-
The production of neutron-rich nuclei and superheavy nuclei is a widely studied topic in nuclear physics and astrophysics [1−4]. Some superheavy nuclides have been synthesized using fusion-evaporation reactions. Elements with atomic numbers Z = 107−113 have been synthesized using cold fusion [1, 2], whereas those with atomic numbers Z = 114−118 have been synthesized using hot fusion [4−10]. However, the cross-section for synthesizing superheavy nuclides with higher proton numbers using fusion-evaporation reactions has almost reached the detectable limit. To date, it is approximately seven neutrons away from the center of the island of stability. The search for new methods to synthesize neutron-rich heavy nuclei has become a pressing issue. Multinucleon transfer (MNT) reactions have recently gained significant attention for their effectiveness in synthesizing neutron-rich heavy nuclei [11−16].
Several experiments highlighted the effectiveness of the MNT reaction in synthesizing neutron-rich nuclei. For instance, in 2015, Watanabe et al. [17] measured the production cross-section of neutron-rich nuclides around N = 126 at GANIL. The findings reveal that the production cross-section of the neutron-rich heavy nuclei via the MNT reactions is approximately four orders of magnitude higher than that of the fragmentation reactions, indicating a significant advantage of MNT reactions in producing neutron-rich isotopes. Additionally, Wuenschel et al. [18] investigated the reaction 238U+232Th with an energy range of 6.1−7.5 MeV·u−1, demonstrating the capability of MNT reactions to produce a certain number of neutron-rich nuclides with proton numbers up to 116. This provides strong confidence in the synthesis of superheavy nuclei via MNT reactions.
The semi-classical theoretical approaches for studying the MNT reaction primarily include the dinuclear system (DNS) model [19−23], GRAZING model [24], and multidimensional dynamical model based on Langevin equations [25, 26]. Microscopic theoretical approaches, such as the time-dependent Hartree-Fock (TDHF) [27−30], improved quantum molecular dynamics (IQMD) [31, 32], and stochastic mean-field (SMF) approaches [33], are used for the MNT reaction. Despite the diversity of available theoretical methods, a comprehensive understanding of the complex mechanisms involved in MNT reactions remains a challenge. No single theory has emerged as universally applicable to different problems posed by MNT reactions. Therefore, it is imperative to continually refine and enhance theoretical frameworks with respect to MNT reactions.
In contrast to typical fusion-evaporation reactions, MNT reactions produce neutron-rich isotopes with an anisotropic and wide angular distribution [34]. The production cross-section of these neutron-rich nuclei varies with respect to the measurement angle. Theoretical analysis of the angular distribution of the MNT reaction products not only aids in collecting and separating reaction products in experiments in a better manner but also improves the relevant theoretical models of the MNT reaction.
In several studies, the angular distribution of MNT reactions has been investigated. For example, in Refs. [35, 36], the DNS model is employed to analyze the angular distribution of the reaction 136Xe + 208Pb. By solving a master equation that accounts for dynamical deformation and assuming that the scattering angle is influenced by the dynamical deformation of two interacting nuclei, which in turn affects the moment of inertia of the dinuclear system, the final distribution of the scattering angle can be derived. This approach allows the theoretical angular distribution to closely match experimental data. In Ref. [37], the angular distribution of MNT reaction products in the reaction 206Pb + 118Sn is examined by coupling Langevin dynamics iteratively with the master equation.
In this study, we introduce a new method to describe the angular distribution of the MNT reaction products based on the DNS model. The angular distributions of the MNT reaction products, such as those in reactions 136Xe + 208Pb and 136Xe + 209Bi, are examined.
-
The state evolution of a dinuclear system can be described by the master equation [38−40]. We denote the probability distribution of a dinuclear system as
$ P\left({Z}_{1}, {{N}_{1},E}_{1},t\right) $ , indicating the probability of observing the projectile-like fragments with proton number Z1 and neutron number N1 in all possible states at time t. The two-dimension master equation can be described as follows:$\begin{aligned}[b] \frac{{\rm d}P\left({Z}_{1},{{N}_{1},E}_{1},t\right)}{{\rm d}t}=\;&{\sum }_{{Z}_1'}{W}_{{Z}_{1},{Z}_1'}\left(t\right)\left[{d}_{{Z}_{1},{N}_{1},{E}_{1}}P({Z}_1',{N}_{1},{E}_1',t)-{d}_{{Z}_1',{N}_{1},{E}_1'}P({Z}_{1},{N}_{1},{E}_{1},t)\right]\\&+{\sum }_{{N}_1'}{W}_{{N}_{1},{N}_1'}\left(t\right)\left[{d}_{{{Z}_{1},N}_{1},{E}_{1}}P\left({Z}_{1},{N}_1',{E}_1'',t\right)-{d}_{{Z}_{1},{N}_1',{E}_1''}P({Z}_{1},{N}_{1},{E}_{1},t)\right]\\&-\left[{\Lambda }_{{Z}_{1},{N}_{1},t}^{qf}\left(\Theta \right)+{\Lambda }_{{Z}_{1},{N}_{1},t}^{fis}\left(\Theta \right)\right]\cdot P({Z}_{1},{{N}_{1},E}_{1},t),\end{aligned} $

(1) where
$ {E}_{1} $ denotes the local excitation energy, and${W}_{{Z}_{1},{Z}_1'}$ denotes the mean transition probability from state$ {(Z}_{1},{N}_{1}) $ to state$({Z}_{1}',{N}_{1})$ . Furthermore,$ {d}_{{Z}_{1},{N}_{1},{E}_{1}} $ denotes the number of possible microscopic states of a dinuclear system in the macroscopic state$ {(Z}_{1},{N}_{1}) $ .$ {\Lambda }_{{Z}_{1},{N}_{1},t}^{qf}\left(\Theta \right) $ and$ {\Lambda }_{{Z}_{1},{N}_{1},t}^{fis}\left(\Theta \right) $ denote the quasi-fission rate and fission rate, respectively. It is important to note that the first and second terms of Eq. (1) represent the changes in the probability distribution induced by proton and neutron transitions between distinct states, while the last term represents a decrease in the probability distribution due to quasi-fission and fission. In practical applications, once the transition probability is determined, the probability distribution of a certain state at time t can be readily derived by solving the master equation. -
The angular distribution of nuclear reactions can be described by classical or semi-classical scattering theories [41, 42]. Typically, the classical approximation of the angular distribution can be expressed as [43−45]
$ \frac{{\rm d}\sigma }{{\rm d}\mathrm{\Theta }}=2\pi {\sum }_{n}{b}_{n}{\left|\frac{{\rm d}{b}_{i}}{{\rm d}\mathrm{\Theta }}\right|}_{{b}_{i}={b}_{n}} ,$

(2) where
$ \mathrm{\Theta } $ denotes the deflection angle, and b denotes the impact parameter. When the projectile collides with the target with energy E, the projectile moves along the Coulomb trajectory at the interaction radius R and forms a composite system with the target. At this time, the projectile and target rotate together at a certain angle$ \Delta \theta $ :$ \Delta \theta =\pi -{\theta }_{i}\left({E}_{i},{l}_{i}\right)-{\theta }_{f}\left({E}_{f},{l}_{f}\right)-\mathrm{\Theta }\left({l}_{i}\right). $

(3) The composite system undergoes nucleon transfer during the interaction time, and the Coulomb angles in Eq. (3) are determined by the corresponding energy and impact parameters (subscripts
$ i $ and$ f $ denote incident and exit, respectively):$ {\theta }_{i,f}=\mathrm{arcsin}\frac{2{b}_{i,f}/R+{\epsilon }_{i,f}}{\sqrt{4+{\epsilon }_{i,f}^{2}}}-\mathrm{arcsin}\frac{1}{\sqrt{(2/{\epsilon }_{i,f}{)}^{2}+1}}, $

(4) where
$ \epsilon ={Z}_{1}{Z}_{2}{\rm e}^{2}/\left(Eb\right) $ , and$ R $ denotes the interaction radius, considered as$ R=1.36\left({A}_{1}^{1/3}+{A}_{2}^{1/3}\right)+0.5 $ . Equation (4) describes the relationship among the Coulomb deflection angles$ {\theta }_{i,f} $ , E, and b. The deflection function comprises the Coulomb deflection angle and nuclear deflection angle, denoted as$ \mathrm{\Theta }\left({l}_{i}\right) $ , which represents the scattering angle at the corresponding impact parameter. Furthermore, it denotes the experimental scattering angle and can be expressed as$ \mathrm{\Theta }\left({l}_{i}\right)={\mathrm{\Theta }}_{C}\left({l}_{i}\right)+{\mathrm{\Theta }}_{N}\left({l}_{i}\right). $

(5) The Coulomb deflection angle
$ {\mathrm{\Theta }}_{C}\left({b}_{i}\right) $ and nuclear deflection angle$ {\mathrm{\Theta }}_{N}\left({l}_{i}\right) $ have the following forms:$ {\mathrm{\Theta }}_{C}\left({b}_{i}\right)=2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{{Z}_{1}{Z}_{2}{\rm e}^{2}}{2E{b}_{i}}\right) $

(6) $ {\mathrm{\Theta }}_{N}\left({l}_{i}\right)=-\beta \cdot {\mathrm{\Theta }}_{c}^{gr}\cdot \frac{{l}_{i}}{{l}_{gr}}{\left(\frac{\delta }{\beta }\right)}^{{l}_{i}/{l}_{gr}}, $

(7) where
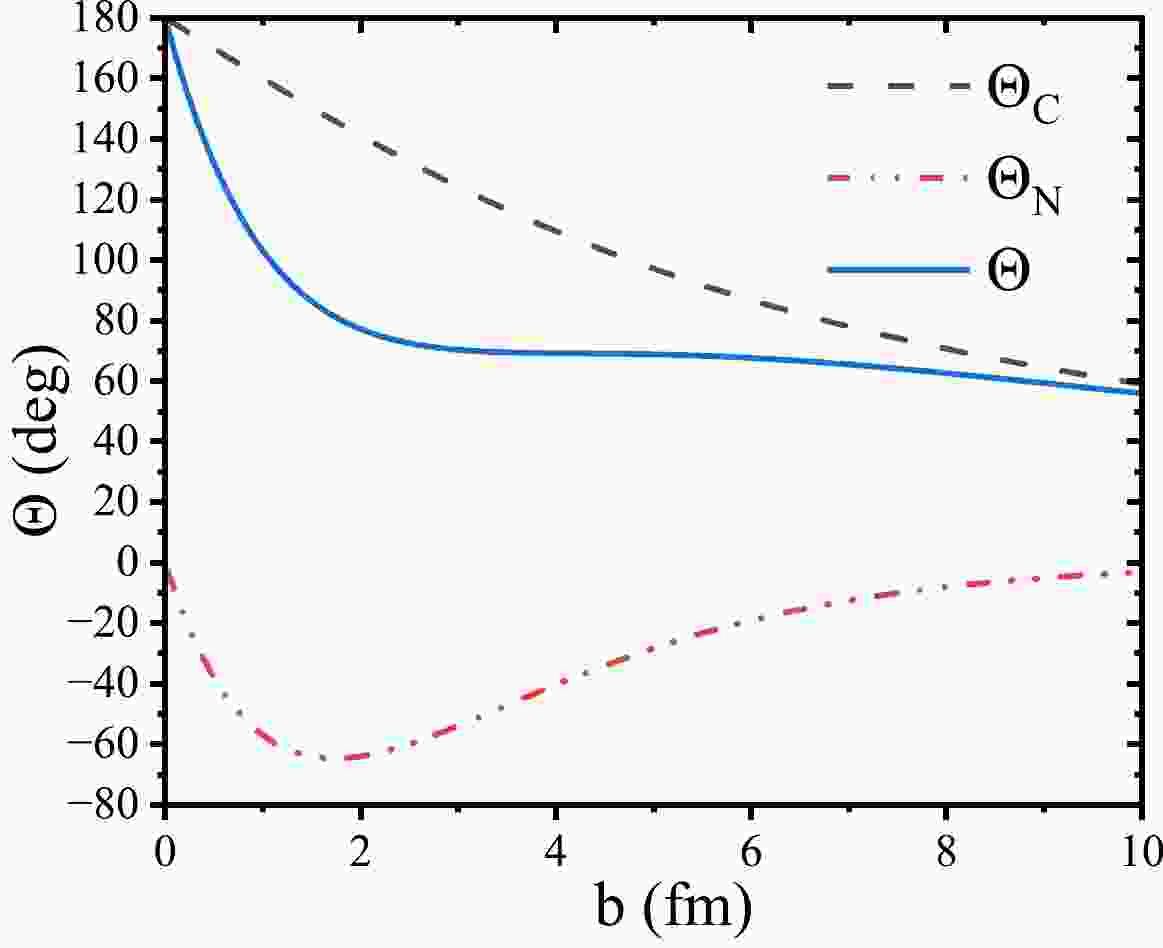
$ {l}_{gr} $ denotes the grazing angular momentum, and$ {\mathrm{\Theta }}_{c}^{gr} $ denotes the Coulomb deflection angle on the grazing trajectory. The expression of parameters$ \delta $ and$ \beta $ can be found in Ref. [46]. The relationship among the Coulomb deflection angle, nuclear deflection angle, and total deflection angle is illustrated in Fig. 1. For a more detailed description of the deflection function approach, see Refs. [43, 44]. In a dinuclear system,$ \Delta \theta $ can be derived through the integration of${\rm d}\mathrm{\Theta }/{\rm d}t$ over the interaction time${\tau }_{\rm int}$ :
Figure 1. (color online) Deflection function of reaction 136Xe+ 208Pb at incident energy
${E}_{\rm c.m.}$ = 526 MeV.$ \Delta \theta ={\int }_{0}^{{\tau }_{int}}{\rm d}t\frac{{\rm d}\Theta }{{\rm d}t}={\int }_{0}^{{\tau }_{int}}{\rm d}t\frac{\hslash {l}_{i}\left(t\right)}{\left\langle{{\mathcal{J}}_{\rm rel}}\right\rangle}, $

(8) $\left\langle{{\mathcal{J}}_{\rm rel}}\right\rangle$ denotes the mean relative moment of inertia. As time$ t $ progresses,$ \Delta \theta $ , determined by Eq. (8) and Eq. (3), becomes consistent. Hence, the interaction time at the corresponding angular momentum can be obtained. Note that the scattering angle calculated via the deflection function approach is the average scattering angle corresponding to the impact parameters, and the angular distribution defined by Eq. (2) is similar to the delta-function. In the classical angular distribution, each impact parameter corresponds to a specific scattering angle. However, due to the quantum effects and fluctuations, the scattering angle corresponding to an impact parameter is represented as a probability distribution. Therefore, we introduce a Gaussian distribution$ f\left[\mathrm{\Theta },\overline{\mathrm{\Theta }}\left({b}_{i}\right)\right] $ [47] into the classical angular distribution. Then, the angular distribution considering fluctuations can be expressed as$ \frac{{\rm d}\sigma }{{\rm d}\mathrm{\Theta }}=2\pi {\sum }_{i}\frac{{b}_{i}}{(2\pi {\sigma }_{\mathrm{\Theta }}^{2}{)}^{1/2}}\mathrm{exp}\left\{-\frac{{\left[{{\Theta - \overline \Theta }}\left({b}_{i}\right)\right]}^{2}}{2{\sigma }_{\mathrm{\Theta }}^{2}\left({b}_{i}\right)}\right\}\cdot \Delta b, $

(9) $ {\sigma }_{\mathrm{\Theta }}^{2} $ denotes the variance, which determines the width of the distribution [48]:$\begin{aligned}[b] {\sigma }_{\Theta }^{2}\left({b}_{i},t\right)=\;&2{C}^{2}T\frac{{J}_{\rm int}}{{J}_{\rm rel}\cdot {J}_{\rm tot}}{\tau }_{l}^{2}\\&\cdot \left[\frac{t}{{\tau }_{l}}-\frac{1}{2}\text{exp}\left(-\frac{2}{{\tau }_{l}}\right)+2\text{exp}\left(-\frac{t}{{\tau }_{l}}\right)-\frac{3}{2}\right], \end{aligned} $

(10) where
${\mathcal{J}}_{\rm int}$ ,${\mathcal{J}}_{\rm rel}$ , and${\mathcal{J}}_{\rm tot}$ denote the interaction moment of inertia, relative moment of inertia, and total moment of inertia, respectively. Furthermore,$ {\tau }_{l} $ denotes the relaxation time of angular momentum, and$ T $ denotes the nucleus temperature. To obtain a more appropriate distribution, we set a constant factor$ C $ and consider$ C=2.5 $ in this study ($ 1\le C\le 3 $ ).By considering the derivative of the proton number and neutron number using Eq. (9), a differential cross-section of the angular distribution can be derived. This provides a triple differential cross-section:
$ \begin{aligned}[b]\frac{{\rm d}{\sigma }^{3}}{{\rm d}{N}_{1}{\rm d}{Z}_{1}{\rm d}\mathrm{\Theta }}=\;&2\pi {\sum }_{i}\frac{{b}_{i}}{(2\pi {\sigma }_{\mathrm{\Theta }}^{2}{)}^{1/2}}\mathrm{exp}\left\{-\frac{{\left[\mathrm{\Theta }-{\overline\Theta }\left({b}_{i}\right)\right]}^{2}}{2{\sigma }_{\mathrm{\Theta }}^{2}\left({b}_{i}\right)}\right\}\\&\times P[{Z}_{1},{N}_{1},{\tau }_{\mathrm{i}\mathrm{n}\mathrm{t}}({b}_{i}\left)\right]\cdot \Delta b , \end{aligned} $

(11) where
$ P[{Z}_{1},{N}_{1},{\tau }_{\mathrm{i}\mathrm{n}\mathrm{t}}({b}_{i}\left)\right] $ denotes the probability distribution of the product with proton number$ {Z}_{1} $ and neutron number$ {N}_{1} $ at the corresponding angular momentum. Similarly, according to the Eq. (11), the double differential cross-section, such as${\rm d}{\sigma }^{2}/{\rm d}A{\rm d}\mathrm{\Theta }$ and${\rm d}{\sigma }^{2}/{{\rm d}l}_{i}{\rm d}\mathrm{\Theta }$ , can also be derived. Analysis of these differential cross-sections offers a deeper insight into the distribution characteristics of production cross-sections in MNT reactions. -
To evaluate the applicability of our model in describing the angular distribution of the MNT reaction, we calculate the angular distribution of reactions, including 136Xe+208Pb and 136Xe+209Bi.
Figure 2 shows the angular distribution of projectile-like fragments (PLFs) (128 < A < 144) and target-like fragments (TLFs) (200 < A < 216) of the reaction 136Xe+ 208Pb at laboratory energies
$ {E}_{\mathrm{l}\mathrm{a}\mathrm{b}} $ = 870 MeV and 1020 MeV with the experimental data from Ref. [49]. In this reaction, only the part with total kinetic energy loss greater than 40 MeV is considered. Our model is in good agreement with the experimental data for both projectile-like fragments (PLFs) and target-like fragments (TLFs) at different incident energies. At an incident energy of 870 MeV, the peak angles of the angular distribution for PLFs and TLFs are approximately 45° and 50°, respectively, and the height and width aspects of the angular distributions are in good agreement with the experimental data. At a higher incident energy of 1020 MeV, the peak angles of the angular distribution for PLFs and TLFs are approximately 35° and 58°, respectively. Notably, the peak angle of PLFs is smaller when compared to$ {E}_{\mathrm{l}\mathrm{a}\mathrm{b}} $ = 870 MeV, whereas the peak angle of TLFs is larger due to the smaller Coulomb deflection angle induced by the larger incident energy. However, at$ {E}_{\mathrm{l}\mathrm{a}\mathrm{b}} $ = 1020 MeV, the peak angle of the TLFs is slightly smaller than the experimental results. The peak angle of the PLFs matches the experimental data well, and the cross section of the PLFs generated at large angles is slightly lower than the experimental value. This discrepancy can be due to the fact that the dynamical deformation of the interacting nuclei was not considered, and the inclusion of this dynamical deformation in future studies is expected to improve this result.
Figure 2. (color online) Angular distribution of projectile-like fragments (128 < A < 144) and target-like fragments (200 < A < 216) of the reaction 136Xe+208Pb at different incident energies.
To assess the universality of our model for different reactions, we calculated the angular distribution of reactions, including 136Xe+209Bi, 86Kr+166Er, 84Kr+209Bi, and 84Kr+208Pb. Figure 3 shows the comparison between the predicted angular distributions and corresponding experimental data. For the reaction 136Xe+209Bi, at the incident energies of
$ {E}_{\mathrm{l}\mathrm{a}\mathrm{b}} $ = 940 MeV (Ec.m.= 569 MeV) and 1130 MeV(Ec.m.= 685 MeV), the angular distribution cross-sections predicted by our model are in good agreement with the experimental data [50, 51]. In the 86Kr+166Er reaction, although the calculations are in general agreement with the experimental data [44], there are differences at small angles where the predictions underestimate the experimental data. We hypothesize that similar distributions may exist in the form of double Gaussians, controlling for larger and smaller angles, respectively. For reactions such as 84Kr+209Bi, 84Kr+208Pb, and 136Xe+208Pb, our model effectively characterizes the main features of the angular distribution. However, its peak is slightly overestimated when compared to the experimental data [52−54]. It should be noted that, although our model cannot perfectly predict the angle distribution of all reactions, the deviations from experimental data are minor and fall within an acceptable range. This paves the way for future model improvements. Overall, the model we have developed to predict the angular distribution of MNT reaction products shows good applicability across a wide range of reactions and incident energies.From the deflection function analysis, it becomes apparent that the angular distribution of reaction products is highly influenced by the incident angular momentum. To further explore this relationship, we investigated the double differential cross-section (
${\rm d}{\sigma }^{2}/{{\rm d}l}_{i}{\rm d}\mathrm{\Theta }$ ) for the reaction 136Xe+208Pb in the center-of-mass system at an energy of${E}_{\mathrm{c.}\mathrm{m.}}$ = 526 MeV. The double differential cross-sections are shown in Fig. 4, where the left and right panels illustrate the double differential cross-sections of all PLFs and TLFs, respectively. The horizontal axis represents the angular momentum$ l $ , and the vertical axis represents the scattering angle${\theta }_{\rm c.m.}$ in the center-of-mass system. As shown, the major products are distributed at positions with a relatively high angular momentum. Furthermore, they exhibit a broad angular distribution within the range of$ 50\hslash < l < 100\hslash $ . As the angular momentum increases, a clear trend emerges: the angular distribution centers of PLFs shift toward smaller angles, while the centers of TLFs move toward larger angles. This phenomenon arises primarily due to the influence of Coulomb repulsion effects. During collisions involving small parameters, strong Coulomb repulsion leads to the forward emission of TLFs. Conversely, as collision parameters increase, the Coulomb repulsion diminishes, causing the angular distribution centers of TLFs to gradually shift towards larger angles. As can be observed from the left panels, the angular distribution centers of PLFs exhibit the opposite trend with a change in collision parameters.
Figure 4. (color online) Double differential cross-sections
${\rm d}{\sigma }^{2}/{{\rm d}l}_{i}{\rm d}\mathrm{\Theta }$ of reaction 136Xe+208Pb at${E}_{\mathrm{c.}\mathrm{m.}}$ = 526 MeV.The angular distribution of the products with different charge numbers in the MNT reaction is different. To gain a deeper understanding, we examined the double differential cross-sections (
${\rm d}{\sigma }^{2}/{\rm d}Z{\rm d}\mathrm{\Theta }$ ) of the reactions 36Xe+209Bi and 136Xe+208Pb at various incident energies. Figure 5(a) and (b) illustrate the double differential cross-sections for the 136Xe + 209Bi reaction at incident energies of${E}_{\mathrm{c.}\mathrm{m.}}$ = 569 MeV and${E}_{\mathrm{c.}\mathrm{m.}}$ = 685 MeV, respectively. The analysis reveals that the main production cross-section is concentrated around the projectile nucleus within a certain angle range. Specifically, for${E}_{\mathrm{c.}\mathrm{m.}}$ = 569 MeV, the peak position of the cross section varies between 63° and 67°, while at${E}_{\mathrm{c.}\mathrm{m.}}$ = 685 MeV, it ranges between 47° and 52°. When the angle or charge deviates from the central region, a rapid decrease in production cross-section is observed. Even small deviations of three to four units in either charge or angle lead to a reduction in cross-section to less than half of its central value. We can obtain a considerable production cross-section in a wide range of angles when the system transfers nucleons toward the mass symmetry direction. Conversely, transferring nucleons in the direction of mass asymmetry results in a narrow angular distribution. The double differential cross-sections of the reaction 136Xe+208Pb at${E}_{\mathrm{c.}\mathrm{m.}}$ = 526 MeV and 677 MeV are shown in Fig. 5(c) and (d), respectively. The conclusions drawn from these data are similar to those based on the 136Xe + 209Bi reaction. To better confirm the aforementioned conclusions, the relationship between the total kinetic energy (TKE) of fragments near the entrance channel and number of transferred protons is examined, as illustrated in Fig. 6. The left (136Xe+209Bi) and right (136Xe+208Pb) sides of Fig. 6 represent the changes in production cross-sections with respect to the total kinetic energy when transferring 3 to 6 protons. When transferring the same number of protons, the cross-section along the mass-symmetric direction is higher than that along the mass-asymmetric direction, which also suggests that the reaction system tends to evolve toward a mass-symmetric direction.
Figure 5. (color online) Double differential cross-sections
${\rm d}{\sigma }^{2}/{\rm d}Z{\rm d}\mathrm{\Theta }$ of the reaction 136Xe+209Bi with${E}_{\mathrm{c.}\mathrm{m.}}$ =569 MeV (a) and 685 MeV (b). The double differential cross-sections${\rm d}{\sigma }^{2}/{\rm d}Z{\rm d}\mathrm{\Theta }$ of reaction 136Xe+ 208Pb with${E}_{\mathrm{c.}\mathrm{m.}}$ =526 MeV (c) and 677 MeV (d).
Figure 6. (color online) Relationship between the total kinetic energy of fragments near the entrance channel and proton number.
The MNT reaction has attracted significant attention for its role in populating neutron-rich nuclei around N = 126 [49, 55]. Hence, we calculated the angular distribution of N = 126 isotones in various reaction channels. Figure 7(a) shows the change in the angular distribution of N = 126 isotones with projectile proton numbers (Z = 51−57) when the target nucleus is 208Pb. The peak angle in the distribution indicates the optimal detection angle for experimentation. It is observed that, as the proton number increases, the peak angle gradually decreases, while the distribution width remains relatively unchanged. Regarding charge equilibration, the N/Z ratio of 208Pb is 1.54. When the N/Z ratio of the projectile nucleus is greater than 1.54, there is a tendency to transfer protons from the target nucleus, which is conducive to producing neutron-rich nuclei with fewer protons than the target nucleus. Conversely, when the N/Z ratio of the projectile nucleus is below 1.54, the production cross-section of N = 126 neutron-rich nuclei can be reduced to a certain extent. According to these observations and those from Fig. 7(c), the optimal detection angle becomes smaller with an increase in projectile proton number. This shift primarily arises from the influence of proton number and radius on the total deflection angle. Here, an increase in proton number results in a decrease in Coulomb deflection angle for TLFs, while the change in radius causes negligible impact on the nuclear deflection angle. Figure 7 (b) and (d) show the influence of the projectile neutron number on the angular distribution of N = 126 isotones, while keeping the proton number constant. It is worth noting that an increase in radius leads to a rise in final scattering angle. However, this trend is not evident, and this phenomenon may become more significant when the effects of dynamical deformation are further considered.

Figure 7. (color online) Relationships of the angular distribution of N = 126 isotones with the (a) projectile proton number and (b) projectile neutron number at
${E}_{\mathrm{c.}\mathrm{m.}}$ = 526 MeV. The optimal detection angle of N = 126 isotones varies with the (c) projectile proton number (with N=82) and (d) projectile neutron number (with Z=54). -
Based on the DNS model, we propose a method to investigate the angular distribution of MNT reaction products, employing the deflection function approach. We calculated the angular distributions of products for the reactions 136Xe+208Pb, 136Xe+209Bi, 86Kr+166Er, 84Kr+209Bi, and 84Kr+208Pb. Theoretical results are in good agreement with the experimental data, verifying the accuracy and reliability of the method in predicting the angular distribution in the MNT reaction.
The dependence of angular distribution on incident angular momentum is examined, and the results show that most products are distributed in positions with a relatively large angular momentum, and a wide angular distribution within the range of
$ 50\hslash < l < 100\hslash $ is observed. Calculations of the double differential cross-sections${\rm d}{\sigma }^{2}/{\rm d}Z{\rm d}\mathrm{\Theta }$ of reactions 136Xe+208Pb and 136Xe+209Bi indicate that the reaction system tends to evolve toward symmetry. As the system evolves along the mass symmetry direction, the center of the angular distribution shifts toward the backward angle, and a large production cross-section and broad angular distribution are observed. However, when the system evolves along the mass asymmetry direction, the production cross-section is smaller and concentrated around the grazing angle. This implies that we should focus on products around the backward angle for detecting heavy nuclei-rich nuclides, while for detecting superheavy nuclides, we should focus on products near the grazing angle. Additionally, we investigate the influence of varying projectiles on the angular distribution of N = 126 isotones at the same incident energy. The results reveal that, as the proton number increases, the optimal detection angle for N = 126 isotones gradually decreases. Furthermore, as the neutron number increases, the optimal detection angle increases slightly. These insights provide valuable guidance for experimental detection methodologies.
Angular distribution of products in multinucleon transfer reactions
- Received Date: 2024-05-31
- Available Online: 2024-10-15
Abstract: A method based on the dinuclear system (DNS) is proposed to describe the angular distribution of products in multinucleon transfer (MNT) reactions. By considering fluctuation effects, the angular distributions of reactions involving 136Xe+208Pb, 136Xe+209Bi, 86Kr+166Er, 84Kr+209Bi, and 84Kr+208Pb are examined, demonstrating good agreement with experimental data. Moreover, the double differential cross-sections (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: