-
Constraining the equation of state (EOS) of neutron stars (NSs) is one of the most fundamental and significant problems in nuclear physics and astrophysics [1−5]. Over the last few years, observation of several objects, such as GW170817 [6], PSR J0740+6620 [7−10] and PSR J0030+0451 [11, 12], has created excellent opportunities to study the EOS of NSs.
It is a common assumption that the pressure inside an NS is isotropic. However, observation of exotic compact objects, such as the secondary component of GW190814 with a measured mass between 2.50 and 2.67
$ M_{\odot} $ ($ M_{\odot} $ is the solar mass) [13] and the black widow pulsar PSR J0952–0607 with a measured mass of M = 2.35$ \pm $ 0.17$ M_{\odot} $ [14], have aroused interest in anisotropic NSs. It is concluded by [15] that even if the system is initially assumed to be isotropic, physical processes are expected in stellar evolution, such as dissipative fluxes, energy density inhomogeneities, or the appearance of shear in the fluid flow, which will always tend to produce pressure anisotropy. The occurrence of pressure anisotropy due to some exotic phenomena, such as pion-condensation [16, 17] or kaon-condensation [18], strong magnetic field [19−30], the existence of a solid core [30, 31], a mixture of two fluids [32], superfluidity [33], and viscosity, may be a source of local anisotropy [34−37]. Please see Refs. [38, 39] for a review. There is also much research focused on anisotropic NSs [40−44].As many properties of NSs depend directly on the choice of the EOS, there is still a great deal of uncertainty in the understanding of the EOS of high-density nuclear matter, which means that there is also a great deal of uncertainty in the NS properties. To constrain the EOS from NS observation, one can use machine learning [45−47] or Bayesian Inference [48, 49]. Besides, it is expected to establish an EOS-insensitive universal relation between the observables and unobservables. Over the past few decades, many relations have been built, such as the I-LOVE-Q relations [50], quasi-universal relations for static and rapid rotating NSs [51], relations between EOS parameters and canonical NSs [52], and relations between other properties [53−60]. In addition, the universal relations between anisotropic NSs have also been studied [61, 62].
The TOV equation helps us calculate the NS global properties based on the EOS; conversely, using the TOV equation to obtain EOS constraints from NS observation might be a worthwhile approach. Recently, the scaled TOV equation has been deduced and then used to constrain the core states and access to the ultimate limit for the pressure and energy density [63, 64], which offered us a novel approach to gain insight into the relations between the global properties of NSs and the core EOS through universal relations and have a high consistency with previous research in understanding the basic problems regarding NSs. Considering that the existence of anisotropic NSs cannot be excluded by current observation and previous research focusing on anisotropic NSs has only shown how the pressure anisotropy affects the NS global properties, this work aims to further solve the effect on the extraction of the NS core EOS.
In the present work, we aim to deduce the dimensionless TOV equation for anisotropic NSs and further investigate the anisotropy effect while extracting the central EOS of PSR J0740+6620. 36 EOSs with a maximum mass larger than 1.8
$ M_{\odot} $ are employed in this work. These include (1) 5 consistent relativistic mean-field (CRMF) EOSs, such as G2* [65], IU-FSU [66], and TW99 [67]; (2) 19 DDRMF and NLRMF EOSs, such as DD [68], DD-ME1 [69], DD-LZ1 [70], NL1 [71], NLZ [72], NLSV1 [73], and TM1 [74]; (3) 9 microscopic EOSs, such as the ALF2 [75] EOS based on hybrid (nuclear+quark) matter, APR3 EOS [76] based on variational calculations of two-nucleon and three-nucleon interactions, ENG [77] and MPA1 [78] EOS based on the Dirac-Brueckner-Hartree-Fock method, and WFF1 EOS [79] based on different two-nucleon and three-nucleon potentials; and (4) 3 EOSs based on the quark mean-field bag (QMFB) model by incorporating the bag confinement mechanism: QMFL40, QMFL60, and QMFL80 [80].This paper is organized as follows. In Sec. II, the process of deducing the dimensionless TOV equation of anisotropic NSs is presented. In Sec. III, the effect of anisotropy in extracting the central EOS is given and discussed. Finally, a summary is given in Sec. IV. To simplify the equations, the geometric units G = c =1 are adopted.
-
Considering a static and spherically symmetric equilibrium distribution of matter, the energy-momentum tensor (
$ T^{\mu\nu} $ ) is defined as [21, 81]$ T^{\mu\nu}=p_{t}g^{\mu\nu}+(\varepsilon+p_{t})u^{\mu}u^{\nu}+(p_{r}-p_{t})k^{\mu}k^{\nu}, $

(1) where
$ g^{\mu\nu} $ is the space-time metric,$ u^{\mu} $ is the 4-velocity of the fluid,$ k^{\mu} $ is the radial unit vector, and$ p_{t} $ ,$ p_{r} $ , and$ \varepsilon $ are the tangential pressure, radial pressure, and energy density, respectively. These 4-vectors satisfy the following conditions:$ k^{\mu}k_{\mu}=1, u^{\mu}k_{\mu}=0. $

(2) The Schwarzschild metric for the star having a spherically symmetric and static configuration is described as
$ {\rm d}s^{2}=e^{\nu}{\rm d}t^{2}-e^{\lambda}{\rm d}r^{2}-r^{2}{\rm d}\theta ^{2}-r^{2}{\rm sin}^{2}\theta {\rm d}\varphi^{2}. $

(3) To exactly calculate the global properties of NSs, one should indeed take into account the magnetic field, rotation, and thus deformation that deviates from spherical symmetry. However, it was noted by Pattersons et al. that even with strong anisotropy and slow rotation, with a mass increase, the star becomes more spherical [82]. Overall, as we ignore the effect of rotation and focus on the maximum mass of an anisotropic NS, we assume spherical symmetry is still valid. Thus, the modified Tolman-Oppenheimer-Volkoff (TOV) equation can be obtained by solving Einstein's equations as [83]
$ \frac{{\rm d}p_{r} }{{\rm d}r} =-\frac{(\varepsilon +p_{r})(m+4\pi r^{3}p_{r} )}{r^{2}-2mr} +\frac{2 \sigma}{r}, $

(4) $ \qquad\qquad\qquad\frac{{\rm d}m}{{\rm d}r} =4\pi r^{2}\varepsilon, $

(5) where
$\sigma \equiv p_{t} -$ $ p_{r} $ is the anisotropy parameter, and m is the enclosed mass corresponding to radius r. Equations (4) and (5) can be integrated from center r =0, m = 0,$ p_{r} $ =$p_{\rm rc}$ ($p_{\rm rc}$ is the radial central pressure) to the surface r = R, m = M,$ p_{r} $ = 0. -
In this work, we use two popular models, namely, the BL [83] and H models [84]. These two models are based on the following assumptions [85, 86]:
(i) The anisotropy should vanish at the origin, i.e.,
$ P_{r}=P_{t} $ at r=0;(ii) The pressure and energy density must be positive, i.e.,
$ P_{r} $ ,$ P_{t} $ ,$ \varepsilon < $ 0;(iii) The radial pressure and energy density must be monotonically decreasing, i.e.,
$ \dfrac{{\rm{d}}P_{r}}{{\rm{d}} r} $ and$ \dfrac{{\rm{d}}\varepsilon }{{\rm{d}} r} < $ 0;(iv) The anisotropic fluid configurations with different conditions, such as the null energy (
$ \varepsilon > $ 0), dominant energy ($ \varepsilon $ +$ P_{r} > $ 0,$ \varepsilon $ +$ P_{t} > $ 0), and strong energy ($ \varepsilon $ +$ P_{r} $ +2$ P_{t} > $ 0), must be satisfied inside the star;(v) The speed of sound inside the star must obey
$ 0 <c_{s,r}^{2}< 1 $ ,$ 0 <c_{s,t}^{2}< 1 $ , where$ c_{s}^{2} $ =$ \dfrac{\partial P}{\partial \varepsilon } $ .For the BL model, the relation between
$ p_{t} $ and$ p_{r} $ is given as$ p_{t} =p_{r}+\frac{\lambda _{\rm BL} }{3} \frac{(\varepsilon+3p_{r})(\varepsilon+p_{r})r^{3}}{r-2m}, $

(6) where
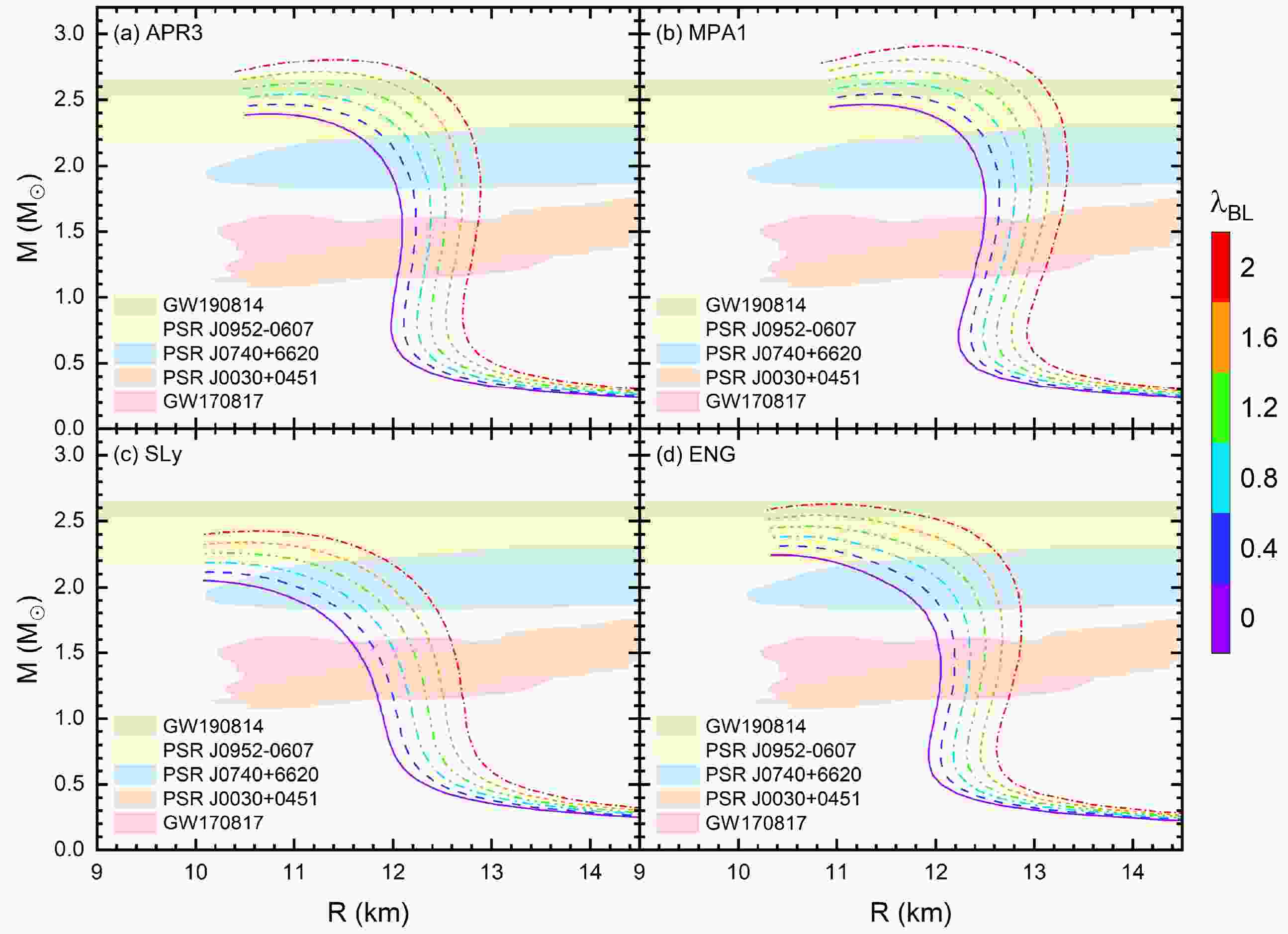
$\lambda_{\rm BL}$ represent the measure of anisotropy. Previous research has given the limit for the BL model, −2$\leqslant \lambda_{\rm BL} \leqslant$ 2 [21]. With the increased positive value of$\lambda_{\rm BL}$ , the model will give out a higher tangential pressure, resulting in a higher mass at a fixed radius. However, with the decrease of the negative value of$\lambda_{\rm BL}$ , the model will give out a smaller tangential pressure, and thus, a smaller mass with a smaller corresponding radius, which may lead to a negative tangential pressure. In this work, we only consider the positive value of$\lambda_{\rm BL}$ .To illustrate the effect of anisotropy, the M-R relation of several selected EOSs based on the BL model is shown in Fig. 1. Each coloured region corresponds to an observational constraint, and different colours of the curves represent different values of
$\lambda_{\rm BL}$ , where the purple solid one refers to an isotropic NS and the red short-dotted one is the highest anisotropy. It can be seen that the introduction of anisotropy plainly increases the maximum mass and corresponding radius of NSs, as the positive value of$\lambda_{\rm BL}$ in the BL model means a higher tangential pressure that can stabilize the structure. Nevertheless, even with such a great change in the M-R curve, all the results still satisfy the observational constraints. Moreover, the introduction of anisotropy makes the M-R curve fall into the interval of GW190814 secondary, which provides a possible mechanism to support the currently observed most massive NS.
Figure 1. (color online) M-R curves for anisotropic NSs based on the BL model. Different colours of the curves represent different values of
$\lambda_{\rm BL}$ , where the red short-dotted one is the highest anisotropy, and the purple solid one is isotropic. The green rectangle is the mass constraint from GW190814 secondary with a mass$ M = 2.59 _{-0.09}^{+0.08} M_{\odot} $ [13]. The yellow rectangle is the mass constraint from black widow pulsar PSR J0952–0607 with a mass$ M = 2.35_{-0.17}^{+0.17} M_{\odot} $ [14]. The pink, orange, and blue areas correspond to the mass-radius constraints from GW170817 [6], PSR J0030+0451 [11], and PSR J0740+6620 [8], respectively.For the H model, Ref. [81] also gives the limit −2
$ \leqslant \lambda _H \leqslant $ 2. For comparison, we only adopt 0$ \leqslant \lambda _H \leqslant $ 2. The relation between$ p_{t} $ and$ p_{r} $ is given by$ p_{t} =p_{r}-2\lambda _{H}p_{r}\frac{m}{r}. $

(7) The M-R relation of the same selected EOSs based on the H model is shown in Fig. 2. Compared with Fig. 1, it is shown that the introduction of anisotropy based on the H model decreases the maximum mass and corresponding radius of NSs, as the positive value of
$ \lambda _{H} $ means a lower tangential pressure, resulting in a less massive NS.
Figure 2. (color online) Same as Fig. 1 but for the H model.
-
To constrain the central EOS of NS matter by using certain astrophysical data, such as observed NS radii and masses without using any specific EOS, Refs. [63, 64] propose a new way to gain insight into NS cores and provide us a direct way to explain the universal relation, which is developed from perturbatively analyzing the dimensionless Tolman-Oppenheimer-Volkoff (TOV) equation. However, considering the effect of the anisotropic pressure mentioned above, some corrections to the dimensionless TOV equation need to be proposed.
Noting that G = c =1, defining S =
$(4\pi\varepsilon_{c})^{-{1}/{2}}$ ($ \varepsilon _{c} $ is the central energy density), one can get the reduced mass$ \widehat{m}\equiv{m}/{S} $ , radius$ \widehat{r}\equiv{r}/{S} $ , radial pressure$ \widehat{p}_{r}\equiv{p_{r}}/{\varepsilon _{c}} $ , tangential pressure$ \widehat{p}_{t}\equiv{p_{t}}/{\varepsilon_{c}} $ , and energy density$ \widehat{\varepsilon} \equiv{\varepsilon}/{\varepsilon _{c}} $ , which changes Eqs. (4) and (5) as follows:$ \frac{{\rm d}\widehat{p}_{r}}{{\rm d}\widehat{r}} =-\frac{(\widehat{\varepsilon}+\widehat{p}_{r})(\widehat{m}+\widehat{r}^{3}\widehat{p}_{r})}{\widehat{r}^{2}-2\widehat{m}\widehat{r}} +\frac{2(\widehat{p}_{t}-\widehat{p}_{r})}{\widehat{r}}, $

(8) $ \quad\qquad\qquad\qquad\frac{{\rm d}\widehat{m}}{{\rm d}\widehat{r}} =\widehat{r}^{2}\widehat{\varepsilon}. $

(9) As there exists a difference in tangential pressure between the different models, the BL model and H model will be discussed separately. For the BL model, according to Eq. (6), by using the reduced radial pressure
$ \widehat{p}_{r} $ , reduced tangential pressure$ \widehat{p}_{t} $ and other properties in reduced form, Eq. (6) now becomes$ \widehat{p}_{t} =\widehat{p}_{r}+\frac{\lambda _{\rm BL} }{12\pi} \frac{(\widehat{\varepsilon}+3\widehat{p}_{r})(\widehat{\varepsilon}+\widehat{p}_{r})\widehat{r}^{3}}{\widehat{r}-2\widehat{m}}. $

(10) Because we only focus on the EOS of the core region and the densest matter inside the NS, which is close to the origin, in this case, the radial coordinate can be viewed as a small parameter and thus can be expanded. The
$ \widehat{\varepsilon} $ ,$ \widehat{p}_{r} $ ,$ \widehat{p}_{t} $ , and$ \widehat{m} $ can be expanded in polynomials in terms of dimensionless radial coordinates:$ \;\;\;\; \widehat{\varepsilon} = 1+a_{1} \widehat{r}+a_{2} \widehat{r}^{2}+a_{3} \widehat{r }^{3}+\cdots, $

(11) $ \;\;\widehat{p}_{r} = \widehat{p}_{\rm rc}+b_{1} \widehat{r}+b_{2} \widehat{r}^{2}+b_{3} \widehat{r }^{3}+\cdots, $

(12) $ \;\;\widehat{p}_{t} = \widehat{p}_{tc}+c_{1} \widehat{r}+c_{2} \widehat{r}^{2}+c_{3} \widehat{r }^{3}+\cdots, $

(13) $ \;\;\widehat{m} = d_{1} \widehat{r}+d_{2} \widehat{r}^{2}+d_{3} \widehat{r}^{3}+\cdots. $

(14) Putting these into Eqs. (8)–(10), matching the coefficients, and ignoring the higher order (as we only focus on the core region of the maximum mass of NS, which will be mostly governed by the core region, the ignorance of the higher order will lead to a small effect, as shown in the APPENDIX of [63]), one has
$b_{1}=0, ~ c_{1}=0, ~d_{1}=0, d_{2}=0, ~d_{3}=1/3$ , and$ \begin{aligned}[b] b_{2} =&\frac{1}{6} \left(\frac{\lambda _{\rm BL}}{2\pi} -1\right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right), \; c_{2} \\=&\frac{1}{6} \left(\frac{\lambda _{\rm BL}}{\pi} -1\right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right). \end{aligned} $

(15) The boundary condition
$ \widehat{p}_{r}=0 $ means$\widehat{p}_{\rm rc}$ +$ b_{2}\widehat{r}^{2} $ =0; thus,$\widehat{r}=\sqrt{-\widehat{p}_{\rm rc}/b_{2}}$ , i.e.,$ \widehat{r}=\left[\dfrac{6\widehat{p}_{\rm rc}}{\left(1-\dfrac{\lambda _{\rm BL}}{2\pi} \right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right)} \right]^{{1}/{2} }, $

(16) which is then multiplied by the scale
$S\equiv(4\pi \varepsilon_{c})^{-{1}/{2}} \sim \varepsilon_{c}^{-{1}/{2}}$ . Then, the stellar radius$R \sim \varepsilon_{c}^{-{1}/{2}} \widehat{r}$ turns out to be$ R\sim \beta \equiv \frac{1}{\sqrt{\varepsilon_{c}}} \left[\dfrac{\widehat{p}_{rc}}{\left(1-\dfrac{\lambda _{\rm BL}}{2\pi} \right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right)} \right]^{{1}/{2} }. $

(17) Noting that
$ d_{1}=d_{2}=0, d_{3}=1/3 $ , we have$ \widehat{m}=\widehat{r}^{3}/3 $ . Multiplied by the scale S, the stellar mass$M \sim \varepsilon_{c}^{-{1}/{2}} \widehat{r}^{3}$ becomes$ M\sim \alpha \equiv \frac{1}{\sqrt{\varepsilon_{c}}} \left[\dfrac{\widehat{p}_{\rm rc}}{\left(1-\dfrac{\lambda _{\rm BL}}{2\pi} \right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right)} \right]^{{3}/{2}}. $

(18) To simplify the expression, the symbols β and α are used in Eqs. (17) and (18) (κ and γ in Eqs. (19) and (20)) to denote the formula. The H model has a similar process but a different result, due to their difference in tangential pressure, that is (see APPENDIX A for details),
$ R\sim \kappa \equiv \frac{1}{\sqrt{\varepsilon_{c}}} \left[\frac{\widehat{p}_{\rm rc}}{4\lambda _{H}\widehat{p}_{\rm rc}+ (\widehat{p}_{\rm rc}+1)(3\widehat{p}_{\rm rc}+1)} \right]^{{1}/{2}}, $

(19) $ M\sim \gamma \equiv \frac{1}{\sqrt{\varepsilon_{c}}} \left[\frac{\widehat{p}_{\rm rc}}{4\lambda _{H}\widehat{p}_{\rm rc}+ (\widehat{p}_{\rm rc}+1)(3\widehat{p}_{\rm rc}+1)} \right]^{{3}/{2}}. $

(20) The distinction between Eqs. (17) and (18) and Eqs. (19) and (20) lies in the denominator. The BL model adds a coefficient that only depends on the value of
$\lambda_{\rm BL}$ , while the H model adds a linear term that is related to the value of$ \lambda_{H} $ and$\widehat{p}_{\rm rc}$ . It is also clear that when$\lambda _{\rm BL}$ =0 or$ \lambda _H $ =0, Eqs. (17)–(20) revert to the isotropic case [63].The relaions of M – α (M – γ) and R – β (R – κ) for a given value of
$\lambda_{\rm BL}$ ($ \lambda_{H} $ ) are shown in Fig. 3 (Fig. 4). Each point represents the maximum mass configuration of the chosen EOS, and each colour of the points corresponds to a particular value of$\lambda_{\rm BL}$ ($ \lambda_{H} $ ), resulting in different degrees of anisotropy. The orange region represents the mass and radius constraint from PSR J0740+6620,$ M = 2.08 ^{+0.07}_{-0.07} M_{\odot} $ ,$ R = 12.39 ^{+1.30}_{-0.98} $ km [7, 8]. For the BL model, the relations of Mmax – α and RMmax – β are shown in Fig. 3, and its fitting formulas for$\lambda _{\rm BL}$ = 0, 0.4, 1.2, and 2 are given by
Figure 4. (color online) Relation of the Mmax – γ (left) and RMmax – κ (right). The meaning of the orange region is the same as in Fig. 3.
$ \begin{array}{*{20}{l}} M_{\lambda_{\rm BL}=0}^{\rm max} = 0.172_{-0.007}^{+0.007}\times10^{4}\alpha-0.062_{-0.094}^{+0.094}, \\ M_{\lambda_{\rm BL}=0.4}^{\rm max} = 0.151_{-0.005}^{+0.005}\times10^{4}\alpha+0.040_{-0.084}^{+0.084}, \\ M_{\lambda_{\rm BL}=1.2}^{\rm max} = 0.123_{-0.003}^{+0.003}\times10^{4}\alpha+0.065_{-0.062}^{+0.062}, \\ M_{\lambda_{\rm BL}=2}^{\rm max} = 0.096_{-0.001}^{+0.001}\times10^{4}\alpha+0.158_{-0.038}^{+0.038}. \end{array} $

(21) $ \begin{array}{*{20}{l}} R_{\lambda_{\rm BL}=0}^{M\max} = 0.969_{-0.043}^{+0.043}\times10^{3}\beta+1.052_{-0.462}^{+0.462}, \\[6.5pt] R_{\lambda_{\rm BL}=0.4}^{M\max} = 0.903_{-0.037}^{+0.037}\times10^{3}\beta+1.323_{-0.414}^{+0.414}, \\[6.5pt] R_{\lambda_{\rm BL}=1.2}^{M\max} = 0.826_{-0.031}^{+0.031}\times10^{3}\beta+1.280_{-0.400}^{+0.400}, \\[6.5pt] R_{\lambda_{\rm BL}=2}^{M\max} = 0.730_{-0.031}^{+0.031}\times10^{3}\beta+1.463_{-0.458}^{+0.458}. \end{array} $

(22) Obviously, for a given value of
$\lambda_{\rm BL}$ , there exists a linear correlation between Mmax and α or RMmax and β. For Mmax – α, when$\lambda _{\rm BL}$ = 0, 0.4, 1.2, and 2, the Pearson's coefficient is 0.975, 0.979, 0.990, and 0.997, respectively. For RMmax – β, when$\lambda _{\rm BL}$ = 0, 0.4, 1.2, and 2, the Pearson's coefficient is 0.968, 0.973, 0.977, 0.970, respectively. The reason mass is more dependent on α is that mass is mostly contributed by the core region, while for radius, it will be more influenced by the crustal region that does not appear in the expression of β. It is also important to note that with the increase in anisotropy, the slope of both relations decreases, implying the tendency for mass (radius) to increase as α (β) slows down owing to the tangential pressure, which plays a more important role in stabilizing the structure.The relations of Mmax – γ and RMmax – κ for the H model are presented in Fig. 4, and its fitting formulas are given by
$ \begin{array}{*{20}{l}} M_{\lambda_{H}=0}^{\rm max} = 0.172_{-0.007}^{+0.007}\times10^{4}\alpha-0.062_{-0.094}^{+0.094}, \\ M_{\lambda_{H}=0.4}^{\rm max} = 0.248_{-0.013}^{+0.013}\times10^{4}\gamma-0.332_{-0.135}^{+0.135}, \\ M_{\lambda_{H}=1.2}^{\rm max} = 0.478_{-0.040}^{+0.040}\times10^{4}\gamma-1.086_{-0.251}^{+0.251}, \\ M_{\lambda_{H}=2.0}^{\rm max} = 0.779_{-0.060}^{+0.060}\times10^{4}\gamma-1.773_{-0.264}^{+0.264}. \end{array} $

(23) $ \begin{array}{*{20}{l}} R_{\lambda_{H}=0}^{M\rm max} = 0.969_{-0.043}^{+0.043}\times10^{3}\beta+1.052_{-0.462}^{+0.462}, \\ R_{\lambda_{H}=0.4}^{M\rm max} = 1.159_{-0.060}^{+0.060}\times10^{3}\kappa+0.388_{-0.566}^{+0.566}, \\ R_{\lambda_{H}=1.2}^{M\rm max} = 1.741_{-0.123}^{+0.123}\times10^{3}\kappa-2.490_{-0.960}^{+0.960}, \\ R_{\lambda_{H}=2.0}^{M\rm max} = 2.213_{-0.249}^{+0.249}\times10^{3}\kappa-4.370_{-1.708}^{+1.708}. \end{array} $

(24) The meaning of the orange region is the same as in Fig. 3. Although the slope changes with the given value of
$ \lambda _{H} $ again, it is contrary to the trend of the BL model. Furthermore, the Pearson's coefficient for Mmax – γ relations when$ \lambda _{H} $ = 0, 0.4, 1.2, and 2 is 0.975, 0.955, 0.899, 0.913, respectively, while it is 0.968, 0.957, 0.924, 0.837 for the RMmax – κ relations, respectively. In the BL model, an increasing positive parameter results in an increasing repulsive force that can support a larger mass and is more affected by the core region. However, in the H model, it indicates an attractive force that results in a smaller maximum mass. As a result, the radius will be less affected by the core region, leading to a decreasing Pearson's coefficient for RMmax – κ relations with increasing$ \lambda _{H} $ . -
From Eqs. (17)-(20), it is shown that the combination of central pressure and energy density can explain the maximum mass and corresponding radius. Thus, the observation of maximum mass and its radius of NS will lead to a constraint on the central pressure and energy density. With further observation of NSs, one can decrease the uncertainty of core-state EOS, which still cannot be achieved by ab initio calculation. For the BL model, combining Eqs. (17), (18), (21), and (22), one can obtain Eq. (25). One would find that both sides of Eq. (25) still contain the pressure term; to separate the pressure term, one should guess the functional form between pressure and energy density.
$ \begin{aligned}[b]p_{\rm rc}^{M-\rm constraint}=&DA^{\tfrac{2}{3}}\varepsilon^{\tfrac{4}{3}}_{c}(3\widehat{p}^{2}_{\rm rc}+4\widehat{p}_{\rm rc}+1), p_{\rm rc}^{R-\rm constraint}\\ = & DB^{2}\varepsilon_{c}^{2}(3\widehat{p}^{2}_{\rm rc}+4\widehat{p}_{\rm rc}+1),\end{aligned} $

(25) and
$ D\equiv(1-\dfrac{\lambda _{\rm BL} }{2\pi}), \; A\equiv\dfrac{\dfrac{M_{\rm max}}{M_{\odot}}-b}{k}, \; B\equiv\dfrac{\dfrac{R_{M\rm max} }{\rm km}-b}{k}, $

(26) where k and b are the slope and intercept with the y-axis corresponding to each formula in Eqs. (21) and (22), respectively. Assuming that
$ p_{rc} $ can also be written in the polynomials of central energy density$ \varepsilon_{c} $ ,$ \begin{aligned}[b] p_{\rm rc}^{M-\rm constraint}=&DA^{\tfrac{2}{3}}\varepsilon_{c}^{\tfrac{4}{3}}\Big(1+aA^{\tfrac{2}{3}}\varepsilon_{c}^{\tfrac{1}{3}}+bA^{\tfrac{4}{3}}\varepsilon^{\tfrac{2}{3}_{c}} \\& + cA^{\tfrac{6}{3}}\varepsilon^{\tfrac{3}{3}}_{c}+\cdots\Big), \end{aligned}$

(27) $ p_{\rm rc}^{R-\rm constraint}=DB^{2}\varepsilon_{c}^{2}(1+aB^{2}\varepsilon_{c}+bB^{4}\varepsilon^{2}_{c}+cB^{6}\varepsilon^{3}_{c}+\cdots). $

(28) Putting the Eqs. (27) and (28) back into Eq. (25) separately, matching their coefficients, the coefficients turn out to be
$ a=4D,\; ~~ b=19D^{2},~~ c=100D^{3},~~ \cdots $

(29) Thus, Eq. (25) becomes
$ \begin{aligned}[b] p_{\rm rc}^{M-\rm constraint} =& DA^{\tfrac{2}{3}}\varepsilon_{c}^{\tfrac{4}{3}} \Big(1+4DA^{\tfrac{2}{3}}\varepsilon_{c} ^{\tfrac{1}{3}}+19D^{2}A^{\tfrac{4}{3}}\varepsilon_{c}^{\tfrac{2}{3}}\\&+100D^{3}A^{\tfrac{6}{3}}\varepsilon_{c} ^{\tfrac{3}{3}}+\cdots \Big),\end{aligned} $

(30) $ \begin{aligned}[b] p_{\rm rc}^{R-\rm constraint}=&DB^{2}\varepsilon_{c}^{2}\Big(1+4DB^{2}\varepsilon_{c}+19D^{2}B^{4}\varepsilon_{c}^{2}\\&+100D^{3}B^{6}\varepsilon_{c}^{3}+\cdots \Big).\end{aligned} $

(31) However, causality should also be considered when constraining the central EOS. Using Eq. (18) and the boundary condition
$ {{\rm{d}}M}/{{\rm{d}} \varepsilon _{c} }=0 $ , the sound speed square is obtained as (see APPENDIX B for details)$ c_{s}^2 \equiv \frac{{\rm{d}}p_{\rm rc}}{{\rm{d}} \varepsilon_{c}} =\widehat{p}_{\rm rc}\left(\frac{1+3\widehat{p}_{\rm rc}^2+4\widehat{p}_{\rm rc}}{3\left(1-3\widehat{p}_{\rm rc}^2\right)}+1 \right), $

(32) which has the same form as the isotropic NS, so the sound speed constraint does not change with the value of
$\lambda _{\rm BL}$ , giving the same limit$\widehat{p}_{\rm rc}$ = 0.374 [63]. Using Eq. (30)–(32), we can now constrain the central EOS.To show the effect of anisotropy on the extracted central EOS of PSR J0740+6620, the results for the BL model according to Eqs. (30) and (31) are shown in Fig. 5. For
$\lambda _{\rm BL}$ = 0.4 in the left panel and$\lambda _{\rm BL}$ = 2 in the right panel, compared to the isotropic case, the striped area indicates the intersection of the M and R constraint. As anisotropy increases, the R constraint gives a stiffer result, while the M constraint yields a softer result. Consequently, the central pressure is lower for the same energy density, owing to the tangential pressure playing a more significant role in stabilizing the star. For$\lambda_{\rm BL}$ = 0.4, the left panel shows that the extracted central energy density range changed from 546–1056 MeV/fm3 to 510–1005 MeV/fm3, and the extracted radial central pressure range changed from 87–310 MeV/fm3 to 76–271 MeV/fm3. For$\lambda_{\rm BL}$ = 2, the extracted central energy density changed to 412–822 MeV/fm3, and the extracted radial central pressure changed to 50–165 MeV/fm3. Note that both results are also consistent with the causality constraint.
Figure 5. (color online) Central EOS of PSR J0740+6620 [7, 8] extracted from the BL model based on Eqs. (30) and (31) for
$\lambda _{\rm BL}$ = 0.4 (left) and$\lambda _{\rm BL}$ = 2 (right) compared with the isotropic case. Suffix "M" ("R") represents the result combining mass (radius) observation data with Eq. (30) (Eq. (31)). The abbreviation "Iso" stands for isotropic NS, while "Aniso" stands for anisotropic NS, and "Co" stands for the intersection of mass and radius constraint bands. The black line indicates the causality constraint from Eq. (32). The green-striped region results from isotropic NS and the red-striped region from anisotropic NS.For the H model, according to Eqs. (19), (20), (23) and (24), the relations change into the following form:
$ \begin{aligned}[b] P_{\rm rc}^{M-\rm constraint} =&A^{\tfrac{2}{3}}\varepsilon_{c} ^{\tfrac{4}{3}} \Big(1+DA^{\tfrac{2}{3}}\varepsilon_{c} ^{\tfrac{1}{3}}+(D^{2}+3)A^{\tfrac{4}{3}}\varepsilon_{c}^{\tfrac{2}{3}}+ \\& (D^{3}+9D )A^{\tfrac{6}{3}}\varepsilon_{c} ^{\tfrac{3}{3}}+\cdots \Big), \end{aligned} $

(33) $ \begin{aligned}[b]P_{\rm rc}^{R-\rm constraint}=&B^{2}\varepsilon_{c}^{2}\left(1+DB^{2}\varepsilon_{c}+(D^{2}+3)B^{4}\varepsilon_{c}^{2}+\right.\\&\left.(D^{3}+9D)B^{6}\varepsilon_{c}^{3}+\cdots\right), \end{aligned}$

(34) where
$ D\equiv4+4\lambda _{H}, \; A\equiv\dfrac{\dfrac{M_{\rm max}}{M_{\odot}}-b}{k}, \; B\equiv\dfrac{\dfrac{R_{M\rm max} }{\rm km}-b}{k}, $

(35) and the meanings of k and b are the same as in the BL model.
In addition, the sound speed square of the H model becomes
$ c_{s}^2 \equiv \frac{{\rm{d}}p_{\rm rc}}{{\rm{d}} \varepsilon_{c}} =\widehat{p}_{\rm rc}\left(\frac{1+3\widehat{p}_{\rm rc}^2+(4+4\lambda _{H} )\widehat{p}_{\rm rc}}{3(1-3\widehat{p}_{\rm rc}^2)}+1\right). $

(36) Comparing Eq. (32) with Eq. (36), it is found that the two models have different results by causality constraints; the BL model does not change with the value of
$\lambda_{\rm BL}$ , while the H model will change with the value of$ \lambda_{H} $ , resulting in different maximum$\widehat{p}_{\rm rc}$ . The difference origins of Eqs. (6) and (7) then occur in Eqs. (17) and (18) and Eqs. (19) and (20), representing different ways the anisotropy affects the central radial pressure. The extracted EOS based on the H model is shown in Fig. 6. As the anisotropy changes, the causality boundary gives different constraints: for$ \lambda _{H} $ = 0.4,$\widehat{p}_{\rm rc}$ = 0.354, but$\widehat{p}_{\rm rc}$ = 0.303 for$ \lambda _{H} $ = 2. Also, the M and R constraint bands change with the introduction of anisotropy. For$ \lambda_{H} $ = 0.4, the left panel shows that the extracted central energy density range changed from 546–1056 MeV/fm3 to 626–1164 MeV/fm3, and the extracted radial central pressure range changed from 87–310 MeV/fm3 to 104–409 MeV/fm3. For$ \lambda_{H} $ = 2, the extracted central energy density range changed to 894–995 MeV/fm3, and the extracted radial central pressure range changed to 220–301 MeV/fm3.
Figure 6. (color online) Same as Fig. 5 but for H model. The causality constraint is from Eq. (36).
To directly demonstrate how
$ \widehat{p}_{rc} $ changes with a given value of$ \lambda _{H} $ , we show it in Fig. 7. The pink line is the constraint of γ, while the orange line means that causality is obeyed. Note that the denominator of Eqs. (19) and (20), namely,$1+3\widehat{p}_{\rm rc}^2+(4+4\lambda _{H})\widehat{p}_{\rm rc}$ , should larger than 0 for each given value of$ \lambda _{H} $ , and the causality means that Eq. (36) should larger than 0 and smaller than 1. This gives another constraint that varies with the given$ \lambda _{H} $ ; when both conditions are satisfied, it becomes the blue – striped region in Fig. 7. Therefore, it is noticed that with the changing$ \lambda _{H} $ , the maximum$\widehat{p}_{\rm rc}$ will change significantly. -
The presence of a strong magnetic field, superfluidity, and other situations will cause anisotropy, leading to an apparent change in the stellar structure. Observations of several exotic compact objects have been made through observation; these fascinating objects possess unknown properties that have motivated the research of anisotropic NSs.
Recently, Refs. [63, 64] derived the dimensionless TOV equation for isotropic NSs and then extracted the central EOS under the observational data of PSR J0740+6620, which greatly reduced uncertainty of the EOS of NS core matter. In this work, we present the anisotropic dimensionless TOV equation to facilitate the extraction of the central EOS of anisotropic NSs. The results indicate that anisotropy will have a non-negligible impact on the extraction of the central EOS of PSR J0740+6620. In the BL model, for
$\lambda_{\rm BL}$ = 0.4, the extracted central energy density$ \varepsilon_{c} $ changed from 546–1056 MeV/fm3 to 510–1005 MeV/fm3, and the extracted radial central pressure$p_{\rm rc}$ changed from 87–310 MeV/fm3 to 76–271 MeV/fm3. For$\lambda_{\rm BL}$ = 2, the extracted$ \varepsilon_{c} $ and$p_{\rm rc}$ changed to 412–822 MeV/fm3 and 50–165 MeV/fm3, respectively. In the H model, for$ \lambda_{H} $ = 0.4, the extracted$ \varepsilon_{c} $ changed to 626–1164 MeV/fm3, and the extracted$p_{\rm rc}$ changed 104–409 MeV/fm3. For$ \lambda_{H} $ = 2, the extracted$ \varepsilon_{c} $ changed to 894–995 MeV/fm3, and the extracted$p_{\rm rc}$ changed to 220–301 MeV/fm3. Additionally, the introduction of anisotropy will result in different causality constraints; for the BL model, it shares the same limit with the isotropic one,$ \widehat{p}_{rc} $ = 0.374 [63], while for the H model, it changes with the given value of$ \lambda_H $ , e.g., for$ \lambda _{H} $ = 0.4,$\widehat{p}_{\rm rc}$ = 0.354, but$\widehat{p}_{\rm rc}$ = 0.303 for$ \lambda _{H} $ = 2. It is worth noting that with the different values of$\lambda_{\rm BL}$ ($ \lambda_{H} $ ), the result will differ significantly. In short, a positive$\lambda_{\rm BL}$ or negative$ \lambda_{H} $ will give a softer EOS region, while a negative$\lambda_{\rm BL}$ or positive$ \lambda_{H} $ will give a stiffer EOS region.Although the existence of a strong magnetic field is considered to be the reason for anisotropy, not all NSs are capable of such strong magnetic fields. Ref. claimed that for a quark star, when the baryon density is approximately 3
$ n_0 $ ($ n_0= 0.16 $ fm–3 is the normal nuclear matter density), the transverse pressure$ P_{\bot} $ (which is perpendicular to the magnetic field) and longitudinal pressure$P_{//}$ (which is parallel to the magnetic field) start to split out at B ≈ 1.5×1017 G, B ≈ 4.5×1017 G for 5$ n_0 $ and B ≈ 6×1017 G for 7$ n_0 $ . It is also calculated by Ref. [87] that if one takes the assumption$ p_t $ =$ p_{r} $ +$ \dfrac{B^{2}}{4\pi} $ , when the central magnetic field is B0 ≈ 1018 G, then$ p_t $ -$ p_{r} \le200 $ MeV·fm-3. In Ref. [42], the anisotropy parameter$\lambda_{\rm BL}$ is still independent of the distributions of a magnetic field in the modified BL model. In subsequent work, it might be worth connecting them and further investigating the effect of magnetic field and anisotropy. -
One can expand
$ \widehat{\varepsilon} $ ,$ \widehat{p_{r}} $ ,$ \widehat{p_{t}} $ , and$ \widehat{m} $ as$ \widehat{\varepsilon} = 1+a_{1} \widehat{r}+a_{2} \widehat{r}^{2}+a_{3} \widehat{r }^{3}+\cdots, $

(A1) $ \widehat{p}_{r} = \widehat{p}_{rc}+b_{1} \widehat{r}+b_{2} \widehat{r}^{2}+b_{3} \widehat{r }^{3}+\cdots, $

(A2) $ \widehat{p}_{t} = \widehat{p}_{tc}+c_{1} \widehat{r}+c_{2} \widehat{r}^{2}+c_{3} \widehat{r }^{3}+\cdots, $

(A3) $ \widehat{m} = d_{1} \widehat{r}+d_{2} \widehat{r}^{2}+d_{3} \widehat{r }^{3}+\cdots. $

(A4) For the BL model, matching their coefficients according to Eqs. (8)–(10), we have
$b_{1}=0,~ c_{1}=0,~ d_{1}=0, d_{2}=0,~ d_{3}=1/3$ , and$ 2b_{2}=-(\widehat{p}_{\rm rc}+1)(\widehat{p}_{\rm rc}+\frac{1}{3})+2(c_{2}-b_{2}), $

(A5) $ c_{2}-b_{2}=\frac{\lambda_{\rm BL}}{4\pi} \left(\widehat{p}_{\rm rc}+1\right)\left(\widehat{p}_{\rm rc}+\frac{1}{3}\right). $

(A6) Thus, one can obtain
$ \begin{aligned}[b] b_{2} &=\frac{1}{6} \left(\frac{\lambda _{\rm BL}}{2\pi} -1\right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right),\\ c_{2} &=\frac{1}{6} \left(\frac{\lambda _{\rm BL}}{\pi} -1\right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right).\end{aligned} $

(A7) Boundary condition
$ \widehat{p}_{r}=0 $ means$\widehat{p}_{\rm rc}$ +$ b_{2}\widehat{r}^{2} $ =0; thus,$\widehat{r}=\sqrt{-\widehat{p}_{\rm rc}/b_{2}}$ , i.e.,$ \widehat{r}=\left(\frac{6\widehat{p}_{\rm rc}}{\left(1-\dfrac{\lambda _{\rm BL}}{2\pi} \right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right)} \right)^{\tfrac{1}{2} }, $

(A8) then multiplied by the scale
$ S\equiv(4\pi \varepsilon_{c})^{-\tfrac{1}{2}} \sim \varepsilon_{c}^{-\tfrac{1}{2}} $ , the stellar radius R turns out to be$ R\sim \dfrac{1}{\sqrt{\varepsilon_{c}}} \left(\dfrac{\widehat{p}_{\rm rc}}{\left(1-\frac{\lambda _{\rm BL}}{2\pi} \right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right)} \right)^{\tfrac{1}{2} }. $

(A9) Noting that
$ d_{3}=1/3 $ , thus$ \widehat{m}=\widehat{r}^{3}/3 $ , multiplied by the scale S, the stellar mass M becomes$ M\sim \dfrac{1}{\sqrt{\varepsilon_{c}}} \left(\dfrac{\widehat{p}_{\rm rc}}{\left(1-\dfrac{\lambda _{\rm BL}}{2\pi} \right) \left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right)} \right)^{\tfrac{3}{2}}. $

(A10) Once the relation of Eq. (A9) or (A10) is obtained (as we have shown in Eqs. (21)−(22)), it can be changed as
$ \begin{aligned}[b] &p_{\rm rc}^{M-\rm constraint}=DA^{\tfrac{2}{3}}\varepsilon^{\tfrac{4}{3}}_{c}\left(3\widehat{p}^{2}_{\rm rc}+4\widehat{p}_{\rm rc}+1\right), \\&p_{\rm rc}^{R-\rm constraint}=DB^{2}\varepsilon_{c}^{2}\left(3\widehat{p}^{2}_{\rm rc}+4\widehat{p}_{\rm rc}+1\right), \end{aligned} $

(A11) where
$ D\equiv\left(1-\dfrac{\lambda _{\rm BL} }{2\pi}\right), A\equiv\dfrac{\dfrac{M_{\rm max}}{M_{\odot}}-b}{k},B\equiv\dfrac{\dfrac{R_{M\rm max}}{\rm km}-b}{k}, $

(A12) and k and b are the slope and intercept with the y-axis corresponding to each formula in Eqs. (21) and (22), respectively; for example, when
$\lambda _{\rm BL}$ = 0.4,$ D=1-({0.4}/{2\pi}) $ ,$A=({M_{\rm max}}/ {M_{\odot}}-0.0402)/{1506}$ ,$B=({{R_{M\rm max}}/{\rm km}-1.3229})/ {903}$ .Eq. (A9) can also be written in the following form (here, we only show the process of deducing from Eq. (A9); for Eq. (A10) it has a similar process):
$ p_{\rm rc}^{R-\rm constraint}=DB^{2}(3{p^{2}_{\rm rc}}+4p_{\rm rc}\varepsilon_{c}+\varepsilon_{c}^{2}). $

(A13) Assuming that
$p_{\rm rc}$ can also be written in the polynomials of central energy density$ \varepsilon_{c} $ ,$ p_{\rm rc}^{R-\rm constraint}=DB^{2}\varepsilon_{c}^{2}(1+aB^{2}\varepsilon_{c}+bB^{4}\varepsilon^{2}_{c}+cB^{6}\varepsilon^{3}_{c}+\cdots). $

(A14) Putting Eq. (A14) back into Eq. (A13), and matching the coefficients, one has
$ a=4D,\; b=19D^{2},\; c=100D^{3},\cdots $

(A15) Finally, the central EOS can be extracted from Eq. (A9):
$\begin{aligned}[b] p_{\rm rc}^{R-\rm constraint}=&DB^{2}\varepsilon_{c}^{2}(1+4DB^{2}\varepsilon_{c}+19D^{2}B^{4}\varepsilon_{c}^{2}\\&+100D^{3}B^{6}\varepsilon_{c}^{3}+\cdots). \end{aligned} $

(A16) For Eq. (A10), it becomes
$ \begin{aligned}[b] p_{\rm rc}^{M \rm constraint} =&DA^{\tfrac{2}{3}}\varepsilon_{c} ^{\tfrac{4}{3}}\left(1+4DA^{\tfrac{2}{3}}\varepsilon_{c} ^{\tfrac{1}{3}}+19D^{2}A^{\tfrac{4}{3}}\varepsilon_{c}^{\tfrac{2}{3}}\right.\\&\left.+100D^{3}A^{\tfrac{6}{3}}\varepsilon_{c} ^{\tfrac{3}{3}}+\cdots\right).\end{aligned} $

(A17) For the H model, Eq. (7) can be changed into
$ \widehat{p}_{t}=\widehat{p}_{r}-2\lambda _{H} \widehat{p}_{r} \frac{\widehat{m}}{r}, $

(A18) combining with Eq. (8) and Eq. (9), it has
$ b_{1}=0, ~c_{1}=0, d_{1}=0, ~d_{2}=0, ~d_{3}=1/3 $ , and$ 2b_{2}=-\left(\widehat{p}_{\rm rc}+1\right)\left(\widehat{p}_{\rm rc}+\frac{1}{3}\right)+2\left(c_{2}-b_{2}\right), $

(A19) $ c_{2}-b_{2}=-\frac{2}{3}\lambda _{H} \widehat{p}_{\rm rc}. $

(A20) Thus,
$ \begin{aligned}[b]&b_{2}=-\frac{1}{6}\left[\left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right)+4\lambda _{H}\widehat{p}_{\rm rc}\right], \\& c_{2} =-\frac{1}{6}\left[\left(\widehat{p}_{\rm rc}+1\right)\left(3\widehat{p}_{\rm rc}+1\right)+8\lambda _{H}\widehat{p}_{\rm rc}\right], \end{aligned} $

(A21) and
$ \begin{aligned}[b] & R\sim \frac{1}{\sqrt{\varepsilon_{c}}} \left(\frac{\widehat{p}_{\rm rc}}{4\lambda _{H}\widehat{p}_{\rm rc}+(\widehat{p}_{\rm rc}+1)(3\widehat{p}_{\rm rc}+1)}\right)^{\tfrac{1}{2}}, \\& M\sim \frac{1}{\sqrt{\varepsilon_{c}}} \left(\frac{\widehat{p}_{\rm rc}}{4\lambda _{H}\widehat{p}_{\rm rc}+(\widehat{p}_{\rm rc}+1)(3\widehat{p}_{\rm rc}+1)} \right)^{\tfrac{3}{2}}. \end{aligned} $

(A22) The central EOS becomes
$ \begin{aligned}[b]p_{\rm rc}^{M-\rm constraint} =&A^{\tfrac{2}{3}}\varepsilon_{c} ^{\tfrac{4}{3}}\left(1+DA^{\tfrac{2}{3}}\varepsilon_{c} ^{\tfrac{1}{3}}+\left(D^{2}+3\right)A^{\tfrac{4}{3}}\varepsilon_{c}^{\tfrac{2}{3}}\right.\\&\left.+\left(D^{3}+9D\right)A^{\tfrac{6}{3}}\varepsilon_{c} ^{\tfrac{3}{3}}+\cdots \right),\end{aligned} $

(A23) $\begin{aligned}[b] p_{\rm rc}^{R-\rm constraint}=&B^{2}\varepsilon_{c}^{2}(1+DB^{2}\varepsilon_{c}+(D^{2}+3)B^{4}\varepsilon_{c}^{2} \\&+(D^{3}+9D)B^{6}\varepsilon_{c}^{3}+\cdots), \end{aligned} $

(A24) where
$ D\equiv4+4\lambda_{H}, \; A\equiv\dfrac{\dfrac{M_{\rm max}}{M_{\odot}}-b}{k}, \; B\equiv\dfrac{\dfrac{R_{M\rm max} }{\rm km}-b}{k}, $

(A25) and the meanings of k and b are the same as for the BL model.
-
For the BL model, one has
$ M\sim \frac{1}{\sqrt{\varepsilon_{c}}} \left(\frac{\widehat{p}_{\rm rc}}{4\lambda _{H}\widehat{p}_{\rm rc}+(\widehat{p}_{\rm rc}+1)(3\widehat{p}_{\rm rc}+1)} \right)^{\tfrac{3}{2}}, $

(B1) which is a function of central energy density
$ \varepsilon_{c} $ . Taking the derivative of M with respect to$ \varepsilon_{c} $ gives$ \frac{{\rm{d}}M}{{\rm{d}}\varepsilon_{c}}=\frac{M(\varepsilon_{c})}{2\varepsilon_{c}}\left[3\left(\frac{\varepsilon_{c}}{p_{\rm rc}}\frac{{\rm{d}}p_{\rm rc}}{{\rm{d}}\varepsilon_{c}}-1\right)\frac{1-3\widehat{p}_{\rm rc}^{2}}{1+\widehat{p}_{\rm rc}^{2}+4\widehat {p}_{\rm rc}} -1\right]. $

(B2) In addition, the derivative of
$ \widehat{R} $ with respect to$\widehat{p}_{\rm rc}$ gives$ \frac{{\rm{d}}\widehat{R}}{{\rm{d}}\widehat{p}_{\rm rc}}=\widehat{R}\frac{1-3\widehat{p}_{\rm rc}^{2}}{2\widehat{p}_{\rm rc}+8\widehat{p}_{\rm rc}^{2}+6\widehat{p}_{\rm rc}^{3}}, $

(B3) and the derivative of
$\widehat{p}_{\rm rc}$ with respect to$ \varepsilon_{c} $ gives$ \frac{{\rm{d}}\widehat{p}_{\rm rc}}{{\rm{d}}\varepsilon_{c}}=\frac{{\rm{d}}\frac{{p}_{\rm rc}}{\varepsilon_{c}}}{{\rm{d}}\varepsilon_{c}}=\frac{1}{\varepsilon_{c}}\left(\frac{{\rm{d}}p_{\rm rc}}{{\rm{d}}\varepsilon_{c}}-\frac{p_{\rm rc}}{\varepsilon_{c}} \right). $

(B4) $ {{\rm{d}}M}/{{\rm{d}}\varepsilon_{c}}=0 $ givesthe expression of sound speed square$s_{r,c}^{2}\equiv {\rm{d}}p_{\rm rc}/{\rm{d}}\varepsilon_{c}$ as$ c_{r,s}^2 \equiv \frac{{\rm{d}}p_{\rm rc}}{{\rm{d}} \varepsilon_{c}} =\widehat{p}_{\rm rc}\left(\frac{1+3\widehat{p}_{\rm rc}^2+4\widehat{p}_{\rm rc}}{3(1-3\widehat{p}_{\rm rc}^2)}+1\right), $

(B5) which is the same as in Ref. [63, 64].
For the H model, it becomes
$ c_{r,s}^2 \equiv \frac{{\rm{d}}p_{\rm rc}}{{\rm{d}} \varepsilon_{c}} =\widehat{p}_{\rm rc}\left(\frac{1+3\widehat{p}_{\rm rc}^2+(4+4\lambda _{H} )\widehat{p}_{\rm rc}}{3(1-3\widehat{p}_{\rm rc}^2)}+1\right). $

(B6) -
Besides the observation of PSR J0740+6620, the observation of a 1.4
$ M_{\odot} $ NS also gives a new constraint on NS radii: 11.96$ < R_{1.4} < $ 14.26 km [11], and 11.52$ < $ $ R_{1.4} < $ 13.85 km [12]. Here, we take the revised result 11.80$ < R_{1.4} < $ 13.10 km [9]. Thus, as above, we can get the relation and EOS constraint from the radius observation of PSR J0030+0451. However, for the maximum mass NS, different EOSs predict a different maximum mass and corresponding radius, but for the canonical NS, it predicts a different radius but with the same mass. Thus, we can only use the radius observation of PSR J0030+0451 now, with the future observation of the moment of inertia imposing another constraint on the central EOS of PSR J0030+0451.For the BL model, we have
$ \begin{array}{*{20}{l}} R_{\lambda_{\rm BL}=0}^{1.4} = 0.671\times10^{3}\beta+2.783, \\ R_{\lambda_{\rm BL}=0.4}^{1.4} = 0.354\times10^{3}\beta+6.765, \\ R_{\lambda_{\rm BL}=1.2}^{1.4} = 0.311\times10^{3}\beta+7.353, \\ R_{\lambda_{\rm BL}=2}^{1.4} = 0.255\times10^{3}\beta+8.232. \end{array} $

(C1) with r =0.948, 0.598, 0.517, 0.421 for
$\lambda _{\rm BL}$ =0, 0.4, 1.2, 2.0.For the H model, we have
$ \begin{array}{*{20}{l}} R_{\lambda_{H}=0}^{1.4} = 0.671\times10^{3}\beta+2.783, \\ R_{\lambda_{H}=0.4}^{1.4} = 0.423\times10^{3}\beta+6.136, \\ R_{\lambda_{H}=1.2}^{1.4} = 0.428\times10^{3}\beta+6.614, \\ R_{\lambda_{H}=2}^{1.4} = 0.435\times10^{3}\beta+7.075. \end{array} $

(C2) with r =0.948, 0.698, 0.752, 0.783 for
$ \lambda _{H} $ =0, 0.4, 1.2, 2.0.The constraint region from the BL model is shown in the Fig. C1. As we have concluded, the pressure anisotropy also affects the extraction of the central EOS of NSs. However, compared to the result from PSR J0740+6620, the constraints from PSR J0030+0451 have a greater uncertainty, which comes from the crust effect in the low mass NS.

Figure C1. EOS extracted from the radius observation of PSR J0030+0451[9] for (a)
$ \lambda _{\rm BL} $ =0.4 and (b)$ \lambda _{\rm BL} $ =2.0.
Anisotropic pressure effect on central EOS of PSR J0740+6620 in the light of dimensionless TOV equation
- Received Date: 2024-06-03
- Available Online: 2024-10-15
Abstract: It is generally agreed upon that the pressure inside a neutron star is isotropic. However, a strong magnetic field or superfluidity suggests that the pressure anisotropy may be a more realistic model. We derived the dimensionless TOV equation for anisotropic neutron stars based on two popular models, namely, the BL and H models, to investigate the effect of anisotropy. Similar to the isotropic case, the maximum mass





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: