Is dark energy necessary for the sustainability of traversable wormholes?

The concept of a wormholes (WH) as a tunnel-like structure in the spacetime continuum connecting two regions of a manifold or two separate universes was initiated by Einstein and Rosen [1] and developed by Morris and Thorne (MT) [2]. The MT proposal was beset with several problems relating to the throat not remaining open sufficiently long to allow even a photon to pass through. However, it was conjectured in Ref. [2] that suitable geometries may be found such that even humans can pass through WHs. These are known as traversable WHs. Theoretically, it is then possible to entertain the idea of time travel. Bronnikov [3] considered the novel construction of cylindrically symmetric WHs, where one end exists in a 4 dimensional spacetime and the other opens up into a 6 dimensional geometry, and discussed their possible observable features to aid the search. It is also required that WHs be horizon and singularity free everywhere [4].

A central requirement for a WH throat to form in general relativity is the violation of the null energy condition (NEC); consequently, the existence of exotic types of matter fields is implied. Physically, this suggests that a negative density facilitates a repulsive gravitational force, which is required to keep the WH throat open. Originally, MT WHs were studied to obtain solutions, followed by later verification of whether the NEC was violated. Subsequently, Visser [5, 6] contemplated commencing by gluing together two asymptotically flat spacetime manifolds and using the junction conditions to establish conditions for the existence of WHs. These conditions invariably amounted to a violation of the NEC at the outset. For example, Kar and Sahdev [7] solved the Einstein equations after prescribing an with trace-free energy momentum. This corresponds to the Casimir stress energy and has the feature of necessary NEC violation, making it ideal in the study of WHs. (Note that fluids with the Casimir effect are considered exotic in this study. Generally, exotic fluid is taken to mean dark energy, but this is not the case in this article.) Evidently this stipulation has not been extensively studied in the literature. Kar and Sahdev [7] reduced the defining equation to a nonlinear second order differential equation after a restrictive prescription of the redshift function as the de facto temporal potential. The choice led to a negative gradient with no singularities or horizons emerging. Following the success of this process, they proceeded to join two spacetime manifolds as per the Visser scheme and generated two equations from the junction conditions, which they solved to construct a viable WH solution. This idea of using the Casimir stress energy has ostensibly not been applied in modified gravity theories. This is surprising because NEC violation is guaranteed, which is highly desirable in WH modeling. This strongly motivates us to use this in constructing viable WHs in $ f(R, T) $ theory.

The Casimir effect is well known in standard physics as an attractive force between neutral parallel plates in a vacuum. This force is a result of the vacuum energy of quantum fields and is a pure quantum effect. The Casimir effect is one of the few phenomena in physics that can create an observable effect of negative energy density. Between the plates, the energy density can become effectively negative compared to the free vacuum. This unusual behavior makes it a good candidate for an actual mechanism to generate negative energy. The Casimir effect is significant in WH physics primarily as a theoretical example of how negative energy densities, necessary for the existence of a stable WH, might be achieved in a controlled physical setting. Garattini [8] analyzed the Casimir effect for WH physics and developed a viable traversable WH model assuming such an EoS.

While the focus of this investigation revolves around the effect of the Casimir stress energy, which has the characteristics of exotic matter but is a laboratory proven extraordinary feature of standard physics, the question of whether exotic matter fields are compulsory in ensuring an open WH throat is certainly worth considering. In the present context, we could ask whether the modifications to the field equations introduced by the $ f(R, T) $ Lagrangian, specifically the addition of a scale dependent trace of the energy momentum tensor, could alter the geometry sufficiently, thus obviating the need for exotic matter. Sporadic research along these lines have appeared in the literature in the case of $ f(R, T) $ gravity. For instance, in [9], some WH models not demanding exotic matter are reported. Note that the possibility of avoiding exotic matter to keep WH throats open has been addressed in several other theories. For example, through the involvement of a scalar field in Brans-Dicke gravity, exotic fields are not required to sustain the geometry of open WHs [10−12]. Bahamonde et al. [13] constructed $ f(R) $ gravity models for the universe with WHs that generally do not require exotic matter; however, the general relativity case $ f(R) = R $ cannot avoid exotic matter [13]. Zubair et al. [14] commenced a study of WHs in $ f(R, T) $ gravity but then specialized to a quadratic form of $ f(R) $ theory and concluded from their models that exotic matter was not required to sustain the WH. Despite these results, question remains as to whether mechanisms that can sustain WHs exist in standard physics. A recent investigation by Nojiri et al. [15, 16] introduced a novel approach to the study of WHs in modified gravity. The comprehensive studies presented in Refs. [17−45] provide detailed information on various examples of traversable WH solutions in different modified gravity theories, highlighting the exciting research in this field. For this reason, we study this possibility.

However, why should $ f(R, T) $ theory be of interest among the many alternatives to general relativity? It is well known that $ f(R, T) $ theory has succeeded in explaining a cornerstone problem in gravitation, namely, the observed accelerated expansion of the universe, which the standard theory cannot deal with without appealing to dark matter and dark energy [46]. Moreover, $ f(R, T) $ theory admits astrophysical models that comply with the elementary requirements for stellar distributions [47]. One major trade-off with $ f(R, T) $ is that energy conservation is sacrificed. This is also true for other viable theories such as unimodular gravity [48−50], Rastall theory [51−54], and Weyl quadratic theory [55−57] and its generalization by Dirac [58−61]. In the context of WHs, the loss of energy conservation is not necessarily a negative feature given that NEC violation is demanded and loss of energy into a WH is probable.

The question of whether WHs are realistic physical entities is interesting. Specifically, we are interested in what observational signatures would indicate the presence of WHs. Some observational protocols have recently emerged. For instance Piotrovich et al. [62] expressed the view that active galactic nuclei are WH mouths instead of supermassive black holes as is the prevailing view. They demonstrated that accreting flows generate collisions inside WHs, and gamma ray radiation is the consequence. In their view, if such radiation were detected, it would serve as solid proof for the existence of WHs. Therefore, it is unsurprising that WHs have attracted considerable attention in the literature. Some configurations that have been studied include Chaplygin gas and dark matter as the source of phantom energy [63−72]. Geometric effects such as torsion, nonmetricity, or higher curvature and higher dimensional terms may also account for exotic matter in some modified theories of gravity. Additionally, Lobo [73] and Visser [74] considered more factors that could explain exotic matter.

Deng and Meng [75] constructed traversable WHs by assuming the presence of dark energy. In their study, they appealed to certain astrophysical observations to dismiss other WH solutions. They produced 6 models, one of which was asymptotically flat, whereas the other 5 were constructed from matter spatially distributed near the throat of the WH. Some researchers have found novel ways to obviate exotic matter [76, 77]. Blazquez-Salcedo et al. [78] generated a class of singularity-free traversable WHs in Einstein-Dirac-Maxwell theory without resorting to exotic matter. They made use of two massive fermions that admit asymptotically flat WH solutions. A physically reasonable traversable WH model was developed in Ref. [79] without the mirror symmetry of Ref. [78]. Another viable approach is to use the thin-shell formalism [80, 81]. In this method, Lobo [82] explained that suitable patches of a manifold can be pasted together such that the violation of the NEC occurs only on a thin shell.

WHs exhibit different properties depending on the gravitational field theory being used. In some theories, exotic matter is not required for WHs to exist. This has been shown by Pavlovic and Sossich [83] and Harko et al. [84] in the case of $ f(R) $ theory. De Benedictis and Horvat [85] demonstrated the throat of a WH in the context of $ f(R) $ gravity. Sharif and Zahra [86] investigated the role of pressure anisotropy in the formation of WHs in the presence of a barotropic EoS, whereas Eiroa and Aguirre [87] studied thin-shell Lorentzian WHs in $ f(R) $ theory. Traversable WHs in $ f(R) $ gravity were considered by Mazharimousavi and Halilsoy [88], and Godani and Samanta [89] examined the role of various redshift functions on WH structure and generated several new solutions.

This article is structured as follows. In Sec. II, we briefly review the field equations of $ f(R,T) $ theory. In Sec. III, we express the corresponding field equations for spherically symmetric and static spacetimes in $ f(R,T) $ gravity and present an equation of state (EoS) that reduces to a traceless energy momentum tensor. The structure equation for standard energy conditions is presented in Sec. IV. We then construct analytic WH solutions for different types of redshift and shape functions in Sec. V. In Sec. VI, we investigate the deflection angle of a light ray passing close to a WH. Finally, we provide a conclusion in Sec. VII.

Various modified gravity theories have been proposed to extend general relativity. The $ f(R,T) $ gravity model [46], which originates from the combination of curvature-matter coupling theory, has many applications in describing the current Universe. Let us start from the $ f(R,T) $ action given by

where g is the determinant of the metric $ g_{\mu\nu} $, and $ {\cal{L}}_m $ denotes the action of matter. $ f(R,T) $ is an arbitrary function of the Ricci scalar R (Ricci scalar) and T (trace of the energy-momentum tensor).

Variations in action (1) with respect to metric $ g_{\mu\nu} $ lead to the modified field equations of $ f(R,T) $ gravity, yielding

where $ f_R \equiv \partial f/\partial R $, $ f_T \equiv \partial f/\partial T $, and $ \square \equiv \nabla_\mu\nabla^\mu $ is the d'Alembertian operator with a covariant derivative represented by $ \nabla_\mu $. Here, the auxiliary tensor $ \Theta_{\mu\nu} $ is defined in terms of the variation in $ T_{\mu\nu} $ as

Taking the trace of the field equations (2), we can obtain a relation between R and T of the form

where $ \Theta = g^{\mu\nu}\Theta_{\mu\nu} $ is the trace of $ \Theta_{\mu\nu} $. Finally, we obtain the covariant derivative of the stress-energy tensor and use the field equations in (2), which yield [90]

Interestingly, Eq. (5) is not conserved owing to the interaction between the curvature and matter sectors. Moreover, non-conservation leads to nongeodesic motion of particles. In the case of $ f(R,T) $ gravity, the functional form of f is not unique. Many $ f(R,T) $ models exhibit interesting features; however, we continue our investigation by considering the simplest functional form of $ f(R,T) = R+ 2\beta T $ [46], i.e., the usual Einstein-Hilbert term plus a T dependent function $ f(T ) $. This model has been widely applied in astrophysical scenarios and also explains the accelerated expansion of the Universe in an elegant manner. Using the particular form function, we rewrite Eqs. (2), (4), and (5) as

where $ G_{\mu\nu} $ is the Einstein tensor.

To study the WH structure, we start by considering the static spherically symmetric metric ansatz in Schwarzschild coordinates in the form

which is in the form of the MT metric [2]. Here, $ \Phi(r) $ is known as the redshift function, and $ b(r) $ is the shape function. The range of the radial coordinate r is $ r\geqslant {r_0} $ , with a minimum value at $ b(r_0) = r_0 $. This can be interpreted as the ‘throat’ of the WH, with the circumference of a circle given by $ 2\pi r $. More precisely, the shape function should satisfy the flaring-out condition, i.e., $ \dfrac{b(r)-rb^{\prime}(r)}{b^2(r)}>0 $ [2], which is provided by the mathematics of embedding. This implies another restriction $ b^{\prime}(r_0) < 1 $ at the throat. In addition, the shape function obeys $ b(r)-r \leqslant 0 $. Nevertheless, $ \Phi(r) $ must be finite everywhere to ensure the absence of an event horizon.

Here, we adopt an anisotropic fluid form that describes the matter sector. Such a tensor can be written as

where $ \rho = \rho(r) $ is the energy density, $ p_r = p_r(r) $ and $ p_t = p_t (r) $ are the radial and transverse pressures, respectively, $ u^\mu $ is the 4-velocity, $ \chi^{\mu} $ is the unit radial vector with $ \chi_{\mu}\chi^{\mu} = 1 $, and $ g_{\mu\nu} $ is the metric tensor. The anisotropy factor is given by $ \sigma = p_t-p_r $.

It is well known from the definition of the matter Lagrangian for isotropic/anisotropic fluid that the energy-momentum tensor is not unique. We can choose either $ {\cal{L}}_m = {\cal{P}} $ or $ {\cal{L}}_m = -\rho $. In this study, we consider $ {\cal{L}}_m = {\cal{P}} $, where $ {\cal{P}} \equiv (p_r+ 2p_t)/3 $ [91−93], which allows us to rewrite Eq. (3) as $ \Theta_{\mu\nu} = -2T_{\mu\nu} + {\cal{P}}g_{\mu\nu} $. By taking the covariant divergence of Eq. (8), we obtain the result

Note that the standard conservation equation does not hold for this theory. If we take $ \beta = 0 $, we can recover the conservation of the energy-momentum tensor for the general relativistic case. Finally, combining Eqs. (9) and (10) and the gravitational equation (6), we obtain the following expressions:

where the prime stands for differentiation with respect to r. Finally, we have three independent Eqs. (12)–(14) with five unknown quantities, i.e., $ \Phi(r) $, $ b(r) $, $ \rho(r) $, $ p_r(r) $ , and $ p_t(r) $. Evidently, this system is underdetermined, and we are free to make any two assumptions to generate a physically reasonable WH solution.

For the sake of simplicity, we can consider an EoS of the form [12]

With these considerations, we may express the EM tensor using Eq. (15) as $ T = -\rho+p_r+ 2p_t = \rho(1-\omega)/ \omega $. In particular, the EoS (15) reduces to a traceless EoS, i.e., $ T = 0 $ for $ \omega = 1 $, and the situation is related to the Casimir effect. By choosing this particular EoS, the authors of [94, 95] have reported WH solutions in higher dimensional gravity theory. Most importantly, this EoS has the feature of necessarily violating the NEC, which is required to maintain the throat of a WH in the open position via the repulsive gravitational effect induced by the negative density. In light of these considerations, i.e., $ \omega = 1 $, we endeavor to construct WH models in the context of $ f(R,T) $ gravity.

This section is devoted to discussing some properties of the stress-energy tensor that will be useful when analyzing the energy conditions. The violation of the NEC, at least in a neighborhood, is the most salient feature of these space-times from the perspective of general relativity [2]. As a result, we search for the existence of WH solutions in $ f(R,T) $ theory with suitable energy conditions such that the matter field violates the NEC. Given the stress-energy tensor (10), the NEC is given by

whereas the WEC asserts that

and the expression for the SEC implies

The above expressions prove useful when searching for WH solutions with NEC violation preferably not originating from exotic matter, such as dark energy.

Here, we begin by finding WH solutions with two different types of redshift functions and one shape function, considering that $ f(R,T) = R+ 2\beta T $. For the WH to be traversable, we consider $ \Phi^{\prime}(r) = 0 $ and $ \Phi(r) = \log \left(1+\dfrac{r_0}{r}\right) $. This choice guarantees that the redshift function is finite everywhere, and consequently, the geometry is horizon free. Finally, we consider the shape function $ b(r) = \dfrac{r_0^2}{r} $, which ensures an asymptotically flat spacetime satisfying the flaring-out condition at the WH throat. These assumptions simplify the field equations significantly and provide particularly intriguing solutions, as shown below.

The simplest approach is to consider $ \Phi^{\prime}(r) = 0 $ , implying WHs with zero tidal forces. In this context, Eqs. (12)–(14) with EoS (15) provide the system

From the system of Eqs. (19)–(21), we may express $ p_r $ and $ p_t $ in terms of b and $ b^{\prime} $ in the form

Substituting $ p_r $ and $ p_t $ given in Eqs. (21)–(23), we obtain the shape function $ b(r) = C $. Using the condition $ b(r_0 ) = r_0 $, we can write $ b(r) = r_0 $, which is constant. Substituting these values into Eqs. (19)–(20), we obtain the components of the energy-momentum tensor $ \rho(r) = 0 $, $ p_r(r) = -\dfrac{r_0}{2 (\beta +4 \pi ) r^3} $, and $ p_t(r) = \dfrac{r_0}{4 (\beta +4 \pi ) r^3} $. This is a physically untenable situation because the energy density is zero while $ p_r = -2p_t $. Thus, considering $ \Phi^{\prime}(r) = 0 $ is not suitable for describing spherically symmetric WH solutions in $ f(R,T) $ gravity. Interestingly, zero-tidal-force WHs with isotropic pressure and a single matter source are also not possible in general relativity (see Ref. [7]).

The second case we consider is logarithmic: $\Phi(r) = \log \left(1+\dfrac{r_0}{r}\right)$. In this model, the field equations (12)–(14) with EoS (15) reduce to the system

Now, the first two equations give the expressions for $ p_r $ and $ p_t $ in terms of b and $ b^{\prime} $,

Substituting the expressions for $ p_r $ and $ p_t $ into Eq. (27), we arrive at the following master equation:

Eq. (29) is routinely solved in the form

using the condition $ b(r_0) = r_0 $. At the throat, $b'(r_0) = \dfrac{6 \pi }{\beta +9 \pi }-1 < 1$. This imposes the restriction $ -6 \pi <\beta <-3 \pi $, for which $ 0< b'(r_0)<1 $. Moreover, we verify that $ \dfrac{b(r)}{r}\to 0 $ as $ r\to \infty $ , which confirms the asymptotic flatness. Using Eq. (30), we plot the shape function for $ \beta = -4.5 \pi $ (dot-dashed), $ \beta = -5\pi $ (dashed), and $ \beta = -5.5 \pi $ (dotted) in the left panel of Fig. 1, when $ r_0 = 1 $.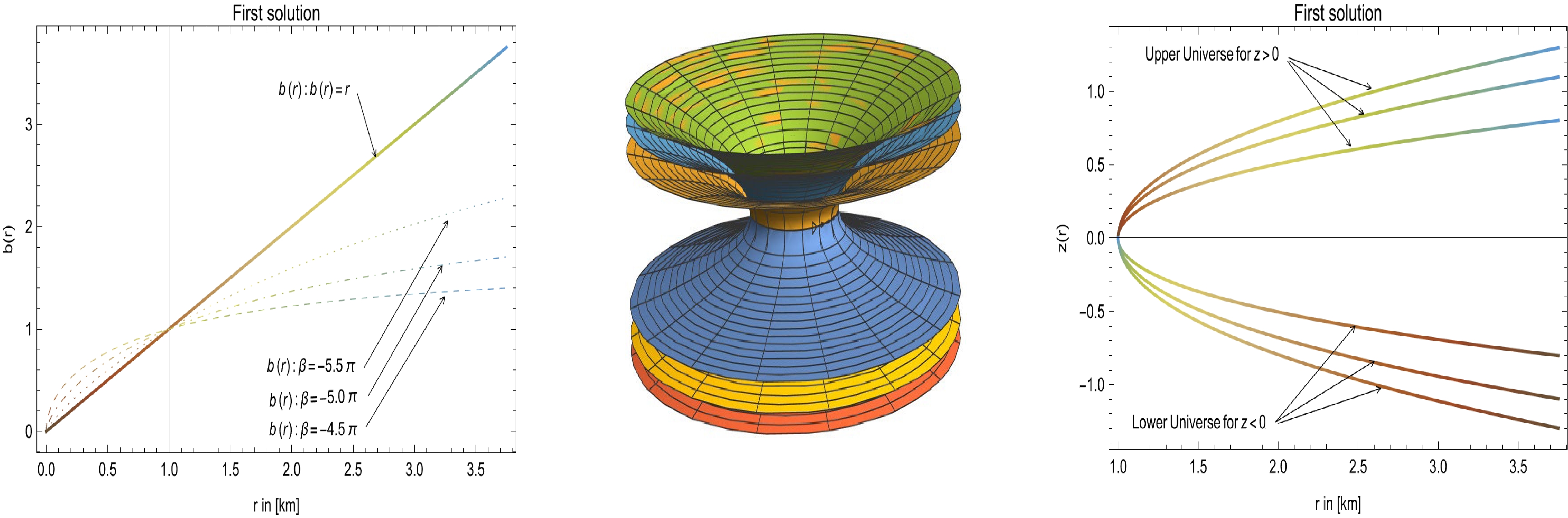

Figure 1.  (color online) Left panel: Behavior of $ b(r) = r $ (solid black), and other curves are plotted for $ b(r) $ given in Eq. (30), which shows $ b(r) < r $. Here, we consider a specific redshift function $ \Phi(r) = \log \left(1+\dfrac{r_0}{r}\right) $ and plot $ b(r) $ for $ \beta = -4.5 \pi $ (solid), $ \beta = - 5\pi $(dashed), and $ \beta = -5.5 \pi $ (dot-dashed). Middle panel: Using Eqs. (30) and (31), we plot the embedded diagram, which provides valuable insights into the geometry and topology of the WH configurations. Right panel: Using Eqs. (30) and (31), we plot the embedded surface $ z(r) $, which provides valuable insights into the geometric structure and characteristics of the embedded surface. In all cases, we consider $ \omega = 1 $, which reduces to a traceless EMT, with $ T = 0 $. See the text for specific choices of the considered parameters.

To better understand the shape function, we find the equation for the embedding surface,

In Fig. 1 (middle and right panels), we present the embedding diagram and embedded surface $ z(r) $ with Eqs. (30) and (31). The location of the WH throat is defined by the black ring that connects two distinct universes.

Using Eqs. (27)–(28) and Eq. (30), we find the following relationships:

where $u(r) = \left(\dfrac{\beta r+6 \pi r+3 \pi r_0}{\beta r+9 \pi r}\right)^{{\beta }/{(3 \pi )}}$. For $ r> r_0 = 1 $, we plot ρ, $ \rho+p_r $ , and $ \rho+p_t $ as functions of r in Fig. 2. It is clear that both $ \rho+p_r $ and $ \rho+p_t $ tend to zero as $ r \to \infty $. For $ -6 \pi <\beta <-3 \pi $, energy density is negative outside the throat while $ \rho+p_r >0 $ and $ \rho+p_t <0 $. As shown in Fig. 2 , the NEC is violated outside the throat. The parameters of the solution are $ -6 \pi <\beta <-3 \pi $ and $ r_0 = 1 $ .

Figure 2.  (color online) Here, we consider a specific redshift function $ \Phi(r) = \log \left(1+\dfrac{r_0}{r}\right) $ and plots of the specific stress-energy profile for ρ (Left panel), $ \rho+p_r $ (Middle panel), and $ \rho+p_t $ (Right panel) versus r. In all cases, we consider $ \omega = 1 $, which reduces to a traceless EMT, with $ T = 0 $. See the text for specific choices of the considered parameters.

At the throat, $ r = r_0 $, we have

It is evident that $ (\rho+ p_r)|_{r_0} \gtrless 0 $ depending on the values of $ -6 \pi <\beta < -3 \pi $. In the region $ -4 \pi <\beta < -3 \pi $ , we have $ (\rho+ p_r)|_{r_0} < 0 $, and $ (\rho+ p_r)|_{r_0} > 0 $ for $ -6 \pi <\beta < -4 \pi $. Moreover, the situation is merely reversed for the NEC along the transverse direction (at the throat), i.e., $ (\rho+ p_t)|_{r_0} \lessgtr 0 $. Note that equations are not-valid for $ \beta = -4 \pi $. From these observations, we can infer that the model violates the NEC throughout the spacetime, and consequently, WEC violation also occurs.

Here, we are also interested in quantifying the total amount of exotic matter through the ''volume integral quantifier'' (VIQ) used by Kar and Sahdev [96]. This can be achieved through the definite integral (with a cut-off of the stress-energy at $ a>r_0 $):

and using Eq. (33), we have

where

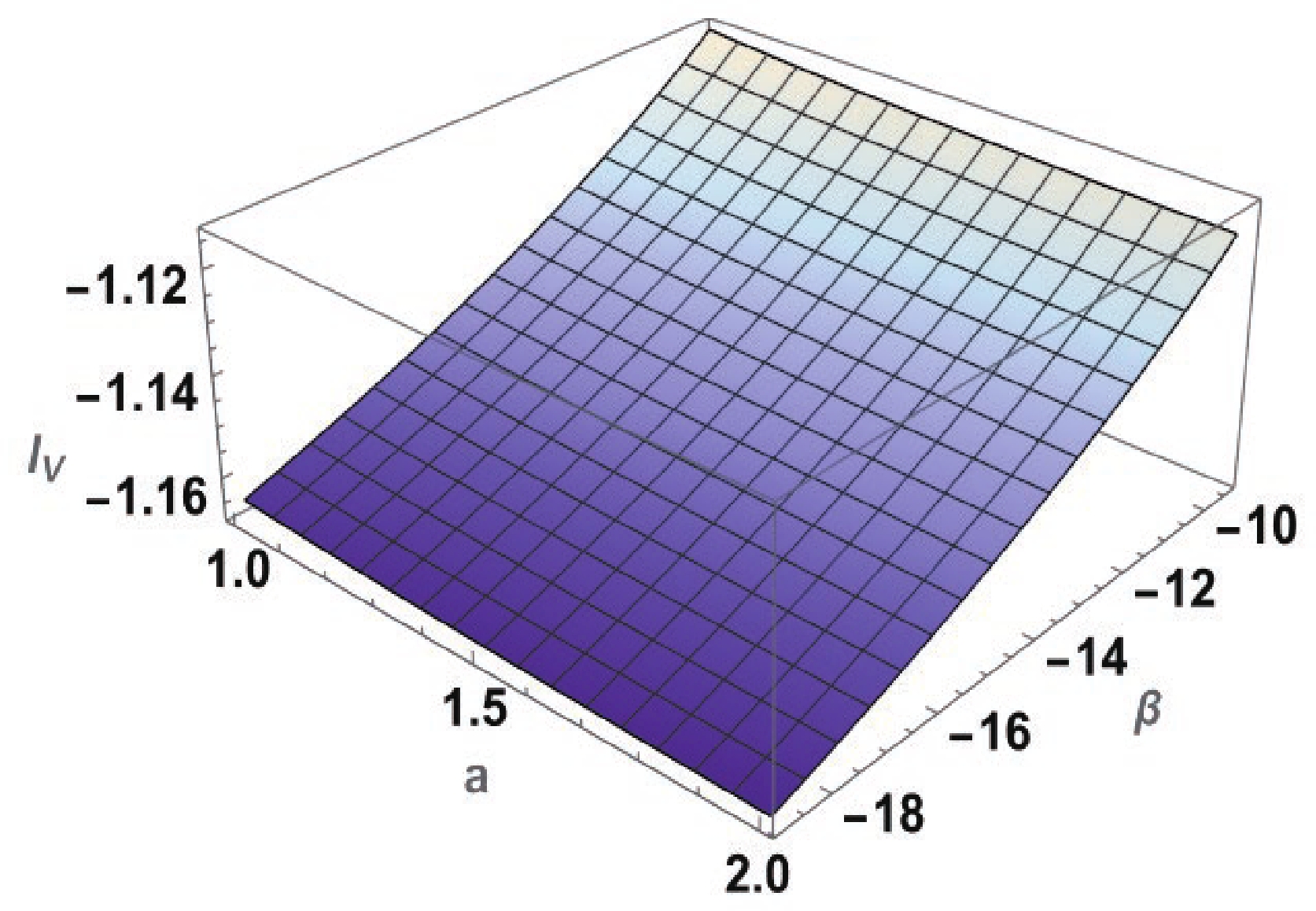
After carefully reviewing Eq. (38), we can conclude that $I_V = \int\left(\rho+p_r\right)\mathrm{d}V \to 0$ when taking the limit $ a \to r_0 $. For more clarity, we plot Fig. 3, which shows that we can theoretically construct a traversable WH with a small amount of NEC violating matter within the specified range $ -6 \pi <\beta <-3 \pi $.

Figure 3.  (color online) Total amount of exotic matter, obtained using Eq. (38). This graph shows that $ I_V \to 0 $ when taking the limit $ a \to r_0 $.

Here, we consider a widely used specific form function given by $ b(r) = \dfrac{r_0^2}{r} $. Notably a generalized version of this shape function appears in the work of Tripathy [97]. However, in his study, the author commenced by referring to 'tideless' forces amounting to $ \phi = 0 $. Thereafter, he adopted the classical Casimir force variation density as $ -\dfrac{1}{a^4} $ , where a is the separation between two charged plates. Based on these, he obtained the shape function above. In addition, he was interested in quantum effects and the generalized uncertainty principle (GUP). Zubair et al. [98] followed a similar approach to Tripathy; however, to fix the geometry of the models, they assumed the existence of conformal Killing vectors. This placed a restriction on the metric potentials, that is, on the shape function profile. Our approach is different. We take the conventional understanding of vanishing tidal forces as $\dfrac{\mathrm{d}\phi}{\mathrm{d}r} = 0$ and then postulate forms of the shape function with the desired properties for a viable WH. In Fig. 4, we plot the shape function $ b(r) $ along with the embedding diagram and embedded surface $ z(r) $ using $ b(r) = \dfrac{r_0^2}{r} $ and Eq. (31).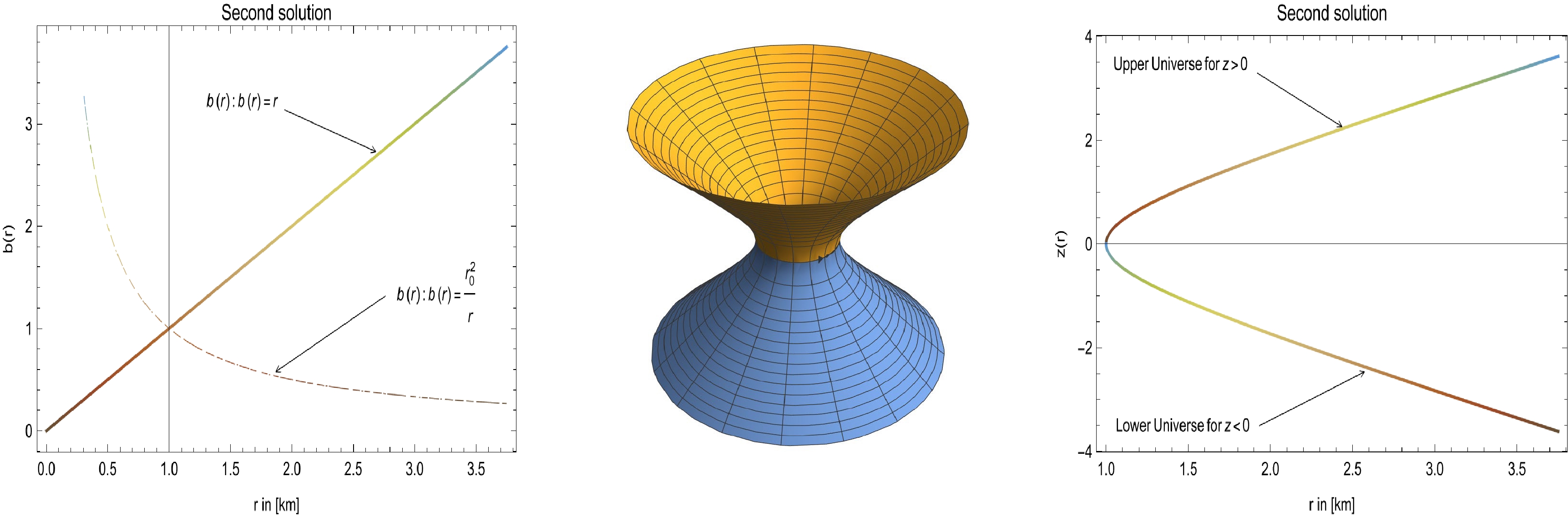

Figure 4.  (color online) Left panel: Behavior of $ b(r) = r $ (solid black), and other curves are plotted for $ b(r) $ given by $b(r) = {r_0^2}/{r}$ , which shows $ b(r) < r $. Middle panel: Using the shape function $b(r) = {r_0^2}/{r}$ and Eq. (31), we plot the embedded diagram, which provides valuable insights into the geometry and topology of the WH configurations. Right panel: Using the shape function $b(r) = {r_0^2}/{r}$ and Eq. (31), we plot the embedded surface $ z(r) $, which provides valuable insights into the geometric structure and characteristics of the embedded surface. In all cases, we consider $ \omega = 1 $, which reduces to a traceless EMT, with $ T = 0 $. See the text for specific choices of the considered parameters.

Considering Eqs. (12)–(14) with EoS (15), we obtain the following expressions:

Solving Eqs. (44)–(72), we obtain the expressions for $ p_r $ and $ p_t $ in terms of b and $ b^{\prime} $,

and substituting $ p_r $ and $ p_t $ into Eq. (73), we obtain the following relationship:

which may be integrated to yield the solution

where $ {\cal{A}} = \sqrt{\dfrac{(\beta +6 \pi ) r_0^2}{\beta +3 \pi }} $ , and $ c_1 $ and $ c_2 $ are integration constants, which, at the throat, reduce to

We must impose the condition $ \cos\left(c_1\right) >0 $ to ensure a regular solution. Thus, $ \Phi(r) $ is finite at the throat. Moreover, we know that the range of $ \cos(x) $ is $ -1\leqslant \cos(x) \leqslant 1 $, and $ \ln(x) $ exists only when $ x >0 $. Then, the proposed range of $0 < \cos (x) = \cos \left[ {{\cal{A}}}/{{(\sqrt{2} r_0)}} \cot ^{-1}\left( {r_0}/{\sqrt{r^2-r_0^2}} \right)-c_1 \right] \leqslant 1$ , for which $ \ln(x) $ is defined. If we consider the maximum value of $ \cos \left(x\right) = 1 $ , then $ \ln(x) = 0 $. Moreover, $\cot ^{-1}\left({r_0}/{\sqrt{r^2-r_0^2}}\right) \to \cot ^{-1}(0) = {\pi}/{2}$ as $ r\to \infty $. This gives $\ln\left[ \cos \left(\dfrac{\pi}{2} \dfrac{{\cal{A}}}{{\sqrt{2} r_0}} -c_1\right)\right]$ a finite value, as the range of $ \cos (x) $ is finite. Finally, we arrive at the conclusion that $ \Phi(r) $ given in Eq. (78) is finite as $ r\to \infty $ ; therefore, this solution now reflects a traversable WH.

Considering the redshift function (78) and inserting the field equations (74)–(75) into Eq. (15), we obtain

where $ {\cal{A}} = \sqrt{\dfrac{(\beta +6 \pi ) r_0^2}{\beta +3 \pi }} $ , and $\theta = \dfrac{1}{\sqrt{2} r_0}\bigg[\sqrt{2} r_0 c_1-{\cal{A}} \cot ^{-1} $ $ \bigg(\dfrac{r_0}{\sqrt{r^2-r_0^2}}\bigg)\bigg] $. In Fig. 5, we plot ρ, $ \rho+p_r $ , and $ \rho+p_t $. For this case, we plot a diagram considering different values of β. From Fig. 4, we see that the energy density and two components for $ \rho+p_r $ and $ \rho+p_t $ are negative outside the throat, i.e., $ r> r_0 = 1 $. This means that the NEC is always violated outside the throat radius for $ \beta > -3 \pi $. For the configurations with $ \beta < -6 \pi $, it is interesting that the WEC (and also the NEC) is satisfied, as shown in the right panel of Fig. 4. Note that $ -6 \pi<\beta < -3 \pi $ is not an allowable range for WH construction from the form of $ {\cal{A}} $.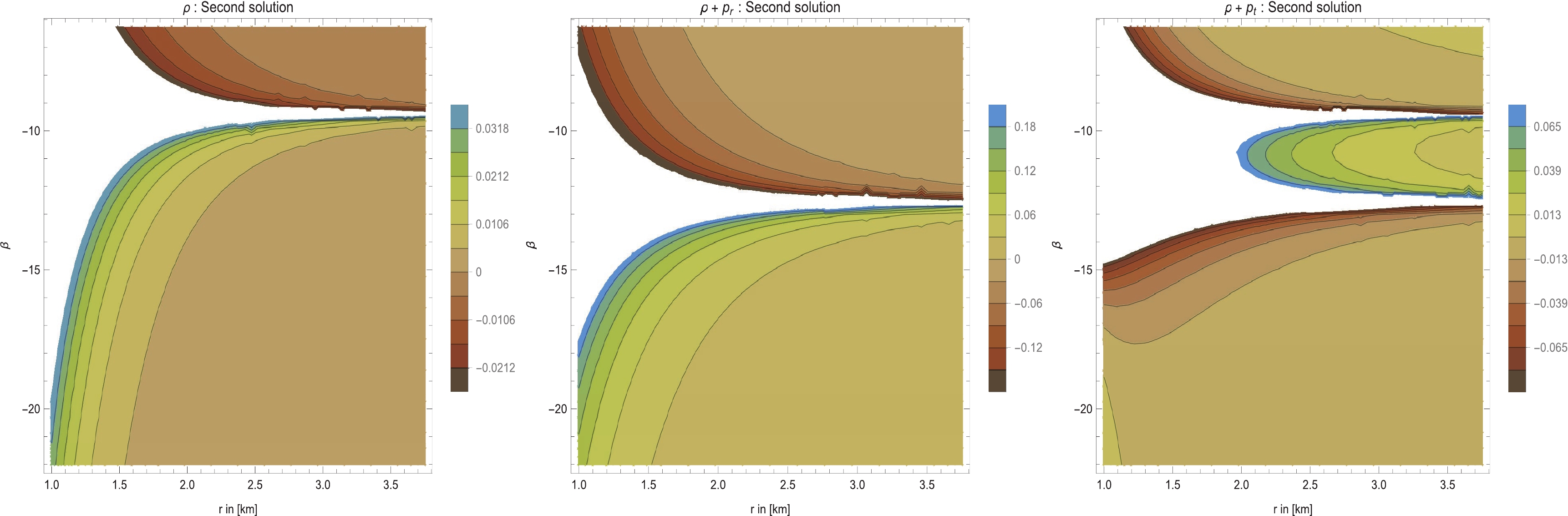

Figure 5.  (color online) Here, we consider a specific shape function $ b(r) = \dfrac{r_0^2}{r} $ and plots of the specific stress-energy profile for ρ (Left panel), $ \rho+p_r $ (Middle panel), and $ \rho+p_t $ (Right panel) versus r. In all cases, we consider $ \omega = 1 $, which reduces to a traceless EMT, with $ T = 0 $. See the text for specific choices of the considered parameters.

The NEC at the throat is given by

It is clear that $ (\rho+ p_{r,t})|_{r_0} <0 $ when $ \beta > -3 \pi $. Thus, the NEC is always violated for $ \beta > -3 \pi $. Conversely, we can verify that $ (\rho+ p_{r,t})|_{r_0} >0 $ for $ \beta < -6 \pi $. This would imply that ρ, $ \rho+p_r $, and $ \rho+p_t $ are always positive when $ \beta < -6 \pi $. As a closing remark, we state that realistic physical mechanisms such as the Casimir effect exist to support the geometry of traversable WHs. Therefore, exotic matter fields in the form of dark energy are not necessary. This is important because experimental support for dark energy is absent to date, whereas the Casimir phenomenon is a laboratory proven counter-intuitive effect.

We now consider the VIQ to evaluate the total amount of exotic matter. Using Eqs. (53) and (37), we can discuss the amount of exotic matter. The full analytical integration is not feasible because of the complicated nature of the expressions. Thus, we perform numerical integration for specific values of $ \beta = -2 \pi $ and $ c_1 = 1 $ with $ \tan \theta \approx \theta $ for small values of θ. Finally, we have

As a result, $ I_V \to 0 $ when $ a\to r_0 $. For greater transparency, we plot Fig. 6 for the range $ -3\pi<\beta<0 $ , where we find that $ \rho+p_r<0 $.

Figure 6.  (color online) Total amount of exotic matter, obtained using Eq. (53). This graph shows that $ I_V \to 0 $ when taking the limit $ a \to r_0 $.

Here, we consider the specific model for $ b(r) = r_0+\gamma r_0 \left(1-\dfrac{r_0}{r}\right) $ [99], where $ 0 < \gamma< 1 $ is of particular interest in generating WH solutions satisfying the condition $ b'(r_0)<1 $. In Fig. 7, we plot the shape function $ b(r) $ along with the embedding diagram and embedded surface $ z(r) $ corresponding to the above-mentioned shape function. Now, we take the field equations (12)–(14) with EoS (15) to obtain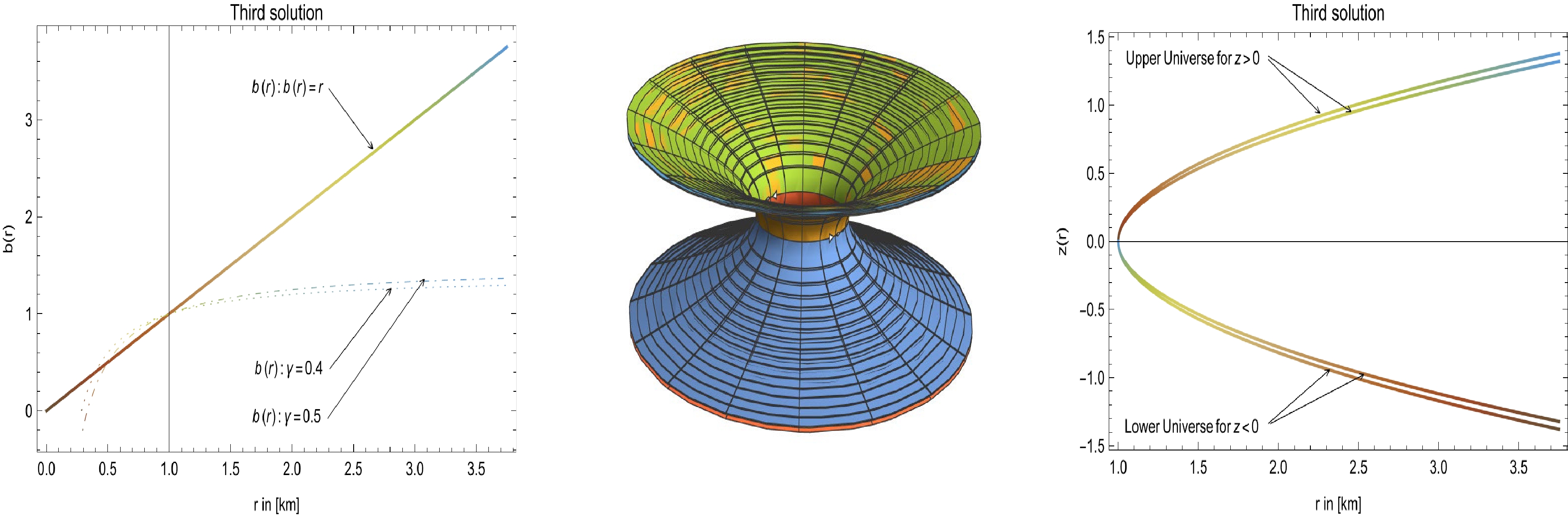

Figure 7.  (color online) Left panel: Behavior of $ b(r) = r $ (solid black), and other curves are plotted for $ b(r) $ given by $ b(r) = \dfrac{r_0^2}{r} $ , which shows $ b(r) < r $. Middle panel: Using the shape function $ b(r) = r_0+\gamma r_0 \left(1-\dfrac{r_0}{r}\right) $ and Eq. (31), we plot the embedded diagram, which provides valuable insights into the geometry and topology of the WH configurations. Right panel: Using the shape function $ b(r) = r_0+\gamma r_0 \left(1-\dfrac{r_0}{r}\right) $ and Eq. (31), we plot the embedded surface $ z(r) $, which provides valuable insights into the geometric structure and characteristics of the embedded surface. In all cases, we consider $ \omega = 1 $, which reduces to a traceless EMT, with $ T = 0 $. See the text for specific choices of the considered parameters.

Here, $ k(r) = 6 r (r-r_0) (r-\gamma r_0) $ , and $ l(r) = 3 r_0 (\gamma r+r-\gamma r_0) $. Eqs. (58) and (59) enable us to obtain explicit expressions for $ p_r $ and $ p_t $ in terms of b and $ b^{\prime} $,

Inserting $ p_r $ and $ p_t $ into Eq. (60), we obtain the following relationship:

which may be integrated to yield the solution

where $ {\cal{K}} = \sqrt{-\dfrac{(\beta +6 \pi ) \gamma r_0^2}{\beta +3 \pi }} $ , and $ k_1 $ and $ k_2 $ are integrating constants, which, at the throat, reduce to

At this juncture, we note a few considerations to maintain the regularity of the solution. We must impose $ \cos\left(k_1\right) >0 $ so that $ \Phi(r) $ is finite at the throat. Interestingly, we find that the present case is similar to our previous case; thus, we do not repeat our discussion here. We may conclude that $ \Phi(r) $ given in Eq. (64) is finite as $ r\to \infty $, which permits a horizonless solution.

Inserting the redshift function (64) into expressions (61)–(62) and using Eq. (15), we finally have

where $ {\cal{M}}(r) = \sqrt{r-\gamma r_0} {\cal{K}} \tan \left( k_1 - \dfrac{\sqrt{2} {\cal{K}} \tanh ^{-1} \left(\dfrac{\sqrt{\gamma } \sqrt{r - r_0}}{\sqrt{r-\gamma r_0}}\right)}{\sqrt{\gamma } r_0} \right) $. Having obtained the solutions for the matter fields, we plot ρ, $ \rho+p_r $ , and $ \rho+p_t $ in Fig. 8. It is important to emphasize that the region for the domain is $ -6 \pi<\beta < -3 \pi $ , where the WH is valid (see the expression for $ {\cal{K}} $). Note that $ \beta = -4\pi $ and $ \beta = -3 \pi $ are points of discontinuity where the solution is not valid. Fig. 8 depicts the behavior of the stress-energy components for $ -6 \pi<\beta < -3 \pi $ and $ \gamma = 0.5 $. Observing the figure, we find that ρ and $ \rho+p_r $ are negative, whereas $ \rho+p_t $ is positive outside the throat, i.e., $ r> r_0 = 1 $. This clearly indicates that the NEC is violated outside the throat radius within the specified region.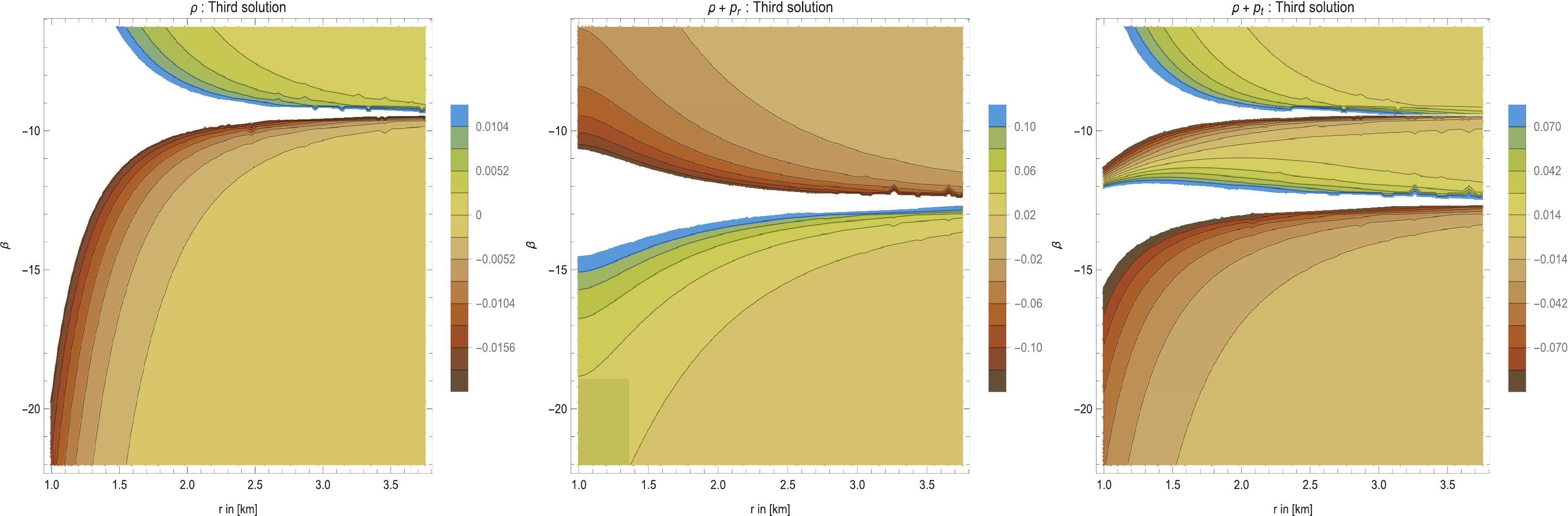

Figure 8.  (color online) Here, we consider a specific shape function $ b(r) = r_0+\gamma r_0 \left(1-\dfrac{r_0}{r}\right) $ and plots of the specific stress-energy profile for ρ (Left panel), $ \rho+p_r $ (Middle panel), and $ \rho+p_t $ (Right panel) versus r. In all cases, we consider $ \omega = 1 $, which reduces to a traceless EMT, with $ T = 0 $. See the text for specific choices of the considered parameters.

The NEC at the throat is given by

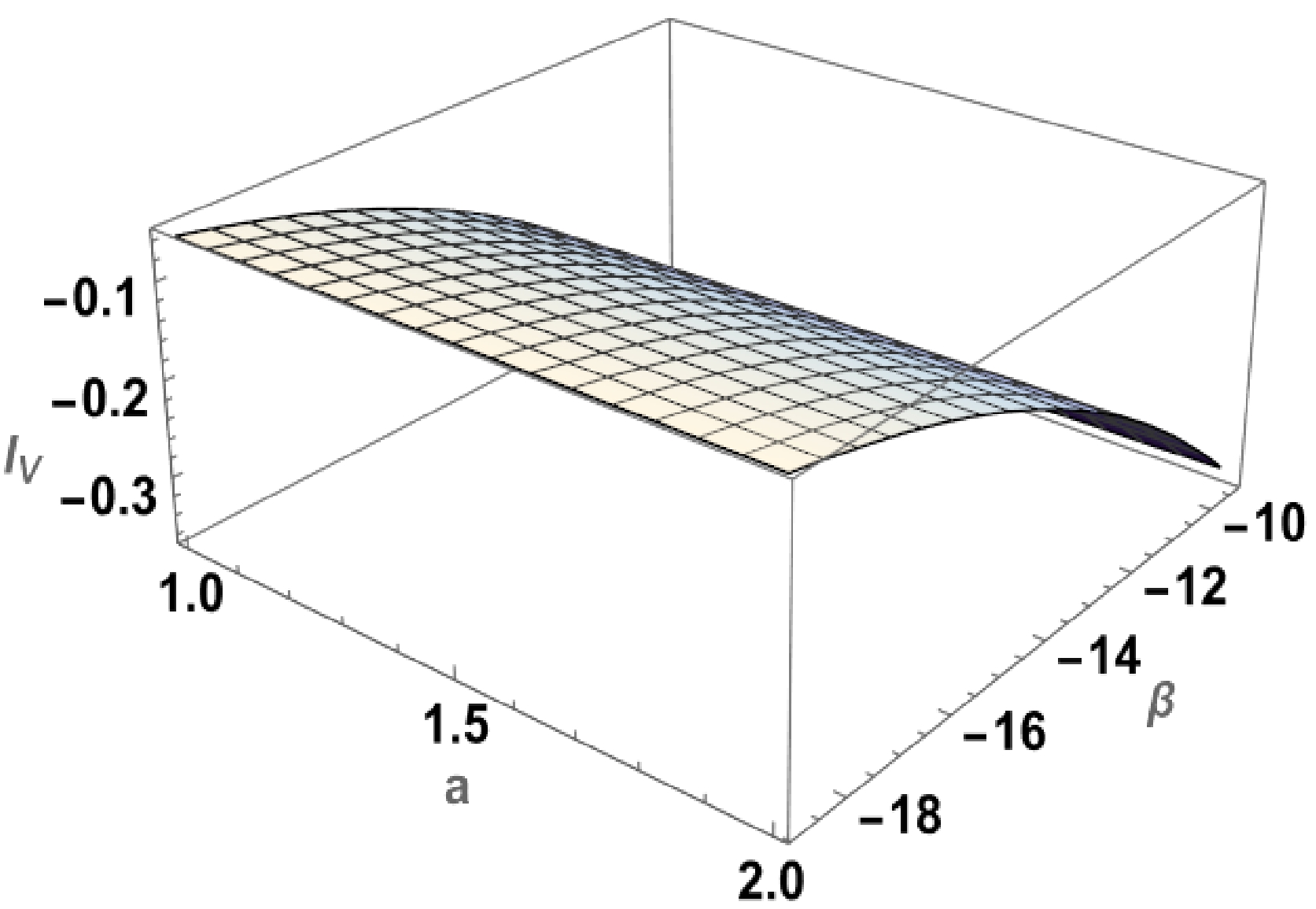
In this case, $ (\rho+ p_{r})|_{r_0} <0 $ and $ (\rho+ p_{t})|_{r_0} \lessgtr 0 $ when $ -4 \pi<\beta < -3 \pi $. Conversely, $ (\rho+ p_{r})|_{r_0} >0 $ and $(\rho+ p_{t})|_{r_0} < 0$ when $ -6 \pi<\beta < -4 \pi $. Thus, it is clear that the NEC is always violated.

Finally, we determine the total amount of exotic matter through the VIQ. Thus, using Eqs. (37) and (71), we obtain an approximate analytical solution for the definite integral with a cut-off of the stress-energy at $ a>r_0 $:

where $ l_1 = \sqrt{2}\sqrt{a-r_0} \sqrt{a-\gamma r_0} $ , and $ l_2 = \tanh ^{-1} \left(\dfrac{a-\sqrt{r-r_0} \sqrt{a-\gamma r_0}}{\sqrt{\gamma } r_0}\right) $. Figure 9 is illustrated for$ \gamma = 0.5 $, $ k_1 = 1 $ , and varying β in the domain $ -6 \pi<\beta < -3 \pi $ , where the WH solution is valid. Observing Fig. 9 , we may infer that the amount of exotic matter can be made arbitrarily small through a judicious choice of the parameter space.

Figure 9.  (color online) Total amount of exotic matter, obtained using Eq. (67). This figure clearly indicates that the total amount of exotic matter can be negligible depending on the model parameters.

To explore the deviation angle of photons from null geodesics, we begin by introducing a comprehensive line element that embodies both spherically symmetric and static characteristics [100, 101]. This line element can be represented as follows:

To characterize the trajectory of an object in free fall with respect to the underlying geometry [101], we make use of the geodesic equation. This equation establishes a relationship between the momentum one-forms of the object and the spacetime's geometry. It can be mathematically expressed as follows:

In this scenario, we assign the parameter λ to represent the affine parameter. It is important to emphasize that if the components of $ g_{\alpha\nu} $ do not vary with respect to $ x^\beta $ for a fixed index β, then $ p_\beta $ remains constant throughout the motion. By exclusively considering the equatorial slice with $ \theta = \pi/2 $, we discover that all the components $ g_{\alpha\beta} $ in Eq. (73) become independent of t, θ, and ϕ. As a result, we can identify the corresponding Killing vector fields $ \delta^{\mu}\alpha \partial\nu $ , with α as a cyclic coordinate. By designating the constants of motion as $ p_t $ and $ p_\phi $, we can delve into the analysis of the system's dynamics using the following expressions:

Here, E and L denote the energy and angular momentum of the photon, respectively. With this in mind, we can express the geodesic equation as

where the overdot notation represents differentiation with respect to the affine parameter λ. Continuing on from the previous analysis, we can straightforwardly obtain the radial null geodesic as

To provide a more precise formulation, we can express the equation for the photon trajectory in terms of the impact parameter $ \mu = L/E $ as

Now, let us consider a photon source with radius $ r_s $ that affects the underlying geometry. To determine the deflection angle of the photons, we must identify the conditions under which the photons can reach the surface. This occurs when a solution $ r_0 $ satisfies the conditions $ r_0 > r_s $ and $ \dot{r}^2 = 0 $, where $ r_0 $ represents the distance of closest approach or the turning point. In this scenario, the impact parameter can be expressed as

In the regime of weak gravity, it becomes apparent that $ \mu \approx \sqrt{{\cal{F}}(r_0)} $. Therefore, if a photon originates from the polar coordinate limit defined as $ \lim\limits_{r \rightarrow \infty} \left( r, -\dfrac{\pi}{2}-\dfrac{\alpha}{2} \right) $, passes through the turning point located at $ (r_0, 0) $, and approaches $ \lim\limits_{r \rightarrow \infty} \left( r, \dfrac{\pi}{2}+\dfrac{\alpha}{2} \right) $, we can define the deflection angle of the photon as α. This deflection angle, denoted by α, is dependent on $ r_0 $ [102] and can be explicitly derived from Eq. (79) as

For the chosen metric coefficients in the $ {\cal{WH}} $ geometry, we can now easily determine the deflection angle of photons in $ f(R, T) $ gravity by numerically integrating the formulas mentioned above, considering the shape functions specified by Eqs. b(r) = $r_0 \left(\dfrac{ 6\pi r+3 \pi r_0+ \beta r}{(\beta +9\pi)r }\right)^{{(3\pi+\beta)}/{(3\pi)}}$, $ b(r) = \dfrac{r_0^2}{r} $, and $ b(r) = r_0+ \gamma r_0 \left(1-\dfrac{r_0}{r}\right) $. Figure 10 shows the plots illustrating the phenomenon at hand. A negative deflection angle indicates the presence of repulsive gravity. To validate this phenomenon, we introduce the concept of the photon deflection angle on the WH. As stated in [103], in the presence of repulsive gravity acting on photons, the deflection angle becomes negative in the spacetime. Remarkably, the deflection angle consistently maintains negative values for all values of $ r_0 $ in the three solutions. This consistent negativity can be interpreted as a manifestation of the repulsive gravity effect.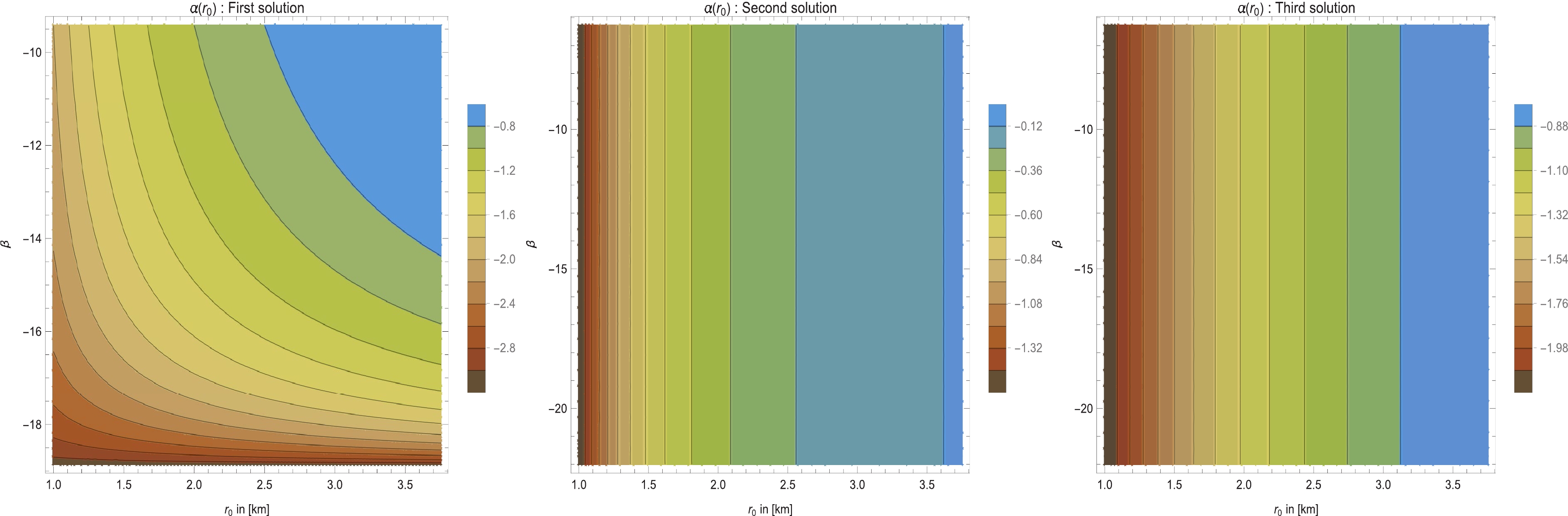

Figure 10.  (color online) Behavior of the numerical results of the photon deflection angle, represented by the quantity $ \alpha(r_0) $, for three solutions. These plots demonstrate the negative deflection angle, indicating the repulsive nature of gravity in the three solutions. In all cases, we consider $ \omega = 1 $, which reduces to a traceless EMT, with $ T = 0 $. See the text for specific choices of the considered parameters.

Invoking the Casimir effect along with suitable shape and redshift functions, we present complete analytical solutions for static and spherically symmetric asymptotically flat WH geometries in the background of $ f(R,T) $ theory. The novelty of our work lies in the use of the Casimir stress energy, which is known to produce negative density and is necessary for the emergence of WHs. The negative density causes a repulsive gravitational behavior, which sustains the opening of the WH throat. In contrast, most treatments of WHs rely on the negative density arising from exotic fluids such as dark energy. The Casimir effect has the advantage of being laboratory confirmed, whereas dark energy is a speculative entity currently lacking empirical observational evidence. Invoking the Casimir behavior in the study of WH geometry has attracted only limited attention historically. In our study, we adopt the approach of Kar and Sahadev [7], which to the best of our knowledge, has not been attempted before. A similar endeavor by Tripathi [97] utilized the quantum effect variation in density with plate-distance as well as considering the generalized uncertainty principle.

We elect to study $ f(R,T) $ gravity, which is a generalization of $ f(R) $ gravity such that the gravitational Lagrangian density depends on R (Ricci scalar) and T (stress-energy tensor). Part of the motivation for $ f(R,T) $ gravity is the coupling between geometry and matter, which has extensive applications in astrophysics and cosmology, and because this peculiarity has not featured in the literature on $ f(R, T) $ theory.

In the geometrical representation, we analyze different energy conditions and investigate the effects of the coupling constant β on the WH structure. At the outset, we show that a sustainable WH cannot be possible for $ \Phi^{\prime}(r) = 0 $ , thereby ruling out WHs with vanishing tidal forces as is the case in the standard theory. Subsequently, by considering $ \Phi(r) = \log \left(1+\dfrac{r_0}{r}\right) $, we show that viable WH solutions exist provided that the coupling parameter β is constrained as $ -6 \pi <\beta <-3 \pi $. In Fig. 1, we show that the shape function $ b(r) $ in Eq. (30) satisfies all the necessary requirements; however, the NEC is violated throughout the spacetime, and consequently, WEC violation also occurs. This is welcome in WH geometry and physics. Finally, we consider $ b(r) = \dfrac{r_0^2}{r} $ as a form function and derive the stress energy tensor components. In this process, the obtained redshift function $ \Phi(r) $ in Eq. (78) is finite everywhere. This is a clear indication that spacetime has no event horizons. Moreover, we show that the WEC is satisfied throughout the entire spacetime by considering a negative value of the coupling constant, $ \beta < -6 \pi $. In addition to our investigations into energy conditions, we also delve into the repulsive effect of gravity. Our findings reveal that the existence of repulsive gravity results in a negative deflection angle. To validate this phenomenon, we introduce the concept of the photon deflection angle on the WH. As documented in [103], when photons are subjected to repulsive gravity, this deflection angle becomes negative within the spacetime. Importantly, it is worth noting that the deflection angle consistently maintains negative values across all values of $ r_0 $ in the three solutions. This consistent negativity can be interpreted as a manifestation of the repulsive gravity effect.

This study shows that the Casimir stress energy is an ideal candidate for the study of WHs, and in future studies, we shall consider its effect in other modified gravitational field theories.

In accordance with the visiting associateship scheme, A. Pradhan is grateful to IUCAA, Pune, India, for providing support and facilities.