Polytropic gas cosmology and late-time acceleration

The accelerated expansion of the Universe, observed in the late 1990s through measurements of distant supernovae, presented a paradigm-shifting discovery in cosmology. This phenomenon, commonly known as the late-time acceleration, indicates that the Universe is expanding at an ever-increasing rate [1, 2]. Although the cause of this acceleration is still a mystery [3, 4], it is believed that the primary driving force could be a mysterious form of energy dominating gravity. This mysterious and pervasive form of energy is widely known as dark energy (DE).

The nature of DE and its implications for the fate of the Universe have become central topics of investigation in modern cosmology. The most important feature of this form of energy is its equation of state (EoS). The EoS parameter ($ w=p/\rho $, where p and ρ represent the pressure and energy density of the DE, respectively) plays a crucial role in characterizing the behavior of DE. The EoS parameter determines how the energy density of DE changes as the Universe expands. Different values of w correspond to different types of DE candidates, each with distinct properties.

The range of possible values for w allows us to explore various models of dark energy and their implications for the Universe. There are several candidates for DE discussed in the scientific literature. The simplest and most widely known candidate is the cosmological constant (Λ) [5, 6]. This corresponds to a constant value of the EoS parameter $ w = -1 $, meaning that the energy density remains constant as the Universe expands. The cosmological constant is consistent with the observed accelerated expansion but lacks a theoretical explanation for its value. Quintessence is a dynamical scalar field that pervades the Universe and has a varying EoS parameter [7−12]. It allows for a range of values for w between –1 and 1/3, representing different behaviors of DE. Quintessence models provide a framework for exploring the dynamics and evolution of DE. Phantom energy has an EoS parameter of $ w < -1 $. It exhibits even more rapid expansion than quintessence or a cosmological constant. Phantom energy models [13, 14] have intriguing implications, including the potential for a "Big Rip" scenario or its smoothing form [15, 16], where the Universe is torn apart in the future. Some theories propose modifications to the laws of gravity at cosmological scales to explain the accelerated expansion. These modifications can effectively mimic DE behavior without invoking a specific DE candidate. Examples include modified gravity theories like the Dvali-Gabadadze-Porrati (DGP) model or $ f(R) $ gravity. However, these are just a few examples of the many candidates for DE that have been proposed and studied in the scientific literature.

Another interesting candidate of DE is the Chaplygin gas, which attempts to explain both DE and dark matter within a unified framework [17−24]. Its EoS is different from the usual EoS for normal matter or DE, and it gives rise to some intriguing properties; for example, one of the remarkable features of Chaplygin gas is that it exhibits an attractive behavior at early times, similar to dark matter, and a repulsive behavior at late times, resembling dark energy. This duality allows Chaplygin gas to explain both the clustering properties of dark matter and the observed accelerated expansion of the Universe. The EoS parameter provides a powerful tool to characterize and differentiate between these candidates, allowing us to better understand the nature of DE and its role in shaping the evolution of the Universe.

By examining the theoretical foundations, observational evidence, and cosmological implications, we seek to shed light on the enigmatic properties of DE and explore the efficacy of another candidate of DE, polytropic gas EoS, in modeling late-time acceleration. Polytropic gas EoS [25] is an extension of the ideal gas law and has found widespread use in various branches of physics, including astrophysics and cosmology. The polytropic gas EoS relates pressure, density, and temperature for a given system, incorporating power-law relationships between these quantities. In the context of cosmological modeling, the polytropic gas EoS has garnered significant attention due to its ability to represent diverse DE models [26−29]. By applying suitable polytropic indices and parameterizations, the polytropic gas EoS can effectively capture the properties of different DE candidates, such as quintessence and phantom energy. This flexibility enables the polytropic gas EoS to provide a unified framework for studying various scenarios of late-time acceleration [30].

The polytropic gas EoS offers a powerful approach to model late-time acceleration in cosmology. By incorporating the polytropic gas EoS into the equations of motion and continuity of the Universe, it becomes possible to investigate the effects of different DE models on cosmic expansion. This modeling framework allows for the exploration of the parameter space of the polytropic indices and EoS parameters to accurately reproduce observational data. Furthermore, the polytropic gas EoS provides a means to understand the thermodynamic properties of dark energy and its interaction with other cosmic components, such as dark matter and baryonic matter [31]. By incorporating these interactions, cosmological models based on the polytropic gas EoS can shed light on the interplay between DE and other fundamental constituents of the Universe. The polytropic gas EoS emerges as a versatile modeling framework that can effectively capture the dynamics of different DE candidates. By leveraging the flexibility of the polytropic gas EoS, cosmologists can investigate the implications of various DE scenarios on the late-time acceleration of the Universe. This approach holds the potential to deepen our understanding of DE, its interaction with other cosmic components, and the ultimate fate of the Universe. Thus, we are interested in exploring the polytropic gas EoS in this work, and our main goal is to apply it to some observational datasets. To distinguish the cosmological behavior of the PDFM and ΛCDM models, we use two different diagnostic tools, namely, statefinder [32, 33] and $ O_m $ Diagnostic [34], which have been used in several recent works (e.g., see [35−37]).

The remainder of this paper is structured as follows: In Sec. II, we present a general overview of the PDFM. The methodology and observational data are presented in Sec. III. In Sec. IV, we check our model with $ H(z) $, type Ia supernovae, Gamma-Ray Bursts, and binned Quasars distance modulus datasets. The geometrical behaviour of the model is discussed through the cosmographic parameters, Statefinder Diagnostic, and $ O_m $ Diagnostic in Sec. V. Sec. VI discusses the information criteria. Finally, Sec. VII presents a conclusion.

In this section, we give a brief review of the generalized EoS that may unify cold dark matter and DE by combining a linear and polytropic EoS. Introduced in [38], the pressure of this fluid labeled $p_{f}$ is given by

where constants ω, B, and η characterise the model. In our setup, we assume that the energy density of this generalized fluid is a sum of the energy density of the cold dark matter, $\rho_{\rm cdm}$, and the energy density of DE, $\rho_{\rm de}$, i.e., $ \rho_{f}=\rho_{\text{cdm}}+\rho_{\text{de}} $, and its pressure $p_{f}=p_{\text{cdm}}+p_{\text{de}}=p_{\text{de}}$. In the literature, the linear part of Eq. (1) mimics the well-known EoS of radiation for $ \omega=1/3 $, pressureless dust for $ \omega=0 $, stiff matter for $ \omega=1 $, and cosmological constant for $ \omega=-1 $.

In what follows, we analyze the polytropic dark fluid model in the context of the FLRW with the metric given by

where $ k=1,0,-1 $ for a closed, flat, and open geometry, respectively. In this setup, the first Friedmann equation is

where $ \rho_i $ stands for the energy density of each component of the budget of the Universe, i.e., $ i=r $, b, and ${f}$ for radiation, baryon, and polytropic dark fluid, respectively. We use the standard convention $ a_0= 1 $, where the subscript $ 0 $ denotes the present time. In this paper, we consider that the energy density $\rho_{f}$ and pressure $p_{f}$ fulfill the EoS for a polytropic dark fluid model [25], i.e., we take $ \omega=0 $ in Eq. (1):

where $ B>0 $ and the polytropic index η are model constants. We consider that the polytropic fluid is a mixture of a non-interacting cold dark matter and DE density. Furthermore, we neglect the radiation part in our study as we are interested in late cosmology. Modern cosmological observations suggest a spatially flat Universe consistent with the cosmological principle. However, accurately determining cosmic curvature and understanding the FLRW metric have become crucial in contemporary cosmology [39−41], particularly due to the challenges of cosmic-curvature tension and possible deviations from General Relativity [42, 43]. Some recent progress made in these aspects can be found in the literature based on recent observations [44−46]. Therefore, in a flat Universe, the first Friedmann Eq. (3) becomes

where $ H=\dot{a}/a $ is the Hubble rate. Moreover, the energy densities and pressures of different species of the Universe fulfill the following energy conservation equations:

where the subscript i represents the polytropic fluid, i.e., cold dark matter, DE, and pressureless baryonic matter.

By using the dimensionless density parameters

one can rewrite the Friedmann equation as follows:

Substituting Eq. (4) into Eq. (6), the polytropic gas energy density in terms of the redshift, $ z=\dfrac{1}{a}-1 $, can be written as

where

and $\rho_{f_0}$ is the polytropic energy density at present time. Also, the energy density of the baryonic matter is

It is worth mentioning that the polytropic energy density in Eq. (10) provides a comprehensive picture of DM and DE. Indeed, Eq. (10) easily interpolates between a non-relativistic matter phase, $\rho_{f} \propto(1+z)^{3}$, in the past and a negative-pressure DE regime, $p_{f}=-\rho_{f}$, at late time. As a result, within the framework of the unified DM-DE scenario, the polytropic energy density may be rewritten as

By using Eqs. (6), (9), and (13), one can obtain the energy densities of CDM and DE, respectively, as follows:

Using Eqs. (7), (12), and (15), the Friedmann equation (Eq. (5)) becomes

In this section, we conduct a thorough comparison between PDFM's predictions and observational data. Our goal is to explore the constraints imposed on the model by utilizing two distinct observational datasets: the observational $ H(z) $ data (OHD), type Ia supernovae (SNIa), Gamma-Ray Bursts (GRBs), and binned Quasars (Q) distance modulus datasets. By comparing the model's predictions with these cosmological data, we can determine the best-fit values of three free parameters of PDFM, denoted as $\Omega_{{b0}}$, β, and η, with the present-day value of the Hubble function h in our analysis. To constrain the parameters of our cosmological model, we adopt a rigorous and widely-used approach based on Bayesian statistics. This technique involves the use of likelihood functions and the application of the Markov Chain Monte Carlo (MCMC) method. The Bayesian framework provides a robust framework for parameter estimation by quantifying the probability of obtaining a certain set of model parameters given the observational data.

In this section, we describe the methodology employed to determine the best-fit values of the four free parameters $\Omega_{{b0}}$, β, η, and $ H_{0} $ of the PDFM, which aims to unify dark matter and DE within a unified framework. MCMC is a powerful statistical technique that allows us to sample from complex and high-dimensional parameter spaces. It is particularly suited for exploring the parameter spaces of cosmological models and finding their best-fit values. In our study, we utilize MCMC to efficiently sample parameter spaces and estimate the posterior distribution of the model parameters given observational data. We use observational data, including OHD, SNIa, GRBs, and Q. These datasets provide valuable constraints on the expansion history and geometry of the Universe. The likelihood function is constructed based on the comparison between model predictions and the observational data. Assuming Gaussian errors for each dataset, the likelihood can be expressed as

where $ \theta = (\Omega_{{b0}}, \beta, \eta, {H_{0}}), $ represents the vector of model parameters, $ x_{\text{obs},i} $ is the observed value of the i-th data point, $ x_{\text{th},i}(\theta) $ is the theoretical prediction of the model, and $ \sigma_i $ is the standard deviation of the measurement. To ensure physically plausible values for model parameters, we impose informative prior distributions on the parameters. The priors encapsulate our prior knowledge or beliefs about parameter values before considering the observational data. The posterior distribution of model parameters is given by Bayes' theorem:

MCMC techniques are then employed to sample from the posterior distribution and explore the parameter space. The Markov chains converge to the regions of parameter space that best explain the observational data. To assess the goodness of fit and compare different models, we compute model likelihoods using the Bayesian evidence [47−50]. Model selection criteria, such as the Bayesian Information Criterion (BIC) [51] or Akaike Information Criterion (AIC) [52], are used to identify the most suitable model given the data.

In our analysis, we utilize thirty-one data points obtained through the OHD technique for determining the Hubble parameter. This method provides direct information about the Hubble function at various redshifts, extending up to $ z \lesssim 2 $. OHD data is favored for its reliability, relying on age differences between passively evolving galaxies originating at the same time but with slight redshift separations. This allows us to compute $ \Delta z / \Delta t $, making CC data preferable over absolute age determinations for galaxies [53]. The selected OHD data points are from independent sources [54−60], unaffected by the Cepheid distance scale or specific cosmological models. However, they do rely on robust stellar population synthesis techniques for modeling stellar ages (for more details, refer to [56, 58, 61−64] for analyses related to OHD systematics). We evaluate the goodness of fit using the $ \chi_{\rm CC}^{2} $ estimator:

where $ H\left(z_{i}, \theta\right) $ represents the theoretical Hubble parameter values at redshift $ z_{i} $ with model parameters denoted as θ. The observational data for the Hubble parameter at $ z_{i} $ is given by $ H_{\mathrm{obs}}\left(z_{i}\right) $, with an associated observational error of $ \sigma_{H}\left(z_{i}\right) $.

The Pantheon+ dataset is a compilation of observations of SNIa that have been recently released [65]. It consists of 1701 SNIa data points covering a redshift range from 0.001 to 2.3. SNIa observations have been instrumental in the discovery of the accelerating expansion of the Universe and are widely used to study the nature of the component driving this expansion. SNIa are incredibly luminous astrophysical objects and are considered to be standard candles, which means their intrinsic brightness can be used to measure relative distances. The Pantheon+ dataset provides valuable information for studying the nature of the accelerating Universe. The chi-square statistic is commonly used to compare observational data with theoretical models. In the case of the Pantheon+ dataset, the chi-square values are calculated using the following expression:

where $ \vec{D} $ represents the difference between the observed apparent magnitudes $ m_{Bi} $ of SNIa and the expected magnitudes given by the cosmological model. The term $ \mathbf{C}_{\text{Pantheon+}} $ denotes the covariance matrix provided with the Pantheon+ data, which includes both statistical and systematic uncertainties. The distance modulus $ \mu_{\text{model}} $ is a measure of the distance to an object, defined as

where $ D_L(z) $ represents the luminosity distance, which is calculated for a flat homogeneous and isotropic FLRW Universe as

The Pantheon+ dataset differs from the previous Pantheon sample as it breaks the degeneracy between the absolute magnitude M and Hubble constant $ H_0 $. This is achieved by rewriting the vector $ \vec{D} $ in terms of the distance moduli of SNIa in the Cepheid hosts. The distance moduli in the Cepheid hosts, denoted as $ \mu_i^{\text{Ceph}} $, are measured independently using Cepheid calibrators. This allows for the independent constraint of the absolute magnitude M. The modified vector $ \vec{D'} $ is defined as

With this modification, the chi-square equation for the Pantheon+ dataset can be rewritten as

Expanding our observational scope further, we introduce 24 binned quasar distance modulus data from [66] spanning a redshift range of $ 0.16<z<5.93 $ and a subset of 162 Gamma Ray Bursts (GRBs) [67] spanning a redshift range of $ 1.44<z<8.1 $. In this context, we define the $ \chi^2 $ function as

Here, $\mu_{g}$ denotes the vector encapsulating the differences between the observed and theoretical distance moduli for each individual GRB. Similarly, for our examination of 24 compact radio quasar observations [66] spanning redshifts in the range of $ 0.46\leq z\leq 2.76 $, we establish the $ \chi^2 $ function as

In this context, $\mu_{q}$ represents the vector capturing the disparities between the observed and theoretical distance moduli for each quasar. The total $ \chi^2 $ function is given by the sum of the individual contributions:

These $ \chi^2 $ functions provide a quantitative measure of the agreement between the observed data and theoretical predictions, allowing for the determination of the best-fit values for the model parameters. Figure 1 shows the constraints on the parameters of the Polytropic Model, with the 1σσ and 2σσ confidence contours. Table 1 provides the 95% confidence level constraints on the cosmological parameters for the Polytropic Model.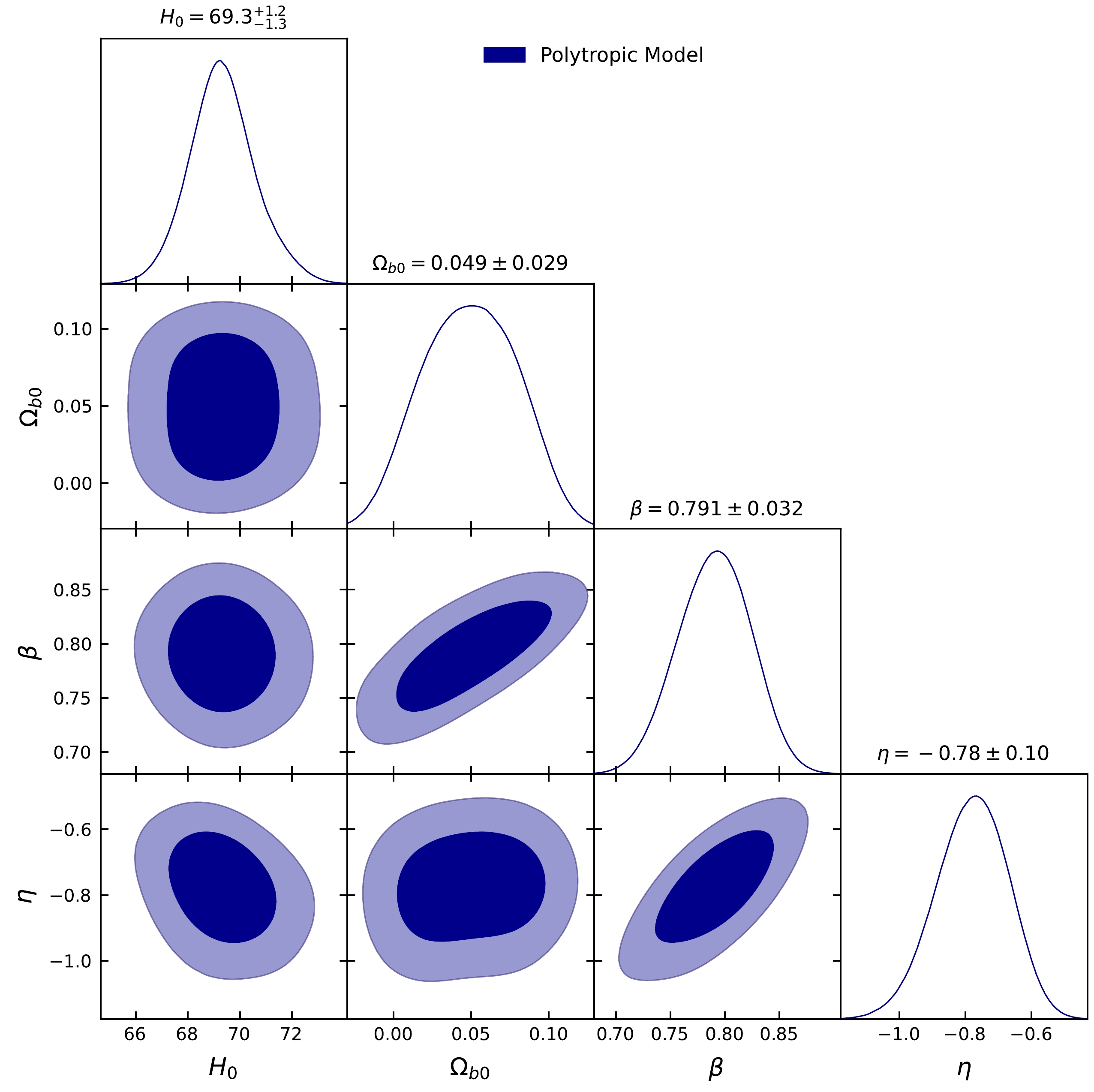

Figure 1.  (color online) T1D posterior distributions and 2D marginalized confidence contours at $ 1\sigma $ and $ 2\sigma $ for the PDFM using OHD, SNIa, GRB, and Q dataset.

MCMC Results
Model	Priors	Parameters	Best fit Value
ΛCDM Model	$ [50, 100] $	$ H_{0} $	$ 69.355 ^{\pm 1.045}_{\pm 2.591} $
PDFM Model	$ [50, 100] $	$ H_{0} $	$ 69.326 ^{\pm 1.108}_{\pm 2.203} $
	$ [0,0.15] $	$ \Omega_{\mathrm{b0}} $	$ 0.049^{\pm 0.033}_{\pm 0.048} $
	$ [0, 1] $	β	$ 0.790^{\pm 0.034}_{\pm 0.064} $
	$ [-1.,-0.5] $	η	$ -0.778^{\pm 0.105}_{\pm 0.242} $

Table 1.  Summary of the MCMC results using OHD, SNIa, GRB, and Q datasets.

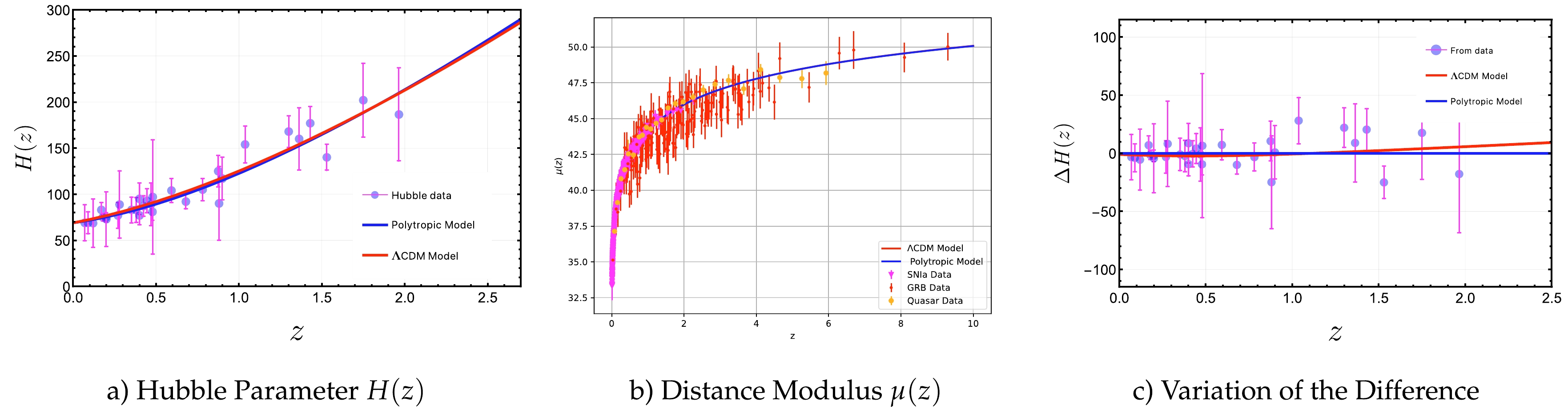
After determining the best-fit values of the free parameters of the PDFM model, it is essential to compare its predictions with observational data and the well-established ΛCDM paradigm. This step allows us to assess the model's viability and its ability to explain observed phenomena in the Universe. By contrasting the model predictions with observational data, we can evaluate the agreement and identify any discrepancies or deviations from the standard ΛCDM framework. Figure 2 illustrates the comparison between the PDFM and ΛCDM models using various observational datasets, including Observational Hubble Data, Type Ia Supernovae, Gamma-Ray Bursts, and Quasars. This comprehensive analysis enables us to validate or refine the proposed cosmological model and advance our understanding of the underlying physical processes driving the evolution of the Universe.

Figure 2.  (color online) Evolution of the Hubble parameter, distance modulus, variation of the difference, and apparent magnitude as functions of redshift for the PDFM and ΛCDM models.

We evaluate the compatibility of the PDFM, depicted by the red line, with a set of 36 OHD measurements represented by blue dots, accompanied by corresponding error bars illustrated by the pink line. As a point of reference, we include the well-established ΛCDM paradigm with $\Omega_{ {m0}}=$ 0.3 and $ \Omega_\Lambda = $ 0.7, indicated by a black dotted line. The comparative analysis is presented in Fig. 2(a), which provides crucial insights into the compatibility between PDFM and the dataset, as well as its alignment with the ΛCDM paradigm. The results of this analysis reveal a remarkable agreement between the PDFM model and the 36 measurements of OHD, as well as with the predictions of the ΛCDM paradigm. The PDFM model demonstrates a close alignment with the dataset, showcasing its ability to accurately reproduce the expansion history of the Universe, as inferred from the CC data. This compelling alignment further supports the validity and credibility of the PDFM model in explaining the observed cosmic evolution.

We have conducted a comprehensive comparison of the distance modulus function, $\mu(z)$, within the frameworks of the PDFM (blue line) and ΛCDM (red line) models. This comparison utilizes a dataset comprising 1071 SNIa measurements (magenta dots), 162 GRB measurements (red dots), and 24 binned Quasar data points (orange dots). The distance modulus function, a key quantity in cosmology, characterizes the apparent brightness of distant celestial objects, such as supernovae, enabling accurate distance estimations. In Fig. 2(b), the graphical representation demonstrates a remarkable agreement between the predictions of the PDFM model and the observational data from SNIa, GRB, and Quasar measurements, as well as with the predictions of the ΛCDM model. The close alignment of the PDFM model with the dataset suggests that it provides a robust fit for the various types of observational data and is consistent with the ΛCDM paradigm. The excellent agreement between the PDFM model and diverse observational data indicates that it is a viable alternative or complement to the ΛCDM model. This suggests that the PDFM model accurately describes cosmic expansion and the behavior of DE.

In Fig. 2(c), we present the relative differences between PDFM and the ΛCDM paradigm using 36 OHD measurements. The plot effectively illustrates the behavior of both models across a range of redshifts. Notably, for redshift values below $ z<0.5 $, both models exhibit remarkably similar behaviors. However, as redshift increases, subtle discrepancies become apparent between the two models. It is evident that these deviations become more pronounced beyond a critical redshift, approximately $ z\approx 2 $. The emergence of these variations at higher redshifts suggests the presence of distinctive features or alternative mechanisms at play within the framework of PDFM. Importantly, it should be emphasized that these discrepancies gradually diminish as one transitions to lower redshifts. This trend indicates a convergence between the two models as redshift values decrease, highlighting the intricate interplay and potential convergence of cosmic dynamics between PDFM and the ΛCDM paradigm.

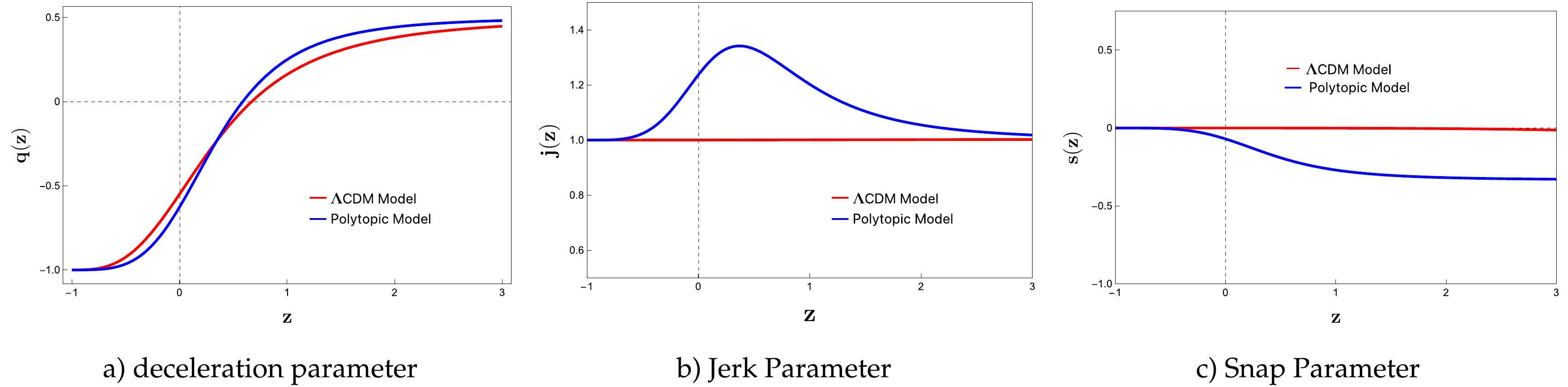
Cosmographic parameters, based on a series expansion of the scale factor [68−70], provide valuable insights into the Universe's behavior and evolution in the context of the PDFM. These parameters include Hubble parameter ($ H(z) $), deceleration parameter ($ q(z) $), Jerk parameter ($ j(z) $), and Snap parameter ($ s(z) $). By studying these parameters as functions of redshift, we can investigate the acceleration history and understand the interplay between the PDFM, baryonic matter, and other cosmic components. The cosmographic approach allows us to probe the Universe's dynamics, infer DE's nature, and explore the underlying physics driving cosmic acceleration. Figure 3 shows the evolution of the PDFM and ΛCDM models for $ q(z) $, $ j(z) $, and $ s(z) $. By analyzing these parameters and comparing them with observational data, we can gain insights into the Universe's nature and test the validity of the PDFM.

Figure 3.  (color online) Evolution of various cosmography parameters with respect to redshift (z). The red line represents the ΛCDM model, while the blue line represents the PDFM.

The deceleration parameter, $ q(z) $, characterizes the Universe's expansion dynamics, providing information on the rate of change of the expansion with time. It is defined as

where $ H(z) $ is the Hubble parameter and $ \dot{H}(z) $ is the derivative of the Hubble parameter with respect to cosmic time. The deceleration parameter classifies the expansion behavior: $ q(z) > 0 $ indicates decelerated expansion, dominated by matter's gravitational pull; $ q(z) < 0 $ indicates accelerated expansion, suggesting DE's presence; and $ q(z) = 0 $ marks a transition between deceleration and acceleration. Studying $ q(z) $ helps understand the dynamic Universe, the interplay between components, and the influence of polytropic dark fluid and baryonic matter on cosmic evolution. Figure 3(a) compares the deceleration parameter (q) between the PDFM and ΛCDM models across different cosmological epochs, represented by redshift (z). At high redshifts, the models diverge, with the ΛCDM model predicting $ q \approx 0.468 $ and PDFM predicting $ q \approx 0.487 $. As z approaches 0 (the present day), the difference between the models diminishes. The PDFM predicts $ q \approx -0.542 $, indicating accelerated expansion, while the ΛCDM model predicts $ q \approx -0.582 $, suggesting slightly slower acceleration. At $ z = -1 $, both models converge to a de Sitter phase with $ q = -1 $. The transitional redshift ($ z_{tr} $) where q crosses zero differs slightly between the models, with the PDFM predicting $z_{\rm tr} \approx 0.652$ and the ΛCDM model predicting $z_{\rm tr} \approx 0.732$. This suggests that the PDFM predicts a slightly earlier transition to an accelerating Universe.

The jerk parameter, j, generalizes familiar cosmological parameters like the scale factor $ a(t) $ and deceleration parameter q. Its significance lies in characterizing cosmic dynamics beyond conventional parameters. Mathematically, j is expressed as

The jerk parameter provides valuable insights into cosmic evolution, distinguishing between DE proposals and connecting them to conventional Universe models. A specific value of j links different DE hypotheses to the standard ΛCDM model, e.g., $ j = 1 $ corresponds to the flat ΛCDM model. Understanding j is crucial for exploring cosmic expansion dynamics and transitions. Figure 3(b) depicts the redshift dependence of the jerk parameter (j). Notably, the PDFM predicts a higher value of $ j \approx 1.073 $, exceeding the ΛCDM model's value of $ j = 1 $. As the Universe evolves, the jerk parameter increases, reaching a present-day value of $ j_0 \approx 1.202 $. In the future, the jerk parameter of the proposed model converges towards $ j \approx 1 $, aligning with the jerk value of the ΛCDM model. This convergence suggests that the proposed model and standard ΛCDM model will exhibit similar cosmic evolution in the long term.

The snap parameter, also known as "jounce," offers a deeper understanding of cosmic dynamics, providing insights beyond traditional parameters. This dimensionless parameter, denoted as s, is derived from the fourth time derivative of the expansion factor $ a(t) $. Mathematically, it is defined as

Notably, in the context of the ΛCDM model, the snap parameter takes on a specific value: $ s = 0 $. Figure 3(c) illustrates the evolution of the snap parameter (s) with redshift (z) in the PDFM. At high redshift, $ s \approx -0.441 $, decreasing to $ s_0 \approx -0.1455 $ at present day. In the future, the PDFM predicts $ s \approx 0 $, converging with the ΛCDM model. This convergence implies a long-term Universe with near-zero curvature, where the fourth derivative of the scale factor approaches a constant value, indicating a stable and nearly flat Universe.

The Statefinder and $ O_{m} $ diagnostic tests are vital for distinguishing between different DE models and understanding cosmic evolution. Figure 4 shows the evolution of the Statefinder pair and $ O_{m} $ for the PDFM model, highlighting its dynamic behavior.

Figure 4.  (color online) Evolution of the Statefinder and $ O_{m} $ diagnostic profiles in the PDFM represented by the blue lines.

The statefinder diagnostic pair $ {s, j} $ is a powerful tool for investigating DE models and understanding their nature based on higher-order derivatives of the scale factor [71]. These dimensionless parameters provide a model-independent way to analyze cosmic characteristics of DE. The statefinder pair can be computed by

Specific ${j, \;s}$ pairs have well-known interpretations in standard DE models. For example, $ {j, s} = {1, 0} $ corresponds to the ΛCDM model, while $ {j, s} = {1, 1} $ corresponds to the SCDM model. The $ j-s $ plane can be divided into regions representing distinct DE models, such as quintessence-like ($ s > 0 $) and phantom-like ($ s < 0 $) models. Deviations from $ {j, s} = {1, 0} $ can indicate an evolutionary process from phantom-like to quintessence-like behavior. Similarly, specific combinations of the deceleration parameter q and statefinder parameter j are associated with well-known models, such as ${q, \;j} = {-0.5,\; 1}$ for the ΛCDM model, ${q, \;j} = {0.5,\; 1}$ for the SCDM model, and ${q, \;j} = {-1, \;1}$ for the de Sitter point. Figure 4(b) illustrates the evolution of the ${s,\; j}$ profile. In the $ {s, j} $ plane, the PDFM model initially predicts the values in the ranges $ j > 1 $ and $ s < 0 $, corresponding to Chaplygin gas. This suggests a potential variability in the EoS for DE, indicating a dynamic rather than static nature. Ultimately, the PDFM model converges to the fixed point corresponding to the ΛCDM model. Figure 4(b) also illustrates the evolution of the $ {q, j} $ profile, which reveals that the PDFM model initially emerges from the Standard Cold Dark Matter (SCDM) point, corresponding to the coordinates $ (0.5, 1) $ in the $ {q, j} $ plane. As the PDFM model evolves, the $ {q, j} $ profile ultimately converges to the de Sitter point at $ (-1, 1) $ in the $ {q, j} $ plane, representing a Universe entirely dominated by a cosmological constant or a DE component with equivalent properties, characterized by a constant expansion rate.

In our research, we employ a robust DE diagnostic called the $O_{m}$ diagnostic, originally introduced by [34]. This diagnostic is particularly noteworthy for its simplicity, relying solely on the directly measurable Hubble parameter $H(z)$ obtained from observations. The $O_{m}$ diagnostic serves as a valuable tool for distinguishing among different cosmological scenarios, specifically discerning the cosmological constant indicative of a standard ΛCDM model.

where $w_0 = -1$ implies ΛCDM with $O_{m} = \Omega_{m0}$. Meanwhile, $w_0 > -1$ (or $w_0 < -1$) implies quintessence (or phantom) scenarios with $O_{m} > \Omega_{m0}$ (or $O_{m} < \Omega_{m0}$) [72]. The evolution of the matter density parameter, $ \Omega_m $, is illustrated in Fig. 4(c). At high redshift, the value of $ \Omega_m $ exceeds $ \Omega_{m0} $, indicating that the PDFM model is situated in the quintessential field. As redshift decreases, $ \Omega_m $ falls below $ \Omega_{m0} $, exhibiting phantom behavior.

To assess the viability of any model, a thorough understanding of information criteria (IC) is essential. The AIC [52, 73−76] is commonly employed as a general IC tool. The AIC serves as an approximate measure of the Kullback-Leibler information divergence and asymptotically provides an unbiased estimator of this divergence. The AIC for Gaussian estimation is given by $\text{AIC}= -2\ln ({\cal L}_{\text{max}})+2\kappa+\dfrac{2\kappa(\kappa+1)}{N-\kappa-1}$, where $ {\cal L}_{\text{max}} $ denotes the maximum likelihood function, κ represents the total number of free parameters in the model, and N is the total number of data points used. As the assumption is often $ N\gg 1 $ for the models considered, the formula simplifies to the original AIC form, $\text{AIC}= -2\ln ({\cal L}_{\text{max}})+2\kappa$. When comparing multiple models, the differences in IC values can be quantified as $\triangle\text{AIC}= \text{AIC}_{\text{PDEM Model}}-\text{AIC}_{\Lambda\text{CDM Model}}= \triangle\chi^{2}_{\text{min}}+ 2\triangle\kappa$. The range of $ \triangle\text{AIC} $ that is considered more favorable is $ (0,2) $. A less favorable range of $ \triangle\text{AIC} $ is $ (4,7) $, while values exceeding $ \triangle\text{AIC}>10 $ provide less support for the model. In addition to the AIC, the $\rm BIC$ [51, 77, 78] also contributes to model selection. Like the AIC, the $\rm BIC$ considers the trade-off between goodness-of-fit and model complexity. However, the $\rm BIC$ incorporates a stronger penalty for models with more parameters. This promotes the selection of simpler models, helping to guard against overfitting. In the context of $\Delta\rm BIC$, the similar principles apply compared with $\Delta\rm AIC$. A lower $\Delta\rm BIC$ indicates stronger support for a particular model, and the magnitude of the difference is informative. Based on the values presented in Table 2, we can provide a comprehensive comparison between the Polytropic Model and the ΛCDM model. For the ΛCDM model, $ \chi^2_{\text{min}} $ is 1229.75 with a $ \chi^2_{\text{red}} $ of 0.976. Its AIC is 1235.75, and because this model serves as the reference, both $\Delta\rm AIC$ and $\Delta\rm BIC$ are 0. The BIC for ΛCDM is 1251.18. The PDFM model shows a slightly lower $ \chi^2_{\text{min}} $ of 1228.82 with the same $ \chi^2_{\text{red}} $ value of 0.976, suggesting a comparable fit quality to ΛCDM. However, its AIC is slightly higher at 1236.82, resulting in a $\Delta\rm AIC$ of 1.07, indicating that PDFM is still strongly supported but slightly less so than ΛCDM. The BIC for PDFM is 1257.39, leading to a $\Delta\rm BIC$ of 6.21, which suggests that PDFM is moderately disfavored compared to ΛCDM when penalizing for model complexity.

Model	$\chi_{\min}^{2}$	$\chi_{\rm red}^{2}$	$\rm AIC $	$ \Delta\rm AIC $	$\rm BIC $	$ \Delta\rm BIC $
ΛCDM	1229.75	0.976	1235.75	0	1251.18	0
PDFM	1228.82	0.976	1236.82	1.07	1257.39	6.21

Table 2.  Summary of $ {\chi_{\text{min}}^2} $, $ \chi_{\text {red }}^2 $, $\rm A I C $, $\triangle\text{AIC}, \rm BIC, \triangle\text{BIC}$.

In this paper, we introduced the PDFM, a novel approach that unifies cold dark matter and DE within a single, versatile framework. This model is characterized by four parameters: the present-day Hubble parameter $ H_0 $, the baryon density parameter $ \Omega_{b0} $, and two additional constants β and η. By applying the PDFM to the FLRW metric, we derive expressions for the energy densities, pressures, and the DE EoS. Our analysis reveals that the PDFM can smoothly transition between different cosmic epochs, from radiation-like behavior to late-time acceleration. To validate the model, we employed MCMC analysis to constrain the parameters using a diverse range of observational datasets, including OHD, SNIa, GRB, and quasars. Our results show that the best-fit values for the PDFM model are $ H_0 = 69.326 ^{\pm 1.108}{\pm 2.203} $, $\Omega{b0} = 0.049^{\pm 0.033}\pm {0.048}$, $ \beta = 0.790^{\pm 0.034}{\pm 0.064} $, and $\eta = -0.778^{\pm 0.105}_{\pm 0.242}$. The corresponding confidence contours are presented in Fig. 1. Our analysis demonstrates that the PDFM model provides an excellent fit to the observational data, with a close alignment with the ΛCDM paradigm, particularly at low redshifts. This suggests that the PDFM model is a viable alternative or complement to the standard model of cosmology. The PDFM model exhibits a rich and complex cosmological evolution, with distinct features that differentiate it from the standard ΛCDM model. The deceleration, jerk, and snap parameters all exhibit unique behaviors, indicating a dynamic and evolving DE component. The PDFM model predicts a slightly earlier transition to an accelerating Universe, with a higher value of the jerk parameter and lower value of the snap parameter at present day. The $ s-j $ and $ q-j $ profiles reveal a fascinating evolution, with the PDFM model initially exhibiting characteristics of Chaplygin gas and ultimately converging to the fixed point corresponding to the ΛCDM model. This convergence suggests that the PDFM model will exhibit similar cosmic evolution to the standard model in the long term, with a near-zero curvature and a stable, nearly flat Universe. The $ O_{m} $ diagnostic test demonstrates that the PDFM model exhibits a transition from a quintessential to phantom regime, highlighting its complex and dynamic characteristics. A comparative analysis between the ΛCDM and PDFM models reveals that both models offer a similar fit to the observational data, as indicated by their close $ \chi^2_{\min} $ and $ \chi^2_{\text{red}} $ values. However, the ΛCDM model is favored due to its lower AIC and BIC values. The ΔAIC of 1.07 for the PDFM model suggests it is still strongly supported but slightly less so than ΛCDM. Meanwhile, the ΔBIC of 6.21 for PDFM indicates moderate disfavor when model complexity is considered. Therefore, ΛCDM remains the preferred model, balancing goodness of fit and simplicity more effectively. The PDFM model provides a novel approach to unifying cold dark matter and DE within a single framework, offering a more comprehensive understanding of the Universe's evolution. The PDFM model exhibits a dynamic and evolving DE component, which can help explain the observed acceleration of the Universe's expansion. The PDFM model provides a viable alternative or complement to the standard ΛCDM model, offering a new perspective on the Universe's evolution and fate. The PDFM model predicts a rich and complex cosmological evolution, with distinct features that differentiate it from the standard ΛCDM model. The PDFM model's dynamic DE component can provide insights into the nature of DE, which remains one of the biggest mysteries in modern cosmology. The PDFM model aims to address the limitations of the standard ΛCDM model, which has been shown to have some inconsistencies with observational data.