-
The LIGO and Virgo observations, as well as the M87
$ ^* $ black hole shadow captured by Event Horizon Telescope, have proven the existence of black holes [1−5]. Since then, black holes and their properties have become more relevant and fascinating subjects among researchers. Hawking temperature is a key concept in black hole thermodynamics and is of significance to understand the nature of black holes. Hawking [6, 7] proposed thermal radiation for studies on the quantum effects near the event horizon of black holes. Several methods for calculation of the Hawking temperature of black holes have been reported [8−11]. The semiclassical tunneling method proposed by Kraus, Parikh, and Wilczek [12−15] is widely used to evaluate the Hawking temperature for different types of black holes. In these studies, the radial null geodesic method has been used to derive the Hawking temperature in accordance with the semiclassical Wentzel–Kramers–Brillouin (WKB) approximation. Another tunneling method to derive the Hawking temperature is the Hamilton-Jacobi method [16], which is an extension of the complex path analysis reported by Padmanabhan et al. [17−19]. Remarkable results were obtained using this technique [20−25]. The tunneling probability has been corrected after consideration of the effects of backreaction and self-gravitation to evaluate the Hawking temperature and semiclassical black hole entropy [26, 27]. The effects of the generalized uncertainty principle (GUP) in the tunneling formalism for Hawking radiation have been extensively studied [28−37], and the quantum corrected Hawking temperature has been calculated.According to string theory and quantum gravity theory, the Lorentz invariance, which is a fundamental principle in physics, is broken down in the high-energy case [38−40]. The Lorentz dispersion relation is required to be modified in the high-energy case. The magnitude of this correction term shoud be in Planck scale [41−43]. Based on the Lorentz invariance violation (LIV), the Klein-Gordon and Dirac equations are required to be modified for the curved spacetime [44−47]. This leads to corrections of physical quantities such as black hole quantum tunneling radiation, temperature, entropy, and other thermodynamic quantities. Thus, the tunneling radiation of bosons and fermions under LIV is a promising area of research. In the last few years, based on LIV modification, many researchers have studied the corrected tunneling radiation for different types of black holes [48−56].
Hawking and Page [57] discovered a phase transition between the Schwarzschild-anti-de Sitter (SAdS) black hole and thermal AdS space. Chamblin et al. [58] investigated the first-order phase transition in Reissner-Nordstrom-AdS (RNAdS) black holes and explored the analogy of the phase transition to a van der Waals liquid-gas system in both canonical and grand canonical ensembles. Further, treating the cosmological constant as a thermodynamic pressure
$P=-{\Lambda}/({8 \pi})$ and its conjugate quantity as a thermodynamical volume, the phase transitions and critical behaviors of a RNAdS black hole in an extended phase space have been studied [59−61]. These phase transitions of the RNAdS black hole in the extended phase space are similar to the van der Waals liquid-gas system's phase transitions. Moreover, the critical exponents are the same as those of the van der Waals liquid-gas system. The$ P-V $ criticality of black holes in different modified theories of gravitation has been extensively studied [62−68]. The van der Waals liquid-gas system analogous to the$ P-v $ criticality of a charged dynamical (Vaidya) AdS black hole, including the equation of state and critical exponents, has also been studied [69]. Further, a van der Waals-like liquid-gas phase transition has been observed in the$ T-S $ plane of the black hole [70].For the van der Waals liquid-gas system, above the critical temperature
$ T_c $ , the isothermal curve shows a similar behavior to the experimental results. However, below$ T_c $ , there exists an oscillating region, which violates the condition of stable equilibrium. The theoretical prediction and experimental results are reconciled by substituting the oscillating part of the isotherm with a horizontal isobar that satisfies the Maxwell's equal area law. The Maxwell's equal area law has been studied [60, 71−73] in the$ P-v $ plane. Further, the construction of the Maxwell's equal area law has been extended in the$ P-V $ and$ T-S $ planes [74−78]. However, no research has been carried out on the construction of a Maxwell's equal area law under LIV modification. Our study aims to construct a Maxwell's equal area law under LIV for a Vaidya-Bonner-de Sitter (VBdS) black hole in an extended phase space.The correction of quantum tunneling radiation of fermions from the VBdS black hole induced by LIV is presented in Section II. In Section III, we study the Maxwell equal area law of the VBdS black hole in the extended phase space and obtain the positions of phase transition under LIV modification for different conjugate variables
$ P-v $ ,$ P-V $ , and$ T-S $ . In Section IV, under LIV modification, we present the entropy correction and calculate the modified Helmholtz free energy, internal energy, and enthalpy. In Section V, the stability of the VBdS black hole under LIV is discussed through Gibbs free energy, heat capacity, and Hessian matrix. The last section presents the conclusions. -
The metric of the nonstationary VBdS black hole in an advanced Eddington-Finkelstein coordinate system
$ (v, r, \theta, \phi) $ is defined by [79]$ \begin{aligned}[b] {\rm d} s^2 =\; &-\bigg(1-\frac{2M}{r} + \frac{Q^2}{r^2}-\frac{\Lambda}{3}r^2\bigg){\rm d}v^2 + 2 {\rm d}v \; {\rm d}r \cr &+ r^2({\rm d}\theta^2 + \sin^2\theta {\rm d}\phi^2), \end{aligned} $

(1) where v indicates the Eddington time,
$ M=M(v) $ and$ Q=Q(v) $ are the mass and charge of the black hole, respectively, and Λ is the cosmological constant. The four vector electromagnetic potentials$ A_{\mu} $ of the VBdS black hole are$A_{\mu}=\Big(\dfrac{Q}{r}, 0, 0, 0\Big)$ . The nonzero contravariant components of the VBdS black hole are$ \begin{aligned}[b] g^{11} =\;& \bigg(1-\frac{2M}{r} + \frac{Q^2}{r^2}-\frac{\Lambda}{3}r^2\bigg), g^{10} = g^{01}=1,\\ g^{22} =\;& \frac{1}{r^2},\, g^{33} = \frac{1}{r^2\sin^2\theta}. \end{aligned} $

(2) As the space-time represented by Eq. (1) is spherically symmetric, the event horizon is necessarily a null surface
$ r_h=r_h(v) $ that satisfies the null hypersurface condition:$ g^{ab}\frac{\partial F}{\partial x^a}\frac{\partial F}{\partial x^b}=0, $

(3) with
$ F(v,r)=0 $ . Using Eq. (1) in Eq. (3), the horizon equation and mass of the VBdS black hole are$ 1-\frac{2M}{r_h}+\frac{Q^2}{r_h^2}-\frac{\Lambda}{3}r_h^2 -2\dot{r_h}=0 $

(4) and
$ M=\frac{r_h}{2}+ \frac{Q^2}{2r_h} -r_h\dot{r}_h - \frac{\Lambda r_h^3}{6} $

(5) respectively, where
$\dot{r}_h = \dfrac{{\rm d} r_h}{{\rm d}v}.$ -
Regarding string theory and quantum gravity, the following relation has been reported [41, 80−82]:
$ \tilde{P}_0^2 = \tilde{P}^2 + m^2-(\lambda \tilde{P}_0)^i \tilde{P}^2, $

(6) where
$ \tilde{P} $ and$ \tilde{P}_0 $ represent the momentum and energy of a particle with a static mass of m, respectively. The constant term λ is in the magnitude of Planck scale, which is determined from the LIV theory by Eq. (6). The value of i is unity in the Liouville string theory. A modified form of the Dirac equation is determined by Eq. (6) for$ i=2 $ [43]. The Rarita-Schwinger-Hamilton-Jacobi equation is [48]$ \begin{aligned}[b] & g^{\mu\nu}(\partial_\mu \Psi + eA_\mu)(\partial_\nu \Psi + eA_\nu) + m^2 - 2\lambda m (\partial_v \Psi + eA_0) \\ & g^{0i}\partial_i \Psi -\lambda^2[(\partial_v \Psi + eA_0)g^{0j}\partial_j \Psi]^2 = 0, \end{aligned} $

(7) where
$ \mu,\nu = 0,1,2,3 $ and$ i,j=1,2,3 $ . The action of the fermion can be obtained by Eq. (7), and the corresponding modified Hawking temperature of the VBdS black hole can be calculated. Eq. (7) is a highly accurate dynamic equation due to the presence of the term$ O(\lambda^2) $ and involvement of LIV. Using Eq. (2) in Eq. (7), we obtain$ \begin{aligned}[b] &\frac{\Delta}{r^2}\bigg(\frac{\partial \Psi}{\partial r}\bigg)^2 + \frac{1}{r^2}\bigg(\frac{\partial \Psi}{\partial \theta}\bigg)^2 + \frac{1}{r^2\sin^2\theta}\bigg(\frac{\partial \Psi}{\partial \phi}\bigg)^2 \\ & \;\; + 2\bigg(\frac{\partial \Psi}{\partial v} + eA_0\bigg) \bigg(\frac{\partial \Psi}{\partial r}\bigg) -2\lambda m \bigg(\frac{\partial \Psi}{\partial v} + eA_0\bigg)\bigg(\frac{\partial \Psi}{\partial r}\bigg) \\ &\;\; -\lambda^2\bigg(\frac{\partial \Psi}{\partial v} + eA_0\bigg)^2\bigg(\frac{\partial \Psi}{\partial r}\bigg)^2 = 0, \end{aligned} $

(8) where
$ \Delta=r^2-2Mr + Q^2- \dfrac{\Lambda}{3}r^4. $ As the action Ψ involved in the above equation is a function of the coordinates$ v, r, \theta, \phi, $ the action Ψ can be derived by using the tortoise coordinate transformation. Therefore, the tortoise coordinate transformation is defined by$ \begin{aligned}[b] r_* =\;& r+\frac{1}{2\kappa} \ln\frac{r-r_h(v)}{r_h(v_0)},\\ v_* =\;& v-v_0, \end{aligned}$

(9) where κ and
$ r_h(v) $ are the surface gravity and location of the event horizon, respectively.$ v_0 $ is the initial time where the fermions exit across the event horizon. The tortoise coordinate transformation describes the spacetime geometry outside the event horizon of the VBdS black hole. In this case,$ r_* $ approaches negative infinity near the event horizon of the VBdS black hole and positive infinity when it tends to the infinite point. Eq. (9) can be written as$ \begin{aligned}[b] \frac{\partial}{\partial r}=\;&\frac{1+2\kappa(r-r_h)}{2\kappa(r-r_h)}\frac{\partial}{\partial r_*}, \\ \frac{\partial}{\partial v}=\;&\frac{\partial}{\partial v_*}-\frac{\dot{r}_h}{2\kappa(r-r_h)}\frac{\partial}{\partial r_*}. \end{aligned} $

(10) To study the modified Hawking temperature, the action S can be defined as
$ \Psi = R (v_*, r_*)+ X(\theta, \phi), $

(11) and let
$ \frac{\partial R}{\partial v_*} = \frac{\partial \Psi}{\partial v_*} = -\omega, $

(12) where ω is the energy of the particle. Using Eqs. (9)−(12) in Eq. (8), we obtain
$ \begin{aligned}[b] &\frac{1}{2\kappa (r-r_h)}\bigg[\frac{ \Delta}{r^2}\Big(1 + 2\kappa (r-r_h)\Big)^2 - 2\dot{r}_h \big(1 + 2\kappa (r-r_h)\big) \\ &\; + 2\lambda m \dot{r}_h\big(1 + 2\kappa (r-r_h)\big) -\lambda^2 \bigg(\frac{\partial R}{\partial v_*} + eA_0\bigg)^2 \\ &\; \big(1 + 2\kappa (r-r_h)\big)^2 \bigg] \bigg(\frac{\partial R}{\partial r_*}\bigg)^2 + 2\bigg(\frac{\partial R}{\partial v_*} + eA_0\bigg) \\ &\;(1-\lambda m) \big(1 + 2\kappa (r-r_h)\big)\bigg(\frac{\partial R}{\partial r_*}\bigg)+ 2\kappa (r-r_h) \\ &\;\Big[m^2 + o(\lambda^2)\Big] =0. \end{aligned} $

(13) To obtain the first-order term of λ in the final result, by multiplying both sides of the above equation by
$ 2\kappa(r-r_h) $ and setting the limit as$ r\longrightarrow r_h $ , we obtain$ \bigg(\frac{\partial R}{\partial r_*}\bigg)^2 - 2(1-\lambda m)(\omega - \omega_0)\bigg(\frac{\partial R}{\partial r_*}\bigg) = 0, $

(14) where
$ \omega_0 = eQ/r_h $ . To derive the surface gravity near the horizon of the VBdS black hole, the limiting value of the coefficient$ \left(\dfrac{\partial R}{\partial r_*}\right)^2 $ is set as unity:$ \begin{aligned}[b] &\lim\limits_{\substack{r\to r_h \\ v\to v_0}} \frac{1}{2\kappa (r-r_h)r^2}\bigg[\Delta[1 + 2\kappa (r-r_h)]- 2r^2\dot{r}_h \\ &\;\;+ 2\lambda m r^2\dot{r}_h -\lambda^2 r^2 (\omega-\omega_0)^2 \left\lbrace 1 + 2\kappa (r-r_h)\right\rbrace \bigg] = 1. \end{aligned} $

(15) Using the above equation, the surface gravity κ is calculated to be
$ \kappa = \frac{1}{2(1-2\dot{r}_h)r_h^3} \bigg[r_h^2 -Q^2 - \Lambda r_h^4 - 2r_h^2\dot{r}_h(1 + 2\lambda m) \bigg]. $

(16) Using Eq. (10) in Eq. (14), we obtain
$ \frac{\partial R}{\partial r} = \frac{1 + 2\kappa (r-r_h)}{2\kappa (r-r_h)}(1-\lambda m) \Big[(\omega-\omega_0)\pm (\omega-\omega_0)\Big]. $

(17) By integrating Eq. (17) and applying Feynman prescription near the horizon of the black hole, we obtain
$ R_{\pm} = \frac{\pi {\rm i}}{2\kappa} (1-\lambda m)\Big[(\omega-\omega_0)\pm (\omega-\omega_0)\Big], $

(18) where
$ R_+ $ and$ R_- $ are the outgoing and ingoing waves, respectively, near the event horizon of the black hole. The tunneling probability of fermions is calculated near the event horizon of the VBdS black hole in accordance with the semiclassical approximation:$ \begin{aligned}[b] \Gamma =\;& \exp (-2 {\rm{Im}} \,\Psi) = \exp (-2 {\rm{Im}} \,R_{\pm}) \\ =\;& \exp \bigg[-\frac{2\pi(\omega-\omega_0)}{\kappa_0}\bigg] = \exp \bigg(-\frac{\omega-\omega_0}{\it T}\bigg),\end{aligned} $

(19) where
$ \kappa_0 = \kappa/(1-\lambda m) $ represents the modified surface gravity of the VBdS black hole according to the Lorentz invariance theory. As Eq. (19) is similar to the Boltzamann formula, the Hawking temperature of the black hole is derived to be$ \begin{aligned}[b] T &=\frac{\kappa_0}{2\pi} \\ & = \frac{r_h-M-2r_h\dot{r}_h(1+m \lambda)-\lambda^2(\omega-\omega_0)^2r_h- \dfrac{2\Lambda}{3}r_h^3}{2\pi\left[2Mr_h -Q^2+\lambda^2(\omega-\omega_0)^2r_h^2+\dfrac{\Lambda}{3}r_h^4\right](1-\lambda m)}.\end{aligned} $

(20) According to Eq. (20), the Hawking temperature and tunneling rate of the VBdS black hole are modified due to the presence of the correction term λ. By applying the binomial expansion for
$ (1-\lambda m)^{-1} $ and ignoring the higher power of λ, Eq. (20) can be written as$ T =T_h + \frac{\lambda m}{4\pi r_h(1-2\dot{r}_h)}\left(1-\frac{Q^2}{r_h^2}-\Lambda r_h^2-3\dot{r}_h\right), $

(21) where
$ T_h $ is the original Hawking temperature of the VBdS black hole in the absence of the LIV theory,$ T_h = \frac{1-\dfrac{Q^2}{r_h^2}-\Lambda r_h^2-2\dot{r}_h}{4\pi r_h(1-2\dot{r}_h)}. $

(22) 
Figure 1. (color online) Original and modified Hawking temperatures of the VBdS black hole versus the radius of the event horizon
$ r_h $ for$ Q=0.1 $ ,$ \lambda=1 $ ,$ \Lambda=0.1 $ ,$ m=0.1 $ , and$ \dot{r_h}=0.3 $ .In our analysis, we consider the cosmological constant Λ as a thermodynamic pressure P
$ \begin{align} P=-\dfrac{\Lambda}{8 \pi}. \end{align} $

(23) As
$ \Lambda>0 $ in the de Sitter space, P is negative. Although it is more appropriate to consider P as a tension rather than as a pressure, we shall continue to refer to it as pressure. The thermodynamics of de Sitter black holes have been studied by treating the positive cosmological constant as thermodynamic pressure [61, 64, 83, 84]. The corresponding conjugate thermodynamic volume is$ \begin{align} V=\dfrac{4}{3} \pi r_{h}^3. \end{align} $

(24) -
In this section, we investigate the corresponding Maxwell's equal area law of the VBdS black hole under the LIV theory. The equation of state of the VBdS black hole under the LIV theory can be obtained from Eq. (21), and can be written as
$ f(T,P,V)=0 $ . We construct the phase transition of the VBdS black hole in$ P-\tilde{v} $ ,$ P-V $ , and$ T-S $ , based on the Maxwell's equal area law. -
The equation of state for the VBdS black hole under the LIV theory is obtained from Eq. (21):
$ \begin{align} P=\dfrac{T(1-2\, \dot{r_h})}{2r_h (1+m \lambda)}+\dfrac{Q^2}{8\pi r_{h}^4}-\dfrac{\Sigma}{8\pi r_h^{2} (1+m \lambda)}. \end{align} $

(25) where
$ \Sigma = 1 + \lambda m -2\dot{r}_h - 3\lambda m \dot{r}_h $ . The equation of state is reduced to$ \begin{align} P=\dfrac{T(1-2 \, \dot{r_h})}{\tilde{v} (1+m \lambda)}+\dfrac{2 Q^2}{\pi \tilde{v}^4}-\dfrac{\Sigma}{2 \pi \tilde{v}^2 (1+m \lambda)}, \end{align} $

(26) where
$ \tilde{v}=2 r_h $ is the specific volume. Eq. (26) is used to illustrate$ P-\tilde{v} $ curves at a constant Q for a given temperature T.According to Fig. 2, there is a phase where one value of the pressure P corresponds to three different values of
$ \tilde{v} $ in the isothermal curves below the critical temperature$ T_c $ . Experiment results show that there should be a horizontal isobar in the isotherm to represent the condensation line where the gas coexists with the liquid.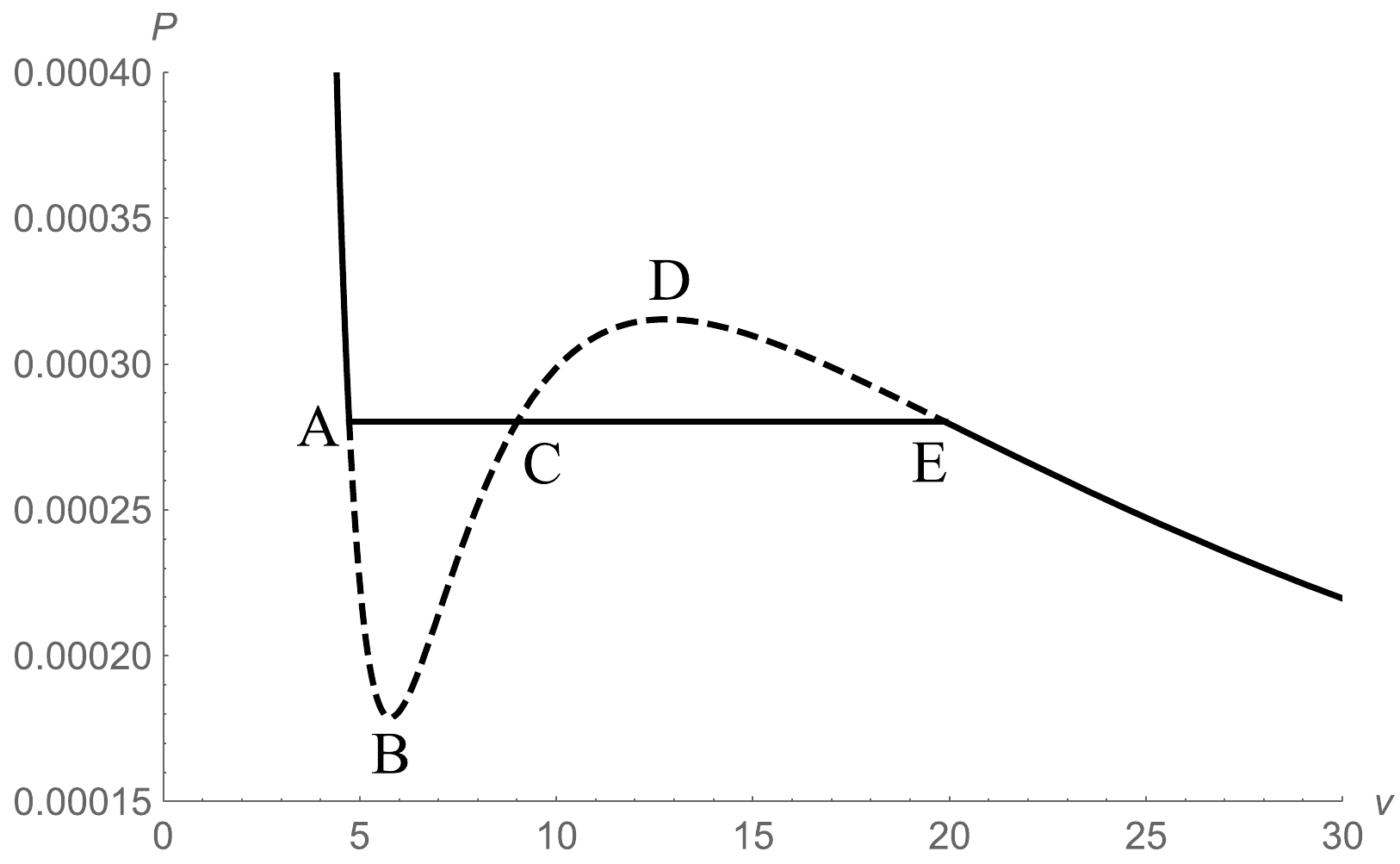
Figure 2.
$ P-\tilde{v} $ diagram below the critical temperature$ T_c $ .$ m=0.1 $ ,$ Q=1 $ ,$ \dot{r_h}=0.3 $ , and$ \lambda=0.1 $ .The thermodynamic system's chemical potential should satisfy
$ \begin{align} {\rm d}\mu=-S {\rm d} T + V {\rm d}P. \end{align} $

(27) In the isotherm transformation, the difference in chemical potential between two states with pressures P and
$ P_0 $ should be$ \begin{align} \mu-\mu_0=\int_{P_0}^{P} V{\rm d}P. \end{align} $

(28) According to Fig. 2, the black hole is in the "gas" phase at point E. However, the black hole is entirely in the "liquid" phase at point A. Furthermore, the region between A and E may be considered as a coexistence phase. As the segment BD defies the equilibrium criteria, the oscillating portion of the curve between A and E cannot be the coexistence line. The chemical potentials are the same at points A and E, which is the thermodynamic condition for phase equilibrium. Using Eq. (28), we obtain
$ \begin{align} \int_{\rm EDCBA} \tilde{v}\; {\rm d} P=0, \end{align} $

(29) showing that area ABC is equal to area CDE.
We find the position of the points A and E for the VBdS black hole under LIV and discuss the effect caused by the LIV parameter λ.
The specific volumes at the boundary of the two-phase coexistence area with a temperature
$ T_0<T_c $ are$ \tilde{v}_1 $ and$ \tilde{v}_2 $ for the VBdS black hole. The corresponding equal-area isobar$ P=P_0 $ is defined by the event horizon radius$ r_h $ and is lower than the critical pressure$ P_c $ . Thus, according to the Maxwell's equal area law, we obtain$ \begin{aligned}[b] P_0 \left( \tilde{v}_2-\tilde{v}_1\right)=\;& \int_{\tilde{v}_1}^{\tilde{v}_{2}} P\; {\rm d}\tilde{v} \\ =\;&\int_{r_1}^{r_2} \left( \dfrac{T_0(1-2 \dot{r_h})}{2 r (1+m \lambda)}+\dfrac{ Q^2}{8\pi r^4}-\dfrac{\Sigma}{8 \pi r^2} \right) 2 {\rm d}r. \end{aligned} $

(30) Thus,
$ \begin{aligned}[b] 2 P_0 \left(r_2-r_1\right)=\;& \dfrac{T_0 \left(1-2 \dot{r_h}\right)}{\left(1+m\lambda\right)} \ln\left( \dfrac{r_2}{r_1} \right)- \dfrac{Q^2}{12\pi}\left( \dfrac{1}{r_2^{3}}-\dfrac{1}{r_1^{3}} \right) \\ &+\dfrac{\Sigma}{4\pi \left(1+m\lambda\right)} \left( \dfrac{1}{r_2}-\dfrac{1}{r_1} \right). \end{aligned} $

(31) According to Eq. (25), we obtain
$ \begin{align} &P_0=\dfrac{T_0(1-2 \dot{r_h})}{2r_1 (1+m \lambda)}+\dfrac{Q^2}{8\pi r_{1}^4}-\dfrac{\Sigma}{8\pi r_1^{2}} \end{align} $

(32) and
$ \begin{align} & P_0=\dfrac{T_0(1-2 \dot{r_h})}{2r_2 (1+m \lambda)}+\dfrac{Q^2}{8\pi r_{2}^4}-\dfrac{\Sigma}{8\pi r_2^{2}}, \end{align} $

(33) where
$ r_1 $ and$ r_2 $ are the event horizon radii of$ \tilde{v}_1 $ and$ \tilde{v}_2 $ , respectively.By using Eqs. (32) and (33) and setting
$ x=\dfrac{r_1}{r_2} $ , we obtain$ \begin{aligned}[b] 0= \;& \dfrac{T_0\left(1-2 \dot{r_h} \right)}{\left(1+m\lambda \right)}+\dfrac{Q^2 \left(1+x\right) \left(1+x^2\right)}{4 \pi x^3 r_{2}^3} \\ &-\dfrac{\Sigma (1+x)}{4 \pi r_2 x \left(1+m \lambda\right)} \end{aligned} $

(34) and
$ \begin{aligned}[b] 2 P_0=\; &\dfrac{T_0\left(1-2 \dot{r_h} \right) \left(1+x\right)}{2 r_2 x \left(1+m\lambda \right)}+\dfrac{Q^2 \left(1+x^4\right) }{8 \pi x^4 r_{2}^4} \\ &-\dfrac{\Sigma (1+x^2)}{8 \pi r_2^{2} x^2 \left(1+m \lambda\right)}. \end{aligned} $

(35) Eq. (31) can be written as
$ \begin{aligned}[b] 2P_0=\;&\dfrac{Q^2 (1+x+x^2)}{12 \pi x^3 r_{2}^4}-\dfrac{\Sigma}{4 \pi x r_{2}^2 \left(1+m\lambda \right)} \\ & -\dfrac{T_0 \ln x \left(1-2 \dot{r_h} \right)}{r_2 \left(1+m \lambda\right) \left(1-x\right)}. \end{aligned} $

(36) Using Eqs. (35) and (36), we obtain
$ \begin{aligned}[b] & \dfrac{4 \pi r_2 x T_0 \left(1-2 \dot{r_h}\right) \left(1-x^2+2x \ln{x} \right) -\Sigma \left(1-x\right)^3}{\left(x-1\right) \left(1+m \lambda\right)} \\ =\;& \dfrac{Q^2 \left(1-x\right)^2 \left(3x^2+4x+3\right)}{3 r_{2}^2 x^2}. \end{aligned} $

(37) Utilizing Eq. (34) in Eq. (37), we obtain
$ \begin{align} r_{2}^2=\dfrac{Q^2 \left(1+m \lambda\right)}{3 \Sigma } \times \dfrac{y_1(x)}{y_2(x)}, \end{align} $

(38) where
$ \begin{align*} & y_1(x)= 4-4x^3 +3 \left(1+x+x^2+x^3\right)\ln{x}, \\ \; \; \; &y_2(x)=x^2 \left[ 2-2x+(1+x) \ln{x}\right]. \end{align*} $

When
$ x \rightarrow 1 $ ,$ r_1=r_2=r_c $ . Therefore, using Eq. (38), we obtain$ \begin{align} r_c^{2}=& \dfrac{Q^2 \left(1+m \lambda\right)}{3 \Sigma } \lim_{x \to 1} \dfrac{y_1(x)}{y_2(x)}. \end{align} $

(39) By using the L'Hopital rule, Eq. (39) becomes
$ \begin{align} r_c=\left\lbrace \dfrac{6Q^2\left(1+m \lambda \right)}{\Sigma}\right\rbrace^{\frac{1}{2}}. \end{align} $

(40) Thus,
$ \begin{align} & \tilde{v}_c=\dfrac{2 Q\sqrt{6 \left(1+m\lambda\right)} }{\sqrt{\Sigma}} \end{align} $

(41) and
$ \begin{align} & T_c= \dfrac{\Sigma^\frac{3}{2}}{3\sqrt{6} \pi Q \left(1-2\dot{r_h}\right) \sqrt{1+m \lambda}}. \end{align} $

(42) By substituting
$ r_2 $ in Eq. (34) and using$ T_0=\chi T_c $ , we obtain$ \begin{align} 2\sqrt{2} \chi x^3 \left( \dfrac{y_1(x)}{y_2(x)}\right)^\frac{3}{2}=9 (1+x) \left[ x^2 \dfrac{y_1(x)}{y_2(x)} -3x^2-3 \right]. \end{align} $

(43) We plot the pressure P according to the specific volume
$ \tilde{v} $ for different values of T and λ in Figs. 3 and 4, respectively, and show the simulated phase transition and boundary of the two-phase coexistence based on isotherms in the$ P-\tilde{v} $ diagram. According to Fig. 3, when the temperature increases, the isobar in the isotherm becomes shorter. The boundaries of the isobar coincide when the temperature reaches its critical value. Moreover, Fig. 4 shows that, under the influence of LIV, the phase transition process becomes longer. Further, the comparison of the original and the modified pressures shows that the phase transition occurs at a lower pressure due to LIV.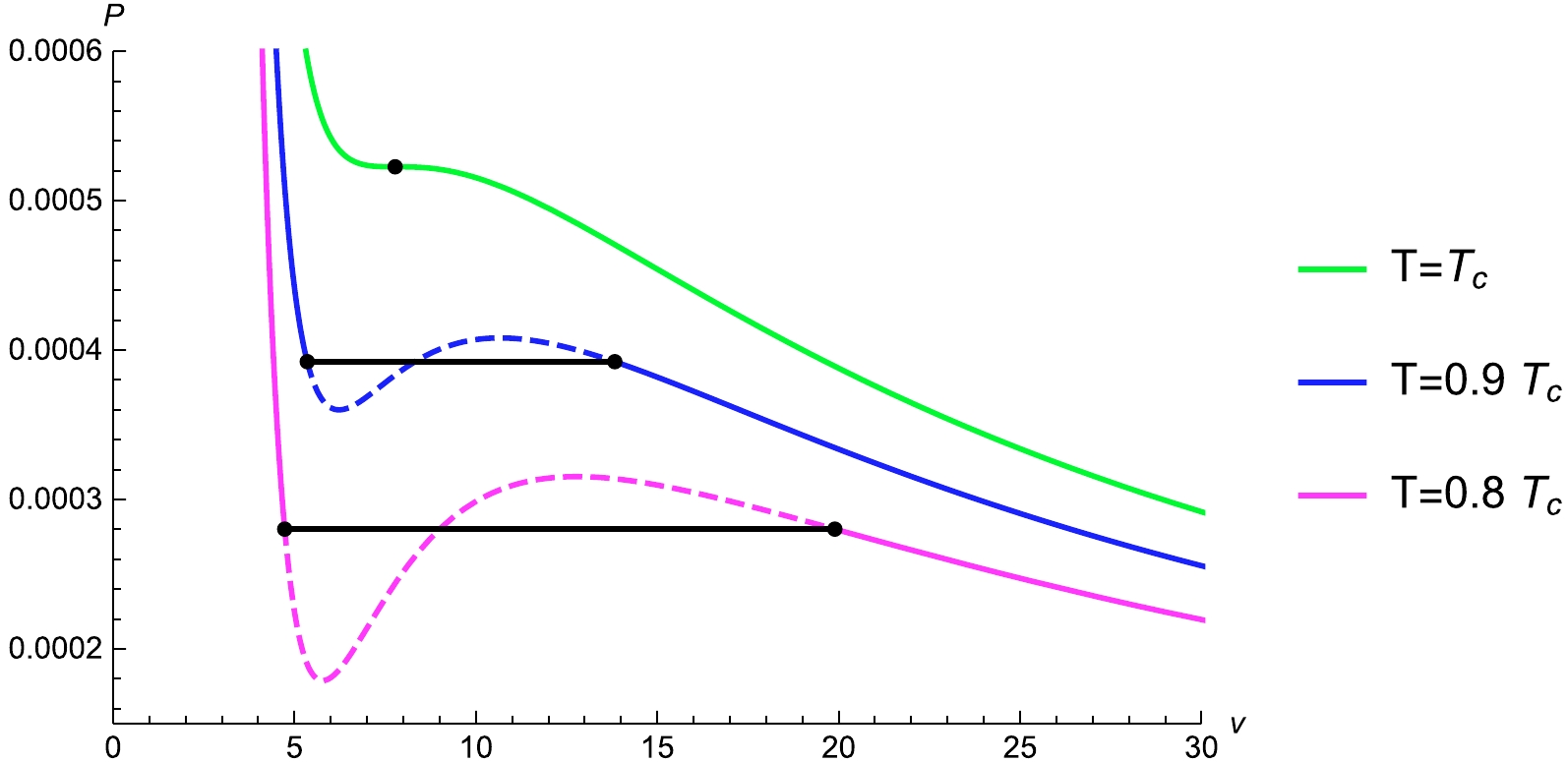
Figure 3. (color online) Simulated phase transition (black solid lines) and boundary of a two-phase coexistence based on isobars in the
$P-\tilde{v}$ diagram for the VBdS black hole under the LIV theory with$ m=0.1 $ ,$ Q=1 $ ,$ \dot{r_h}=0.3 $ , and$ \lambda=0.1 $ . The temperature of the isotherms decreases from top to bottom.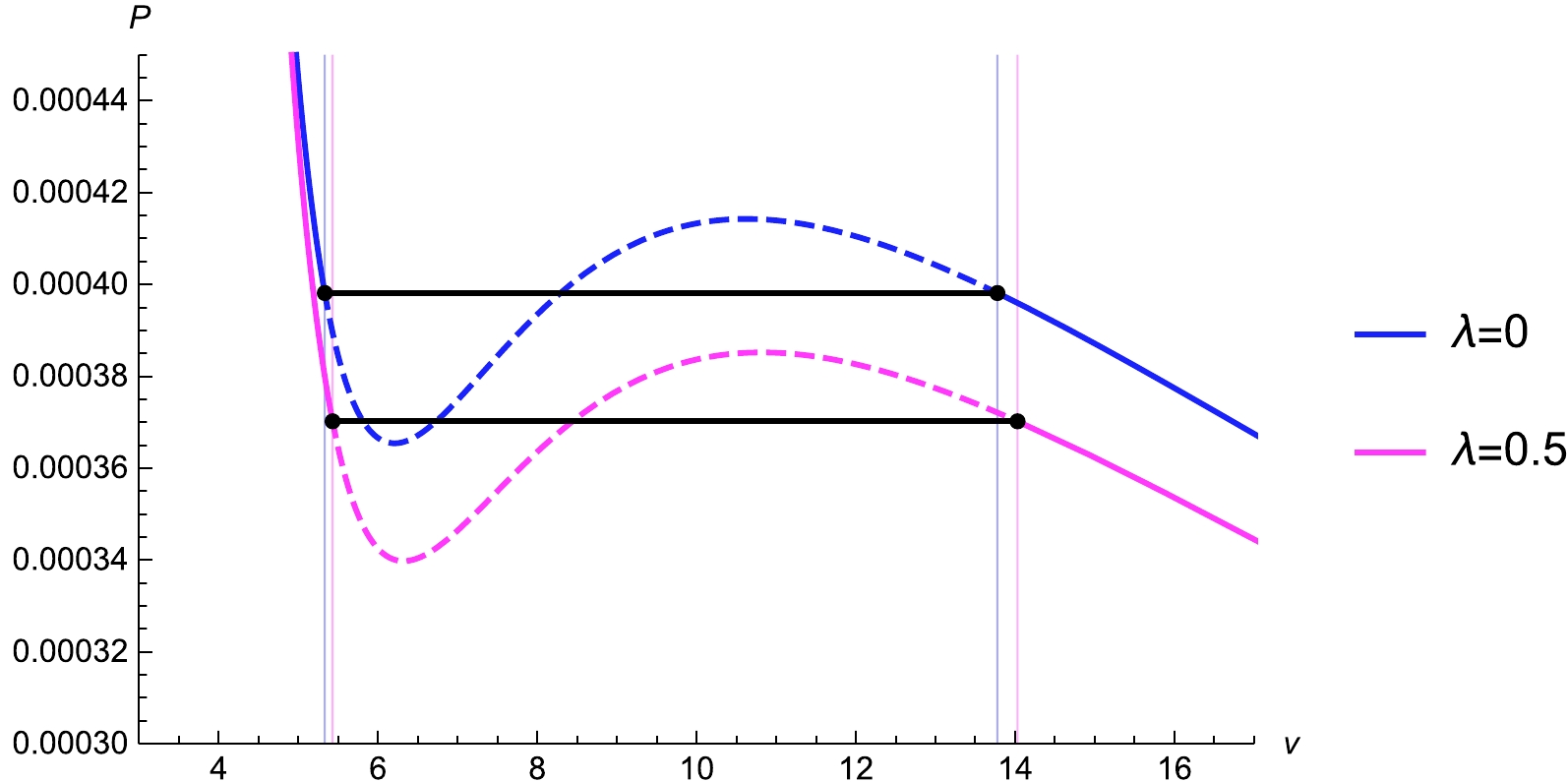
Figure 4. (color online) Simulated phase transition (black solid lines) and boundary of a two-phase coexistence for
$ T<T_c $ in the$ P-\tilde{v} $ diagram for (a)$ \lambda=0 $ (top) and (b)$ \lambda=0.5 $ (bottom) with fixed$ m=0.1 $ ,$ Q=1 $ , and$ \dot{r_h}=0.3 $ .The numerical values of x,
$ r_1 $ ,$ r_2 $ ,$ \tilde{v}_1 $ ,$ \tilde{v}_2 $ , and$ P_0 $ for different values of λ for the VBdS black hole under the LIV theory are presented in Table 1, which shows that x decreases as χ decreases, but λ does not affect it.$ r_2 $ and$ \tilde{v}_2 $ increase with λ but decrease with the increase in χ. However,$ P_0 $ decreases with the increase in λ but increases with the increase in χ.λ χ x $ r_1 $ 

$ r_2 $ 

$ v_1 $ 

$ v_2 $ 

$ P_0 $ 

0 1 1 3.87298 3.87298 7.74597 7.74597 0.000530516 0.9 0.386969 2.66568 6.88861 5.33135 13.7772 0.000398128 0.8 0.237789 2.35641 9.90968 4.71283 19.8194 0.000284384 0.1 1 1 3.88744 3.88744 7.77489 7.77489 0.000522667 0.9 0.386969 2.67563 6.91433 5.35126 13.8287 0.000392237 0.8 0.237789 2.36521 9.94668 4.73043 19.8934 0.000280176 0.5 1 1 3.94405 3.94405 7.88811 7.88811 0.000493299 0.9 0.386969 2.71459 7.01501 5.42919 14.03 0.000370198 0.8 0.237789 2.39966 10.0915 4.79931 20.1831 0.000264433 Table 1. Numerical solutions for x,
$ r_1 $ ,$ r_2 $ ,$ \tilde{v}_1 $ ,$ \tilde{v}_2 $ , and$ P_0 $ for different values of λ with$ m = 0.1 $ ,$ Q=1 $ , and$ \dot{r_h}=0.3 $ . -
In this subsection, we examine the condition under which the conjugate variables (P, V) occur under the Maxwell's equal area law. Further, we discuss the phase transition of the VBdS black hole in the
$ P-V $ diagram based on the Maxwell's equal area law. On the isotherm with a temperature$ T_0 $ $ (T_0< T_c) $ in the$ P-V $ diagram, two points$ (P_0, V_1) $ and$ (P_0,V_2) $ satisfy the Maxwell's equal area law,$ \begin{aligned}[b] P_0(V_2 - V_1)=\;&\int_{V_1}^{V_2} P{\rm d}V = \int_{r_1}^{r_2} \bigg( \dfrac{T_0(1-2 \dot{r_h})}{2 r (1+m \lambda)} \\& +\dfrac{ Q^2}{8\pi r^4} -\dfrac{\Sigma}{8 \pi r^2} \bigg) 4 \pi r^2 {\rm d}r. \end{aligned} $

(44) By Eq. (44), we derive the relation
$ \begin{aligned}[b] 2P_0 = \;& \frac{3Q^2}{4\pi r_2^4 x(1+x+x^2)} + \frac{3T_0 (1+x)(1-2\dot{r}_h)}{2r_2 (1+\lambda m)(1+x+x^2)} \\ & - \frac{3\Sigma}{4\pi r_2^2(1+x+x^2)(1+\lambda m)}. \end{aligned} $

(45) Similarly, we obtain
$ r_2^2 = \frac{Q^2 (1+4x+x^2)(1+\lambda m)}{\Sigma x^2}. $

(46) At
$ T_0 = \chi T_c $ , when$ 0<\chi<1 $ , we obtain$ \chi = \frac{3\sqrt{6} x (1+x)}{(1+4x + x^2)^{3/2}}. $

(47) The critical state is obtained when
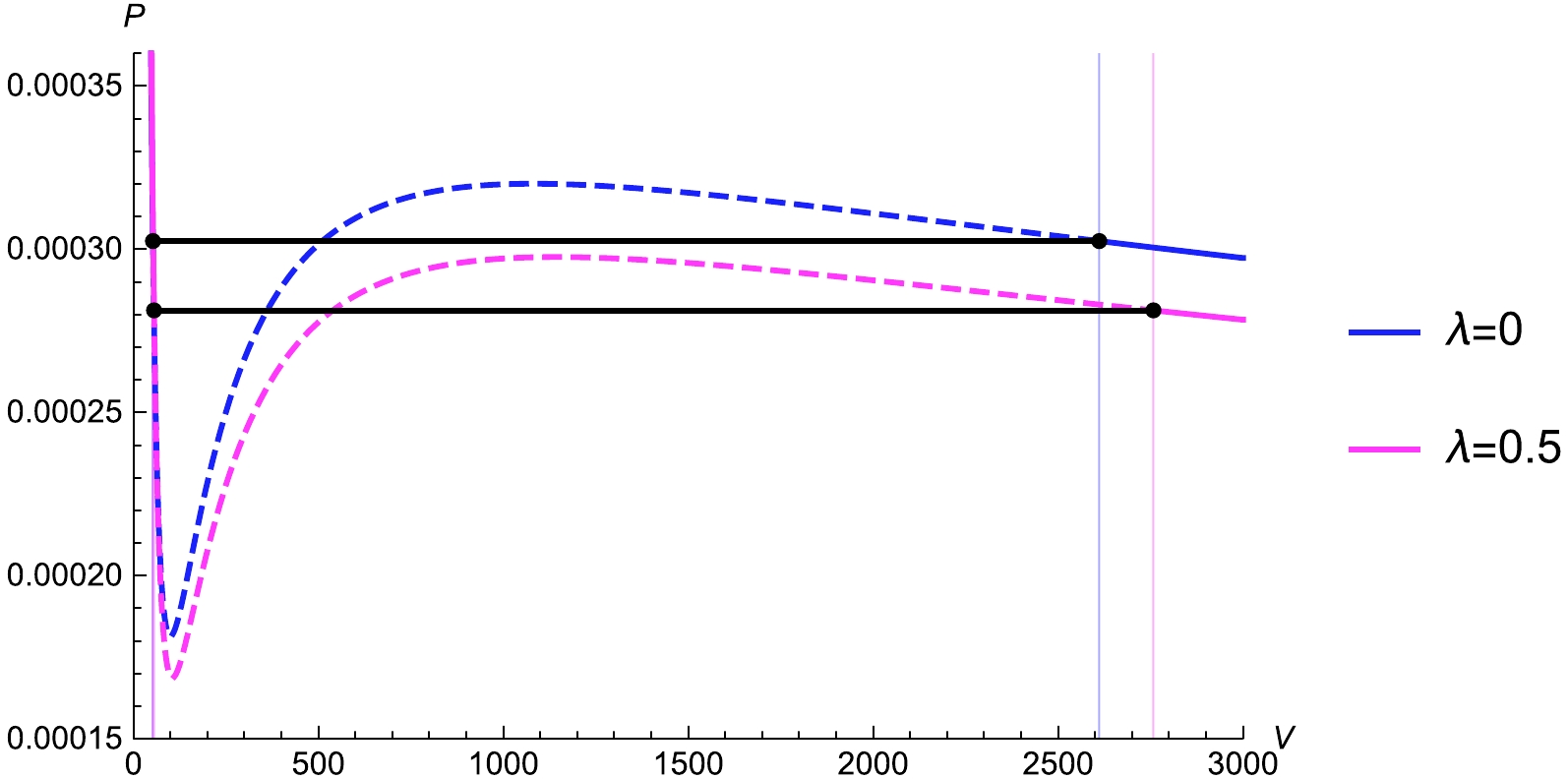
$ x \rightarrow 1 $ , i.e.,$ \chi \rightarrow 1 $ . Using Eqs. (46) and (45), we can solve$ r_2 $ and$ P_0 $ for different values of λ and fixed χ by deriving a specific value of x by Eq. (47). Using the values of$ r_2 $ , we can find the values of$ r_1 $ , and the corresponding values of$ V_1 $ and$ V_2 $ can be obtained. To investigate the impact of the parameter λ on the phase transition processes, by fixing the parameters$ m=0.1 $ ,$ Q=1 $ ,$ \dot{r_h}=0.3 $ , and$ \chi=0.8, 0.9, 1 $ , the values of$ r_1 $ ,$ r_2 $ ,$ V_1 $ ,$ V_2 $ , and$ P_0 $ are obtained. The results are shown in Table 2. x is not related to the LIV parameter λ. With the increase in λ, the values of$ r_2 $ and$ v_2 $ increase, while, with the increase in χ, the values of$ r_2 $ and$ v_2 $ decrease. Further,$ P_0 $ decreases with the increase in λ, which implies that the LIV reduces the pressure of phase transition. We plot the$ P-V $ diagram for different values of χ and λ in Figs. 5 and 6, respectively, and show the isobar representing the process of isothermal phase transition or two-phase coexistence state as that of the van der Waals system. Figure 5 shows that, as the temperature increases, the isothermal phase transition becomes shorter. When the temperature reaches its critical value, it turns into a single point. Further, according to Fig. 6, the isothermal phase transition becomes longer under the influence of LIV. Moreover, the isobar representing the two-phase coexistence occurs at a lower pressure under the influence of the LIV.λ χ x $ r_1 $ 

$ r_2 $ 

$ V_1 $ 

$ V_2 $ 

$ P_0 $ 

0 1 1 3.87298 3.87298 243.347 243.347 0.000530516 0.9 0.404703 2.63752 6.51716 76.8554 1159.48 0.000403993 0.8 0.272204 2.32535 8.5427 52.6691 2611.4 0.000302491 0.1 1 1 3.88744 3.88744 246.083 246.083 0.000522667 0.9 0.404703 2.64736 6.5415 77.7194 1172.52 0.000398015 0.8 0.272204 2.3304 8.5746 53.2613 2640.76 0.000298015 0.5 1 1 3.94405 3.94405 256.99 256.99 0.000493299 0.9 0.404703 2.68592 6.63675 81.1644 1224.49 0.000375652 0.8 0.272204 2.36803 8.69946 55.6221 2757.82 0.00028127 Table 2. Numerical solutions for x,
$ r_1 $ ,$ r_2 $ ,$ V_1 $ ,$ V_2 $ , and$ P_0 $ for different values of λ with$ m = 0.1 $ ,$ Q=1 $ , and$ \dot{r_h}=0.3 $ .
Figure 5. (color online) Simulated phase transition (black solid lines) and boundary of two-phase coexistence based on isobars in the
$ P-V $ diagram for the VBdS black hole under the LIV theory with$ m = 0.1 $ ,$ Q = 1 $ ,$ \dot{r_h} = 0.3 $ , and$ \lambda = 0.1 $ . The temperature of the isotherms decreases from top to bottom. -
In this section, through the Maxwell's equal area law, we construct the phase transition in
$ T-S $ for the VBdS black hole under the LIV theory. The equation of state (Eq. (25)) can be written as$ T=\dfrac{2P \sqrt{S}(1+\lambda m)}{\sqrt{\pi}(1-2 \dot{r_h})}+\dfrac{\Sigma}{4 \sqrt{\pi S}(1-2\dot{r_h})} -\dfrac{Q^2 \sqrt{\pi}(1+\lambda m)}{4 S^\frac{3}{2} (1-2 \dot{r_h})}, $

(48) where
$ S=\pi r_{h}^2 $ is the Bekenstein-Hawking entropy.For given charge Q, LIV parameter λ, and pressure
$ P_0< P_c $ , the entropies at the boundary of the two-phase coexistence region are$ S_1 $ and$ S_2 $ and their corresponding temperature is$ T_0 $ $ (T_0 \leq T_c) $ . Notably, the temperature depends on the horizon radius$ r_h $ . According to the Maxwell's equal area law,$ \begin{aligned}[b] T_0(S_2-S_1) =\;& \int_{S_1}^{S_2} T \; {\rm d}S \\ =\;& \int_{r_1}^{r_2} \frac{2Pr(1+\lambda m)}{1-2\dot{r}_h} + \frac{\Sigma}{4\pi r_h(1-2\dot{r}_h)} \\ &-\frac{Q^2 (1+\lambda m)}{4\pi r_h^3(1-2\dot{r}_h)} 2 \pi r_h {\rm d}r_h. \end{aligned} $

(49) Thus,
$ \begin{aligned}[b] 2\pi T_0 =\;& \frac{-Q^2(1+\lambda m)}{ x(1+x)(1-2\dot{r}_h)r_2^3} +\frac{\Sigma}{(1+x)(1-2\dot{r}_h)r_2} \\ &+\frac{8\pi P_0r_2(1+\lambda m)(1+x+x^2)}{3(1+x)(1-2\dot{r}_h)}, \end{aligned} $

(50) $ \begin{align} T_0 =& \bigg[\frac{-Q^2(1+\lambda m)}{4\pi r_1^3(1-2\dot{r}_h)}+\frac{2P_0r_1(1+\lambda m)}{1-2\dot{r}_h}+\frac{\Sigma}{4\pi r_1(1-2\dot{r}_h)}\bigg] \end{align} $

(51) and
$ \begin{align} T_0 =& \bigg[\frac{-Q^2(1+\lambda m)}{4\pi r_2^3(1-2\dot{r}_h)}+\frac{2P_0r_2(1+\lambda m)}{1-2\dot{r}_h}+\frac{\Sigma}{4\pi r_2(1-2\dot{r}_h)}\bigg]. \end{align} $

(52) By Eqs. (51) and (52), we obtain
$ \frac{Q^2 (1+\lambda m)(1+x+x^2)}{x^3r_2^3}+8\pi P_0(1+\lambda m)r_2 -\frac{\Sigma}{x r_2} =0 $

(53) and
$ \begin{aligned}[b] 8\pi T_0 = \;& \frac{-Q^2 (1+\lambda m)(1+x^3)}{(1-2\dot{r}_h)x^3 r_2^3}+ \frac{\Sigma (1+x)}{(1-2\dot{r}_h)x r_2 } \\ &+ \frac{8\pi P_0r_2 (1+\lambda m)(1+x)}{(1-2\dot{r}_h)} . \end{aligned} $

(54) Using Eqs. (50) and (54), we can derive the relation
$ 8\pi P_0 r_2(1+\lambda m)=\frac{-3 Q^2(1+3x+x^2)(1+\lambda m)}{r_2^3 x^3} +\frac{3\Sigma}{r_2 x}. $

(55) Using Eq. (55), Eq. (53) is reduced to
$ r_2^2 = \frac{Q^2(1+4x+x^2)(1+\lambda m)}{\Sigma \;x^2}. $

(56) By Eq. (53), we obtain
$ P_0 = \frac{3 x^2 \Sigma^2}{8\pi Q^2 (1+4x+x^2)^2 (1+\lambda m)^2}. $

(57) The critical radius
$ r_c =r_1=r_2 $ and critical pressure$ P_c $ are$ r_c =\frac{\sqrt{6}Q(1+ \lambda m)^{\frac{1}{2}}}{\Sigma^{\frac{1}{2}}} $

(58) and
$ P_c= \frac{\Sigma^2}{96\pi Q^2 (1+\lambda m)^2}. $

(59) At
$ P_0 = \chi P_c $ , when$ 0<\chi<1 $ , we obtain$ \chi = \frac{36 x^2}{(1+ 4x + x^2)^2}. $

(60) We plot
$ T-S $ diagrams for different values of χ and λ in Figs. 7 and 8, respectively, and show the isotherms (black solid lines), which represent the simulated phase transition processes derived from the Maxwell's equal area law. According to Fig. 7, the isotherm becomes shorter with the increase in the pressure. Once the pressure reaches its critical point, it converges to a point. For Fig. 8, we consider$ P<P_c $ and plot the$ T-S $ diagrams for$ \lambda=0 $ and 0.5. The phase transition process for$ \lambda=0.5 $ is longer than that at$ \lambda=0 $ , which implies that the LIV increases the phase transition process. We compute the values of x,$ r_1 $ ,$ r_2 $ ,$ S_1 $ ,$ S_2 $ , and$ T_0 $ at$ \chi= $ 0.8, 0.9, 1 and$ \lambda= $ 0, 0.1, 0.5, to determine the influence of these parameters on the simulated phase transition process and two-phase coexistence region. The values are presented in Table 3. x is unrelated to λ.$ r_2 $ and$ S_2 $ are directly proportional to λ but are inversely proportional to χ. Moreover,$ T_0 $ is inversely proportional to λ and directly proportional to χ. Both$ r_2 $ and$ S_2 $ increase with λ but decrease with the increase in χ. However,$ T_0 $ decreases with the increase in λ but increases with χ.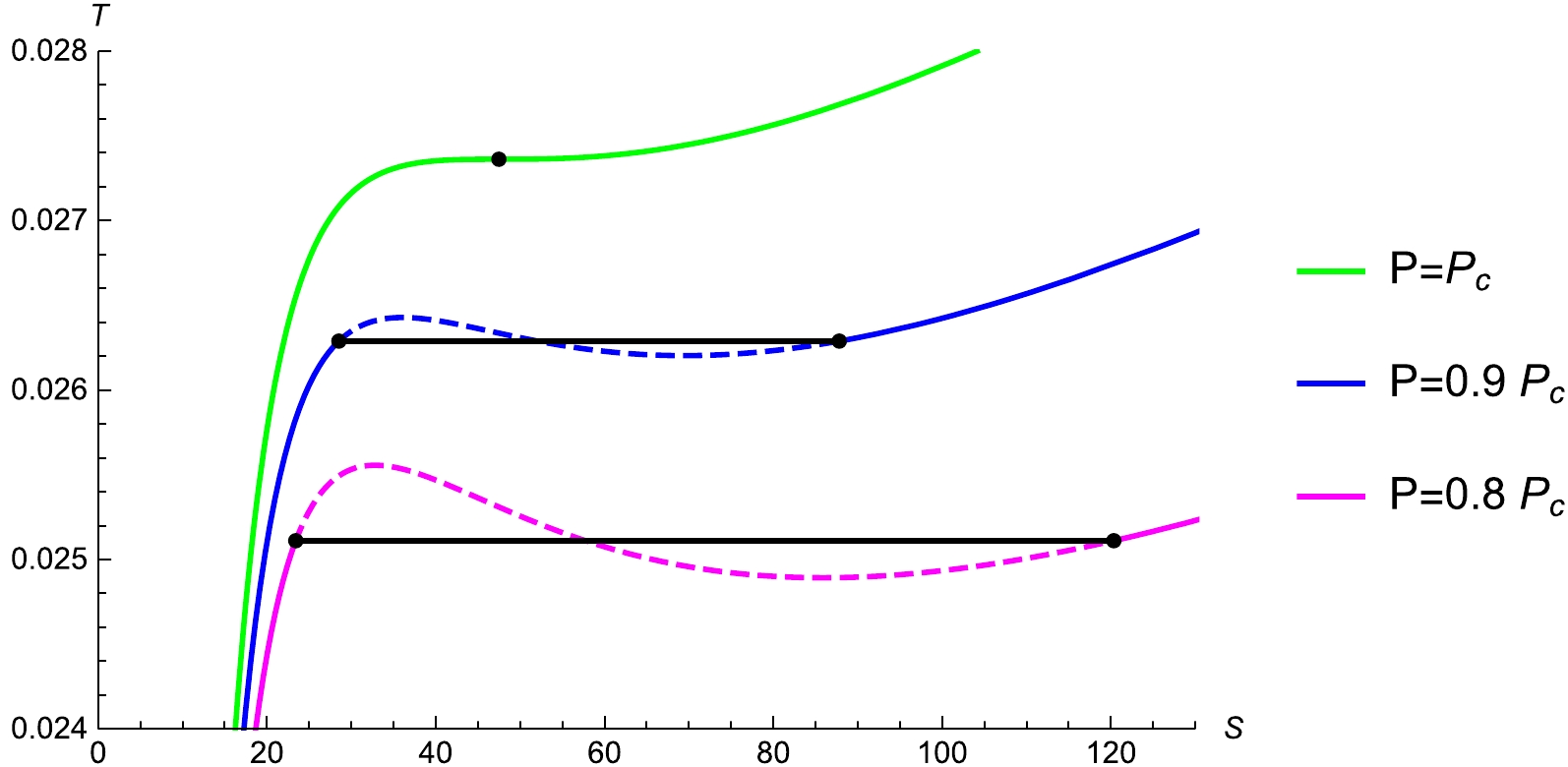
Figure 7. (color online) Simulated phase transition (black solid lines) and boundary of two-phase coexistence based on isobars in the
$ T-S $ diagram for the VBdS black hole under the LIV theory with$ m=0.1 $ ,$ Q=1 $ ,$ \dot{r_h}=0.3 $ , and$ \lambda=0.1 $ . The pressure of the isobars decreases from top to bottom.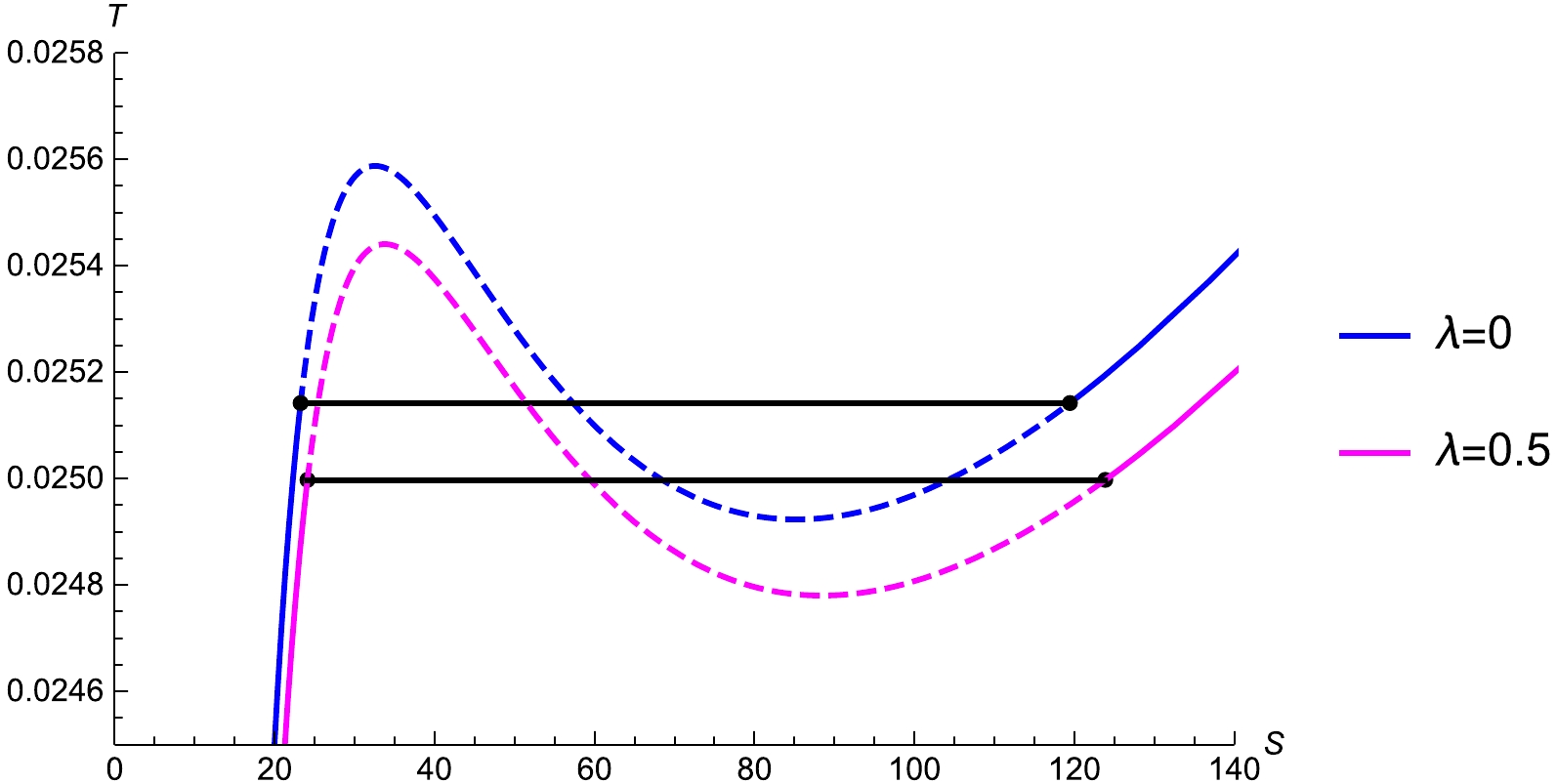
Figure 8. (color online) Simulated phase transition (black solid lines) and boundary of two-phase coexistence for
$ P < P_c $ in the$ T-S $ diagram for (a)$ \lambda = 0 $ (top) and (b)$ \lambda = 0.5 $ (bottom) with fixed$ m = 0.1 $ ,$ Q = 1 $ , and$ \dot{r_h} = 0.3 $ .λ χ x $ r_1 $ 

$ r_2 $ 

$ S_1 $ 

$ S_2 $ 

$ T_0 $ 

0 1 1 3.87298 3.87298 47.1239 47.1239 0.0273958 0.9 0.569919 3.00187 5.26719 28.3095 87.158 0.0263212 0.8 0.441089 2.7198 6.16609 23.2393 119.445 0.0251419 0.1 1 1 3.88744 3.88744 47.4764 47.4764 0.0273621 0.9 0.569919 3.01307 5.28685 28.5213 87.81 0.0262889 0.8 0.441089 2.72995 6.18911 23.4131 120.339 0.0025111 0.5 1 1 3.94405 3.94405 48.8692 48.8692 0.0272384 0.9 0.569919 3.05695 5.36384 29.358 90.386 0.02617 0.8 0.441089 2.76971 6.27924 24.1 123.869 0.0249975 Table 3. Numerical solutions for x,
$ r_1 $ ,$ r_2 $ ,$ S_1 $ ,$ S_2 $ , and$ T_0 $ for different values of λ with$ m = 0.1 $ ,$ Q=1 $ , and$ \dot{r_h}=0.3 $ . -
In this section, we evaluate the corrected entropy under the influence of the LIV theory. To determine the corrected entropy, we use the partition function [85, 86]
$ \begin{align} \tilde{Z}(\beta)= \int_{0}^{\infty} \rho(\tilde{E}) {\rm e}^{-\beta \tilde{E}} {\rm d} \tilde{E}, \end{align} $

(61) where
$ \beta=T^{-1} $ .$ \tilde{E} $ and$ \rho(\tilde{E}) $ are the average energy and quantum density of the system, respectively. We apply the inverse Laplace transformation to obtain the quantum density,$ \begin{aligned}[b] \rho (\tilde{E})&=\dfrac{1}{2 \pi {\rm i}} \int_{\beta_0- {\rm i} \infty}^{\beta_0+ {\rm i} \infty} {\rm e}^{\beta \tilde{E}} \tilde{Z}(\beta) {\rm d}\beta \\ &=\dfrac{1}{2 \pi{\rm i}} \int_{\beta_0- {\rm i} \infty}^{\beta_0+ {\rm i} \infty} {\rm e}^{\tilde{S}(\beta)} {\rm d}\beta, \end{aligned} $

(62) where
$\tilde{S}=\ln (\tilde{Z})+\beta \tilde{E}$ is the corrected entropy for the black hole.Using the steepest descent method at the saddle point
$ \beta_0 $ , the complex integral is calculated such that$ \left(\dfrac{\partial \tilde{S}(\beta)}{\partial \beta}\right)_{\beta_0}=0 $ and$ \dfrac{\partial^2 \tilde{S}}{\partial \beta^2}>0 $ . By further expanding$ \tilde{S}(\beta) $ around the equilibrium$ \beta=\beta_0 $ , we obtain$ \begin{aligned}[b] \tilde{S}(\beta)=\;& S+\dfrac{1}{2} \left(\beta-\beta_0 \right)^2 \left(\dfrac{\partial^2 \tilde{S}(\beta)}{\partial \beta^2}\right)_{\beta_0} \\ &+\text{higher order terms}, \end{aligned} $

(63) where
$ S=\tilde{S} $ is the zero-order entropy and satisfies the relations$ \dfrac{\partial S}{\partial \beta}=0 $ and$ \dfrac{\partial^2 S}{\partial \beta^2}=0 $ at$ \beta=\beta_0 $ . By Eqs. (62) and (63), we derive$ \begin{align} \rho(\tilde{E})=\dfrac{{\rm e}^S}{2\pi {\rm i}} \int_{\beta_0-{\rm i} \infty}^{\beta+ {\rm i} \infty} {\rm e}^{\frac {\left(\beta-\beta_0\right)^2} {2}\frac{\partial^2 \tilde{S}}{\partial \beta^2}} \; {\rm d}\beta. \end{align} $

(64) The expression of quantum density can be further simplified to
$ \begin{align} \rho(\tilde{E})=\dfrac{{\rm e}^S}{\sqrt{2\pi}} \left( \dfrac{\partial^2 \tilde{S}}{\partial \beta^2} \right)^{{-1}/{2}}. \end{align} $

(65) Ignoring the higher-order terms, after simplification, we obtain
$ \begin{align} \tilde{S}=S-\dfrac{1}{2} \; \text{ln}(S T^2). \end{align} $

(66) Using the modified Hawking temperature under the influence of the LIV theory (T) and entropy (S) in Eq. (66), we obtain the corrected entropy under the influence of the LIV theory:
$ \begin{align} \tilde{S} =& \pi r_h^2 + \ln \bigg[\frac{4\sqrt{\pi}(1-2\dot{r}_h)}{\big(\Sigma - \Lambda r_h^2(1+\lambda m)\big) -Q^2(1+\lambda m)r_h^{-2}} \bigg]. \end{align} $

(67) The corrected entropy in the absence of LIV
$ S_c $ is calculated using$ T=T_h $ :$ \begin{align} S_c =& \pi r_h^2 + \ln \bigg[\frac{4\sqrt{\pi} r_{h}^2(1-2\dot{r}_h)}{ -Q^2+r_{h}^2 \left( 1-2 \dot{r_h}-\Lambda r_h^2 \right)} \bigg]. \end{align} $

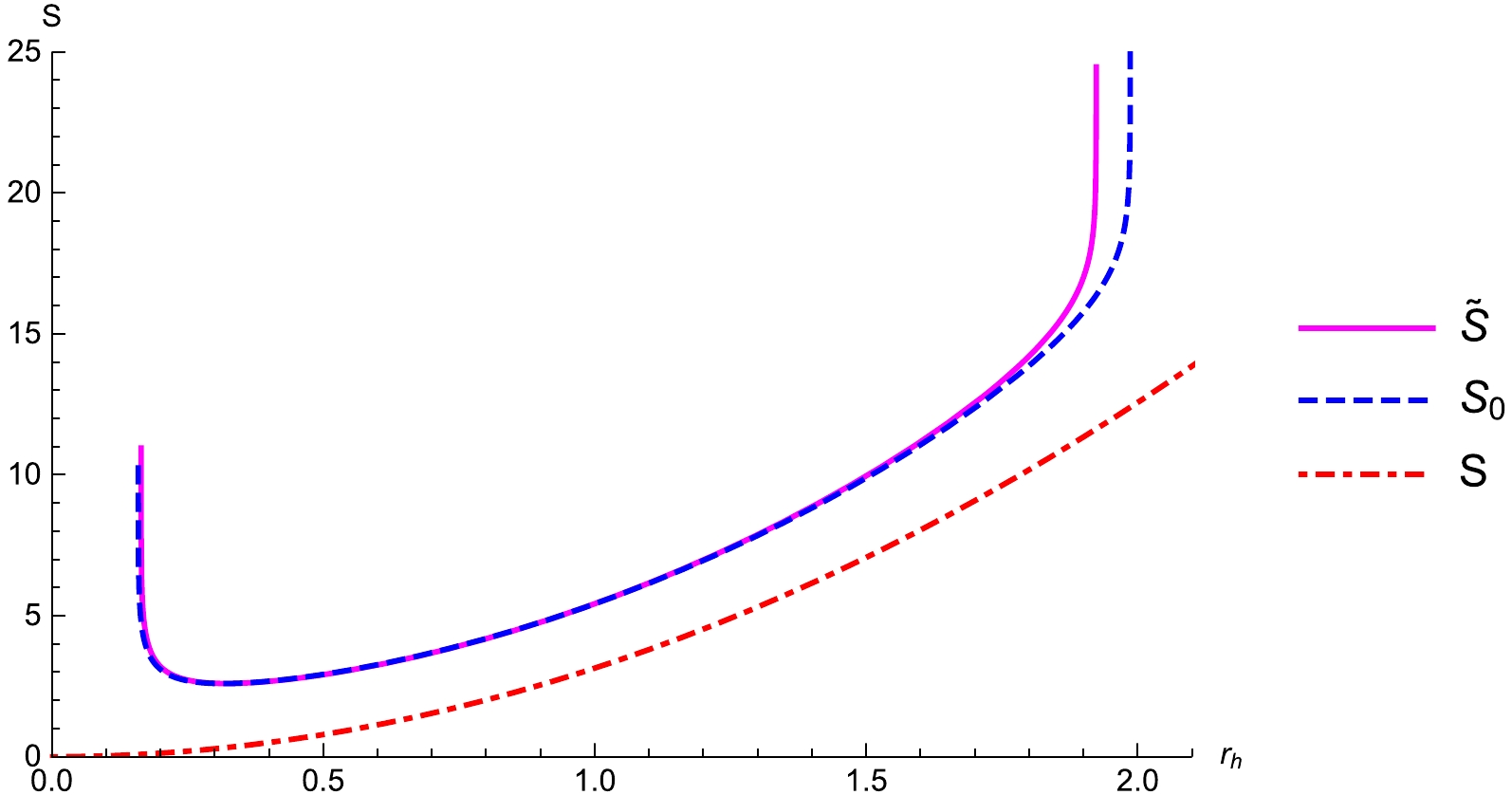
(68) We plot the original entropy S, corrected entropy in the absence of LIV
$ S_c $ , and corrected entropy under the influence of LIV$ \tilde{S} $ in Fig. 9. The original entropy (S) monotonically increases with the radius of the event horizon$ r_h $ . However,$ S_c $ and$ \tilde{S} $ initially decrease, and then increase. The LIV theory does not largely impact a small black hole. However, the LIV theory increases the entropy of a larger black hole. -
We analyze the behaviour of the Helmholtz free energy of the VBdS black hole under the influence of the LIV theory. The Helmholtz free energy is [87]
$ \begin{align} F=-\int \tilde{S} \,{\rm d}T. \end{align} $

(69) Using Eqs. (21) and (67), we obtain the expression of Helmholtz free energy under the influence of the LIV theory:
$ \begin{aligned}[b] F=\;&\frac{1}{12\pi r_h^3(1-2\dot{r}_h)}\bigg[Q^2(2 + 9\pi r_h^2)(1+\lambda m) \\ &+ \pi r_h^6(1+\lambda m)\Lambda + 3r_h^4 \Big\lbrace \big(\pi \Sigma + 2\Lambda(1+\lambda m)\big) \Big\rbrace \cr &- 3 \Big\lbrace r_h^2\big(\Sigma - \Lambda r_h^2(1+\lambda m) \big)-Q^2(1+\lambda m) \Big\rbrace \cr &\times \ln\bigg(\frac{4\sqrt{\pi}(1-2\dot{r}_h)}{\big(\Sigma - \Lambda r_h^2(1+\lambda m)\big) -Q^2(1+\lambda m)r_h^{-2}}\bigg) \bigg]. \end{aligned} $

(70) The Helmholtz free energy without the influence of the LIV theory is
$ \begin{aligned}[b] F_0=\;&\frac{1}{12\pi r_h^3(1-2\dot{r}_h)}\bigg[Q^2(2 + 9\pi r_h^2)+ \pi r_h^6 \Lambda \cr & + 3r_h^4 \Big\lbrace \big(\pi (1-2\dot{r}_h) + 2\Lambda\big) \Big\rbrace \cr & -3 \Big\lbrace r_h^2\big(1-2\dot{r}_h - \Lambda r_h^2 \big)-Q^2 \Big\rbrace \cr & \times \ln\bigg(\frac{4\sqrt{\pi}(1-2\dot{r}_h)}{\big(1-2\dot{r}_h - \Lambda r_h^2\big) -Q^2 \, r_h^{-2}}\bigg) \bigg]. \end{aligned} $

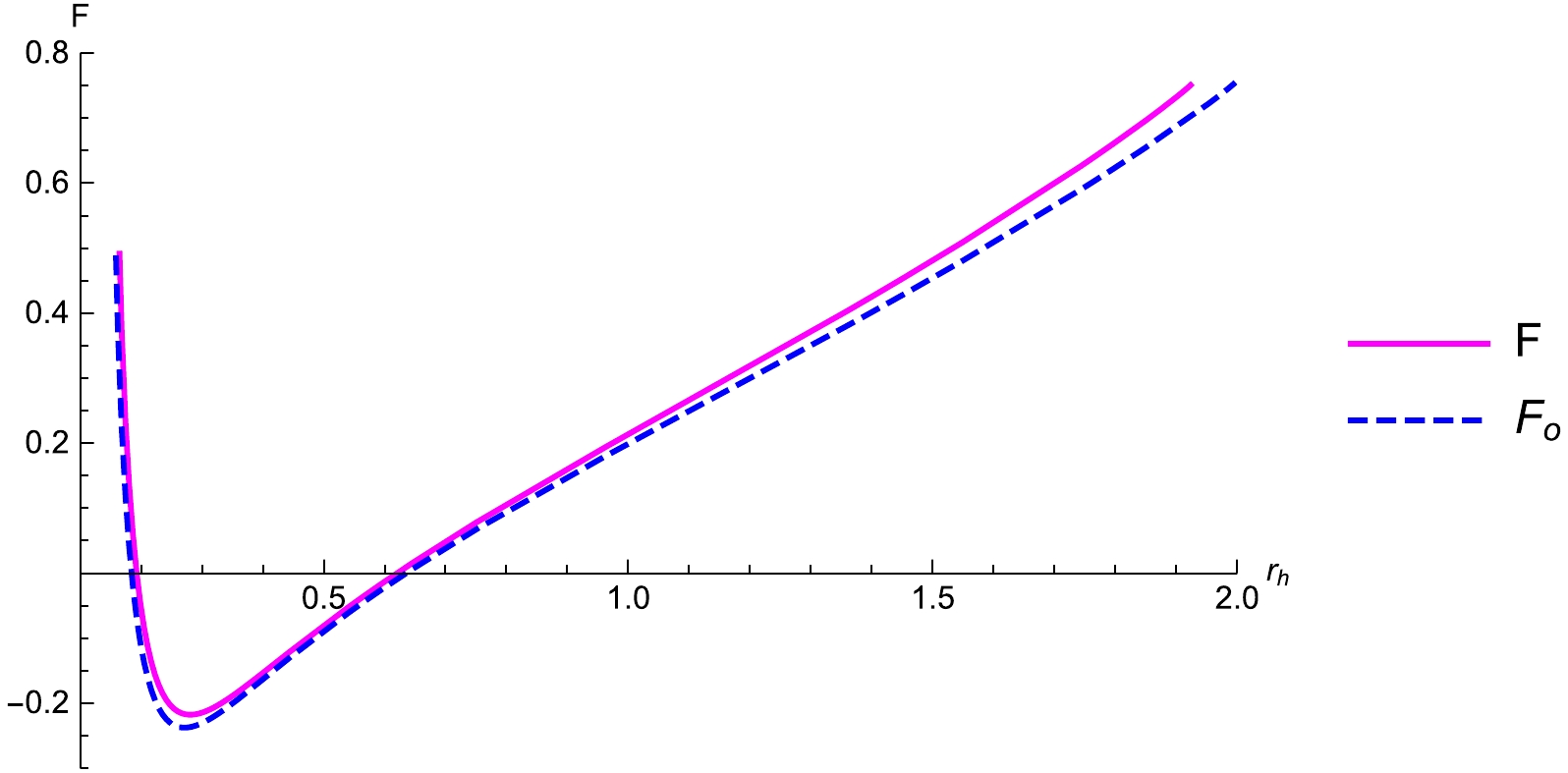
(71) In Fig. 10, we plot the Helmholtz free energy with and without the influence of the LIV theory. The two Helmholtz free energies exhibit similar patterns. Initially they decrease monotonically up to the minimum energy level, and then increase with the increase in the size of the black hole. The LIV theory increases the Helmholtz free energy. In comparison to smaller black holes, larger black holes are more affected by the LIV theory.
-
The internal energy of the VBdS black hole is [88]
$ \begin{align} E= F+T\, \tilde{S}. \end{align} $

(72) Using Eqs. (21), (67), and (70), the internal energy under the LIV theory is calculated to be
$ \begin{aligned}[b] E=\;& \frac{1}{6\pi \, r_h^3 (1-2\dot{r}_h)}\bigg[Q^2(1+3\pi \, r_h^2)(1+\lambda m) \cr +& r_h^4 \Big[3\pi \Big((1 +\lambda m)-\dot{r}_h(1 + 2\lambda m) \Big) + (3-\pi \, r_h^2) \cr &(1 + \lambda m)\Lambda \Big] \bigg]. \end{aligned} $

(73) The internal energy without LIV theory is
$ \begin{aligned}[b] E_0=\;& \frac{1}{6\pi \, r_h^3 (1-2\dot{r}_h)}\bigg[Q^2(1+3\pi \, r_h^2) \cr &+ r_h^4 \Big[3\pi \left(1 -\dot{r}_h \right) + (3-\pi \, r_h^2)\Lambda \Big] \bigg]. \end{aligned} $

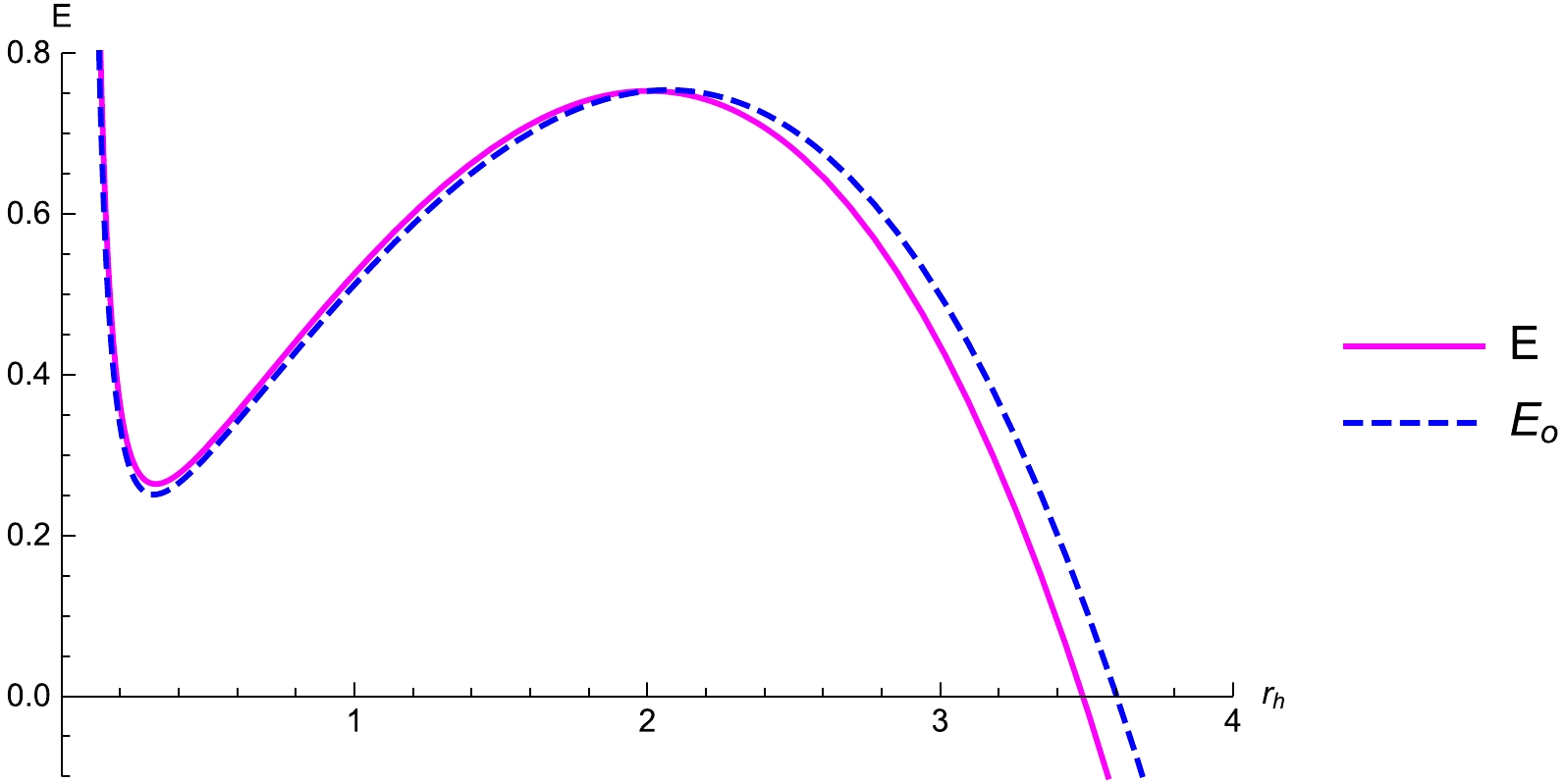
(74) Figure 11 shows the internal energies of the VBdS black hole with and without the influence of the LIV theory. For small black holes, both internal energies are positive and exhibit a fluctuation behaviour. However, the internal energy becomes negative for a large black hole, which reflects the stability of the large black hole. There exists an event horizon radius
$ r_h=r_{h}^* $ below which the internal energy under the LIV theory is higher than the internal energy without the LIV theory, and vice versa for$ r_h>r_{h}^* $ . The value of$ r_h^{*} $ is 2.00781. -
The enthalpy H of the black hole is [87]
$ \begin{align} H= E + P \,V. \end{align} $

(75) We derive the pressure from the Helmholtz free energy:
$ \begin{aligned}[b] P=\;&-\dfrac{{\rm d} F}{{\rm d} V} =\frac{1}{16\pi^2 r_h^6(1-2\dot{r}_h)}\bigg[r_h^2\Big(\Sigma + \Lambda r_h^2(1+\lambda m)\Big) \cr & -3Q^2(1+\lambda m) \bigg] \times \bigg[\pi r_h^2 \cr & + \ln \bigg(\frac{4\sqrt{\pi}(1-2\dot{r}_h)}{\big(\Sigma - \Lambda r_h^2(1+\lambda m)\big) -Q^2(1+\lambda m)r_h^{-2}}\bigg)\bigg]. \cr \end{aligned} $

(76) Using Eqs. (73) and (76), we calculate the enthalpy of the VBdS black hole under the LIV theory:
$ \begin{aligned}[b] H=\;& \frac{1}{12\pi r_h^3 (1-2\dot{r}_h)} \bigg[Q^2(2 + 9\pi r^2)(1+\lambda m) \cr &+ r^4\Big[7\pi\Sigma + (6-\pi r^2)(1+\lambda m)\Lambda \Big] \cr &+ \Big[ r^2\Big\lbrace \Sigma + (1+\lambda m)\Lambda r^2 \Big\rbrace - 3Q^2(1+\lambda m) \Big] \cr \times & \ln \Big[\frac{4\sqrt{\pi}(1-2\dot{r}_h)}{\Sigma - \Lambda r_h^2(1+\lambda m) -Q^2(1+\lambda m)r_h^{-2}}\Big] \bigg]. \end{aligned} $

(77) The enthalpy of the VBdS black hole in the absence of LIV theory is
$ \begin{aligned}[b] H_0=\;& \frac{1}{12\pi r_h^3 (1-2\dot{r}_h)} \bigg[Q^2(2 + 9\pi r^2)+ r^4\Big[7\pi (1-2 \dot{r_h}) \cr & +\Lambda \left( 6-\pi r^2\right) \Big] + \Big[ r^2 \left( 1-2 \dot{r_h} + \Lambda r^2 \right) - 3Q^2 \Big] \cr & \times \ln \Big[\frac{4\sqrt{\pi}(1-2\dot{r}_h)}{1-2\dot{r_h} - \Lambda r_h^2 -Q^2 r_h^{-2}}\Big] \bigg]. \end{aligned} $

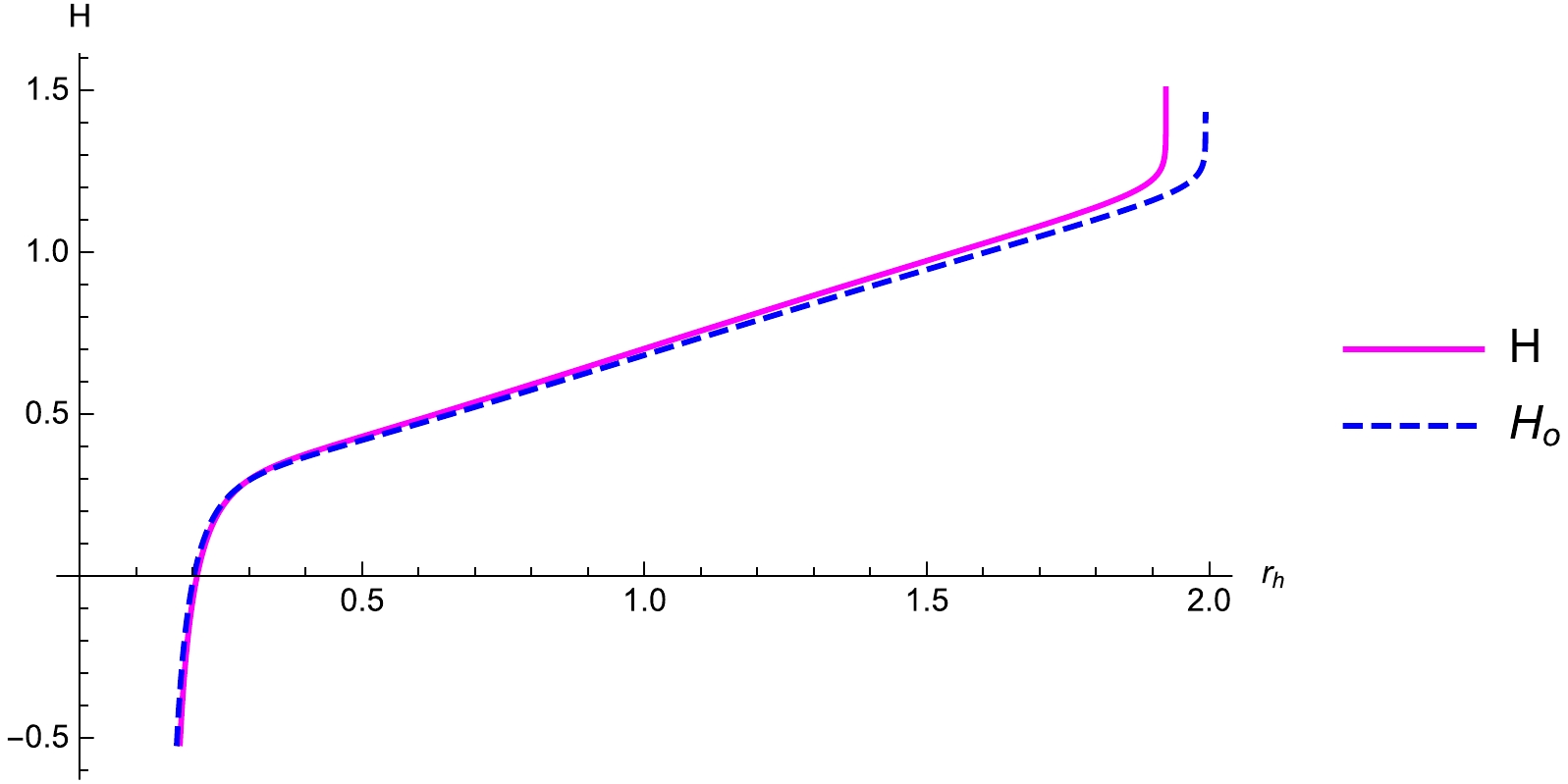
(78) In Fig. 12, the enthalpies of the VBdS black hole with and without the influence of the LIV theory are plotted and illustrate the effect of the LIV theory. The LIV theory does not affect the small black hole, but increases the enthalpy of a large black hole.
-
In this section, we discuss the global and local stabilities of the black hole. The global stability of the black hole is analyzed by using the Gibbs free energy. The local stability is discussed by evaluating the heat capacity and Hessian matrix.
-
When the cosmological constant is interpreted as thermodynamic pressure, a new term
$V {\rm d}P$ arises in the first law of black hole thermodynamics. As a consequence, the mass of the black hole is considered as enthalpy rather than internal energy [89−91]. Thus, the first law of nonrotating charged black hole thermodynamics becomes$ \begin{align} {\rm d}M=T\,{\rm d}S+ V\, {\rm d}P+\Phi \, {\rm d}Q, \end{align} $

(79) where
$\Phi=\dfrac{Q}{r_h}$ is the electric potential. Thus, in the canonical ensemble, the Gibbs free energy of the black hole in the extended phase space is$ \begin{align} G=M-T S. \end{align} $

(80) The modified Gibbs free energy under the LIV theory is obtained by substituting Eqs. (5), (21), and (67) in Eq. (80):
$ \begin{aligned}[b] G =\;& \frac{1}{4\pi r_h^3(1-2\dot{r}_h)}\bigg[2\pi r_h^2(1-2\dot{r}_h) \Big(r_h^2 +Q^2-2r_h^2\dot{r}_h \cr & - \frac{\Lambda}{3}r_h^4 \Big)-\Big\lbrace \Sigma r_{h}^2- (1+\lambda m) \big( Q^2 +\Lambda r_{h}^4 \big) \Big\rbrace \cr & \times \Big(\pi r_h^2 + \ln \Big[\dfrac{4\sqrt{\pi}r_{h}^2(1-2\dot{r}_h)}{ \Sigma r_{h}^2- (1+\lambda m) \big( Q^2 +\Lambda r_{h}^4 \big) } \Big]\Big)\bigg]. \end{aligned} $

(81) The Gibbs free energy in the absence of LIV is
$ \begin{aligned}[b] G_0 =\;& \frac{1}{4\pi r_h^3(1-2\dot{r}_h)}\bigg[2\pi r_h^2(1-2\dot{r}_h) \Big(r_h^2 -Q^2-2r_h^2\dot{r}_h \\ & - \frac{\Lambda}{3}r_h^4 \Big)-\Big( r_{h}^2-2r_{h}^2 \dot{r}_h -Q^2-\Lambda r_{h}^4 \Big) \\ & \times \Big(\pi r_h^2 + \ln \Big[\dfrac{4\sqrt{\pi}r_{h}^2(1-2\dot{r}_h)}{ r_{h}^2-2r_{h}^2 \dot{r}_h -Q^2-\Lambda r_{h}^4 } \Big]\Big)\bigg]. \end{aligned} $

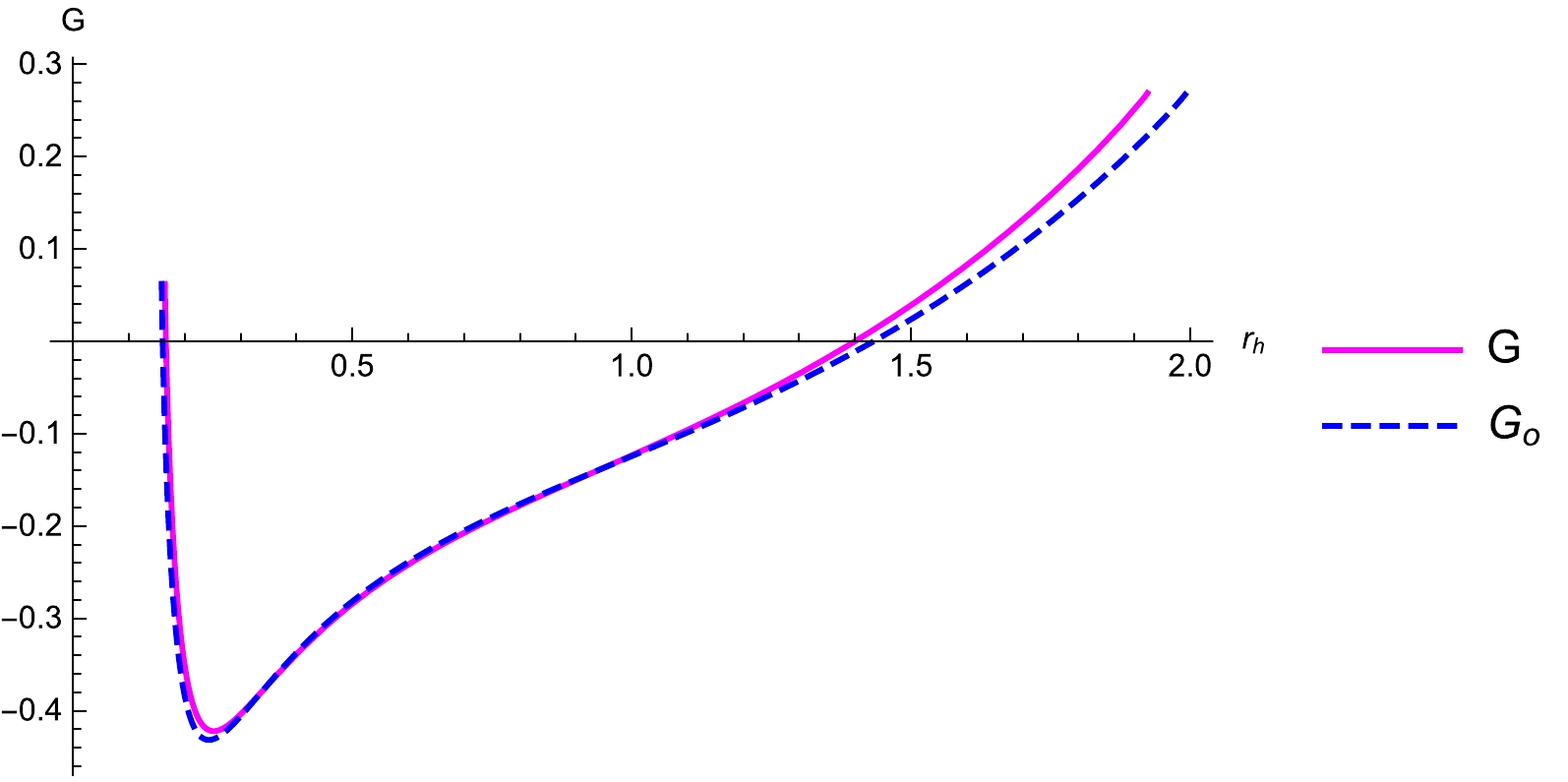
(82) The Gibbs free energy of the black hole provides a vital information about the global stability of the black hole. The preferred phase of the system is that minimizing the Gibbs free energy. The Gibbs free energies under the LIV modification and in the absence of LIV modification are plotted in Fig. 13. Both decrease for a small black hole and increase with the increase in
$ r_h $ . The small black hole has a lower Gibbs free energy, and hence it is globally stable. The large black holes have a higher Gibbs free energy signifying a globally unstable state. Further, the black holes are more unstable under the influence of the LIV theory. -
The heat capacity of the black hole provides a vital information about its phase transitions and thermodynamic local stability. The phase transition point is the point where the heat capacity either vanishes or diverges. The points where the heat capacity vanishes correspond to first-type phase transition whereas the points at which the heat capacity diverges correspond to second-type phase transition. A stable black hole has a positive heat capacity, whereas an unstable black hole has a negative heat capacity.
The heat capacity in the absence of LIV is calculated using Eqs. (22) and (68):
$ \begin{aligned}[b] C_0=\;&T_h\frac{\partial S_c}{\partial T_h} \\ =\;& \frac{2\bigg[Q^2(1+\pi r_h^2)- r_{h}^4 \left\lbrace \Lambda+\pi \left(1-2 \dot{r_h}-r_h^2 \Lambda \right) \right\rbrace \bigg]}{r_{h}^2 \left(1-2 \dot{r_h}+r_h^2 \Lambda \right) - 3Q^2 }.\cr \end{aligned} $

(83) By substituting Eqs. (21) and (67) in Eq. (83), we obtain the modified heat capacity under the influence of the LIV theory:
$ \begin{aligned}[b] C =\;&T\frac{\partial S}{\partial T}= \frac{2}{r_h^2\Big(\Sigma + \Lambda r_h^2(1+\lambda m)\Big) - 3Q^2 (1+\lambda m)} \\ & \bigg[Q^2(1+\lambda m)(1+\pi r_h^2)- \bigg\lbrace \Lambda (1+\lambda m) \\ & +\pi \Big(\Sigma - \Lambda r_h^2(1+\lambda m) \Big) \bigg\rbrace \bigg]. \end{aligned} $

(84) To study the influence of the LIV theory on the phase transition and stability of the black hole, we plot
$ C_0 $ and C in Fig. 14. For the heat capacity in the absence of LIV, the second-type phase transition point is$ r_h=0.271375 $ , while the first-type phase transition points are$ r_h=0.315466 $ and$ r_h=2.07203 $ for the above set of parameters. However, due to the LIV theory, the second-type phase transition point is$ r_h=0.280751 $ , while the first-type phase transition points are$ r_h=0.321609 $ and$ r_h=2.00468 $ . We conclude that the positions of phase transitions are affected by the LIV theory. Notably, both heat capacities are positive for a large horizon radius, which implies stability for large black holes. The stable and unstable ranges of the heat capacities are presented in Table 4.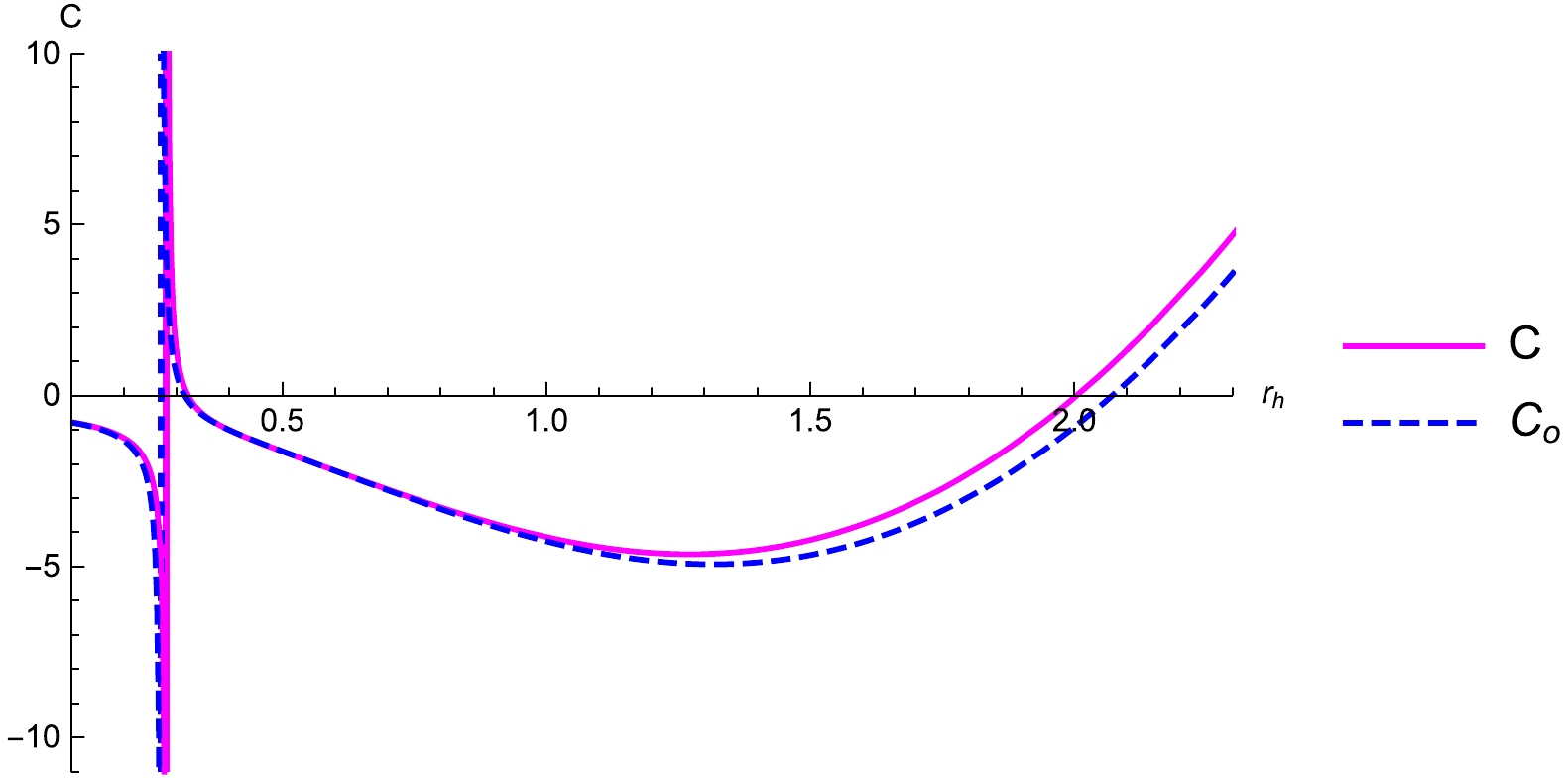
Figure 14. (color online) Heat capacity of the VBdS black hole with and without LIV theory with respect to the radius of the event horizon
$ r_h $ for$ Q=0.1 $ ,$ \lambda=1 $ ,$ \Lambda=0.1 $ ,$ m=0.1 $ , and$ \dot{r_h}=0.3 $ .Stable range Unstable range Heat capacity without LIV theory $ (C_0) $ 

$ 0.271375<r_h< 0.3 $ 

$ 0<r_h< 0.271375 $ 

$ 2.07203<r_h $ 

$ 0.315466<r_h< 2.07203 $ 

Heat capacity with the LIV theory $ (C) $ 

$ 0.280751<r_h< 0.321609 $ 

$ 0<r_h<0.280751 $ 

$ 2.00468<r_h $ 

$ 0.321609<r_h< 2.00468 $ 

Table 4. Stable and unstable ranges of the VBdS black hole with and without LIV theory.
-
Another approach to evaluate the local stability of black holes is by using the Hessian matrix of the Helmholtz free energy. This matrix involves the second-order derivatives of the Helmholtz free energy with respect to the Hawking temperature and chemical potential
$ \left(\phi=\dfrac{\partial M}{\partial Q}\right) $ . The Hessian matrix is defined as$ \begin{align} \mathcal{\tilde{H}} =\left(\begin{array}{c c} \mathcal{\tilde{H}}_{aa} & \mathcal{\tilde{H}}_{ab}\\ \mathcal{\tilde{H}}_{ba} & \mathcal{\tilde{H}}_{bb}\\ \end{array}\right)\;\;\; a,b=1,2, \end{align} $

(85) where
$ \mathcal{\tilde{H}}_{11} = \dfrac{\partial ^2 F}{\partial T^2} $ ,$ \mathcal{\tilde{H}}_{12}=\dfrac{\partial^2 F}{\partial T \, \partial \phi} $ ,$ \mathcal{\tilde{H}}_{21} = \dfrac{\partial^2F}{\partial \phi \, \partial T} $ , and$ \mathcal{\tilde{H}}_{22}= \dfrac{\partial^2 F}{\partial \phi^2} $ . The determinant of the Hessian matrix is zero. Thus, one of the eigenvalue of the matrix (85) is zero. The other eigenvalue is determined by the trace of the matrix. The trace of the Hessian matrix must be positive for the black hole to be locally stable. It is calculated by$ \begin{align} \tau=T_r(\mathcal{\tilde{H}}) = \mathcal{\tilde{H}}_{11} + \mathcal{\tilde{H}}_{22}, \end{align} $

(86) where
$ \begin{aligned}[b] H_{11} =\;& 8\pi r_h^3 (1-2\dot{r}_h)\frac{\Sigma_1}{\Sigma_2},\\ H_{22} =\;&\frac{1}{4\pi Q^2 (1-2\dot{r}_h)} \bigg[ 2(1+\lambda m)(3Q^2 + \Lambda r^4) \\ &+\frac{\Theta}{r_h^2\Big(\Sigma - \Lambda r^2(1+\lambda m)\Big)-Q^2(1+\lambda m)} \\ &\times \ln \bigg\{\frac{4\sqrt{\pi}(1-2\dot{r}_h)}{\big(\Sigma - \Lambda r_h^2(1+\lambda m)\big) -Q^2(1+\lambda m)r_h^{-2}}\bigg\} \bigg]\cr \end{aligned} $

(87) and
$ \Sigma_1 $ ,$ \Sigma_2 $ , and Θ are defined as$ \begin{aligned}[b] \Sigma_1 =\;& Q^2(1+\lambda m)(1+\pi \, r_{h}^2)+r_{h}^4\Big[\Lambda(1+\lambda m)(\pi \,r_{h}^2 -1) \cr &-\Sigma \, \pi\Big],\end{aligned} $

$ \begin{aligned}[b]\Sigma_2 =\;& \Big[3Q^2(1+\lambda m)-\Big(\Sigma + (1+\lambda m)\Lambda r_h^2\Big)r_h^2\Big] \cr &\times \Big[r_h^2\big(\Sigma-\Lambda r_{h}^2(1+\lambda m)\big)-Q^2(1+\lambda m) \Big],\\ \Theta =\;& 2\Big[3Q^4(1+\lambda m)^2 - Q^2 r_{h}^2 (1+\lambda m)\Big\lbrace (1+\pi \, r_{h}^2)\Sigma \cr & + 2\Lambda \,r_{h}^2(2+\pi \, r_{h}^2)(1+\lambda m)\Big\rbrace + r_{h}^6\Big\lbrace \Sigma \, \Lambda(1+\lambda m) \cr & \times (1+\pi \, r_{h}^2) + \pi \, \Sigma^2 + r_{h}^2 \Lambda^2 (1+\lambda m)^2(1-2\pi r_{h}^2) \Big\rbrace \Big]. \end{aligned} $

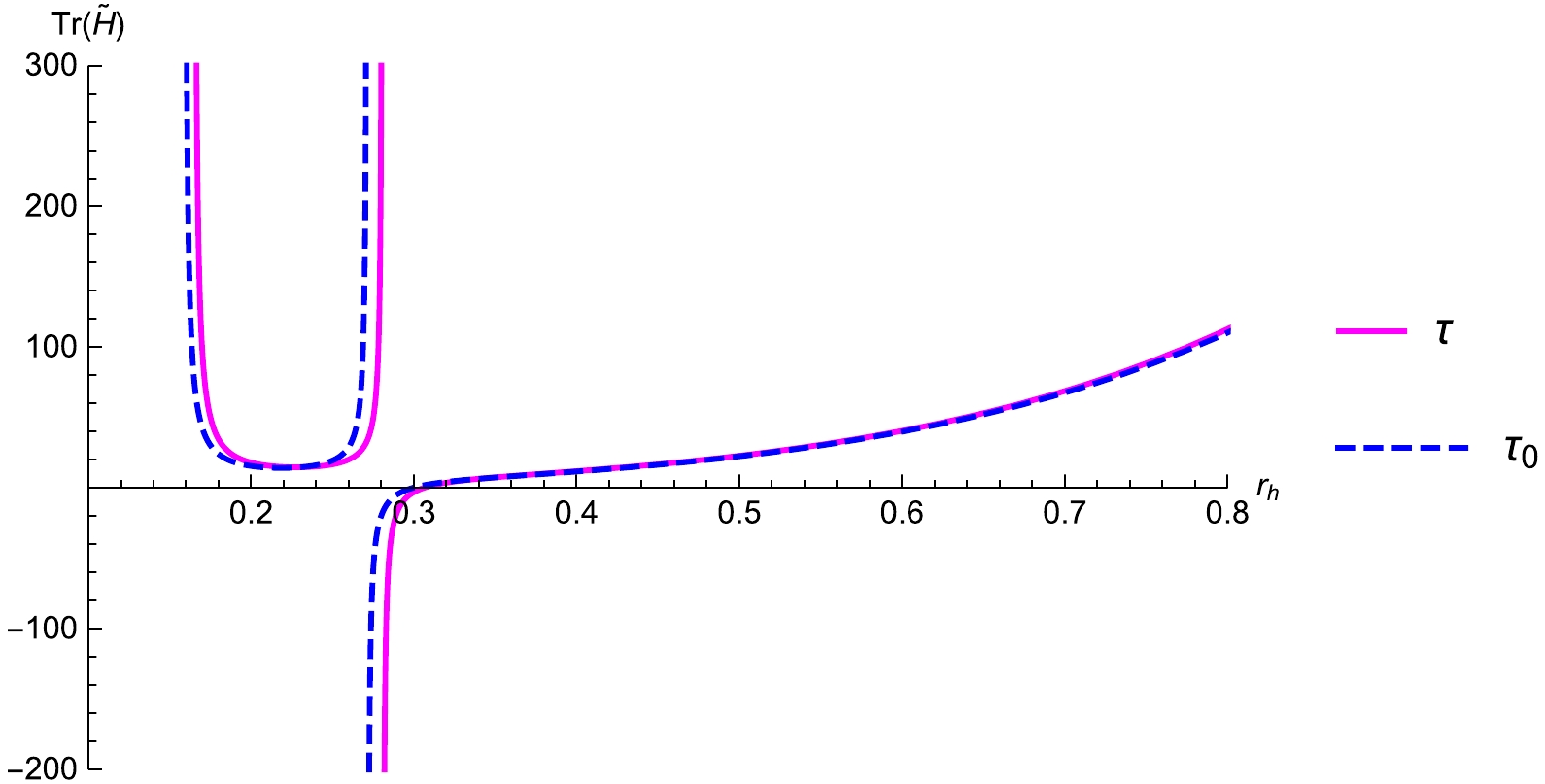
(88) We plot the trace of the Hessian matrix with respect to the event horizon radius in Fig. 15. In the absence of LIV theory, the black holes in the ranges
$ 0.158613< r_h<0.271375 $ and$ 0.299026<r_h<\infty $ are stable, while, under the influence of the LIV theory, the stable ranges are$ 0.164393<r_h<0.280751 $ and$ 0.305731< r_h< \infty $ . The LIV theory affects the stability range of the black hole. The large black holes are locally stable. -
In this study, the quantum tunneling radiation of fermions near the event horizon of a VBdS black hole was investigated by using the Rarita-Schwinger-Hamilton-Jacobi equation under the influence of LIV modification. Based on the LIV modification, the corrected tunneling rate and Hawking temperature were derived and found to be dependent on the LIV parameter and mass of the particle. For
$ \lambda=0 $ , the results are consistent with those in [69]. The thermal fluctuations of the VBdS black hole under the influence of the LIV modification were also investigated. We used first-order logarithmic corrections to calculate the corrected entropy of the VBdS black hole under the LIV modification. Further, the modifications in the thermodynamic quantities such as the Helmholtz free energy, internal energy, enthalpy, Gibbs free energy, and heat capacity due to the LIV modification were studied. Under the influence of the LIV modification, the above thermodynamic quantities tend to increase. Our graphical analysis showed that the LIV modification affects the thermodynamic quantities of large black holes, but it does not affect the small black holes. The stability of the black hole was investigated by using the Gibbs free energy, heat capacity, and Hessian matrix. The local stability range of the VBdS black hole under the LIV modification is presented in Table 4. The large black holes are locally stable.Further, the thermodynamic behaviour of the VBdS black hole in the extended phase space was discussed. By treating the cosmological constant as a thermodynamic pressure, we derived the equation of state under the LIV modification. Similar to the van der Waals liquid-gas system, in the isotherms of the VBdS black holes, we observed a region where the condition of stable equilibrium is violated. The unphysical oscillating part in the isotherm should be replaced by an isobar, which represents the liquid-gas coexistence line. For different conjugate variables,
$ P-\tilde{v} $ ,$ P-V $ , and$ T-S $ , we investigated the phase transitions and positions of the boundary of two-phase coexistence using the Maxwell's equal area law and influence of the LIV modification on the phase transition points. In the$ P-\tilde{v} $ and$ P-V $ planes, the length of the isobar decreases with the increase in the temperature. Further, the LIV modification increases the length of the phase transition, and the transition of the liquid phase to the gas phase occurs at a lower pressure. Similarly, in the$ T-S $ diagram, the increase in the pressure tends to decrease the length of the isobar. The liquid-gas coexistence region in the$ T-S $ diagram increases, and the phase transition occurs at a lower temperature under the LIV modification. -
We thank the anonymous reviewers for the valuable suggestions and comments to improve the paper.
-
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Maxwell's equal area law for Vaidya-Bonner-de Sitter black hole under Lorentz invariance violation
- Received Date: 2024-04-18
- Available Online: 2024-11-15
Abstract: In this study, we investigate the tunneling of fermions with arbitrary spin near the event horizon of a nonstationary Vaidya-Bonner-de Sitter (VBdS) black hole under Lorentz invariance violation (LIV). The modified Hawking temperature of VBdS black holes is calculated by using tortoise coordinate transformation, Feynman prescription, and Wentzel–Kramers–Brillouin approximation. By considering the cosmological constant as a thermodynamic pressure in the extended phase space, we construct a Maxwell's equal area law under LIV and study the phase transitions of VBdS black hole in





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: