Dynamical study of T_ss systems using the chiral quark model

In 1964, Gell-Mann [1] and Zweig [2] proposed the conventional quark model, suggesting that mesons and baryons are composed of $ q\bar{q} $ and qqq, respectively. At that time, most hadrons were properly explained by this model. However, over the past two decades, there has been an influx of new experimental data unveiling properties of hadronic states that challenge the predictions of the conventional quark model, such as X(3872) [3], Y(4626) [4], and $ Z_{c}(3900) $ [5]. These exotic hadronic states provide a valuable platform for a deeper understanding of the properties of low-lying Quantum Chromodynamics (QCD).

In 2021, the LHCb Collaboration reported a new state $ T_{cc}^{+} $(3875) in the $ D^{0}D^{0}\pi $ mass distribution with a mass $ M=3875.1+\delta m_{\exp} $, where $ \delta m_{\exp}=-273\pm61\pm5^{+11}_{-14} $ keV, and a width $ \Gamma=410\pm165\pm43^{+18}_{-38} $ keV [6, 7]. This notably narrow width indicates that it is a long-living exotic state. Its spin-parity quantum number is $ J^{P}=1^{+} $. The minimal quark content of $ T_{cc}^{+} $(3875) is $ cc\bar{u}\bar{d} $, which means that, unlike the three hidden-charm tetraquark states mentioned above, there can be no annihilation for such a component. These interesting properties have attracted theoretical attention and motivated research globally [8−48]. It is generally assumed that $ T_{cc}^{+} $ is a molecular state, a compact tetraquark, or a triangle singularity. For example, in Ref. [8], by using a coupled-channel approach, the authors suggested that $ T_{cc}^{+} $ is a hadronic molecule generated by the interactions in the $ D^{*+}D^{0} $ and $ D^{*0}D^{+} $ channels. In Ref. [9], they also argued that $ T_{cc}^{+} $ is a molecule state in the framework of chiral unitary theory. Moreover, S. S. Agaev et al. [10] proposed that $ T_{cc}^{+} $ is a compact structure by employing the QCD three-point sum rule method. In Refs. [11, 12], the authors proposed that this state may be a triangle logarithmic singularity.

In addition to the T_cc state, double-bottom ($ T_{bb} $) tetraquark states have also been investigated in various theoretical frameworks. In Ref. [13], also using a coupled-channel approach, the authors proposed that $ \bar{B}^{*}\bar{B}^{*} $ states with $ IJ^{P}=01^{+},11^{+} $ might be good molecular candidates. In Ref. [14], J. Cheng et al. employed a heavy diquark-antidiquark symmetry (HDAS) and the chromomagnetic interaction (CMI) model to study $ bb\bar{n}\bar{n} $ ($ n=u,\; d $) tetraquark states. The results show that the lowest energy of $ bb\bar{n}\bar{n} $ with $ IJ^{P}=01^{+} $ is approximately 116 MeV below the $ \bar{B}\bar{B}^{*} $ threshold. In Ref. [15], Lin et al. investigated the P-wave $ T_{bb}^{-} $ states in the diquark-antidiquark framework by employing the quark model. In the $ \rho $-mode with $ 1^{1}P_{1} $ $ [bb]_{\bar{3}}^{0}[\bar{u}\bar{d}]_{3}^{0} $ configuration, its energy is approximately 18 MeV lower than the $ \bar{B}\bar{B} $ threshold, which means it can establish a compact bound state.

Furthermore, theoretical investigations have explored other partners ($ T_{bc} $, $ T_{bc\bar{s}} $, $ T_{cc\bar{s}} $, $ T_{bb\bar{s}} $) of T_cc. In the case of$ T_{bc} $, $ T_{bc\bar{s}} $ states, in Ref. [18] the authors employed a nonrelativistic quark model and found that $ T_{bc} $ with $ IJ^{P}=00^{+} $ and 01⁺, $ T_{bcs} $ with $\frac{1}{2}0^{+}$, $\frac{1}{2}1^{+}$ can form a bound state. The high-spin states $ T_{bc} $ with $ 02^{+} $ and $ T_{bc\bar{s}} $ with $\frac{1}{2}2^{+}$ can decay into D-wave $ \bar{B}D $ and $ \bar{B}_{s}D $, although they are below the $ \bar{B}^{*}D^{*} $ and $ \bar{B}_{s}^{*}D^{*} $ thresholds, respectively. The QCD sum rule has also been used to calculate $ T_{bc} $ and $ T_{bc} $ [16, 17]. In Ref. [16], the authors suggested that for the $ T_{bc\bar{s}} $ states with $ J^{P}=0^{+} $ and $ 1^{+} $, both masses are below the corresponding thresholds ($ D^{(*)}\bar{B}^{(*)} $). In Ref. [17], the results show that the masses of $ T_{bc\bar{s}} $ tetraquark states are below the thresholds of $ \bar{B}_{s}D $ and $ \bar{B}^{*}_{s}D $ final states for the scalar and axial-vector channels, respectively. Regarding $ T_{cc\bar{s}} $ and $ T_{bb\bar{s}} $ tetraquark states, in Ref. [18], the authors argued that $ T_{cc\bar{s}} $ is not a bound state, but they obtained a shallow bound state for the $ T_{bb\bar{s}} $ tetraquark state with $IJ^{P}= {\frac{1}{2}}1^{+}$. Applying the color-Coulomb potential in the diquark-antidiquark framework at the heavy quark limit [19], the $ T_{bb\bar{s}} $ state becomes bound into compact structures. However, in Ref. [20], the authors reported that $ T_{cc\bar{s}} $ can establish a stable state against the strong interaction. Further results and discussions on the partners of T_cc can be found in Refs. [49−59].

While T_cc partners involving heavy quarks have been extensively studied, limited attention has been given to double strangeness partner (T_ss) tetraquark states. Thus, the investigation of bound and resonant states in the T_ss system is both interesting and necessary.

The structure of the paper is as follows. Section II provides a brief description of the quark model and wave functions. Section III introduces the real-scaling method. Section IV details the ³P₀ method. Section V presents our results and discussion.

In this study, we primarily investigated the dynamics of the $ s\bar{q}s\bar{q} $ system using the chiral quark model. This model is an excellent potential framework because it effectively explains hadron interactions, including mass, kinetic, and potential terms, which can be expressed as

where m denotes the quark mass, $ \mu $ represents the reduced mass, and $ \vec{p} $ is the relative momentum between quarks. The form of $ \mu $ is

In the $ s\bar{q}s\bar{q} $ system, s and q can be approximately regarded as identical quarks. Consequently, the exchange of Goldstone bosons between s and q plays a significant role. Therefore, our potential includes the confinement potential, one-gluon exchange potential, and Goldstone boson exchange potential, expressed as follows:

Goldstone boson exchange mainly stems from the spontaneous chiral symmetry breaking, a fundamental characteristic of QCD. This results in a long-range attractive force between quarks. In our chiral quark model, the chiral part of the Hamiltonian, ($ V_{\pi}(r_{ij}) $+$ V_{\eta}(r_{ij}) + $ $ V_{K}(r_{ij}) $+ $ V_{\sigma}(r_{ij}) $), can be expressed as

where $ {\boldsymbol{\sigma}} $ represents the Pauli matrices acting on the spin wave functions of the T_ss system, and $ {\boldsymbol{\lambda}}^{a} $ denotes the Gell-Mann matrices acting on the flavor wave functions of the T_ss system. $ Y(x) $ is the Yukawa function, explicitly given by $Y(x)={e^{-x}}/{x}$. $ \Lambda_{\chi} $ serves as the cut-off parameter, and $ g^2_{ch}/4\pi $ denotes the Goldstone-quark coupling constant. The masses of Goldstone bosons are denoted by $ m_{\pi} $, $ m_{\eta} $, and $ m_{K} $, while $ m_{\sigma} $ is determined by the relation

One of the characteristics of QCD is quark confinement, which suggests that quarks cannot be separated. This corresponds to the confinement potential in the Hamiltonian. Unlike other potential forms in the quark model, the confinement potential is not directly derived from the field theory. Consequently, it typically appears in three common forms: linear [60], quadratic [61], and screened[62] confinement potentials. These potentials share the common feature of exhibiting strong attraction at short distances. The distinction lies in the fact that, owing to screening effects, screened confinement potential can describe well the spectra of light mesons including excited states. Given that the $ s\bar{q}s\bar{q} $ system involves light mesons (K/K^*), we employed the screened confinement potential in this study. Its specific form is expressed as

where $ {\boldsymbol{\lambda}}^{c} $ denotes $S U(3)$ color Gell-Mann matrices, and $ a_{c} $ and $ \mu_c $ are model parameters.

The one-gluon exchange potential $V_{\rm oge}(r_{ij})$ reflects the QCD characteristic of asymptotic freedom. It plays a crucial role in the quark model by offering intermediate-range attractive forces. This potential generally consists of a Coulomb term and a color-magnetic term. It reads

where $ \alpha_s $ is the QCD-inspired strong coupling constant, which is determined by fitting experimental meson data. Generally, the heavier the quark, the smaller the coupling constant between quarks. All the parameters are determined by fitting the meson spectrum, from light to heavy, taking into account only a quark-antiquark component. They are listed in Table 1.

Quark masses	$ m_u=m_d $(MeV)	313
	$ m_{s} $(MeV)	555
Goldstone bosons	$\Lambda_{\pi}=\Lambda_{\sigma}(\rm fm^{-1})$	4.2
	$\Lambda_{\eta}=\Lambda_{K}(\rm fm^{-1})$	5.2
	$ g_{ch}^2/(4\pi) $	0.54
	$ \theta_p(^\circ) $	–15
Confinement	$ a_{c} $ (MeV)	430
	$ \mu_{c} $($ fm^{-1} $)	0.7
	$ \Delta $(MeV)	181.1
OGE	$ \alpha_{qq} $	0.54
	$ \alpha_{qs} $	0.48
	$ \alpha_{ss} $	0.42
	$ \hat{r}_0 $(MeV)	28.17

Table 1.  Quark model parameters ($ m_{\pi}=0.7 $ $\rm fm^{-1} $, $ m_{\sigma}=3.42 $ $\rm fm^{-1} $, $ m_{\eta}=2.77 $ $\rm fm^{-1} $, $ m_{K}=2.51 $ $\rm fm^{-1} $).

The T_ss system has two important structures: the molecular ($ s\bar{q} $-$ s\bar{q} $) and diquark ($ ss $-$ \bar{q}\bar{q} $) configurations. At the quark level, these are expressed as the product of four components: color, spin, flavor, and orbital parts. According to QCD, any quark system, including multi-quark states, must be colorless. Therefore, the color wave function of a four-quark system can be obtained by two coupled color-singlet clusters, $ {\bf{1}} \otimes {\bf{1}} $,

Additionally, the color wave function of a colorless four-quark system can also be obtained by coupling two color-octet wave functions, $ {\bf{8}} \otimes {\bf{8}} $,

These two color wave functions correspond to the molecular configurations. Regarding the diquark structure, the color wave functions are constructed in a similar manner to the coupling of two color-octet states into a color-singlet four-quark wave function. Specifically, it involves coupling $ {\bf{3}} \otimes \bar{{\bf{3}}} $ and $ {\bf{6}} \otimes \bar{{\bf{6}}} $ to form a colorless four-quark system. The wave function can be expressed as

In contrast to color wave functions, the spin of antiquarks and quarks is indistinguishable. Therefore, diquark and molecular structures share the same spin wave function. Given that we are studying the T_ss system with total spin 1, its wave function exists in three possible configurations, namely $ {\bf{0}} \otimes {\bf{1}} $ ($ S_1 $), $ {\bf{1}} \otimes {\bf{0}} $ ($ S_2 $), and $ {\bf{1}} \otimes {\bf{1}} $ ($ S_3 $),

The flavor wave functions of the sub-clusters for the two structures are

In this case, the subscripts of $ \chi_{I,I_z}^{fm(d)i} $ denote the isospin and its third component, while the superscripts specify the structure (fm for the molecular configuration and $ fd $ for the diquark configuration) and the index. Considering the isospin of T_cc, the isospin of T_ss is set to zero. Thus, the total flavor wave function can be coupled in two possible ways: $ {\bf{\frac{1}{2}}} \otimes {\bf{\frac{1}{2}}} $ (molecular configuration, $ F_1 $) and $ {\bf{0}} \otimes {\bf{0}} $ (diquark configuration, $ F_2 $). The total flavor wave functions can be written as

Given that the T_ss system has positive parity, we set all orbital quantum numbers to zero. Consequently, its spatial wave function can be represented as

The spatial wave functions for the three relative motions involved here are expanded using the Gaussian Expansion Method (GEM):

with normalization constant

The coefficients $ c_n $ are variational parameters determined through dynamic optimization. The Gaussian size parameters follow a geometric progression,

Here, $ r_n $ denotes the Gaussian size parameter for the n-th term, with $ r_1 $ and $r_{n_{\max}}$ as the initial parameters.

The total wave function is constructed as the direct product of the orbital, spin, color, and flavor wave functions. Thus, the complete wave function of the system is expressed as

Here, $ {\cal{A}} $ denotes the antisymmetrization operator. For the $ s\bar{q}s\bar{q} $ system, where the two subsystems are identical, $ {\cal{A}} $ is defined as 1-(13)-(24)+(13)(24). Subsequently, to determine the eigen-energies of the system utilizing the Rayleigh-Ritz variational principle, we solve the Schrödinger equation:

The real-scaling method was first proposed by Taylor [63] to study resonance states in electron-molecule systems. Owing to its success in explaining a substantial amount of experimental data, Hiyama et al. [64] applied this method at the quark level to search for the $ P_c $ states in the $ qqqc\bar{c} $ system. Subsequently, we introduced this method to the tetraquark system for the first time and successfully explained particles [65−69] such as Y(4626), X(2900), and $ \Upsilon $(10753).

The real-scaling method involves systematically scaling the width of Gaussian functions between two groups using a scaling factor denoted as $ \alpha $, $ R \rightarrow \alpha R $. As $ \alpha $increases, the width of the Gaussian functions expands, leading to variations in the system energy. If a stable structure is present, it remains unaffected by the changes in Gaussian function widths. Within the framework of this method, bound states do not exhibit decay behavior owing to the absence of corresponding decay channels, and thus manifest as horizontal lines, as shown in Fig. 1(a). Conversely, resonance states, which have several decay channels, strongly couple with scattering channels and decay to the relevant threshold channels. This is depicted in Fig. 1(b) by two downward-sloping lines that demonstrate avoid-crossing behavior. Given that resonance states are stable structures, the avoid-crossing structure may reappear as the scaling factor$ \alpha $ increases. However, a larger $ \alpha $ results in a more complex calculation process. Therefore, for computational efficiency, we set$ \alpha $ to range from 1.0 to 3.0. Within this range, most resonance states exhibit repeated avoid-crossing structures. The real-scaling method allows for the calculation of the decay width of stable states. The calculation equation is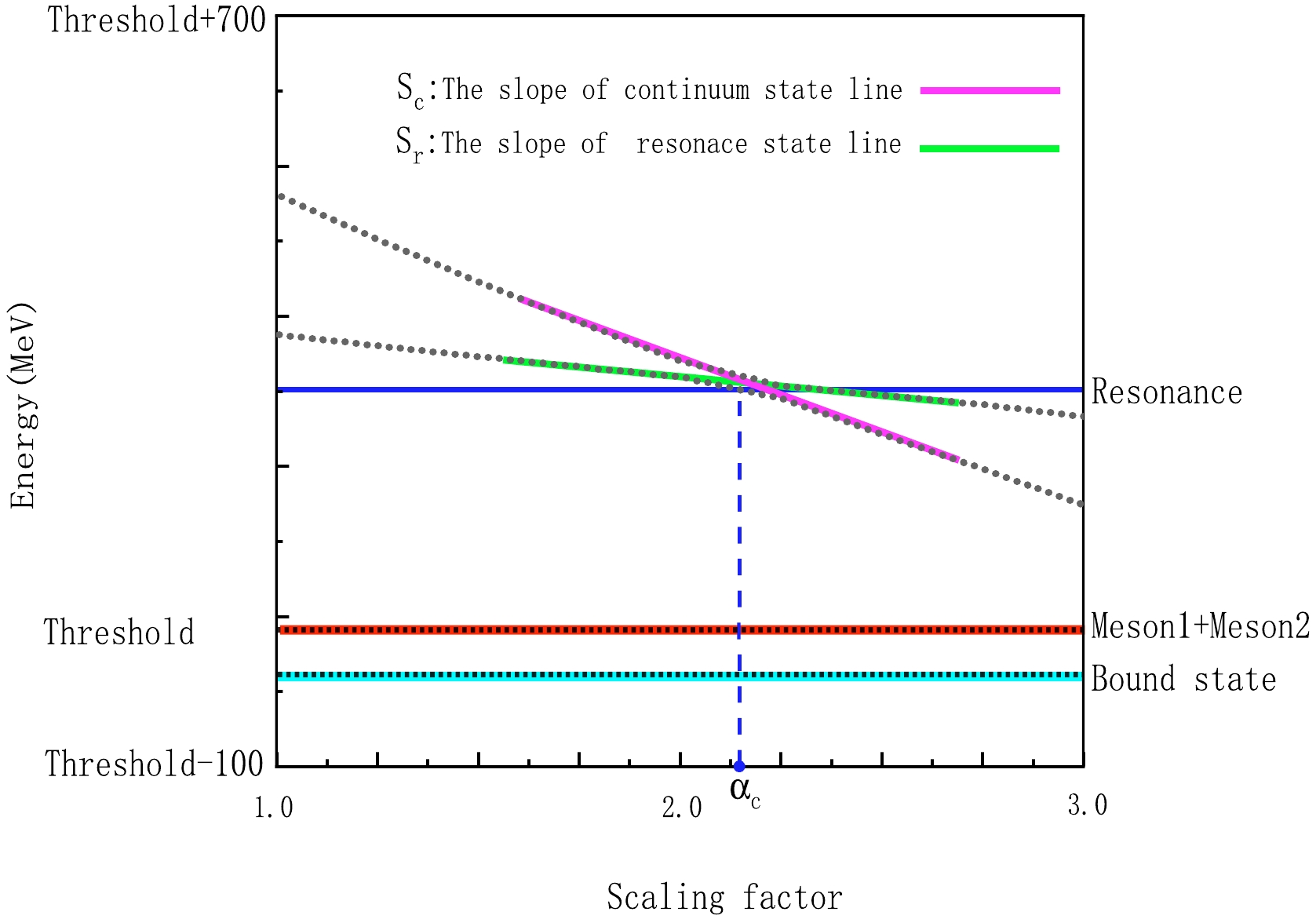

Figure 1.  (color online) Two forms of stable states, namely bound state (horizontal line) and resonance state (avoid-crossing structure), for the real-scaling method. The red line represents the threshold, while the light blue line indicates the bound state. The avoid-crossing structure formed by the red line represents the scattering state, whereas the green line represents a genuine resonance.

Based on the discussion above, in the framework of the real-scaling method, the avoid-crossing structure represents a resonant state, while the horizontal line indicates a bound state. Therefore, the decay width calculation given by Eq. (21) is applicable only to the decay width of resonant states. Here, $ \alpha_c $ denotes the $ \alpha $ coordinate corresponding to the avoid-crossing structure, while $ V(\alpha_c) $ represents the energy difference at the avoid-crossing point between the two lines; "$ slope_r $" and "$ slope_s $" indicate the slopes of these two lines.

The ³P₀ model is extensively employed in the calculation of meson decay widths [70, 71]. It posits that a meson in the vacuum excites a pair of quark-antiquark with momenta $ {\bf{p}}_3 $ and $ {\bf{p}}_4 $, respectively. The probability of their production is determined by a parameter $ \gamma $, which is generally determined by an overall fitting of the strong decay width of hadrons. Thus, one obtains $ \gamma=6.95 $ for $ u\bar{u} $ and $ d\bar{d} $ pair creation, and $ \gamma=6.95/\sqrt{3} $ for $ s\bar{s} $ pair creation [72]. The flavor wave function of the quark-antiquark pair is given by $\phi_{0} =(u\bar{u} + d\bar{d} + s\bar{s})/ {\sqrt{3}}$, and the color wave function is $\omega_{0} = (r\bar{r} + g\bar{g} + b\bar{b})/{\sqrt{3}}$. The operator in the model is

The S-matrix element for the process $ A \rightarrow B + C $ is expressed as

where $ {\bf{P}}_B $ and $ {\bf{P}}_C $ are the momenta of B and C mesons in the final state; they satisfy $ {\bf{P}}_A = {\bf{P}}_B + {\bf{P}}_C = 0 $ in the center-of-mass frame of meson A. $ {\cal{M}}^{M_{J_A}M_{J_B}M_{J_C}} $ is the helicity amplitude of the process $ A \rightarrow B + C $, which can be obtained as

with the momentum space integral

where $ {\bf{P}}={\bf{P}}_B=-{\bf{P}}_C $, $ {\bf{p}}={\bf{p}}_3 $, and $ m_3 $ is the mass of the created quark $ q_3 $. To analyze the results and compare the theoretical results with experimental data, the partial wave amplitude $ {{\cal{M}}}^{JL}(A\rightarrow BC) $ is often employed. It is related with the helicity amplitude by the Jacob-Wick formula [73]:

Finally, the decay width is calculated as

where a nonrelativistic phase-space is assumed,

with $ M_A $, $ M_B $, $ M_C $ being the masses of the mesons involved. In this study, for computational convenience, we transformed the transition operator T from the momentum space to the coordinate space. The specific form is

Here, $ {\bf{R}}_{AV}={\bf{R}}_A-{\bf{R}}_V $ is the relative coordinate between the source particle "A" and the created quark-antiquark pair in the vacuum, with

The convergence factor ${\rm e}^{-r^2/(4f^2)}$ in the modified operator $ T_2 $ accounts primarily for energy considerations of the quark-antiquark pairs created in the vacuum, confirming the difficulty of creating high-energy quark-antiquark pairs. The damping factor ${\rm e}^{-R_{AV}^2/{R_0}^2}$ reflects that the created quark-antiquark pair should not be too far from the originating particle. Finally, the parameter $ \gamma = 6.95 $ was initially obtained by fitting the heavy-flavor meson $ c\bar{c} $. However, a previous study of ours demonstrated that this parameter cannot be directly applied to the calculation of mass shifts in the light meson spectrum [74]. In this context, we need to calculate the decay of the light meson K^*. Therefore, we first obtained a new value for $ \gamma $ by fitting the experimental data for $ \rho \rightarrow \pi\pi $. The values of the parameters $ R_0 $ and f were ultimately determined by fitting the masses of light mesons,

We systematically studied the bound and resonant states in T_ss. We coupled the diquark and molecular structures to explore potential bound states, denoted as KK^*. Within the framework of the four-quark model, the KK^* states cannot decay via strong interactions into other two-meson channels. Therefore, the decay width of bound states KK^* can only originate from the process of $K^{*} \rightarrow K \pi$. Using the ³P₀ model, we first calculated the decay width of K^* in vacuum based on previously fitted parameters of light mesons. Then, we calculated the decay width of K^* when bound in the KK^* state, taking into account the effects of binding energy. By comparing these two results, we estimated the decay width of the bound state KK^*. Finally, we employed the real-scaling method to systematically identify resonant states in the energy range from 1.4 to 2.8 GeV and calculated their decay widths.

Table 2 summarizes the results of the bound-state calculations. Owing to symmetry restrictions, the molecular structure of the T_ss system with 01⁺ involves four physical channels: two color singlets, KK^* and K^*K^*, and their corresponding color octets. Meanwhile, the diquark structure of the T_ss system contains only two physical channels: $ [ss]_6^0[\bar{q}\bar{q}]_{\bar{6}}^1 $ and $ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $.

Channel	$ |S_i F_j C_k\rangle(\Psi^{i,j,k}) $	E	Mixed
KK*	$ |111\rangle $	1393
$ [K]_8[K^{*}]_8 $	$ |112\rangle $	1959
K*K*	$ |311\rangle $	1816
[K*]8[K*]8	$ |312\rangle $	1797
coupled-molecular-channels:			1392
$ [ss]_6^0[\bar{q}\bar{q}]_{\bar{6}}^1 $	$ |124\rangle $	1974
$ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $	$ |223\rangle $	1543
coupled-diquark-channels:			1484
complete coupled-channels:			1328
Threshold (K+K*):			1392

Table 2.  Results of the bound state calculations in the $ s\bar{q}s\bar{q} $ system (unit: MeV).

The energy of KK^* is 1393 MeV, which is 1 MeV above the threshold (1392 MeV). Its color octet state, $ [K]_8[K^{*}]_8 $, has an energy of 1959 MeV, which is significantly higher than the threshold energy, indicating that neither of these channels form bound states. By contrast, K^*K^* has an energy of 1816 MeV, whereas its color octet state, [K^*]₈[K^*]₈, has an energy of 1797 MeV. This energy is not only lower than that of $ [K]_8[K^{*}]_8 $ but also lower than the energy of K^*K^*. This can be attributed to the fact that, within the quark model, strong attractive forces are more likely to occur between double vector mesons [75]. We performed channel coupling for these four molecular states. The results indicate that, although K^*K^* and [K^*]₈[K^*]₈ exhibit strong attractive interactions, the coupling effect still do not lower the energy of the lowest energy channel KK^* below the threshold. Similarly, owing to symmetry constraints, the diquark structure contains only two physical channels, $ [ss]_6^0[\bar{q}\bar{q}]_{\bar{6}}^1 $ and $ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $. Among these, the $ 3 \times \bar{3} $ configuration has a relatively low energy of 1543 MeV, approximately 100 MeV above the threshold energy, whereas the $ 6 \times \bar{6} $ configuration has a much higher energy and is heavier than all the molecular structures. This suggests that the diquark structure with $ 3 \times \bar{3} $ exhibits stronger attraction. Subsequently, we performed structural mixing of the two physical channels in the diquark structure and the four physical channels in the molecular structure. The calculation results indicate that a bound state, B(1320), with a binding energy of 60 MeV was obtained. The composition analysis reveals that the molecular state KK^* contributes 82% to B(1320), while the $ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $ state contributes 13%, as shown in Table 3. The root-mean-square distance of B(1320) shows that the distance between internal quarks is approximately 1 fm, directly confirming that B(1320) is predominantly a molecular state.

State	KK*	$ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $	K*K*	[K*]8[K*]8	$ r_{s\bar{s}} $	$ r_{s\bar{q}} $	$ r_{\bar{q}\bar{q}} $
B(1320)	82%	13%	3%	2%	1.0	1.1	1.3

Table 3.  Main components of the bound state and root-mean-square distance among the internal quarks (unit: fm).

Similar to the decay width of T_cc, which mainly comes from $ DD^{*} \rightarrow DD + \pi $, the decay width of the predicted bound state B(1320) should mainly result from $ KK^{*} \rightarrow KK + \pi $. T_cc has a binding energy of 1 MeV and hence only minimally affects the phase space for $ DD^{*} \rightarrow DD + \pi $, resulting in a decay width almost equal to that of $ D^{*} $. In contrast to T_cc, B(1320) has a binding energy of 60 MeV, which substantially reduces the phase space for $ KK^{*} \rightarrow KK + \pi $. As a result, the decay width of B(1320) is expected to be less than that of K^*. To estimate the decay width of the bound state in the T_ss system (KK^*), we distributed the binding energy of 60 MeV equally between the two particles K and K^*. Consequently, the energy of K^* in KK^* had to be corrected by reducing it by approximately 30 MeV. The decay width of K^*, after this mass correction, provides the decay width of the bound state in the T_ss system (KK^*). Employing the ³P₀ model, we calculated the decay widths of K^* and K^* within the bound state KK^* separately. The results are listed in Table 4. We observed, that owing to the influence of the binding energy, the decay width of K^* decreased from 20 to 17 MeV. Therefore, we hypothesize that the width of the bound state B(1320) we obtained should be approximately 3 MeV smaller than the experimentally observed width of K^*.

State	$ K\pi $	State	$ K\pi $
K*	20 MeV	K* in the KK*	17 MeV

Table 4.  Comparison of the calculated decay widths of K^* in vacuum and in the KK^* bound state.

In the quark model, resonances can form through two types of mechanism: the first involves strong attraction between mesons, resulting in resonance states, and the second involves resonance formation due to attractive interactions between colorful structures. Given that, in the T_ss bound state calculations, every single channel is a scattering state, the first mechanism does not apply. Thus, we focused on identifying resonances under the second mechanism framework.

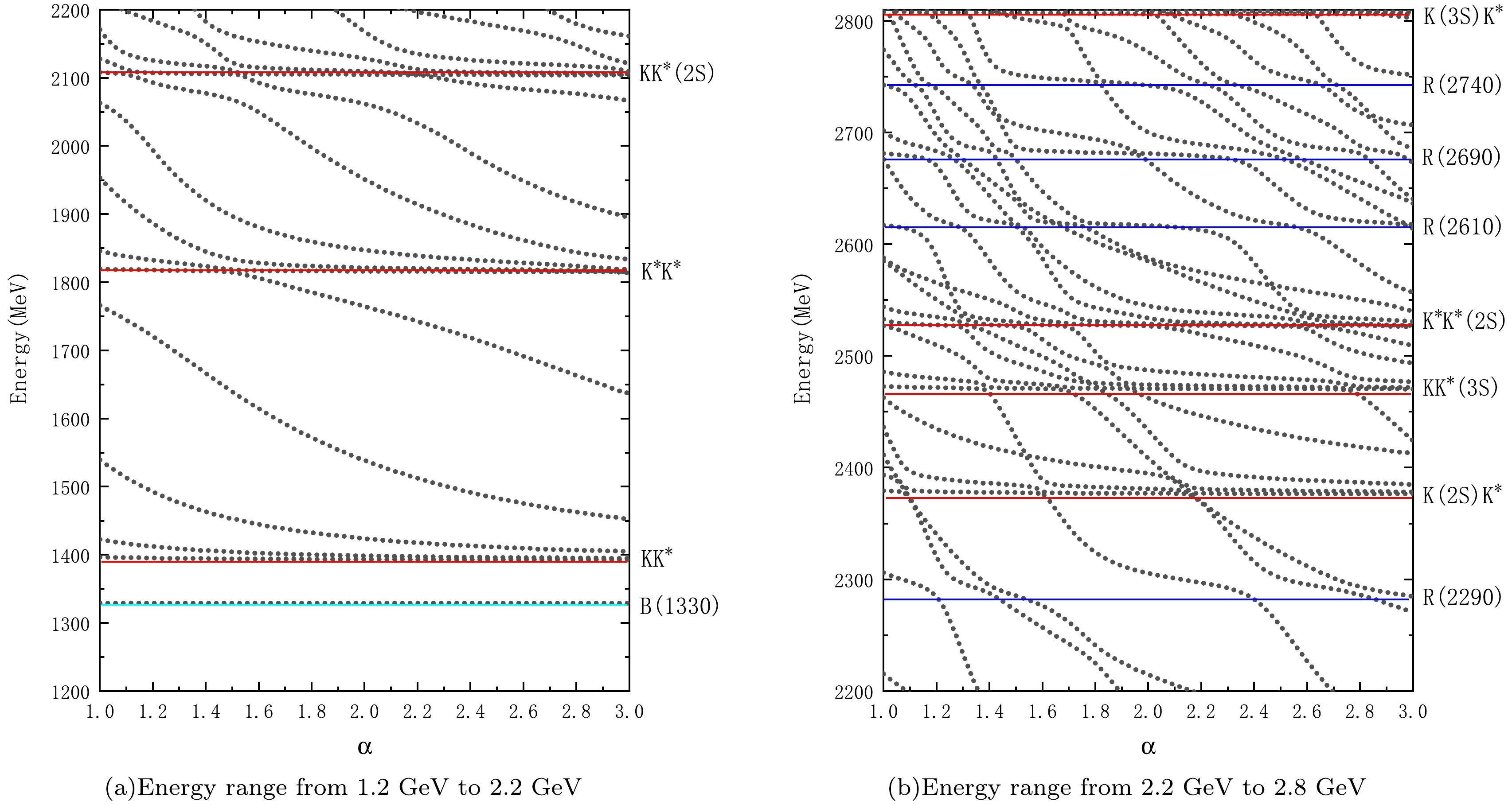
In the T_ss system, there are four colorful structures: two diquark configurations, $ [ss]_6^0[\bar{q}\bar{q}]_{\bar{6}}^1 $ and $ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $, and two color-octet states, $ [K]_8[K^{*}]_8 $ and [K^*]₈[K^*]₈. We first performed channel coupling of these four colorful structures. According to our calculations, within the energy range of 1.4−2.8 GeV, we identified 13 possible candidates of resonance in the T_ss system. These resonances, denoted as E (energy), are listed in Table 5 along with their corresponding color structure compositions. The majority of the candidates are located around 2.6 GeV, indicating several genuine resonances at this energy level. Subsequently, we employed the real-scaling method to evaluate the stability of these resonances and obtained the results presented in Fig. 2. As shown in Fig. 2, most of the resonance candidates decayed into their corresponding threshold channels. Only four resonances, R(2290), R(2610), R(2690), and R(2740), survived the coupling process with the scattering channels. The resonance R(2290) primarily originated from the previous resonance candidate E(2313). As the scaling factor $ \alpha $ increased, the calculational space changed, causing the energy of E(2313) to drop to 2290 MeV, where it stabilized and formed an avoid-crossing structure at $ \alpha=1.2 $. The energies of most resonance candidates are concentrated around 2.6 GeV. Note that the other three genuine resonances that survive after coupling with the scattering channels also have energies near 2.6 GeV. By comparing the energy levels, we can infer that resonance R(2620) likely originated from candidate E(2618), resonance R(2680) from candidate E(2682), and resonance R(2740) from candidate E(2751). We also calculated the percentage contributions of each channel and the root-mean-square distance between quarks for these resonances, as listed in Table 6. This table shows that each resonance has a significant [K^*]₈[K^*]₈ component. From our previous bound state calculations, we already observed that the energy of [K^*]₈[K^*]₈ is lower than that of K^*K^*, indicating a strong attraction between [K^*]₈[K^*]₈. Given that these four resonances contain substantial colorful structure components, their internal quark distances are small, within 1 fm. Additionally, their decay widths are all less than 10 MeV.

Resonances	$ [ss]_6^0[\bar{q}\bar{q}]_{\bar{6}}^1 $	$ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $	$ [K]_8[K^{*}]_8 $	[K*]8[K*]8
E(1484)	8.7%	83.3%	1.1%	6.9%
E(1875)	68.2%	1.0%	12.8%	18.0%
E(2099)	12.0%	63.4%	5.6%	18.9%
E(2229)	1.3%	69.0%	18.6%	11.1%
E(2313)	68.3%	9.2%	8.4%	14.1%
E(2345)	0.9%	59.6%	21.1%	18.4%
E(2541)	17.0%	56.0%	15.3%	11.7%
E(2618)	34.9%	9.9%	31.5%	23.6%
E(2631)	2.9%	59.3%	25.5%	12.1%
E(2669)	18.4%	33.0%	8.2%	40.4%
E(2681)	4.3%	49.1%	42.2%	6.3%
E(2726)	45.5%	19.2%	11.4%	23.9%
E(2751)	1.4%	60.7%	18.3%	19.5%

Table 5.  Candidates for resonant states in the $ s\bar{q}s\bar{q} $ system (unit: MeV).

Figure 2.  (color online) Energy spectrum of the T_ss system obtained from the real-scaling method.

state	width	KK*	$ [K]_8[K^{*}]_8 $	K*K*	[K*]8[K*]8	$ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $	$ [ss]_6^0[\bar{q}\bar{q}]_{\bar{6}}^1 $	$ r_{s\bar{s}} $	$ r_{s\bar{q}} $	$ r_{\bar{q}\bar{q}} $
R(2290)	10.2	17.2%	8.0%	9.8%	36.4%	5.8%	22.4%	1.1	1.2	1.4
R(2620)	5.3	19.6%	24.8%	0.9%	36.3%	15.0%	3.2%	1.2	1.4	1.5
R(2680)	5.8	5.4%	25.5%	15.1%	28.9%	7.3%	17.6%	1.2	1.3	1.4
R(2740)	1.9	7.4%	14.5%	1.6%	35.1%	0.3%	40.1%	0.9	1.0	1.2

Table 6.  Decay widths of the resonance states, main components of the resonance states (unit: MeV), and root-mean-square distances (unit: fm) in the $ ss\bar{q}\bar{q} $ system.

In the framework of the chiral quark model, we systematically investigated the bound states and resonances of the T_ss ($ s\bar{q}s\bar{q} $ with 01⁺) system. Using the method of Gaussian expansion, we considered four physical channels, KK^* and K^*K^*, and their corresponding color octets, $ [K]_8[K^{*}]_8 $ and [K^*]₈[K^*]₈, in the molecular structure, as well as two physical channels, $ [ss]_6^0[\bar{q}\bar{q}]_{\bar{6}}^1 $ and $ [ss]_3^1[\bar{q}\bar{q}]_{\bar{3}}^0 $, in the diquark structure, and performed coupled-channel calculations for these two structures.

The bound state calculations reveal a deeply bound state, B(1330), with KK^* as its primary component. We hypothesize that the main decay width of this bound state arises from the decay process $ K^{*} \rightarrow K + \pi $. Thus, using the ³P₀ model, we calculated the decay width of K^* to be 20 MeV. However, the binding energy of B(1330), approximately 60 MeV, directly affects the decay phase space of K^*. By distributing this binding energy equally between K^* and K, we estimated that the energy of K^* should be reduced by approximately 30 MeV during the decay process. Consequently, the decay width of the bound state B(1330) in the T_ss system is estimated to be 17 MeV. Subsequently, we employed the real-scaling method to calculate the resonances. These results indicate that we obtained four resonances, R(2290), R(2610), R(2690), and R(2740), primarily composed of colorful structure components. Their decay widths are all within 10 MeV, and the internal quark distances are around 1 fm.

Given the current interest in T_cc, with much attention focused on its heavy-flavor partner, there is limited research on the light-flavor partner of T_cc. Therefore, we suggest that related experiments must be conducted to search for the predicted bound states and resonances in the T_ss system.