Systematic study of cross section for proton-induced reactions on neodymium up to 65 MeV using TALYS-1.96 code

The estimation of the cross sections (CSs) of charged particle induced reactions is important for the design of an accelerator-driven system (ADS), the production of radioisotopes, and the verification of various nuclear models [1−3]. It is also important for understanding the origin of p-nuclei under astrophysical conditions [4]. Natural neodymium (Nd) is composed of 7 long-lived stable isotopes, ¹⁴²Nd (27.2%), ¹⁴³Nd (12.2%),¹⁴⁴Nd (23.8%), ¹⁴⁵Nd (8.3%), ¹⁴⁶Nd (17.2%), ¹⁴⁸Nd (5.7%), and ¹⁵⁰Nd (5.6%). Nd can be used as a target for producing radioisotopes such as ¹⁴⁹Pm and ^140,141Nd, which are medically important and usable for therapeutic purposes [5–8].

Knowledge of the production CSs of proton induced reactions on natural Nd is also important for the experimental observation of doube β decay. ¹⁵⁰Nd, which is one of the 7 long-lived naturally occurring isotopes of ^natNd, is a highly promising candidate for the observation of neutrinoless double β decay ($ \beta\beta0\nu $) with a large Q-value of 3371.38±0.20 keV [9]. Because the expected signal strength of the double β decay of ¹⁵⁰Nd is extremely weak, a reduction in background is required. Currently, there are three ongoing experiments in which the neutrinoless double β decay of ¹⁵⁰Nd is being studied: the Sudbury Neutrino Observatory plus liquid scintillator (SNO+) [10], Drift chamber Beta-ray analyzer (DCBA) [11], and SuperNEMO [12]. A background component in the double β decay experiment is the decay of long-lived radioisotopes such as ¹⁴³Pm, ¹⁴⁴Pm, ¹⁴⁶Pm, ¹⁴⁸Pm and ¹⁴⁷Nd, produced in natural Nd by its reaction with a proton from cosmic rays. Therefore, the excitation functions of proton induced reactions on natural Nd must be measured.

The goal of this study was to perform a systematic investigation of the theoretical estimation of the production CSs of various medically important isotopes of lanthanides via proton induced reactions on neodymium and to compare the calculated CSs with the experimental results obtained till date in various experiments (using natural and enriched Nd targets). Such systematic studies are important for validating the theoretical calculations performed using TALYS code (version 1.96) [13], considering various optical model potentials (OMPs), level density models (LDMs), and preequilibrium models (PEs).

For this study, the experimental data of Olkowsky et al. [14, 15], Lebeda et al. [16, 17], Banerjee et al. [18], Yang et al. [1], and Tarkanyi et al. [19] were used. In the work of Olkowsky et al., the CSs of ^149,150Pm produced via proton-induced reactions on ¹⁵⁰Nd were measured. The chosen energy range of the incident proton beam was from 6.9 to 10.84 MeV. In the work of Lebeda et al. [16, 17], proton-induced reactions on natural neodymium (^natNd) were investigated in the 5−35 MeV energy range to measure the production CSs of different radionuclides. Similarly, in the work of Banerjee et al. [18], the excitation function of ¹⁵⁰Nd(p, xnyp) reactions was measured using the stacked-foil activation technique with a 97.65% enriched ¹⁵⁰Nd target. The chosen proton energy range was 7–15 MeV. In [18], the absolute CSs for the ¹⁵⁰Nd(p, n)¹⁵⁰Pm, ¹⁵⁰Nd(p, 2n)¹⁴⁹Pm, and ¹⁵⁰Nd(p; d, pn)¹⁴⁹Nd reactions were carefully measured at various proton energy values ranging from 7–15 MeV for the first time. It is worth emphasizing that the dead time of the detectors used by Banerjee et al. [18] was significantly lower (≤10%) than that allowed by Lebeda et al. [16, 17], i.e., (≤40%). In the work of Yang et al. [1], the production CSs of ^natNd(p, x) reactions were determined using the stacked-foil activation technique for proton energies up to 45 MeV. In the work of Tarkanyi et al. [19], the excitation functions of ^natNd(p, x) nuclear reactions were measured up to an energy of 65 MeV using the stacked foil activation technique and high resolution γ-spectrometry.

In this study, a systematic investigation of the theoretical estimations of the CSs of ^{150,149,148,146,144,143,141}Pm and ^149,147Nd nuclei was performed via proton-induced reactions on a neodymium target using TALYS code for incident proton beams with energies up to 65 MeV. TALYS is a theoretical nuclear model code in which photons, neutrons, protons, deuterons, $ ^3 $He, and $ ^4 $He can be used as projectiles in the energy range of 1 keV to 200 MeV for target elements with a mass of 12 and heavier [13]. It utilizes state-of-the-art nuclear reaction models and includes direct reaction, preequilibrium emission, and compound reaction mechanisms. The various experimental results taken from EXFOR [15] and the literature were compared with the theoretically calculated values based on the TALYS-1.96 code. In this study, theoretical calculations for each individual reaction were first conducted using various LDMs in the default mode. Subsequently, various combinations of nuclear model parameters were used to fine tune the estimated CSs with the observed experimental results. Finally, calculations were performed using adjusted global parameters for the purpose of fine tuning. The level density parameters were calculated using the six different choices of LDMs available in TALYS-1.96. In TALYS, the six LDMs used for calculating nuclear reaction CSs are as follows: (i) LDM-1: constant temperature model [20] + Fermi gas model [21] (default); (ii) LDM-2: back-shifted Fermi gas model [21]; (iii) LDM-3: generalized superfluid model [22, 23] (iv) LDM-4: microscopic model of Goriely [24] based on Hartree-Fock calculations; (v) LDM-5: microscopic combinatorial model of Goriely-Hilaire [25]; (vi) LDM-6: microscopic level density based on temperature dependent Hartree-Fock-Bogoliubov calculations [26] using the D1M Gogny force.

In the Fermi gas model, the level density parameter 'a' can be derived from D₀, which is the s-wave average neutron resonance spacing (in keV) at the neutron separation energy. The experimental value of D₀ for ¹⁵⁰Nd was obtained from the RIPL-3 database [27] and compared with the theoretical values predicted by the TALYS code for each LDM. The values of D₀ are listed in Table 1.

In TALYS, the contribution of the compound nucleus is calculated using the Hauser-Feshbach model [28]. The preequilibrium contribution is calculated using the exciton [29] and multistep direct/compound models. Moreover, the OMP by Koning-Delaroche (KD) [30] is used. To consider the γ-ray emission channel, TALYS uses a fixed γ-ray strength function (γSF) model. In the present study, the Brink-Axel (BA) Lorentzian [31, 32] and Kopecky-Uhl (KU) generalized Lorentzian [33] were used as the γSFs.

In this study, a combination of various input parameters and models were used assuming that the CSs of nuclear reactions are dependent on the nuclear level densities (NLDs), OMPs, and γ SFs.

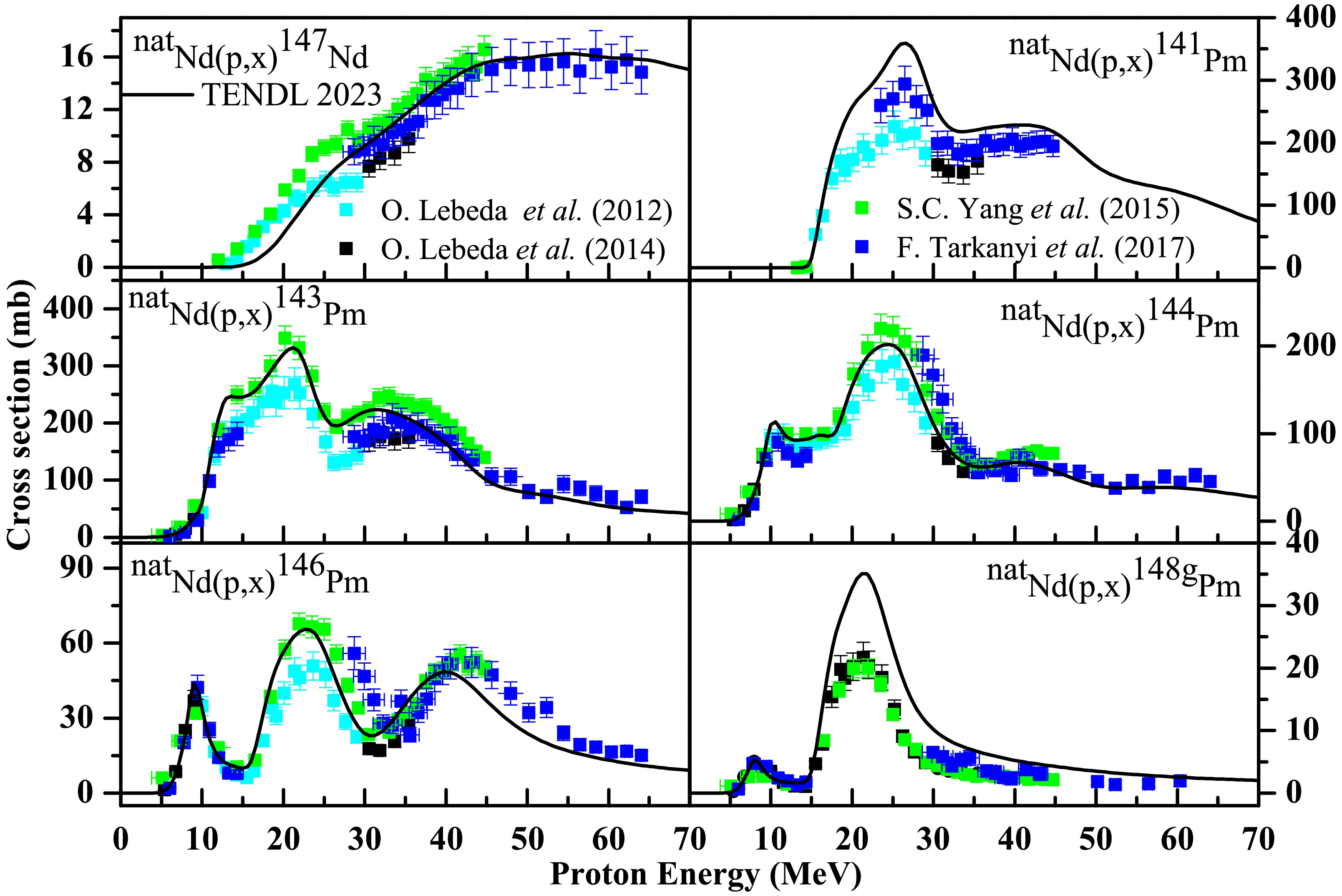
The results of the production CSs of ^150,149Pm and ¹⁴⁹Nd reported by Banerjee et al. [18] are shown in panels (a), (b), and (c) of Fig. 1, along with the literature data of Lebeda et al. [16, 17] and Olkowsky et al. taken from the EXFOR compilation [15]. These data were compared with the evaluated data from the TENDL-2023 [34] database. Note that the CS values obtained by Lebeda et al. via bombardment of protons on a natural ¹⁵⁰Nd target were scaled up to the absolute values obtained by Banerjee et al. [18] considering the isotopic enrichment of ¹⁵⁰Nd. This is because Banerjee et al. [18] used an enriched ¹⁵⁰Nd target. Similarly, in Fig. 2, the measured CS data of ^{148,146,144,143,141}Pm and ¹⁴⁷Nd taken from the EXFOR compilation [15] and produced experimentally via proton-induced reactions on ^natNd by Lebeda et al. [16, 17], Yang et al. [1], and Tarkanyi et al. [19] are shown and compared with the evaluated data from the TENDL-2023 [34] database.

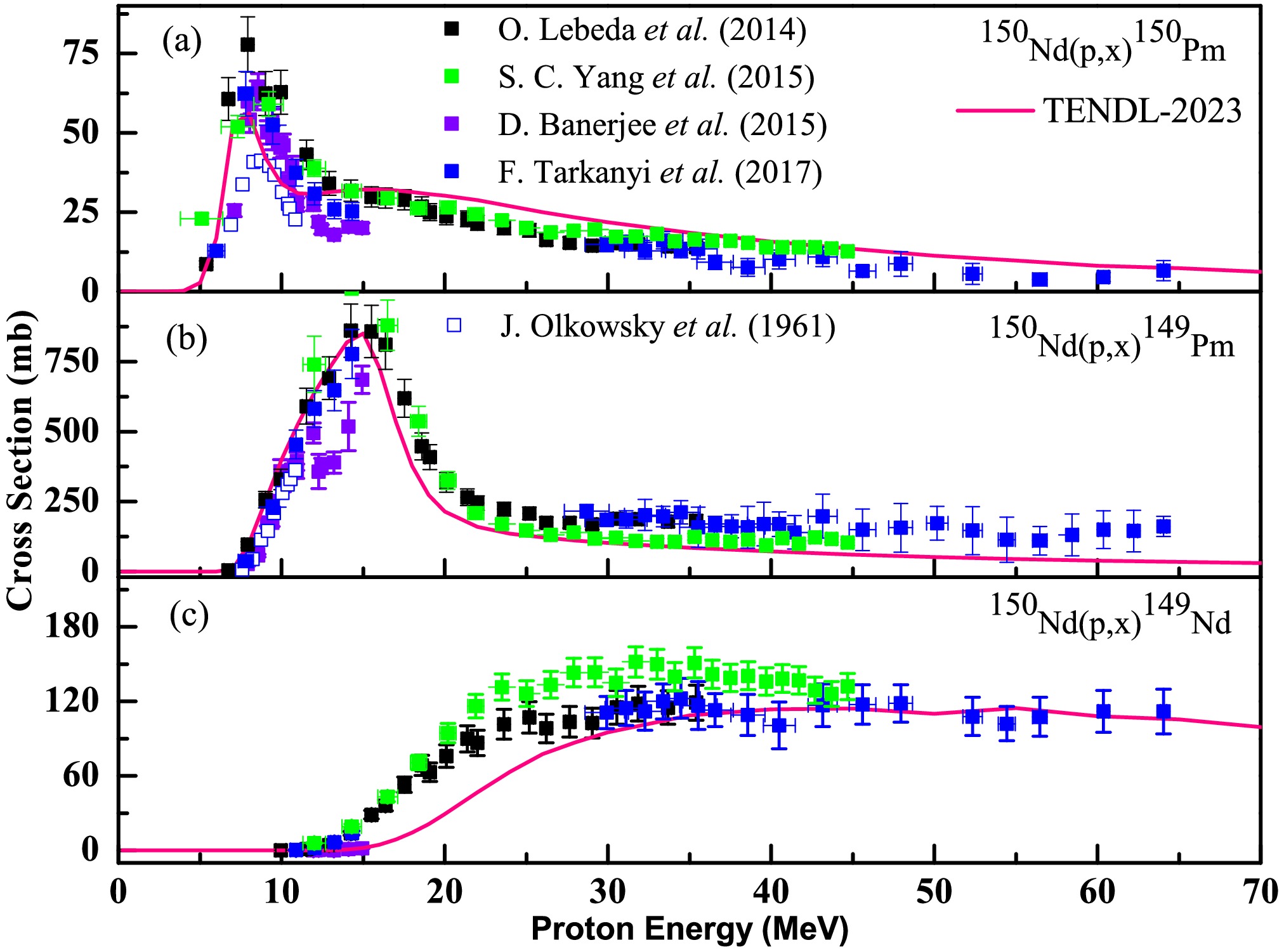
Figure 1.  (color online) Data of Banerjee et al. [18] for the (a) ¹⁵⁰Nd(p, n)¹⁵⁰Pm, (b) ¹⁵⁰Nd(p, 2n)¹⁴⁹Pm, and (c) ¹⁵⁰Nd(p; d, $ pn $)¹⁴⁹Nd reactions compared with the previously published results of Olkowsky et al. [14] taken from the EXFOR database [15], Yang et al. [1], Tarkanyi et al. [19], and Lebeda et al. [16, 17], along with the TENDL-2023 data [34].

Figure 2.  (color online) Experimental data of ^natNd(p, x)^{148g,146,144,143,141}Pm and ¹⁴⁷Nd taken from the EXFOR database [15], along with the TENDL-2023 data [34].

TALYS calculations were performed for the ¹⁵⁰Nd(p, x) ^150,149Pm,¹⁴⁹Nd, ^natNd(p, x)^{148,146,144,143,141}Pm, and ¹⁴⁷Nd reactions using the default parameters with different phenomenological and microscopic LDMs along with KD local OMPs and a simplified model Lorentzian (SMLO) E1 γSF. Along with the default mode, theoretical calculations were also performed using a combination of various model parameters for each of the above mentioned reactions to fine tune the theoretical results with the experimental data. The results of the theoretical calculations (both using the default mode and using different combinations of model parameters) for the various reactions are shown in Figs. 3 to 12.

Figure 3.  (color online) Experimental data for the ¹⁵⁰Nd(p, x)¹⁵⁰Pm reaction from the previous works of Yang et al. [1], Olkowsky et al. [14], Lebeda et al. [16, 17], Banerjee et al. [18], and Tarkanyi et al. [19] compared with the (a) phenomenological and (b) microscopic level density model calculations based on TALYS code with the default option. Discrepancies were observed between the experimental data and the theoretically predicted cross section values at various energies calculated using six different level density models in the default mode.

Figure 12.  (color online) Experimentally measured data for the ^natNd(p, x)¹⁴⁷Nd reaction obtained from the literature compared with the phenomenological theoretical calculations based on TALYS code with different combinations of model parameters. The dotted and red continuous lines indicate the theoretically estimated CSs using TALYS in the default mode and using different combinations of model parameters, respectively.ers, respectively.

For the ¹⁵⁰Nd(p, x)¹⁵⁰Pm reaction (Fig. 3), the constant temperature model in the default mode could effectively reproduce the variation trend in the CS data reported by the various groups up to a proton energy of 10 MeV. Beyond this energy and up to 35 MeV, the theoretical results generated by the constant temperature model overestimated the experimental data reported by Banerjee et al. [18], Lebeda et al. [16, 17], Yang et al. [1], and Tarkanyi et al. [19]. In the 35–45 MeV proton energy range, the theoretically calculated CSs using the constant temperature model matched well with the data reported by Yang et al. [1], and in the 45−65 MeV range, they matched closely with the data reported by Tarkanyi et al. [19]. The results of the back shifted Fermi gas model in its default mode matched the experimental results reported by Banerjee et al. [18] only up to a proton energy of $\sim$12.5 MeV. They matched the variation and magnitude trends of the results reported by Lebeda et al. [16, 17] reasonably well up to an energy of 17.5 MeV. Beyond this and up to 30 MeV, a discrepancy was observed between the theoretical and experimental results. Beyond this energy, the CS prediction of this model matched well with the data reported by Yang et al. [1] in the 35−45 MeV range and with those by Tarkanyi et al. [19] in the 45−65 MeV range. At a proton energy of 11−15 MeV, a discrepancy was observed between the theoretical calculations of the generalized superfluid model in the default mode and the results reported by Banerjee et al. [18]. The shape and magnitude of the excitation function produced by this model matched well with the results reported by Olkowsky et al. [14] in the 5−10 MeV range. In the 15–35 MeV range, they matched well with those of Lebeda et al. and Yang et al. [1]. Beyond 35 MeV, the predictions of this model matched only with the data of Tarkanyi et al. [19]. The default theoretical results of all the microscopic LDMs (i.e., LDM-4, LDM-5, and LDM-6) (see panel-(b) of Fig. 3) overestimated the experimental results reported by Lebeda et al. [16, 17], Yang et al. [1], and Banerjee et al. [18] beyond a proton energy of 11–12 MeV and up to 35 MeV. Beyond 35 MeV, they matched closely with the data reported by Yang et al. [1] up to 45 MeV and with those of Tarkanyi et al. [19] in the 45−65 MeV range. The variation pattern of the theoretical results of all the phenomenological and microscopic LDMs was similar to that reported by Olkowsky et al. in the 6−11 MeV range.

Considering the large discrepancies between the measured CSs and the theoretical results from TALYS using default parameters, the theoretical values were revised with different combinations of nuclear models and/or model parameters in an attempt to reproduce the experimental results more accurately. Simultaneously, the OMPs, LDMs, and PEs, which are of utmost importance, were individually adjusted. For example, the behavior of the constant temperature model was significantly improved by combining the KD local optical potential with the Brink-Axel Lorentzian as the gamma strength function and preequmode 3 as the PE. The response of the back-shifted Fermi gas model was improved by combining the KD local dispersive model with the Brink-Axel Lorentzian and preeqmode 3. For both of the above LDMs, the parameters "asys" and "fullhf" were enabled to match with the experimental data. The parameter "asys" is a flag to use all level density parameters from systematics by default and "gshell" is used to include the damping of shell effects with excitation energy in single-particle level densities. The generalized superfluid model was improved by combining the KD global potential with the Brink-Axel Lorentzian. For this model, the parameters "asys" and "gshell" were enabled. The response of the microscopic models of Goriely and Goriely-Hilaire was improved via the combination of the KD global OMP and KU generalized Lorentzian γSF along with preequilibrium model 3. For the former microscopic model of Goriely, the parameter "gshell" was enabled. Similarly, the behavior of the microscopic model of the Goriely-Hilaire Gogny force was improved by combining the KD global OMP with the Brink-Axel Lorentzian and preequilibrium model 3. For all the aforementioned phenomenological and microscopic LDMs, the parameter "fullhf" was enabled and the Hofmann-Richert-Tepel-Weidenm$ \ddot{u} $ller (HRTW) model was used. This is worth mentioning that the parameter "fullhf" takes care of j-l coupling in the Hauser-Feshback theory. See Fig. 4 and Table 2 for further details.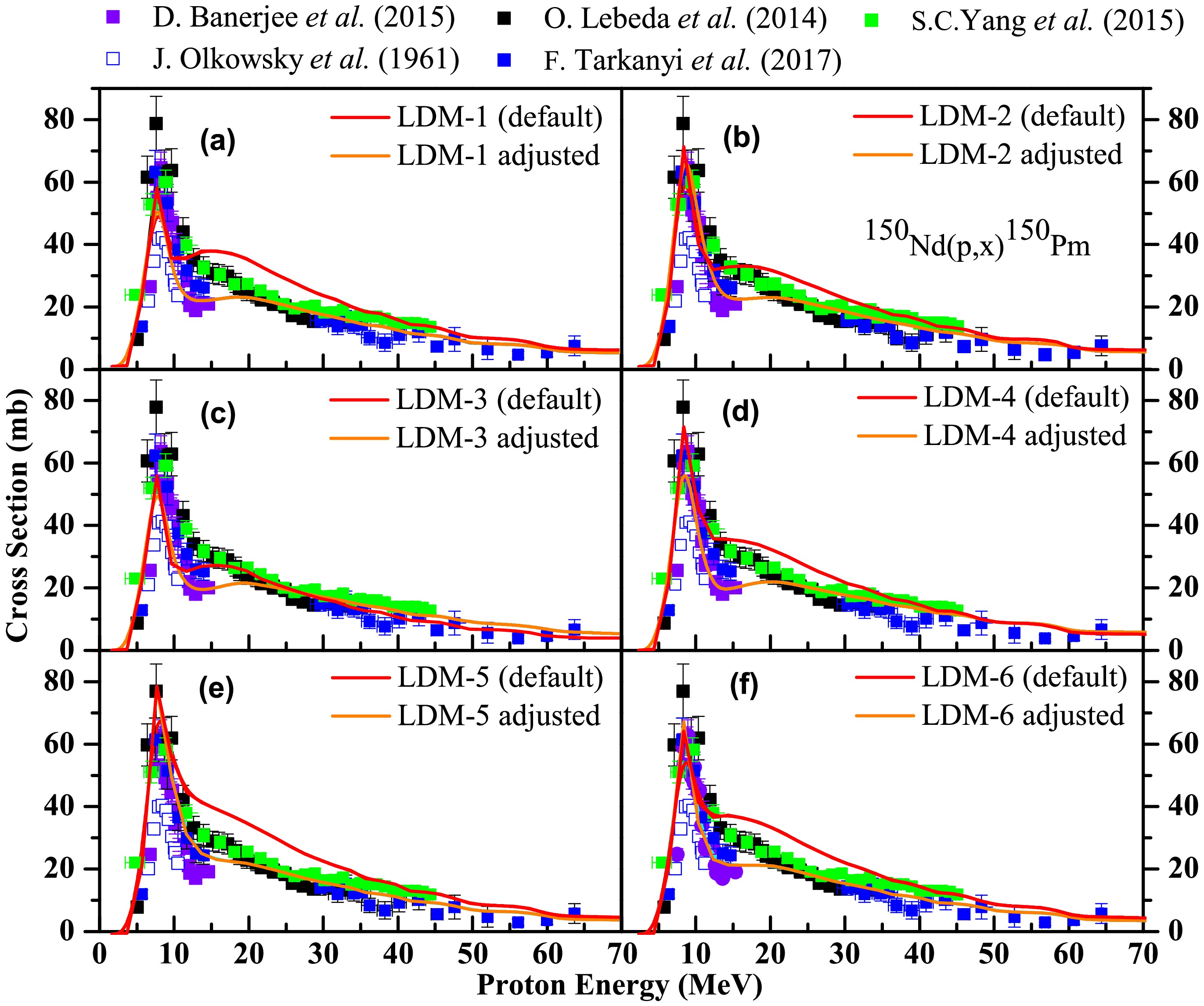

Figure 4.  (color online) Experimentally measured data for the ¹⁵⁰Nd(p, x)¹⁵⁰Pm reaction obtained from the literature compared with the phenomenological theoretical calculations based on TALYS code with different combination of nuclear models and model parameters. The red and sky-blue continuous lines indicate the theoretically estimated CSs using TALYS in the default mode and using different combinations of model parameters, respectively

Similarly, for the ¹⁵⁰Nd(p, x)¹⁴⁹Pm reaction (Fig. 5), the excitation function generated by the theoretical calculations of all the phenomenological and microscopic models peaked at approximately 15 MeV. Up to this energy value, the theoretical results calculated by the various models matched the experimentally calculated CS values reasonably well (except the CS values at proton energies of 12.44, 13.21, 14.10, and 14.94 MeV reported by Banerjee et al. [18]). Beyond the peak value, the phenomenological LDMs underestimated the CS values. Although the microscopic LDMs produced results with a trend similar to that of the experimental results, a small overestimation and underestimation was observed at some energy values in the 15–65 MeV range.

Figure 5.  (color online) Experimentally measured data for the ¹⁵⁰Nd(p, x)¹⁴⁹Pm reaction obtained from the literature compared with the phenomenological theoretical calculations based on TALYS code with different combinations of nuclear models and/or model parameters. The red and yellow continuous lines indicate the theoretically estimated CSs using the default mode and different combinations of nuclear models, respectively.

However, to improve the behavior of the constant temperature model, a combination of the KD local OMP and Brink-Axel Lorentzian was used along with enabled "asys" and "gshell" parameters. Similarly, for the back-shifted Fermi gas and generalized superfluid models, the combinations of the KD local dispersive model & KU generalized Lorentzian and KD global & Brink-Axel Lorentzian were used as the OMP and γSF, respectively. The parameter "asys" was also enabled for these LDMs to improve their behavior. For the microscopic models of Goriely & Goriely-Hilaire, the combination of the KD global OMP and KU generalized lorentizian γSF was used along with the enabled parameters of "gshell" and/or "asys." For the LDM of the Goriely-Hilaire Gogny force, the KD global OMP was combined with KU generalized Lorentzian. Moreover, for all the above LDMs, widthmode 2 (i.e., HRTW model) was used and the "fullhf" parameter was enabled. The parameter "widthmode" was used to include a model for width mode fluctuation corrections in compound nucleus calculations. For all the LDMs, preequilibrium model 4, i.e., the multi-step direct or compound model, was used. Refer to Fig. 5 and Table 3 for more details.

For the ¹⁵⁰Nd(p, x)¹⁴⁹Nd reaction (Fig. 6), the excitation functions generated by the theoretical calculations of all the LDMs (both phenomenological and microscopic) satisfactorily followed the variation and magnitude trends of the experimental data reported by the various groups up to 30 MeV. Beyond this energy, the theoretical calculations overestimated the CS values and did not provide satisfactory results in the default mode.

Figure 6.  (color online) Experimentally measured data for the ¹⁵⁰Nd(p, x)¹⁴⁹Nd reactions obtained from the literature compared with the phenomenological theoretical calculations based on TALYS code in the default mode and with different combinations of model parameters. The dotted and continuous lines indicate the theoretically estimated CSs using TALYS in the default mode and using different combinations of model parameters, respectively

However, the responses of the various LDMs ranging from LDM-1 to LDM-6 improved significantly for ¹⁵⁰Nd(p, x)¹⁴⁹Nd reactions when the PE was changed from preeqmode 2 (default exciton model) to preeqmode 3 (numerical transition rates with an optical model for collision probability). Fig. 6 shows the effect of the change in the preequilibrium mode on the response of the different LDMs for the respective reaction channels.

For the ^natNd(p, x)^148gPm reaction (Fig. 7), the predictions of the theoretical calculations based on both the phenomenological and microscopic LDMs matched reasonably well up to a proton energy of 15 MeV and beyond 30 MeV. In the 15–30 MeV proton energy range, the various LDMs used in the default mode overestimated the CS values when compared to the experimental data reported by the various groups. Moreover, as shown in Figs. 7(a) and 7(b), slight changes in the peak position of the excitation functions were observed with the variation in the LDM.

Figure 7.  (color online) Experimental data for the ^natNd(p, x)^148gPm reaction reported by various groups taken from EXFOR [15] compared with the calculations using (a) phenomenological and (b) microscopic level density models and (c) different gamma strength functions (γSFs) based on the TALYS code. No significant improvement was observed from the use of different γSFs when compared with the default run using different LDMs.

However, no significant improvement was observed in the CS values for the ^natNd(p, x)^148gPm reaction despite using different gamma strength functions (such as strength-1 to strength-9), as shown in Fig. 7(c), compared to those of the default run using the six LDMs.

For the ^natNd(p, x)¹⁴⁶Pm reaction, as shown in Fig. 8, the constant temperature and back-shifted Fermi gas models in the default mode predicted the CS values fairly well up to 40 MeV; however, beyond this value, the models underestimated the CS values. The generalized superfluid model also provided satisfactory result up to 35 MeV, after which mismatch between the experimental results and theoretical prediction was observed. Similarly, discrepancies were observed between the theoretical predictions made using the microscopic LDMs in the default mode and the experimental results beyond 40 MeV.

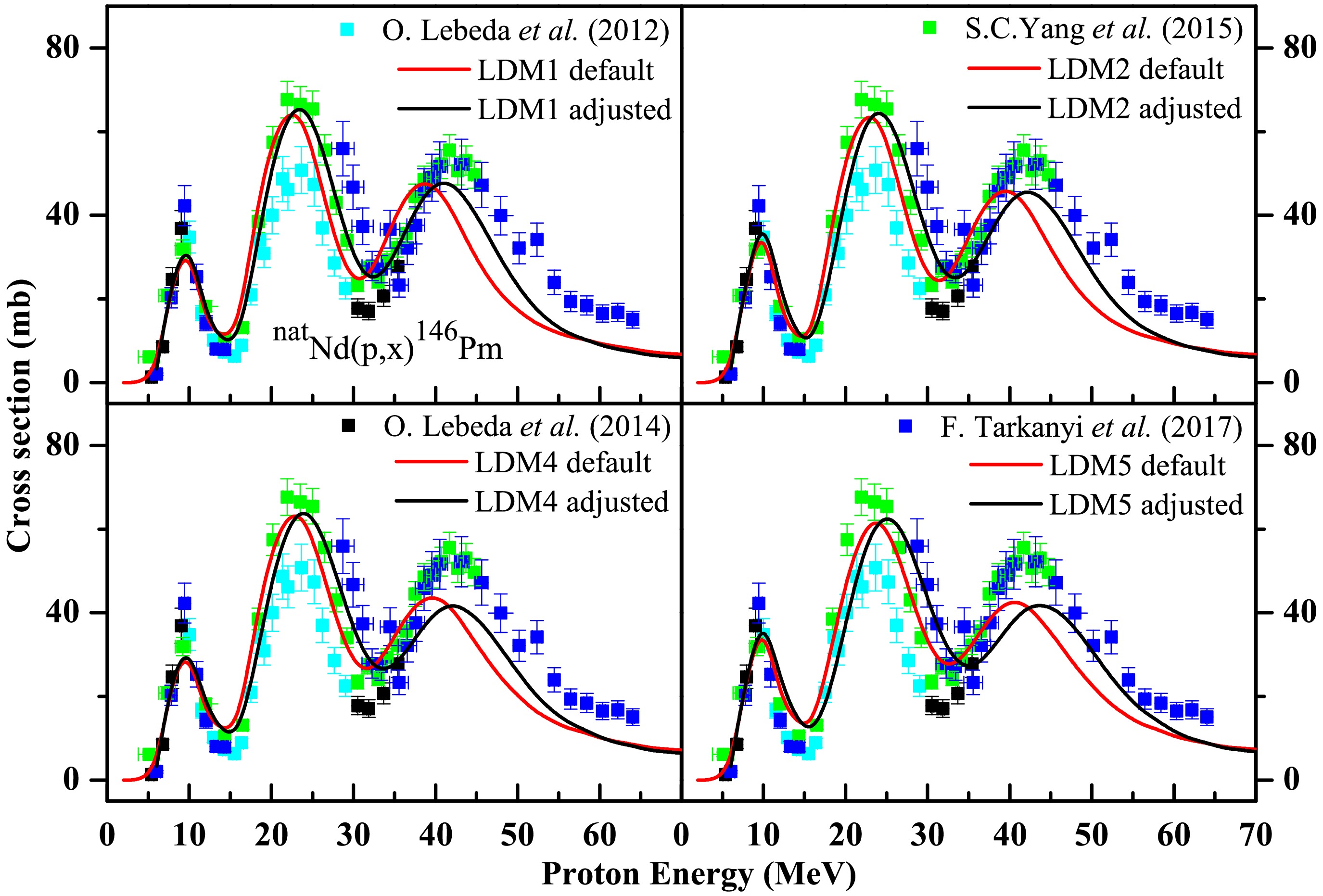
Figure 8.  (color online) Experimentally measured data for the ^natNd(p, x)¹⁴⁶Pm reaction obtained from the literature compared with the phenomenological theoretical calculations based on TALYS code with different combinations of model parameters. The red and black continuous lines indicate the theoretically estimated CSs using TALYS in the default mode and using different combinations of model parameters, respectively. As no significant improvement in the response was observed in the case of LDM-3 and LDM-6 using different combinations of model parameters w.r.t. the TALYS run with NLDs in the default mode, these figures have not been included here.

However, for this reaction, the response of LDMs such as LDM-1, LDM-2, LDM-4, and LDM-5 improved significantly when the KU generalized Lorentzian strength function (i.e., strength 1) was used along with preeqmode 3 and the Bauge-Delaroche JLM potential. As no significant improvement was observed in the case of LDM-3 and LDM-6 after using different combinations of nuclear model parameters, the respective plots have not been included in Fig. 8.

For the ^natNd(p, x)^144,143Pm reactions, the theoretically estimated CS values (as shown in Figs. 9 and 10, respectively) generated using the various LDMs (LDM-1 to LDM-6) in the default mode matched the experimental data reported by the various groups reasonably well.

Figure 9.  (color online) Experimental data for the ^natNd(p, x)¹⁴⁴Pm reaction reported by various groups taken from EXFOR [15] compared with the six level density model calculations (i.e., LDM-1 to LDM-6) based on TALYS code with the default option.

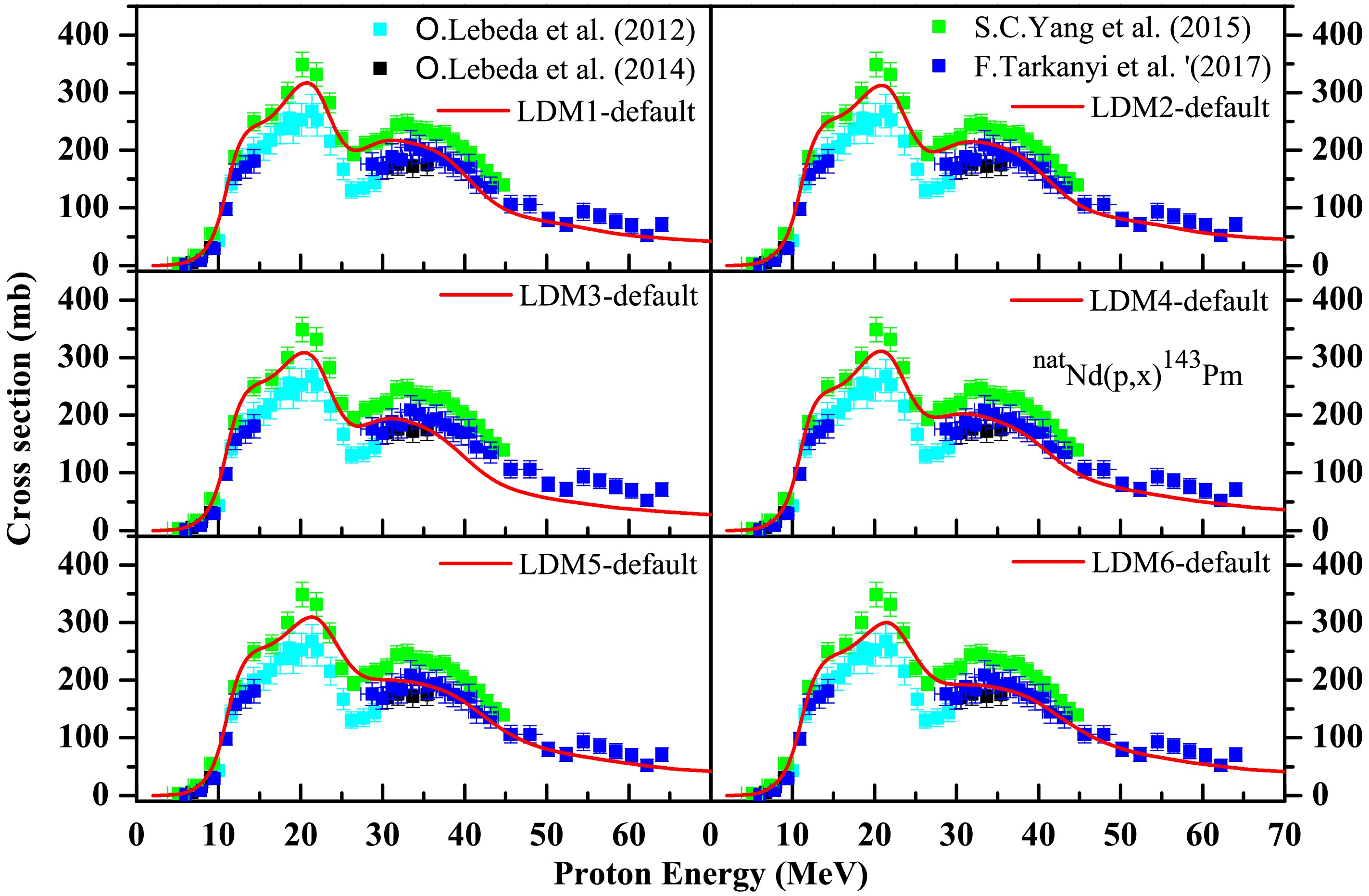
Figure 10.  (color online) Experimental data for the ^natNd(p, x)¹⁴³Pm reaction reported by various groups taken from EXFOR [15] compared with the six level density model calculations based on TALYS code with the default option.

For the ^natNd(p, x)¹⁴¹Pm reaction (Fig. 11), the phenomenological LDMs in the default mode predicted the CS values reasonably well in the 10–65 MeV range; however, in the 20–30 MeV range, these models overestimated the CS values. In the 35–65 MeV range, the microscopic LDMs (particularly LDM-5 and LDM-6) failed to suitably predict the CS values when used in the default mode.

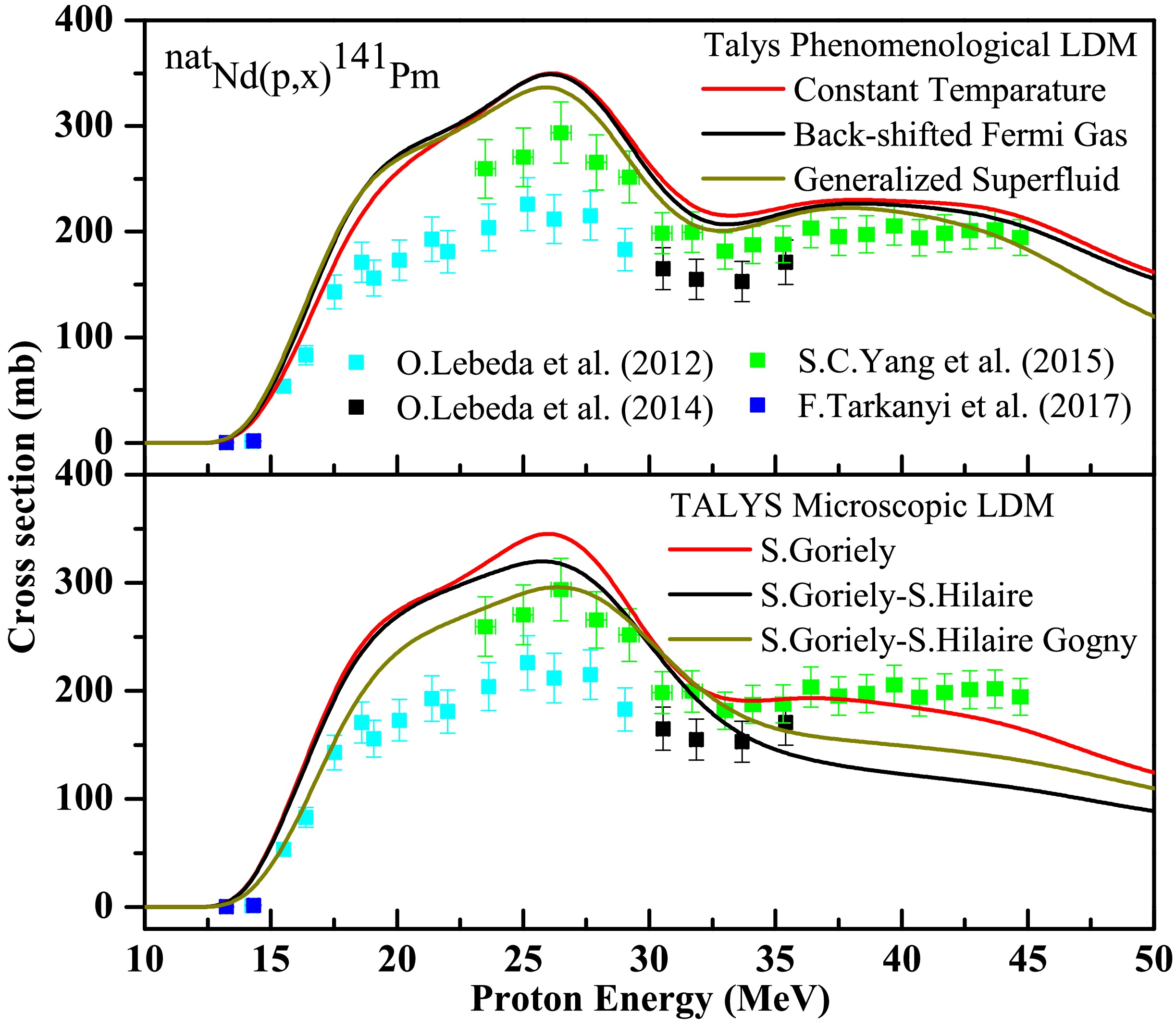
Figure 11.  (color online) Experimental data for the ^natNd(p, x)¹⁴¹Pm reaction taken from EXFOR [15] compared with the (a) phenomenological and (b) microscopic level density model calculations based on TALYS code with the default option.

No significant improvement was observed in the CS values by using different combinations of nuclear models and model parameters compared to those of the default run using the six LDMs.

In the case of the ^natNd(p, x)¹⁴⁷Nd reaction (Fig. 12), the constant temperature and back-shifted Fermi gas models predicted the CS values well up to a proton beam energy of 50 MeV, after which the CS values were slightly overestimated. The generalized superfluid model failed to suitably predict the CS values in the 30–65 MeV range when used in the default mode. Similarly, the CS values for the ^natNd(p, x)¹⁴⁷Nd reaction was over estimated by the microscopic LDMs (particularly LDM-5 and LDM-6) beyond 40 MeV.

However, the responses of the various LDMs ranging from LDM-1 to LDM-6 changed significantly for ¹⁵⁰Nd(p, x)¹⁴⁷Nd reactions when the PE was changed from the default exciton model to preequimode 3. Fig. 12 shows the effect of the change in the preequilibrium mode on the responses of different LDMs for the respective reaction channels.

In this study, as well as from the different combinations of nuclear models and/or model parameters, an alternate process was also adopted to fit the various experimental data using the OMP parameters available in the TALYS code. One motive behind this exercise was to verify the sensitivity of the theoretical CS calculation on the OMP parameters. To fit the ¹⁵⁰Nd(p, x)¹⁵⁰Pm data using the TALYS code, the diffuseness parameter of the volume-central potential for the proton OMP (a_v) was reduced by 20% from its default value and the PE was changed from the default exciton to preeqmode 3, where the collision rates are based on the optical model. To fit the ¹⁵⁰Nd(p, x)¹⁴⁹Pm data, the diffuseness parameter a_v was reduced by 10% from its default value and the PE was changed from the default exciton to the multistep direct or compound model. Similarly, for ^natNd(p, x)^144,143Pm reactions, the theoretical results were fine tuned by reducing the radius parameter of the volume-central part of the proton OMP (i.e., r_v) value by 10% from its default value. Similarly, for the ^natNd(p, x)¹⁴¹Pm data, the value of r_v was decreased by 30% and a_v was increased by 20%. For the ^natNd(p, x)^149,147Nd reactions, the values of r_v and a_v were reduced by 10% and 20%, respectively, from their default values for the purpose of fine tuning. These systematic studies revealed that adjustment of the diffuseness and radius parameters, often coupled with changes in the preequilibrium mode (from the default exciton mode), leads to excellent agreement between the theoretical predictions made by TALYS and the experimental data taken from the literature, in most of the aforementioned reaction channels. Fig. 13 shows the effect of the above alterations in the OMP parameters (a_v and/or r_v) and the preequilibrium mode wherever needed.

Figure 13.  (color online) Experimentally measured CS data for the ^natNd(p, x)^{150,149,144,143}Pm,^149,147Nd reactions obtained from the literature compared with the default theoretical calculations based on TALYS code and with the adjusted diffuseness and/or radius global parameters of the volume-central part of the proton OMP. The black and red continuous lines indicate the theoretically estimated CSs using TALYS with the default mode and with adjusted OMP parameters, respectively.

In summary, the CSs of the ¹⁵⁰Nd(p, x)^150,149Pm,¹⁴⁹Nd, ^natNd(p, x)^{148,146,144,143,141}Pm, and ¹⁴⁷Nd reactions were theoretically calculated via the TALYS-1.96 code using both the default mode and a combination of different nuclear reaction models and model parameters available in TALYS. The CSs estimated theoretically using the TALYS code with six LDMs in the default mode were compared with the experimental CSs available in the literature reported by various experimental groups. Several discrepancies between theoretical estimates and experimental results were obtained when TALYS was run in its default mode. However, the various theoretically estimated CSs were found to be in good agreement with the experimentally observed data when certain specific nuclear parameters and models were used in combination. The impact of the various PEs and γSF on the CS calculation was also revealed in this study. Moreover, the sensitivity of the theoretically calculated CSs w.r.t the diffuseness and radius parameters of the volume-central part of the proton OMP was investigated. As shown, variation of the above OMP parameters can lead to satisfactory fine tuning of the calculated CSs for most of the reaction channels opened via proton induced reactions on an Nd target.

The theoretically estimated CSs for long-lived radioisotopes such as ¹⁴³Pm, ¹⁴⁴Pm, ¹⁴⁶Pm, ¹⁴⁸Pm, and ¹⁴⁷Nd produced via proton induced reactions on ^natNd are important for the estimation of their production rates, which are used to define the maximum allowed time for neodymium exposure on Earth's surface and the necessary cooling times before deploying the isotope in the SNO+ β-decay experiment.

As the energy values of the incident proton in this study extended up to 65 MeV, it is important to note that the contribution of the preequilibrium mechanism to the total reaction cross section attained significance at energies above 10 MeV.

The author would like to thank ICFAI University Tripura for all their help and support in carrying out the research. The author would also like to acknowledge the helpful discussions with Dr. Bibhabasu De and Mr. Songshaptak De.