Study of the semileptonic decays ${{\boldsymbol\Upsilon}({\bf 1}{\boldsymbol S}){\bf\to}{\boldsymbol B}_{(\boldsymbol c)}{\boldsymbol\ell}\bar{\boldsymbol\nu}_{\boldsymbol\ell}} $

Low-lying quarkonia systems such as $ \Upsilon(1S) $ mostly decay through intermediate gluons or photons produced by the annihilation of the parent $ \bar{q}q $ pair. As a result, strong and radiative decays of $ \Upsilon(1S) $ have been widely studied both theoretically and experimentally. Meanwhile, weak decays of $ \Upsilon(1S) $ have attracted less attention. Owing to the significant progress in the improvement of collider luminosity over recent years, a large amount of rare weak decays have been observed. In particular, the rare semileptonic decay of the charmonium $ J/\psi\to D\ell^+\nu_{\ell} $, ($ \ell = e,\mu $), was considered one of the main research topics at the BESIII experiment [1]. In 2021, BESIII reported a search for the decay $ J/\psi\to D e^+\nu_e $ based on a sample of $ 10.1\times 10^9 $ $ J/\psi $ events [2]. The results placed an upper limit of the branching fraction of $\mathcal{B}(J/\psi\to D e^+\nu_e+\rm{c.c.}) < 7.1 \times 10^{-8}$ at the 90% confidence level (CL). Note that this upper limit was improved by a factor of 170 compared to the previous value [3]. In 2023, using the same $ J/\psi $ event sample, BESIII searched for the semimuonic channel for the first time and found an upper limit of $\mathcal{B}(J/\psi\to D \mu^+\nu_\mu+\rm{c.c.}) < 5.6 \times 10^{-7}$ at the 90% CL [4]. These upper limits are still considerably larger than standard model (SM) predictions, which are of the order of $ 10^{-11} $ [5−9]. Nevertheless, the experimental data implied constraints on several new physics (NP) models that could enhance the branching fractions to the order of 10⁻⁵ [10]. In light of the extensive search for rare charmonium decays, it is reasonable to explore similar decays of the bottomonium $ \Upsilon(1S) $.

The semileptonic decays $ \Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell $, where $\ell = e,\mu,\tau,$ have been investigated in several theoretical studies. However, there are few such studies, and the existing predictions differ. The first calculation of decays $\Upsilon(1S)\to B_c\ell\bar{\nu}_\ell$ was performed by Dhir, Verma, and Sharma [7] in the framework of the Bauer-Stech-Wirbel model. They obtained $\mathcal{B}(\Upsilon(1S)\to B_c e \bar{\nu}_e)= \big(1.70^{+0.03}_{-0.02}\big)\times 10^{-10}$ and $\mathcal{B}(\Upsilon(1S)\to B_c \tau \bar{\nu}_\tau)=\big(2.9^{+0.05}_{-0.02}\big)\times 10^{-11}$. However, in this study, the authors only considered the $ \Upsilon(1S)\to B_c $ transition. In 2017, Wang et al. calculated the decays $ \Upsilon(1S)\to B^{(*)}_{(c)}\ell\bar{\nu}_\ell $ using the Bethe-Salpeter method [9]. The results for the $ \Upsilon(1S)\to B_c $ case were $\mathcal{B}(\Upsilon(1S)\to B_c e \bar{\nu}_e)= \big(1.37^{+0.22}_{-0.19}\big)\times 10^{-10}$ and $\mathcal{B}(\Upsilon(1S)\to B_c \tau \bar{\nu}_\tau)=\big(4.17^{+0.58}_{-0.52}\big) \times 10^{-11}$. The results of the two studies above only marginally agree. Considering the ratio of branching fractions, namely, $R(\Upsilon(1S)\to B_c)=\mathcal{B}(\Upsilon(1S)\to B_c \tau \bar{\nu}_\tau)/\mathcal{B}(\Upsilon(1S) \to B_c e \bar{\nu}_e)$, $ R(\Upsilon(1S)\to B_c) $ was estimated to be approximately $ 0.17\pm 0.01 $ (Dhir et al.) and $ 0.30\pm 0.09 $ (Wang et al.). The results implied a tension at $ 1.5\; \sigma $ between the two studies. Moreover, in 2016, Chang et al. considered the decays $ \Upsilon(nS)\to B_c\ell\bar{\nu}_\ell $ ($ n=1,2,3 $) based on nonrelativistic QCD (NRQCD) [11]. They found $R(\Upsilon(1S) \to B_c)= 0.24^{+0.02}_{-0.01}$, which agrees with the results by Wang et al. but disagrees with those by Dhir et al. Therefore, it is necessary to provide more theoretical predictions for these decays.

There is another interesting aspect of the $ \Upsilon(1S)\to B_c\ell\bar{\nu}_\ell $ decay: at the quark level, it is induced by the transition $ b\to c\ell\bar{\nu}_\ell $. For more than a decade, tensions between experimental data and the SM predictions for the ratios of the branching fractions $ R_D=\mathcal{B}(B^0\to D \tau \bar{\nu}_\tau)/ \mathcal{B}(B^0\to D e \bar{\nu}_e) $ and $ R_{D^*}=\mathcal{B}(B^0\to D^* \tau \bar{\nu}_\tau)/\mathcal{B}(B^0\to D^* e \bar{\nu}_e) $ could not be eliminated. This is known in the community as ''the $ R_{D^{(*)}} $ puzzle,'' which hints at a possible violation of lepton flavor universality (LFU) and has motivated a significant search for NP in the semileptonic decays $ B^0\to D^{(*)} \ell \bar{\nu}_\ell $ (see, e.g., [12, 13] and references therein). Thus, the decay $ \Upsilon(1S)\to B_c\ell\bar{\nu}_\ell $ is a reasonable candidate for probing possible NP beyond the SM.

The weak decays of hadrons, such as $ \Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell $ , are characterized by the interplay of strong and weak interactions. Although the structure of the weak interaction in semileptonic decays is well established, the strong interaction in the hadronic transitions $ \Upsilon(1S)\to B_{(c)} $ can only be calculated using nonperturbative methods. Hadronic transitions are often parameterized by invariant form factors. In this study, the hadronic form factors of the semileptonic decays of $ \Upsilon(1S) $ are calculated in the framework of the covariant confined quark model (CCQM) developed previously by our group. One of the advantages of our model is the ability to calculate the form factors in the entire physical range of momentum transfer without any extrapolation.

The remainder of the paper is organized as follows. In Sec. II, we present the relevant theoretical formalism for the calculation of the semileptonic decays $\Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell$. In Sec. III, we briefly introduce the CCQM and demonstrate the calculation of the hadronic form factors in our model. Subsequently, we present our numerical results in Sec. IV and conclude in Sec. V.

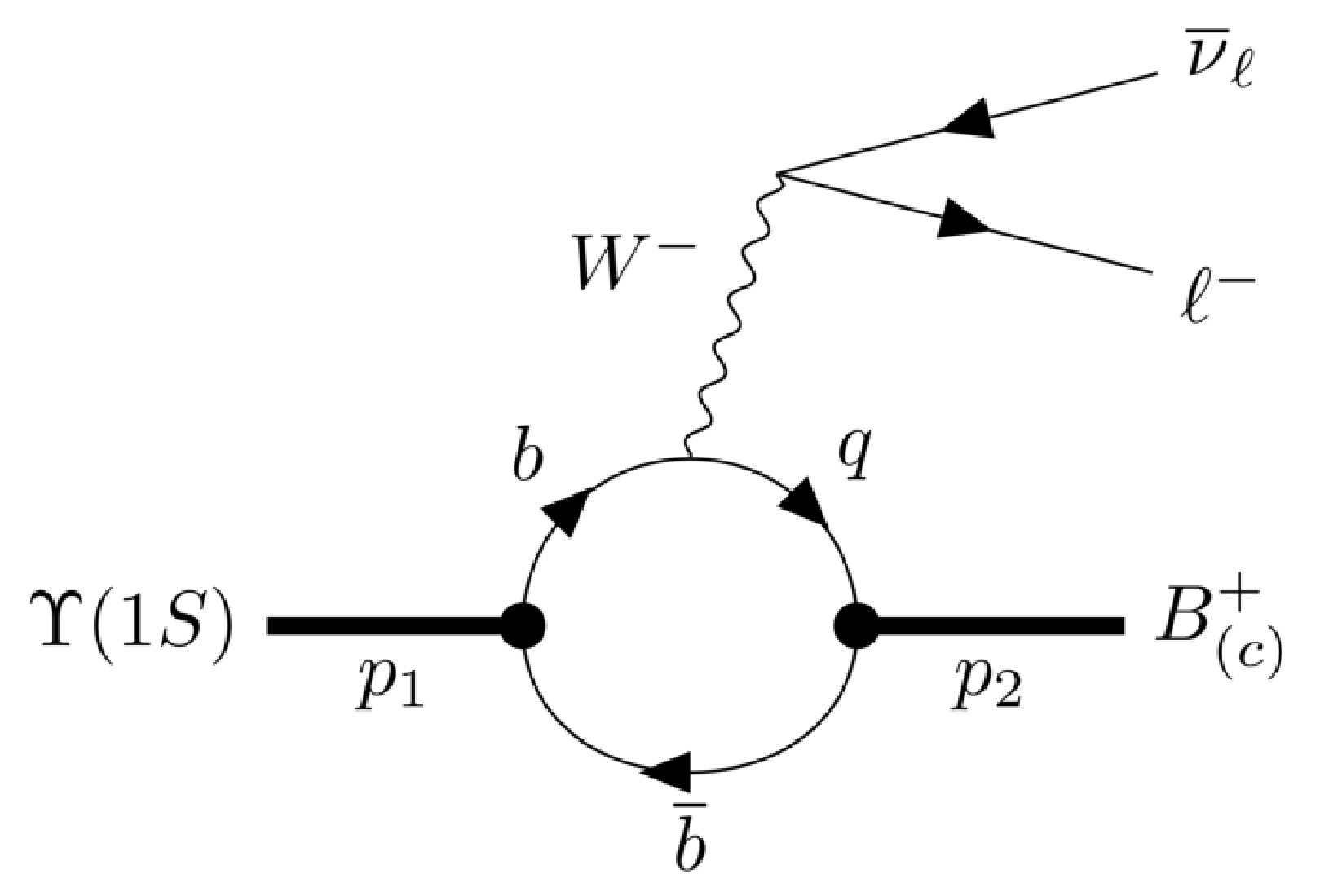
In the CCQM, the semileptonic decays $\Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell$ are described by the Feynman diagram shown in Fig. 1. The effective Hamiltonian for the semileptonic decays $ \Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell $ is given by

Figure 1.  Feynman diagram for semileptonic decays $ \Upsilon(1S)\to $$ B_{(c)}\ell\bar{\nu}_\ell $.

where $ q = (u, c) $, $ G_F $ is the Fermi constant, $ V_{qb} $ is the Cabibbo-Kobayashi-Maskawa matrix element, and $O^\mu= \gamma^\mu(1-\gamma_5)$ is the weak Dirac matrix with left chirality. The invariant matrix element of the decays is written as

The squared matrix element can be written as a product of the hadronic tensor $ H_{\mu\nu} $ and leptonic tensor $ L^{\mu\nu} $:

The leptonic tensor for the process $ W^-_{\rm{off-shell}}\to \ell^-\bar \nu_\ell $ $ \left( W^+_{\rm{off-shell}}\to \ell^+ \nu_\ell \right) $ is given by [14]

where the upper/lower sign refers to the two $ (\ell^-\bar\nu_\ell)/(\ell^+\nu_\ell) $ configurations. The sign change is due to the parity violating part of the leptonic tensors. In our case, we must use the upper sign in Eq. (4).

The hadronic matrix element in Eq. (2) is often parameterized as a linear combination of Lorentz structures multiplied by scalar functions, namely, invariant form factors that depend on the momentum transfer squared. For the $ V \to P $ transition, we have

where $ q=p_1-p_2 $, $ p=p_1+p_2 $, $ m_1 = m_{\Upsilon(1S)} $, $ m_2 = m_{B_{(c)}} $, and $ \epsilon_1 $ is the polarization vector of $ \Upsilon(1S) $, such that $ \epsilon_1^\dagger\cdot p_1 = 0 $. The particles are on-shell, i.e., $ p_1^2=m_1^2=m^2_{\Upsilon(1S)} $ and $ p_2^2=m_2^2=m^2_{B_{(c)}} $. The form factors $ A_0(q^2) $, $ A_{\pm}(q^2) $, and $ V(q^2) $ are calculated later in our model. In terms of the invariant form factors, the hadronic tensor reads as

where

Finally, by summing the vector polarizations, we obtain the decay width

where $ m_1=m_{\Upsilon(1S)} $, $ m_2=m_{B_{(c)}} $, and $ s_1 =(p_{B_{(c)}}+p_{\ell})^2 $. The upper and lower bounds of $ s_1 $ are given by

where $ \lambda(x,y,z) \equiv x^2+y^2+z^2-2(xy+yz+zx) $ is the Källén function.

The CCQM has been used for approximately three decades as a tool for hadronic calculations. The model has been introduced in great detail within many studies by our group, for instance, in Refs. [15−17], and successfully employed to explore the various decays of not only mesons and baryons, but also tetraquarks, pentaquarks, and other multiquark states [18−27]. In this paper, we only list the main features of the model for concision and to focus more on the new results.

The CCQM is based on an effective interaction Lagrangian describing the coupling of hadrons to their constituent quarks. The coupling of a meson $ M(q_1 \bar q_2) $ to its constituent quarks $ q_1 $ and $ \bar q_2 $ is described by the nonlocal Lagrangian (see, e.g., Ref. [17])

Here, $ g_M $ is the meson-quark coupling constant, $ \Gamma_M $ is the relevant Dirac matrix (or a string of Dirac matrices) chosen appropriately to describe the spin quantum numbers of the meson field $ M(x) $, and the vertex function $ F_M(x,x_1,x_2) $ characterizes the finite size of the meson. To satisfy translational invariance, the vertex function must obey the identity $ F_M(x+a,x_1+a,x_2+a) \, = \, F_M(x,x_1,x_2) $ for any given four-vector a. In what follows, we adopt a specific form for the vertex function, which satisfies the above translation invariance relation.

where $ \Phi_M $ is a correlation function of the two constituent quarks with masses $ m_1 $ and $ m_2 $. The variable $ w_i $ is defined by $ w_i=m_i/(m_1+m_2) $ such that $ w_1+w_2=1 $. In principle, the Fourier transform of the correlation function, which we denote by $ \Phi_M(-p^2) $, can be calculated from the solutions of the Bethe-Salpeter equation for the meson bound states [28].

The authors of Ref. [29] found that, using various forms for the vertex function, the basic hadron observables were insensitive to the details of the functional form of the hadron-quark vertex function. Therefore, we use this observation as a guiding principle and choose a simple Gaussian form for the Fourier transform of the correlation function $ \Phi_{M}(-p^2) $. The minus sign is chosen to emphasize that we are working in Minkowski space.

where the parameter $ \Lambda_M $ characterizes the size of the meson. Because $ p^2 $ becomes $ -p_E^2 $ in Euclidean space, the form (12) has the appropriate falloff behavior in the Euclidean region. We must reiterate that any choice for $ \Phi_M $ is appropriate as long as it falls off sufficiently fast in the ultraviolet region of Euclidean space to render the Feynman-diagram ultraviolet finite.

Recently, we also considered a more complicated structure for the vertex functions. In Ref. [30], we introduced the vertex functions as Gaussian multiplying some polynomial to describe the radial excitations of the charmonium and bottomonium as follows:

where $ \Phi_{V}(-k^{2})=\exp(k^2/\Lambda^2_V) $. Here, we assumed that the different radial excitations cannot pass into each other through a quark loop. We called this assumption the orthogonality condition. This condition allowed us to determine the numerical values of the coefficients $ c_{m+n-1} $ in the allowed region of $ p^{2} $ for a certain quarkonium spectrum.

The quark-meson coupling is obtained using the compositeness condition [31, 32]

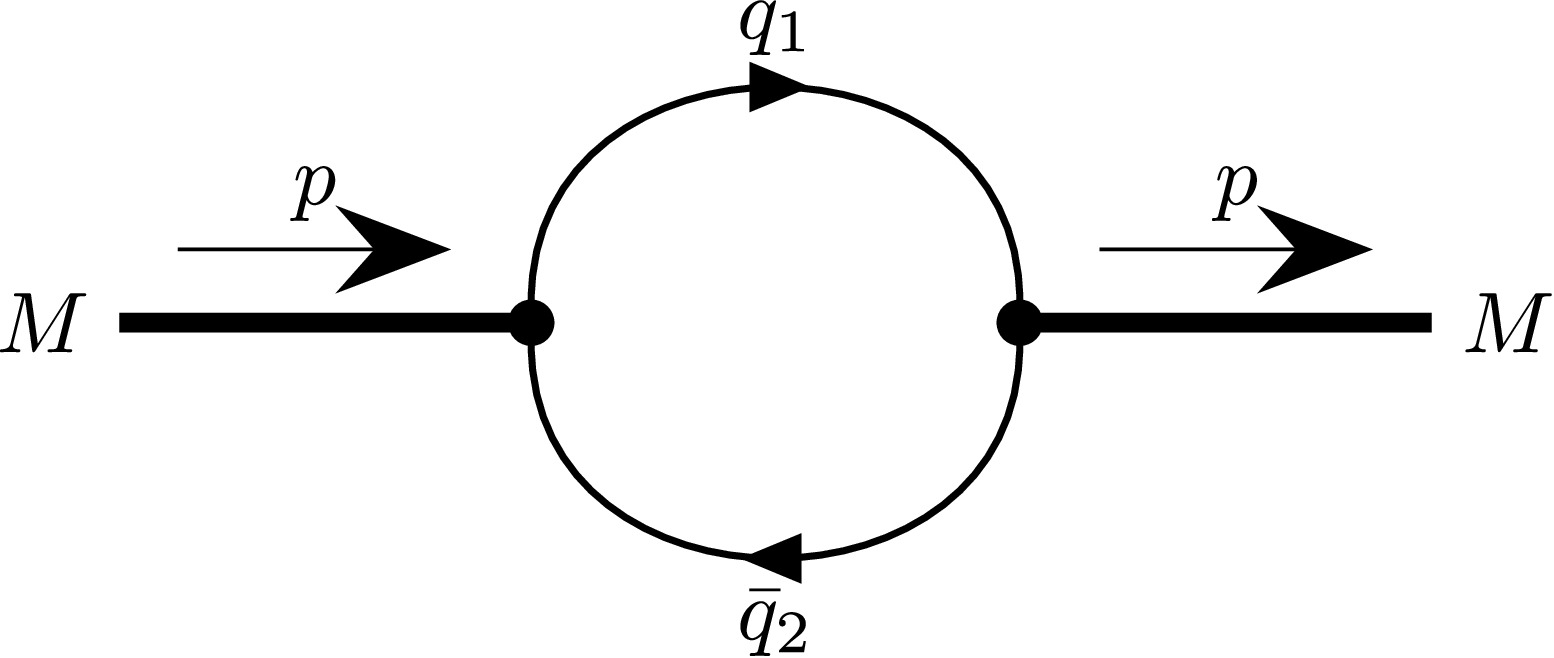
where $ Z_M $ is the wave function renormalization constant of the meson M, and $ \Pi'_M $ is the derivative of the meson mass function.

The meson mass function in Eq. (13) is defined by the Feynman diagram shown in Fig. 2 and has the following form:

Figure 2.  One-loop self-energy diagram for a meson.

where

is the quark propagator.

The CCQM has several free parameters, including the constituent quark masses $ m_q $, hadron size parameters $ \Lambda_H $, and a universal cutoff parameter λ, which guarantees the confinement of constituent quarks inside hadrons. These parameters are obtained by fitting to available experimental data and/or lattice QCD. Once they are fixed, the CCQM can be used to calculate hadronic quantities in a straight-forward manner. The parameters relevant to this study are listed in Table 1.

$ m_{u/d} $	$ m_s $	$ m_c $	$ m_b $	$ \Lambda_B $	$ \Lambda_{B_c} $	$ \Lambda_{\Upsilon(1S)} $	λ
0.241	0.428	1.67	5.04	1.96	2.73	4.03	0.181

Table 1.  Quark masses, meson size parameters, and infrared cutoff parameter (all in GeV).

In the CCQM, the hadronic matrix element of the semileptonic decays $ \Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell $ is given in the diagram in Fig. 1 and is written as

where k is the loop momentum, and $ w_{ij}=m_{q_j}/(m_{q_i}+m_{q_j}) $ $ (i,j=1,2,3) $.

The form factors are then calculated using standard one-loop calculation techniques (see, e.g., Ref. [33]). The main steps are as follows. First, the Gaussian form of the vertex functions in Eq. (12) is substituted into Eq. (17). Second, the Fock-Schwinger representation is used for the quark propagator

Third, the integrals are treated over the Fock-Schwinger parameters $ 0\le \alpha_i<\infty $ by introducing an additional integration, which converts the set of these parameters into a simplex:

Note that Feynman diagrams are calculated in the Euclidean region, where $ p^2=-p^2_E $. The vertex functions fall off in the Euclidean region; therefore, no ultraviolet divergence appears. To avoid possible thresholds in the Feynman diagram, we introduce a universal infrared cutoff, which effectively guarantees the confinement of quarks within hadrons.

Each form factor for the semileptonic transition $ \Upsilon(1S)\to B_{(c)} $ is finally transformed into three-fold integrals of the general form

The expressions for $ f(t\alpha_1,t\alpha_2) $ are obtained using our FORM code. The numerical calculation of the three-fold integrals is performed using FORTRAN codes with the help of the NAG library (see appendix).

Before listing our numerical results, we briefly discuss the estimation of the theoretical errors in our approach. We reiterate that all phenomenological quark models of hadrons are simplified physics pictures; therefore, it is difficult to treat the theoretical error rigorously. The main source of uncertainties originates from the free parameters listed in Table 1. They are obtained by a least-squares fit of leptonic and electromagnetic decay constants to experimental data and/or lattice QCD, and the allowed deviation in the fit is in the range 5%–10%. This range can be used as a reasonable estimation of the model's errors. Moreover, the CCQM has been applied to study a broad range of hadron decay processes, and we find that our predictions often agree with experimental data within 10%. Therefore, we estimate the theoretical error of the predictions in this study to be approximately 10%.

Note that the 10% error arises from the existence of free parameters in the model, which are determined through a fit to the experimental data (see Ref. [34]). These fitted parameters carry their own uncertainties, and these uncertainties propagate through to the form factors and decay widths. As a result, the overall error remains below 10%. The errors associated with the numerical calculation of the multifold integrals are negligible, as we use a highly reliable subroutine from the NAG library. This ensures that the precision of the numerical integration does not contribute significantly to the overall error. More details on the NAG subroutine are given in the appendix.

In Fig. 3 , we present the form factors of the $\Upsilon(1S) \to B_{(c)}$ transitions in the full range of momentum transfer $ 0\le q^2 \le q^2_{\rm{max}} = (m_{\Upsilon(1S)}-m_{B_{(c)}})^2 $. Note that in the CCQM, the form factors are directly calculated in the entire physical range without the extrapolation typically observed in lattice QCD and the QCD sum rules. We then parameterize the $ q^2 $ dependence of the form factors using a general dipole approximation

Figure 3.  (color online) Our results for the form factors of the $ \Upsilon(1S) \to B $ (left) and $ \Upsilon(1S) \to B_c $ (right) transitions.

The dipole-approximation parameters for the $ \Upsilon(1S) \to B_{(c)} $ form factors are displayed in Table 2. We also list the values of the form factors at zero recoil, i.e., at $ q^2_{\rm{max}} $. We compare the form factors at maximum recoil $ (q^2 = 0) $ with those of other theoretical studies in Table 3.

	$ \Upsilon(1S)\to B $					$ \Upsilon(1S)\to B_c $
	$ A_0 $	$ A_+ $	$ A_- $	V		$ A_0 $	$ A_+ $	$ A_- $	V
$ F(0) $	0.46	0.013	1.03	0.38		2.54	0.27	2.56	1.23
a	3.93	8.99	5.64	5.63		3.49	4.91	4.57	4.54
b	3.41	21.9	8.34	8.37		2.83	7.43	5.93	5.89
$ F(q^2_{\rm{max}}) $	1.28	0.18	4.78	1.75		3.96	0.50	4.59	2.19

Table 2.  Parameters of the dipole approximation for the $ \Upsilon(1S)\to B_{(c)} $ form factors and the form-factor values at zero recoil $ q^2_{\rm{max}} $.

	$ \Upsilon(1S)\to B $					$ \Upsilon(1S)\to B_c $
	$ A_0(0) $	$ A_+(0) $	$ A_-(0) $	$ V(0) $		$ A_0(0) $	$ A_+(0) $	$ A_-(0) $	$ V(0) $
This study	0.46	0.013	1.03	0.38		2.54	0.27	2.56	1.23
BSW [7]						$ 3.06^{+0.10}_{-0.05} $	$ 0.38^{+0.06}_{-0.09} $		$ 1.61^{+0.01}_{-0.01} $
Ref. [35]						4.99	1.01		1.01
NRQCD [11]						3.46	0.51		1.66
BS [9]	0.20	0.031	0.29	0.15		1.63	0.26	1.28	0.80

Table 3.  Form factors at maximum recoil $ q^2=0 $ in the CCQM and other theoretical studies. The values in the row labeled BS were obtained based on the form-factor graphs of Ref. [9] and private communication with its authors.

We present our results for the branching fractions of the semileptonic decays $ \Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell $ ($ \ell = e,\mu,\tau $) in Table 4. We also show the relevant predictions of other theoretical studies for comparison. Our predictions agree well with the Bethe-Salpeter-approach results [9]. Regarding the results obtained using the Bauer-Stech-Wirbel model [7], the branching fractions for the electron and muon modes agree with ours; however, that for the tau mode disagrees. The results obtained in NRQCD [11] for the branching fractions are larger than those in other studies, including ours.

Channel	Unit	This study	BS [9]	BSW [7]	NRQCD [11]
$ \Upsilon(1S)\to B e \bar\nu_e $	$ 10^{-13} $	5.96	$ 7.83^{+1.40}_{-1.20} $
$ \Upsilon(1S)\to B \mu \bar\nu_\mu $	$ 10^{-13} $	5.95	$ 7.82^{+1.40}_{-1.20} $
$ \Upsilon(1S)\to B \tau \bar\nu_\tau $	$ 10^{-13} $	3.30	$ 5.04^{+0.92}_{-0.79} $
$ \Upsilon(1S)\to B_c e \bar\nu_e $	10−10	1.84	$ 1.37^{+0.22}_{-0.19} $	$ 1.70^{+0.03}_{-0.02} $	$ 5.58^{+3.32\,\,+0.14\,\,+0.08}_{-1.54\,\,-0.12\,\,-0.18} $
$ \Upsilon(1S)\to B_c \mu \bar\nu_\mu $	10−10	1.83	$ 1.37^{+0.22}_{-0.19} $	$ 1.69^{+0.04}_{-0.02} $	$ 5.58^{+3.32\,\,+0.14\,\,+0.08}_{-1.54\,\,-0.12\,\,-0.18} $
$ \Upsilon(1S)\to B_c \tau \bar\nu_\tau $	$ 10^{-11} $	4.74	$ 4.17^{+0.58}_{-0.52} $	$ 2.90^{+0.05}_{-0.02} $	$ 13.0^{+7.7\,\,+0.3\,\,+0.2}_{-3.5\,\,-0.3\,\,-0.4} $

Table 4.  Branching fractions of the $ \Upsilon(1S) $ semileptonic decays in the CCQM, Bethe-Salpeter (BS) approach [9], Bauer-Stech-Wirbel (BSW) model [7], and NRQCD framework [11].

It is interesting to consider the ratio $ R_{B_{(c)}}\equiv\mathcal{B}(\Upsilon(1S)\to B_{(c)} \tau \bar{\nu}_\tau)/\mathcal{B}(\Upsilon(1S)\to B_{(c)} \ell \bar{\nu}_\ell) $, $ (\ell = e,\mu) $, where a large part of theoretical and experimental uncertainties cancels. Note that the key advantage in considering this ratio is the cancellation of various uncertainties. Specifically, the hadronic form factors, which describe the $ \Upsilon(1S) \to B_c $ transition and carry theoretical uncertainties, largely cancel out. Similarly, uncertainties from radiative corrections, including QCD, QED, and electroweak interactions, also cancel out owing to their similar impacts on both decay channels in the ratio. Additionally, CKM-matrix-element uncertainties are eliminated, as they affect both processes identically. These cancellations make the ratio a particularly clean observable for studying potential deviations from the SM and probing NP effects.

Eqs. (23) and (24) list all available predictions for $ R_{B_{(c)}} $ to date:

Our results for the ratios $ R_{B} $ and $ R_{B_c} $ agree well with those in the BS approach. Meanwhile, the result for $ R_{B_c} $ in the BSW model is approximately two times smaller than the BS and our predictions. Moreover, the NRQCD prediction for $ R_{B_c} $ is very close to ours. Therefore, we propose that the value $ R_{B_c}\simeq 0.3 $ is a reliable prediction.

As already mentioned in the introduction, the semileptonic decay $ \Upsilon(1S)\to B_{c}\ell\bar{\nu}_\ell $ is induced by the quark-level transition $ b\to c\ell\bar{\nu}_\ell $ and can be linked with the $ R_D^{(*)} $ anomaly. Therefore, it is interesting to probe the possible NP effects in the $ \Upsilon(1S) $ semitauonic decay. Based on the current status of the anomalies, we assume that NP only affects leptons of the third generation and modify the effective Hamiltonian for the quark-level transition $ b \to c \tau^- \bar{\nu}_{\tau} $ as follows:

where the four-fermion operators are written as

Here, $ P_{L,R}=(1\mp\gamma_5)/2 $ are the left and right projection operators, and $ V_{L,R} $ are the complex Wilson coefficients governing the NP contributions. In the SM, $ V_{L,R}=0 $.

The invariant matrix element of the semileptonic decay $ \Upsilon(1S)\to B_{c}\tau\bar{\nu}_\tau $ is then written as

Note that the axial hadronic currents do not contribute to the $ P\to P^\prime $ transition. Therefore, assuming that NP appears in both the $ \bar{B}^0\to D $ and $ \bar{B}^0\to D^* $ transitions, the case of pure $ V_R-V_L $ coupling is ruled out. Therefore, the branching fraction $ \mathcal{B}(\Upsilon(1S)\to B_{c}\tau\bar{\nu}_\tau) $ is modified according to

By assuming the dominance of only one NP operator at a time, the allowed regions for the NP Wilson coefficients $ V_{L(R)} $ are obtained using experimental data for the ratios of branching fractions $R_D= 0.344\pm 0.026$, $R_{D^*}= 0.285\pm 0.012$ [36], and $ R_{J/\psi}=0.71\pm 0.17\pm 0.18 $ [37], the upper limit $ {\cal{B}}(B_c\to \tau\nu) \leq $ 10% from the LEP1 data [38], and the longitudinal polarization fraction of the $ D^* $ meson, $ F_L^{D^*}({B} \to D^{\ast} \tau\bar{\nu}_\tau)=0.43\pm 0.06\pm 0.03 $ [39]. The relevant form factors for the transitions $ B\to D^{(*)} $ and $ B_c\to J/\psi $ were calculated in Ref. [40]. In Fig. 4, we show the allowed regions for V_L and V_R within 2σ, and in each region, we find a best-fit value and mark it with an asterisk.

Figure 4.  (color online) Constraints on the complex Wilson coefficients V_L and V_R from the measurements of $ R_D $, $ R_{D^*} $, $ R_{J/\psi} $, and $ F_L^{D^*}({B} \to D^{\ast} \tau\nu_\tau) $ within 2σ and from the branching fraction $ {\cal{B}}(B_c\to\tau\nu_\tau)\leq $ 10%. The allowed regions are indicated in light-blue, and the asterisks indicate the best-fit values.

We summarize our predictions for the branching fraction $ \mathcal{B}(\Upsilon(1S)\to B_c \tau \bar{\nu}_\tau) $ and the ratio of branching fractions $ R_{B_c} $ in Table 5. The row labeled SM (CCQM) contains our predictions within the SM with the CCQM form factors. The predicted intervals for the observables in the presence of NP are given in correspondence with the 2σ allowed regions of the NP Wilson coefficients depicted in Fig. 4. Note that the V_L NP scenario can enhance the physical observables by a factor of 6.

Quantity	SM (CCQM)	VR	VL
$ 10^{11}\times\mathcal{B}(\Upsilon(1S)\to B_c \tau \bar{\nu}_\tau) $	4.74	(4.77, 7.07)	(4.74, 27.3)
$ R_{B_c} $	0.26	(0.26, 0.39)	(0.26, 1.50)

Table 5.  Observables in the SM and in the presence of NP.

Finally, it is worth mentioning the possibility of experimental observation of the semileptonic decays $ \Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell $. As noted in Ref. [11], a branching fraction of the order of 10⁻¹⁰ of the decays $ \Upsilon(1S)\to B_c\ell\bar{\nu}_\ell $ is almost impossible to achieve at LHCb, CMS, and Belle-II. Although the accumulated number of $ \Upsilon(1S) $ samples at these colliders can be as large as 10¹⁰–10¹¹, the low reconstruction efficiency (assumed to be several percent) makes it extremely difficult to observe any significant signal. Even if NP effects enhance the branching fractions by an order of magnitude (in the case of semitauonic decay), studying these decays experimentally remains a challenge (see Ref. [11] for more details).

This paper presents a new study of the semileptonic decays $ \Upsilon(1S)\to B_{(c)}\ell\bar{\nu}_\ell $, where $ \ell = e,\mu,\tau, $ inspired by the recent search for similar rare weak decays of $ J/\psi $ at BESIII. The relevant form factors for the $ \Upsilon(1S)\to B_{(c)} $ transitions are calculated in the entire momentum transfer squared region within the framework of the CCQM. Predictions of the branching fractions and their ratios are reported and compared with those of other theoretical studies. A good agreement is found with the results of the Bethe-Salpeter approach. However, our prediction of the ratio of branching fractions $R_{B_{(c)}}\equiv\mathcal{B}(\Upsilon(1S)\to B_{(c)} \tau \bar{\nu}_\tau)/ \mathcal{B}(\Upsilon(1S) \to B_{(c)} \ell \bar{\nu}_\ell)$ disagrees with the Bauer-Stech-Wirbel model prediction. We predict $ R_{B_c}=0.26 $ and $ R_{B}=0.55 $ , which are close to the values $ R_{B_c}=0.30 $ and and $ R_{B}=0.64 $ obtained in the Bethe-Salpeter approach. We also extend the SM effective Hamiltonian for the $ b\to c\tau\bar{\nu}_\tau $ transition by including left- and right-handed four-fermion operators of dimension six. The relevant Wilson coefficients are obtained based on experimental data. Using the 2σ allowed regions for these coefficients, we find that the branching fraction of the tau mode and the ratio $ R_{B_c} $ can be enhanced by approximately an order of magnitude. There have been few theoretical calculations for $ \Upsilon(1S) $ semileptonic decays to date. Therefore, this study provides more insights for experimental testing of the SM and the search for NP at future colliders.

C. T. T. and H. C. T. thank HCMC University of Technology and Education for supporting their work and scientific collaboration.

For numerical calculations of multifold integrals, we use the NAG subroutine d01fcf.

For instance, in the case of threefold integrals:

external FA0: function supplied by the user (our form factor)

eps=10⁻⁵: the relative errors acceptable by the user

maxpts=10000000: the maximum number of integrand evaluations

minpts=0: the minimum number of integrand evaluations

lenwrk=500000

wrkstr(500000)

ifail=0

ndim =3: the number of dimensions

finval: contains the best estimate obtained for the integral

acc: contains the estimated relative error in finval

　do 20 k=1,3

a(k)=0.d0

b(k)=1.d0

　20 continue

call d01fcf(ndim,a,b,minpts,maxpts,FA0,eps,acc,lenwrk,wrkstr,finval,ifail)

　A0=finval

acc=10⁻⁴.