Rotational properties and blocking effects in N = 152 isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf

I. INTRODUCTION

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

The possibility of a deformed shell gap at $N=152$ was suggested by the systematics of the alpha-particle energies around the $A=250$ mass region [1]. This large gap enhances the stability of isotopes at $N=152$ and results in large values of the moment of inertia (MOI) compared to those of the neighboring isotopes [2]. Over the past decade, many in-beam spectroscopy studies have been performed on the $N=152$ even-even (e.g., ²⁴⁸Cm, ²⁵⁰Cf, ²⁵²Fm, ²⁵⁴No, and ²⁵⁶Rf) and odd-A (e.g., ²⁴⁹Bk, ²⁵¹Es, and ²⁵⁵Lr) isotones [3−5]. These observed rotational bands, associated with MOIs and alignment properties, can reveal detailed information on the single-particle level structure in light superheavy nuclei.

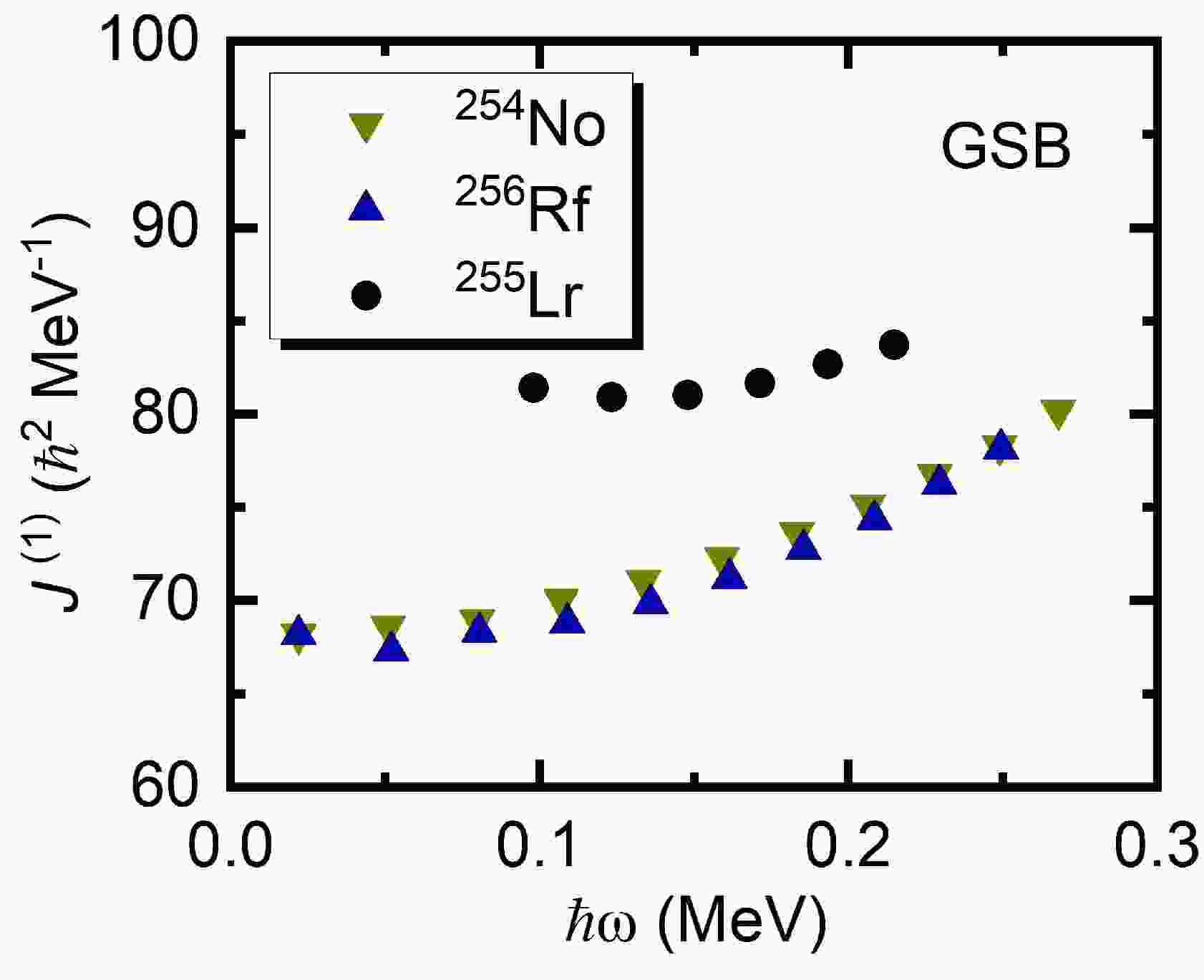
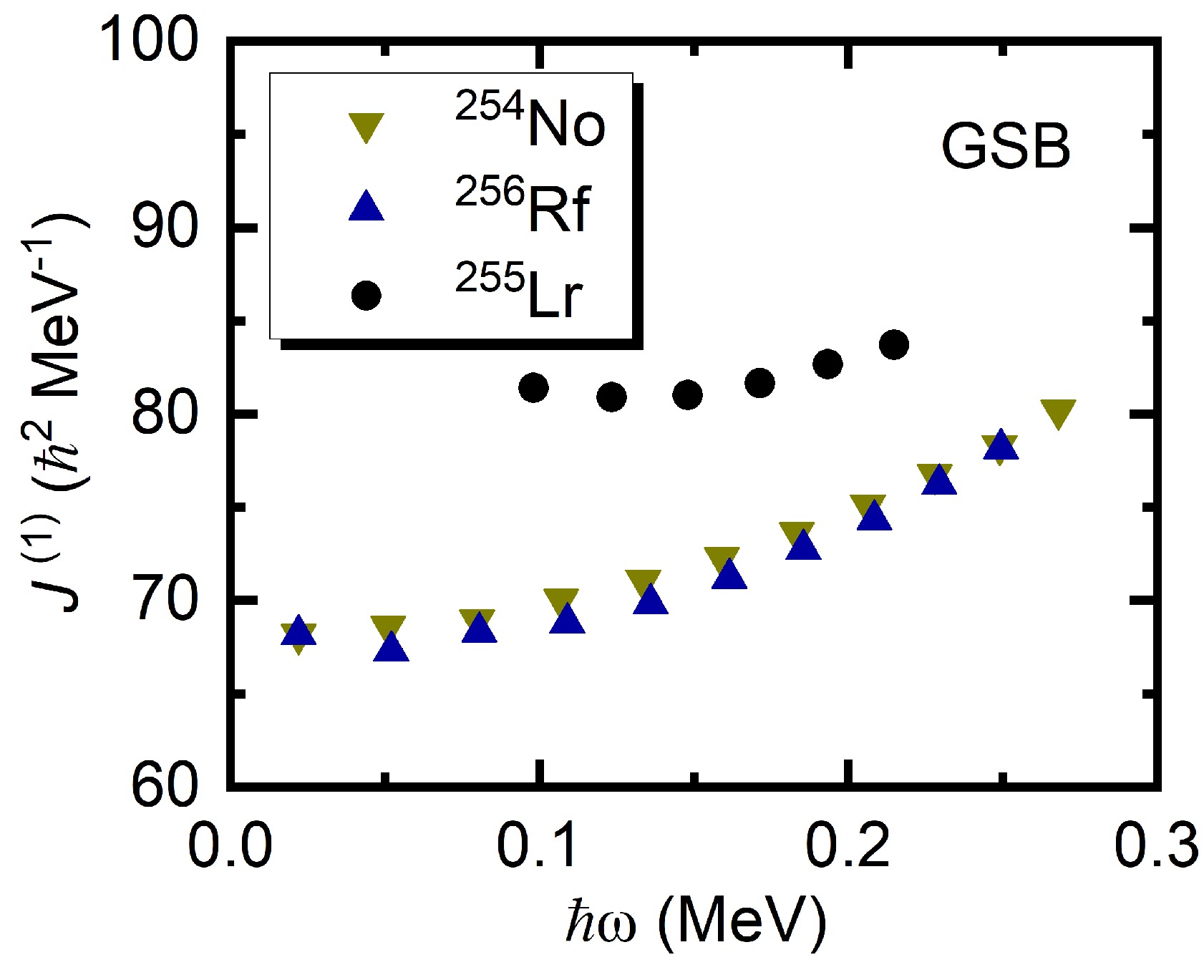
Ground-state bands (GSBs) with identical transition energies (within 2 keV) in the A ~ 250 actinide nuclei were reported in Ref. [6]. To the best of our knowledge, the identical transition energies of the recently observed GSBs in the heavier $N=152$ isotones ²⁵⁴No [7] and ²⁵⁶Rf [2] have not previously been reported. A comparison of the experimental kinematic MOI $J^{(1)}$ of the GSBs in the $N=152$ isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf is shown in Fig. 1. The experimental data are taken from Refs. [2, 5, 7]. The kinematic MOI $J^{(1)}$ values are nearly identical for the GSBs in the even-even nuclei ²⁵⁴No and ²⁵⁶Rf, whereas for their odd-A neighbor nucleus ²⁵⁵Lr, there is an remarkable increase in $J^{(1)}$ for the GSB. Furthermore, the odd-even difference in MOI gradually decreases with increasing rotational frequency ω. These issues require further investigation.

Figure 1

Figure 1.  (color online) Experimental kinematic moments of inertia $J^{(1)}$ for the GSBs in the N = 152 isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf. The experimental data are taken from Refs. [2, 5, 7].

DownLoad: Full-Size Img PowerPoint

In this study, the rotational properties and blocking effects of the $N=152$ isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf are investigated using the cranked shell model (CSM), with the pairing correlations treated via the particle-number-conserving (PNC) method. It is well known that the MOIs of normally deformed bands are sensitive to nuclear pairing correlations and Pauli blocking effects. In the PNC-CSM method, the CSM Hamiltonian, including monopole and quadrupole pairing correlations, is diagonalized directly in a truncated Fock space. Thus, the particle number is conserved and the Pauli blocking effects are exactly considered.

II. THEORETICAL FRAMEWORK

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

For an axially symmetric nucleus in the rotating frame, the CSM Hamiltonian with pairing is $H_\mathrm{CSM}=H_{\rm Nil} - \omega J_{x} +H_\mathrm{P}$. $H_{\rm Nil}=\sum h_{\rm Nil}$ is the Nilsson Hamiltonian, $\xi (\eta)$ is the eigenstate of the single-particle Hamiltonian $h_{\xi (\eta)}$, and $\overline{\xi} (\overline{\eta})$ is the corresponding time-reversed state. $-\omega J_{x}$ is the Coriolis interaction with cranking frequency ω about the x axis (perpendicular to the nuclear symmetry z axis). The pairing $H_\mathrm{P}$ includes monopole $H_\mathrm{P}(0)= -G_{0} \sum_{\xi\eta}a_{\xi}^{\dagger}a_{\overline{\xi}}^{\dagger}a_{\overline{\eta}}a_{\eta}$ and quadrupole $H_\mathrm{P}(2)= -G_{2} \sum_{\xi\eta}q_{2}(\xi)q_{2}(\eta)a_{\xi}^{\dagger}a_{\overline{\xi}}^{\dagger}a_{\overline{\eta}}a_{\eta}$ pairing correlations, where $q_{2}(\xi) = \sqrt{{16\pi}/{5}}\langle \xi |r^{2}Y_{20}|\xi\rangle$ is the diagonal element of the stretched quadrupole operator, and $G_{0}$ and $G_{2}$ are the average monopole and quadrupole pairing strengths, respectively.

In the PNC method for the pairing correlations, the CSM Hamiltonian $H_{\rm CSM}$ is diagonalized in a sufficiently large cranked many-particle configuration (CMPC) space without particle-quasiparticle transformation; thus, the Pauli blocking effects on pairing are treated consistently and exactly. The eigenstate of $H_{\rm CSM}$ can be expressed as $|\psi\rangle = \sum_{i}C_{i}|i\rangle$, where $C_i$ is real, and $|i\rangle=|\mu_1 \mu_2 \cdots \mu_n\rangle$ is a CMPC defined as the n-particle occupation on the cranked Nilsson orbitals. The particle occupation probability of the cranked Nilsson orbital μ in the state $|\psi\rangle$ is $n_{\mu} = \sum_{i}|C_{i}|^{2}P_{i \mu}$, where $P_{i \mu} = 1$ if μ is occupied in $|i\rangle$ , otherwise, $P_{i \mu} = 0$ . The kinematic MOI of the eigenstate $|\psi\rangle$ is $J^{(1)}=\langle\psi|J_x|\psi\rangle/{\omega}=\sum_{\mu} j^{(1)}(\mu)+$ $\sum_{\mu<\nu} j^{(1)}(\mu\nu)$, where $j^{(1)}(\mu)=[\langle \mu |j_x| \mu \rangle n_{\mu}]/\omega$ is the direct contribution, and $j^{(1)}(\mu\nu)=2[\langle \mu |j_x|\nu\rangle\sum_{i<j}(-)^{M_{i \mu}+M_{j \nu}}C_iC_j]/\omega$ is the interference term. The details of PNC calculations are given in Refs. [8, 9].

III. RESULTS AND DISCUSSIONS

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

The Nilsson parameters κ and μ are taken from Ref. [10]. The values of proton $\kappa_5$, $\mu_5$ and neutron $\kappa_6$, $\mu_6$ are modified slightly to fit the single-particle level sequence when the high-order deformation $\varepsilon_6$ is considered [11−13]. The deformations are used as input parameters in the PNC-CSM calculations. For the neighboring isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf, the deformation parameter $\varepsilon_2=0.260$ is chosen to be close to the experimental value [14], and $\varepsilon_4=0.020$ and $\varepsilon_6=0.045$ are chosen, referring to the deformations predicted by the finite range droplet model [15].

In principle, the effective pairing strengths $G_{0}$ and $G_{2}$ can be determined by the experimental odd-even differences in nuclear binding energies. They are also connected with the dimensions of the truncated CMPC space. In these calculations for ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf, the CMPC space is entirely constructed in the proton $N=5$, 6 and neutron $N=6$, 7 major shells, and the dimensions of the CMPC space are approximately 1000. For the even-even nuclei ²⁵⁴No and ²⁵⁶Rf, the corresponding effective pairing strengths are $G_{0} = 0.25$ MeV and $G_{2} = 0.02$ MeV for both protons and neutrons. For the odd-even nucleus ²⁵⁵Lr, the pairing strengths are slightly smaller for protons, that is, $G_{0p} = 0.15$ MeV and $G_{2p} = 0.02$ MeV, and those for neutrons are the same with even-even nuclei. The stability of the PNC-CSM calculations against the change in the dimensions of the CMPC space has been investigated in Refs. [9, 16].

The cranked Nilsson levels near the Fermi surface of ²⁵⁴No for protons and neutrons are shown in Fig. 2. The signature $\alpha=+1/2$ and $\alpha=-1/2$ levels are denoted by solid and dotted lines, respectively. The $Z = 100$ gap for protons and $N=152$ gap for neutrons are consistent with the experiment and the results predicted by the Woods-Saxon potential [17]. Based on such a sequence of single-particle levels, the experimental ground state with the configuration $\pi [521]1/2$ and the first excited state with the configuration $\pi [514]7/2$ in ²⁵⁵Lr ($Z=103$) can be reproduced well.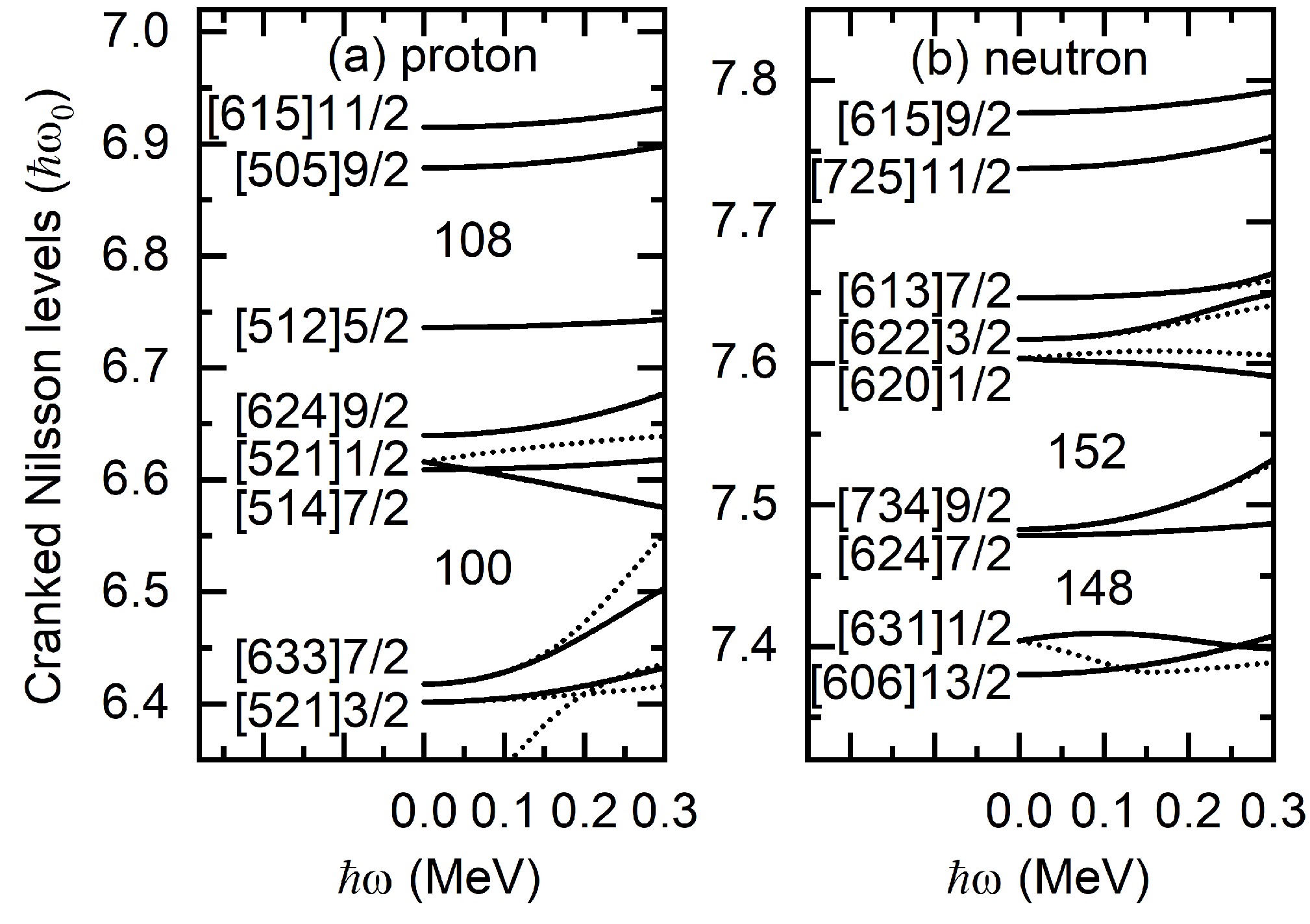

Figure 2

Figure 2.  Cranked Nilsson levels near the Fermi surface of ²⁵⁴No for protons and neutrons. The signature $\alpha = +1/2$ and $\alpha = -1/2$ levels are denoted by solid and dotted lines, respectively.

DownLoad: Full-Size Img PowerPoint

Figure 3 shows the experimental and calculated kinematic MOIs of the GSBs in ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf, which are denoted by solid squares and lines, respectively. The experimental kinematic MOI can be extracted using $J^{(1)}(I)=(2I+1)\hbar^{2}/E_{\gamma}(I+1 \rightarrow I-1)$. For ²⁵⁵Lr, the signature $\alpha=-1/2$ band has not been observed, and only the experimental and calculated MOIs of the signature $\alpha=+1/2$ band in ²⁵⁵Lr are shown.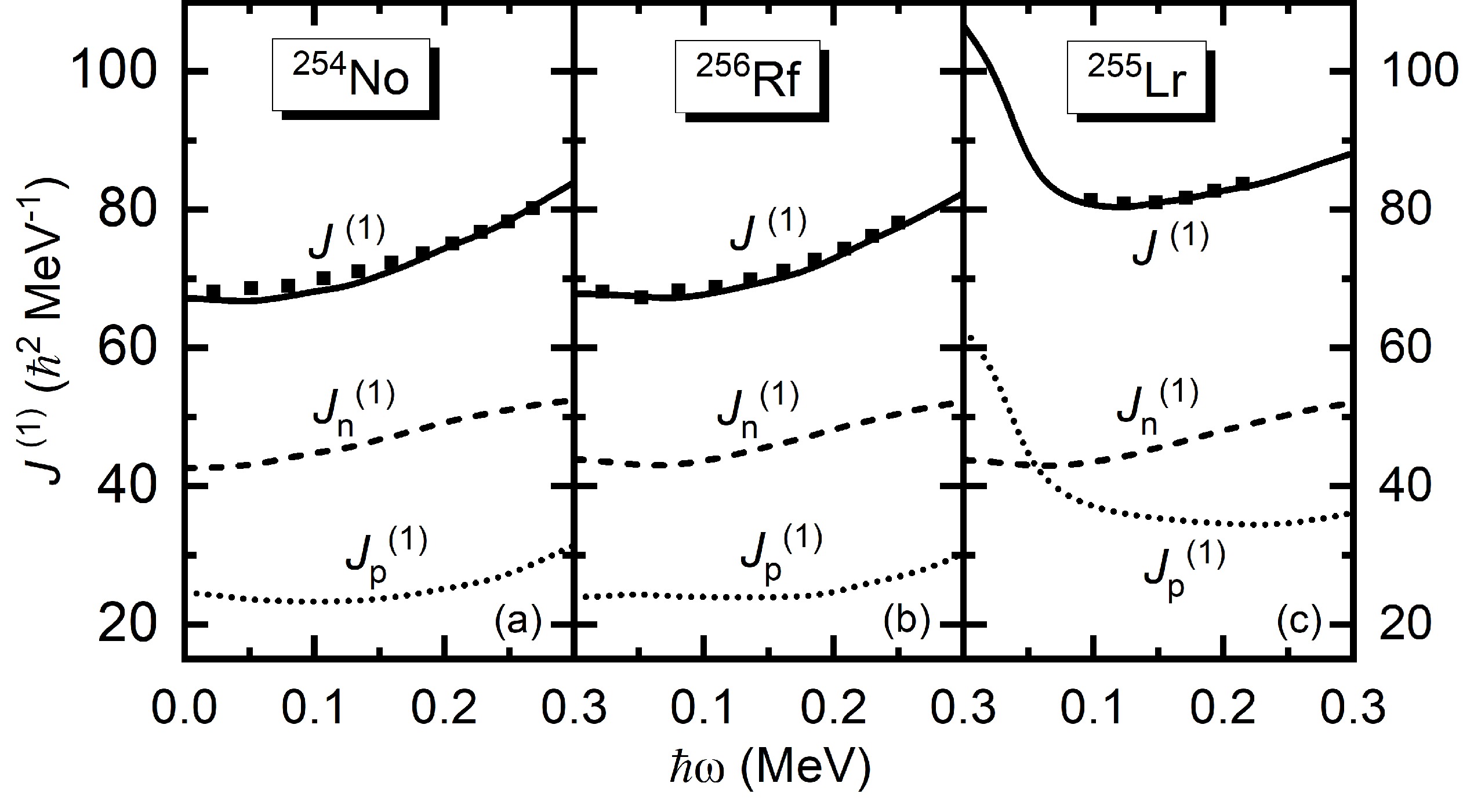

Figure 3

Figure 3.  Experimental and calculated kinematic moments of inertia $J^{(1)}$ for the GSBs in the $N=152$ isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf. The experimental data are denoted by squares, which are taken from Refs. [2, 5, 7]. The PNC-CSM calculations are denoted by lines. $J_n^{(1)}$ and $J_p^{(1)}$ represent the separate contributions to $J^{(1)}$ from neutrons and protons, respectively.

DownLoad: Full-Size Img PowerPoint

As shown in Figs. 3(a) and 3(b), the observed near identity of $J^{(1)}$ for the GSBs in ²⁵⁴No and ²⁵⁶Rf is reproduced satisfactorily by the PNC-CSM calculations. In Fig. 3(c), the experimental $J^{(1)}$ of the odd-A nucleus ²⁵⁵Lr is larger than those of the neighboring even-even nuclei ²⁵⁴No and ²⁵⁶Rf by approximately 15 $\hbar^{2}$ to 5 $\hbar^{2}$MeV, with the observed frequency $\hbar\omega$ increasing from approximately $\hbar\omega=0.10$ to 0.20 MeV, which is also reproduced well by the PNC-CSM calculation. In addition, the calculation shows that $J^{(1)}$ for the GSB in ²⁵⁵Lr is larger than those in neighboring nuclei by approximately 40 $\hbar^{2}$ MeV at $\hbar\omega=0$ MeV. As shown in Figs. 3(a)−3(c), the contributions to $J^{(1)}$ from neutrons ($J_n^{(1)}$) are nearly the same for the GSBs in these three isotones. The observed identity of $J^{(1)}$ in the neighboring even-even nuclei ²⁵⁴No and ²⁵⁶Rf, as well as the large difference in $J^{(1)}$ in the odd-A nucleus ²⁵⁵Lr, primarily stem from contributions to $J^{(1)}$ from protons ($J_p^{(1)}$).

Figure 4 shows the occupation probability $n_{\mu}$ of each proton orbital μ (including both $\alpha = \pm 1/2$) near the Fermi surface for the GSBs in ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf. As shown in Fig. 4(a), both the proton $\pi [514]7/2$ and $\pi [521]1/2$ orbitals are nearly half occupied ($n_\mu \approx 1$) for ²⁵⁴No. This can be understood as the $\pi [514]7/2$ and $\pi [521]1/2$ orbitals being close to each other [see Fig. 2], and relatively strong pairing correlations are expected between these two orbitals. Compared to the case of ²⁵⁴No, two additional protons in ²⁵⁶Rf partially occupy the proton $\pi [514]7/2$, $\pi [521]1/2$, and $\pi[624]9/2$ orbitals. Owing to the proton $Z=100$ subshell, the orbitals under this subshell are almost completely occupied ($n_\mu \approx 2$).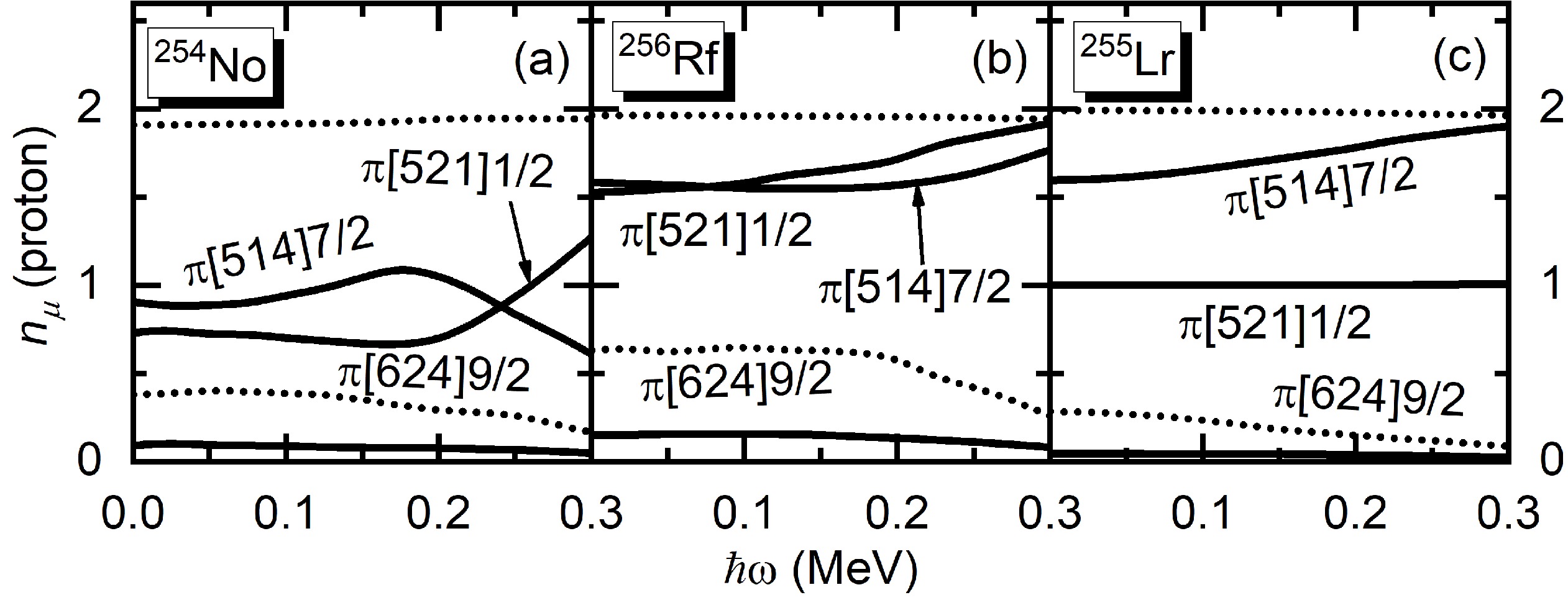

Figure 4

Figure 4.  Occupation probabilities $n_{\mu}$ of each cranked proton orbital μ (including both $\alpha=\pm 1/2$) near the Fermi surface for the GSBs in the $N=152$ isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf. The Nilsson orbitals far above ($n_{\mu} \approx 0$) and far below the Fermi surface ($n_{\mu} \approx 2$) are not shown.

DownLoad: Full-Size Img PowerPoint

Unlike the case of ²⁵⁴No and ²⁵⁶Rf, as shown in Fig. 4(c), the $\pi [521]1/2$ orbital is half occupied ($n_{\mu}$ $\approx$ 1) over the entire frequency. Except for the $\pi [521]1/2$ orbital, the other cranked Nilsson orbitals are either fully occupied ($n_{\mu}$ $\approx$ 2) or empty ($n_{\mu}$ $\approx$ 0). This is understandable from Fig. 2, which shows that the Fermi surface of ²⁵⁵Lr ($Z=103$) is just located at the proton $\pi [521]1/2$ orbital at $\hbar\omega=0$ MeV. The cranked Nilsson orbitals $\pi [514]7/2$ and $\pi [521]1/2$ ($\alpha=+1/2$) are close to each other over the entire rotational frequency; thus, the $\pi [514]7/2$ orbital is nearly fully occupied and the $\pi [521]1/2$ orbital is half occupied.

The PNC-CSM calculations can provide detailed information on the contributions to the MOIs $J^{(1)}$ from each cranked orbital, including the direct contribution $j^{(1)}(\mu)$ and interference term $j^{(1)}(\mu\nu)$. The calculated $j^{(1)}(\mu)$ and $j^{(1)}(\mu\nu)$ from the proton major $N=5$ and $N=6$ shells for the GSBs in ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf are shown in Fig. 5. The sum of the contributions from the proton orbitals below the $Z=100$ subshell (blue dashed lines) is almost the same for all the isotones. Compared to ²⁵⁴No, the contributions to $J^{(1)}$ from two additional protons, partially occupying the proton orbitals $\pi [514]7/2$, $\pi [521]1/2$, and $\pi [624]9/2$, are almost negligible for GSBs in ²⁵⁶Rf. These lead to the near identity of the total $J^{(1)}$ for the neighboring even-even GSBs in ²⁵⁴No and ²⁵⁶Rf. In contrast, the blocking of the nucleon on the proton orbital $\pi [521]1/2$ leads to a significant increase in proton $j^{(1)}([521]1/2)$ for the GSB in the low frequency region of the odd-A nucleus ²⁵⁵Lr [see Fig. 5(c)]. However, owing to the Coriolis antipairing effect, the blocking effects become weakened with increasing frequency. As shown in Figs. 5(a)−5(c), the differences in $j^{(1)}([521]1/2)$ of the GSBs of the odd-A nucleus and neighboring even-even nuclei decrease with increasing rotational frequency $\hbar\omega$ . Therefore, as shown in Fig. 3, $J^{(1)}_p$ of the GSB in the odd-A nucleus ²⁵⁵Lr exhibits significant deviations from those in the neighboring even-even nuclei.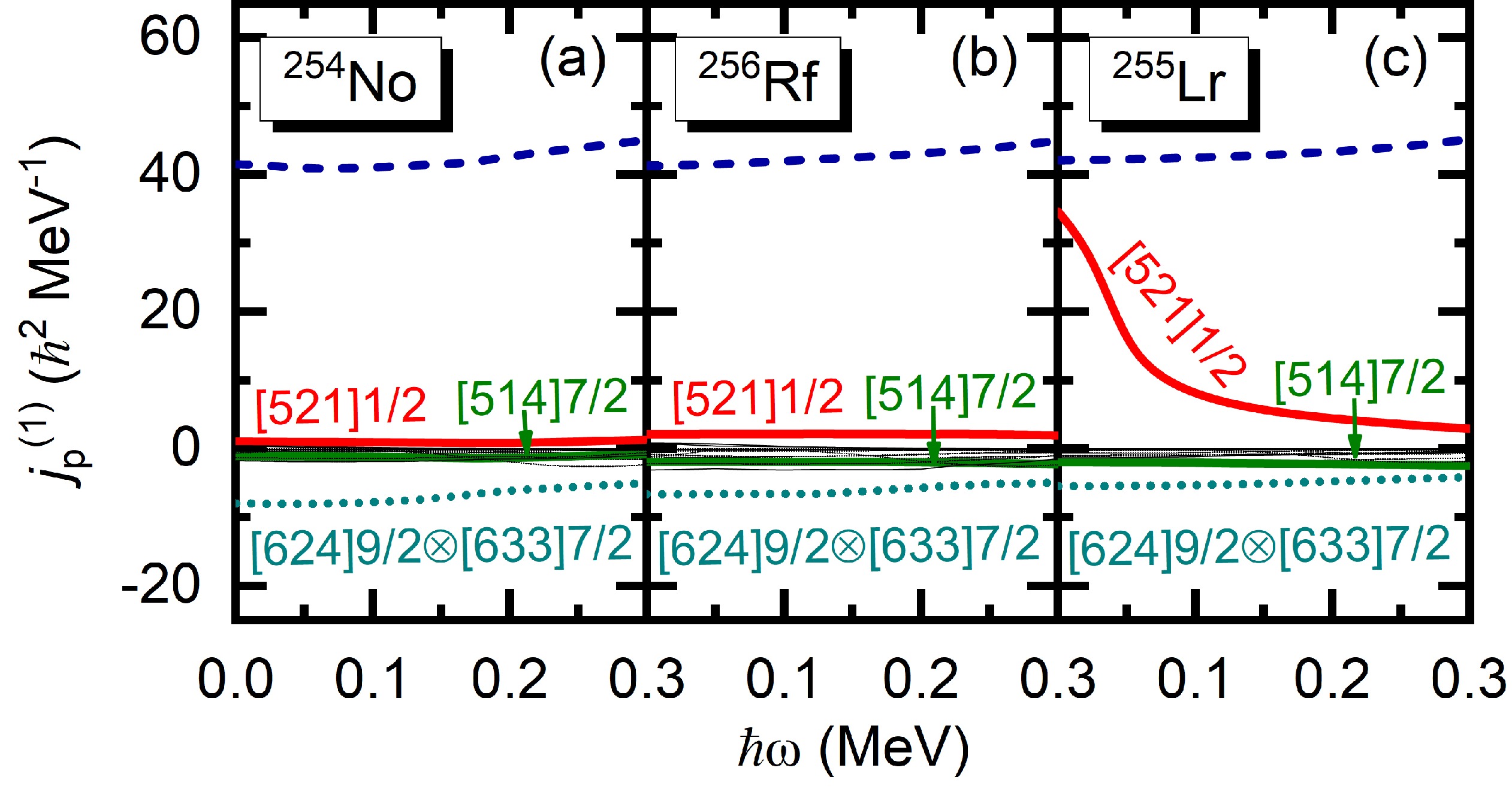

Figure 5

Figure 5.  (color online) Calculated contributions to $J_p^{(1)}$ from each cranked proton orbital, including the direct contribution $j^{(1)}(\mu)$ (solid lines) and interference term $j^{(1)}(\mu\nu)$ (dotted lines), for the GSBs in the $N=152$ isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf. The sum of the contributions from orbitals under the $Z=100$ subshell is denoted by blue dashed lines. $j^{(1)}(\mu)$ and $j^{(1)}(\mu\nu)$ are denoted simply by μ and $\mu\otimes\nu$, respectively.

DownLoad: Full-Size Img PowerPoint

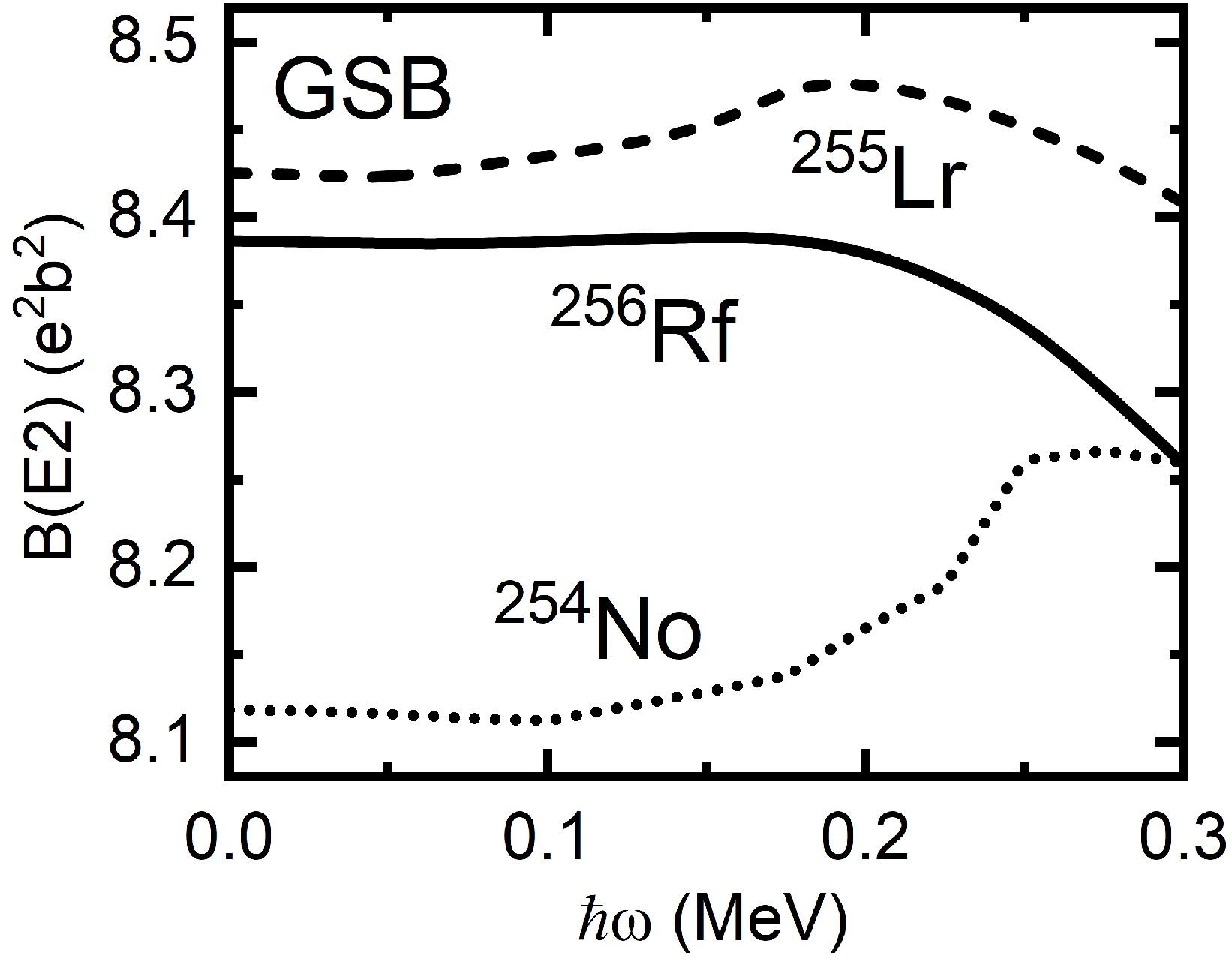
The electronic quadrupole transition probabilities $B(E2)$ are important quantities for testing the nuclear wavefunctions and deducing the quadrupole collectivities. In the semiclassical approximation, the transition probabilities $B(E2)$ can be obtained as $B(E2)= {3} \langle \psi|Q_{20}^{p}|\psi\rangle/ {8}$, where $|\psi\rangle$ is the eigenstate of the CSM Hamiltonian, and $Q_{20}^{p}$ corresponds to the laboratory quadrupole moment of protons, $Q_{20}^{p}=r^{2}Y_{20}=\sqrt{{5}/{16 \pi}}(3 z^{2}-r^{2})$. Note that the valence single-particle space is constructed in the major shells from $N=0$ to $N=6$ for protons, and there is no effective charge involved in the calculation of the $B(E2)$ values. Because the same deformation parameters are used to calculate the $B(E2)$ values for all $N=152$ isotones, the different behaviors of $B(E2)$ values along an isotonic chain are purely a microscopic effect of the nuclear many-body wavefunctions.

Figure 6 demonstrates the calculated $B(E2)$ values as a function of rotational frequency $\hbar\omega$ for the GSBs of ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf. Because more valence nucleons participate in the collective behavior, the $B(E2)$ value of ²⁵⁵Lr (²⁵⁶Rf) is larger than that of ²⁵⁴No by approximately 0.30 $e^{2}b^{2}$ (0.27 $e^{2}b^{2}$) at low frequency. The $B(E2)$ values remain almost constant at $\hbar\omega<0.20$ MeV, which indicates that these isotones have stable rotor characteristics with large collectivities in the low frequency region. At high rotational frequency, the behaviors of the $B(E2)$ values for the GSBs of ²⁵⁵Lr, ²⁵⁶Rf, and ²⁵⁴No are different. The $B(E2)$ values in ²⁵⁵Lr and ²⁵⁶Rf decrease at $\hbar\omega>0.20$ MeV, whereas that in ²⁵⁴No increases in this frequency region. This difference is easy to understand because the level $\pi [514]7/2$ crosses $\pi [521]1/2$ [see Fig. 2(a)], which leads to a structural change in the many-body wave functions.

Figure 6

Figure 6.  Calculated $B(E2)$ values as a function of rotation frequency $\hbar\omega$ for the GSBs of ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf.

DownLoad: Full-Size Img PowerPoint

IV. SUMMARY

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

In summary, the GSBs in the $N = 152$ isotones ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf are investigated using the CSM, with the pairing correlations treated via a PNC method. The Pauli blocking effects are considered exactly in the PNC method. The experimentally kinematic MOIs $J^{(1)}$ are reproduced well by the PNC-CSM calculations, and the contributions to $J^{(1)}$ from neutrons are nearly the same for these isotones.

The variation in $J^{(1)}$ versus frequency exhibits a remarkable identity for the neighboring even-even isotones ²⁵⁴No and ²⁵⁶Rf. This is because the two additional protons in ²⁵⁶Rf are partially occupied by the proton $\pi [514]7/2$, $\pi [521]1/2$, and $\pi [624]9/2$ orbitals, but the contributions to $J^{(1)}$ are negligible compared to ²⁵⁴No.

Compared to the case of the neighboring nuclei ²⁵⁴No and ²⁵⁶Rf, there is a nearly 50% increase in $J^{(1)}$ for the odd-A nucleus ²⁵⁵Lr. Detailed theoretical investigations show that the increase in $J^{(1)}$ is mainly caused by the contribution of proton $j^{(1)}([521]1/2)$ owing to the blocking of the nucleon on the proton $\pi [521]1/2$ orbital in ²⁵⁵Lr.

The electronic quadrupole transition probabilities $B(E2)$ among ²⁵⁴No, ²⁵⁵Lr, and ²⁵⁶Rf are investigated using the semiclassical approximation, with the microscopic wave function obtained via the PNC-CSM method. Compared to the $B(E2)$ values of ²⁵⁵Lr and ²⁵⁶Rf, the different behavior of the $B(E2)$ value of ²⁵⁴No at $\hbar\omega>0.20$ MeV is predicted to be due to the level $\pi [514]7/2$ crossing $\pi [521]1/2$.

References