Angularity in Higgs boson decays via H→gg at NNLL' accuracy

Since the experimental discovery of the Higgs boson, the final piece of the Standard Model, the continuous operation of the Large Hadron Collider (LHC) and the ATLAS and CMS experiments [1, 2] have achieved significant success in the refined study of the Higgs boson, for example, determining the Higgs couplings with top quarks [3, 4] and bottom quarks [5, 6]. At the LHC, the significantly large background restricts the accuracy of measurements on the Higgs signal strength to not below 5% [7] and complicates the probing of Yukawa couplings of the light fermions of first two generations [8−16]. The sensitivity to Higgs self-interactions is also weak [17−20]. Future experimental proposals to probe its properties and rare decay modes of the Higgs boson with higher accuracy have been presented, e.g., the International Linear Collider [21], Circular Electron-Positron Collider (CEPC) [22], CLIC [23], and FCC-ee [24]. In the future electron-positron colliders, most of the possible decay channels of Higgs boson can be studied with high precision, and the total width of the Higgs boson can be reconstructed in a model independent manner.

Hadronic decay of the Higgs boson, where the final state consists of hadrons, is one of the dominant decay modes that will be extensively studied in Higgs factories. The hadronic decay is initiated by quarks and gluons. The former are induced by Yukawa-coupling operator $ H\to q\bar q $ and the latter by an effective gluon operator $ H\to gg $ through the top-quark loop, which we refer to as the quark and gluon channels, respectively. Event shapes are the classic observables designed to describe the geometry of final hadrons. An application of event shapes for Higgs decay is discussed in [25], where analysis with several event shapes enables the constraining of the Yukawa coupling of light quarks. Studies on event shapes in Higgs decays include fixed-order results at the next-to-leading order (NLO) corresponding to $ {\cal{O}}( \alpha_s^2) $ relative to the Born rate [26−30], resummed results of thrust at next-to-next-to-leading logarithmic accuracy (NNLL') for gluon channel [31], NNLL' matched to the NLO [32], and approximate N³LL' accuracy [33]. Angularity distributions are available at NNLL' for the quark channel, at NLL' for the gluon channel [34], and at NNLL in a groomed version for the gluon channel [35].

Angularity is a class of event shapes defined by a continuous weight parameter a that controls sensitivity to the rapidity parameter as

where $ m_H $ is the Higgs mass, the sum goes over all the final particle i having a transverse momentum $ {\bf{p}}^i_\perp $, and rapidity $ \eta_i $ is measured with respect to the thrust axis, which is an axis that minimizes the value of thrust $\tau_{a=0}$. For the change in a, angularity $ \tau_a $ is sensitive to a collinear particle with large rapidity $ |\eta|\gg 1 $ and less sensitive to a soft particle with smaller rapidity $ |\eta|\sim {\cal{O}}(1) $. In other words, by regulating the value of a, we can control the relative contribution between the collinear and soft particles or modes. With its continuous parameter a, the angularity enables us to interpolate the parameter region between the thrust $ (a=0) $ and jet broadening $ (a=1) $ and further extrapolate beyond this region. The infrared-safe region of a is $ - \infty < a < 2 $, where perturbation theory is valid. For the region $ a \geq 2 $, the angularity is sensitive to collinear splitting and becomes infrared-unsafe. In the framework of the soft-collinear effective theory (SCET) [36−40], the factorization of the angularity distribution in the small $ \tau_a $ region and resummation of Sudakov logarithms of $ \tau_a $ are established and studied in the thrust-like region $ a<1 $ in $ e^+e^- $ [41−43] and DIS [44] and the broadening-like region $ a \sim 1 $ in $ e^+e^- $ [45−47]. Studies have also been conducted on variants with a recoil-free axis [48], a vector transverse momentum [49], and two joint angularities [50]. In this work, we focus on an improved prediction of the region $ a<1 $.

The gluon channel starting at $ \alpha_s^2 $ is known to suffer from large perturbative uncertainties compared with the quark channel. The angularity distribution for the gluon channel is only available at NLL', which is one order lower than that of the quark channel [34]. The primary focus of this work is improving the gluon channel, resummed up to NNLL' accuracy and matched up to NLO accuracy. The most crucial part is to determine a remaining term, the two-loop constant of the gluon-jet function in the factorization, and to compute the fixed-order distribution at NLO for angularity in Higgs hadronic decay.

The remainder of the paper is organized as follows. In Sec. II, we first review the factorization formula for angularity distribution, which is used for the resummation of logarithmic terms. In Sec. III.A, we review the determination strategy of the jet-function constant that utilizes a fit to fixed-order distribution. In Sec. III.B, we discuss the one-loop constant to illustrate a fit form with fractional power. In Sec. III.C, we determine the two-loop constant in the quark- and gluon-jet function using Tikhonov regularization to handle ill-posed fit. In Sec. IV, we present our prediction of angularity distribution resummed at NNLL' accuracy and matched to the NLO fixed-order distribution and discuss leading and subleading nonperturbative (NP) corrections. Finally, we conclude the paper in Sec. V.

At the small angularity limit, the final state hadrons can be treated as nearly back-to-back jets in the rest frame of the Higgs boson. Similar to $ e^+ e^- \to q\bar{q} $, in the framework of the soft-collinear-effective theory (SCET) [36, 37, 39, 51, 52], the factorization formula for the Higgs boson decay is given by [26, 41, 42]

where $ i=q, g $ represent the quark and gluon channel, respectively. The Born decay rates are $ \Gamma_B^g(\mu)= \dfrac{m_H^3 \alpha^2_s(\mu) }{72 \pi^3 v^2} $ and $ \Gamma_B^q(\mu)= \dfrac{m_H C_A y^2_q(\mu) }{16 \pi } $. The Wilson coefficient $ C^g_t(m_t, \mu) $ corresponds to the top-quark loop coupled to two gluons [53−58], whereas for the quark, $ C^q_t(m_t, \mu)=1 $. $ C^i_S(m_H, \mu) $ represents the hard coefficient that can be determined by integrating out the hard fluctuations near the hard scale $ m_H $. These hard coefficients are defined from the matching to the SCET and can be obtained from $ Hq\bar{q} $ and $ Hgg $ form factors that are available up to the three-loop order [41, 59−61]. The angularity soft functions $ S^i( \tau_a,\mu) $ describing soft emissions are available up to the two-loop order [43, 62, 63] for both the quark and gluon, which are related by the Casimir scaling. The angularity jet functions $ J^i ( \tau_a,\mu) $ describe the collinear emission along the direction of the initial quark or gluon. The quark-jet function is known up to two-loop order, the gluon-jet function at the one-loop order [42, 43] has been known for a long time, whereas the remaining constant term in the two-loop gluon-jet function became available recently [64]. Here, one of the main tasks of this paper is to independently compute the two-loop constant using the method described in Sec. III.

In Eq. (2), the convergence in perturbation theory may break down owing to the presence of Sudakov logarithms of $ \tau_a $. At a small $ \tau_a $ limit, the logarithm exhibits singular behavior. A standard method of curing this behavior is through the resummation of these large logs in momentum space [65, 66] or Laplace space [67, 68]. Here, we work in Laplace space, where the transformation and factorization in Eq. (2) is expressed as

where $ \nu_a $ is the conjugate variable, and $ \tilde{J}^i $ and $ \tilde{S}^i $ are the jet and soft functions in the Laplace space, respectively.

A generic form of $G=\{C_t,\;C_s,\;\tilde{J},\;\tilde{S}\}$ in the fixed-order expansion in the strong coupling constant $ \alpha_s $ is given in Eq. (23) and is composed of cusp $ \Gamma( \alpha_s) $ and non-cusp $ \gamma( \alpha_s) $ anomalous dimensions and constant terms. The large logs present in each function G are resummed using the renormalization group (RG) evolution starting from natural scales $ \mu_G $ to the desired scale μ, where the scales $ \mu_G $ are selected as a physical momentum that minimizes the logs. Details of the resummation are given in Appendices A and B.

At each order of $ \alpha_s $, log L terms behave as $ \alpha_s^n L^{k} $, where $ 0\le k\le 2n $. In logarithmic accuracy, the power counting of log L is $ \alpha_s L\sim {\cal{O}}(1) $. Subsequently, terms such as $ \alpha_s^n L^{n+1}\sim {\cal{O}}(1/ \alpha_s) $ are called leading log (LL), terms such as $ \alpha_s^n L^{n}\sim {\cal{O}}(1) $ are next-to-leading log (NLL), and terms such as $ \alpha_s^n L^{n-k}\sim {\cal{O}}( \alpha_s^k) $ are N$ ^k $LL. At LL accuracy, the cusp anomalous dimension $ \Gamma( \alpha_s) $ of each function and QCD beta function $ \beta( \alpha_s) $ are required; at NLL accuracy, non-cusp anomalous dimensions $ \gamma( \alpha_s) $ begin to contribute; at NNLL accuracy, one-loop constant terms are required. At our target accuracy of NNLL' two-loop order, constant terms should be added to NNLL accuracy. Table 1 summarizes the logarithmic accuracy and relevant n-order ingredients in $ \alpha_s $ such as $\Gamma( \alpha_s),\; \beta( \alpha_s),\; \gamma( \alpha_s)$ and constant terms, which are given in Appendices A and C.

	$\Gamma(\alpha_s)$	$\gamma(\alpha_s)$	$\beta(\alpha_s)$	Constant in $\{C_t,C_s,J, S\}[\alpha_s]$
LL	$\alpha_s$	1	$\alpha_s$	1
NLL(')	$\alpha_s^2$	$\alpha_s$	$\alpha_s^2$	$1 (\alpha_s)$
NNLL(')	$\alpha_s^3$	$\alpha_s^2$	$\alpha_s^3$	$\alpha_s (\alpha_s^2)$

Table 1.  Resummation accuracy N$^k$LL and primed accuracy N$^k$LL$'$. Individual ingredients necessary at the corresponding accuracy: cusp and non-cusp anomalous dimensions, beta function, and hard, jet, and soft functions.

Because our main focus is the gluon channel, computing the two-loop constant term for the gluon-jet function and NNLL' resummation of the gluon channel, henceforth, we set $ i=g $ in Eqs. (2) and (3) and omit the superscript.

In this section, we discuss the determination of the two-loop constant term in the gluon-jet function necessary at NNLL' accuracy.

The constant is determined using the NLO fixed-order result via the strategy in [43, 60, 69]. In the determination, we introduce a fitting function, which improves numerical accuracy of the constant. The fitting function assumes the asymptotic form for the nonsingular part used in the thrust [66] when $ a\le 0 $ and contains additional terms with fractional powers associated with recoil corrections obtained in [45] when $ a>0 $.

We first quickly review the strategy in Sec. III.A. Subsequently, we begin with the one-loop constant by using the LO result to illustrate and test recoil corrections in the fitting to nonsingular part in Sec. III.B. In Sec. III.C, we determine the two-loop constants of the quark- and gluon-jet functions by using NLO results in the quark and gluon channels, respectively.

The SCET factorization formula in Eq. (2) reproduces the singular terms of the fixed-order QCD result when it is expanded and truncated at a fixed order in $ \alpha_s $. The singular part can be expressed as

where the rate is normalized using the Born rate $ \Gamma_B= \Gamma_B(m_H) $ at $ \mu=m_H $, a constant term A contains contributions from constant terms of the jet function and soft and hard functions, and the subscript $ + $ on a function B implies the plus distribution in $ \tau_a $. The term A is also contained in the fixed-order QCD result, which can be expressed as a sum of singular part in Eq. (4) and a nonsingular part $ r( \tau_a) $ as

Because the same A appears in Eqs. (4) and (5), the constant of jet function can be determined from the fixed-order result. However, in practice, the analytical results at NLO that can capture the delta function term Eq. (5) is not available for the angularity distribution.

We numerically compute the angularity distribution using the codes used in predicting thrust distribution [26], where matrix elements are generated using OᴘᴇɴLᴏᴏᴘs [70−72] in part and the phase space is integrated using a Monte Carlo (MC) simulation with the Vegas algorithm [73]. The numerical computation cannot capture the term A owing to the delta function $ \tau_a=0 $ in Eq. (5). Therefore, we use the total decay rate $ \Gamma_t $, which is the integration of Eq. (5) and is given in [74] for the quark channel and in [55] for the gluon channel. The rate has the following form:

where the plus distribution B in Eq. (5) vanishes upon integration, and $ r_c $ is a reminder function $ r_c( \tau_a,1) $ at $ \tau_a=0 $ that is defined by the accumulated nonsingular part $ r( \tau_a) $ from $ \tau_a $ to 1 as

In the last equality, $ r(\tau_a) $ is estimated by obtaining the difference between Eqs. (4) and (5).

Note that in the numerical approach, we cannot compute Eq. (7) at $ \tau_a=0 $. The remainder function is computed down to small $ \tau_a \ll 1 $ regions instead, and an approximate value of $ r_c $ is obtained by obtaining a fit using an asymptotic form in the region and extrapolating the fit to $ \tau_a=0 $. Subsequently, the value of A can be obtained by subtracting the approximate value from Eq. (6). The fit method improves the accuracy of determining A. For example, in the thrust limit, the error of A at NLO in the gluon channel reduces from 2.6% to 0.7% using the fit with data above $ \tau_a=10^{-4} $, and this corresponds to a decrease from 20% to 5% in the constant term.

In this subsection, we discuss the determination of the one-loop constant using the LO QCD result to illustrate the fit to the nonsingular part and test the effect of recoil corrections.

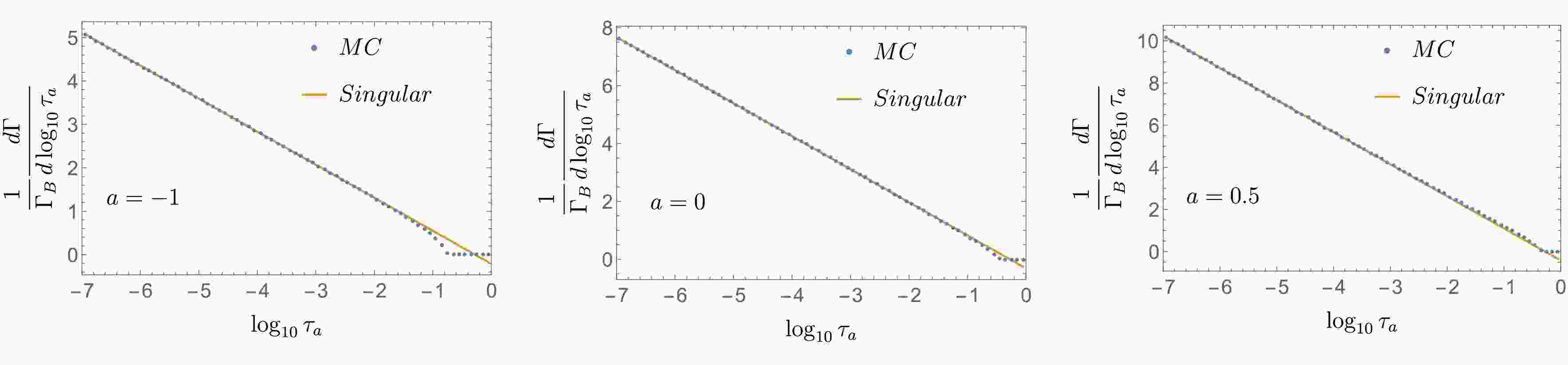
We obtain the LO angularity distribution from $ 10^{10} $ MC events and bin the distribution in logarithmic space. In Fig. 1, the MC distribution in the gluon channel is compared with the singular distribution at three values of the angularity parameter $ a=-1, 0, $ and $ 0.5 $. In the limit of $ \tau_a\rightarrow 0 $, as expected, the MC agrees well with the singular part, whereas in the relatively large $ \tau_a $ region, they exhibit significant differences owing to the large nonsingular part.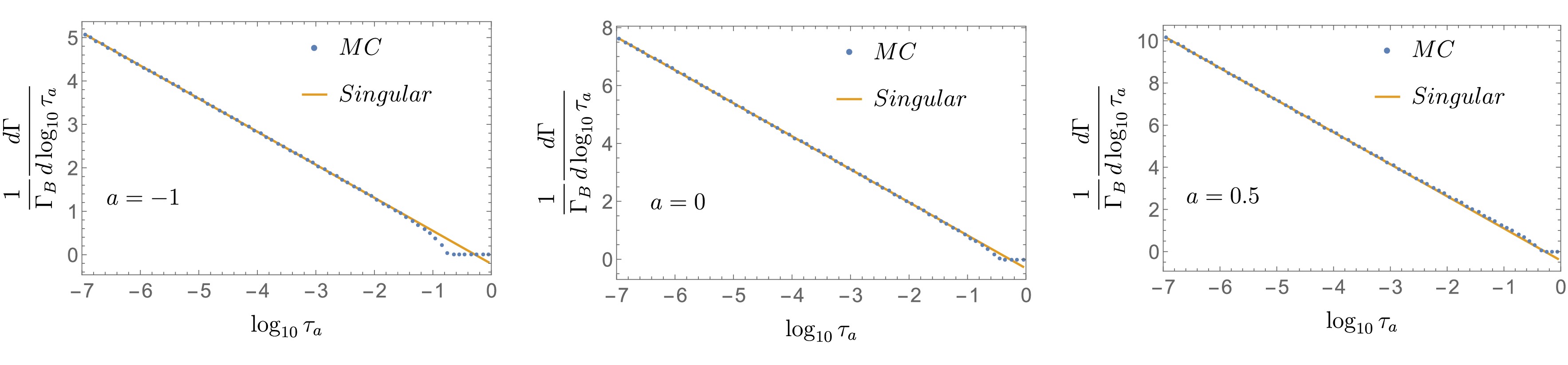

Figure 1.  (color online) LO MC distribution (dots) and singular distribution (solid line) in the gluon channel.

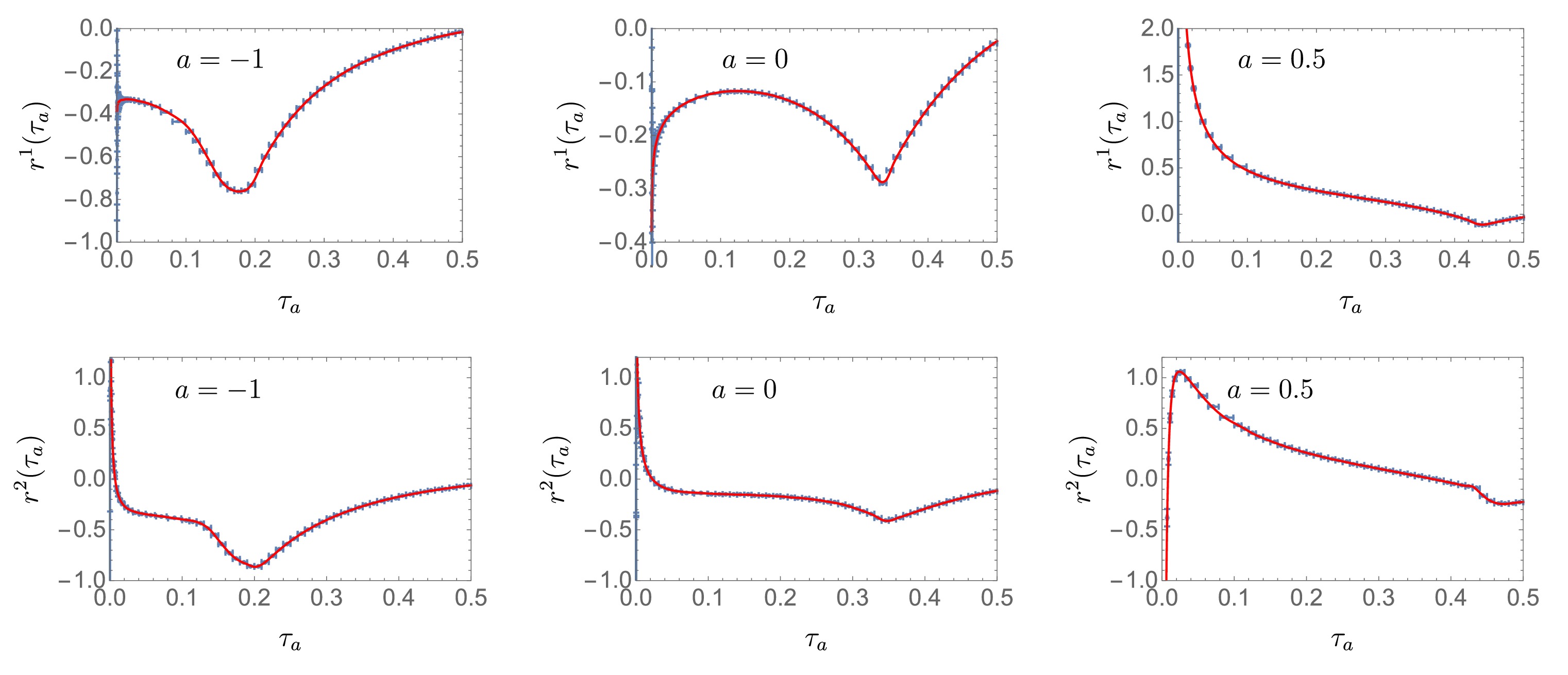
Subsequently, we obtain nonsingular results $ r( \tau_a) $, as shown in Fig. 2, by obtaining the difference between MC and singular results. In $ a\le 0 $, the nonsingular $ r( \tau_a) $ follows an asymptotic form as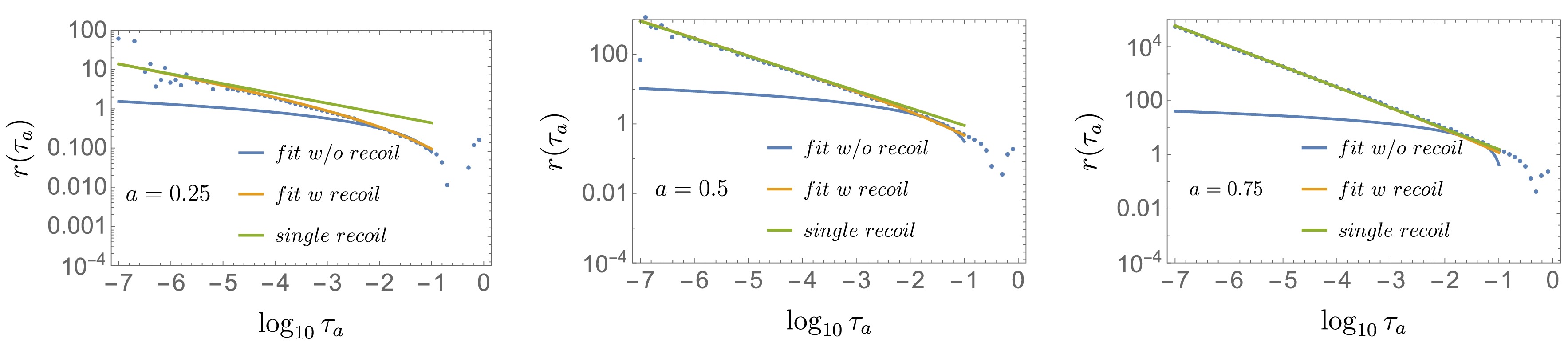

Figure 2.  (color online) LO nonsingular part (dots) and fit results with and without recoil corrections (blue and orange, respectively) and fit only with recoil corrections.

We can fit with above form to the nonsingular part to improve accuracy in the small $ \tau_a $ region when the data suffer from large uncertainties.

In contrast, for $ a>0 $, the nonsingular part has subleading singular terms that are more significant contributions than those in Eq. (8) and become increasingly large with increasing a. According to the SCET power counting of angularity, collinear and soft momenta respect the following scaling:

where λ is a small parameter in the SCET and is defined by the observable $ \lambda^{2-a}\sim \tau_a $. The collinear momentum $ p_c^\mu $ along a unit vector $ \hat n $ is expressed in the light-cone coordinates, and the three components are $ n\cdot p_c $, $ \bar n \cdot p_c $, and $ p_c^\perp $, where $ n=(1,\hat n) $ and $ \bar n =(1, -\hat n) $. For angularity $ a\lesssim 0 $, the thrust axis is insensitive to transverse recoil by soft radiation, i.e., $ p^\perp_c \gg p^\perp_s $, but for $ a\rightarrow 1 $, the recoil effect is significant, i.e., $ p^\perp_c\sim p^\perp_s $. The recoil corrections obtained from the one-loop soft function in [45] are given by

where the color factor $ C_i=C_F $ and $ C_A $ for the quark and gluon channels, respectively, and $ \lceil x \rceil $ is the ceiling function. The series sum becomes a single term $ \dfrac{c_1}{\tau^{a}} $ for $ a\in (0,1/2] $, two terms $ \dfrac{c_1}{\tau^{a}}+\dfrac{c_2}{\tau^{2a-1}} $ for $ a\in (1/2,2/3] $, three terms $ \dfrac{c_1}{\tau^{a}}+\dfrac{c_2}{\tau^{2a-1}}+\dfrac{c_3}{\tau^{3a-2}} $ for $ a\in (2/3,3/4] $, etc. The recoil corrections are characterized by the fractional power, which is still suppressed compared with the singular terms $ \ln^n \tau_a/ \tau_a $, but they are greater than typical power corrections $ \ln^n \tau_a $ in Eq. (8). The coefficients $ c_n $ for $ n=1,2,3 $ are given by

In our fit, the coefficients are set to free parameters that are determined by the fit to data. The effect of recoil corrections is shown in Fig. 2, where three fit results using a form in Eq. (8) without any recoil corrections (blue), a form with both Eqs. (8) and (10) (orange), and a form with only recoil terms in Eq. (10) without Eq. (8) (green). We observe that the fitting results in orange and green agree with Eq. (11).

At $ a=0.25 $, the fit with both terms in Eqs. (8) and (10) is valid, whereas at $ a = 0.5 $ and $ 0.75 $, the fit with only recoil terms in Eq. (10) can mostly describe the data. As a increases, the recoil corrections become larger and dominate over typical power corrections in Eq. (8), and the fit without the recoil cannot describe the behavior of nonsingular data.

Figure 3 shows the remainder function $ r_c( \tau_a,1) $ (dots) obtained by integrating $ r( \tau_a) $ in Fig. 2, fit curves similar to Fig. 2, and exact value of $ r_c $ (horizontal gray line) obtained from the exact singular part and LO total rate. When selecting fit regions (red), plateau regions are excluded to test the prediction of the fit result.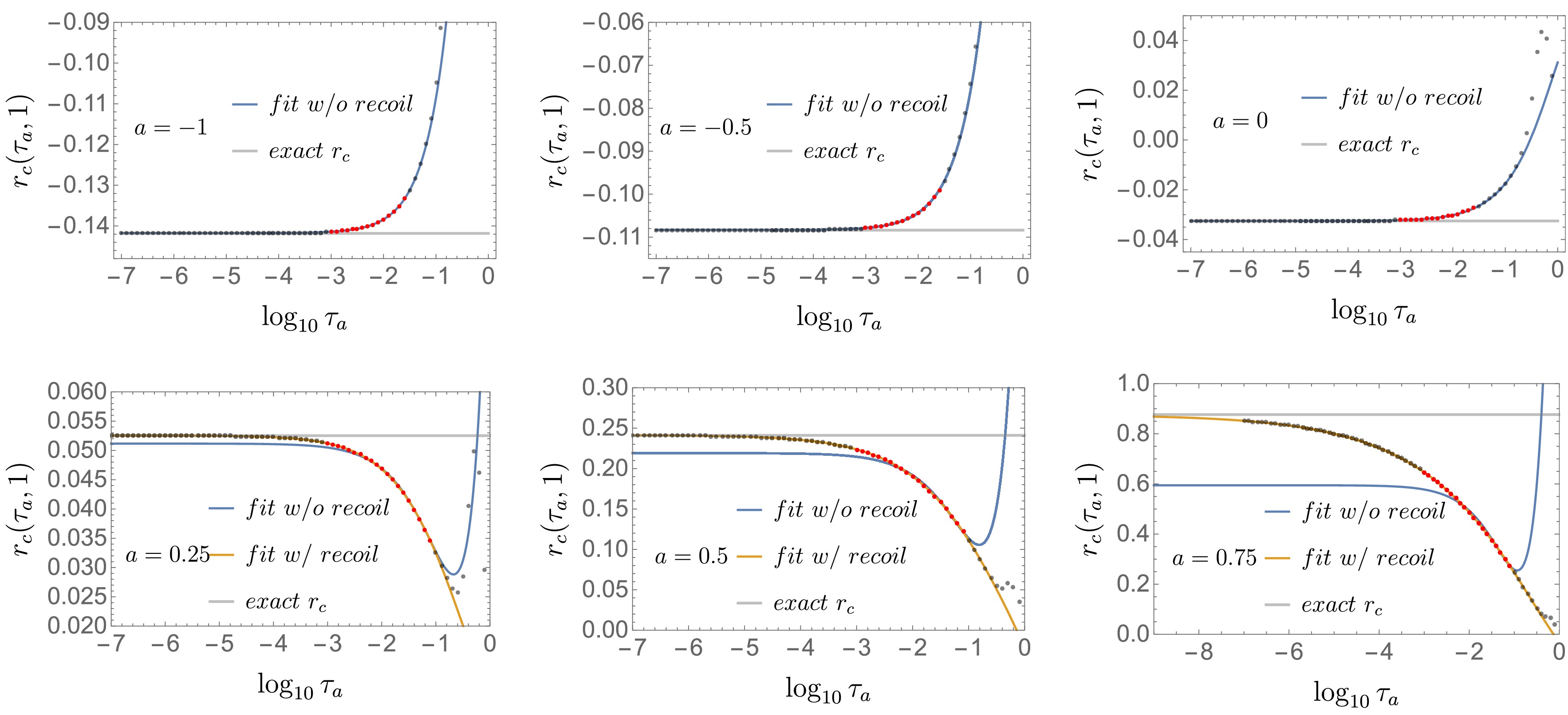

Figure 3.  (color online) Remainder function (dots) at LO in the gluon channel, and fit result with and without recoil corrections (blue and orange respectively) to data in the fit regions (red).

The fits with recoil corrections extrapolate well to the exact values of $ r_c $ in $ a>0 $, whereas fits without recoil corrections extrapolate well to the exact value in $ a \le 0 $ and begin to deviate from the value for $ a>0 $. The fact that data for $ r_c( \tau_a,1) $ exhibit a plateau region, which corresponds with the exact value of $ r_c $, does not motivate such a fit and extrapolation because fine-tuning errors in the difference between the LO fixed-order and singular part are not as significant as those at NLO. We again emphasize that the purpose of this subsection is to illustrate the significance of including recoil corrections in the fits and obtain the NLO fit with those terms.

Following the same strategy, we determine the two-loop constant of the jet function using the NLO total rate [55], NLO fixed-order obtained from MC simulations, and two-loop singular part obtained from Eq. (2).

We also perform a fit to the nonsingular part by including recoil-correction terms for $ a>0 $. However, their scaling behavior at NLO is currently unknown. We make a conjecture regarding the scaling behavior, test this conjecture in the quark channel, and then apply it to the gluon channel. Our conjecture is that dominant scaling behavior can be inferred from crossing terms between the one-loop jet function and recoil corrections from the one-loop soft function. In this conjecture, we assume that recoil corrections from the two-loop soft function and one- and two-loop jet functions will not produce more singular terms. The convolution of singular terms $ \ln^k \tau_a $ from the jet function and recoil corrections of a form in Eq. (10) yields

where $ \alpha_{n,k} $ are fit parameters. For the region $ 0<a\le 1/2 $, $ n=1 $ and Eq. (12) reduces to

We must also include typical integer-power corrections of the form

where $ \alpha_k $ are fit parameters. These terms are leading contributions for $ a\le 0 $ as Eq. (12) has no recoil corrections. The form in Eq. (14) becomes $ r_c+ \tau_a \sum\nolimits_{k=0}^3 \tilde{\alpha}_k \ln^k \tau_a $ in the remainder function $ r_c( \tau_a,1) $, and the value of $ r_c $ is determined from the fitting to $ r_c( \tau_a,1) $ data obtained from Eq. (7).

A subtlety of the fit with recoil corrections in $ a>0 $ is that eight or more fit parameters make the fit ill-posed, and an ordinary chi-square fit cannot constrain these parameters properly. We adopt Tikhonov regularization [75], in which a regularization term $ \lambda | \Gamma{\bf{x}}|^2 $ is added to the chi-square and tames the ill-posed fit, where λ is a regularization parameter, and Γ is a Tikhonov matrix. More details about the regularization and our choice of λ and Γ are discussed in Appendix D.

Figure 4 shows the nonsingular part of the angularity distribution in the quark and gluon channels at $ a=0.25 $ and 0.5 and the fitting results using terms in both Eqs. (12) and (14). The fit curves describe the data well. We also examine the small $ \tau_a $ region beyond the range in the figure and check the relative importance of the LL term in Eq. (12). At $ a=0.25 $, the fit result with the LL is qualitatively similar to that with all three terms in Eq. (12). However, at $ a=0.5 $, the LL alone cannot explain the data and including subleading-log terms in the fit form provides significant improvement. Therefore, we include all three terms from Eq. (12) in our fit.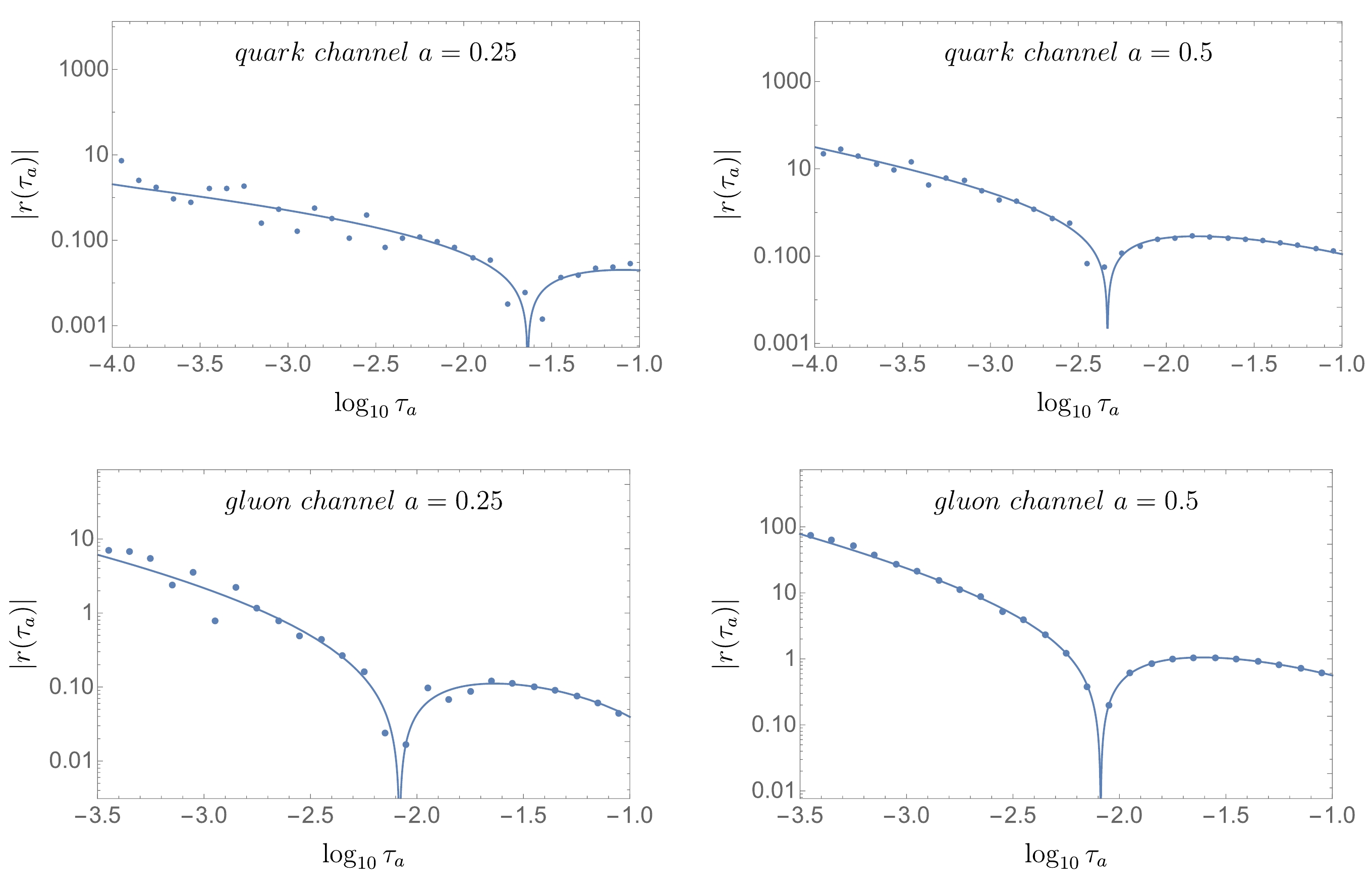

Figure 4.  (color online) NLO nonsingular parts (dots) at a = 0.25 and 0.5 for the quark (upper) and gluon (lower) channels and fit curves (blue) including recoil corrections.

When $ r_c $ is determined from the fit, we can obtain the two-loop constant $ c_{\tilde{J}}^{2} $ from the following relation:

where $ \Delta_a= \Gamma_t/ \Gamma_B-\left[A-2\left(\tfrac{ \alpha_s}{4\pi}\right)^2 c_{\tilde{J}}^{2}\right] $ is obtained by rewriting Eq. (6), and the term in square bracket is simply the sum of all contributions except for missing $ c_{\tilde{J}}^{2} $; hence, it is determined from the singular part. We determine the constants at seven values of $ a=-1+n/4 $, where $n=\{0,1,2,\cdots, 6\}$, for which numerical values of $ \Delta_a $ for quark and gluon channels are

where we set $ \alpha_s=0.1127 $.

According to the procedure described in previous sections, we numerically obtained the remainder function $ r_c( \tau_a,1) $ in the quark channel for seven values of angularity parameters from $ 10^{11} $ MC events computed on an Intel Xeon Platinum 9242 CPU for about 3k CPU hours with an IR cutoff $ \alpha_{\rm{cut}}=10^{-11} $ on a dimensionless variable $ y_{ij,k} $ in the dipole subtraction [76−78].

The remainder function in Fig. 5 tends to have larger uncertainties in the small $ { \tau_a} $ region around $ 10^{-4} $ and below owing to fine-tuning with large cancellations between fixed-order and singular parts. In the plots for $ a\le 0 $, we can read plateau regions approaching existing results [43] (horizontal gray line) and determine $ r_c $, and hence the two-loop constant $ c_{\tilde{J}}^{2} $, using Eq. (15). The value of $ r_c $ is determined by extrapolating the fit curve (blue) to $ \tau_a=0 $ with a fit form obtained by integrating Eq. (14). In selection of the fit region (red dots with error bar), we eliminate the plateau region to test the asymptotic forms.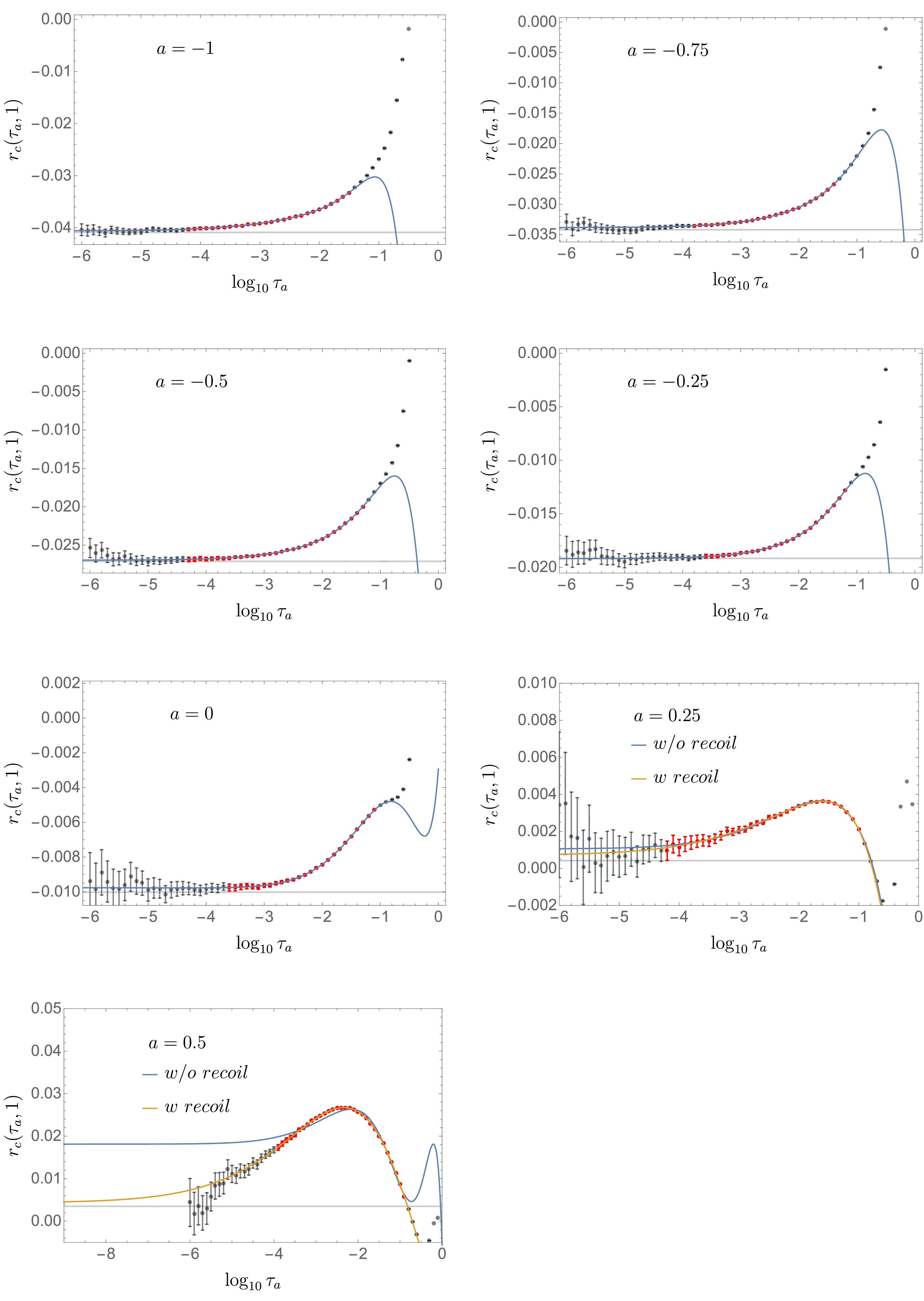

Figure 5.  (color online) NLO remainder function r_c(τ_a,1) (gray and red dots with error bars) in the quark channel, and fit results without recoil corrections (blue) and with corrections (orange) to the selected region of data (red dots with error bar) compared with existing values of r_c (horizontal gray line).

In contrast, for $ a>0 $, a plateau is hardly observed from the data, and two fit results with and without recoil corrections (orange and blue, respectively) are shown in the figure. A plateau region would appear in a smaller $ \tau_a $ region as a increases because the recoil corrections such as $ \tau_a^{n(1-a)} $ slow the convergence of the remainder functions further. It is not accessible from MC results computed with double precision of machine variables. As indicated in Fig. 4, the fit with recoil corrections at $ a=0.5 $ clearly extrapolates to the value of $ r_c $ close to the existing value [64, 79] (horizontal gray line). Our values of $ c_{\tilde{J}}^{2} $ are given in Table 2 and agree reasonably with existing results in [43, 64, 79]. We note that our fit region does not include the plateau region, and our results in Table 2 tend to have larger uncertainties than those that could have been obtained from the best fit including the plateau region because our purpose in the quark channel is to verify fitting with the asymptotic form.

$c_{\tilde{J}}^{2}\backslash a$	−1	−0.75	−0.5	−0.25	0	0.25	0.5
This work	$65.43\pm0.91$	$40.41\pm1.02$	$16.52\pm0.36$	$-9.10\pm1.16$	$-36.84\pm0.72$	$-55.36\pm0.69$	$-3.18\pm2.13$
Ref. [43]	$66^{-5.2}_{-3.5}$	$42.3_{-3.3}^{+5.1}$	$17.3_{-2.5}^{+3.2}$	$-9.34_{-2.48}^{+2.76}$	$-36.3_{-2.4}^{+2.7}$	$-57.6_{-3.2}^{+3.8}$	$-79.8^{+39.7}_{-24.9}$
Ref. [64]*	67.8	43.1	18.2	−8.7	−34.9	−53.6	−0.22
* The values are read from plots in the thesis and would have errors of a few percent.

Table 2.  Two-loop constant $c_{\tilde{J}}^{2}$ of the quark-jet function for angularity.

In the fit region (red dots with error bars), we take a set of fit regions $ \{ \tau_a^{\rm{low}}\,, \tau_a^{\rm{high}} \} $ and obtain a set of $ r_c $ values and statistical uncertainties from fitting to the regions. For the systematic uncertainty, which primarily results from the IR cutoff and higher-power corrections, we obtain the maximum deviation of $ r_c $ from its averaged value in the set. We obtain our central value from the averaged $ r_c $ and our uncertainty from the sum of the systematic and averaged-statistical uncertainties in quadrature. Specifically, the set $ \{ \tau_a^{\rm{low}}\,, \tau_a^{\rm{high}} \} $ is obtained from all possible combinations for pairs from nine succeeding points for the$ \log_{10} \tau_a^{\rm{low}} $ domain, separated by a step size of $ 0.1 $ and similarly five succeeding points for the $ \log_{10} \tau_a^{\rm{high}} $ domain. Our selection criterion for the $ \tau_a^{\rm{high}} $ domain is that it should be robust against higher-power corrections and we select $ \{-1.6+0.4(1+a) , -1.2+ 0.4(1+a)\} $. The criterion for the $ \tau_a^{\rm{low}} $ domain is that it should be insensitive to IR cutoff. We scan all available domains of nine succeeding points and select the domain giving least that gives the least standard deviation for $ r_c $. We also explore the effect of the cutoff $ \alpha_{\rm{cut}} $ by comparing our standard value $ \alpha_{\rm{cut}}=10^{-11} $ with larger value $ 10^{-8} $ in Appendix E.

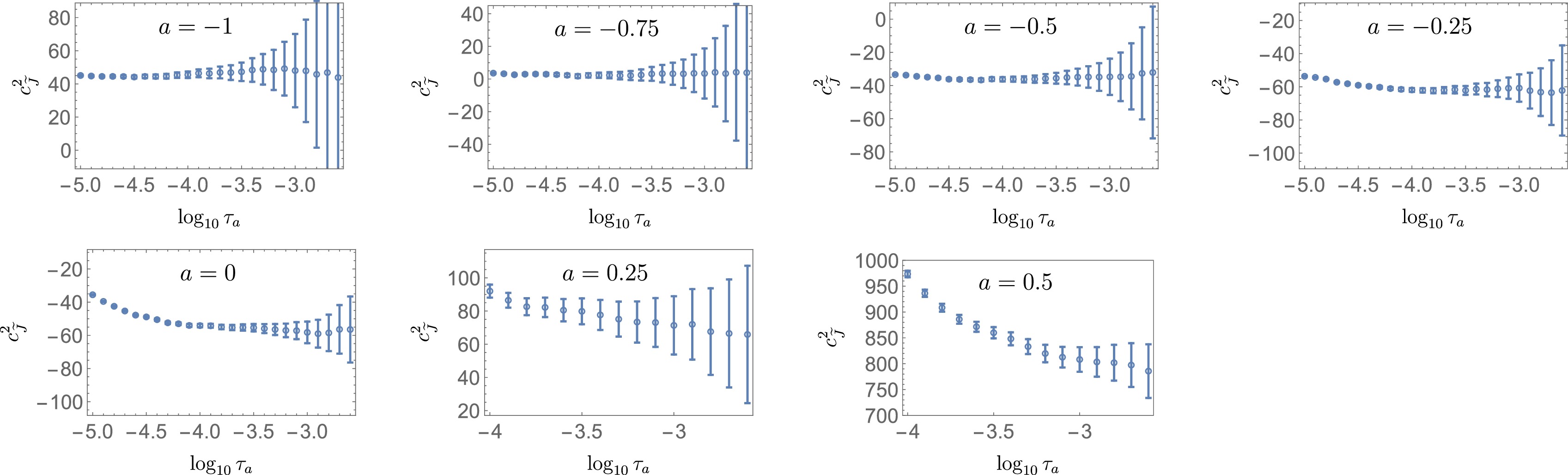
Now, we determine the two-loop constant of the angularity gluon-jet function and compare our results to values given in [64]. The procedure is essentially the same as that described in Sec. III.C.1, and we describe only the difference from that section.

We use the same number of $ 10^{11} $ MC events with a larger cutoff $ \alpha_{\rm{cut}}=10^{-8} $ in the gluon channel. Figure 6 shows the NLO remainder function $ r_c( \tau_a,1) $ (gray and red dots with error bar) obtained from MC events compared with fit results (blue) for the selected region of data (red dots) and $ r_c $ values in [64] (horizontal gray line). The fits for $ a\le 0 $ were performed without the recoil corrections, whereas those for $ a>0 $ were performed with the recoil corrections. Unlike the quark channel, we do not observe any plateau regions at any value of a; hence, fitting with the asymptotic form in Eqs. (12) and (14) is essential in the gluon channel.

Figure 6.  (color online) NLO remainder function r_c(τ_a,1) (gray and red dots with error bar) in the gluon channel, and fit results (blue) from the selected region (red dots with error bar) compared with existing values of r_c (horizontal gray line).

Owing to a more severe cutoff effect, the fit regions are narrowed. The domains of $ \log_{10} \tau_a^{\rm{low}} $ reduces to seven succeeding points for non-positive a and $ \log_{10} \tau_a^{\rm{high}} $ to five points for positive a.

The cutoff effect on the value of $ c_{\tilde{J}}^{2} $ in the gluon channel is shown in Appendix E. Table 3 shows our two-loop constant $ c_{\tilde{J}}^{2} $ converted from $ r_c $ values using Eq. (15), and our values have reasonable agreement with those values reported in [64].

$c_{\tilde{J}}^{2} \backslash a$	−1	−0.75	−0.5	−0.25	0	0.25	0.5
This work	$44.19\pm1.70$	$2.10\pm2.75$	$-36.43\pm1.65$	$-62.08\pm2.49$	$-54.55\pm2.60$	$75.09\pm10.99$	$814.48\pm28.71$
Ref. [64]*	37.18	−4.59	−40.27	−56.95	−55.73	69.21	776.61
* The values are read from plots in the thesis and would have errors of a few percent.

Table 3.  Two-loop constant $c_{\tilde{J}}^{2}$ of the gluon-jet function for angularity.

In this section, we present the angularity distribution at NNLL' matched to the fixed-order NLO results, which is $ {\cal{O}}( \alpha_s^2) $ correction relative to the Born rate $ \Gamma_B(\mu) $. The distribution is composed of two parts:

where $\dfrac{{\rm d} \Gamma^{\rm{res}}}{{\rm d} \tau_a}$ is the resummed singular part, and $ r(\tau_a,\mu_{\rm{ns}}) $ is the nonsingular part at a scale $ \mu_{\rm{ns}} $, including all subleading-power corrections of $ \tau_a $ at NLO. As described in Sec. II, we perform the log resummation by RG-evolving the functions in the factorization equation Eq. (3). We provide a final expression in Eq. (54), and the detailed procedure is summarized in Appendices A and B. The nonsingular part matched our full distribution in Eq. (17) to the fixed-order result as defined in Eq. (5). Including this is important because the unphysical behavior of singular terms in the large $ \tau_a $ region can be corrected by adding the nonsingular part. Note that in Eq. (17), $ \Gamma_B= \Gamma_B(m_H) $ is the Born decay rate at the scale of Higgs mass. Hence, both the singular and nonsingular parts contain a prefactor $ \Gamma_B(\mu)/ \Gamma_B(m_H)= \alpha_s(\mu)^2/ \alpha_s(m_H)^2 $.

We also compute a cumulative distribution by integrating Eq. (17) from 0 to $ \tau_a $ as

where $ \Omega=\eta_S+2\eta_J $ is the sum of integrated anomalous dimensions of the jet and soft functions, which are defined in Eqs. (40) and (41). When the resummation is turned off, Ω reduces to zero and cancels against the same factor in ${\rm d} \Gamma^{\rm{res}}/{\rm d} \tau_a$ such that $ \Gamma_c ( \tau_a) $ remains finite.

The nonsingular part in Eq. (17) can be expressed in a scale independent form satisfying ${\rm d}r\left(\tau_a, \mu\right)/{\rm d}\mu=0$ as

where $ r^1( \tau_a) $ and $ r^2( \tau_a) $ are the LO and NLO coefficients, respectively, and depend only on $ \tau_a $. The scale dependency on $ \mu_{\rm{ns}} $ is made explicit with the logarithmic term proportional to $ 3\beta_0 r^1 $, which is cancelled by the same term generated by the scale variation of the lower-order term proportional to $ r^1( \tau_a) $. Compared with the nonsingular part in $ e^+e^- $ angularity [43], the log term differs from that in [43] by a factor of 3 owing to an additional prefactor $ \alpha_s( \mu_{\rm{ns}})^2 $ from the Born rate $ \Gamma_B^g(\mu) $, which is absent in $ e^+e^- $ angularity.

An analytic expression of the nonsingular part is unknown except for the thrust limit $ a=0 $, and it is determined numerically from MC events obtained in Sec. III.C. We interpolate the remainder function obtained from MC events instead of interpolating the nonsingular part because the binned nonsingular part inherits uncertainties by an amount of the bin size in the x-axis, whereas with its integration, the remainder function, does not at the end of each bin. Subsequently, we obtain the nonsingular part by taking the numerical differentiation of the interpolated remainder function.

To maintain a good precision of the interpolation in both small and large $ \tau_a $ regions, the spectrum of $ r^n( \tau_a) $ is divided into two regions, below and above a point $ \tau_a=0.1 $. Below the point, MC data are binned in log space from a lower bound $ \log_{10} \tau_a^{\rm{low}} $ to the point with a step size of 0.1, where the lower bound is –7 at LO and –4 or –5 at NLO. Above the point, the MC data are binned in linear space $ \tau_a $ up to 1 with a step size of 0.01. At NLO, MC data in small $ \tau_a $ regions tend to be significantly biased by the cutoff effect, as shown in Fig. A1, and the fit function is instead used to describe points below $ \tau_a=0.1 $. Subsequently, the interpolation functions $ r_{\log_{10} }^n( \tau_a) $ and $ r_{\rm{lin}}^n ( \tau_a ) $ in two regions are joined smoothly using the method in [43]: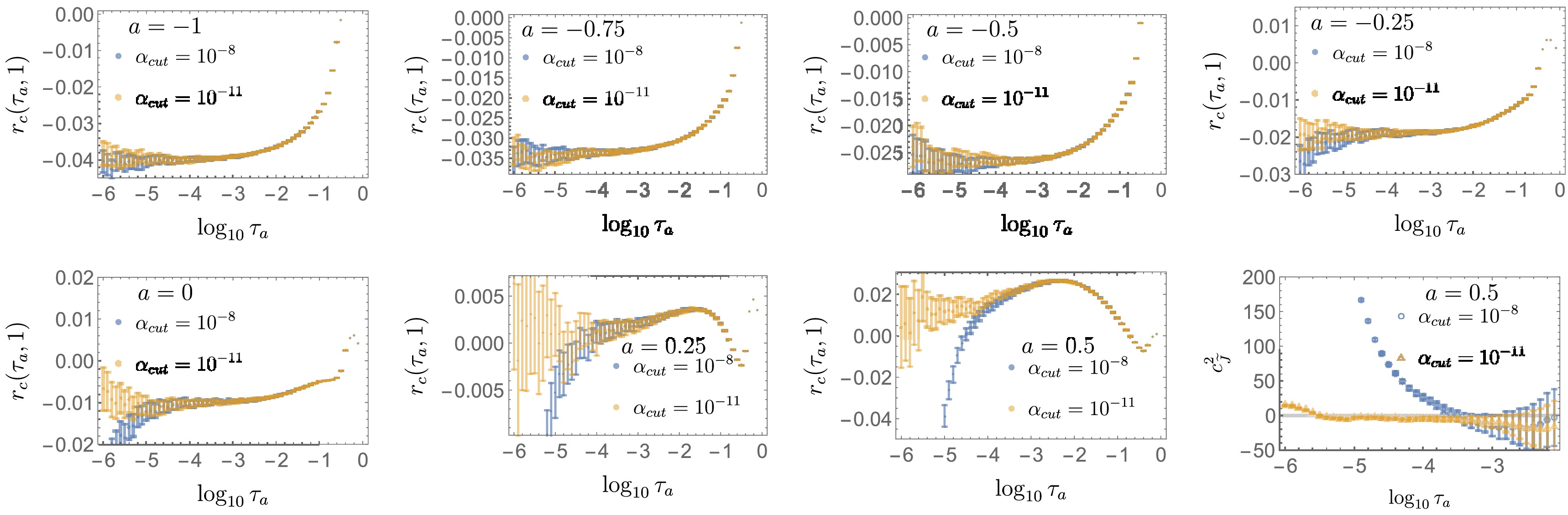

Figure A1.  (color online) NLO remainder functions for α_cut = 10⁻¹¹ (blue) and for 10⁻⁸ (yellow) at seven different values of a. The last plot shows the prediction of a two-loop constant $c_{\tilde{J}}^{2}$ as a function of the lower bound τ_a^low for α_cut = 10⁻¹¹ and 10⁻⁸.

where $f\left(z, z_0, \epsilon\right)=1 /\left(1+{\rm e}^{-\left(z-z_0\right) / \epsilon}\right)$ is a transition function.

Nonsingular distributions with error bars at LO (first row) and NLO (second row) are shown in Fig. 7, and the red curves are the interpolations joined using Eq. (20). Note that the nonsingular is not a physical quantity and can be negative, whereas the full distribution in Eq. (17) is physical and positive definite.

Figure 7.  (color online) LO (upper) and NLO (lower) coefficients of the nonsingular part r(τ_a,µ_ns) at a = −1, 0, 0.5.

For the numerical calculation of distribution, we must select proper scales: hard scales $ \mu_{C_t} $, $ \mu_{C_S} $, soft scale $ \mu_S $, and jet scale $ \mu_J $. In the choice, we must consider the $ \tau_a $ distribution divided by three regions: the peak region $ \left(\tau_{a} \sim 2 \Lambda_{\rm QCD} / m_H \ll 1\right) $, tail region $ \left(2 \Lambda_{\rm QCD} /m_H \ll \tau_{a} \ll 1\right) $, and far-tail region $ ( \tau_a\sim 1) $. The tail region is the region where $ \tau_a $ remains small and resummation is effective. In the region, the natural choice is the canonical scales $\mu_{C_t,C_S}= m_H,\, \mu_{J} = m_H \tau_a^{1/(2-a)},\, \mu_S = m_H \tau_a$ that minimize the logarithms in each function. In the far-tail region, $ \mu_i \sim {\cal{O}}(m_H) $ and we can set all scales to be hard scales $ \mu_i=m_H $, which is a conventional choice in fixed-order perturbation theory. The peak region is dominated by a NP effect and our perturbative approach is invalid. Before approaching the peak region, we must stop scales running into $ \Lambda_{\rm QCD} $ and freeze them in the perturbative region well above $ \Lambda_{\rm QCD} $. We can design a profile function $ \mu_i( \tau_a) $ that is a smooth function of $ \tau_a $ satisfying the above criteria [65, 66, 80]. Here, we adopt the profile functions and scale variations to estimate the perturbative uncertainty designed for the $ e^+e^- $ angularity in [43], and we modify a parameter $ t_2(a) $ to be $ 0.43\times 0.674^{1 - 1.913a} $, which is the value of $ \tau_a $ where singular and nonsingular parts of the gluon channel are the same in size and, beyond the point, all scales smoothly transit to the hard scale. We also adopt the choice of [43] for a scale $ \mu_{\rm{ns}} $ in the nonsingular part.

Figure 8 shows our resummed results at NNLL'+ $ {\cal{O}}( \alpha_s^2) $ accuracy (red) for angularity distribution (first and second rows), relative uncertainties (third row), and cumulative distributions (fourth row) at three values of $ a=-1 $, 0, and 0.5 and results at a lower accuracy: NLL (green) and NNLL$ +O( \alpha_s) $ (blue) for comparison. The band at each accuracy represents the perturbative uncertainty estimated using scale variations in the profile function. The distributions normalized using the Born rate in the first row hardly overlap between different accuracies, and the peak of distribution increases by 100% from NLL to NNLL and 50 % from NNLL to NNLL' because of large perturbative corrections as in the total rate. The distributions normalized using their own area in the second row exhibit reasonable overlapping within the uncertainties between different accuracy, which indicates a perturbative convergence of the resummation. In the third row, the perturbative uncertainties with respect to central values reduce to about 20% at the NNLL', which is about half of the NLL uncertainties. However, the reduction rate with increasing accuracy is rather slow compared with the quark channel of many gluon initiated processes. $ c_{\tilde{J}}^{2} $ uncertainties in Table 3 propagate to the distribution and the values also exhibit deviations from the two-loop results in Ref. [64]. Their effect in the distribution are as large as 0.8%, which is negligible compared with the perturbative uncertainties at this level of accuracy. In the fourth row, the cumulative distribution is normalized by the total rate at the corresponding order in $ \alpha_s $. We can observe that the cumulative distribution reduces to the total rate in the far-tail region. In this region, resummation is turned off and the resummed distribution in Eq. (17) reduces to the fixed-order result in Eq. (5).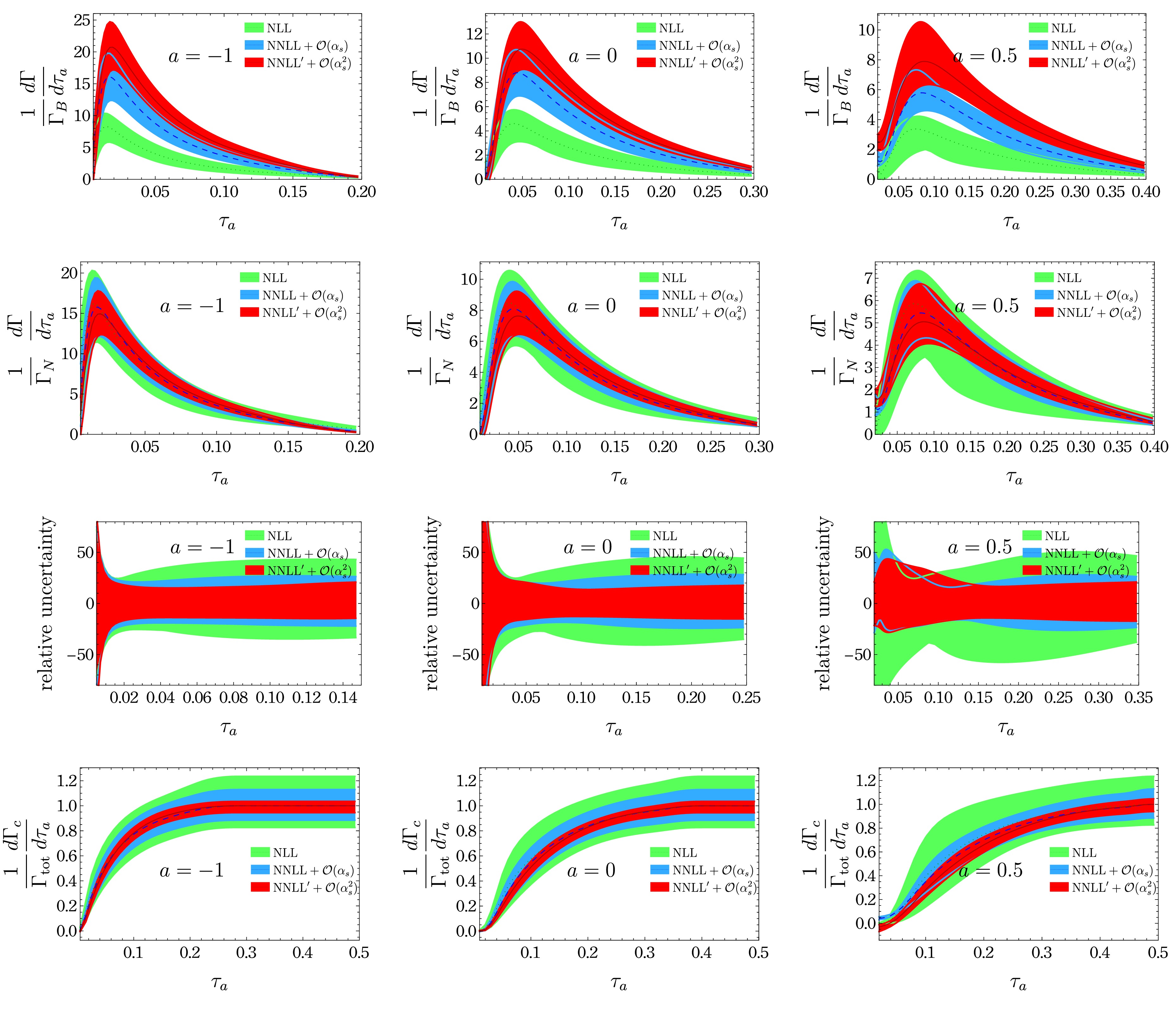

Figure 8.  (color online) First and second rows: Angularity distributions at three values of a = −1, 0, 0.5 for the gluon channel in Higgs decay. The bands indicate perturbative uncertainties. The first row is normalized by the Born rate Γ_B and the second by the area covered by the resummed distribution Γ_N at the corresponding order. Third row: Relative perturbative uncertainty in percentage. Bottom row: Cumulative distributions normalized using the total rate.

We observe a generic feature of the distribution that the shape becomes broad and the peak moves to the right with increasing a because, for a given jet scale, $ \mu_J=m_H \tau_a^{1/(2-a)} $, increasing a scales up the value of $ \tau_a $. However, this is not true for the soft scale $ \mu_S=m_H \tau_a $, where a does not change the scale of $ \tau_a $. Both of them affect the distribution and make its change as a function of a nontrivial. The peak of the distribution is an essential feature of the resummation, known as the Sudakov exponent, which is $ {\rm e}^{-\frac{2 \alpha_s C_A }{\pi}\ln^2 \tau_a} $ at LL accuracy and cures the singular behavior $ \ln \tau_a/ \tau_a $, and the peak position of the gluon channel is rather located at a large $ \tau_a $ compared with that in the quark channel due to the Casimir scaling.

Figure 8 shows the pure perturbative contribution without the NP effect such as hadronization that can be included by introducing an NP model [65, 81, 82] or power correction with a universal NP parameter $ \Omega \sim {\cal{O}}( \Lambda_{\rm{QCD}}) $ [83], which can be further refined with a scheme subtracting renormalon ambiguities [69, 84]. The parameter Ω captures a leading NP correction and shifts the perturbative distribution. Hence, the first moment of $ \tau_a $ is

where the superscript 'had' is for the hadron level that can be measured in an experiment or simulated in event generators, and 'pert' is for pure perturbative results at the parton level. Eq. (21) includes the quark and gluon channels $ \Omega=f_q\Omega_q+f_g \Omega_g $, where $f_{i}= \Gamma^{i}_{\rm tot}/( \Gamma^q_{\rm tot}+ \Gamma^g_{\rm tot})\approx 0.9$ and $ 0.1 $ for the quark and gluon fractions, respectively. For the quark channel $ \Omega_q^{ee}\approx 0.35 $ GeV from the $ e^+e^- $ thrust analysis [66] and assuming Casimir scaling estimates $ \Omega_g\approx C_A/C_F\Omega_q $. We can determine $ \Omega_g $ in Higgs factories using the known value of $ \Omega_q^{ee} $.

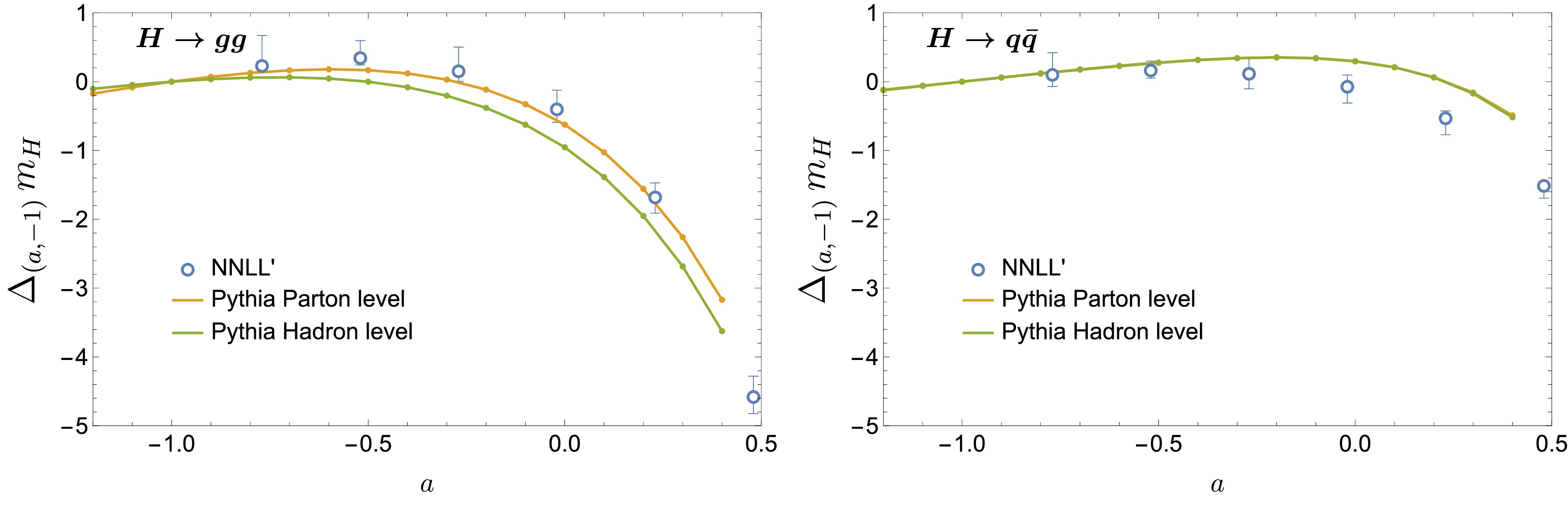
Equation (21) predicts a dependence $ (1-a)^{-1} $ in the Ω term that can be easily identified using a comparison experiment and theory predictions in a space [85]. We can also test if the a dependence in the Ω term is comparable to the hadronization model in event generators. Figure 9 shows the difference $ \langle \tau_{{a}}^{\rm{had}} \rangle-\langle \tau_{{a}}^{\rm{pert}} \rangle $ with a weight $ (1-a)m_H $ obtained from Pythia simulations for the quark and gluon channels. The y values correspond to $ 2\Omega_q $ for the quark and $ 2\Omega_g $ for the gluon and would weakly depend on a via the subleading term $ {\cal{O}}(\Lambda_{\rm{QCD}}^2/m_H^2) $ in Eq. (21). While the quark channel is consistent with the a dependence, and $ \Omega_q^{\rm{pythia}}\approx 0.2 $ GeV roughly agrees with $ \Omega_q^{ee} $ within a factor of two, the gluon channel exhibits a rather stronger a dependence ranging as $ \Omega_g^{\rm{pythia}}\approx 0.2\sim 0.6 $ GeV in the order of $ \Lambda_{\rm{QCD}} $. Their relative contributions are $ f_q\Omega_q^{\rm{pythia}}\approx 0.2 $ and $ f_g \Omega_g^ {\rm{pythia}}\approx 0.02\sim 0.06 $, where the gluon contributions are suppressed and the a dependence would become soft. Measurements in future Higgs factories can justify the value of $ \Omega_g $. If the Pythia value is different from the measurement, it can be obtained from another source such as large perturbative corrections at higher orders absent in Pythia that have been absorbed into hadronization parameters fitted to experimental data.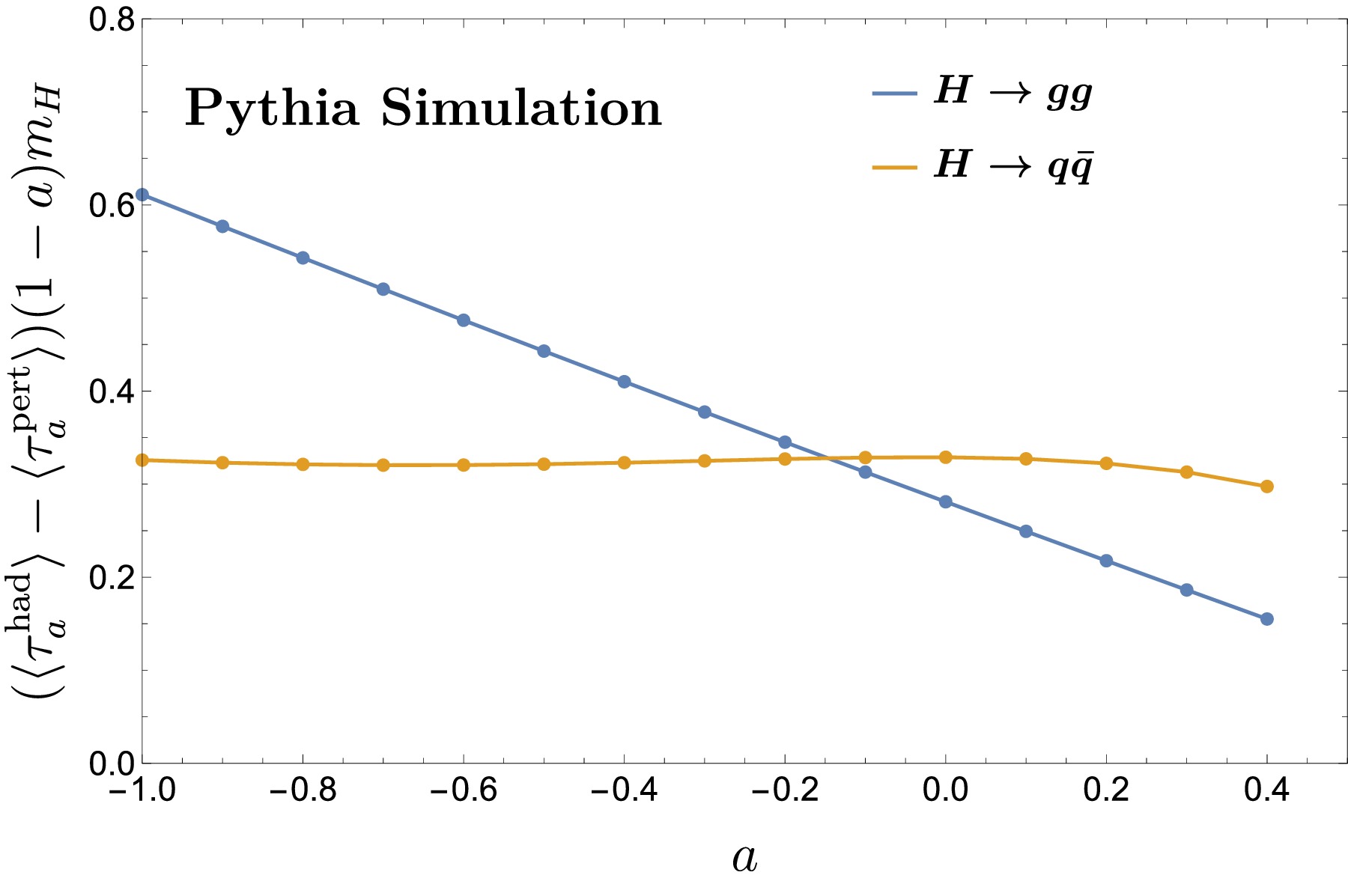

Figure 9.  (color online) Difference between $\langle \tau_{{a}}^{\rm{had}} \rangle$ at the hadron level and $\langle \tau_{{a}}^{\rm{pert}} \rangle$ at the parton level from a Pythia simulation for the gluon channel (blue) and quark channel (orange).

The subleading NP corrections of $ {\cal{O}}( \Lambda_{\rm{QCD}}^2/m_H^2) $ in Eq. (21) can be studied from higher-moment or cumulant analysis. In $ e^+e^- $ thrust [86], the second thrust cumulant, which is completely insensitive to $ \Omega^q $ enables us to determine a subleading correction $ \Omega_2^{'q}(0) $, which is the sum of two contributions: one from the leading thrust factorization and the other from a power correction $ \Omega^q_{1,1}(0)\sim \Lambda_{\rm{QCD}}^2 $ multiplied by a perturbative part. This can be extended to $ e^+e^- $ angularity to determine $ \Omega_2^{'q}(a) $ at nonzero a and to the angularity in Higgs decay to determine corresponding corrections in the gluon channel. Following the convention of [86], the correction $ {\cal{O}}( \Lambda_{\rm{QCD}}^2/m_H^2) $ in Eq. (21) can be parameterized as $ 2M_{0,1}(a) \,\Omega_{1,1}(a)/m_H^2 $, where $ \Omega_{1,1}(a) $ is the correction appearing in the second cumulant, and $ M_{0,1}(a) $ accounts for a perturbative part. Another method to study the subleading NP corrections is to obtain the difference between moments as in [87, 88] at two points in a space:

where the leading correction Ω is cancelled in the second line, and the subtracted moment $ \Delta_{(a,a')} $ is sensitive to the subleading correction that can be expressed as a difference of the quantity $ 2(1-a)M_{0,1}(a) \,\Omega_{1,1}(a)/m_H^2 $ at two points a and $ a' $. By comparing experimental measurement and perturbative predictions, we can determine the correction. The subtracted moment with angularity provides additional information different from that obtained from thrust cumulant analysis. Hence, it is a useful tool for extracting information on subleading NP corrections. Figure 10 shows our perturbative predictions of Eq. (22) at NNLL' accuracies compared with Pythia simulations at parton and hadron levels for the gluon channel (left) and quark channel (right). The Pythia results in the gluon channel exhibit a notable difference between parton and hadron levels, whereas the difference in the quark channel is very small. This analysis can be performed for different colliders such as the Electron-Ion Collider [89] with DIS trust and angularity [44, 81, 82, 90] and can determine NP corrections.

Figure 10.  (color online) Prediction of the subtracted moment ∆_(a,−1) as a function of a from resummed results at NNLL' compared with Pythia simulations at parton and hadron levels for the quark channel (left) and gluon channel (right).

We present improved predictions of angularity distribution $ \tau_a $ in hadronic decays of the Higgs boson via an effective operator $ H\to gg $ that suffers from large perturbative uncertainties compared with the other contribution via the Yukawa interaction $ H\to q\bar q $. The distribution is improved by resumming large logarithms of angularity at NNLL' accuracy in the SCET framework and by matching the resummed results to the fixed-order result at NLO.

To achieve NNLL' accuracy, we independently determine a remaining ingredient, a two-loop constant of the gluon-jet function for angularity. We observe that our values of the constant agree reasonably with the values in the literature. In the determination of the constant, significant contamination occurs from subleading singular corrections slowly suppressed in the small $ \tau_a $ limit. To estimate the correction, we use asymptotic forms in the small $ \tau_a $ region and fit it to the nonsingular part of the fixed-order result. The asymptotic form for $ a\le 0 $ is $ \sum\limits_{k}\alpha_k \ln^k \tau_a $, which is one power-suppressed by the singular part, and for $ 0<a\le 1/2 $, it has additional terms with fractional power $ \sum\limits_{k}\alpha_{1,k} \ln^k \tau_a/( \tau_a)^{a} $, which is conjectured from recoil corrections in a one-loop soft function. The form in $ a> 0 $ has eight degrees of freedom, and the fitting result is sensitive to noise; hence, it is ill-posed. We observe that it can be handled by adopting Tikhonov regularization that reduces the sensitivity to noise.

We also consider NP corrections in the angularity. The corrections receive two contributions, one from the quark channel and the other from the gluon channel. Additionally, by using the value known for the quark in $ e^+e^- $ experiment, the gluon contribution can be determined from measurement in Higgs factories. A Pythia simulation shows that the quark channel is comparable to the prediction of leading-power correction for the angularity, whereas the gluon channel is considerably different from the prediction in a dependence and magnitude estimated from Casimir scaling. We also consider a subtracted moment $ \Delta_{(a,a')} $ defined by the difference between moments of $ \tau_a $ at a and $ a' $ that mitigates the leading correction. Hence, it is sensitive to subleading corrections. The subtracted moment as a function of a is an independent direction from the cumulant analysis and provides additional information to the subleading correction.

Here, we summarize the functions appearing in the factorization in the gluon channel, and the tag g representing the gluon is implied implicitly. In Laplace space, each function $ G=\{C_t,C_S,\tilde{J},\tilde{S}\} $ in Eq. (3) can be expressed as follows:

where $ \Gamma_{G}^n=-\dfrac{j_{G} \kappa_{G}}{2} \Gamma_n $. $ \Gamma_n $, $ \gamma_G^n $, and $ c_G^n $ are coefficients of the universal cusp and non-cusp anomalous dimensions $ \Gamma_{\rm{cusp}} ( \alpha_s) $ and $ \gamma_G ( \alpha_s) $ and of a constant term $ c_G $ in $ \alpha_s $ expansion as

where $ \beta_n $ and $ \Gamma_n $ are given in Appendix C and $ \gamma_G^n $ and $ c_G^n $ are given in Appendices A.1 and A.2, respectively. The factors $ j_{G} $ and $ \kappa_{G} $ and log $ L_G $ are summarized in Table A1.

	$C_t$	$C_S$	$\tilde{J}$	$\tilde{S}$
$j_G$	1	1	2-a	1
$\kappa_G$	0	2	-2/(1-a)	4/(1-a)
$L_G$	$\ln \frac{m_t}{\mu_{C_t}} $	$\ln \frac{i m_H}{\mu_{C_S}} $	$\ln \left[\frac{m_H}{\mu_{\tilde J}}\left(\nu e^{\gamma_{E}}\right)^{-1 / j_{\tilde J}}\right] $	$\ln \left[\frac{m_H}{\mu_{\tilde S}}\left(\nu e^{\gamma_{E}}\right)^{-1 / j_{\tilde S}}\right]$

Table A1.  j_G, $\kappa_G $, L_G, and L_G for the functions $G=\{C_t, C_S, \tilde J, \tilde S\} $.

Each term in Eq. (A1) can be transformed into the momentum space using the inverse Laplace transformation as follows:

where the distribution function $ {\cal{L}}_n(\tau) $ is defined by

The anomalous dimension of the function G is defined by the renormalization group (RG) equation as

From scale independence of the factorization in Eq. (3), we have a consistence relation:

where the first term is from the Born rate $ \Gamma_B \propto \alpha_s^2 $. The non-cusp anomalous dimensions of $ C_t $ [53−58] and $ C_S $ [61] are given by

The quark soft anomalous dimension is given in [42, 91], and gluon soft anomalous dimension can be obtained from the quark soft anomalous dimension using a Casimir scaling $ C_F\to C_A $.

where we have made the a-dependence of the anomalous dimension explicit, and

where

which vanish for thrust case $ a=0 $. Here, we give numerical results at the values of a used in the MC simulation in Table A2.

a	−1.0	−0.75	−0.5	−0.25	0.0	0.25	0.5
$\gamma_1^{C A} $	1.0417	5.8649	9.8976	13.190	15.795	17.761	19.132
$ \gamma_1^{n f}$	−0.9571	0.5284	1.8440	2.9751	3.9098	4.6398	5.1613

Table A2.  $\gamma_1^{CA} $ and $ \gamma_1^{nf}$ for the quark angularity soft anomalous dimensions.

Subsequently, we can obtain $ \gamma_J( \alpha_s) $, which is given by Eq. (A7).

Content terms in $ C_t $ [53−58] and $ C_S $ [61] are given by

The constant term of quark soft functions is known to one-loop for generic values of a analytically [42], and the two-loop constant is determined numerically for generic a in [62]. The gluon soft function can be obtained from quark soft function constant by a Casimir scaling $ C_F\to C_A $. In Laplace space,

where

The one-loop constant of gluon jet function [92, 93] in Laplace space is given by

where

Note that in Eq. (A14), the minus sign of $ \pi^2/6 $ term is opposite to that in Eq. (11) of Ref. [93], which we believe is a typo because following their recipe results in the minus and our numerical result for $ c_{\tilde{J}}^{1} $ is consistent with the minus.

The two-loop constant is numerically obtained and is given in Table A3.

a	−1.0	−0.75	−0.5	−0.25	0.0	0.25	0.5
$ c_2^{C A}$	−22.430	−29.170	−36.398	−44.962	−56.499	−74.717	−110.55
$c_2^{n f} $	27.315	28.896	31.589	36.016	43.391	56.501	83.670

Table A3.  $c_2^{CA} $ and $c_2^{nf} $ for the constant term of quark angularity soft functions.

The large logs in $ C_t $, $ C_S $, $ \tilde{J} $, and $ \tilde{S} $ can be resummed using the RG evolution starting from natural scales, in which the logs are small, to an arbitrary scale μ. The solution of RGE in Eq. (A15) shares the following structure:

where $ K_G $ and $ \eta_G $ are integrations of $ \gamma_G(\mu) $ in Eq. (A6) from $ \mu_G $ to μ

After replacing $\dfrac{{\rm d} \mu'}{\mu'}$ by ${\rm d} \alpha_s/\beta( \alpha_s)$, we define three integrals as

In Appendix C, we present results of integration performed order by order in $ \alpha_s $. We define $ K_G $ and $ \eta_G $ as

Now, we review conversion of resummed results in Laplace space back to the momentum space using the inverse Laplace transformation

To make the inverse integration simple, we replace all ν-dependent log by derivative operators as $ L_G\to \partial_{\eta_G}/j_G $ in the fixed-order function $ G(\nu,\mu) $ in Eq. (A1) and rewrite the resummed function in Eq. (38) as

where $ g(\partial_{\eta_G})=G(\nu,\mu)\vert_{L_G\to \partial_{\eta_G}/j_G} $. We observe that Eq. (B6) is equivalent to Eq. (B1).

At $ {\cal{O}}(\alpha_s) $, we have the fix-order function $ g(\partial_{\eta_G}) $:

Using an identity of inverse transformation

Equation (B6) becomes the resummed function in momentum space as

where the logarithm in $ \tau_a $ is defined by

The resummed distribution is the product of the jet and soft functions expressed in a form of Eq. (B6); thus, $ \eta_G $ in Eq. (B8) is replaced by the sum $ \Omega=\eta_S+2\eta_J $. Finally, we obtain

where

In the numerical calculation, we set $ \mu_{C_t}=\mu_{C_S} $ to be the hard scale $ \mu_H $ and vary them simultaneously for a scale variation. By shifting the derivative by $ L_G( \tau_a) $ all the exponents in Eq. (B9) can be moved in the front as

The operators $ [\partial_{\Omega}+j_G L_G( \tau_a)]^n $ turns into poly-logarithms:

where

We would like to note that operators in crossing terms such $ \alpha_s^2 s_1j_1 $ are not simply the square of the second line in Eq. (B14) and must be carefully expended as

Our final form of the resummed result is given by

Here, we summarize the coefficient of cusp-anomalous and beta function and integrals defined in Eq. (B3) in the resummation.

To the NNLL order, we require up to three-loop cusp anomalous dimension for the gluon [94, 95], which is related to the quark channel by the ratio of the eigenvalues $ C_i $ of the quadratic Casimir operators up to three-loop order [94]: $ \dfrac{\Gamma_{\rm{cusp}}^q(\alpha_s)}{C_F}=\dfrac{\Gamma_{\rm{cusp}}^g(\alpha_s)}{C_A} $. Note that this is different from the soft function where all the $ C_F $ are replaced by $ C_A $. Here, we give cusp anomalous dimension for the gluon without the subscript g.

The beta function expanded in powers of $ \alpha_s $ is given by

The beta-function coefficients [96, 97] are

An expansion of Eq. (B3) in powers of $ \alpha_s $ is

Here, $ r = \alpha_s(\mu)/\alpha_s(\mu_0) $. Solving the beta function to three-loop order yileds the running coupling as

where $ X\equiv 1+\alpha_s(\mu_0)\beta_0 \ln(\mu/\mu_0)/(2\pi) $. In our numerical calculations, we take the full NNLL results in Eq. (C4) for $ K_{ \Gamma,\gamma},\eta_ \Gamma $ and in Eq. (C5).

For a known matrix A and vector $ {\bf{b}} $, a least-square method involves determining a vector $ {\bf{x}} $ such that it minimizes the square residuals $ |A{\bf{x}}-{\bf{b}} |^2 $, where $ |\cdot|^2 $ is the vector squared. In our problem, $ {\bf{b}}_i $ is the value of the remainder function at $ i_{\rm{th}} $ bin, $ {\bf{x}}_j $ is the $ j_{\rm{th}} $ parameter in the fit function, and $ A_{ij} $ is the value of the $ j_{\rm{th}} $ term of the fit function at the $ i_{\rm{th}} $ bin. $ \hat{x}=(A^T A)^{-1}A^T{\bf{b}} $ is the solution to zero gradient of the square residuals. However, in some cases, matrix $ A^T A $ is nearly singular and sensitive to small changes in data such as noise. In these cases, regression is considered to be ill-posed, and generally regularization aids in improving the result. We adopt Tikhonov regularization [75], in which a regularization term is included in the squared residuals $ |A{\bf{x}}-{\bf{b}}|^2+\lambda | \Gamma{\bf{x}}|^2 $, where λ is a regularization parameter, and Γ is a Tikhonov matrix. With the introduction of the regularization term, the solution to zero gradient is $ \hat{x}=(A^T A+\lambda\Gamma^T\Gamma)^{-1}A^T{\bf{b}} $, where $ \lambda\Gamma^T\Gamma $ tames the singularity of $ A^T A $.

The regularization depends on the choice of regularization parameter λ and Tikhonov matrix Γ. We take the identity matrix for Γ in our analysis. We also test with discrete first- and second-order derivative matrices that yield $ \Gamma{\bf{x}}=(x_2-x_1,\cdots, x_n-x_{n-1})^T $ and $ (x_3-2x_2+x_1,\cdots, x_n+2x_{n-1}-x_{n-2})^T $, and they essentially provide results consistent with that with the identity matrix. The regularization parameter should be assigned carefully, a very small value cannot tame the singularity, whereas too large a value would distort the feature of the remainder function. We select the value of parameter that produces a robust fit result against variations of upper and lower bounds of the fit region. We observe that for non-positive a cases, the value of the regularization parameter is small $ \lambda=10^{-4} $, which is essentially equivalent to ordinary least-square, i.e., $ \lambda= 0 $. For a positive a, the parameter is larger $ \lambda= 10^3(10^1) $ for $ a=0.25 $ and $ \lambda= 10^4(10^3) $ for $ a=0.5 $ in the quark (gluon) channel.

We explore the effect of the cutoff $ \alpha_{\rm{cut}} $ in the quark channel by comparing our standard value $ \alpha_{\rm{cut}}=10^{-11} $ and larger value $ 10^{-8} $, as shown in Fig. A1. Their differences are hardly visible in $ a< 0 $ in given ranges of $ \tau_a $ and become visible in $ a\ge0 $. The last plot in Fig. A1 shows the constant $ c_{\tilde{J}}^{2} $ as a function of $ \tau_a^{\rm{low}} $ at $ a=0.5 $. While the value of constant stays still in the domain $ \log_{10} \tau_a^{\rm{low}}\in\{-4.5,-2.6\} $ for $ \alpha_{\rm{cut}}=10^{-11} $, for $ \alpha_{\rm{cut}}=10^{-8} $, it begins to change at approximately $ \log_{10} \tau_a^{\rm{low}}=-3.5 $ and below. This implies that the fit regions for $ \alpha_{\rm{cut}}=10^{-11} $ in Fig. 5 is insensitive to the cutoff effect. For $ \alpha_{\rm{cut}}=10^{-8} $, we use same the criteria and obtain $ c_{\tilde{J}}^{2}=-55.90\pm1.84 $ at $ a=0.25 $ and $ -10.33\pm11.44 $ at $ a=0.5 $, which are consistent with the values in Table 2.

Figure A2 shows the cutoff effect in the gluon channel as a function of $ \tau_a^{\rm{low}} $ with a constant $\log_{10} \tau_a^{\rm{high}}= -1.4+0.4\,(1+a)$. Similar to the quark channel, larger a values tend to suffer from greater cutoff effect $ c_{\tilde{J}}^{2} $. Using the results, our fit regions are selected to avoid the cutoff effect as described in the main body of the paper.

Figure A2.  (color online) Two-loop constant $c_{\tilde{J}}^{2}$ as a function of lower bound τ_a^low with fixed-upper bound log₁₀ τ_a^high = −1.4+0.4(1+a) at α_cut = 10⁻⁸