-
The proposal of black-hole thermodynamics has, to some extent, become a bridge connecting general relativity, classical thermodynamics, and quantum mechanics. With the establishment of the four laws of black-hole thermodynamics, the study of its properties has become one of the most active research topics in theoretical physics [1−8]. General Relativity is widely regarded as a low-energy effective field theory (EFT) of gravity. Understanding how quantum gravity influences low-energy EFTs is crucial in regimes where quantum gravity effects become significant. Although black holes are often treated as classical objects, their solutions have offered remarkable insights into quantum gravity. The Swampland program was introduced to identify constraints that quantum gravity imposes on EFTs [9−15]. Within this framework, the Weak Gravity Conjecture (WGC) serves as one such constraint, proposing that any EFT with a U(1) gauge field coupled to gravity must contain a charged state with a charge-to-mass ratio greater than one [16]. WGC can be examined through correction terms [17−38], which introduce higher-derivative corrections. Goon and Penco observed that a derivative in free energy can be equivalently applied to the action [19]. They further defined these corrections using a perturbative parameter linked to the cosmological constant.
It is well-known that in de Sitter (dS) spacetime, when certain conditions are satisfied by the parameters of the spacetime, a region exists where both the black-hole and cosmological horizons coexist [39]. In this coexistence region, the curve of the spacetime mass M as a function of r has two extrema, corresponding to masses
$ {M_N} $ and$ {M_C} $ . Ref. [40] applied the theory proposed in [19] to study the relation$ M \to {M_N} $ in Reissner-Nordström-de Sitter (RNdS), Kerr-de Sitter (KdS), and Kerr-Newman-de Sitter (KNdS) spacetimes, confirming the universality of the thermodynamic relation in dS black holes. Furthermore, these results suggest that WGC is still applicable in the dS spacetime. Given the coexistence region in the dS spacetime with two extrema, the extremum N is the intersection point where the positions of the black-hole and cosmological horizons are equal. In the coexistence region$ M \to {M_N} $ , the spacetime can evolve along either the black-hole or cosmological horizon. Ref. [40] only discusses the four-dimensional case, specifically the approach to the extremum along the black-hole horizon in the coexistence region. No previous study has addressed the scenario of approaching the extremum along the cosmological horizon or the cases in higher-dimensional spacetimes. In this study, combining the first law of thermodynamics in the dS spacetime, we investigated the universal relation proposed by Goon and Penco in dS black holes [19]. We extended the approach proposed in Ref. [40] to examine the behavior as one approaches the extrema along both the black-hole and cosmological horizons and to study the approach to the minimum extremum from the region where both horizons coexist, providing a universal relation,$ \mathop {\lim }\limits_{T \to 0} {\left( {\frac{{\partial {M_N}}}{{\partial \eta }}} \right)_{{X_i}}} = \mathop {\lim }\limits_{T \to 0} {\left( { - T\frac{{\partial S}}{{\partial \eta }}} \right)_{M,{X_i}}} = \mathop {\lim }\limits_{T \to 0} {\left( { - {{\bar X}_J}\frac{{\partial {X_j}}}{{\partial \eta }}} \right)_{M,{X_{i \ne j}}}}, $

(1) where
$ {X_i} $ represents the state function of the spacetime. Given that the studied examples involve higher-dimensional spacetimes with double rotational parameters, the conclusions obtained are more universally applicable.This paper is organized as follows. Sec. II discusses the universal relation of a non-linear magnetic-charged black hole in dS spacetime, analyzing the influence of charge and the cosmological constant on the coexistence region of both horizons. Sec. III explores the universal relation in five-dimensional dS hairy spacetime. Sec. IV examines a charged five-dimensional spacetime with double rotation, deriving a universal relation. Finally, Sec. V provides a summary.
-
Einstein gravity coupled to the non-linear electromagnetic field in the four-dimensional dS spacetime is described by the action [39]
$ S = \int {{\mathrm{d}^4}} x\sqrt { - g} \left[ {\frac{1}{{16\pi }}\left( {R - \frac{\Lambda }{2}} \right) - \frac{1}{{4\pi }}L(F)} \right], $

(2) where R is the scalar curvature of the dS spacetime, Λ
$ (\Lambda = 3/{l^2}) $ is the positive cosmological constant, and$ L(F) $ is a function of the invariant$ {F_{\mu \nu }}{F^{\mu \nu }}/4 = F $ with$ {F_{\mu \nu }} = {\partial _\mu }{A_\nu } - {\partial _\nu }{A_\mu } $ being the field strength of the non-linear electromagnetic field. In this paper, the non-linear electrodynamic term$ L(F) $ is explicitly expressed as$ L(F) = \frac{{3M}}{{{{\left| Q \right|}^3}}}\frac{{{{(2{Q^2}F)}^{3/2}}}}{{{{\left[ {1 + {{(2{Q^2}F)}^{3/4}}} \right]}^2}}}, $

(3) where M and Q are the mass and charge of the system, respectively. A static and spherical symmetric dS black hole of mass M and magnetic charge Q is expressed as
$ f(r) = 1 - \frac{{2M{r^2}}}{{{r^3} + {Q^3}}} - \frac{{{r^2}}}{{{l^2}}}, $

(4) According to Refs. [19, 37, 40], the cosmological constant becomes a perturbation parameter, yielding
$ S = \int {{\mathrm{d}^4}} x\sqrt { - g} \left[ {\frac{1}{{16\pi }}\left( {R - \frac{{(1 + \eta )\Lambda }}{2}} \right) - \frac{1}{{4\pi }}L(F)} \right], $

(5) where η is a very small constant. This correction shifts the metric function in Eq. (4),
$ f(r) = 1 - \frac{{2M{r^2}}}{{{r^3} + {Q^3}}} - \frac{{(1 + \eta )}}{{{l^2}}}{r^2}, $

(6) and the relation between the black-hole mass M and its horizon radius is established from the equation of the horizons
$ f(r) = 0 $ as$ M = \frac{{r_{ + ,c}^3 + {Q^3}}}{{2r_{ + ,c}^2}}\left( {1 - \frac{{(1 + \eta )}}{{{l^2}}}r_{ + ,c}^2} \right),$

(7) In the extended phase space, the entropy S, magnetic charge Q, and thermodynamic pressure P are regarded as a complete set of extensive thermodynamic variables. Their corresponding conjugating quantities, which are intensive thermodynamic variables, are the temperature T, chemical potential Φ, and thermodynamic volume V. Thus, the first law of the thermodynamics is established on the event and cosmological horizons, respectively, as follows:
$ \begin{aligned}[b] &\mathrm{d}M = {T_ + }\mathrm{d}{S_ + } + {\Phi _ + }\mathrm{d}Q + {V_ + }\mathrm{d}P, \\&\mathrm{d}M = - {T_c}\mathrm{d}{S_c} + {\Phi _c}\mathrm{d}Q + {V_c}\mathrm{d}P, \end{aligned} $

(8) where the minus sign in front of
$ T_c $ arises because the surface gravity of the cosmological horizon is negative. According to the conventional definition,$ T_c $ is negative. We have that$ \begin{aligned}[b] &{T_{ + ,c}} = \pm \frac{{f'({r_{ + ,c}})}}{{4\pi }} = \frac{{r_{ + ,c}^3 - 2{Q^3} - 3(1 + \eta )r_{ + ,c}^5/{l^2}}}{{4\pi {r_{ + ,c}}(r_{ + ,c}^3 + {Q^3})}},\;\;P = - \frac{\Lambda }{{8\pi }},\\ &{\Phi _{ + ,c}} = {\left( {\frac{{\partial M}}{{\partial Q}}} \right)_{{r_{ + ,c}}}} = \frac{{3{Q^2}}}{{2r_{ + ,c}^2}}\left( {1 - \frac{{(1 + \eta )}}{{{l^2}}}r_{ + ,c}^2} \right),\\&{S_{ + ,c}} = \pi r_{ + ,c}^2\left( {1 - \frac{{2{Q^3}}}{{r_{ + ,c}^3}}} \right), \end{aligned} $

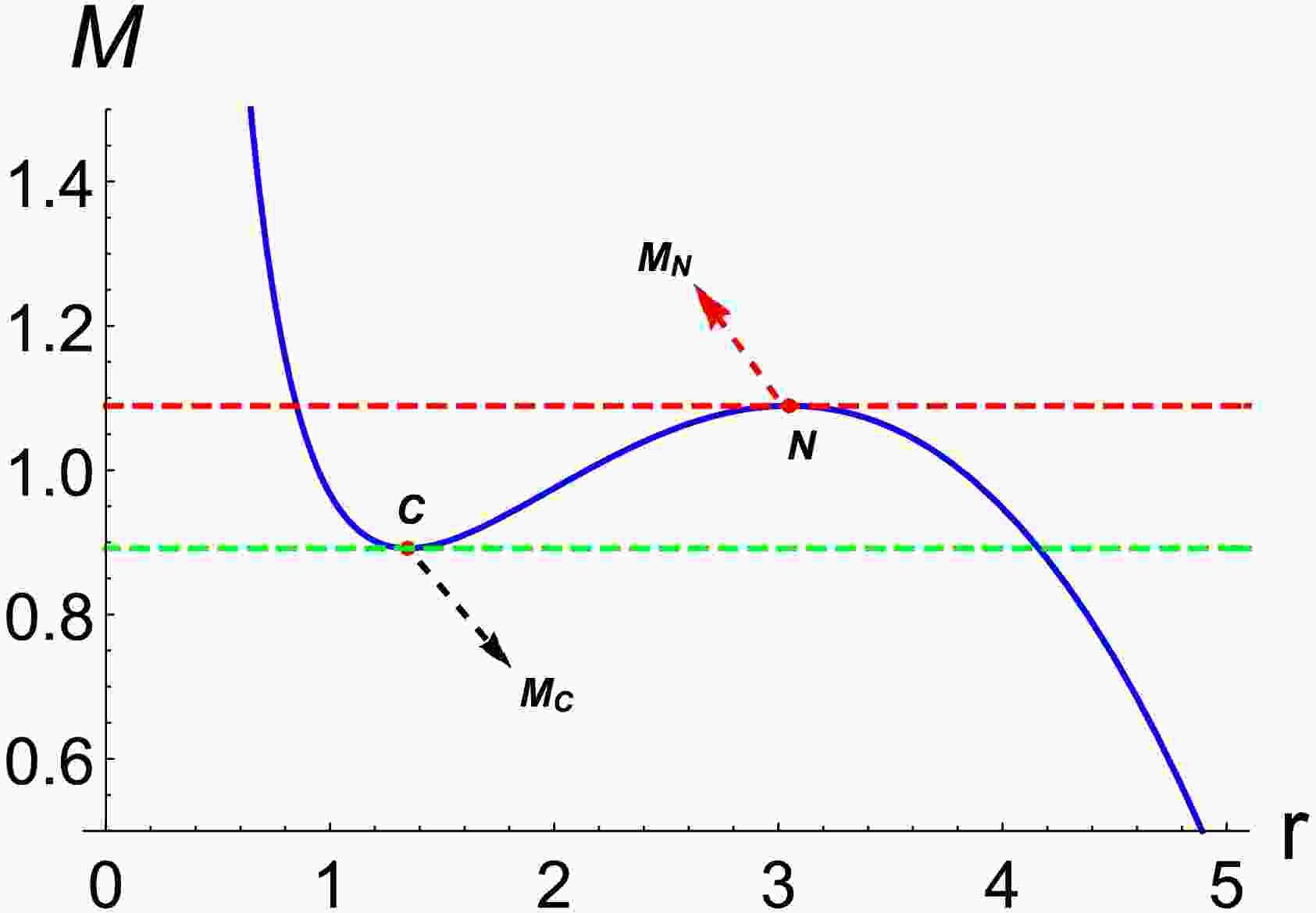
(9) and from Eq. (7), we can obtain the
$ M-r $ curve shown in Fig. 1. We know that when Q and$ {l^2}/(1 + \eta) $ are given, the spacetime energy satisfies$ {M_C} \le M \le {M_N} $ . In this case, the non-linear charged dS (NLC-dS) spacetime has an inner black-hole horizon$ {r_ - } $ , a black-hole horizon$ {r_ + } $ , and a cosmological horizon$ {r_ c } $ . At the local maximum point N, the black-hole and cosmological horizons coincide, representing the highest energy state in which both horizons coexist, corresponding to$ M = {M_N} $ . The black hole at this point is known as the Nariai black hole, whose event horizon radius$ {r_ N } $ is the largest positive real solution of the following equation:$ \frac{{3(1 + \eta )}}{{{l^2}}}r_{N,C}^5 - r_{N,C}^3 + 2Q_{N,C}^3 = 0, $

(10) Given that
$ M = {M_C} $ , the inner horizon$ {r_ - } $ and event horizon$ {r_ +} $ coincide. Such a black hole is called a cold black hole, whose event horizon radius${r_{{\rm{cold}}}}$ is the remaining positive real solution of Eq. (9). From Eqs. (7) and (10), we know that when the charges Q and l in the spacetime remain constant,$ {r_{N,C}} $ is a function of η. When η changes, it causes a corresponding change in the energy at point N, given by$ \begin{aligned}[b]{\left( {\frac{{\partial {M_{N,C}}}}{{\partial \eta }}} \right)_Q} =\;& - \frac{{(r_{N,C}^3 + {Q^3})}}{{2r_{N,C}^2}}\frac{{r_{N,C}^2}}{{{l^2}}} \\&+ \frac{1}{2}\left( {1 - \frac{{3(1 + \eta )r_{N,C}^2}}{{{l^2}}} - \frac{{2{Q^3}}}{{r_{N,C}^3}}} \right)\frac{{\partial {r_{N,C}}}}{{\partial \eta }}, \end{aligned}$

(11) and when the energy M remains constant, according to Eq. (7), a change in η causes a corresponding change in the charge Q and horizon position
$ {r_{ +,c}} $ given by$ \begin{aligned}[b] 0 =\;& \frac{{3{Q^2}}}{{2r_{ + ,c}^2}}\left( {1 - \frac{{(1 + \eta )}}{{{l^2}}}r_{ + ,c}^2} \right)\mathrm{d}Q - \frac{{r_{ + ,c}^3 + {Q^3}}}{{2{l^2}}}\mathrm{d}\eta \\&+ \frac{\partial }{{\partial {r_{ + ,c}}}}\left[ {\frac{{r_{ + ,c}^3 + {Q^3}}}{{2r_{ + ,c}^2}}\left( {1 - \frac{{(1 + \eta )}}{{{l^2}}}r_{ + ,c}^2} \right)} \right]\mathrm{d}{r_{ + ,c}}, \end{aligned} $

(12) i.e.,
$\begin{aligned}[b] {\left( {\frac{{\partial Q}}{{\partial \eta }}} \right)_M} =\;& \frac{1}{{{\Phi _{ + ,c}}}}\Bigg\{ \frac{{r_{ + ,c}^3 + {Q^3}}}{{2{l^2}}} - \Bigg[ \frac{{r_{ + ,c}^3 - 2{Q^3}}}{{2r_{ + ,c}^3}}\\& + \frac{{3(1 + \eta )r_{ + ,c}^2}}{{2{l^2}}} \Bigg]\frac{{\partial {r_{ + ,c}}}}{{\partial \eta }} \Bigg\}. \end{aligned}$

(13) At point N, the black-hole and cosmological horizons coincide, and the radiation temperature of both horizons is zero. Therefore, when approaching point N from the coexistence region of both horizons, regardless of whether it is along the black-hole or cosmological horizon, we have that
$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial {M_{N,C}}}}{{\partial \eta }}} \right)_Q} = - \frac{{(r_{N,C}^3 + {Q^3})}}{{2{l^2}}} = - {\Phi _{ + ,c}}{\left( {\frac{{\partial {Q_N}}}{{\partial \eta }}} \right)_M}. $

(14) At point C, the black-hole and inner horizons coincide, and the radiation temperature of the black-hole horizon is zero. However, the radiation temperature of the cosmological horizon at the corresponding energy point is not zero. Therefore, when approaching point C along the black-hole horizon in the coexistence region, we have that
$ \mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\partial {M_C}}}{{\partial \eta }}} \right)_Q} = - \frac{{(r_C^3 + {Q^3})}}{{2{l^2}}} = \mathop {\lim }\limits_{{T_ + } \to 0} - {\Phi _ + }{\left( {\frac{{\partial {Q_C}}}{{\partial \eta }}} \right)_M}. $

(15) From Eqs. (14) and (15), we observe that in the dS spacetime with a coexistence region of two horizons, when the thermodynamic quantities of the spacetime approach the endpoints of the coexistence region, i.e., at points N and C, the perturbations in entropy S and energy M satisfy the expression
$ \mathop {\lim }\limits_{{T_ + } \to 0} {\left( { - {T_ + }\frac{{\partial {S_ + }}}{{\partial \eta }}} \right)_{M,Q}} = \mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\partial {M_N}}}{{\partial \eta }}} \right)_Q}. $

(16) Moreover, the perturbations in charge Q and energy M satisfy Eqs. (14) and (15). From these equations, we know that the perturbation relations are not only applicable to the case of approaching the extremum along the black-hole horizon, but also hold when approaching the extremum along the cosmological horizon. By using Eqs. (14) and (16), we can generalize the perturbation relations to dS spacetimes that satisfy the first law of thermodynamics, i.e.,
$ \begin{aligned}[b] \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial {M_{N,C}}}}{{\partial \eta }}} \right)_{{X^i}}} =\;& \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} - {\Phi _{ + ,c}}{\left( {\frac{{\partial Q}}{{\partial \eta }}} \right)_{{X^i}}} \\=\;& \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( { - {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)_{M,{X^i}}} \\=\;& \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} - {\bar X^j}{\left( {\frac{{\partial {X^j}}}{{\partial \eta }}} \right)_{Q,{X^{i \ne j}}}}. \end{aligned} $

(17) In this equation,
$ {X^i} $ and$ {\bar X^i} $ are a pair of conjugate state parameters of the thermodynamic system.$ {X^i} $ is the spacetime parameter obtained after removing Q. -
Although we are interested in Einstein gravity, we focused our investigation in the context of Lovelock gravity minimally coupled to a Maxwell field. The scalar hair is conformally coupled to gravity via the dimensionally extended Euler densities in terms of the rank four tensor [41, 42]:
$ \mathrm{d}{s^2} = - f(r)\mathrm{d}{t^2} + {f^{ - 1}}\mathrm{d}{r^2} + {r^2}\mathrm{d}\Omega _2^2, $

(18) with the horizon function expressed as
$ f(r) = 1 - \frac{{8M}}{{3\pi {r^2}}} - \frac{{\Lambda {r^2}}}{6} - \frac{H}{{{r^3}}} + \frac{{4\pi {Q^2}}}{{3{r^4}}}, $

(19) where M, H, and Q are mass, hair parameter, and charge respectively; Λ is the cosmological constant. According to Refs. [19, 37, 40], the cosmological constant becomes the perturbation parameter, yielding a black hole with three positive horizons: the black-hole event horizon
$ {r_ + } $ , internal (Cauchy) horizon$ {r_ - } $ , and cosmological horizon$ {r_c} $ [41]. From Eq. (19), we obtain$ M = \frac{{3\pi r_{ + ,c}^2}}{8} - \frac{{\pi (1 + \eta )\Lambda r_{ + ,c}^4}}{{16}} - \frac{{3\pi H}}{{8{r_{ + ,c}}}} + \frac{{{\pi ^2}{Q^2}}}{{2r_{ + ,c}^2}}, $

(20) The Hawking radiation temperature of the black-hole and cosmological horizons is given by
$ {T_{ +, c}} = \pm \left( {\frac{1}{{2\pi {r_{ + ,c}}}} - \frac{{(1 + \eta )\Lambda {r_{ + ,c}}}}{{6\pi }} - \frac{{2{Q^2}}}{{3r_{ + ,c}^5}} + \frac{H}{{4\pi r_{ + ,c}^4}}} \right), $

(21) and the thermodynamic quantities corresponding to the two horizons satisfy the first law of thermodynamics and the Smarr relation [41]:
$ \delta M = \pm {T_{ + ,c}}\delta {S_{ + ,c}} + {V_{ + ,c}}\delta P + {\phi _{ + ,c}}\delta Q + {k_{ + ,c}}\delta H, $

(22) where
$ \Lambda = - 8\pi P $ . The thermodynamic quantities corresponding to the two horizons are the entropy$ {S_{ +,c}} $ , thermodynamic volume$ {V_{ +,c}} $ , and electric potentials$ {\phi _{ +,c}} $ and$ {\phi _{ +,c}} $ , expressed respectively as follows:$ {S_{ + ,c}} = \frac{{{\pi ^2}r_{ + ,c}^3}}{2},{V_{ + ,c}} = \frac{{{\pi ^2}r_{ + ,c}^4}}{2},{\phi _{ + ,c}} = \frac{{{\pi ^2}Q}}{{r_{ + ,c}^2}},{k_{ + ,c}} = - \frac{{3\pi }}{{8{r_{ + ,c}}}}. $

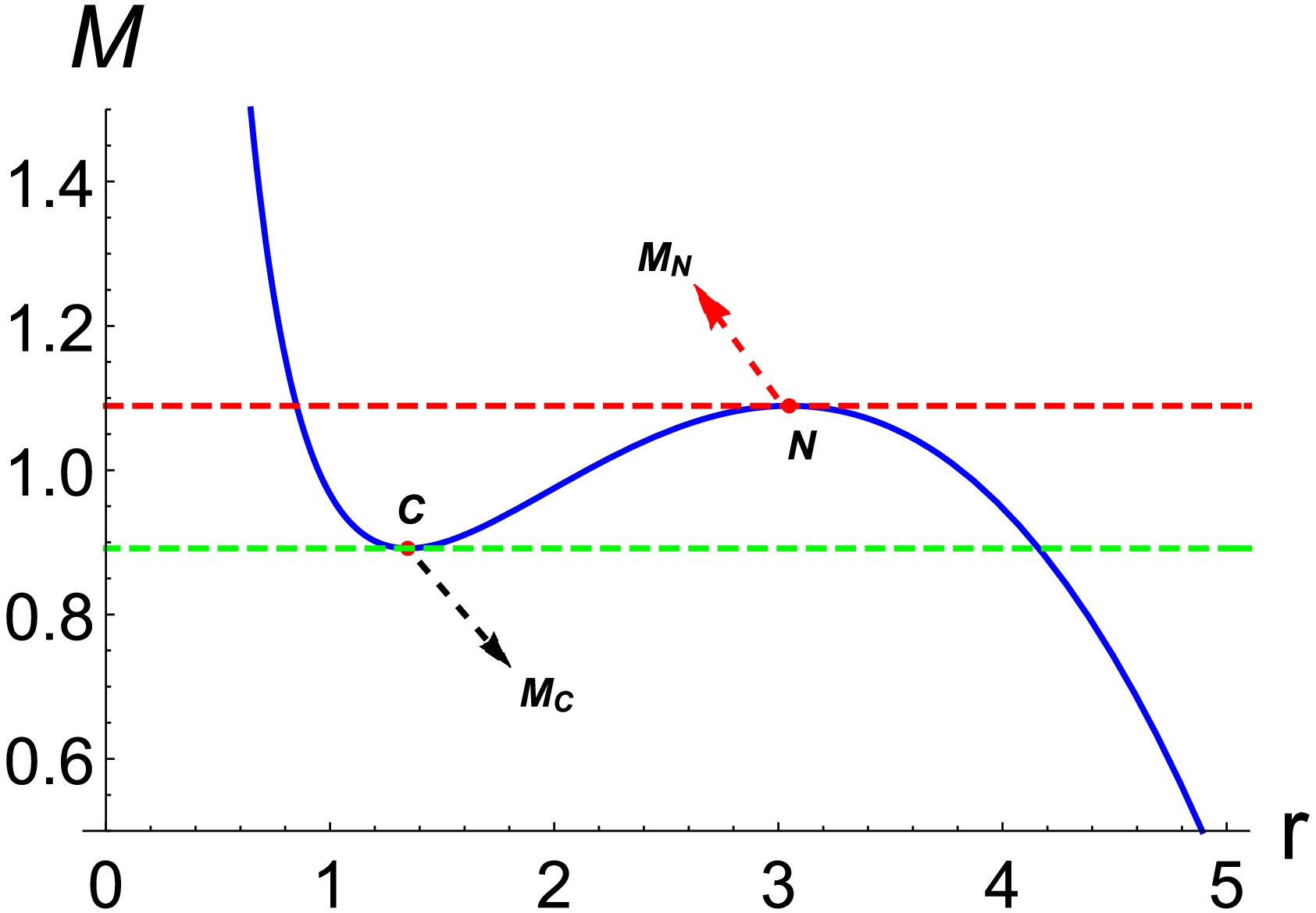
(23) From Eq. (20), we can obtain the
$ M - r $ curve for$ Q = 1 $ ,$ H = 1 $ , and$ (1 + \eta)\Lambda = 0.45 $ . Figure 2 shows that when Q,$ (1 + \eta)\Lambda $ and H are given, the spacetime energy satisfies$ {M_C} \le M \le {M_N} $ , and the five-dimensional dS hairy spacetime has an inner black-hole horizon$ {r_ - } $ , a black-hole horizon$ {r_ + } $ , and a cosmological horizon$ {r_c} $ . At the local maximum point N, the black-hole and cosmological horizons coincide. This point represents the largest energy point where both the black-hole and cosmological horizons coexist. The corresponding black hole is known as the Nariai black hole, whose event horizon radius$ {r_N} $ is the largest positive real solution of the following equation:$ \frac{{3\pi {r_{N,C}}}}{4} - \frac{{\pi (1 + \eta )\Lambda r_{N,C}^3}}{4} + \frac{{3\pi H}}{{8r_{N,C}^2}} - \frac{{{\pi ^2}{Q^2}}}{{r_{N,C}^3}} = 0, $

(24) According to Eqs. (20) and (24), when the charges Q, Λ, and H in the spacetime remain constant,
$ {r_{N,C}} $ is a function of η. When η changes, it causes a corresponding change in the energy at point N given by$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial {M_{N,C}}}}{{\partial \eta }}} \right)_{Q,\Lambda ,H}} = - \frac{{3\pi \Lambda r_{N,C}^4}}{{48}}. $

(25) When the energy M, Λ, and H remain constant, we can deduce from Eq. (20) that when η changes, it causes changes in the charge Q and horizon position
$ {r_{ +,c}} $ . The relationship between these changes is given by$ \begin{aligned}[b] 0 =\;& - \frac{{\pi \Lambda r_{ + ,c}^4}}{{16}}\mathrm{d}\eta + \frac{{{\pi ^2}Q}}{{r_{ + ,c}^2}}\mathrm{d}Q \\&+ \Bigg( {\frac{{3\pi {r_{ + ,c}}}}{4} - \frac{{\pi (1 + \eta )\Lambda r_{ + ,c}^3}}{4} + \frac{{3\pi H}}{{8r_{ + ,c}^2}} - \frac{{{\pi ^2}{Q^2}}}{{r_{ + ,c}^3}}} \Bigg)\mathrm{d}{r_{ + ,c}}, \end{aligned} $

(26) i.e.,
$ \begin{aligned}[b] {\left( {\frac{{\partial Q}}{{\partial \eta }}} \right)_{M,\Lambda ,H}}=\;& \frac{1}{{{\Phi _{ + ,c}}}}\Bigg[ \frac{{\pi \Lambda r_{ + ,c}^4}}{{16}} - \Bigg( \frac{{3\pi {r_{ + ,c}}}}{4} - \frac{{\pi (1 + \eta )\Lambda r_{ + ,c}^3}}{4}\\& + \frac{{3\pi H}}{{8r_{ + ,c}^2}} - \frac{{{\pi ^2}{Q^2}}}{{r_{ + ,c}^3}} \Bigg)\frac{{\partial {r_{ + ,c}}}}{{\partial \eta }} \Bigg]. \end{aligned} $

(27) Figure 2 shows that at point N, the black-hole and cosmological horizons coincide, and the radiation temperature of both horizons is zero. Therefore, when the spacetime approaches point N from the coexistence region of both horizons, regardless of whether it is along the black-hole or cosmological horizon, we have that
$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial {M_{N,C}}}}{{\partial \eta }}} \right)_{Q,\Lambda ,H}} = - \frac{{\pi \Lambda r_{N,C}^4}}{{16}} = - \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\Phi _{ + ,c}}{\left( {\frac{{\partial Q}}{{\partial \eta }}} \right)_{M,\Lambda ,H}}. $

(28) At point C, the black-hole and inner horizons coincide, and the radiation temperature of the black-hole horizon is zero. However, at the same energy point, the radiation temperature of the cosmological horizon is not zero. Therefore, when approaching point C from the coexistence region of the black-hole horizon, we have that
$\mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\partial {M_C}}}{{\partial \eta }}} \right)_{Q,\Lambda ,H}} = - \frac{{\pi \Lambda r_C^4}}{{16}} = - \mathop {\lim }\limits_{{T_ + } \to 0} {\Phi _ + }{\left( {\frac{{\partial Q}}{{\partial \eta }}} \right)_{M,\Lambda ,H}}. $

(29) When η changes, the change in entropy is given by
$ \frac{{\partial {r_{ + ,c}}}}{{\partial \eta }} = \pm \frac{{\Lambda r_{ + ,c}^2}}{{24\pi {T_{ + ,c}}}}, $

(30) $ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( { - {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)_{M,Q,\alpha }} = \mp \frac{{\Lambda \pi r_N^4}}{{16\pi }}. $

(31) When the energy Q, Λ, and H remain constant, we find from Eq. (20) that when η changes, the corresponding change in M is given by
$ \begin{aligned}[b] {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{Q,\Lambda ,H}} =\;& - \frac{{\pi \Lambda r_{ + ,c}^4}}{{16}} + \frac{{3{\pi ^2}r_{ + ,c}^2}}{2}\Bigg( \frac{1}{{2\pi {r_{ + ,c}}}} - \frac{{(1 + \eta )\Lambda {r_{ + ,c}}}}{{6\pi }} \\&+ \frac{H}{{4\pi r_{ + ,c}^4}} - \frac{{2{\pi ^2}{Q^2}}}{{3r_{ + ,c}^5}} \Bigg)\frac{{\partial {r_{ + ,c}}}}{{\partial \eta }},\\ &\mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{Q,\Lambda ,H}} = - \frac{{\pi \Lambda r_N^4}}{{16}}. \end{aligned} $

(32) From Eqs. (31) and (32), we obtain
$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( { - {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)_{\Lambda ,Q,H}} = \mp \frac{{\Lambda \pi r_N^4}}{{16\pi }} = \pm \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial {M_N}}}{{\partial \eta }}} \right)_{\Lambda ,Q,H}}. $

(33) Similarly, it can be proved that
$ \mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\partial {M_C}}}{{\partial \eta }}} \right)_{Q,\Lambda ,H}} = - \frac{{\Lambda \pi r_N^4}}{{16\pi }} = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( { - {T_ + }\frac{{\partial {S_ + }}}{{\partial \eta }}} \right)_{H,Q,\Lambda }}. $

(34) When the energy M, Λ, and Q remain constant, we find from Eq.(20) that when η changes, it causes corresponding changes in H and the horizon position
$ {r_{ +,c}} $ . The relationships for these changes are given by$ \begin{aligned}[b] 0 =\;& - \frac{{\pi \Lambda r_{ + ,c}^4}}{{16}}d\eta - \frac{{3\pi }}{{8{r_{ + ,c}}}}\mathrm{d}H \\&+ \left( {\frac{{3\pi {r_{ + ,c}}}}{4} - \frac{{\pi (1 + \eta )\Lambda r_{ + ,c}^3}}{4} + \frac{{3\pi H}}{{8r_{ + ,c}^2}} - \frac{{{\pi ^2}{Q^2}}}{{r_{ + ,c}^3}}} \right)\mathrm{d}{r_{ + ,c}}, \end{aligned} $

(35) i.e.,
$ \begin{aligned}[b] {\left( {\frac{{\partial H}}{{\partial \eta }}} \right)_{M,\Lambda ,Q}} =\;& \frac{1}{{{k_{ + ,c}}}}\Bigg[ \frac{{\pi \Lambda r_{ + ,c}^4}}{{16}} - \Bigg( \frac{{3\pi {r_{ + ,c}}}}{4} - \frac{{\pi (1 + \eta )\Lambda r_{ + ,c}^3}}{4}\\& + \frac{{3\pi H}}{{8r_{ + ,c}^2}} - \frac{{{\pi ^2}{Q^2}}}{{r_{ + ,c}^3}} \Bigg)\frac{{\partial {r_{ + ,c}}}}{{\partial \eta }} \Bigg]. \end{aligned} $

(36) Figure 3 shows that at point N, the black-hole and cosmological horizons coincide, and the radiation temperature of both horizons is zero. Therefore, when approaching point N from the coexistence region of both horizons, regardless of whether it is along the black-hole or cosmological horizon, we have that
$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial {M_{N,C}}}}{{\partial \eta }}} \right)_{Q,\Lambda ,H}} = - \frac{{\pi \Lambda r_{N,C}^4}}{{16}} = - \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {k_{ + ,c}}{\left( {\frac{{\partial H}}{{\partial \eta }}} \right)_{M,\Lambda ,Q}}. $

(37) -
In this section, we verify the relation for a charged-dS rotating black hole in
$ n = 5 $ . A charged-dS rotating black hole in the$ n = 5 $ solution comprises axially symmetric black holes with an axis of rotation. The action is identical to the SdS action, leading to a process similar to the SdS case. The$ n = 5 $ Kerr-Newman-dS metric for a rotating charged black hole with a positive cosmological constant reads [2, 43, 44]$ \begin{aligned}[b] \mathrm{d}{s^2} =\; & - \frac{{R[(1 + {g^2}{r^2}){\rho ^2}\mathrm{d}t + 2q\nu ]\mathrm{d}t}}{{{\Xi _a}\Xi {}_b{\rho ^2}}} \\&+ \frac{{2q\nu \omega }}{{{\rho ^2}}} + \frac{f}{{{\rho ^4}}}{\left( {\frac{{Rdt}}{{{\Xi _a}\Xi {}_b}} - \omega } \right)^2}\\ & + \frac{{{\rho ^2}\mathrm{d}{r^2}}}{\Delta } + \frac{{{\rho ^2}\mathrm{d}{\theta ^2}}}{R} + \frac{{{r^2} + {a^2}}}{{{\Xi _a}}}{\sin ^2}\theta \mathrm{d}{\varphi ^2}\\& + \frac{{{r^2} + {b^2}}}{{{\Xi _b}}}{\cos ^2}\theta \mathrm{d}{\psi ^2}, \end{aligned} $

(38) $ \phi = \frac{{\sqrt 3 q}}{{{\rho ^2}}}\left( {\frac{{R\mathrm{d}t}}{{{\Xi _a}{\Xi _b}}} - \omega } \right), $

(39) where
$ \begin{aligned}[b] &\nu = b{\sin ^2}\theta \mathrm{d}\varphi + a{\cos ^2}\theta \mathrm{d}\psi,\\&\omega = a{\sin ^2}\theta \frac{{\mathrm{d}\varphi }}{{{\Xi _a}}} + b{\cos ^2}\theta \frac{{\mathrm{d}\psi }}{{{\Xi _b}}},\\ &R = 1 + {a^2}{g^2}{\cos ^2}\theta + {b^2}{g^2}{\sin ^2}\theta,\\& \Delta = \frac{{({r^2} + {a^2})({r^2} + {b^2})(1 - {g^2}{r^2}) + {q^2} + 2abq}}{{{r^2}}} - 2m,\\ &{\rho ^2} = 1 + b{\sin ^2}\theta + a{\cos ^2}\theta ,\\&{\Xi _a} = 1 + {a^2}{g^2},{\Xi _b} = 1 + {b^2}{g^2},\\&f = 2m{\rho ^2} - {q^2} - 2abq{g^2}{\rho ^2}. \end{aligned} $

(40) The thermodynamic quantities are [44, 45]
$ \begin{aligned}[b] &M = \frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}},\\&m = \frac{{({r^2} + {a^2})({r^2} + {b^2})(1 - {g^2}{r^2}) + {q^2} + 2abq}}{{2{r^2}}},\\&{J^a} = \frac{{\pi [2am + qb(1 - {a^2}{g^2})]}}{{4\Xi _a^2{\Xi _b}}},\\& {J^b} = \frac{{\pi [2bm + qb(1 - {a^2}{g^2})]}}{{4\Xi _b^2{\Xi _a}}},\\& Q = \frac{{\sqrt 3 \pi q}}{{4{\Xi _a}{\Xi _b}}}. \end{aligned} $

(41) where r represents either the position of the black-hole horizon
$ {r_+ } $ or the position of the cosmological horizon$ {r_c} $ . For the black-hole horizon, we have that$ \begin{aligned}[b] &{T_ + } = \frac{{r_ + ^4[1 - {g^2}(2r_ + ^2 + {a^2} + {b^2})] - {{(ab + q)}^2}}}{{2\pi {r_ + }[(r_ + ^2 + {a^2})(r_ + ^2 + {b^2}) + abq]}},\end{aligned} $

$ \begin{aligned}[b]& {S_ + } = \frac{{{\pi ^2}[(r_ + ^2 + {a^2})(r_ + ^2 + {b^2}) + abq]}}{{2{\Xi _a}{\Xi _b}{r_ + }}},\\&\Omega _ + ^a = \frac{{a(r_ + ^2 + {b^2})(1 - {g^2}r_ + ^2) + bq}}{{(r_ + ^2 + {a^2})(r_ + ^2 + {b^2}) + abq}},\\ & \Omega _ + ^b = \frac{{b(r_ + ^2 + {a^2})(1 - {g^2}r_ + ^2) + aq}}{{(r_ + ^2 + {a^2})(r_ + ^2 + {b^2}) + abq}},\\ &{\phi _ + } = \frac{{\sqrt 3 qr_ + ^2}}{{(r_ + ^2 + {a^2})(r_ + ^2 + {b^2}) + abq}}. \end{aligned} $

(42) For the cosmological horizon, we have that
$ \begin{aligned}[b] &{T_c} = - \frac{{r_c^4[1 - {g^2}(2r_c^2 + {a^2} + {b^2})] - {{(ab + q)}^2}}}{{2\pi {r_c}[(r_c^2 + {a^2})(r_c^2 + {b^2}) + abq]}},\\&{S_c} = \frac{{{\pi ^2}[(r_c^2 + {a^2})(r_c^2 + {b^2}) + abq]}}{{2{\Xi _a}{\Xi _b}{r_c}}},\\ &\Omega _c^a = \frac{{a(r_c^2 + {b^2})(1 - {g^2}r_c^2) + bq}}{{(r_c^2 + {a^2})(r_c^2 + {b^2}) + abq}},\\&\Omega _c^b = \frac{{b(r_c^2 + {a^2})(1 - {g^2}r_c^2) + aq}}{{(r_c^2 + {a^2})(r_c^2 + {b^2}) + abq}},\\&{\phi _c} = \frac{{\sqrt 3 qr_c^2}}{{(r_c^2 + {a^2})(r_c^2 + {b^2}) + abq}}. \end{aligned} $

(43) The thermodynamic quantities of the spacetime satisfy the first law of thermodynamics,
$ \begin{array}{*{20}{l}} \mathrm{d}M = \pm {T_{ + ,c}}\mathrm{d}{S_{ + ,c}} + \sum\limits_j {\Phi _{ + ,c}^j} \mathrm{d}{Q^j} + \sum\limits_j {\Omega _{ + ,c}^j}\mathrm{d}{J^j} + {V_{ + ,c}}\mathrm{d}P, \end{array} $

(44) where
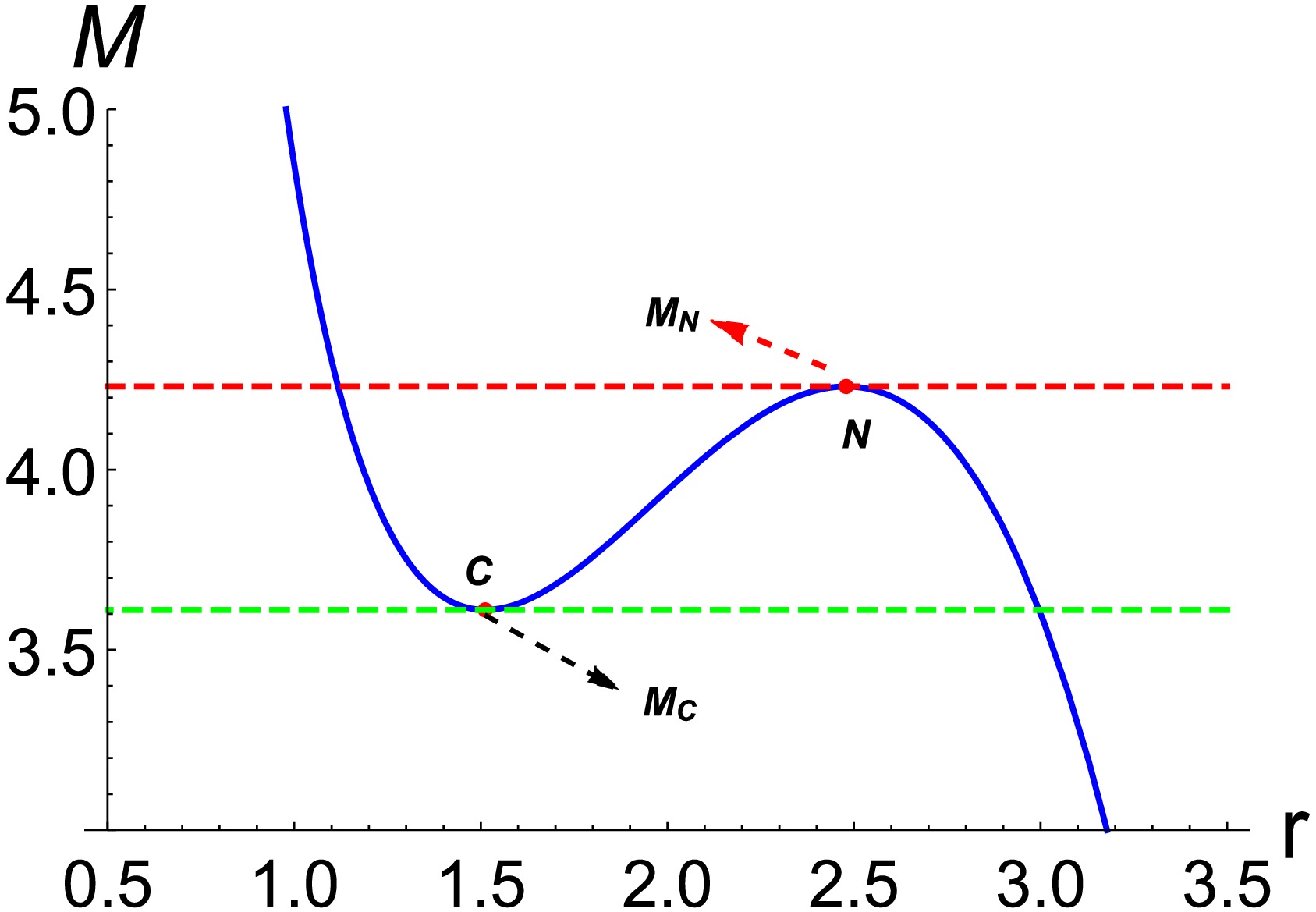
$ {r_{ +,c}} $ represents the positions of the black-hole and cosmological horizons, respectively. According to Eq. (44),$ M = M({S_{ +,c}},{J^j},{Q^j},P) $ . According to Refs. [19, 32, 37], the cosmological constant becomes a perturbation parameter η, where η is a very small constant. Using Eq. (41), we can represent the relationship between the horizon position$ {r_{ +,c}} $ and mass M in the spacetime when$ a = 0.001 $ ,$ b = 0.05 $ ,$ q = 0.1 $ , and$ g = 0.5 $ , which is represented by the$ M - r $ curve.Figure 3 shows that when
$ M > {M_N} $ , there is no horizon in the spacetime. When$ M = {M_N} $ , the black-hole horizon position$ {r_ + } $ coincides with the cosmological horizon position$ {r_c} $ , and such a black hole is called Nariai black hole, whose event horizon radius$ {r_N} $ is the largest positive real solution. As$ M = {M_C} $ , the inner horizon$ {r_ - } $ and event horizon$ {r_ + } $ coincide, and such a black hole is called cold black hole, whose event horizon radius$ {r_{cold}} $ is the remaining positive real solution. When$ {M_C} < M < {M_N} $ , the spacetime has a coexistence region between the black-hole horizon$ {r_ + } $ and cosmological horizon$ {r_c} $ . When$ M < {M_N} $ , the spacetime has the cosmological horizon$ {r_c} $ only. When the spacetime parameters$ {J^j} $ ,$ {Q^j} $ , q, and P remain constant, the changes in M and entropy$ {S_{ +,c}} $ caused by a perturbation in η are given by$ \begin{aligned}[b] \frac{{\mathrm{d}M}}{{\mathrm{d}\eta }} =\;& \frac{{\partial M}}{{\partial {S_{ + ,c}}}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }} = \pm {T_{ + c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}\\&+ \frac{\partial }{{\partial \eta }}\left[ {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right], \end{aligned} $

(45) $\begin{aligned}[b]& \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\mathrm{d}M}}{{\mathrm{d}\eta }}} \right)_{{J^a},{J^b},Q,P}} \\=\;& \frac{\partial }{{\partial \eta }}\left[ {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right]. \end{aligned}$

(46) When M remains constant, the change in
$ {S_{ +,c}} $ caused by a perturbation in η is given by$\begin{aligned}[b] 0 =\;& \frac{\partial }{{\partial \eta }}\left[ {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right] \\&+ \frac{{\partial M}}{{\partial {S_{ + ,c}}}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}.\end{aligned} $

(47) From Eq. (44), we can obtain that
$ \begin{aligned}[b] 0 =\;& \frac{\partial }{{\partial \eta }}\left[ {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right] \\&\pm {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}. \end{aligned} $

(48) From Eqs. (46) and (48), we obtain that
$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\mathrm{d}M}}{{\mathrm{d}\eta }}} \right)_{{J^a},{J^b},Q,P}} = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \left( { \mp {T_{ + ,c}}{{\left( {\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)}_{M,{J^a},{J^b},Q,P}}} \right). $

(49) When
$ {T_{ +,c}} \to 0 $ corresponds to$ M \to {M_{N,C}} $ and the coexistence region of both horizons approaches point N, the uncontrolled evolution can proceed along either the black-hole or cosmological horizon. When the coexistence region of both horizons approaches point C, only the radiation temperature associated with the black-hole horizon becomes zero at point C. Consequently, the evolution can only proceed along the black-hole horizon toward point C, that is,$ \mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\mathrm{d}M}}{{\mathrm{d}\eta }}} \right)_{{J^a},{J^b},Q,P}} = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \left( { - {T_ + }{{\left( {\frac{{\partial {S_ + }}}{{\partial \eta }}} \right)}_{M,{J^a},{J^b},Q,P}}} \right), $

(50) and when M remains constant, the changes in Q and entropy
$ {S_{ +,c}} $ caused by a perturbation in η are given by$ \begin{aligned}[b] 0 =\; &\frac{\partial }{{\partial Q}}\left( {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right)\frac{{\partial Q}}{{\partial \eta }}+ \frac{\partial }{{\partial \eta }}\left[ {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right]\\ & + \frac{\partial }{{\partial {S_{ + ,c}}}}\left( {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right)\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}. \end{aligned} $

(51) From Eq. (44), we can obtain that
$ \begin{aligned}[b] 0 = {\Phi _{ + ,c}}\frac{{\partial Q}}{{\partial \eta }} + \frac{\partial }{{\partial \eta }}\left[ {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right] \pm {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}. \end{aligned} $

(52) From Eqs. (46) and (49), we obtain that
$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\mathrm{d}M}}{{\mathrm{d}\eta }}} \right)_{{J^a},{J^b},Q,P}} = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \left( { - {\Phi _{ + ,c}}{{\left( {\frac{{\partial Q}}{{\partial \eta }}} \right)}_{M,{J^a},{J^b},P}}} \right). $

(53) When M remains constant, the changes in
$ {J^{a,b}} $ caused by a perturbation in η are given by$ 0 = \Omega _{ + .c}^{a,b}\frac{{\partial {J^{a,b}}}}{{\partial \eta }} + \frac{\partial }{{\partial \eta }}\left[ {\frac{{\pi m(2{\Xi _a} + 2{\Xi _b} - {\Xi _a}{\Xi _b}) - 2\pi qab{g^2}({\Xi _a} + {\Xi _b})}}{{4\Xi _a^2\Xi _b^2}}} \right] \pm {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}. $

(54) From Eq. (46) and Eq. (54), we obtain that
$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\mathrm{d}M}}{{\mathrm{d}\eta }}} \right)_{{J^a},{J^a},Q,P}} = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \left( { - \Omega _{ + ,c}^a{{\left( {\frac{{\partial {J^a}}}{{\partial \eta }}} \right)}_{M,{J^b},Q,P}}} \right) = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \left( { - \Omega _{ + ,c}^b{{\left( {\frac{{\partial {J^b}}}{{\partial \eta }}} \right)}_{M,{J^a},Q,P}}} \right). $

(55) When the system approaches point N from the coexistence region of both horizons, we have that
$ \begin{aligned}[b] \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\mathrm{d}M}}{{\mathrm{d}\eta }}} \right)_{{J^a},{J^b},Q,P}} =\;& \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \left( { - \Omega _{ + ,c}^a{{\left( {\frac{{\partial {J^a}}}{{\partial \eta }}} \right)}_{M,{J^b},Q,P}}} \right) = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \left( { - \Omega _{ + ,c}^b{{\left( {\frac{{\partial {J^b}}}{{\partial \eta }}} \right)}_{M,{J^a},Q,P}}} \right)\\ =\;& \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \left( { - {\Phi _{ + ,c}}{{\left( {\frac{{\partial Q}}{{\partial \eta }}} \right)}_{M,{J^j},Q,P}}} \right) = \mp {T_{ + ,c}}{\left( {\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)_{M,{J^j},Q,P}}. \end{aligned} $

(56) When the system approaches point C from the coexistence region of both horizons, we have that
$ \mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\mathrm{d}M}}{{\mathrm{d}\eta }}} \right)_{{J^j},Q,P}} = \mathop {\lim }\limits_{{T_ + } \to 0} \left( { - \Omega _ + ^i{{\left( {\frac{{\partial {J^i}}}{{\partial \eta }}} \right)}_{M,J(i),Q,P}}} \right) = \mathop {\lim }\limits_{{T_ + } \to 0} \left( { - {\Phi _ + }{{\left( {\frac{{\partial Q}}{{\partial \eta }}} \right)}_{M,{J^j},P}}} \right) = \left( { - {T_ + }{{\left( {\frac{{\partial {S_ + }}}{{\partial \eta }}} \right)}_{M,{J^j},Q,P}}} \right). $

(57) Thus, Eqs. (56) and (57) can be extended to any spacetime with multiple parameters as long as the state parameters of the spacetime satisfy the first law of thermodynamics:
$ \begin{array}{*{20}{l}} \mathrm{d}M = \pm {T_{ + ,c}}d{S_{ + ,c}} + \sum\limits_i {{{{\rm{\bar X}}}_i}} \mathrm{d}{X^i}, \end{array} $

(58) and when the spacetime approaches the maximum energy value at point N from the coexistence region of both horizons, we have that
$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{{X^i}}} = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( { \pm {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)_{M,{X^i}}} = - \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \bar X_{ + ,c}^j{\left( {\frac{{\partial {X^j}}}{{\partial \eta }}} \right)_{M,{X^{i \ne j}}}}. $

(59) When the spacetime approaches the minimum energy value at point C from the coexistence region of both horizons, we have that
$ \mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{{X^i}}} = \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( { - {T_ + }\frac{{\partial {S_ + }}}{{\partial \eta }}} \right)_{M,{X^i}}} = - \mathop {\lim }\limits_{{T_ + } \to 0} \bar X_ + ^j{\left( {\frac{{\partial {X^j}}}{{\partial \eta }}} \right)_{M,{X^{i \ne j}}}}. $

(60) where
$ {X^j} $ and$ {\bar X^j} $ are a pair of conjugate state parameters that satisfy the thermodynamic system. -
From the above discussion, it can be concluded that when the energy M in the spacetime is a function of the state parameters and satisfies the first law of thermodynamics, under the condition that other state function
$ {X^i} $ remains constant, when the spacetime perturbation parameter η changes, the energy M and horizon position in the spacetime also change. The relationship between these changes is given by Eqs. (11), (32) and (46). When the spacetime evolves from the coexistence of two horizons towards the maximum energy corresponding to the coexistence of both horizons, the relationship between the changes in energy M and horizon position (entropy) satisfies$ \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{{X^i}}} = {\left( { \pm {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)_{M,{X^i}}}. $

(61) In this equation, the positive and negative signs correspond to the cases when approaching point N from the coexistence region of both horizons along the black-hole and cosmological horizons, respectively. When approaching point C from the coexistence region of both horizons, we have that
$ \mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{{X^i}}} = {\left( { - {T_ + }\frac{{\partial {S_ + }}}{{\partial \eta }}} \right)_{M,{X^i}}}. $

(62) When the perturbation parameter η changes, it causes one of the state functions
$ {X^i} $ in the state function$ {X^j} $ to vary with η, while the other state functions remain unchanged. The relationship is given by$ {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{{X^i}}} = {\left( {\frac{{\partial M}}{{\partial {X^j}}}\frac{{\partial {X^j}}}{{\partial \eta }}} \right)_{{X^{i \ne j}}}} + {\left( {\frac{{\partial M}}{{\partial S}}\frac{{\partial S}}{{\partial \eta }}} \right)_{{X^i}}}. $

(63) When the energy M remains constant, Eq. (63) can be expressed as
$ \begin{aligned}[b]& {\left( {\frac{{\partial M}}{{\partial {X^j}}}\frac{{\partial {X^j}}}{{\partial \eta }}} \right)_{M,{X^{i \ne j}}}} + {\left( {\frac{{\partial M}}{{\partial S}}\frac{{\partial S}}{{\partial \eta }}} \right)_{M,{X^i}}} \\=\;& {\left( {{{\bar X}^j}\frac{{\partial {X^j}}}{{\partial \eta }}} \right)_{M,{X^{i \ne j}}}} + {\left( { \pm {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)_{M,{X^i}}} = 0. \end{aligned} $

(64) From Eqs. (62) and (64), we can obtain the universal relation at the maximum energy point N corresponding to the coexistence region of two horizons approaching the coexistence region of both horizons. The relation is given by
$ \begin{aligned}[b] \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{{X^i}}} =\;& \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} {\left( { \mp {T_{ + ,c}}\frac{{\partial {S_{ + ,c}}}}{{\partial \eta }}} \right)_{M,{X^i}}} \\=\;& - \mathop {\lim }\limits_{{T_{ + ,c}} \to 0} \bar X_{ + ,c}^j{\left( {\frac{{\partial {X^j}}}{{\partial \eta }}} \right)_{M,{X^{i \ne j}}}}, \end{aligned} $

(65) and from the coexistence region of both horizons approaching the minimum energy point C corresponding to the coexistence region of both horizons, the universal relation is given by
$ \begin{aligned}[b] \mathop {\lim }\limits_{{T_ + } \to 0} {\left( {\frac{{\partial M}}{{\partial \eta }}} \right)_{{X^i}}} =\;& \mathop {\lim }\limits_{{T_ + } \to 0} {\left( { - {T_ + }\frac{{\partial {S_ + }}}{{\partial \eta }}} \right)_{M,{X^i}}} \\=\;& - \mathop {\lim }\limits_{{T_ + } \to 0} \bar X_ + ^j{\left( {\frac{{\partial {X^j}}}{{\partial \eta }}} \right)_{M,{X^{i \ne j}}}}. \end{aligned} $

(66) From the above analysis, we obtained the variation law of the state parameters of the system as the perturbation parameter η changes at the endpoint of the coexistence region of both horizons in the dS spacetime. It is concluded that as long as the state parameters of the spacetime satisfy the first law of thermodynamics, Eqs. (65) and (66) remain valid. We extended the conclusions provided in Refs. [19, 37] to the endpoints of the coexistence region of two horizons in any dS spacetime. Our method is simple to compute and the process is clear, offering a pathway to further investigate the physical properties of the coexistence region of two horizons in the dS spacetime.
The exploration of the proportional relationship between corrected mass and entropy provides a pathway to understanding WGC, which offers intriguing insights into the realm of quantum gravity. Studies such as the present one contribute to a deeper comprehension of this fundamental aspect of physics.
Universal thermodynamic relations with constant corrections for five-dimensional de Sitter spacetime
- Received Date: 2024-11-16
- Available Online: 2025-03-15
Abstract: In this study, we built upon the method proposed by Goon and Penco for analyzing the universality of thermodynamic relations with corrections in de Sitter (dS) black holes. Additionally, based on our analysis of non-linear magnetically charged black holes in dS spacetime, five-dimensional dS hairy spacetime, and five-dimensional charged-dS rotating black holes, we demonstrate the universality of thermodynamic relations in dS black holes. This establishes a universal conjecture relating shifted thermodynamic quantities for arbitrary black-hole backgrounds. We consider that these universal relations will offer new insights into the realm of quantum gravity.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: