Investigation of heavy particle radioactivity and spontaneous fission of even-Z superheavy nuclei

In the ground state, an unstable nuclear system attains stability either by expelling ionized particles or radiation. Owing to this, three principle decay processes fall in this category: alpha (α), beta (β), and gamma (γ) emissions. However, in addition to these decay channels, cluster (or heavy cluster) radioactivity and spontaneous fission (SF) are equally important for investigating the ground state dynamics of heavy and superheavy elements. Among these, SF was discovered during the investigation of the decay of the $^{235}$U nucleus into two comparable fragments after capturing a neutron [1]. The division of a nucleus into two massive parts was called nuclear fission. The study opened a new window for nuclear physicists to observe unstable heavy and superheavy nuclei through SF process. In particular, for the superheavy mass region, the probability of fission is paramount owing to a high Coulomb repulsion. Hence, the $Z^2/A$ factor plays an important role in the segregation of fission fragments. Moreover, the magicity at Z = 114, 120, 126 and N = 172, 184 magic shells is another milestone while investigating fission barriers for superheavy nuclei. Precisely, the calculated shell correction energies at superheavy magic shells provide stability against prompt fission and further aid in investigating the island of stability [2−4]. This signifies the importance of the interplay between shell effects and Coulomb repulsion for SF process. Even and odd nucleons also influence the SF events. In odd nuclear systems, an unpaired nucleon significantly hinders the fission process [5−7]. Therefore, ground state fission, which often dominates in $108\leq Z$$\leq 114$ and $170 \leq N$$\leq 180$ mass regions, is affected by various parameters that should be accounted for when investigating its dynamics [8, 9]. Owing to this, the preformed cluster model (PCM) [10−16] is applied in this analysis to study the SF half-lives ($T_{\rm SF}$) of $Z=112$ and $Z=114$ isotopes. The shell effects of the parent nuclei and fissioning fragments are duly incorporated along with the liquid drop potential. In addition, the deformation effects are included up to $\beta_{2i}$ within the hot optimum orientation approach [17]. Moreover, the roles of different versions of proximity potentials, namely Prox-77 [18], Prox-00 [19], Mod Prox-00 [20], Prox-88 [21] and Prox-BW-91 [21], are tested to calculate $T_{\rm SF}$ of $Z=112$ and 114 nuclear systems.

The ground state decay mechanism is significantly affected by the doubly magic $^{208}$Pb nucleus, leading to the emission of exotic clusters with $Z_{\rm cluster} > 28$. This process is called heavy particle radioactivity (HPR) [16, 22, 23]. Generally, the decay phenomenon lying between α-emission and SF events is called cluster (or heavy particle) radioactivity. Note that the peculiar decay mode was first investigated for trans-lead nuclei with $Z = 87-96$. The emission of $^{14}$C, $^{20}$O, $^{23}$F, $^{22,24-26}$Ne clusters [24−27] is primarily observed in this mass region. Subsequently, Poenaru et al. [22, 23] extended the research on superheavy nuclei with $Z_{\rm parent} > 110$ through the analytic super asymmetric fission (ASAF) model. Various methodologies, such as the unified fission model (UFM) [28−31], generalized liquid drop model (GLDM) [32−35], universal decay law (UDL) [36, 37], density dependent cluster model [38], universal curve (UNIV) [39], unified description (UD) formula [40], scaling law of Horoi [41], PCM [10−16], and AKRA (from the Author Akrawy) [42], were developed to address the heavy cluster emission. Among the mentioned methodologies, the PCM assumes the clusters to be preformed inside the parent nucleus with a finite value of the preformation factor ($P_0$). The preformation probability ($P_0$) is calculated by solving the Schrodinger equation for the dynamic flow of charges and masses or through empirical formulas [43−47]. Thereafter, the cluster in the parent nucleus is assumed to penetrate with available Q-value through the interaction barrier. Based on this, the PCM is applied in this work to understand the HPR of $Z=112-120$ nuclear systems in terms of the preformation factor and penetration probability of clusters. Santhosh et al. [48] addressed the ASAF data [49] by calculating α-decay and heavy cluster decay probabilities of superheavy isotopes. However, the present analysis, through the PCM, focuses on following points:

(1) The primary aim of this work is to test the effect of different proximity potentials, namely Prox-77 [18], Prox-00 [19], Mod Prox-00 [20], Prox-88 [21], and Prox-BW-91 [21], on heavy cluster emission and SF in even-Z superheavy nuclei.

(2) The role of the Z-dependent radius [50] in various proximity potentials is investigated to address both phenomena.

The remainder of this paper is organized as follows: the methodology is described in Section II, including the framework of the PCM. Various versions of the proximity potentials are also briefly discussed. The calculations and results are discussed in Section III. Finally, the outcomes are summarized in Section IV.

The PCM [10−16] based on the quantum mechanical fragmentation theory (QMFT) [51, 52] has been developed by adopting Gamow's theory of the penetration of emitted particles/fragments. In this paper, instead of a square well or harmonic potential, a more realistic nuclear proximity potential is used. Using different versions of proximity potentials (described in subsequent subsections), we calculate the SF and cluster emission half-lives by including cluster and daughter preformation probabilities (${P_0}$), barrier impinging frequency (${f_0}$), and barrier penetrability (P), which are calculated as

here, $P_0$ and P refer to the η and R motions of the fragments, respectively, and the third factor of Eq. (1) can be calculated as

Here, $f_0$ is depicted as the impinging or assault frequency of the cluster, where ${R_0}$ is the radius of the parent nucleus. The impinging frequency $f_0$ is nearly constant ${\sim}$ $10^{21}{\rm s^{-1}}$ for cluster and SF processes.

Within the QMFT, the preformation probability $P_0$ is calculated by solving the Schrödinger equation, and the potential required for this mechanism is called the fragmentation potential $V_R(\eta)$, which is calculated as

Here, the binding energies of the two fragments, $B_i (i= 1,2)$, are obtained from Audi's experimental compilation [53] and the theoretical estimates of Möller et al. [54]. The Möller-Nix et al. binding energies are included for those nuclear systems that are absent in [53]. The binding energies are essentially the sum of the liquid drop component $V_{\rm LDM}$ and δU (empirical shell corrections [55]). The second term reflects the Coulomb interaction, and $V_P$is the nuclear proximity potential. In this paper, different versions of proximity potentials are used, namely Prox-77, Prox-00, Mod Prox-00, Prox-88, and Prox-BW-91. A brief account of these potentials is given below:

Prox-77 is based on the pocket formula of Blocki [18] and is calculated as the product of surface constant, universal function, and mean curvature radius:

Here, the mean curvature radius ($\overline{R}$) is

with

and

The universal function is parameterized as

respectively, for $s_0\le 1.2511$ and $s_0\ge 1.2511$.

The surface energy constant used for this potential is calculated as

Here, N and Z are the total neutrons and protons, respectively, of the considered nuclear system.

In Prox-88 [21], the γ term is modified, and the revised surface energy constant is given by

In this version of the proximity potential, the universal function is obtained from Myers and Swiatecki [19], which is expressed as

The nuclear charge radius is included in Prox-00, which is calculated as

The surface energy constant used for this potential is

For further details of the coefficients, see Refs. [19, 56].

In this version of the potential [20], the nuclear charge radius is slightly different from the one used earlier in Prox-00 and is given by

This proximity potential [21] is expressed as

with

Here, a=0.63 fm, $R_0$$=R_1$$+R_2+0.29$, and $R_i$ is defined as

The surface energy constant used for this potential is

The Coulomb potential [57, 58] for two charge fragments is given by

Here, $Y_\lambda^{(0)}(\theta_i)$ is the spherical harmonic function, and deformations $\beta_{\lambda i}$ (we use only $\beta_{2i}$) are taken from Ref. [54].

The roles of dynamic deformations of cluster and residual nuclei are discussed in [59, 60], where the nuclear shape parametrization depends on several dynamical degrees of freedom. In contrast, in the PCM [10−16], the Schrödinger equation is solved as a function of the mass-asymmetry parameter $\eta=(A1-A2)/(A1+A2)$ to obtain the relative formation probability of the most probable fragments in the exit channel. As the relative probability of all fragments of exit channel is required in the collective clusterization process adopted in the PCM, the use of dynamical deformations makes the task very complex. Therefore, static deformations are used in this analysis.

The stationary Schrödinger equation of motion at a fixed R-value is given as

The mass parameters ($B_{\eta\eta}(\eta)$) are the conventional hydrodynamical masses of Kröger and Scheid [61]. For cluster emission and other ground state decay processes, only the ground state (ν=0) solution is relevant. Therefore, the first turning point is reached with the normalized fractional cluster preformation probability $P_0$ at a fixed $R (= R_a)$ and is calculated as

Instead of calculating the radial Schrödinger equation for R motion, the penetration probability P is determined using the WKB approximation.

This means that tunnelling starts at $R =R_a$ and ends at $R =R_b$ with $V_{Rb}=Q$, and between $P_a$ and $P_b$, the de-excitation probability ($W_i$) is assumed to be equal to unity [62]. Here, $R_a$ = $R_1$ + $R_2 + \Delta R$ is taken as the initial turning point. The relative separation distance $\Delta R$ between two fragments or clusters $A_i$ is assumed to account for the neck formation effects. $\Delta R$ is used as a model parameter that is optimized with reference to available data.

The radius parameters used in Prox-77, Prox-88, and Prox-BW-91 are mass dependent. However, the radii included in Prox-00 and Mod Prox-00 are A and Z dependent. Hence, the role of the Z-dependent radius is also tested for Prox-77, Prox-88, and Prox-BW-91 potentials, which can be calculated through the relation given by [50]

This paper focuses on the ground state decay of $Z=112-120$ nuclear systems using the PCM [10−16]. This work is divided into two subsections: Part A comprises the decay analysis of heavy particle emission. Broadly, heavy cluster radioactivity from Cn, Fl, Lv, Og, and 120 isotopes are investigated by inculcating different proximity potentials, namely Prox-77 [18], Prox-00 [19], Mod Prox-00 [20], Prox-88 [21], and Prox-BW-91 [21] through the hot-deformed fragmentation approach. The ground state deformation effects are included up to $\beta_{2i}$. Note that the radii included in Prox-77, Prox-88, and Prox-BW-91 potentials are mass number (A) dependent. Subsequently, proximity versions are modified by introducing Z-dependent radius parameters of the fragments given by Eq. (25). With the mentioned cases of proximity potentials, the decay half lives are calculated and compared with the estimates of [49]. Furthermore, Part B is designed to understand the SF half-lives of $Z=112-120$ superheavy nuclei. Various proximity potentials are tested by including A and Z dependent radii.

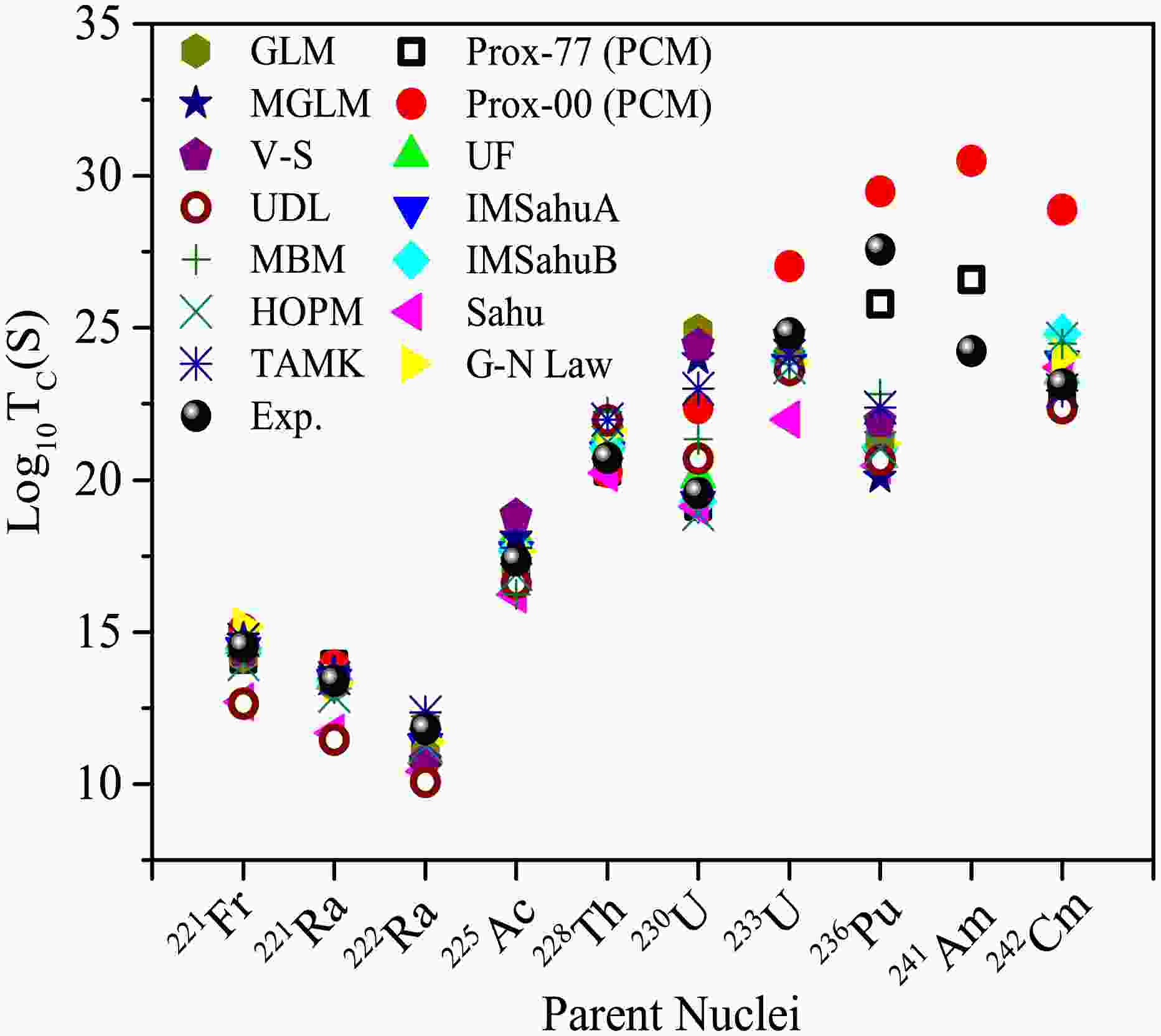
The cluster emission from heavy and superheavy nuclei is explored to understand the ground state nuclear dynamics. In the heavy mass region, particularly for the trans-lead nuclei, clusters such as $^{14}$C, $^{20}$O, $^{24}$Ne,$^{28}$Mg, and $^{34}$Si are emitted corresponding to Pb-daughter nuclei. Figure 1 is plotted to address this for Fr-Cm nuclear systems. Note that the analysis of clusters in this mass region is primarily introduced to analyze the role of Prox-00 and Prox-77 potentials on cluster radioactivity to extend the analysis to address the heavy cluster emission from superheavy mass region. Furthermore, the decay half-lives of C-Si clusters are also addressed in Ref. [15] with various proximity versions using the binding energies of [54]. However, the present cluster analysis is conducted for Audi's experimental binding energies [53]. We clearly observe in Fig. 1 that the PCM calculated half-lives using Prox-77 and Prox-00 potentials agree closely with experimental estimates. The calculations with semi-empirical models [40, 63−67] agree well with PCM based log$_{10}$$T_C$ data.

Figure 1.  (color online) Cluster decay half-lives plotted as a function of parent nuclei in the trans-lead region. PCM based results of the Prox-77 and Prox-00 proximity versions are presented and compared with experimental data and calculations of semi-empirical formulas [40, 63−67].

In the systematic search for nuclear decay modes, the fragmentation profile of $Z=112-120$ nuclear systems is plotted in Fig. 2(a) as a function of light fragment mass ($A_2$). The fragmentation behavior is plotted for $^{282}$Cn, $^{284}$Fl, $^{292}$Lv,$^{294}$Og, and $^{300}$120 even-even nuclear systems for β$_{2i}$-hot deformed approach at best fitted neck-length parameters obtained for Prox-00. Hot orientations are considered at the lowest interaction radius corresponding to highest potential. Fig. 2(a) shows that minima in the fragmentation potential are obtained at SF and heavy cluster regions; hence, they are considered as the prominent decay modes for $Z=112-120$ superheavy nuclei. Another striking observation that this figure shows is for $^{282}$Cn and $^{284}$Fl nuclear systems, the minimum potential is observed in the SF region compared with the heavy cluster emission region. However, as we move towards heavier nuclei i.e.,$^{292}$Lv,$^{294}$Og, and $^{300}$120, the minima in potential is observed in the cluster region. This indicates that as we approach heavier Z-nuclei, the possibility of heavy particle radioactivity increases compared with SF. This observation is in agrement with Refs. [8, 9]. Furthermore, Fig. 2(b) shows the roles of different proximity potentials on the heavy particle emission and SF processes. In this study, $^{284}$Fl nucleus is considered. Interestingly, the emission of the $^{78}$Ge cluster remains intact with the inclusion of different versions of proximity potentials. Moreover, the SF region also remains the same with Prox-77, Prox-00, Mod Prox-00, Prox-88, and Prox-BW-91 potentials.

Figure 2.  (color online) Fragmentation potential plotted as a function of light fragment mass ($A_2$) for $^{282}$Cn, $^{284}$Fl, $^{292}$Lv,$^{294}$Og,$^{300}$120 even-even nuclear systems for the Prox-00 potential. The regions of heavy cluster emission and spontaneous fission (SF) are indicated in the plot. (b) is presented to check the effect of the different proximity potentials on decay path of superheavy nuclei; precisely the fragmentation of $^{284}$Fl is included here.

The discussion of Fig. 2(a) signifies the dominance of heavy cluster emission and SF decay modes. Based on this, the mass distribution is plotted in Fig. 3 to observe the decay trajectories of $Z=112-120$ superheavy nuclei. Note that the figure is presented for the Prox-00 potential. The figures show that the cluster emission is primarily governed through the Pb-nuclei that appears as the complementary fragment. Heavy cluster emission occurs via the binary decay of heavy cluster (HC)+ lead (Pb) fragments. This decay mode is purely associated with the shell effects of Pb nuclei. In contrast, the SF peaks are reinforced via highly deformed fission fragments. For the decay of Lv $(Z=116)$, Og $(Z=118)$, and $Z=120$ nuclear systems, the SF decay is purely observed around asymmetric fragments having a higher value of quadrupole deformations ($\beta_{2i}$), as depicted in Fig. 3(c)−(e). Interestingly, for Cn $(Z=112)$ and Fl $(Z=114)$ superheavy nuclei, SF is mostly observed around the symmetric region (except for the heavier isotopes of Z=114) with octupole deformations ($\beta_{3i}$) $(-0.054-(-0.136)$ for $^{144-148}$Ba and $-0.042-(-0.128)$ for $^{144-148}$La) and quadrupole deformations ($\beta_{2i}$) (see Fig. 3(a)−(b)). Note that the emergence of an SF region is shown at the neck-length parameters of heavy cluster emission for a comparative analysis. However, a complete discussion of the SF process is presented in Section III.B.

Figure 3.  (color online) Preformation probability plotted as a function of fragment mass to investigate the decay modes of (a) Cn, (b) Fl, (c) Lv, (d) Og, and (e) 120 isotopes using the Prox-00 potential. The peaks of Pb-fragments can be clearly visualized. The SF region is also shown in this figure for $Z=112-120$ superheavy nuclear systems.

In the superheavy mass region with $Z \geq 110$, the heavier clusters $Z _e$$> 28$ are observed along with the doubly magic daughter $^{208}$Pb. To analyze the emitted heavy clusters, we plot the fragmentation potential for all the nuclei under consideration, i.e., $^{281-285}$Cn, $^{284-294}$Fl, $^{291-293}$Lv, $^{294-295}$Og, and $^{299-302}$120 in Fig. 4. The figure clearly shows that for $Z=112$ isotopes, Zn clusters are emitted. Precisely, $^{73-74}$Zn are probable emitted clusters from $^{281,282}$Cn nuclei, whereas $^{283,284,285}$Cn systems emit $^{76}$Zn, $^{77}$Zn, and $^{78}$Zn clusters, as shown in Fig. 4. Similarly, $^{78,80-82,84}$Ge clusters are emitted from $^{284-294}$Fl nuclear systems at the fixed values of the neck-length parameters in the range of 1$\pm$0.2 fm, as shown in Fig. 4. Furthermore, selenium ($^{84-85}$Se), krypton ($^{84,86-88}$Kr), and strontium ($^{91-94}$Sr) clusters are expected candidates emitted from $Z=116$ ($^{291-293}$Lv), Z=118 ($^{294-295}$Og), and $Z=120$ ($^{299-302}$120) nuclei, respectively. The emitted clusters obtained from the potential minima correspond with the one as given by Poenaru et al. [49] along with some new clusters such as $^{73}$Zn, $^{78}$Zn, $^{84}$Kr, and $^{88}$Kr.

Figure 4.  (color online) Fragmentation potential plotted for the heavy fragment mass region to analyze the emitted heavy clusters from different isotopes of superheavy nuclei in the charge spectrum of $Z=112-120$.

Next, we attempt to address the heavy cluster decay half-lives (log$_{10}$T_C) of $Z=112-120$ nuclear systems in reference to the ASAF data [49]. The cluster decay half-lives calculated in this work are the half-lives of the most probable emitted cluster that correspond with the ones obtained with the ASAF model. Hence, the Prox-77 [18] potential is used, as it is widely applied to address decay dynamics. The PCM calculated half-lives (log$_{10}$T_C) for different isotopes are plotted in Fig. 5(a). For the Prox-77 potential, the cluster decay half-lives of $Z=112$ and $Z=114$ isotopes are calculated within the estimates of ASAF calculations [49]. However, the decay half-lives cannot be addressed through Prox-77 for $Z \geq 116$. In addition to the mentioned proximity potential, Prox-BW-91 [21], which is based on the Woods-Saxon parametrization concept, is included in the calculations. Prox-BW-91 is the refined version of the Prox-CW-76 potential [56]. Hence, instead of both, Prox-BW-91 is used to investigate the heavy cluster radioactivity. Again, $^{281-285}$112 isotopes exhibit good aggrement with ASAF measurements. However, some isotopes of $Z=114$ ($^{284-288}$114) can be addressed through the BW-91 approach within the fixed range of $\Delta R \sim 0.4-0.5$ fm but not for $Z \geq 116$ nuclei, as shown in Fig. 5(a). Next, Prox-88 [21], a modified version of Prox-77, is included in the calculations. With Prox-88, half-lives are harmonized with ASAF data only for $^{281-285}$112 superheavy nuclei at $\Delta R \sim 1.0$ fm values. Lower magnitudes of half-life values are obtained for $Z=114$ isotopes. Finally, log$_{10}$T_C of $Z \geq 116$ nuclei cannot be achieved within the application of the Prox-88 potential, as shown in Fig. 5(a). Therefore, as the magnitude of the potentials start decreasing from Prox-77, more nuclei begin to deviate from the estimated cluster decay half-lives (see Fig. 5(b)). As lower potentials are not effective, Prox-00 [19] and Mod Prox-00 [20] potentials are used in the calculations as they have larger magnitudes than Prox-77, as plotted in Fig. 5(b). The ASAF half-lives [49] are nicely addressed with Prox-00 and Mod Prox-00 potentials for all cases under consideration.

Figure 5.  (color online) (a) Comparison of the ASAF estimates [49] and PCM calculations of log$_{10}$T_C. The A-dependent radii in different versions of proximity potentials are used to calculate decay half-lives. (b) Variation in the scattering potential V (MeV) as a function of internuclear radius or range R (fm) for the decay of $^{284}$Fl into $^{78}$Ge+$^{206}$Pb reaction with A-dependent radius parameters included for Prox-77, Prox-00, Mod Prox-00, Prox-88, and Prox-BW-91. The inset in Fig. 5(b) represents the scattering potential of Lv, Og and Z = 120 with the inclusion of the Prox-77 potential.

To investigate further, we plot the scattering potential for the $^{284}$Fl$\rightarrow$$^{78}$Ge+$^{206}$Pb reaction in Fig. 5(b) by introducing the aforementioned proximity potentials. Note that $^{282-284}$Cn, $^{284-294}$Fl, $^{292}$Lv,$^{294}$Og, and $^{300-302}$120 even-even nuclei and $^{281-285}$Cn, $^{287-289}$Fl, $^{293}$Lv, $^{295}$Og, and $^{299-301}$120 even-odd nuclear systems are discussed in this analysis, but Fig. 5(b) is plotted only for $^{284}$Fl as the other nuclei have similar scattering behaviors. The figure shows that highest potential is obtained for Prox-00 followed by Mod Prox-00, Prox-77, Prox-BW-91, and Prox-88. Interestingly, for the $Z=114$ nuclear system, the scattering potential is well above the Q-value (shown by the dotted horizontal arrow) for all proximity potentials and hence provide a suitable path for heavy cluster penetration. However, the inset in Fig. 5(b), which is plotted for Z = 116, 118, and 120 nuclei using the Prox-77 potential, shows that the barrier height is significantly lower than the Q-value for cluster emission; hence, tunnelling is not possible. This justifies why the half-lives are not addressed for $Z \geq 116$ using Prox-77. A similar trend occurs for Prox-88 and Prox-BW-91 potentials, which is not addressed here to avoid repetition. To rectify this, we introduce a new set of binging energies prescribed by Wang et al. [68] for two extreme nuclei under consideration, i.e., $^{282}$Cn and $^{302}$120. Interestingly, the same results are observed for both nuclei, as mentioned earlier for Audi's case [53]. Broadly speaking, the half-lives of $Z=112$ can be achieved with Prox-77 potential; however, the $^{302}$120 nuclear system also cannot be addressed through Prox-77 with a new set of binging energies [68]. Similarly, the half-lives for $Z=112$ and $Z=120$ agree well with ASAF measurements for the Prox-00 potential, as shown in Table 1. The table compares the results of the Audi [53] and Wang [68] binding energies at the same neck-length parameters for the Prox-00 potential.Table 1 shows that log$_{10}$$T_c$ calculated for $Z=112$ and $Z=120$ isotopes do not vary significantly with both sets of binding energies. Furthermore, the fragmentation potential for these are shown in Fig. 6, which shows that the structure of the fragmentation potential remains the same with a minor variation in the magnitude. The results in terms of decay half-lives and fragmentation potentials are nearly identical for both binding energies; hence, in the subsequent analysis, Audi's [53] binding energies are used.

Parent	Ref. [53]			Ref. [68]		Ref. [49]ASAF/s
	Q/MeV	Log$_{10}$$T_C$/s		Q/MeV	Log$_{10}$$T_C$s
$^{282}$Cn	244.46	10.15		246.3	9.01	9.29
$^{302}$120	318.1	−5.05		318.4	−5.91	−5.26

Table 1.  PCM calculated log$_{10}$$T_C$ for $^{282}$Cn and $^{302}$120 nuclei using Prox-00 potential using the Audi [53] and Wang [68] binding energies. ASAF calculated half-lives are also given in the table.

Figure 6.  (color online) Comparison of fragmentation potentials using the Audi [53] and Wang [68] binding energies for the decay of (a) $^{302}$120 and (b) $^{282}$Cn parent nuclei.

The radius parameters of Prox-00 and Mod Prox-00 are mass number (A) and neutron excess (N-Z) dependent, as shown by Eqs. (12) and (14), respectively. However, the radii for Prox-77, Prox-88, and Prox- BW-91 are exclusively mass number dependent. As matter density distribution of nucleus differs from proton density, it will be of interest to include the Z-dependent radius (see Eq. (25)) in these proximity potentials. This can be an alternative to addressing the log$_{10}$$T_c$ of $Z \geq 116$ nuclei instead of a new set of binding energies. Figure 7(a) shows the scattering behavior for Prox-77, Prox-88, Prox-00, and Prox-BW-91 with Z-dependent radii. Figure 7(a) clearly shows that the magnitude of the scattering potential is significantly uplifted with the inclusion of Z-dependent radius in Prox-77, Prox-88, and Prox-BW-91 potentials.

Figure 7.  (color online) (a) Variation of scattering potential V (MeV) as a function of internuclear radius or range R (fm) for Z-dependent radii in Prox-77, Prox-88, Prox-BW-91 and Prox-00 potentials. (b) shows the comparison of radius parameter with the use of A-dependent and Z-dependent equations. (c) is plotted to show the variation of the penetration probability for the same channel for Prox-77, Prox-88 and Prox-BW-91 potentials with A and Z dependent radius parameters.

For instance, the barrier height ($V_B$) in Fig. 5(b) for $^{284}$Fl is $\sim$ 271 MeV, which becomes modified to 285 MeV by including the Z-dependent radius in the Prox-77 potential. Similarly, the barrier heights for A-dependent and Z-dependent radius for Prox-88 for the same nuclear system are 267 and 279 MeV, respectively. The $V_B$ for Prox-BW-91 is noted as 292 MeV for Z-dependent radius. The maximum change in the barrier height is measured for Prox-00 potential which is calculated as 311 MeV by replacing the Eq. (12) with exclusive Z-dependent case. It is relevant to mention that Eq. (25) dependent Prox-00 potential is discussed here simply to explore that whether Z-dependent radius parameters work for this case or not. Interestingly, the pocket starts vanishing for this potential. Hence, the clear reason for not including Eq. (25) in Prox-00 is justified to address the dynamics of heavy cluster emission. The same is true for Mod Prox-00 potential. Further Fig. 7(b) is plotted for Prox-77, Prox-88, Prox-BW-91, Prox-00, and Mod Prox-00 radius parameters, alongwith the Z-dependent radius given by Eq. (25). Interestingly, Z-dependant radius parameters are lower in magnitude than mass dependant radii for Prox-77, Prox-88, and Prox-BW-91; however, closer to the one obtained in Prox-00 case. The decrement in radius parameters becomes reason for enhancement in $V_B$ by including Z-dependence in radii and further decrease in the barrier penetrability (see Fig. 7(c)) for the mentioned nuclear system. This figure clearly shows that the penetration probability decreases for Eq. (25) dependent radii. Hence, we observe that the higher barrier height and lower penetration probability are required to address the cluster emission through Z-dependent radius compared with A-dependent radius parameters.

By including the Z-dependent radii in Prox-77, Prox-88 and Prox-BW-91, better results can be visualized in Fig. 8(a) compared with the previous case. The log$_{10}$T_C agrees well with ASAF data for $Z \geq 116$ nuclei, as depicted in the figure. Moreover, the neck-length parameters $(\Delta R)$ are also plotted in Fig. 8(b) for $Z=112-120$ nuclei for Z-dependent radius. It is clearly depicted from the figure that higher neck is required for the Z-dependent radii for calculating the half-lives as compared to A-dependent radius parameters for Prox-77, Prox-88 and Prox-BW-91 proximity potentials.

Figure 8.  (color online) (a) PCM calculated log$_{10}$ $T_C$ (sec) including Z-dependent radius parameters in Prox-77, Prox88 and Prox-BW-91 potentials. (b) Neck-length parameter variation for different proximities using A and Z-dependent radius parameters.

Figure 9 shows the branching ratios of $Z=112-118$ superheavy nuclei. The branching ratio of cluster emission ($b_c$) relative to alpha decay can be calculated as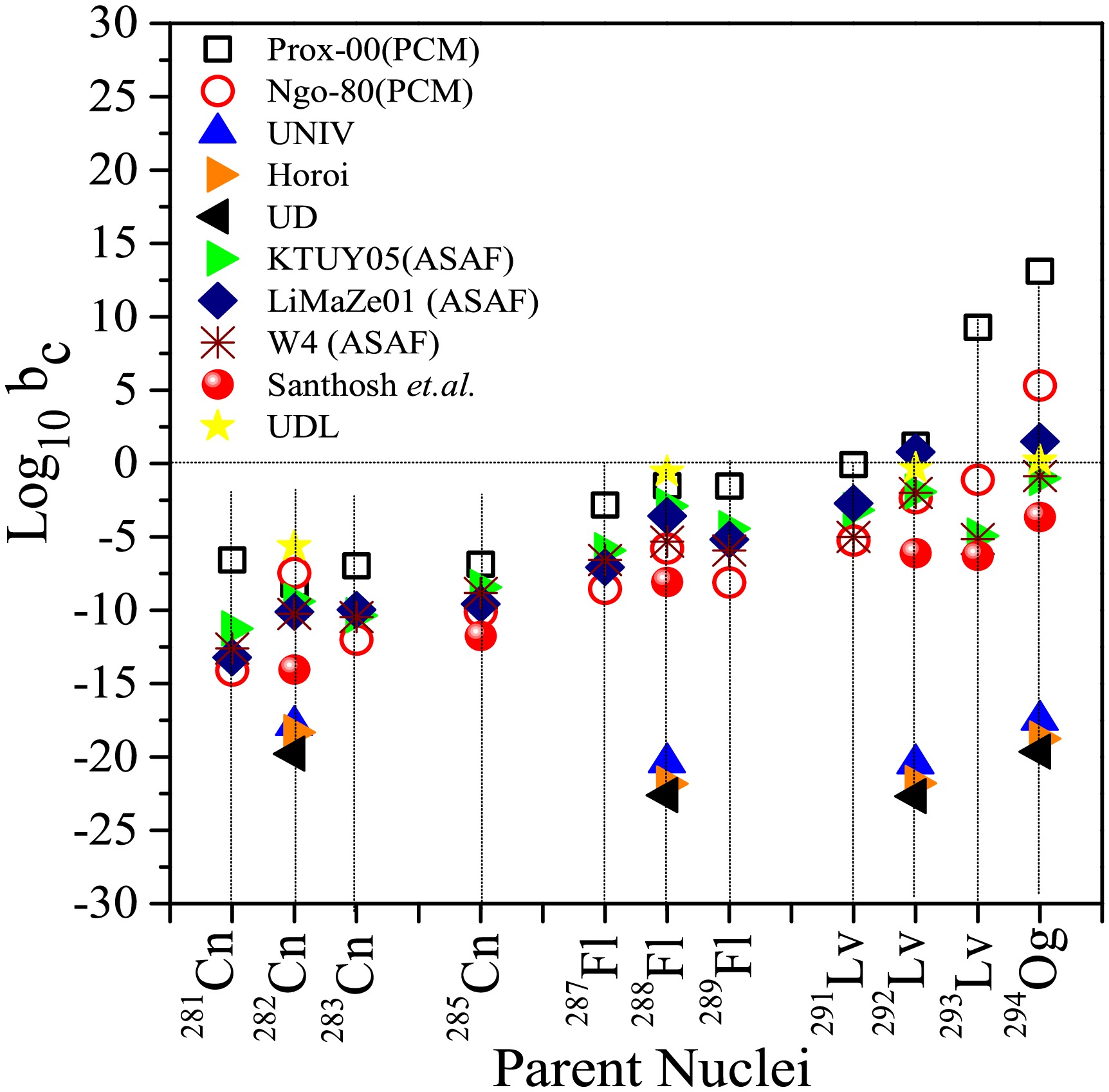

Figure 9.  (color online) Branching ratios calculated using Prox-00 and Prox-Ngô-80 potentials. The results are compared with UNIV [39], Horoi [41], UD [40], UDL [36], ASAF with LiMaZe01 [23], KTUY05 [23], and W4 [49] mass tables. The measurements of Santhosh et al. [48] are also shown in the figure and compared with PCM fitted values.

Note that the branching ratios are calculated only for those nuclear systems for which the experimental α-decay half-lives are available. The selected systems are depicted in Fig. 9. For the calculations of alpha decay, two proximity potentials are introduced, namely Prox-00 and Prox-Ngô-80, with reference to a recent study [69]. The branching ratios agree closely with ASAF measurements (LiMaZe01 [23], KTUY05 [23], and W4 [49] mass tables) and UDL data [36] for the Prox-00 potential for most nuclear systems. However, much higher log$_{10}$$b{_c}$ values are calculated for $^{293}$Lv and $^{294}$Og nuclei. To rectify this, we introduce the Ngô-80 proximity [70]. The branching ratios for extreme nuclei (i.e., $^{293}$Lv and $^{294}$Og) decrease with the Ngô-80 potential and agree well with ASAF and UDL measurements. The log$_{10}$$b_c$ of Santhosh $et~ al.$ [48] is also presented in Fig. 9 and compared with the calculated PCM values. The branching ratios with the Prox-Ngô-80 potential agree closely with Santhosh $et~ al.$'s data. However, lower branching ratios are reported with UNIV estimates [39], UD estimates [40], and the scaling law of Horoi $et~ al.$ [41].

In this section, the SF half-lives of $^{282,284}$Cn and $^{284,286}$Fl even-Z nuclear systems [71] are calculated using different versions of proximity potentials, as in the previous section. Furthermore, the half-live predictions are conducted for $Z=116-120$ isotopes at different neck-length parameters. Note that even-even superheavy nuclei are considered because fission hindrance persists owing to unpaired neutrons or protons in even-odd and odd-odd nuclear systems. First, the results for $^{282}$Cn, $^{284}$Cn, $^{284}$Fl, and $^{286}$Fl nuclei are tabulated in Table 2 with the inclusion of Prox-00, Mod Prox-00, Prox-77 (A, Z), Prox-88 (Z), and Prox-BW-91 (Z) potentials. Here, the half-lives calculated using Prox-88 and Prox-BW-91 with A-dependent radii are not included, which is clarified in Fig. 10(a). The scattering potential in Fig. 10(a) indicates that the barrier height for Prox-88 (A) is lower than the Q-value for the $^{138}$Ce+ $^{146}$Ba decay channel of the $^{284}$Fl nuclear system. Similarly, Prox-BW-91 is not appropriate for addressing the SF of the $^{284}$Fl nucleus as the barrier height approximately matches the Q-value of the decay; hence, fission fragments cannot easily penetrate the barrier. In contrast, other potentials mentioned in Fig. 10 appear to work for SF processes of superheavy nuclear systems. The same is true for $^{282,284}$Cn and $^{286}$Fl nuclear systems. Among the mentioned potentials, the SF half-lives overestimate the experimental data [61] to a much higher extent for Prox-77 (Z) and Prox-BW-91 (Z) potentials. However, reasonably good agreement is obtained with the inclusion of Prox-77 (A), Prox-00, and Mod Prox-00 potentials. Table 2 leads to a fact that Prox-00 and Prox-77 (A) give more appropriate results for $Z=112$ and $Z=114$ superheavy nuclei. However, the aim of this analysis is to select the best version of the proximity potential to address the SF process. Owing to this, Fig. 10(b) indicates that Prox-77 (A) can be applied to $Z \leq 116$ nuclear systems ($^{284}$Fl and $^{282}$Cn) because for higher superheavy systems the Q-value overestimates the barrier height. Hence, Prox-00 is the best proximity to handle SF half-lives for superheavy mass regions.

Nucleus	$T_{\rm SF}^{\rm Expt.}$/ms	Prox-77(A)			Prox-77(Z)			Prox-00			Mod Prox-00			Prox-88 (Z)			Prox-BW-91(Z)
		$\Delta R$/fm	$T_{\rm SF}$/ms		$\Delta R$/fm	$T_{\rm SF}$/ms		$\Delta R$/fm	$T_{{\rm{SF}}}$/ms		$\Delta R$/fm	$T_{\rm SF}$/ms		$\Delta R$/fm	$T_{\rm SF}$/ms		$\Delta R$/fm	$T_{\rm SF}$/ms
$^{282}$Cn	0.91	0.946	0.98		0.959	1.09$\times$10$^{5}$		1.075	1.6		1.110	1.5		1.214	12.9		0.65	3.2$\times$10$^{6}$
$^{284}$Cn	98	0.945	84.8		0.972	1.15$\times$10$^{6}$		1.075	76.9		1.109	29.9		1.220	0.18		0.65	5.1$\times$10$^{8}$
$^{284}$Fl	2.5	0.894	2.06		0.940	1.63$\times$10$^{2}$		1.005	1.6		1.111	11.6		1.173	3.50		0.62	8.38$\times$10$^{5}$
$^{286}$Fl	120	0.950	0.55		0.956	1.9$\times$10$^{5}$		1.035	150		1.074	264		1.197	134		0.62	2.95$\times$10$^{8}$

Table 2.  Comparison of PCM calculated spontaneous decay half-lives ($T_c$) with experimental data [71] for Z = 112 and 114 superheavy nuclei by including Prox-77 (A, Z), Prox-88 (Z), Prox-BW-91 (Z), Prox-00, and Mod Prox-00 proximity potentials.

Figure 10.  (color online) (a) Scattering potential plotted as a function of the interaction range for the fission channel emitted from $^{284}$Fl nuclear system using various versions of proximity potentials. (b) Scattering potentials for $Z=112-116$ superheavy nuclei with the inclusion of the Prox-77 potential.

Thus, Prox-00 is the most probable proximity version that can handle the ground state emission such as heavy particle radioactivity and SF simultaneously. Moreover, the Z-dependence in the proximity potentials are effective only for the heavy particle emission and are not appropriate for addressing the SF half-lives of superheavy nuclei. Owing to this, the SF half-lives are calculated using the Prox-00 potential at different neck-length parameters in the range 1−1.1 fm in Fig. 11 for $^{292}$Lv, $^{294}$Og, and $^{300,302}$120 nuclei, which can provide a testing ground for future experiments on SF. Figure 11 shows that the fission half-lives decrease with increasing neck-length parameters.

Figure 11.  SF half-lives calculated using the Prox-00 potential for $^{292}$Lv $^{294}$Og, $^{300}$120, and $^{302}$120 superheavy nuclei.

Finally, the total kinetic energy (TKE) is calculated for $Z=112-120$ nuclei by introducing Coulomb and proximity potentials at the scission point of the barrier. The Q (value)= TKE+TXE, where TKE is total kinetic energy of the decay fragments, and TXE is the total excitation energy. Because the parent and daughter nuclei are considered in the ground state, Q$\sim$ TKE. Figure 12 shows the calculated TKE and experimental [72] and theoretical estimates of Refs. [73−75]. The PCM calculated TKE magnitudes lie in the range of 320−365 MeV, which are significantly higher than the experimental values. Hence, the formula for calculating TKE values is again revisited and a factor of 0.7 is introduced when calculating the $V_C$ and $V_P$ at the scission point of fission fragments of $^{282}$Cn, $^{284}$Cn, $^{284}$Fl, $^{286}$Fl, $^{292}$Lv, $^{294}$Og, $^{300}$120, and $^{302}$120 nuclear systems. The formula for estimating TKE given by [73] agrees well with experimental TKE data [72]. This formula is developed by introducing the modified version of the Coulomb potential (see Ref. [73]). Hence, the modification of the traditional expression of Coulomb potential to address TKE values is justified. The same argument is considered for the TKE calculation of binary fragmentation in Unik $et~al.$ [74] and Viola [75] systematics. Both fit the experimental data well. Owing to this, the Coulomb and proximity potentials in PCM are modified to attain the experimental TKE values, which are now calculated as ($V_C$+$V_P$)$\times$0.7 to acquire the experimental TKE values. Note that ($V_C$+$V_P$)$\times$0.65 is used for the temperature dependent case, where the emission from the hot and rotating compound nucleus is included [76].

Figure 12.  (color online) PCM calculated TKE values for $Z=112-120$ superheavy nuclei alongwith the formulae given by [73−75]. The estimated values are compared with experimental TKE data [72].

The heavy particle radioactivity and spontaneous fission phenomena are addressed through the PCM for $Z=112-120$ (even-Z) superheavy nuclei. The fragmentation structure reveals that up to $Z=114$, there are higher chances of spontaneous fission, whereas heavy particle radioactivity starts competing for heavier superheavy nuclei ($Z > 114$). Additionally, the preformation structure shows that the heavy clusters are primarily governed through magic shell effects, whereas spontaneous fission is reinforced by the higher order deformations of the decaying fission fragments. The cluster decay half-lives are calculated via Prox-77, Prox-88, Prox-BW-91, Prox-00, and Mod Prox-00 proximity potentials using A-dependant radius. However, the Z-dependent radius parameter is used to determine the corresponding barrier characteristics, potentials, and decay half-lives, and a comparison is made with the A-dependant case. A larger barrier height, neck-length parameter$(\Delta R)$, and lower penetrability are observed for Z-dependent case compared with A-dependent radius parameter used in different proximity potentials. The branching ratios are also calculated through Prox-00 and Prox-Ngô-80 potentials and compared with UNIV, UD, UDL, Horoi, and ASAF measurements. The log$_{10}$($b_c$) values are also compared with Santhosh et al. Good agreement with Prox-Ngô-80 is obtained for $Z=112-118$ superheavy nuclei. Furthermore, the cluster decay and spontaneous fission half-lives of nuclei up to $Z \leq 114$ have reasonable agrement with ASAF data using Prox-77(A). For heavier nuclei ($Z > 114$), Prox-00 (T_C, T_SF), Mod Prox-00 (T_C, T_SF), and Prox-77(Z) (T_C) appear to be better options to address half-lives. Finally, the TKE values are calculated and compared with experimental data.