Sub-barrier fusion cross sections: role of Pauli blocking and isospin asymmetry

The fusion process in the sub-barrier energy region is crucial for numerous interesting issues in both nuclear physics and astrophysics [1, 2]. By clarifying the details of fusion dynamics, our understanding of astrophysical processes such as carbon and oxygen burning may be further improved [3−5]. Fusion reactions also play an important role in the synthesis of new nuclides and superheavy elements [6−8]. Although substantial progress has been made using the cold and hot fusion reactions, the production of heavier elements remains challenging because the fusion process is, generally, strongly blocked by both Coulomb barrier and Pauli repulsion. An example that has received particular attention is the hindrance of fusion far below the Coulomb barrier [9−11], that is, the unexpected falloff in the measured fusion excitation functions of systems such as ${\rm{^{58}Ni+{}^{58}Ni}}$, ${\rm{^{90}Zr+{}^{92}Zr}}$, ${\rm{^{60}Ni+{}^{89}Y}}$, and ${\rm{^{64}Ni+{}^{64}Ni}}$. This has introduced a new challenge in theoretical descriptions and experimental observation [12−14].

Fusion at deep sub-barrier energies provides an effective probe for the internal details of the nucleus-nucleus (NN) potential. Theoretical efforts have been devoted to interpreting fusion hindrance phenomena by refining the internal part of NN interactions. For example, a large diffuseness parameter in the Woods-Saxon form of the NN potential was employed to fit experimental data [15−17], indicating the necessity of refining the inner part of conventional Woods-Saxon parameterization. Similarly, a calibrated repulsive core in the NN potential was proposed in Ref. [18] to simulate the effect of nuclear incompressibility in the inner region, which yielded good agreement between the theory and fusion data. Moreover, the density-constrained time-dependent Hartree-Fock theory was applied to describe the hindrance problem, in which the Pauli energy contribution to the nucleus-nucleus interaction was considered [19, 20]. Recently, inspired by the inverse process of $\alpha$-cluster decay [21−23], a Pauli blocking potential derived from microscopic in-medium wave functions was incorporated into the coupled-channel method to better account for the repulsive core and hindrance phenomena [24, 25]. Both the $\alpha$-induced and $n\alpha$-induced fusion reactions were analyzed in detail, and the shallow ''pocket" in the inner region resulting from Pauli blocking was found to play a non-trivial role in explaining the abrupt decrease in quantum tunneling probability during the fusion process [24−27].

Although many studies have been conducted on hindrance phenomena at extreme sub-barrier energies, the density overlapping process of the projectile-target system and the Pauli blocking involved in the fusion process are not yet fully understood. In addition, there has been a clear experimental observation of the dependence of sub-barrier suppression on the structure of the interacting nuclei [10]. In particular, the nuclear isospin effect is considered to play a role in the Pauli blocking process after two nuclei contact and affect the onset of sub-barrier fusion hindrance [28−31]. A better understanding of the nuclear isospin dependence of the fusion hindrance of very neutron-rich nuclei will be helpful for the synthesis of superheavy nuclei using radioactive beams [32]. In this study, we propose an improved Pauli blocking potential $V_{Pi}^{n\alpha}$ with explicit isospin asymmetries and perform coupled-channel calculations for a number of systems, namely, ${\rm{^{16}O+{}^{72,74}Ge}}$, $^{92} {\rm{Zr}}$, ${\rm{^{142,144}Nd}}$, ${\rm{^{144,148}Sm}}$, $^{208} {\rm{Pb}}$ , $^{12} {\rm{C}}+{ }^{198} {\rm{Pt}}$, and $^{208} {\rm{Pb}}$. A comparison of different isospin asymmetric systems may shed more light on fusion hindrance phenomena and the isospin effect in low-energy nuclear reactions involving exotic nuclei far from the stability line.

The remainder of this paper is organized as follows. In Sec. II, the coupled-channel formalism and double-folding potential are presented, and the construction of the isospin-dependent Pauli blocking potential is explained in detail. In Sec. III, we first present the Pauli potentials in different fusion systems and then compare the calculated total and partial fusion cross sections, astrophysical S factors, and mean square deviation from experimental data. The isospin effect in different fusion systems is also discussed. Finally, Sec. IV presents a summary.

The well-established coupled-channel model has been widely adopted in the calculations of fusion reactions [17, 33−35] and addresses the coupling between nuclear intrinsic motion and the relative motion of the colliding nuclei [1, 12]. By imposing the isocentrifugal approximation, the angular momentum of the relative motion is replaced by the total angular momentum J, and the coupled-channel Schrödinger equations can be written as

where E is the bombarding energy in the center-of-mass frame, $\epsilon_n$ is the excitation energy of the n-th channel, J is the total angular momentum of the fusion system, $u_n(R)$ is the radial wave function of the n-th channel of the fusion system, and $V(R)$ is the total potential, which consists of Coulomb and nuclear interactions, i.e., V(R) = $V_C(R)+V_N(R)$. $V_C(R)$ and $V_N(R)$ are obtained via the double-folding procedure, as discussed in Section II.A. Matrix elements of the coupling Hamiltonian $V_{nm}$ are given by the sum of $V_{nm}^N$ and $V_{nm}^C$, which represent the nuclear and Coulomb components, respectively. The matrix elements are discussed in Section II.B.

The Michigan-3-Yukawa (M3Y) double-folding potential [36] is suitable for the description of fusion cross sections, which incorporates the nucleon distributions of the reacting nuclei [37]. However, the M3Y potential is known to overestimate the experimental fusion cross sections at deep sub-barrier energies. A microscopic Pauli blocking potential obtained by solving the in-medium four-nucleon wave equation [21] can greatly improve the exchange term in the standard M3Y potential. Here, we propose an isospin-dependent Pauli potential $V_{Pi}^{n\alpha}$ based on our previous calculations [25]. The M3Y+Pauli double-folding nucleus-nucleus potential $V_N(R)$ and the Coulomb potential $V_C(R)$ are defined as follows:

where R is the separation of the centers of mass of two reacting nuclei, $|{\boldsymbol{s}}|\; ({\boldsymbol{s}}={\boldsymbol{R}}-{\boldsymbol{r}}_{{\boldsymbol{1}}}+{\boldsymbol{r}}_{{\boldsymbol{2}}})$ is the distance between a nucleon in the target and a nucleon in the projectile, $\rho_{1}$ denotes the nucleon density distribution of the target, i.e., the sum of the proton and neutron densities, $\rho_{2}$ is the nucleon density distribution of the projectile, and $\rho_{1p}$ and $\rho_{2p}$ are the proton density distributions of the two participants. The density-dependent nucleon-nucleon interaction $g(|{\boldsymbol{s}}|)$ follows the form

where the multiplier $F(\rho)$ is given by $F(\rho) = C[1+ \alpha \exp (-\beta \rho)]$ , and the values of the parameters C, $\alpha$ , and $\beta$ are taken from Ref. [38]. We focus on the $n\alpha$ + target fusion systems, namely, the ${\rm{^{12}C}}$ and ${\rm{^{16}O}}$ groups. For the ${\rm{^{12}C}}$ group, the fitted strengths of the Yukawa interactions are ${{c_{1}=9989\;\rm MeV\cdot fm}}$ and ${{c_{2}=3023\rm\; MeV\cdot fm}}$. The fitted strengths ${{c_{1}=2954.5\rm\; MeV\cdot fm}}$ and ${{c_{2}=1554\rm\; MeV\cdot fm}}$ are used for the ${\rm{^{16}O}}$ group. The neutron ${(k=n)}$ and proton ${(k=p)}$ density distributions of the target nuclei are taken in the standard Fermi form [39],

where $C_{k}$ and $a_{k}$ are the half-density radius and diffuseness, respectively, and their values are taken from Ref. [40]. $\rho_{0k}$ is the normalization coefficient. The modified Gaussian form is used for the density distributions of projectiles, where the parameters $\omega$ and $\gamma$ are obtained by fitting the corresponding root-mean-square (rms) radii, and $\rho_{02}$ is determined by integrating the density distribution equivalent to the corresponding mass number [41, 42],

To relate the density distribution of projectile $\rho_{p}$ to that of the $\alpha$ particle $\rho_{\alpha}$, an $\alpha$-cluster distribution function inside the nucleus, $\rho_{c}(r)$, was proposed [25],

in which the distribution of the $\alpha$ particle is described as the widely used Gaussian form

Combining Eqs. (6), (7), and (8) and using the Fourier transform technique, we can obtain the distribution function of $\alpha$ clusters,

in which

From the above discussion, the ${n\alpha}$ Pauli blocking potential can be obtained by utilizing a single folding procedure

where $V_{pi}^{\alpha}$ is the isospin-dependent Pauli blocking potential between the target and a single $\alpha$ particle. For homogeneous systems, the Pauli blocking potential for an $\alpha$ projectile (2n+2p) is microscopically obtained by solving the in-medium Schrödinger equations [21−23]. With the Jacobian momenta ${\boldsymbol{p}}_{1}={\boldsymbol{P}}/4+{\boldsymbol{k}}/2+{\boldsymbol{k}}_{12},\; {\boldsymbol{p}}_{2}={\boldsymbol{P}}/4+{\boldsymbol{k}}/2 -{\boldsymbol{k}}_{12}, \; {\boldsymbol{p}}_{3}= {\boldsymbol{P}}/4-{\boldsymbol{k}}/2+{\boldsymbol{k}}_{34},\;{\boldsymbol{p}}_{4}={\boldsymbol{P}}/4-{\boldsymbol{k}}/2-{\boldsymbol{k_{34}}}$, the in-medium Schrödinger equation is given by

where the centroid of the $\alpha$-cluster is considered to be at rest (P=0) in homogeneous nuclear matter. The effective in-medium interaction ${\tilde V}_4 ({\boldsymbol{k}},{\boldsymbol{k}}_{12},{\boldsymbol{k}}_{34};{\boldsymbol{k}}', {\boldsymbol{k}}'_{12},{\boldsymbol{k}}'_{34};{\boldsymbol{P}})$ contains the external mean field ${\tilde V}_4^{\rm{ext}}$ experienced by the $\alpha$ projectile as well as the intrinsic nucleon-nucleon interaction ${\tilde V}_4^{\rm{intr}}$ modified by Pauli blocking

with the nucleon-nucleon interaction defined as a Gaussian form factor

and the states below the Fermi sphere $k_F=(3 \pi^2 \rho_B/2)^{1/3}$ are blocked out. $\rho_B$ represents the baryon density, defined as $\rho_B=\rho_n+\rho_p$. ${\tilde W}({\boldsymbol{P}})$ is decomposed into ${\tilde W}({\boldsymbol{P}})= {\tilde W}^{\text{ext}}({\boldsymbol{P}})+{\tilde W}^{\text{intr}}({\boldsymbol{P}})$. By performing a variational calculation on the intrinsic part, the in-medium equation can be solved with a Gaussian ansatz,

with $\varphi_{\tau}({\boldsymbol{p}})={\rm{e}}^{-\frac{{\boldsymbol{p}}^2}{2a}} \Theta\left[p-k_{\rm{F}}\right]$. We must evaluate the normalization factor N of the trial function as well as the kinetic and potential energies. For each density $\rho_B$, the minimum of the intrinsic energy ${\tilde W}^{\text{intr}}(\rho_B)$ must be found with the ansatz, and Pauli blocking for an $\alpha$ projectile embedded in the nuclear medium is considered. Thus, the Pauli blocking potential is obtained for homogeneous nuclear matter via

where $E_{\alpha}^{(0)}=-28.3$ MeV is the bound-state energy for $\alpha$ particles in the zero-density limit. Here, a fit formula is given to simulate the result of the microscopic calculation within the variational approach,

For imbalanced systems, it is difficult to perform variational calculations. Recently, we performed microscopic calculations for isospin asymmetric systems [43]. The Pauli blocking potential is reduced for imbalanced systems. In this study, we improve the Pauli blocking potential by including a new term related to the isospin asymmetry of the target, i.e.,

where $\delta(r)$ is the isospin asymmetry defined as $\delta(r)= (\rho_{1n}(r)-\rho_{1p}(r))/(\rho_{1n}(r)+\rho_{1p}(r))$.

Now, we discuss the explicit form of the coupling Hamiltonian for heavy-ion fusion reactions. It has been demonstrated that the low-lying collective excitations of colliding nuclei during fusion have a significant impact on the fusion cross section by modifying the potential between the colliding nuclei, especially at sub-barrier colliding energies [2, 44−46]. The surface vibration of the colliding nuclei, as a type of collective excitation, is considered in our calculation. The Hamiltonian for the coupling of the relative motion to the surface vibration of the nucleus is introduced by considering the change in the nucleus radius in the potential. Taking the target as an example, the change in its radius, considering the deformation during fusion, can be expressed by a dynamical operator $\hat O$,

The surface vibration of the nucleus is approximated by a harmonic oscillator; thus, the dynamical operator is given by

where $\lambda$ and $\beta_{\lambda}$ are the multipolarity of the vibrational mode and the corresponding deformation parameter, respectively, and $a_{\lambda 0}^{\dagger}$ and $a_{\lambda 0}$ denote the creation and annihilation operators of the phonon, respectively. Hence, the matrix element of this operator between the n-phonon state $|n\rangle$ and the m-phonon state $|m\rangle$ is obtained as

By numerically diagonalizing the matrix $\hat O$, $\hat{O}|\alpha\rangle = \lambda_{\alpha}|\alpha\rangle$, where $\lambda_{\alpha}$ and $|\alpha\rangle$ are the eigenvalues and eigenvectors of $\hat O$, the nuclear coupling matrix elements are evaluated as

where $\widetilde{V}_{N}\left(R, \hat{O}_{\lambda}\right) =V_{N}\left(R-\hat{O}_{\lambda}\right)$.

The Coulomb coupling matrix elements $V_{nm}^C$ are calculated using the linear coupling approximation [12],

Again, the total coupling matrix element is determined by adding the values of $V_{nm}^N$ and $V_{nm}^C$. The detailed structure inputs for describing the excitation of low-lying states in fusing partners are listed in Table 1.

${\rm{Nuclei}}$	$\lambda^\pi$	$E_x$/MeV	$\beta_{\lambda}$	References
$^{12} {\rm{C}}$	$2^+$	4.440	0.590	[47]
$^{16} {\rm{O}}$	$3^-$	6.130	0.729	[18]
	$2^+$	6.917	0.349	[18]
$^{28} {\rm{Si}}$	$2^+$	1.779	-0.407	[48]
	$3^-$	6.879	0.401	[48]
$^{30} {\rm{Si}}$	$2^+$	2.235	0.330	[49]
	$3^-$	5.488	0.275	[49]
$^{72} {\rm{Ge}}$	$2^+$	0.834	0.240	[50]
$^{74} {\rm{Ge}}$	$2^+$	0.596	0.285	[50]
$^{92} {\rm{Zr}}$	$2^+$	0.934	0.101	[51]
	$3^-$	2.340	0.174	[51]
$^{100} {\rm{Mo}}$	$2^+$	0.536	0.230	[48]
	$3^-$	1.908	0.220	[48]
$^{142} {\rm{Nd}}$	$2^+$	1.575	0.092	[52]
	$3^-$	2.084	0.127	[52]
$^{144} {\rm{Nd}}$	$2^+$	0.696	0.120	[53]
	$4^+$	1.314	0.060	[53]
$^{144} {\rm{Sm}}$	$2^+$	1.660	0.087	[51]
	$3^-$	1.810	0.151	[51]
$^{148} {\rm{Sm}}$	$2^+$	0.555	0.140	[54]
	$3^-$	1.160	0.190	[54]
$^{198} {\rm{Pt}}$	$2^+$	0.407	0.110	[55]
	$3^-$	1.500	0.100	[55]
$^{208} {\rm{Pb}}$	$3^-$	2.615	0.111	[18]
	$5^-$	3.198	0.059	[18]

Table 1.  Deformation parameters $\beta_{\lambda}$ of vibrational states along with their corresponding excitation energies $E_x$ used in the coupled channel calculations for different nuclei. $\lambda^\pi$ denotes the multipolarity and parity of a state.

The total fusion cross section is obtained by summing the partial fusion cross sections,

in which the penetrability $P_J$ is given by

where $k_{n}\left(R_{\min }\right)$ is the local wave number for the n-th channel at the minimum position of the Coulomb pocket, and $k_{0}$ is that for the entrance channel. In CCFULL, coupled-channel equations are solved by using the incoming wave boundary condition (IWBC) and integrating the equations directly with the modified Numerov method. The transmission coefficient $T_{n}$ of the n-th channel satisfies

where $\chi_{n m}(R)$ is the wave function of the m-th channel obtained from $u_{n}(R)$.

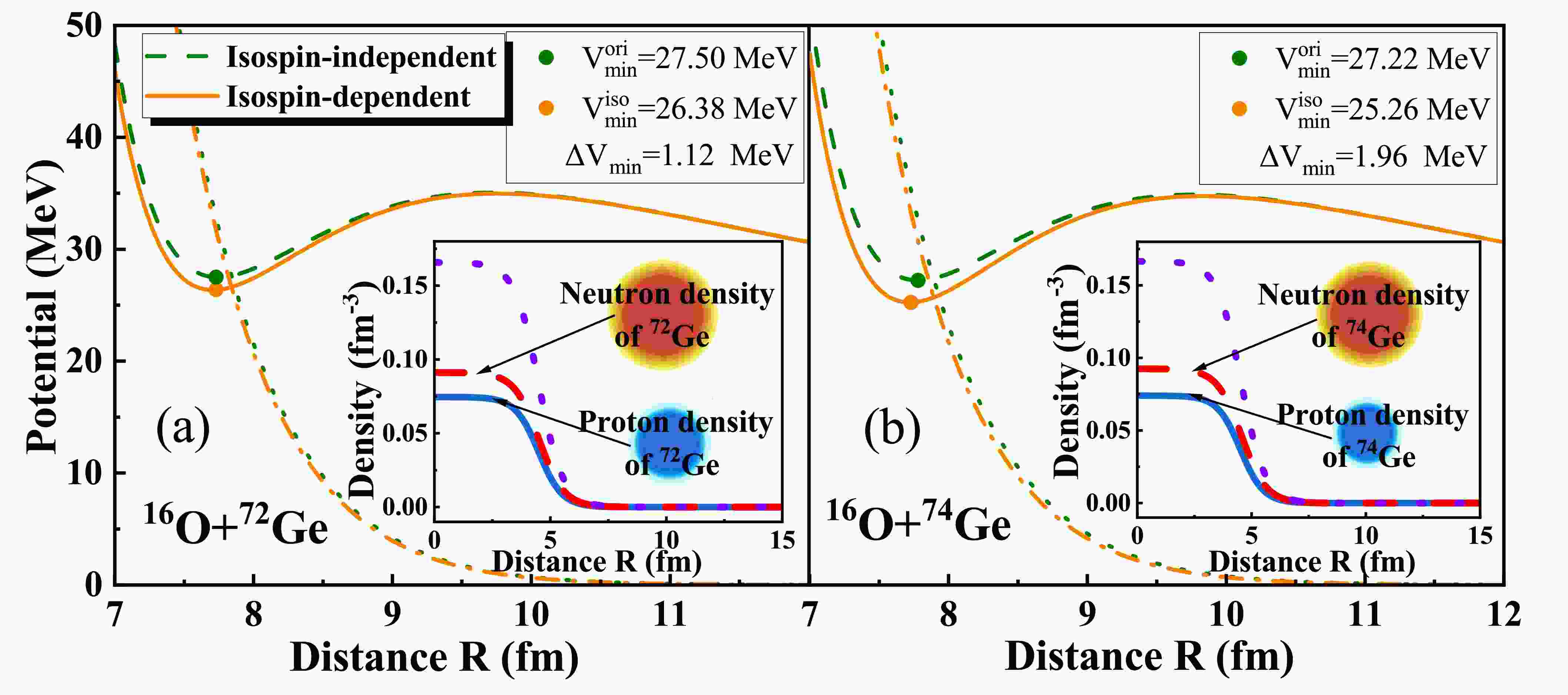
We adopt ${\rm{^{16}O+{}^{72,74}Ge}}$ as a representative example. The nucleus-nucleus potentials calculated with and without the isospin dependent term and the nucleon density distributions of targets are displayed in Fig. 1. For both the fusion systems, the isospin effect leads to lower Pauli blocking potentials and, in turn, deeper pockets and narrower barriers compared with the isospin-independent ones. For the ${\rm{^{16}O+{}^{74}Ge}}$ fusion reaction with larger isospin asymmetry, the variation in the minimum energy of the pocket, $\Delta {V}_{\min }=1.96$ ${\rm{MeV}}$, is larger than that for the ${\rm{^{16}O+{}^{72}Ge}}$ system, $\Delta {V}_{\min }=1.12$ ${\rm{MeV}}$. Note that the Coulomb repulsion of the two systems is identical; hence, the difference between the $\Delta {V}_{\min}$ values mainly originates from the Pauli blocking potential.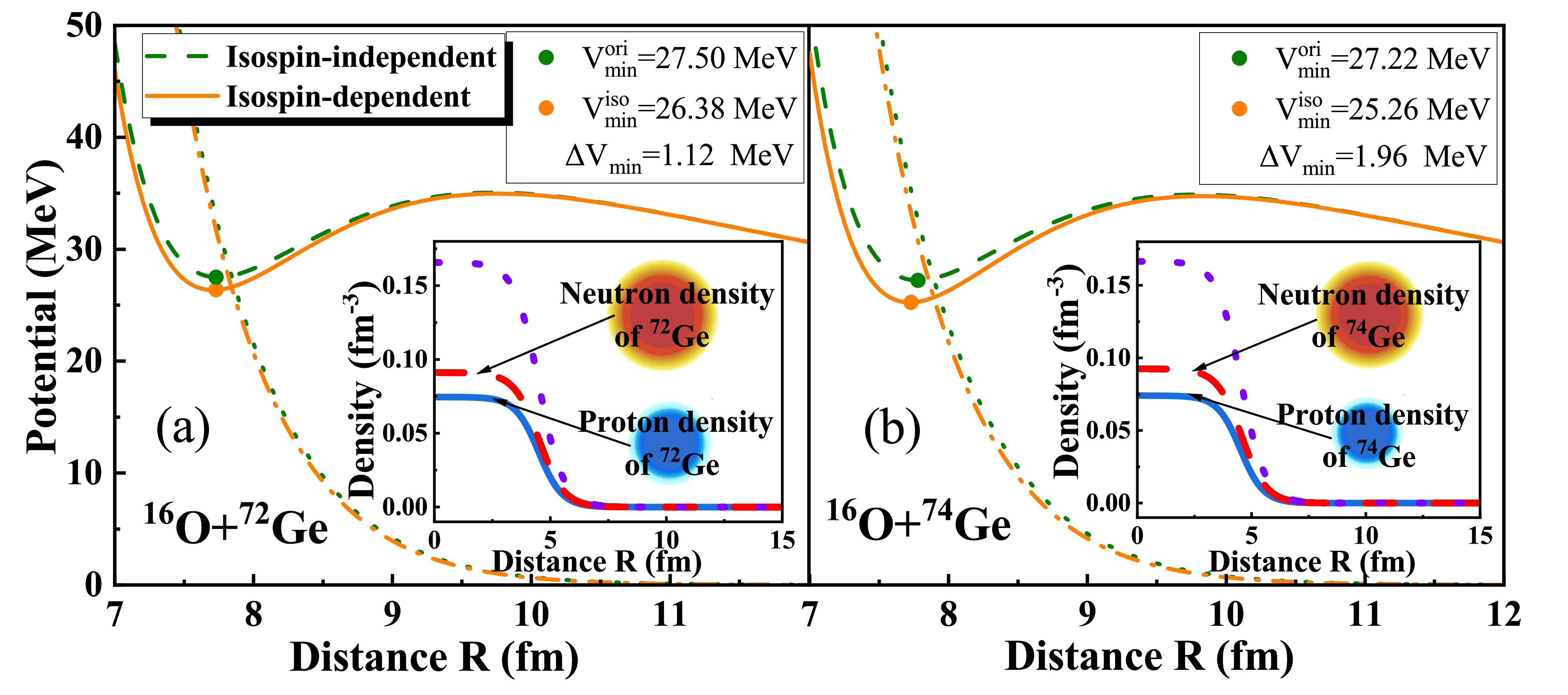

Figure 1.  (color online) (a) Potentials of the fusion reaction ${\rm{^{16}O+{}^{72}Ge}}$ and the nucleon density distributions of the target ${\rm{^{72}Ge}}$. The orange dotted-dashed line represents the Pauli blocking potential, and the orange solid line represents the total potential, calculated by including the isospin effect. The green dotted line represents the Pauli blocking potential, and the green dashed line represents the total potential, calculated without the isospin effect. The nucleon density distributions are shown in the insert, in which the red dashed line denotes the neutron density distribution, the blue solid line denotes the proton density distribution, and the violet dotted line is the sum of the neutron and proton densities of the target. (b) Potentials of the fusion reaction ${\rm{^{16}O+{}^{74}Ge}}$ and the nucleon density distributions of the target ${\rm{^{74}Ge}}$.

A similar phenomenon can also be found in other systems, as shown in Fig. 2. For all the $^{16}{\rm{O}}$ -target systems, $\Delta {{V}}_{\min }$ as a function of the isospin asymmetry of the target $I=(N-Z)/A$ is shown in the insert. The isospin effect is more evident for the target with larger I, and the variation in the minimum pocket energy, $\Delta {{V}}_{\min }$, increases linearly with I. For instance, $^{16} {\rm{O}}+{ }^{208} {\rm{Pb}}$ exhibits the greatest variation in the minimum energy. Note that the barrier penetration probability has an exponential dependence on the barrier properties. A small change in the pocket position by the isospin effect will result in a non-negligible effect on the theoretical fusion cross sections, especially at sub-barrier energies.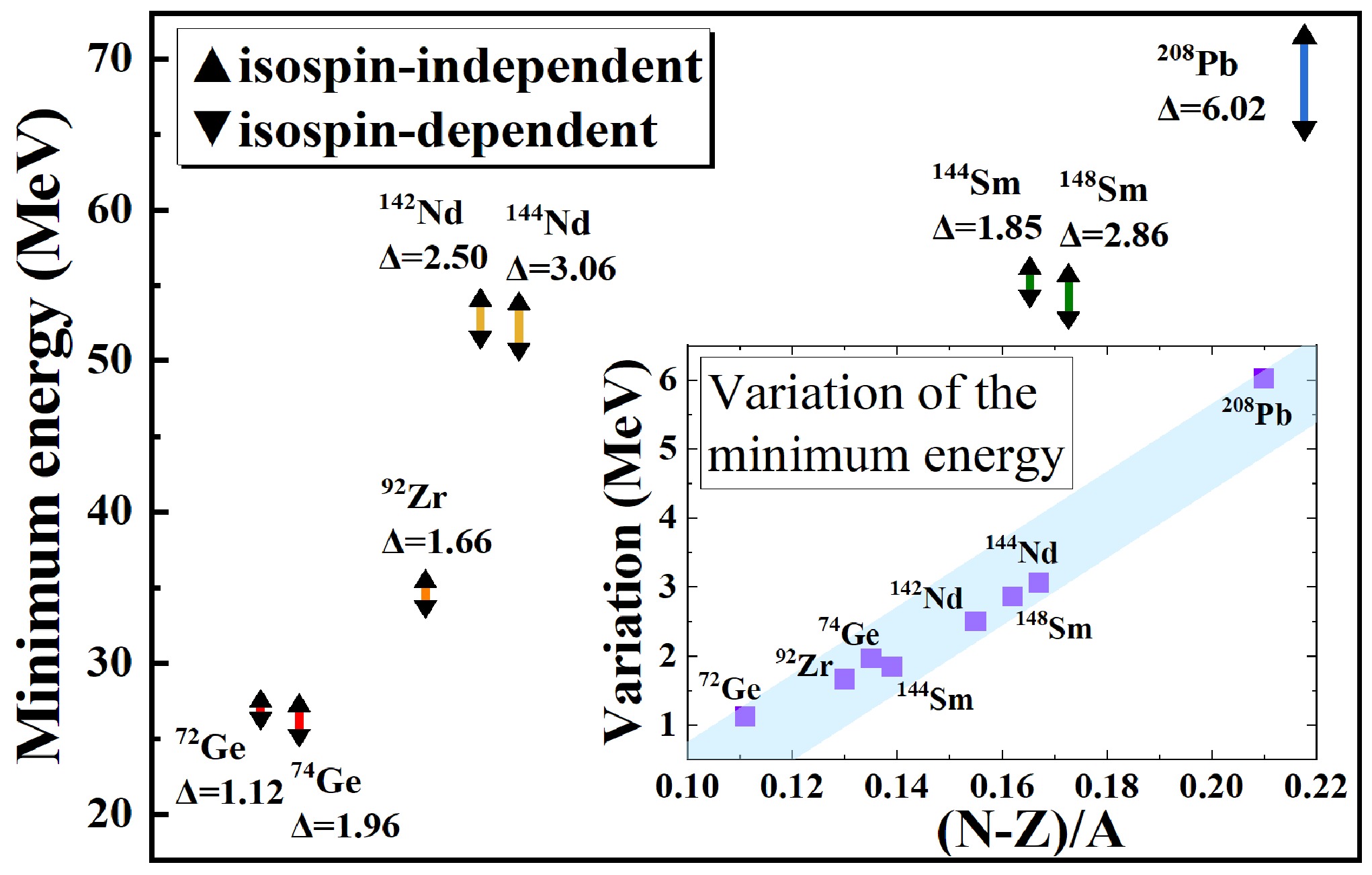

Figure 2.  (color online) Variation in the minimum pocket energy after introducing the isospin-dependent term in the Pauli blocking potential. The triangles and inverted triangles denote the minimum energies of the pockets obtained by the isospin-independent and isospin-dependent Pauli blocking potentials, respectively. For all the calculated ¹⁶O-target systems, $\Delta { {V}}_{\min }$ as a function of the isospin asymmetry of the target, $I=(N-Z)/A$, is shown in the insert.

The fusion excitation functions of the ${\rm{^{16}O+{}^{72,74}Ge}}$ and ${\rm{^{16}O+^{144,148}Sm}}$ systems are shown in Fig. 3, performed by the CCFULL [56]. The experimental fusion cross sections can be effectively reproduced by including the isospin effect in the Pauli blocking potential, whereas the results calculated without this effect underestimate the data at sub-barrier energies, especially for the ${\rm{^{144,148}Sm}}$ targets. At near and above barrier energies, there is no obvious difference between the isospin-dependent and isospin-independent results. This is because at high incident energies, a compound nucleus is assumed to be formed before the two colliding nuclei strongly overlap [57]; thus, the Pauli blocking effect is relatively weaker. As the incident energy decreases toward sub-barrier energies, owing to the large density overlap, the Pauli blocking effect becomes increasingly important, especially for isospin symmetric systems.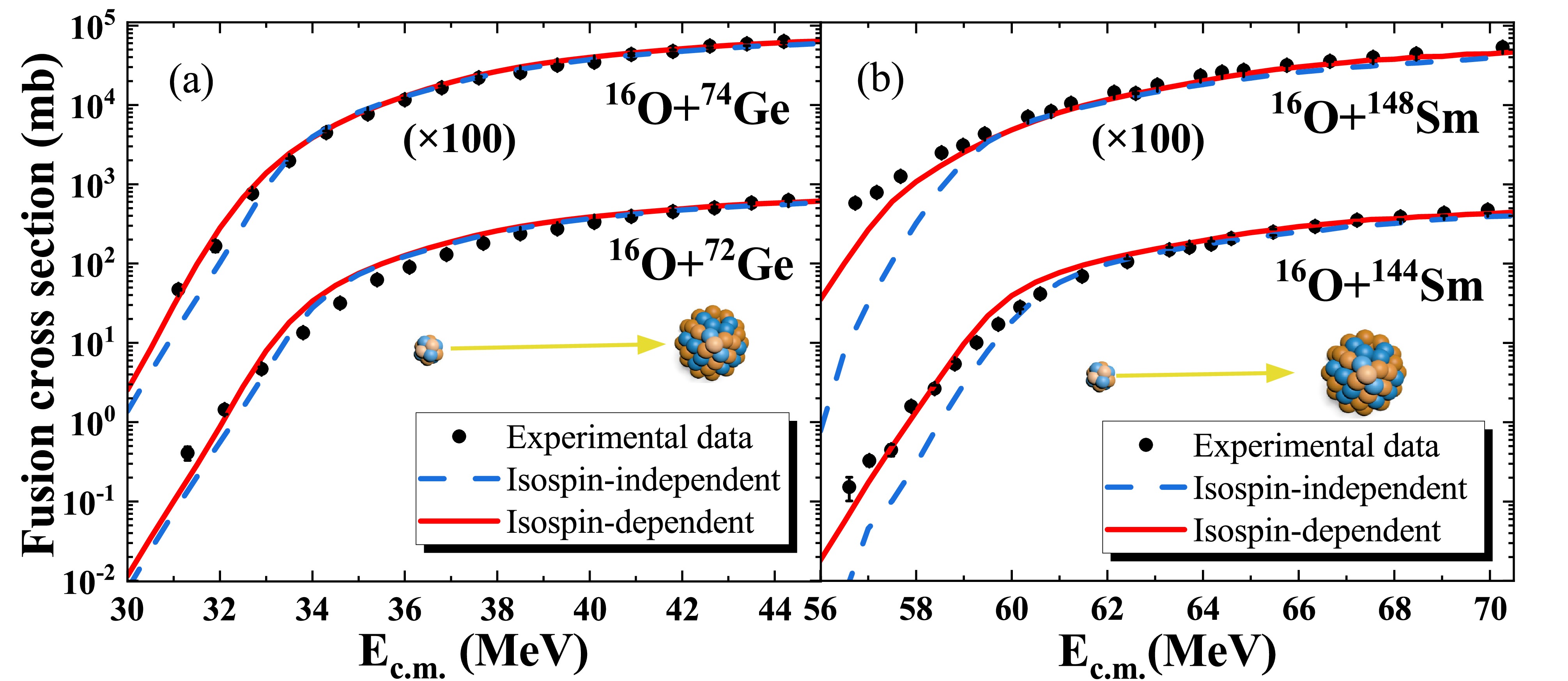

Figure 3.  (color online) (a) Comparison of the fusion cross sections of the $\mathrm{^{16}O+{}^{72}Ge}$ and $\mathrm{^{16}O+{}^{74}Ge}$ systems calculated using isospin-independent (blue dashed lines) and isospin-dependent (red solid lines) Pauli blocking potentials. (b) Comparison of the fusion cross sections of the $\mathrm{^{16}O+{}^{144}Sm}$ and $\mathrm{^{16}O+{}^{148}Sm}$ systems. Note that the results for the $\mathrm{^{16}O+{}^{74}Ge}$ and $\mathrm{^{16}O+{}^{148}Sm}$ reactions have been multiplied by 100. The experimental data are taken from Refs. [54, 58, 59].

Detailed insights into the fusion process can be obtained from the angular momentum dependence of fusion cross sections. Fig. 4 shows the partial fusion cross sections of the reactions ${\rm{^{16}O+{}^{72,74}Ge}}$ calculated at several specified experimental incident energies, namely, 32.1 and 31.3 MeV for the ${\rm{{}^{72}Ge}}$ target and 31.9 and 31.1 MeV for the ${\rm{{}^{74}Ge}}$ target. It is evident that the isospin effect enhances the partial fusion cross sections. For example, the maximum partial fusion cross section at 32.1 MeV for the ${\rm{^{16}O+{}^{72}Ge}}$ system increases from 0.102 to 0.174 mb. Higher angular momentum components with $J>12$ also contribute to the total fusion cross sections after considering the isospin effect.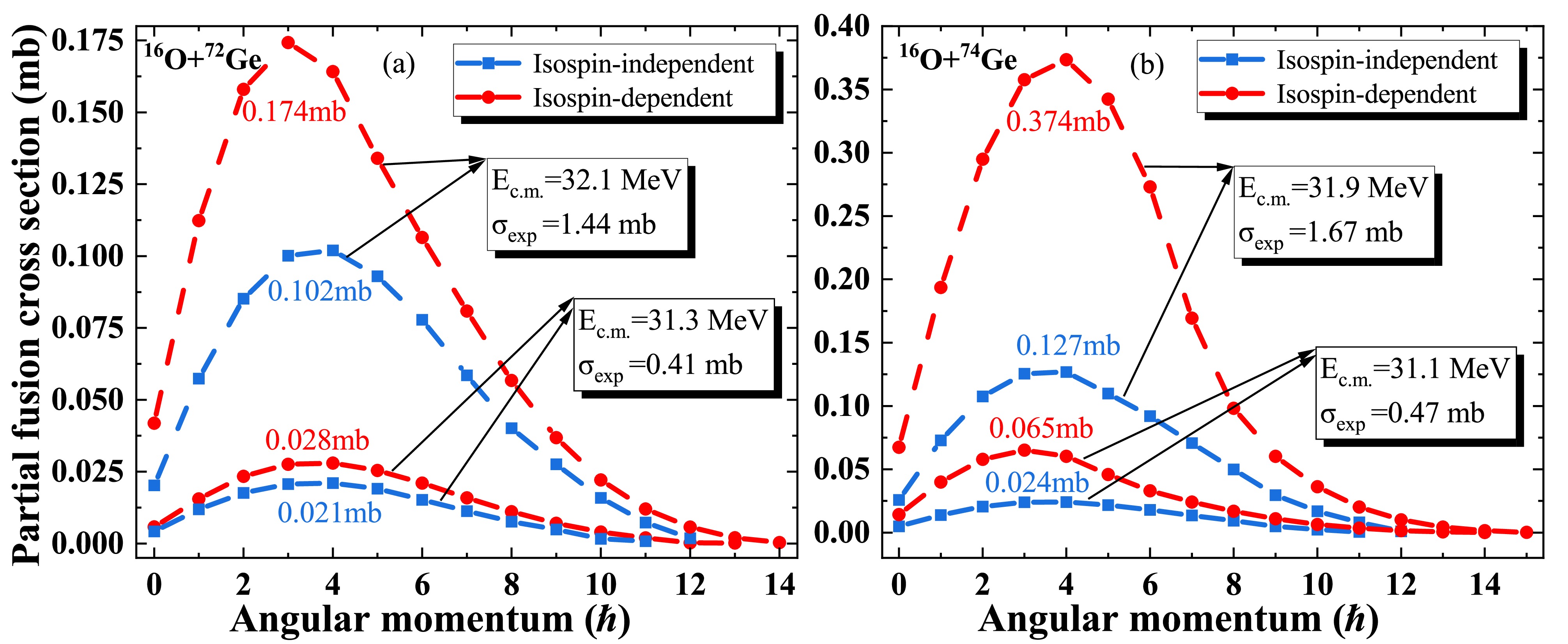

Figure 4.  (color online) (a) Partial fusion cross sections of the ${\rm{^{16}O+{}^{72}Ge}}$ system calculated using isospin-independent (blue lines with squares) and isospin-dependent (red lines with circles) Pauli blocking potentials. (b) Partial fusion cross sections of the ${\rm{^{16}O+{}^{74}Ge}}$ system. The experimental total fusion cross sections at specified sub-barrier energies are given in boxes [58].

To further explore the isospin dependence of Pauli blocking potentials, we calculate the fusion cross sections of more systems, including $^{16} {\rm{O}}+{ }^{92} {\rm{Zr}}$, $^{16} {\rm{O}}+{ }^{208} {\rm{Pb}}$, $^{12} {\rm{C}}+{ }^{198} {\rm{Pt}}$ , and $^{12} {\rm{C}}+{ }^{208} {\rm{Pb}}$. The best-fit global values of the Yukawa interaction strength for the ¹⁶O- and ¹²C-induced reactions and the mean square errors (MSEs) are given in Table 2. The MSEs are used to obtain the goodness of fit for all studied systems.

$\rm{Systems}$	MSE values (isospin-independent)	MSE values (isospin-dependent)	Ref.
$^{16} \mathrm{O}+{ }^{72} \mathrm{Ge}$	0.3649	0.3165	[58]
$^{16} \mathrm{O}+{ }^{74} \mathrm{Ge}$	0.0520	0.0565	[58]
$^{16} \mathrm{O}+{ }^{92} \mathrm{Zr}$	0.2168	0.2428	[60]
$^{16} \mathrm{O}+{ }^{142} \mathrm{Nd}$	0.2739	0.2575	[53]
$^{16} \rm{O}+{ }^{144} \rm{Nd}$	0.8545	0.7659	[61]
$^{16} \rm{O}+{ }^{144} \rm{Sm}$	0.2490	0.2107	[59]
$^{16} \rm{O}+{ }^{148} \rm{Sm}$	0.2843	0.2437	[54]
$^{16} \rm{O}+{ }^{208} \rm{Pb}$	0.8256	0.2983	[62]
$^{12} \rm{C}+{ }^{198} \rm{Pt}$	0.0123	0.0087	[63]
$^{12} \rm{C}+{ }^{208} \rm{Pb}$	0.1443	0.1364	[64]
Total	3.2776	2.5370

Table 2.  Comparison of the mean square errors (MESs) calculated with and without the isospin term. For the $^{16} \mathrm{O}$ group, the best-fit global values of ${c_{1}}$ and ${c_{2}}$ are ${c_{1}=2902{\rm \;MeV \cdot fm}}$ and ${c_{2}=1575{\rm \;MeV \cdot fm}}$ for the isospin-independent case, and ${c_{1}=2954.5{\rm \;MeV \cdot fm}}$ and ${c_{2}=1554{\rm \;MeV \cdot fm}}$ for the isospin-dependent case. For the $^{12} \mathrm{C}$ group, the best-fit values are ${c_{1}=10015.5{\rm \;MeV \cdot fm}}$ and ${c_{2}=3109{\rm \;MeV \cdot fm}}$ for the isospin-independent case, and ${c_{1}=9989{\rm \;MeV \cdot fm}}$ and ${c_{2}=3023{\rm \;MeV \cdot fm}}$ for the isospin-dependent case. The last column lists the corresponding references from which the experimental data are extracted.

where $\sigma_{\rm th}$ and $\sigma_{\rm exp}$ represent the theoretical and experimental total fusion cross sections, respectively, and N is the number of experimental points used for fitting in each fusion system. The values of the MSEs calculated using the isospin-independent and isospin-dependent Pauli blocking potentials are compared in Table 2. The MSE value of the system with the largest isospin asymmetry, $^{16} {\rm{O}}+{ }^{208} {\rm{Pb}}$, improves most obviously among all the calculated fusion systems. The total MSE-values with the isospin term for the $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ groups are found to be smaller than those without the isospin term, indicating that the Pauli potentials "felt" by the target nuclei with larger isospin asymmetries are effectively lower than those with smaller isospin asymmetries.

Recently, an experimental study on the sub-barrier fusion of $^{28} {\rm{Si}}+{ }^{100} {\rm{Mo}}$ observed a tendency of the astrophysical S factor to develop a maximum, which is a clear indication of hindrance [48]. It is noted in Ref. [48] that coupled-channel calculations performed with the best-fit Woods-Saxon potential cannot easily reproduce the flat trend of S at the lowest energy. Interestingly, in the present study, it is found that M3Y+isospin-dependent Pauli blocking essentially improves the data fit. The calculated fusion cross sections of $^{28} {\rm{Si}}+{ }^{100} {\rm{Mo}}$ and the conversion to the S factor are given in Fig. 5 (a). As shown, M3Y+isospin-dependent Pauli blocking yields good agreement with the experimental flat trend of the S factor, especially at deep sub-barrier energies [48]. Similarly, in a lighter fusion system $^{28} {\rm{Si}}+{ }^{30} {\rm{Si}}$, large deviations from the experimental fusion cross sections and the optical model predictions have been observed [65]. By introducing isospin-dependent Pauli blocking, the experimental fusion cross sections and S factors are reproduced relatively well, as shown in Fig. 5 (b). We also predict the maximum of the S factor at 25.10 MeV for the $^{28} {\rm{Si}}+{ }^{30} {\rm{Si}}$ system and 65.44 MeV for the $^{28} {\rm{Si}}+{ }^{100} {\rm{Mo}}$ system, whereas the isospin-independent results predict earlier onsets of hindrance. This could be verified by future precise measurements of fusion cross sections down to deeper energies, which will allow us to locate the hindrance threshold energy.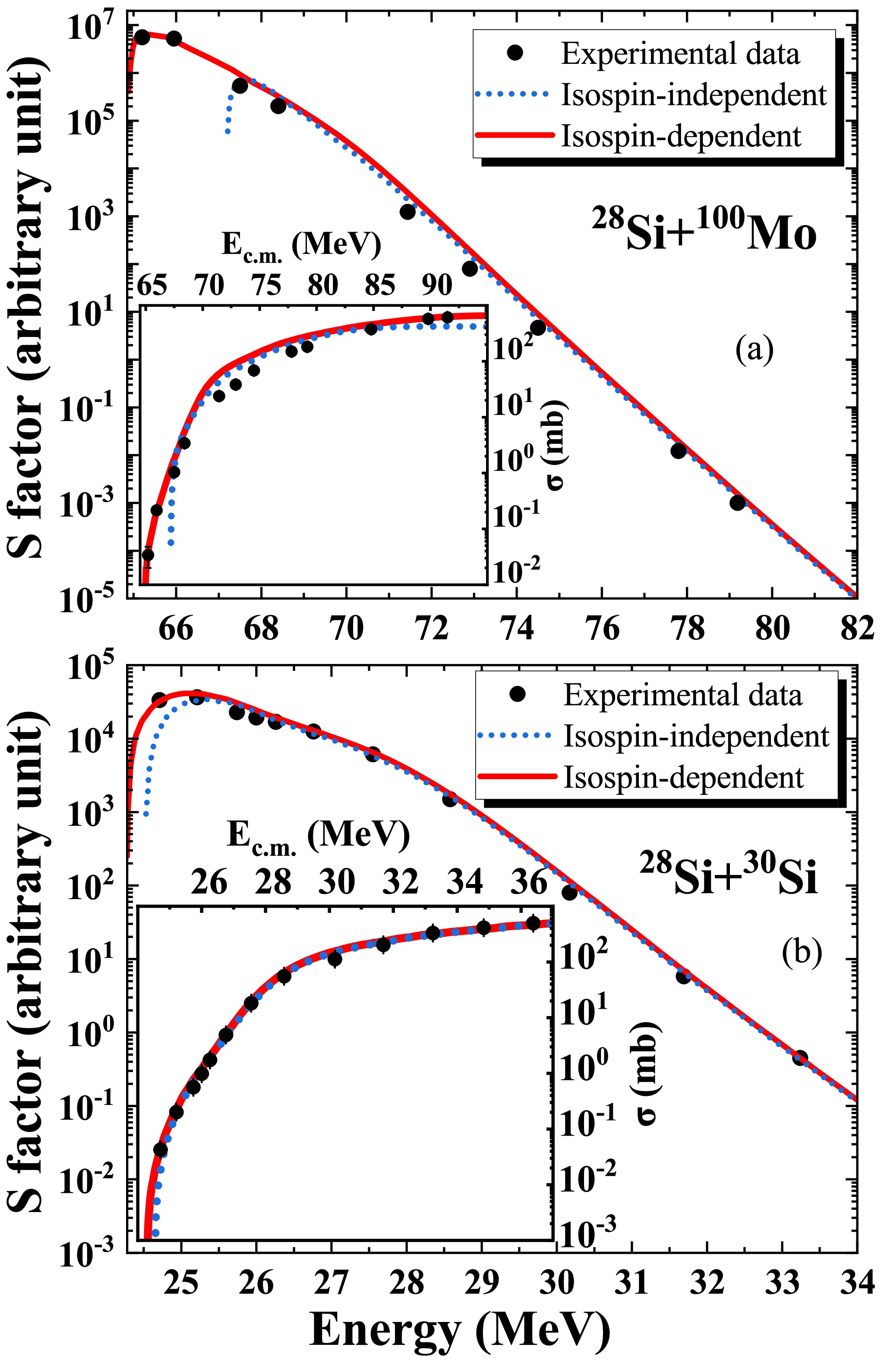

Figure 5.  (color online) (a) Excitation function and astrophysical S factor of the $^{28} {\rm{Si}}+{ }^{100} {\rm{Mo}}$ system. The red solid lines are the isospin-dependent results, which are compared with the isospin-independent results (blue dotted lines). (b) Same as (a), but for the $^{28} {\rm{Si}}+{ }^{30} {\rm{Si}}$ system. The experimental data are taken from Refs. [48, 65].

We investigate the effects of Pauli blocking and isospin asymmetry on the cross sections of fusion reactions, especially at deep sub-barrier energies. The microscopic treatment of the density overlapping process and Pauli blocking of isospin asymmetric fusion systems is difficult and should be tackled by solving complex in-medium equations. In this study, by incorporating the isospin effect, the Pauli blocking effect is found to be significant for isospin symmetric targets and slightly reduced for targets with large isospin asymmetries. For the fusion systems ${\rm{^{16}O+{}^{72,74}Ge}}$, $^{92} {\rm{Zr}}$, ${\rm{^{142,144}Nd}}$, ${\rm{^{144,148}Sm}}$, and $^{208} {\rm{Pb}}$ and the systems $^{12} {\rm{C}}+{ }^{198} {\rm{Pt}}$ and $^{208} {\rm{Pb}}$, the involved potential pockets become deeper and lead to enhanced fusion cross sections compared with the isospin-independent results. The agreement between the calculated fusion cross sections and the experimental data is largely improved by considering the isospin effect. The total MSE is reduced from 3.2776 to 2.5370 for the ¹⁶O-target and ¹²C-target systems. Moreover, the calculated astrophysical S factors agree well with the data for both the $^{28} {\rm{Si}}+{ }^{100} {\rm{Mo}}$ and $^{28} {\rm{Si}}+{ }^{30} {\rm{Si}}$ systems, and the onset of hindrance down to the lower energy region is predicted with isospin-dependent Pauli blocking.