Muon g − 2 with SU(2)_L multiplets

I. INTRODUCTION

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

Even after the discovery of the standard model (SM) Higgs, we must resolve several challenges such as non-zero neutrino masses and a muon anomalous magnetic dipole moment (muon $g-2$) that would indicate the necessity for physics beyond the SM. New results on muon $g-2$ are reported by the E989 collaboration at Fermilab [1, 2]:

Furthermore, the combined results of the previous Brookhaven National Laboratory (BNL) measurement suggests that muon $g-2$ deviates from the SM prediction by 5.1σ [1−23]:

Although results of the hadron vacuum polarization (HVP) estimated by recent lattice calculations [24−26] may weaken the necessity of a new physics effect, Refs. [27−29] ¹ show that the lattice results imply new tensions with the HVP extracted from $e^+ e^-$ data and the global fits to the electroweak precision observables. However, we note that such tensions occur only in the large $q^2$ region, whereas a shift in the $e^+e^-$ hadronic cross section for a momentum transfer below 1 GeV (e.g. from $e^+e^- \to \pi^+ \pi^-$) does not exhibit this problem. In addition, the CMD-3 collaboration [30] released results on the cross section of $e^+ e^- \to \pi^+ \pi^-$ that disagree at the $(2.5-5) \sigma$ level with all previous measurements that weaken the deviation of muon $g-2$. Thus, the origin of the anomaly is controversial, and further experimental/theoretical explorations are required. If muon $g-2$ suggests new physics, we expect new particles and interactions. To explain the sizable muon $g-2$ in a natural manner using Yukawa couplings, ² we would require one-loop contributions with a chiral flip by a heavy fermion mass inside a loop diagram [33−36]. Otherwise, the Yukawa couplings would exceed the perturbation limit, or mediator masses that are too light are required.

A simple method to extend the SM to resolve these problem is the introduction of new fields that are $S U(2)_L$ multiplets [36−48]. For example, neutrino masses can be induced by adding a Higgs triplet with hypercharge 1, which is known as a type-II seesaw mechanism [49−54]. We can also expect that a sizable contribution to muon $g-2$ is obtained by adding a vector-like fermion multiplet in addition to a scalar multiplet in which a chiral flip occurs inside a loop picking up a vector-like fermion mass. Additionally, multiple electric charges of components in large multiplets can enhance the muon $g-2$ value. In addition to explaining the muon $g-2$ anomaly and neutrino masses, large $S U(2)_L$ multiplet fields would induce interesting signatures at collider experiments as they contain multiply-charged particles.

In this paper, we explain the sizable muon $g-2$ via $S U(2)_L$ multiplet fields without any additional symmetries. More concretely, we add an $S U(2)_L$ quartet vector-like fermion ψ with hypercharge $1/2$, one triplet Higgs Δ with hypercharge 1, and one quartet scalar $H_4$ with hypercharge $3/2$. The quartet fermion plays an crucial role in explaining the sizable muon $g-2$ causing the chiral flip in terms of its mass term and through mixing of triplet and quartet bosons. In addition, the neutrino mass matrix is simply induced via a type-II scenario via the Yukawa interactions between the lepton doublet and triplet Higgs field. The choice of the $S U(2)_L$ quartet vector-like fermion ψ is suitable for obtaining Yukawa interactions of $\bar L_L \Delta^\dagger \psi_R$ for muon $g-2$; we can have a similar term with a $S U(2)_L$ doublet vector-like fermion, but we would also have an undesired term of $\bar L_L \psi_L^c$ inducing unnecessary mixing between the SM lepton and vector-like fermion. Subsequently, we require $H_4$ to make the Yukawa term $\bar \psi_L h_4 e_R$ have a chiral flip in the loop diagram inducing muon $g-2$. Additionally, note that we should consider constraints on the vacuum expectation values (VEVs) of $S U(2)_L$ multiplet scalar fields because they deviate the ρ-parameter from 1. After formulating our model, we conduct a numerical analysis and search for the allowed region in our parameter space, and we discuss the collider physics, focusing on productions of multiply-charged particles in the model.

The remainder of this paper is organized as follows. In Sec. II, we introduce our model and formulate the Yukawa and Higgs sectors, oblique ρ parameter, neutral fermion masses including the active neutrino masses, lepton flavor violations (LFVs), and muon $g-2$. In Sec. III, we present a numerical analysis of muon $g-2$ and discuss collider physics. Finally, we provide the summary of our results and the conclusion in Sec. IV.

II. MODEL SETUP AND CONSTRAINTS

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

In this section, we introduce our model. For the fermion sector, we introduce one family of vector-like fermions ψ with $(4,{1/2})$, where each content in parentheses represents the charge assignment of the SM gauge groups ($S U(2)_L, U(1)_Y$). For the scalar sector, we add a triplet scalar field Δ with $(3,1)$, which achieves a type-II seesaw mechanism and a quartet scalar field $H_4$ with $(4,{3/2})$, where the SM-like Higgs field is denoted as H. Here, we express the components of multiplets as

where $\tilde h^0 = \dfrac 1{\sqrt2} (h^0 + v_h + {\rm i} G^0)$, and the triplet can be expressed as $H_3 = ( \delta^{0}, \delta^{+}, \delta^{++})^T$. Neutral components of scalar fields develop VEVs denoted by $\{ \langle H\rangle, \langle \Delta \rangle, \langle H_4 \rangle \} \equiv \{v_h, v_\Delta, v_4 \}/\sqrt2$, which induce the spontaneous electroweak symmetry breaking. All the field contents and their assignments are summarized in Table 1, where the quark sector is exactly the same as in the SM. The renormalizable lepton Yukawa Lagrangian under these symmetries is given by

Table 1

Table 1.  Charge assignments of the our lepton and scalar fields under $S U(2)_L\times U(1)_Y$, where the lower index i is the number of family that runs over $1-3$, all of them are singlets under $S U(3)_C$, and the quark sector is the same as the SM one.

	$L_{L_i}$	$e_{R_i}$	ψ	H	Δ	$H_4$
$S U(2)_L$	${\bf{2}}$	${\bf{1}}$	${\bf{4}}$	${\bf{2}}$	${\bf{3}}$	${\bf{4}}$
$U(1)_Y$	$-\dfrac12$	$-1$	$\dfrac12$	${\dfrac12}$	$1$	$\dfrac32$

DownLoad: CSV

Show Table

hereafter, we implicitly symbolize the gauge invariant contracts of $S U(2)_L$ index in brackets [$\cdots$], indices $(i,j) = 1$-$3$ are the family numbers, and $y_\ell$ is assumed to be diagonal matrix with real parameters without loss of generality. Subsequently, the mass eigenvalues of charged-leptons are defined by $m_\ell = y_\ell v_h/\sqrt2 = {\rm{Diag}}(m_e, m_\mu, m_\tau)$. In our model, the scalar potential is given by

where we omit details of trivial quartet terms with Δ and $H_4$ for simplicity and assume their couplings are small. The non-trivial scalar potential is given by

where $\mu_1$ plays a crucial role in inducing muon $g-2$, as we show later.

Here, we discuss the advantage of selecting a $S U(2)$ quartet for the scalar and fermion. First, we would like to have interaction terms of $\overline{L_L} \Delta^\dagger \psi_R$, $\overline{\psi_L} H_4 e_R$, and $H^\dagger \Delta^\dagger H_4$ to obtain chirality flip enhancement for muon $g-2$ while achiving the neutrino mass via a type-II seesaw. We can generalize the $S U(2)_L$ representation of ψ and $H_4$ to be ${\bf{N}}$ if it satisfies ${\bf{N}} \times {\bf{3}} \times {\bf{2}} \supset {\bf{1}}$ to obtain these terms. The minimal choice is an ${\bf{N}} = 2$ writhing new scalar and fermion as $H_2$ and $\psi'$, but this case induces non-desired terms such as $\overline{L_L} \psi'^c_L$ and $\overline{\psi'^c_R} H_2 e_R$. These terms would induce non-negligible mixing of the SM charged leptons and exotic charged fermions. Thus, we select ${\bf{N}} = {\bf{4}}$ to avoid these unnecessary terms. The choice of a larger multiplet also enhances muon $g-2$ as we have more contributions from components in multiplets. In addition, the choice of ${\bf{N}} = {\bf{4}}$ induces interesting phenomenology at the collider experiments as it provides multiply-charged particles inside a multiplet.

A VEVs of scalar fields and ρ-parameter

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

Non-zero VEVs of scalar fields are obtained by solving the stationary conditions

Here, we explicitly express the first two terms of Eq. (9) as

where we consider them in unitary gauge. Assuming $v_4, v_\Delta \ll v_h$ and small couplings for trivial quartet couplings, we obtain the VEVs approximately as

Thus, small values of $v_\Delta$ and $v_4$ are naturally obtained when mass parameters $\mu_\Delta$ and $\mu_{H_4}$ are larger than the electroweak scale.

The electroweak ρ parameter deviates from unity owing to the nonzero values of $v_\Delta$ and $v_4$ at the tree level as follows:

where the VEVs satisfy the relation $v \equiv \sqrt{v_h^2+v_\Delta^2+v_4^2} \simeq 246$ GeV. Here, we consider the current constraint on parameter ρ; $\rho = 1.00038 \pm 0.00020$ [55]. If we take $v_X \equiv v_\Delta = v_4$, the upper bound of $v_X$ is

when we require ρ to be within the 2σ level. In our analysis, we select $v_\Delta \sim v_4 \sim 1$ GeV for simplicity ³. Note that ther smallness of VEVs of triplet and quartet scalars in the model can be obtained using large values of $\mu_\Delta$ and $\mu_4$, as in Eq. (12). The smallness of VEVs can be maintained as long as these parameters are larger than cubic coupling $\mu_{1,2}$ even under radiative correction. Although higher order radiative correction would affect the VEVs, we can tune these free parameters to make VEVs small in general.

Finally, we briefly discuss the vacuum stability of the scalar potential. In the model, we select scales of $\mu_\Delta$ and $\mu_{H_4}$ that are much larger than the VEVs of scalar fields. Thus, we obtain

and the other second derivatives of the potential are much smaller. This condition will be maintained after diagonalizing mass matrices of scalar bosons, and the original components are approximately mass eigenstates because the off-diagonal components of mass matrices are much smaller than the diagonal components. Thus, the stability of the vacuum can be guaranteed by the positive values of $\mu_\Delta^2$ and $\mu_{H_4}^2$ in the model. Additionally, we assume all the coupling constants associated with quartic terms in the potential to be positive to require the absence of directions in the scalar field space for which the potential is not bounded from below.

B Masses of new particles

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

The scalars and fermions with large $S U(2)_L$ multiplets provide exotic charged particles. The mass terms of $H_4$, Δ, and ψ are approximately given by

where we have ignored contributions from quartet terms in the scalar potential assuming they are sufficiently small. Thus, components in ψ have a degenerate mass $M_\psi$, where a small mass shift appears at the loop level [56], but we ignore it in the following analysis. The triply charged scalar mass is given by $m_{H^{+++}} = \mu_{H_4}$, whereas we have $\delta^\pm-\phi^\pm_4$, $\delta^{\pm\pm}-\phi^{\pm\pm}_4$, and $\delta^0-\phi^0_4$ mixings through the $\mu_1$ term that lead to a sizable muon $g-2$, as we discuss in the following. We express the mass eigenstates and mixings as follows:

where $c_{a},s_{a}$ are the short-hand notations of $\cos a,\sin a$, respectively, with $a\equiv(\alpha,\beta,\gamma)$. The mass eigenvalues and mixing angles are given by

Notice here that we neglect the mixing between the SM Higgs and other neutral scalar bosons by selecting related parameters to be sufficiently small, and we do not discuss experimental constraints related to the SM Higgs boson assuming its couplings are SM like. For example, the mixing between $\delta^0$ and $h^0$ is estimated using $\mu_1 v_4/\mu_\Delta^2$. The mixing angle is approximately $2 \times 10^{-3}$ if $v_\Delta = 1$ GeV, $\mu_1 = \mu_{H_4} = 1.2 M_\psi$, $\mu_\Delta = 0.8 M_\psi$, and $M_\psi = 1$ TeV, which is the maximal angle in our numerical analysis. The mixing angle $2 \times 10^{-3}$ is sufficiently small to satisfy experimental constraints regarding Higgs boson measurement.

C Neutral fermion masses

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

After the spontaneous symmetry breaking, the neutral fermion mass matrix in the basis of $\Psi^0_L\equiv (\nu_L^c, \psi_R,\psi_L^{c})^T$ is given by

where $m_\nu^{(II)}\equiv y_\nu v_\Delta$, $m_D\equiv {y_D v_\Delta}/\sqrt3$, $m_R\equiv {2 g_R v_\Delta}/3$, and $m_L\equiv {2 g_L v_\Delta}/3$. Achieving the block diagonalizing, we determine the active neutrino mass matrix:

The second term in the above equation corresponds to inverse seesaw, but its matrix rank is one. Thus, we simply expect that the neutrino oscillation data are dominantly described by the first term $m_{\nu_{}}^{(II)}$. Notice here that we require the following constraint to achieve $m_{\nu_{}}\approx m_{\nu_{}}^{(II)}$:

It can be obtained by requiring $m_L$ to be small; for example, if $m_D \sim 1$ Gev and $M_\psi = 1$ TeV, we select $m_L \ll 10^{-3}$ GeV. We can make $m_L$ small because $g_L$ is a free parameter. Here, we also assume $m_D$ to be negligibly small compared with $M_\psi$ to evade the mixing between the SM charged-leptons and exotic charged fermions. In this case, no mixing occurs between the active neutrinos and heavier neutral fermions. Thus, the heavier neutral mass eigenvalues diag[$D_1,D_2$] are given by unitary matrix $V_N$ as $D = V_N M_N V_N^T$, where

Here, we assume $m\equiv m_R = m_L$ for simplicity.

The active neutrino mass matrix is diagonalized using $D_\nu = U_{\rm{MNS}} m_\nu U_{\rm{MNS}}^T$, where $U_{\rm{MNS}}$ is the Maki-Nakagawa-Sakata mixing matrix [55]. This suggests that we simply parametrize $y_\nu$ as follows:

Basically, we can achieve neutrino mass and mixing tuning Yukawa couplings $y_{\nu_{ij}}$ that are the same as the type-II seesaw mechanism. Thus, we do not discuss neutrino masses further in this paper.

D Lepton flavor violations (LFVs) and muon $g-2$

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

In our model, LFV processes and muon $g-2$ are induced from Yukawa interactions associated with couplings $\{ y_D,\ f \}$. The relevant terms are explicitly given by

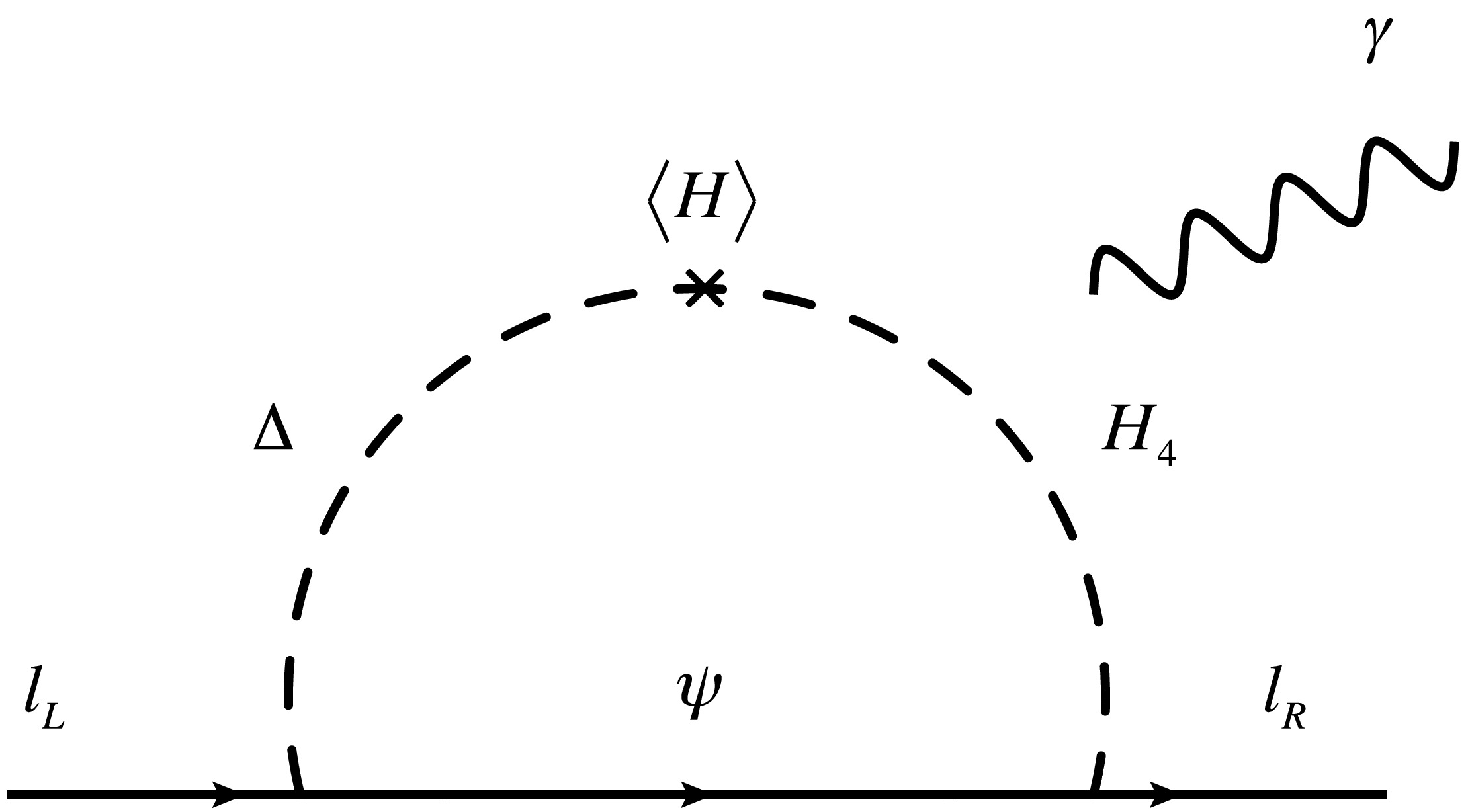
Considering scalar mixing in Eqs. (17)−(19), contributions to $\ell \to \ell' \gamma$ and muon $g-2$ are given by the one-loop diagram in Fig. 1. Branching ratios (BRs) of LFV processes are expressed as follows:

Figure 1

Figure 1.  Feynman diagram to generate muon $g-2$ and $\ell \to \ell' \gamma$ processes.

DownLoad: Full-Size Img PowerPoint

Dominant contributions to amplitudes $a_L$ and $a_R$ are given by

where $a,k$ run over $1,2$. $m_{d_k},m_{c_k},m_{h_k}$ are respectively the mass eigenvalues for singly-charged bosons $H_{1,2}^{\pm}$ in Eq. (17), doubly-charged ones $H_{1,2}^{\pm\pm}$ in Eq. (18), and neutral ones $H_{1,2}^{0}$ in Eq. (19); the loop functions are given by

The current experimental upper bounds on BRs of LFV processes are given by [58, 59]

We impose these constraints in our numerical analysis below. Moreover, note that trilepton decay modes $\mu(\tau) \to \bar eee$ and $\tau \to \{\bar\mu \mu \mu, \bar\mu \mu e, \mu \mu\bar e, \bar\mu e e,\mu\bar e e \}$ can be mediated by doubly charged Higgs via the Yukawa interaction of $\overline{L^c} \Delta L$. However, the corresponding Yukawa coupling in our case is too small to achieve the neutrino mass because we have selected $v_\Delta \sim 1$ GeV. Thus, we can simply neglect these trilepton decays of μ and τ.

Muon $g-2$; $\Delta a_\mu$ results from the same diagram as LFVs, and it is formulated by the following expression:

The recent data informs us thet $\Delta a_\mu = (24.9\pm4.9)\times 10^{-10}$ [1, 2] at the 1σ C.L. Note that $a_{L,R}$ does not have chiral suppression because the vector-like lepton mass $M_\psi$ is picked inside the loop. The simplest method to obtain the sizable muon $g-2$ is to set $f_{1,3} = y_{D_{1,3}} = 0$, taking $f_2$ and $y_{D_2}$ to be of order one. Thus, we need not consider the constraints of LFVs. In the next subsection, we will demonstrate this through a numerical analysis.

Note that one-loop level vertex corrections for $Z \bar{\mu} \mu$ and $h \bar{\mu} \mu$ interactions can be associated with Yukawa coupling $y_{D_2}$ and $f_2$ achieving a sizable muon $g-2$ that modify $Z(h) \to \bar\mu \mu$ decay modes. Typically, we can satisfy experimental constraints when we have chiral enhancement for muon $g-2$. We would have a strong constraint from $Z \to \bar\mu \mu$ if we do not have chirality flip enhancement, and such an enhancement is one advantage of our model.

E RG evolution of gauge couplings

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

Here, we briefly discuss the renormalization group evolution of gauge coupling under the existence of new particles. For illustration, we consider $U(1)_Y$ gauge coupling $g_Y$ and check the scale in which it becomes strong. We determine the energy evolution of $g_Y$, including contributions from $\{ \psi, H_4, \Delta \}$, such that

where μ is a reference energy scale, and we select $m_{in} = m_Z$ and $M = 1$ TeV; $m_{in}$ and M are the initial and threshold mass scales, respectively. Thus, we observe that $g_Y$ becomes $\mathcal{O}(1)$ at approximately $\mu = 10^{32}$ GeV, which is much larger than the Planck scale. The evolution of $S U(2)_L$ gauge coupling does not change significantly, and electroweak gauge couplings do not exhibit strong interaction below the Planck scale in the model.

III. NUMERICAL ANALYSIS AND PHENOMENOLOGY

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

In this section, we perform a numerical analysis using scanning free parameters and explore the region to explain muon $g-2$, considering LFV constraints. Thereafter, we consider collider physics focusing on the production of multiply-charged fermions and scalar bosons.

A Numerical analyses on muon ${\boldsymbol{g-2}}$

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

Now that the formalulations have been presented, we perform a numerical analysis considering LFV constraints and muon $g-2$. First, we randomly select the following input parameters:

where we select $|f_2|$ and $|y_{D_2}|$ to be larger than other Yukawa couplings to obtain a sizable muon $g-2$. Note that splittings of masses of components in the same scalar multiplets are small and we can evade the constraints from oblique parameters [57]. Additionally, we take $\mu_2 = 0$ for simplicity.

Figure 2 represents the values of muon $g-2$ in terms of the mass parameter $M_\psi$, where each point corresponds to one parameter set within the range of Eq. (41) allowed by LFV constraints that satisfy a value of muon $g-2$ in $3 \sigma$. The black dashed line shows the best fit value of muon $g-2$, the blue points are within 1σ, the yellow ones are within 2σ, and the red ones are within 3σ of the experimental value. Thus, we find that $M_\psi \lesssim 15(8.5)$ TeV is preferred for obtaining muon $g-2$ within the $3(1) \sigma$ C.L. in our scenario. In addition, we show branching ratios of LFV processes for the same parameter sets in Fig. 3, where the left and right plots represent ${\rm BR}(\mu \to e \gamma)$ and ${\rm BR}(\tau \to \mu \gamma)$ as functions of Max$[|f_1|, |y_{D_1}|]$ and Max$[|f_3|, |y_{D_3}|]$, respectively, and the colors of the points are the same as in Fig. 2. We find that $|f_{1}|(|y_{D_1}|)$ should be smaller than $\sim 10^{-4}$ to avoid a stringent constraint from ${\rm BR}(\mu \to e \gamma)$, whereas the constraint on $f_3 (y_{D_3})$ is much looser. Here, we omit a plot for ${\rm BR}(\tau \to e \gamma)$ because it is not correlated to muon $g-2$ and it tends to be much smaller than the experimental limit.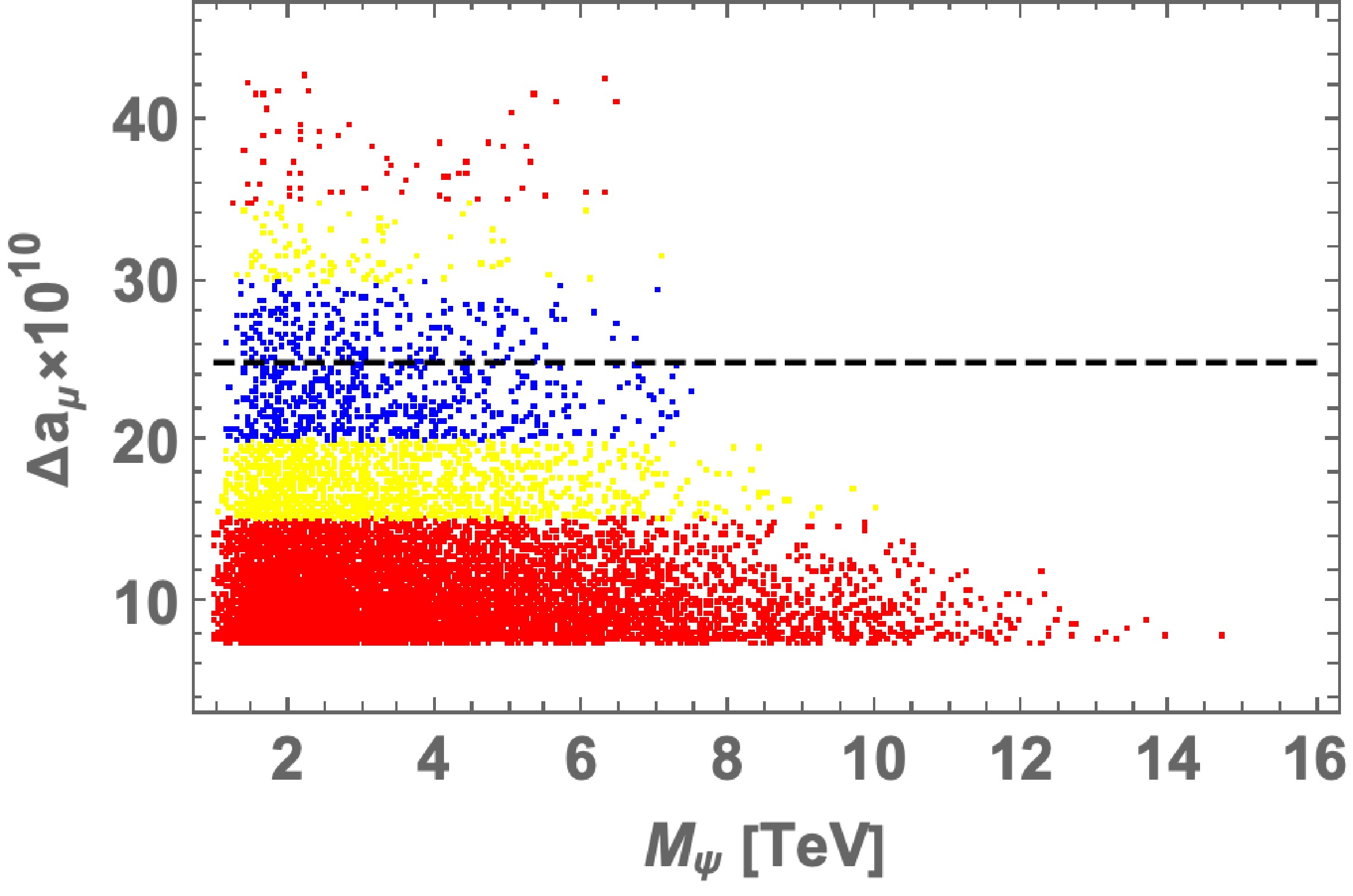

Figure 2

Figure 2.  (color online) Random plot of muon $g-2$ in terms of the mass parameter $M_\psi$ within the range of Eq. (41), where we impose LFV constraints. The black dashed line represents the best fit value of muon $g-2$, the blue points are within 1σ, the yellow ones are within 2σ, and the red ones are within 3σ of the experimental value.

DownLoad: Full-Size Img PowerPoint

Figure 3

Figure 3.  (color online) Left and right plots show ${\rm BR}(\mu \to e \gamma)$ and ${\rm BR}(\tau \to \mu \gamma)$ as functions of Max$[|f_1|, |y_{D_1}|]$ and Max$[|f_3|, |y_{D_3}|]$ for parameter sets satisfying muon $g-2$ within $3 \sigma$; the colors of points are the same as in Fig. 2. The horizontal dashed line indicates the current upper bound of the BRs.

DownLoad: Full-Size Img PowerPoint

Next, we also demonstrate a simple analysis to obtain a sizable muon $g-2$ setting $f_{1,3} = y_{D_{1,3}} = 0$, taking $f_2$ and $y_{D_2}$ to be free parameters. This is because we can enhance muon $g-2$ without inducing LFVs. Figure 4 represents the region achieving muon $g-2$ within the $3 \sigma$ C.L. on the parameter space of the valid Yukawa coupling $y_{D_2}$ and $f_2$, fixing the other input parameters as follows: $M_\psi = \{1, 3, 5\}$ TeV as indicated on the plots, $\mu_{H_4} = 1.2 M_\psi$, $\mu_\Delta = 0.8 M_\psi$, $m = 10$ GeV, and $\mu_1 = \mu_{H_4}$. The black solid curves represent the parameter region providing the best fit value of muon $g-2$. We find that less than order one Yukawa couplings are sufficient to determine the best fit value of muon $g-2$ even when the fermion mass is of the order 3 TeV.

Figure 4

Figure 4.  (color online) Region achieving muon $g-2$ within the 3σ C.L. for $M_\psi = \{1, 3, 5\}$ TeV on $\{y_{D_2}, f_2 \}$ plane, where we select $\mu_1=\mu_{H_4} = 1.2 M_\psi$, $\mu_\Delta = 0.8 M_\psi$, $m = 10$ GeV, and $y_{D_{1,3}} = f_{1,3} =0$. The parameters on the black curve provide the best fit value of muon $g-2$.

DownLoad: Full-Size Img PowerPoint

B Collider physics

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

Here, we briefly discuss the collider signature of the model, focusing on the pair productions of new particles with the highest electrical charge in $H_4$ and ψ. They can be produced via electroweak gauge interactions that are given by

where we omit other terms that are irrelevant in our calculation below. We consider the production processes

in a hadron collider experiment. Here, we estimate the production cross sections using the CalcHEP 3.8 [60] package, implementing the relevant interactions applying the CTEQ6 parton distribution functions (PDFs) [61]. In Fig. 5, the cross sections are shown as functions of exotic charged particle masses for the center of mass energies of $\sqrt{s} = 14, 27$ and 100 TeV as reference values. We find that the $\overline{\psi^{++}} \psi^{++}$ production cross section is larger than that of $H^{+++}H^{---}$ by one order.

Figure 5

Figure 5.  (color online) Cross sections for $pp \to H^{+++}H^{---}$ and $pp \to \psi^{++} \psi^{--}$ with center of mass energies of 14, 27, and 100 TeV.

DownLoad: Full-Size Img PowerPoint

Exotic charged particles can decay via Yukawa couplings in Eq. (7). Here, we assume the relation among mass parameters as $\mu_\Delta < M_\psi < \mu_{H_4}$ for illustration. Thus, the dominant decay modes of $H^{+++}$ and $\psi^{++}$ are $H^{+++} \to \ell^+ \psi^{++}$ and $\psi^{++} \to \nu_\ell \delta^{++}$, respectively, where the decay widths are given by

Note that here we consider $\delta^{++} \simeq H_1^{++}$, assuming a small mixing angle for simplicity. The mixing angle β between doubly charged scalars is estimated using $|\beta| \simeq \Delta M^2_{++}/\mu^2_{H_4} \sim \mu_1 v_h/\mu^2_{H_4}$, and it can be small; $|\beta | < 0.1$ is achieved through $\mu_1 \lesssim \mu_{H_4}/2$ for $\mu_{H_4} = 1.2$ TeV, and the approximation above is reasonable. Note that the branching ratio of these processes are 1 when the mass difference between components in the multiplets is sufficiently small. In addition, $\delta^{++}$ dominantly decays into the $W^+ W^+$ mode considering $v_\Delta \sim \mathcal{O}(1)$ GeV. Thus, the decay chains provide signatures from $H^{+++}H^{---}$ and $\psi^{++} \psi^{-}$ such that

where $\nu (\bar \nu)$ indicates any neutrino (anti-neutrino) flavor. For signals, we consider a pair of the same sign W bosons decays into leptons, whereas a pair of the other same sign decays into jets. The signals at the detectors are

where j and ${\not {E}}_T$ indicate jet and missing transverse momentum, respectively. In Table 2, we provide the expected number of events given by the products of luminosity L, production cross section σ, and BRs for the corresponding final state for some benchmark points (BPs) of $M_\psi (m_{H^{+++}})$ assuming an integrated luminosity of $L = 1$ ab^–1 and $m_{\delta^{++}} < M_\psi$ to enable the decay mode of $\psi^{++} \to \delta^{++} \nu$. Thus, we find that the mass scale of approximately 1 TeV can be explored using $\sqrt{s} = 14$ TeV with sufficient integrated luminosity that will be achieved by the High-Luminosity-LHC experiment. In particular, the signal from $\overline{\psi^{++}} \psi^{++}$ is promising as the cross section is larger than that of $H^{+++} H^{---}$.

Table 2

Table 2.  Expected numbers of events for our signals in some BPs of $M_\psi (m_{H^{+++}}$) with an integrated luminosity of $L = 1$ ab$^{-1}$.

$\sqrt{s}$/TeV	14					27					100
$M_\psi (m_{H^{+++}})$/GeV	1000	1250	1500	1750		1000	1500	2000	2500		2000	3000	4000	6000
$L \cdot \sigma \cdot {\rm BR}$ [Signal 1]	324.	82.	23.	7.		2221.	319.	65.	16.		1954.	373.	103.	14.
$L \cdot \sigma \cdot {\rm BR}$ [Signal 2]	22.	5.	1.	0.		188.	24.	4.	1.		181.	33.	8.	1.

DownLoad: CSV

Show Table

Next, we perform a simple numerical simulation study to examine the possibility of testing our signal at the LHC 14 TeV including the detector effect. For illustration, signal 1 in Eq. (50) is considered because the expected number of events is larger than the other signal. We also fix a doubly charged scalar mass to $m_\delta \equiv m_{\delta^{\pm \pm}} = 500$ GeV and $H^{\pm \pm \pm}$ mass as 2000 GeV for simplicity. The possible SM background (BG) processes for the signal are expressed as follows:

where q indicates any quarks and these processes provides charged leptons, missing transverse momentum, and jets after the decay of gauge bosons. Note that it is more straightforward and even precise to directly generate charged leptons, jets, and missing transverse energy events as BG in the simulation study. However, generating final states containing many particles such as 8 particle states $\ell^\pm \ell^\pm 4j \nu \nu$ is difficult. Thus, we generate the final states in Eq. (52) in our simulation study; note that, in this case, the number of BG events would be slightly underestimated. We estimate the cross sections of these BG processes and find

which are estimated using ${\mathrm{MADGRAPH5}}$ [63]. Subsequently, we perform a numerical simulation to generate events for the signal and BG using ${\mathrm{MADGRAPH5}}$ by implementing the model using FeynRules 2.0 [64]. The events are passed to ${\mathrm{PYTHIA}}$ ${\mathrm{8}}$ [65] to manage hadronization, initial-state radiation (ISR), and final-state radiation (FSR) effects and the decays of SM particles, and we apply ${\mathrm{Delphes}}$ [66] to simulate the detector level. We apply the selection of events at the detector level such that

Here, we consider the minimum number of jets as 3 to avoid reducing signal events significantly.

Fig. 6 shows kinetic distributions for signal and BG events, where we apply integrated luminosity $L = 1$ ab^–1 and consider the $\ell^- \ell^-$ case in the event section Eq. (54) (results for $\ell^+ \ell^+$ are almost the same); the left-hand plot shows the distribution of the transverse momentum of $\ell^-_1$ ($\ell_{1(2)}$ is the charged lepton with the (second) highest transverse momentum), the center plot shows the distribution of the transverse momentum of $\ell^-_2$, and the right-hand plot shows the distribution of the missing transverse momentum. The solid black histogram indicates the signal, whereas the gray filled histogram is for BG events where all BG events are summed. Here, the number of events is estimated as $N_{\rm{event}} = L \sigma N_{\rm{Selected}}/N_{\rm{Generated}}$, where $N_{\rm{Select}}$ is the number of events after the selection, $N_{\rm{Generated}}$ is the number of originally generated events using ${\mathrm{MADEVENT5}}$, σ is a cross section for each process, and L is the integrated luminosity. We find that $P_T(\ell^-)$ and the missing transverse momentum of signal tend to be larger than those of the BG. We also show distributions for invariant masses of the same sign leptons and three jets in Fig. 7, where we consider three jets because we have selected the minimal number of jets as three. We find that the signal distribution of the three-jet invariant mass is centered around the mass of $\delta^{\pm \pm}$ because the jets in the signal events primarily result from the decay chain $\delta^{\pm \pm} \to W^\pm W^\pm \to jjjj$.

Figure 6

Figure 6.  Left: Distribution of transverse momentum of $\ell^-_1$. Center: Distribution of transverse momentum of $\ell^-_2$. Right: Distribution of missing transverse momentum. The solid black histogram indicates signal, and the gray filled histogram is for BG events. Here, $\ell_{1(2)}$ is the charged lepton with the (second) highest transverse momentum. The applied luminosity and masses of new particles are given in the plots.

DownLoad: Full-Size Img PowerPoint

Figure 7

Figure 7.  Left: Distribution of invariant mass of same sign charged lepton. Right: Distribution of invariant mass of three jets. The indication of histograms is the same as Fig. 6.

DownLoad: Full-Size Img PowerPoint

Based on the kinetic distributions, we apply kinematical cuts

where ${\not {E}}_T$ is the missing transverse energy (momentum) that is the same as the missing $p_T$ in Fig. 6. For illustration, we show the number of signal events before and after the cut in Eq. (55) for the $\ell^- \ell^-$ case and estimate the discovery significance using the formula

where $N_S$ and $N_{\rm BG}$ are the number of signal and total BG events, respectively. We find that the kinematical cuts can significantly reduce the number of backgrounds, whereas the number of signal events does not reduce significantly. In particular, we find the cut of missing transverse energy improves signal to background ratio effectively. Subsequently, we can obtain a larger significance S after imposing cuts as shown in Table 3. Finally, in Fig. 8, we show the required integrated luminosity to achieve the discovery significance $S =$ 1, 3, 5, where kinematical cuts Eq. (55) are applied and both $\ell^+ \ell^+$ and $\ell^- \ell^-$ cases are summed. We find that the $M_\psi \lesssim 1060$ GeV region can be in reach of discovery at the high-luminosity LHC with $L = 3000$ fb^–1. We expect that more mass regions explaining muon $g-2$ can be tested if we perform a higher energy experiment like 100 TeV collider in the future [62].

Table 3

Table 3.  Number of events before and after kinematical cuts for the event selection of $\ell^- \ell^- +$jets.

	$N_{\rm signal}$	$N_{ZZZ}$	$N_{ZW^+W^-}$	$N_{ZZW^\pm}$	$N_{4Z}$	$N_{2W^+W^-}$	$N_{ZZW^+W^-}$	$N_{ZZZW^\pm}$	$N_{W^\pm W^\pm qq}$	S
Before cuts	33.4	$7.83$	$13.6$	$53.5$	$0.0819$	$10.3$	$3.02$	$0.313$	$747$	$1.15$
With cuts	15.4	0.001	$0.378$	$0.832$	$0.00234$	$0.458$	$0.192$	$0.00524$	$3.74$	$5.67$

DownLoad: CSV

Show Table

Figure 8

Figure 8.  (color online) Integrated luminosity to achieve the discovery significance $S=1,3,5$ where kinematical cuts Eq. (54) are applied and both $\ell^+ \ell^+$ and $\ell^- \ell^-$ cases are summed. The center of mass energy is $\sqrt{s} = 14$ TeV.

DownLoad: Full-Size Img PowerPoint

IV. SUMMARY AND DISCUSSION

• I. INTRODUCTION
• II. MODEL SETUP AND CONSTRAINTS
•      A VEVs of scalar fields and ρ-parameter
•      B Masses of new particles
•      C Neutral fermion masses
•      D Lepton flavor violations (LFVs) and muon $g-2$
•      E RG evolution of gauge couplings
• III. NUMERICAL ANALYSIS AND PHENOMENOLOGY
•      A Numerical analyses on muon ${\boldsymbol{g-2}}$
•      B Collider physics
• IV. SUMMARY AND DISCUSSION

In this paper, we have proposed a simple extension of the SM without additional symmetry by introducing large $S U(2)_L$ multiplet fields such as a quartet vector-like fermion and quartet and triplet scalar fields. These multiplet fields can induce a sizable muon $g-2$ owing to new Yukawa couplings at the one-loop level, where we do not have chiral suppression by light lepton mass as we select a heavy fermion mass term changing chirality inside a loop diagram. The triplet scalar field can induce neutrino masses after developing its VEV by type-II seesaw mechanism.

We have performed a numerical analysis searching for a parameter space that explains muon $g-2$ and allowed by LFV constraints. We find that muon $g-2$ can be explained when the new multiplets mass scale are less than approximately $\mathcal{O}(10)$ TeV. We also discuss collider physics focusing on the production of multiply-charged fermions/scalars via proton-proton collisions. We have performed a simulation study for $\sqrt{s} = 14$ TeV fixing some parameters for illustration. The signal/background events are generated, and we find relevant kinematical cuts to reduce the background via kinematical distributions. Subsequently, we have investigated the effect of cuts and shown discovery significance after imposing the cuts. A mass scale of 1 TeV can be explored using $\sqrt{s} = 14$ TeV with sufficient integrated luminosity that will be achieved by the High-Luminosity-LHC experiment. Additionally, most of mass region explaining muon $g-2$ can be tested if we achieve a higher energy experiment such as that at the 100 TeV collider.

1The effect in modifying HVP for muon $$\begin{document}$ g-2 $\end{document}$$ and electroweak precision test are also discussed previously in Ref. [31].

2If one explains it via new gauge sector such as $$\begin{document}$ U(1)_{L_\mu-L_\tau} $\end{document}$$ , chiral flip is not needed but narrow region as for the gauge coupling and its mass [32].

3Here we just choose the value around the upper limit from $$\begin{document}$ \rho $\end{document}$$ -parameter. In this case we should require tiny Yukawa coupling ( $$\begin{document}$ y_\nu < 10^{-9} $\end{document}$$ ) for neutrino mass generated by type-II seesaw mechanism. We can get smaller $$\begin{document}$ v_\Delta $\end{document}$$ by adjusting the parameters in the scalar potential.

References