Coexistence and band mixing in ^114,116Cd

Nuclear structure studies involving band mixing at low energies have attracted significant interest from both experimental and theoretical perspectives [1−11]. Among the most successful approaches is the simple two-state mixing model [12−14]. Other widely used approaches include phenomenological models and the Interacting Boson Model (IBM), which provide strong evidence for band mixing involving multi-particle-hole excitations [15−23]. Band mixing configurations can be associated with shape coexistence phenomena resulting from multi-particle-hole (np-nh) excitations, which effectively describe vibrational (normal) and rotational (intruder) states near closed-shell nuclei, particularly those around proton numbers $ Z \sim 50 $ and $ Z \sim 82 $ [20, 21]. Consequently, numerous configurations with nearly identical excitation energies can coexist [24, 25]. This proximity in energy levels leads to strong mixing between the lowest-lying vibrational and rotational states, complicating the assignment of specific configuration labels. Recent studies have further explored configuration mixing in the rotational and vibrational limits [16, 17]. Fortune et al. have described the band mixing between the ground and excited states of $ K = 0 $ and/or $ K = 2 $ bands in even-even nuclei [12−14, 19], highlighting the intricate interplay between these states.

Considerable attention has been dedicated to the study of Cd isotopes, as demonstrated by a substantial body of literature [10, 11, 26, 27]. Recently, several manuscripts have provided comprehensive summaries of the properties of normal and intruder states in these isotopes [20]. An earlier study by Deleze et al. [28] investigated mixed ground-state and intruder bands in ¹¹⁴Cd using neutron capture and ¹¹⁰Pd$ (\alpha, 2n) $ reaction spectroscopy. Their findings identified regular configurations for transitions such as $ 2^+_1 \rightarrow 0^+_1 $ and $ 2^+_2 \rightarrow 0^+_{1,2} $ and intruder configurations for transitions such as $ 0^+_2 \rightarrow 2^+_1 $ and $ 2^+_3 \rightarrow 0^+_{1,2} $. An intruder band built on the 1380-keV level of ¹¹⁶Cd was identified by Juutinen et al. [29]. Additionally, Kadi et al. studied multiphonon quadrupole vibrational states and intruder structures in ¹¹⁶Cd using the $ (n, n' \gamma) $ reaction [30]. Their experiments revealed that the band mixing in ¹¹⁶Cd is weaker than that in lighter Cd isotopes. The study also highlighted challenges in explaining the decay behavior of the lowest excited states in ¹¹⁶Cd owing to the complex interplay between intruder structures and multiphonon vibrational excitations.

Band mixing phenomena are prominently observed in Cd isotopes, particularly between the three-phonon levels and intruder bands, as detailed by Garrett et al. [8]. In ¹¹⁴Cd, the intruder excitations, notably the $ 2^+ $ states (2048-keV level), are considered candidates for three-phonon states and exhibit significant mixing with vibrational states, as indicated by their decay properties and energy levels. In contrast, the mixing scenario in ¹¹⁶Cd differs, as the $ 4^+ $ and $ 2^+ $ levels do not exhibit as strong a degree of mixing as observed in ¹¹⁴Cd. These studies have significantly enhanced our understanding of band mixing behavior in Cd isotopes.

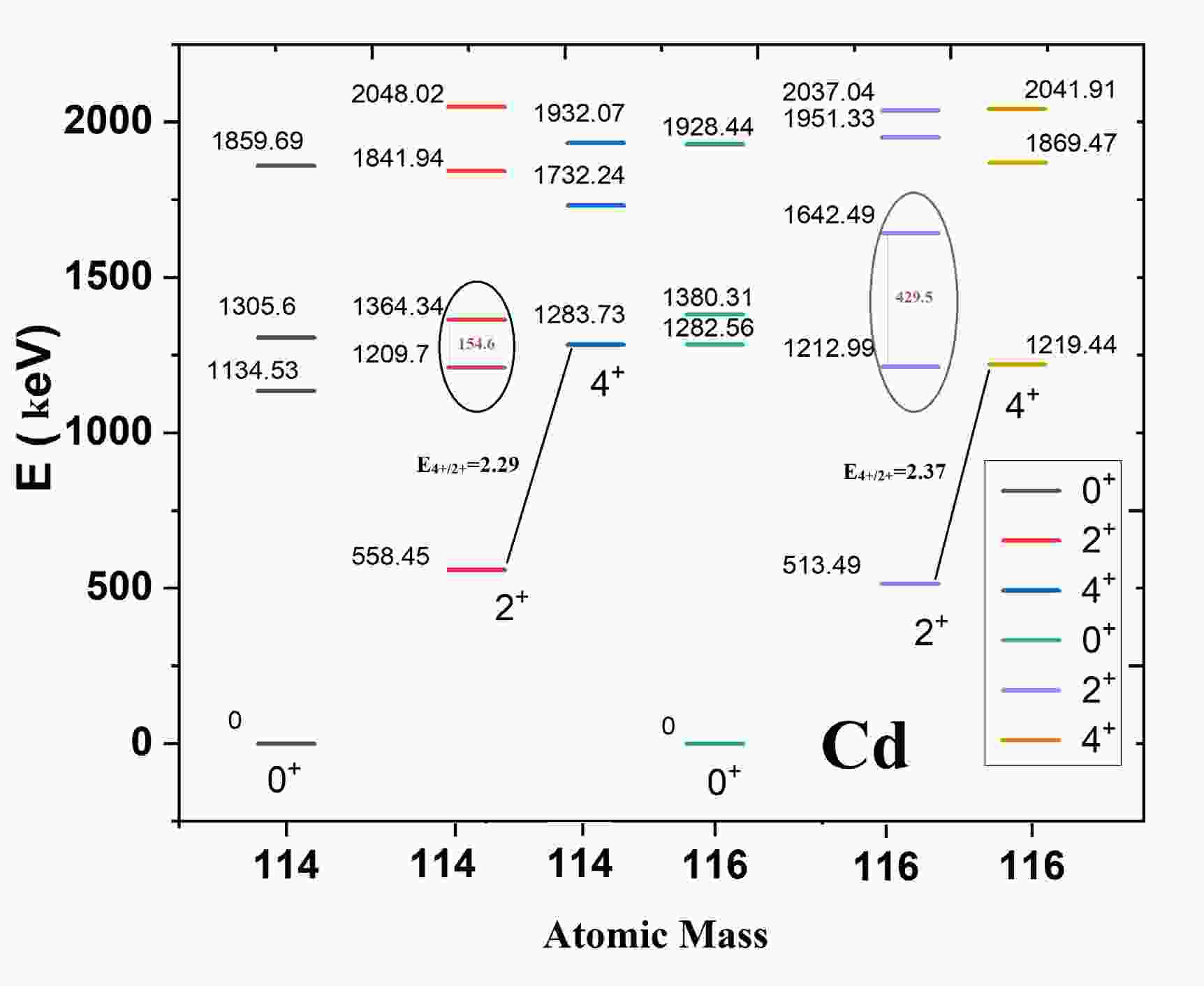
Nuclei such as Cd isotopes, located near the $ Z = 50 $ closed proton shell or near the middle of the $ N = 50-82 $ major neutron shell, exhibit strong collective behavior [8]. In this section, I illustrate this collectivity. The ground states of ¹¹⁴Cd and ¹¹⁶Cd share vibrational characteristics, whereas their excited states exhibit differences owing to the presence of intruder states with deformed rotational characteristics, as shown in Fig. 1. The small energy differences between states may indicate strong mixing within the intruder configurations, as highlighted in the figure, a topic that will be revisited later. For pure vibrational states, the ratio $ E(4^+_1)/E(2^+_1) $ is expected to be 2.0. However, in ¹¹⁴Cd and ¹¹⁶Cd, this ratio deviates, with values of approximately 2.29 and 2.37, respectively, suggesting deviations from purely vibrational behavior. Similarly, the ratios of the rotational state energies $ E(0^+_{{\rm{rot}}}) $ to the ground $ 2^+ $ state are 2.03 for ¹¹⁴Cd and 2.49 for ¹¹⁶Cd, further emphasizing the differences in their collective behaviors and the influence of band mixing.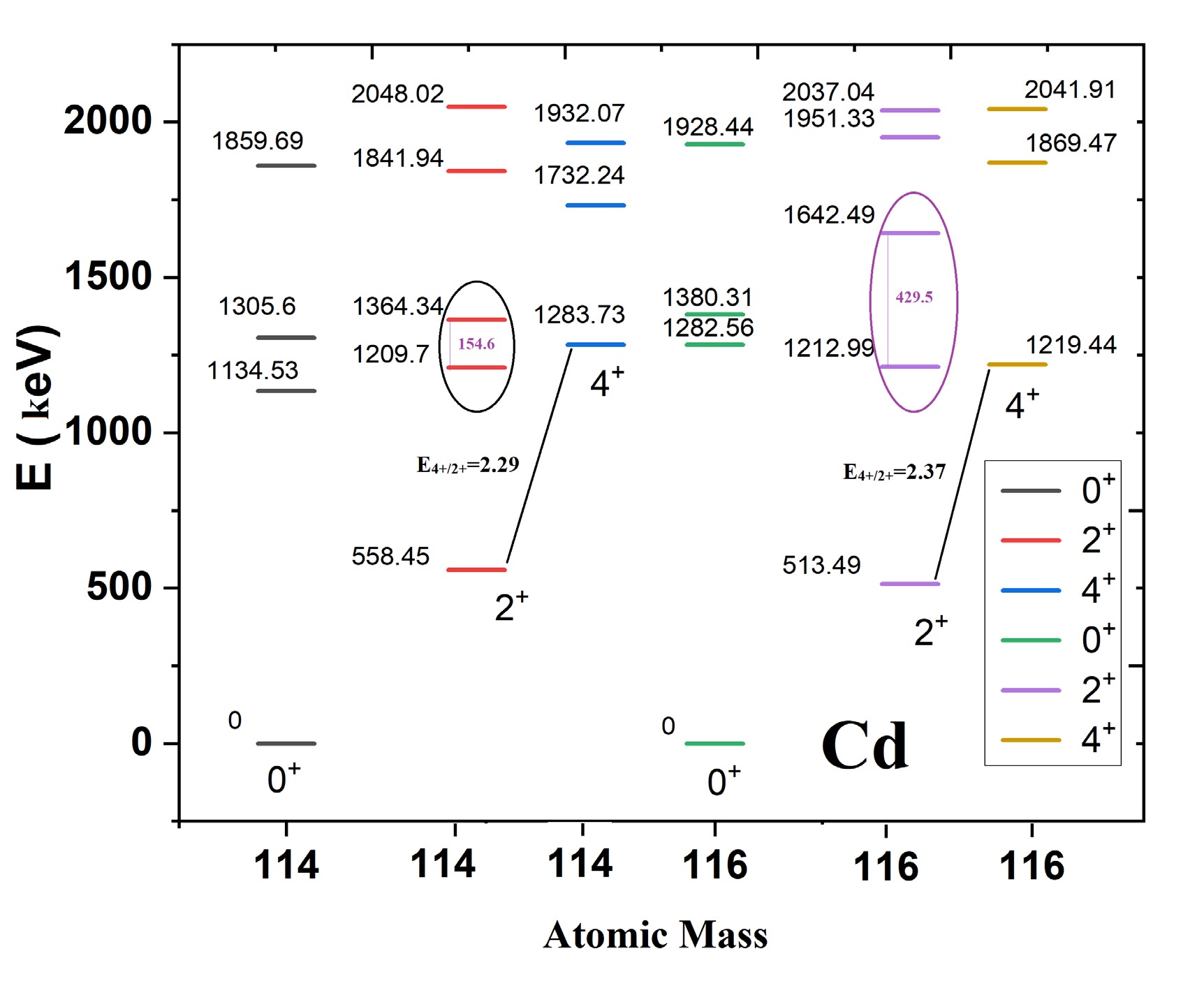

Figure 1.  (color online) Similarity and differences in ground states with vibrational characteristics and excited rotational bands. Exp data are taken from [31].

The irregularities observed in the energy systematics of nuclear states for ^106-122Cd isotopes indicate a decrease in collectivity within the ground-state band as the spin increases, resulting in heightened sensitivity to subtle variations in the wave function [30]. These variations are likely influenced by sub-shell effects or are indicative of underlying mixing mechanisms, as reported by Garrett et al. [8]. The rotational states exhibit a dependence on $ J(J+1) $ with a linear pattern, as depicted in Fig. 2. This pattern suggests that mixing is more pronounced in excited bands rather than in ground bands. The validity of this claim will be demonstrated using the simple two-state mixing model in the following section. Additionally, the linear nature of Band 3 in rotational states, observed in both ¹¹⁴Cd and ¹¹⁶Cd, will be further explored to understand its implications.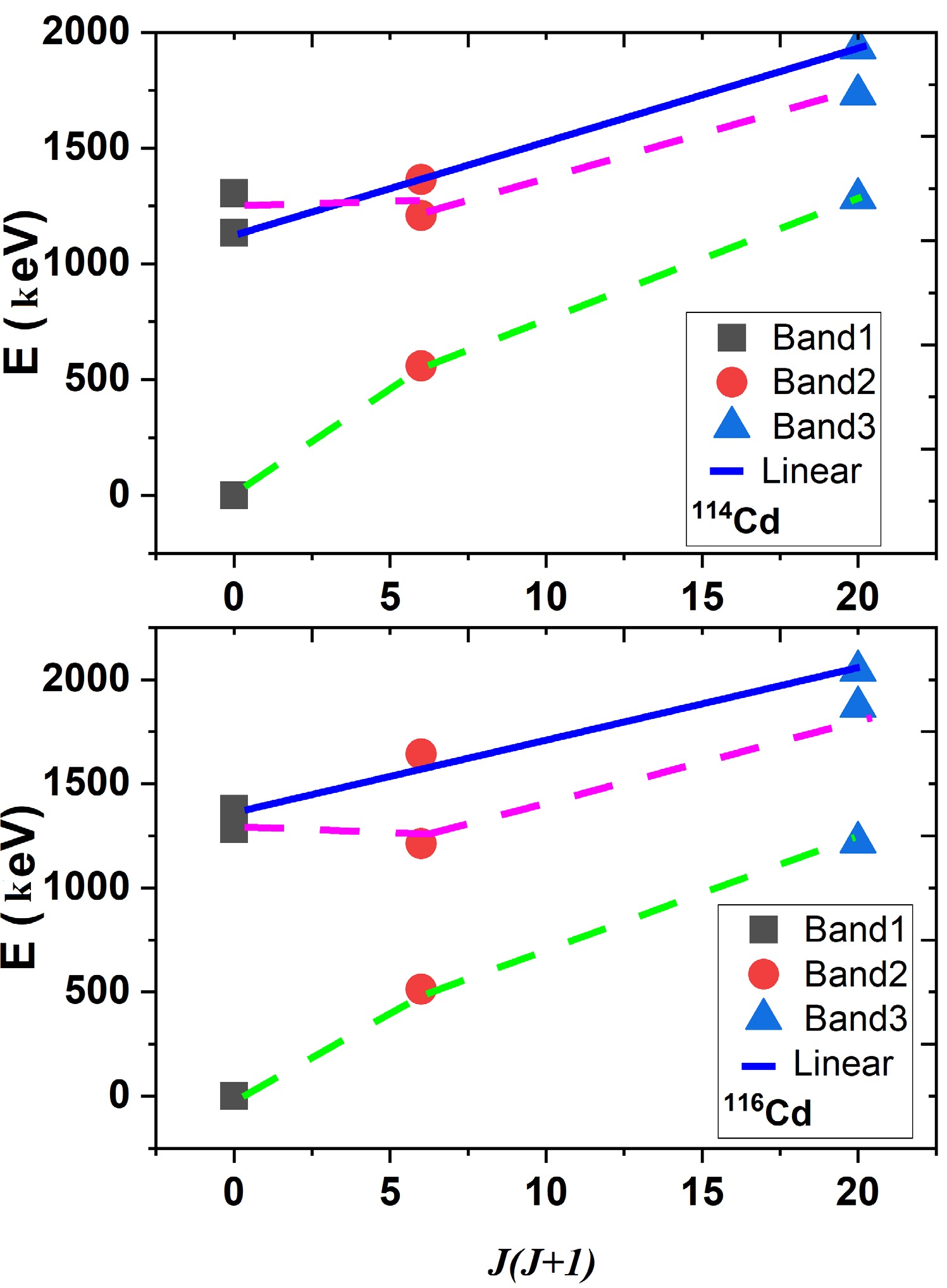

Figure 2.  (color online) Energies of the first three bands with a linear pattern of $ J(J+1) $ in ¹¹⁴Cd and ¹¹⁶Cd.

Moreover, $ ^{114}{\rm{Cd}} $ exhibits greater overall collectivity than $ ^{116}{\rm{Cd}} $, as indicated by the summed $ \sum M^{2}_{i} $ (W.u.) from $ M_{0} $ to $ M_{7} $. For $ ^{114}{\rm{Cd}} $, the summed strength is 528.31 (W.u.), whereas in $ ^{116}{\rm{Cd}} $, it is only 239.05 (W.u.), further emphasizing the differences in collective behavior between these isotopes.

Given the likelihood that the two-phonon normal bands and intruder rotational bands are strongly mixed in both nuclei, I have summed the transitions for the second and third $ 0^+ $ bands, as well as for the $ 2^+ $ bands. This approach simplifies the system into four available bands: two $ 0^+ $ bands ($ 0^+_1 $, $ 0^+_{2,3} $) and two $ 2^+ $ bands ($ 2^+_1 $, $ 2^+_{2,3} $). By summing the squares of the transition matrix elements $ M $, we conserve the overall transition strengths. The transition matrix elements among these four bands are provided in Table 1. Based on this framework, we can now examine the band mixing present in some ground and excited states. Following the assumptions outlined in Ref. [12], our analysis begins by considering that the structures originating from the excited $ 0^+_2 $states in ^114-116Cd exhibit rotational bands with deformations comparable to those of their respective ground-state bands. This similarity is expected if both intruder and normal candidates coexist. According to the guidelines in Refs. [12, 18, 19], I utilize the effective $ \Delta K = 0 $ coupling approach to explore the implications of a simple two-state mixing model. This analysis reveals significant magnitudes in the E2 transition amplitudes between the deformed intruder and normal vibrational state bands, which notably deviate from the expected leading-order intensity relations [32]. These findings underscore the complex interaction between intruder and vibrational configurations in the band structure of these isotopes.

			114Cd			116Cd			114Cd			116Cd
Label	Initial	Final	$ B(E2) $[$ a $]	M(E2)[$ b $]		$ B(E2) $[$ a $]	M(E2)[$ b $]		M(E2)[$ c $]	M(E2)[$ d $]		M(E2)[$ c $]	M(E2)[$ d $]
$ M_0 $	$ 2^+_1 $	$ 0^+_g $	31.1(19)	12.46		33.5(12)	12.94		13.22	11.08		12.30	12.18
$ M_1 $	$ 0^+_2 $	$ 2^+_1 $	27.4(17)	5.23		0.79(22)	0.88		1.04	8.50		0.03	0.06
$ M_2 $	$ 2^+_2 $	$ 0^+_g $	0.48(6)	1.54		1.11(18)	2.35		0.30	−		0.09	0.18
$ M_3 $	$ 2^+_2 $	$ 0^+_2 $	3.4(7)	4.12		−	−		3.12	−		−	−
$ M_4 $	$ 0^+_3 $	$ 2^+_g $	0.0026(4)	0.05		30(6)	5.47		−	−		−	5.16
$ M_5 $	$ 2^+_3 $	$ 0^+_g $	0.33(4)	1.28		1.1(4)	2.34		−	2.10		2.13	−
$ M_6 $	$ 2^+_3 $	$ 0^+_2 $	65(9)	18.02		−	−		−	18.83		−	−
$ M_7 $	$ 0^+_3 $	$ 2^+_1 $	−	−		30(6)	5.47		−	−		−	−
			114Cd			116Cd			114Cd	116Cd
Label	Initial	Final	$ B(E2) $[$ e $]	M(E2)[$ f $]		$ B(E2) $[$ e $]	M(E2)[$ f $]		M(E2)[$ g $]	M(E2)[$ g $]
1	$ 2^+_1 $	$ 0^+_g $	46	15.16		36	13.41		12.37	12.68
2	$ 0^+_2 $	$ 2^+_1 $	2.9	1.7		9.5	3.08		0.32	0.42
3	$ 2^+_2 $	$ 0^+_g $	3.2	4		1.9	3.08		0.75	0.42
4	$ 2^+_2 $	$ 0^+_2 $	11	7.41		1.7	2.91		6.53	2.07
$a$) Used $B(E2)$ (W.u.) from [31] and $\bf{M}^{\bf{2}}(\bf{E2})$ = ($2J_{i}+1) B(E2; i \rightarrow f$). $b$) Used from exp data, $c$) Used from TSMM (fit1), and $d$) Used from TSMM (fit2). $e$) Used $B(E2)$ from [33]. $f$) Used from IBM and $g$) Used from TSMM.

Table 1.  $ E2 $ transition matrix elements (W.u.) for $ 0\leftrightarrow 2 $ transitions in ¹¹⁴Cd and ¹¹⁶Cd. Note that $ B(E2) $is expressed in Weisskopf units (W.u.), whereas M(E2) is expressed in units of $(({\rm{W.u.}})^{1/2})$.

where $ M_i $ is the intrinsic matrix element for the transition. The presence of intruder states leads to inevitable band mixing, which is crucial for explaining the $ B(E2) $ values observed in ¹¹⁴Cd and ¹¹⁶Cd. A simple two-state model is particularly effective when intruder states are involved in the mixing process. Typically, band mixing occurs between normal ground states and excited intruder states, reflecting the coexistence of different nuclear configurations. This coexistence is characterized by the mixing of normal and intruder configurations, significantly influencing the nuclear structure. If all the transition matrix elements $ M(E2) $ are known, a detailed mixing analysis for transitions between $ 0\leftrightarrow2 $ states can be performed. I have applied the simple two-state mixing model to analyze the $ 0\leftrightarrow2 $ transitions in both ¹¹⁴Cd and ¹¹⁶Cd, revealing the extent of mixing between normal and intruder states in these nuclei. For the mixing model, we have

for $ 0_g^+ $ and $ 0_{2,3}^+ $ states,

for the ground state $ 2_g^+ $ and the higher-lying states $ 2_{2,3}^+ $, where $ 2_{2,3}^+ $ denotes either the second or third $ 2^+ $ state based on the experimental data. The coefficients $ c $ and $ d $ represent the mixing amplitudes between the basis states $|\phi\rangle_{(g)}$ (ground band) and $|\phi\rangle_{(e)}$ (excited band). The states $ 0_{2}^{+} $ and $ 0_{3}^{+} $, as well as $ 2_{2}^{+} $ and $ 2_{3}^{+} $, have distinct wave functions. The notation $ (0,2)_{2,3}^{+} $ indicates either the second or third states, used when the identification of these states depends on the selected solution. To construct the wave functions for the mixed states, we determine the coefficients based on experimental data and the theoretical framework of band mixing. The orthonormality conditions, $ a^2 + b^2 = 1 $, and $ c^2 + d^2 = 1, $ ensure the proper normalization of the wave functions. This approach provides a clear and systematic method for obtaining the coefficients and ensuring the orthonormality of the mixed wave functions.

A unique determination for the two-state model exists based on Refs. [12−14, 18, 19]. Here, I define the matrix elements $ M_g $ and $ M_e $ to connect $ 0^{+} $ and $ 2^{+} $ states. To ensure clarity, Eq. (4) represents the reduced transition matrix elements for the electric quadrupole transitions. The reduced transition matrix elements are defined as follows:

Furthermore, I assume that, for the band mixing of the ground and excited states, the $ g $ states are not connected to the $ e $ states by the $ E2 $ operator. I select eight transitions, connecting $ 0\leftrightarrow2 $ from $ M_0-M_7 $ in Fig. 3.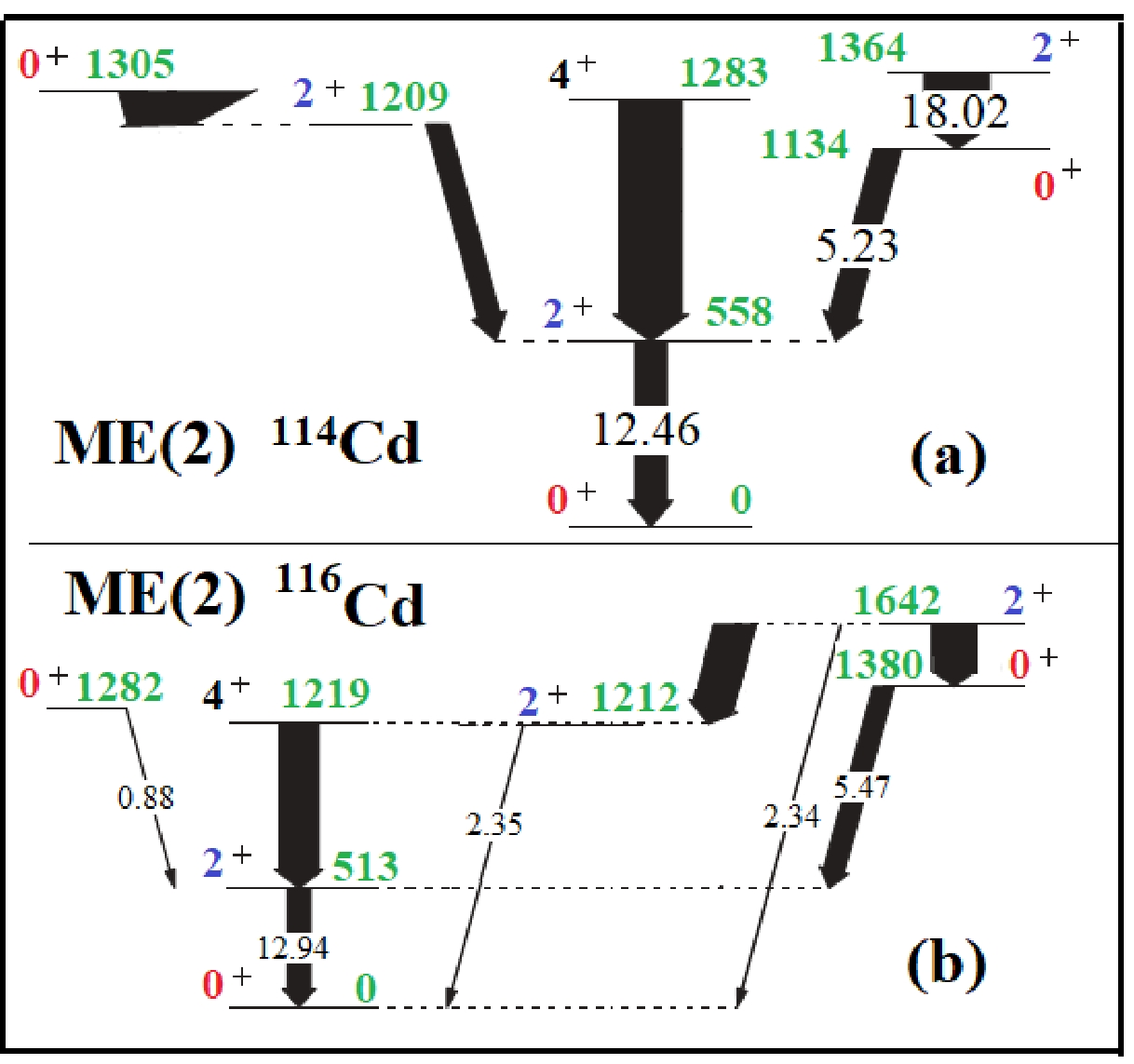

Figure 3.  (color online) Transition matrix elements for connecting $ 0\leftrightarrow2 $ transitions in ¹¹⁴Cd and ¹¹⁶Cd.

The four transition matrix elements $ M_0-M_3 $ for $ ^{114}\mathrm{Cd} $ and $ M_0-M_2 $ and $ M5 $ for $ ^{116}\mathrm{Cd} $, listed in Table 1, can be expressed as linear combinations of basis states $ M $. Including elements such as $ M_4-M_7 $ would necessitate experimental knowledge of transitions such as $ B(E2) $ from $ 0_3^+ $ to $ 2_1^+ $, which are currently unknown. Another possible scenario considers transitions $ M_6 $ instead of $ M_3 $ for $ ^{114}\mathrm{Cd} $, and $ M_0-M_2 $ and $ M_7 $ for $ ^{116}\mathrm{Cd} $. For example, if $ M_6 $ is considered instead of $ M_3 $ in $ ^{114}\mathrm{Cd} $, the resulting parameters are as follows: $ a = 0.92, c = 0.87, M_g = 10.96, M_e = 19.71 $. Similarly, for $ ^{116}\mathrm{Cd} $, transitions $ M_0-M_2 $ and $ M_7 $ are included in the analysis, involving states $ 0_1^+ $, $ 0_2^+ $, $ 0_3^+ $, $ 2_1^+ $, and $ 2_2^+ $, as shown in Table 1. Considering $ M_5 $ for $ ^{116}\mathrm{Cd} $ is one option; alternatively, $ M_7 $ provides an option with the following resulting parameters: $a = 0.16,\; c = 0.24, \; M_g = 5.16, M_e = 13.30$. These alternative sets of transitions lead to different solutions for the mixing coefficients and matrix elements, illustrating the flexibility of the model within the constraints of the experimental data. The results of these alternative scenarios are summarized in Table 2. This analysis underscores the importance of careful selection of transitions to ensure consistency with the two-state mixing framework and to account for the limitations imposed by the available experimental information. Because different sets of $ E2 $transition matrix elements are considered in the TSMM, distinct solutions corresponding to each set of matrix elements are obtained. For clarity, we present two representative solutions, labeled as fit 1 and fit 2, in Table 1.

Quantity	114Cd	114Cd alt.$ [a] $	114Cd $ [b] $	114Cd $ [c] $	116Cd	116Cd alt. $ [a] $	116Cd $ [b] $	116Cd $ [c] $
a	0.43	0.39	0.26	0.92	0.09	0.03	0.26	0.16
c	0.22	0.01	0.35	0.87	0.19	0.17	0.26	0.24
$ M_g $	3.12	4.39	6.53	10.96	2.13	2.45	2.07	5.16
$ M_e $	13.80	13.51	16.15	19.71	13.21	13.15	14.24	13.30
$a$) fitting from negative sign of $M_2$. $b$) fitting from IBM [33]. $c$) fitting considering $ M_0{-}M_2 $ and $M6$ for 114Cd and $ M_0{-}M_2 $ and $M7$ for 116Cd.

Table 2.  Results of fitting for $ 0\leftrightarrow 2 $ transitions in ¹¹⁴Cd and ¹¹⁶Cd.

For instance, the matrix element $ \langle 0_1 \| M(E2) \| 2_1 \rangle = acM_g +bdM_e $, and similar expressions apply for other transitions. This approach enables the extraction of the experimental quantities for each nucleus and the determination of wave-function mixing amplitudes, which are also provided in Table 1. To ensure robustness, I repeated the analysis with the matrix element $ M2 $ set negative, and these results are labeled as "alt." in the tables. The alternative solution exhibits reduced mixing in both nuclei, consistent with the two-state mixing model. During the fitting process of the experimental $ 0 \leftrightarrow 2 $ transitions in ¹¹⁴Cd, the transition matrix elements for the ground ($ g $) and excited ($ e $) bands were approximately 3.12 and 13.8 W.u., and 4.39 and 13.51 W.u., with corresponding ratios of 0.22 and 0.32 for different fitting sets, labeled as fit 1 and fit 2. A similar extraction was performed for the IBM transitions, yielding transition matrix elements of about 6.53 and 16.15 W.u. for the $ g $ and $ e $ bands, respectively, with a ratio of 0.40.

The results of fitting the two-state mixing model calculations for the $ 0 \leftrightarrow 2 $ transitions in ¹¹⁶Cd indicate that the transition matrix elements for the ground ($ g $) and excited ($ e $) bands are approximately 2.13 and 13.21 W.u., with a ratio of 0.16 for fit 1. For fit 2, these amplitudes are 2.45 and 13.15 W.u., resulting in a ratio of 0.18. In the IBM transition analysis, the corresponding values for the $ g $ and $ e $ bands are about 2.07 and 14.24 W.u., with a ratio of 0.14. This suggests that the ratios of the transition matrix elements from the IBM model correspond well with those obtained from our two-state mixing model, particularly for connecting $ 0 \leftrightarrow 2 $ transitions in ¹¹⁶Cd. These findings indicate that the transition matrix elements associated with the $ e $ bands are significantly stronger than those of the $ g $ bands, demonstrating the dominant influence of intruder states. Mixing is particularly pronounced in ¹¹⁴Cd and is similar when comparing the $ 0 \leftrightarrow 2 $ transitions and fitted wave-function amplitudes from the IBM model. The ratios $ M_g/M_e $ for both the two-state mixing model and the IBM calculations are depicted in Fig. 4, highlighting the consistency between these approaches and further validating the observed trends in band mixing behavior.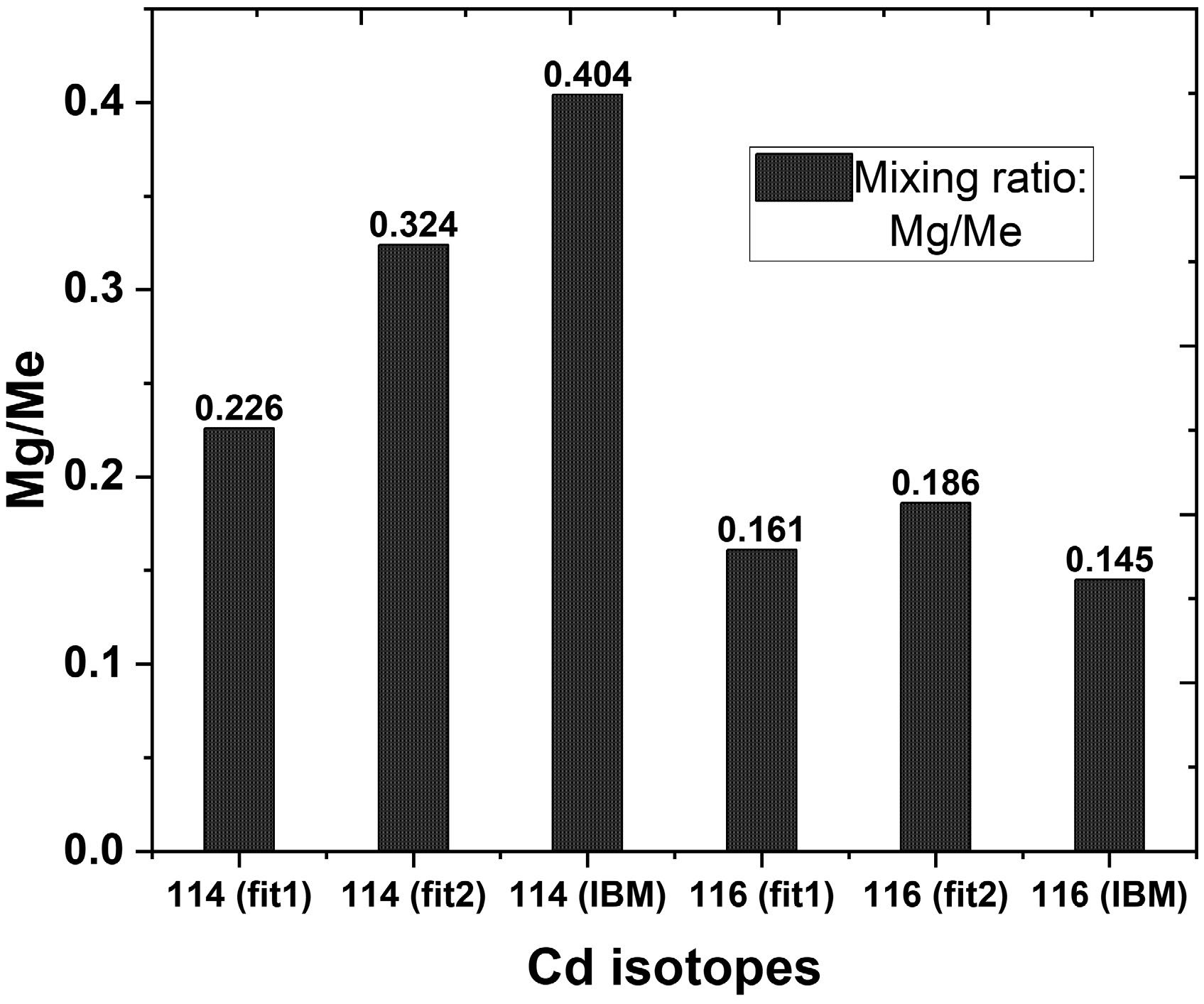

Figure 4.  Comparison of $ M_g/M_e $ratios for the two-state mixing model and IBM calculation for ¹¹⁴Cd and ¹¹⁶Cd.

For $ M_g $ and $ M_e $, we establish that $ M_e > M_g $. It is well-established that Cd isotopes exhibit vibrational characteristics at their lowest energy levels, with an intruder deformed rotational band appearing at slightly higher energies. Our calculations and fitting of the excited band validate the experimental rotational behavior, which follows the $ J(J+1) $ pattern with a linear trend, as shown in Fig. 2. This explains why this pattern is more prominent in $ e $ bands than in $ g $ bands. Furthermore, the extracted values from the two-state mixing model for ¹¹⁴Cd are greater than those obtained from the IBM calculation, whereas the reverse is observed for ¹¹⁶Cd.

Next, I examine a key indicator of band mixing: the mixing potential, which is defined based on the level spacing. The level spacing of low-lying states is crucial for characterizing band mixing. By combining the spacings of the ground and rotational intruder states with the mixing amplitudes, one can derive the matrix elements responsible for this mixing. Consequently, for each nucleus, the mixing potentials between the $ 0^+ $ and $ 2^+ $ bands are given by $ V_0 = ab \Delta E0 $ and $ V_2 = ab \Delta E2 $, respectively. In these equations, $ \Delta E $ is the energy differences of selected states. The results of these comparisons are detailed in Table 3. Using the interaction matrix elements from a two-state model, I can assess the strength of the collectivity of the basis states.

Quantity	114Cd	114Cd alt.$ [a] $	114Cd $ [b] $	116Cd	116Cd alt. $ [a] $	116Cd $ [b] $
$ V_0 $	397.45	374.99	274.90	114.44	38.42	310.78
$ V_2 $	228.17	215.27	157.81	62.40	20.95	169.45
$a$) fitting from negative sign of $M_2$. $b$) fitting from IBM [33].

Table 3.  Mixing matrix elements in ¹¹⁴Cd and ¹¹⁶Cd.

Based on the analysis of two-state mixing model and IBM, the results in Table 3, the mixing potential for ¹¹⁴Cd is higher than that for ¹¹⁶Cd.

In a study by Gavrielov et al. [1], the partial dynamical symmetry analysis characterizes various states in Cd isotopes based on their wave-function compositions. Their findings indicate a strong dominance of the normal component, suggesting minimal mixing with intruder states. However, for increased angular momenta and mid-shell nuclei such as ¹¹⁴Cd, the intruder states ($ 0^+_i $ and $ 2^+_i $, where i denotes intruder states) exhibit intermediate mixing while still predominantly displaying the normal component. In contrast, my observations reveal significant mixing in ¹¹⁴Cd. Specifically, I have identified band mixing in the intruder states of ¹¹⁶Cd through band mixing amplitudes, particularly focusing on the second excited $ 0^+ $ state at 1380 keV and extending to other members of the band. This result is consistent with previous studies suggesting that the 1380 keV $ 0^+ $ state, rather than the 1282 keV $ 0^+ $ state, along with the 1642 keV $ 2^+ $ state in ¹¹⁶Cd, might belong to a potential intruder band. This finding supports the notion of a complex nuclear structure with various energy levels and transitions in the Cd isotopes, as reflected in the partial level scheme of the isotopes studied. When the intruder band in ¹¹⁶Cd is compared with the ground-state band of the ¹²⁴Ba isotone, we observe that the influence of mixing with other states on the band member energies is minimal. This comparison underscores that the intruder $ 0^+ $state in ¹¹⁶Cd can be interpreted as a two-quadrupole phonon state in the vibrator model. This interpretation is supported by the significant differences observed in the $ B(E2: 0^+_2 \rightarrow 2^+_1) $ = 0.79(22) W.u. and $ B(E2: 0^+_3 \rightarrow 2^+_1) $ = 30.0(6) W.u. values, which indicate varying degrees of collectivity and transitions within the nucleus.

The role of mixing in even-even Cd isotopes remains a compelling area of investigation, particularly concerning the unique electromagnetic properties of their low-lying bands. While certain characteristics can be attributed to a strong mixing of vibrational and intruder bands, as highlighted in previous studies (e.g., [8]), there exist indications of a scenario with minimal or no mixing. The central unresolved problem is the extent to which proton-intruder configurations contribute to the collective behavior of these nuclei in their low-lying bands. This presents a complex and intriguing puzzle in nuclear structure physics. The interplay between mixing and the role of intruder states in shaping the electromagnetic properties of these isotopes continues to challenge our understanding and prompts further investigation into the detailed mechanisms governing nuclear structure in Cd isotopes.

I have compared various nuclear properties, including energy spectra and $ E2 $ transition rates, between ¹¹⁴Cd and ¹¹⁶Cd. These nuclei, well-known for their normal and intruder states in the medium mass region, have been examined with a focus on $ E2 $ transition rates. A configuration mixing scheme is employed to analyze the lowest normal and intruder states of the $ 0^+ $ and $ 2^+ $bands. The results reveal that ¹¹⁴Cd exhibits greater collectivity than ¹¹⁶Cd, with a more pronounced mixing behavior observed in ¹¹⁴Cd.

I would like to express my deepest gratitude to H. T. Fortune, now deceased, whose invaluable contributions and expertise greatly enriched this study.