Weak magnetic effect in quark-gluon plasma and local spin polarization

Thermodynamic characteristics can be effectively inferred through experimental measurements once a system reaches local thermal equilibrium. As indicated by the equilibrium density operator, $ \lg \hat \rho\sim \alpha \hat N - \beta_\mu \hat p^\mu + \omega_{\mu\nu} \hat M^{\mu\nu}/2 $ (cf. Ref. [1]), the constants of motion $ (\hat N, \hat p^\mu, \hat M^{\mu\nu}) $, which usually correspond to gauge symmetry group and the Poincaré group generators, are conjugate to the thermodynamic variables: chemical potential over temperature ($ \alpha=\mu/T $), fluid four-velocity over temperature ($ \beta_\mu = u_\mu/T $), and the thermal vorticity tensor ($ \omega_{\mu\nu}=\omega^{\rm th}_{\mu\nu}\equiv-\dfrac{1}{2}(\partial_\mu \beta_\nu - \partial_\nu \beta_\mu) $). Since these constants of motion are experimental observables, the chemical potential, temperature, and other physical quantities can be obtained by measuring charge, momentum, and angular momentum of particles in a thermal system.

Such measurements have been made extensively, particularly in high-energy heavy-ion experiments. For instance, the observed hadron spectra – momentum distribution – reveals the temperature, baryon chemical potential, and flow velocity of a quark-gluon plasma (QGP) [2, 3]. Other differential measurements, including the hadron collective flow and flow correlations, indicate that the space-time distribution of temperature in the QGP fireball originates hydrodynamically from an almond-shape geometry [4−6].

Recently, the study has been advanced to the analysis of hadron spin polarization to elucidate the rotational nature of QGP [7−12]. Indeed, assuming that QGP achieves local thermal equilibrium, spin-1/2 particles are expected to be polarized owing to thermal vorticity [13−17]. Following the Cooper-Frye formula [13, 18],

with $ n_F $ the Fermi-Dirac distribution, $ \epsilon^{\mu\alpha\beta\sigma} $ the totally antisymmetric Levi-Civita symbol, and $ \omega_{\mu\nu}=\omega^{\rm th}_{\mu\nu} $, the global spin polarization of Lambda hyperons emitted from a hyper-surface Σ can be successfully characterized [9−11, 19−21].

However, thermal vorticity fails to describe the differential spectrum of the Lambda spin polarization, which is often referred to as the local spin polarization (see Ref. [15] for a recent review). In particular, when the thermal voticity is projected along the beam axis (z-axis), it yields an azimuthal distribution of the Lambda spin polarization with a sign that is opposite to experimental observations [22−27]. This discrepency has triggered extensive research into spin generation through QGP beyond thermal vorticity and the local thermal equilibrium condition [28−37].

In this Letter, with respect to the conversion of quark spin from QGP fluid, we introduce the dissipative effect induced by a weak external magnetic field. It has been noticed that for a field strength $ |eB|\ll m_\pi^2 $, where $ m_\pi $ is the pion mass, and when the bulk evolution of QGP is barely affected, quarks can be driven slightly out of local thermal equilibrium [38, 39]. The out-of-equilibrium effect leads to a correction in the quark distribution function, which, for quark species with electric charge Q, is [39]

where $ \sigma_{\rm el} $ is the electrical conductivity, $ \chi_{\rm ch} $ is an effective charge susceptibility, and $ F^{\mu\nu} $ is the electromagnetic field strength tensor. Equation (2) is a scalar function solution where the quark spin is averaged. Correspondingly, when the weak magnetic field is considered, the conversion of quark spin is modified, and the Cooper-Frye formula in Eq. (1) becomes

In realistic heavy-ion collisions, since the magnetic field is created and orientated out of the reaction plane, the $ p_\mu F^{\mu\nu}u_\nu $ factor in Eq. (2) results in a dipole structure in the azimuthal angle distribution. Therefore, the extra $ \delta f_{\rm EM} $ does not contribute to the globle spin polarization in terms of local spin polarization. However, it is potentially significant. Eq. (3) is the major result of this Letter.

We use the natural units throughout the letter. We use the $ g^{\mu\nu}=(+,-,-,-) $ matrix convetion and take $ \epsilon^{0123}=1 $ for the Levi-Civita symbol.

In the presence of an electromagnetic field, the evolution of quarks with spin degrees of freedom in QGP medium satisfies the Boltzmann-Vlasov equation [40−42]:

Note that the quark distribution function is a Hermian matrix in the spin subspace, $ \mathscr{F}= \mathscr{F}^\dagger $. For QGP close to local thermal equilibrium, the collision kernal can be linearized via the relaxation time approximation. In principle, relaxation time $ \tau_R $ is a function of $ p\cdot u $, depending on microscopic dynamics. In this Letter, we take the so-called quadratic ansatz reported in Ref. [43]: $ \tau_R = \bar{\tau} p\cdot u/T $, where $ \bar\tau $ is a free parameter determined by transport coefficients ¹. Because quarks in QGP are dominated by strong and electromagnetic forces, the collision kernel, as well as the parameter $ \bar\tau $, are expected even with respect to the charge conjugation symmetry. Accordingly, subject to a charge conjugation transformation, Eq. (4) applies to anti-quarks. In the following, we focus on the derivation of quarks, while results associated with anti-quarks can be inferred upon charge conjugate symmetry.

Using the Chapman-Enskog method, with the knowledge of the equilibrium quark distribution function [13],

Eq. (4) can be solved in steps [39, 40]. In Eq. (5), $ U(p) $ is the amalgamated spinor solution for free spin up and spin dowm fermions: $ U(p) = (u_+(p), u_-(p)) $ and $ \overline{{U}}(p)= U^\dagger \gamma^0 $. The matrix $ X(x,p) $ is identified as $X(x,p) \equiv $ $ \left({\rm e}^{\beta\cdot p} \exp{\left[-\dfrac{1}{2}\omega_{\mu\nu}\Sigma^{\mu\nu}\right]}+1\right)^{-1}\,,$ where $\Sigma^{\mu\nu}= \dfrac{\rm i}{4}[\gamma^\mu,\gamma^\nu]$is the relativistic rotation generator realized through the gamma matrix. At the leading order of $ |eB|/T^2 $, $ \mathscr{F} = \mathscr{F}_{{{\rm{eq}}}} + \delta \mathscr{F}_{\rm EM} $, where the dissipative correction is

with

To derive Eq. (6), we used the Dirac equation $ (\not {p}-m)U(p)=0 $, which implies that $ F^{\mu\nu}p_\mu \dfrac{\partial}{\partial p^\nu} U(p)=0 $ and $ F^{\mu\nu}p_\mu \dfrac{\partial}{\partial p^\nu} \overline{{U}}(p)=0 $. The hermiticity of $ \delta \mathscr{F}_{{{\rm{eq}}}} $ can be verified with respect to the condition $ Y^\dagger = \gamma^0 Y \gamma^0 $.

In accordance with the dissipative correction in the conserved current of hydrodynamics, the dissipative correction in the phase-space distribution function satisfies the Landau's matching condition. In particular, for a QGP medium with local charge neutrality, the leading order dissipative correction to the current is driven by the external electromagnetic field:

where the trace $ {{{\rm{tr}}}}_2 $ is taken in the spin subspace and the summation takes considers flavors and colors. To evaluate the trace, using trace cyclicity, the condition that $ U(p)\overline{{U}}(p)=\sum_{\rm spin} u(p) \bar u(p)=\not {p}+m $, and the vanishing trace of three gamma matrices, for quarks with electric charge Q,

In the above expression,$ n_F $prime indicates a derivativative with respect to $ p\cdot u/T $. For instance, $ n_F'= -n_F(1-n_F) $. A couple of comments are in order. First, we have used the approximated identity in the derivation [13]: $ {{{\rm{tr}}}}_2\left[\exp\left(\dfrac{n}{2}\omega_{\alpha\beta}\Sigma^{\alpha\beta}\right)\right] \approx 4 + \dfrac{n^2}{2} \omega^{\alpha\beta}\omega_{\alpha\beta} $. Secondly, substituting the trace back to the matching condition, Eq. (8) yields an expression that relates $ \bar\tau $ to the electrical conductivity $ \sigma_{\rm el} $. In the limit $ \omega\to 0 $, one arrives at the standard relation $ \sigma_{\rm el} = \bar\tau\chi_{\rm el} $ [39]. Accordingly, up to a factor of two, whcih amounts to a summation over spin, the first term in Eq. (9) can be identified as the scalar function $ \delta f_{\rm EM} $. In sum, as expected, in a non-rotating system, the spin averaged quark distribution function reduces to $ \dfrac{1}{2}{{{\rm{tr}}}}_2 \mathscr{F}= n_F + \delta f_{\rm EM} $.

The Cooper-Frye formula in Eq. (1) is a variant of the the Pauli-Lubanski pseudo-vector,

where $ S^{\rho\sigma} $ corresponds to the angular momentum operator. Spin polarization of particles emitted from QGP, in particular, can be described when $ \Pi^{\rm PL}_\mu $ is evaluated on a hypersurface that meets the freeze out condition in heavy-ion collisions and as the averaged expectation of particles in phase space. As has been shown previously [13], because $ S^{\mu\nu} $ has contributions only from spin, it can be determined from the spind density tensor in relation to the quark distribution function in a QGP that is out of local thermal equilibrium [40]:

where the rank-2 tensor function is

Accordingly, the average with respect to the quark spectrum is

Following the Cooper-Frye prescription [44] and integrating over a hypersurface, Eqs. (12) and (13) lead to Eq. (3). Note that the derivation does not reply on the the explicit form of $ \omega^{\mu\nu} $. Hence, Eq. (3) applies when other contributions beyond the thermal vorticity tensor, including the shear-induced polarization, are considered.

In realistic heavy-ion collisions, the collision region must be an electromagentic field pointing out of the reaction plane, namely, $ {\boldsymbol B} = B_y\hat y $. Although the field strength is expected to be initally strong, it drops drastically [45−52]. The magnetic field likely becomes weak when the QGP medium is formed and begins expand hydrodynamically [51, 52]. Although the magnetic effect in QGP is too weak to influence the bulk medium evolution, it has been shown to be significant for some signatures, including thermal photon spectrum anisotropy [38, 39] and thermal di-lepton polarization [53].

In a weak magnetic field, as indicated by Eq. (3), although quark polarization by QGP rotation remains unchanged, the quark spin configuration in phase space can be dramatically different. To demonstrate this effect, we apply Eq. (3) to the hydrodynamical modeling of QGP evolution and calculate the spin polarization of s-quarks emitted from the chemincal freeze-out hypersurface. Because the spin of a Lambda hyperon is dominantly carried by the s-quark, as u-, d- and s-quark coalesce [54], the calculation is expected to provide a good approximation to the polarization of the Lambda hyperon. Of course, as a consequence of approximate chiral symmetry breaking during the coalescence, we leave the s-quark mass $ m_s $ as a free parameter.

With respect to the isobar collision systems with $ \sqrt{s_{NN}}=200 $ GeV, we conduct hydrodynamical simulations using the 3+1D MUSIC program [55]. Initial conditions are chosen and calibrated according to the centrality class determined by charged particle multiplicity and a longitudinal profile that reproduces rapidity dependent direct flow [56]. To capture the thermal vorticity associated with the elliptic and triangular initial geometry, we deform the optical Glauber model distribution with a finite ellipticity and triangularity following the prescription introduced in Ref. [57]. In addition to the standard set of parameters that have been used in hydrodynamical modeling, such as the shear and the bulk viscosities, we used the mean value of electrical conductivity $ \sigma_{\rm el}/T = 1 $, with respect to the pQCD expectation $ \sigma_{\rm el}/T\in [0.2,2] $ [58, 59] ². To avoid complexity from unknown space-time evolution, for the magnetic field, we take $ {\boldsymbol B}= B\Gamma(\eta_s)\hat y $, with B representing a constant parameter and the space-time rapidity dependence $ \Gamma(\eta_s) $ determined from the retarded potential solution [50]. In this way, $ |eB| $ is the time-average field strength in the center of the QGP.

Lambda local spin polarization along the beam axis can be quantified when it is decomposed into sine Fourier modulations. Under the local thermal equilibrium condition, the local thermal vorticities in QGP are expected from the medium response to the elliptic and triangular geometries. As shown in Fig. 1, we solve the Lambda local spin polarization for RuRu collisions with impact parameter $ b=7 $ fm and $ m_s=0.8 $ GeV. Indeed, in Fig. 1 (a), where $ w_{\mu\nu} $ is identified as $ w^{\rm th}_{\mu\nu} $, without a magnetic field, the negative second-order and third-order modulations of the local spin polarization are obtained. It is interesting to notice that the magnitude for the second order is larger, which is consistent with the hierarchy between elliptic and triangular flow.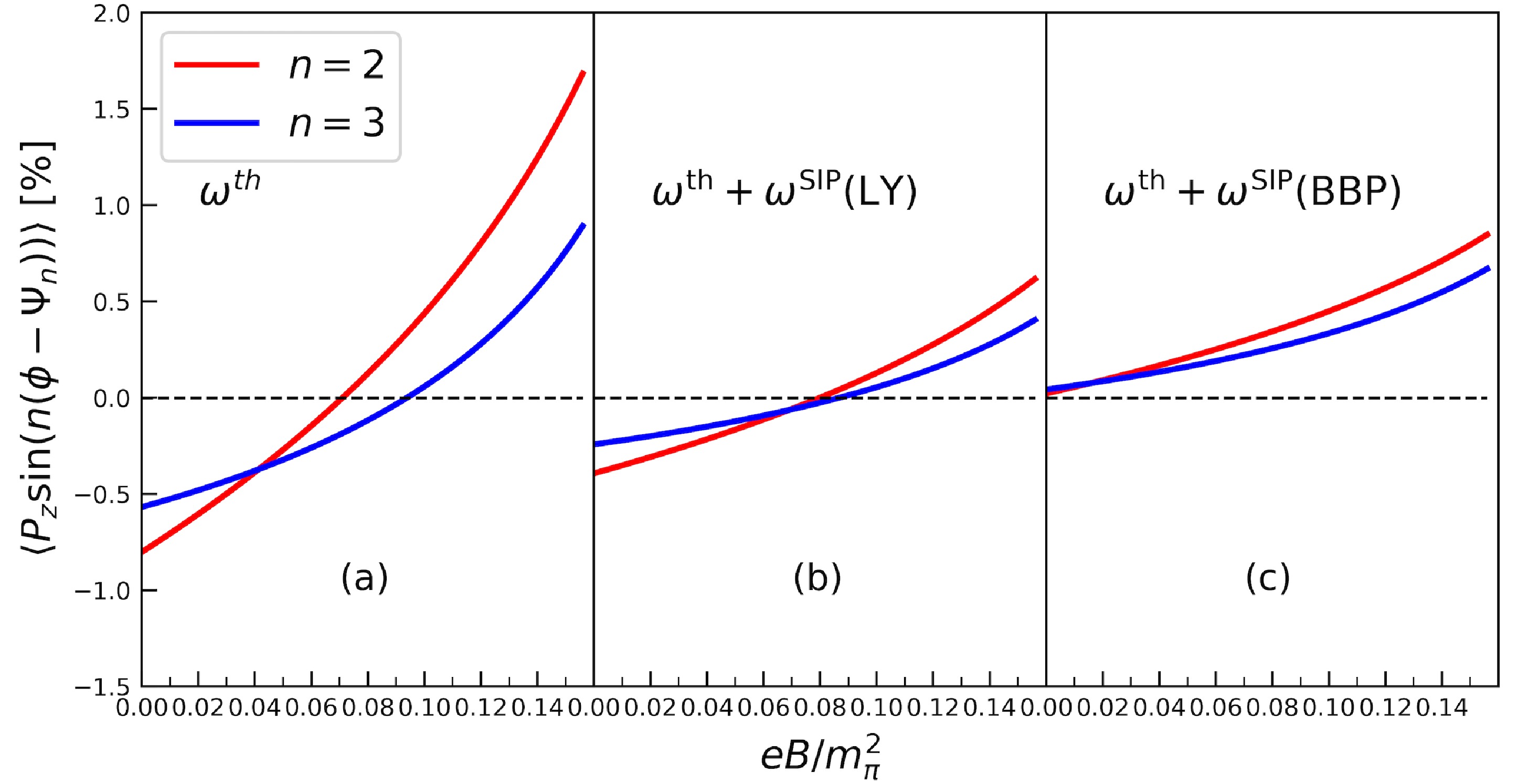

Figure 1.  (color online) Dependence of the second-order modulation (red) and the third-order modulation (blue) of Lambda local spin polarization on the magnetic field.

To resolve the sign problem of the Lambda local spin polarization, a number of contributions have been proposed beyond thermal vorticity [31−35]. Of particular interest, the shear tensor $ \xi_{\mu\nu} = \frac{1}{2}(\partial_\mu \beta_\nu + \partial_\nu \beta_\mu) $, which appears in systems in local thermal equilibrium, gives rise to the so-called shear-induced polarization $ \omega^{\rm SIP}_{\mu\nu} $. Corresponding to the two types of formulation, $ \omega^{\rm SIP}_{\mu\nu}({\rm LY}) $ by Liu and Yin [32] and $ \omega^{\rm SIP}_{\mu\nu}({\rm BBP}) $ by Becattini, Bucciantini, and Palermo [33], with the replacement $ \omega_{\mu\nu}\to \omega^{\rm th}_{\mu\nu} + \omega^{\rm SIP}_{\mu\nu} $ in Eq. (3), we re-calculate the Lambda local spin polarization. Results are shown in Fig. 1 (b) and (c).

In summary, Fig. 1 shows the following. First, in all cases, with the magnetic field introduced, both modulations in the local spin polarization increase monotonically. Eventually, with a weak magnetic field, they become positive regardless of the contribution from shear-induced polarization. We emphasize that the sign change of the local polarization reflects the more significant influence of $ \delta f_{\rm EM} $ in the weighted integral with respect to local vorticity at the freeze-out hypersurface. That is, in Eq. (2), $ \delta f_{\rm EM} $ can overwhelm $ n_F $ in terms of the conversion of local spin. However, it does not imply $ |\delta f_{\rm EM}|>|n_F| $. Secondly, the second-order modulation appears more sensitive to the magnetic field than third-order modulation, while sensitivity is reduced by shear-induced polarization. Lastly, and importantly, although the shear-induced polarization can make the local Lambda spin polarization positive [60], the second-order modulation being greater than third-order modulation is an unambiguous signature associated with the magnetic field. All of these qualitative features are not affected by the s-quark mass although for smaller $ m_s $, spin conversion from the QGP is earsier, which effectively reduces the required field strength.

Experimental observables, especially centrality dependent Lambda local spin polarization, can be well captured in the presence of a weak magnetic field. Although our current calculation is approximate, we achieve excellent characterizations with $ m_s=0.8 $ GeV and $ w_{\mu\nu} = \omega^{\rm th}_{\mu\nu}+w^{\rm SIP}_{\mu\nu} $(BBP). As shown in Fig. 2 (a), the STAR measured $ n=2 $ modulation of the Lambda local spin polarization in the isobar systems can be reproduced [61], with the the centrality dependent $ |eB| $ extracted and given in Fig. 2 (b) (blue symbols). The error bars in Fig. 2 (b) are from experimental uncertainties and$ \sigma_{\rm el}/T\in [0.2, ~2] $. For comparison, in Fig. 2 (b), the estimated field strength from the direct photon $ v_2 $ in AuAu collisions are shown as well [39]. It is interesting to notice that the extracted field strength grows towards peripheral collisions. The third-order modulation of the Lambda local spin polarization can be described in the same field strength, and the results are shown as the green shaded band in Fig. 2 (a).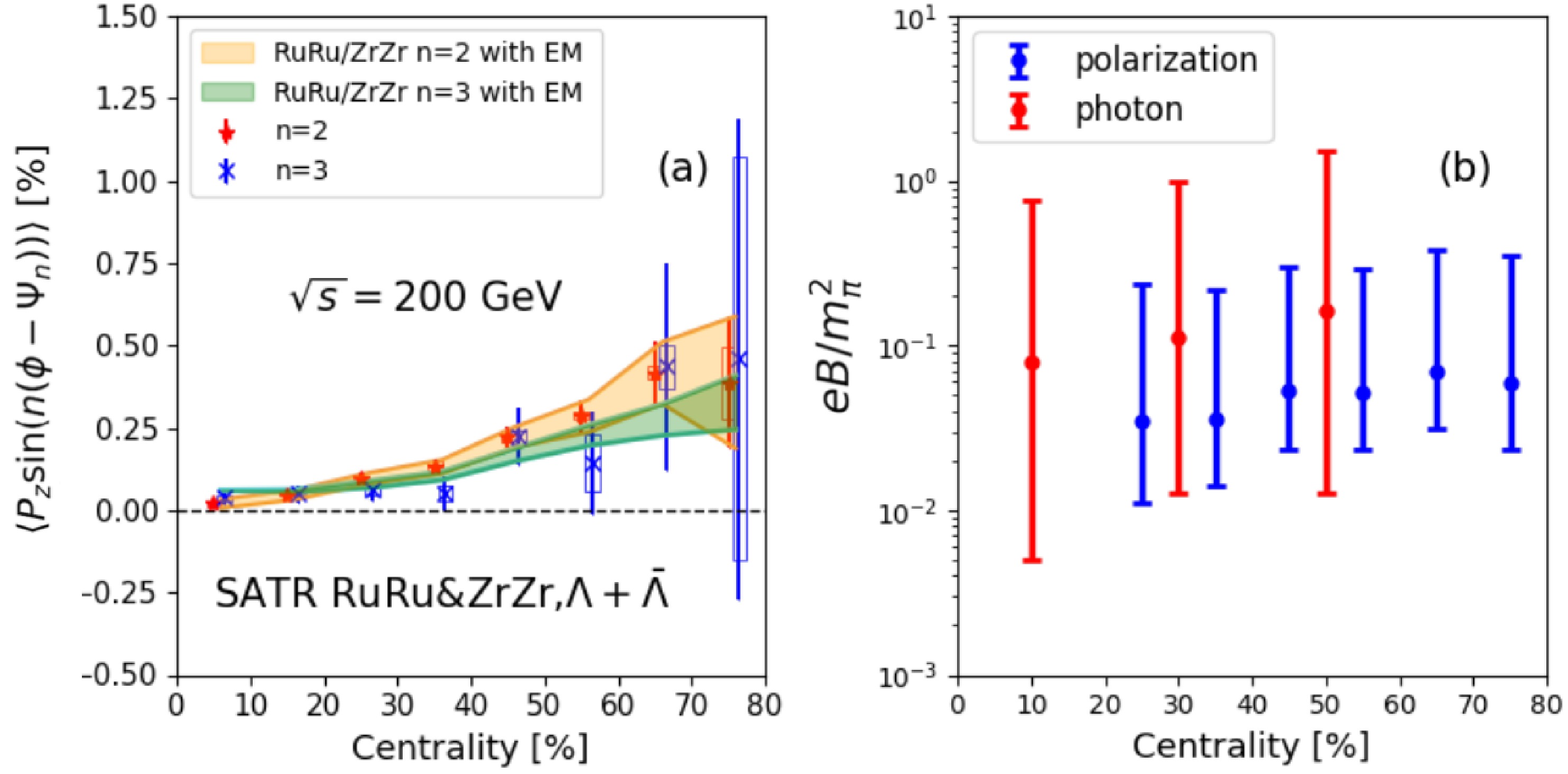

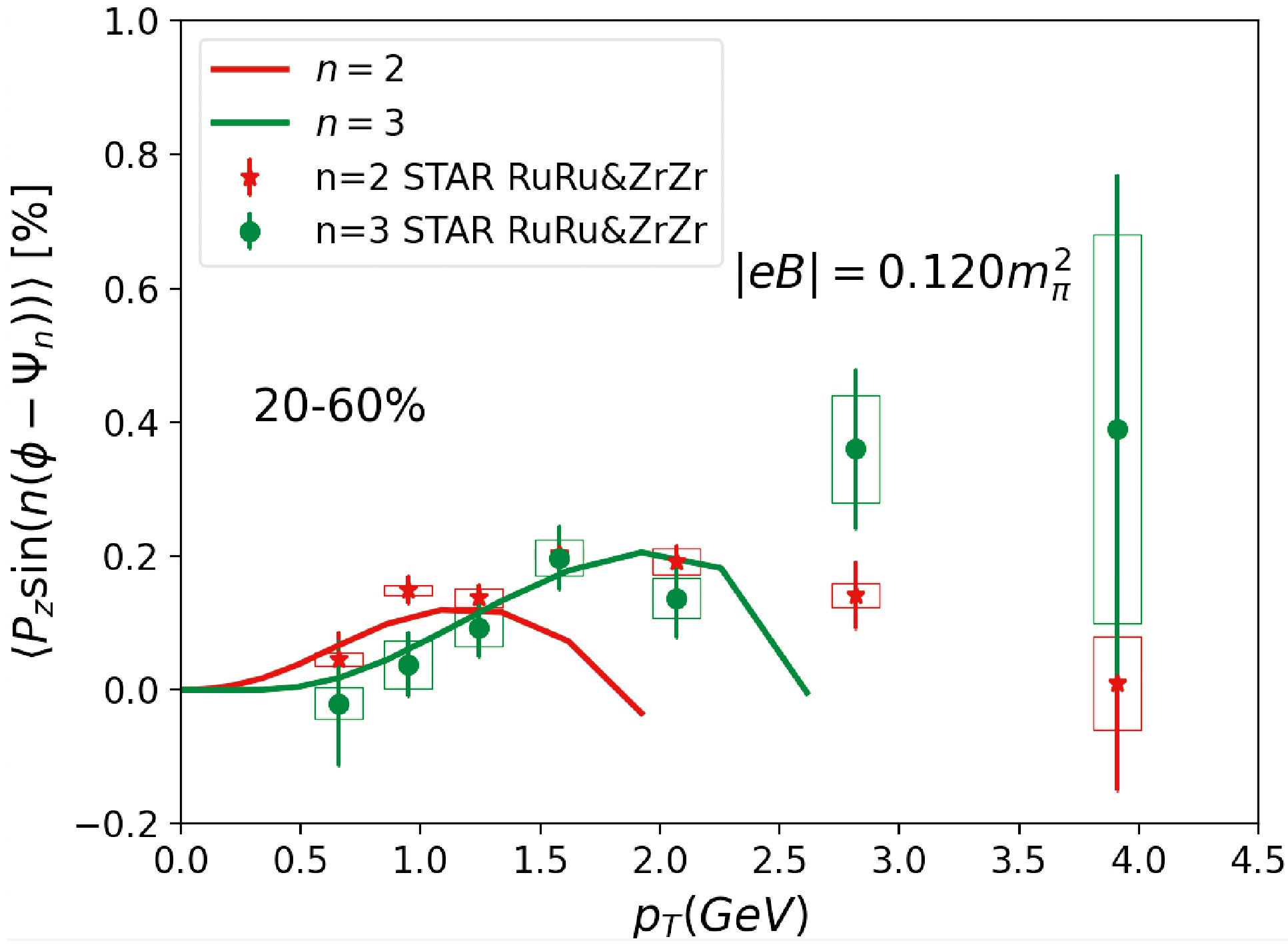
Figure 2.  (color online) (a) Centrality dependent Lambda local spin polarization from the isobar collisions: symbols are experimental results from the STAR collaboration [61] while the shaded band corresponds to theoretical results with magnetic field for $ \omega=\omega^{\rm th} + \omega^{\rm SIP} $ (BBP). (b) Centrality dependence of the magnetic field extracted according to the Lambda local spin polarization (blue symbols) and the direct photon elliptic flow (red symbols) [39].

In the centrality class 20% − 60%, the STAR collaboration also measured the transverse momentum dependent local spin polarization for the Lambda hyperon [61]. Although the ordering in Fig. 2 (a) is not obvious, as shown in Fig. 3, from the $ p_T $ dependent Lambda local spin polarization, in the low $ p_T $ region, a larger $ n=2 $ modulation is observed than in $ n=3 $. As we emphasized previously, this ordering indicates the presence of a weak magnetic field. Moreover, our theoretical calculation gives a consistent description of the $ p_T $ dependence. The deviations at large $ p_T $, where hydrodynamics becomes invalid and perturbative contributions to spin local polarization can be important, should not be a surprise.

Figure 3.  (color online) Transverse momentum dependent Lambda local spin polarization for the $ n=2 $ (red) and $ n=3 $ (green) modes of the isobar collisions in the 20%−60% centrality class.

For the conversion of quark spin from QGP, and consequently, the spin polarization of Lambda hyperon, we observed a novel effect originating from the weak magnetic field. Unlike coupling via a finite magnetic moment of the hyperon $ \mu_\Lambda $, namely, $ \omega_{\mu\nu}\to \omega_{\mu\nu} + Q F_{\mu\nu} \mu_\Lambda/T $ [14], this novel effect reflects a small dissipative correction in the quark phase space distribution. The weak magnetic effect can be crucial to the observed Lambda local spin polarization, not only because it correctly captures the sign observed in experiments, but also because it determines the ordering of the second- and third-order modulations of the local spin polarization. Using hydrodynamical simulations, the experimentally measured Lambda local spin polarization can be well understood. The required fields in different centralities, as shown in Fig. 2 (b), are consistent with the estimations based on direct photon elliptic flow. These are indeed weak fields as they satisfy $ |eB|\ll m_\pi^2 $. In fact, using the mean value from Fig. 2 (b), the time integrated value can be obtained as $\mathscr{B}=\int {\rm d}t eB\lesssim 50$ MeV, which is too weak to induce splitting in global polarization between Λ and $ \bar \Lambda $ [62].

We are grateful to Xiangyu Wu for providing us the centrality classifications with eccenticity parameters for the isobar systems.