-
Unstable states are ubiquitous phenomena in contemporary physics, manifesting across various disciplines such as molecular physics, nuclear physics, and particle physics. In hadronic physics, the prevalence of unstable resonances is particularly notable within the context of strong interactions, where new resonant states are frequently encountered and documented. These resonances assume significance in unraveling the fundamental characteristics of hadrons and their interactions, perpetuating their investigation as a vibrant research area within the field of particle physics.
To explore the characteristics of unstable states across diverse branches of physics, several models sharing a similar conceptual framework have independently emerged. Among these models, the Friedrichs model is prominent as a simple non-relativistic Hamiltonian that couples a bare discrete state to a bare continuous state [1]. Within this model, the solutions for unstable generalized eigenstates can be rigorously obtained and expressed in terms of the bare states. In the quantum field theory, the Lee model was developed to investigate the properties of field renormalization [2]. This model considers two nucleon states, denoted as N and V, which can be converted to each other by absorbing or emitting a bosonic θ particle through processes
$ V\rightleftharpoons N+\theta $ . Analogous models can be found in various domains, such as the Jaynes-Cummings model in quantum optics [3] and the Anderson model in condensed matter physics [4]. In this article, we collectively refer to these models as the Friedrichs-Lee (FL) model, highlighting their common conceptual foundation. The generalized eigenstates of the full interacting Hamiltonian within the FL model can be explicitly determined in terms of the original discrete state and the continuum states.The original FL model, which involves only one discrete and one continuous state, is often considered as a toy model owing to its simplicity. It is often employed to comprehend the properties of bound, virtual, and resonant states that appear in the scattering processes. When the bare discrete state is above the continuum threshold, its pole position moves to the second sheet and becomes a pair of resonance poles. If the bare discrete state is below the threshold, an accompanied virtual state pole would appear on the second sheet when the interaction is turned on. In addition to these states generated from the bare discrete states, there could also be dynamically generated states from the singularities of the interaction vertices [5]. The mathematical background of describing the unstable states is the Rigged Hilbert Space (RHS) quantum mechanics [6−8], rather than the conventional Hilbert space. In the RHS quantum mechanics, Hamiltonian H, as an Hermitian operator, could have generalized complex eigenvalues and the related eigenstates corresponding to the pole of the S-matrix that lies on the unphysical sheet of the analytically continued energy plane, commonly referred to as the Gamow states. The Friedrichs model was also extended to include more continuous or discrete states and with a more realistic interaction vertex function. Thus, it has been extensively applied in a wide range of realistic scenarios, particularly to study hadronic scattering processes [9−14]. Furthermore, coupled-channel models sharing similar characteristics have demonstrated success in describing various resonance phenomena in different physical systems [15−25]. The widespread applicability and efficacy of these models in describing resonance phenomena render them as effective tools in studying the properties of unstable states in different physical contexts.
In hadron physics, the usual effective field theory calculation of the scattering amplitude encounter challenges pertaining to unitarity and analyticity. The perturbative S-matrix generally fails to generate bound states or resonance poles on the analytically continued Riemann surface of the energy plane. Various unitarization methods are used to address this, such as the K-matrix method. The typical K-matrix parameterization of the S-matrix such as,
$S=\dfrac {1-{\rm i}\,K}{1+{\rm i}\,K}$ , lacks a dynamical origin and enforces unitarity by hand. However, this parametrization does not guarantee the absence of unphysical spurious poles, including those located in the complex energy plane of the first Riemann sheet, which violates causality. In contrast, the FL model achieves unitarity as a consequence of its dynamics, and the Hermitian property of the Hamiltonian ensures the absence of spurious poles in the first Riemann sheet. These are the immediate advantages of these types of models over the K-matrix parameterization.While notable achievements have been made in the application of such models, certain aspects still require further improvement. From a quantum field theory perspective, the previous model only considers the contribution of intermediate s-channel discrete states to the amplitude. However, other types of interactions are not included. The first one results from the crossed channels in the two-to-two scattering amplitude, where the intermediate particle can also appear as the t- or u-channel propagators. The second one involves the contact interactions, such as the four-point vertex. When a partial wave projection is performed, both of these interactions can be represented by continuum-continuum interactions. These interactions introduce a mild background to the final experimental observation, potentially interfering with the s-channel resonances and modifying the lineshape. It is crucial to include these background contributions in the analysis of the experimental data while preserving analyticity and unitarity. The commonly used Breit-Wigner parametrization to parameterize the t- or u-channel resonance and a polynomial to parameterize the background would violate the unitarity. A naïve K-matrix unitarization may introduce unexpected spurious poles in the S-matrix. Thus, incorporating the continuum-continuum interactions into the FL-like models could overcome these problems. However, a general continuum-continuum interaction renders the model no longer solvable. In Refs. [10, 26], a particular form of separable interaction involving the continuum states is introduced, where the interaction vertex function between the discrete states and the continuum also appears as the factors of the separable interaction between two continuum states. The Hamiltonian is
$ \begin{aligned}[b] H=\;&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{i=1}^N \int_{a_i}^\infty \mathrm d \omega \,\omega|\omega;i\rangle\langle \omega;i| \\ &+\sum_{i,j=1}^C v_{ij}\Big(\int_{a_i}^\infty\mathrm d \omega f_i(\omega)|\omega;i\rangle\Big)\Big(\int_{a_j}^\infty\mathrm d \omega f^*_j(\omega)\langle \omega;j|\Big) \\ &+\sum_{j=1}^D\sum_{i=1}^C \Bigg[ u_{ji}^*|j\rangle\Big(\int_{a_i}^\infty\mathrm d \omega f^*_i(\omega)\langle \omega;i|\Big)\\&+ u_{ji}\Big(\int_{a_i}^\infty\mathrm d \omega f_i(\omega)|\omega;i\rangle \Big) \langle j| \Bigg], \end{aligned} $

(1) where form factor
$ f_i(\omega) $ is associated with the i-th continuum state$ |\omega;i\rangle $ , both for its interaction with different discrete states and interaction with other continuum states. Two aspects of this model could be improved. First, the interaction between discrete states$ |j\rangle $ and the continuum could be extended to general function$ f_{ij}(\omega) $ for a more realistic description of the strong interaction in the real world. Using the quark pair creation (QPC) model as an example, the interaction between a meson and their decay products is expressed as a complicated integration between the wave function for the three states and the pair production vertex [12, 27]. Thus, the form of the interaction function depends both on the discrete state and the continuum. Second, the interaction between the continuum states need not be factorized using the same factors as the interaction between the discrete state and the continuum. In this paper, we demonstrate that after factorizing the continuum-continuum interaction independent of the discrete-continuum interaction, the model remains exactly solvable. In principle, the extra continuum-continuum interaction should be the residue interaction after subtracting the s-channel intermediate discrete state contribution, which could have no relation with the discrete-continuum interaction. Whether this interaction can be expressed as a separable potential remains an open question. Some physical applications of the separable potentials in discussing real world problems already exist, for example, describing the interaction between the open-flavor and hidden-flavor channels in momentum space [28]. Our formalism differs from this implementation by two key advances. First, we parameterize all continuum-continuum couplings via separable potentials without distinction between open-flavor and hidden-flavor channels. This enables a more general description of coupled-channel systems. Second, through the projection of potentials onto angular momentum eigenstates through spherical harmonic expansion, the three-dimensional momentum integration reduces to a one-dimensional radial integral. This systematically eliminates angular variables, significantly simplifying both numerical implementation and analytical discussion of momentum dynamics. Moreover, generally, a square-integrable interaction potential between continuum states could be expanded using a series of general separable basis. We can also expand both the discrete-continuum interaction vertex and continuum-continuum interaction vertices using the same function basis. Thus, the study of such separable potentials may have broader physical applications. In this paper, our focus is on these two types of improvements: the incorporation of a more general discrete-continuum interaction and various separable continuum-continuum interactions among multiple bare discrete and continuum states in the FL model. By rigorously solving the eigenstates for the Hamiltonian, we obtain the "in'' and "out'' states, the scattering S-matrix, the discrete state solution, and other mathematical physics properties. Our aim is to establish a solid foundation for the further phenomenological applications of the FL model by including these additional physical features.We organize the remainder of the paper as follows. In Sec. II, the solution of the FL model with more general interactions between discrete and continuum states is derived. Sec. III discusses a case with extra separable continuum-continuum interactions. Sec. IV studies a case when the interaction potential between continuum states can be approximated by a sum of separable potentials and considers cases when both the continuum-continuum potential and continuum-discrete potentials are approximated by a truncated series. In Sec. V, as an application, we consider some simple examples and discuss the behavior of the discrete states after turning on various interactions. Sec. VI provides the conclusion.
-
First, we consider a system with D types of discrete states and C types of continuum states, where C and D denote the numbers of the continuum and discrete states, respectively. If no interaction exists, the mass of the j-th discrete state
$ |j\rangle $ is$ M_j $ , whereas the energy spectrum of the n-th continuum state ranges as$ [a_n,\infty) $ with threshold energy$ a_n $ . The interaction between the j-th discrete and n-th continuum states can be generally represented by coupling function$ f_{jn}(\omega) $ . The full Hamiltonian can be expressed as$ \begin{align} H=&H_0+H_I, \end{align} $

(2) where free Hamiltonian
$ H_0 $ can be expressed explicitly as$ \begin{align} H_0=&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{n=1}^C \int_{a_n}^\infty \mathrm d \omega \,\omega|\omega;n\rangle\langle \omega;n|, \end{align} $

(3) and interaction part
$ H_I $ is$ \begin{aligned}[b] H_I=\;&\sum_{j=1}^D\sum_{n=1}^C \Bigg[ |j\rangle\Bigg(\int_{a_n}^\infty\mathrm d \omega f^*_{jn}(\omega)\langle \omega;n|\Bigg)\\&+ \Bigg(\int_{a_n}^\infty\mathrm d \omega f_{jn}(\omega)|\omega;n\rangle \Bigg) \langle j| \Bigg]. \end{aligned} $

(4) The free eigenstates are orthogonal to each other and the normalization conditions satisfy
$ \langle i|j\rangle=\delta_{ij} $ ,$ \langle i|\omega;n\rangle=0 $ and$ \langle \omega;n|\omega';n'\rangle=\delta(\omega-\omega')\delta_{nn'} $ . For simplicity, we first assume that no degenerate threshold and degenerate discrete states exist. If degenerate states with the same threshold and same interactions with the other states exist, the corresponding solutions will also be degenerate with the same expression after the interactions are turned on, and we will consider them as one state with degenerate degrees of freedom, similar to different magnetic quantum numbers in the absence of a magnetic field. If the states with degenerate threshold partake in different interactions, the following discussion will not be modified significantly. We will return to this case later.The general solution for energy eigenvalue problem
$ H|\Psi(E)\rangle=E|\Psi(E)\rangle $ can be represented as a linear combination of the discrete and continuum states:$ \begin{align} |\Psi(E)\rangle=\sum_{i=1}^D \alpha_i(E)|i\rangle+\sum_{n=1}^C\int_{a_n} \mathrm d\omega \psi_n(E,\omega)|\omega;n\rangle, \end{align} $

(5) where the
$ \alpha_i(E) $ and$ \psi_n(E,\omega) $ functions are defined as the coefficient functions of the discrete and continuum states, respectively. By substituting this ansatz into the eigenvalue equation and carefully examining the coefficients preceding the discrete and continuum states, we can derive two distinct sets of equations:$ \begin{aligned}[b] &(M_j-E)\alpha_j(E)+\sum_{n=1}^C \int_{a_n}^\infty \mathrm d \omega f^*_{jn}(\omega)\psi_n(E,\omega)=0\,,\\&\quad \mathrm{for } \ j=1,\dots,D \end{aligned} $

(6) $ \begin{aligned}[b] &\sum_{j=1}^D\alpha_j (E)f_{jn}(\omega)+(\omega-E)\psi_n(E,\omega)=0\,,\\ &\quad \mathrm{for} \ \ n=1,\dots C,\ \ \mathrm{and}\ \ \omega>a_n. \end{aligned} $

(7) An important observation to make is that the formula exhibits a nontrivial complexity, which does not appear in the single-channel scenario. Specifically, for a given energy range
$ a_l < \omega < a_{l+1} $ , only l equations are present in Eq. (7).Consequently, the eigenvalue problem yields both continuum and discrete solutions. These solutions correspond to different regimes of the spectrum, which will be addressed carefully in the following.
1. Continuum state solutions
When energy E is above the highest threshold, that is
$ E>a_C $ , there will be C continuum states when the interactions are turned on; therefore, the m-th continuum solution will be$ \begin{aligned}[b]& |\Psi_m(E)\rangle=\sum_{i=1}^D \alpha_{mi}(E)|i\rangle+\sum_{n=1}^C\int_{a_n} \mathrm d\omega \psi_{mn}(E,\omega)|\omega;n\rangle,\\& \quad m=1,2,\dots,C\,. \end{aligned} $

(8) However, when energy E is lower than the highest threshold, e.g.,
$ E\in[a_l,a_{l+1}) $ ,$ l<C $ , there will be l degenerate continuum eigenstates,$ m=1,2\dots,l $ , and the other states are not well-defined below their thresholds and are set to$ \mathbf 0 $ . To remove the ambiguity of the degenerate states, we require that when the interaction is turned off, i.e.,$ f_{jm}(\omega)\to 0 $ ,$ |\Psi_m\rangle $ tends to free continuum state$ |E;m\rangle $ . We expect that, when eigenvalue$ E\in[a_1,a_2] $ , we can solve$ \alpha_{1,i} $ and$ \psi_{1,i} $ in$ |\Psi_1(E)\rangle $ and then analytically extend these parameters to$ E\in[a_2,a_3] $ to solve$ |\Psi_2(E)\rangle $ , etc. Thus, the eigenfunctions can be uniquely determined. From Eq. (6,7) in terms of the coefficients in Eq. (8), coefficient function$ \psi_{mn}(E,\omega) $ before the continuum state in different energy regions can be expressed as$ \begin{aligned}[b] (\mathrm{ for}\ n\le l) \quad \psi_{mn}(E,\omega)=\;&\gamma_n\delta_{mn}\delta(\omega-E)\\&+\frac 1{E-\omega\pm {\rm i}\, 0}\sum_{j=1}^D \alpha_{mj}(E)f_{jn}(\omega)\,, \\ (\mathrm{ for}\ n> l) \quad \psi_{mn}(E,\omega)=&\frac 1{E-\omega\pm {\rm i}\, 0}\sum_{j=1}^D \alpha_{mj}(E)f_{jn}(\omega)\,. \end{aligned} $

This equation can be concisely expressed in one equation by using Heaviside step function
$ \Theta(x) $ :$ \begin{aligned}[b] \psi^\pm_{mn}(E,\omega)=\;&\gamma_n\delta_{mn}\delta(\omega-E)\Theta(E-a_n)\\&+\frac 1{E-\omega\pm {\rm i}\, 0}\sum_{j=1}^D f_{jn}(\omega)\alpha_{mj}(E)\,. \end{aligned} $

(9) Notice that
$ \psi^{\pm}_{mn} $ is a generalized function, and to distinguish between different integral contours, we have included$\pm {\rm i}\,0$ in the denominator of the integral in Eq. (8). The$ \psi^+ $ state corresponds to the coefficient for the in-state, whereas$ \psi^- $ corresponds to those of the out-state. For the convenience of the future discussions, we will omit superscripts$ \pm $ in the notations. The appropriate superscript can be easily inferred based on the context. When there is a need to explicitly indicate the in-state or out-state, we will use the superscript accordingly.Inserting this equation back into Eq. (6), we can obtain the equations for coefficient functions
$ \alpha_{mk}(E) $ for$ m=1,2,\dots l $ $ \begin{aligned}[b] &-\sum_{k=1}^D\alpha_{mk}(E)\Big[\delta_{kj}(E-M_j)-\sum_{n=1}^C\int_{a_n}^\infty\mathrm d\omega\, \frac{f_{kn}(\omega)f^*_{jn}(\omega)}{E-\omega\pm {\rm i}\,0}\Big]\\&\quad+ \sum_{n=1}^C\gamma_m(E)\delta_{mn}f^*_{jn}(E)=0. \end{aligned} $

(10) With many different discrete and continuum states involved, the representation becomes much more complex than the simplest version. The formula and derivation procedure can be simplified by introducing the matrix form. In the following, the matrices are represented in bold type, the dot symbol "
$ \cdot $ " represents the matrix product, and the matrix element is expressed in the form of$ (\boldsymbol\eta)_{ij} $ . For example, Eq. (10) can be expressed in matrix form as$ \begin{align} - \boldsymbol \alpha^\pm(E)\cdot \boldsymbol \eta_\pm(E)+\boldsymbol \gamma(E)\cdot \mathbf f^\dagger(E) =0\,, \end{align} $

where
$ \boldsymbol \alpha $ and$ \mathbf f $ are the$ C\times D $ and$ D\times C $ matrices for coefficients$ \alpha_{mk} $ and$ f_{jm} $ , respectively. Matrix$ \boldsymbol\gamma $ is defined as a diagonal matrix of dimension$ C\times C $ $ (\boldsymbol \gamma)_{mn}(E)=\gamma_n\delta_{mn}\Theta(E-a_n), $

whose diagonal elements
$ \gamma_n $ can differ in principle for different n values, and the values can be determined by the normalization conditions. The$ \boldsymbol\eta_\pm $ matrix, the inverse of the resolvent function matrix, has dimension$ D\times D $ , and every matrix element is$ \begin{align} (\boldsymbol \eta_\pm)_{kj}(E) =(E-M_j)\delta_{kj}-\sum_{n=1}^C\int_{a_n}^\infty\mathrm d\omega\, \frac{f_{kn}(\omega)f^*_{jn}(\omega)}{E-\omega\pm {\rm i}\,0}. \end{align} $

(11) Generally, the determinant of the η matrix does not vanish for
$ a_l<E<a_{l+1} $ , and matrix$ \boldsymbol\alpha^\pm $ can be represented as$ \begin{align} \boldsymbol \alpha^\pm(E)= \boldsymbol \gamma(E)\cdot \mathbf f^\dagger(E)\cdot\boldsymbol \eta_{\pm}^{-1}(E). \end{align} $

Inserting this result into Eq. (9), coefficient functions
$ \psi_{mn} $ before the continuum states can be obtained in matrix representation:$ \begin{align*} \boldsymbol \psi^\pm(E,\omega)=\boldsymbol\gamma\delta(\omega-E)+\frac 1{E-\omega\pm {\rm i}\,0}\boldsymbol \gamma(E)\cdot \mathbf f^\dagger(E)\cdot\boldsymbol \eta_\pm^{-1}(E)\cdot \mathbf f(\omega). \end{align*} $

The solution of the continuum eigenstate can then be expressed as
$ \begin{aligned}[b] |\Psi^\pm_m(E)\rangle=\;&\sum_{i=1}^D \alpha^\pm_{mi}(E)|i\rangle+\sum_{n=1}^C\int \mathrm d\omega \psi^\pm_{mn}(E,\omega)|\omega;n\rangle \\=\;&\gamma_m\Theta(E-a_m)|E,m\rangle+\sum_{k=1}^D\big( \boldsymbol \gamma(E)\cdot \mathbf f^\dagger(E)\cdot\boldsymbol \eta_\pm^{-1}(E)\big)_{mk}\\&\times\Bigg(|k\rangle+\sum_{n=1}^C\int_{a_n} {\rm d} \omega\frac {f_{kn}(\omega)}{E-\omega\pm {\rm i}\,0}|\omega;n\rangle\Bigg)\,. \end{aligned} $

(12) Note that in energy region
$ a_l<E<a_{l+1} $ , wave function$ |\Psi^\pm_m\rangle $ for$ m>l $ should vanish. Another required condition is that, when coupling function$ f_{jn} $ vanishes,$ |\Psi^\pm_m(E)\rangle $ tends to$ |E,m\rangle $ . Therefore, coefficient$ \gamma_m $ is determined to be 1. We can check that the normalization satisfies$ \langle \Psi^\pm_m(E)|\Psi^\pm_n(E')\rangle=\delta(E-E')\delta_{mn} $ . From the perspective of the scattering theory,$ |\Psi^+\rangle $ is the "in" state and$ |\Psi^-\rangle $ is the "out" state; therefore, the S-matrix can be obtained by inner product of the "in" and "out" states as$ \begin{aligned}[b]&\langle \Psi^-_m(E)|\Psi^+_n(E')\rangle=\gamma_m^*\gamma_n\delta(E-E') -2\pi {\rm i}\,\delta(E-E')\big(\boldsymbol\gamma(E')\\ &\cdot \mathbf f^\dagger(E')\cdot\boldsymbol \eta_+^{-1\dagger}(E)\cdot \mathbf f(E) \cdot\boldsymbol \gamma^\dagger(E) \big)_{nm} \\ =\;&\delta(E-E')\big[ \boldsymbol \gamma\cdot\big(1 -2\pi {\rm i}\, \mathbf f^T(E)\cdot\boldsymbol \eta_+^{-1}(E)\cdot \mathbf f^*(E) \big)\cdot \boldsymbol \gamma\big]_{nm}. \end{aligned} $

(13) The
$ \boldsymbol\eta_\pm(E) $ function can be analytically extended to the complex E plane with$ \eta_+(E) $ and$ \eta_-(E) $ coinciding with$ \boldsymbol \eta(E) $ on the upper and lower edges of the real axis above the thresholds, respectively. We can also define the analytically continued S-matrix as$ \mathbf S=1 -2\pi {\rm i}\, \mathbf f^T(E)\cdot\boldsymbol \eta^{-1}(E)\cdot \mathbf f^*(E), $

(14) where E is analytically continued to the complex energy plane, and only when E is real and on the upper edge of the cut above the lowest threshold
$ a_1 $ is the S-matrix the physical one. Given the presence of C continuous states with distinct thresholds,$ 2^C $ different Riemann sheets generally exist for the analytically continued S-matrix. Because only the Riemann sheets nearest to the physical region affect the physical S-matrix the most, we label the m-th sheet as the Riemann sheet continued from the physical region$ (a_m,a_{m+1}) $ , where the first sheet in which the physical S-matrix resides is called the physical sheet by convention.Note that the formula of the scattering matrix in Eq. (14) has important phenomenological applications. For example, in studying the particle-particle scattering processes, the two particles that collide or those final states (often called channels in the scattering experiments) form continuum states, whereas the intermediate resonance states are considered the discrete states. The
$ (n,m) $ -th element of the scattering matrix in Eq. (14) can describe the scattering amplitudes from the channel of the n-th continuum state to the m-th channel. The coupled-channel unitarity is naturally satisfied among all the related scattering amplitudes owing to the apparent relation$ \mathbf S\mathbf S^\dagger= I $ . Furthermore, when the coupling function between the discrete and continuum states is reliably described by some dynamical models, the physical observables, such as cross sections, can be predicted or calculated [28].2. Discrete state solutions:
In Eqs. (6) and (7), if eigenvalue
$ E\notin [a_n,\infty) $ for$ n=1,\dots, C $ ,$\pm {\rm i}\, 0$ need not be introduced in the denominator of the integrand, we have$ \psi_n(E,\omega)=\frac 1{E-\omega}\sum_j f_{jn}(\omega)\alpha_j(E)\,, \quad (\mathrm{for} \ n=1,\dots C) $

(15) $ \begin{aligned}[b] (\boldsymbol\alpha(E)\cdot \boldsymbol \eta(E))_j=\;&\sum_{k=1}^D\alpha_k(E)\Bigg[\delta_{kj}(M_j-E)\\&-\sum_{m=1}^C\int_{a_m}^\infty\mathrm d\omega\, \frac{f_{km}(\omega)f^*_{jm}(\omega)}{\omega-E}\Bigg]=0\,,\\&\quad (\mathrm{for } \ j=1,\dots,D)\,. \end{aligned} $

(16) To obtain nonzero solutions of
$ \alpha_k(E) $ , the condition$ \det \boldsymbol\eta(E)=0 $ is necessary. This condition implies that discrete energy solutions may exist for this equation, which generally correspond to the poles of the S-matrix elements. If solutions exist on the first sheet, they must reside on the real axis below the lowest threshold because the eigenvalue of a Hermitian Hamiltonian for a normalizable eigenstate should be real. Additionally, solutions can also exist on the unphysical sheets, which may correspond to complex conjugate resonance poles on the complex energy plane or to virtual state poles located on the real axis below the lowest threshold. At least D discrete solutions may tend to the bare discrete states, i.e.,$ \alpha^{(l)}_k\to \delta_{kl} $ and$ E\to M_l $ for$ l=1,2,\dots, D $ , as all coupling function$ f_{ln}\to 0 $ . Furthermore, there could also be other solutions corresponding to dynamically generated states that do not go to the bare states when the interactions are switched off. Generally, the solutions does not exhibit degeneracy, indicating that the poles for S-matrix are simple poles. If the degenerate solutions occur for$ \det \boldsymbol\eta(E)=0 $ , this implies that two or more poles may coincide and form a higher order pole. This scenario is considered to be accidental and only occurs for some special coupling functions. For our discussion, we will not consider this special case and assume that the solutions are non-degenerate. Subsequently, for each energy solution$ E_i $ , we can also determine eigenvector$ \alpha^{(i)}_k(E_i) $ and$ \psi^{(i)}_n(E_i,\omega) $ , and the wave function of discrete state is expressed as$ \begin{align} |\Psi^{(i)}(E_i)\rangle=\sum_{j=1}^D \alpha^{(i)}_j(E_i)\Big(|j\rangle+\sum_{n=1}^C\int_{a_n} \mathrm d\omega \frac{f_{jn}(\omega)}{E_i-\omega}|\omega;n\rangle\Big). \end{align} $

(17) When
$ E_i $ lies on the real axis of the first Riemann sheet below the lowest threshold, this wave function corresponds to a bound state. In this case, the integrals in$ \eta(E_i) $ and$ \alpha_k^{(i)}(E_i) $ are real. The normalization for this state is well defined, and$ \alpha_k^{(i)}(E_i) $ can be selected such that$ \begin{aligned}[b] 1=&\sum_{jk}^{D} \alpha_k^{(i)}(E_i)\Big(\delta_{jk}+\sum_{m=1}^C\int_{a_m} {\rm d} \omega\frac{f_{km}(\omega)f^*_{jm}(\omega)}{(E_i-\omega)^2}\Big)\alpha_j^{(i)*}(E_i) \\=&\sum_{jk}^D\alpha^{(i)}_{k}(E_i)\eta_{kj}'(E_i)\alpha^{(i)*}_{j}(E_i)\,, \end{aligned} $

(18) with
$ \eta'_{kj}(E) $ being the derivative of$ \eta_{kj}(E) $ w.r.t. E. This equation has a probabilistic explanation. The first term on the right-hand side represents the probability of finding the bare discrete states in the bound state, whereas the second one represents those of determining the bare continuum states in it. If we define$ Z^{(i)}_k=|\alpha_k^{(i)}(E_i)|^2, $

$ \begin{aligned}[b] X^{(i)}_m=\sum_{k,j=1}^D\alpha_k^{(i)}(E_i)\Big(\int_{a_m} {\rm d} \omega\frac{f_{km}(\omega)f^*_{jm}(\omega)}{(E_i-\omega)^2}\Big)\alpha_j^{(i)*}(E_i), \end{aligned} $

(19) then
$ Z^{(i)}\equiv \sum_k Z^{(i)}_k $ is called the elementariness and$ X^{(i)}\equiv \sum_{m=1}^CX^{(i)}_m $ is called the compositeness for the bound state. When solution$ E_i $ resides on the unphysical sheet, the integral contour must be deformed to bypass the pole position in different integrals, as shown in Fig. 1. For resonance poles on the m-th sheet, the integral contour for the first m-th integral should be deformed accordingly, following the contour shown in Fig. 1. In such cases, the usual normalization may not be well-defined, as the integral contour for the pole and its conjugate pole are not consistent. Therefore, the normalization must be defined through the inner product of the state and its conjugate state that corresponds to the conjugate pole. The resulting normalization is similar to Eq. (18) with$ E_i $ replaced by the pole position on the unphysical sheet and the integral contour suitably deformed. However, note that the probabilistic interpretation of each term in the sum will no longer hold, as the terms may not be real or positive for poles on the unphysical plane.Next, we study the case with the degenerate threshold. If different continuum states exist with the same threshold
$ a_n $ , with degeneracy$ h_n $ , we must add another label κ to the continuum to denote the different continuum states sharing the same threshold,$ |\omega,n\kappa\rangle $ . Thus, all the indices in the equations labeling the continuum states would include the additional indices κ to label the degenerate states, for example,$ f_{in}(\omega) $ ,$ \alpha_{ni} $ ,$ \gamma_m $ ,$ \psi_{mn} $ , and$ \Psi_m $ become$ f_{i,n\kappa} $ ,$ \alpha_{n\kappa, i} $ ,$ \gamma_{m\kappa} $ , and$ \psi_{m\kappa,n\kappa'} $ .$ \mathfrak h=\sum_{n=1}^C h_n $ continuum states will exist. The sum over the continuum states must also sum over κ. Matrix$ \boldsymbol\gamma $ is defined as$ \gamma_{m\kappa,n\kappa'}(E)=\delta_{mn}\delta_{\kappa,\kappa'}\Theta(E-a_n) $ . The$ \mathbf f $ matrix becomes a$ D\times \mathfrak h $ matrix and$ \boldsymbol \eta $ is still a$ D\times D $ matrix. With all these changes, the previous discussion and equations can be smoothly used in this case. -
In the previous case, we considered a scenario in which a bare continuum state is only coupled to the bare discrete states but not to the other continuum states. However, when the direct interactions between continuum states become significant, it is more appropriate to include the corresponding term in the interaction Hamiltonian
$ H_I $ . Analytically solving the Hamiltonian with a general continuum-continuum interaction is generally not feasible. Therefore, in this section, we focus on a case with a separable interaction, which still enables an exactly solvable solution.The Hamiltonian including D discrete states and C continua with factorizable self-interacting contact terms can be expressed as
$ \begin{aligned}[b] H=\;&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{n=1}^C \int_{a_n}^\infty \mathrm d \omega \,\omega|\omega;n\rangle\langle \omega;n| \\ &+\sum_{m,n=1}^C v_{mn}\Bigg(\int_{a_m}^\infty\mathrm d \omega g_m(\omega)|\omega;m\rangle\Bigg)\Bigg(\int_{a_n}^\infty\mathrm d \omega g^*_n(\omega)\langle \omega;n|\Bigg) \\ &+\sum_{j=1}^D\sum_{n=1}^C \Bigg[ |j\rangle\Bigg(\int_{a_n}^\infty\mathrm d \omega f^*_{jn}(\omega)\langle \omega;n|\Bigg)\\&+ \Bigg(\int_{a_n}^\infty\mathrm d \omega f_{jn}(\omega)|\omega;n\rangle \Bigg) \langle j| \Bigg]. \end{aligned} $

(20) In this case, new coupling constants
$ v_{mn} $ between two continuum states have been incorporated in the interaction terms, and$ v_{mn}=v_{nm}^* $ is satisfied to meet the Hermiticity requirement. Form-factor functions$ g_n(\omega) $ are involved in the interaction between two continuum states, and$ f_{jn}(\omega) $ represents the interaction vertex between the j-th discrete and n-th continuum states. We assume that the$ f_{jn} $ matrix is of full rank; otherwise, we can always construct a decoupled state using a linear combination of the discrete or continuum states. For simplicity, we first assume that the coupling constant matrix$ v_{mn} $ is non-degenerate and will return to the degenerate$ v_{mn} $ case later.Similar to the previous case, we will also solve Hamiltonian eigenfunction
$ H|\Psi(E)\rangle=E|\Psi(E)\rangle $ . The eigenstate of the Hamiltonian with eigenvalue E can be be expanded in terms of the discrete and continuum states as$ \begin{align} |\Psi(E)\rangle=\sum_{i=1}^D \alpha_i(E)|i\rangle+\sum_{n=1}^C\int_{a_n} \mathrm d\omega \psi_n(E,\omega)|\omega;n\rangle. \end{align} $

(21) Inserting this ansatz into the eigenvalue equation and projecting to the discrete eigenstates or the continuum ones, we find two sets of equations:
$ \begin{align} & (M_j-E)\alpha_j(E)+A_j(E)=0,\quad j=1,\dots,D \end{align} $

(22) $ \begin{aligned}[b] &\sum_{j=1}^D\alpha_j (E)f_{jn}(\omega)+(\omega-E)\psi_n(E,\omega)+\sum_{m=1}^Cv_{nm}B_m(E)g_n(\omega)=0, \\&\quad n=1,\dots,C, \quad \mathrm{and\ }\omega>a_n \\[-15pt]\end{aligned} $

(23) where two new integration functions
$ A_j(E) $ and$ B_n(E) $ have been defined as$ \begin{aligned}[b]& A_j(E)\equiv\sum_{n=1}^C\int_{a_n}^\infty\mathrm d\omega\, f^*_{jn}(\omega)\psi_n(E,\omega), \\& B_n(E)\equiv\int_{a_n}^\infty\mathrm d\omega\, g^*_n(\omega)\psi_n(E,\omega). \end{aligned} $

(24) Because we have assumed that continuum-continuum coupling constants
$ v_{mn} $ are not degenerate, C-independent$ B_n(E) $ functions exist. In contrast, if$ v_{mn} $ matrix is degenerate, the only change is that fewer$ g_n $ and$ B_n $ functions will exist.Similarly, as discussed previously, if the eigenvalue
$ E\in [a_l,a_{l+1}) $ for$ l< C $ , there should be l continuum solutions$ |\Psi_m(E)\rangle $ ,$ m=1,2,\dots, l $ with the same eigenvalue E. As the interactions are gradually deactivated, these continuum solutions should tend to well-defined states$ |E,m\rangle $ . This ensures that in the absence of interactions, the continuum solutions can be uniquely determined as the continuum states$ |E,m\rangle $ , thus eliminating any ambiguity in their characterization. This requirement guarantees a smooth transition from the interacting system to the non-interacting system.Under these specific conditions, the l contiuum state solutions for
$ a_l<E<a_{l+1} $ coincide with the first l states for$ E>a_C $ . Consequently, it is sufficient to solve for the solutions when$ E>a_C $ , and then the first l solutions can be obtained for the$ E<a_l $ range. For each continuum state$ |\Psi_m(E)\rangle $ with$ E>a_C $ , the corresponding coefficients are denoted as$ \alpha_{jm} $ ,$ \psi_{nm}(E,\omega) $ ,$ A_{jm} $ , and$ B_{nm} $ as in Eqs. (21), (22), and (23). Subsequently, we can obtain$ \begin{align} &\alpha^\pm_{jm}(E)=\frac1{E-M_j}A^\pm_{jm}(E), \end{align} $

(25) $ \begin{aligned}[b] \psi^\pm_{nm}(E,\omega)=\;&\delta_{nm}\delta(\omega-E)+\frac 1{E-\omega\pm {\rm i}\,0}\\&\times\Bigg(\sum_{j=1}^D \frac{A^\pm_{jm}(E) f_{jn}(\omega)}{E-M_j}+\sum_{n'=1}^C v_{nn'}B^\pm_{n'm}(E)g_n(\omega)\Bigg) \,. \end{aligned} $

(26) The procedure of solving Eq. (26) is straightforward but intricate. The strategy is to apply the operations
$\sum_n\int_{a_n} {\rm d}\omega f^*_{jn}(E)\times$ and$\sum_n v^*_{nm'}\int {\rm d} \omega g^*_{n}(\omega)\times$ on the left-hand side of Eq. (26). After this, we can derive the following expressions:$ \begin{align} 0 = f_{jm}^*(E)-\sum_{j'=1}^D\frac{ A_{j'm}(E)}{E-M_{j'}}\Bigg(\delta_{j'j}(E-M_{j'})-\sum_{n=1}^C\int_{a_n} {\rm d}\omega\frac {f_{j'n}(\omega)f_{jn}^*(\omega)}{E-\omega\pm {\rm i}\, 0}\Bigg) +\sum_{n'=1}^C\bigg(B_{n'm}(E)\sum_{n=1}^Cv_{nn'}\int_{a_n}\frac{f^*_{jn}(\omega)g_n(\omega)}{E-\omega\pm {\rm i}\, 0}\bigg)\,, \end{align} $

(27) $ \begin{align} 0&= v^*_{mm'}g^*_m(E)+\sum_{j=1}^D\alpha_{jm}\sum_{n=1}^Cv^*_{nm'} \int_{a_n}\frac {f_{jn}(\omega)g_{n}^*(\omega)}{E-\omega\pm {\rm i}\,0}-\sum_{n'=1}^CB_{n'm}(E)\Bigg(v^*_{n'm'}-\sum_{n=1}^Cv^*_{nm'}v_{nn'}\int_{a_n}\frac{g_n(\omega)g^*_n(\omega)}{E-\omega\pm {\rm i}\,0}\Bigg). \end{align} $

(28) The matrix representation proves to be a valuable tool in simplifying the derivation process and achieving concise results. In this context, we introduce matrices
$ \mathbf{Y} $ and$ \mathbf{F} $ with$ (C+D) \times C $ dimension, matrices$ \mathbf{V}^A $ and$ \mathbf{V}^B $ with dimensions$ D \times D $ and$ C \times C $ , respectively, matrices$ \mathbf{V}^{AB} $ and$ \mathbf{V}^{BA} $ with dimensions$ D \times C $ and$ C \times D $ , respectively, and finally, a$ (C+D) \times (C+D) $ matrix$ \mathbf{M} $ encompassing$ \mathbf{V}^A $ ,$ \mathbf{V}^B $ ,$ \mathbf{V}^{AB} $ , and$ \mathbf{V}^{BA} $ as follows$ \begin{aligned}[b]&(\mathbf Y)_{jm}=\alpha_{jm}=\frac{A_{jm}(E)}{E-M_j},\quad (\mathbf F)_{jm}= f_{jm}^*,\quad \mathrm{for}\ m=1,\cdots,C;j=1,\cdots,D, \\&(\mathbf Y)_{mn}=B_{m-D,n},\quad(\mathbf F)_{mn}=v^*_{n,m-D}g^*_n, \quad \mathrm{for}\ n=1,\cdots,C; m=D+1,\cdots,D+C, \end{aligned} $

(29) $ \begin{aligned}[b](\mathbf V^A)_{ij}=\;&\delta_{ij}(E-M_i)-\sum_{n=1}^C\int_{a_n}{\rm d}\omega\frac {f_{jn}(\omega)f_{in}^*(\omega)}{E-\omega\pm {\rm i}\,0}, \quad \mathrm{for}\ i=1,\cdots,D; j=1,\cdots,D, \\ (\mathbf V^B)_{mn}=&\Big(v_{mn}-\sum_{l=1}^C v_{ml}v_{ln}\int_{a_l}\frac{g_l(\omega)g^*_l(\omega)}{E-\omega\pm {\rm i}\,0}\Big), \quad \mathrm{for}\ m=1,\cdots,C; n=1,\cdots,C, ,\\ (\mathbf V^{AB})_{im}=&-\sum_{n=1}^Cv_{n,m}\int_{a_n}\frac{f^*_{in}(\omega)g_n(\omega)}{E-\omega\pm {\rm i}\,0}, \quad \mathrm{for}\ i=1,\cdots,D; m=1,\cdots,C, \\ (\mathbf V^{BA})_{mj}=&-\sum_{n=1}^C v^*_{nm}\int_{a_n}\frac{f_{j,n}(\omega)g^*_{n}(\omega)}{E-\omega\pm {\rm i}\,0}, \quad \mathrm{for}\ j=1,\cdots,D; m=1,\cdots,C, \\ \mathbf M_{IJ}=&\begin{pmatrix} \mathbf V^A(E)&\mathbf V^{AB}(E)\\ \mathbf V^{BA}(E)&\mathbf V^{B}(E)\end{pmatrix}_{IJ}, \quad \mathrm{for}\ I,J=1,\cdots,C+D\,. \end{aligned} $

(30) Similar to coefficients α and ψ, we have omitted superscript
$ \pm $ in the notations of matrices$ \mathbf Y $ ,$ \mathbf V $ , and$ \mathbf M $ , which can be inferred from the surrounding context. With these matrices, Eqs. (27) and (28) can be expressed in matrix form$ \begin{align} \mathbf M\cdot \mathbf Y=\mathbf F. \end{align} $

(31) or in component form
$ \sum_{j=1}^DV^A_{ij}(E) \alpha_{jm}(E)+\sum_{n=1}^CV^{AB}_{in}(E)B_{nm}(E)=f_{im}^*(E)\,, $

(32) $ \sum_{j=1}^DV^{BA}_{nj}(E)\alpha_{jm}(E)+\sum_{n'=1}^CV^B_{nn'}(E)B_{n'm}(E)=g^*_{m}(E)\delta_{m,n}\,. $

(33) Before proceeding further, let us examine some properties of these matrices. From relation
$ v^*_{mn}=v_{nm} $ , we can observe the following symmetric properties:$ \begin{aligned}[b]& (\mathbf V^{A+})^*_{ij}=(\mathbf V^{A-})_{ji},\quad (\mathbf V^{B+})^*_{mn}=(\mathbf V^{B-})_{nm}, \\& (\mathbf V^{AB+})^*_{jn}=(\mathbf V^{BA-})_{nj}\,, \quad \mathbf M^{+\dagger}=\mathbf M^-. \end{aligned} $

(34) When
$ v_{mn} $ ,$ f_{jm}(\omega) $ , and$ g_n(\omega) $ are real for real ω values, these function matrices possess real analyticity. Consequently, they can be analytically continued to the entire complex E plane and satisfy the Schwartz reflection property. Moreover, the analytically continued function matrices can relate the$ +i0 $ and$ -i0 $ counterparts, representing the limits on the upper and lower edges along the real axis above the threshold. If$ v_{mn} $ ,$ f_{jm}(\omega) $ , and$ g_n(\omega) $ are complex, the function matrices will no longer be real analytic, but the determinant of matrix$ \mathbf M $ , denoted as$ \det \mathbf M $ , remains real analytic. Thus, the analytically continued determinant exhibits the Schwartz reflection symmetry,$ \det \mathbf M(z)=\det \mathbf M^{*}(z^*) $ .In general,
$ \det \mathbf M $ is nonzero for general real E values above the lowest threshold; otherwise, if$ \det \mathbf M=0 $ for all real E values, the$ v_{mn} $ matrix would be degenerate and some continuum state would be decoupled from the other continuum states. decouples would occur in the continuum-continuum interaction, which is not our assumption at present. As a result,$ \mathbf M $ has an inverse, and$ \mathbf Y $ can be obtained using$ \mathbf Y= \mathbf M^{-1}\cdot \mathbf F $ . Thus, by inserting$ A_{jm}(E) $ or$ \alpha_{jm}(E) $ and$ B_{nm} $ into Eq. (26), we obtain coefficients$ \psi^\pm_{nm} $ , and the continuum eigenstates are solved to be$ \begin{aligned}[b] |\Psi^\pm_m(E)\rangle =\;& |E,m\rangle+\sum_{j=1}^D \alpha^\pm_{jm}(E)\\&\times\Big(|j\rangle+\sum_{n=1}^C\int_{a_n} \mathrm d\omega \frac {f_{jn}(\omega)}{E-\omega\pm {\rm i}\,0} |\omega;n\rangle\Big)\\&+\sum_{n,n'=1}^C v_{nn'}B^\pm_{n'm}(E)\int_{a_n} \mathrm d\omega \frac {g_n(\omega)}{E-\omega\pm {\rm i}\,0} |\omega;n\rangle \end{aligned} $

(35) for
$ E>a_m $ . Upon comparison with Eq. (12), this solution is different only in the last term, stemming from the presence of separable potential. Importantly, we can confirm that the solution retains the previous normalization condition,$ \langle \Psi^\pm_m(E)|\Psi^\pm_n(E')\rangle=\delta(E-E')\delta_{mn} $ . This normalization condition guarantees the orthogonality of the wave functions, ensuring their compatibility and consistency within the framework of the problem.The S-matrix can be obtained as
$ \begin{aligned}[b] S_{mn}(E,E') =\delta_{mn}\delta(E-E')-2\pi {\rm i}\delta(E-E')\end{aligned} $

$ \begin{aligned}[b] \Big(\sum_{IJ=1}^{D+C} (\mathbf F^{\dagger})_{mI}(\mathbf M^+)^{-1}_{IJ}( \mathbf F_{Jn})\Big)\,, \end{aligned} $

(36) or
$ \mathbf S(E,E') =\mathbf I\delta(E-E')-2\pi {\rm i}\delta(E-E') \mathbf F^{\dagger}\cdot (\mathbf M^+)^{-1}\cdot \mathbf F\, $

(37) in a simplified matrix form. For a more thorough derivation of the normalization and meticulous calculation of the S-matrix, please refer to Appendix A, where we provide a detailed presentation of the calculations, offering a comprehensive and in-depth derivation of the normalization condition and the S-matrix.
Subsequently, our attention turns toward the derivation of discrete eigenstates. The eigenvalues for the discrete states does not coincide with the spectrum of the continuum states. Thus, using condition
$ E\notin [a_i,\infty) $ for$ i=1,\dots, C $ , we can solve Eq. (23) and obtain$ \begin{align} \alpha_j(E)=&\frac1{E-M_j}A_j(E), \end{align} $

(38) $ \begin{align} \psi_n(E,\omega) =&\frac 1{E-\omega}\Big(\sum_{j=1}^D {\alpha_{j}(E) f_{jn}(\omega)}+\sum_{n'=1}^C v_{nn'}B_{n'}(E)g_n(\omega)\Big) \,. \end{align} $

(39) By multiplying Eq. (39) with
$ f^*_{jn}(\omega) $ and$ v^*_{nm}g_n^*(\omega) $ separately and subsequently summing over n and integrating w.r.t. variable ω, we arrive at the following expressions:$ \begin{align} 0 &=-\sum_{j'=1}^D\frac{ A_{j'}(E)}{E-M_{j'}}\Big(\delta_{j'j}(E-M_{j'})-\sum_{n=1}^C\int_{a_n} {\rm d}\omega\frac {f_{j'n}(\omega)f_{jn}^*(\omega)}{E-\omega}\Big) +\sum_{n'=1}^C\bigg(B_{n'}(E)\sum_{n=1}^Cv_{nn'}\int_{a_n}\frac{f^*_{jn}(\omega)g_n(\omega)}{E-\omega}\bigg)\,, \end{align} $

(40) $ \begin{align} 0 &=\sum_{j=1}^D\sum_{n=1}^Cv^*_{nm}\frac{ A_{j}(E)}{E-M_j} \int_{a_n}\frac {f_{jn}(\omega)g_{n}^*(\omega)}{E-\omega}-\sum_{n'=1}^CB_{n'}(E)\bigg(v^*_{n'm}-\sum_{n=1}^Cv^*_{nm}v_{nn'}\int_{a_n}\frac{g_n(\omega)g^*_n(\omega)}{E-\omega}\bigg)\,. \end{align} $

(41) The expressions obtained in these two equations deviate from Eqs. (27) and (28) by the absence of the first terms on the right-hand side. Analogous to the definition in Eq. (30), we can introduce matrices
$ \mathbf V^A $ ,$ \mathbf V^{AB} $ ,$ \mathbf V^{BA} $ ,$ \mathbf V^B $ , and$ \mathbf M $ as the analytic continuation of the matrices in Eq. (30) and$\begin{aligned}[b] \mathbf X^T=\;& \bigg(\frac{A_1}{E-M_1},\dots,\frac{A_D}{E-M_D}, B_1,\dots, B_C \bigg)\\ =\;&(\alpha_1,\dots,\alpha_D,\dots B_1,\dots, B_C)\,. \end{aligned}$

Thus, Eqs. (40) and (41) can be expressed as
$ \mathbf M\cdot \mathbf X=0. $

To obtain nonzero solutions for vector
$ \mathbf X $ , we must satisfy the condition that the determinant of$ \mathbf M $ is equal to zero, i.e.,$ \det \mathbf M(E)=0 $ . By analytically continuing this equations to different Riemann sheets and solving it on each sheet, we can determine the generalized discrete eigenvalues.When the generalized eigenvalues are determined, vector
$ \mathbf X $ can be solved for each eigenvalue. Substituting the solutions for$ \alpha_j $ and$ B_n $ into Eq. (39), we obtain the discrete solution from Eq. (21) for each generalized energy eigenvalue:$ \begin{aligned}[b] |\Psi^{(i)}(E_i)\rangle=\;&\sum_{j=1}^D \alpha^{(i)}_j(E_i)\Big(|j\rangle+\sum_{n=1}^C\int_{a_n} \mathrm d\omega \frac{f_{jn}(\omega)}{E_i-\omega}|\omega;n\rangle\Big)\\&+\sum_{n,n'=1}^C v_{nn'}B^{(i)}_{n'}(E_i)\int_{a_n} \mathrm d\omega \frac {g_n(\omega)}{E_i-\omega} |\omega;n\rangle, \end{aligned} $

(42) where superscript
$ (i) $ denotes the i-th discrete solution. The solution for$ \mathbf X $ is only determined up to a normalization. On the first Riemann sheet, the zeros of$ \det \mathbf M $ can only be located on the real axis below$ a_1 $ due to the hermicity of the Hamiltonian. These zeros correspond to the discrete eigenvalues$ E_b $ . The associated states can have a finite norm, and we can impose the normalization condition on the coefficients to ensure$ \begin{aligned}[b] 1=\;& \sum_{i=1}^D|\alpha_i(E_b)|^2+\sum_{n=1}^C\int_{a_j}^\infty {\rm d}\omega \frac 1{(E_b-\omega)^2}\\&\times\Big|\sum_{j=1}^D {\alpha_{j}(E_b) f_{jn}(\omega)}+\sum_{n'=1}^C v_{nn'}B_{n'}(E_b)g_n(\omega)\Big|^2 \\ =\;&\mathbf X(E_b)\cdot \mathbf M'(E_b)\cdot \mathbf X^*(E_b)\,. \end{aligned} $

(43) Within the framework described earlier, each term in the summation can be interpreted as the probability of finding the corresponding bare state within the bound state. However, complex energy solutions could also be present on different unphysical sheets. As the determinant of
$ \mathbf M $ is a real analytic function, these complex eigenvalue solutions appear as complex conjugate pairs.As already mentioned,
$ 2^C $ distinct Riemann sheets exist. However, for our specific purposes, we focus solely on solutions$ E_R $ that reside on the lower half Riemann sheet closest to the physical sheet. These solutions have a significant impact on the physical S-matrix elements. Because$ E_R $ lies on a nearby unphysical sheet, the evaluation of the matrix value of$ \mathbf M $ at this point requires deforming the integral contours to the corresponding sheet around$ E_R $ defined in matrices$ \mathbf V $ and$ \mathbf M $ in Eq. (30), as illustrated in Fig. 1 [5]. Additionally, in the state solution Eq. (42), the integral contours are also deformed similarly. The normalization requirement of these states may resemble Eq. (43), but with$ E_b $ replaced by$ E_R $ , and the integral contour adjusted accordingly following the deformation depicted in Fig. 1. However, note that no probabilistic explanations are available for each terms in the sum, as they may not be real. Additionally, there can also be real solutions below the lowest threshold$ a_1 $ on unphysical sheets, which correspond to virtual states. Similar to the resonant states, the corresponding integral contours should be deformed in Eqs. (42) and (30) for these states.If coupling constant matrix
$ v_{mn} $ is degenerate, certain continuum states may decouple from the contact interaction. This enables us to select a suitable set of continuum basis states in which the decoupled states do not appear in the contact interaction terms. A more general hamiltonian can be expressed as$ \begin{aligned}[b] H=\;&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{n=1}^C \int_{a_n}^\infty \mathrm d \omega \,\omega|\omega;n\rangle\langle \omega;n| \\ &+\sum_{m,n=1}^r\sum_{m',n'=1}^C v_{mn}\Big(\int_{a_m}^\infty\mathrm d \omega { g_{mm'}(\omega)}|\omega;m'\rangle\Big)\\&\times\Big(\int_{a_n}^\infty\mathrm d \omega { g^*_{nn'}(\omega)}\langle \omega;n'|\Big) \\ &+\sum_{j=1}^D\sum_{n=1}^C \Bigg[ |j\rangle\Big(\int_{a_n}^\infty\mathrm d \omega { f^*_{jn}(\omega)}\langle \omega;n|\Big)\\&+ \Big(\int_{a_n}^\infty\mathrm d \omega {f_{jn}(\omega)}|\omega;n\rangle \Big) \langle j| \Bigg]\,, \end{aligned} $

(44) where r is the rank of the continuum-continuum coupling constant matrix, and
$ v_{mn} $ ,$ m,n=1,\cdots,r $ is a non-degerate matrix. Notice that in general, although we are discussing the degererate case where$ r<C $ , this general interaction even applies when$ r>C $ , which may correspond to the case we will discuss in the next section. Because v is a Hermitian matrix, it can always be diagonalized and be selected as$ v_{mn}=\lambda_m\delta_{mn} $ for$ m,n=1,\cdots,r $ . When$ g_{mm'}\propto \delta_{mm'} $ , it reduces to the original case (20). The solution to the engenvalue problem for this Hamiltonian is straightforward as before. The difference of the results from the nondegerate case is roughly to change the definition of$ B_n $ in Eq. (24) using$ B_n= \sum_{l=1}^C \int g_{nl}\psi_l $ ($ n=1,\cdots,r $ ) and replace factor$ v_{nm} g_n $ to$ \sum_{l=1}^r v_{lm}g_{ln} $ in each equation. For a different continuum solution$ B_n $ , we would require another index m to denote the corresponding continuum solution, i.e.,$ B_{nm} $ ,$ (n=1,\cdots,r; m=1,\cdots,C) $ . Note that the range of the first subindex of$ g_{ln} $ and$ B_{nm} $ is from$ 1 $ to r and the second one from$ 1 $ to C. Thus, the summation over the first subindex of$ g_{ln} $ and$ B_{nm} $ must be from$ 1 $ to r.A special case is when
$ r=1 $ , and we can set$ v_{11}=1 $ and$ g_{1n}= v_n g_{n}(E)\equiv (\mathbf g)_n $ , where$ v_n $ is a constant and$ g_n(E) $ is a coupling function. Thus, we can rename$ B_{1m} $ to$ B_m^\pm(E)\equiv B^\pm _{1m}=\sum_{n=1}^C v_n \int {\rm d}\omega g_n(E)\psi^\pm_{nm}(E) $ . The$ \mathbf M $ matrix in Eq. (30) can be represented as$ \begin{align} \mathbf M_{IJ}=&\begin{pmatrix}\eta& -\mathfrak f \\-\mathfrak f^{{\text ‡} T}& \mathfrak g \end{pmatrix}, \quad \mathrm{for}\ I,J=1,\cdots,D+1\,, \end{align} $

(45) $ \begin{aligned}[b] \eta_{ij}(E)=&\delta_{ij}(E-M_i)-\sum_{n=1}^C\int_{a_n} {\rm d} \omega\frac {f_{jn}(\omega)f_{in}^*(\omega)}{E-\omega\pm {\rm i}\,0}, \\&\quad \mathrm{for}\ i=1,\cdots,D; j=1,\cdots,D, \end{aligned} $

(46) $ \begin{align} \mathfrak g(E)=\Big(1-\sum_{l=1}^C\int_{a_l}\frac{v_lg_{l}(\omega)v^*_lg^*_{l}(\omega)}{E-\omega\pm {\rm i}\,0}\Big) \,, \end{align} $

(47) $ \begin{align} \mathfrak f_i=\sum_{m'=1}^C\int_{a_{m'}}\frac{f^*_{im'}(\omega)v_{m'}g_{m'}(\omega)}{E-\omega\pm {\rm i}\,0}, \quad \mathrm{for}\ i=1,\cdots,D; \end{align} $

(48) $ \begin{align} \mathfrak f^{\text ‡}_j=\sum_{m=1}^C\int_{a_{m}}\frac{f_{j,m}(\omega)v_m^*g^*_{m}(\omega)}{E-\omega\pm {\rm i}\,0}, \quad \mathrm{for}\ j=1,\cdots,D; \end{align} $

(49) For the continuum eigenstate solutions,
$ \alpha_{jm} $ and$ B_m $ are solved as$ \begin{align} \alpha_{jm}=&(\eta^{-1}\cdot \mathbf f_m^*)_j+(\eta^{-1}\cdot \mathfrak f)_jB_m\,, \end{align} $

(50) $ \begin{align} B_m=&\frac{ \mathfrak f^{{\text ‡} T}\cdot \eta^{-1}\cdot \mathbf f^*_{m}+(\mathbf g^*(E))_m}{\mathfrak g(E)-\mathfrak f^{{\text ‡} T} \cdot\eta^{-1}\cdot \mathfrak f }\,, \quad m=1,\ldots,C, \end{align} $

(51) where we have defined vector
$ (\mathbf f_m)_i=f_{im} $ ,$ i=1,\cdots,D $ . Subsequently, the S-matrix can be obtained as$ \begin{align} S_{mn}(E,E')=&\delta_{mn}\delta(E-E')-2\pi {\rm i}\delta(E-E')\Big( \mathbf f_{m}\cdot( \eta^+)^{-1}\cdot \mathbf f^*_n(E) \end{align} $

(52) $ \begin{align} &+\frac{\big(\mathbf f_{m}\cdot( \eta^+)^{-1}\cdot \mathfrak f^+(E) + (\mathbf g(E))_{m}\big) \big(\mathfrak f^{+{\text ‡} T}\cdot ( \eta^+)^{-1}\cdot \mathbf f^*_{n}+(\mathbf g^*(E))_n\big)}{\mathfrak g^+(E)-\mathfrak f^{+{\text ‡} T} \cdot( \eta^+)^{-1}\cdot \mathfrak f^+ }\Big)\,. \end{align} $

(53) With the S-matrix, the observable scattering cross section can be obtained to compare with the experiments.
In the perspective of the effective field theory, discrete state
$ j_0 $ becomes decoupled when its mass$ M_{j_0} $ significantly exceeds the system's characteristic energy scale. This fundamental principle was exemplified in Weinberg's seminal work [29], where two equivalent formulations were constructed: the full theory contains the discrete state explicitly in the free Hamiltonian, whereas the reduced theory eliminates the discrete state by introducing a specific potential renormalization. Weinberg demonstrated their equivalence when$ M_{j_0}\to \infty $ , provided the potentials satisfy the matching conditions that encode the decoupling dynamics. In our present scenario, we can also construct a low energy effective Hamiltonian without this discrete state and include an effective contact interaction of the continuum states after we integrate out the intermediate discrete state in the s channel. The corresponding interaction term can be expressed using separable contact effective interaction terms as$ -\sum_{m,n=1}^C\int {\rm d} \omega \frac{f_{j_0m}(\omega)}{\sqrt{M_{j_0}}}|\omega;m\rangle\langle \omega;n|\frac{f^*_{j_0n}(\omega)}{\sqrt{M_{j_0}}}. $

(54) This interaction is similar to the previous special case with
$ r=1 $ by replacing$ v_{11}\to v_{j_0j_0}=-1 $ ,$ g_{1n}\to g_{j_0 n}= \dfrac{f_{j_0 n}}{\sqrt{M_j}} $ , and matrix elements$ v_{j_0,n}=0 $ and$ g_{mm'}=g_m\delta_{mm'} $ . It effectively adds one extra rank to the original$ v_{mn} $ matrix. To solve this eigenvalue problem, using Eq. (30) and the discussion after Eq. (44), we will have a row and column in$ \mathbf V^B $ from Eq. (54), with$ \begin{aligned}[b]& \mathbf V^B_{j_0j_0}=-1-\sum_{l=1}^C\int_{a_l}\frac{f_{j_0l}(\omega)f^*_{j_0l}(\omega)/M_{j_0}}{(E-\omega\pm {\rm i}\,0)}\,,\\& \mathbf V^B_{j_0n}=\sum_{l=1}^C\int_{a_l}\frac{v_{ln}g_{l}(\omega)f^*_{j_0l}(\omega)/\sqrt{M_{j_0}}}{(E-\omega\pm {\rm i}\,0)}. \end{aligned} $

(55) $ \mathbf V^{AB} $ will have corresponding matrix elements$ \begin{align} \mathbf V^{AB}_{ij_0}=&\sum_{n=1}^C\int_{a_n}\frac{f^*_{in}(\omega)f_{j_0n}(\omega)/\sqrt{M_{j_0}}}{E-\omega\pm {\rm i}\,0}\,, \end{align} $

(56) and similar for
$ \mathbf V^{BA} $ .$ \mathbf F $ will have element$ \mathbf F_{j_0,n}=-f^*_{j_0 n}/ \sqrt{M_{j_0}} $ . Alternatively, we can start from the original Hamiltonian with the discrete state and take the large$ M_{j_0} $ limit. From Eq. (30), taking$ M_{j_0} $ to be much larger than E in$ \mathbf V^{A}_{j_0j_0} $ , we factorize$ M_{j_0} $ and take$ E/M_{j_0}\to0 $ , i.e., making replacement$\mathbf V^{A}_{j_0j_0}\to M_{j_0} \Big(-1- \dfrac 1 {M_{j_0}}\times \sum_{n=1}^C\int_{a_n}{\rm d}\omega \dfrac{f_{j_0n}(\omega)f^*_{j_0n}(\omega)}{E-\omega\pm {\rm i}\,0}\Big)$ . Similarly, after$ M_{j_0} $ is factorized out from$ \mathbf V^A_{j_0 j_0} $ and$ \sqrt{M_{j_0}} $ from$ \mathbf V^A_{ij_0} $ ,$ \mathbf V^A_{j_0i} $ ,$ \mathbf V^{AB}_{j_0m} $ ,$ \mathbf V^{BA}_{mj_0} $ , these matrix elements are of the same form as the corresponding matrix elements in$ \mathbf V^{AB} $ ,$ \mathbf V^{BA} $ ,$ \mathbf V^B $ in Eqs. (56) and (55) as if we are directly solving the decoupled Hamiltonian as constructed above Eq. (54). We then find that the S-matrices obtained using the two approaches are the same. -
In scenarios in which the interaction potential can be reasonably approximated as separable potentials, wherein the potential can be expressed as the product of two components associated with the ingoing and outgoing states, the problem can be effectively addressed and hold practical significance. Now, the problem is how to approximate a potential using the separable potentials. Before addressing this problem, let us review how a general contact interaction arises in the elastic and nonelastic scattering.
As discussed in the previous section, the Hamiltonian of a most general model with multiple discrete and continuum states and their interactions can be expressed as
$ \begin{align} H=&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{n=1}^C \int_{a_n}^\infty {\rm d} \omega \,\omega|\omega;n\rangle\langle \omega;n| \\ &+\sum_{m,n=1}^C \int_{a_m}^\infty {\rm d} \omega' \int _{a_n} {\rm d} \omega V_{mn}(\omega',\omega)|\omega';m\rangle \langle \omega;n| \\ &+\sum_{j=1}^D\sum_{n=1}^C \int_{a_n}^\infty {\rm d} \omega \Big( f^*_{jn}(\omega) |j\rangle\langle \omega;n|+f_{jn }(\omega)|\omega;n\rangle \langle j|\Big). \end{align} $

In the context of nonrelativistic scattering, i.e., when the in-state and out-state are composed of the same two-particle content, in the angular momentum representation, these continuum states can be expressed as
$ |\omega,n\rangle= \sqrt{\mu p}|p,JM;lS\rangle $ , where$ J,M,l,S $ are the quantum numbers for total angular mentum, magnetic angular momentum, relative orbital angular momentum, and total spin, respectively, and are collectedly denoted using n, and$ a_n $ denotes the threshold. Here, p represents the radial momentum, μ is the reduced mass, and$ \omega=\dfrac{p^2}{2\mu}+a_n $ represents the total energy. The normalization of the continuum states is selected such that the inner product between two continuum states is given by$ \langle \omega',n'|\omega,n\rangle= \delta_{n'n}\delta(\omega-\omega') $ . Momentum space potential$ V_{mn}(\omega',\omega) $ can be derived from coordinate space potential$ V( {\mathbf r}) $ . For simplicity, we consider only the rotational invariant potential. Potential function$ V_{mn}(\omega',\omega) $ results from the matrix elements$V_{n'n}(\omega',\omega)\equiv\langle \omega',n'|V|\omega, n\rangle= \sqrt{\mu' p'}\, \sqrt{\mu p}$ $ \langle p'JMl'S'|V|pJMlS\rangle $ . The simplest example is when the in-states and out-states are composed of the same spinless particles, i.e., elastic scattering. If we know coordinate-space potential$ V(r) $ , then momentum-space potential$ V(k',k) $ can be expressed in terms of coordinate-space potential$ V(r) $ as follows:$ \begin{align} \langle k',l',m'|V|k,l,m\rangle=\frac{\delta_{l'l}\delta_{m'm} }{k'k}\int r^2 \mathrm dr \frac 2\pi {\hat j}_{l}(k'r) V(r) {\hat j}_{l}(kr), \end{align} $

(57) where
$ {\hat j}(z) $ represents the Riccati-Bessel function.When the in-states and out-states can have different particle compositions, we can generalize potential
$ V(\omega',\omega) $ accordingly. In addition to the angular momentum quantum numbers, labels n and$ n' $ can also denote the different particle compositions$ |\omega,n\rangle $ . If the potential in coordinate space,$ V( {\mathbf r}', {\mathbf r}) $ , in the center-of-mass system, is invariant under rotation, it can be expressed as a function of$ {\mathbf r}^2, {\mathbf r}'^2 $ , and$ {\mathbf r}\cdot {\mathbf r}' $ . Here,$ {\mathbf r} $ and$ {\mathbf r}' $ represent the positions of the in-state and out-state relative coordinates, respectively. For a spinless particle system, the matrix elements for in-states and out-states can be expressed as follows:$ \begin{aligned}[b] V_{n'n}(\omega',\omega)\equiv\;&\langle n' \omega'lm|V|n,\omega lm\rangle\\=\;&\int {\rm d} {\mathbf r} {\rm d} {\mathbf r}'\langle n',\omega'lm| {\mathbf r}'\rangle V( {\mathbf r}', {\mathbf r})\langle {\mathbf r}|n,\omega lm\rangle\nonumber \\=\;&\frac2\pi\big(\frac{\mu'\mu}{p'p} \big)^{1/2}\int {\rm d}r {\rm d}r' {\hat j}_l(pr) {\hat j}_l(p'r'){\tilde V_{l}(r',r)}\,, \nonumber\\ \tilde V_{l}(r',r)\delta_{ll'}\delta_{mm'}=\;&rr'\int {\rm d}\Omega {\rm d}\Omega' Y^*_{l'm'}( \hat {\mathbf r}')Y_{lm}( \hat {\mathbf r}){\tilde V( {\mathbf r}', {\mathbf r})}\,. \end{aligned} $

The Wigner-Ekart theorem has been employed to account for the spherical symmetry of the potential
$ V( {\mathbf r}', {\mathbf r}) $ . When the in-state and out-state can have spins, the total angular momentum are conserved, but the orbital angular momentum can differ. We can include different orbital angular momentum and total spin quantum numbers$ lS $ and$ l'S' $ into n and$ n' $ to label different in-states and out-states,$ \begin{aligned}[b] V_{n'n}(\omega',\omega)\equiv\;&\langle n' \omega'JM|V|n,\omega JM\rangle\nonumber =\frac2\pi\big(\frac{\mu'\mu}{p'p} \big)^{1/2}\\&\times\int {\rm d} r {\rm d}r'\sum_{ll'SS'} {\hat j}_l(pr) {\hat j}_{l'}(p'r'){\tilde V_{ll'SS'}^{JM}(r',r)}, \\ \tilde V_{ll'SS'}^{JM}(r',r)=\;&rr'\sum_{mm'm_sm_s'}\int {\rm d}\Omega {\rm d}\Omega' Y^*_{l'm'}( \hat {\mathbf r}')Y_{lm}(\hat {\mathbf r}){\tilde V_{SS'}( {\mathbf r}', {\mathbf r})}\\&\times C^{JM}_{lmSm_s}C^{JM}_{l'm'S'm_s'}\,, \end{aligned} $

where
$ C^{JM}_{lmSm_s} $ is the Clebsch-Gordon coefficient. To make further progress, we also assume that the potential is square integrable for both$ \omega' $ and ω, and the same for the interaction vertex between the discrete and continuum states$ f_{jn}(\omega) $ , that is$ \int_{a_m} {\rm d}\omega'\int_{a_n} {\rm d} \omega |V_{mn}(\omega',\omega)|^2=\mathrm{finite}\,,\quad \int_{a_n} {\rm d}\omega |f_{jn}(\omega)|^2=\mathrm{finite}. $

The Hamiltonian for general potentials
$ V_{mn}(\omega',\omega) $ has no exact solutions. However, it is well known that such a potential can be expanded using a sum of separable potentials [30]. For continuum states$ |\omega,m\rangle $ , we can select a set of complete basis functions$ \tilde g_{m\rho}(\omega) $ , with$\int_{a_m} {\rm d}\omega \tilde g^*_{m\rho}(\omega)\tilde g_{m\delta}(\omega)= \delta_{\rho\delta}$ and$ \sum_\delta \tilde g_{m\delta}(\omega')\tilde g_{m\delta}(\omega)= \delta(\omega'-\omega) $ . The basis sets for different continuum states, i.e., for different m and n, need not be the same. Potential$ V_{mn}(\omega',\omega) $ can then be expanded as$ V_{mn}(\omega',\omega)=\sum\limits_{\rho\delta} v_{mn,\rho\delta }\tilde g_{m\rho}(\omega)\tilde g^*_{n\delta}(\omega). $

In the following, we will use Greek letters ρ and δ to label the basis, and repeated Greek letters are summed over without the explicit sum symbol, and the sum symbol for the Latin letters would still remain explicit. The coefficient matrix composed of
$ v_{mn,\rho\delta} $ is Hermitian$ v_{mn,\rho\delta}=v^*_{nm,\delta\rho} $ and should be non-degenerate. In general, there are infinite number of bases, and the sum of δ and ρ is up to infinity. Because expansion coefficients$ v_{mn,\rho\delta} $ are small at a sufficiently large order, we can make an approximation and truncate the series to a finite order N, i.e.,$ v_{mn,\rho\delta}=0 $ for$ \rho,\delta>N $ . Subsequently, the general Hamiltonian for multiple continuum states and discrete states can be recast as$ \begin{aligned}[b] H =\;&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{n=1}^C \int_{a_n}^\infty \mathrm d \omega \,\omega|\omega;n\rangle\langle \omega;n| \\ &+\sum_{m,n=1}^C v_{mn,\rho\delta}\Big(\int_{a_m}^\infty\mathrm d \omega' \tilde g_{m\rho}(\omega')|\omega';m\rangle\Big)\\&\times\Big(\int_{a_n}^\infty\mathrm d \omega \tilde g^*_{n\delta}(\omega)\langle \omega;n|\Big) \\ &+\sum_{j=1}^D\sum_{n=1}^C \Bigg[ |j\rangle\Big(\int_{a_n}^\infty\mathrm d \omega f^*_{jn}(\omega)\langle \omega;n|\Big)\\&+\Big(\int_{a_n}^\infty\mathrm d \omega f_{jn} (\omega)|\omega;n\rangle \Big) \langle j| \Bigg]\,. \end{aligned} $

(58) We can take
$ m\rho $ and$ n\delta $ as the row and column indices and diagonalize matrix$ v_{mn,\rho\delta} $ . Thus, the problem reduces to the similar case in the last part of the last section when degenerate$ v_{mn} $ is discussed. Here, the rank of$ v_{mn,\rho\delta} $ is greater than C, as indicated in the last section. Alternatively, we can also directly solve the problem as before in the following. The general eigenstate for this eigenvalue problem can be expanded using the bare discrete and continuum states:$ \begin{align} |\Psi(E)\rangle =&\sum_{i=1}^D \alpha_i(E)|i\rangle+\sum_{n=1}^C\int_{a_n} \mathrm d\omega \psi_{n}(E,\omega)|\omega;n\rangle. \end{align} $

(59) Similar to previous sections, for
$ |\Psi_m\rangle $ , the corresponding$ \alpha_i $ and$ \psi_n $ will have another index m, i.e.,$ \alpha_{im} $ and$ \psi_{nm} $ .With the same procedures as the previous section, the approximate properly normalized continuum states can be solved as
$ \begin{aligned}[b] |\Psi^\pm_m(E)\rangle =\;&|E;m\rangle+\sum_{j=1}^D \alpha^\pm_{jm}(E)\\&\times\Big(|j\rangle+ \sum_{n=1}^C\int_{a_n} \mathrm d\omega\frac{f_{jn}(\omega)}{E-\omega\pm {\rm i}\,0} |\omega;n\rangle\Big)\\ & +\Big( \sum_{n,n'=1}^Cv_{nn',\delta'\rho}\psi^\pm_{n'm\rho}(E)\int_{a_n} \mathrm d\omega\frac{\tilde g_{n\delta'}(\omega)}{E-\omega\pm {\rm i}\,0} |\omega;n\rangle\Big), \end{aligned} $

(60) where
$ \alpha^\pm_{im}(E) $ and$ \psi^\pm_{n'm\rho}(E)\equiv\int_{a_n}^\infty \psi_{n'm}(\omega)\tilde g_{n\rho}(\omega) $ can be solved as in Eq. (B11). Thus, the S-matrix can be obtained,$ \begin{aligned}[b] \langle \Psi_m^-(E)|\Psi_n^+(E')\rangle=\;&\delta_{mn}\delta(E-E')\\& -2\pi {\rm i} \delta(E-E')\Big(\tilde{\bf F}^\dagger_m \cdot (\tilde{\bf M}^+)^{-1}\cdot \tilde{\bf F}_m \Big), \end{aligned} $

(61) where matrix
$ \tilde{\mathbf M}^+ $ with dimension$ (D+NC)\times (D+NC) $ and vector$ \tilde {\mathbf F}_m $ with dimension$ (D+NC) $ are defined in Eq. (B7). The detailed calculation is given in Appendix B. The discrete eigenvalues can be obtained by solving Eq.$ \det \tilde {\mathbf M}(E)=0 $ . The discrete state corresponding to eigenvalue$ E_i $ can be expressed as$ \begin{aligned}[b] |\Psi^{(i)}(E_i)\rangle =\;&\sum_{i=1}^D \alpha^{(i)}_{j}(E_i)\Big(|j\rangle+ \int_{a_n} \mathrm d\omega\frac{f_{jn}(\omega)}{E_i-\omega} |\omega;n\rangle\Big) \\&+\sum_{n'=1}^C v_{nn',\delta'\rho}\psi^{(i)}_{n'm\rho}(E_i)\int_{a_n} \mathrm d\omega\frac{\tilde g_{n\delta'}(\omega) }{E_i-\omega} |\omega;n\rangle\,, \end{aligned} $

(62) where the integral contour must be deformed for
$ E_i $ on unphysical sheets as before.Note that although we have selected
$ g_{m\delta} $ as orthogonal function sets, we do not use this orthogonal property in solving the problem. Thus, as long as we can approximate the Hamiltonian using the separable interaction as in Eq. (58) without orthogonal conditions for$ g_{m\delta} $ functions, the solution applies.Next, we could go further and expand interaction function
$ f_{jm}(\omega) $ using the same set of basis$ \tilde g_{m\delta}(\omega) $ as in the corresponding contact interaction involving continuum state$ |\omega,m\rangle $ ,$ f_{jm}(\omega)=\sum\limits_{\delta}f_{jm\delta}\tilde g_{m\delta}(\omega),\quad f_{jm\delta}=\int {\rm d}\omega\, f_{jm}(\omega)\tilde g^*_{m\delta}(\omega)\,, $

and also make an approximation by truncating the series to the N-th order the same as in the contact terms, that is,
$ f_{jm\delta}=0 $ for$ \delta>N $ . This may reduce the dimension of matrix$ \tilde{\mathbf M} $ and may also simplify the numerical calculation. Subsequently, the general Hamiltonian for multiple continuum and discrete states can be recast as$ \begin{aligned}[b] H=\;&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{n=1}^C \int_{a_n}^\infty \mathrm d \omega \,\omega|\omega;n\rangle\langle \omega;n| \\ &+\sum_{m,n=1}^C v_{mn,\rho\delta}\Big(\int_{a_m}^\infty\mathrm d \omega' \tilde g_{m\rho}(\omega')|\omega';m\rangle\Big)\\&\times\Big(\int_{a_n}^\infty\mathrm d \omega \tilde g^*_{n\delta}(\omega)\langle \omega;n|\Big) \\ &+\sum_{j=1}^D\sum_{n=1}^C \Bigg[f^*_{jn\delta} |j\rangle\Big(\int_{a_n}^\infty\mathrm d \omega \tilde g^*_{n\delta}(\omega)\langle \omega;n|\Big)\\&+ f_{jn\delta } \Big(\int_{a_n}^\infty\mathrm d \omega \tilde g_{n\delta}(\omega)|\omega;n\rangle \Big) \langle j| \Bigg]\,. \end{aligned} $

(63) This case is similar to those discussed in [10, 26], where the same form factor posseses the continuum both in the discrete-continuum and continuum-continuum interactions. Using the eigenstate ansatz
$ \begin{aligned}[b] |\Psi(E)\rangle =&\sum_{i=1}^D \alpha_{i}(E)|i\rangle+\int_{a_n} \mathrm d\omega \psi_{n}(E,\omega)|\omega;n\rangle \\ =&\sum_{i=1}^D \alpha_i(E)|i\rangle+\sum_{n=1}^C\psi_{n\delta}(E)\int_{a_n} \mathrm d\omega \tilde g_{n\delta}(\omega)|\omega;n\rangle\,, \end{aligned} $

(64) we can proceed solving the eigenvalue problem similar to the previous section, the details of which are given in Appendix C. The properly normalized continuum state can be solved and expressed as
$ \begin{aligned}[b] |\Psi^\pm_m(E)\rangle =\;&\sum_{i=1}^D \alpha^\pm_{im}(E)|i\rangle+|E,m\rangle+\sum_{n=1}^C\sum_{n'=1}^C\psi^\pm_{n'm\rho}(E) V_{n\delta',n'\rho}(E)\\&\times\int_{a_n} \mathrm d\omega \frac{\tilde g_{n\delta'}(\omega)}{E-\omega\pm {\rm i}\,0} |\omega;n\rangle \end{aligned} $

(65) where
$ \alpha^\pm_{im} $ and$ \psi^\pm_{nm\rho} $ can be solved using Eq. (C9). The S-matrix can be obtained:$ \begin{aligned}[b]& \langle \Psi_m^-(E)|\Psi_n^+(E')\rangle\\=\;&\delta_{mn}\delta(E-E')-2\pi {\rm i}\delta(E-E')\\&\times\sum_{n=1}^C\sum_{n'=1}^C\psi^{-*}_{n'm\rho}(E') V^*_{n\delta',n'\rho}(E') \tilde g^*_{n\delta'}(E) \\=\;&\delta_{mn}\delta(E-E')-2\pi {\rm i}\delta(E-E')(\tilde {\mathbf F}_m^\dagger\cdot (\tilde {\mathbf W}^+)^{-1} \cdot \tilde {\mathbf F}_n) \end{aligned} $

(66) where
$ NC\times NC $ matrix$ \tilde {\mathbf W}^+ $ and$ NC $ dimensional vector$ \tilde {\mathbf F}_m $ are defined in Eqs. (C8) and (C7), respectively. Similar to the previous section, the generalized energy eigenvalues for the discrete state can be obtained from$ \det \tilde {\mathbf M}(E)=0 $ , and for each eigenvalue$ E_i $ ,$ \psi_{n\rho}^{(i)} $ can be solved from$ \tilde {\mathbf M}\cdot \tilde {\mathbf Y}=0 $ , where matrices$ \tilde {\mathbf M} $ and$ \tilde {\mathbf Y} $ are defined in Eqs. (C6) and (C7), respectively. Thus, we have the discrete eigenstates$ \begin{aligned}[b] |\Psi^{(i)}(E_i)\rangle=\;&\sum_{n'=1}^C\psi^{(i)}_{n'\rho}(E_i)\Big[\sum_{j=1}^D \frac{f^*_{jn'\rho} }{E_i-M_j} |j\rangle\\&+V_{n\delta',n'\rho}(E_i)\int_{a_n}{\rm d} \omega\frac{\tilde g_{n\delta'}(\omega)}{E_i-\omega} |\omega;n\rangle\Big] \\ \mathrm{with \,}\;& \tilde {\mathbf Y}^{(i)\dagger}(E_i)\cdot \mathbf V(E_i)\cdot \tilde{\mathbf W}'(E_i)\cdot \mathbf V(E_i)\cdot \tilde {\mathbf Y}^{(i)}(E_i)=1 \end{aligned} $

(67) with integral contour deformed for resonances and virtual states as before.
-
When contact interactions are involved, we can explore the effect of introducing small couplings on the mass of the discrete states in a general manner. Analyzing pole trajectories as couplings vary offers valuable insights into particle properties. This type of analysis proves useful in elucidating the origin of certain states observed in the experiments utilizing Friedrichs-like models or similar formulas derived from the dispersive models. Notably, Refs. [21, 31−34] demonstrated how pole trajectories of various states provide valuable clues regarding the possible nature of these particles. Moreover, such analyses may provide qualitative guidance in understanding the interaction properties from the spectrum. To illustrate this, we focus on the exponential form factor, a frequently employed form factor in the literature. Using this form factor as an example, we discuss the properties of the bound states while varying the couplings. For simplicity, we consider a two-channel case in which the threshold for the two continuum states are denoted as
$ a_1 $ and$ a_2 $ with$ a_1<a_2 $ .The basic consideration is as follows: At the leading order, where the interactions are absent, the discrete state is determined by the condition
$ E-\mu=0 $ , with the bare mass being the solution. When a small coupling constant λ is turned on, we must consider an equation of the form$ E-\mu+\lambda \chi(E)=0 $ ($ \lambda>0 $ ), where$ \chi(E) $ is real and small in the vicinity of$ E=\mu $ . The next-to-leading-order solution can be expressed as$ E=\mu-\lambda \chi(\mu) +O(\lambda^2) $ . The sign of$ \chi(\mu) $ enables us to determine the tendency of the solution's behavior. If we know that$ \chi(E) $ is a monotonic function, either positive definite or negative definite, we can determine the direction in which the solution will shift as λ increases continuously. For example, if$ \chi(E) $ is a positive decreasing function, the solution will move downward as λ becomes increasingly positive. More generally, when we replace the left-hand side of the leading-order equation$ E-\mu=0 $ with another increasing function, i.e.,$ \zeta(E)=0 $ , the addition of another positive increasing function will cause the zero point to shift to the left (Fig. 2).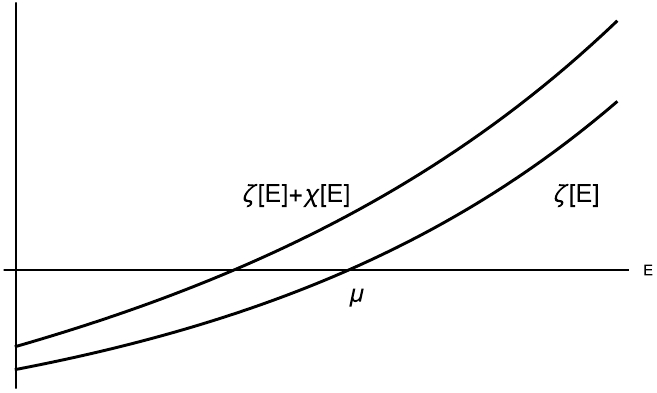
Figure 2. Monotonically increasing function
$ \zeta(E) $ that satisfies$ \zeta(\mu)=0 $ . The solution for$ \zeta(E)+\chi(E)=0 $ is smaller than μ if$ \chi(E) $ is a monotonically increasing positive function.We must also examine the behavior of the dispersion integral defined as
$G(E)=\int_a^\infty {\rm d}\omega \dfrac{ |f(\omega)|^2}{E-\omega +{\rm i}\,0}$ . When$ E<a $ , the integral behaves as a purely negative decreasing function. For$ E>a $ , the imaginary part is$ -\pi |f(E)|^2 $ , which is purely negative in this region. The real part corresponds to the principal value integral in$ G(E) $ . Near the threshold, the real part is negative and increasing with E, passing through the zero point$ \hat E $ and reaching a positive maximum, and then decreases back towards zero as E approaches infinity. See Fig. 3 for an example. Typically, the integrand includes phase space factor$ \rho(E)\propto \sqrt{E-a_1} $ , which suppresses the integrand near threshold a, which causes a higher value of$ \hat E $ . See Fig. 3 for a case with$ |f(\omega)|^2=\sqrt{\omega-a_1} {\rm e}^{-E/\Lambda} $ . We observe that$ \mathrm{Re}G(E) $ becomes positive only when E approaches Λ, which characterizes the inverse of the interaction range. If the energy range of interest is significantly smaller than Λ, then$ \mathrm{Re} G(E) $ remains negative. In the following, we will primarily focus on this region.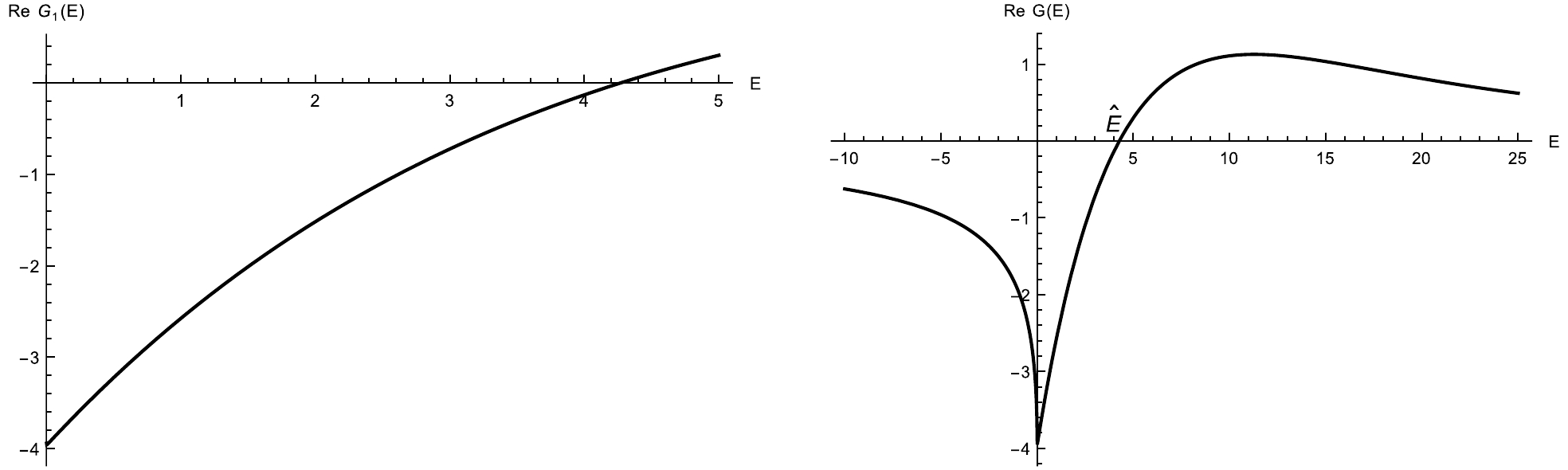
Figure 3. General behavior of the real part of the
$G(E)=\int_{a}^\infty {\rm d}\omega \frac{|f(\omega)|^2}{E-\omega+{\rm i}\epsilon}$ function using$|f(\omega)|^2=\sqrt{\omega-a} {\rm e}^{-\omega/\Lambda}$ , with$ \Lambda=5 $ ,$ a=0 $ . If the interested energy region is much smaller than Λ, then$ \mathrm {Re} G(E)<0 $ .With this preparation, we can explore some interesting and instructive simple cases that are relevant to the phenomenological analysis of the spectrum.
First, we consider the cases with only continuum states.
1. In the presence of a single continuum and self interaction
$ v_{11} $ , if$ v_{11} $ is sufficiently negative (i.e., attractive), a bound state will emerge at$ E_0<a_1 $ .This is the simplest case. The
$ \mathbf M $ matrix reduces to a function$ M_{11}=v_{11}(1-v_{11}G_1(E)), $

where
$G_1=\int_{a_1}^\infty {\rm d}\omega \dfrac{|g_1(\omega)|^2}{E-\omega+{\rm i}\,\epsilon}$ , and$ a_1 $ is the threshold. Because$ G_1(E) $ is negative and continuously decreasing for$ E<a_1 $ with$ \lim_{E\to -\infty} G_1(E)=0 $ , as shown in Fig. (3), for$ M_{11} $ to have a zero point at$ E_0<a_1 $ , coupling$ v_{11} $ must satisfy condition$ v_{11}< 1/G_1(a_1) $ .2. With a second continuum state included, we can examine the coupled-channel effect on the dynamical bound state of the lower channel discussed in previous case when
$ v_{11}<0 $ .The
$ \mathbf M $ matrix becomes$ \begin{align} \mathbf M=&\begin{pmatrix}v_{11}(1-v_{11}G_1(E))-|v_{12}|^2G_2(E)\\v_{12}(1-v_{11}G_1(E))-v_{12}v_{22}G_2(E) \\ v_{21}(1-v_{11}G_1(E))-v_{22}v_{21}G_2(E)\\v_{22}(1-v_{22}G_2(E))-|v_{12}|^2G_1(E) \end{pmatrix}, \\ G_i=&\int_{a_i}^\infty {\rm d}\omega \frac{|g_i(\omega)|^2}{E-\omega+{\rm i}\,\epsilon}, \end{align} $

(68) where
$ a_1 $ and$ a_2 $ are the thresholds for the two channels with$ a_1<a_2 $ . The determinant can be calculated to be$ \begin{aligned}[b]\det \mathbf M=\;& (\det \mathbf v)\Big(1-v_{11}G_1(E)-v_{22}G_2(E)\\&+(\det \mathbf v) G_1(E)G_2(E)\Big)\,,\\ \mathbf v=\;&\begin{pmatrix} v_{11}&v_{12}\\v_{21}&v_{22}\end{pmatrix}\,. \end{aligned}$

Note that because
$ v_{12} $ appears only in$ \det \mathbf v $ in the form of$ |v_{12}|^2 $ , the phase or sign of$ v_{12} $ is irrelavent to this result in this context.We consider four cases progressively. In each case, we first present the result and then provide the reasoning behind it.
(a) When
$ v_{12}\neq 0 $ and$ v_{22}=0 $ , the coupled channel effect will play a role of attractive interaction, causing the bound state to shift from$ E_0 $ to a deeper energy level$ E_{0b} $ , i.e.,$ E_{0b}<E_0 $ .This can be demonstrated by directly calculating the determinant of
$ \mathbf M $ , yielding$ \begin{align} \det \mathbf M=-|v_{12}|^2\Big(1-v_{11}G_1(E)-|v_{12}|^2G_1(E)G_2(E)\Big)\,. \end{align} $

(69) At
$ E<a_1 $ , the last term$ -|v_{12}|^2G_1(E)G_2(E) $ in the bracket is negative and decreasing, whereas term$ -v_{11}G_1(E) $ is also negative and decreasing. Following similar reasoning as illustrated in Fig. 2, E must be much smaller to have a zero point of$ \det\mathbf M $ , denoted as$ E_{0b} $ . This discussion does not rely on the smallness of the coupling; therefore, it is also valid for strong interaction.(b) When a sufficiently small
$ v_{22} $ is then turned on, the result depends on the sign of$ v_{22} $ . A negative$ v_{22} $ causes the bound state to shift to a deeper energy level, whereas a positive$ v_{22} $ results in a shallower bound state.The contribution from
$ v_{22} $ to$ \det \bf M $ at the zero point$ E_{0b} $ can be expressed as$\begin{aligned}[b]& -v_{22}|v_{12}|^2(v_{11}v_{22}-|v_{12}|^2)G_1(E_{0b})G^2_2(E_{0b})\\&\sim v_{22}|v_{12}|^4G_1(E_{0b})G^2_2(E_{0b})+O(v_{22}^2)\,.\end{aligned} $

When
$ v_{22} $ is negative, indicating a more attractive interaction, this term contributes positively to$ \det \mathbf M $ for$ E<a_1 $ , thereby negatively affecting the terms in the bracket of Eq. (69). This results in the bound state shifting deeper from$ E_{0b} $ , moving away from the threshold. Conversely, when$ v_{22} $ is positive, the bound state becomes shallower, moving upward from$ E_{0b} $ . Therefore, when both$ v_{12} $ and a positive$ v_{22} $ are present, the direction of the bound state's movement from$ E_0 $ depends on the competition between the effects of$ v_{22} $ and$ v_{12} $ .(c) For a large
$ |v_{22}| $ , when$ v_{22}>0 $ , we can conclude that the bound state will be located to the left of$ E_0 $ but to the right of$ E_{0b} $ .This can be understood by expressing
$ \det \mathbf M $ as follows:$ \begin{aligned}[b] \det \mathbf M=\;& (\det \mathbf v)(1-v_{22}G_2(E))\Big(1-v_{11}G_1(E)\\&-\frac{|v_{12}|^2}{1-v_{22}G_2(E)} G_1(E)G_2(E)\Big) \end{aligned} $

(70) and by considering the positivity of
$ -v_{22}G_2(E) $ in the last term in the bracket for$ E<a_1 $ . As$ v_{22} $ increases, the absolute value of the last term in the bracket deceases. Thus, when a positive$ v_{22} $ is turned on from$ 0 $ to$ \infty $ , the bound state moves from$ E_b $ to$ E_0 $ .(d) When a negative
$ v_{22} $ is introduced, starting from zero and becomes increasingly negative, the bound state will shift deeper from$ E_{0b} $ to$ -\infty $ .This occurs because, for fixed E, term
$ 1-v_{22}G_2(E) $ in the denominator of the last term in the bracket approaches zero, leading to a divergence of that term. To cancel the first two finite terms, E must become increasingly negative such that$ |G_2(E)| $ decreases sufficiently, enabling the last term to remain finite and effectively cancel the first two terms in the bracket. Consequently, this will cause the bound state to shift deeper from$ E_{0b} $ to$ -\infty $ .3. Similar to the previous case, when only an attractive interaction exists in the second channel, i.e.,
$ v_{22}<0 $ with$ v_{11}=v_{12}=0 $ , a dynamically generated bound state ($ E_b $ ) can exist below$ a_2 $ and is assumed to be above$ a_1 $ , satisfying condition$ 1/G_{22}(a_1)<v_{22}<1/G_{22}(a_2) $ . We can then examine the effect of turning on the first channel on the bound state spectrum of the second channel. We consider two cases.(a) When a small
$ v_{12} $ is introduced while keeping$ v_{11}=0 $ , the bound state will transit to the second sheet. Whether the mass of the state increases or decreases depends on the sign of$ \mathrm{Re} G_1(E_b) $ . A negative$ \mathrm{Re} G_1(E_b) $ will cause the mass of the state tend to decrease, whereas a positive$ \mathrm{Re} G_1(E_b) $ will lead to an increase in the mass.In this case, we have
$ \begin{align} \det \mathbf M=-|v_{12}|^2\Big(1-v_{22}G_2(E)-|v_{12}|^2G_1(E)G_2(E)\Big)\,. \end{align} $

(71) Consider solving
$ \det M=0 $ in the powers of$ v_{12} $ using iteration. Because$ E_b>a_1 $ , the$ G_1(E) $ factor in the last term contributes an imaginary term of$ -\pi {\rm i} |g_1(E)|^2 $ . Combining this with the other factors yields a negative imaginary part on the order of$ |v_{12}|^2 $ in the bracket. For$ \det M=0 $ to hold, the state corresponding to$ E_b $ must move into the complex plane, enabling term$ -v_{22}G_2(E) $ to generate a negative imaginary part of order$ v^2_{12} $ to cancel the imaginary part of the last term in the bracket. Thus, E must have a negative imaginary part, and with the$ +{\rm i}\epsilon $ in the definition of$ G_i(E) $ , the pole moves continuously to the second Riemann sheet. This is consistent with the common knowledge that the resonance poles cannot reside on the physical sheet. Whether the mass of the pole is increasing or decreasing depends on the the sign of the leading real part of the last term, which is determined by examining$\mathrm{Re} G_1(E_b)=P.V.\int_{a_1}^\infty {\rm d}\omega \dfrac{|g_1(\omega)|^2}{E_b-\omega}$ . If this value is negative (positive) the mass will decrease (increase). This is owing to$ G_2(E) $ being negative and decreasing for$ E<a_2 $ , leading to a negative (positive) contribution from the real part of the last term in the bracket. In the example illustrated in Fig. 3, when Λ is much larger than$ a_2 $ , where$ \mathrm{Re} G_1(E) $ is negative and monotonically increasing near$ E_b $ , turning on the$ v_{12} $ will cause the mass of the dynamically generated state (from$ E_b $ ) in the second channel to decrease.(b) When a small
$ |v_{11}| $ is also turned on, as long as$ |v_{11}| $ is sufficiently small, the result will be the same as previous case.Similar to the previous case,
$ \det \mathbf M $ can be expressed as$ \begin{aligned}[b] \det \mathbf M=\;& (\det \mathbf v)(1-v_{11}G_1(E))\Big((1-v_{22}G_2(E)\\&-\frac{|v_{12}|^2}{1-v_{11}G_1(E)} G_1(E)G_2(E)\Big) \end{aligned} $

$ \begin{aligned}[b] =\;& (\det \mathbf v)(1-v_{11}G_1(E))\Big((1-v_{22}G_2(E)\\&-\frac{|v_{12}|^2\big(1-v_{11}(\mathrm{Re} G_1(E)-i \mathrm{Im} G_1(E))\big)}{|1-v_{11}G_1(E)|^2} G_1(E)G_2(E)\Big) \end{aligned} $

(72) Compared with (71), an extra factor
$ 1/(1- v_{11}G_1) $ exists in the$ |v_{12}|^2 $ term. The difference is of order$ O(v_{11}|v_{12}|^2) $ , and therefore, for sufficiently small$ |v_{11}| $ , the result would be the same as in the previous case.4. A bound state could also be generated from the pure
$ v_{12} $ interaction with no self-interaction, i.e.,$ v_{11}= v_{22}=0 $ , regardless of the sign of$ v_{12} $ . In this case,$ v_{12} $ acts as an attractive interaction.If
$ v_{11}=v_{22}=0 $ ,$ \det \mathbf M=-|v_{12}|^2(1-|v_{12}|^2G_1(E)G_2(E)) $ . Because both$ G_1(E) $ and$ G_2(E) $ are negative and decreasing for E below the first threshold, a solution to$ \det \mathbf M=0 $ can exist when$ |v_{12}|^2 $ is sufficiently large, specifically when$ |v_{12}|^2>1/(G_1(a_1)G_2(a_1))) $ . When$ |v_{12}|^2 $ decreases, the bound state will go up through the threshold to the second Riemann sheet, becoming a virtual state or a resonance. Thus, activating only$ v_{12} $ is equivalent to enhance the attractive interaction when only two continuum states exist.Next, we add a discrete state of bare mass μ with coupling vertex functions to the two continua,
$ f_1(\omega) $ and$ f_2(\omega) $ . Now$ \mathbf M $ matrix becomes$ \mathbf M=\begin{pmatrix} (E-\mu)-\mathcal F_1(E)-\mathcal F_2(E)& -v_{11}\mathcal F^g_{1}(E)-v_{21}\mathcal F^g_{2}(E)&- v_{12}\mathcal F^g_{1}(E)-v_{22}\mathcal F^g_{2}(E) \\ -v_{11}\mathcal F^{g{\text ‡}}_{1}(E)-v^*_{21}\mathcal F^{g{\text ‡}}_{2}(E)&v_{11}(1-v_{11}G_1(E))-|v_{12}|^2G_2(E)&v_{12}(1-v_{11}G_1(E))-v_{12}v_{22}G_2(E) \\ -v^*_{12}\mathcal F^{g{\text ‡}}_{1}(E)-v_{22}\mathcal F^{g{\text ‡}}_{2}(E)&v_{21}(1-v_{11}G_1(E))-v_{22}v_{21}G_2(E)&v_{22}(1-v_{22}G_2(E))-|v_{12}|^2G_1(E) \end{pmatrix} $

(73) where
$\mathcal F_{n}=\int_{a_n}{\rm d}\omega\dfrac {f_{n}(\omega)f_{n}^*(\omega)}{E-\omega+{\rm i}\,0}$ ,$\mathcal F^g_{n}=\int_{a_n} {\rm d}\omega\dfrac {f^*_{n}(\omega)g_{n}(\omega)}{E-\omega+ {\rm i}\,0}$ ,$\mathcal F^{g{\text ‡}}_{n}=\int_{a_n} {\rm d}\omega\dfrac {f_{n}(\omega)g^*_{n}(\omega)}{E-\omega+ {\rm i}\,0}$ .We examine three different cases.
1. One bare discrete state coupled with two continuum states with
$ v_{ij}=0 $ .When only the interaction between the discrete state and continuum states exists, i.e.,
$ v_{11}=0,~ v_{12}=0, ~ v_{22}=0 $ , we need only to examine$ \begin{align} M_{11}\equiv(E-\mu)-\mathcal F_1(E)-\mathcal F_2(E)=0. \end{align} $

(74) By default, we will consider
$ \mu\ll \Lambda $ and$ \mathrm {Re} \mathcal F_1(\mu)<0 $ similar to Fig. 3.(a) When
$ \mu<a_1 $ , because$ \mathcal F_1(E) $ and$ \mathcal F_2(E) $ for$ E<a_1 $ are negative and decreasing, the solution, denoted as$ E_\mu $ , will be less than μ. This indicates that when the discrete state lies below both continuum states, turning on the interaction between the discrete and continuum states causes the discrete state to move deeper below the thresholds.(b) For
$ a_1<\mu<a_2 $ , when sufficiently weak interactions$ f_1 $ and$ f_2 $ are gradually turned on, the discrete state would move to the second sheet and the mass will decrease.In this case, only
$ \mathcal F_{1,2} $ contributions near μ are significant to the shift of the zero point, as observed in the iteration solution. With$ \mathcal F_2(\mu)<0 $ , and assuming$ \mathrm{Re} \mathcal F_1(\mu) <0 $ (as observed in the case of exponential form factor with$ \mu\ll \Lambda $ ), a weak interaction between the discrete state and the two continua will also lead to a decrease in the mass of the discrete state. Because$ \mathcal F_1(\mu) $ has a negative imaginary part, the energy of the discrete state solution and$ -\mathcal F_2(E) $ will develop negative imaginary parts to cancel it. Consequently, the discrete state will move continuously to the complex plane of the second Riemann sheet.(c) When
$ \mu>a_2 $ , similar to the previous case, the discrete state will go to the third Riemann sheet and the mass will decrease.The discussion is similar to the previous item. When
$ \mu\ll \Lambda $ , we find that$ \mathrm {Re}(\mathcal F_{1,2}(\mu)) <0 $ , and these terms act as attractive interactions, driving the mass of the discrete state downward. The negative imaginary parts of$ \mathcal F_{1,2}(\mu) $ result in the solution moving down to the third sheet of the Riemann surface.This may provide an understanding of why most of the open-flavor effects tend to cause the mass of the
$ c\bar c $ state to be smaller [35]: Λ in the corresponding system is sufficiently large or the interaction range is so small such that$ \mathrm {Re}(\mathcal F_{1,2}(\mu)) <0 $ .2. One bare discrete state coupled with two continuum states with
$ v_{11}\neq 0 $ .Now, proceeding from previous case, we gradually turn on
$ v_{11}\neq 0 $ and leave$ v_{12}=v_{22}=0 $ . Subsequently, we must examine the zero point of the determinant of the first$ 2\times 2 $ submatrix, denoted as$ \mathbf M_{12} $ $ \begin{align} \det \mathbf M_{12}=& ((E-\mu)-\mathcal F_1-\mathcal F_2)(v_{11}(1-v_{11}G_1(E))) - (v_{11}^2\mathcal F^g_{1}\mathcal F^{g{\text ‡}}_{1}) \end{align} $

(75) $ \begin{align} =&v_{11}(1-v_{11}G_1(E))\left((E-\mu)-\mathcal F_1-\mathcal F_2 - \frac{(v_{11}^2\mathcal F^g_{1}\mathcal F^{g{\text ‡}}_{1})}{v_{11}(1-v_{11}G_1(E))}\right). \end{align} $

(76) (a) We first consider
$ E_\mu<a_1 $ . We continue to use$ E_\mu $ to denote the solution to$ M_{11}=(E-\mu)-\mathcal F_1-\mathcal F_2=0 $ , meaning that the discrete state is renormalized from bare mass μ to$ E_\mu $ by turning on$ f_1 $ and$ f_2 $ . Another bound state may be dynamically generated by the continuum-continuum interaction$ v_{11} $ , denoted by$ E_0 $ , which results from the solution to$ 1-v_{11}G_1(E)=0 $ when$ f_1=0 $ , as discussed in case 2. We would examine the effect of turning on$ v_{11} $ on the bound state$ E_\mu $ and then the effect of turning on$ f_{1,2} $ on the bound state$ E_0 $ .● The simplest case is when
$ v_{11}>0 $ , no bound state is developed by the pure continuum-continuum interaction. Turning on$ v_{11} $ will cause the bound state to move upward toward the threshold from$ E_\mu $ .This occurs because at
$ E=E_\mu $ , the last term in Eq. (75) becomes$ |v_{11}\mathcal F^g_{1}(E_\mu)|^2>0 $ and$ (v_{11}(1-v_{11}G_1(E_\mu)))>0 $ , whereas$ \mathcal F_{1,2}(E_\mu) $ are negative. Thus, turning on$ v_{11} $ has the opposite effect of$ \mathcal F_{1,2} $ on the discrete state. Therefore, the state moves upward from the previous solution$ E_\mu $ toward the threshold.● If
$ v_{11}<0 $ , the bound state would always move down from$ E_\mu $ .We first consider a case when
$ |v_{11}| $ is sufficiently small, such that$ |v_{11}\mathcal F^g_{1}(E_\mu)|^2/(v_{11}(1-v_{11}G_1(E_\mu)))<0 $ . This condition will cause the discrete states corresponding to$ E_\mu $ to move downward. A larger$ |v_{11}| $ may generate a zero point of$ (1-v_{11}G_1(E)) $ at$ E_0<a_1 $ , indicating a bound state at$ E_0 $ that moves down from the threshold$ a_1 $ when$ f_1(\omega)=0 $ . Because at$ E_\mu<E_0 $ ,$ \dfrac{v_{11}^2|\mathcal F^g_{1}(E_\mu)|^2}{(v_{11}(1-v_{11}G_1(E_\mu)))}<0 $ , if$ \mathcal F^g_{1}(E) $ continues to decrease similar to$ G_{1,2}(E) $ for$ E<E_0 $ , the previous result remains valid for large$ |v_{11}| $ . In this case, when negative$ v_{11} $ is activated and becomes increasingly negative, the bound state generated from μ consistently moves down.● For the bound state from
$ E_0 $ , switching on small interaction$ f_1(\omega) $ will cause the bound state to move upward toward the threshold.The reasoning is as follows. Because
$ E_0 $ moves down from the threshold as$ v_{11} $ becomes increasingly negative, we have$ E_\mu<E_0 $ and$ (E_0-\mu)-\mathcal F_1(E_0)-\mathcal F_2(E_0)>0 $ . Subsequently, the negativity of term$ \dfrac{v_{11}\mathcal F^g_{1}\mathcal F^{g{\text ‡}}_{1}}{(E-\mu)-\mathcal F_1-\mathcal F_2} $ causes the bound state corresponding to$ E_0 $ to shift upward toward the threshold. Therefore, in this case, turning on$ f_1 $ appears to activate a repulsive interaction that decelerates the downward movement of the state at$ E_0 $ as$ v_{11} $ becomes more attractive. However, turning on$ f_2 $ will reduce this deceleration effect, because$ -\mathcal F_2 $ is positive and$ \dfrac{v_{11}^2\mathcal F^g_{1}\mathcal F^{g{\text ‡}}_{1}}{(E-\mu)-\mathcal F_1-\mathcal F_2} $ will become smaller.(b) Next we examine the case when
$ a_1<\mu<a_2 $ ,$ f_{1,2}(\omega) $ is sufficiently small,$ v_{12}=v_{22}=0 $ , and$ \mathrm{Re}\mathcal F_1(\mu)<0 $ , to observe the effect of turning on small$ v_{11} $ . By iterating once, we have an approximation to the solution$ \begin{align} E_1=\mu+\mathcal F_1(\mu)+\mathcal F_2(\mu) + \frac{v_{11}\mathcal F^g_{1}(\mu)\mathcal F^{g{\text ‡}}_{1}(\mu)}{1-v_{11}G_1(\mu)} \end{align} $

(77) Expanding to
$ O(v_{11}) $ , we have$ \begin{aligned}[b] \mathrm{Re} E_1=\;&\mu+ \mathrm{Re}\mathcal F_1(\mu)+\mathcal F_2(\mu)+ v_{11}[|\mathrm{P.V.}\mathcal F^g_{1}(\mu)|^2\\&-\pi^2|f_1(\mu)g(\mu)|^2]+O(v_{11}^2)\,, \end{aligned} $

(78) $ \begin{align} \mathrm {Im} E_1=&-\pi \big(|f_1(\mu)|^2+2 v_{11} \mathrm {Re}[\mathcal F_1^g(\mu) f_1(\mu)g^*(\mu)]\big)+O(v_{11}^2)\,, \end{align} $

(79) where
$ \mathrm {P.V.} $ means the principal value part. Thus, the effect of turning on$ v_{11} $ on the mass is determined by the$ v_{11} $ term in Eq. (78). If it is positive (negative), it will play an attractive (repulsive) role. Whether the width will be broader depends on the positivity or negativity of the second term in the bracket of Eq. (79), respectively. Using our example form factor,$ \mathrm {Re}\mathcal F_1^g(\mu)\mathrm {Re}( f_1^*(\mu)g(\mu))<0 $ , a positive (negative)$ v_{11} $ causes a broader (narrower) resonance.(c) When
$ \mu>a_2 $ , both$ \mathcal F_{1,2} $ have imaginary parts and Eqs. (78) and (79) change to$ \begin{aligned}[b] \mathrm{Re} E_1=\;&\mu+ \mathrm{Re}\mathcal F_1(\mu)+\mathrm{Re}\mathcal F_2(\mu)+ v_{11}[|\mathrm{P.V.}\mathcal F^g_{1}(\mu)|^2\\&-\pi^2|f_1(\mu)g(\mu)|^2]+O(v_{11}^2)\,, \end{aligned} $

(80) $ \begin{aligned}[b] \mathrm {Im} E_1=\;&-\pi \big(|f_1(\mu)|^2+|f_2(\mu)|^2\\&+2 v_{11} \mathrm {Re}[\mathcal F_1^g(\mu) f_1(\mu)g^*(\mu)]\big)+O(v_{11}^2)\,. \end{aligned} $

(81) The analysis and result are similar to the previous case.
3. One bare discrete state coupled with two continuum states with
$ v_{12}\neq 0 $ .Let us now discuss the effect of nonzero
$ v_{12} $ and set$ v_{11}=v_{22}=0 $ . Then, the$ \mathbf M $ matrix becomes$ \begin{align*} \mathbf M= \begin{pmatrix} (E-\mu)-\mathcal F_1(E)-\mathcal F_2(E) & -v_{21}\mathcal F^g_{2}(E) & - v_{12}\mathcal F^g_{1}(E) \\ -v^*_{21}\mathcal F^{g{\text ‡}}_{2}(E) & -|v_{12}|^2G_2(E) & v_{12} \\ -v^*_{12}\mathcal F^{g{\text ‡}}_{1}(E) & v_{21} & -|v_{12}|^2G_1(E) \end{pmatrix} \end{align*} $

and
$ \begin{aligned}[b] \det \mathbf M=\;&|v_{12}|^2\Big(-\big((E-\mu)-\mathcal F_1(E)-\mathcal F_2(E)\big)\\&\big(1-|v_{12}|^2 G_1(E)G_2(E)\big) \\&+|v_{12}|^2\big(\mathcal F^g_2(E)\mathcal F^{g{\text ‡}}_2(E)G_1(E)+\mathcal F^g_1(E)\mathcal F^{g{\text ‡}}_1(E)G_2(E)\big) \\ &+v_{12}^*\mathcal F^{g{\text ‡}}_1(E)\mathcal F^g_2(E)+v_{12}\mathcal F^{g}_1(E)\mathcal F^{g{\text ‡}}_2(E)\Big). \end{aligned} $

(82) This time
$ v_{12} $ appears not only in$ |v_{12}|^2 $ but also in linear terms.When
$ v_{12}=0 $ , the bare state at$ E=\mu $ is renormalized to$ E_\mu<a_1 $ , which satisfies$ (E_\mu-\mu)-\mathcal F_1(E_\mu)-\mathcal F_2(E_\mu)=0 $ . When coupling$ v_{12} $ is turned on, the position of this bound state will shift. The result depends on the sign of the last line in Eq. (82) near the bound state. If this term is negative, the effect of turning on$ v_{12} $ will be to pull the bound state downward. Conversely, if it is positive, a small$ |v_{12}| $ will initially cause the bound state from$ E_\mu $ to move upward. However, as$ |v_{12}| $ becomes sufficiently large, the state will eventually move downward.The reasoning is as follows. For
$ E<a_1 $ , the$ |v_{12}|^2 $ term in the second line of Eq. (82) is always negative and decreases with E. The linear terms of$ v_{12}^{(*)} $ in the third line takes the form$ 2\mathrm {Re} [v_{12} \mathcal F^{g{\text ‡}}_{1}(E) \mathcal F^g_{2}(E)] $ .We first consider a special case when the two terms in the last line are too small compared with the second line and can be ignored, for example,
$ |\mathcal F_2^g|\ll |\mathcal F_1^g| $ and$ |\mathcal F_2^g|\ll |G_2| $ .● When
$ |v_{12}|^2 $ is sufficiently small, factor$ 1-|v_{12}|^2 G_1(E)G_2(E)>0 $ for$ E<E_\mu $ , and the effect of the purely negative second line is to push the discrete state downward from$ E_\mu $ as$ |v_{12}| $ increases from zero.● When
$ |v_{12}|^2 $ becomes sufficiently large, such that the solution to$ 1-|v_{12}|^2 G_1(E)G_2(E)=0 $ generates$ E_b $ , which comes down from the threshold$ a_1 $ , we can expect$ E_\mu<E_b $ because$ E_\mu $ is already below the threshold$ a_1 $ . Given that$ G_1(E)G_2(E)>0 $ and increases with respect to E below the threshold$ a_1 $ , we still have$ 1-|v_{12}|^2 G_1(E)G_2(E)>0 $ for$ E<E_b $ . Thus, the discrete state generated from the bare state always moves away from the threshold.● We can also examine the effect of the second line on the bound state generated from
$ E_b $ . Because we have$ (E_b-\mu)-\mathcal F_1(E_b)-\mathcal F_2(E_b)>0 $ , the effect of the negative second line is to decelerate the bound state from moving down or to pull it toward the threshold$ a_1 $ .Thus, the second line of Eq. (82) plays the role of an effective attractive interaction, dragging the bound state generated from the bare discrete state downward, whereas it functions as an effective repulsive interaction for the bound state resulting from the continuum-continuum interaction.
If the last two terms on the last line cannot be ignored, they will add complexity to the discussion. If the sum of these two term is negative, it will play a similar role to the second line, whereas if it is positive, it will have the opposite effect and compete with the second line. Because it is of order
$ v_{12} $ , it may contribute more significantly than the second term for very small$ v_{12} $ . If this is the case, when$ v_{12} $ is activated, the third line will initially dominate the second line. If both interaction vertices$ f_i $ and$ g_i $ are real positive exponential functions, as in the exponential form factor example, the sign of the last line will correspond to$ \mathrm {Re}v_{12} $ . A small positive$ \mathrm{Re} v_{12} $ will cause the bare discrete state to move upward toward the threshold. However, as$ \mathrm{Re} v_{12} $ increases, the terms in the second line will dominate, dragging the discrete state down from$ E_\mu $ and decelerating the one from$ E_b $ from descending. Additionally, the third line may become sufficiently large such that the bound state from$ E_b $ collides with the bound state generated from$ E_\mu $ as$ |v_{12}| $ increases, and then they may separate again into two bound states, one moving downward and the other upward.In more complicated cases, the results may be intricate and may not present a simple picture. The previous cases serve as examples for analyzing the effects of the different interaction in various scenarios and qualitatively understanding the behavior of the pole positions.
-
This paper presents several improvements to the Friedrichs model, aiming to provide a more comprehensive description of coupled channel scattering in real-world scenarios. First, we investigate scenarios involving multiple discrete and continuum states, focusing on the general interaction between these discrete and continuum states. Second, we consider the inclusion of continuum-continuum interactions, employing a more general separable interaction that is independent of the interaction between the discrete and continuum states. Notably, this extended model remains exactly solvable. Third, we address scenarios in which the square integrable interaction between the continuum states takes a non-separable form, rendering it non-solvable. However, we propose an approach to approximate this potential by expanding it in terms of a selected basis set, effectively expressing it as a truncated series of separable potentials. Consequently, at a finite order, this potential becomes solvable. To simplify the analysis, we also suggest utilizing the same basis set for expanding both the discrete-continuum interaction and continuum-continuum potential. A few simple examples are discussed to analyse the behaviors of the masses of the discrete states when different interactions are turned on, which may be useful in qualitatively understanding the spectrum in the coupled channel system. A few interesting results may also be useful for the systems where the couplings between states can be tuned such as the cold atom systems.
This discussion establishes a theoretical foundation for the application of the Friedrichs model in various contexts, including hadron physics and other areas involving coupled channel scattering and intermediate resonances. To utilize the model effectively, we must first model the interaction between the discrete-continuum and continuum-continuum components. Subsequently, the continuum-continuum potential can be approximated using a series of separable potentials, enabling resonance searches or S-matrix calculations. An advantageous aspect of this model is the automatic preservation of unitarity in the S-matrix while avoiding the presence of spurious poles on the first Riemann sheet. In contrast, the conventional K-matrix parameterization lacks control over spurious poles on the physical sheet.
However, a remaining challenge lies in determining the continuum-continuum interactions in a reasonable manner. Further research is required to develop suitable approaches for obtaining these interaction terms in a manner that satisfies the physical expectations and provides reliable results in various real world applications.
-
The normalization of the continuum state using the coefficients in Eqs. (25) and (26) can be calculated as follows:
$ \begin{aligned}[b] \langle \Psi^\pm_m(E)|\Psi^\pm_n(E')\rangle=\;&\sum_{i=1}^D\alpha_{im}^*(E)\alpha_{in}(E')+\delta_{mn}\delta(E-E') +\frac 1{E-E'\mp {\rm i}\,0}\Bigg(\sum_{j=1}^D \frac{A^*_{jm}(E) f^*_{jn}(E')}{E-M_j}+\sum_{n'=1}^C v^*_{nn'}B^*_{n'm}(E)g^*_n(E')\Bigg) \\& +\frac 1{E'-E\pm {\rm i}\,0}\Bigg(\sum_{j=1}^D \frac{A_{jm}(E') f_{jn}(E)}{E'-M_j} +\sum_{n'=1}^C v_{nn'}B_{n'm}(E')g_n(E)\Bigg) \\&+\sum_{m'=1}^C\int_{a_{m'}} {\rm d}\omega\underbrace{\frac 1{E-\omega\mp {\rm i}\,0}\frac 1{E'-\omega\pm {\rm i}\,0}}_{\frac1{E'-E\pm i0}\big(\frac 1{E-\omega\mp i0}-\frac 1{E'-\omega\pm {\rm i}\,0}\big) }\Bigg(\sum_{j=1}^D \frac{A^*_{jm}(E) f^*_{jm'}(\omega)}{E-M_j}+\sum_{n'=1}^C v^*_{m'n'}B^*_{n'm}(E)g^*_{m'}(\omega)\Bigg) \\&\times\Bigg(\sum_{j'=1}^D \frac{A_{j'n}(E') f_{j'm'}(\omega)}{E'-M_{j'}}+\sum_{n''=1}^C v_{m'n''}B_{n''n}(E')g_{m'}(\omega)\Bigg). \end{aligned} $

(A1) Note that we have omitted the
$ \pm $ superscripts in coefficients$ \alpha_{im} $ ,$ A_{jm} $ , and$ B_{mn} $ because they all have the same superscript of$ \pm $ . Using the definitions in Eq. (30), Eqs. (32) and (33), the last two lines can be reduced as$ \begin{aligned}[b] & \frac1{E'-E\pm {\rm i}\,0}\Big[\sum_{j,j'=1}^D{ \alpha^{\pm*}_{jm}(E)}\big(\delta_{jj'}(E-E'){ -V^{\pm*}_{j'j}(E)}+{ V^{\pm}_{jj'}(E')}\big){\alpha^\pm_{j'n}(E')} +\sum_{j=1}^D\sum_{n''=1}^C{ \alpha^{\pm*}_{jm}(E)}\big({ -\sum_{m'}V^{\pm BA*}_{m'j}(E)v_{m'n''}}+ {V^{\pm AB}_{jn''}(E')}\big) { B^\pm_{n''n}(E')} \\&+\sum_{j'=1}^D\sum_{n'=1}^C{ B^{\pm*}_{n'm}}\big({ -V^{\pm AB*}_{j'n'}(E)}+\sum_{m'=1}^Cv^*_{m'n'}{ V^{\pm BA}_{j'm'}}\big){ \alpha^\pm_{j'n}(E')}+\sum_{n',n'',m'=1}^C{ B^{\pm*}_{n'm}(E)}\big({ -V^{\pm B*}_{m'n'}(E)v_{m'n''}}+v^*_{m'n'}{ V^{\pm B}_{m'n''}(E')}\big){ B^\pm_{n''n}(E')}\Big] \end{aligned} $

$ \begin{aligned}[b] =\;&-\sum_{j=1}^D\alpha^{\pm*}_{jm}(E)\alpha^\pm_{jn}(E)+ \frac1{E'-E\pm {\rm i}\,0}\Bigg[\sum_{j'=1}^D({ -f_{j'm}(E)})\alpha^\pm_{j'n}(E')+\alpha^{\pm*}_{j'm}(E){ f^*_{j'n}(E')}) \\& +\sum_{n',m'=1}^C({-\delta_{mm'}g_m(E)} v_{m'n'}B^\pm_{n'n}(E')+B^{\pm*}_{n'm}(E)v^*_{m'n'}{ g^*_{m'}(E')\delta_{m'n})}\Bigg]. \end{aligned} $

Thus, they cancel with the terms in Eq. (A1) except for the
$ \delta(E-E') $ term. The S-matrix can also be obtained by$ \begin{aligned}[b] \langle \Psi^-_m(E)|\Psi^+_n(E')\rangle=\;&\sum_{i=1}^D \sum_{i=1}^D\alpha_{im}^{-*}(E)\alpha^+_{in}(E')+\delta_{mn}\delta(E-E') \\& +\Bigg(\frac 1{E-E'- {\rm i}\,0}{-2\pi {\rm i}\delta(E-E')}\Bigg)\Bigg(\sum_{j=1}^D \frac{A^{-*}_{jm}(E) f^*_{jn}(E')}{E-M_j}+\sum_{n'=1}^C v^*_{nn'}B^{-*}_{n'm}(E)g^*_n(E')\Bigg) \\& +\frac 1{E'-E+ {\rm i}\,0}\Bigg(\sum_{j=1}^D \frac{A^+_{jm}(E') f_{jn}(E)}{E'-M_j} +\sum_{n'=1}^C v_{nn'}B^+_{n'm}(E')g_n(E)\Bigg) \\&+\sum_{m'=1}^C\int_{a_{m'}} {\rm d}\omega\underbrace{\frac 1{E-\omega+ {\rm i}\,0}\frac 1{E'-\omega+ {\rm i}\,0}}_{\frac1{E'-E+ {\rm i}\,0}\big(\frac 1{E-\omega+ {\rm i}\,0}-\frac 1{E'-\omega+ {\rm i}\,0}\big)}\Bigg(\sum_{j=1}^D \frac{A^{-*}_{jm}(E) f^*_{jm'}(\omega)}{E-M_j}+\sum_{n'=1}^C v^*_{m'n'}B^{-*}_{n'm}(E)g^*_{m'}(\omega)\Bigg) \\&\times\Bigg(\sum_{j'=1}^D \frac{A^+_{j'n}(E') f_{j'm'}(\omega)}{E'-M_{j'}}+\sum_{n''=1}^C v_{m'n''}B^+_{n''n}(E')g_{m'}(\omega)\Bigg). \end{aligned} $

(A2) We have used
$\dfrac 1{E-\omega+ {\rm i}\,0}\dfrac 1{E'-\omega+ {\rm i}\,0}=\dfrac1{E'-E+ {\rm i}\,0}\big(\dfrac 1{E-\omega- {\rm i}\,0}-\dfrac 1{E'-\omega+ {\rm i}\,0}\big)-2\pi {\rm i}\delta(E-\omega) \dfrac 1{E'-\omega+ {\rm i}\,0}=\dfrac1{E'-E+ {\rm i}\,0} \big(\dfrac 1{E-\omega+ {\rm i}\,0}-\dfrac 1{E'-\omega+ {\rm i}\,0}\big)$ . Because$\delta(E'-E)\big(\dfrac 1{E-\omega+ {\rm i}\,0}-\dfrac 1{E'-\omega+ {\rm i}\,0}\big)=0$ ,$ {\rm i}\,0 $ in the first factor does not have any effect. The last two lines can be reduced to$ \begin{aligned}[b] & \frac1{E'-E+ {\rm i}\,0}\Bigg[\sum_{j,j'=1}^D{ \alpha^{-*}_{jm}(E)}\big(\delta_{jj'}(E-E'){ -V^{-*}_{j'j}(E)}+{ V^+_{jj'}(E')}\big){\alpha^+_{j'n}(E')} +\sum_{j=1}^D\sum_{n''=1}^C{ \alpha^{-*}_{jm}(E)}\Bigg({ -\sum_{m'}V^{- BA*}_{m'j}(E)v_{m'n''}}+ { V^{+ AB}_{jn''}(E')}\Bigg) { B^+_{n''n}(E')} \\&+\sum_{j'=1}^D\sum_{n'=1}^C{ B^{-*}_{n'm}}\Bigg({ -V^{- AB*}_{j'n'}(E)}+\sum_{m'=1}^Cv^*_{m'n'}{ V^{+ BA}_{j'm'}}\Bigg){ \alpha^+_{j'n}(E')} +\sum_{n',n'',m'=1}^C{ B^{-*}_{n'm}(E)}\Bigg({ -V^{- B*}_{m'n'}(E)v_{m'n''}}+v^*_{m'n'}{ V^{+ B}_{m'n''}(E')}\Bigg){ B^+_{n''n}(E')}\Bigg] \\=\;&-\sum_{j=1}^D\alpha^{-*}_{jm}(E)\alpha^+_{jn}(E)+ \frac1{E'-E+ {\rm i}\,0}\Bigg[\sum_{j'=1}^D({ -f_{j'm}(E)})\alpha^+_{j'n}(E')+\alpha^{-*}_{j'm}(E){ f^*_{j'n}(E')}) \\&+\sum_{n',m'=1}^C({-\delta_{mm'}g_m(E)} v_{m'n'}B^+_{n'n}(E')+B^{-*}_{n'm}(E)v^*_{m'n'}{ g^*_{n}(E')\delta_{m'n})}\Bigg]. \end{aligned} $

These terms cancel with the other terms except the terms with
$ \delta(E-E') $ . For$ E=E' $ and is real, the final sum inside the square bracket will be zero:$ \Big[\sum_{j'=1}^D({ -f_{j'm}(E)}\alpha^+_{j'n}(E)+\alpha^{-*}_{j'm}(E){ f^*_{j'n}(E)}) +\sum_{n',m'=1}^C({-\delta_{mm'}g_m(E)} v_{m'n'}B^+_{n'n}(E)+B^{-*}_{n'm}(E)v^*_{m'n'}{ g^*_{m'}(E)\delta_{m'n})}\Big]=0, $

which can be derived directly from Eqs. (32) and (33). Thus, the S-matrix can be derived:
$ \begin{aligned}[b] S_{mn}(E,E')=\;&\delta(E-E')-2\pi {\rm i}\delta(E-E')\Big(\sum_{j=1}^D \frac{A^{-*}_{jm}(E) f^*_{jn}(E')}{E-M_j}+\sum_{n'=1}^C v^*_{nn'}B^{-*}_{n'm}(E)g^*_n(E')\Big) \\ =\;&\delta(E-E')-\pi {\rm i} \delta(E-E')\Big(\sum_{j=1}^D\big({ \alpha^{-*}_{jm}(E) f^*_{jn}(E')}+{ f_{j'm}(E)\alpha^+_{j'n}(E')}\big) +\sum_{n'=1}^C \big({ v^*_{nn'}B^{-*}_{n'm}(E)g^*_n(E')}+ { v_{mn'}B^+_{n'n}(E)g_m(E')}\big)\Big)\,. \end{aligned} $

From the definition of
$ \mathbf Y $ and$ \mathbf F $ in Eq. (29) and solving$ \mathbf Y $ from Eq. (31), we can reformulate the previous equation using the matrices and obtain Eq. (36). -
This section provides the details for solving the eigenstate problem for the Hamiltonian in Section IV. After approximating the general contact potential as the sum of the separable potentials, the approximated Hamiltonian for multiple continuum and discrete states is shown in Eq. (58), which is copied here for completeness:
$ \begin{aligned}[b] H =\;&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{n=1}^C \int_{a_n}^\infty \mathrm d \omega \,\omega|\omega;n\rangle\langle \omega;n| \\ &+\sum_{m,n=1}^C v_{mn,\rho\delta}\Big(\int_{a_m}^\infty\mathrm d \omega' { \tilde g_{m\rho}(\omega')}|\omega';m\rangle\Big)\\&\times\Big(\int_{a_n}^\infty\mathrm d \omega { \tilde g^*_{n\delta}(\omega)}\langle \omega;n|\Big) \\ &+\sum_{j=1}^D\sum_{n=1}^C \Bigg[ |j\rangle\Big(\int_{a_n}^\infty\mathrm d \omega { f^*_{jn}(\omega)}\langle \omega;n|\Big)\\&+\Big(\int_{a_n}^\infty\mathrm d \omega { f_{jn} (\omega)}|\omega;n\rangle \Big) \langle j| \Bigg]\,. \end{aligned} $

(B1) The general eigenstate for this eigenvalue problem can be expanded using the bare discrete and bare continuum states:
$ \begin{align*} |\Psi(E)\rangle =&\sum_{i=1}^D \alpha_i(E)|i\rangle+\sum_{n=1}^C\int_{a_n} \mathrm d\omega \psi_{n}(E,\omega)|\omega;n\rangle\,. \end{align*} $

The proceeding derivation goes in parallel with the process in Section III. With this ansatz, the eigenvalue problem can be reduced to the following equations:
$ \begin{aligned}[b] (&M_j-E)\alpha_j(E)+A_j(E)= 0,\quad j=1,\dots,D \\ &\sum_{j=1}^D\alpha_j (E)f_{jn}(\omega)+(\omega-E)\psi_{n}(E,\omega)\\&\;\;+\sum_{m=1}^Cv_{nm,\rho\delta}{ \psi_{m\delta}(E)} \tilde g_{n\rho}(\omega) =0, \quad n=1,\dots,C, \quad\mathrm{and\ }\omega>a_n \end{aligned} $

where we have defined
$ \begin{aligned}[b]& A_j(E) =\sum_{n=1}^C\int_{a_n}^\infty\mathrm d\omega\, f^*_{jn}(\omega)\psi_n(E,\omega), \\& \psi_{n\delta}(E)=\int {\rm d}\omega \psi_{n}(E,\omega)\tilde g^*_{n\delta}(\omega). \end{aligned} $

(B2) There are C continuum eigenstate solutions and
$ |\Psi(E)\rangle $ ,$ \alpha_i $ ,$ \psi_{n\delta} $ , and$ A_{j}(E) $ require another index m to denote different continuum solutions, i.e.,$ |\Psi_m(E)\rangle $ ,$ \alpha_{im}(E) $ ,$ \psi_{nm\delta}(E) $ , and$ A_{jm}(E) $ . Similar to Section III, we require that$ |\Psi_m(E)\rangle $ tends to$ |E,m\rangle $ as the interactions are turned off and consider the C continuum solutions for$ E>a_C $ . Then, the above equations can be reduced to$ \alpha^\pm_{jm}(E)=\frac1{E-M_j}A^\pm_{jm}(E)\,, $

(B3) $ \begin{aligned}[b] \psi^\pm_{nm}(E,\omega) =\;&\delta_{nm}\delta(E-\omega)+ \sum_{j=1}^D \frac{\alpha^\pm_{jm}(E)f_{jn}(\omega)}{E-\omega\pm {\rm i}\,0}\\&+\sum_{n'=1}^C v_{nn',\delta'\rho}\frac{\psi^\pm_{n'm\rho}(E)\tilde g_{n\delta'}(\omega)}{E-\omega\pm {\rm i}\,0}. \end{aligned} $

(B4) By applying operation
$\sum_n \int_{a_n} {\rm d}\omega f^*_{jn}(\omega)\times$ and operations$\sum_{n\delta}v^*_{nm',\rho'\delta}\int_{a_n} {\rm d}\omega\tilde g^*_{n\delta}(\omega)\times$ on (B4), we respectively obtain$ \begin{align} 0=-f^*_{jm}(E)+\sum_{j'=1}^D\Big((E-M_{j'})\delta_{jj'}- \sum_{n=1}^C\int_{a_n} {\rm d}\omega\frac{f_{j'n}(\omega)f^*_{jn}(\omega)}{E-\omega\pm {\rm i}\,0}\Big)\frac{A^\pm_{j'm}(E)}{E-M_{j'}} -\sum_{n',n=1}^C v_{nn',\delta'\rho}\psi^\pm_{n'm\rho}(E)\int_{a_n} {\rm d} \omega\frac{f^*_{jn}(\omega)\tilde g_{n\delta'}(\omega)}{E-\omega\pm {\rm i}\,0}\,, \end{align}$

(B5) $ \begin{align} 0= -v^*_{mm',\delta\rho'}\tilde g^*_{m\delta}(E)-\sum_{j=1}^D { \alpha^\pm_{jm}(E)}\sum_{n=1}^Cv^*_{nm',\delta\rho'} \int_{a_n} {\rm d}\omega \frac{{ f_{jn}(\omega)}\tilde g_{n\delta}^*(\omega)}{E-\omega\pm {\rm i}\,0} + \sum_{n'}^C\psi^\pm_{n'm\rho}(E) \bigg[v^*_{n'm',\rho\rho'}-\sum_{n=1}^Cv^*_{nm',\delta\rho'}v_{nn',\delta'\rho}\int_{a_n} {\rm d}\omega \frac{\tilde g_{n\delta'}(\omega)\tilde g_{n\delta}^*(\omega)}{E-\omega\pm {\rm i}\,0}\bigg]. \end{align} $

(B6) These two equations correspond to previous Eq. (27) and (28). Notice that the differences here are Greek letters and the sums. Similar to the vectors and matrices defined in Eqs. (29)−(30), we define
$ \begin{aligned}[b] &(\tilde {\mathbf F}_m)_{m'\rho'}=v^*_{mm',\delta\rho'}\tilde g^*_{m\delta}(E)\,,\quad (\tilde {\mathbf F}_m)_j=f^*_{jm}(E)\,,\quad m=1,\dots, C; j=1,\dots,D; \delta=1,2,\dots, N \\ &(\tilde {\mathbf Y}_m(E))_{j}=\alpha_{jm}(E) \,,\quad(\tilde {\mathbf Y}_m)_{n'\rho}=\psi^\pm_{n'm\rho}(E)\,, \quad j=1,\dots,D; m,n'=1,\dots,C;\rho=1,2,\dots, N \end{aligned} $

(B7) $ \begin{aligned}[b] &\tilde {\mathbf V}^{BB}_{m'\rho',n'\rho}=v^*_{n'm',\rho\rho'}-\sum_{n=1}^Cv^*_{nm',\delta\rho'}v_{nn',\delta'\rho}\int_{a_n} {\rm d}\omega \frac{\tilde g_{n\delta'}(\omega)\tilde g_{n\delta}^*(\omega)}{E-\omega\pm {\rm i}\,0},\quad m',n'=1,2,\dots,C; \rho',\rho=1,2,\dots, N \\&\tilde {\mathbf V}^{AA}_{jj'}=(E-M_{j'})\delta_{jj'}- \sum_{n=1}^C\int_{a_n} {\rm d}\omega\frac{f_{j'n}(\omega)f^*_{jn}(\omega)}{E-\omega\pm {\rm i}\,0},\quad j,j'=1,2,\dots, D \\& \tilde {\mathbf V}^{AB}_{j,n'\rho}=-\sum_{n=1}^Cv_{nn',\delta'\rho}\int_{a_n} {\rm d}\omega\frac{f^*_{jn}(\omega)\tilde g_{n\delta'}(\omega)}{E-\omega\pm {\rm i}\,0}, \quad j=1,\dots,D; n'=1,\dots, C;\rho=1,2,\dots, N \\& \tilde {\mathbf V}^{BA}_{m'\rho',j}=-\sum_{n=1}^Cv^*_{nm',\delta\rho'} \int_{a_n} {\rm d}\omega \frac{{ f_{jn}(\omega)}\tilde g_{n\delta}^*(\omega)}{E-\omega\pm {\rm i}\,0}, \quad j=1,\dots,D; m'=1,\dots, C;\rho'=1,2,\dots, N \\ &\tilde{\mathbf M}_{IJ}=\begin{pmatrix} \tilde {\mathbf V}^{AA}(E)&\tilde {\mathbf V}^{AB}(E)\\ \tilde {\mathbf V}^{BA}(E)&\tilde {\mathbf V}^{BB}(E)\end{pmatrix}_{IJ}.\quad IJ=1,\dots,D, D+1,\dots, D+NC\,. \end{aligned} $

(B8) We still have
$ \tilde {\bf M}^{+\dagger} =\tilde {\bf M}^- $ . With these matrices, Eqs. (B5) and (B6) can be expressed as$ \tilde {\bf M}\cdot \tilde {\bf Y}_m=\tilde {\bf F}_m $

or
$ \begin{aligned} \sum_{j=1}^D\tilde{\bf V}^{AA}_{ij}(E) \alpha_{jm}(E)+\sum_{n'=1}^C\tilde{\bf V}^{AB}_{i,n'\rho}(E) \psi_{n'm\rho}(E)=f^*_{im}(E), \end{aligned} $

(B9) $ \begin{aligned} \sum_{j=1}^D\tilde{\bf V}^{BA}_{n\delta,j}(E) \alpha_{jm}(E) + \sum_{n'=1}^C\tilde{\bf V}^{BB}_{n\delta,n'\rho}(E) \psi_{n'm\rho}(E) = v^*_{nn',\delta\rho}(E)\tilde g^*_{m\rho}(E). \end{aligned} $

(B10) As earlier,
$ \tilde{\mathbf M} $ is still independent of m, but$ \tilde {\mathbf F}_m $ depends on m. If an infinite number of bases are used, matrix$ \tilde {\mathbf M} $ and vectors$ \tilde{\bf F}_m $ and$ \tilde {\mathbf Y} $ are infinite dimensional. Now, we have considered that the bases selected sufficiently well and have made a truncation to a finite order N of the expansion of potential$ V_{nn'} $ i.e.,$ v_{nn',\delta\rho}=0 $ for$ \delta,\rho > N $ . Thus,$ \tilde {\bf M} $ is a$ (D+N C)\times (D+ NC) $ matrix. In general, matrix$ \tilde {\bf M} $ is non-degenerate for$ E>a_m $ , and$ \tilde{\bf Y}_m $ can be solved:$ \tilde{\bf Y}_m(E)=\tilde{\bf M}^{-1}\cdot \tilde {\bf F}_m. $

(B11) With all the
$ \psi^\pm_{nm\rho}(E) $ and$ \alpha^\pm_{jm}(E) $ values at hand, the approximate continuum solutions are solved as$ \begin{aligned}[b] |\Psi^\pm_m(E)\rangle =\;&\sum_{i=1}^D \alpha^\pm_{im}(E)|i\rangle+|E;m\rangle+ \sum_{n=1}^C\int_{a_n} \mathrm d\omega\frac{1}{E-\omega\pm {\rm i}\,0} \Big(\sum_{j=1}^D \alpha^\pm_{jm}(E)f_{jn}(\omega) +\sum_{n'=1}^C v_{nn',\delta'\rho}\psi^\pm_{n'm\rho}(E)\tilde g_{n\delta'}(\omega) \Big)|\omega;n\rangle\, \\ =\;&|E;m\rangle+\sum_{j=1}^D \alpha^\pm_{jm}(E)\Big(|j\rangle+ \sum_{n=1}^C\int_{a_n} \mathrm d\omega\frac{f_{jn}(\omega)}{E-\omega\pm {\rm i}\,0} |\omega;n\rangle\Big) +\Big( \sum_{n,n'=1}^Cv_{nn',\delta'\rho}\psi^\pm_{n'm\rho}(E)\int_{a_n} \mathrm d\omega\frac{\tilde g_{n\delta'}(\omega)}{E-\omega\pm {\rm i}\,0} |\omega;n\rangle\Big). \end{aligned} $

(B12) We can check that the normalization is
$\langle \Psi_m^\pm(E)|\Psi_n^\pm(E')\rangle= \delta_{mn}\delta(E-E')$ . The S-matrix can be obtained:$ \begin{aligned}[b] \langle \Psi_m^-(E)|\Psi_n^+(E')\rangle=\;&\delta_{mn}\delta(E-E') \\&-2\pi {\rm i}\delta(E-E')\Big(\tilde{\bf F}^\dagger_m \cdot (\tilde{\bf M}^+)^{-1}\cdot \tilde{\bf F}_m \Big). \end{aligned} $

(B13) For discrete eigenvalues and discrete eigenstates, Eq. (B4) will not have the delta function, and we have
$ \tilde {\bf M} \cdot \tilde {\bf Y}=0, $

where
$ \tilde {\bf Y} $ is defined similar to Eq. (B7) without subindex m. The generalized energy eigenvalues for the discrete state can be obtained from$ \det \tilde {\mathbf M}(E)=0 $ , and eigenvector$ \tilde {\bf Y} $ can be obtained with proper normalization selected as in the previous section. Thus, the i-th discrete state can be expressed as$ \begin{aligned}[b] |\Psi^{(i)}(E_i)\rangle =\;&\sum_{i=1}^D \alpha^{(i)}_{j}(E_i)\Big(|j\rangle+ \int_{a_n} \mathrm d\omega\frac{f_{jn}(\omega)}{E_i-\omega} |\omega;n\rangle\Big) \\&+\sum_{n'=1}^C v_{nn',\delta'\rho}\psi^{(i)}_{n'm\rho}(E_i)\int_{a_n} \mathrm d\omega\frac{\tilde g_{n\delta'}(\omega) }{E_i-\omega} |\omega;n\rangle\,, \\ &\mathrm {with\ } \tilde {\mathbf Y}^{(i)}(E_i)\cdot \tilde {\mathbf M}'(E_i)\cdot \tilde {\mathbf Y}^{(i)*}(E_i)=1 \end{aligned} $

(B14) where
$ \tilde {\mathbf M}'(E) $ is the derivative of the matrix w.r.t.$ E_i $ , and the integral contour must be deformed for$ E_i $ on unphysical sheets as before. -
This section solves the eigenstates for the Hamiltonian in Eq. (63) where both the contact potential and vertex are expanded using function bases
$ \tilde g_{n\delta} $ , which we reproduce here for completeness:$ \begin{align} H=\;&\sum_{i=1}^D M_i|i\rangle\langle i|+\sum_{n=1}^C \int_{a_n}^\infty \mathrm d \omega \,\omega|\omega;n\rangle\langle \omega;n| \\ &+\sum_{m,n=1}^C v_{mn,\rho\delta}\Big(\int_{a_m}^\infty\mathrm d \omega' { \tilde g_{m\rho}(\omega')}|\omega';m\rangle\Big)\\&\times\Big(\int_{a_n}^\infty\mathrm d \omega { \tilde g^*_{n\delta}(\omega)}\langle \omega;n|\Big)\end{align} $

$ \begin{aligned}[b] &+\sum_{j=1}^D\sum_{n=1}^C \Bigg[f^*_{jn\delta} |j\rangle\Big(\int_{a_n}^\infty\mathrm d \omega { \tilde g^*_{n\delta}(\omega)}\langle \omega;n|\Big)\\&+{ f_{jn\delta }} \Big(\int_{a_n}^\infty\mathrm d \omega \tilde g_{n\delta}(\omega)|\omega;n\rangle \Big) \langle j| \Bigg]. \end{aligned} $

(C1) This case is similar to those discussed in [10, 26], where the same form factor for the continuum before both in the discrete-continuum and continuum-continuum interaction. Using the eigenstate ansatz
$ \begin{aligned}[b] |\Psi(E)\rangle =\;&\sum_{i=1}^D \alpha_{i}(E)|i\rangle+\int_{a_n} \mathrm d\omega \psi_{n}(E,\omega)|\omega;n\rangle \\ =\;&\sum_{i=1}^D \alpha_i(E)|i\rangle+\sum_{n=1}^C\psi_{n\delta}(E)\int_{a_n} \mathrm d\omega \tilde g_{n\delta}(\omega)|\omega;n\rangle\,, \end{aligned} $

(C2) and proceeding in solving the eigenvalue problem similarly to the previous section, we find that
$ A_j $ in Eq. (B2) becomes$ A_j(E) =\sum\limits_{n=1}^C \, f^*_{jn\delta}\psi_{n\delta}(E). $

For the m-th continuum solution
$ |\Psi_m(E)\rangle $ , coefficients$ \alpha_i $ ,$ \psi_n $ , and$ \psi_{n\delta} $ take another subindex m and Eqs. (B3) and (B4) become$ \alpha^\pm_{jm}(E)=\frac1{E-M_j}A^\pm_{jm}(E)=\frac1{E-M_j}\sum_{n'=1}^C f^*_{jn'\rho}\psi^\pm_{n'm\rho}(E), $

(C3) $ \psi^\pm_{nm}(E,\omega) =\delta_{nm}\delta(E-\omega)+ \sum_{n'=1}^C\psi^\pm_{n'm\rho}(E) V_{n\delta',n'\rho}(E)\frac{\tilde g_{n\delta'}(\omega)}{E-\omega\pm {\rm i}\,0}, $

(C4) where
$ V_{n\delta',n'\rho}(E) $ is defined as the matrix elements of a$ NC\times NC $ matrix$ \mathbf V $ $ (\mathbf V{ (E)})_{n\delta',n'\rho}= \sum\limits_{j=1}^D\frac{f_{jn\delta'}f^*_{jn'\rho}}{E-M_j} + v_{nn',\delta'\rho}, $

which should be be non-degenerate for general E. Multiplying
$ \tilde g_{n\delta}^*(\omega) $ to above Eq. (C4) and integrating w.r.t ω, we obtain$ \begin{aligned}[b] \delta_{nm}\tilde g^*_{n\delta}(E)=\;& \sum_{n'=1}^C\psi^\pm_{n'm\rho}(E) \bigg[\delta_{nn'}\delta_{\rho\delta}\\&-V_{n \delta',n'\rho}(E)\int_{a_n} {\rm d}\omega \frac{\tilde g_{n\delta'}(\omega)\tilde g_{n\delta}^*(\omega)}{E-\omega\pm {\rm i}\,0}\bigg]. \end{aligned} $

(C5) We define
$ NC\times NC $ matrix$ \tilde {\mathbf M} $ and$ NC $ dimensional vector$ \tilde {\bf F}_m $ ,$ \tilde {\bf Y}_m $ as$ \tilde {\mathbf M}_{n\delta,n'\rho}=\delta_{nn'}\delta_{\rho\delta}-V_{n \delta',n'\rho}(E)\int_{a_n} {\rm d}\omega \frac{\tilde g_{n\delta'}(\omega)\tilde g_{n\delta}^*(\omega)}{E-\omega\pm {\rm i}\,0}, $

(C6) $ (\tilde {\mathbf F}_m)_{n\delta}=\delta_{nm}\tilde g^*_{n\delta}(E)\,,\quad (\tilde {\mathbf Y}_m)_{n'\rho}=\psi^\pm_{n'm\rho}(E). $

(C7) Thus, Eq. (C5) can be expressed as
$ \tilde {\mathbf F}_m=\tilde{ \mathbf M}\cdot \tilde{\mathbf Y}_m $ . Note that$ \tilde{\mathbf M} $ is independent of the m-th solution, but$ \tilde {\mathbf F}_m $ depends on m. To observe the real analyticity of$ \det \tilde {\mathbf M} $ , we define$ \begin{aligned}[b] (\tilde{\bf W}^\pm)_{n\delta,n'\rho}=\;&(\tilde {\bf M}^\pm\cdot \mathbf V^{-1})_{n\delta,n'\rho}\\=\;&{\mathbf V}^{-1}_{n\delta,n'\rho}-\delta_{nn'}\int_{a_n} {\rm d}\omega \frac{\tilde g_{n\rho}(\omega)\tilde g_{n\delta}^*(\omega)}{E-\omega\pm {\rm i}\,0}, \end{aligned} $

(C8) and then we have
$ \tilde {\mathbf M}^\pm=\tilde{\mathbf W}^\pm\cdot \mathbf V $ . Because$ (\tilde {\mathbf W}^\pm(E))^\dagger = \tilde {\mathbf W}^\mp(E) $ and$ \mathbf V(E) $ is Hermitian for real E,$ \det\tilde {\mathbf M}^{\pm \dagger }(E)= \det\tilde {\mathbf M}^{\mp}(E) $ . Therefore, the analytically continued$ \det \tilde {\mathbf M}(E) $ with$ \det\tilde {\mathbf M}^{+}(E) $ and$ \det\tilde {\mathbf M}^{-}(E) $ on the upper and lower edges of the cut above the threshold satisfies the Schwartz reflection relation,$ \det\tilde {\mathbf M}^{*}(E)=\det\tilde {\mathbf M}(E^*) $ .Subsequently, in general, matrix
$ \tilde {\bf M} $ is non-degenerate for$ E>a_m $ , and$ \tilde{\bf Y}_m $ can be solved:$ \psi^\pm_{nm\rho}(E)=(\tilde{\bf Y}_m(E))_{n\rho}=(\tilde{\bf M}^{-1}\cdot \tilde {\bf F}_m)_{n\rho}=(\tilde{\bf M}^{-1})_{n\rho,m\delta} \tilde g_{m\delta}(E). $

(C9) With all the
$ \psi^\pm_{nm\rho}(E) $ values for$ \rho\le N $ at hand, all$ \alpha^\pm_{jm}(E) $ and$ \psi^\pm_{nm}(E,\omega) $ can also be obtained. Thus, the continuum state can be approximated as$ \begin{aligned}[b] |\Psi^\pm_m(E)\rangle =\;&\sum_{i=1}^D \alpha^\pm_{im}(E)|i\rangle+|E,m\rangle+\sum_{n=1}^C\sum_{n'=1}^C\psi^\pm_{n'm\rho}(E) V_{n\delta',n'\rho}(E)\\&\times\int_{a_n} \mathrm d\omega \frac{\tilde g_{n\delta'}(\omega)}{E-\omega\pm {\rm i}\,0} |\omega;n\rangle. \end{aligned} $

(C10) We can check that the normalization is
$ \langle \Psi_m^\pm(E)|\Psi_n^\pm(E')\rangle= \delta_{mn}\delta(E-E') $ . The S-matrix can be obtained as$ \begin{aligned}[b] \langle \Psi_m^-(E)|\Psi_n^+(E')\rangle=\;&\delta_{mn}\delta(E-E')-2\pi {\rm i}\delta(E-E')\\&\times\sum_{n=1}^C\sum_{n'=1}^C\psi^{-*}_{n'm\rho}(E') V^*_{n\delta',n'\rho}(E') \tilde g^*_{n\delta'}(E) \\=&\delta_{mn}\delta(E-E')-2\pi {\rm i} \delta(E-E')\\&\times(\tilde {\mathbf F}_m^\dagger\cdot (\tilde {\mathbf W}^+)^{-1} \cdot \tilde {\mathbf F}_n). \\[-15pt] \end{aligned} $

(C11) Similar to the previous section, the generalized energy eigenvalues for the discrete state can be obtained from
$ \det \tilde {\mathbf M}(E)=0 $ , and for each eigenvalue$ E_i $ ,$ \psi_{n\rho}^{(i)} $ can be solved from$ \tilde {\mathbf M}\cdot \tilde {\mathbf Y}=0 $ . Thus, we have the discrete eigenstates,$ \begin{aligned}[b] |\Psi^{(i)}(E_i)\rangle=\;&\sum_{n'=1}^C\psi^{(i)}_{n'\rho}(E_i)\Bigg[\sum_{j=1}^D \frac{f^*_{jn'\rho} }{E_i-M_j} |j\rangle \\&+{ \sum_{n=1}^C}V_{n\delta',n'\rho}(E_i)\int_{a_n} {\rm d}\omega\frac{\tilde g_{n\delta'}(\omega)}{E_i-\omega} |\omega;n\rangle\Bigg], \\ \mathrm{with }\quad& \tilde {\mathbf Y}^{(i)\dagger}(E_i)\cdot \mathbf V(E_i)\cdot \tilde{\mathbf W}'(E_i)\cdot \mathbf V(E_i)\cdot \tilde {\mathbf Y}^{(i)}(E_i)=1 \end{aligned} $

(C12) with integral contour deformed for resonances and virtual states as earlier.
On the generalized Friedrichs-Lee model with multiple discrete and continuous states
- Received Date: 2024-11-11
- Available Online: 2025-08-15
Abstract: In this study, we present several improvements of the non-relativistic Friedrichs-Lee model with multiple discrete and continuous states while retaining its solvability. Our findings establish a solid theoretical basis for the exploration of resonance phenomena in scenarios involving multiple interfering states across various channels. The scattering amplitudes associated with the continuum states naturally adhere to coupled-channel unitarity, rendering this framework particularly valuable for investigating hadronic resonant states appearing in multiple coupled channels. Moreover, this generalized framework exhibits a wide-range applicability, enabling investigations into resonance phenomena across diverse physical domains, including hadron physics, nuclear physics, optics, cold atom physics, etc.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
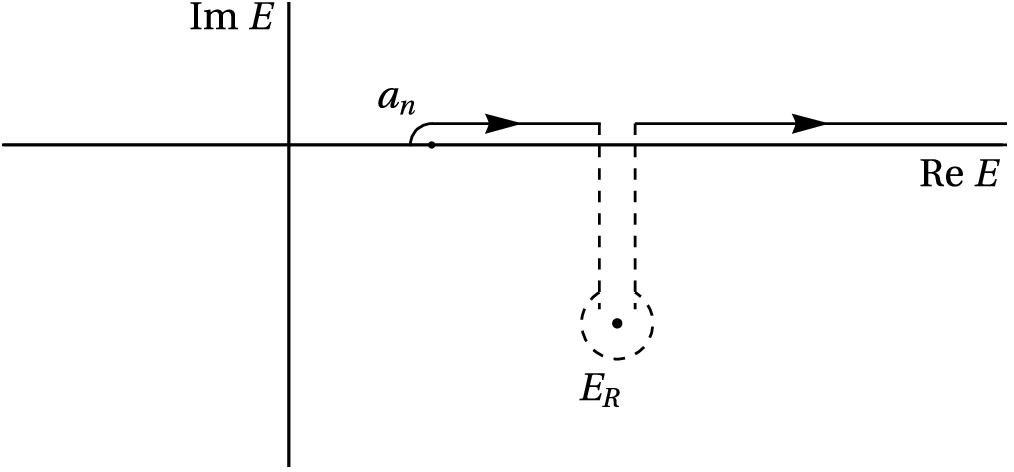










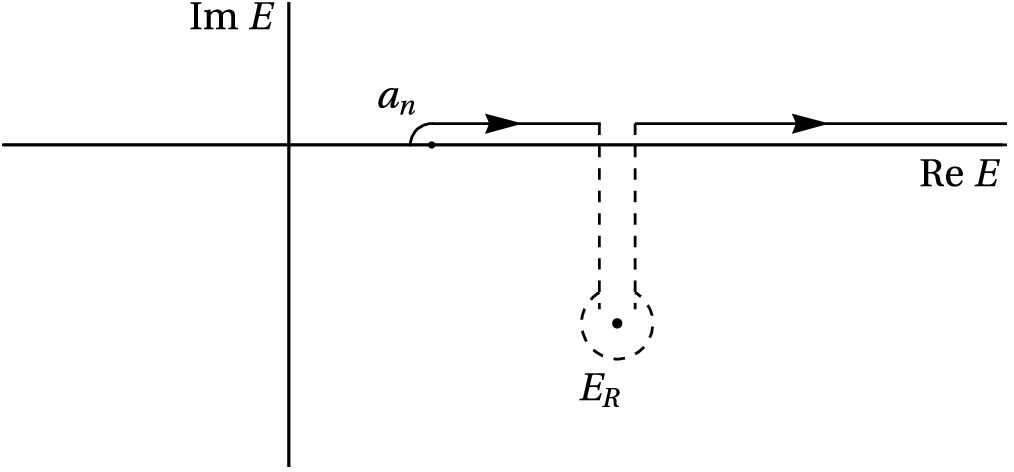



 DownLoad:
DownLoad: