-
The synthesis of superheavy elements (SHEs) [1] has gained considerable attention following the recent expansion of the periodic table, driven by the discovery of elements with higher atomic numbers. Under particular laboratory conditions, these radioactive elements with atomic numbers greater than 103 (Z
$ >103 $ ) can only be synthesized by the fusion of two nuclei. In the formation of SHEs, this is impeded by a dynamical non-equilibrium phenomenon known as quasifission [2]. In reactions involving heavy elements, quasifission (QF) and fusion-fission (FF) are the predominant processes, significantly hindering the production of an evaporation residue at higher excitation energies. Quasifission has become highly significant in heavy-ion nuclear physics due to its strong impact on compound nucleus formation and SHE synthesis [3].Many theoretical and experimental studies have been conducted on the quasifission process. From one such theoretical result, the systematic time-dependent Hartree-Fock (TDHF) simulations of collisions were studied by Simenel et al. [4], which indicated that the mass equilibration between fragments in quasi-fission had stopped. Heavy-ion reaction investigations by Godbey et al. [5] found that the TDHF theory and its extensions are a useful theoretical tool to study quasifission. Comparing the reaction using the 244Pu target to the 239Pu case reported by Guo et al. [6] showed that the quasifission significantly decreased and the survival probability increased by approximately one order of magnitude. Nasirov et al. [7] showed that the reduced quasifission yield is due to overlapping mass-angle distributions. Hammerton et al. [8] showed that the dynamics of quasifission exhibit an extensive reliance on the compound nuclei N/Z. McGlynn et al. [9] revealed that the quasifission trajectories can be interpreted in terms of the underlying potential energy surface for low excitation energies.
Experimental studies on quasifission by Hinde et al. [10] revealed that the static deformation and spherical magic numbers of the colliding nuclei significantly influence the quasifission times in collisions at energies near the capture barrier. Further, Itkis et al. [11] showed that the time scale of quasifission was an indirect observable that provides insights into the intermediate stages of the SHE formation process. Quasifission typically occurs on a shorter time scale compared to compound nucleus formation. Heavy-ion reactions forming superheavy nuclei are dominated by quasifission and deep inelastic collisions, limiting compound nucleus formation. These nuclei predominantly undergo fission, revealing important formation cross-sections, fission barriers, and survival probabilities. Recent studies, focusing on mass-energy distributions via the CORSET spectrometer, provide key insights into these processes [12].
Gupta et al. [13] systematically studied quasifission and fusion–fission lifetimes in heavy-ion fusion reactions for superheavy element (SHE) synthesis, which show longer quasifission lifetimes in successful reactions. The performance lifetimes depend on the energy, angular momentum, and deformation parameters. Manjunatha et al. [14] analyzed quasifission and fusion-fission lifetimes for Z=120 synthesis using the dinuclear system model. Further, the influence of projectile-target orientation and angular momentum on quasifission barriers was investigated in detail by Gupta et al. [15], who also investigated Coulomb fission and quasifission lifetimes [16].
The synthesis of SHEs continues to challenge nuclear physicists, with quasifission (QF) being a significant barrier in the formation of compound nuclei. Despite extensive theoretical and experimental studies, many aspects of the quasifission process remain poorly understood, motivating further investigation. Identifying optimal projectile-target combinations, beam energies, and orientation angles is essential for minimizing quasifission and maximizing fusion probabilities, which is crucial for achieving measurable evaporation residue cross-sections. To facilitate the synthesis of SHEs, it is important to gain a comprehensive understanding of quasifission mechanisms. A systematic study of quasifission lifetimes across the SHE region (
$ 104\le Z\le 120 $ ) is necessary to enhance the prediction of reaction dynamics and optimize experimental conditions. A detailed investigation into these aspects will provide critical insights into the dynamics of SHE formation and improve strategies for successful synthesis. -
The dinuclear system's nucleus-nucleus interaction potential [17] is expressed as
$ \begin{aligned}[b] V(R,Z_i,\beta_{2i},\ell)=\;& V_c(R,Z_i,\beta_{2i}) \\&+V_N(R,Z_i,\beta_{2i}) + V_{\rm rot}(\ell,\beta_{2i}). \end{aligned} $

(1) Here,
$ i=1,2 $ identifies whether the parameter belongs to the projectile (i = 1) or target (i = 2), where$ Z_i $ accounts for the atomic number of nucleus i, and$ \beta_{2i} $ corresponds to the quadrupole deformation parameter of nucleus i, which accounts for nuclear shape effects. R represents the distance between the two centers,$ V(R,Z_i,\beta_{2i},\ell) $ denotes the nucleus-nucleus potential,$ V_C $ corresponds to the Coulomb potential,$ V_N $ is the nuclear potential, and$ V_{\rm rot} $ signifies the rotational potential. The terms$ V_C $ and$ V_{\rm rot} $ were evaluated using the set of equations explained in [14, 17]. The term$ V_N $ is evaluated as explained in literature [18], in which the proximity 2010 potential has been considered in the evaluation of the nuclear potential.The quasifission lifetime of an excited asymmetric dinuclear system (DNS) [14, 17, 19] is given by
$ \begin{align} \tau_{qf}=\frac{1}{\lambda_{qf}}, \end{align} $

(2) where
$ \lambda_{qf} $ represents the quasifission decay constant, expressed as$ \begin{aligned}[b] \lambda_{qf}=\; & \frac{\omega_m}{2\pi\omega_{qf}}\left(\sqrt{\left(\frac{\Gamma}{2\hbar}\right)^2+ \omega_{qf}^2}-\frac{\Gamma}{2\hbar}\right) \\& \exp\left(-\frac{B_{qf}(Z,A,\ell)}{\Theta_{\rm DNS}(Z,A)}\right) \end{aligned} $

(3) The term Γ denotes the average width of the single-particle states near the Fermi surface, typically taken as 2 MeV.
$ \omega_m $ and$ \omega_{qf} $ represent the frequencies of the harmonic oscillator and inverted harmonic oscillator, respectively [14]. The quasifission barrier ($ B_{qf}(Z,A,\ell) $ ) in the dinuclear system is given by$ B_{qf}(Z,A,l)=V(R_b,Z,A,\beta_{2i},\ell)- V(R_m,Z,A,\beta_{2i},\ell) $

(4) where
$ \ell $ is the angular momentum. The term$ \beta_{2i} $ is the quadrupole deformation parameter of projectile and target, whose values are obtained from [20, 21].$ R_m $ and$ R_b $ are the distances at which the potential is minimum and maximum in the DNS system, respectively. The nucleus-nucleus potential is minimum at distance$ R=R_m $ [17]. The local temperature$ \Theta_{\rm DNS} $ is expressed as$ \begin{align} \Theta_{\rm DNS}(Z,A)=\sqrt{\left(\frac{E_{\rm DNS}-B_{qf}}{a}\right)}. \end{align} $

(5) The excitation energy of DNS is expressed as
$ \begin{align} E_{\rm DNS}=E_{\rm cm}-V(R_m),\end{align} $

(6) where
$ E_{\rm cm} $ is the center of mass energy. -
We investigated quasifission lifetimes of SHEs in the region
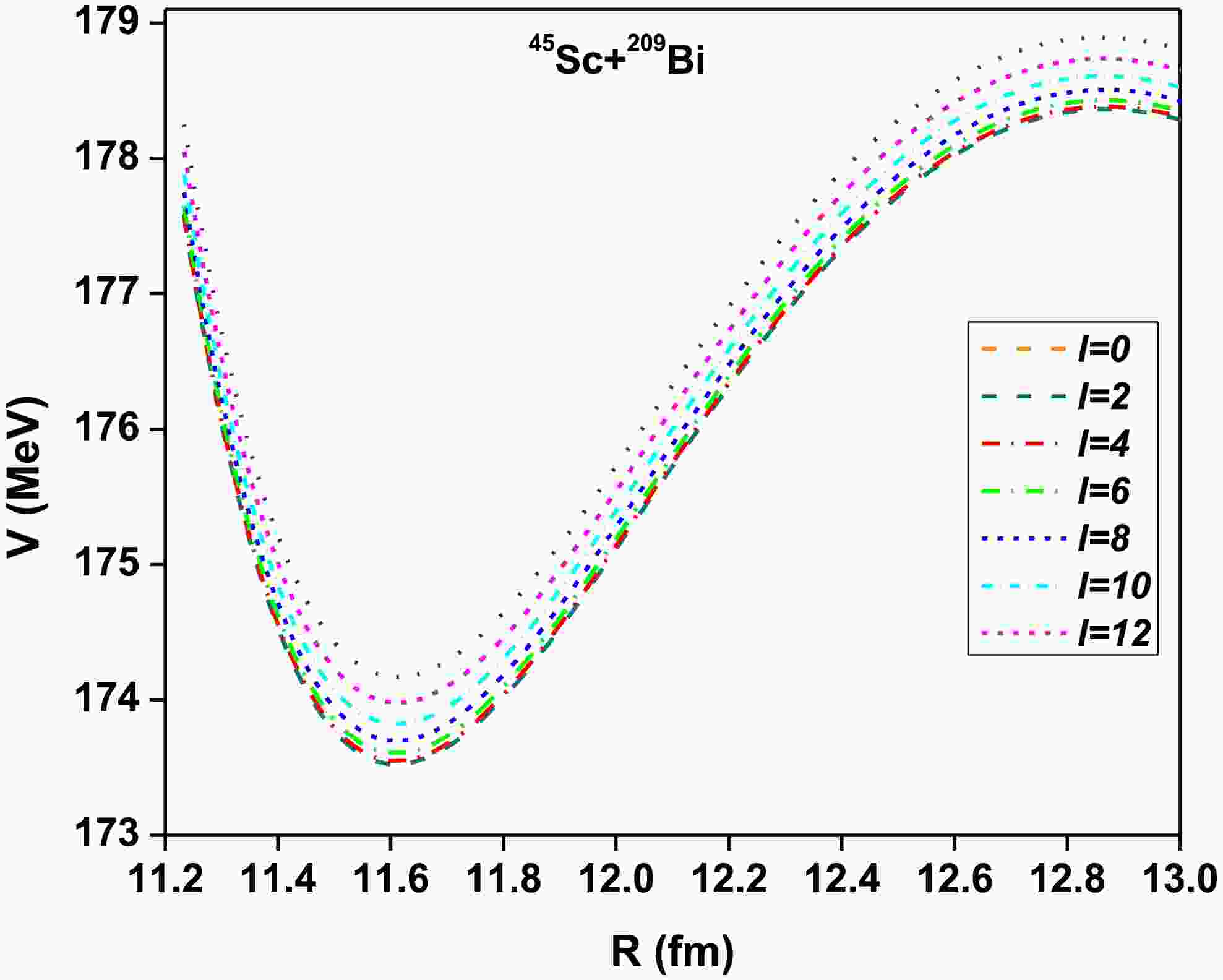
$ 104\le Z\le 120 $ and mass number region$ 243 \le A \le 301 $ . From this perspective, we considered different projectile-target combinations. For the projectile, the selected atomic and mass numbers are between$ 20\le Z\le 30 $ and$ 40\le A\le 70 $ , respectively. Similarly, the target's atomic and mass numbers range between$ 74\le Z\le 98 $ and$ 180\le A\le 252 $ , respectively. Likewise, we studied approximately 1946 fusion reactions in the SHEs in the region$ 104\le Z\le 120 $ . For each projectile-target combination, the nucleus-nucleus potential is evaluated by maintaining orientation angles$ \alpha_1=90^\circ $ and$ \alpha_2=90^\circ $ . Figure 1 shows a plot of the nucleus-nucleus interaction potential of the dinuclear system with the mean distance between their centers. The studied nucleus-nucleus potential is specifically for the reaction 45Sc+209Bi, and different curves have been plotted for different values of angular momentum ($ \ell= $ 0, 2, 4, 6, 8, 10, 12). The total potential decreases as R increases, showing the behavior of the nucleus-nucleus interaction potential where the repulsive Coulomb and attractive nuclear forces interact. As$ \ell $ increases, the potential barrier shifts upward, indicating a centrifugal effect due to angular momentum. In addition, the barrier height increases with$ \ell $ , which is consistent with the additional rotational energy introduced by higher angular momentum.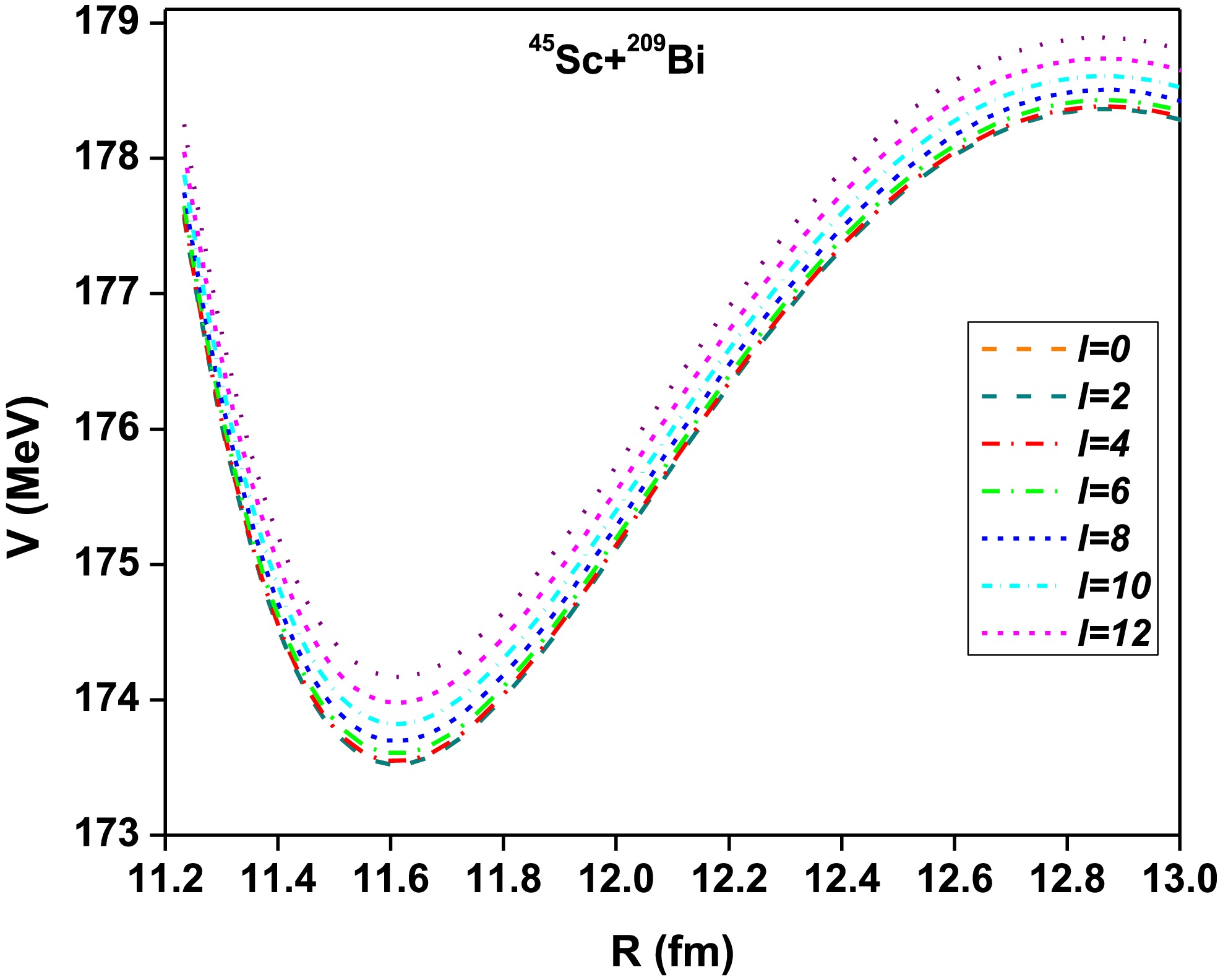
Figure 1. (color online) Variation of nucleus-nucleus interaction potential of the dinuclear system with the mean distance between their centers for different angular momenta, with orientation angles of the projectile and target fixed at
$ \alpha_1=90^\circ $ and$ \alpha_2=90^\circ $ .Once the minimum and maximum potentials were identified, the quasifission barriers were evaluated using Eq. (4). For instance, we plotted the effect of angular momentum on quasifission barriers for the fusion reaction of 45Sc+209Bi, as presented in Fig. 2. As
$ \ell $ increases,$ B_{qf} $ gradually decreases. The values of$ B_{qf} $ range approximately between 4.84 MeV and 4.72 MeV, showing a relatively small variation over the entire range of$ \ell $ .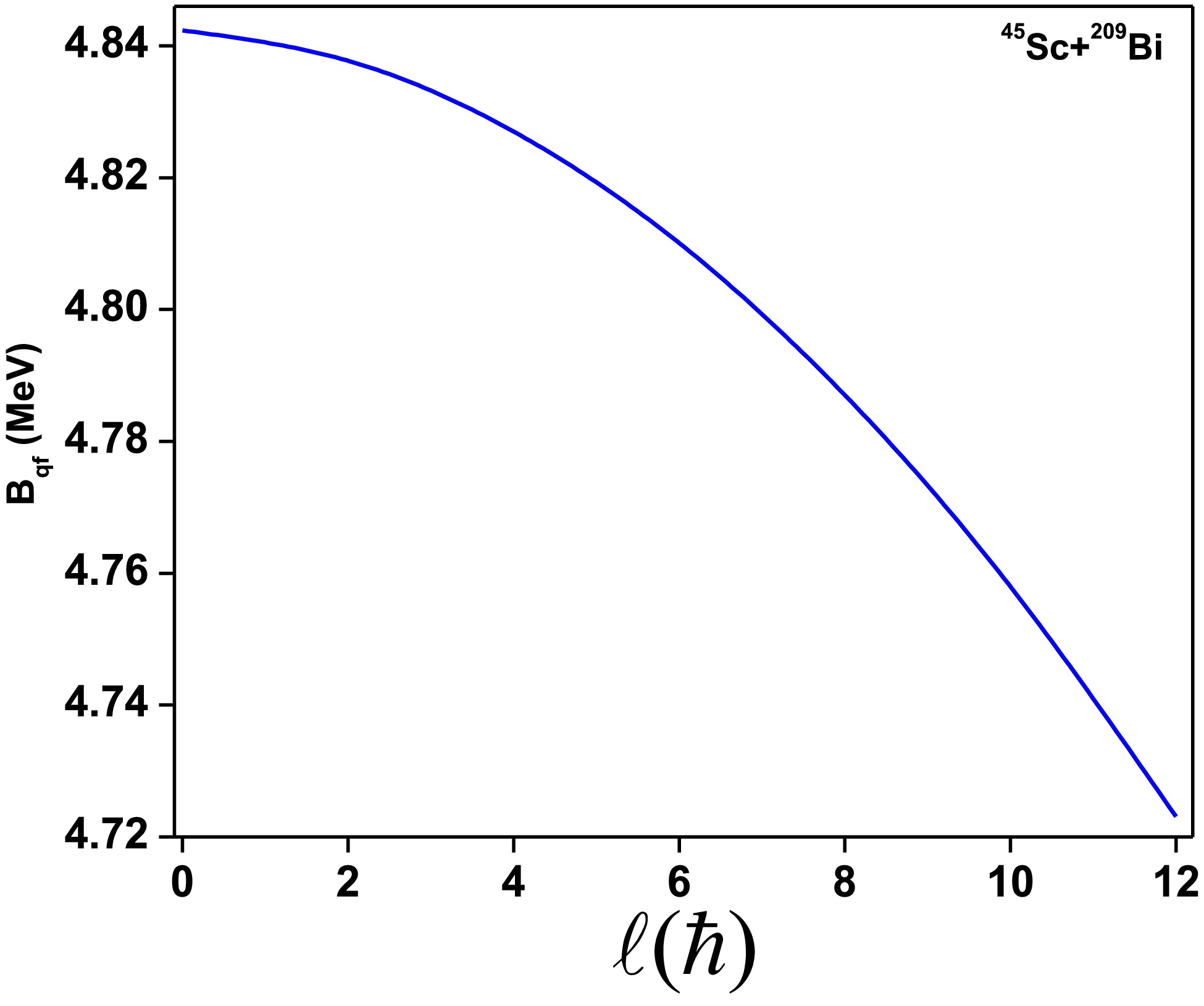
Figure 2. (color online) Quasifission barrier as a function of angular momentum for the fusion reaction of 45Sc+209Bi.
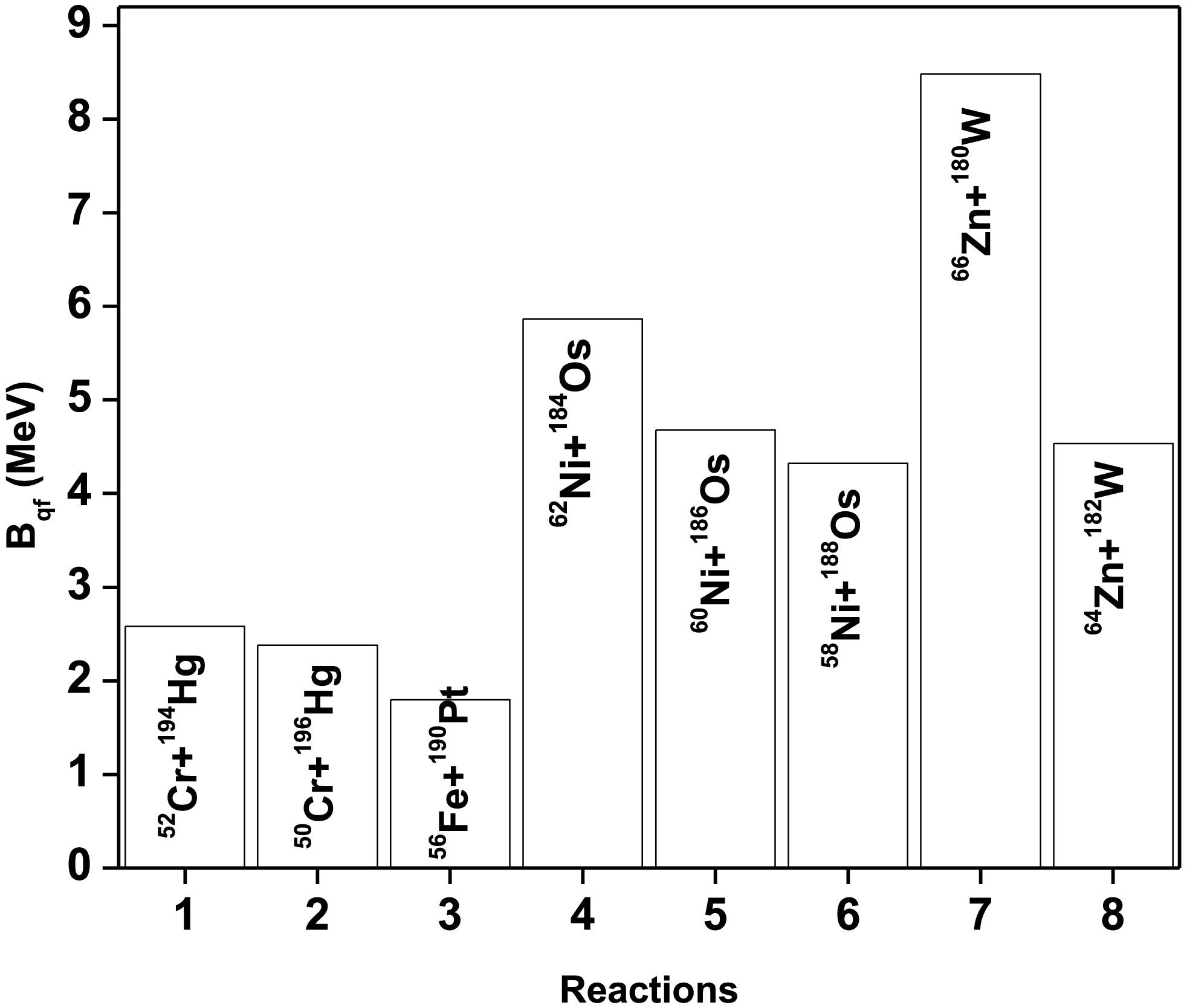
For each isotope, we get different projectile-target combinations. For the formation of compound nuclei 246Rf, we considered 8 possible projectile-target combinations: 52Cr+194Hg, 50Cr+196Hg, 56Fe+190Pt, 62Ni+ 184Os, 60Ni+186Os, 58Ni+188Os, 66Zn+180W, and 64Zn+182W. The quasifission barriers obtained for these studied fusion reactions are plotted in Fig. 3.
$ B_{qf} $ was observed to be larger for 66Zn+180W than for other studied fusion reactions. Similarly, a smaller$ B_{qf} $ value was noticed for the 56Fe+190Pt fusion reaction. Larger$ B_{qf} $ values are more favorable for synthesizing superheavy elements, as they resist quasifission and enhance fusion probability. Meanwhile, smaller values of$ B_{qf} $ correspond to the reactions where the likelihood of quasifission is the highest. Hence, in each isotope, we have identified larger$ B_{qf} $ values.We identified larger
$ B_{qf} $ values for fusion reactions forming Rutherfordium (Rf) isotopes (Z=104). Approximately 190 fusion reactions were analyzed for the production of isotopes ranging from 242Rf to 260Rf. Figure 4 depicts the variation of the quasifission barrier,$ B_{qf} $ , as a function of the compound nuclei's mass numbers. The analysis revealed a general trend where$ B_{qf} $ increases with the mass number of the compound nuclei, reaching a peak value of 8.5 MeV for$ ^{249}_{145} $ Rf. This maximum value is notably higher than those of neighboring nuclei, indicating enhanced stability against quasifission. Following this maximum,$ B_{qf} $ gradually decreases with increasing mass number. However, secondary maxima are observed at$ ^{246}_{142} $ Rf with 7.98 MeV and$ ^{252}_{148} $ Rf with 8.23 MeV, suggesting regions of increased stability in these nuclei. Furthermore, a third maximum is identified at$ ^{257}_{153} $ Rf with a$ B_{qf} $ value of 6.22 MeV. These distinct maxima reflect variations in the quasifission barrier with respect to the mass numbers of compound nuclei.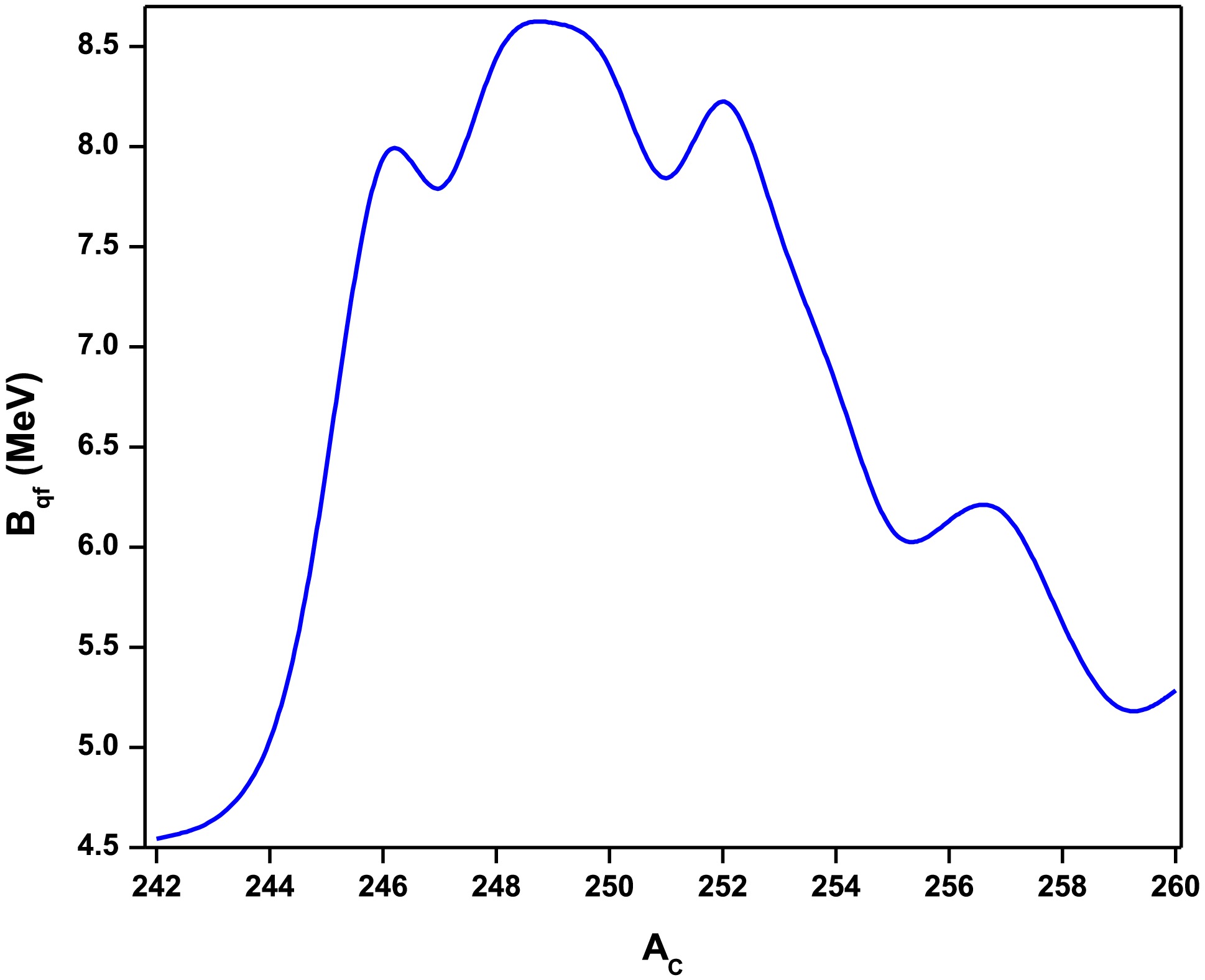
Figure 4. (color online) Larger quasifission barriers obtained for fusion reactions forming isotopes of 242Rf to 260Rf as a function of mass number of compound nuclei.
Furthermore, the quasifission lifetimes were evaluated using Eq. (3). The lifetime of the quasifission process is typically in the range of
$ 10^{-20} $ to$ 10^{-18} $ s. Figure 5 shows a plot of quasifission lifetimes obtained for the fusion reactions forming Rutherfordium (Rf) in the superheavy region of 105 ≤ Z ≤ 120. For each isotope, we have identified larger Bqf values. Figure 6 presents a heat map of quasifission barriers ($ B_{qf}$ ) for various combinations of projectile and target atomic numbers that lead to the formation of compound nuclei within the atomic number range 104 ≤ Z ≤ 120. The lower quasifission barriers range from 0 MeV to 3.464 MeV, as represented by purple to dark cyan. However, higher$B_{qf} $ values were observed up to 8.66 MeV, indicated by a color range from light cyan to red. The larger quasifission barriers were observed for Nc > 161. In addition, we noticed larger$B_{qf} $ values for Z=104 to 106; for Z=114, larger$ B_{qf}$ values above 6 MeV were observed. We also observed that, as the neutron number of each Z increases, the quasifission barriers also increase, particularly for Z > 108. For instance, the neutron number of compound nuclei (Nc) varies from 143 to 168 with Z=108. Here, the quasifission barriers range between 1.7 MeV and 8.66 MeV, as clearly represented by a blue to red color transition.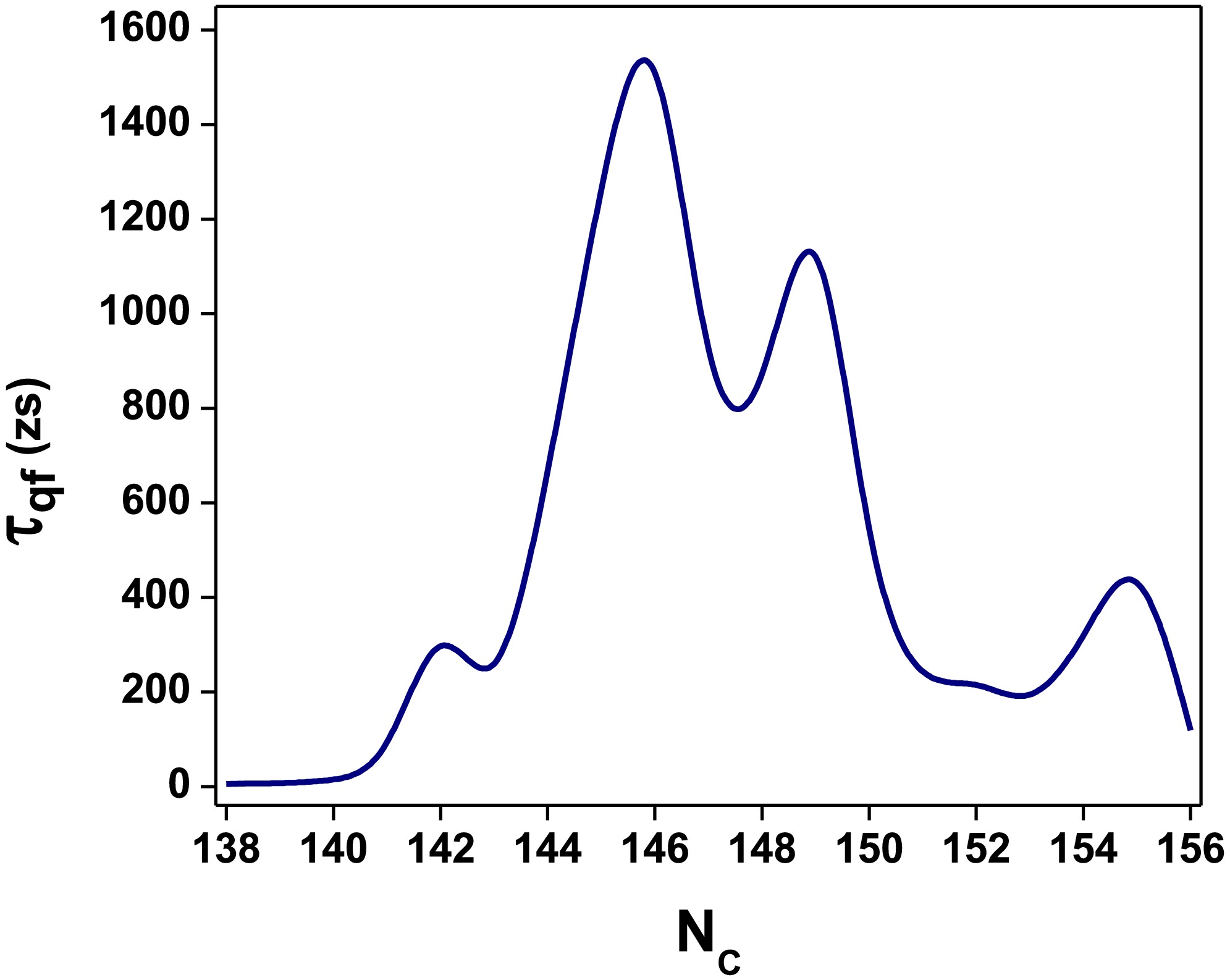
Figure 5. (color online) Quasifission lifetimes obtained for fusion reactions forming Rutherfordium (Rf) isotopes (Z=104).
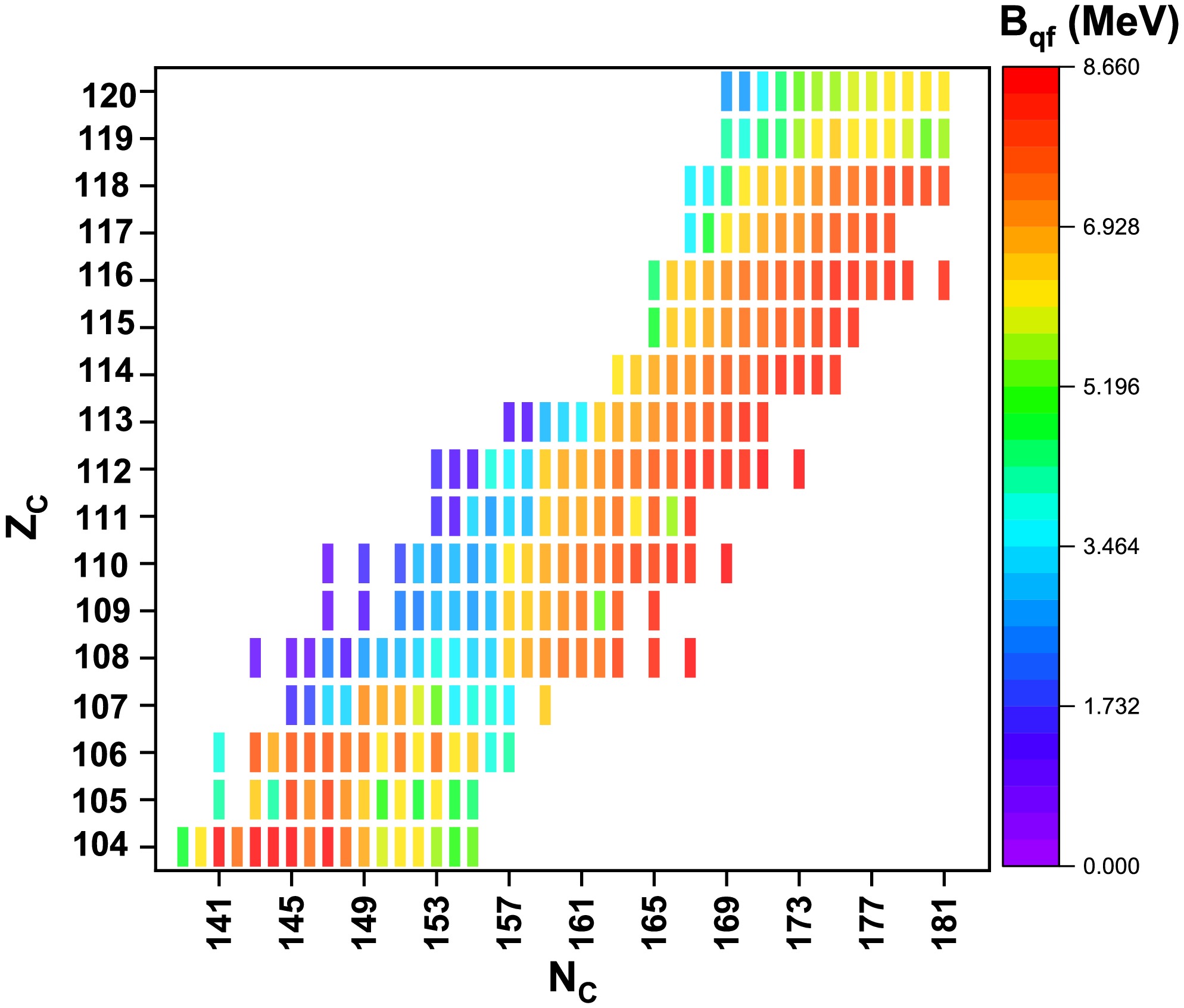
Figure 6. (color online) Map illustrating the quasifission barriers (
$ B_{qf} $ ) for various combinations of projectile and target atomic numbers, leading to the formation of compound nuclei within the atomic number range$ 104\le Z\le 120 $ . The map uses a color gradient, where an increase in$ B_{qf} $ values is represented by a transition from purple to red.Furthermore, we identified larger quasifission lifetimes in each isotope of the compound nuclei in the range of 104 ≤ Z ≤ 120, and these are portrayed as a heat map in Fig. 7. From the map, it can be observed that the lifetimes vary between 0.1 and 2040 zs, as indicated by a color range from purple to red. Values above 1632 zs were observed for
$^{249}_{145} $ Rf,$^{248}_{143} $ Db,$^{260}_{154} $ Sg, and$^{263}_{156} $ Hs. However, in all other cases, the quasifission lifetimes were less than 1632 zs.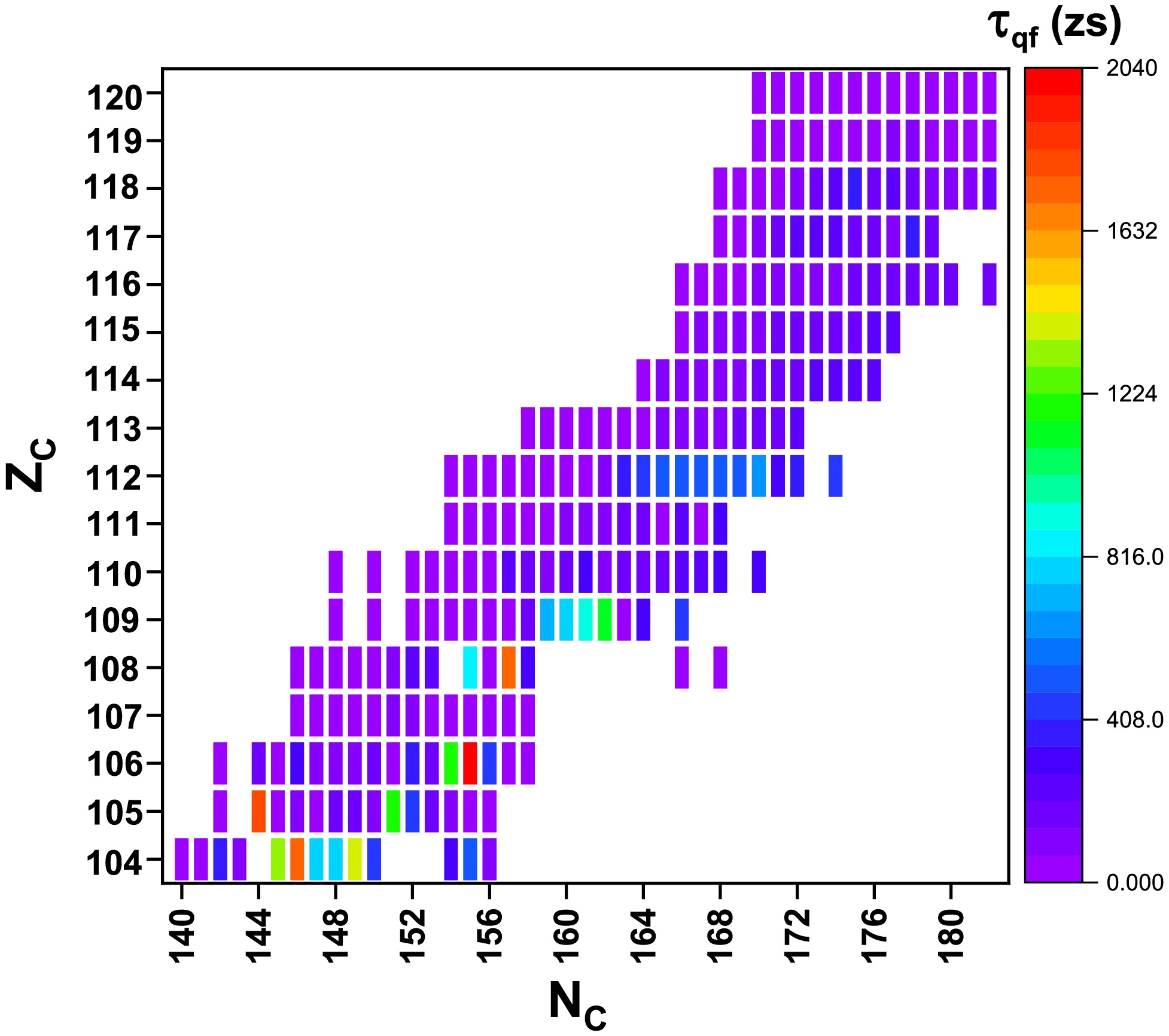
Figure 7. (color online) Map illustrating the quasifission lifetimes for various combinations of projectile and target atomic numbers, leading to the formation of compound nuclei within the atomic number range
$ 104\le Z\le 120 $ . The map uses a color gradient, where an increase in$ \tau_{qf} $ values is represented by a transition from purple to red.Further, we plot the angular dependent quasifission lifetimes for each atomic number in Fig. 8(a). The plot reveals a gradual decrease in quasifission lifetimes with increasing atomic number of the compound nuclei. For Z=120, the lifetimes diminish to as low as 253 zs, indicating reduced stability against quasifission as atomic number increases. However, larger quasifission lifetimes were observed for 64Ni+196Pt, leading to the formation of compound nuclei
$ ^{260}_{106} $ Sg with a quasifission lifetime of 659 zs. Further, larger quasifission lifetimes were observed for the 46Ti+210Bi, 61Ni+202Hg, 43Ca+227Ac, and 45Sc+252Cf fusion reactions. The corresponding angular momentum values are plotted in Fig. 8(b). Here, the angular momentum was varied between$ 91\hbar $ and$ 135\hbar $ . The lowest value of$ 91\hbar $ was observed for the reaction of 61Ni+202Hg; similarly, a higher value of$ 135 \hbar $ was observed for the 48Ca+250Cm reaction. These$ \ell $ -values were taken from the Nuclear video project [22].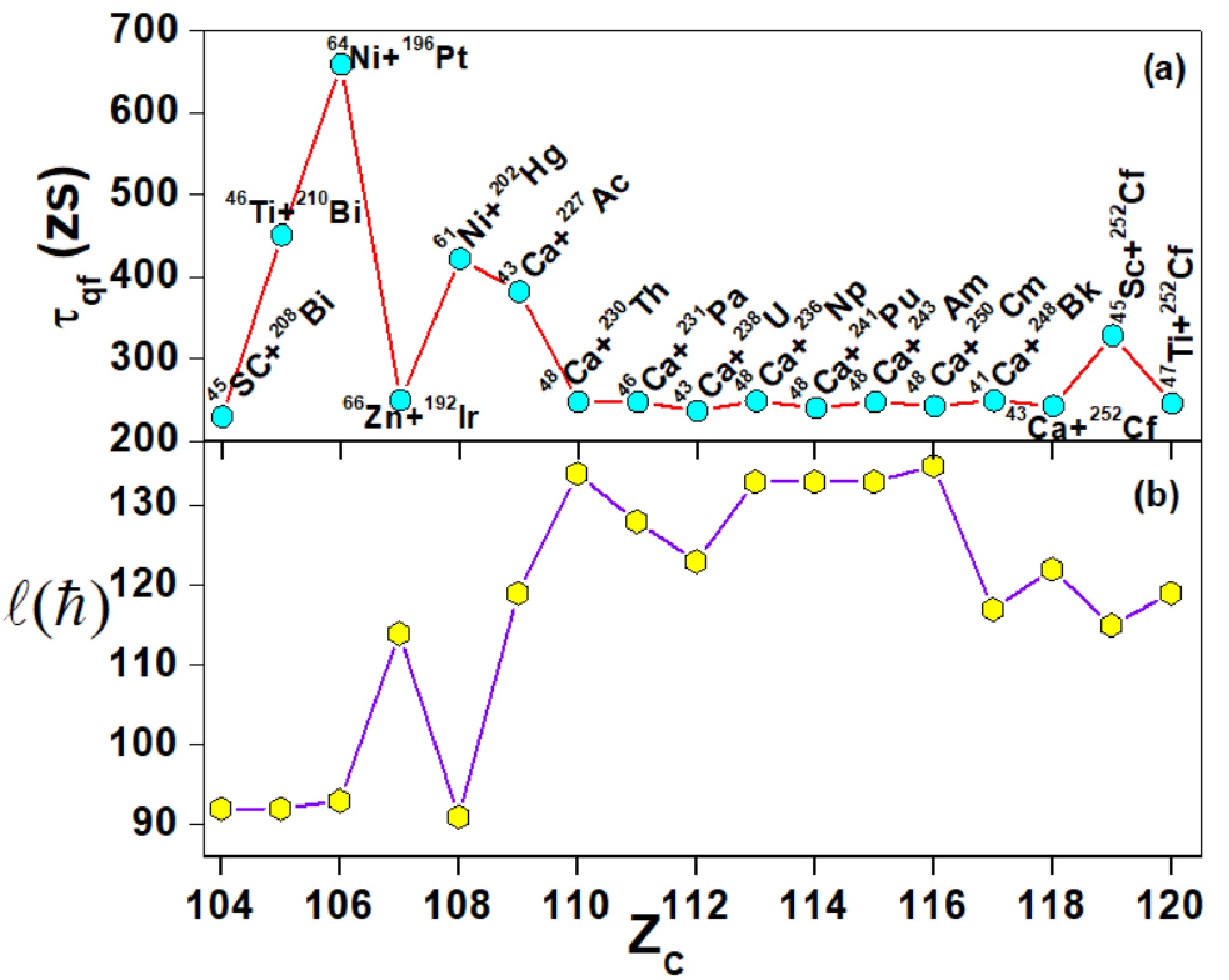
Figure 8. (color online) (a) Larger quasifission lifetimes and (b) angular momentum as a function of compound nuclei's atomic number in the range
$ 104\le Z\le 120 $ .Furthermore, the model was tested by comparing quasifission lifetimes with the experimentally available data [23, 24] as summarized in Table 1. From the comparison, it was observed that the present work (PW) values are generally lower than those in the references, except for some reactions (34S+186W and 238U+48Ca) where the PW showed significantly larger lifetimes. For reactions with 238U as a target, the PW values are closer to those in literature but still show systematic differences. In case of 48Ti+186W, a reduction in the PW values by half was observed. In the case of 34S+186W and 238U+48Ca, a significant increase in quasifission lifetimes was observed in the PW than in literature. For 238U+64Ni, 238U+58Fe, and 238U+48Ti, the PW values are lower and closely aligned with literature values, indicating some consistency with the present model. The discrepancies between theoretical and experimental quasifission lifetimes arise due to several key limitations in the present model. This study employed the nuclear proximity 2010 model, which, while effective, does not fully capture dynamical effects, shell structure influences, and nucleon transfer mechanisms that significantly impact quasifission. Additionally, quasifission lifetimes were derived using a decay constant approach, assuming a well-defined transition from the dinuclear system to quasifission. However, real reactions involve stochastic fluctuations in mass and angular distributions, leading to deviations from measured lifetimes. Further, in our study, we considered a fixed nuclear orientation (
$ \alpha_1 = 90^\circ $ and$ \alpha_2= 90^\circ $ ) and did not fully account for orientation-dependent fusion probabilities, which are crucial for deformed nuclei. Furthermore, shell corrections and energy dissipation mechanisms were not explicitly included, though the experimental results suggest they strongly influence quasifission barriers. From Fig. 8, we observed smaller lifetimes corresponding to 48Ca-induced fusion reactions, but these lifetimes were found to be smaller when compared to those of neighboring nuclei. This suggests a distinct behavior in fusion dynamics for 48Ca-induced reactions. Moreover, it has been experimentally [25] observed that the evaporation residue cross-sections corresponding to these superheavy elements are in the range of picobarns (pb). Hence, this may support the fact that, as quasifission lifetimes decrease, the production cross-sections reduce from the nb to pb range in the region of Z=104 to 118.Reaction $ E_{\rm cm} $ /MeV

$ \ell $ 

$ \tau_{qf} /{\rm zs} $ 

Ref. PW 48Ti+186W 245 124 10 [23] 5 64Ni+184W 341 124 5 [23] 1.01 34S+186W 180 116 10 [23] 55.25 238U+27Al 146 113 $ \approx $ 12.7 [24]

2.5 238U+48Ca 216 135 3.7 [24] 31.5 238U+45Sc 227 122 3.2 [24] 8.5 238U+48Ti 240 123 2.9 [24] 5.25 238U+58Fe 280 118 2.6 [24] 1.25 238U+64Ni 303 115 2.5 [24] 1.26 -
We investigated the quasifission lifetimes of SHEs in the atomic number range
$ 104\le Z \le 120 $ and mass number range$ 243\le A\le 301 $ . To achieve this, we considered various projectile-target combinations. The projectiles selected had atomic numbers in the range$ 20\le Z\le 30 $ and mass numbers of$ 40\le A\le 70 $ . Similarly, the targets had atomic numbers in the range$ 74\le Z\le 98 $ and mass numbers of$ 180\le A\le 252 $ . The nucelus-nucleus potential was evaluated by considering the nuclear proximity 2010 model. The quasifission barriers were evaluated by taking the difference between minimum and maximum potentials. The quasifission barrier was found to be maximum at$ \ell=0 $ . Furthermore, quasifission barriers and lifetimes were evaluated in the fusion reactions leading to the formation of compound nuclei in the superheavy region$ 104\le Z\le 120 $ . A heat map (Fig. 7) of quasifission lifetimes for compound nuclei ($ 104\le Z\le 120 $ ) revealed lifetimes ranging from 0.1 to 2040 zs, indicated by a color range from purple to red. Lifetimes above 1600 zs were identified for$ ^{249}_{145} $ Rf,$ ^{248}_{143} $ Db,$ ^{260}_{154} $ Sg, and$ ^{263}_{156} $ Hs, while others were below 1600 zs. The quasifission lifetimes showed a gradual decrease with increasing atomic number, reducing to 0.1 zs for Z=120, indicating a decline in stability against quasifission with higher atomic numbers. Furthermore, the influence of angular momentum on quasifission barriers showed a decline with increasing atomic number. The shortest lifetime of 253 zs occurred at Z=120, while longer lifetimes, such as 659 zs for 64Ni+196Pt, indicated greater stability. The present model was validated by comparing quasifission lifetimes with available data. PW values were generally lower than references, except for 34S+186W and 238U+48Ca, showing significant increases. For 238U-based reactions, the PW aligned better, though systematic differences existed.
A comprehensive analysis of quasifission lifetimes in the superheavy element region 104 ≤ Z ≤ 120
- Received Date: 2025-01-08
- Available Online: 2025-08-15
Abstract: We analyzed quasifission lifetimes of superheavy elements (SHEs) in the atomic number range





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: