Effects of nucleon-nucleon short-range correlation on fragment generation in isotopic nuclear reactions

The saturation character of nuclear matter reveals a balance between long-range attractive and short-range repulsive forces within a nuclear interaction. This short-range aspect of nuclear forces engenders correlations among nucleon pairs, particularly neutron-proton (n-p) pairs, which results in nucleons in the ground state populating the phase space having momenta exceeding the Fermi momentum [1−5]. The high-momentum tail (HMT) phenomenon, resulting from nucleon-nucleon short-range correlations (SRCs), has been validated through proton removal experiments using high-energy electrons or protons [6−11]. Recent experiments with high momentum transfers indicate that nuclei in the ground state can form nucleon pairs characterized by high relative momentum and low center-of-mass momentum [12−16]. Such findings reveal that approximately 20% of nucleons in the ground state exist in these paired states, focusing interest on these intricate nucleon correlations [17−21]. Furthermore, the HMT profile typically exhibits a $ C/k^4 $ tail across all nuclei, ranging from deuterons to much heavier nuclei [22−25]. In the nucleon momentum distribution within the HMT, the ratio of n-p SRCs to p-p or n-n SRCs is approximately 18 in heavier nuclei [26, 27] but significantly lower in lighter nuclei (A<5) [28]. Consequently, the nucleon component in the HMT is markedly isospin dependent, indicating distinct structures in the high-momentum wave function, particularly in lighter nuclei.

Using the isospin- and momentum-dependent transport model, we can study the isospin effect in intermediate-energy heavy-ion collisions (HICs) through some isospin-sensitive observables, such as nucleonic collective flows, the free neutron-to-proton ratio ($ n/p $), and the $ \pi^{-}/\pi^{+} $ ratio [29−33]. They have been shown to be considerably sensitive to the HMT [34−36]. Additionally, the quantum molecular dynamics transport model can better explain the multi-fragmentation and production of fragments in intermediate-energy HICs [37−40]. Because of the effects of nucleon-nucleon SRCs on fragments and light clusters, e.g., triton and $ ^3 {\rm{He}}$ are studied with central $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$ collisions at $ E_{\text{beam}} = 120 $ MeV/u. Before this work, we first constructed the HMT of the initializing nucleus in phase space. Thereafter, the gas-phase nucleons sensitive to the HMT was studied using the transport model with the HMT of the initializing nucleus and compared with experimental data. Additionally, as a verification of the constructed HMT, we provide evidentiary support for the subsequent study of fragments and light clusters.

In the QMD-like models, the wave function for each nucleon is represented by a Gaussian wave packet [41, 42] as follows:

where $ {\boldsymbol{r}}_{i}(t) $ and $ {\boldsymbol{p}}_{i}(t) $ are the centers of the $ i^{th} $ nucleon in the coordinate and momentum space, respectively. $ \sigma_{r} $ is the width of the Gaussian wave packet depending on the mass number of the nucleus in $ \sigma_{r} = 0.92+0.08A^{1/3} $ fm [43]. After performing a Wigner transformation for Eq. (1), we obtain the Wigner density as

with

The $ i^{th} $ nucleon density distributions in the coordinate and momentum space are

and

respectively, and the total density distribution is the sum of all nucleons in reaction systems.

In the LQMD model, the temporal evolutions of the baryons (nucleons and resonances) and mesons in the reaction system under the self-consistently generated mean-field are governed by Hamilton’s equations of motion [44−48]. Based on the Skyrme interactions, isospin-, density-, and momentum-dependent Hamiltonians have been constructed. The Hamiltonian of baryons consists of the relativistic energy, effective interaction potential, and momentum related components. The effective interaction potential is composed of the Coulomb potential and local interactions.

The local interaction potential is derived from the energy-density functional in the form $ U_{\mathrm{loc}}=\int_{ }^{ }V_{\mathrm{loc}}(\rho(\boldsymbol{r}))\mathrm{d}\boldsymbol{r} $. The functional $ \int V_{\mathrm{loc}} $ can be expressed as

where $ \rho_{{n}} $, $ \rho_{{p}} $, and $ \rho=\rho_{\mathrm{\mathit{n}}}+\rho_{\mathrm{\mathit{p}}} $ are the neutron, proton, and total densities, respectively, and $ \delta=(\rho_{\mathrm{\mathit{n}}}-\rho_{\mathrm{\mathit{p}}})/(\rho_{\mathrm{\mathit{n}}}+\rho_{\mathrm{\mathit{p}}}) $ is the isospin asymmetry. The parameters α, β, γ, $ g_{\mathrm{sur}} $, $ g_{\mathrm{sur}}^{\mathrm{iso}} $, and $ \rho_{0} $ are set to –215.7 MeV, 142.4 MeV, 1.322, 23 MeV·fm², –2.7 MeV·fm², and 0.16 fm^-3, respectively. $ E_{\mathrm{sym}}^{\mathrm{loc}}(\rho) = 26.25\left(\rho / \rho_0\right)^{0.5} $ is the local part of the symmetry energy, which leads to soft-symmetry energy and the effective mass splitting of $ m_{\mathrm{\mathit{n}}}^* > m_{\mathrm{\mathit{p}}}^* $ to obtain the symmetry energy of 31.5 MeV at saturation density. In the LQMD model, a Skyrme-type momentum-dependent potential is used [44, 45].

where $ C_{\tau, \tau} = C_{\mathrm{mom}}(1+x), $ $ C_{\tau,\tau^{\prime}} = C_{\mathrm{mom}}(1-x)\left(\tau \neq \tau^{\prime}\right) $, and the isospin symbols $ \tau(\tau^{\prime}) $ represent the proton or neutron. The parameters $ C_{\mathrm{mom}} $ and $ \epsilon $ are determined by fitting the real part of the optical potential as a function of the incident energy from the proton-nucleus elastic scattering data, and the obtained values of $ C_{\mathrm{mom}} $ and $ \epsilon $ are 1.76 MeV and 500 $ \mathrm{c}^{2}/\mathrm{GeV}^{2} $, respectively. Thus, the effective mass of the nuclear medium at saturation density is $ m^*/m = 0.75 $. The parameter x is the strength of the isospin splitting, for which a value of –0.65 is adopted in this study, and the mass splitting in the nuclear medium is $ m_\mathrm{n}^* > m_\mathrm{p}^* $ [49].

The initial density distributions of nucleons in the projectile and target result from the density distributions of stable nuclei selected by the self-evolution of nucleons in the LQMD model. Each nucleus is divided into many spherical shells centered around its center of mass. By using the local Thomas-Fermi approximation in each shell of radius r, we can calculate the local Fermi momenta of neutrons and protons in each shell using

where $ \rho(r) $ is given by Eq. (4). The Fermi momentum obtained using Eq. (8) can provide nuclear momentum space information using the Monte Carlo sampling method.

We use a nucleon momentum distribution with an HMT reaching $ \lambda k_{F_{n,p}} = 2.0 k_{F_{n,p}} $ [50], where $ \lambda=k_{\mathrm{max}}/k_F $ is the high momentum cutoff parameter, and $ k_{F_{n,p}} $ is the neutron or proton Fermi momentum [51, 52]. According to the n-p dominance model [26, 27], 20% of nucleons with equal numbers of neutrons and protons are inside the HMT. The momentum distribution for nucleons with HMTs in initialization is expressed as

and

keeping 20% fraction of total nucleons in the HMT, i.e.,

with the normalization condition

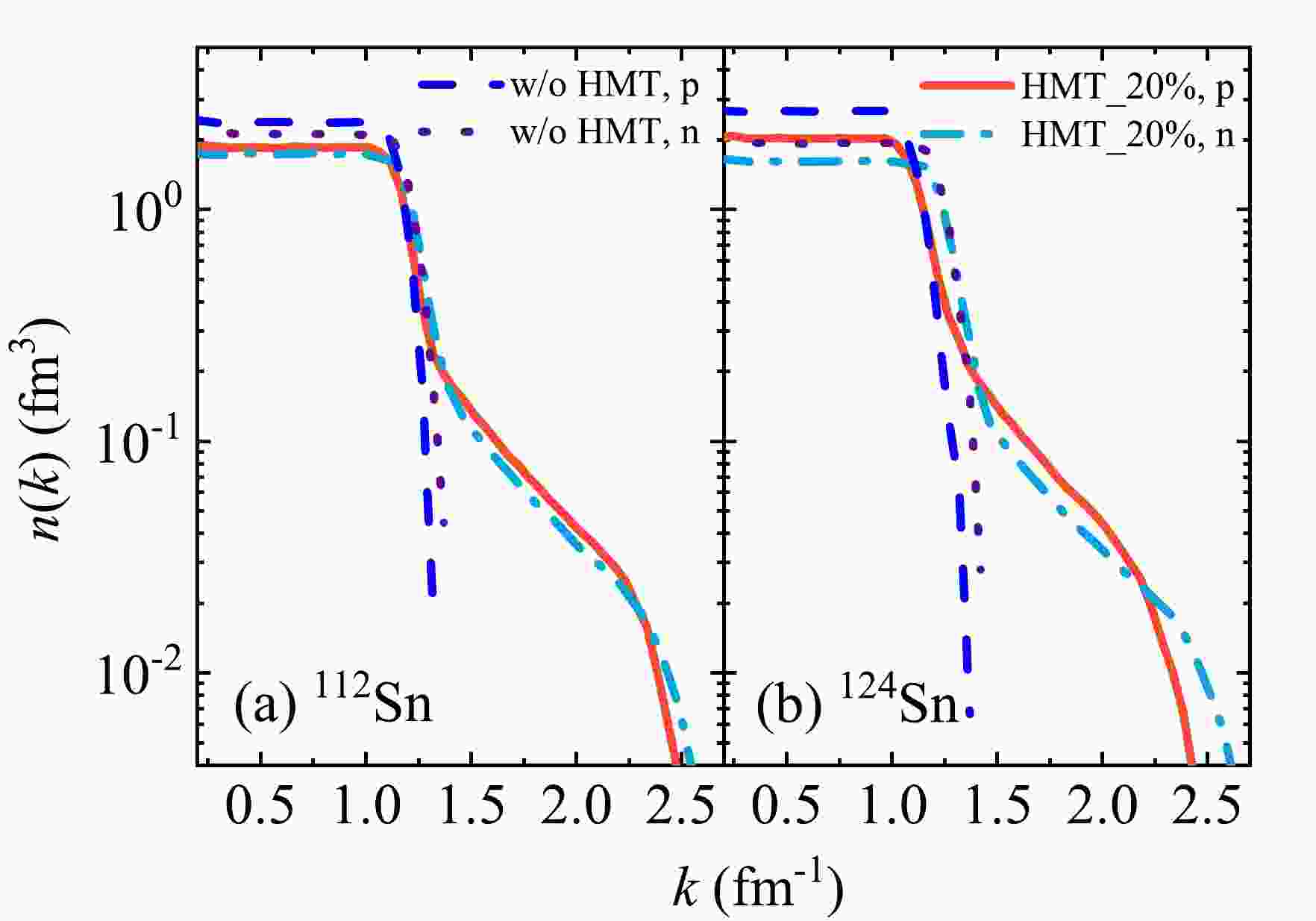
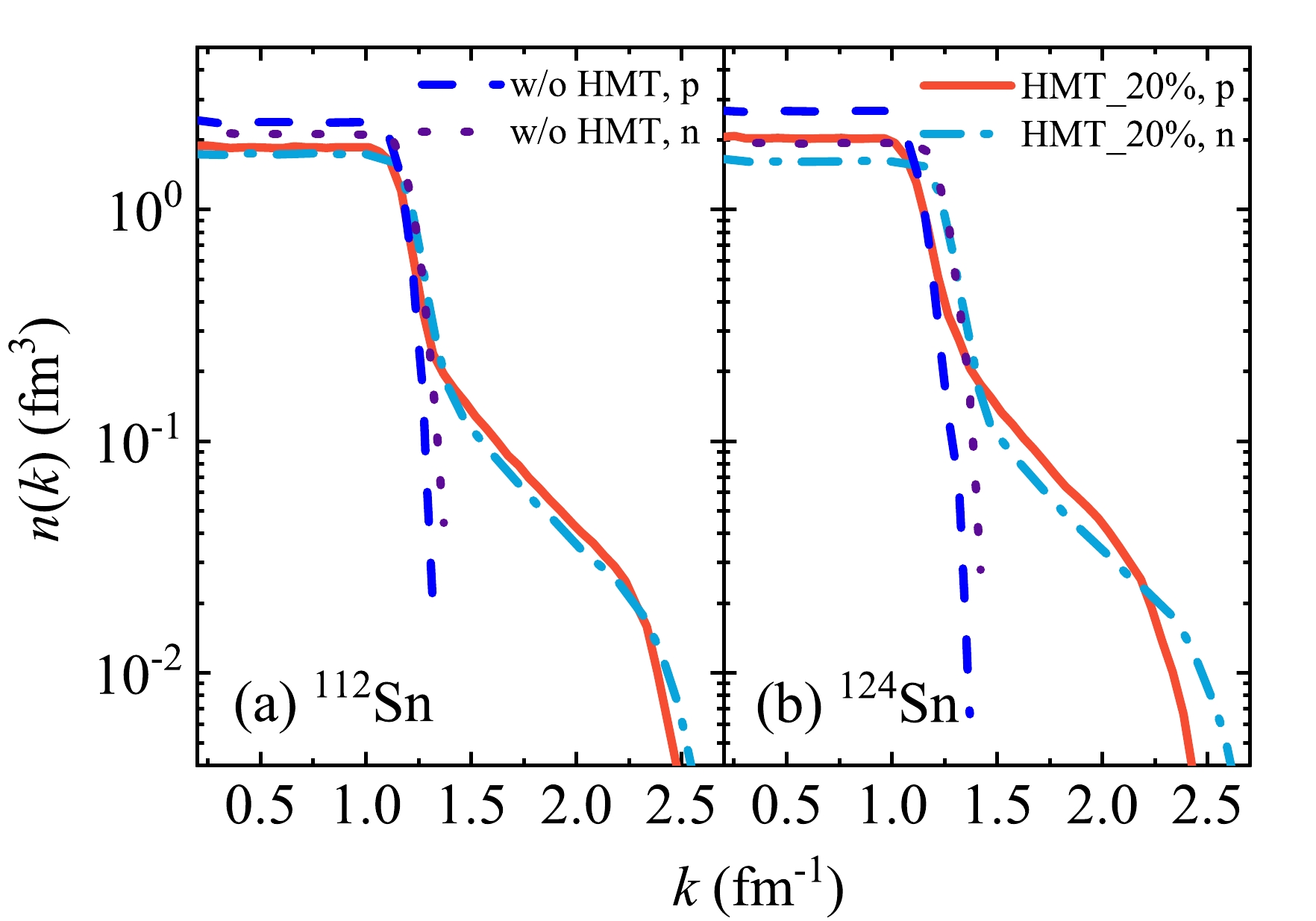
The parameters $ C_{1} $ and $ C_{2} $ in Eq. (10) are determined automatically from the above equations. The calculation of momentum distribution also uses the form of the Gaussian wave packet in Eq. (5).

The HMT is strongly isospin dependent, and the isotopes $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ have been applied to the study of isospin effects. Therefore, the HMTs of $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ are constructed as shown in Fig. 1. The nucleon momentum distributions with and without HMTs are compared. Compared with the ideal gas case, protons in the neutron-rich nucleus $ ^{124} {\rm{Sn}}$ have a higher probability than neutrons of possessing momenta exceeding the nuclei without HMT momentum [53]. This phenomenon results from the n-p dominance model, which dictates that equal numbers of neutrons and protons must populate the HMT.

Figure 1.  (color online) Comparison between nucleon momentum distribution n(k) of $^{112}{\rm{Sn}}$ and $^{124}{\rm{Sn}}$ with and without HMTs. The normalization condition is $ \int_0^{\lambda k_F}n(k)k^2\mathrm{d}k=1. $

Because the performance of nucleons is relevant to the isospin-dependent HMT, the observables should be kinetic-energy or momentum spectra with isospin correlations. The central collisions of the isotopic nuclear systems A = $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ and B = $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$ are simulated at $ E_{\mathrm{beam}} $ = 120 MeV/u and an impact parameter $ b = 0-3 $ fm to investigate the effects of the HMT on the kinetic-energy spectra of neutron-to-proton ratios ($ R_{n/p} $) from the yields of gas-phase fragments (nucleons, hydrogen, and helium isotopes) in Fig. 2. These particles, emitted perpendicular to the beam direction with a cut at the polar angle of $ 70^{\circ}<\theta_{\mathrm{c.m.}}<110^{\circ} $ $ (\cos\theta_{\mathrm{c.m.}} = p_{z}/ $ $ \sqrt{p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}) $, are analyzed. The nucleons in the gas phase of the experimental data are obtained by combining the free nucleons with those bound in light isotopes with $ 1 < A < 5 $ [54, 55]. As shown in Fig. 2, the value of the gas-phase $ R_{n/p} $ without the HMT is clearly higher than that with the HMT, both in $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$ collisions. The HMT is induced by SRCs, and the n-p pairs are predominant. This predominance implies that in the high-kinetic energy region, neutrons and protons tend to appear as correlated pairs, resulting in reduced $ R_{n/p} $. The reduction in the $ n/p $ ratio will tend to approach 1, and the extent of the reduction will become smaller as the isospin asymmetry of the reaction system decreases. Therefore, the HMT effect in neutron-rich reaction systems is more noticeable. In both $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$ collisions under the influence of soft symmetry energy and the effective mass splitting of $ m_\mathrm{n}^{\ast} > m_\mathrm{p}^{\ast} $, the gas-phase $ R_{n/p} $ with the HMT is closer to the experimental data than that without the HMT. In contrast, the bump structure around the energy of 20 MeV/u results from the competition of free nucleons and light fragments to $ R_{n/p} $. The light fragments with Z $ \leq $ 2 are primarily produced at low kinetic energy and have smaller $ n/p $ ratios than the free nucleons [46].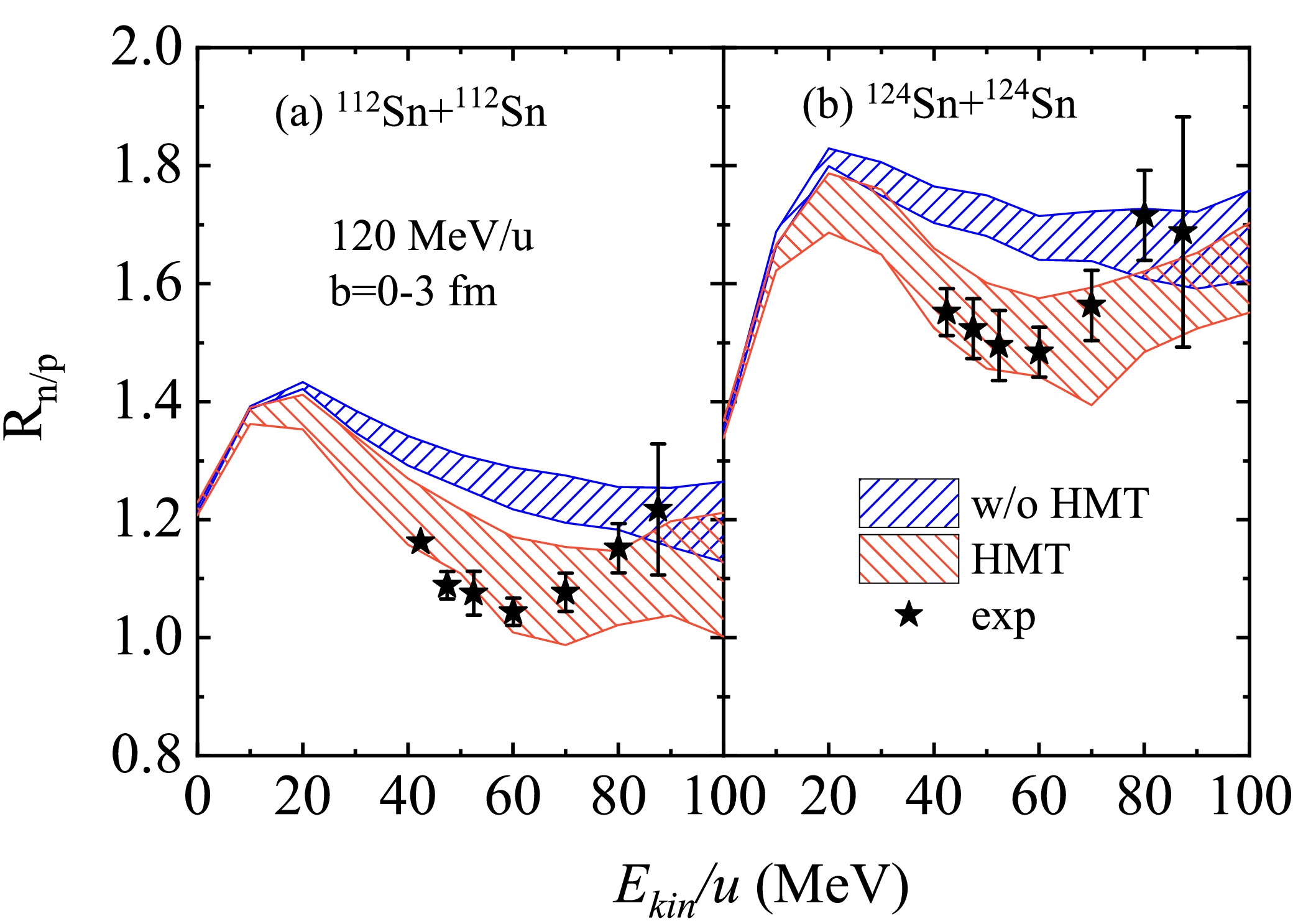

Figure 2.  (color online) Effects of the HMT on the kinetic-energy spectra of neutron-to-proton ratios from the yields of gas-phase fragments (nucleons, hydrogen and helium isotopes) [panels (a) and (b)] in $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$ reactions at the beam energy $ E\mathrm{_{beam}} $ = 120 MeV/u in the transverse direction $ 70^{\circ}<\theta_{\mathrm{c.m.}}<110^{\circ} $.

The kinetic energy spectra of the gas-phase double neutron-to-proton ratios ($ DR_{n/p} = R_{n/p}(B)/R_{n/p}(A) $) have been calculated at $ E_{\mathrm{beam}} $ = 120 MeV/u in the transverse direction $ 70^{\circ}<\theta_{\mathrm{c.m.}}<110^{\circ} $ with and without the HMT, as shown in Fig. 3. However, the $ DR_{n/p} $ with or without the HMT is less sensitive to the experimental data becuase the HMT has the same effect on neutron-rich and -deficient systems. Therefore, the $ DR_{n/p} $ serves as a good experimental observable for other isospin effects, such as symmetry energy and nucleon effective mass splitting, because it can be considered without taking into account the HMT, neutron measurement efficiency, and influence of the Coulomb energy.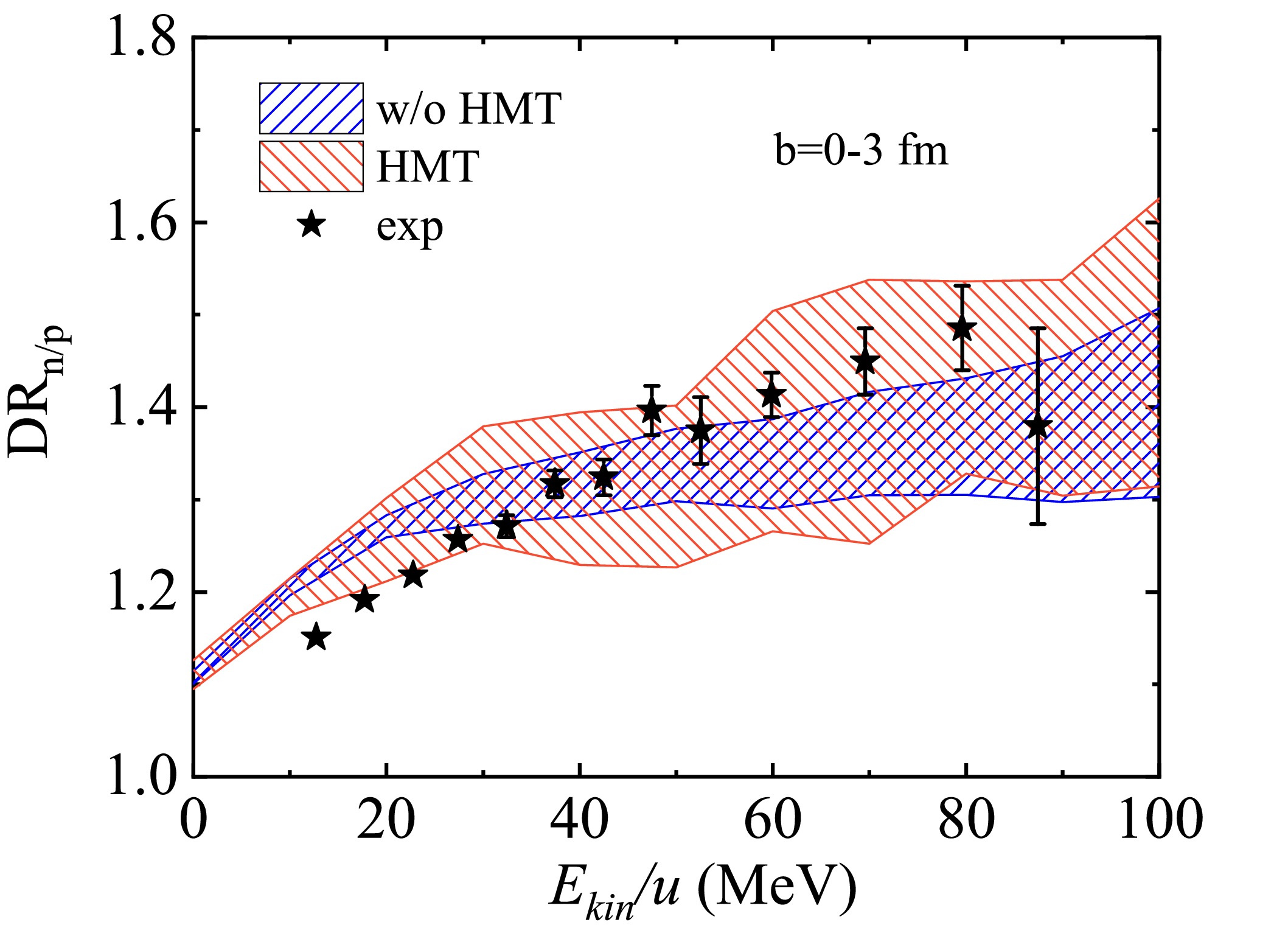

Figure 3.  (color online) Effects of the HMT on the kinetic-energy spectra of the double neutron-to-proton ratios of gas-phase nucleons in collisions of $^{124}{\rm{Sn}}$ + $^{124}{\rm{Sn}}$ over $^{112}{\rm{Sn}}$ + $^{112}{\rm{Sn}}$ at the beam energy $ E\mathrm{_{beam}} $ = 120 MeV/u in the transverse direction $70^{\circ}<\theta_{\mathrm{c.m.}}<110^{\circ}$.

Among gas-phase nucleons, light clusters such as triton and $ ^{3} {\rm{He}}$ constitute essential components. Therefore, analyzing the triton-to-$ ^{3} {\rm{He}}$ ratio enables us to further explore the isospin-dependent effects within gas-phase nucleons and establish an understanding of the dynamics of light clusters under the influence of the HMT. Figure 4 shows the triton-to-$ ^{3} {\rm{He}}$ ratio as a function of the total momentum in the peripheral collisions of 120 MeV/u $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$. The triton-to-$ ^{3} {\rm{He}}$ ratio is sensitive to the HMT. Moreover, the value of the triton-to-$ ^{3} {\rm{He}}$ ratio with the HMT is much smaller than that without the HMT, particularly at high momenta. This is because the HMT emanates from SRCs, where n-p pairs dominate. This dominance suggests that neutrons and protons in the high-momentum region are more likely to form correlated pairs, leading to a decrease in the triton-to-$ ^{3} {\rm{He}}$ ratio. For the peripheral collisions, because more (less) energetic nucleons are from the HMT (nucleon-nucleon collisions), the larger effects of the HMT on the triton-to-$ ^{3} {\rm{He}}$ ratio are expected.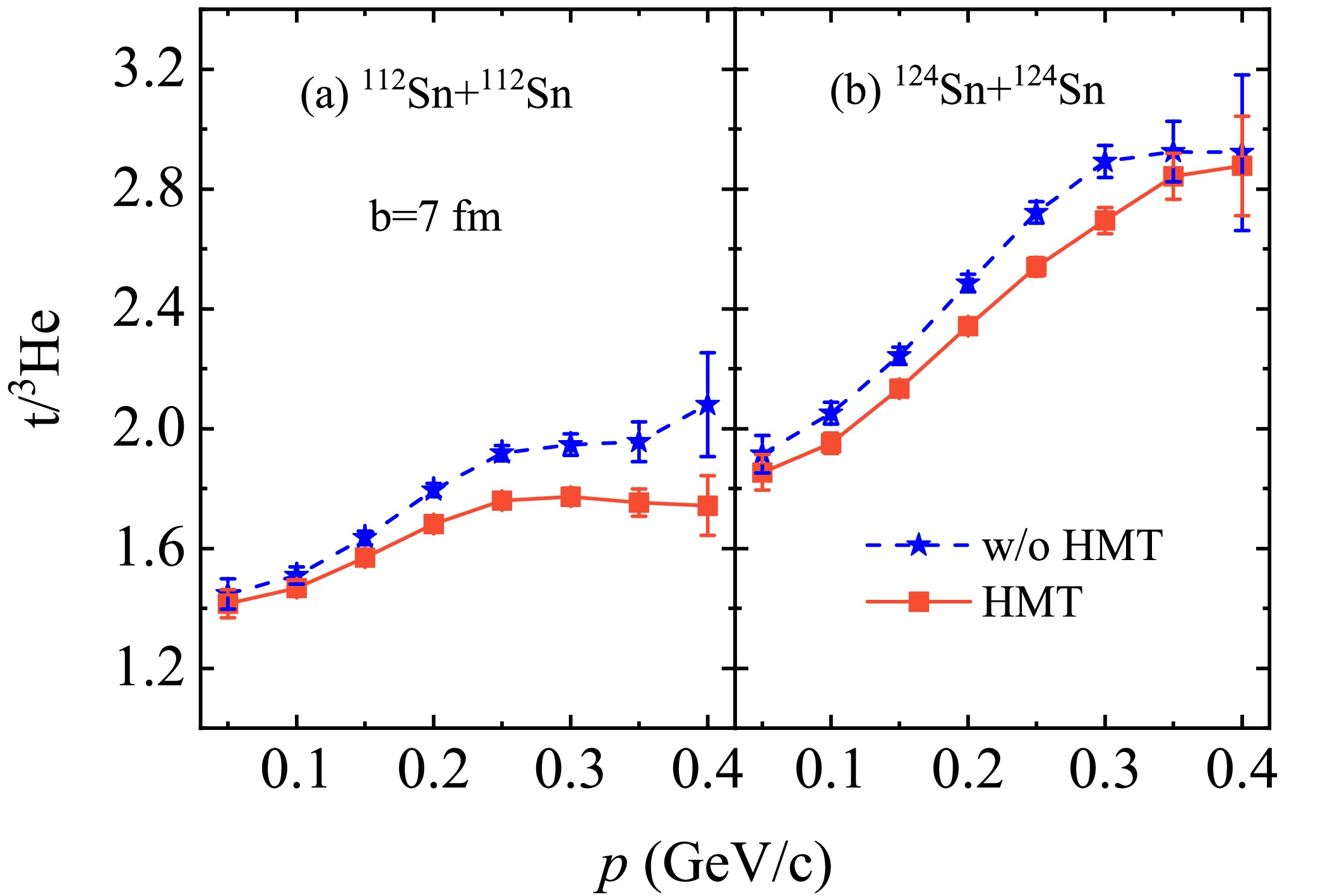

Figure 4.  (color online) Effects of the HMT on the triton-to-$^{3}{\rm{He}}$ ratio as a function of total momentum in the Sn+Sn reactions at 120 MeV/u with different reaction systems.

Light clusters, such as triton and $ ^{3} {\rm{He}}$, offer insights into isospin dynamics under the influence of the HMT. We extend this analysis to heavier fragments whose production involves more complex interactions and structural dynamics. Figure 5 shows multiplicity distributions of fragments produced in HICs with and without the HMT in the peripheral collisions of $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$. The yields of fragments decrease with the increasing fragment charge with or without the HMT and are not affected by the different isotope reaction systems. However, more yields of very light fragments and less yields of heavier fragments with the HMT are obtained compared with and without the HMT. Because the very light fragments are mostly pre-equilibrium emissions, the momentum correlations among nucleons increase the coalescence probability among nucleons. Thus, more light fragments are produced. The heavier fragments are primarily deexcited remnants of the reaction, and heavier fragments are produced with smaller nucleon momenta (i.e., without the HMT).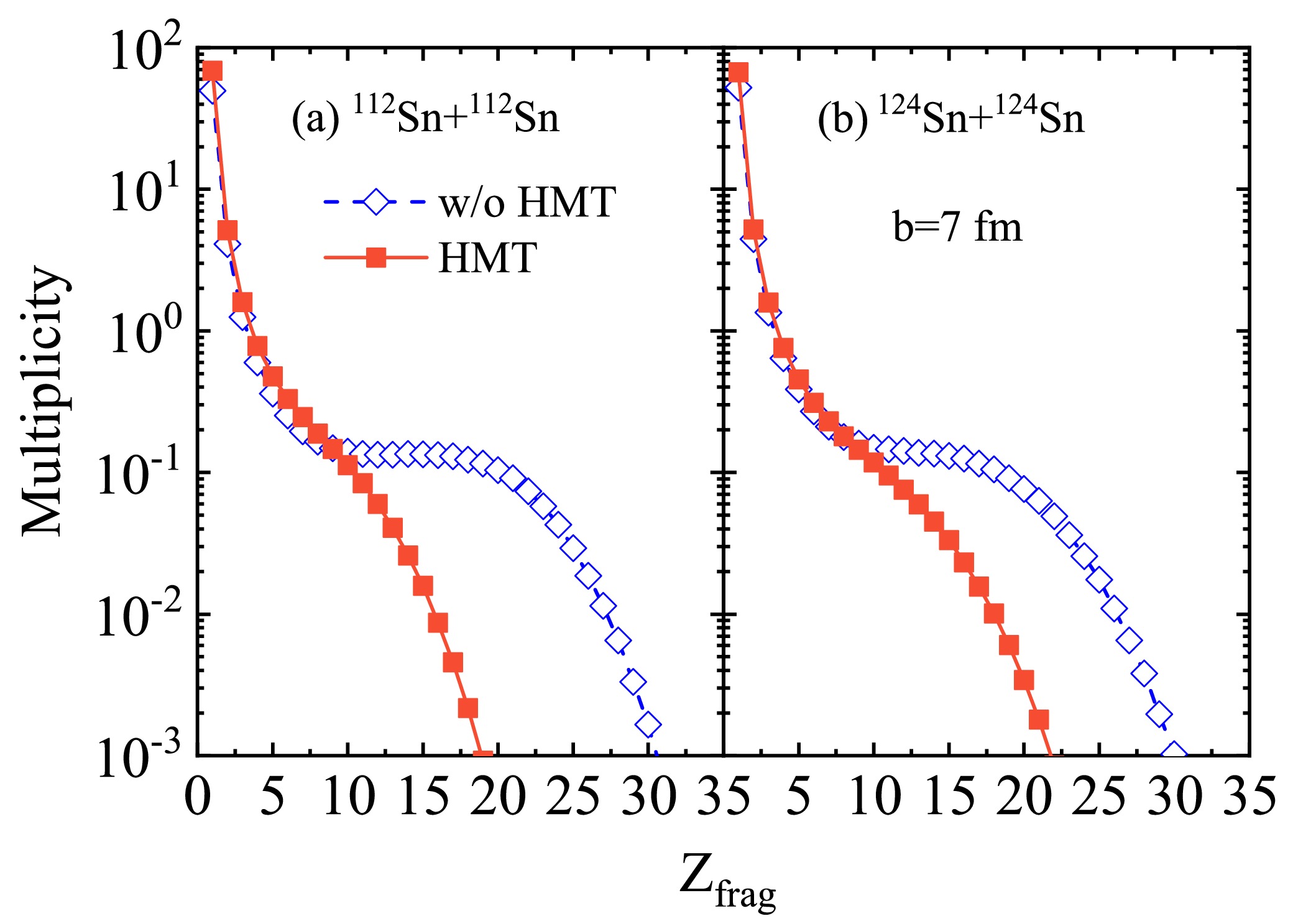

Figure 5.  (color online) Effects of the HMT on the multiplicities of fragments as a function of fragment charge in the Sn+Sn reactions at 120 MeV/u with different reaction systems.

Owing to the dominant isospin dependence of short-range correlation pairs, in addition to the multiplicity distribution, the influence of the HMT should also be reflected in the average neutron-to-proton ratio $ \langle N/Z\rangle $ of the fragments. Figure 6 shows the $ \langle N/Z\rangle $ as a function of the fragment charge number $ A_{\mathrm{frag}} $ for the $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ reactions (left panel) and $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$ reactions (right panel) at the incident beam energy of 120 MeV/u with and without the HMT in semiperipheral collision. Furthermore, to show more clearly the isospin effects of produced isobars, we analyze the average neutron-to-proton ratio $ \langle N/Z\rangle $ of produced isobars, which is defined as [56]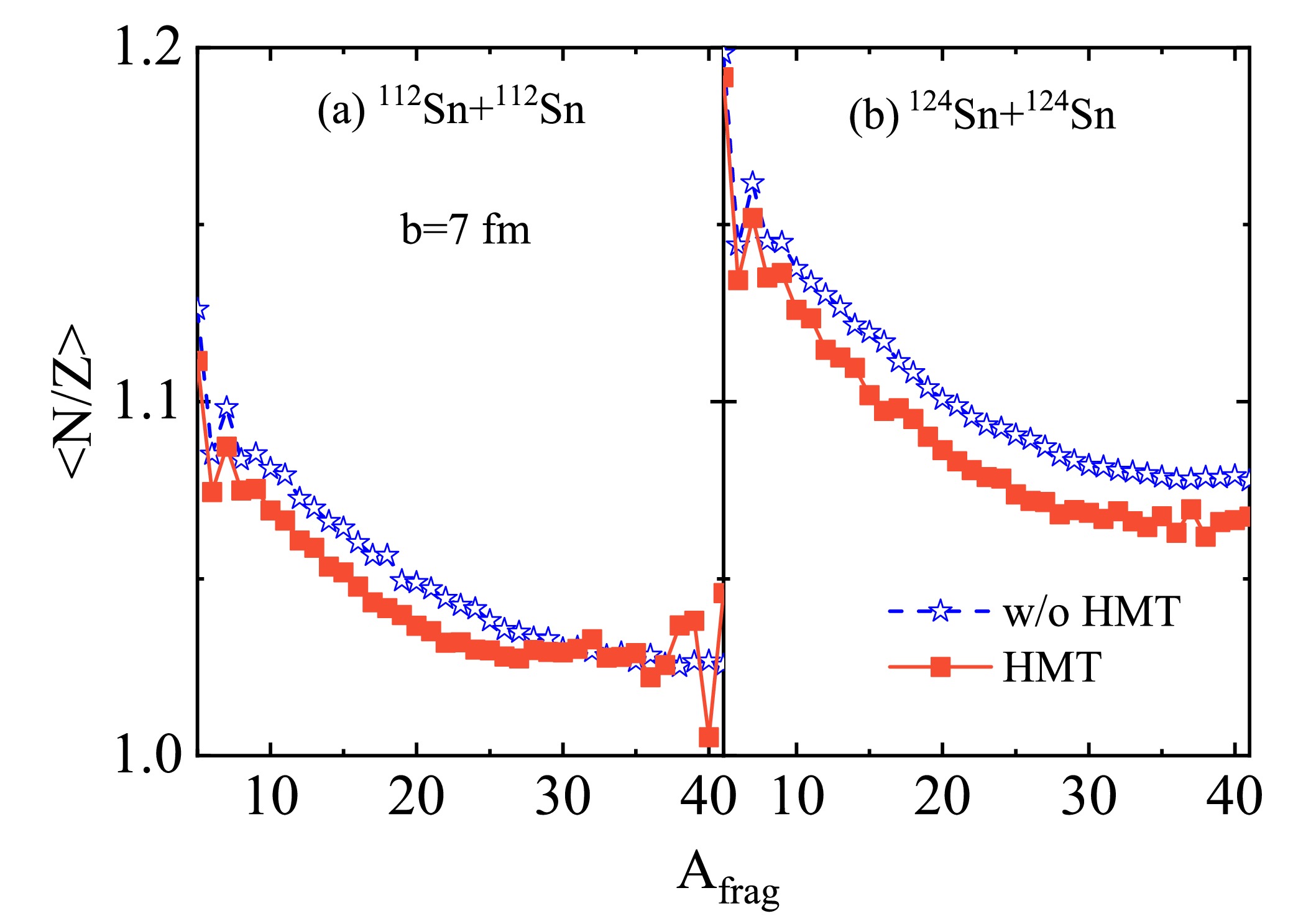

Figure 6.  (color online) Effects of the HMT on the average neutron-to-proton ratio $\langle N/Z\rangle$ as a function of charge number $ A\mathrm{_{frag}} $ in the Sn+Sn reactions at 120 MeV/u with different reaction systems.

where $ \sum Y\left({ }^A X_Z\right) $ denotes the yield of the isobar $ {}^AX_Z $ of the nuclear mass number A; the summation is conducted over all different isobars. The $ A\mathrm{_{frag}} $ distribution of the average neutron-to-proton ratio $ \langle N/Z\rangle $ is sensitive to the HMT particularly for heavier fragments from Fig. 6. Moreover, we can observe that $ \langle N/Z\rangle $ with the HMT decreases more sharply than that without the HMT, particularly for heavier isobars. This is understandable because the HMT causes de-excitation of remnants easily and often more neutrons are emitted for neutron-rich system. Thus, the neutron-rich $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$ reaction system is more sensitive to the HMT than the $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ reaction system in the $ A\mathrm{_{frag}} $ distribution of $ \langle N/Z\rangle $.

In this work, the effects of nucleon-nucleon SRCs leading to the HMT are studied in isotopic nuclear reactions at $ E_{\mathrm{beam}}= $ 120 MeV/u using the LQMD transport model. The HMT is incorporated into the initialization of nucleons of the isotopes of $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ in phase space. An analysis of single and double ratios of gas phase neutron and proton spectra shows that the HMT affects single ratios but not double ratios in 120 MeV/u $ ^{112} {\rm{Sn}}$ + $ ^{112} {\rm{Sn}}$ and $ ^{124} {\rm{Sn}}$ + $ ^{124} {\rm{Sn}}$ reactions. Therefore, the double ratios can serve as a good experimental observable for other isospin effects. The ratio of triton-to-$ ^3 {\rm{He}}$, such as the single ratios of gas-phase neutrons and protons, is influenced by the HMT, with its effects being more pronounced in neutron-rich reaction systems. The single ratios with the HMT are consistent with the experimental data, but the double ratios, whether with or without the HMT, can fit better to the experimental data. Finally, the isospin-dependent HMT significantly alters the fragment multiplicity distribution and average neutron-to-proton ratio of produced isobars. Interestingly, the average neutron-to-proton ratio of heavier isobars influenced by the HMT is also more pronounced in neutron-rich systems. The production of heavier fragments primarily originates from the de-excitation of remnants, which is influenced by the HMT. This differs from the production mechanism of light clusters.