-
Charmonium, the bound state of charm and anti-charm quarks governed by the strong force, is analogous to the ‘hydrogen atom’ in the study of meson spectroscopy [1, 2]. Due to its heavy mass, the velocity of the charm quark is relative slow and therefore the system can be well described by a non-relativistic potential model [3]. By now, the charmonium spectroscopy below the open-charm threshold is well established [4], and a precise study of them is important and necessary for a stringent test of the theory of the strong interaction, quantum chromodynamics (QCD). The
$ \chi_{cJ} $ (spin$ J = 0,1,2) $ charmonia are P-wave$ c\overline{c} $ states split by spin-orbit and tensor forces. At the moment, the$ \chi_{c1} $ and$ \chi_{c2} $ masses are precisely measured using a scan approach with$ p\bar{p} $ annihilation by the E760 [5] and E835 [6] experiments, and by the LHCb [7] experiment in$ pp $ collisions, whereas a precise$ \chi_{c0} $ mass measurement is relatively marginal, with an uncertainty about five times larger [8, 9] than that of$ \chi_{c1,c2} $ . Improved precision on the$ \chi_{c0} $ mass is important for probing the spin structure of the strong force, such as the fine structure splitting$ M(^3P_2)-M(^3P_0) $ , and the singlet-triplet splitting$ M(^1P_1)-M_{\rm{cog}}(^3P_J) $ , where$ M_{\rm{cog}}(^3P_J) $ is the center-of-gravity of the triplet. This helps precisely determine the spin-orbit and tensor forces.We also lack knowledge about the precise width of
$ \chi_{c0} $ [4] compared to its$ J = 1,\; 2 $ partners [5−7]. A precise width measurement of$ \chi_{c0} $ serves as an essential input for studying the$ \chi_{c0} $ decay, such as the$ E1 $ transition partial width, light hadron decay width, etc. Furthermore, lattice QCD calculations show an excited scalar glueball candidate with mass in the range of$ 2.8-3.7 $ GeV [10−13], and the$ \chi_{c0} $ might contain a gluonic admixture due to the presence of such a nearby glueball. In this sense, the precise$ \chi_{c0} $ width provides valuable knowledge to investigate the excited glueball spectrum, which was used to explain the$ \gamma^*\to(c\bar{c})(c\bar{c}) $ cross section discrepancy [14] between perturbative QCD calculations [15, 16] and the experimental measurement [17].The decay of
$ \chi_{c0} $ to light hadrons proceeds predominately via two-gluon exchanges (color-singlet) [18]. The decay widths of the simplest pseudo-scalar final state$ \pi^+\pi^- $ and$ K^+K^- $ are expected to be identical within SU(3) flavor symmetry. This simple feature also applies to other$ 0^{++} $ systems, such as the light glueball candidates$ f_0(1500) $ and$ f_0(1710) $ [4]. However, the couplings of$ f_0(1710) $ to the$ \pi^+\pi^- $ and$ K^+K^- $ final states differ significantly [19, 20] due to a so-called 'Chiral Suppression' effect [21, 22]. Therefore, a precise measurement of the branching fraction (BF)$ \chi_{c0}\to \pi^+\pi^-/ K^+K^- $ , together with its full width, provides an ideal testing ground for the study of decays of the glueball candidates. In addition, the color-octet component also plays an important role in charmonium decays, and these precise BF measurements can help to constrain the non-pertubative parameters in QCD calculations [18, 23, 24] and to allow us to finally understand the decay dynamics of charmonium states.In this Letter, a precise mass and width measurement of
$ \chi_{c0} $ is achieved via$ \chi_{c0}\to \pi^+\pi^-/ K^+K^- $ decays. The decay BFs of$ \chi_{c0,c2}\rightarrow\pi^{+}\pi^{-}/K^{+}K^{-} $ are precisely measured as well. The analysis is performed using a$ \psi(3686) $ data sample consisting of$ (107.7\pm0.6)\times10^{6} $ events taken in 2009 and$ (345.4\pm2.6)\times10^{6} $ events taken in 2012 [25] at BESIII. The$ \chi_{c0,c2} $ states are produced copiously in the radiative transition$ \psi(3686)\to\gamma\chi_{c0,c2} $ .The BESIII detector is described in detail elsewhere [26]. Simulated Monte Carlo (MC) samples produced with a GEANT4-based [27] MC simulation software package, which includes the geometric description of the detector as well as its response, are used to determine detection efficiencies, optimize the selection criteria, and estimate background contributions. Signal MC samples of
$ \psi(3686)\rightarrow\gamma\chi_{c0,c2}\rightarrow\gamma\pi^{+}\pi^{-}/\gamma K^{+}K^{-} $ are produced. Each channel contains 400,000 signal events. In the simulation, the$ \psi(3686) $ resonance is generated with KKMC [28, 29], which includes initial-state-radiation and the beam energy spread. The decays of$ \psi(3686)\to\gamma\chi_{c0,c2}\to \gamma \pi^+\pi^-/ \gamma K^+K^- $ are simulated with the angular distribution taken into account using a previous multipole amplitude measurement by BESIII [30].To investigate the potential background, an inclusive MC sample containing the same number of
$ \psi(3686) $ events as data is simulated. This sample includes the production of the$ \psi(3686) $ resonance, the ISR production of the$ J/\psi $ , and the continuum processes incorporated in KKMC [28, 29]. All particle decays are modeled with EVTGEN [31, 32] using BFs either taken from the Particle Data Group (PDG) [4], when available, or otherwise modeled with LUNDCHARM [33, 34] for all remaining unknown charmonium decays. Final state radiation (FSR) from charged final state particles is incorporated using the PHOTOS package [35]. Di-muon and Bhabha MC samples, each containing one million events, are generated with the Babayaga generator [36] for further background studies.For the
$ \psi(3686)\rightarrow\gamma\chi_{c0,c2}\rightarrow\gamma\pi^{+}\pi^{-}/\gamma K^{+}K^{-} $ signal events of interest, the final states have two high-momentum charged tracks and an energetic radiative photon, with an energy of 261 (128) MeV in the$ \chi_{c0}\; (\chi_{c2}) $ case, due to the large mass gap between$ \psi(3686) $ and$ \chi_{c0,c2} $ . Charged tracks detected in the multi-layer drift chamber (MDC) are required to be within the polar angle range$ \vert \cos\theta\vert<0.93 $ , where θ is defined with respect to the z axis, which is the symmetry axis of the MDC. For each good charged track, the distance of closest approach to the interaction point (IP) must be less than 10 cm along the z axis, and less than 1 cm in the transverse plane. A candidate event is required to have two good charged tracks with zero net charge.Photon candidates are identified using isolated showers in the electromagnetic calorimeter (EMC). The deposited energy of each shower must be more than 25 MeV in the barrel region (
$ \vert \cos\theta\vert< 0.80 $ ) and more than 50 MeV in the end-cap region ($ 0.86 <\vert \cos\theta\vert< 0.92 $ ). To exclude showers that originate from charged tracks, the angle subtended by the EMC shower and the position of the closest charged track at the EMC must be greater than 10 degrees as measured from the IP. To suppress electronic noise and showers unrelated to the event, the difference between the EMC time and the event start time is required to be within [0, 700] ns. At least one good photon candidate is required in an event.To improve the momentum resolution of final state particles and further suppress background, a four-constraint (4C) kinematic fit which constrains the four-momentum of two charged tracks and a photon to the initial
$ \psi(3686) $ four-momentum is performed. The two charged tracks are assumed to be either$ \pi^+\pi^- $ or$ K^+K^- $ , and the corresponding kinematic fit chi-squares ($ \chi^2_{\gamma \pi^+\pi^-} $ and$ \chi^2_{\gamma K^+K^-} $ ) are obtained. An event is assigned as$ \gamma \pi^+\pi^- $ if$ \chi^2_{\gamma \pi^+\pi^-}<\chi^2_{\gamma K^+K^-} $ , otherwise as$ \gamma K^+K^- $ . The radiative photon candidate is selected as the one that yields the smallest$ \chi^2 $ from the 4C kinematic fit if there are multiple photon candidates within one event. The$ \chi^{2} $ of the kinematic fit is further required to be less than 60 for$ \gamma\pi^{+}\pi^{-} $ events and 56 for$ \gamma K^{+}K^{-} $ events, which are optimized by maximizing the Figure-of-Merit$ S/\sqrt{(S + B)} $ , where S represents the number of normalized events from signal MC samples according to BFs from the PDG [4], and B is the total number of normalized background events estimated from the inclusive, Bhabha and di-muon MC samples.For
$ \gamma\pi^{+}\pi^{-} $ events, there are radiative Bhabha and$ \psi(3686)\rightarrow(\gamma) e^{+}e^{-} $ backgrounds. To remove these electrons, the deposited energy of each charged track in the EMC is required to be less than 1.34 GeV. Electrons passing through the EMC gap ($ 0.81<\left|\cos \theta\right|<0.86 $ ), which has no crystals between the barrel and end-cap regions, can further survive. To remove these remaining electrons, the$ \mathrm{d}E/\mathrm{d}x $ of a charged particle measured by the MDC is used. For charged tracks falling into the gap region, the$ |\chi_{{\mathrm{d}E}/{\mathrm{d}x}}(\pi)| $ [26] is required to be less than 2, where$ \chi_{{\mathrm{d}E}/{\mathrm{d}x}}(\pi) $ is the pull value of$ \mathrm{d}E/\mathrm{d}x $ based on the pion hypothesis. The most significant background comes from radiative di-muon and$ \psi(3686)\to(\gamma) \mu^+\mu^- $ events due to serious π and μ mis-identification. These non-peaking background processes are precisely known [4] and can be well simulated at BESIII.For
$ \gamma K^{+}K^{-} $ events, the background level is much lower due to the higher kaon mass. There are some remaining backgrounds from radiative Bhabha,$ \psi(3686)\rightarrow (\gamma) e^{+}e^{-} $ , and$ \psi(3686)\rightarrow \pi^{0}\pi^{0} J/\psi\to \pi^0 \pi^0 e^+e^- $ , which are effectively vetoed by requiring the deposited energy of both kaons in the EMC to be less than 1.34 GeV. Since no particle identification is applied to high momentum pions and kaons, there is cross-contamination between$ \gamma \pi^+\pi^- $ and$ \gamma K^+K^- $ events. According to MC simulation studies, the cross-contamination ratio is small ($ <1 $ %). For$ \gamma K^+K^- $ events, the background contribution from$ \gamma \pi^+\pi^- $ cross-contamination is fixed via MC simulation, and vice versa.After applying the event selection criteria mentioned above, the obtained
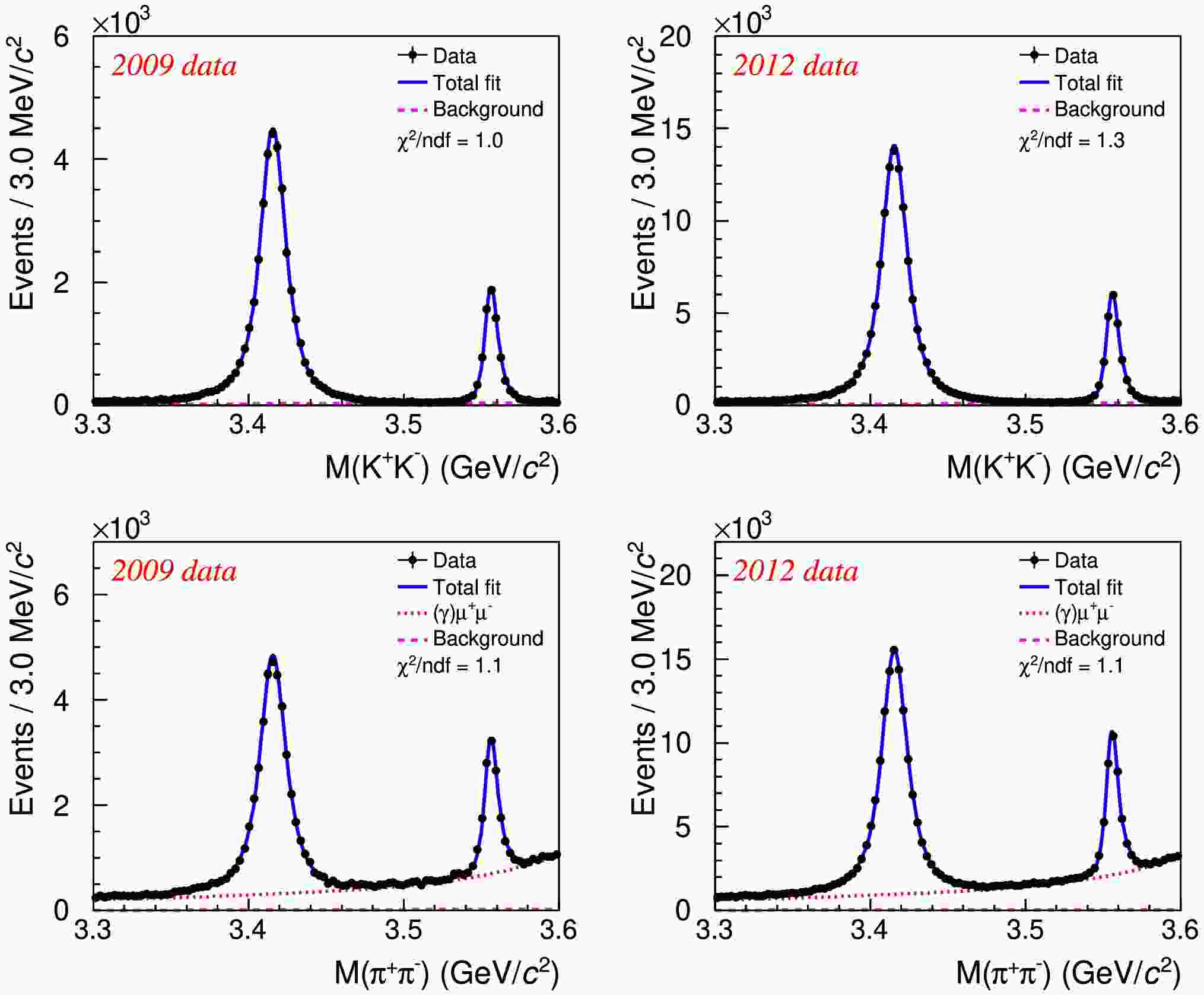
$ M(\pi^{+}\pi^{-}) $ and$ M(K^{+}K^{-}) $ invariant mass distributions from data are shown in Fig. 1, where significant numbers of$ \chi_{c0,c2} $ signal events are observed. To measure the mass and width of$ \chi_{c0} $ , as well as the BFs of$ \chi_{c0,c2}\to \pi^+\pi^-/ K^+K^- $ , an unbinned maximum likelihood fit is performed to the$ \gamma \pi^+\pi^- $ and$ \gamma K^+K^- $ data events simultaneously. In the fit, the BFs of$ \chi_{c0,c2}\to \pi^+\pi^- $ and$ \chi_{c0,c2}\to K^+K^- $ are shared as common parameters between data taken in different years. To avoid using the absolute momentum scale, and therefore significantly improve the mass precision of$ \chi_{c0} $ , the mass split between$ \chi_{c2} $ and$ \chi_{c0} $ ,$ \Delta M_{20} \equiv M( \chi_{c2})-M( \chi_{c0}) $ , is measured instead. Even in this case, the quality of the 2012 data is not as good as the 2009 data due to the worse MDC inner chamber performance during data taking [37], which bring in considerable systematic effects from discrepancies between data and MC simulation. Therefore, only the 2009 data are used for mass and width measurements, i.e.$ \Delta M_{20} $ and the full width Γ of$ \chi_{c0} $ are shared as common parameters in$ \gamma \pi^+\pi^- $ and$ \gamma K^+K^- $ data events taken in 2009.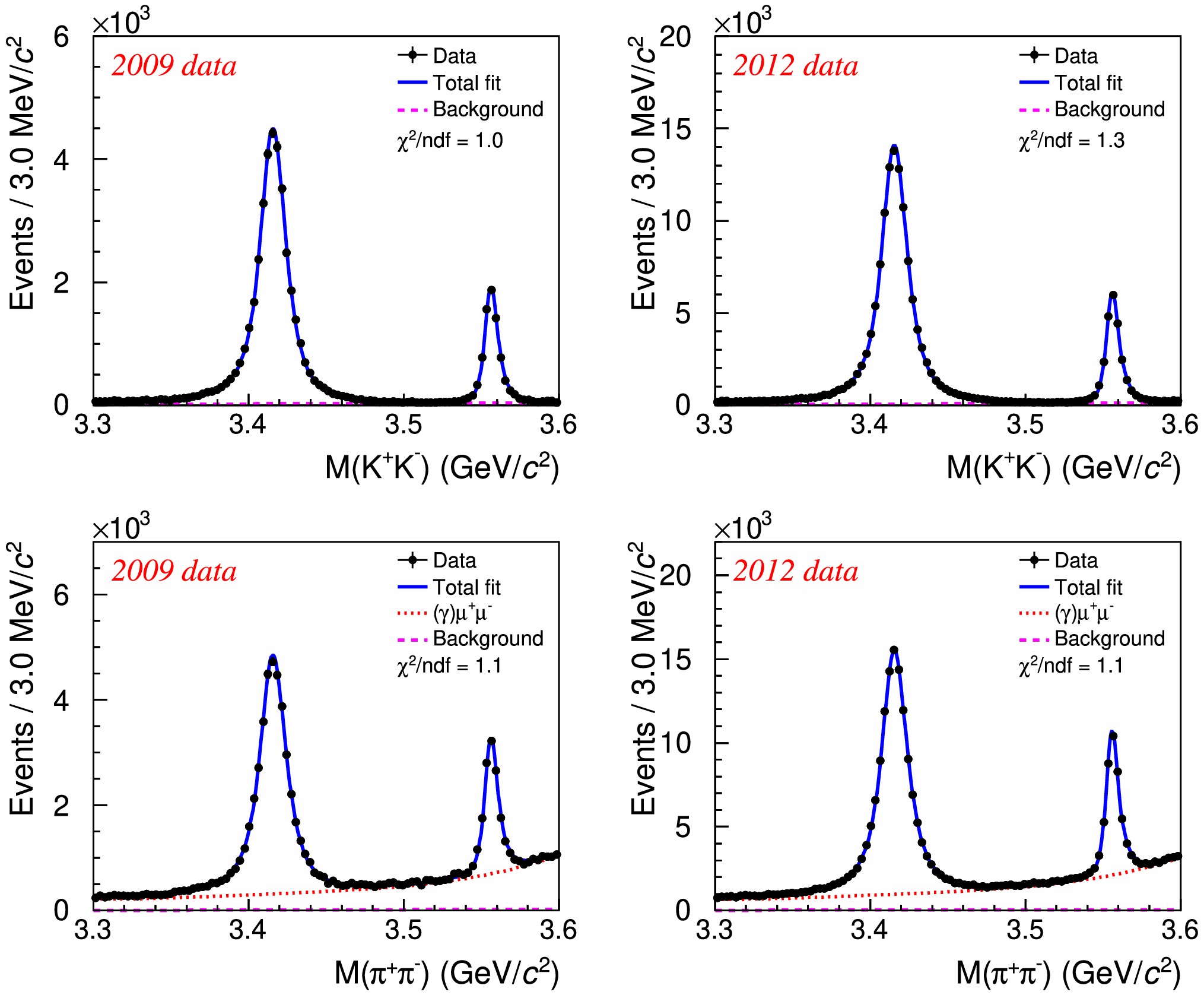
Figure 1. (color online) The
$ K^+K^- $ (top row) and$ \pi^+\pi^- $ (bottom row) invariant mass distributions from$ \psi(3686) $ data taken in 2009 (first column) and 2012 (second column) with fit results overlaid. The black dots with error bars are data, the blue solid curves represent the total fit results, the red dotted lines in bottom panels represent the background component from$ (\gamma) \mu^+\mu^- $ , and the pink dashed lines represent all other background components.The signal probability-density-function (PDF) is parameterized as
$ \begin{array}{l} [{\rm{BW}}^2(\sqrt{s}) \times {\cal{PS}}^{2}_1(\sqrt{s}) \times {\cal{D}}^{2}(\sqrt{s}) \\ \times {\cal{PS}}^2_2(\chi_{c0,c2}\rightarrow\pi^+\pi^-/K^+K^-)\times \epsilon(\sqrt{s})]\otimes {\rm{Resolution}}, \end{array} $

(1) where
$ {\rm{BW}}(\sqrt{s}) $ is a relativistic Breit-Wigner (BW) amplitude defined as$ {\rm{BW}}(\sqrt{s}) = \frac{1}{s-M^{2}+ {\rm i} M \Gamma \dfrac{p}{p^{\prime}}\dfrac{M}{\sqrt{s}}}, $

(2) where
$ \sqrt{s} $ is the$ \pi^+\pi^-/ K^+K^- $ invariant mass, while M and Γ are the mass and constant width of$ \chi_{c0,c2} $ , respectively, and$ p\; (p^\prime) $ is the momentum of daughter particles in the rest frame of the mother particle with mass$ \sqrt{s}\; (M) $ . In the$ E1 $ radiative transition$ \psi(3686)\to\gamma\chi_{c0,c2} $ , the decay width is proportional to a phase space factor$ {\cal{PS}}_1(\sqrt{s}) $ [38, 39] defined as$ {\cal{PS}}_1(\sqrt{s}) = \left(\dfrac{E_{\gamma}}{E^{0}_{\gamma}}\right)^{3/2}, $

(3) where
$ E_{\gamma} $ is the radiative photon energy and$ E^{0}_{\gamma} $ corresponds to the photon energy at the$ \chi_{c0,c2} $ mass M. An additional damping factor${\cal{D}}(\sqrt{s}) = \left(\dfrac{(E^{0}_{\gamma})^2}{E^{0}_{\gamma} E_{\gamma}+(E^{0}_{\gamma}-E_{\gamma})^{2}}\right)^{1/2}$ [40] is also introduced to suppress the higher energy tail.$ {\cal{PS}}_2(\chi_{c0,c2}\rightarrow\pi^{+}\pi^{-}/K^{+}K^{-}) $ is the phase space factor of$ \chi_{c0,c2} $ decaying into$ \pi^+\pi^-/ K^+K^- $ [4]. The signal PDF is corrected by a mass-dependent efficiency curve$ \epsilon(\sqrt{s}) $ , which is obtained by MC simulation studies and varies within 1% for the interested mass region, thus parameterized as a linear function. The$ \chi_{c0,c2} $ resonance line shapes are further convolved with Gaussian functions to account for the detector resolution. In the fit, the$ \chi_{c2} $ width is fixed to the known value [4], and the resolution difference between data and MC simulation measured from$ \chi_{c2} $ data events is used to calibrate that for$ \chi_{c0} $ .The shapes of dominant background sources are described by polynomial functions. For
$ \gamma K^+K^- $ events, the background is low and parameterized as a free second-order polynomial. The small cross-contamination contribution from$ \gamma \pi^+\pi^- $ events is fixed via MC simulation. For$ \gamma \pi^{+} \pi^{-} $ events, the dominating$ (\gamma) \mu^+\mu^- $ background is represented by a fourth-order polynomial, which is fixed according to normalized MC events for$ \psi(3686)\to(\gamma) \mu^+\mu^- $ and di-muon processes. Other extra backgrounds with a small contribution ($ \sim 3 $ % of the total background) are parameterized as a free second-order polynomial.Figure 1 shows the fit results. The mass split between
$ \chi_{c2} $ and$ \chi_{c0} $ is measured to be$ \Delta M_{20}\equiv M(\chi_{c 2})-M(\chi_{c 0}) = (140.54\pm0.07 $ ) MeV/$ c^2 $ . Taking the world average mass$ M( \chi_{c2}) = (3556.17\pm0.07) $ MeV/$ c^2 $ [4] as input, the$ \chi_{c0} $ mass is calculated to be$ M( \chi_{c0}) = (3415.63\pm0.07 $ ) MeV/$ c^2 $ . The width of$ \chi_{c0} $ is measured to be$ \Gamma(\chi_{c0}) = (12.52\pm 0.12) \; {\rm{MeV}} $ . The uncertainties here are statistical only.The systematic uncertainties in the mass split and
$ \chi_{c0} $ width measurements mainly come from the signal and background PDF shapes as well as the damping factor, momentum-dependent scale, and possible interference effect. In the nominal fit model, a BW function with a mass-dependent width, i.e. Eq. (2), is used to describe the$ \chi_{c0,c2} $ state. An alternative shape with a constant width BW function is investigated. The difference with respect to the nominal measurement for$ \Delta M_{20} $ is 0.04 MeV/$ c^2 $ and for the$ \chi_{c0} $ full width$ \Gamma( \chi_{c0}) $ is 0.08 MeV, which are taken as systematic uncertainties. A damping factor also appears in the signal PDF. We take another form$ {\cal{D}}(\sqrt{s}) = {\rm e}^{-{E_{\gamma}^2}/({8\beta^2})} $ , where$ \beta = 65.0\pm2.5\; {\rm{MeV}} $ from the CLEO-c Collaboration [41]. The difference on the measurements of$ \Delta M_{20} $ and$ \Gamma( \chi_{c0}) $ is 0.01 MeV/$ c^2 $ and 0.01 MeV, respectively.The uncertainty due to background in the fit is studied in several aspects. The free background components are described by second-order polynomials for both
$ \gamma \pi^+\pi^- $ and$ \gamma K^+K^- $ events. Changing this component to a third-order polynomial either for$ \gamma \pi^+\pi^- $ or$ \gamma K^+K^- $ events yields differences on the measurements, which are 0.02 MeV/$ c^2 $ for$ \Delta M_{20} $ and 0.04 MeV for$ \Gamma( \chi_{c0}) $ . Interference between$ \chi_{c0,c2} $ resonances and continuum is observed in low-mass regions [42], and we account for this by adding the continuum component coherently to the signal PDF. The resulting difference for$ \Delta M_{20} $ is 0.01 MeV/$ c^2 $ and$ \Gamma( \chi_{c0}) $ is 0.08 MeV. For$ \gamma \pi^+\pi^- $ events, the dominant background comes from$ (\gamma) \mu^+\mu^- $ . Varying the output cross section from Babayaga [36] by$ \pm1\sigma $ for MC simulated background normalization yields a difference of 0.02 MeV/$ c^2 $ for$ \Delta M_{20} $ and 0.02 MeV for$ \Gamma( \chi_{c0}) $ . The shape parameters of this background component are also varied within$ \pm1\sigma $ , which yields a difference of 0.01 MeV/$ c^2 $ for$ \Delta M_{20} $ and 0.02 MeV for$ \Gamma( \chi_{c0}) $ . The momentum-dependent scale is simulated by MC. The systematic uncertainty due to the difference between data and MC is studied by correcting the MC distribution of final-state particle momenta to data with$ \chi_{c2} $ events, which yields a variation of 0.04 MeV/$ c^2 $ for$ \Delta M_{20} $ and 0.01 MeV for$ \Gamma( \chi_{c0}) $ .Table 1 summarizes all these sources and their corresponding contributions. Assuming all the sources are independent, the total systematic uncertainty is obtained by adding each individual source in quadrature, which is 0.07 MeV/
$ c^2 $ for$ \Delta M_{20} $ and 0.13 MeV for$ \Gamma( \chi_{c0}) $ .Source $ \Delta M_{20} $ /(

$ {{{\rm{MeV}}}/{\rm{c}}^2} $ )

$ \Gamma( \chi_{c0}) $ /

$ {\rm{MeV}} $ 

Signal shape $ 0.04 $ 

$ 0.08 $ 

Damping factor $ 0.01 $ 

$ 0.01 $ 

Polynomial background $ 0.02 $ 

$ 0.04 $ 

Interference effect 0.01 0.08 Number of $ (\gamma) \mu^+\mu^- $ background

$ 0.02 $ 

$ 0.02 $ 

Shape of $ (\gamma) \mu^+\mu^- $ background

$ 0.01 $ 

$ 0.02 $ 

Momentum dependent scale $ 0.04 $ 

$ 0.01 $ 

Total $ 0.07 $ 

$ 0.13 $ 

Table 1. Sources of systematic uncertainties and their contributions to
$ \Delta M_{20} $ and$ \Gamma( \chi_{c0}) $ measurements.The BF of
$ \chi_{c0,c2}\to \pi^+\pi^-/ K^+K^- $ is calculated as$ {\cal{B}} = \frac{N_{\rm{sig}}}{N_{\rm{tot}}[\psi(3686)]\epsilon{\cal{B}}[\psi(3686)\to\gamma\chi_{c0,c2}]}, $

(4) where
$ N_{\rm{sig}} $ is the number of observed$ \chi_{c0,c2} $ signal events from the fit,$ N_{\rm{tot}}[\psi(3686)] $ is the total number of collected$ \psi(3686) $ events [25],$ \epsilon$ is the detection efficiency of$ \gamma \pi^+\pi^-/\gamma K^+K^- $ events, and$ {\cal{B}}[\psi(3686)\to\gamma\chi_{c0,c2}] $ is the BF of the$ E1 $ radiative transition [4]. In practice, a simultaneous fit is performed and the BFs are shared between different data sets. The BFs are measured to be$ {\cal{B}}(\chi_{c0} \rightarrow K^{+} K^{-}) = (6.36 \pm 0.02) \times 10^{-3} $ ,$ {\cal{B}}(\chi_{c0} \rightarrow \pi^{+} \pi^{-}) = (6.06 \pm 0.02) \times 10^{-3} $ ,$ {\cal{B}}(\chi_{c2} \rightarrow K^{+} K^{-}) = (1.22 \pm 0.01) \times 10^{-3} $ , and$ {\cal{B}}(\chi_{c2} \rightarrow \pi^{+} \pi^{-}) = (1.61 \pm 0.01) \times 10^{-3} $ , respectively, where all the uncertainties are statistical only. Table 2 lists the detection efficiencies for each data set.$ \epsilon(\gamma\pi^{+}\pi^{-}) $ 

$ \epsilon(\gamma K^{+}K^{-}) $ 

2009 $ \chi_{c0} $ 

$ 0.644\pm0.001 $ 

$ 0.589\pm0.001 $ 

2009 $ \chi_{c2} $ 

$ 0.667\pm0.001 $ 

$ 0.624\pm0.001 $ 

2012 $ \chi_{c0} $ 

$ 0.634\pm0.001 $ 

$ 0.577\pm0.001 $ 

2012 $ \chi_{c2} $ 

$ 0.658\pm0.001 $ 

$ 0.613\pm0.001 $ 

Table 2. The detection efficiencies for
$ \gamma \pi^+\pi^- $ and$ \gamma K^+K^- $ data events taken in different years.The systematic uncertainties in the BF measurements mainly come from the total number of
$ \psi(3686) $ events, detection efficiencies, signal and background PDF shapes, possible interference effect, fit range, 4C kinematic fit, and intermediate BFs.The total number of
$ \psi(3686) $ events is measured by counting inclusive hadronic events, with an uncertainty of$ 0.7 $ % [25]. Detection efficiencies include tracking, photon detection, decay angular distributions, and selection criteria. The uncertainty of photon detection is measured to be 0.5% per photon by studying the$ e^+e^- \rightarrow \gamma \mu^+\mu^- $ process and 0.5% is assigned for this analysis. Pion and kaon tracks have a momentum above 1 GeV. The tracking efficiency of such tracks is above$ 99 $ % at BESIII, by studying$ e^+e^-\to \pi^+\pi^- \pi^+\pi^- $ and$ J/\psi\to K^*K $ events. According to the two-dimensional (2D,$ p_t $ vs.$ \cos\theta $ ) tracking efficiencies of data and MC simulation, the uncertainty in each bin is obtained. The final uncertainty due to tracking is estimated as a weighted average over 2D bins.Decay angular distributions also affect the detection efficiencies. Considering the helicity amplitudes and correlation coefficients measured by BESIII [30], 100 sets of two correlated helicity amplitude parameters are obtained via a 2D sampling. The resulting changes in detection efficiencies, and therefore the corresponding changes of BFs from the simultaneous fit, are taken as systematic uncertainties. The uncertainties due to the pion/kaon EMC deposit energy requirement and fit range are studied using a Barlow test [43], by changing a series of EMC deposit energies and fit ranges. All the alternative choices give results within 1σ of the nominal result, which means these two sources can be ignored.
For the 4C kinematic fit, a correction of the pull distribution of charged track parameters is applied to the MC simulation [44]. The uncertainties are taken as half of the efficiency difference with or without helix parameter corrections. The uncertainties on the BFs for
$ \psi(3686)\rightarrow\gamma\chi_{c0} $ ($ 2.1 $ %) and$ \psi(3686)\rightarrow\gamma\chi_{c2} $ ($ 2.1 $ %) are taken from the PDG [4]. The uncertainties due to the signal shape, damping factor and background are studied using the same method as the mass split and width measurement. The cross-contaminations between$ \gamma \pi^+\pi^- $ and$ \gamma K^+K^- $ events are studied via MC simulations, with input BFs updated by this measurement. The fluctuations due to BFs are taken as systematic uncertainties.Table 3 summarizes all these sources and their contributions to the BF measurements. Assuming all the sources are independent, the total systematic uncertainties are obtained by adding them in quadrature. The largest systematic uncertainty comes from the intermediate BFs, and all other sources contribute about 1.2%.
Source $ \gamma\pi^{+}\pi^{-} $ 

$ \gamma K^{+}K^{-} $ 

$ \chi_{c0} $ 

$ \chi_{c2} $ 

$ \chi_{c0} $ 

$ \chi_{c2} $ 

$ N_{\rm{tot}} $ [

$ \psi(2S) $ ]

$ 0.7 $ 

$ 0.7 $ 

$ 0.7 $ 

$ 0.7 $ 

Tracking $ 0.1 $ 

$ 0.1 $ 

$ 0.2 $ 

$ 0.1 $ 

Photon $ 0.5 $ 

$ 0.5 $ 

$ 0.5 $ 

$ 0.5 $ 

Polynomial background $ 0.6 $ 

$ 0.2 $ 

$ 0.1 $ 

$ 0.1 $ 

Interference effect 0.4 0.0 0.4 0.0 Number of $ (\gamma)\mu^{+}\mu^{-} $ background

$ 0.1 $ 

$ 0.4 $ 

$ 0.1 $ 

$ 0.1 $ 

Shape of $ (\gamma)\mu^{+}\mu^{-} $ background

$ 0.2 $ 

$ 0.1 $ 

$ 0.1 $ 

$ 0.1 $ 

Cross contamination 0.0 0.0 0.0 $ 0.1 $ 

Damping factor $ 0.1 $ 

$ 0.2 $ 

$ 0.1 $ 

$ 0.1 $ 

Signal shape $ 0.1 $ 

$ 0.2 $ 

$ 0.1 $ 

$ 0.1 $ 

Angular distribution ... $ 0.1 $ 

... 0.0 4C kinematic fit $ 0.3 $ 

$ 0.2 $ 

$ 0.7 $ 

$ 0.8 $ 

Sum $ 1.2 $ 

$ 1.1 $ 

$ 1.2 $ 

$ 1.2 $ 

Intermediate BF $ 2.1 $ 

$ 2.1 $ 

$ 2.1 $ 

$ 2.1 $ 

Total $ 2.4 $ 

$ 2.4 $ 

$ 2.4 $ 

$ 2.4 $ 

Table 3. Sources of systematic uncertainties and their contributions (in %) to BF measurements. ''...'' means a non-applicable option.
In summary, a precise measurement of the
$ \chi_{c0} $ resonance parameters and the$ \chi_{c0,c2}\to \pi^+\pi^-/ K^+K^- $ decay BFs is performed at BESIII by analyzing$ \psi(3686) $ data events. The mass split between$ \chi_{c2} $ and$ \chi_{c0} $ is measured to be$ \Delta M_{20} = (140.54\pm0.07\pm0.07)\; {\rm{MeV}}/c^2 $ . Taking the$ \chi_{c2} $ world average mass as input, the$ \chi_{c0} $ mass is determined to be$ M( \chi_{c0}) = (3415.63\pm0.07\pm0.07\pm0.07 $ ) MeV/$ c^2 $ , where the first uncertainty is statistical, the second systematic, and the third from the$ \chi_{c2} $ mass uncertainty. This is the most precise$ \chi_{c0} $ mass measurement to date. It is a bit higher ($ 1.42\pm0.49 $ MeV/$ c^2 $ ) than the BES measurement [8], while it agrees well with the E835 measurement [9]. Our measurement improves the precision of the$ \chi_{c0} $ mass over previous individual measurements by a factor of four [8, 9]. The full width of$ \chi_{c0} $ is measured to be$ \Gamma( \chi_{c0}) = (12.52\pm0.12\pm0.13)\; {\rm{MeV}} $ . It agrees with the BES measurement quite well within$ 1\sigma $ [8] and improves the precision by an order of magnitude. These measurements have a big impact on our knowledge about the$ \chi_{c0} $ resonance parameters [4], and are expected to play a crucial role in our understanding of the strong force governing the$ c\bar{c} $ system [39, 45]. A comparison of our results with other measurements as well as the PDG world average is shown in Fig. 2.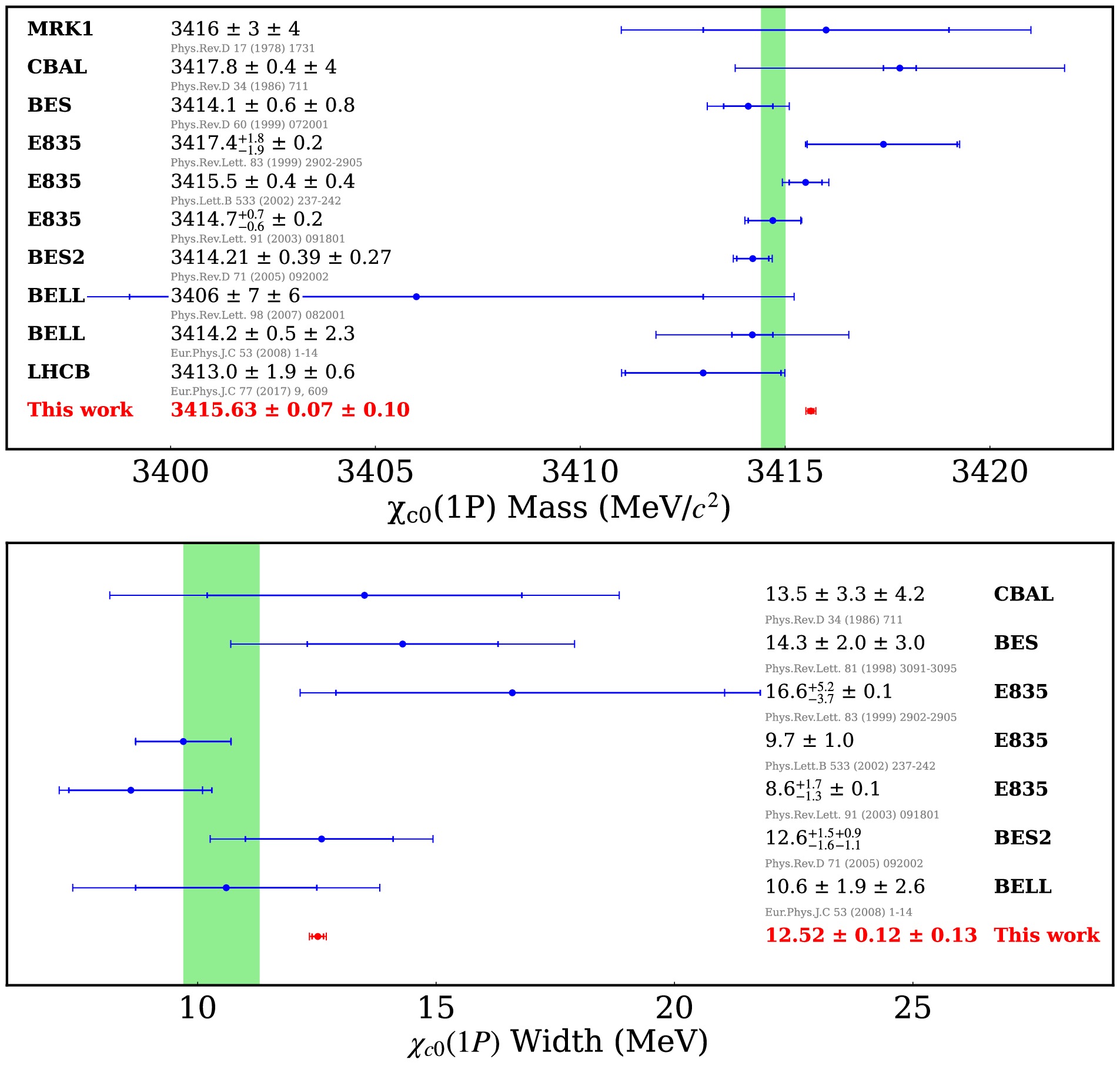
Figure 2. (color online) Comparison of the
$ \chi_{c0} $ resonance parameters measurements. The light green bands represent the PDG world average [4].The decay BFs are measured to be
$ \begin{array}{l} {\cal{B}}( \chi_{c0}\to K^+K^-) = (6.36\pm0.02\pm0.08\pm0.13)\times10^{-3}, \\ \;\; {\cal{B}}( \chi_{c0}\to \pi^+\pi^-) = (6.06\pm0.02\pm0.07\pm0.13)\times10^{-3}, \\ {\cal{B}}( \chi_{c2}\to K^+K^-) = (1.22\pm0.01\pm0.02\pm0.03)\times10^{-3}, \\ \;\;{\cal{B}}( \chi_{c2}\to \pi^+\pi^-) = (1.61\pm0.01\pm0.02\pm0.04)\times10^{-3}, \end{array} $

where the first uncertainties are statistical, the second systematic, and the third come from
$ {\cal{B}}[\psi(3686)\rightarrow \gamma\chi_{c0,c2}] $ [4]. These measurements agree with the CLEO-c result within$ 1\sigma $ [46], and improve the precision by more than threefold. Interestingly, the ratio of BFs$ {\cal{R}} = \dfrac{{\cal{B}}( \chi_{c0}\to \pi^+\pi^-)}{{\cal{B}}( \chi_{c0}\to K^+K^-)} = (0.95\pm0.01\pm0.01) $ demonstrates no obvious ‘Chiral Suppression’ is observed for this$ 0^{++} $ system, which supports the theoretical analysis in Ref. [47, 48]. This behavior is also quite different from the case of the$ f_0(1710) $ [19, 20], therefore challenging the scalar glueball interpretation of the$ f_0(1710) $ state [21]. It implies$ f_0(1710) $ might contain a substantial$ s\bar{s} $ component, which aligns with the model calculations in Ref. [49, 50]. Combining our precisely measured$ {\cal{R}} $ value, which constrains the glueball fraction in$ f_0(1710) $ , with future theoretical improvements will advance our understanding of QCD.
HTML
-
The BESIII Collaboration thanks the staff of BEPCII and the IHEP computing center for their strong support. We are also grateful to Prof. Chen Ying for the inspiring discussion on glueballs.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: