-
Clustering is an intriguing phenomenon inside nuclear many-body systems, appearing abundantly in different mass regions across the nuclide chart. The clustering phenomenon unveils an alternative perspective on the basic structures within the atomic nucleus [1, 2]. Due to the strongly correlated nucleon motions, some particles with high degrees of symmetry under certain circumstances can be regarded as substructures, such as the enormously stable α particle [3]. In fact, the α-cluster concept has been applied to investigate a series of typical nuclei above double shell closures [4−10], giving good descriptions of electromagnetic transitions, energy spectra, α scattering, and α-emission widths. However, explorations of the cluster structures of heavy nuclei are more challenging because of both the mean-field effects and limitations of experimental technology. Therefore, much more attention has been paid to clustering phenomena for the systems of
$ n\alpha $ or$ n\alpha $ plus other particles in light-mass region [11−13], especially for the exotic cluster states. Recently, many 4α events have been recorded with full particle identification, providing new evidence for the Hoyle-like structure in 16O [14]. The excited 0+ state with a gas-like characteristic was found via microscopic five-body calculations, implying the existence of 5α condensate state in 20Ne [15].Despite α-clustering being a common occurrence throughout the above regions, the measurements of energy levels and electromagnetic transition rates for cluster states appear to be more difficult when it comes to odd-mass nuclei owing to the interaction in collective excitations of few-body [16] and relatively small cross sections corresponding to astrophysical energies. Fortunately, the widely discussed cluster states close to the thresholds in favorable nuclei 19F and 21Ne can be identified via the three-nucleon and α-particle transfer reactions [17, 18]. From a theoretical perspective, new insights into the clustering phenomena in odd-A nuclei with the spin-orbit coupling effects can be obtained by studying the weak-coupling interplay [19] between the cluster and residual core. Meanwhile, the energy spectra and electromagnetic transitions around 20Ne have been observed experimentally, with implications for nuclear astrophysical field [16, 20−32]. Besides, the existence of cluster states in heavier odd-mass nuclei has been a topic of interest in recent years. The spectroscopic properties, including spin parities and α-particle partial widths, of possible cluster states in these nuclei, such as 43Sc, 59Cu, and 93Mo [33, 34], have a significant impact on the astrophysical nucleosynthesis process.
In recent decades, some progress has been achieved in the microscopic comprehension of clustering phenomena rooted in the configuration mixing. Starting from the generator coordinate method (GCM), orthogonality condition model (OCM), and resonating group method (RGM), various new microscopic models and methods have been developed to interpret the α-cluster states for light nuclei, such as the Tohsaki-Horiuchi-Schuck-Röpke (THSR) wave function [12, 15], antisymmetrized molecular dynamics (AMD) [35−37], and Monte Carlo Shell Model (MCSM) [38]. In addition to these cluster models, the binary cluster-core model [7−9, 39−41], which treats the picture of target nucleus as the cluster constituted by strongly correlated nucleons orbiting the inert core, has been used to successfully describe the spectroscopic properties from light to heavy nuclei, including several odd-A nuclei [39, 42]. In our previous work [7, 8], we systematically investigated the parity doublet bands and electromagnetic transitions for α-cluster states above double shell closures within the BCM and Monte Carlo bootstrap method, resulting in good agreement with the available data plus uncertainty evaluation.
One objective of this study is to give satisfactory calculations of the electromagnetic transition rates and energy levels in the field of astrophysical interest with the extra cluster spin-orbit potential in the same framework of "three-nucleon or α-cluster + core" configurations for 19F and 21Ne to verify the reliability of such a binary cluster-core model. The other aim is to check or prove the role of cluster degrees of freedom in heavier odd-mass nuclei, such as 43Sc, 59Cu, and 93Mo. The remainder of this article is organized as follows. Section II presents the theoretical framework of the calculations of energy spectra and electromagnetic transition strengths. In Sec. III, the numerous results and discussions on cluster states in the above nuclei are given. A brief summary with additional remarks is given in the last section.
-
Clustering is an intriguing phenomenon inside nuclear many-body systems, appearing abundantly in different mass regions across the nuclide chart. The clustering phenomenon unveils an alternative perspective on the basic structures within the atomic nucleus [1, 2]. Due to the strongly correlated nucleon motions, some particles with high degrees of symmetry under certain circumstances can be regarded as substructures, such as the enormously stable α particle [3]. In fact, the α-cluster concept has been applied to investigate a series of typical nuclei above double shell closures [4−10], giving good descriptions of electromagnetic transitions, energy spectra, α scattering, and α-emission widths. However, explorations of the cluster structures of heavy nuclei are more challenging because of both the mean-field effects and limitations of experimental technology. Therefore, much more attention has been paid to clustering phenomena for the systems of
$ n\alpha $ or$ n\alpha $ plus other particles in light-mass region [11−13], especially for the exotic cluster states. Recently, many 4α events have been recorded with full particle identification, providing new evidence for the Hoyle-like structure in 16O [14]. The excited 0+ state with a gas-like characteristic was found via microscopic five-body calculations, implying the existence of 5α condensate state in 20Ne [15].Despite α-clustering being a common occurrence throughout the above regions, the measurements of energy levels and electromagnetic transition rates for cluster states appear to be more difficult when it comes to odd-mass nuclei owing to the interaction in collective excitations of few-body [16] and relatively small cross sections corresponding to astrophysical energies. Fortunately, the widely discussed cluster states close to the thresholds in favorable nuclei 19F and 21Ne can be identified via the three-nucleon and α-particle transfer reactions [17, 18]. From a theoretical perspective, new insights into the clustering phenomena in odd-A nuclei with the spin-orbit coupling effects can be obtained by studying the weak-coupling interplay [19] between the cluster and residual core. Meanwhile, the energy spectra and electromagnetic transitions around 20Ne have been observed experimentally, with implications for nuclear astrophysical field [16, 20−32]. Besides, the existence of cluster states in heavier odd-mass nuclei has been a topic of interest in recent years. The spectroscopic properties, including spin parities and α-particle partial widths, of possible cluster states in these nuclei, such as 43Sc, 59Cu, and 93Mo [33, 34], have a significant impact on the astrophysical nucleosynthesis process.
In recent decades, some progress has been achieved in the microscopic comprehension of clustering phenomena rooted in the configuration mixing. Starting from the generator coordinate method (GCM), orthogonality condition model (OCM), and resonating group method (RGM), various new microscopic models and methods have been developed to interpret the α-cluster states for light nuclei, such as the Tohsaki-Horiuchi-Schuck-Röpke (THSR) wave function [12, 15], antisymmetrized molecular dynamics (AMD) [35−37], and Monte Carlo Shell Model (MCSM) [38]. In addition to these cluster models, the binary cluster-core model [7−9, 39−41], which treats the picture of target nucleus as the cluster constituted by strongly correlated nucleons orbiting the inert core, has been used to successfully describe the spectroscopic properties from light to heavy nuclei, including several odd-A nuclei [39, 42]. In our previous work [7, 8], we systematically investigated the parity doublet bands and electromagnetic transitions for α-cluster states above double shell closures within the BCM and Monte Carlo bootstrap method, resulting in good agreement with the available data plus uncertainty evaluation.
One objective of this study is to give satisfactory calculations of the electromagnetic transition rates and energy levels in the field of astrophysical interest with the extra cluster spin-orbit potential in the same framework of "three-nucleon or α-cluster + core" configurations for 19F and 21Ne to verify the reliability of such a binary cluster-core model. The other aim is to check or prove the role of cluster degrees of freedom in heavier odd-mass nuclei, such as 43Sc, 59Cu, and 93Mo. The remainder of this article is organized as follows. Section II presents the theoretical framework of the calculations of energy spectra and electromagnetic transition strengths. In Sec. III, the numerous results and discussions on cluster states in the above nuclei are given. A brief summary with additional remarks is given in the last section.
-
As mentioned previously, the BCM is a clear and effective cluster model, in which the target nucleus is assumed as the strongly correlated cluster orbiting the inert core composed of the residual nucleons. The wave functions and corresponding energies of relative motion between the cluster and core can be determined by direct solution of the two-body radial Schrödinger equation, which is given by
$ \left[ {\frac{{ - {\hbar ^2}}}{{2\mu }}{\nabla ^2} + V(r)} \right]\left| {n,l} \right\rangle = {E_{nl}}\left| {n,l} \right\rangle . $

(1) Here, μ, n, and l are the reduced mass of the two-body system and principal and orbital quantum numbers, respectively. The total interaction potential
$ V(r) $ is the key point of the cluster-core structure, containing the local nuclear potential, repulsive Coulomb part, cluster spin-orbit interaction, and centrifugal term, as follows:$ V(r)=V_{N}(r)+V_{C}(r)+V_{\rm so}(r) + \dfrac{\hbar^{2}l(l+1)}{2\mu r^{2}}. $

(2) The Coulomb potential
$ V_{C}(r) $ is regarded as that of the uniformly charged spherical core of radius$ R_C $ interacting with a point cluster. In terms of the nuclear potential$ V_N(r) $ , note that the conventional Woods-Saxon (W.S.) potentials often behave inversely in high-lying levels. There is also a typical shortcoming of compressed spectra in describing the ground-state rotational bands caused by the semi-microscopic double folding potentials [43−45]. To eliminate these dilemmas, the W.S. + W.S.3 approach was developed to refine the shape of nuclear potential in accordance with the energy spectra and half-lives of charged-particle emissions simultaneously [46]. A slightly modified variant of the W.S. potential mixture plus the terms of λ and σ subsequently optimizes these circumstances, leading to a good description of the excitation energies and$ B(E2) $ transition rates. The cluster-core potential of (1+Gaussian) (W.S.+W.S.3) shape is therefore chosen as the nuclear part, as in our previous studies [7, 8], namely,$ \begin{aligned}[b] V_{N}(r)=\; &-V_{0}\left[1+\lambda \exp \left(-\frac{r^{2}}{\sigma^{2}}\right)\right] \\&\times \left\{\frac{b}{1+\exp [(r-R)/a]} + \frac{1-b}{\big\{1+\exp [(r-R)/3a]\big\}^{3}}\right\}, \end{aligned} $

(3) where the values of depth
$ V_0 $ , diffuseness a, mixing parameter b, and parameters λ and σ are introduced in the following process. The nuclear parameter R is assumed to be equivalent to the Coulomb radius$ R_C $ for minimizing the number of adjustable parameters, which is obtained by reproducing the experimental bandhead of the parity doublet bands. In general, spin-orbit splitting is not considered in even-even nuclei because of the zero spins of the cluster and residual core, while the spin-orbit coupling potential cannot be neglected in the calculations of the odd-mass region, which is related to the nuclear potential$ V_N(r) $ of Eq. (3) in the usual way [39, 42] by$ V_{\rm so}(r)=-V_{\rm so}\left(\dfrac{\hbar}{m_{\pi}c}\right)^{2}\frac{1}{r}\ \bigg|\dfrac{\mathrm{d}V_N(r)}{\mathrm{d}r}\bigg|\ \mathit{\boldsymbol{l}}\cdot\mathit{\boldsymbol{\sigma}}. $

(4) Here, (
$ \hbar $ /$ m_{\pi}c $ )2 = 2 fm2, and$ \mathit{\boldsymbol{\sigma}} $ is the spin of triton or 3He and odd-mass core in the different configurations.$ V_{\rm so} $ is the potential depth of the spin-orbit part, which can adjust the ordering and spacing of energy levels.Based on the shell-model theory, the nucleons inside the cluster should lie completely in certain orbitals outside the frozen core, which are characterized by orbital angular momentum l and internal node n of wave function, namely, the principal quantum number in the Eq. (1). The values of n and l are allowed by the Wildermuth condition,
$ G=2n+l=\sum\limits_{i}\big(g_i^{A_d+A_c}-g_i^{A_c}\big). $

(5) The global quantum number G, identifying the energy bands of states, can be obtained after fixing the values of the oscillator and interior quantum numbers
$ g_i^{A_d+A_c} $ and$ g_i^{A_c} $ . Subsequently, the node n can be determined by the orbital angular momentum l. The condition G$ \geqslant $ $ G_{\mathrm{g.s.}} $ is taken into account when describing the parity doublet bands for odd-A nuclei, where$ G_{\mathrm{g.s.}}$ is connected with the ground states. In the present study, the global quantum numbers G, employed in the α-core structures in 19F, 21Ne, 43Sc, 59Cu, and 93Mo, are fixed as 8, 8, 12, 12, and 16, respectively. For the triton or 3He cluster states, the values of G are set to 6, 6, 9, 9, and 12 in the systems of "t + 16O," "3He + 18O," "t + 40Ca," "t + 56Ni," and "3He + 90Zr," respectively.In the framework of BCM, the electromagnetic transitions of the cluster states belong to a special case of "single-particle" transition. For example, the entire α cluster is viewed as a single particle during the transition instead of four separate nucleons undergoing the change of shell-model states. In this way, the reduced dipole transition strength
$ B(E1) $ [42] for the cluster-core relative motion from the initial state$ j_i $ of the$ K_i $ -band to the final state$ j_f $ of$ K_f $ -band is evaluated by$ B(E1; j_i \rightarrow j_f) = \dfrac{3}{4\pi} |\langle j_iK_i10|j_fK_f \rangle|^{2}{\beta_1}^{2}\langle r\rangle ^{2} $

(6) with
$ \beta_1 = \dfrac{Z_cA_d - Z_dA_c}{A_d + A_c}, $

(7) and
$ \left\langle r\right\rangle\left\langle=\right\rangle\int_{ }^{ }ru_{l_ij_i}(r)u_{l_fj_f}(r)\mathrm{d}r. $

(8) The quadrupole transition rate
$ B(E2) $ [42] is given by$ B(E2; j_i \rightarrow j_f) = \dfrac{5}{4\pi} |\langle j_iK_i20|j_fK_f \rangle|^{2}{\beta_2}^{2}\langle r^{2}\rangle ^{2} $

(9) with
$ \beta_2 = \dfrac{Z_cA_d^{2} + Z_dA_c^{2}}{(A_d + A_c)^{2}}, $

(10) and
$ \langle r^{2}\rangle = \int r^{2}u_{l_ij_i}(r)u_{l_fj_f}(r)\mathrm{d}r. $

(11) $ Z_c $ and$ A_c $ are the proton and mass numbers of the cluster, respectively, and$ Z_d $ and$ A_d $ are those of the residual core.$ u_{lj}(r) $ is the radial wave function associated with the momenta l and j for the cluster states. It is convenient to compare the calculated results of electromagnetic transition rates with the observed data by using the Weisskopf unit (W.u.) in the following forms:$ 1\mathrm{W.u.}=\dfrac{0.81}{4\pi}(A_c+A_d)^{\frac{2}{3}}\mathrm{e}^2\mathrm{fm^2} $

(12) for B(E1) values and
$ 1\mathrm{W.u.}=\dfrac{0.747}{4\pi}(A_c+A_d)^{\frac{4}{3}}\mathrm{e}^2\mathrm{fm^4} $

(13) for B(E2) values. These two transition strengths in Weisskopf units vary with the mass numbers of the target nuclei.
-
As mentioned previously, the BCM is a clear and effective cluster model, in which the target nucleus is assumed as the strongly correlated cluster orbiting the inert core composed of the residual nucleons. The wave functions and corresponding energies of relative motion between the cluster and core can be determined by direct solution of the two-body radial Schrödinger equation, which is given by
$ \left[ {\frac{{ - {\hbar ^2}}}{{2\mu }}{\nabla ^2} + V(r)} \right]\left| {n,l} \right\rangle = {E_{nl}}\left| {n,l} \right\rangle . $

(1) Here, μ, n, and l are the reduced mass of the two-body system and principal and orbital quantum numbers, respectively. The total interaction potential
$ V(r) $ is the key point of the cluster-core structure, containing the local nuclear potential, repulsive Coulomb part, cluster spin-orbit interaction, and centrifugal term, as follows:$ V(r)=V_{N}(r)+V_{C}(r)+V_{\rm so}(r) + \dfrac{\hbar^{2}l(l+1)}{2\mu r^{2}}. $

(2) The Coulomb potential
$ V_{C}(r) $ is regarded as that of the uniformly charged spherical core of radius$ R_C $ interacting with a point cluster. In terms of the nuclear potential$ V_N(r) $ , note that the conventional Woods-Saxon (W.S.) potentials often behave inversely in high-lying levels. There is also a typical shortcoming of compressed spectra in describing the ground-state rotational bands caused by the semi-microscopic double folding potentials [43−45]. To eliminate these dilemmas, the W.S. + W.S.3 approach was developed to refine the shape of nuclear potential in accordance with the energy spectra and half-lives of charged-particle emissions simultaneously [46]. A slightly modified variant of the W.S. potential mixture plus the terms of λ and σ subsequently optimizes these circumstances, leading to a good description of the excitation energies and$ B(E2) $ transition rates. The cluster-core potential of (1+Gaussian) (W.S.+W.S.3) shape is therefore chosen as the nuclear part, as in our previous studies [7, 8], namely,$ \begin{aligned}[b] V_{N}(r)=\; &-V_{0}\left[1+\lambda \exp \left(-\frac{r^{2}}{\sigma^{2}}\right)\right] \\&\times \left\{\frac{b}{1+\exp [(r-R)/a]} + \frac{1-b}{\big\{1+\exp [(r-R)/3a]\big\}^{3}}\right\}, \end{aligned} $

(3) where the values of depth
$ V_0 $ , diffuseness a, mixing parameter b, and parameters λ and σ are introduced in the following process. The nuclear parameter R is assumed to be equivalent to the Coulomb radius$ R_C $ for minimizing the number of adjustable parameters, which is obtained by reproducing the experimental bandhead of the parity doublet bands. In general, spin-orbit splitting is not considered in even-even nuclei because of the zero spins of the cluster and residual core, while the spin-orbit coupling potential cannot be neglected in the calculations of the odd-mass region, which is related to the nuclear potential$ V_N(r) $ of Eq. (3) in the usual way [39, 42] by$ V_{\rm so}(r)=-V_{\rm so}\left(\dfrac{\hbar}{m_{\pi}c}\right)^{2}\frac{1}{r}\ \bigg|\dfrac{\mathrm{d}V_N(r)}{\mathrm{d}r}\bigg|\ \mathit{\boldsymbol{l}}\cdot\mathit{\boldsymbol{\sigma}}. $

(4) Here, (
$ \hbar $ /$ m_{\pi}c $ )2 = 2 fm2, and$ \mathit{\boldsymbol{\sigma}} $ is the spin of triton or 3He and odd-mass core in the different configurations.$ V_{\rm so} $ is the potential depth of the spin-orbit part, which can adjust the ordering and spacing of energy levels.Based on the shell-model theory, the nucleons inside the cluster should lie completely in certain orbitals outside the frozen core, which are characterized by orbital angular momentum l and internal node n of wave function, namely, the principal quantum number in the Eq. (1). The values of n and l are allowed by the Wildermuth condition,
$ G=2n+l=\sum\limits_{i}\big(g_i^{A_d+A_c}-g_i^{A_c}\big). $

(5) The global quantum number G, identifying the energy bands of states, can be obtained after fixing the values of the oscillator and interior quantum numbers
$ g_i^{A_d+A_c} $ and$ g_i^{A_c} $ . Subsequently, the node n can be determined by the orbital angular momentum l. The condition G$ \geqslant $ $ G_{\mathrm{g.s.}} $ is taken into account when describing the parity doublet bands for odd-A nuclei, where$ G_{\mathrm{g.s.}}$ is connected with the ground states. In the present study, the global quantum numbers G, employed in the α-core structures in 19F, 21Ne, 43Sc, 59Cu, and 93Mo, are fixed as 8, 8, 12, 12, and 16, respectively. For the triton or 3He cluster states, the values of G are set to 6, 6, 9, 9, and 12 in the systems of "t + 16O," "3He + 18O," "t + 40Ca," "t + 56Ni," and "3He + 90Zr," respectively.In the framework of BCM, the electromagnetic transitions of the cluster states belong to a special case of "single-particle" transition. For example, the entire α cluster is viewed as a single particle during the transition instead of four separate nucleons undergoing the change of shell-model states. In this way, the reduced dipole transition strength
$ B(E1) $ [42] for the cluster-core relative motion from the initial state$ j_i $ of the$ K_i $ -band to the final state$ j_f $ of$ K_f $ -band is evaluated by$ B(E1; j_i \rightarrow j_f) = \dfrac{3}{4\pi} |\langle j_iK_i10|j_fK_f \rangle|^{2}{\beta_1}^{2}\langle r\rangle ^{2} $

(6) with
$ \beta_1 = \dfrac{Z_cA_d - Z_dA_c}{A_d + A_c}, $

(7) and
$ \left\langle r\right\rangle\left\langle=\right\rangle\int_{ }^{ }ru_{l_ij_i}(r)u_{l_fj_f}(r)\mathrm{d}r. $

(8) The quadrupole transition rate
$ B(E2) $ [42] is given by$ B(E2; j_i \rightarrow j_f) = \dfrac{5}{4\pi} |\langle j_iK_i20|j_fK_f \rangle|^{2}{\beta_2}^{2}\langle r^{2}\rangle ^{2} $

(9) with
$ \beta_2 = \dfrac{Z_cA_d^{2} + Z_dA_c^{2}}{(A_d + A_c)^{2}}, $

(10) and
$ \langle r^{2}\rangle = \int r^{2}u_{l_ij_i}(r)u_{l_fj_f}(r)\mathrm{d}r. $

(11) $ Z_c $ and$ A_c $ are the proton and mass numbers of the cluster, respectively, and$ Z_d $ and$ A_d $ are those of the residual core.$ u_{lj}(r) $ is the radial wave function associated with the momenta l and j for the cluster states. It is convenient to compare the calculated results of electromagnetic transition rates with the observed data by using the Weisskopf unit (W.u.) in the following forms:$ 1\mathrm{W.u.}=\dfrac{0.81}{4\pi}(A_c+A_d)^{\frac{2}{3}}\mathrm{e}^2\mathrm{fm^2} $

(12) for B(E1) values and
$ 1\mathrm{W.u.}=\dfrac{0.747}{4\pi}(A_c+A_d)^{\frac{4}{3}}\mathrm{e}^2\mathrm{fm^4} $

(13) for B(E2) values. These two transition strengths in Weisskopf units vary with the mass numbers of the target nuclei.
-
As mentioned above, the nuclear properties of cluster states in 19F and 21Ne have been reported for three-nucleon and α transfer reactions in recent decades. Nevertheless, some experimental information around the A = 20 region, such as energy levels, electromagnetic transition rates, spins and parities, remains somewhat ambiguous owing to the intricate structures within the odd-A nuclei and limitations of experimental techniques. These spectroscopic properties are vital to the generation of heavy elements in astrophysical environments [20−32] and deepening the theoretical understanding of many-body physics, with particular relevance to the clustering phenomena in odd mass nuclei. Furthermore, the 17O + α reaction rates have great influence on the efficiency of the weak s process occurring in massive and asymptotic giant branch stars. The rates of the 17O(α, γ)21Ne and 17O(α, n)20Ne reactions [30−32] strongly depend on the energy levels of α-cluster states approaching the thresholds in 21Ne [20], which have attracted more attention in the region of interest for astrophysics.
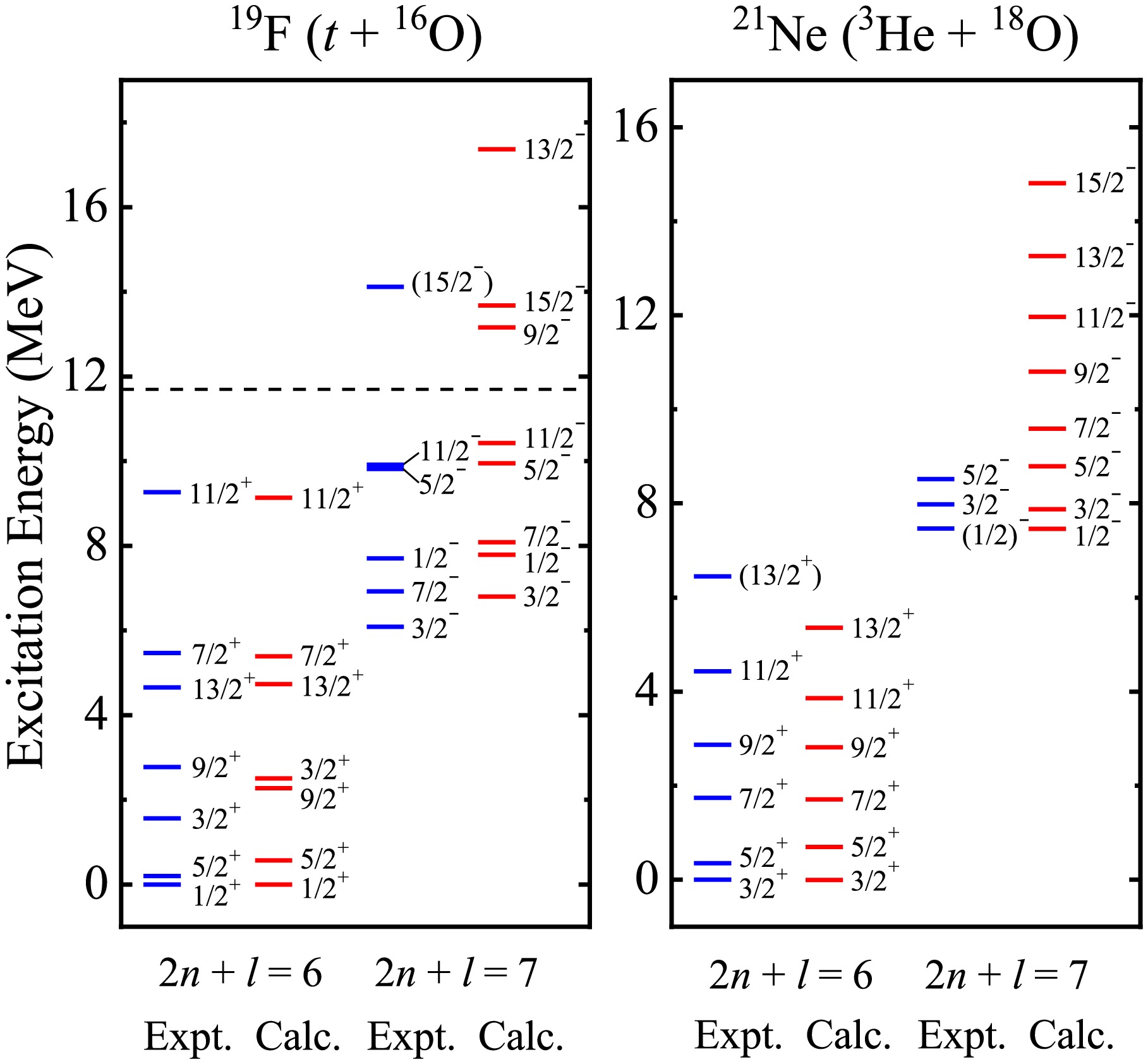
Considering this, the energy spectra and reduced transition strengths of cluster states around 20Ne are initially calculated, serving as a test on the binary cluster-core model. The theoretical energy levels of α-cluster and three-nucleon structures for 19F and 21Ne compared with the observed data are shown in Figs. 1 and 2, where the dashed lines represent the cluster thresholds. The nuclear parameters for 19F (α + 15N) and 21Ne (α + 17O) in Eq. (3) are
$ V_0 $ = 235.00 MeV, a = 0.70 fm, b = 0.19, λ = 0.10, and σ = 0.20 fm, which are consistent with the findings in our previous work [8]. The values of b, λ, and σ remain constant in all cases to reduce the number of free parameters. According to the previous empirical systematics and constant reasonable attempts,$ V_0 $ = 190.00 MeV and a = 0.90 fm are applied to describe the three-nucleon cluster states in the following process, which are close to those of other studies [40, 47−49]. The key point is the inclusion of the spin-orbit coupling potential, which gives rise to the splitting of energy levels with the same orbital angular momentum l. With the bootstrap method [7, 8], the depths$ V_{\rm so} $ can then be separately fixed as 0.058, 0.005, and –0.018 MeV for t-cluster states in 19F and α-cluster and 3He-cluster states in 21Ne, respectively. As for the "α + 15N" configuration of 19F,$ V_{\rm so} $ = 0.003 MeV corresponds to the 2n + l = 8 band, and$ V_{\rm so} $ = –0.018 MeV corresponds to the 2n + l = 9 band. The complete parity doublet bands have been compared with Ref. [42], where the spin-orbit coupling effect was not introduced in the α-core structure for 19F. The energy spectra of cluster states for 19F and 21Ne have been well reproduced within the BCM, along with reasonable predictions for further levels without experimental counterparts. It is observed that the degree of energy level splitting, which is very sensitive to spin-orbit potential depth, rises with growth of the absolute value of$ V_{\rm so} $ . Moreover, the energy spacing coming from the same l is found to increase with increasing l in a certain energy band. The agreement of our results with experimental data proves that the BCM is equally reliable for describing the cluster states and possesses robust model predictive capability in light odd-A nuclei, thereby offering assistance in theoretical analysis of cluster phenomena and experimental design about the essential reactions of (α, n) and (α, γ) in the astrophysical s process. It is noted that the calculations of above two configurations are performed based on mutually orthogonal wave functions and two disjoint bases. In addition, the assignments of energy levels and electromagnetic transition strengths are related to Wildermuth condition, which contributes to different global quantum numbers G of different configurations in the same nucleus. Hence, there will be no conflicts in the assignment of energy levels and electromagnetic transitions in these two cluster states. The calculations here can be served as a preliminary attempt to explore the possible cluster states in odd-A nuclei with two configurations in the framework of BCM plus the spin-orbit coupling. In fact, there may exist some possible mixed states between triton and α-cluster, which deserve further investigations within the coupled-channels formalism in the future work.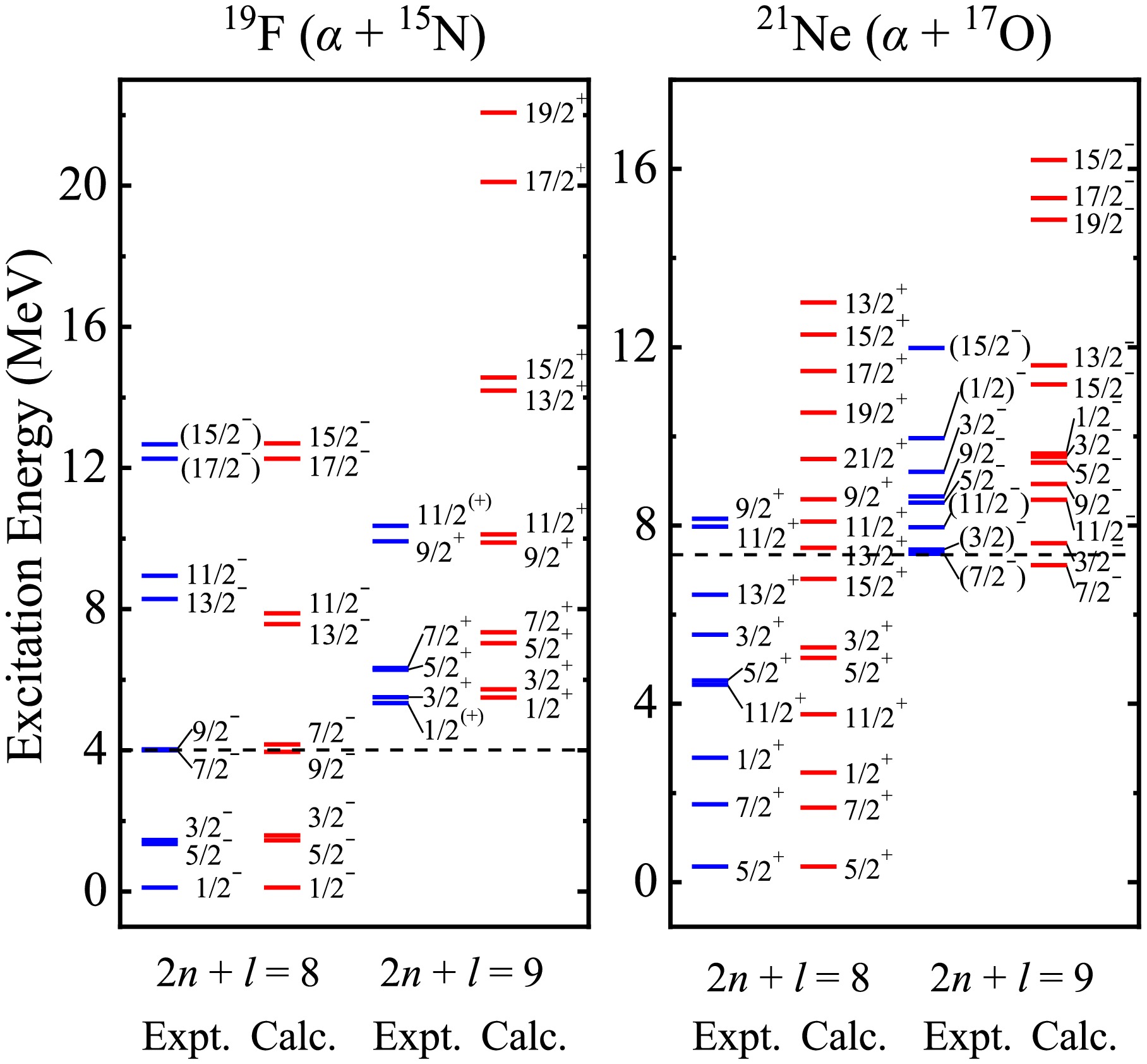
Figure 1. (color online) Comparisons of the calculated parity doublet bands of 2n + l = 8 and 9 for α-cluster states in 19F (α + 15N) and 21Ne (α + 17O) with the experimental data [20, 42, 50], where the dashed lines dictate the α-cluster breakup thresholds. The intrinsic spins of 15N and 17O are 1/2- and 5/2+, respectively.
As is well known, analyzing the spectra is a direct way to study the spectroscopic properties of cluster states. The enhancement of reduced electromagnetic transition rates is an effective symbol of cluster states. Once the wave functions are generated by the above procedure, the
$ B(E1) $ and$ B(E2) $ transition probabilities between successive band members can then be obtained by Eqs. (6) and (9). For further examination of the BCM, a comparison of obtained reduced quadrupole transition strengths with available data and other related calculations for cluster states in 19F and 21Ne is presented in Table 1. The first column denotes the target nuclei with the clusters. The third and fourth columns indicate the theoretical$ B(E2) $ values and experimental data, respectively. For 19F, the$ B(E2)_{1} $ values in the fifth column are from the vibron-fermion model with SU(3)$ \times $ U(2) limit [56], i.e., the extension of the U(3) vibron model. The calculated results for$ B(E2)_{2} $ based on the GCM [57] with the "α + 15N" configuration are plotted in the last column. Obviously, the$ B(E2) $ values have been well reproduced within the BCM for both nuclei despite the overestimation for the transition 11/2-$ \rightarrow $ 7/2- in 19F (α + 15N), which is comparable with the$ B(E2)_1 $ and$ B(E2)_2 $ values. The present$ B(E2) $ values are in accordance with these two calculations, except for the 11/2+$ \rightarrow $ 7/2+ and 11/2+$ \rightarrow $ 13/2+ transitions for 19F in Ref. [57]. This implies that there are some mixed cluster states of triton and α-particle in the low-lying energy region, which presents difficulties in both experimental detection and theoretical research. The transition rates of 5/2+$ \rightarrow $ 1/2+ with 5.36 W.u., 3/2+$ \rightarrow $ 5/2+ with 2.40 W.u., and 9/2+$ \rightarrow $ 5/2+ with 6.21 W.u. in 19F are very close to the recent results of 6.45 W.u., 2.65 W.u., and 6.41 W.u. in Ref. [59], respectively, where the$ B(E2) $ values are determined using the USDB nuclear shell model interaction. The calculations of$ B(E2) $ values in this study for 21Ne agree with the$ B(E2)_{1} $ values in the fifth column of Table 1, which are obtained in the framework of CSM [58]. Additionally, reasonable predictions of$ B(E2) $ values for these two nuclei are displayed in Table 1, especially for α-cluster states approaching the thresholds in the region of astrophysical interest. These selected levels of negative-parity bands in 21Ne may belong to the α-cluster states due to large$ B(E2) $ strengths.Nuclei Transition $ B(E2)_{{\rm{calc.}}} $ 

$ B(E2)_{{\rm{expt.}}} $ 

$ B(E2)_{1} $ 

$ B(E2)_{2} $ 

19F(α) 5/2− $ \rightarrow $ 1/2−

19.53 21.60 $ \pm $ 0.40

20.00 18.10 19F(α) 3/2− $ \rightarrow $ 1/2−

19.69 21.89 18.00 19F(α) 3/2− $ \rightarrow $ 5/2−

8.54 7.50 19F(α) 7/2− $ \rightarrow $ 5/2−

2.68 3.13 2.20 19F(α) 7/2− $ \rightarrow $ 3/2−

24.30 25.71 21.00 19F(α) 9/2− $ \rightarrow $ 5/2−

26.36 28.00 $ \pm $ 6.00

22.51 23.70 19F(α) 9/2− $ \rightarrow $ 7/2−

1.66 1.30 19F(α) 13/2− $ \rightarrow $ 9/2−

23.56 19.00 $ \pm $ 2.00

19F(α) 11/2− $ \rightarrow $ 7/2−

23.80 8.10 $ \pm $ 2.00

23.88 18.80 19F(α) 11/2− $ \rightarrow $ 9/2−

0.91 1.28 0.60 19F(α) 11/2− $ \rightarrow $ 13/2−

0.84 19F(t) 5/2+ $ \rightarrow $ 1/2+

5.36 6.95 $ \pm $ 0.08

6.95 6.20 19F(t) 3/2+ $ \rightarrow $ 1/2+

5.77 6.95 8.00 19F(t) 3/2+ $ \rightarrow $ 5/2+

2.40 3.10 2.80 19F(t) 9/2+ $ \rightarrow $ 5/2+

6.21 8.20 $ \pm $ 0.90

8.09 5.80 19F(t) 13/2+ $ \rightarrow $ 9/2+

3.93 3.20 $ \pm $ 0.40

5.27 2.90 19F(t) 7/2+ $ \rightarrow $ 5/2+

0.72 0.81 0.90 19F(t) 7/2+ $ \rightarrow $ 3/2+

6.70 7.28 12.80 19F(t) 7/2+ $ \rightarrow $ 9/2+

0.55 0.78 0.50 19F(t) 11/2+ $ \rightarrow $ 9/2+

0.20 0.50 19F(t) 11/2+ $ \rightarrow $ 13/2+

0.21 0.07 19F(t) 11/2+ $ \rightarrow $ 7/2+

4.91 22.8 21Ne(α) 7/2+ $ \rightarrow $ 5/2+

$ ^{\rm{a}} $ 

14.62 11.00 $ \pm $ 4.00

21Ne(α) 1/2+ $ \rightarrow $ 5/2+

$ ^{ \rm a} $ 

42.22 21Ne(α) 11/2+ $ ^{\rm{c}} $ 

$ \rightarrow $ 7/2+

$ ^{\rm{a}} $ 

15.75 21Ne(α) 5/2+ $ ^{\rm{b}} $ 

$ \rightarrow $ 5/2+

$ ^{\rm{a}} $ 

0.69 21Ne(α) 5/2+ $ ^{\rm{b}} $ 

$ \rightarrow $ 7/2+

18.90 21Ne(α) 5/2+ $ ^{\rm{b}} $ 

$ \rightarrow $ 1/2+

13.50 21Ne(α) 3/2+ $ \rightarrow $ 5/2+

$ ^{\rm{a}} $ 

0.08 21Ne(α) 3/2+ $ \rightarrow $ 7/2+

19.12 21Ne(α) 3/2+ $ \rightarrow $ 1/2+

13.68 21Ne(α) 3/2+ $ \rightarrow $ 5/2+

$ ^{\rm{b}} $ 

36.16 21Ne(α) 13/2+ $ \rightarrow $ 11/2+

$ ^{\rm{c}} $ 

3.53 21Ne(α) 3/2− $ ^{\rm{d}} $ 

$ \rightarrow $ 7/2−

49.31 21Ne(α) 11/2− $ \rightarrow $ 7/2−

41.01 21Ne(α) 5/2− $ \rightarrow $ 7/2−

52.52 21Ne(α) 5/2− $ \rightarrow $ 3/2−

$ ^{\rm{d}} $ 

68.43 21Ne(α) 9/2− $ \rightarrow $ 7/2−

23.83 21Ne(α) 9/2− $ \rightarrow $ 11/2−

20.27 21Ne(α) 9/2− $ \rightarrow $ 5/2−

43.41 21Ne(3He) 5/2+ $ \rightarrow $ 3/2+

20.58 24.30 $ \pm $ 2.00

24.16 21Ne(3He) 7/2+ $ \rightarrow $ 3/2+

7.04 9.30 $ \pm $ 0.80

10.08 21Ne(3He) 7/2+ $ \rightarrow $ 5/2+

10.54 11.00 $ \pm $ 4.00

15.10 21Ne(3He) 9/2+ $ \rightarrow $ 5/2+

10.90 15.70 $ \pm $ 2.20

15.10 21Ne(3He) 9/2+ $ \rightarrow $ 7/2+

7.94 9.00 $ \pm $ 5.00

9.87 21Ne(3He) 11/2+ $ \rightarrow $ 7/2+

7.50 17.94 21Ne(3He) 11/2+ $ \rightarrow $ 9/2+

2.85 6.00 $ \pm $ 4.00

6.91 21Ne(3He) 13/2+ $ \rightarrow $ 9/2+

8.57 19.72 21Ne(3He) 13/2+ $ \rightarrow $ 11/2+

3.69 5.05 $ ^{\rm{a}} $ 

$ E(5/2^{+}) $ = 0.351 MeV.

$ ^{\rm{b}} $ 

$ E(5/2^{+}) $ = 4.526 MeV.

$ ^{\rm{c}} $ 

$ E(11/2^{+}) $ = 4.433 MeV.

$ ^{\rm{d}} $ 

$ E(3/2^{-}) $ = 7.465 MeV.

Table 1. Comparison of the theoretical
$ B(E2) $ values with the experimental data [50−52] and other associated studies for 19F and 21Ne. The comparative theoretical results of the$ B(E2)_1 $ and$ B(E2)_2 $ values in 19F are from Ref. [56] and Ref. [57], respectively, where the$ B(E2)_{1} $ values are based on the SU(3)$ \times $ U(2) limit of the vibron-fermion model, and the$ B(E2)_{2} $ values are obtained within the generator coordinate method (GCM). The comparative results of$ B(E2)_{1} $ values for 21Ne are based on the cluster shell model (CSM) [58]. All the quadrupole transition probabilities presented here are in Weisskopf units (W.u.).The electromagnetic dipole transitions are often considered as another important indicator of cluster states. In past decades, some interesting events of enhanced
$ B(E1) $ values [60−64] have been observed from light to heavy nuclei, attracting widespread attention in nuclear physics. In this study, the$ E1 $ transitions occur in 19F from the G = 9 to G = 8 band of α-cluster states and from the negative- to positive-parity levels of t-cluster states. Table 2 shows the$ B(E1) $ values for 19F in comparison with measured quantities and the aforementioned calculations. General agreement with experimental data is obtained for the "α + 15N" configuration, except for the transition 5/2+$ \rightarrow $ 3/2-, which is close to the theoretical$ B(E1)_1 $ and$ B(E1)_2 $ values. Nonetheless, the strong dipole transition probabilities of triton states are given within the BCM at approximately two orders of magnitude larger than the available data. As Ref. [42] discussed, the relatively large difference between the two configurations comes from the recoil terms of Eqs. (7) and (10), giving rise to larger$ B(E1) $ rates for triton states by a factor of 16 than the case of α-core structure. Meanwhile, these states may have impure cluster structures, namely, the mixing states between α and t cluster levels or between cluster and non-cluster states, leading to uncertainties in the measurements. Such an enhancement of$ B(E1) $ values of t-cluster states in the 19F we calculated has not yet been experimentally observed. Similarly, the reproduction of$ E1 $ transitions by other models is generally unsatisfactory [42, 56, 57], e.g., the relatively small results in the calculations with the algebraic approach [56]. A consistent investigation of this problem in odd mass nuclei relies on additional experimental data, which is hoped to be useful for the ongoing or forthcoming experiments on the nuclear structures.Nuclei Transition $ B(E1)_{{\rm{calc.}}} $ 

$ B(E1)_{{\rm{expt.}}} $ 

$ B(E1)_{1} $ 

$ B(E1)_{2} $ 

19F(α) 3/2+ $ \rightarrow $ 1/2−

18.20 7.00 4.83 11.20 19F(α) 3/2+ $ \rightarrow $ 5/2−

31.10 9.80 5.06 8.70 19F(α) 3/2+ $ \rightarrow $ 3/2−

3.56 2.00 19F(α) 5/2+ $ \rightarrow $ 5/2−

0.86 2.10 $ \pm $ 0.50

0.24 1.20 19F(α) 5/2+ $ \rightarrow $ 3/2−

12.62 1.20 $ \pm $ 0.40

5.80 16.80 19F(α) 5/2+ $ \rightarrow $ 7/2−

18.06 19F(α) 7/2+ $ \rightarrow $ 5/2−

16.94 19F(α) 7/2+ $ \rightarrow $ 7/2−

0.60 19F(α) 7/2+ $ \rightarrow $ 9/2−

19.24 19F(t) 1/2− $ \rightarrow $ 1/2+

269.90 19F(t) 1/2− $ \rightarrow $ 3/2+

43.83 19F(t) 3/2− $ \rightarrow $ 1/2+

302.24 5.10 $ \pm $ 1.40

19F(t) 3/2− $ \rightarrow $ 5/2+

448.23 3.2 $ \pm $ 1.00

19F(t) 3/2− $ \rightarrow $ 3/2+

49.80 19F(t) 5/2− $ \rightarrow $ 5/2+

26.52 19F(t) 5/2− $ \rightarrow $ 3/2+

371.31 19F(t) 5/2− $ \rightarrow $ 7/2+

257.23 19F(t) 7/2− $ \rightarrow $ 5/2+

462.97 12.00 $ \pm $ 2.00

0.03 5.20 19F(t) 7/2− $ \rightarrow $ 9/2+

316.95 1.7 $ \pm $ 0.50

0.002 4.00 19F(t) 7/2− $ \rightarrow $ 7/2+

9.06 0.08 19F(t) 11/2− $ \rightarrow $ 9/2+

510.58 3.90 $ \pm $ 1.20

19F(t) 11/2− $ \rightarrow $ 13/2+

133.48 0.33 $ \pm $ 0.16

In fact, the excited states of atomic nuclei, especially in light even-even nuclei, are strongly characterized by α clustering, contributing to various α-cluster configurations as the excitation energy increases. For heavier nuclei, the picture of clusters becomes unclear, resulting from the complex interactions among nucleons, not to mention the interplay with nucleon degree. Meanwhile, the symmetry breaking [65] from the spin-orbit force and mean-field effect would be stronger, suppressing the α-like correlations in this region. Therefore, it is of great significance to extend the α-cluster concept to heavier nuclei. Inspired by the successful application of cluster-core structures around 20Ne, the BCM is generalized to heavier nuclei approaching the shell closures, such as 43Sc, 59Cu, and 93Mo, which can provide a good testing ground to confirm the persistence of cluster states. The obtained energy spectra for nuclei 43Sc, 59Cu, and 93Mo with α and three-nucleon clusters are compared with the suggested experimental counterparts in Figs. 3 and 4, respectively. To ensure the applicability of BCM within the same parameterization, the nuclear parameters in Eq. (3) are the same as before, and the spin-orbit parameter
$ V_{\rm so} $ = 0.003 MeV, consistent with the case of the negative-parity band in 19F (α + 15N), is employed in both configurations of these three nuclei. Satisfactory theoretical parity doublet bands and predictions have been obtained in the framework of BCM, as shown in the Figs. 3 and 4, suggesting that the available levels correspond to possible cluster states in heavier nuclei with odd mass. It should be noted that 93Mo exhibits rich information of energy levels below 5 MeV, but no corresponding energy levels have been observed in the region from 5 to 10 MeV [55]. This reflects the theoretical prediction of the$ 2n + l $ = 13 band for 3He-cluster states awaiting additional experimental confirmation. Meanwhile, the energy bands of α-cluster states are more intricate than those of other configurations on account of the inclusion of the spin-orbit coupling effect. For example, the number of energy levels coming from one certain orbital angular momentum l is 2 for the 3He-cluster states in 93Mo, while the maximum number could even reach 10 for the α-cluster states. This seems to indicate that the α cluster tends to form more easily than other clusters within nuclei and plays a dominant role in the mixed states.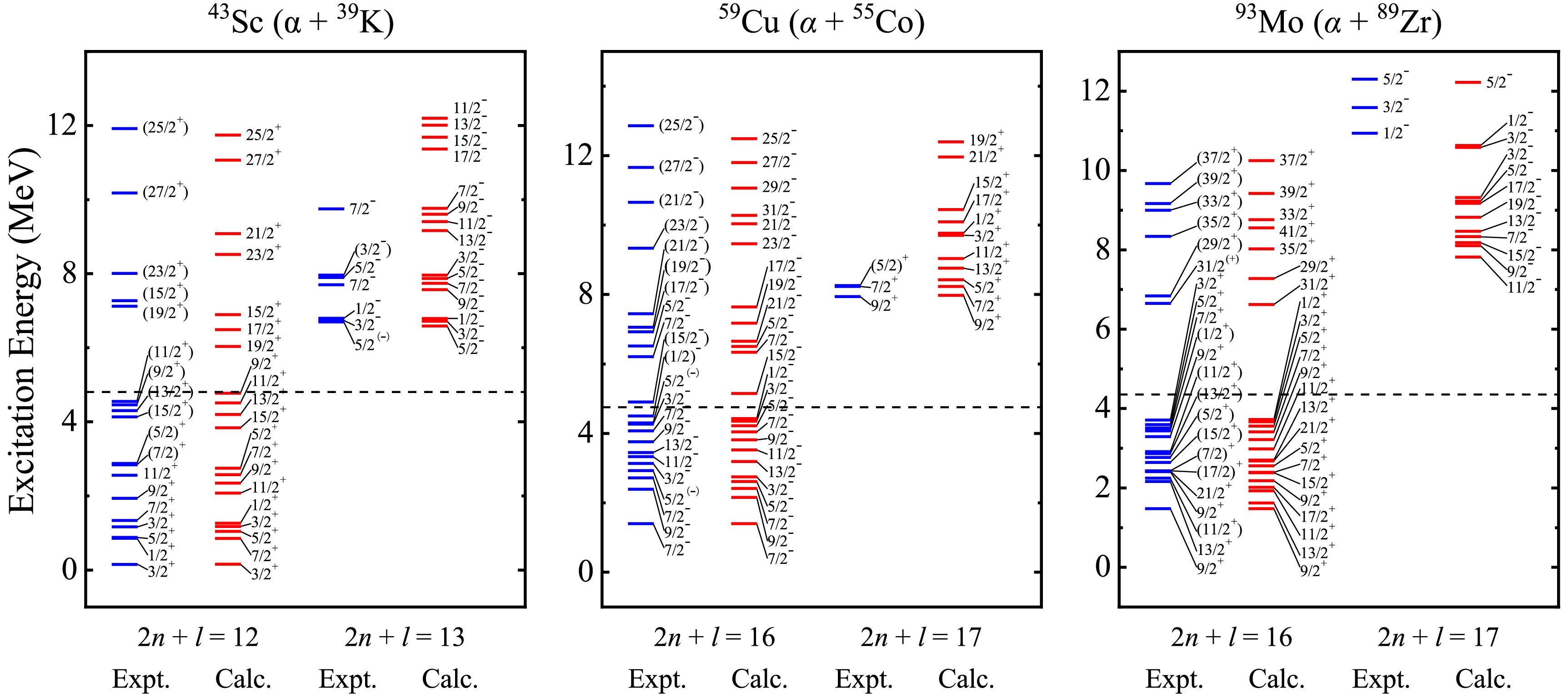
Figure 3. (color online) Comparisons of the calculated doublet parity bands with available candidates [50] for α-cluster states in heavier nuclei, where the dashed lines denote the α-cluster thresholds. The intrinsic spins of 39K, 55Co, and 89Zr are 3/2+, 7/2-, and 9/2-, respectively.
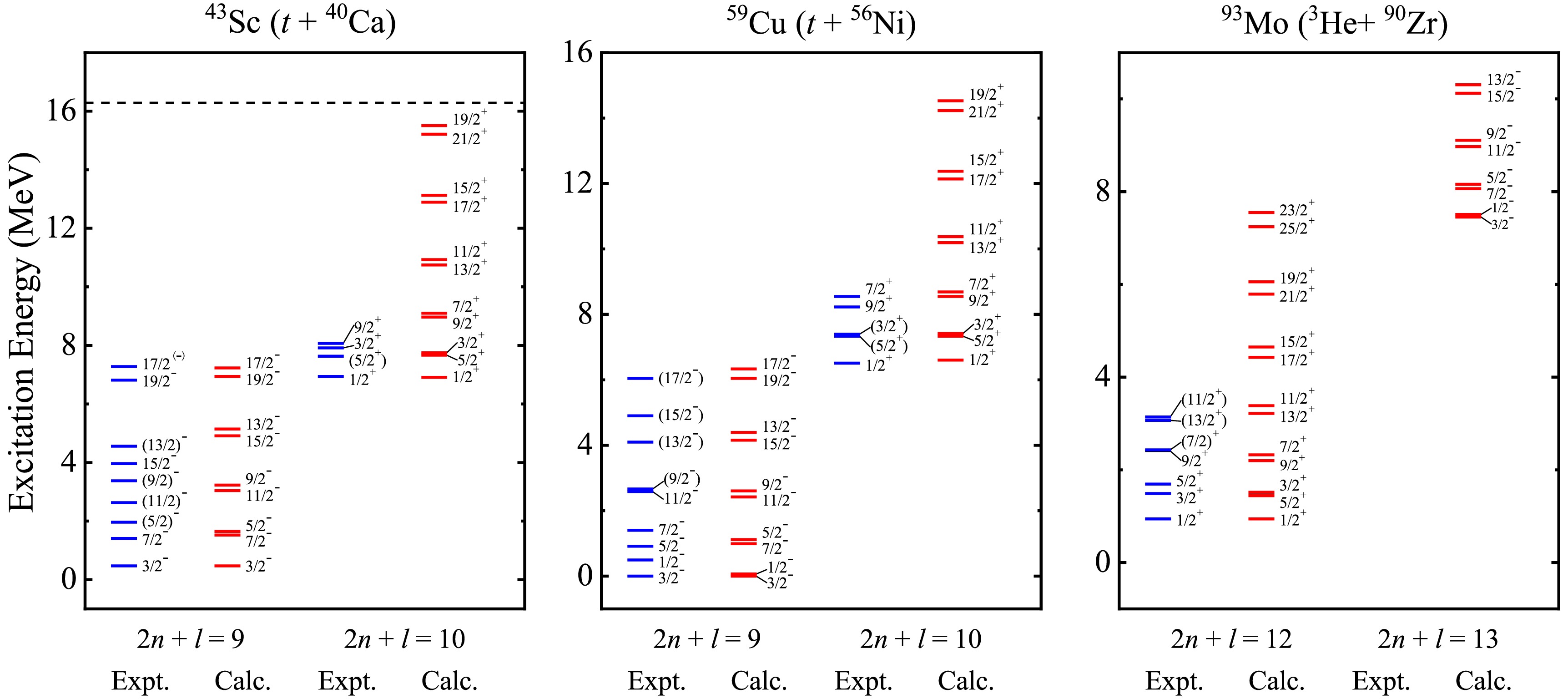
Figure 4. (color online) Same as Fig. 3 but for triton and 3He cluster states.
As with 19F and 21Ne, we have systematically investigated the electromagnetic quadrupole transitions with two different configurations for 43Sc, 59Cu, and 93Mo within the BCM. The calculated
$ B(E2) $ values are displayed in Table 3, where one can see an overall agreement of the results and experimental data despite the underestimation in the transitions of 7/2-$ \rightarrow $ 3/2- and 11/2-$ \rightarrow $ 7/2- in 43Sc (t + 40Ca). All the results verify that α clustering is a stable feature from light to heavier nuclei, including the odd-A nuclei. There might be fewer cluster structures of 3H and 3He in this region. Additionally, the existence of clustering phenomena in heavy nuclei is still an open question, which deserves further study within the coupled-channels formalism. We hope this study can provide new insights into nuclear structures.Nuclei(cluster) $ J^{\pi}_i(E^{\rm{expt.}}_i) $ 

$ J^{\pi}_f(E^{\rm{expt.}}_f) $ 

$ B(E2)_{{\rm{calc.}}} $ 

$ B(E2)_{{\rm{expt.}}} $ 

43Sc(α) 5/2+(0.881) 3/2+(0.152) 23.08 13.00 $ \pm $ 5.00

43Sc(α) 3/2+(1.159) 1/2+(0.856) 13.56 $< 180.00 $ 

43Sc(α) 3/2+(1.159) 5/2+(0.881) 34.80 $< 180.00 $ 

43Sc(α) 7/2+(1.338) 3/2+(0.152) 9.56 20.00 $ \pm $ 9.00

43Sc(α) 7/2+(1.338) 5/2+(0.881) 14.42 46.00 $ \pm $ 24.00

43Sc(α) 9/2+(1.933) 5/2+(0.881) 13.79 15.00 $ \pm $ 4.00

43Sc(α) 9/2+(1.933) 7/2+(1.338) 9.00 3.30 $ \pm $ 1.60

43Sc(α) 11/2+(2.554) 7/2+(1.338) 16.17 20.00 $ \pm $ 3.00

43Sc(t) 7/2-(1.408) 3/2-(0.473) 2.62 24.00 $ \pm $ 9.00

43Sc(t) 5/2-(1.963) 3/2-(0.473) 6.30 4.40 $ \pm $ 2.50

43Sc(t) 11/2-(2.635) 7/2-(1.408) 4.09 43.00 $ \pm $ 16.00

59Cu(t) 1/2-(0.492) 3/2-(0) 4.83 $< 300.00 $ 

59Cu(t) 5/2-(0.914) 3/2-(0) 0.66 $< 2.90 $ 

59Cu(t) 7/2-(1.399) 3/2-(0) 2.98 17.00 $ \pm $ 8.00

59Cu(t) 7/2-(1.399) 5/2-(0.914) 0.34 1.30 $ \pm $ 0.80

93Mo(α) 13/2+(2.162) 9/2+(1.477) 12.26 3.30 $ \pm $ 0.50

93Mo(α) 11/2+(2.247) 9/2+(1.477) 4.32 3.70 $ ^{+1.90}_{-2.10} $ 

93Mo(α) 17/2+(2.430) 13/2+(2.162) 12.95 4.48 $ \pm $ 0.23

-
As mentioned above, the nuclear properties of cluster states in 19F and 21Ne have been reported for three-nucleon and α transfer reactions in recent decades. Nevertheless, some experimental information around the A = 20 region, such as energy levels, electromagnetic transition rates, spins and parities, remains somewhat ambiguous owing to the intricate structures within the odd-A nuclei and limitations of experimental techniques. These spectroscopic properties are vital to the generation of heavy elements in astrophysical environments [20−32] and deepening the theoretical understanding of many-body physics, with particular relevance to the clustering phenomena in odd mass nuclei. Furthermore, the 17O + α reaction rates have great influence on the efficiency of the weak s process occurring in massive and asymptotic giant branch stars. The rates of the 17O(α, γ)21Ne and 17O(α, n)20Ne reactions [30−32] strongly depend on the energy levels of α-cluster states approaching the thresholds in 21Ne [20], which have attracted more attention in the region of interest for astrophysics.
Considering this, the energy spectra and reduced transition strengths of cluster states around 20Ne are initially calculated, serving as a test on the binary cluster-core model. The theoretical energy levels of α-cluster and three-nucleon structures for 19F and 21Ne compared with the observed data are shown in Figs. 1 and 2, where the dashed lines represent the cluster thresholds. The nuclear parameters for 19F (α + 15N) and 21Ne (α + 17O) in Eq. (3) are
$ V_0 $ = 235.00 MeV, a = 0.70 fm, b = 0.19, λ = 0.10, and σ = 0.20 fm, which are consistent with the findings in our previous work [8]. The values of b, λ, and σ remain constant in all cases to reduce the number of free parameters. According to the previous empirical systematics and constant reasonable attempts,$ V_0 $ = 190.00 MeV and a = 0.90 fm are applied to describe the three-nucleon cluster states in the following process, which are close to those of other studies [40, 47−49]. The key point is the inclusion of the spin-orbit coupling potential, which gives rise to the splitting of energy levels with the same orbital angular momentum l. With the bootstrap method [7, 8], the depths$ V_{\rm so} $ can then be separately fixed as 0.058, 0.005, and –0.018 MeV for t-cluster states in 19F and α-cluster and 3He-cluster states in 21Ne, respectively. As for the "α + 15N" configuration of 19F,$ V_{\rm so} $ = 0.003 MeV corresponds to the 2n + l = 8 band, and$ V_{\rm so} $ = –0.018 MeV corresponds to the 2n + l = 9 band. The complete parity doublet bands have been compared with Ref. [42], where the spin-orbit coupling effect was not introduced in the α-core structure for 19F. The energy spectra of cluster states for 19F and 21Ne have been well reproduced within the BCM, along with reasonable predictions for further levels without experimental counterparts. It is observed that the degree of energy level splitting, which is very sensitive to spin-orbit potential depth, rises with growth of the absolute value of$ V_{\rm so} $ . Moreover, the energy spacing coming from the same l is found to increase with increasing l in a certain energy band. The agreement of our results with experimental data proves that the BCM is equally reliable for describing the cluster states and possesses robust model predictive capability in light odd-A nuclei, thereby offering assistance in theoretical analysis of cluster phenomena and experimental design about the essential reactions of (α, n) and (α, γ) in the astrophysical s process. It is noted that the calculations of above two configurations are performed based on mutually orthogonal wave functions and two disjoint bases. In addition, the assignments of energy levels and electromagnetic transition strengths are related to Wildermuth condition, which contributes to different global quantum numbers G of different configurations in the same nucleus. Hence, there will be no conflicts in the assignment of energy levels and electromagnetic transitions in these two cluster states. The calculations here can be served as a preliminary attempt to explore the possible cluster states in odd-A nuclei with two configurations in the framework of BCM plus the spin-orbit coupling. In fact, there may exist some possible mixed states between triton and α-cluster, which deserve further investigations within the coupled-channels formalism in the future work.
Figure 1. (color online) Comparisons of the calculated parity doublet bands of 2n + l = 8 and 9 for α-cluster states in 19F (α + 15N) and 21Ne (α + 17O) with the experimental data [20, 42, 50], where the dashed lines dictate the α-cluster breakup thresholds. The intrinsic spins of 15N and 17O are 1/2- and 5/2+, respectively.
As is well known, analyzing the spectra is a direct way to study the spectroscopic properties of cluster states. The enhancement of reduced electromagnetic transition rates is an effective symbol of cluster states. Once the wave functions are generated by the above procedure, the
$ B(E1) $ and$ B(E2) $ transition probabilities between successive band members can then be obtained by Eqs. (6) and (9). For further examination of the BCM, a comparison of obtained reduced quadrupole transition strengths with available data and other related calculations for cluster states in 19F and 21Ne is presented in Table 1. The first column denotes the target nuclei with the clusters. The third and fourth columns indicate the theoretical$ B(E2) $ values and experimental data, respectively. For 19F, the$ B(E2)_{1} $ values in the fifth column are from the vibron-fermion model with SU(3)$ \times $ U(2) limit [56], i.e., the extension of the U(3) vibron model. The calculated results for$ B(E2)_{2} $ based on the GCM [57] with the "α + 15N" configuration are plotted in the last column. Obviously, the$ B(E2) $ values have been well reproduced within the BCM for both nuclei despite the overestimation for the transition 11/2-$ \rightarrow $ 7/2- in 19F (α + 15N), which is comparable with the$ B(E2)_1 $ and$ B(E2)_2 $ values. The present$ B(E2) $ values are in accordance with these two calculations, except for the 11/2+$ \rightarrow $ 7/2+ and 11/2+$ \rightarrow $ 13/2+ transitions for 19F in Ref. [57]. This implies that there are some mixed cluster states of triton and α-particle in the low-lying energy region, which presents difficulties in both experimental detection and theoretical research. The transition rates of 5/2+$ \rightarrow $ 1/2+ with 5.36 W.u., 3/2+$ \rightarrow $ 5/2+ with 2.40 W.u., and 9/2+$ \rightarrow $ 5/2+ with 6.21 W.u. in 19F are very close to the recent results of 6.45 W.u., 2.65 W.u., and 6.41 W.u. in Ref. [59], respectively, where the$ B(E2) $ values are determined using the USDB nuclear shell model interaction. The calculations of$ B(E2) $ values in this study for 21Ne agree with the$ B(E2)_{1} $ values in the fifth column of Table 1, which are obtained in the framework of CSM [58]. Additionally, reasonable predictions of$ B(E2) $ values for these two nuclei are displayed in Table 1, especially for α-cluster states approaching the thresholds in the region of astrophysical interest. These selected levels of negative-parity bands in 21Ne may belong to the α-cluster states due to large$ B(E2) $ strengths.Nuclei Transition $ B(E2)_{{\rm{calc.}}} $ 

$ B(E2)_{{\rm{expt.}}} $ 

$ B(E2)_{1} $ 

$ B(E2)_{2} $ 

19F(α) 5/2− $ \rightarrow $ 1/2−

19.53 21.60 $ \pm $ 0.40

20.00 18.10 19F(α) 3/2− $ \rightarrow $ 1/2−

19.69 21.89 18.00 19F(α) 3/2− $ \rightarrow $ 5/2−

8.54 7.50 19F(α) 7/2− $ \rightarrow $ 5/2−

2.68 3.13 2.20 19F(α) 7/2− $ \rightarrow $ 3/2−

24.30 25.71 21.00 19F(α) 9/2− $ \rightarrow $ 5/2−

26.36 28.00 $ \pm $ 6.00

22.51 23.70 19F(α) 9/2− $ \rightarrow $ 7/2−

1.66 1.30 19F(α) 13/2− $ \rightarrow $ 9/2−

23.56 19.00 $ \pm $ 2.00

19F(α) 11/2− $ \rightarrow $ 7/2−

23.80 8.10 $ \pm $ 2.00

23.88 18.80 19F(α) 11/2− $ \rightarrow $ 9/2−

0.91 1.28 0.60 19F(α) 11/2− $ \rightarrow $ 13/2−

0.84 19F(t) 5/2+ $ \rightarrow $ 1/2+

5.36 6.95 $ \pm $ 0.08

6.95 6.20 19F(t) 3/2+ $ \rightarrow $ 1/2+

5.77 6.95 8.00 19F(t) 3/2+ $ \rightarrow $ 5/2+

2.40 3.10 2.80 19F(t) 9/2+ $ \rightarrow $ 5/2+

6.21 8.20 $ \pm $ 0.90

8.09 5.80 19F(t) 13/2+ $ \rightarrow $ 9/2+

3.93 3.20 $ \pm $ 0.40

5.27 2.90 19F(t) 7/2+ $ \rightarrow $ 5/2+

0.72 0.81 0.90 19F(t) 7/2+ $ \rightarrow $ 3/2+

6.70 7.28 12.80 19F(t) 7/2+ $ \rightarrow $ 9/2+

0.55 0.78 0.50 19F(t) 11/2+ $ \rightarrow $ 9/2+

0.20 0.50 19F(t) 11/2+ $ \rightarrow $ 13/2+

0.21 0.07 19F(t) 11/2+ $ \rightarrow $ 7/2+

4.91 22.8 21Ne(α) 7/2+ $ \rightarrow $ 5/2+

$ ^{\rm{a}} $ 

14.62 11.00 $ \pm $ 4.00

21Ne(α) 1/2+ $ \rightarrow $ 5/2+

$ ^{ \rm a} $ 

42.22 21Ne(α) 11/2+ $ ^{\rm{c}} $ 

$ \rightarrow $ 7/2+

$ ^{\rm{a}} $ 

15.75 21Ne(α) 5/2+ $ ^{\rm{b}} $ 

$ \rightarrow $ 5/2+

$ ^{\rm{a}} $ 

0.69 21Ne(α) 5/2+ $ ^{\rm{b}} $ 

$ \rightarrow $ 7/2+

18.90 21Ne(α) 5/2+ $ ^{\rm{b}} $ 

$ \rightarrow $ 1/2+

13.50 21Ne(α) 3/2+ $ \rightarrow $ 5/2+

$ ^{\rm{a}} $ 

0.08 21Ne(α) 3/2+ $ \rightarrow $ 7/2+

19.12 21Ne(α) 3/2+ $ \rightarrow $ 1/2+

13.68 21Ne(α) 3/2+ $ \rightarrow $ 5/2+

$ ^{\rm{b}} $ 

36.16 21Ne(α) 13/2+ $ \rightarrow $ 11/2+

$ ^{\rm{c}} $ 

3.53 21Ne(α) 3/2− $ ^{\rm{d}} $ 

$ \rightarrow $ 7/2−

49.31 21Ne(α) 11/2− $ \rightarrow $ 7/2−

41.01 21Ne(α) 5/2− $ \rightarrow $ 7/2−

52.52 21Ne(α) 5/2− $ \rightarrow $ 3/2−

$ ^{\rm{d}} $ 

68.43 21Ne(α) 9/2− $ \rightarrow $ 7/2−

23.83 21Ne(α) 9/2− $ \rightarrow $ 11/2−

20.27 21Ne(α) 9/2− $ \rightarrow $ 5/2−

43.41 21Ne(3He) 5/2+ $ \rightarrow $ 3/2+

20.58 24.30 $ \pm $ 2.00

24.16 21Ne(3He) 7/2+ $ \rightarrow $ 3/2+

7.04 9.30 $ \pm $ 0.80

10.08 21Ne(3He) 7/2+ $ \rightarrow $ 5/2+

10.54 11.00 $ \pm $ 4.00

15.10 21Ne(3He) 9/2+ $ \rightarrow $ 5/2+

10.90 15.70 $ \pm $ 2.20

15.10 21Ne(3He) 9/2+ $ \rightarrow $ 7/2+

7.94 9.00 $ \pm $ 5.00

9.87 21Ne(3He) 11/2+ $ \rightarrow $ 7/2+

7.50 17.94 21Ne(3He) 11/2+ $ \rightarrow $ 9/2+

2.85 6.00 $ \pm $ 4.00

6.91 21Ne(3He) 13/2+ $ \rightarrow $ 9/2+

8.57 19.72 21Ne(3He) 13/2+ $ \rightarrow $ 11/2+

3.69 5.05 $ ^{\rm{a}} $ 

$ E(5/2^{+}) $ = 0.351 MeV.

$ ^{\rm{b}} $ 

$ E(5/2^{+}) $ = 4.526 MeV.

$ ^{\rm{c}} $ 

$ E(11/2^{+}) $ = 4.433 MeV.

$ ^{\rm{d}} $ 

$ E(3/2^{-}) $ = 7.465 MeV.

Table 1. Comparison of the theoretical
$ B(E2) $ values with the experimental data [50−52] and other associated studies for 19F and 21Ne. The comparative theoretical results of the$ B(E2)_1 $ and$ B(E2)_2 $ values in 19F are from Ref. [56] and Ref. [57], respectively, where the$ B(E2)_{1} $ values are based on the SU(3)$ \times $ U(2) limit of the vibron-fermion model, and the$ B(E2)_{2} $ values are obtained within the generator coordinate method (GCM). The comparative results of$ B(E2)_{1} $ values for 21Ne are based on the cluster shell model (CSM) [58]. All the quadrupole transition probabilities presented here are in Weisskopf units (W.u.).The electromagnetic dipole transitions are often considered as another important indicator of cluster states. In past decades, some interesting events of enhanced
$ B(E1) $ values [60−64] have been observed from light to heavy nuclei, attracting widespread attention in nuclear physics. In this study, the$ E1 $ transitions occur in 19F from the G = 9 to G = 8 band of α-cluster states and from the negative- to positive-parity levels of t-cluster states. Table 2 shows the$ B(E1) $ values for 19F in comparison with measured quantities and the aforementioned calculations. General agreement with experimental data is obtained for the "α + 15N" configuration, except for the transition 5/2+$ \rightarrow $ 3/2-, which is close to the theoretical$ B(E1)_1 $ and$ B(E1)_2 $ values. Nonetheless, the strong dipole transition probabilities of triton states are given within the BCM at approximately two orders of magnitude larger than the available data. As Ref. [42] discussed, the relatively large difference between the two configurations comes from the recoil terms of Eqs. (7) and (10), giving rise to larger$ B(E1) $ rates for triton states by a factor of 16 than the case of α-core structure. Meanwhile, these states may have impure cluster structures, namely, the mixing states between α and t cluster levels or between cluster and non-cluster states, leading to uncertainties in the measurements. Such an enhancement of$ B(E1) $ values of t-cluster states in the 19F we calculated has not yet been experimentally observed. Similarly, the reproduction of$ E1 $ transitions by other models is generally unsatisfactory [42, 56, 57], e.g., the relatively small results in the calculations with the algebraic approach [56]. A consistent investigation of this problem in odd mass nuclei relies on additional experimental data, which is hoped to be useful for the ongoing or forthcoming experiments on the nuclear structures.Nuclei Transition $ B(E1)_{{\rm{calc.}}} $ 

$ B(E1)_{{\rm{expt.}}} $ 

$ B(E1)_{1} $ 

$ B(E1)_{2} $ 

19F(α) 3/2+ $ \rightarrow $ 1/2−

18.20 7.00 4.83 11.20 19F(α) 3/2+ $ \rightarrow $ 5/2−

31.10 9.80 5.06 8.70 19F(α) 3/2+ $ \rightarrow $ 3/2−

3.56 2.00 19F(α) 5/2+ $ \rightarrow $ 5/2−

0.86 2.10 $ \pm $ 0.50

0.24 1.20 19F(α) 5/2+ $ \rightarrow $ 3/2−

12.62 1.20 $ \pm $ 0.40

5.80 16.80 19F(α) 5/2+ $ \rightarrow $ 7/2−

18.06 19F(α) 7/2+ $ \rightarrow $ 5/2−

16.94 19F(α) 7/2+ $ \rightarrow $ 7/2−

0.60 19F(α) 7/2+ $ \rightarrow $ 9/2−

19.24 19F(t) 1/2− $ \rightarrow $ 1/2+

269.90 19F(t) 1/2− $ \rightarrow $ 3/2+

43.83 19F(t) 3/2− $ \rightarrow $ 1/2+

302.24 5.10 $ \pm $ 1.40

19F(t) 3/2− $ \rightarrow $ 5/2+

448.23 3.2 $ \pm $ 1.00

19F(t) 3/2− $ \rightarrow $ 3/2+

49.80 19F(t) 5/2− $ \rightarrow $ 5/2+

26.52 19F(t) 5/2− $ \rightarrow $ 3/2+

371.31 19F(t) 5/2− $ \rightarrow $ 7/2+

257.23 19F(t) 7/2− $ \rightarrow $ 5/2+

462.97 12.00 $ \pm $ 2.00

0.03 5.20 19F(t) 7/2− $ \rightarrow $ 9/2+

316.95 1.7 $ \pm $ 0.50

0.002 4.00 19F(t) 7/2− $ \rightarrow $ 7/2+

9.06 0.08 19F(t) 11/2− $ \rightarrow $ 9/2+

510.58 3.90 $ \pm $ 1.20

19F(t) 11/2− $ \rightarrow $ 13/2+

133.48 0.33 $ \pm $ 0.16

In fact, the excited states of atomic nuclei, especially in light even-even nuclei, are strongly characterized by α clustering, contributing to various α-cluster configurations as the excitation energy increases. For heavier nuclei, the picture of clusters becomes unclear, resulting from the complex interactions among nucleons, not to mention the interplay with nucleon degree. Meanwhile, the symmetry breaking [65] from the spin-orbit force and mean-field effect would be stronger, suppressing the α-like correlations in this region. Therefore, it is of great significance to extend the α-cluster concept to heavier nuclei. Inspired by the successful application of cluster-core structures around 20Ne, the BCM is generalized to heavier nuclei approaching the shell closures, such as 43Sc, 59Cu, and 93Mo, which can provide a good testing ground to confirm the persistence of cluster states. The obtained energy spectra for nuclei 43Sc, 59Cu, and 93Mo with α and three-nucleon clusters are compared with the suggested experimental counterparts in Figs. 3 and 4, respectively. To ensure the applicability of BCM within the same parameterization, the nuclear parameters in Eq. (3) are the same as before, and the spin-orbit parameter
$ V_{\rm so} $ = 0.003 MeV, consistent with the case of the negative-parity band in 19F (α + 15N), is employed in both configurations of these three nuclei. Satisfactory theoretical parity doublet bands and predictions have been obtained in the framework of BCM, as shown in the Figs. 3 and 4, suggesting that the available levels correspond to possible cluster states in heavier nuclei with odd mass. It should be noted that 93Mo exhibits rich information of energy levels below 5 MeV, but no corresponding energy levels have been observed in the region from 5 to 10 MeV [55]. This reflects the theoretical prediction of the$ 2n + l $ = 13 band for 3He-cluster states awaiting additional experimental confirmation. Meanwhile, the energy bands of α-cluster states are more intricate than those of other configurations on account of the inclusion of the spin-orbit coupling effect. For example, the number of energy levels coming from one certain orbital angular momentum l is 2 for the 3He-cluster states in 93Mo, while the maximum number could even reach 10 for the α-cluster states. This seems to indicate that the α cluster tends to form more easily than other clusters within nuclei and plays a dominant role in the mixed states.
Figure 3. (color online) Comparisons of the calculated doublet parity bands with available candidates [50] for α-cluster states in heavier nuclei, where the dashed lines denote the α-cluster thresholds. The intrinsic spins of 39K, 55Co, and 89Zr are 3/2+, 7/2-, and 9/2-, respectively.

Figure 4. (color online) Same as Fig. 3 but for triton and 3He cluster states.
As with 19F and 21Ne, we have systematically investigated the electromagnetic quadrupole transitions with two different configurations for 43Sc, 59Cu, and 93Mo within the BCM. The calculated
$ B(E2) $ values are displayed in Table 3, where one can see an overall agreement of the results and experimental data despite the underestimation in the transitions of 7/2-$ \rightarrow $ 3/2- and 11/2-$ \rightarrow $ 7/2- in 43Sc (t + 40Ca). All the results verify that α clustering is a stable feature from light to heavier nuclei, including the odd-A nuclei. There might be fewer cluster structures of 3H and 3He in this region. Additionally, the existence of clustering phenomena in heavy nuclei is still an open question, which deserves further study within the coupled-channels formalism. We hope this study can provide new insights into nuclear structures.Nuclei(cluster) $ J^{\pi}_i(E^{\rm{expt.}}_i) $ 

$ J^{\pi}_f(E^{\rm{expt.}}_f) $ 

$ B(E2)_{{\rm{calc.}}} $ 

$ B(E2)_{{\rm{expt.}}} $ 

43Sc(α) 5/2+(0.881) 3/2+(0.152) 23.08 13.00 $ \pm $ 5.00

43Sc(α) 3/2+(1.159) 1/2+(0.856) 13.56 $< 180.00 $ 

43Sc(α) 3/2+(1.159) 5/2+(0.881) 34.80 $< 180.00 $ 

43Sc(α) 7/2+(1.338) 3/2+(0.152) 9.56 20.00 $ \pm $ 9.00

43Sc(α) 7/2+(1.338) 5/2+(0.881) 14.42 46.00 $ \pm $ 24.00

43Sc(α) 9/2+(1.933) 5/2+(0.881) 13.79 15.00 $ \pm $ 4.00

43Sc(α) 9/2+(1.933) 7/2+(1.338) 9.00 3.30 $ \pm $ 1.60

43Sc(α) 11/2+(2.554) 7/2+(1.338) 16.17 20.00 $ \pm $ 3.00

43Sc(t) 7/2-(1.408) 3/2-(0.473) 2.62 24.00 $ \pm $ 9.00

43Sc(t) 5/2-(1.963) 3/2-(0.473) 6.30 4.40 $ \pm $ 2.50

43Sc(t) 11/2-(2.635) 7/2-(1.408) 4.09 43.00 $ \pm $ 16.00

59Cu(t) 1/2-(0.492) 3/2-(0) 4.83 $< 300.00 $ 

59Cu(t) 5/2-(0.914) 3/2-(0) 0.66 $< 2.90 $ 

59Cu(t) 7/2-(1.399) 3/2-(0) 2.98 17.00 $ \pm $ 8.00

59Cu(t) 7/2-(1.399) 5/2-(0.914) 0.34 1.30 $ \pm $ 0.80

93Mo(α) 13/2+(2.162) 9/2+(1.477) 12.26 3.30 $ \pm $ 0.50

93Mo(α) 11/2+(2.247) 9/2+(1.477) 4.32 3.70 $ ^{+1.90}_{-2.10} $ 

93Mo(α) 17/2+(2.430) 13/2+(2.162) 12.95 4.48 $ \pm $ 0.23

-
In summary, the investigations of parity doublet bands and electromagnetic transition properties have been extended to the odd mass region around 20Ne within the binary cluster-core model plus the extra nuclear spin-orbit potential. These nuclear properties approaching α thresholds are crucial inputs for the origins of heavy elements from the s process in massive stars. The good agreement of our results for cluster states based on the "α + core" and "t or 3He + core" configurations (except for the
$ B(E1) $ values of t-cluster states) with available data and other calculations for 19F and 21Ne from the GCM, phenomenological algebraic model, and CSM demonstrates the reliability and model predictive capacity of BCM. Moreover, the better theoretical$ B(E1) $ values of α-cluster states reveal that the α-cluster ingredients occupy a prominent position in the mixed states constituted with t or 3He clusters. Encouraged by this, the present physical picture is applied to describe the cluster states for 43Sc, 59Cu, and 93Mo. The calculated energy spectra and$ B(E2) $ values are found to be consistent with measured data, implying the persistence of cluster states in heavier odd-A nuclei and the reasonableness of the present framework. It is expected to be helpful to comprehend the role that cluster degrees of freedom play in the structural knowledge of odd mass nuclei. -
In summary, the investigations of parity doublet bands and electromagnetic transition properties have been extended to the odd mass region around 20Ne within the binary cluster-core model plus the extra nuclear spin-orbit potential. These nuclear properties approaching α thresholds are crucial inputs for the origins of heavy elements from the s process in massive stars. The good agreement of our results for cluster states based on the "α + core" and "t or 3He + core" configurations (except for the
$ B(E1) $ values of t-cluster states) with available data and other calculations for 19F and 21Ne from the GCM, phenomenological algebraic model, and CSM demonstrates the reliability and model predictive capacity of BCM. Moreover, the better theoretical$ B(E1) $ values of α-cluster states reveal that the α-cluster ingredients occupy a prominent position in the mixed states constituted with t or 3He clusters. Encouraged by this, the present physical picture is applied to describe the cluster states for 43Sc, 59Cu, and 93Mo. The calculated energy spectra and$ B(E2) $ values are found to be consistent with measured data, implying the persistence of cluster states in heavier odd-A nuclei and the reasonableness of the present framework. It is expected to be helpful to comprehend the role that cluster degrees of freedom play in the structural knowledge of odd mass nuclei.
Investigation of cluster states around 20Ne including spin-orbit coupling and its extension to heavier nuclei
- Received Date: 2025-05-03
- Available Online: 2025-12-15
Abstract: Clustering, as a fundamental dynamical feature existing widely in many-body systems, has aroused tremendous interest in nuclear physics over the last few decades. The α-cluster concept has been used successfully to describe the energy spectra and electromagnetic transitions for a series of nuclei above the doubly magic core. In the present study, we have systematically investigated the spectroscopic properties of three-nucleon and α-cluster states in 19F and 21Ne within the binary cluster-core model (BCM) plus the extra spin-orbit potential. The calculated energy levels and electromagnetic transition strengths, with few exceptions, are in good agreement with experimental data, confirming the reliability and integrity of BCM. Furthermore, such a BCM is extended to the case of cluster states approaching shell closures in heavier nuclei, such as 43Sc, 59Cu, and 93Mo, leading to satisfactory reproductions and predictions on energy levels and reduced transition rates. It is expected that the present study can provide further insight into the cluster degrees of freedom in odd-A nuclei.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: