-
The study of strong gravitational lensing provides a profound window into the nature of spacetime and the properties of black holes. This phenomenon, predicted by Einstein's theory of general relativity [1, 2], occurs when light from a distant source is bent by the gravitational field of a massive object, such as a black hole, thus resulting in multiple images or highly magnified and distorted images of the source [3]. Strong gravitational lensing not only offers insights into the structure and dynamics of black holes but also serves as a powerful tool for probing fundamental physics under extreme conditions [4].
In recent years, the Event Horizon Telescope (EHT) has revolutionized our understanding of black holes by capturing the images of the shadows of supermassive black holes at the center of the galaxy
$ \mathrm{M}87^* $ [5, 6] and at the center of the Milky Way [7, 8]. These unprecedented observations provide a unique opportunity to test various black hole models and theories of gravity [9]. Previous research has investigated the lensing properties of black holes in various modified gravity frameworks [10−14]. However, the gravitational lensing effects of black holes described by non-linear electrodynamics, such as the Dyonic ModMax model, remain underexplored.Recent studies have explored gravitational lensing in non-linear electrodynamics, including the Dyonic ModMax model, placing focus on weak lensing, plasma effects, and black hole shadows [15−20]. However, strong lensing and the interplay of dual charges with rotation remain underexplored [21, 22]. The Dyonic ModMax model’s duality and conformal invariance offer unique lensing signatures [23, 24]. This study investigates strong lensing in Dyonic ModMax black holes and proposes novel observational tests to constrain model parameters using future telescope data [16, 17], thereby addressing primary and relativistic images in the strong gravitational field regime.
The Dyonic ModMax black hole model extends the conventional Maxwell theory by incorporating a modification through nonlinear electrodynamics, which leads to distinct spacetime features that are absent in other modified gravity models [25]. Among the intriguing models that have emerged is the Dyonic ModMax black hole, which incorporates modifications to Maxwell's electrodynamics that lead to novel predictions about the behavior of light and matter in the vicinity of the black hole [26−28].
This article presents a theoretical investigation of strong gravitational lensing around Dyonic ModMax black holes. We aim to place constraints on the parameters of the Dyonic ModMax black hole model by analyzing and comparing the lensing effects with EHT observations. We begin by reviewing the key aspects of gravitational lensing theory [29] and the Dyonic ModMax black hole solution [30−32]. Subsequently, we derive the lensing observables, such as the angular position and magnification of the lensed images, and examine how these are influenced by the unique features of the Dyonic ModMax black hole.
Our study is motivated by the need to explore alternative gravity theories and to understand how deviations from classical general relativity manifest in observational phenomena [33−41]. The Dyonic ModMax black hole serves as a test case for these explorations by providing insights that could extend to other modified gravity theories. By comparing our theoretical predictions with the empirical data from the EHT [42−51], we aim to identify distinctive signatures of the Dyonic ModMax black hole and determine the feasibility of this model in explaining the observed characteristics of black hole shadows and lensing patterns.
The results of this investigation will not only shed light on the viability of the Dyonic ModMax black hole model but also contribute to the broader effort to test the limits of general relativity and explore new physics in the strong gravity regime [38, 52−55]. Through this theoretical and observational synergy, we seek to deepen our understanding of black holes and the fundamental laws governing our universe [56−58].
In this paper, we estimate the deflection angle of the light rays and the time delay of the signals from two relativitic images. We show that time delays between relativistic images are indeed measurable in most supermassive black holes cases. Moreover, we learn that in a first approximation, the time delay between consecutive relativistic images is proportional to the minimum impact angle. The ratio between these two observables is merely the distance of the lens, which can be estimated following precise guidelines and without bias. This paper is structured as follows: in Sect. II, we briefly explain the Dyonic ModMax black hole solution and obtain horizon properties. In Sect. III, we provide the main results of the gravitational lensing in the case of strong field regime. In Sect. IV, we derive a general expression for the time delay as well as consider the Dyonic ModMax spacetime case and calculate the time delay for supermassive black holes at the center of several galaxies such as Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA). Finally, Sect. V concludes the paper.
-
The study of strong gravitational lensing provides a profound window into the nature of spacetime and the properties of black holes. This phenomenon, predicted by Einstein's theory of general relativity [1, 2], occurs when light from a distant source is bent by the gravitational field of a massive object, such as a black hole, thus resulting in multiple images or highly magnified and distorted images of the source [3]. Strong gravitational lensing not only offers insights into the structure and dynamics of black holes but also serves as a powerful tool for probing fundamental physics under extreme conditions [4].
In recent years, the Event Horizon Telescope (EHT) has revolutionized our understanding of black holes by capturing the images of the shadows of supermassive black holes at the center of the galaxy
$ \mathrm{M}87^* $ [5, 6] and at the center of the Milky Way [7, 8]. These unprecedented observations provide a unique opportunity to test various black hole models and theories of gravity [9]. Previous research has investigated the lensing properties of black holes in various modified gravity frameworks [10−14]. However, the gravitational lensing effects of black holes described by non-linear electrodynamics, such as the Dyonic ModMax model, remain underexplored.Recent studies have explored gravitational lensing in non-linear electrodynamics, including the Dyonic ModMax model, placing focus on weak lensing, plasma effects, and black hole shadows [15−20]. However, strong lensing and the interplay of dual charges with rotation remain underexplored [21, 22]. The Dyonic ModMax model’s duality and conformal invariance offer unique lensing signatures [23, 24]. This study investigates strong lensing in Dyonic ModMax black holes and proposes novel observational tests to constrain model parameters using future telescope data [16, 17], thereby addressing primary and relativistic images in the strong gravitational field regime.
The Dyonic ModMax black hole model extends the conventional Maxwell theory by incorporating a modification through nonlinear electrodynamics, which leads to distinct spacetime features that are absent in other modified gravity models [25]. Among the intriguing models that have emerged is the Dyonic ModMax black hole, which incorporates modifications to Maxwell's electrodynamics that lead to novel predictions about the behavior of light and matter in the vicinity of the black hole [26−28].
This article presents a theoretical investigation of strong gravitational lensing around Dyonic ModMax black holes. We aim to place constraints on the parameters of the Dyonic ModMax black hole model by analyzing and comparing the lensing effects with EHT observations. We begin by reviewing the key aspects of gravitational lensing theory [29] and the Dyonic ModMax black hole solution [30−32]. Subsequently, we derive the lensing observables, such as the angular position and magnification of the lensed images, and examine how these are influenced by the unique features of the Dyonic ModMax black hole.
Our study is motivated by the need to explore alternative gravity theories and to understand how deviations from classical general relativity manifest in observational phenomena [33−41]. The Dyonic ModMax black hole serves as a test case for these explorations by providing insights that could extend to other modified gravity theories. By comparing our theoretical predictions with the empirical data from the EHT [42−51], we aim to identify distinctive signatures of the Dyonic ModMax black hole and determine the feasibility of this model in explaining the observed characteristics of black hole shadows and lensing patterns.
The results of this investigation will not only shed light on the viability of the Dyonic ModMax black hole model but also contribute to the broader effort to test the limits of general relativity and explore new physics in the strong gravity regime [38, 52−55]. Through this theoretical and observational synergy, we seek to deepen our understanding of black holes and the fundamental laws governing our universe [56−58].
In this paper, we estimate the deflection angle of the light rays and the time delay of the signals from two relativitic images. We show that time delays between relativistic images are indeed measurable in most supermassive black holes cases. Moreover, we learn that in a first approximation, the time delay between consecutive relativistic images is proportional to the minimum impact angle. The ratio between these two observables is merely the distance of the lens, which can be estimated following precise guidelines and without bias. This paper is structured as follows: in Sect. II, we briefly explain the Dyonic ModMax black hole solution and obtain horizon properties. In Sect. III, we provide the main results of the gravitational lensing in the case of strong field regime. In Sect. IV, we derive a general expression for the time delay as well as consider the Dyonic ModMax spacetime case and calculate the time delay for supermassive black holes at the center of several galaxies such as Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA). Finally, Sect. V concludes the paper.
-
Dyonic ModMax black hole space-time singularities have been extensively studied in GR with NED [17, 28, 59−61]. However, here we focus on a new black hole solution in GR with NED using an exotic field referred to as the Dyonic ModMax field. The action can be written as
$ S=\int_{ }^{ }\sqrt{-g}\Bigg[\frac{1}{8\pi\kappa}R+L(x,y)\Bigg]\mathrm{d}^4x, $

(1) where
$ L(x,y)=x\mathrm{cos}\mathrm{h}\gamma+\sqrt{x^2+y^2}\mathrm{sinh}\gamma , \quad\quad\rm{where}\, $

(2) $ x = \frac{1}{4}F_{\mu\nu}F^{\mu\nu} \quad\quad {\rm and}\quad\quad y = \frac{1}{4}F_{\mu\nu}\tilde{F}^{\mu\nu} $

(3) are the electromagnetic Lorentz invariants in terms of the electromagnetic tensor
$ F_{\mu\nu} $ and its dual$ \tilde F_{\mu\nu} : = \frac 12 \epsilon_{\mu\nu\sigma\rho} F^{\sigma\rho} $ . From the ModMax Lagrangian, the Plebański dual variable reads [30, 62]$ \begin{aligned}[b] P_{\mu\nu} : =\;& -L_x F_{\mu\nu} - L_y \tilde F_{\mu\nu} = \left[ \cosh \gamma - \frac x{(x^2 + y^2)^{1/2}} \sinh \gamma \right] F_{\mu\nu} -\\&\frac {y \sinh \gamma}{(x^2 + y^2)^{1/2}} \tilde F_{\mu\nu}. \end{aligned} $

Its dual is
$ \tilde P_{\mu\nu} = \left[ \cosh \gamma - \frac x{(x^2 + y^2)^{1/2}} \sinh \gamma \right] \tilde F_{\mu\nu} +\frac {y \sinh \gamma}{(x^2 + y^2)^{1/2}} F_{\mu\nu}. $

The modified Maxwell field equation is given by
$ \nabla_\mu P^{\mu \nu} = 0. $

(4) Additionally, the Einstein equations can be expressed as
$ R^\mu _ \nu - \frac{1}{2} \delta^\mu _\nu R + \Lambda \delta^\mu _\nu = 8 \pi T ^\mu _ \nu . $

(5) Here, the energy momentum tensor
$ T^\mu_\nu $ is given by [30]$ \begin{aligned} 8 \pi T ^\mu _ \nu = - F^{\mu \beta} P _{\beta \nu } + \delta^\mu _\nu L = F^{\mu \beta}(L_x F_{\beta \nu }+ L_y \tilde{F}_{\beta \nu} ) + \delta^\mu _\nu L \end{aligned}. $

(6) To solve the Einstein equation, we choose following anzats:
$ \mathrm{d}s^2 = -f(r) \mathrm{d} t^2+f(r)^{-1} \mathrm{d} r^2+r^2(\mathrm{d} \theta^2 +\sin^2 \theta \mathrm{d}\phi^2 ) . $

(7) In this paper, we consider only asymptotically flat configurations; therefore, we choose
$ \Lambda = 0 $ in Eq. (5). First we take$ A_\mu = (\Phi(r), 0, 0, Q_m \cos \theta) $ to consider the dyonic solution. In this case, we get$ F_{\mu \nu} = - \Phi_{I , r} \delta^0 _{[ \mu} \delta^1 _{ \nu ]} - Q_m \sin \theta \delta^2 _{[ \mu} \delta^3 _{ \nu ]}. $

(8) Therefore,
$ \begin{aligned}[b] x = \; &\frac{1}{2}\left(- \Phi^2_{, r} + \frac{Q^2 _m}{r^4}\right), \ y = -\frac{\Phi_{, r} Q_m}{r^2}, \\& (x^2 + y^2)^{1/2} = \frac{1}{2}\left(- \Phi^2_{, r} + \frac{Q^2 _m}{r^4}\right), \end{aligned} $

(9) and it is straightforward to show that the only non-vanishing Pleban'ski variables are
$ \begin{aligned}[b] P_{01} =\;& - (\cosh{\gamma} + \sinh{\gamma}) \Phi_{,r} = -\mathrm{e}^\gamma \Phi{,r} , \\P_{23} =\;& - (\cosh{\gamma} - \sinh{\gamma}) Q_m \sin{\theta} = - \mathrm{e}^{- \gamma}Q_m \sin {\theta} . \end{aligned} $

(10) We can express the electric potential as
$ \Phi(r) = \frac{Q_e\cdot \mathrm{e}^{-\gamma}}{r}. $

(11) This condition sets a conservation low for
$ P_{01} $ . In this case, the gravitational field equations read$ \begin{aligned}[b] - \frac{m_{, r}}{r^2} =\; &- \frac{(Q^2 _e + Q^2 _m)\cdot \mathrm{e}^{- \gamma}}{2 r^4}, \\ - \frac{m_{, rr}}{2 r} = \; &\frac{(Q^2 _e + Q^2 _m)\cdot \mathrm{e}^{- \gamma}}{2 r^4} , \end{aligned}$

(12) and the solution of this system of equations is
$ m(r) = M - \frac{(Q^2 _e + Q^2 _m)\cdot \mathrm{e}^{- \gamma}}{2 r}. $

(13) Finally, we can find the lapse function of the metric Eq.(7):
$ f(r) = 1-\frac{2 M}{r}+\frac{(Q_\mathrm{e}^2 + Q_m^2)\cdot \mathrm{e}^{-\gamma}}{r^2} , $

(14) where
$ Q_e $ and$ Q_m $ are the electric and magnetic charge of the black hole, respectively, and γ is related to a constant screening factor for the charge of the black hole, which corresponds to the nonlinear parameter [32]. If we choose$ \gamma = 0 $ , Maxwell's theory is recovered. Additionally, by choosing$ Q_e = Q_m = 0 $ the Schwarzschild case is easily obtained. To analyze the horizon properties of such a black hole, we set$ f(r) = 0 $ . Under this condition, the event horizon can be determined using the following expression:$ r_h = M \pm \sqrt{\left(M^{2} - (Q_{e}^{2} + Q_{m}^{2}\right)\cdot \mathrm{e}^{-\gamma}}. $

(15) This paper examines only the motion of a photon, which is a neutral, massless particle. Thus, we can define Q as
$ Q_\mathrm{e}^2 + Q_m^2 = Q^2 $ . We can obtain the maximum value of black hole charge using Eq. (15) as follows:$ 0 < Q < M\cdot \mathrm{e}^{-\gamma/2}. $

(16) Eq. (15) thus clearly indicates that the Q and γ parameters negatively affect the horizon radius, and Eq. (16) provides the boundary values for charge Q in terms of M and γ.
-
Dyonic ModMax black hole space-time singularities have been extensively studied in GR with NED [17, 28, 59−61]. However, here we focus on a new black hole solution in GR with NED using an exotic field referred to as the Dyonic ModMax field. The action can be written as
$ S=\int_{ }^{ }\sqrt{-g}\Bigg[\frac{1}{8\pi\kappa}R+L(x,y)\Bigg]\mathrm{d}^4x, $

(1) where
$ L(x,y)=x\mathrm{cos}\mathrm{h}\gamma+\sqrt{x^2+y^2}\mathrm{sinh}\gamma , \quad\quad\rm{where}\, $

(2) $ x = \frac{1}{4}F_{\mu\nu}F^{\mu\nu} \quad\quad \rm{and}\quad\quad y = \frac{1}{4}F_{\mu\nu}\tilde{F}^{\mu\nu} $

(3) are the electromagnetic Lorentz invariants in terms of the electromagnetic tensor
$ F_{\mu\nu} $ and its dual$ \tilde F_{\mu\nu} : = \frac 12 \epsilon_{\mu\nu\sigma\rho} F^{\sigma\rho} $ . From the ModMax Lagrangian, the Plebański dual variable reads [30, 62]$ \begin{aligned}[b] P_{\mu\nu} : =\;& -L_x F_{\mu\nu} - L_y \tilde F_{\mu\nu} = \left[ \cosh \gamma - \frac x{(x^2 + y^2)^{1/2}} \sinh \gamma \right] F_{\mu\nu} -\\&\frac {y \sinh \gamma}{(x^2 + y^2)^{1/2}} \tilde F_{\mu\nu}. \end{aligned} $

Its dual is
$ \tilde P_{\mu\nu} = \left[ \cosh \gamma - \frac x{(x^2 + y^2)^{1/2}} \sinh \gamma \right] \tilde F_{\mu\nu} +\frac {y \sinh \gamma}{(x^2 + y^2)^{1/2}} F_{\mu\nu}. $

The modified Maxwell field equation is given by
$ \nabla_\mu P^{\mu \nu} = 0. $

(4) Additionally, the Einstein equations can be expressed as
$ R^\mu _ \nu - \frac{1}{2} \delta^\mu _\nu R + \Lambda \delta^\mu _\nu = 8 \pi T ^\mu _ \nu . $

(5) Here, the energy momentum tensor
$ T^\mu_\nu $ is given by [30]$ \begin{aligned} 8 \pi T ^\mu _ \nu = - F^{\mu \beta} P _{\beta \nu } + \delta^\mu _\nu L = F^{\mu \beta}(L_x F_{\beta \nu }+ L_y \tilde{F}_{\beta \nu} ) + \delta^\mu _\nu L \end{aligned}. $

(6) To solve the Einstein equation, we choose following anzats:
$ \mathrm{d}s^2 = -f(r) \mathrm{d} t^2+f(r)^{-1} \mathrm{d} r^2+r^2(\mathrm{d} \theta^2 +\sin^2 \theta \mathrm{d}\phi^2 ) . $

(7) In this paper, we consider only asymptotically flat configurations; therefore, we choose
$ \Lambda = 0 $ in Eq. (5). First we take$ A_\mu = (\Phi(r), 0, 0, Q_m \cos \theta) $ to consider the dyonic solution. In this case, we get$ F_{\mu \nu} = - \Phi_{I , r} \delta^0 _{[ \mu} \delta^1 _{ \nu ]} - Q_m \sin \theta \delta^2 _{[ \mu} \delta^3 _{ \nu ]}. $

(8) Therefore,
$ \begin{aligned}[b] x = \; &\frac{1}{2}\left(- \Phi^2_{, r} + \frac{Q^2 _m}{r^4}\right), \ y = -\frac{\Phi_{, r} Q_m}{r^2}, \\& (x^2 + y^2)^{1/2} = \frac{1}{2}\left(- \Phi^2_{, r} + \frac{Q^2 _m}{r^4}\right), \end{aligned} $

(9) and it is straightforward to show that the only non-vanishing Pleban'ski variables are
$ \begin{aligned}[b] P_{01} =\;& - (\cosh{\gamma} + \sinh{\gamma}) \Phi_{,r} = -\mathrm{e}^\gamma \Phi{,r} , \\P_{23} =\;& - (\cosh{\gamma} - \sinh{\gamma}) Q_m \sin{\theta} = - \mathrm{e}^{- \gamma}Q_m \sin {\theta} . \end{aligned} $

(10) We can express the electric potential as
$ \Phi(r) = \frac{Q_e\cdot \mathrm{e}^{-\gamma}}{r}. $

(11) This condition sets a conservation low for
$ P_{01} $ . In this case, the gravitational field equations read$ \begin{aligned}[b] - \frac{m_{, r}}{r^2} =\; &- \frac{(Q^2 _e + Q^2 _m)\cdot \mathrm{e}^{- \gamma}}{2 r^4}, \\ - \frac{m_{, rr}}{2 r} = \; &\frac{(Q^2 _e + Q^2 _m)\cdot \mathrm{e}^{- \gamma}}{2 r^4} , \end{aligned}$

(12) and the solution of this system of equations is
$ m(r) = M - \frac{(Q^2 _e + Q^2 _m)\cdot \mathrm{e}^{- \gamma}}{2 r}. $

(13) Finally, we can find the lapse function of the metric Eq.(7):
$ f(r) = 1-\frac{2 M}{r}+\frac{(Q_\mathrm{e}^2 + Q_m^2)\cdot \mathrm{e}^{-\gamma}}{r^2} , $

(14) where
$ Q_e $ and$ Q_m $ are the electric and magnetic charge of the black hole, respectively, and γ is related to a constant screening factor for the charge of the black hole, which corresponds to the nonlinear parameter [32]. If we choose$ \gamma = 0 $ , Maxwell's theory is recovered. Additionally, by choosing$ Q_e = Q_m = 0 $ the Schwarzschild case is easily obtained. To analyze the horizon properties of such a black hole, we set$ f(r) = 0 $ . Under this condition, the event horizon can be determined using the following expression:$ r_h = M \pm \sqrt{\left(M^{2} - (Q_{e}^{2} + Q_{m}^{2}\right)\cdot \mathrm{e}^{-\gamma}}. $

(15) This paper examines only the motion of a photon, which is a neutral, massless particle. Thus, we can define Q as
$ Q_\mathrm{e}^2 + Q_m^2 = Q^2 $ . We can obtain the maximum value of black hole charge using Eq. (15) as follows:$ 0 < Q < M\cdot \mathrm{e}^{-\gamma/2}. $

(16) Eq. (15) thus clearly indicates that the Q and γ parameters negatively affect the horizon radius, and Eq. (16) provides the boundary values for charge Q in terms of M and γ.
-
This section investigates the strong gravitational lensing effect in the spacetime described in Eq. (7). The photon sphere radius can be determined using the following expression [63]:
$ \frac{g^\prime_{\theta\theta}(r)}{g_{\theta\theta}(r)}- \frac{g^\prime_{tt}(r)}{g_{tt}(r)} = 0, $

(17) where
$ \prime $ is the differentiation with respect to the radial coordinate r. From Eqs. (7) and (17), we get$ r_m = \frac{3M +\sqrt{9M^2-8Q^2 \mathrm{e}^{-\gamma}}}{2} . $

(18) The specific energy and angular momentum can be written as
$ E\equiv-g_{\mu\nu}t^{\mu} \kappa^{\nu} = \frac{\Delta}{r^2}\dot{t}, $

(19) and
$ L\equiv g_{\mu\nu}\phi^{\mu}\kappa^\nu = r^2\dot{\phi} , $

(20) where
$ \Delta = f(r)\cdot r^2 $ and$ \kappa_\mu $ is the killing vector. The impact parameter is an important quantity and is defined as$ b\equiv\frac{L}{E} = \frac{r^4\dot{\phi}}{\Delta\dot{t}}. $

(21) Additionally, we assume that the motion occurs in the equatorial plane,
$ \theta = \pi/2 $ . Under this assumption, the equations of motion in the radial direction can be obtained as$ \dot{r}^2 = \frac{\Delta^2}{r^4}\dot{t}^2-\Delta\dot{\phi}^2, $

(22) or
$ \dot{r}^2 = V(r), $

(23) where
$ V(r) $ is the effective potential for the motion of the photon and is expressed as$ V(r)\equiv \mathrm{e}^2-\frac{\Delta}{r^4}L^2. $

(24) We consider that the light beam coming from infinity is deflected at the closest distance
$ r = r_0 $ and travels to infinity. At the closest distance,$ \dot{r} $ vanishes and the following formula is obtained from Eq. (22) for the critical impact parameter at the closest distance: [63]$ b(r_0) = \frac{r_0^2}{\sqrt{\Delta(r_0)}}. $

(25) Using the above equation, we can define the critical impact parameter as
$ b_c(r_m)\equiv \lim\limits_{r_0\to r_m}b(r_0) = \lim\limits_{r_0\to{r_m}}\frac{r_o^2}{\sqrt{\Delta(r_0)}}. $

(26) The critical impact parameter is defined such that photons with an impact parameter of
$ b < b_c $ fall into the black hole. Parameter$ b(r_0) $ can be expanded in the power of$ r_0-r_m $ as$ b(r_0) = b_c(r_m)+\frac{3M r_m-4Q^2 \mathrm{e}^{-\gamma}}{2(M r_m-\epsilon M^2)^{\tfrac{3}{2}}}(r_0-r_m)^2+O((r_0-r_m)^3). $

(27) From Eq. (22), we can establish the following relationship between r and ϕ:
$ \left(\frac{\mathrm{d}r}{\mathrm{d}\phi}\right)^2=r^4\left(\frac{1}{b^2}-\frac{\Delta}{r^4}\right), $

(28) which can alternatively be expressed in terms of the deflection angle
$ \alpha(r_0) $ of the light beam as$ \alpha = I(r_0)-\pi, $

(29) where
$ I(r_0)\equiv2\int_{r_0}^{\infty}\frac{\mathrm{d}r}{r^2\sqrt{\dfrac{1}{b^2}-\dfrac{\Delta}{r^4}}}. $

(30) By introducing a variable z, defined as
$ z\equiv 1-\frac{r}{r_0}, $

(31) $ I(r_0) $ can be rewritten as$ I(r_0)=\int_{ }^{ }f(z,r_0)\mathrm{d}z, $

(32) where
$ { f(z,r_0) = \frac{2r_0}{\sqrt{c_1(r)z+c_2(r_0)z^2 + c_3(r_0)z^3 + c_4(r_0)z^4}}}, $

(33) $ c_1(r_0)\equiv2(r^2_0-3M r_0 +2Q^2 \mathrm{e}^{-\gamma}), $

(34) $ c_2(r_0)\equiv-r^2_0 +6 M r_0 -6Q^2 \mathrm{e}^{-\gamma}, $

(35) $ c_3(r_0)\equiv -2 M r_0 + 46Q^2 \mathrm{e}^{-\gamma}, $

(36) $ c_4(r_0)\equiv - Q^2 \mathrm{e}^{-\gamma}. $

(37) $ I(r_0) $ can be split into two parts, i.e., a divergent part$ I_D $ ($ r_0 $ ) and a regular part$ I_R $ ($ r_0 $ ): I($ r_0 $ ) =$ I_D $ ($ r_0 $ )+$ I_R $ ($ r_0 $ ). The divergent part is expressed as$ I_D(r_0)=\int_0^1f_D(z,r_0)\, \mathrm{d}z, $

(38) where
$ f_D(z,r_0) = \frac{2r_0}{\sqrt{c_1(r_0)z+c_2(r_0)z^2}}, $

(39) and the result is
$ \begin{aligned}[b] I_D(r_0) =\;& \frac{4r_0}{\sqrt{-r_0^2+6 M r_0-6 Q^2 \mathrm{e}^{-\gamma}}}\\&\log\frac{\sqrt{-r_0^2+6 M r_0-6 Q^2 \mathrm{e}^{-\gamma}}+\sqrt{r_0^2-2Q^2 \mathrm{e}^{-\gamma}}}{2(r_0^2-3 M r_0+2 Q^2 \mathrm{e}^{-\gamma})}. \end{aligned} $

(40) In the strong deflection limit
$ r_0\rightarrow r_m $ , Eq. (40) is expressed as$ \begin{aligned}[b] I_D(b) = \;&-\bar{a}\mathrm{log}\left(\frac{b}{b_c}-1\right)+\bar{a} \mathrm{log}\frac{2(3M r_m-4 Q^2 \mathrm{e}^{-\gamma})}{M r_m-Q^2 \mathrm{e}^{-\gamma}}+\\&O((b-b_c)\mathrm{log}(b-b_c)), \end{aligned} $

(41) where
$ \bar{a} $ is given by$ \bar{a} = \frac{r_m}{\sqrt{3M r_m-4Q^2 \mathrm{e}^{-\gamma}}}. $

(42) Additionally, the regular part
$ I_R $ is defined as$ I_R(r_0)\equiv\int_0^1f_R(z,r_0)\, \mathrm{d}z, $

(43) where
$ f_R(z,r_0)\equiv f(z,r_0)-f_D(z,r_0). $

(44) As we are investigating the deflection angle in the strong field limit
$ r_0 \rightarrow r_m $ , we consider$ \lim\limits_{r_0\to{r_m}}f_R(z,r_0) = \frac{2r_m}{z\sqrt{c_2(r_m)+c_3(r_m)z+c_4(r_m)z^2}}-\frac{2r_m}{z\sqrt{c_2(r_m)}}. $

(45) Following some calculations, the analytical expression can be written as
$ \begin{aligned}[b] I_R(b) = \;&\bar{a}\,\log\Bigg[\frac{4(3M r_m-4Q^2 \mathrm{e}^{-\gamma})^2}{M^2 r_m^2(M r_m-Q^2 \mathrm{e}^{-\gamma})}\times(2\sqrt{M r_m-Q^2 \mathrm{e}^{-\gamma}} \\&-\sqrt{3M r_m-4Q^2 \mathrm{e}^{-\gamma}})^2\Bigg]+O((b-b_c)\log(b-b_c)). \end{aligned} $

(46) Eventually, the bending angle of the light rays
$ \alpha(b) $ in the strong deflection limit$ b\rightarrow b_c $ is given by [63]$ \alpha(b) = -\bar{a} \log\left(\frac{b}{b_c}-1\right)+\bar{b}+O\Bigg((b-b_c)\log(b-b_c)\Bigg), $

(47) where
$ \overline{a} $ and$ \overline{b} $ are expressed as$ \overline{a} = \frac{r_m}{\sqrt{3M r_m -4 Q^2 \mathrm{e}^{-\gamma}}} $

(48) $ \begin{aligned}[b] \overline{b} =\;& \overline{a}\log\Bigg[\frac{8(3 M r_m - 4 Q^2 \mathrm{e}^{-\gamma})^2}{M^2 r^2_m(M r_m -Q^2 \mathrm{e}^{-\gamma})^2}\times\\&\Bigg(2\sqrt{M r_m - M^2}-\sqrt{3Mr_m-4 Q^2 \mathrm{e}^{-\gamma}}\Bigg)^2\Bigg]-\pi , \end{aligned} $

(49) respectively. Table 1 lists values for
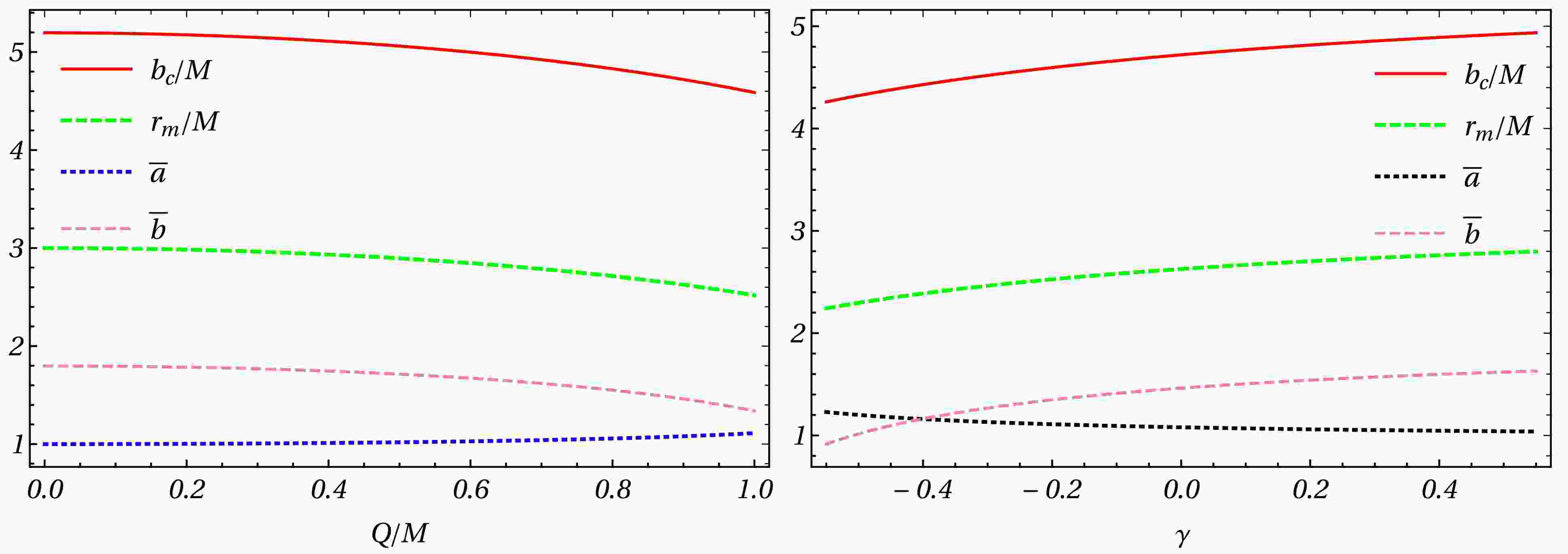
$ b_c/M $ , where$ \overline{a} $ and$ \overline{b} $ denote the lensing coefficients as functions of the charge of the black hole Q/M and γ parameters. When the black hole is non-charged$ (Q/M = 0) $ , we obtain$ b_c = 3\sqrt{3}M $ ,$ \overline{a} = 1 $ , and$ \overline{b} = -0.40023 $ . When$ Q/M = 0.6 $ , we obtain$ b_c = 4.59M $ ,$ \overline{a} = 1.1092 $ and$ \overline{b} = -0.4085 $ , which indicates that in the case of the Dyonic ModMax black hole, the quantity$ b_c $ will be smaller than that for the Schwarzschild case. Fig. 1 indicates that coefficient$ \overline{a} $ increases while$ \overline{b} $ ,$ b_c $ ,$ r_m $ decrease with increasing values of$ Q/M $ . Fig. 2 shows the deflection angle$ \alpha_D(b) $ as a function of b for different values of Q/M and γ. The deflection angle for Dyonic ModMax black holes (see Fig. 2) monotonically decreases with the impact parameter b and the deflection angle$ \alpha_D(b)\rightarrow \infty $ as$ b\rightarrow b_c $ . Notably, the deflection angle for Dyonic ModMax black holes decreases with increasing values of b. By contrast, for an impact parameter whose value is similar to the critical impact parameter (see Fig. 2), the deflection angle$ \alpha_D(b) $ decreases for increasing values of both Q/M and γ:γ $ {Q/M} $ 

$ \bar{a} $ 

$ \bar{b} $ 

$ {b_c/R_s} $ 

0 0.0 1 -0.40023 2.59808 -0.5 0.4 1.03512 -0.396203 2.47728 -0.5 0.8 1.58337 -1.08685 1.94022 0.0 0.4 1.01974 -0.397184 2.49912 0.0 0.8 1.12317 -0.413638 2.27299 0.5 0.4 1.01147 -0.398215 2.55523 0.5 0.8 1.05727 -0.396916 2.41483 Table 1. Estimated for the strong lensing coefficients
$ \overline{a} $ ,$ \overline{b} $ and the critical impact parameter$ b_c/R $ for Dyonic ModMax Black hole Spacetime. The values for$ Q/M=0 $ and$ \gamma=0 $ correspond to a Schwarzschild black hole.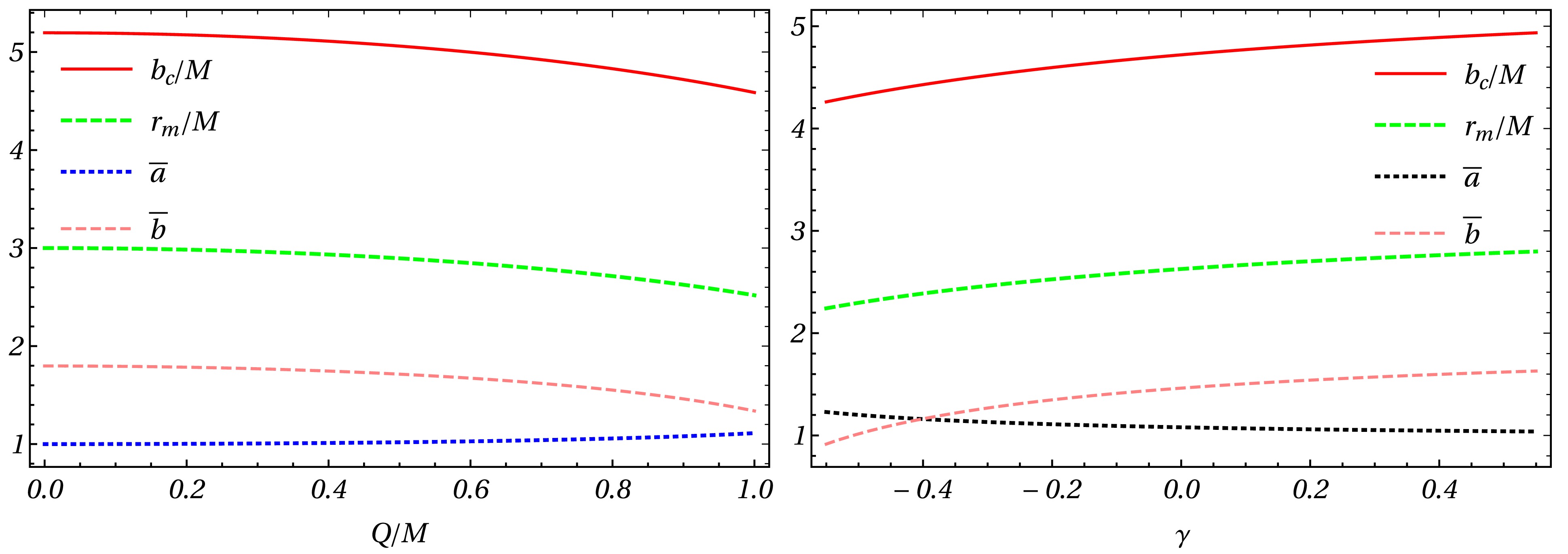
Figure 1. (color online) Quantities
$ b_c/M , r_m/M, \overline{a}, $ and$ \overline{b} $ in the Dyonic ModMax spacetime as functions of Q/M and γ.$ \overline{a} = 1 $ and$ \overline{b} = -0.4002 $ at$ Q/M = 0, \gamma = 0 $ correspond to the values of a Schwarzschild black hole.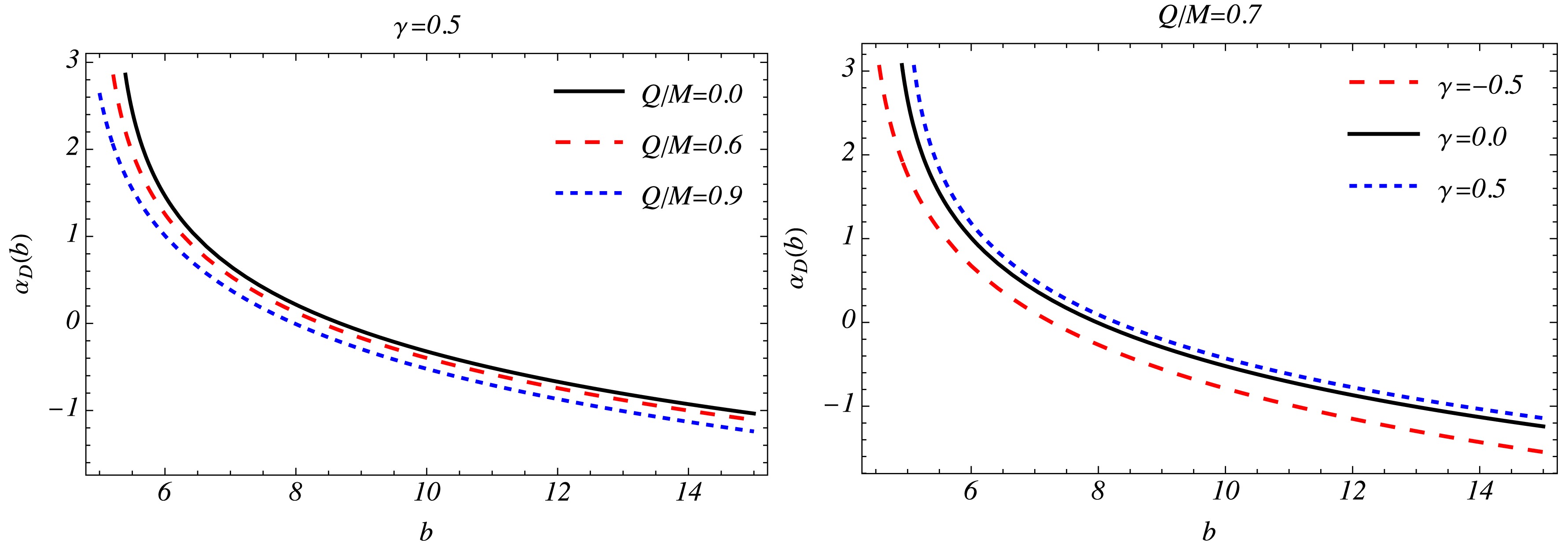
Figure 2. (color online) Variation in deflection angle for Dyonic ModMax black hole spacetime as a function of the impact parameter b for different values of
$ Q/M $ (left) and γ (right).$ \beta = \theta-\frac{D_{LS}}{D_{OS}}\Delta\alpha_n. $

(50) Here,
$ \Delta\alpha = \alpha-2n\pi $ is the offset of the deflection angle looping over$ 2n\pi $ and n is an integer; β is the angular position of the source and θ is the angular position of the image from the optic axis. The distance between the observer and the lens and between the observer and the source are denoted by$ D_{OL} $ and$ D_{OS} $ , respectively. Using Eqs. (47) and (50), the position of the nth relativistic image can be approximated as [63]$ \theta_n = \theta^0_n+\frac{b_c e_n (\beta-\theta^0_n)D_{OS}}{\overline{a} D_{LS} D_{OL}}, $

(51) where
$ e_n = \mathrm{e}^{\left(\tfrac{\overline{b}}{\overline{a}}-\tfrac{2 n \pi}{\overline{a}}\right)}. $

(52) $ \theta^0_n $ denotes the image positions corresponding to$ \alpha = 2n\pi $ . As gravitational lensing conserves surface brightness, the magnification is the quotient of the solid angles subtended by the nth image and the source ([63−65]). The magnification of the nth relativistic image is expressed as [63]$ \mu_n = \left(\frac{\beta}{\theta} \frac{d\beta}{d\theta}\right)^{-1} = \frac{b^2_c e_n (1+e_n)D_{OS}}{\overline{a}\beta D_{LS}D^2_{OL}}. $

(53) The first relativistic image is the brightest one, and the magnifications decrease exponentially with n. The magnifications are proportional to
$ 1/D^2_{OL} $ , which is a very small factor and thus causes the relativistic images to be very faint, unless the value of β is close to zero, i.e., nearly perfect alignment. Having obtained the deflection angle (Eq. (47), (48), and (49)), we calculate three observables of relativistic images (see Table 3, Fig. 3, 4 and 5), the angular position of the asymptotic relativistic images ($ \theta_\infty $ ), the angular separation between the outermost and asymptotic relativistic images($ s_\infty $ ), (see Fig. 4) and the relative magnification of the outermost relativistic image with respect to the other relativistic images ($ r_{\rm mag} $ )(see Fig. 5) [63].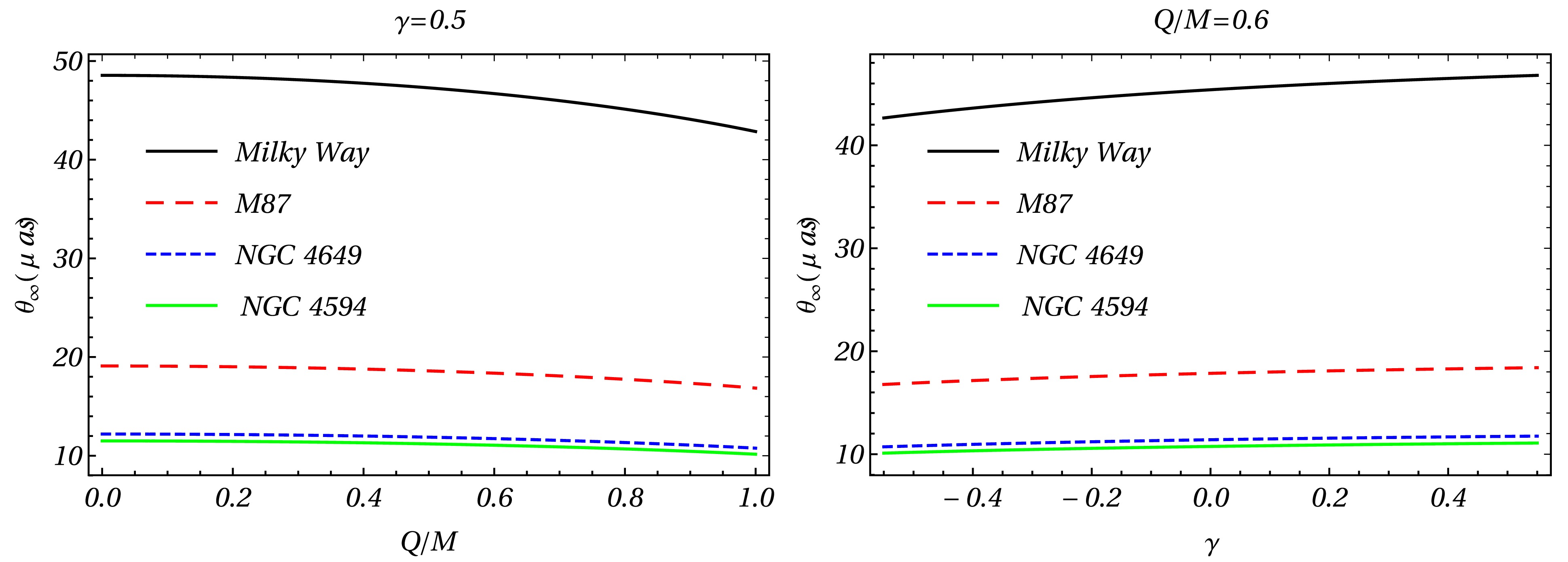
Figure 3. (color online) Behavior of lensing observables
$ \theta_\infty $ as a function of parameters Q/M and γ in the strong field limit obtained by considering the spacetime around the compact object.Galaxy M( $ M_\odot $ )

$ D_{OL} $ (Mpc)

$ M/D_{OL} $ 

$ \Delta T^S_{2,1}(Schw) $ 

$ \Delta T^S_{2,1}(DM) $ 

Milky Way $ 3.61 \times10^6 $ 

0.00762 $ 2.26467\times10^{-11} $ 

11.4968 8.748 "NGC4486(M87)" $ 3.0 \times10^9 $ 

16.1 $ 8.90733 \times10^{-12} $ 

8021 7270 NGC4649 $ 2.0 \times10^9 $ 

16.8 $ 5.6908 \times10^{-12} $ 

8021 7270 NGC4697 $ 1.7 \times10^8 $ 

11.7 $ 6.94569 \times10^{-13} $ 

5347.34 4846.67 NGC5128(cenA) $ 2.4\times10^8 $ 

4.2 $2.73158 \times10^{-12} $ 

454.53 411.97 Table 3. Time delay between two relativistic images of different galaxies.

Figure 4. (color online) Behavior of lensing observables
$ s_\infty $ as a function of parameters Q/M and γ in the strong field limit obtained by considering the spacetime around the compact object.
Figure 5. (color online) Graph illustrating the relationship between the contact parameter
$ r\mathrm{_{mag}} $ and the parameter ϵ.$ \theta_\infty = \frac{b_c}{D_{OL}}, $

(54) $ s = \theta_1-\theta_\infty = \theta_\infty \mathrm{e}^{\left(\tfrac{\overline{b}}{\overline{a}}-\tfrac{2 n \pi}{\overline{a}}\right)}, $

(55) $ r_{\rm mag} = \frac{5 \pi}{\overline{a} \log{10}}. $

(56) γ Q/M Milky Way NGC4486 NGC4649 $ r\mathrm{_{mag}} $ 

$ \theta_{\infty}(\mathrm{\mu as}) $ 

$ S(\mathrm{\mu as}) $ 

$ \theta_{\infty}(\mathrm{\mu as}) $ 

$ S(\mathrm{\mu as}) $ 

$ \theta_{\infty}(\mathrm{\mu as}) $ 

$ S(\mathrm{\mu as}) $ 

0.0 0.0 48.5447 0.0607535 19.0935 0.0238954 12.1986 0.0152665 6.82188 -0.5 0.4 46.2876 0.0729555 18.2057 0.0286946 11.9974 0.0183327 6.59044 -0.5 0.8 36.2528 0.345028 14.2589 0.135705 11.3382 0.0867007 4.30845 0.0 0.4 47.2071 0.067439 18.5674 0.0265249 11.8625 0.0169465 6.68985 0.0 0.8 42.4706 0.109304 16.7044 0.0429911 10.6723 0.0274666 6.07378 0.5 0.4 47.744 0.0645842 18.7786 0.0254021 11.9974 0.0162291 6.74453 0.5 0.8 45.1208 0.081358 17.7468 0.0319995 11.3382 0.0204441 6.45234 Table 2. Angular position of asymptotic relativistic images (
$ \theta_\infty $ ), angular separation between the outermost and asymptotic relativistic images ($ s_\infty $ ), and relative magnification of the outermost relativistic image with respect to other relativistic images ($ r_{\mathrm{mag}} $ ) for Milky Way, NGC4486, and NGC4649 for the case in which the charge of the black hole Q/M and γ parameters are fixed.The strong deflection limit coefficients
$ \overline{a} $ ,$ \overline{b} $ and the critical impact parameter values can be obtained using the measured values of s,$ r_{\mathrm{mag}} $ , and$ \theta_\infty $ . If$ \theta_\infty $ represents the asymptotic position of a set of images in the limit$ n \rightarrow\infty $ , then we consider that only the outermost image$ \theta_1 $ is resolved as a single image and all the remaining images are packed together at$ \theta_\infty $ . The measured values can be compared with those predicted by the theoretical models to check the nature of the black hole. Table 3 lists the observable values corresponding to various values of γ and Q. The results indicate that the Dyonic ModMax black hole exhibits unique and distinguishable observable characteristics compared to other configurations.One of the important conclusions in the study of deflection angle is that we can constrain the Dyonic ModMax spacetime parameter using EHT observation. Eq. (54) can be used to ascertain the specific values of these parameters that may be used to align the diameters of the M87* and Sgr A* BH, as determined by EHT. The angular size of the image of BH M87* is reported to be
$ \theta_d=42\pm3\ \, \rm{\mu as} $ . The mass and distance of M87* from the solar system is$ M = 6.5\times 10^9 M_\odot $ and$ d = 16.8 $ Mpc, respectively [7, 66]. The constraints on M87* are depicted in the left panel of Fig. 6, which reveals a limited boundary region for the charge for negative values of γ , and a significantly larger region for positive values of γ. More specificly, the parameter constraints are$ 0.7\ge Q>0.4 $ and$ \gamma\ge-0.5 $ . The observational data of the supermassive BH Sgr A* may be analyzed using the same methodology. A study conducted by Akiyama et al. (2019) determined that the angular diameter of the shadow of the BH Sgr A* is approximately$ \theta_d = 48.7 \pm7\, \rm{\mu as} $ with an approximate mass of$ M\simeq4\times10^6M_\odot $ . The distance from Earth is approximately$ d\simeq 8 \, \text{kpc} $ . The results for Sgr A* are shown in the right panel of Fig. 6. The graph indicates that the allowed parameter region for Sgr A* is broader compared to that of M87*, namely$ Q \geqslant 0.3 $ and$ \gamma \geqslant -0.5 $ . This broader range can likely be attributed to the greater observational uncertainties associated with Sgr A*.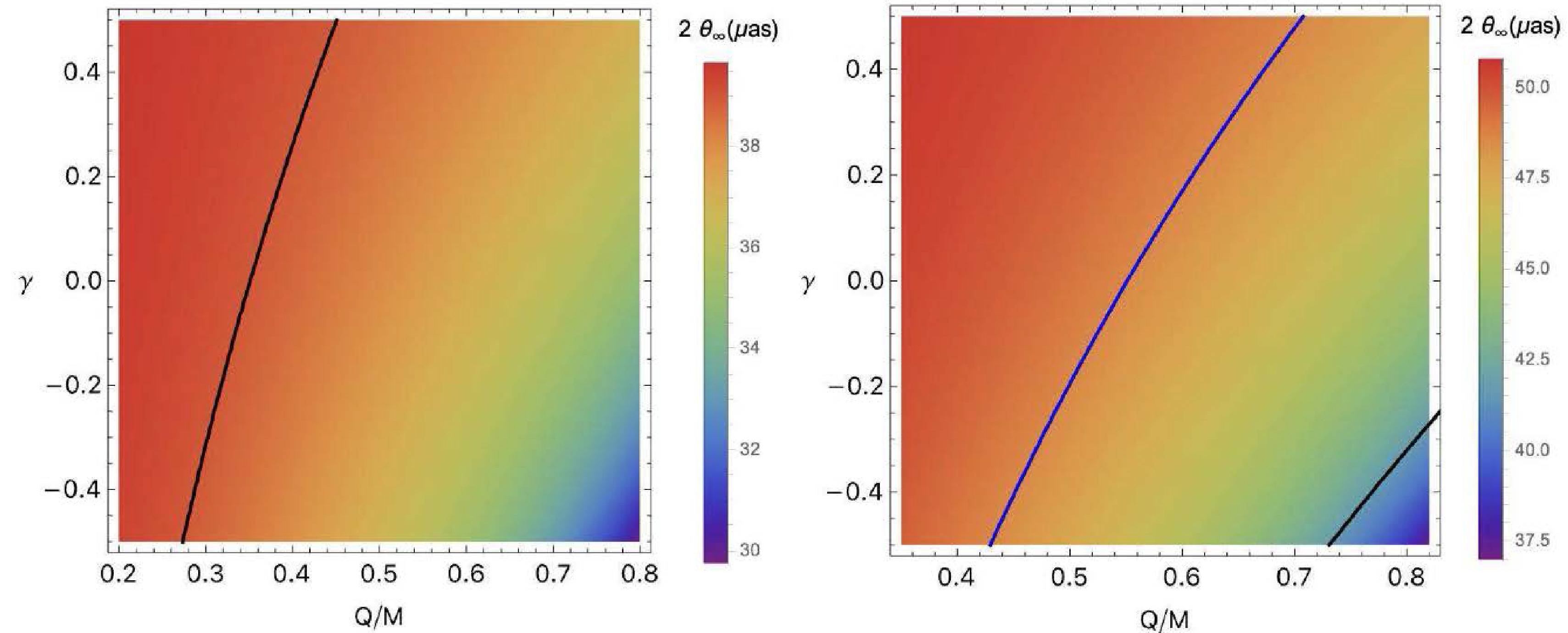
Figure 6. (color online) Constraining parameter obtained using EHT observation for
$ \mathrm{M87}^* $ (left panel) and$ \mathrm{SgrA}^* $ (right panel). The black thick line corresponds to the maximum parameter values and is consistent with the observational results of$ 39\mathrm{\ \mu as} $ for$ \mathrm{M}87^* $ (left panel) and$ 41.7\ \mathrm{\mu as} $ for$ \mathrm{SgrA}^* $ (right panel), while the blue line represents the middle value of the observational results ($ 48.7\ \mathrm{\mu as} $ for$ \mathrm{SgrA}^* $ ). -
This section investigates the strong gravitational lensing effect in the spacetime described in Eq. (7). The photon sphere radius can be determined using the following expression [63]:
$ \frac{g^\prime_{\theta\theta}(r)}{g_{\theta\theta}(r)}- \frac{g^\prime_{tt}(r)}{g_{tt}(r)} = 0, $

(17) where
$ \prime $ is the differentiation with respect to the radial coordinate r. From Eqs. (7) and (17), we get$ r_m = \frac{3M +\sqrt{9M^2-8Q^2 \mathrm{e}^{-\gamma}}}{2} . $

(18) The specific energy and angular momentum can be written as
$ E\equiv-g_{\mu\nu}t^{\mu} \kappa^{\nu} = \frac{\Delta}{r^2}\dot{t}, $

(19) and
$ L\equiv g_{\mu\nu}\phi^{\mu}\kappa^\nu = r^2\dot{\phi} , $

(20) where
$ \Delta = f(r)\cdot r^2 $ and$ \kappa_\mu $ is the killing vector. The impact parameter is an important quantity and is defined as$ b\equiv\frac{L}{E} = \frac{r^4\dot{\phi}}{\Delta\dot{t}}. $

(21) Additionally, we assume that the motion occurs in the equatorial plane,
$ \theta = \pi/2 $ . Under this assumption, the equations of motion in the radial direction can be obtained as$ \dot{r}^2 = \frac{\Delta^2}{r^4}\dot{t}^2-\Delta\dot{\phi}^2, $

(22) or
$ \dot{r}^2 = V(r), $

(23) where
$ V(r) $ is the effective potential for the motion of the photon and is expressed as$ V(r)\equiv \mathrm{e}^2-\frac{\Delta}{r^4}L^2. $

(24) We consider that the light beam coming from infinity is deflected at the closest distance
$ r = r_0 $ and travels to infinity. At the closest distance,$ \dot{r} $ vanishes and the following formula is obtained from Eq. (22) for the critical impact parameter at the closest distance: [63]$ b(r_0) = \frac{r_0^2}{\sqrt{\Delta(r_0)}}. $

(25) Using the above equation, we can define the critical impact parameter as
$ b_c(r_m)\equiv \lim\limits_{r_0\to r_m}b(r_0) = \lim\limits_{r_0\to{r_m}}\frac{r_o^2}{\sqrt{\Delta(r_0)}}. $

(26) The critical impact parameter is defined such that photons with an impact parameter of
$ b < b_c $ fall into the black hole. Parameter$ b(r_0) $ can be expanded in the power of$ r_0-r_m $ as$ b(r_0) = b_c(r_m)+\frac{3M r_m-4Q^2 \mathrm{e}^{-\gamma}}{2(M r_m-\epsilon M^2)^{\tfrac{3}{2}}}(r_0-r_m)^2+O((r_0-r_m)^3). $

(27) From Eq. (22), we can establish the following relationship between r and ϕ:
$ \left(\frac{\mathrm{d}r}{\mathrm{d}\phi}\right)^2=r^4\left(\frac{1}{b^2}-\frac{\Delta}{r^4}\right), $

(28) which can alternatively be expressed in terms of the deflection angle
$ \alpha(r_0) $ of the light beam as$ \alpha = I(r_0)-\pi, $

(29) where
$ I(r_0)\equiv2\int_{r_0}^{\infty}\frac{\mathrm{d}r}{r^2\sqrt{\dfrac{1}{b^2}-\dfrac{\Delta}{r^4}}}. $

(30) By introducing a variable z, defined as
$ z\equiv 1-\frac{r}{r_0}, $

(31) $ I(r_0) $ can be rewritten as$ I(r_0)=\int_{ }^{ }f(z,r_0)\mathrm{d}z, $

(32) where
$ { f(z,r_0) = \frac{2r_0}{\sqrt{c_1(r)z+c_2(r_0)z^2 + c_3(r_0)z^3 + c_4(r_0)z^4}}}, $

(33) $ c_1(r_0)\equiv2(r^2_0-3M r_0 +2Q^2 \mathrm{e}^{-\gamma}), $

(34) $ c_2(r_0)\equiv-r^2_0 +6 M r_0 -6Q^2 \mathrm{e}^{-\gamma}, $

(35) $ c_3(r_0)\equiv -2 M r_0 + 46Q^2 \mathrm{e}^{-\gamma}, $

(36) $ c_4(r_0)\equiv - Q^2 \mathrm{e}^{-\gamma}. $

(37) $ I(r_0) $ can be split into two parts, i.e., a divergent part$ I_D $ ($ r_0 $ ) and a regular part$ I_R $ ($ r_0 $ ): I($ r_0 $ ) =$ I_D $ ($ r_0 $ )+$ I_R $ ($ r_0 $ ). The divergent part is expressed as$ I_D(r_0)=\int_0^1f_D(z,r_0)\, \mathrm{d}z, $

(38) where
$ f_D(z,r_0) = \frac{2r_0}{\sqrt{c_1(r_0)z+c_2(r_0)z^2}}, $

(39) and the result is
$ \begin{aligned}[b] I_D(r_0) =\;& \frac{4r_0}{\sqrt{-r_0^2+6 M r_0-6 Q^2 \mathrm{e}^{-\gamma}}}\\&\log\frac{\sqrt{-r_0^2+6 M r_0-6 Q^2 \mathrm{e}^{-\gamma}}+\sqrt{r_0^2-2Q^2 \mathrm{e}^{-\gamma}}}{2(r_0^2-3 M r_0+2 Q^2 \mathrm{e}^{-\gamma})}. \end{aligned} $

(40) In the strong deflection limit
$ r_0\rightarrow r_m $ , Eq. (40) is expressed as$ \begin{aligned}[b] I_D(b) = \;&-\bar{a}\mathrm{log}\left(\frac{b}{b_c}-1\right)+\bar{a} \mathrm{log}\frac{2(3M r_m-4 Q^2 \mathrm{e}^{-\gamma})}{M r_m-Q^2 \mathrm{e}^{-\gamma}}+\\&O((b-b_c)\mathrm{log}(b-b_c)), \end{aligned} $

(41) where
$ \bar{a} $ is given by$ \bar{a} = \frac{r_m}{\sqrt{3M r_m-4Q^2 \mathrm{e}^{-\gamma}}}. $

(42) Additionally, the regular part
$ I_R $ is defined as$ I_R(r_0)\equiv\int_0^1f_R(z,r_0)\, \mathrm{d}z, $

(43) where
$ f_R(z,r_0)\equiv f(z,r_0)-f_D(z,r_0). $

(44) As we are investigating the deflection angle in the strong field limit
$ r_0 \rightarrow r_m $ , we consider$ \lim\limits_{r_0\to{r_m}}f_R(z,r_0) = \frac{2r_m}{z\sqrt{c_2(r_m)+c_3(r_m)z+c_4(r_m)z^2}}-\frac{2r_m}{z\sqrt{c_2(r_m)}}. $

(45) Following some calculations, the analytical expression can be written as
$ \begin{aligned}[b] I_R(b) = \;&\bar{a}\,\log\Bigg[\frac{4(3M r_m-4Q^2 \mathrm{e}^{-\gamma})^2}{M^2 r_m^2(M r_m-Q^2 \mathrm{e}^{-\gamma})}\times(2\sqrt{M r_m-Q^2 \mathrm{e}^{-\gamma}} \\&-\sqrt{3M r_m-4Q^2 \mathrm{e}^{-\gamma}})^2\Bigg]+O((b-b_c)\log(b-b_c)). \end{aligned} $

(46) Eventually, the bending angle of the light rays
$ \alpha(b) $ in the strong deflection limit$ b\rightarrow b_c $ is given by [63]$ \alpha(b) = -\bar{a} \log\left(\frac{b}{b_c}-1\right)+\bar{b}+O\Bigg((b-b_c)\log(b-b_c)\Bigg), $

(47) where
$ \overline{a} $ and$ \overline{b} $ are expressed as$ \overline{a} = \frac{r_m}{\sqrt{3M r_m -4 Q^2 \mathrm{e}^{-\gamma}}} $

(48) $ \begin{aligned}[b] \overline{b} =\;& \overline{a}\log\Bigg[\frac{8(3 M r_m - 4 Q^2 \mathrm{e}^{-\gamma})^2}{M^2 r^2_m(M r_m -Q^2 \mathrm{e}^{-\gamma})^2}\times\\&\Bigg(2\sqrt{M r_m - M^2}-\sqrt{3Mr_m-4 Q^2 \mathrm{e}^{-\gamma}}\Bigg)^2\Bigg]-\pi , \end{aligned} $

(49) respectively. Table 1 lists values for
$ b_c/M $ , where$ \overline{a} $ and$ \overline{b} $ denote the lensing coefficients as functions of the charge of the black hole Q/M and γ parameters. When the black hole is non-charged$ (Q/M = 0) $ , we obtain$ b_c = 3\sqrt{3}M $ ,$ \overline{a} = 1 $ , and$ \overline{b} = -0.40023 $ . When$ Q/M = 0.6 $ , we obtain$ b_c = 4.59M $ ,$ \overline{a} = 1.1092 $ and$ \overline{b} = -0.4085 $ , which indicates that in the case of the Dyonic ModMax black hole, the quantity$ b_c $ will be smaller than that for the Schwarzschild case. Fig. 1 indicates that coefficient$ \overline{a} $ increases while$ \overline{b} $ ,$ b_c $ ,$ r_m $ decrease with increasing values of$ Q/M $ . Fig. 2 shows the deflection angle$ \alpha_D(b) $ as a function of b for different values of Q/M and γ. The deflection angle for Dyonic ModMax black holes (see Fig. 2) monotonically decreases with the impact parameter b and the deflection angle$ \alpha_D(b)\rightarrow \infty $ as$ b\rightarrow b_c $ . Notably, the deflection angle for Dyonic ModMax black holes decreases with increasing values of b. By contrast, for an impact parameter whose value is similar to the critical impact parameter (see Fig. 2), the deflection angle$ \alpha_D(b) $ decreases for increasing values of both Q/M and γ:γ $ {Q/M} $ 

$ \bar{a} $ 

$ \bar{b} $ 

$ {b_c/R_s} $ 

0 0.0 1 -0.40023 2.59808 -0.5 0.4 1.03512 -0.396203 2.47728 -0.5 0.8 1.58337 -1.08685 1.94022 0.0 0.4 1.01974 -0.397184 2.49912 0.0 0.8 1.12317 -0.413638 2.27299 0.5 0.4 1.01147 -0.398215 2.55523 0.5 0.8 1.05727 -0.396916 2.41483 Table 1. Estimated for the strong lensing coefficients
$ \overline{a} $ ,$ \overline{b} $ and the critical impact parameter$ b_c/R $ for Dyonic ModMax Black hole Spacetime. The values for$ Q/M=0 $ and$ \gamma=0 $ correspond to a Schwarzschild black hole.
Figure 1. (color online) Quantities
$ b_c/M , r_m/M, \overline{a}, $ and$ \overline{b} $ in the Dyonic ModMax spacetime as functions of Q/M and γ.$ \overline{a} = 1 $ and$ \overline{b} = -0.4002 $ at$ Q/M = 0, \gamma = 0 $ correspond to the values of a Schwarzschild black hole.
Figure 2. (color online) Variation in deflection angle for Dyonic ModMax black hole spacetime as a function of the impact parameter b for different values of
$ Q/M $ (left) and γ (right).$ \beta = \theta-\frac{D_{LS}}{D_{OS}}\Delta\alpha_n. $

(50) Here,
$ \Delta\alpha = \alpha-2n\pi $ is the offset of the deflection angle looping over$ 2n\pi $ and n is an integer; β is the angular position of the source and θ is the angular position of the image from the optic axis. The distance between the observer and the lens and between the observer and the source are denoted by$ D_{OL} $ and$ D_{OS} $ , respectively. Using Eqs. (47) and (50), the position of the nth relativistic image can be approximated as [63]$ \theta_n = \theta^0_n+\frac{b_c e_n (\beta-\theta^0_n)D_{OS}}{\overline{a} D_{LS} D_{OL}}, $

(51) where
$ e_n = \mathrm{e}^{\left(\tfrac{\overline{b}}{\overline{a}}-\tfrac{2 n \pi}{\overline{a}}\right)}. $

(52) $ \theta^0_n $ denotes the image positions corresponding to$ \alpha = 2n\pi $ . As gravitational lensing conserves surface brightness, the magnification is the quotient of the solid angles subtended by the nth image and the source ([63−65]). The magnification of the nth relativistic image is expressed as [63]$ \mu_n = \left(\frac{\beta}{\theta} \frac{d\beta}{d\theta}\right)^{-1} = \frac{b^2_c e_n (1+e_n)D_{OS}}{\overline{a}\beta D_{LS}D^2_{OL}}. $

(53) The first relativistic image is the brightest one, and the magnifications decrease exponentially with n. The magnifications are proportional to
$ 1/D^2_{OL} $ , which is a very small factor and thus causes the relativistic images to be very faint, unless the value of β is close to zero, i.e., nearly perfect alignment. Having obtained the deflection angle (Eq. (47), (48), and (49)), we calculate three observables of relativistic images (see Table 3, Fig. 3, 4 and 5), the angular position of the asymptotic relativistic images ($ \theta_\infty $ ), the angular separation between the outermost and asymptotic relativistic images($ s_\infty $ ), (see Fig. 4) and the relative magnification of the outermost relativistic image with respect to the other relativistic images ($ r_{\rm mag} $ )(see Fig. 5) [63].
Figure 3. (color online) Behavior of lensing observables
$ \theta_\infty $ as a function of parameters Q/M and γ in the strong field limit obtained by considering the spacetime around the compact object.Galaxy M( $ M_\odot $ )

$ D_{OL} $ (Mpc)

$ M/D_{OL} $ 

$ \Delta T^S_{2,1}(Schw) $ 

$ \Delta T^S_{2,1}(DM) $ 

Milky Way $ 3.61 \times10^6 $ 

0.00762 $ 2.26467\times10^{-11} $ 

11.4968 8.748 "NGC4486(M87)" $ 3.0 \times10^9 $ 

16.1 $ 8.90733 \times10^{-12} $ 

8021 7270 NGC4649 $ 2.0 \times10^9 $ 

16.8 $ 5.6908 \times10^{-12} $ 

8021 7270 NGC4697 $ 1.7 \times10^8 $ 

11.7 $ 6.94569 \times10^{-13} $ 

5347.34 4846.67 NGC5128(cenA) $ 2.4\times10^8 $ 

4.2 $2.73158 \times10^{-12} $ 

454.53 411.97 Table 3. Time delay between two relativistic images of different galaxies.

Figure 4. (color online) Behavior of lensing observables
$ s_\infty $ as a function of parameters Q/M and γ in the strong field limit obtained by considering the spacetime around the compact object.
Figure 5. (color online) Graph illustrating the relationship between the contact parameter
$ r\mathrm{_{mag}} $ and the parameter ϵ.$ \theta_\infty = \frac{b_c}{D_{OL}}, $

(54) $ s = \theta_1-\theta_\infty = \theta_\infty \mathrm{e}^{\left(\tfrac{\overline{b}}{\overline{a}}-\tfrac{2 n \pi}{\overline{a}}\right)}, $

(55) $ r_{\rm mag} = \frac{5 \pi}{\overline{a} \log{10}}. $

(56) γ Q/M Milky Way NGC4486 NGC4649 $ r\mathrm{_{mag}} $ 

$ \theta_{\infty}(\mathrm{\mu as}) $ 

$ S(\mathrm{\mu as}) $ 

$ \theta_{\infty}(\mathrm{\mu as}) $ 

$ S(\mathrm{\mu as}) $ 

$ \theta_{\infty}(\mathrm{\mu as}) $ 

$ S(\mathrm{\mu as}) $ 

0.0 0.0 48.5447 0.0607535 19.0935 0.0238954 12.1986 0.0152665 6.82188 -0.5 0.4 46.2876 0.0729555 18.2057 0.0286946 11.9974 0.0183327 6.59044 -0.5 0.8 36.2528 0.345028 14.2589 0.135705 11.3382 0.0867007 4.30845 0.0 0.4 47.2071 0.067439 18.5674 0.0265249 11.8625 0.0169465 6.68985 0.0 0.8 42.4706 0.109304 16.7044 0.0429911 10.6723 0.0274666 6.07378 0.5 0.4 47.744 0.0645842 18.7786 0.0254021 11.9974 0.0162291 6.74453 0.5 0.8 45.1208 0.081358 17.7468 0.0319995 11.3382 0.0204441 6.45234 Table 2. Angular position of asymptotic relativistic images (
$ \theta_\infty $ ), angular separation between the outermost and asymptotic relativistic images ($ s_\infty $ ), and relative magnification of the outermost relativistic image with respect to other relativistic images ($ r_{\mathrm{mag}} $ ) for Milky Way, NGC4486, and NGC4649 for the case in which the charge of the black hole Q/M and γ parameters are fixed.The strong deflection limit coefficients
$ \overline{a} $ ,$ \overline{b} $ and the critical impact parameter values can be obtained using the measured values of s,$ r_{\mathrm{mag}} $ , and$ \theta_\infty $ . If$ \theta_\infty $ represents the asymptotic position of a set of images in the limit$ n \rightarrow\infty $ , then we consider that only the outermost image$ \theta_1 $ is resolved as a single image and all the remaining images are packed together at$ \theta_\infty $ . The measured values can be compared with those predicted by the theoretical models to check the nature of the black hole. Table 3 lists the observable values corresponding to various values of γ and Q. The results indicate that the Dyonic ModMax black hole exhibits unique and distinguishable observable characteristics compared to other configurations.One of the important conclusions in the study of deflection angle is that we can constrain the Dyonic ModMax spacetime parameter using EHT observation. Eq. (54) can be used to ascertain the specific values of these parameters that may be used to align the diameters of the M87* and Sgr A* BH, as determined by EHT. The angular size of the image of BH M87* is reported to be
$ \theta_d=42\pm3\ \, \rm{\mu as} $ . The mass and distance of M87* from the solar system is$ M = 6.5\times 10^9 M_\odot $ and$ d = 16.8 $ Mpc, respectively [7, 66]. The constraints on M87* are depicted in the left panel of Fig. 6, which reveals a limited boundary region for the charge for negative values of γ , and a significantly larger region for positive values of γ. More specificly, the parameter constraints are$ 0.7\ge Q>0.4 $ and$ \gamma\ge-0.5 $ . The observational data of the supermassive BH Sgr A* may be analyzed using the same methodology. A study conducted by Akiyama et al. (2019) determined that the angular diameter of the shadow of the BH Sgr A* is approximately$ \theta_d = 48.7 \pm7\, \rm{\mu as} $ with an approximate mass of$ M\simeq4\times10^6M_\odot $ . The distance from Earth is approximately$ d\simeq 8 \, \text{kpc} $ . The results for Sgr A* are shown in the right panel of Fig. 6. The graph indicates that the allowed parameter region for Sgr A* is broader compared to that of M87*, namely$ Q \geqslant 0.3 $ and$ \gamma \geqslant -0.5 $ . This broader range can likely be attributed to the greater observational uncertainties associated with Sgr A*.
Figure 6. (color online) Constraining parameter obtained using EHT observation for
$ \mathrm{M87}^* $ (left panel) and$ \mathrm{SgrA}^* $ (right panel). The black thick line corresponds to the maximum parameter values and is consistent with the observational results of$ 39\mathrm{\ \mu as} $ for$ \mathrm{M}87^* $ (left panel) and$ 41.7\ \mathrm{\mu as} $ for$ \mathrm{SgrA}^* $ (right panel), while the blue line represents the middle value of the observational results ($ 48.7\ \mathrm{\mu as} $ for$ \mathrm{SgrA}^* $ ). -
The time difference is caused by the photons taking different paths as they wind the black hole, thus leading to a time delay between different images. If the time signals of the first image and other packed images can be distinguished, then the time spent by the photon to wind around the black hole is given by [67]
$ {\tilde{T}(b) = \overline{a}\log{\left(\frac{b}{b_c}-1\right)} + \overline{b} +O(b-b_c)} . $

(57) As the images are highly demagnified, and the separation between the images is of the order of microarcseconds, we must at least distinguish the outermost relativistic image from the rest. Additionally, we assume the source to be variable, which generally is abundant in all galaxies; otherwise, there is no time delay to measure. For spherically symmetric black holes, the time delay between the first and second relativistic image is expressed as [67]
$ \Delta T^s_{2,1} = 2 \pi b_c = 2\pi D_{OL}\theta_\infty. $

(58) Using Eq. (58), if we can measure the time delay accurately and the critical impact parameter with negligible error, we can obtain the distance of the black hole accurately.Table 3 compares several galaxies representing Schwarzschild and Dyonic ModMax spacetime. In the Dyonic ModMax spacetime, the time delays
$ \Delta T^s_{2.1} $ between two distinct relativistic images are comparatively smaller than the fixed value of Q/M and γ in the Schwarzschild cases. We have also analytically derived the time delays$ \Delta T^s_{2.1} $ between the first and second-order relativistic images for various astronomical objects including the Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA) with the help of data obtained from Ref. [65]. Using this analysis, we have shown that if we have an independent observation for the time delay, we can strongly constrain the Dyonic ModMax space time parameters Q and γ owing to a distinguishable difference in the measured time delay. -
The time difference is caused by the photons taking different paths as they wind the black hole, thus leading to a time delay between different images. If the time signals of the first image and other packed images can be distinguished, then the time spent by the photon to wind around the black hole is given by [67]
$ {\tilde{T}(b) = \overline{a}\log{\left(\frac{b}{b_c}-1\right)} + \overline{b} +O(b-b_c)} . $

(57) As the images are highly demagnified, and the separation between the images is of the order of microarcseconds, we must at least distinguish the outermost relativistic image from the rest. Additionally, we assume the source to be variable, which generally is abundant in all galaxies; otherwise, there is no time delay to measure. For spherically symmetric black holes, the time delay between the first and second relativistic image is expressed as [67]
$ \Delta T^s_{2,1} = 2 \pi b_c = 2\pi D_{OL}\theta_\infty. $

(58) Using Eq. (58), if we can measure the time delay accurately and the critical impact parameter with negligible error, we can obtain the distance of the black hole accurately.Table 3 compares several galaxies representing Schwarzschild and Dyonic ModMax spacetime. In the Dyonic ModMax spacetime, the time delays
$ \Delta T^s_{2.1} $ between two distinct relativistic images are comparatively smaller than the fixed value of Q/M and γ in the Schwarzschild cases. We have also analytically derived the time delays$ \Delta T^s_{2.1} $ between the first and second-order relativistic images for various astronomical objects including the Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA) with the help of data obtained from Ref. [65]. Using this analysis, we have shown that if we have an independent observation for the time delay, we can strongly constrain the Dyonic ModMax space time parameters Q and γ owing to a distinguishable difference in the measured time delay. -
We draw the following conclusions through this investigation:
● The radius of the spherical photon orbit
$ r_m $ , the critical impact parameter$ b_c $ , the lensing coefficient$ \bar{b} $ , the deflection angle$ \alpha_D(b) $ , and the angular position$ \theta_\infty $ decrease with increasing values of Q, while the lensing coefficient$ \bar{a} $ and angular separation$ s_\infty $ exhibit the opposite trend. Consequently, the parameter γ behaves inversely to Q.● Additionally, we illustrated the constraining in the Dyonic ModMax spacetime with EHT observations using parametric space graphs.
● We analytically derived the time delays
$ \Delta T^s_{2.1} $ between first and second-order relativistic images for the Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA). We conclude that the time delay is larger for supermassive black holes of higher mass as compared to lighter black holes.● Graphical and tabular results revealed the dependence of the deflection angle on parameters Q and γ. Notably, when γ is negative, the deflection angle decreases more sharply, while positive values of γ tend to smooth out this variation. EHT observations, especially those related to the shadow diameters of the
$ \mathrm{M}87^* $ and$ \mathrm{SgrA}^* $ black holes, were used to establish experimental constraints on these parameters. For$ \mathrm{M}87^* $ , the parameters are constrained by$ 0.7\ge Q>0.4 $ and$ \gamma\ge-0.5 $ , whereas for$ \mathrm{SgrA}^* $ , the allowed parameter space is broader, i.e$ Q \geqslant 0.3 $ and$ \gamma \geqslant -0.5 $ , due to larger observational uncertainties. -
We draw the following conclusions through this investigation:
● The radius of the spherical photon orbit
$ r_m $ , the critical impact parameter$ b_c $ , the lensing coefficient$ \bar{b} $ , the deflection angle$ \alpha_D(b) $ , and the angular position$ \theta_\infty $ decrease with increasing values of Q, while the lensing coefficient$ \bar{a} $ and angular separation$ s_\infty $ exhibit the opposite trend. Consequently, the parameter γ behaves inversely to Q.● Additionally, we illustrated the constraining in the Dyonic ModMax spacetime with EHT observations using parametric space graphs.
● We analytically derived the time delays
$ \Delta T^s_{2.1} $ between first and second-order relativistic images for the Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA). We conclude that the time delay is larger for supermassive black holes of higher mass as compared to lighter black holes.● Graphical and tabular results revealed the dependence of the deflection angle on parameters Q and γ. Notably, when γ is negative, the deflection angle decreases more sharply, while positive values of γ tend to smooth out this variation. EHT observations, especially those related to the shadow diameters of the
$ \mathrm{M}87^* $ and$ \mathrm{SgrA}^* $ black holes, were used to establish experimental constraints on these parameters. For$ \mathrm{M}87^* $ , the parameters are constrained by$ 0.7\ge Q>0.4 $ and$ \gamma\ge-0.5 $ , whereas for$ \mathrm{SgrA}^* $ , the allowed parameter space is broader, i.e$ Q \geqslant 0.3 $ and$ \gamma \geqslant -0.5 $ , due to larger observational uncertainties.
Theoretical study of Strong gravitational lensing around Dyonic ModMax black hole: constraints from EHT observations
- Received Date: 2025-07-21
- Available Online: 2025-12-15
Abstract: In this study, we investigate the properties of the Dyonic ModMax black hole solution using strong gravitational lensing. Additionally, we calculate the time delay between two relativistic images of a background object. First, we analyze expressions for the photon orbits in the spacetime of the Dyonic ModMax black hole. To obtain observational consequences, we provide expressions for the observable quantities, such as angular radius and magnifications. The numerous observations suggest that many nearby galaxies contain supermassive central black holes. In our model, such a supermassive black hole can be characterized by two additional parameters: γ and Q. Notably, the bending angle





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: