-
Black holes (BHs) are described by solutions to Einstein's General Relativity (GR), such as the Schwarzschild [1, 2] and Kerr [3] metrics, which predict event horizons beyond which no information can escape. However, these classical descriptions are challenged at extremely high densities and energies, where quantum gravitational effects become significant. In recent years, there has been growing interest in quantum-corrected black holes [4−6], which incorporate modifications inspired by theories of quantum gravity, such as loop quantum gravity [7−10], string theory [11, 12], or generalized uncertainty principles [13, 14]. These quantum corrections alter the near-horizon geometry and can significantly influence the dynamics of accretion disks and their associated radiation properties.
GR cannot incorporate quantum principles and fails to resolve the singularities associated with the cosmological Big Bang and black holes. Quantum theories of gravity offer a potential solution by incorporating quantum effects. Loop Quantum Gravity (LQG), a non-perturbative theory of quantum gravity [15], has been extensively applied to singularity resolution in loop quantum cosmology (see, e.g., [16−22]). Notably, models of black hole solutions within LQG have been developed in recent years, and have focused on LQG black hole solutions, for instance, including the regular, static self-dual black hole solution obtained via a mini-superspace polymerization procedure [23], which exhibits self-duality linked to T-duality [24, 25]. Substantial research explores quantum effects within the LQG framework, providing insights into the nature of quantum black hole solutions [26−34], and phenomenological studies of loop quantum black holes are increasingly prevalent [35−46].
Accretion disks are fundamental structures surrounding compact astrophysical objects, including black holes, neutron stars, and white dwarfs. These disks form when matter spirals inward due to gravitational forces, gradually losing angular momentum and converting gravitational potential energy into radiation. The study of accretion disks is crucial for understanding high-energy astrophysical phenomena, such as quasars [47, 48], X-ray binaries [49−51], and active galactic nuclei (AGN) [52, 53]. In the context of black holes, the radiation emitted from accretion disks serves as a powerful observational tool, offering insights into the spacetime geometry and the physical properties of black holes themselves.
The radiation emitted by accretion disks around quantum-corrected black holes is of particular interest, as it can reveal deviations from GR due to quantum corrections predicted by loop quantum gravity. These deviations stem from modifications in spacetime curvature [54], the potential existence of quantum remnants [55, 56], and alterations to the causal structure near the event horizon. Consequently, the electromagnetic spectrum, luminosity, and temporal variability of the radiation from these disks are expected to differ significantly from those of classical black holes. Studying these differences offers a pathway to indirect observational evidence for quantum gravitational effects, advancing efforts toward a unified theory of quantum gravity [57].
This study aims to explore the radiation properties of such a thin accretion disk using the geometrically thin and optically thick Novikov-Thorne disk model [58, 59] around the quantum-corrected black hole, focusing on how quantum corrections affect the flux of the electromagnetic radiation, the accretion disk's temperature, spectral and differential luminosities. By comparing these properties with the Schwarzschild BH [1, 2], we seek to identify potential observational tests for the existence of quantum corrections. Such investigations are not only crucial for advancing our understanding of black hole physics but also for probing the fundamental nature of spacetime and gravity.
This paper is organized as follows: In Sec. II we briefly review a quantum-corrected BH spacetime. In Sec. III, we briefly introduce the Novikov-Thorne model. Additionally, we explore the innermost stable circular orbits (ISCO) parameters and the radiative efficiency. Further, we analyze the radiative properties of the accretion disk of the quantum-corrected BH in Sec. IV. Finally, we give our concluding remarks in Sec. V. Throughout this paper, we use the
$ (-, +, +, +) $ signature for the spacetime metric and a system of units in which we set$ G=c=1 $ , unless the constants are directly stated. -
Black holes (BHs) are described by solutions to Einstein's General Relativity (GR), such as the Schwarzschild [1, 2] and Kerr [3] metrics, which predict event horizons beyond which no information can escape. However, these classical descriptions are challenged at extremely high densities and energies, where quantum gravitational effects become significant. In recent years, there has been growing interest in quantum-corrected black holes [4−6], which incorporate modifications inspired by theories of quantum gravity, such as loop quantum gravity [7−10], string theory [11, 12], or generalized uncertainty principles [13, 14]. These quantum corrections alter the near-horizon geometry and can significantly influence the dynamics of accretion disks and their associated radiation properties.
GR cannot incorporate quantum principles and fails to resolve the singularities associated with the cosmological Big Bang and black holes. Quantum theories of gravity offer a potential solution by incorporating quantum effects. Loop Quantum Gravity (LQG), a non-perturbative theory of quantum gravity [15], has been extensively applied to singularity resolution in loop quantum cosmology (see, e.g., [16−22]). Notably, models of black hole solutions within LQG have been developed in recent years, and have focused on LQG black hole solutions, for instance, including the regular, static self-dual black hole solution obtained via a mini-superspace polymerization procedure [23], which exhibits self-duality linked to T-duality [24, 25]. Substantial research explores quantum effects within the LQG framework, providing insights into the nature of quantum black hole solutions [26−34], and phenomenological studies of loop quantum black holes are increasingly prevalent [35−46].
Accretion disks are fundamental structures surrounding compact astrophysical objects, including black holes, neutron stars, and white dwarfs. These disks form when matter spirals inward due to gravitational forces, gradually losing angular momentum and converting gravitational potential energy into radiation. The study of accretion disks is crucial for understanding high-energy astrophysical phenomena, such as quasars [47, 48], X-ray binaries [49−51], and active galactic nuclei (AGN) [52, 53]. In the context of black holes, the radiation emitted from accretion disks serves as a powerful observational tool, offering insights into the spacetime geometry and the physical properties of black holes themselves.
The radiation emitted by accretion disks around quantum-corrected black holes is of particular interest, as it can reveal deviations from GR due to quantum corrections predicted by loop quantum gravity. These deviations stem from modifications in spacetime curvature [54], the potential existence of quantum remnants [55, 56], and alterations to the causal structure near the event horizon. Consequently, the electromagnetic spectrum, luminosity, and temporal variability of the radiation from these disks are expected to differ significantly from those of classical black holes. Studying these differences offers a pathway to indirect observational evidence for quantum gravitational effects, advancing efforts toward a unified theory of quantum gravity [57].
This study aims to explore the radiation properties of such a thin accretion disk using the geometrically thin and optically thick Novikov-Thorne disk model [58, 59] around the quantum-corrected black hole, focusing on how quantum corrections affect the flux of the electromagnetic radiation, the accretion disk's temperature, spectral and differential luminosities. By comparing these properties with the Schwarzschild BH [1, 2], we seek to identify potential observational tests for the existence of quantum corrections. Such investigations are not only crucial for advancing our understanding of black hole physics but also for probing the fundamental nature of spacetime and gravity.
This paper is organized as follows: In Sec. II we briefly review a quantum-corrected BH spacetime. In Sec. III, we briefly introduce the Novikov-Thorne model. Additionally, we explore the innermost stable circular orbits (ISCO) parameters and the radiative efficiency. Further, we analyze the radiative properties of the accretion disk of the quantum-corrected BH in Sec. IV. Finally, we give our concluding remarks in Sec. V. Throughout this paper, we use the
$ (-, +, +, +) $ signature for the spacetime metric and a system of units in which we set$ G=c=1 $ , unless the constants are directly stated. -
Black holes (BHs) are described by solutions to Einstein's General Relativity (GR), such as the Schwarzschild [1, 2] and Kerr [3] metrics, which predict event horizons beyond which no information can escape. However, these classical descriptions are challenged at extremely high densities and energies, where quantum gravitational effects become significant. In recent years, there has been growing interest in quantum-corrected black holes [4−6], which incorporate modifications inspired by theories of quantum gravity, such as loop quantum gravity [7−10], string theory [11, 12], or generalized uncertainty principles [13, 14]. These quantum corrections alter the near-horizon geometry and can significantly influence the dynamics of accretion disks and their associated radiation properties.
GR cannot incorporate quantum principles and fails to resolve the singularities associated with the cosmological Big Bang and black holes. Quantum theories of gravity offer a potential solution by incorporating quantum effects. Loop Quantum Gravity (LQG), a non-perturbative theory of quantum gravity [15], has been extensively applied to singularity resolution in loop quantum cosmology (see, e.g., [16−22]). Notably, models of black hole solutions within LQG have been developed in recent years, and have focused on LQG black hole solutions, for instance, including the regular, static self-dual black hole solution obtained via a mini-superspace polymerization procedure [23], which exhibits self-duality linked to T-duality [24, 25]. Substantial research explores quantum effects within the LQG framework, providing insights into the nature of quantum black hole solutions [26−34], and phenomenological studies of loop quantum black holes are increasingly prevalent [35−46].
Accretion disks are fundamental structures surrounding compact astrophysical objects, including black holes, neutron stars, and white dwarfs. These disks form when matter spirals inward due to gravitational forces, gradually losing angular momentum and converting gravitational potential energy into radiation. The study of accretion disks is crucial for understanding high-energy astrophysical phenomena, such as quasars [47, 48], X-ray binaries [49−51], and active galactic nuclei (AGN) [52, 53]. In the context of black holes, the radiation emitted from accretion disks serves as a powerful observational tool, offering insights into the spacetime geometry and the physical properties of black holes themselves.
The radiation emitted by accretion disks around quantum-corrected black holes is of particular interest, as it can reveal deviations from GR due to quantum corrections predicted by loop quantum gravity. These deviations stem from modifications in spacetime curvature [54], the potential existence of quantum remnants [55, 56], and alterations to the causal structure near the event horizon. Consequently, the electromagnetic spectrum, luminosity, and temporal variability of the radiation from these disks are expected to differ significantly from those of classical black holes. Studying these differences offers a pathway to indirect observational evidence for quantum gravitational effects, advancing efforts toward a unified theory of quantum gravity [57].
This study aims to explore the radiation properties of such a thin accretion disk using the geometrically thin and optically thick Novikov-Thorne disk model [58, 59] around the quantum-corrected black hole, focusing on how quantum corrections affect the flux of the electromagnetic radiation, the accretion disk's temperature, spectral and differential luminosities. By comparing these properties with the Schwarzschild BH [1, 2], we seek to identify potential observational tests for the existence of quantum corrections. Such investigations are not only crucial for advancing our understanding of black hole physics but also for probing the fundamental nature of spacetime and gravity.
This paper is organized as follows: In Sec. II we briefly review a quantum-corrected BH spacetime. In Sec. III, we briefly introduce the Novikov-Thorne model. Additionally, we explore the innermost stable circular orbits (ISCO) parameters and the radiative efficiency. Further, we analyze the radiative properties of the accretion disk of the quantum-corrected BH in Sec. IV. Finally, we give our concluding remarks in Sec. V. Throughout this paper, we use the
$ (-, +, +, +) $ signature for the spacetime metric and a system of units in which we set$ G=c=1 $ , unless the constants are directly stated. -
The Oppenheimer-Snyder model [60] is a significant model for describing BHs. However, this model faces problems due to the Big Bang singularity, which suggests the model provides an incomplete description of black hole formation and the early universe. Moreover, it neglects quantum effects. Therefore, the authors of Ref. [61] suggested a quantum-corrected BH model in the framework of LQG. These quantum effects prevent the formation of a spacetime singularity through modifications to the Schwarzschild solution. In this chapter, we review the static and spherically symmetric quantum-corrected BH in Boyer–Lindquist coordinates
$ (t, r, \theta, \phi) $ as given by [61, 62].$ \begin{eqnarray} \begin{aligned} {\rm d} s^2=&-f(r){\rm d} t^2+f(r)^{-1}{\rm d} r^2+r^2{\rm d}\Omega^2, \end{aligned} \end{eqnarray} $

(1) where
$ \begin{eqnarray} f(r)=\left(1-\frac{2G M}{r}+\frac{\alpha G^2M^2}{r^4}\right)\, , \end{eqnarray} $

(2) where M refers to the Arnowitt–Deser–Misner mass, while
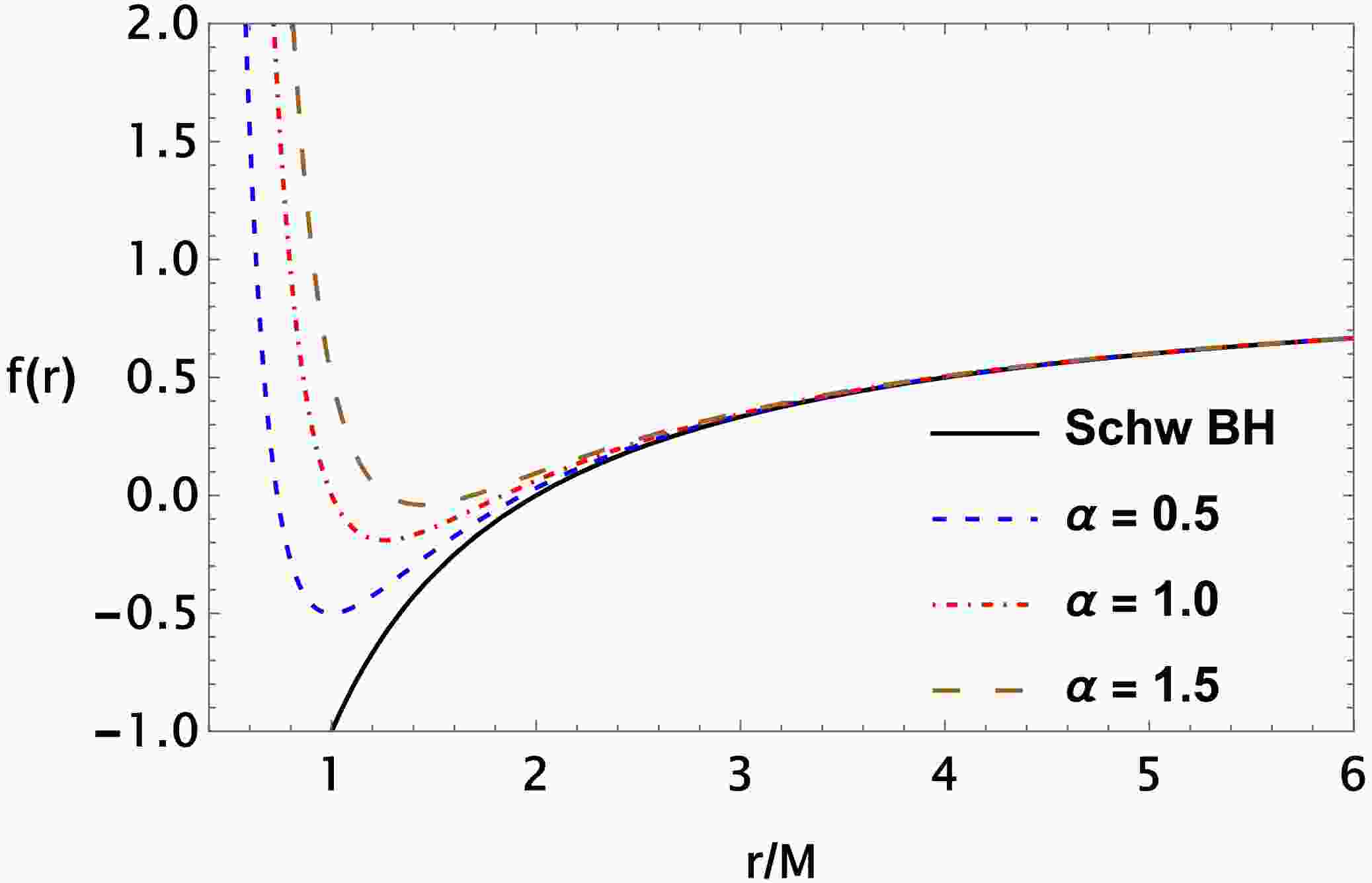
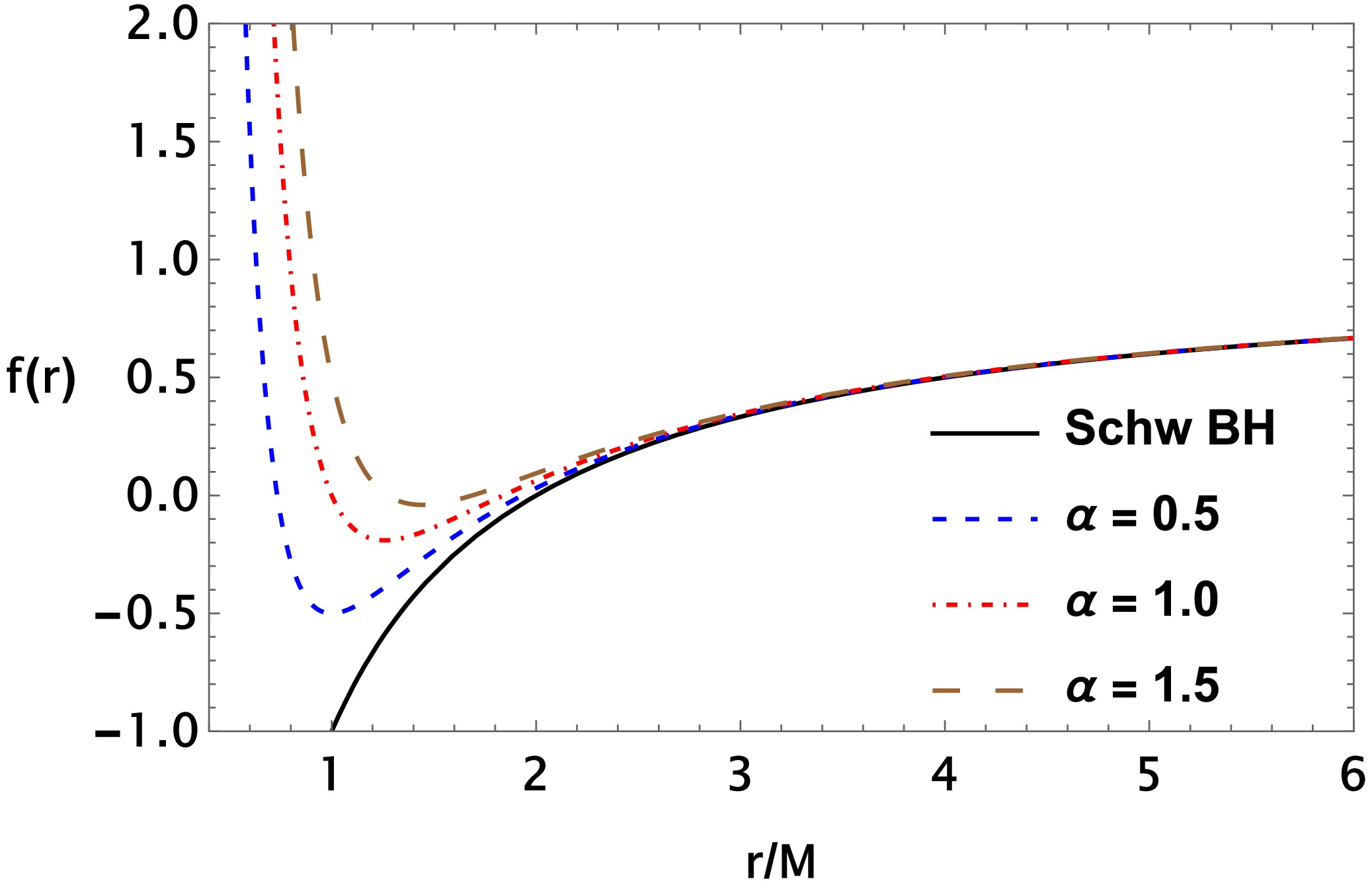
$ \alpha=16\sqrt{3}\pi\gamma^3\ell_p^2 $ represents the quantum correction parameter, with the Planck length$ \ell_p=\sqrt{G\hbar} $ and the Barbero–Immirzi parameter γ. For simplicity in further analysis, we will treat α as a dimensionless quantity by rescaling it as$ \alpha \to \alpha/M^2 $ and adopting units where$ G = c = \hbar = 1 $ . Note that the given metric reduces to the Schwarzschild BH in the$ \alpha \to 0 $ limit. It is worth noting that the Barbero–Immirzi parameter γ plays a crucial role in LQG, where the spectrum of quantum geometry operators depends on its value. For example, one can quantize the area of a surface and the volume of a space region in units of$ \gamma l_p^2 $ and$ \gamma^{3/2} l_p^{3} $ , respectively [63]. In Fig. 1, we demonstrate the radial profile of the metric function of the quantum-corrected BH for different values of the α parameter. As can be observed from this figure, the zeros of the metric function correspond to the location of the horizons of the quantum-corrected BH. In addition, as the quantum correction parameter α increases, the Cauchy and event horizons become closer to each other. -
The Oppenheimer-Snyder model [60] is a significant model for describing BHs. However, this model faces problems due to the Big Bang singularity, which suggests the model provides an incomplete description of black hole formation and the early universe. Moreover, it neglects quantum effects. Therefore, the authors of Ref. [61] suggested a quantum-corrected BH model in the framework of LQG. These quantum effects prevent the formation of a spacetime singularity through modifications to the Schwarzschild solution. In this chapter, we review the static and spherically symmetric quantum-corrected BH in Boyer–Lindquist coordinates
$ (t, r, \theta, \phi) $ as given by [61, 62].$ \begin{eqnarray} \begin{aligned} {\rm d} s^2=&-f(r){\rm d} t^2+f(r)^{-1}{\rm d} r^2+r^2{\rm d}\Omega^2, \end{aligned} \end{eqnarray} $

(1) where
$ \begin{eqnarray} f(r)=\left(1-\frac{2G M}{r}+\frac{\alpha G^2M^2}{r^4}\right)\, , \end{eqnarray} $

(2) where M refers to the Arnowitt–Deser–Misner mass, while
$ \alpha=16\sqrt{3}\pi\gamma^3\ell_p^2 $ represents the quantum correction parameter, with the Planck length$ \ell_p=\sqrt{G\hbar} $ and the Barbero–Immirzi parameter γ. For simplicity in further analysis, we will treat α as a dimensionless quantity by rescaling it as$ \alpha \to \alpha/M^2 $ and adopting units where$ G = c = \hbar = 1 $ . Note that the given metric reduces to the Schwarzschild BH in the$ \alpha \to 0 $ limit. It is worth noting that the Barbero–Immirzi parameter γ plays a crucial role in LQG, where the spectrum of quantum geometry operators depends on its value. For example, one can quantize the area of a surface and the volume of a space region in units of$ \gamma l_p^2 $ and$ \gamma^{3/2} l_p^{3} $ , respectively [63]. In Fig. 1, we demonstrate the radial profile of the metric function of the quantum-corrected BH for different values of the α parameter. As can be observed from this figure, the zeros of the metric function correspond to the location of the horizons of the quantum-corrected BH. In addition, as the quantum correction parameter α increases, the Cauchy and event horizons become closer to each other. -
The Oppenheimer-Snyder model [60] is a significant model for describing BHs. However, this model faces problems due to the Big Bang singularity, which suggests the model provides an incomplete description of black hole formation and the early universe. Moreover, it neglects quantum effects. Therefore, the authors of Ref. [61] suggested a quantum-corrected BH model in the framework of LQG. These quantum effects prevent the formation of a spacetime singularity through modifications to the Schwarzschild solution. In this chapter, we review the static and spherically symmetric quantum-corrected BH in Boyer–Lindquist coordinates
$ (t, r, \theta, \phi) $ as given by [61, 62].$ \begin{eqnarray} \begin{aligned} {\rm d} s^2=&-f(r){\rm d} t^2+f(r)^{-1}{\rm d} r^2+r^2{\rm d}\Omega^2, \end{aligned} \end{eqnarray} $

(1) where
$ \begin{eqnarray} f(r)=\left(1-\frac{2G M}{r}+\frac{\alpha G^2M^2}{r^4}\right)\, , \end{eqnarray} $

(2) where M refers to the Arnowitt–Deser–Misner mass, while
$ \alpha=16\sqrt{3}\pi\gamma^3\ell_p^2 $ represents the quantum correction parameter, with the Planck length$ \ell_p=\sqrt{G\hbar} $ and the Barbero–Immirzi parameter γ. For simplicity in further analysis, we will treat α as a dimensionless quantity by rescaling it as$ \alpha \to \alpha/M^2 $ and adopting units where$ G = c = \hbar = 1 $ . Note that the given metric reduces to the Schwarzschild BH in the$ \alpha \to 0 $ limit. It is worth noting that the Barbero–Immirzi parameter γ plays a crucial role in LQG, where the spectrum of quantum geometry operators depends on its value. For example, one can quantize the area of a surface and the volume of a space region in units of$ \gamma l_p^2 $ and$ \gamma^{3/2} l_p^{3} $ , respectively [63]. In Fig. 1, we demonstrate the radial profile of the metric function of the quantum-corrected BH for different values of the α parameter. As can be observed from this figure, the zeros of the metric function correspond to the location of the horizons of the quantum-corrected BH. In addition, as the quantum correction parameter α increases, the Cauchy and event horizons become closer to each other. -
According to the Novikov-Thorne model [58], the accretion disk must be optically thick and geometrically thin near the quantum-corrected black hole. However, the accretion disk is extremely thin in vertical size while it extends significantly in the horizontal direction. This results in a negligible vertical size compared to its extensive horizontal extension. Therefore, its height h is much smaller than the radius r of the disk, which extends in the horizontal direction, i.e.,
$ h \ll r $ . Based on the properties of the thin accretion disk formed around the quantum-corrected black hole and the hydrodynamic equilibrium of the disk, the vertical entropy and pressure gradients are considered negligible in the accreting matter. The heat generated by stress and dynamical friction cannot accumulate in the accretion disk, as it is efficiently cooled by the thermal radiation emitted from the disk's surface. Hence, this results in a stabilized thin disk, with its inner edge situated in a stable orbit around the black hole, where the plasma follows Keplerian motion in these stable orbits. We now define the energy efficiency based on the radiation rate of the photon energy emitted from the disk's surface [58, 64]. One can write the corresponding equation as$ \eta=1-{{\cal{E}}_{\rm ISCO}}\ . $

(3) We can see from the equation above that the efficiency can be determined by the measured energy at the ISCO. Therefore, it is important to determine the ISCO parameters
$ r_{\rm ISCO} $ ,$ {\cal L}_{\rm ISCO} $ , and$ {\cal E}_{\rm ISCO} $ . To achieve this, it is necessary to consider the dynamics of test particles around the quantum-corrected BH. One can write the standard form of the effective potential for the radial motion of the test particles as follows [65].$ \begin{equation} V_{\rm eff}(r)=-1+\dfrac{{\cal{E}}^2 g_{\phi \phi}+2 {\cal{E}} {\cal{L}} g_{t \phi}+{\cal{L}}^2 g_{tt}}{g^2_{t \phi}-g_{tt}g_{\phi \phi}}\, , \end{equation} $

(4) where
$ {\cal{E}}=E/m $ and$ {\cal{L}}=L/m $ refer to the specific energy and angular momentum. It is worth noting that the metric functions are given by$ g_{tt}=-f(r) $ and$ g_{\phi \phi}=r^2\sin^2\theta $ , with$ g_{t\phi}=0 $ for a static and spherically symmetric black hole. Consequently, we can express the conserved quantities in terms of the metric tensors in the following form:$ \begin{equation} {\cal{E}}=-\dfrac{g_{tt}}{\sqrt{-g_{tt}-\Omega^2 g_{\phi \phi}}}\, , \end{equation} $

(5) and
$ \begin{equation} {\cal{L}}=\dfrac{\Omega g_{\phi \phi}}{\sqrt{-g_{tt}-\Omega^2 g_{\phi \phi}}}\, , \end{equation} $

(6) where Ω is the orbital angular velocity of the test particles, as given by [66−68].
$ \begin{equation} \Omega=\dfrac{{\rm d} \phi}{{\rm d} t}=\sqrt{-\dfrac{g_{tt,r}}{g_{\phi \phi,r}}}\ . \end{equation} $

(7) We also consider motion in the equatorial plane,
$ \theta = \pi/2 $ . According to the Novikov-Thorne model, the inner edge of the accretion disk can be determined by the ISCO radius, which is defined by the following conditions:$ \begin{equation} V_{\rm eff}(r)=0, \quad V'_{\rm eff}(r)=0, \quad V''_{\rm eff}(r)=0. \end{equation} $

(8) Using the above-mentioned conditions, we can find the ISCO parameters and the radiative efficiency. The results are demonstrated in Table 1. One can see from this table that ISCO parameters decrease slightly under the influence of the quantum correction parameter α. In contrast, there is a slight increase in radiative efficiency with the increase of the α parameter. It should be noted that the first row of Table 1 refers to the corresponding values for the Schwarzschild BH.
α $r_{\rm ISCO}$ 

${{\cal{L}}}_{\text{ISCO}}$ 

${\cal{E}}_{\text{ISCO}}$ 

η% 0.0 6.00000 3.46410 0.942809 5.71910 0.2 5.96909 3.45925 0.942588 5.74121 0.4 5.93746 3.45430 0.942361 5.76393 0.6 5.90505 3.44925 0.942127 5.78729 0.8 5.87181 3.44411 0.941887 5.81133 1.0 5.83769 3.43885 0.941639 5.83609 Table 1. The innermost stable circular orbit (ISCO) parameters and the radiative efficiency of the accretion disk are tabulated for different values of the quantum correction parameter α.
-
According to the Novikov-Thorne model [58], the accretion disk must be optically thick and geometrically thin near the quantum-corrected black hole. However, the accretion disk is extremely thin in vertical size while it extends significantly in the horizontal direction. This results in a negligible vertical size compared to its extensive horizontal extension. Therefore, its height h is much smaller than the radius r of the disk, which extends in the horizontal direction, i.e.,
$ h \ll r $ . Based on the properties of the thin accretion disk formed around the quantum-corrected black hole and the hydrodynamic equilibrium of the disk, the vertical entropy and pressure gradients are considered negligible in the accreting matter. The heat generated by stress and dynamical friction cannot accumulate in the accretion disk, as it is efficiently cooled by the thermal radiation emitted from the disk's surface. Hence, this results in a stabilized thin disk, with its inner edge situated in a stable orbit around the black hole, where the plasma follows Keplerian motion in these stable orbits. We now define the energy efficiency based on the radiation rate of the photon energy emitted from the disk's surface [58, 64]. One can write the corresponding equation as$ \eta=1-{{\cal{E}}_{\rm ISCO}}\ . $

(3) We can see from the equation above that the efficiency can be determined by the measured energy at the ISCO. Therefore, it is important to determine the ISCO parameters
$ r_{\rm ISCO} $ ,$ {\cal L}_{\rm ISCO} $ , and$ {\cal E}_{\rm ISCO} $ . To achieve this, it is necessary to consider the dynamics of test particles around the quantum-corrected BH. One can write the standard form of the effective potential for the radial motion of the test particles as follows [65].$ \begin{equation} V_{\rm eff}(r)=-1+\dfrac{{\cal{E}}^2 g_{\phi \phi}+2 {\cal{E}} {\cal{L}} g_{t \phi}+{\cal{L}}^2 g_{tt}}{g^2_{t \phi}-g_{tt}g_{\phi \phi}}\, , \end{equation} $

(4) where
$ {\cal{E}}=E/m $ and$ {\cal{L}}=L/m $ refer to the specific energy and angular momentum. It is worth noting that the metric functions are given by$ g_{tt}=-f(r) $ and$ g_{\phi \phi}=r^2\sin^2\theta $ , with$ g_{t\phi}=0 $ for a static and spherically symmetric black hole. Consequently, we can express the conserved quantities in terms of the metric tensors in the following form:$ \begin{equation} {\cal{E}}=-\dfrac{g_{tt}}{\sqrt{-g_{tt}-\Omega^2 g_{\phi \phi}}}\, , \end{equation} $

(5) and
$ \begin{equation} {\cal{L}}=\dfrac{\Omega g_{\phi \phi}}{\sqrt{-g_{tt}-\Omega^2 g_{\phi \phi}}}\, , \end{equation} $

(6) where Ω is the orbital angular velocity of the test particles, as given by [66−68].
$ \begin{equation} \Omega=\dfrac{{\rm d} \phi}{{\rm d} t}=\sqrt{-\dfrac{g_{tt,r}}{g_{\phi \phi,r}}}\ . \end{equation} $

(7) We also consider motion in the equatorial plane,
$ \theta = \pi/2 $ . According to the Novikov-Thorne model, the inner edge of the accretion disk can be determined by the ISCO radius, which is defined by the following conditions:$ \begin{equation} V_{\rm eff}(r)=0, \quad V'_{\rm eff}(r)=0, \quad V''_{\rm eff}(r)=0. \end{equation} $

(8) Using the above-mentioned conditions, we can find the ISCO parameters and the radiative efficiency. The results are demonstrated in Table 1. One can see from this table that ISCO parameters decrease slightly under the influence of the quantum correction parameter α. In contrast, there is a slight increase in radiative efficiency with the increase of the α parameter. It should be noted that the first row of Table 1 refers to the corresponding values for the Schwarzschild BH.
α $r_{\rm ISCO}$ 

${{\cal{L}}}_{\text{ISCO}}$ 

${\cal{E}}_{\text{ISCO}}$ 

η% 0.0 6.00000 3.46410 0.942809 5.71910 0.2 5.96909 3.45925 0.942588 5.74121 0.4 5.93746 3.45430 0.942361 5.76393 0.6 5.90505 3.44925 0.942127 5.78729 0.8 5.87181 3.44411 0.941887 5.81133 1.0 5.83769 3.43885 0.941639 5.83609 Table 1. The innermost stable circular orbit (ISCO) parameters and the radiative efficiency of the accretion disk are tabulated for different values of the quantum correction parameter α.
-
According to the Novikov-Thorne model [58], the accretion disk must be optically thick and geometrically thin near the quantum-corrected black hole. However, the accretion disk is extremely thin in vertical size while it extends significantly in the horizontal direction. This results in a negligible vertical size compared to its extensive horizontal extension. Therefore, its height h is much smaller than the radius r of the disk, which extends in the horizontal direction, i.e.,
$ h \ll r $ . Based on the properties of the thin accretion disk formed around the quantum-corrected black hole and the hydrodynamic equilibrium of the disk, the vertical entropy and pressure gradients are considered negligible in the accreting matter. The heat generated by stress and dynamical friction cannot accumulate in the accretion disk, as it is efficiently cooled by the thermal radiation emitted from the disk's surface. Hence, this results in a stabilized thin disk, with its inner edge situated in a stable orbit around the black hole, where the plasma follows Keplerian motion in these stable orbits. We now define the energy efficiency based on the radiation rate of the photon energy emitted from the disk's surface [58, 64]. One can write the corresponding equation as$ \eta=1-{{\cal{E}}_{\rm ISCO}}\ . $

(3) We can see from the equation above that the efficiency can be determined by the measured energy at the ISCO. Therefore, it is important to determine the ISCO parameters
$ r_{\rm ISCO} $ ,$ {\cal L}_{\rm ISCO} $ , and$ {\cal E}_{\rm ISCO} $ . To achieve this, it is necessary to consider the dynamics of test particles around the quantum-corrected BH. One can write the standard form of the effective potential for the radial motion of the test particles as follows [65].$ \begin{equation} V_{\rm eff}(r)=-1+\dfrac{{\cal{E}}^2 g_{\phi \phi}+2 {\cal{E}} {\cal{L}} g_{t \phi}+{\cal{L}}^2 g_{tt}}{g^2_{t \phi}-g_{tt}g_{\phi \phi}}\, , \end{equation} $

(4) where
$ {\cal{E}}=E/m $ and$ {\cal{L}}=L/m $ refer to the specific energy and angular momentum. It is worth noting that the metric functions are given by$ g_{tt}=-f(r) $ and$ g_{\phi \phi}=r^2\sin^2\theta $ , with$ g_{t\phi}=0 $ for a static and spherically symmetric black hole. Consequently, we can express the conserved quantities in terms of the metric tensors in the following form:$ \begin{equation} {\cal{E}}=-\dfrac{g_{tt}}{\sqrt{-g_{tt}-\Omega^2 g_{\phi \phi}}}\, , \end{equation} $

(5) and
$ \begin{equation} {\cal{L}}=\dfrac{\Omega g_{\phi \phi}}{\sqrt{-g_{tt}-\Omega^2 g_{\phi \phi}}}\, , \end{equation} $

(6) where Ω is the orbital angular velocity of the test particles, as given by [66−68].
$ \begin{equation} \Omega=\dfrac{{\rm d} \phi}{{\rm d} t}=\sqrt{-\dfrac{g_{tt,r}}{g_{\phi \phi,r}}}\ . \end{equation} $

(7) We also consider motion in the equatorial plane,
$ \theta = \pi/2 $ . According to the Novikov-Thorne model, the inner edge of the accretion disk can be determined by the ISCO radius, which is defined by the following conditions:$ \begin{equation} V_{\rm eff}(r)=0, \quad V'_{\rm eff}(r)=0, \quad V''_{\rm eff}(r)=0. \end{equation} $

(8) Using the above-mentioned conditions, we can find the ISCO parameters and the radiative efficiency. The results are demonstrated in Table 1. One can see from this table that ISCO parameters decrease slightly under the influence of the quantum correction parameter α. In contrast, there is a slight increase in radiative efficiency with the increase of the α parameter. It should be noted that the first row of Table 1 refers to the corresponding values for the Schwarzschild BH.
α $r_{\rm ISCO}$ 

${{\cal{L}}}_{\text{ISCO}}$ 

${\cal{E}}_{\text{ISCO}}$ 

η% 0.0 6.00000 3.46410 0.942809 5.71910 0.2 5.96909 3.45925 0.942588 5.74121 0.4 5.93746 3.45430 0.942361 5.76393 0.6 5.90505 3.44925 0.942127 5.78729 0.8 5.87181 3.44411 0.941887 5.81133 1.0 5.83769 3.43885 0.941639 5.83609 Table 1. The innermost stable circular orbit (ISCO) parameters and the radiative efficiency of the accretion disk are tabulated for different values of the quantum correction parameter α.
-
In this section, we explore the flux produced by an accretion disk of a quantum-corrected black hole. It is worth noting that an accretion disk is composed of gas and dust moving in stable orbits around a black hole or neutron star. Gas and dust can lose energy and angular momentum due to the influence of the surrounding geometry as they begin to orbit the compact object. Consequently, the orbits of the gas and dust shift toward the inner edge of the accretion disk, eventually causing them to descend toward the compact object. This process leads to accretion disk radiation, where gas and dust heat up and release energy as radiation. We expect that the quantum-corrected black hole parameters can affect the accretion disk radiation. In particular, the α parameter of the black hole can influence the gas and dust in the surrounding accretion disk, leading to a highly ionized state within the disk. As a result of the ionization process, high-energy radiation is emitted as X-rays, which can be detected. The radiation from the accretion disk around a black hole is considered a powerful tool for investigating key aspects of the disk and may have significant implications for observational studies. One can write the equation for the flux of the electromagnetic radiation as follows [58, 59, 69].
$ \begin{equation} {\cal{F}}(r)=-\dfrac{\dot{M_0}}{4 \pi \sqrt{g}}\dfrac{\Omega_{,r}}{(E-\Omega L)^2} \int _{r_{\rm ISCO}}^r (E-\Omega L) L_{,r} {\rm d} r\, , \end{equation} $

(9) where g is the determinant of the three-dimensional subspace
$ g=\sqrt{-g_{tt}g_{rr}g_{\phi \phi}} $ with ($ t, r, \phi $ ) coordinates. The quantity$ {\cal{F}}(r) $ is defined as a function of$ \dot{M_0} $ , which represents the accretion rate of the disk mass and is treated as unknown. However, for simplicity, one can set$ \dot{M_0}=1 $ .One can derive the flux of the electromagnetic radiation using Eqs. (5) and (6). It is complicated to derive analytically; thus, we explore it numerically in Fig. 2. It can be shown from this figure that the value of the flux of electromagnetic radiation increases with the increasing α parameter. We note that the blue line corresponds to the Schwarzschild BH case in this figure. In addition, we turn to the disk temperature, which is another important quantity of electromagnetic radiation. The flux of the black body radiation can be written as
$ {\cal{F}}(r)=\sigma T^4 $ , where σ is the Stefan-Boltzmann constant. We can plot the radial dependence of the disk temperature and energy for different values of the α parameter in Fig. 3. It can be seen from this figure that there is a slight increase under the influence of the α parameter. One can plot the temperature by a "density plot" in Fig. 4 to provide more information. From Fig. 4, it is evident that the dark region is located within the inner edge of the accretion disk, while the red areas represent regions where the disk's temperature reaches its peak value.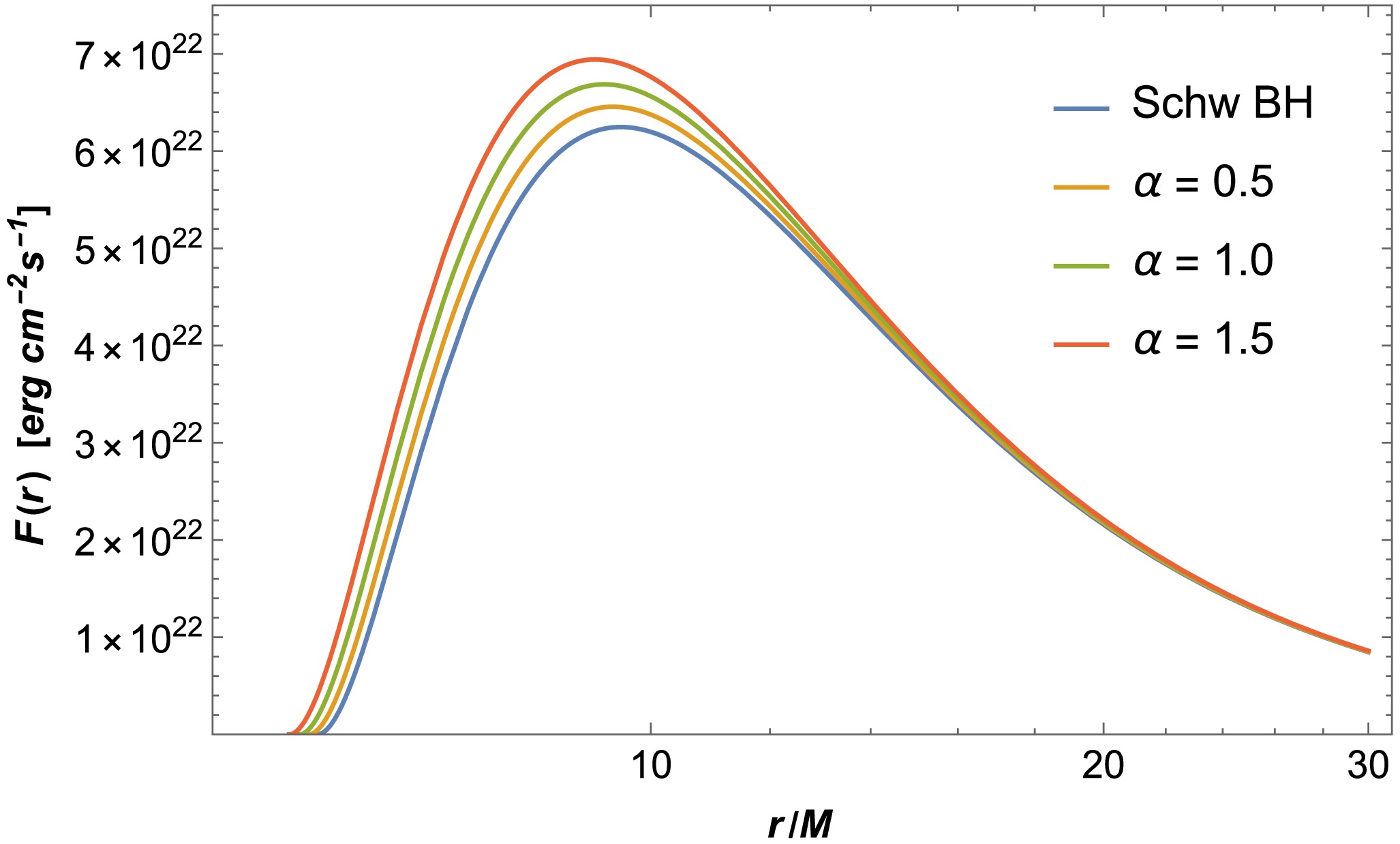
Figure 2. (color online) The radial profile of the flux of electromagnetic radiation from the accretion disk for different values of the quantum correction parameter α.
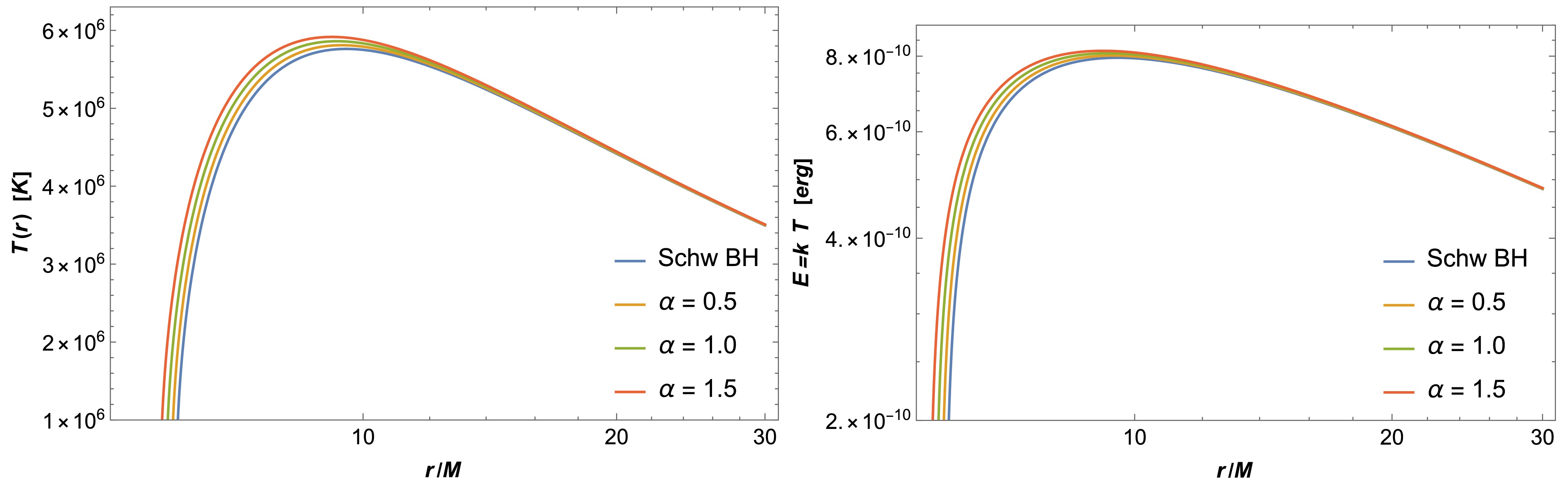
Figure 3. (color online) The radial profile of the temperature of the accretion disk is analyzed for different values of the quantum correction parametα.
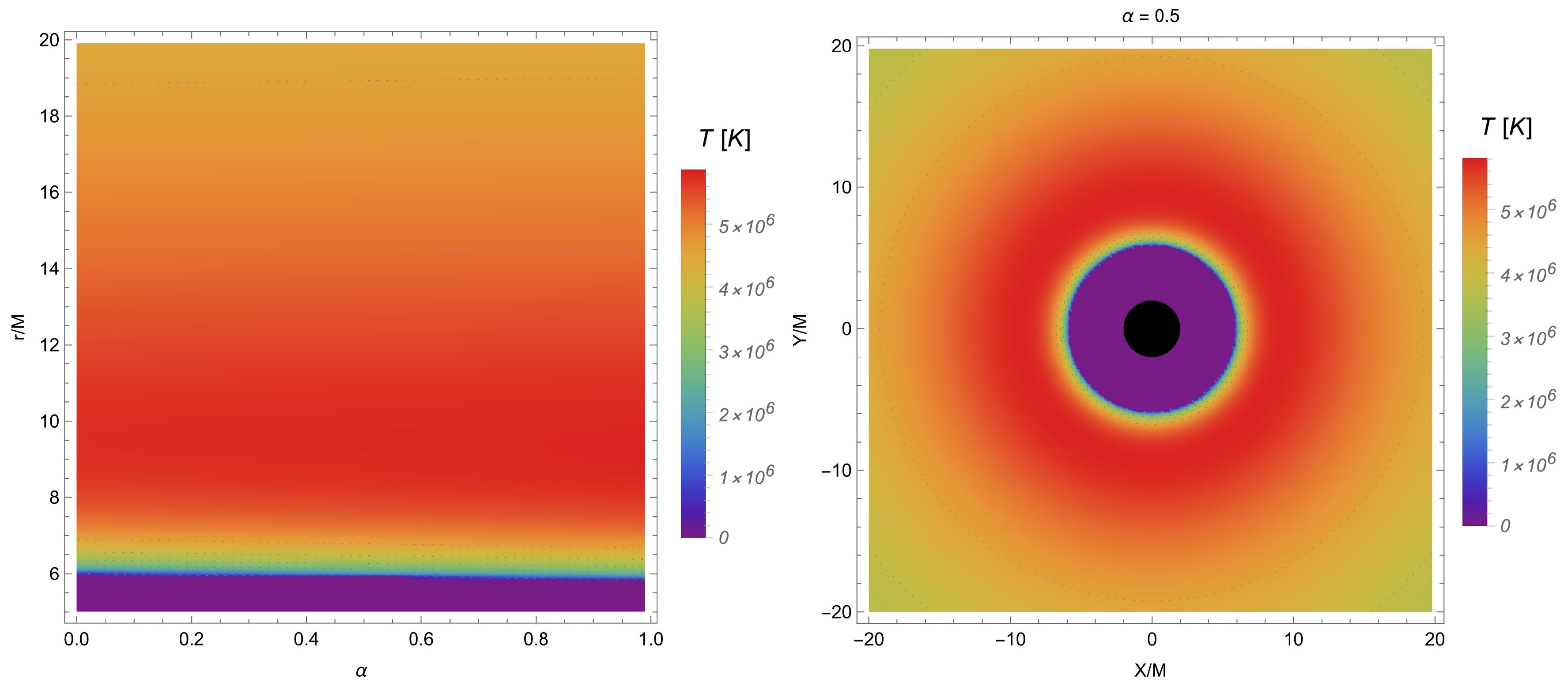
Figure 4. (color online) The temperature profile of the accretion disk is plotted for different values of the quantum correction parameter α. The left panel refers to the parameter space (r, α). The right panel depicts the density plot of the temperature of the accretion disk at the equatorial
$ X-Y $ plane of the quantum-corrected black hole (BH). Here, X and Y are Cartesian coordinates.In addition, we consider the differential luminosity, which is defined as follows [58, 59, 69]
$ \begin{equation} \dfrac{{\rm d} {\cal{L}}_{\infty}}{{\rm d} \ln{r}}=4 \pi r \sqrt{g} E {\cal{F}}(r)\, . \end{equation} $

(10) Here, we note that we have used the numerical method instead of the analytical method. The radial dependence of the differential luminosity of the accretion disk is demonstrated in Fig. 5. We can see from this figure that there is a slight increase with the increase of the α parameter. Note that
$ \alpha=0 $ corresponds to the Schwarzschild-BH case. We then turn to another important quantity of the accretion disk: spectral luminosity. Here, we assume for simplicity that black body radiation can be considered to describe the radiation emission. After that, we can define the spectral luminosity$ {\cal{L}}_{\nu,\infty} $ in terms of the radiation frequency ν [70−80].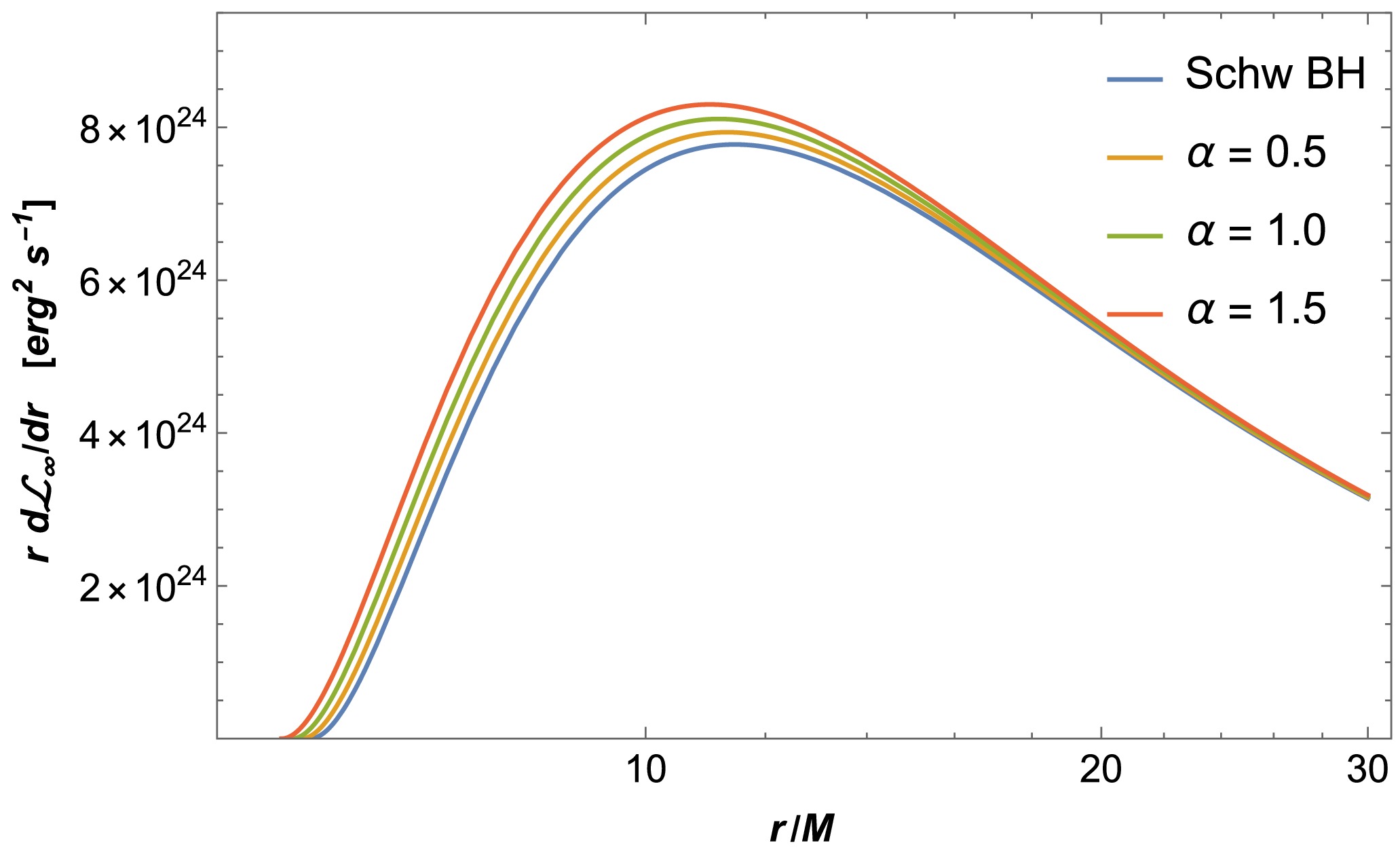
Figure 5. (color online) The radial dependence of the differential luminosity of the accretion disk around the quantum-corrected black hole.
$ \begin{equation} \nu {\cal{L}}_{\nu,\infty}=\dfrac{60}{\pi^3} \int_{r_{\rm ISCO}}^{\infty} \dfrac{\sqrt{g} E}{M^2}\dfrac{(u^t y)^4}{\exp\Big[{\dfrac{u^t y}{(M^2 {\cal{F}})^{1/4}}}\Big]-1} {\rm d}r\, , \end{equation} $

(11) where y equals
$ h \nu /k T_{\star} $ . h and k refer to the Planck constant and the Boltzmann constant, respectively. We emphasize that$ T_{\star} $ is the characteristic temperature associated with the Stefan-Boltzmann law, which is defined as follows:$ \begin{eqnarray} \sigma T_{\star}= \dfrac{\dot{M}_0}{4 \pi M^2}\, , \end{eqnarray} $

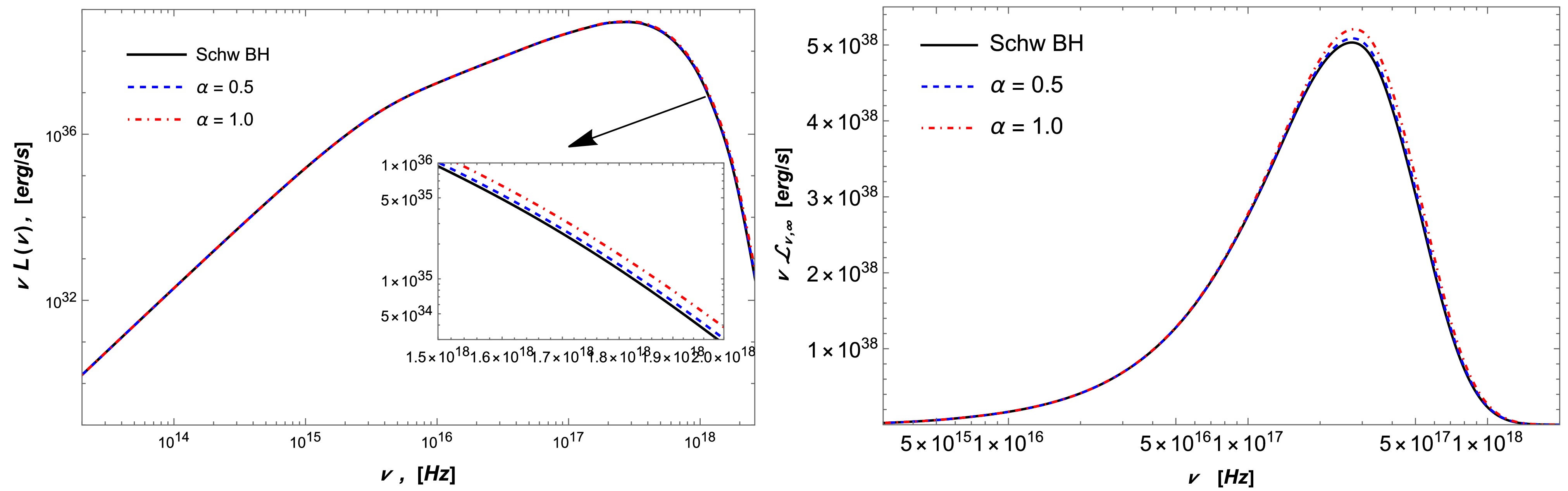
(12) where σ refers to the Stefan-Boltzmann constant. Then, we plot the dependence of the spectral luminosity of the accretion disk around the quantum-corrected BH on the radiation frequency in Fig. 6. As demonstrated in this figure, there is a slight increase under the influence of the α parameter.
-
In this section, we explore the flux produced by an accretion disk of a quantum-corrected black hole. It is worth noting that an accretion disk is composed of gas and dust moving in stable orbits around a black hole or neutron star. Gas and dust can lose energy and angular momentum due to the influence of the surrounding geometry as they begin to orbit the compact object. Consequently, the orbits of the gas and dust shift toward the inner edge of the accretion disk, eventually causing them to descend toward the compact object. This process leads to accretion disk radiation, where gas and dust heat up and release energy as radiation. We expect that the quantum-corrected black hole parameters can affect the accretion disk radiation. In particular, the α parameter of the black hole can influence the gas and dust in the surrounding accretion disk, leading to a highly ionized state within the disk. As a result of the ionization process, high-energy radiation is emitted as X-rays, which can be detected. The radiation from the accretion disk around a black hole is considered a powerful tool for investigating key aspects of the disk and may have significant implications for observational studies. One can write the equation for the flux of the electromagnetic radiation as follows [58, 59, 69].
$ \begin{equation} {\cal{F}}(r)=-\dfrac{\dot{M_0}}{4 \pi \sqrt{g}}\dfrac{\Omega_{,r}}{(E-\Omega L)^2} \int _{r_{\rm ISCO}}^r (E-\Omega L) L_{,r} {\rm d} r\, , \end{equation} $

(9) where g is the determinant of the three-dimensional subspace
$ g=\sqrt{-g_{tt}g_{rr}g_{\phi \phi}} $ with ($ t, r, \phi $ ) coordinates. The quantity$ {\cal{F}}(r) $ is defined as a function of$ \dot{M_0} $ , which represents the accretion rate of the disk mass and is treated as unknown. However, for simplicity, one can set$ \dot{M_0}=1 $ .One can derive the flux of the electromagnetic radiation using Eqs. (5) and (6). It is complicated to derive analytically; thus, we explore it numerically in Fig. 2. It can be shown from this figure that the value of the flux of electromagnetic radiation increases with the increasing α parameter. We note that the blue line corresponds to the Schwarzschild BH case in this figure. In addition, we turn to the disk temperature, which is another important quantity of electromagnetic radiation. The flux of the black body radiation can be written as
$ {\cal{F}}(r)=\sigma T^4 $ , where σ is the Stefan-Boltzmann constant. We can plot the radial dependence of the disk temperature and energy for different values of the α parameter in Fig. 3. It can be seen from this figure that there is a slight increase under the influence of the α parameter. One can plot the temperature by a "density plot" in Fig. 4 to provide more information. From Fig. 4, it is evident that the dark region is located within the inner edge of the accretion disk, while the red areas represent regions where the disk's temperature reaches its peak value.
Figure 2. (color online) The radial profile of the flux of electromagnetic radiation from the accretion disk for different values of the quantum correction parameter α.

Figure 3. (color online) The radial profile of the temperature of the accretion disk is analyzed for different values of the quantum correction parametα.

Figure 4. (color online) The temperature profile of the accretion disk is plotted for different values of the quantum correction parameter α. The left panel refers to the parameter space (r, α). The right panel depicts the density plot of the temperature of the accretion disk at the equatorial
$ X-Y $ plane of the quantum-corrected black hole (BH). Here, X and Y are Cartesian coordinates.In addition, we consider the differential luminosity, which is defined as follows [58, 59, 69]
$ \begin{equation} \dfrac{{\rm d} {\cal{L}}_{\infty}}{{\rm d} \ln{r}}=4 \pi r \sqrt{g} E {\cal{F}}(r)\, . \end{equation} $

(10) Here, we note that we have used the numerical method instead of the analytical method. The radial dependence of the differential luminosity of the accretion disk is demonstrated in Fig. 5. We can see from this figure that there is a slight increase with the increase of the α parameter. Note that
$ \alpha=0 $ corresponds to the Schwarzschild-BH case. We then turn to another important quantity of the accretion disk: spectral luminosity. Here, we assume for simplicity that black body radiation can be considered to describe the radiation emission. After that, we can define the spectral luminosity$ {\cal{L}}_{\nu,\infty} $ in terms of the radiation frequency ν [70−80].
Figure 5. (color online) The radial dependence of the differential luminosity of the accretion disk around the quantum-corrected black hole.
$ \begin{equation} \nu {\cal{L}}_{\nu,\infty}=\dfrac{60}{\pi^3} \int_{r_{\rm ISCO}}^{\infty} \dfrac{\sqrt{g} E}{M^2}\dfrac{(u^t y)^4}{\exp\Big[{\dfrac{u^t y}{(M^2 {\cal{F}})^{1/4}}}\Big]-1} {\rm d}r\, , \end{equation} $

(11) where y equals
$ h \nu /k T_{\star} $ . h and k refer to the Planck constant and the Boltzmann constant, respectively. We emphasize that$ T_{\star} $ is the characteristic temperature associated with the Stefan-Boltzmann law, which is defined as follows:$ \begin{eqnarray} \sigma T_{\star}= \dfrac{\dot{M}_0}{4 \pi M^2}\, , \end{eqnarray} $

(12) where σ refers to the Stefan-Boltzmann constant. Then, we plot the dependence of the spectral luminosity of the accretion disk around the quantum-corrected BH on the radiation frequency in Fig. 6. As demonstrated in this figure, there is a slight increase under the influence of the α parameter.
-
In this section, we explore the flux produced by an accretion disk of a quantum-corrected black hole. It is worth noting that an accretion disk is composed of gas and dust moving in stable orbits around a black hole or neutron star. Gas and dust can lose energy and angular momentum due to the influence of the surrounding geometry as they begin to orbit the compact object. Consequently, the orbits of the gas and dust shift toward the inner edge of the accretion disk, eventually causing them to descend toward the compact object. This process leads to accretion disk radiation, where gas and dust heat up and release energy as radiation. We expect that the quantum-corrected black hole parameters can affect the accretion disk radiation. In particular, the α parameter of the black hole can influence the gas and dust in the surrounding accretion disk, leading to a highly ionized state within the disk. As a result of the ionization process, high-energy radiation is emitted as X-rays, which can be detected. The radiation from the accretion disk around a black hole is considered a powerful tool for investigating key aspects of the disk and may have significant implications for observational studies. One can write the equation for the flux of the electromagnetic radiation as follows [58, 59, 69].
$ \begin{equation} {\cal{F}}(r)=-\dfrac{\dot{M_0}}{4 \pi \sqrt{g}}\dfrac{\Omega_{,r}}{(E-\Omega L)^2} \int _{r_{\rm ISCO}}^r (E-\Omega L) L_{,r} {\rm d} r\, , \end{equation} $

(9) where g is the determinant of the three-dimensional subspace
$ g=\sqrt{-g_{tt}g_{rr}g_{\phi \phi}} $ with ($ t, r, \phi $ ) coordinates. The quantity$ {\cal{F}}(r) $ is defined as a function of$ \dot{M_0} $ , which represents the accretion rate of the disk mass and is treated as unknown. However, for simplicity, one can set$ \dot{M_0}=1 $ .One can derive the flux of the electromagnetic radiation using Eqs. (5) and (6). It is complicated to derive analytically; thus, we explore it numerically in Fig. 2. It can be shown from this figure that the value of the flux of electromagnetic radiation increases with the increasing α parameter. We note that the blue line corresponds to the Schwarzschild BH case in this figure. In addition, we turn to the disk temperature, which is another important quantity of electromagnetic radiation. The flux of the black body radiation can be written as
$ {\cal{F}}(r)=\sigma T^4 $ , where σ is the Stefan-Boltzmann constant. We can plot the radial dependence of the disk temperature and energy for different values of the α parameter in Fig. 3. It can be seen from this figure that there is a slight increase under the influence of the α parameter. One can plot the temperature by a "density plot" in Fig. 4 to provide more information. From Fig. 4, it is evident that the dark region is located within the inner edge of the accretion disk, while the red areas represent regions where the disk's temperature reaches its peak value.
Figure 2. (color online) The radial profile of the flux of electromagnetic radiation from the accretion disk for different values of the quantum correction parameter α.

Figure 3. (color online) The radial profile of the temperature of the accretion disk is analyzed for different values of the quantum correction parametα.

Figure 4. (color online) The temperature profile of the accretion disk is plotted for different values of the quantum correction parameter α. The left panel refers to the parameter space (r, α). The right panel depicts the density plot of the temperature of the accretion disk at the equatorial
$ X-Y $ plane of the quantum-corrected black hole (BH). Here, X and Y are Cartesian coordinates.In addition, we consider the differential luminosity, which is defined as follows [58, 59, 69]
$ \begin{equation} \dfrac{{\rm d} {\cal{L}}_{\infty}}{{\rm d} \ln{r}}=4 \pi r \sqrt{g} E {\cal{F}}(r)\, . \end{equation} $

(10) Here, we note that we have used the numerical method instead of the analytical method. The radial dependence of the differential luminosity of the accretion disk is demonstrated in Fig. 5. We can see from this figure that there is a slight increase with the increase of the α parameter. Note that
$ \alpha=0 $ corresponds to the Schwarzschild-BH case. We then turn to another important quantity of the accretion disk: spectral luminosity. Here, we assume for simplicity that black body radiation can be considered to describe the radiation emission. After that, we can define the spectral luminosity$ {\cal{L}}_{\nu,\infty} $ in terms of the radiation frequency ν [70−80].
Figure 5. (color online) The radial dependence of the differential luminosity of the accretion disk around the quantum-corrected black hole.
$ \begin{equation} \nu {\cal{L}}_{\nu,\infty}=\dfrac{60}{\pi^3} \int_{r_{\rm ISCO}}^{\infty} \dfrac{\sqrt{g} E}{M^2}\dfrac{(u^t y)^4}{\exp\Big[{\dfrac{u^t y}{(M^2 {\cal{F}})^{1/4}}}\Big]-1} {\rm d}r\, , \end{equation} $

(11) where y equals
$ h \nu /k T_{\star} $ . h and k refer to the Planck constant and the Boltzmann constant, respectively. We emphasize that$ T_{\star} $ is the characteristic temperature associated with the Stefan-Boltzmann law, which is defined as follows:$ \begin{eqnarray} \sigma T_{\star}= \dfrac{\dot{M}_0}{4 \pi M^2}\, , \end{eqnarray} $

(12) where σ refers to the Stefan-Boltzmann constant. Then, we plot the dependence of the spectral luminosity of the accretion disk around the quantum-corrected BH on the radiation frequency in Fig. 6. As demonstrated in this figure, there is a slight increase under the influence of the α parameter.
-
In this paper, we studied the radiation properties of the accretion disk around the quantum-corrected BH, and from this work, we can draw the following conclusions. Firstly, we analyzed the test particle motion around the quantum-corrected BH. We explored the ISCO parameters numerically (e.g., the specific energy, angular momentum, and ISCO radius). Further, we explored the flux of electromagnetic radiation using the Novikov-Thorne model. The radial profile of the flux is demonstrated in Fig. 2. It can be seen from this figure that the value of the flux of electromagnetic radiation increases with the increasing quantum correction parameter α. In addition, we studied the temperature of the accretion disk using blackbody radiation. The radial dependence of the disk's temperature is shown in Fig. 3. One can see from this figure that there is an increase with the increase of the α parameter. To be more informative, the accretion disk's temperature profile is plotted using a "color map" in Fig. 4. The left and right panels of this figure correspond to the parameter space (
$ r,\alpha $ ) and the equatorial$ X-Y $ plane, respectively. Moreover, the radial dependence of the differential luminosity was studied, and the corresponding figure is shown in Fig. 5. It is clearly seen in Fig. 5 that there is an increase under the influence of the quantum correction parameter α. Finally, we examined the spectral luminosity of the accretion disk. The dependence of spectral luminosity on the radiation frequency on a logarithmic scale and a regular scale is demonstrated in Fig. 6. It can be seen from this figure that the values of the spectral luminosity increase slightly with the increase of the quantum correction parameter.The quantum-corrected BH solution considered here, a modification of the Schwarzschild BH, addresses the singularity problem. Its geometry, differing from other BH solutions within loop quantum gravity, reveals that the collapse process depends on whether the collapsing matter density reaches the Planck scale. This model thus alters the BH structure compared to the BH solutions in GR. However, the quantum correction parameter is small in realistic scenarios. Current experimental limitations, such as the Event Horizon Telescope's (EHT) resolution (a few Schwarzschild radii), prevent definitive confirmation of quantum BH effects. Higher resolution may potentially reveal quantum effects. Future generations of space- and ground-based telescopes (e.g., LISA, Taiji, LIGO-Virgo, and advanced EHT projects) will be crucial in probing quantum effects on gravitational waves and optical properties with greater precision.
In this work, we examined the Novikov-Thorne model for the accretion disk around the quantum-corrected BH, which is well-suited for studying thermal emission and accurately modeling the thermal components observed in X-ray binaries. Our theoretical investigations of the accretion disk radiation in this framework aim to provide valuable insights for interpreting future astrophysical observations and probing the properties of quantum-corrected BHs. Therefore, our findings can improve our understanding of the radiative properties of quantum-corrected BHs and offer insight into observational deviations from other BH solutions. By analyzing the impact of the quantum correction parameter on the surrounding accretion disk, our theoretical results not only contribute to theoretical knowledge but also pave the way for future observational investigations of extreme spacetime regions near quantum-corrected BHs.
-
In this paper, we studied the radiation properties of the accretion disk around the quantum-corrected BH, and from this work, we can draw the following conclusions. Firstly, we analyzed the test particle motion around the quantum-corrected BH. We explored the ISCO parameters numerically (e.g., the specific energy, angular momentum, and ISCO radius). Further, we explored the flux of electromagnetic radiation using the Novikov-Thorne model. The radial profile of the flux is demonstrated in Fig. 2. It can be seen from this figure that the value of the flux of electromagnetic radiation increases with the increasing quantum correction parameter α. In addition, we studied the temperature of the accretion disk using blackbody radiation. The radial dependence of the disk's temperature is shown in Fig. 3. One can see from this figure that there is an increase with the increase of the α parameter. To be more informative, the accretion disk's temperature profile is plotted using a "color map" in Fig. 4. The left and right panels of this figure correspond to the parameter space (
$ r,\alpha $ ) and the equatorial$ X-Y $ plane, respectively. Moreover, the radial dependence of the differential luminosity was studied, and the corresponding figure is shown in Fig. 5. It is clearly seen in Fig. 5 that there is an increase under the influence of the quantum correction parameter α. Finally, we examined the spectral luminosity of the accretion disk. The dependence of spectral luminosity on the radiation frequency on a logarithmic scale and a regular scale is demonstrated in Fig. 6. It can be seen from this figure that the values of the spectral luminosity increase slightly with the increase of the quantum correction parameter.The quantum-corrected BH solution considered here, a modification of the Schwarzschild BH, addresses the singularity problem. Its geometry, differing from other BH solutions within loop quantum gravity, reveals that the collapse process depends on whether the collapsing matter density reaches the Planck scale. This model thus alters the BH structure compared to the BH solutions in GR. However, the quantum correction parameter is small in realistic scenarios. Current experimental limitations, such as the Event Horizon Telescope's (EHT) resolution (a few Schwarzschild radii), prevent definitive confirmation of quantum BH effects. Higher resolution may potentially reveal quantum effects. Future generations of space- and ground-based telescopes (e.g., LISA, Taiji, LIGO-Virgo, and advanced EHT projects) will be crucial in probing quantum effects on gravitational waves and optical properties with greater precision.
In this work, we examined the Novikov-Thorne model for the accretion disk around the quantum-corrected BH, which is well-suited for studying thermal emission and accurately modeling the thermal components observed in X-ray binaries. Our theoretical investigations of the accretion disk radiation in this framework aim to provide valuable insights for interpreting future astrophysical observations and probing the properties of quantum-corrected BHs. Therefore, our findings can improve our understanding of the radiative properties of quantum-corrected BHs and offer insight into observational deviations from other BH solutions. By analyzing the impact of the quantum correction parameter on the surrounding accretion disk, our theoretical results not only contribute to theoretical knowledge but also pave the way for future observational investigations of extreme spacetime regions near quantum-corrected BHs.
-
In this paper, we studied the radiation properties of the accretion disk around the quantum-corrected BH, and from this work, we can draw the following conclusions. Firstly, we analyzed the test particle motion around the quantum-corrected BH. We explored the ISCO parameters numerically (e.g., the specific energy, angular momentum, and ISCO radius). Further, we explored the flux of electromagnetic radiation using the Novikov-Thorne model. The radial profile of the flux is demonstrated in Fig. 2. It can be seen from this figure that the value of the flux of electromagnetic radiation increases with the increasing quantum correction parameter α. In addition, we studied the temperature of the accretion disk using blackbody radiation. The radial dependence of the disk's temperature is shown in Fig. 3. One can see from this figure that there is an increase with the increase of the α parameter. To be more informative, the accretion disk's temperature profile is plotted using a "color map" in Fig. 4. The left and right panels of this figure correspond to the parameter space (
$ r,\alpha $ ) and the equatorial$ X-Y $ plane, respectively. Moreover, the radial dependence of the differential luminosity was studied, and the corresponding figure is shown in Fig. 5. It is clearly seen in Fig. 5 that there is an increase under the influence of the quantum correction parameter α. Finally, we examined the spectral luminosity of the accretion disk. The dependence of spectral luminosity on the radiation frequency on a logarithmic scale and a regular scale is demonstrated in Fig. 6. It can be seen from this figure that the values of the spectral luminosity increase slightly with the increase of the quantum correction parameter.The quantum-corrected BH solution considered here, a modification of the Schwarzschild BH, addresses the singularity problem. Its geometry, differing from other BH solutions within loop quantum gravity, reveals that the collapse process depends on whether the collapsing matter density reaches the Planck scale. This model thus alters the BH structure compared to the BH solutions in GR. However, the quantum correction parameter is small in realistic scenarios. Current experimental limitations, such as the Event Horizon Telescope's (EHT) resolution (a few Schwarzschild radii), prevent definitive confirmation of quantum BH effects. Higher resolution may potentially reveal quantum effects. Future generations of space- and ground-based telescopes (e.g., LISA, Taiji, LIGO-Virgo, and advanced EHT projects) will be crucial in probing quantum effects on gravitational waves and optical properties with greater precision.
In this work, we examined the Novikov-Thorne model for the accretion disk around the quantum-corrected BH, which is well-suited for studying thermal emission and accurately modeling the thermal components observed in X-ray binaries. Our theoretical investigations of the accretion disk radiation in this framework aim to provide valuable insights for interpreting future astrophysical observations and probing the properties of quantum-corrected BHs. Therefore, our findings can improve our understanding of the radiative properties of quantum-corrected BHs and offer insight into observational deviations from other BH solutions. By analyzing the impact of the quantum correction parameter on the surrounding accretion disk, our theoretical results not only contribute to theoretical knowledge but also pave the way for future observational investigations of extreme spacetime regions near quantum-corrected BHs.
-
We warmly thank the anonymous referees for their valuable comments, which have definitely helped improve the accuracy and quality of the presentation of the manuscript.
-
We warmly thank the anonymous referees for their valuable comments, which have definitely helped improve the accuracy and quality of the presentation of the manuscript.
-
We warmly thank the anonymous referees for their valuable comments, which have definitely helped improve the accuracy and quality of the presentation of the manuscript.
Radiation properties of the accretion disk around a quantum-corrected black hole
- Received Date: 2025-08-14
- Available Online: 2025-12-15
Abstract: In this work, we study the radiation properties of the quantum-corrected black hole (BH). For simplicity, we consider test particles around the quantum-corrected BH. With this aim, we define the important quantities of test particles around the quantum-corrected BH: the effective potential, energy, angular momentum, and innermost stable circular orbit (ISCO). In addition, we explore the radiation properties of the accretion disk around the quantum-corrected BH considering the Novikov-Thorne model. We find that the values of the flux of the electromagnetic radiation and the temperature of the disk increase slightly with the increase of the quantum correction parameter α. To obtain more information, we plot the temperature profile using a color map. Finally, we consider the spectral luminosity of the accretion disk under the influence of the quantum correction parameter α.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: