Refinement of an analytical capture cross section formula

The study of heavy-ion fusion reactions at near-barrier energies [1−7] is of significant importance in nuclear physics, particularly for the synthesis of superheavy nuclei (SHN) [8−14] and the exploration of nuclear structure effects [15−19]. A critical aspect of the study is the accurate calculation of the capture cross sections, which are influenced by complex nuclear structure effects and dynamical processes, such as dynamical deformation and nucleon transfer. These factors couple with the relative motion of the colliding nuclei [20, 21], necessitating sophisticated models to describe the fusion dynamics accurately.

One of the widely used approaches [22−27] to account for these couplings is the introduction of an empirical barrier distribution (EBD). By using a single Gaussian function to parameterize the barrier distribution, the capture cross sections can be expressed as an analytical formula [27, 28], which is named as the EBD method in code KEWPIE2 [29]. The EBD method has demonstrated reasonable success for heavy fusion systems [29, 30] and provides a robust framework for analyzing cold fusion, leading to the synthesis of SHN [28]. While the EBD method works well for heavy systems, its accuracy diminishes for fusion reactions with lighter nuclei owing to oversimplifications. First, the parameters in the original EBD method do not explicitly consider the influence of the surface effects of light nuclei on the barrier height and radius, which leads to an over-prediction of the barrier height and an under-prediction of the barrier radius for light fusion systems, such as ¹⁶O+¹⁶O. Furthermore, the model neglects the influence of the reaction Q-value on the cross section. For instance, the fusion systems ¹³²Sn+^40,48Ca, despite both involving spherical nuclei, exhibit a significant difference in the sub-barrier cross sections owing to their distinct reaction Q-values. The influence of the Q-value on the width of the barrier distribution, which is observed in Ref. [31], is not involved in the EBD method, as the width parameter is only dependent on the deformations of the reaction partners and the average barrier height. As a result of neglecting Q-value effects in the EBD calculations, the data of both reactions ¹³²Sn+^40,48Ca cannot be well reproduced simultaneously. In addition, the influence of deep inelastic scattering (DIS) on the barrier radius for the superheavy systems observed in Refs. [32, 33] is neglected in the EBD method.

To address its limitations for light systems, we present an enhanced version of the EBD formula. The improvements include incorporating the surface effects of light nuclei and the contribution of the competition between the shell and isospin effects to the barrier height. Additionally, we consider the influence of the reaction Q-value on the barrier distribution width and account for DIS effects on the barrier radius for superheavy systems. These refinements substantially enhance the accuracy of the model, enabling a more comprehensive description of fusion reactions across a wide range of systems, from light to superheavy cases.

The remainder of this paper is structured as follows: In Sec. II, the framework of the EBD method and the three key input quantities are introduced. In Sec. III, the results obtained with the proposed formula for a series of reaction systems and some discussions are presented. Finally, a summary is given in Sec. IV.

In the EBD method, the capture cross section is written as [27−29]

where $ X = (E_{\rm c.m.}-V_B)/\sqrt{2}W $. $ E_{\rm c.m.} $ denotes the center-of-mass incident energy. $ V_B $ and W denote the centroid and standard deviation of the Gaussian function, respectively. $ R_B $ denotes the barrier radius.

In this paper, a new version EBD2 of the formula is proposed by refining the three input quantities: $ V_B $, $ R_B $, and W. In Ref. [34], Wen et al. observed that the extracted barrier heights $ V_B $ are approximately linearly proportional to the Coulomb parameter $ Z_1 Z_2/(A_1^{1/3}+A_2^{1/3}) $. In EBD, $ V_B $ is parameterized by a cubic polynomial of the Coulomb parameter [28]. In this study, the average barrier height $ V_B $ (in MeV) is parameterized as

with the Coulomb parameter re-written as

Here, $ Z_1 $ and $ Z_2 $ denote the charge numbers of the projectile nucleus and target, respectively. $ A_1 $ and $ A_2 $ denote the corresponding mass numbers of the reaction partners. The surface correction factor $ F_S=1-Z_1^{-1/3} Z_2^{-1/3} $ is introduced to consider the surface effects of light nuclei and the Coulomb exchange term [35, 36]. The correction term $ \Delta B=\sum {\Delta_i I_i^2} $ in Eq. (2) is used to consider the competition between the shell and isospin effects, with the shell gap $ \Delta_i $ [37] and isospin asymmetry $ I_i=(N_i-Z_i)/A_i $ of the reaction partners ($ i=1 $ for projectile and $ i=2 $ for target). On the one hand, the neutron transfer and neck formation in the reaction process with neutron-rich nuclei can lower the capture barrier and thus enhance the fusion cross sections at sub-barrier energies [23, 38]. On the other hand, for fusion reactions between magic nuclei, the strong shell effect inhibits the lowering of the barrier effect [23]. This competition is evident for the reactions with neutron-rich nuclei ⁴⁸Ca and ¹³²Sn.

The average barrier radius is written as

with $ r_0=1.10 $ fm. The factor $ F_{\rm DIS}= 1+\exp(X_{\rm B}-X_0) $ with the Bass parameter [2] $ X_{\rm B}=\dfrac{Z_1 Z_2}{(A_1^{1/3}+A_2^{1/3})A_1^{1/3}A_2^{1/3}} $ is introduced to consider the influence of DIS on the barrier radius in superheavy systems inspired by the results in Refs. [32, 33]. The dimensionless parameter $ X_0=10.2 $ is determined by the measured capture cross sections of some super-heavy systems [39], such as ⁶⁴Ni + ²³⁸U. Bass concluded that fusion is excluded for the systems with $ X_{\rm B}>12.6 $ [2] owing to the disappearance of the capture pocket.

The standard deviation of the Gaussian function is parameterized as

where $ w_{d}=\sum {|\beta_{2i}| A_i^{1/3}} $ and $ w_i = r_0 A_i^{1/3} \beta_{2i}^2/4\pi $ [28, 29], with the mass numbers $ A_1 $ and $ A_2 $ of the reaction partners, and their quadrupole deformation parameter $ \beta_2 $ taken from the WS4 model [40] for prolate nuclei heavier than ¹⁶O. For oblate nuclei ($ \beta_2<0 $) or those with hexadecapole deformation $ \beta_4<0 $, the corresponding deformation parameter is set as $ \sqrt{\beta_2^2+\beta_4^2}/2 $. In this study, the Q-value dependence of the parameter $ w_0=(V_B+Q)/c_2 $ is introduced to consider the dynamical effects owing to the excitation energy of the reaction system at the capture position, which is approximately proportional to the excitation energy of the compound nuclei. $ N_{\rm CN} $ denotes the neutron number of the compound nucleus. The optimal values for the four parameters $ c_0=0.63 $ MeV, $ c_1=0.015 $ fm^-1, $ c_2=33.0 $ MeV$ \cdot $fm^-1, and $ r_0=1.10 $ fm in Eq. (5) are obtained by varying these parameters and searching for the minimal deviation between the predicted cross sections and the experimental data for 426 fusion reactions (including the systems collected in Refs. [25, 39, 41] except those induced by nuclei lighter than ¹²C). For α-induced fusion reactions, the structure effects could be neglected, and the value of W is simply written as $ W=c_0 + c_1 V_B $.

By substituting the values of $ V_B $, $ R_B $, and W obtained from Eqs. (2)−(5) under the fixed parameters into Eq. (1), the capture cross sections of any selected heavy-ion fusion reactions at energies around the Coulomb barrier can be directly calculated based on the EBD2 formula.

To quantify the influence of the proposed refinements, we first evaluate the accuracy of the two-parameter barrier height formula, i.e., Eq. (2). Fig. 1(a) shows the relative deviations between the calculated barrier heights $ V_B^{\rm th} $ according to Eq. (2) and 382 extracted barrier heights [41] $ V_B^{\rm exp} $ from the measured fusion excitation functions. The results of EBD2 were much better than those of EBD for light systems ($ Z_1 Z_2\le 200 $). The mean value of the relative deviations (RD) in absolute value with respect to the 382 barrier heights was only 1.65% with EBD2, which is much smaller than that of the three-parameter formula in EBD (RD = 2.04%) and that of two-parameter MCW potential [34] (RD = 1.95%). We note that the accuracy of the barrier height formula can be improved in EBD2 by introducing the surface correction factor $ F_S $. In both EBD and MCW, the Coulomb parameter is expressed as $ z=Z_1 Z_2/(A_1^{1/3}+A_2^{1/3}) $ neglecting the correction factor $ F_S $, and the deviations between the model predictions and the data for light fusion systems thus significantly increase. Fig. 1(b) shows the barrier radius coefficient, i.e., $ R_B/(A_1^{1/3}+A_2^{1/3}) $. The squares denote the extracted data [41], which evidently decrease with the charge product $ Z_1 Z_2 $. The line and circles denote the results of EBD (1.16 fm) and EBD2, respectively. The decreasing trend of the data can be remarkably well reproduced by EBD2. In Table 1, we list the calculated barrier parameters according to Eqs. (2)−(5) and the deviation between the experimental data and the calculated $ \sigma_{\rm {cap} } $ by using Eq. (1), which will be discussed later. The barrier radii $ R_B $ are systematically reduced for super-heavy systems owing to the factor $ F_{\rm DIS} $. The values of W also indicate that the barrier distributions broaden for reactions with well-deformed target nuclei, compared with the reactions induced by spherical ones.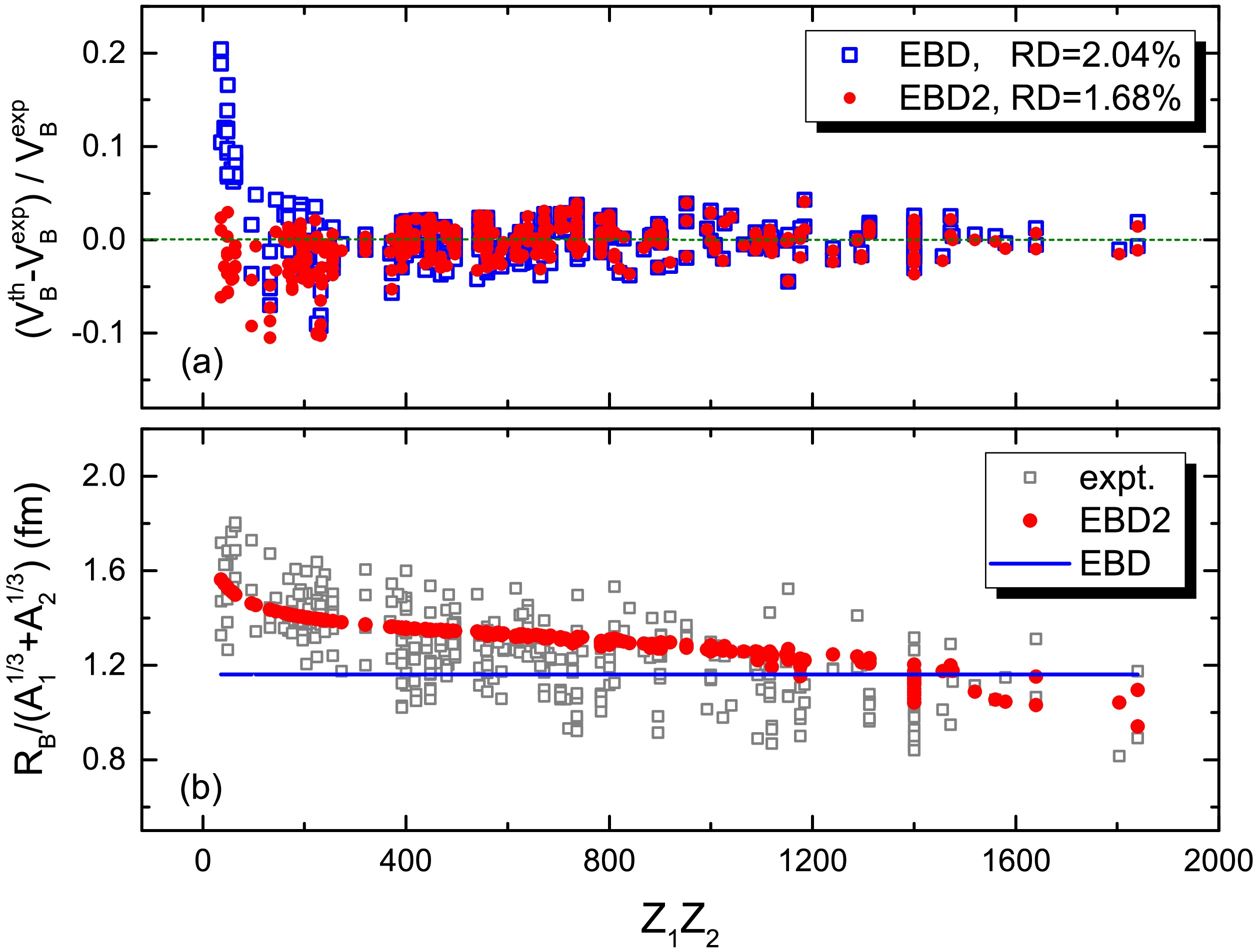

Figure 1.  (color online) (a) Relative deviations between the calculated barrier heights $ V_B^{\rm th} $ and 382 extracted barrier heights [41] $ V_B^{\rm exp} $ for reactions induced by nuclei with $ Z_1\ge 6 $ and $ Z_2\ge 6 $. The squares and circles denote the results of EBD [28, 29] and EBD2, respectively. (b) Barrier radii $ R_B $ scaled by $ A_1^{1/3}+A_2^{1/3} $. The squares and circles denote the extracted reduced barrier radii [41] and the predictions of EBD2 by Eq. (4), respectively. The line denotes the results of EBD [28, 29].

Reaction	$ V_B $/MeV	$ R_B $/fm	W /MeV	$ \chi_{\log}^{2} $
16O+16O	10.04	7.39	0.75	0.041
18O+58Ni	30.69	8.54	1.44	0.011
16O+92Zr	41.39	9.04	1.36	0.039
16O+154Sm	58.93	9.88	2.58	0.007
16O+208Pb	74.35	10.43	1.48	0.109
16O+238U	80.92	10.69	3.03	0.008
40Ca+48Ca	52.67	8.95	1.94	0.023
40Ca+132Sn	115.79	10.08	3.83	0.030
48Ca+132Sn	113.24	10.47	2.33	0.014
48Ca+154Sm	137.12	10.45	4.29	0.011
48Ca+208Pb	174.16	10.38	2.10	0.185
48Ca+238U	191.03	10.23	4.07	0.012
48Ca+248Cm	198.22	10.06	4.09	0.094
54Cr+208Pb	208.39	8.80	2.84	−
54Cr+238U	228.93	8.08	5.24	−
54Cr+244Pu	233.07	7.91	5.26	−
54Cr+243Am	235.98	7.57	4.92	−
54Cr+248Cm	237.65	7.62	5.01	−
64Ni+208Pb	240.66	7.18	2.42	−
64Ni+238U	264.75	6.08	4.76	0.136

Table 1.  Barrier parameters according to Eqs. (2)−(5) for 20 fusion reactions. $ \chi_{\log}^{2} $ denotes the deviation between the measured cross sections and the predicted $ \sigma_{\rm {cap} } $ with EBD2.

In Fig. 2, we show the predicted capture cross sections for six fusion reactions ¹⁶O+¹⁶O, ¹⁸O+⁵⁸Ni, ¹⁶O+⁹²Zr, ¹⁶O+¹⁵⁴Sm, ¹⁶O+²⁰⁸Pb, and ⁶⁴Ni+²³⁸U. The dot-dashed curves and solid curves denote the results of EBD and EBD2, respectively. The experimental data were much better reproduced with EBD2 from the light fusion system ¹⁶O+¹⁶O to the superheavy system ⁶⁴Ni + ²³⁸U. For ¹⁶O+¹⁶O, the results of EBD were much smaller than the experimental data by five orders of magnitude at $ E_{\rm c.m.}=10 $ MeV. The predicted barrier height $ V_B=11.02 $ MeV with EBD was higher than the extracted one by approximately 10%. Simultaneously, the predicted barrier radius $ R_B=5.85 $ fm with EBD was much smaller than the extracted value ($ 8.52 \pm 0.24 $ fm) [41] from the fusion excitation function and the extracted experimental data ($ 8.63 \pm 0.32 $ fm) [45] from the measured elastic scattering angular distribution based on identical-particle interference by approximately 32% (see Fig. 1(b)), which led to the significant under-prediction of the fusion cross sections. For the superheavy system ⁶⁴Ni+²³⁸U, the extracted capture cross sections from the measured mass-total kinetic energy (TKE) distributions were significantly smaller than the predicted results of EBD. EBD2 reproduced the data more accurately, as the factor $ F_{\rm DIS} $ was introduced in the barrier radius to consider the influence of DIS for superheavy systems.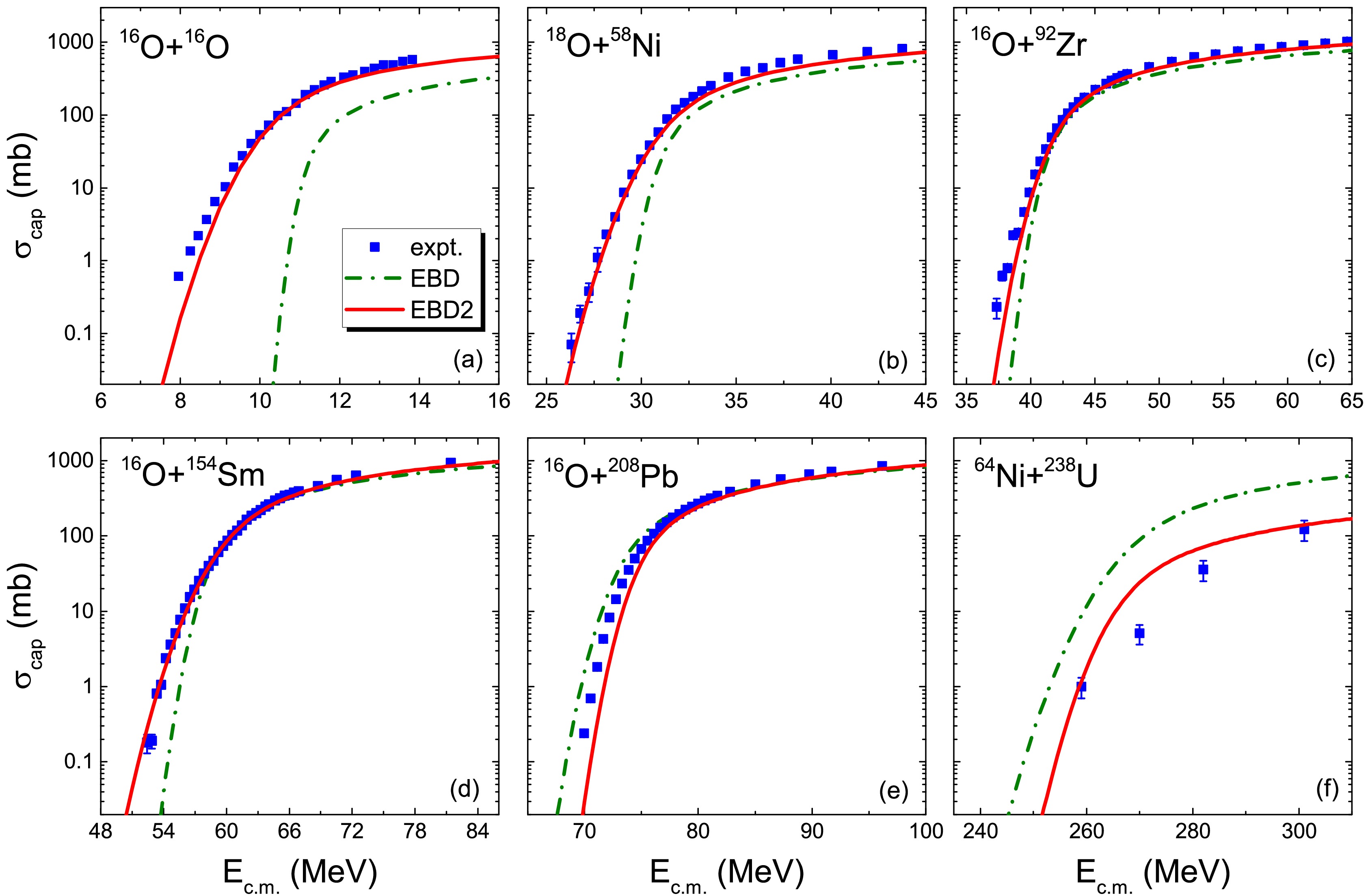

Figure 2.  (color online) Comparison of EBD and EBD2 predictions with the measured capture cross sections for ¹⁶O+¹⁶O [42], ¹⁸O+⁵⁸Ni [43], ¹⁶O+⁹²Zr [44], ¹⁶O+¹⁵⁴Sm [6], ¹⁶O+²⁰⁸Pb [7], and ⁶⁴Ni+²³⁸U [39]. The squares denote the experimental data. The dot-dashed curves and solid curves denote the results of EBD and EBD2, respectively.

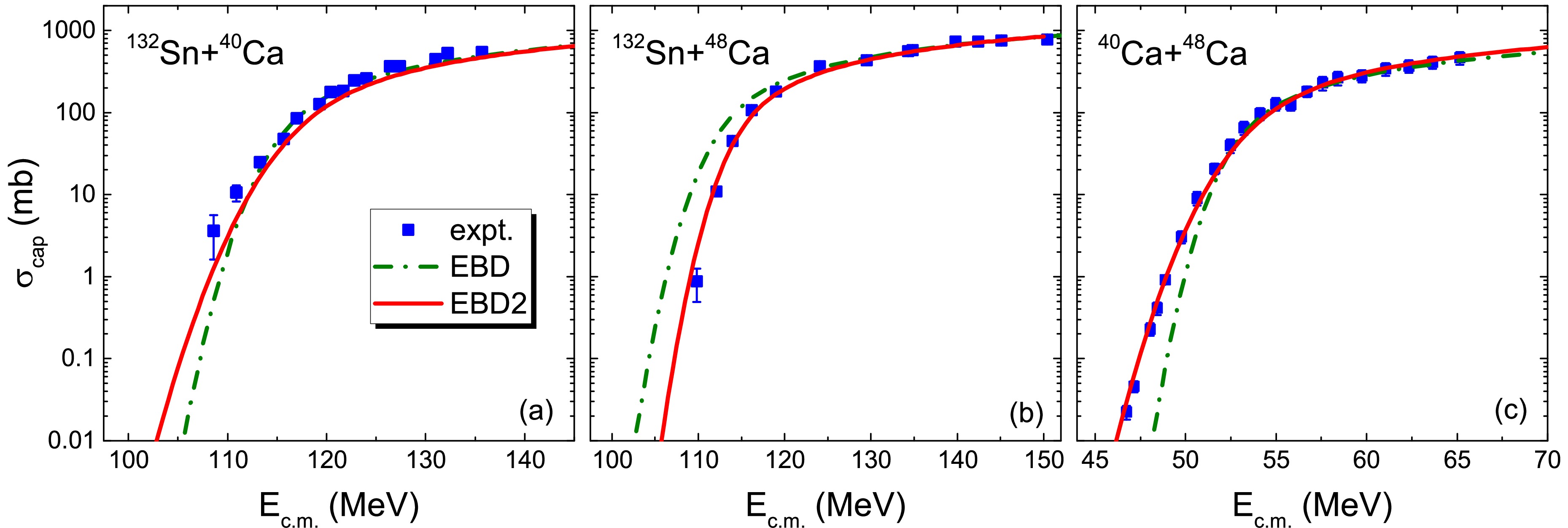
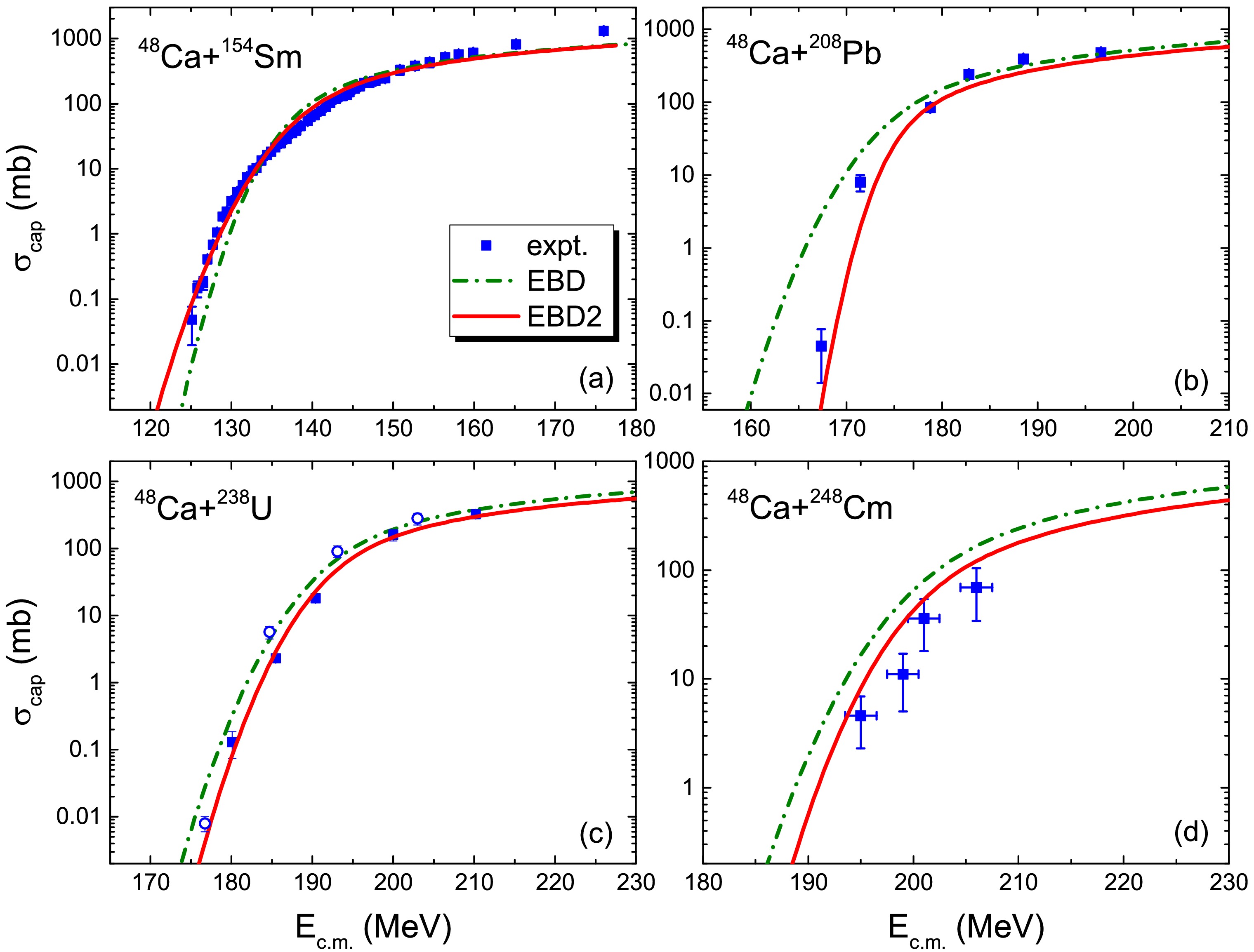
To test the accuracy of the EBD2 formula for describing the fusion reactions induced by neutron-rich doubly-magic nuclei, we showed the predicted capture (fusion) cross sections for ¹³²Sn+^40,48Ca and ⁴⁰Ca + ⁴⁸Ca in Fig. 3. Although both ⁴⁰Ca and ⁴⁸Ca are doubly-magic nuclei, the Q-values in ¹³²Sn+^40,48Ca were different (with $ Q=-52.13 $ MeV for ¹³²Sn+⁴⁰Ca, and $ Q=-75.78 $ MeV for ¹³²Sn+⁴⁸Ca). Although ⁴⁸Ca has eight more neutrons than ⁴⁰Ca, the excitation energy of the compound nucleus in ¹³²Sn+⁴⁸Ca was only 37 MeV, lower than that of ¹³²Sn+⁴⁰Ca by approximately 26 MeV at $ E_{\rm c.m.}=V_B $, owing to the stronger shell effect in ⁴⁸Ca and the isospin effect. In Ref. [31], a relatively higher excitation energy at the capture position can result in stronger effects for dynamical deformations and nucleon transfer in the capture process and broaden the width of the barrier distribution. In EBD2, the parameter $ w_0 $ is directly related to the excitation energy of the compound nuclei in the fusion reaction. The obtained values of W according to Eq. (5) are 3.83 MeV and 2.33 MeV for ¹³²Sn+⁴⁰Ca and ¹³²Sn+⁴⁸Ca, respectively. The model accuracy was significantly improved in EBD2, indicating that the Q-value plays a role in the width of the barrier distribution. In addition, the correction term $ \Delta B $ in Eq. (2) owing to the competition between the shell and isospin effects plays a role in these reactions. For ¹³²Sn+⁴⁸Ca, the barrier height was increased by $ \Delta B=1.28 $ MeV owing to the competition between these two effects, with which the over-prediction of the cross sections from EBD at sub-barrier energies was improved.

Figure 3.  (color online) (a) Same as Fig. 2, but for reactions ¹³²Sn + ^40,48Ca [46] and ⁴⁰Ca + ⁴⁸Ca [47]

In Fig. 4, we show the predicted capture cross sections for four heavy fusion reactions induced by ⁴⁸Ca. We note that the experimental data could be well reproduced by EBD2, particularly for ⁴⁸Ca+²⁰⁸Pb, in which the experimental data were significantly over-predicted by EBD. The squares and circles in Fig. 4(c) denote the experimental data taken from Ref. [50] based on position-sensitive multiwire proportional counters and [39] based on the two-arm time of-flight spectrometer CORSET, respectively. For the reaction leading to the synthesis of SHN ⁴⁸Ca+²⁴⁸Cm, the extracted capture cross sections from the measured mass TKE distributions at energies around the barrier were smaller than the predicted results from EBD. The results of EBD2 were better owing to the introduction of the factor $ F_{\rm DIS} $ to consider the influence of DIS on the barrier radius.

Figure 4.  (color online) (a) Same as Fig. 2, but for reactions ⁴⁸Ca+¹⁵⁴Sm [48], ⁴⁸Ca+²⁰⁸Pb [49], ⁴⁸Ca+²³⁸U [39, 50], and ⁴⁸Ca+²⁴⁸Cm [39]

To further test the accuracy of EBD2, we systematically calculated the capture excitation functions for 426 fusion reactions with $ 35 < Z_1 Z_2 < 2600 $. To analyze the model accuracy, we calculated the mean-square deviation between the predicted cross sections and the experimental data in logarithmic scale (which is called the average deviation $ {\cal{D}} $ in Ref. [25]),

Compared with the traditional definition of $ \chi^{2} $ in which the uncertainty of the cross section is involved, $ \chi_{\log }^{2} $ is more effective to check the trend of cross sections at sub-barrier energies. In Fig. 5, we show the calculated mean-square deviation $ \chi_{\log}^{2} $ as a function of the charge product $ Z_1 Z_2 $. The obtained mean-square deviations with EBD2 were much smaller than those of EBD, particularly for light fusion systems. For 426 fusion reactions, the mean value of $ \chi_{\log}^{2} $ was only 0.113 with EBD2, which is much smaller than the corresponding value with the original EBD (3.485).

Figure 5.  (color online) Mean-square deviation between the predicted cross sections and the experimental data in logarithmic scale. The squares and circles denote the results of EBD and EBD2, respectively.

To test the predictive power of the EBD2 formula, we simultaneously calculated the capture cross sections of two reactions [51] ¹²C+²⁴⁸Cm and ¹⁶O+²⁴⁴Pu, which are not included in the data of the 426 fusion reactions mentioned previously. We note that the measured capture excitation functions for these two reactions could be well reproduced by EBD2. In addition, the fusion cross sections for some α-induced reactions, such as α+¹⁵⁴Sm [52], at energies around the Coulomb barrier could be described well by EBD2.

The capture cross section at a given center-of-mass energy $ E_{\rm c.m.} $ can also be written as the sum of the cross sections for each partial wave J [53],

J represents the relative angular momentum, and $ T(E_{\rm c.m.},J) $ is the penetration probability of the two colliding nuclei overcoming the capture potential barrier in the entrance channel. The reduced mass of the entrance channel is simply given by $ \mu= u A_1 A_2/(A_1+A_2) $. In the EBD2 formula, the corresponding penetration probability $ T(E_{\rm c.m.},J) $ can be approximately expressed as [29]

with the effective barrier $ B_{\rm eff}=V_B+ J(J+1)\hbar^2 /( 2 \mu R_B^2 ) $. In Fig. 6, we show the predicted penetration probabilities and the corresponding capture cross sections for ⁵⁴Cr+²⁴³Am. From Fig. 6(a), we can observe that the obtained penetration probabilities increase gradually from zero to one for head-on collisions and $ T=0.5 $ at the barrier energy of 236 MeV, owing to the introduction of the Gaussian barrier distribution. At $ E_{\rm c.m.}=240 $ MeV, the penetration probability decreases with the angular momentum and reduces to 0.1 at $ J=35 $, which indicates that SHN in this reaction are mainly formed at the central collisions. From Fig. 6(b), we note that the results obtained with Eq. (7) and Eq. (1) are close to each other, which indicates that the approximation in Eq. (8) is sufficiently accurate.

Figure 6.  (color online) (a) Penetration probability $ T (E_{\rm c.m.},J) $with Eq. (8) for ⁵⁴Cr+²⁴³Am. (b) Predicted capture cross sections for ⁵⁴Cr+²⁴³Am with the EBD2 formula. The solid curve and circles denote the results obtained with Eq. (7) and Eq. (1), respectively.

With a refinement to the input quantities of the EBD method, a much more accurate analytical capture cross section formula EBD2 was proposed. The key refinements involved (i) a surface correction to the parameter z and a shell correction term for barrier height calculations, (ii) a Q-value-dependent width term to account for dynamical deformation effects, and (iii) a radius modification incorporating surface effects in light nuclei and DIS in superheavy systems. These refinements substantially improved the model accuracy. The average deviation (in logarithmic scale) between the predicted capture cross sections and the experimental data for 426 reaction systems with $ 35 < Z_1 Z_2 < 2600 $ was systematically calculated. EBD2 reduced the average deviation from 3.485 to 0.113. The surface correction term plays an important role in the fusion barriers for reactions between light nuclei, and a relatively higher excitation energy (related to the reaction Q-value) at the capture position can result in stronger effects for dynamical deformations and nucleon transfer in the capture process, and thus broaden the width of the barrier distribution. The competition between the shell and isospin effects is for reactions with neutron-rich magic nuclei, such as ⁴⁸Ca and ¹³²Sn. For superheavy systems, the influence of DIS needs to be considered for a better description of the capture cross sections. Although the EBD2 method could systematically reproduce the data well, we still note that the measured cross sections for oxygen-induced reactions at above-barrier energies were slightly under-predicted by the EBD2 method, which could be due to the limitation of the single-Gaussian distribution in the calculations. By further adding a correction term from the classic cross section formula $ 0.1 \pi R_B^2(1-V_B/E_{\rm c.m.}) $, the capture cross sections at above-barrier energies could be better reproduced. With the proposed EBD2 formula for better describing the capture cross sections, the evaporation residual cross sections for fusion reactions leading to the synthesis of SHN could be further investigated with less uncertainties.

N. W. is grateful to Min Liu and Hui-Ming Jia for reading the manuscript, and Jinming Chen for calculating the deviations $ \chi_{\log}^{2} $. A capture cross section calculator based on the proposed EBD2 formula is available at http://www.imqmd.com/fusion/EBD2A.html