-
Since Becquerel first observed
$ \alpha $ decay as an unidentified radioactive phenomenon in 1896, this mode of decay has attracted widespread interest from scientists. More than a decade later, Rutherford further characterized this phenomenon as the emission of a 4He particle from the parent nucleus [1]. With the advent of quantum mechanics, Gamow [2], as well as Condon and Gurney [3], attributed this process to quantum tunneling. Since then,$ \alpha $ decay has long been perceived as one of the most powerful tools for investigating unstable, neutron-deficient, and superheavy nuclei, remaining an active area of research in nuclear physics [4−26].With the advancement of techniques, a substantial amount of research has been conducted both experimentally [27, 28] and theoretically [29−39]. Experimentally, a series of superheavy elements have been discovered. For example, the superheavy element with atomic number Z = 118 has been synthesized by 48Ca hot fusion reactions with an actinide Cf target in 2011 [27]. Recently, a new
$ \alpha $ -emitting isotope 214U, produced by the fusion-evaporation reaction$ {}^{182}{\rm{W}}({}^{36}{\rm{Ar}}, 4n){}^{214}{\rm{U}} $ , was identified by employing the gas-filled recoil separator SHANS and the recoil$ \alpha $ -correlation technique [28]. Theoretically, many famous empirical formulas have been proposed to calculate$ \alpha $ decay half-lives. The first one was proposed by Geiger and Nuttal [40] in 1911. Their findings demonstrated that the logarithm of the half-life$ \log_{10} T_{1/2} $ was linearly correlated with the inverse of the square root of$ \alpha $ decay energy$ Q_{\alpha}^{-1/2} $ , which was known as Geiger-Nuttal law (G-N). Since then, several other noteworthy empirical formulas have been successively proposed, including the scaling law Brown formula (SLB) [41]; universal decay law (UDL) [42, 43]; Royer formula [34] along with its improved forms such as the modified Royer formula (MR) and unitary Royer formula (DZR) [44, 45]; Viola-Seaborg formula (VS) [46] proposed in 1966 and further modified to the Viola-Seaborg-Sobiczewski formula (VSS) [47] and modified Viola-Seaborg formula (MVS) [48]; the NRDX formula and the Hatsukawa formula [49]; and more [50−55]. These formulas can effectively describe the half-life of$ \alpha $ decay. Meanwhile, extensive theoretical frameworks, ranging from generalized liquid drop model (GLDM) [56] to microscopic approaches like the density-dependent cluster model (DDCM) [57], have been developed to describe$ \alpha $ decay. These models emphasize the critical role of$ \alpha $ decay preformation factors$ P_\alpha $ in determining$ \alpha $ decay half-lives.Up to now, many microscopical and phenomenological models have been developed to calculate the
$ \alpha $ decay preformation factors$ P_\alpha $ [37, 58−63]. From the microscopical perspective, the R-matrix method [37, 58−60] provides a framework to obtain$ P_\alpha $ through the initial truncated wave functions of parent nuclei. Furthermore, the preformation factors can also be determined using the microscopical Tohsaki-Horiuchi-Schuck-Röpke wave function [61], which demonstrates particular effectiveness in addressing clustering phenomena in light nuclear systems. Using the cluster-configuration shell model, Varga et al. reproduced the experimental decay width of 212Po and obtained its$ \alpha $ decay preformation factor$ P_\alpha $ = 0.23 [37, 60]. However, the calculation of purely microcosmic$ P_\alpha $ is very difficult owing to the complexity of the nuclear many-body problem and the uncertainty of the nuclear potential. In phenomenological models, the preformation factors are typically extracted by calculating the ratio of the$ \alpha $ decay half-lives obtained from the model and the experimental results [63–65]. In 2005, Xu and Ren [62] investigated the experimental$ \alpha $ decay half-lives of medium-mass nuclei with 50 ≤ Z ≤ 82 by employing the DDCM [57]. Their findings indicated that the$ \alpha $ preformation factors are approximately alike for the same kinds of parent nuclei, i.e., with values of 0.43 for even-even nuclei, 0.35 for odd-A nuclei, and 0.18 for odd-odd nuclei. Nevertheless, the obtained preformation factors are strongly model-dependent. Recently, Ahmed et al. [12, 66] proposed a new quantum-mechanical theory named cluster-formation model (CFM) to calculate the$ \alpha $ decay preformation factors$ P_\alpha $ of even-even nuclei, which suggests that the initial state of the parent nucleus should be a linear combination of different possible clusterization states. Subsequently, Deng et al. [67] and Ren et al. [68, 69] extended this model to calculate the preformation factors for odd-A and odd-odd nuclei.In addition to the
$ \alpha $ decay preformation factors, recent studies have also emphasized the effect of deformation and nonlocality on the$ \alpha $ decay half-lives. Deformation, characterized by quadrupole and hexadecapole deformation parameters, modifies the interaction potential between the emitted$ \alpha $ particle and daughter nucleus, leading to a reduction in the$ \alpha $ decay half-life [70]. Meanwhile, nonlocal potentials, such as the energy-dependent Perey-Buck potential and energy-independent but angular momentum-dependent Mumbai potential, lead to a reduction in$ \alpha $ decay half-lives through nonlocal nuclear interactions. Notably, when deformation and nonlocality act together, there is no significant difference in the results for the Perey-Buck model, as the reduction induced by nonlocality in this model is already large. However, the Mumbai model shows that the reduction in$ \alpha $ decay half-life caused by nonlocality alone is relatively small, while the introduction of deformation significantly enhances this effect [70, 71]. These findings indicate that deformation and nonlocality are important factors in calculating$ \alpha $ decay half-life.Assault frequency is also important in the calculation of
$ \alpha $ decay half-life. Starting from classical theory, the assault frequency can be derived as a function of the parameterized$ \alpha $ decay energy and charge radius of the parent nucleus. Therefore, based on the above two points, we propose a model to calculate$ \alpha $ decay half-lives, containing only four adjustable parameters, while the$ \alpha $ decay preformation factor$ P_\alpha $ is calculated through the CFM. The corresponding standard deviation is 0.408 for all 559 nuclei, 0.323 for even-even nuclei, 0.459 for odd-A nuclei, and 0.391 for odd-odd nuclei. In addition, we extend this model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120. For comparison, the formulas of UDL and DZR are also used. The prediction results of these formulas are in good agreement with each other.The remainder of this article is organized as follows. In Sec. II, the theoretical framework for calculating
$ \alpha $ decay half-life is described briefly. In Sec. III, the calculations and discussion related to this framework are presented. Finally, a brief summary is provided in Sec. IV. -
Since Becquerel first observed
$ \alpha $ decay as an unidentified radioactive phenomenon in 1896, this mode of decay has attracted widespread interest from scientists. More than a decade later, Rutherford further characterized this phenomenon as the emission of a 4He particle from the parent nucleus [1]. With the advent of quantum mechanics, Gamow [2], as well as Condon and Gurney [3], attributed this process to quantum tunneling. Since then,$ \alpha $ decay has long been perceived as one of the most powerful tools for investigating unstable, neutron-deficient, and superheavy nuclei, remaining an active area of research in nuclear physics [4−26].With the advancement of techniques, a substantial amount of research has been conducted both experimentally [27, 28] and theoretically [29−39]. Experimentally, a series of superheavy elements have been discovered. For example, the superheavy element with atomic number Z = 118 has been synthesized by 48Ca hot fusion reactions with an actinide Cf target in 2011 [27]. Recently, a new
$ \alpha $ -emitting isotope 214U, produced by the fusion-evaporation reaction$ {}^{182}{\rm{W}}({}^{36}{\rm{Ar}}, 4n){}^{214}{\rm{U}} $ , was identified by employing the gas-filled recoil separator SHANS and the recoil$ \alpha $ -correlation technique [28]. Theoretically, many famous empirical formulas have been proposed to calculate$ \alpha $ decay half-lives. The first one was proposed by Geiger and Nuttal [40] in 1911. Their findings demonstrated that the logarithm of the half-life$ \log_{10} T_{1/2} $ was linearly correlated with the inverse of the square root of$ \alpha $ decay energy$ Q_{\alpha}^{-1/2} $ , which was known as Geiger-Nuttal law (G-N). Since then, several other noteworthy empirical formulas have been successively proposed, including the scaling law Brown formula (SLB) [41]; universal decay law (UDL) [42, 43]; Royer formula [34] along with its improved forms such as the modified Royer formula (MR) and unitary Royer formula (DZR) [44, 45]; Viola-Seaborg formula (VS) [46] proposed in 1966 and further modified to the Viola-Seaborg-Sobiczewski formula (VSS) [47] and modified Viola-Seaborg formula (MVS) [48]; the NRDX formula and the Hatsukawa formula [49]; and more [50−55]. These formulas can effectively describe the half-life of$ \alpha $ decay. Meanwhile, extensive theoretical frameworks, ranging from generalized liquid drop model (GLDM) [56] to microscopic approaches like the density-dependent cluster model (DDCM) [57], have been developed to describe$ \alpha $ decay. These models emphasize the critical role of$ \alpha $ decay preformation factors$ P_\alpha $ in determining$ \alpha $ decay half-lives.Up to now, many microscopical and phenomenological models have been developed to calculate the
$ \alpha $ decay preformation factors$ P_\alpha $ [37, 58−63]. From the microscopical perspective, the R-matrix method [37, 58−60] provides a framework to obtain$ P_\alpha $ through the initial truncated wave functions of parent nuclei. Furthermore, the preformation factors can also be determined using the microscopical Tohsaki-Horiuchi-Schuck-Röpke wave function [61], which demonstrates particular effectiveness in addressing clustering phenomena in light nuclear systems. Using the cluster-configuration shell model, Varga et al. reproduced the experimental decay width of 212Po and obtained its$ \alpha $ decay preformation factor$ P_\alpha $ = 0.23 [37, 60]. However, the calculation of purely microcosmic$ P_\alpha $ is very difficult owing to the complexity of the nuclear many-body problem and the uncertainty of the nuclear potential. In phenomenological models, the preformation factors are typically extracted by calculating the ratio of the$ \alpha $ decay half-lives obtained from the model and the experimental results [63–65]. In 2005, Xu and Ren [62] investigated the experimental$ \alpha $ decay half-lives of medium-mass nuclei with 50 ≤ Z ≤ 82 by employing the DDCM [57]. Their findings indicated that the$ \alpha $ preformation factors are approximately alike for the same kinds of parent nuclei, i.e., with values of 0.43 for even-even nuclei, 0.35 for odd-A nuclei, and 0.18 for odd-odd nuclei. Nevertheless, the obtained preformation factors are strongly model-dependent. Recently, Ahmed et al. [12, 66] proposed a new quantum-mechanical theory named cluster-formation model (CFM) to calculate the$ \alpha $ decay preformation factors$ P_\alpha $ of even-even nuclei, which suggests that the initial state of the parent nucleus should be a linear combination of different possible clusterization states. Subsequently, Deng et al. [67] and Ren et al. [68, 69] extended this model to calculate the preformation factors for odd-A and odd-odd nuclei.In addition to the
$ \alpha $ decay preformation factors, recent studies have also emphasized the effect of deformation and nonlocality on the$ \alpha $ decay half-lives. Deformation, characterized by quadrupole and hexadecapole deformation parameters, modifies the interaction potential between the emitted$ \alpha $ particle and daughter nucleus, leading to a reduction in the$ \alpha $ decay half-life [70]. Meanwhile, nonlocal potentials, such as the energy-dependent Perey-Buck potential and energy-independent but angular momentum-dependent Mumbai potential, lead to a reduction in$ \alpha $ decay half-lives through nonlocal nuclear interactions. Notably, when deformation and nonlocality act together, there is no significant difference in the results for the Perey-Buck model, as the reduction induced by nonlocality in this model is already large. However, the Mumbai model shows that the reduction in$ \alpha $ decay half-life caused by nonlocality alone is relatively small, while the introduction of deformation significantly enhances this effect [70, 71]. These findings indicate that deformation and nonlocality are important factors in calculating$ \alpha $ decay half-life.Assault frequency is also important in the calculation of
$ \alpha $ decay half-life. Starting from classical theory, the assault frequency can be derived as a function of the parameterized$ \alpha $ decay energy and charge radius of the parent nucleus. Therefore, based on the above two points, we propose a model to calculate$ \alpha $ decay half-lives, containing only four adjustable parameters, while the$ \alpha $ decay preformation factor$ P_\alpha $ is calculated through the CFM. The corresponding standard deviation is 0.408 for all 559 nuclei, 0.323 for even-even nuclei, 0.459 for odd-A nuclei, and 0.391 for odd-odd nuclei. In addition, we extend this model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120. For comparison, the formulas of UDL and DZR are also used. The prediction results of these formulas are in good agreement with each other.The remainder of this article is organized as follows. In Sec. II, the theoretical framework for calculating
$ \alpha $ decay half-life is described briefly. In Sec. III, the calculations and discussion related to this framework are presented. Finally, a brief summary is provided in Sec. IV. -
Since Becquerel first observed
$ \alpha $ decay as an unidentified radioactive phenomenon in 1896, this mode of decay has attracted widespread interest from scientists. More than a decade later, Rutherford further characterized this phenomenon as the emission of a 4He particle from the parent nucleus [1]. With the advent of quantum mechanics, Gamow [2], as well as Condon and Gurney [3], attributed this process to quantum tunneling. Since then,$ \alpha $ decay has long been perceived as one of the most powerful tools for investigating unstable, neutron-deficient, and superheavy nuclei, remaining an active area of research in nuclear physics [4−26].With the advancement of techniques, a substantial amount of research has been conducted both experimentally [27, 28] and theoretically [29−39]. Experimentally, a series of superheavy elements have been discovered. For example, the superheavy element with atomic number Z = 118 has been synthesized by 48Ca hot fusion reactions with an actinide Cf target in 2011 [27]. Recently, a new
$ \alpha $ -emitting isotope 214U, produced by the fusion-evaporation reaction$ {}^{182}{\rm{W}}({}^{36}{\rm{Ar}}, 4n){}^{214}{\rm{U}} $ , was identified by employing the gas-filled recoil separator SHANS and the recoil$ \alpha $ -correlation technique [28]. Theoretically, many famous empirical formulas have been proposed to calculate$ \alpha $ decay half-lives. The first one was proposed by Geiger and Nuttal [40] in 1911. Their findings demonstrated that the logarithm of the half-life$ \log_{10} T_{1/2} $ was linearly correlated with the inverse of the square root of$ \alpha $ decay energy$ Q_{\alpha}^{-1/2} $ , which was known as Geiger-Nuttal law (G-N). Since then, several other noteworthy empirical formulas have been successively proposed, including the scaling law Brown formula (SLB) [41]; universal decay law (UDL) [42, 43]; Royer formula [34] along with its improved forms such as the modified Royer formula (MR) and unitary Royer formula (DZR) [44, 45]; Viola-Seaborg formula (VS) [46] proposed in 1966 and further modified to the Viola-Seaborg-Sobiczewski formula (VSS) [47] and modified Viola-Seaborg formula (MVS) [48]; the NRDX formula and the Hatsukawa formula [49]; and more [50−55]. These formulas can effectively describe the half-life of$ \alpha $ decay. Meanwhile, extensive theoretical frameworks, ranging from generalized liquid drop model (GLDM) [56] to microscopic approaches like the density-dependent cluster model (DDCM) [57], have been developed to describe$ \alpha $ decay. These models emphasize the critical role of$ \alpha $ decay preformation factors$ P_\alpha $ in determining$ \alpha $ decay half-lives.Up to now, many microscopical and phenomenological models have been developed to calculate the
$ \alpha $ decay preformation factors$ P_\alpha $ [37, 58−63]. From the microscopical perspective, the R-matrix method [37, 58−60] provides a framework to obtain$ P_\alpha $ through the initial truncated wave functions of parent nuclei. Furthermore, the preformation factors can also be determined using the microscopical Tohsaki-Horiuchi-Schuck-Röpke wave function [61], which demonstrates particular effectiveness in addressing clustering phenomena in light nuclear systems. Using the cluster-configuration shell model, Varga et al. reproduced the experimental decay width of 212Po and obtained its$ \alpha $ decay preformation factor$ P_\alpha $ = 0.23 [37, 60]. However, the calculation of purely microcosmic$ P_\alpha $ is very difficult owing to the complexity of the nuclear many-body problem and the uncertainty of the nuclear potential. In phenomenological models, the preformation factors are typically extracted by calculating the ratio of the$ \alpha $ decay half-lives obtained from the model and the experimental results [63–65]. In 2005, Xu and Ren [62] investigated the experimental$ \alpha $ decay half-lives of medium-mass nuclei with 50 ≤ Z ≤ 82 by employing the DDCM [57]. Their findings indicated that the$ \alpha $ preformation factors are approximately alike for the same kinds of parent nuclei, i.e., with values of 0.43 for even-even nuclei, 0.35 for odd-A nuclei, and 0.18 for odd-odd nuclei. Nevertheless, the obtained preformation factors are strongly model-dependent. Recently, Ahmed et al. [12, 66] proposed a new quantum-mechanical theory named cluster-formation model (CFM) to calculate the$ \alpha $ decay preformation factors$ P_\alpha $ of even-even nuclei, which suggests that the initial state of the parent nucleus should be a linear combination of different possible clusterization states. Subsequently, Deng et al. [67] and Ren et al. [68, 69] extended this model to calculate the preformation factors for odd-A and odd-odd nuclei.In addition to the
$ \alpha $ decay preformation factors, recent studies have also emphasized the effect of deformation and nonlocality on the$ \alpha $ decay half-lives. Deformation, characterized by quadrupole and hexadecapole deformation parameters, modifies the interaction potential between the emitted$ \alpha $ particle and daughter nucleus, leading to a reduction in the$ \alpha $ decay half-life [70]. Meanwhile, nonlocal potentials, such as the energy-dependent Perey-Buck potential and energy-independent but angular momentum-dependent Mumbai potential, lead to a reduction in$ \alpha $ decay half-lives through nonlocal nuclear interactions. Notably, when deformation and nonlocality act together, there is no significant difference in the results for the Perey-Buck model, as the reduction induced by nonlocality in this model is already large. However, the Mumbai model shows that the reduction in$ \alpha $ decay half-life caused by nonlocality alone is relatively small, while the introduction of deformation significantly enhances this effect [70, 71]. These findings indicate that deformation and nonlocality are important factors in calculating$ \alpha $ decay half-life.Assault frequency is also important in the calculation of
$ \alpha $ decay half-life. Starting from classical theory, the assault frequency can be derived as a function of the parameterized$ \alpha $ decay energy and charge radius of the parent nucleus. Therefore, based on the above two points, we propose a model to calculate$ \alpha $ decay half-lives, containing only four adjustable parameters, while the$ \alpha $ decay preformation factor$ P_\alpha $ is calculated through the CFM. The corresponding standard deviation is 0.408 for all 559 nuclei, 0.323 for even-even nuclei, 0.459 for odd-A nuclei, and 0.391 for odd-odd nuclei. In addition, we extend this model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120. For comparison, the formulas of UDL and DZR are also used. The prediction results of these formulas are in good agreement with each other.The remainder of this article is organized as follows. In Sec. II, the theoretical framework for calculating
$ \alpha $ decay half-life is described briefly. In Sec. III, the calculations and discussion related to this framework are presented. Finally, a brief summary is provided in Sec. IV. -
$ \alpha $ decay half-life is defined as$ T_{1/2} = \frac{\ln 2}{\lambda}, $

(1) where
$ \lambda $ is a decay constant that can be obtained by$ \lambda = \nu P P_\alpha. $

(2) Here,
$ \nu $ is the assault frequency, P denotes the penetration probability, and$ P_\alpha $ represents the$ \alpha $ decay preformation factors. The assault frequency$ \nu $ is relevant to the$ \alpha $ decay energy$ Q_\alpha $ and charge radius of the parent nucleus$ R_p $ and can be parameterized as [72]$ \log_{10} \nu = a + b \log_{10} E_\alpha^{1/2} + c \log_{10} R_p, $

(3) where
$ E_\alpha $ is the kinetic energy of the emitted$ \alpha $ particle, which is related to the$ \alpha $ decay energy as follows:$ E_\alpha = \frac{A_p - 4}{A_p} Q_\alpha. $

(4) Here,
$ A_p $ is the mass number of a parent nucleus. Therefore, the assault frequency$ \nu $ can be expressed as$ \log_{10} \nu = a + b \log_{10} (\frac{A_p - 4}{A_p} Q_\alpha)^{1/2} + c \log_{10} R_p, $

(5) where a, b, and c are adjustable parameters. Charge radius
$ R_p $ is given by [73]$ R_{p} = r_0 \left( 1 - r_1 \frac{N_{p} - Z_{p}}{Z_{p}} + r_2 \frac{1}{Z_{p}} \right) Z_{p}^{1/3}, $

(6) where
$ N_p $ is the neutron number of a parent nucleus, and$ Z_p $ is the charge number of a parent nucleus.$ r_0=1.5579 $ fm,$ r_1=-0.0835 $ , and$ r_2=1.0652 $ are taken from Ref. [73].The penetration probability P, calculated by the Wentzel-Kramers-Brillouin (WKB) approximation, is expressed as
$ P=\exp\left\{-\frac{2}{\hbar}\int_{R_0}^{R_2}\sqrt{2\mu\left[V(r)-Q_{\alpha}\right]}\mathrm{d}r\right\}. $

(7) Here,
$ V(r) $ is the total interaction potential between the emitted$ \alpha $ particle and daughter nucleus.$ \mu = m_\alpha m_d/(m_\alpha + m_d) $ is the reduced mass of the$ \alpha $ particle and daughter nucleus in the center-of-mass coordinate, with$ m_d $ and$ m_\alpha $ being the masses of the daughter nucleus and$ \alpha $ particle, respectively.$ R_0 $ and$ R_2 $ are the inner and outer classical turning points of potential barrier, respectively, satisfying the conditions$ V(R_0) = V(R_2) = Q_\alpha $ . Here, the$ \alpha $ decay energy$ Q_\alpha $ can be calculated by$ Q_{\alpha}=M(A,Z)-M(A-4,Z-2)-M(^4\mathrm{He}), $

(8) where
$ M(A, Z) $ ,$ M(A-4, Z-2) $ , and$ M(^4{\rm{He}}) $ are the mass excesses of the parent nucleus, daughter nucleus, and$ \alpha $ particle.In Eq. (7), the total interaction potential between the emitted
$ \alpha $ particle and daughter nucleus$ V(r) $ contains three parts: nuclear potential$ V_N(r) $ , Coulomb potential$ V_C(r) $ , and centrifugal potential$ V_l(r) $ . This can be expressed as$ V(r) = V_N(r) + V_C(r) + V_l(r). $

(9) In the case of favored
$ \alpha $ decay, a schematic diagram of$ \alpha $ -daughter nucleus interaction potential$ V(r) $ is shown in Fig. 1.$ R_1 $ is the position of the highest barrier point. From this figure, we can see that the potential$ V(r) $ is divided into two parts. In the first part with$ r < R_1 $ ($ R_1 = R_d + R_\alpha $ is the separating radius with$ R_d $ and$ R_\alpha $ being the radii of daughter nucleus and emitted$ \alpha $ particle, respectively), the potential$ V(r) $ is expressed as$ V_i(r) $ , while it can be approximated by the Coulomb barrier for the second part with$ r \geq R_1 $ .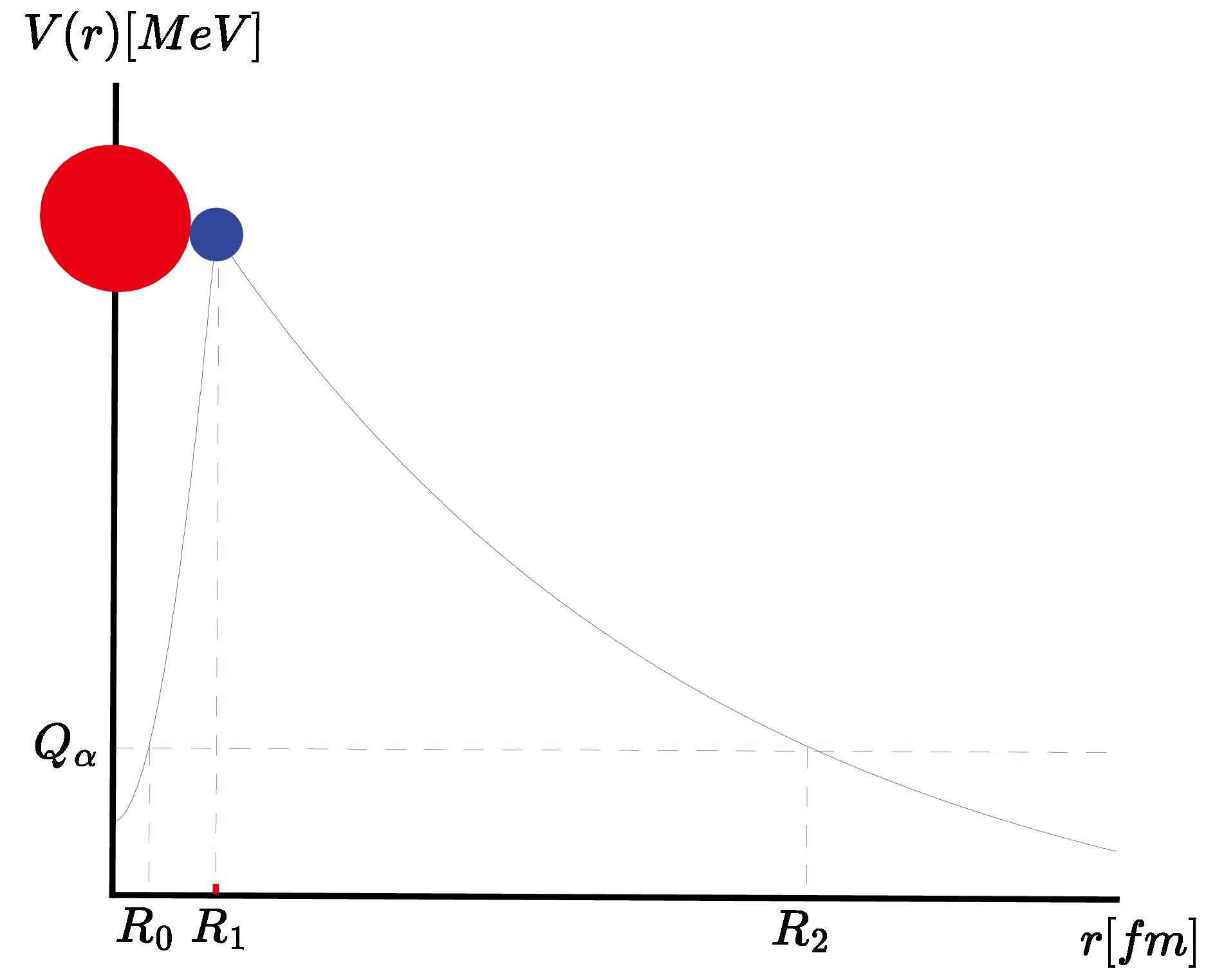
Figure 1. (color online) Schematic diagram of
$\alpha$ -daughter nucleus interaction potential$V(r)$ .From this perspective, the general form of Eq. (7) can be divided into two terms as
$ \begin{aligned}[b]P=\; & \exp\left\{-\frac{2}{\hbar}\int_{R_0}^{R_1}\sqrt{2\mu\left[V_i(r)-Q_{\alpha}\right]}\mathrm{d}r\right\} \\ & \times\exp\left\{-\frac{2}{\hbar}\int_{R_1}^{R_2}\sqrt{2\mu\left(\frac{2Z_de^2}{r}-Q_{\alpha}\right)}\mathrm{d}r\right\},\end{aligned} $

(10) which are denoted as
$ P_1 $ and$ P_2 $ , respectively. The first term$ P_1 $ is the$ \alpha $ decay preformation factors. Due to the complexity of the nuclear potential$ V_N(r) $ ,$ P_1 $ cannot be integrated to obtain an analytical form. Therefore, in this work, we use the CFM to calculate it, as presented in the following. The second term$ P_2 $ can be given in analytical form as$ \begin{aligned}[b] P_2 =\;& \exp \left\{ -\frac{8e^2}{\hbar} \sqrt{2mZ_d} \left( \frac{A_d}{A_p Q \alpha} \right)^{1/2} \right. \\&\left. \times \left[ \arccos \sqrt{X} - \sqrt{X(1-X)} \right] \right\}, \end{aligned} $

(11) where m is the mass of one atomic mass unit, Zd is the charge number of a daughter nucleus. X is the ratio of radius
$ R_1 $ to$ R_2 $ , which can be expressed as$ X = \frac{R_1}{R_2} = r \left( A_d^{1/3} + A_\alpha^{1/3} \right) \times \frac{Q_\alpha}{2 Z_d e^2}. $

(12) Here, r = 1.2249 fm is the radius constant taken from Ref. [74], and
$ A_d $ and$ A_\alpha $ are the mass numbers of the daughter nucleus and$ \alpha $ particle, respectively.According to the calculation of the WKB barrier penetration probability, in the process of favored
$ \alpha $ decay, the angular momentum l carried away by the emitted$ \alpha $ particle is equal to zero. Nevertheless, in the process of unfavored$ \alpha $ decay, the emitted$ \alpha $ particle takes on a non-zero angular momentum, which introduces a non-zero centrifugal potential to the total$ \alpha $ particle-daughter nucleus interaction potential. The presence of the centrifugal potential will lead to a higher total barrier, resulting in a lower pentration probability and ultimately a longer$ \alpha $ decay half-life. There are two methods to deal with this effect on the unfavored$ \alpha $ decay half-lives: introducing the terms of orbital angular momentum$ l(l+1) $ [42, 43, 75−78] or$ \sqrt{l(l+1)} $ [75] into empirical formulas. In this work, we choose$ l(l+1) $ to consider this effect and incorporate it into the original formula presented in Eq. (1). Therefore, the unified formula can be written as$ \begin{aligned}[b] \log_{10} T_{1/2} =\; & \log_{10}(\ln 2) - \log_{10} \nu - \log_{10} P \\ & - \log_{10} P_{\alpha} + dl(l + 1), \end{aligned} $

(13) where d is an adjustable parameter.
-
$ \alpha $ decay half-life is defined as$ T_{1/2} = \frac{\ln 2}{\lambda}, $
(1) where
$ \lambda $ is a decay constant that can be obtained by$ \lambda = \nu P P_\alpha. $
(2) Here,
$ \nu $ is the assault frequency, P denotes the penetration probability, and$ P_\alpha $ represents the$ \alpha $ decay preformation factors. The assault frequency$ \nu $ is relevant to the$ \alpha $ decay energy$ Q_\alpha $ and charge radius of the parent nucleus$ R_p $ and can be parameterized as [72]$ \log_{10} \nu = a + b \log_{10} E_\alpha^{1/2} + c \log_{10} R_p, $
(3) where
$ E_\alpha $ is the kinetic energy of the emitted$ \alpha $ particle, which is related to the$ \alpha $ decay energy as follows:$ E_\alpha = \frac{A_p - 4}{A_p} Q_\alpha. $
(4) Here,
$ A_p $ is the mass number of a parent nucleus. Therefore, the assault frequency$ \nu $ can be expressed as$ \log_{10} \nu = a + b \log_{10} (\frac{A_p - 4}{A_p} Q_\alpha)^{1/2} + c \log_{10} R_p, $
(5) where a, b, and c are adjustable parameters. Charge radius
$ R_p $ is given by [73]$ R_{p} = r_0 \left( 1 - r_1 \frac{N_{p} - Z_{p}}{Z_{p}} + r_2 \frac{1}{Z_{p}} \right) Z_{p}^{1/3}, $
(6) where
$ N_p $ is the neutron number of a parent nucleus, and$ Z_p $ is the charge number of a parent nucleus.$ r_0=1.5579 $ fm,$ r_1=-0.0835 $ , and$ r_2=1.0652 $ are taken from Ref. [73].The penetration probability P, calculated by the Wentzel-Kramers-Brillouin (WKB) approximation, is expressed as
$ P=\exp\left\{-\frac{2}{\hbar}\int_{R_0}^{R_2}\sqrt{2\mu\left[V(r)-Q_{\alpha}\right]}\mathrm{d}r\right\}. $
(7) Here,
$ V(r) $ is the total interaction potential between the emitted$ \alpha $ particle and daughter nucleus.$ \mu = m_\alpha m_d/(m_\alpha + m_d) $ is the reduced mass of the$ \alpha $ particle and daughter nucleus in the center-of-mass coordinate, with$ m_d $ and$ m_\alpha $ being the masses of the daughter nucleus and$ \alpha $ particle, respectively.$ R_0 $ and$ R_2 $ are the inner and outer classical turning points of potential barrier, respectively, satisfying the conditions$ V(R_0) = V(R_2) = Q_\alpha $ . Here, the$ \alpha $ decay energy$ Q_\alpha $ can be calculated by$ Q_{\alpha}=M(A,Z)-M(A-4,Z-2)-M(^4\mathrm{He}), $
(8) where
$ M(A, Z) $ ,$ M(A-4, Z-2) $ , and$ M(^4{\rm{He}}) $ are the mass excesses of the parent nucleus, daughter nucleus, and$ \alpha $ particle.In Eq. (7), the total interaction potential between the emitted
$ \alpha $ particle and daughter nucleus$ V(r) $ contains three parts: nuclear potential$ V_N(r) $ , Coulomb potential$ V_C(r) $ , and centrifugal potential$ V_l(r) $ . This can be expressed as$ V(r) = V_N(r) + V_C(r) + V_l(r). $
(9) In the case of favored
$ \alpha $ decay, a schematic diagram of$ \alpha $ -daughter nucleus interaction potential$ V(r) $ is shown in Fig. 1.$ R_1 $ is the position of the highest barrier point. From this figure, we can see that the potential$ V(r) $ is divided into two parts. In the first part with$ r < R_1 $ ($ R_1 = R_d + R_\alpha $ is the separating radius with$ R_d $ and$ R_\alpha $ being the radii of daughter nucleus and emitted$ \alpha $ particle, respectively), the potential$ V(r) $ is expressed as$ V_i(r) $ , while it can be approximated by the Coulomb barrier for the second part with$ r \geq R_1 $ .
Figure 1. (color online) Schematic diagram of
$\alpha$ -daughter nucleus interaction potential$V(r)$ .From this perspective, the general form of Eq. (7) can be divided into two terms as
$ \begin{aligned}[b]P=\; & \exp\left\{-\frac{2}{\hbar}\int_{R_0}^{R_1}\sqrt{2\mu\left[V_i(r)-Q_{\alpha}\right]}\mathrm{d}r\right\} \\ & \times\exp\left\{-\frac{2}{\hbar}\int_{R_1}^{R_2}\sqrt{2\mu\left(\frac{2Z_de^2}{r}-Q_{\alpha}\right)}\mathrm{d}r\right\},\end{aligned} $
(10) which are denoted as
$ P_1 $ and$ P_2 $ , respectively. The first term$ P_1 $ is the$ \alpha $ decay preformation factors. Due to the complexity of the nuclear potential$ V_N(r) $ ,$ P_1 $ cannot be integrated to obtain an analytical form. Therefore, in this work, we use the CFM to calculate it, as presented in the following. The second term$ P_2 $ can be given in analytical form as$ \begin{aligned}[b] P_2 =\;& \exp \left\{ -\frac{8e^2}{\hbar} \sqrt{2mZ_d} \left( \frac{A_d}{A_p Q \alpha} \right)^{1/2} \right. \\&\left. \times \left[ \arccos \sqrt{X} - \sqrt{X(1-X)} \right] \right\}, \end{aligned} $
(11) where m is the mass of one atomic mass unit, Zd is the charge number of a daughter nucleus. X is the ratio of radius
$ R_1 $ to$ R_2 $ , which can be expressed as$ X = \frac{R_1}{R_2} = r \left( A_d^{1/3} + A_\alpha^{1/3} \right) \times \frac{Q_\alpha}{2 Z_d e^2}. $
(12) Here, r = 1.2249 fm is the radius constant taken from Ref. [74], and
$ A_d $ and$ A_\alpha $ are the mass numbers of the daughter nucleus and$ \alpha $ particle, respectively.According to the calculation of the WKB barrier penetration probability, in the process of favored
$ \alpha $ decay, the angular momentum l carried away by the emitted$ \alpha $ particle is equal to zero. Nevertheless, in the process of unfavored$ \alpha $ decay, the emitted$ \alpha $ particle takes on a non-zero angular momentum, which introduces a non-zero centrifugal potential to the total$ \alpha $ particle-daughter nucleus interaction potential. The presence of the centrifugal potential will lead to a higher total barrier, resulting in a lower pentration probability and ultimately a longer$ \alpha $ decay half-life. There are two methods to deal with this effect on the unfavored$ \alpha $ decay half-lives: introducing the terms of orbital angular momentum$ l(l+1) $ [42, 43, 75−78] or$ \sqrt{l(l+1)} $ [75] into empirical formulas. In this work, we choose$ l(l+1) $ to consider this effect and incorporate it into the original formula presented in Eq. (1). Therefore, the unified formula can be written as$ \begin{aligned}[b] \log_{10} T_{1/2} =\; & \log_{10}(\ln 2) - \log_{10} \nu - \log_{10} P \\ & - \log_{10} P_{\alpha} + dl(l + 1), \end{aligned} $
(13) where d is an adjustable parameter.
-
$ \alpha $ decay half-life is defined as$ T_{1/2} = \frac{\ln 2}{\lambda}, $
(1) where
$ \lambda $ is a decay constant that can be obtained by$ \lambda = \nu P P_\alpha. $
(2) Here,
$ \nu $ is the assault frequency, P denotes the penetration probability, and$ P_\alpha $ represents the$ \alpha $ decay preformation factors. The assault frequency$ \nu $ is relevant to the$ \alpha $ decay energy$ Q_\alpha $ and charge radius of the parent nucleus$ R_p $ and can be parameterized as [72]$ \log_{10} \nu = a + b \log_{10} E_\alpha^{1/2} + c \log_{10} R_p, $
(3) where
$ E_\alpha $ is the kinetic energy of the emitted$ \alpha $ particle, which is related to the$ \alpha $ decay energy as follows:$ E_\alpha = \frac{A_p - 4}{A_p} Q_\alpha. $
(4) Here,
$ A_p $ is the mass number of a parent nucleus. Therefore, the assault frequency$ \nu $ can be expressed as$ \log_{10} \nu = a + b \log_{10} (\frac{A_p - 4}{A_p} Q_\alpha)^{1/2} + c \log_{10} R_p, $
(5) where a, b, and c are adjustable parameters. Charge radius
$ R_p $ is given by [73]$ R_{p} = r_0 \left( 1 - r_1 \frac{N_{p} - Z_{p}}{Z_{p}} + r_2 \frac{1}{Z_{p}} \right) Z_{p}^{1/3}, $
(6) where
$ N_p $ is the neutron number of a parent nucleus, and$ Z_p $ is the charge number of a parent nucleus.$ r_0=1.5579 $ fm,$ r_1=-0.0835 $ , and$ r_2=1.0652 $ are taken from Ref. [73].The penetration probability P, calculated by the Wentzel-Kramers-Brillouin (WKB) approximation, is expressed as
$ P=\exp\left\{-\frac{2}{\hbar}\int_{R_0}^{R_2}\sqrt{2\mu\left[V(r)-Q_{\alpha}\right]}\mathrm{d}r\right\}. $
(7) Here,
$ V(r) $ is the total interaction potential between the emitted$ \alpha $ particle and daughter nucleus.$ \mu = m_\alpha m_d/(m_\alpha + m_d) $ is the reduced mass of the$ \alpha $ particle and daughter nucleus in the center-of-mass coordinate, with$ m_d $ and$ m_\alpha $ being the masses of the daughter nucleus and$ \alpha $ particle, respectively.$ R_0 $ and$ R_2 $ are the inner and outer classical turning points of potential barrier, respectively, satisfying the conditions$ V(R_0) = V(R_2) = Q_\alpha $ . Here, the$ \alpha $ decay energy$ Q_\alpha $ can be calculated by$ Q_{\alpha}=M(A,Z)-M(A-4,Z-2)-M(^4\mathrm{He}), $
(8) where
$ M(A, Z) $ ,$ M(A-4, Z-2) $ , and$ M(^4{\rm{He}}) $ are the mass excesses of the parent nucleus, daughter nucleus, and$ \alpha $ particle.In Eq. (7), the total interaction potential between the emitted
$ \alpha $ particle and daughter nucleus$ V(r) $ contains three parts: nuclear potential$ V_N(r) $ , Coulomb potential$ V_C(r) $ , and centrifugal potential$ V_l(r) $ . This can be expressed as$ V(r) = V_N(r) + V_C(r) + V_l(r). $
(9) In the case of favored
$ \alpha $ decay, a schematic diagram of$ \alpha $ -daughter nucleus interaction potential$ V(r) $ is shown in Fig. 1.$ R_1 $ is the position of the highest barrier point. From this figure, we can see that the potential$ V(r) $ is divided into two parts. In the first part with$ r < R_1 $ ($ R_1 = R_d + R_\alpha $ is the separating radius with$ R_d $ and$ R_\alpha $ being the radii of daughter nucleus and emitted$ \alpha $ particle, respectively), the potential$ V(r) $ is expressed as$ V_i(r) $ , while it can be approximated by the Coulomb barrier for the second part with$ r \geq R_1 $ .
Figure 1. (color online) Schematic diagram of
$\alpha$ -daughter nucleus interaction potential$V(r)$ .From this perspective, the general form of Eq. (7) can be divided into two terms as
$ \begin{aligned}[b]P=\; & \exp\left\{-\frac{2}{\hbar}\int_{R_0}^{R_1}\sqrt{2\mu\left[V_i(r)-Q_{\alpha}\right]}\mathrm{d}r\right\} \\ & \times\exp\left\{-\frac{2}{\hbar}\int_{R_1}^{R_2}\sqrt{2\mu\left(\frac{2Z_de^2}{r}-Q_{\alpha}\right)}\mathrm{d}r\right\},\end{aligned} $
(10) which are denoted as
$ P_1 $ and$ P_2 $ , respectively. The first term$ P_1 $ is the$ \alpha $ decay preformation factors. Due to the complexity of the nuclear potential$ V_N(r) $ ,$ P_1 $ cannot be integrated to obtain an analytical form. Therefore, in this work, we use the CFM to calculate it, as presented in the following. The second term$ P_2 $ can be given in analytical form as$ \begin{aligned}[b] P_2 =\;& \exp \left\{ -\frac{8e^2}{\hbar} \sqrt{2mZ_d} \left( \frac{A_d}{A_p Q \alpha} \right)^{1/2} \right. \\&\left. \times \left[ \arccos \sqrt{X} - \sqrt{X(1-X)} \right] \right\}, \end{aligned} $
(11) where m is the mass of one atomic mass unit, Zd is the charge number of a daughter nucleus. X is the ratio of radius
$ R_1 $ to$ R_2 $ , which can be expressed as$ X = \frac{R_1}{R_2} = r \left( A_d^{1/3} + A_\alpha^{1/3} \right) \times \frac{Q_\alpha}{2 Z_d e^2}. $
(12) Here, r = 1.2249 fm is the radius constant taken from Ref. [74], and
$ A_d $ and$ A_\alpha $ are the mass numbers of the daughter nucleus and$ \alpha $ particle, respectively.According to the calculation of the WKB barrier penetration probability, in the process of favored
$ \alpha $ decay, the angular momentum l carried away by the emitted$ \alpha $ particle is equal to zero. Nevertheless, in the process of unfavored$ \alpha $ decay, the emitted$ \alpha $ particle takes on a non-zero angular momentum, which introduces a non-zero centrifugal potential to the total$ \alpha $ particle-daughter nucleus interaction potential. The presence of the centrifugal potential will lead to a higher total barrier, resulting in a lower pentration probability and ultimately a longer$ \alpha $ decay half-life. There are two methods to deal with this effect on the unfavored$ \alpha $ decay half-lives: introducing the terms of orbital angular momentum$ l(l+1) $ [42, 43, 75−78] or$ \sqrt{l(l+1)} $ [75] into empirical formulas. In this work, we choose$ l(l+1) $ to consider this effect and incorporate it into the original formula presented in Eq. (1). Therefore, the unified formula can be written as$ \begin{aligned}[b] \log_{10} T_{1/2} =\; & \log_{10}(\ln 2) - \log_{10} \nu - \log_{10} P \\ & - \log_{10} P_{\alpha} + dl(l + 1), \end{aligned} $
(13) where d is an adjustable parameter.
-
Within the CFM [12, 66−69], the total clusterization state
$ \Psi $ of the parent nuclei is assumed to be a linear combination of all its n possible clusterization states$ \Psi_i $ . This can be expressed as$ \Psi = \sum\limits_{i=1}^{n} a_i \Psi_i, $
(14) $ a_i = \int \Psi_i^* \Psi \, {\rm d}\tau, $
(15) where
$ a_i $ denotes the superposition coefficient of$ \Psi_i $ , on the basis of the orthogonality condition$ \sum\limits_{i=1}^{n} |a_i|^2 = 1. $
(16) The total wave function is an eigenfunction of the total Hamiltonian H. Similarly, H can be expressed as
$ H = \sum\limits_{i=1}^{N} H_i, $
(17) where
$ H_i $ is the Hamiltonian for the i-th clusterization state$ \Psi_i $ . Because all the clusters describe the same nucleus, they are assumed to share the same total energy E of the total wave function. Therefore, the total energy E can be expressed as$ E = \sum\limits_{i=1}^{n} |a_i|^2 E = \sum\limits_{i=1}^{n} E_{fi}, $
(18) where
$ E_{fi} $ denotes the formation energy of a cluster in the ith clusterization state$ \Psi_i $ . Then, the$ \alpha $ decay preformation factors$ P_\alpha $ can be obtained by$ P_\alpha = \frac{E_{f\alpha}}{E}, $
(19) where
$ E_{f\alpha} $ is the formation energy of the$ \alpha $ cluster. E is composed of$ E_{f\alpha} $ and the interaction energy between the$ \alpha $ cluster and daughter nuclei. In the framework of CFM [12, 67−69], the$ \alpha $ cluster-formation energy$ E_{f\alpha} $ and total energy E can be expressed as four different cases as follows:Case I for even-even nuclei:
$ \begin{aligned}[b] E_{f \alpha} =\;& 3B(A,Z) + B(A - 4,Z - 2) \\ & - 2B(A - 1,Z - 1) - 2B(A - 1,Z), \end{aligned} $
(20a) $ \begin{aligned} E = B(A,Z) - B(A - 4,Z - 2); \end{aligned} $
(20b) Case II for even Z-odd N, i.e., even-odd nuclei:
$ \begin{aligned} E_{f \alpha} =\;& 3B(A - 1,Z) + B(A - 5,Z - 2) \\ & - 2B(A - 2,Z - 1) - 2B(A - 2,Z) , \end{aligned} $
(21a) $ \begin{aligned} E = B(A,Z) - B(A - 5,Z - 2); \end{aligned} $
(21b) Case III for odd Z-even N, i.e., odd-even nuclei:
$ \begin{aligned}[b] E_{f \alpha} =\;& 3B(A - 1,Z - 1) + B(A - 5,Z - 3) \\ & - 2B(A - 2,Z - 2) - 2B(A - 2,Z - 1) , \end{aligned} $
(22a) $ \begin{aligned} E = B(A,Z) - B(A - 5,Z - 3); \end{aligned} $
(22b) Case IV for doubly odd nuclei:
$ \begin{aligned} E_{f \alpha} =\;& 3B(A - 2,Z - 1) + B(A - 6,Z - 3) \\ & - 2B(A - 3,Z - 2) - 2B(A - 3,Z - 1) , \end{aligned} $
(23a) $ \begin{aligned} E = B(A,Z) - B(A - 6,Z - 3); \end{aligned} $
(23b) where
$ B(A,Z) $ denotes the binding energy of the nucleus with mass number A and proton number Z. -
Within the CFM [12, 66−69], the total clusterization state
$ \Psi $ of the parent nuclei is assumed to be a linear combination of all its n possible clusterization states$ \Psi_i $ . This can be expressed as$ \Psi = \sum\limits_{i=1}^{n} a_i \Psi_i, $

(14) $ a_i = \int \Psi_i^* \Psi \, {\rm d}\tau, $

(15) where
$ a_i $ denotes the superposition coefficient of$ \Psi_i $ , on the basis of the orthogonality condition$ \sum\limits_{i=1}^{n} |a_i|^2 = 1. $

(16) The total wave function is an eigenfunction of the total Hamiltonian H. Similarly, H can be expressed as
$ H = \sum\limits_{i=1}^{N} H_i, $

(17) where
$ H_i $ is the Hamiltonian for the i-th clusterization state$ \Psi_i $ . Because all the clusters describe the same nucleus, they are assumed to share the same total energy E of the total wave function. Therefore, the total energy E can be expressed as$ E = \sum\limits_{i=1}^{n} |a_i|^2 E = \sum\limits_{i=1}^{n} E_{fi}, $

(18) where
$ E_{fi} $ denotes the formation energy of a cluster in the ith clusterization state$ \Psi_i $ . Then, the$ \alpha $ decay preformation factors$ P_\alpha $ can be obtained by$ P_\alpha = \frac{E_{f\alpha}}{E}, $

(19) where
$ E_{f\alpha} $ is the formation energy of the$ \alpha $ cluster. E is composed of$ E_{f\alpha} $ and the interaction energy between the$ \alpha $ cluster and daughter nuclei. In the framework of CFM [12, 67−69], the$ \alpha $ cluster-formation energy$ E_{f\alpha} $ and total energy E can be expressed as four different cases as follows:Case I for even-even nuclei:
$ \begin{aligned}[b] E_{f \alpha} =\;& 3B(A,Z) + B(A - 4,Z - 2) \\ & - 2B(A - 1,Z - 1) - 2B(A - 1,Z), \end{aligned} $

(20a) $ \begin{aligned} E = B(A,Z) - B(A - 4,Z - 2); \end{aligned} $

(20b) Case II for even Z-odd N, i.e., even-odd nuclei:
$ \begin{aligned} E_{f \alpha} =\;& 3B(A - 1,Z) + B(A - 5,Z - 2) \\ & - 2B(A - 2,Z - 1) - 2B(A - 2,Z) , \end{aligned} $

(21a) $ \begin{aligned} E = B(A,Z) - B(A - 5,Z - 2); \end{aligned} $

(21b) Case III for odd Z-even N, i.e., odd-even nuclei:
$ \begin{aligned}[b] E_{f \alpha} =\;& 3B(A - 1,Z - 1) + B(A - 5,Z - 3) \\ & - 2B(A - 2,Z - 2) - 2B(A - 2,Z - 1) , \end{aligned} $

(22a) $ \begin{aligned} E = B(A,Z) - B(A - 5,Z - 3); \end{aligned} $

(22b) Case IV for doubly odd nuclei:
$ \begin{aligned} E_{f \alpha} =\;& 3B(A - 2,Z - 1) + B(A - 6,Z - 3) \\ & - 2B(A - 3,Z - 2) - 2B(A - 3,Z - 1) , \end{aligned} $

(23a) $ \begin{aligned} E = B(A,Z) - B(A - 6,Z - 3); \end{aligned} $

(23b) where
$ B(A,Z) $ denotes the binding energy of the nucleus with mass number A and proton number Z. -
Within the CFM [12, 66−69], the total clusterization state
$ \Psi $ of the parent nuclei is assumed to be a linear combination of all its n possible clusterization states$ \Psi_i $ . This can be expressed as$ \Psi = \sum\limits_{i=1}^{n} a_i \Psi_i, $
(14) $ a_i = \int \Psi_i^* \Psi \, {\rm d}\tau, $
(15) where
$ a_i $ denotes the superposition coefficient of$ \Psi_i $ , on the basis of the orthogonality condition$ \sum\limits_{i=1}^{n} |a_i|^2 = 1. $
(16) The total wave function is an eigenfunction of the total Hamiltonian H. Similarly, H can be expressed as
$ H = \sum\limits_{i=1}^{N} H_i, $
(17) where
$ H_i $ is the Hamiltonian for the i-th clusterization state$ \Psi_i $ . Because all the clusters describe the same nucleus, they are assumed to share the same total energy E of the total wave function. Therefore, the total energy E can be expressed as$ E = \sum\limits_{i=1}^{n} |a_i|^2 E = \sum\limits_{i=1}^{n} E_{fi}, $
(18) where
$ E_{fi} $ denotes the formation energy of a cluster in the ith clusterization state$ \Psi_i $ . Then, the$ \alpha $ decay preformation factors$ P_\alpha $ can be obtained by$ P_\alpha = \frac{E_{f\alpha}}{E}, $
(19) where
$ E_{f\alpha} $ is the formation energy of the$ \alpha $ cluster. E is composed of$ E_{f\alpha} $ and the interaction energy between the$ \alpha $ cluster and daughter nuclei. In the framework of CFM [12, 67−69], the$ \alpha $ cluster-formation energy$ E_{f\alpha} $ and total energy E can be expressed as four different cases as follows:Case I for even-even nuclei:
$ \begin{aligned}[b] E_{f \alpha} =\;& 3B(A,Z) + B(A - 4,Z - 2) \\ & - 2B(A - 1,Z - 1) - 2B(A - 1,Z), \end{aligned} $
(20a) $ \begin{aligned} E = B(A,Z) - B(A - 4,Z - 2); \end{aligned} $
(20b) Case II for even Z-odd N, i.e., even-odd nuclei:
$ \begin{aligned} E_{f \alpha} =\;& 3B(A - 1,Z) + B(A - 5,Z - 2) \\ & - 2B(A - 2,Z - 1) - 2B(A - 2,Z) , \end{aligned} $
(21a) $ \begin{aligned} E = B(A,Z) - B(A - 5,Z - 2); \end{aligned} $
(21b) Case III for odd Z-even N, i.e., odd-even nuclei:
$ \begin{aligned}[b] E_{f \alpha} =\;& 3B(A - 1,Z - 1) + B(A - 5,Z - 3) \\ & - 2B(A - 2,Z - 2) - 2B(A - 2,Z - 1) , \end{aligned} $
(22a) $ \begin{aligned} E = B(A,Z) - B(A - 5,Z - 3); \end{aligned} $
(22b) Case IV for doubly odd nuclei:
$ \begin{aligned} E_{f \alpha} =\;& 3B(A - 2,Z - 1) + B(A - 6,Z - 3) \\ & - 2B(A - 3,Z - 2) - 2B(A - 3,Z - 1) , \end{aligned} $
(23a) $ \begin{aligned} E = B(A,Z) - B(A - 6,Z - 3); \end{aligned} $
(23b) where
$ B(A,Z) $ denotes the binding energy of the nucleus with mass number A and proton number Z. -
In 2009, a linear expression for charged-particle emissions was proposed by Qi et al. [42–43] based on the
$ \alpha $ -like R-matrix theory and named as UDL. It can be expressed as$ \log_{10}(T_{1/2}) = a Z_c Z_d \sqrt{\frac{{\cal{A}}}{Q_c}} + b \sqrt{{\cal{A}} Z_c Z_d \left(A_c^{1/3} + A_d^{1/3}\right)} + c, $

(24) where
$ {\cal{A}} = \dfrac{A_c A_d}{A_c + A_d} $ is the reduced mass of the emitted cluster-daughter nucleus system measured in units of the nucleon mass, and a, b, and c are adjustable parameters. -
In 2009, a linear expression for charged-particle emissions was proposed by Qi et al. [42–43] based on the
$ \alpha $ -like R-matrix theory and named as UDL. It can be expressed as$ \log_{10}(T_{1/2}) = a Z_c Z_d \sqrt{\frac{{\cal{A}}}{Q_c}} + b \sqrt{{\cal{A}} Z_c Z_d \left(A_c^{1/3} + A_d^{1/3}\right)} + c, $
(24) where
$ {\cal{A}} = \dfrac{A_c A_d}{A_c + A_d} $ is the reduced mass of the emitted cluster-daughter nucleus system measured in units of the nucleon mass, and a, b, and c are adjustable parameters. -
In 2009, a linear expression for charged-particle emissions was proposed by Qi et al. [42–43] based on the
$ \alpha $ -like R-matrix theory and named as UDL. It can be expressed as$ \log_{10}(T_{1/2}) = a Z_c Z_d \sqrt{\frac{{\cal{A}}}{Q_c}} + b \sqrt{{\cal{A}} Z_c Z_d \left(A_c^{1/3} + A_d^{1/3}\right)} + c, $
(24) where
$ {\cal{A}} = \dfrac{A_c A_d}{A_c + A_d} $ is the reduced mass of the emitted cluster-daughter nucleus system measured in units of the nucleon mass, and a, b, and c are adjustable parameters. -
Based on the Royer formula [34], considering the effect of angular momentum, Deng et al. [45] proposed a formula to calculate
$ \alpha $ decay half-lives, which can be expressed as$ \log_{10} T_{1/2} = a + b A^{1/6} \sqrt{Z} + c \frac{Z}{\sqrt{Q \alpha}} + d l(l + 1) + h. $
(25) Here A, Z,
$ Q_\alpha $ , and l represent the mass number, proton number,$ \alpha $ decay energy of parent nuclei, and angular momentum taken away by the emitted$ \alpha $ particle, respectively. a, b, c, and d are adjustable parameters. The values of h for different$ \alpha $ decay cases are expressed as$ h = \begin{cases} 0, & {\rm{for\ even-even\ nuclei,}} \\ 0.2812, & {\rm{for\ odd}}\ Z-{\rm{even}}\ N\ {\rm{nuclei,}} \\ 0.3625, & {\rm{for\ even}}\ Z-{\rm{odd}}\ N\ {\rm{nuclei,}} \\ 0.7486, & {\rm{for\ odd-odd\ nuclei.}} \end{cases} $
(26) -
Based on the Royer formula [34], considering the effect of angular momentum, Deng et al. [45] proposed a formula to calculate
$ \alpha $ decay half-lives, which can be expressed as$ \log_{10} T_{1/2} = a + b A^{1/6} \sqrt{Z} + c \frac{Z}{\sqrt{Q \alpha}} + d l(l + 1) + h. $
(25) Here A, Z,
$ Q_\alpha $ , and l represent the mass number, proton number,$ \alpha $ decay energy of parent nuclei, and angular momentum taken away by the emitted$ \alpha $ particle, respectively. a, b, c, and d are adjustable parameters. The values of h for different$ \alpha $ decay cases are expressed as$ h = \begin{cases} 0, & {\rm{for\ even-even\ nuclei,}} \\ 0.2812, & {\rm{for\ odd}}\ Z-{\rm{even}}\ N\ {\rm{nuclei,}} \\ 0.3625, & {\rm{for\ even}}\ Z-{\rm{odd}}\ N\ {\rm{nuclei,}} \\ 0.7486, & {\rm{for\ odd-odd\ nuclei.}} \end{cases} $
(26) -
Based on the Royer formula [34], considering the effect of angular momentum, Deng et al. [45] proposed a formula to calculate
$ \alpha $ decay half-lives, which can be expressed as$ \log_{10} T_{1/2} = a + b A^{1/6} \sqrt{Z} + c \frac{Z}{\sqrt{Q \alpha}} + d l(l + 1) + h. $

(25) Here A, Z,
$ Q_\alpha $ , and l represent the mass number, proton number,$ \alpha $ decay energy of parent nuclei, and angular momentum taken away by the emitted$ \alpha $ particle, respectively. a, b, c, and d are adjustable parameters. The values of h for different$ \alpha $ decay cases are expressed as$ h = \begin{cases} 0, & {\rm{for\ even-even\ nuclei,}} \\ 0.2812, & {\rm{for\ odd}}\ Z-{\rm{even}}\ N\ {\rm{nuclei,}} \\ 0.3625, & {\rm{for\ even}}\ Z-{\rm{odd}}\ N\ {\rm{nuclei,}} \\ 0.7486, & {\rm{for\ odd-odd\ nuclei.}} \end{cases} $

(26) -
Based on WKB theory, considering the
$ \alpha $ decay preformation factors$ P_\alpha $ , we propose a model to calculate$ \alpha $ decay half-lives of 559 nuclei from the ground state. Using the minimum standard deviation between experimental data and calculated data as the objective, function whose detailed information is provided later, we obtain the coefficients a, b, c, and d, as shown in the Table 1. To compare the calculated results under the same conditions, we refitted the experimental data and obtained the parameter results for the UDL and DZR, as shown in Tables 2−3. In this study, the standard deviation$ \sigma $ can be defined as follows:Parameters e-e e-o o-o a 21.1958 23.4998 26.7499 b −1.8435 0.7241 2.25913 c 0.5001 −2.8591 −8.4193 d 0 0.2784 0.2721 Table 1. Parameter fitting results of Eq. (13) for three different types of nuclei.
Parameters e-e e-o o-o a 0.4101 0.418 0.4062 b −0.4218 −0.4024 −0.3724 c −21.9524 −23.8632 −24.0723 Table 2. Same as Table 1 but for the UDL.
Parameters e−e e−o o−e o−o a −25.627 −28.22089 −27.1408 28.0910 b −1.1559 −1.0000 −1.1410 −1.1270 c 1.5912 1.5625 1.6251 1.6408 d 0 0.0468 0.0625 0.0625 Table 3. Same as Table 1 but for the DZR.
$ \sigma= \left[ \frac{1}{n} \sum\limits_{i=1}^n \left( \log_{10} T^{{\rm{exp}}}_{1/2} - \log_{10} T^{{\rm{cal}}}_{1/2} \right)^2 \right]^{1/2}, $

(27) where
$ \log_{10} T_{1/2}^{{\rm{exp}}} $ and$ \log_{10} T_{1/2}^{{\rm{cal}}} $ are the logarithmic forms of experimental$ \alpha $ decay half-lives and the calculated ones, respectively. n is the number of nuclei involved in different decay cases. The standard deviation$ \sigma $ of the calculated results for the three models and/or formulas is shown in Table 4. From this table, we can clearly see that the standard deviation$ \sigma $ of our model only is 0.408 for all 559 nuclei, 0.323 for 177 even-even nuclei, 0.459 for 277 odd-A nuclei, and 0.391 for 105 odd-odd nuclei. These values are smaller than those of the UDL and DZR results, which proves that our model achieves satisfactory results.Formulas Total e-e e-o o-o Our model 0.408 0.323 0.459 0.391 UDL 0.589 0.349 0.633 0.632 DZR 0.436 0.337 0.493 0.423 Table 4. Standard deviations
$\sigma$ between experimental$\alpha$ decay half-lives and those calculated using our model, the UDL and the DZR for 177 even-even nuclei, 277 odd-A nuclei, and 105 odd-odd nuclei.To show the concrete results, we use these formulas to calculate
$ \alpha $ decay half-lives of even-even, odd-A, and odd-odd nuclei. The detailed calculated results are listed in Tables 5−7. In these tables, the first three columns represent the parent nucleus, experimentally measured$ \alpha $ decay energy$ Q_\alpha $ , and$ \alpha $ decay preformation factors calculated using the CFM, respectively. The fourth to seventh columns represent the experimental half-life data for$ \alpha $ decay, as well as those calculated using our model, UDL, and DZR in logarithmic form, denoted as$ \log_{10} T^{{\rm{exp}}}_{1/2} $ ,$ \log_{10} T_{1/2}^{{\rm{cal}}} $ ,$ \log_{10} T_{1/2}^{{\rm{UDL}}} $ ,$ \log_{10} T_{1/2}^{{\rm{DZR}}} $ , respectively. For Tables 6−7, the eighth column represents the angular momentum l taken away by the$ \alpha $ particle. These three tables show that our calculated results agree closely with the experimental data for most nuclei, with some exceptions such as 185Pt, 205Ac, 209Bi, 210Po, 227Np, 230Np, 245Bk, 247Cm, 249Cf, 251Fm, 255Md, 257Md, 258Md, 268Hs, and 282Ds.Nuclide $Q_{\alpha}$ 

$P_\alpha$ 

$\log_{10} T_{1/2}^{{\rm{exp}}}$ 

$\log_{10} T_{1/2}^{{\rm{cal}}}$ 

$\log_{10} T_{1/2}^{{\rm{UDL}}}$ 

$\log_{10} T_{1/2}^{{\rm{DZR}}}$ 

146Sm 2.5292 0.1979 15.33 15.31 15.57 15.52 148Sm 1.9870 0.1954 23.30 23.10 23.54 23.43 148Gd 3.2713 0.2017 9.35 9.30 9.44 9.41 150Gd 2.8071 0.2021 13.75 13.67 13.87 13.84 152Gd 2.2039 0.2213 21.53 21.34 21.65 21.61 150Dy 4.3511 0.2360 3.11 3.05 3.10 3.07 152Dy 3.7265 0.2403 6.93 7.01 7.04 7.08 154Dy 2.9451 0.2379 13.98 13.68 13.77 13.83 152Er 4.9341 0.2389 1.06 1.06 1.11 1.06 154Er 4.2801 0.2568 4.68 4.57 4.55 4.60 156Er 3.4811 0.2521 9.99 10.15 10.16 10.25 154Yb 5.4741 0.2349 −0.35 −0.41 −0.33 −0.41 156Yb 4.8091 0.2572 2.41 2.70 2.69 2.73 156Hf 6.0251 0.2703 −1.64 −1.70 −1.66 −1.71 158Hf 5.4051 0.2463 0.81 0.83 0.85 0.85 160Hf 4.9021 0.2546 3.28 3.24 3.21 3.26 162Hf 4.4171 0.2411 5.69 5.94 5.91 5.98 158W 6.6151 0.2408 −2.84 −2.96 −2.84 −2.97 160W 6.0651 0.2732 −0.99 −0.99 −0.98 −0.98 162W 5.6781 0.2441 0.42 0.56 0.57 0.57 164W 5.2781 0.2506 2.22 2.34 2.31 2.36 166W 4.8561 0.2309 4.74 4.46 4.44 4.49 168W 4.5001 0.2357 6.20 6.48 6.44 6.52 180W 2.5153 0.1621 25.70 24.84 25.19 24.99 162Os 6.7651 0.2373 −2.68 −2.67 −2.55 −2.66 164Os 6.4851 0.2708 −1.66 −1.72 −1.70 −1.72 166Os 6.1421 0.2472 −0.59 −0.46 −0.44 −0.46 168Os 5.8161 0.2474 0.68 0.83 0.82 0.85 170Os 5.5361 0.2373 1.89 2.04 2.02 2.05 172Os 5.2241 0.2397 3.21 3.50 3.45 3.52 174Os 4.8711 0.2259 5.25 5.33 5.29 5.36 186Os 2.8212 0.1569 22.80 22.19 22.46 22.29 166Pt 7.2951 0.2381 −3.53 −3.61 −3.47 −3.61 168Pt 6.9851 0.2725 −2.69 −2.65 −2.61 −2.65 170Pt 6.7081 0.2420 −1.86 −1.74 −1.68 −1.74 172Pt 6.4631 0.2545 −0.99 −0.89 −0.88 −0.88 174Pt 6.1833 0.2471 0.06 0.16 0.15 0.16 176Pt 5.8851 0.2605 1.20 1.36 1.30 1.37 178Pt 5.5731 0.2267 2.43 2.72 2.70 2.73 180Pt 5.2761 0.2051 4.03 4.14 4.13 4.15 182Pt 4.9511 0.1868 5.62 5.83 5.85 5.85 184Pt 4.5991 0.1858 7.77 7.88 7.89 7.90 186Pt 4.3201 0.1732 9.73 9.67 9.71 9.70 188Pt 4.0067 0.2161 12.53 11.91 11.86 11.94 190Pt 3.2686 0.2031 19.18 18.48 18.54 18.54 172Hg 7.5251 0.2767 −3.64 −3.61 −3.55 −3.60 174Hg 7.2331 0.2487 −2.70 −2.73 −2.66 −2.72 176Hg 6.8971 0.2674 −1.65 −1.64 −1.64 −1.63 178Hg 6.5773 0.2584 −0.53 −0.52 −0.54 −0.51 180Hg 6.2581 0.2651 0.73 0.68 0.62 0.69 182Hg 5.9951 0.2540 1.89 1.74 1.67 1.75 184Hg 5.6601 0.2418 3.44 3.21 3.13 3.22 186Hg 5.2041 0.2469 5.70 5.46 5.34 5.47 188Hg 4.7091 0.2387 8.72 8.26 8.15 8.29 180Pb 7.4191 0.2476 −2.39 −2.61 −2.55 −2.60 182Pb 7.0651 0.2342 −1.26 −1.47 −1.43 −1.46 184Pb 6.7741 0.2357 −0.21 −0.47 −0.46 −0.46 186Pb 6.4711 0.2301 1.07 0.65 0.63 0.66 188Pb 6.1091 0.2215 2.47 2.10 2.06 2.11 190Pb 5.6971 0.2155 4.24 3.93 3.87 3.94 192Pb 5.2211 0.2040 6.55 6.32 6.26 6.33 194Pb 4.7381 0.1946 9.94 9.11 9.06 9.13 210Pb 3.7927 0.1066 16.57 15.86 16.08 15.85 188Po 8.0831 0.2750 −3.57 −3.97 −3.91 −3.97 190Po 7.6931 0.2619 −2.61 −2.84 −2.81 −2.84 192Po 7.3201 0.2571 −1.49 −1.67 −1.68 −1.67 194Po 6.9871 0.2352 −0.41 −0.55 −0.56 −0.55 196Po 6.6581 0.2160 0.78 0.64 0.63 0.64 198Po 6.3101 0.2032 2.27 2.01 1.99 2.00 200Po 5.9811 0.1837 3.79 3.41 3.41 3.41 202Po 5.7001 0.1767 5.14 4.70 4.69 4.69 204Po 5.4851 0.1579 6.27 5.75 5.77 5.74 206Po 5.3271 0.1452 7.14 6.55 6.60 6.54 208Po 5.2157 0.1350 7.96 7.13 7.20 7.11 210Po 5.4075 0.1059 7.08 6.05 6.23 6.02 212Po 8.9542 0.2210 −6.53 −6.76 −6.46 −6.83 214Po 7.8335 0.2134 −3.79 −3.71 −3.58 −3.78 216Po 6.9063 0.2046 −0.84 −0.65 −0.63 −0.72 218Po 6.1148 0.1956 2.27 2.49 2.45 2.43 194Rn 7.8631 0.2614 −3.11 −2.63 −2.61 −2.62 196Rn 7.6161 0.2563 −2.33 −1.89 −1.89 −1.88 198Rn 7.3501 0.2390 −1.16 −1.04 −1.05 −1.03 200Rn 7.0441 0.2213 0.07 0.00 −0.01 0.01 202Rn 6.7731 0.2094 1.09 0.99 0.97 0.99 204Rn 6.5471 0.1912 2.01 1.85 1.84 1.84 206Rn 6.3841 0.1803 2.74 2.49 2.49 2.48 208Rn 6.2611 0.1626 3.37 2.98 3.02 2.97 210Rn 6.1591 0.1515 3.95 3.39 3.45 3.38 212Rn 6.3853 0.1206 3.16 2.37 2.55 2.35 214Rn 9.2082 0.2291 −6.59 −6.70 −6.42 −6.75 216Rn 8.1975 0.2368 −4.54 −4.04 −3.94 −4.09 218Rn 7.2625 0.2342 −1.47 −1.10 −1.12 −1.15 220Rn 6.4048 0.2208 1.75 2.15 2.06 2.11 222Rn 5.5904 0.2218 5.52 5.92 5.75 5.87 202Ra 7.8801 0.2477 −2.39 −2.03 −2.02 −2.01 204Ra 7.6361 0.2309 −1.22 −1.28 −1.27 −1.26 206Ra 7.4161 0.2186 −0.62 −0.57 −0.57 −0.56 208Ra 7.2731 0.1954 0.10 −0.10 −0.07 −0.10 210Ra 7.1511 0.1871 0.60 0.30 0.34 0.30 214Ra 7.2731 0.1384 0.39 −0.21 −0.36 −0.23 216Ra 9.5251 0.2390 −6.76 −6.79 −6.51 −6.82 218Ra 8.5411 0.2426 −4.59 −4.28 −4.18 −4.32 220Ra 7.5941 0.2393 −1.74 −1.42 −1.45 −1.46 222Ra 6.6777 0.1991 1.53 1.91 1.86 1.88 224Ra 5.7889 0.1840 5.50 5.88 5.79 5.85 226Ra 4.8707 0.1816 10.70 11.09 10.98 11.06 210Th 8.0691 0.2341 −1.80 −1.96 −1.95 −1.95 212Th 7.9581 0.1957 −1.50 −1.65 −1.57 −1.64 214Th 7.8271 0.1951 −1.06 −1.27 −1.20 −1.26 216Th 8.0731 0.1585 −1.58 −2.09 −1.90 −2.09 218Th 9.8491 0.2506 −6.91 −6.89 −6.62 −6.90 220Th 8.9741 0.2432 −4.99 −4.75 −4.62 −4.77 222Th 8.1321 0.2324 −2.65 −2.38 −2.35 −2.39 224Th 7.2991 0.1981 0.02 0.37 0.36 0.35 226Th 6.4531 0.1822 3.27 3.70 3.64 3.68 228Th 5.5202 0.1831 7.78 8.24 8.12 8.22 230Th 4.7700 0.1826 12.38 12.82 12.70 12.80 232Th 4.0816 0.1601 17.65 18.10 18.07 18.07 218U 8.7751 0.1880 −3.45 −3.42 −3.25 −3.41 222U 9.4781 0.2446 −5.33 −5.36 −5.20 −5.36 224U 8.6281 0.2472 −3.40 −3.11 −3.08 −3.11 226U 7.7011 0.2075 −0.57 −0.24 −0.26 −0.24 228U 6.7991 0.1905 2.75 3.12 3.04 3.11 230U 5.9921 0.1871 6.24 6.74 6.61 6.73 232U 5.4136 0.1688 9.34 9.82 9.71 9.81 234U 4.8576 0.1502 12.89 13.29 13.23 13.27 236U 4.5730 0.1532 14.87 15.29 15.23 15.27 238U 4.2698 0.1374 17.15 17.65 17.66 17.62 230Pu 7.1781 0.2015 2.02 2.45 2.36 2.46 232Pu 6.7161 0.1647 4.00 4.31 4.25 4.31 234Pu 6.3101 0.1517 5.72 6.10 6.05 6.10 236Pu 5.8672 0.1398 7.96 8.27 8.24 8.26 238Pu 5.5932 0.1450 9.44 9.73 9.67 9.72 240Pu 5.2558 0.1293 11.32 11.70 11.68 11.68 242Pu 4.9843 0.1326 13.07 13.42 13.39 13.39 244Pu 4.6656 0.1268 15.41 15.64 15.64 15.60 234Cm 7.3651 0.1943 2.28 2.53 2.43 2.54 236Cm 7.0671 0.1573 3.35 3.67 3.64 3.68 238Cm 6.6701 0.1366 5.31 5.32 5.32 5.32 240Cm 6.3978 0.1373 6.42 6.53 6.51 6.53 242Cm 6.2157 0.1222 7.15 7.38 7.39 7.37 244Cm 5.9016 0.1444 8.76 8.96 8.88 8.94 246Cm 5.4751 0.1421 11.17 11.33 11.25 11.31 248Cm 5.1618 0.1462 13.08 13.25 13.15 13.22 238Cf 8.1331 0.1854 −0.08 0.53 0.51 0.57 240Cf 7.7111 0.1496 1.61 1.98 2.00 2.00 242Cf 7.5171 0.1451 2.53 2.66 2.68 2.68 244Cf 7.3290 0.1527 3.19 3.36 3.33 3.37 246Cf 6.8616 0.1551 5.11 5.26 5.18 5.26 248Cf 6.3613 0.1382 7.46 7.52 7.46 7.52 250Cf 6.1285 0.1358 8.62 8.65 8.59 8.64 252Cf 6.2170 0.1463 7.94 8.17 8.07 8.15 254Cf 5.9261 0.1543 9.22 9.66 9.52 9.63 244Fm 8.5461 0.1656 −0.51 −0.13 −0.09 −0.09 246Fm 8.3791 0.1536 0.22 0.37 0.43 0.41 248Fm 7.9950 0.1637 1.54 1.65 1.63 1.67 250Fm 7.5569 0.1491 3.27 3.23 3.20 3.24 252Fm 7.1541 0.1539 4.96 4.80 4.72 4.81 254Fm 7.3073 0.1350 4.07 4.14 4.13 4.15 256Fm 7.0255 0.1546 5.06 5.28 5.18 5.28 252No 8.5481 0.1581 0.56 0.50 0.53 0.54 254No 8.2261 0.1404 1.75 1.55 1.59 1.58 256No 8.5811 0.1533 0.47 0.33 0.37 0.36 256Rf 8.9261 0.1557 0.33 0.00 0.05 0.06 258Rf 9.1961 0.1737 −0.59 −0.85 −0.82 −0.80 260Sg 9.9001 0.1716 −1.77 −2.16 −2.06 −2.09 266Hs 10.3461 0.1566 −2.41 −2.75 −2.58 −2.66 268Hs 9.7651 0.1711 0.15 −1.21 −1.16 −1.14 270Hs 9.0651 0.1555 0.95 0.85 0.84 0.91 270Ds 11.1151 0.1793 −3.69 −4.06 −3.86 −3.95 282Ds 9.1451 0.1958 2.40 1.15 1.02 1.21 286Cn 9.2351 0.1836 1.48 1.55 1.42 1.62 286Fl 10.3551 0.2085 −0.66 −1.04 −1.10 −0.94 288Fl 10.0751 0.1976 −0.19 −0.29 −0.37 −0.20 290Lv 10.9951 0.2069 −2.05 −2.12 −2.12 −1.99 292Lv 10.7851 0.2016 −1.80 −1.61 −1.63 −1.49 294Og 11.8353 0.2112 −3.15 −3.58 −3.49 −3.43 Table 5. Comparison of experimental
$\alpha$ decay half-lives of even-even nuclei with the calculated ones using our model, UDL, and DZR in logarithmic form. The experimental$\alpha$ decay half-lives are taken from Ref. [79]. The$\alpha$ decay energy and mass excess are taken from the latest evaluated atomic mass table AME2020 [80, 81]. The$\alpha$ decay energy and half-lives are in units of MeV and s, respectively.Nuclide $Q_{\alpha} $ /MeV

$P_\alpha$ 

$\log_{10} T^{{\rm{exp}}}_{1/2}$ 

$\log_{10} T^{{\rm{cal}}}_{1/2}$ 

$\log_{10} T_{1/2}^{{\rm{UDL}}}$ 

$\log_{10} T_{1/2}^{{\rm{DZR}}}$ 

l 148Eu 4.5071 0.1400 14.70 15.30 14.33 15.11 0 152Ho 4.0421 0.1682 3.12 3.20 3.03 3.11 0 154Ho 5.0941 0.1714 6.56 6.05 5.77 6.00 0 154Tm 4.3461 0.1709 1.17 1.23 1.20 1.17 0 156Tm 5.5951 0.1835 5.12 5.20 5.06 5.22 0 156Lu 4.7901 0.1678 −0.31 −0.09 −0.03 −0.15 0 158Lu 6.1251 0.1842 3.07 3.76 3.73 3.81 0 158Ta 5.0071 0.1946 −1.31 −1.38 −1.17 −1.35 0 162Ta 6.6951 0.1828 3.68 4.27 3.65 4.06 2 160Re 6.2451 0.1727 −2.26 −1.85 −2.28 −2.17 2 162Re 5.0681 0.1977 −0.95 −0.99 −0.72 −0.91 0 168Re 6.7151 0.1655 4.94 5.52 4.35 5.64 4 166Ir 6.3751 0.1965 −1.95 −1.87 −1.54 −1.79 0 168Ir 5.9551 0.1781 −0.64 −0.62 −0.35 −0.55 0 170Ir 5.9851 0.1792 1.24 1.03 1.27 1.13 0 172Ir 5.6931 0.1711 2.34 1.83 1.11 1.71 3 174Ir 7.1851 0.1730 3.17 2.83 2.36 2.63 2 170Au 6.9251 0.1977 −2.58 −2.67 −2.27 −2.58 0 172Au 6.6951 0.1743 −1.55 −1.79 −1.45 −1.72 0 174Au 6.4351 0.1843 −0.81 −1.03 −0.68 −0.93 0 176Au 6.0581 0.1781 0.14 −0.08 0.24 0.02 0 178Au 5.8311 0.1875 1.32 1.40 1.71 1.56 0 180Au 5.5251 0.1625 3.13 3.11 2.66 2.92 2 182Au 5.2341 0.1464 4.06 4.53 4.00 4.31 2 184Au 4.9121 0.1327 5.19 5.41 5.45 5.45 0 186Au 7.0251 0.1316 7.89 7.56 7.16 7.35 1 178Tl 7.7571 0.1934 −0.39 −0.75 −0.99 −0.90 2 186Bi 7.2631 0.1751 −1.83 −2.66 −2.59 −2.86 1 188Bi 6.8621 0.1691 −1.22 −1.08 −1.04 −1.25 1 190Bi 6.3811 0.1620 0.91 0.31 0.31 0.16 1 192Bi 5.9181 0.1567 2.44 2.17 2.12 2.04 1 194Bi 5.2611 0.1475 4.31 4.17 4.05 4.05 1 196Bi 6.2073 0.1401 7.43 7.14 7.28 7.29 0 212Bi 5.6211 0.0786 4.00 3.98 2.51 4.11 5 214Bi 7.6961 0.0815 6.75 6.68 5.15 6.87 5 192At 7.3341 0.1895 −1.94 −2.19 −1.66 −2.04 0 194At 7.1951 0.1860 −0.54 −1.01 −0.50 −0.83 0 196At 6.8891 0.1695 −0.41 −0.55 −0.09 −0.41 0 198At 6.5961 0.1545 0.66 0.58 0.99 0.71 0 200At 6.3541 0.1447 1.92 1.70 2.06 1.82 0 202At 6.0711 0.1309 3.16 2.75 3.04 2.84 0 204At 5.8871 0.1252 4.16 3.97 4.22 4.06 0 206At 5.7511 0.1116 5.31 5.50 5.01 5.25 2 208At 5.6311 0.1022 6.02 5.53 5.65 5.53 0 210At 7.8172 0.0946 7.22 6.81 6.21 6.48 2 212At 8.9880 0.0784 −0.50 −0.99 −2.35 −0.96 5 214At 7.9500 0.1542 −6.25 −5.99 −5.60 −6.24 0 216At 6.8761 0.1501 −3.52 −3.21 −2.81 −3.33 0 218At 6.0531 0.1438 0.11 1.02 0.71 0.71 2 220At 7.8711 0.1376 3.43 3.78 4.07 3.83 0 198Fr 7.6151 0.1864 −1.82 −1.07 −1.45 −1.08 3 200Fr 7.3861 0.1729 −1.32 −1.22 −0.69 −1.05 0 202Fr 7.1701 0.1594 −0.43 −0.44 0.05 −0.29 0 204Fr 6.9231 0.1502 0.26 0.33 0.78 0.46 0 206Fr 6.7851 0.1368 1.26 1.27 1.66 1.38 0 208Fr 6.6701 0.1283 1.82 1.77 2.13 1.85 0 210Fr 6.5291 0.1152 2.43 2.26 2.57 2.30 0 212Fr 8.5891 0.1068 3.44 3.51 3.10 3.23 2 214Fr 9.1742 0.0893 −2.26 −2.53 −3.79 −2.47 5 216Fr 8.0131 0.1610 −6.15 −5.78 −5.32 −5.95 0 218Fr 6.8001 0.1661 −2.85 −2.69 −2.19 −2.69 0 220Fr 7.9531 0.1635 1.44 1.83 1.90 1.70 1 206Ac 7.7281 0.1668 −1.60 −1.56 −0.99 −1.39 0 208Ac 7.5401 0.0903 −1.01 −0.61 −0.32 −0.70 0 212Ac 7.3521 0.1334 −0.05 −0.21 0.25 −0.12 0 214Ac 9.2411 0.1212 0.94 1.13 0.87 0.90 2 216Ac 9.3831 0.1027 −3.36 −3.58 −4.74 −3.47 5 218Ac 8.3481 0.1688 −6.00 −5.65 −5.12 −5.74 0 220Ac 7.1381 0.1710 −1.58 −2.31 −2.41 −2.55 2 222Ac 6.3271 0.1667 0.70 0.97 1.50 1.15 0 224Ac 5.5061 0.1386 5.02 4.72 4.73 4.62 1 226Ac 8.4151 0.1279 9.23 9.12 8.70 9.00 2 212Pa 8.2751 0.1688 −2.24 −2.31 −1.68 −2.14 0 214Pa 8.0991 0.1404 −1.77 −1.84 −1.30 −1.75 0 216Pa 9.7031 0.1392 −0.98 −0.65 −0.78 −0.84 2 220Pa 7.6931 0.1785 −6.07 −5.78 −5.18 −5.82 0 224Pa 6.9871 0.1623 −0.07 0.49 0.42 0.38 2 226Pa 6.2651 0.1372 2.16 2.43 2.91 2.60 0 228Pa 5.4401 0.1264 6.63 6.47 5.91 6.47 3 230Pa 9.3291 0.1274 10.67 10.50 10.09 10.44 2 224Np 8.3351 0.1742 −4.32 −3.59 −3.59 −3.79 2 226Np 7.5431 0.1739 −1.46 −1.54 −0.86 −1.33 0 228Np 6.7811 0.1451 2.17 1.54 1.74 1.49 1 230Np 5.0081 0.1328 3.96 5.06 4.62 5.11 3 236Np 6.7951 0.1049 15.47 14.83 13.72 15.07 4 234Am 6.2551 0.1153 5.55 6.42 5.41 7.04 5 236Am 5.4691 0.1054 6.73 7.43 7.81 7.65 0 240Am 8.1051 0.1006 10.98 11.70 11.93 11.92 0 234Bk 8.2651 0.1480 1.40 1.36 1.40 1.37 2 240Es 8.1551 0.1308 0.93 1.29 1.61 1.32 1 242Es 7.9451 0.1057 1.49 1.72 1.94 1.66 1 244Es 7.4951 0.1022 2.84 2.43 2.63 2.36 1 246Es 7.6451 0.1068 3.66 3.66 4.24 3.90 0 246Es 7.1611 0.1068 3.66 3.47 3.68 3.44 1 248Es 6.7351 0.1087 5.76 5.65 5.55 5.63 2 252Es 8.9451 0.0958 7.72 7.48 7.28 7.42 2 244Md 8.8951 0.1347 −0.44 −0.16 0.22 −0.14 1 246Md 8.1551 0.1170 −0.04 0.03 0.34 −0.02 1 250Md 7.7451 0.1139 2.88 2.64 2.66 2.62 2 256Md 7.2709 0.0951 4.70 4.38 4.03 4.40 3 258Md 9.1651 0.1081 6.65 5.63 5.86 5.67 1 252Lr 8.8251 0.1096 −0.42 −0.49 0.23 −0.28 0 254Lr 8.8551 0.1102 1.22 1.44 1.23 1.50 3 256Lr 9.3351 0.0992 1.52 0.81 1.10 0.74 1 256Db 9.3351 0.1152 0.38 0.32 0.44 0.31 2 Table 7. Same as Table 6 but for odd-odd nuclei.
Nuclide $Q_{\alpha} $ /MeV

$P_\alpha$ 

$\log_{10} T^{{\rm{exp}}}_{1/2}$ 

$\log_{10} T^{{\rm{cal}}}_{1/2}$ 

$\log_{10} T_{1/2}^{{\rm{UDL}}}$ 

$\log_{10} T_{1/2}^{{\rm{DZR}}}$ 

l 107Te 4.0051 0.1721 −2.34 −2.17 −2.65 −2.97 0 109I 3.9171 0.2638 −0.19 −0.66 −1.60 −1.12 2 113I 2.7061 0.2190 7.30 7.17 6.91 7.24 0 111Xe 3.7151 0.1794 0.85 0.52 0.15 −0.19 0 145Pm 2.3221 0.1659 17.30 17.68 17.51 17.77 0 147Sm 2.3114 0.1588 18.53 18.69 18.52 17.77 0 147Eu 2.9912 0.1723 10.96 11.48 11.41 11.53 0 151Eu 1.9640 0.1789 26.16 25.81 24.97 25.67 2 149Gd 3.0995 0.1581 11.27 11.18 11.10 10.52 0 151Gd 2.6522 0.1611 15.63 15.86 15.78 15.09 0 149Tb 4.0781 0.1835 4.95 5.00 4.29 4.64 2 151Tb 3.4957 0.1799 8.82 9.06 8.38 8.79 2 151Dy 4.1800 0.1796 4.28 4.26 4.24 3.83 0 153Dy 3.5591 0.1864 8.39 8.49 8.53 8.02 0 151Ho 4.6441 0.2212 2.20 2.12 2.18 2.11 0 153Ho 4.0161 0.2207 5.37 5.77 5.89 5.87 0 153Er 4.8021 0.1777 1.84 1.91 1.89 1.56 0 155Er 4.1181 0.1946 6.15 5.73 5.82 5.39 0 153Tm 5.2481 0.2314 0.21 0.19 0.27 0.17 0 155Tm 4.5721 0.2435 3.41 3.50 3.68 3.62 0 157Tm 3.8091 0.2352 7.46 8.37 8.58 8.58 0 155Yb 5.3381 0.1704 0.30 0.39 0.36 0.09 0 155Lu 5.8021 0.2359 −1.12 −1.20 −1.12 −1.24 0 157Hf 5.8751 0.1918 −0.91 −0.96 −0.95 −1.15 0 159Hf 5.2251 0.1778 1.16 1.83 1.89 1.61 0 161Hf 4.6791 0.1871 3.79 4.59 4.72 4.36 0 157Ta 6.2751 0.2821 −1.98 −2.16 −2.01 −2.14 0 159Ta 5.6601 0.2504 0.48 0.24 0.43 0.32 0 159W 6.4551 0.1658 −2.09 −2.16 −2.23 −2.37 0 161W 5.9251 0.1929 −0.25 −0.29 −0.22 −0.42 0 163W 5.5181 0.1747 1.27 1.43 1.51 1.26 0 167W 4.7511 0.1706 4.69 5.22 5.37 5.00 0 163Re 6.0121 0.2520 0.08 −0.32 −0.11 −0.25 0 165Re 5.6951 0.2537 1.03 0.94 1.20 1.07 0 169Re 5.0141 0.2280 5.18 5.12 4.45 5.09 3 163Os 6.6651 0.1625 −2.24 −2.08 −2.12 −2.24 0 165Os 6.3351 0.1892 −1.10 −1.01 −0.94 −1.10 0 167Os 5.9851 0.1750 0.21 0.33 0.42 0.22 0 169Os 5.7131 0.1778 1.40 1.43 1.56 1.33 0 171Os 5.3711 0.1731 2.66 2.97 3.13 2.84 0 173Os 5.0551 0.1765 3.73 4.51 4.72 4.38 0 167Ir 6.5051 0.2598 −1.17 −1.36 −1.14 −1.29 0 169Ir 6.1411 0.2543 −0.18 −0.02 0.24 0.09 0 171Ir 5.8651 0.2397 1.31 1.09 1.37 1.22 0 173Ir 5.5411 0.2365 2.41 2.50 2.81 2.67 0 175Ir 5.4301 0.2195 3.02 3.69 3.30 3.54 2 177Ir 5.0821 0.1885 4.69 4.80 5.06 4.92 0 167Pt 7.1651 0.1611 −3.04 −2.93 −2.99 −3.05 0 169Pt 6.8651 0.1883 −2.16 −2.07 −2.01 −2.11 0 171Pt 6.6051 0.1694 −1.28 −1.17 −1.11 −1.24 0 173Pt 6.3581 0.1808 −0.35 −0.33 −0.21 −0.37 0 177Pt 5.6431 0.1888 2.24 2.54 2.78 2.52 0 179Pt 5.4121 0.1658 3.94 4.34 3.86 3.84 2 181Pt 5.1501 0.1521 4.85 4.98 5.18 4.84 0 183Pt 4.8221 0.1405 6.61 6.80 7.00 6.60 0 185Pt 4.2801 0.1414 7.93 10.24 10.48 9.97 0 173Au 6.8361 0.2665 −1.53 −1.78 −1.52 −1.70 0 175Au 6.5851 0.2543 −0.65 −0.91 −0.64 −0.81 0 177Au 6.2971 0.2617 0.57 0.12 0.44 0.27 0 179Au 5.9811 0.2240 1.51 1.43 1.73 1.56 0 181Au 5.7511 0.1988 2.70 2.45 2.72 2.56 0 183Au 5.4661 0.1768 3.89 3.79 4.06 3.89 0 185Au 5.1800 0.1725 4.98 5.22 5.51 5.34 0 173Hg 7.3751 0.1887 −3.10 −2.95 −2.90 −2.94 0 175Hg 7.0751 0.1720 −2.00 −2.00 −1.94 −2.02 0 177Hg 6.7351 0.1878 −0.93 −0.24 −0.77 −0.61 2 179Hg 6.3511 0.1845 0.14 0.48 0.68 0.51 0 181Hg 6.2841 0.1915 1.12 1.37 0.91 1.01 2 183Hg 6.0381 0.1851 1.90 1.67 1.91 1.70 0 185Hg 5.7721 0.1792 2.91 2.81 3.07 2.82 0 177Tl 7.0671 0.2827 −1.61 −1.81 −1.50 −1.68 0 179Tl 6.7051 0.2677 −0.14 −0.57 −0.23 −0.40 0 181Tl 6.3221 0.2671 1.52 0.85 1.24 1.07 0 181Pb 7.2451 0.1716 −1.41 −1.15 −1.73 −1.51 2 183Pb 6.9281 0.1654 −0.27 −0.11 −0.66 −0.48 2 185Pb 6.6951 0.1686 1.26 0.68 0.17 0.32 2 187Pb 6.3931 0.1663 2.20 1.80 1.33 1.44 2 189Pb 5.9151 0.1622 3.97 3.78 3.37 3.41 2 187Bi 7.7791 0.2413 −1.43 −1.81 −3.14 −1.48 5 189Bi 7.2681 0.2261 −0.16 −0.24 −1.51 0.15 5 191Bi 6.4471 0.2144 1.39 1.17 1.52 1.32 0 193Bi 6.0211 0.1986 3.26 2.95 3.32 3.12 0 195Bi 5.5351 0.1858 5.78 5.23 5.64 5.44 0 209Bi 3.1373 0.0938 26.80 25.45 24.12 25.85 5 211Bi 6.7501 0.0903 2.11 1.56 −0.02 1.57 5 213Bi 5.9881 0.0924 5.12 4.60 3.14 4.73 5 189Po 7.6941 0.1906 −2.46 −1.95 −2.48 −2.22 2 191Po 7.4931 0.1849 −1.66 −2.03 −1.86 −1.90 0 193Po 7.0941 0.1840 −0.40 −0.75 −0.53 −0.61 0 195Po 6.7491 0.1699 0.69 0.48 0.72 0.59 0 197Po 6.4111 0.1577 1.80 1.79 2.05 1.87 0 199Po 6.0741 0.1498 3.64 3.20 3.48 3.25 0 201Po 5.7991 0.1368 4.92 4.46 4.74 4.46 0 203Po 5.4961 0.1329 6.29 6.62 6.24 6.19 2 205Po 5.3251 0.1198 7.19 6.85 7.13 6.76 0 207Po 5.2151 0.1111 7.99 7.46 7.71 7.32 0 209Po 4.9770 0.1037 9.59 8.84 9.08 8.65 0 211Po 7.5946 0.0884 −0.29 −0.85 −2.54 −1.19 5 213Po 8.5357 0.1804 −5.43 −5.35 −5.37 −5.33 0 215Po 7.5263 0.1775 −2.75 −2.53 −2.39 −2.45 0 217Po 6.6621 0.1726 0.20 0.42 0.69 0.53 0 219Po 5.9161 0.1673 3.34 3.51 3.88 3.60 0 191At 7.7141 0.1984 −2.68 −2.35 −2.15 −2.37 0 193At 7.3891 0.2661 −1.54 −1.49 −1.11 −1.33 0 195At 7.1021 0.2380 −0.54 −0.51 −0.14 −0.36 0 197At 7.1051 0.2142 −0.39 −0.51 −0.18 −0.41 0 199At 6.7781 0.1974 0.89 0.67 1.01 0.78 0 201At 6.4731 0.1748 2.07 1.88 2.20 1.97 0 203At 6.2101 0.1656 3.15 2.96 3.30 3.07 0 205At 6.0191 0.1456 4.20 3.83 4.14 3.90 0 207At 5.8731 0.1318 4.81 4.51 4.79 4.56 0 209At 5.7571 0.1209 5.69 5.07 5.33 5.09 0 211At 5.9825 0.0938 4.79 4.08 4.21 3.95 0 213At 9.2537 0.1871 −6.90 −6.73 −6.84 −7.16 0 215At 8.1771 0.1779 −4.43 −4.06 −3.99 −4.30 0 217At 7.2021 0.1679 −1.49 −1.08 −0.87 −1.17 0 219At 6.3421 0.1582 1.78 2.14 2.46 2.17 0 195Rn 7.6941 0.1830 −2.15 −1.93 −1.73 −1.75 0 197Rn 7.4101 0.1814 −1.27 −1.05 −0.81 −0.86 0 199Rn 7.1321 0.1706 −0.23 −0.12 0.14 0.05 0 203Rn 6.6301 0.1527 1.82 1.72 2.00 1.85 0 205Rn 6.3861 0.1407 2.84 3.39 2.99 3.08 2 207Rn 6.2511 0.1340 3.42 3.27 3.55 3.33 0 209Rn 6.1551 0.1219 4.00 3.70 3.95 3.71 0 211Rn 5.9661 0.1142 5.28 5.23 4.79 4.81 2 213Rn 8.2451 0.0978 −1.71 −2.06 −3.75 −2.32 5 215Rn 8.8386 0.1821 −5.64 −5.43 −5.44 −5.36 0 217Rn 7.8881 0.1921 −3.23 −2.92 −2.73 −2.75 0 219Rn 6.9462 0.1932 0.60 0.82 0.49 0.64 2 221Rn 6.1631 0.1851 3.84 3.95 3.71 3.75 2 197Fr 7.8841 0.2692 −2.64 −2.32 −1.95 −2.18 0 199Fr 7.8161 0.2474 −2.18 −2.11 −1.77 −2.00 0 201Fr 7.5191 0.2245 −1.20 −1.17 −0.82 −1.06 0 203Fr 7.2741 0.2080 −0.26 −0.35 0.00 −0.24 0 205Fr 7.0541 0.1858 0.60 0.44 0.78 0.53 0 207Fr 6.8891 0.1724 1.19 1.04 1.37 1.12 0 209Fr 6.7781 0.1527 1.75 1.48 1.77 1.52 0 211Fr 6.6621 0.1400 2.33 1.93 2.21 1.95 0 213Fr 6.9051 0.1096 1.54 1.07 1.21 0.94 0 215Fr 9.5403 0.2012 −7.05 −6.76 −6.82 −7.13 0 217Fr 8.4701 0.2040 −4.66 −4.21 −4.06 −4.37 0 219Fr 7.4491 0.1976 −1.65 −1.20 −0.89 −1.19 0 221Fr 6.4571 0.1823 2.46 3.16 2.90 2.99 2 223Fr 5.5614 0.1799 7.34 7.88 7.17 8.14 4 203Ra 7.7361 0.1746 −1.44 −1.39 −1.15 −1.16 0 205Ra 7.4861 0.1646 −0.66 −0.59 −0.34 −0.38 0 207Ra 7.2691 0.1574 0.21 0.81 0.40 0.61 2 209Ra 7.1431 0.1418 0.67 0.59 0.83 0.74 0 211Ra 7.0421 0.1372 1.10 0.93 1.17 1.07 0 213Ra 6.8621 0.1263 2.27 2.29 1.84 1.99 2 215Ra 8.8621 0.1092 −2.78 −3.04 −4.72 −3.22 5 217Ra 9.1611 0.1850 −5.71 −5.56 −5.54 −5.43 0 219Ra 8.1381 0.1911 −2.05 −2.24 −2.71 −2.41 2 221Ra 6.8801 0.1899 1.40 1.90 1.64 1.78 2 223Ra 5.9790 0.1608 5.99 5.77 5.55 5.55 2 205Ac 7.8061 0.0991 −1.10 −0.04 −0.99 −0.48 3 207Ac 7.8491 0.2218 −1.51 −1.53 −1.16 −1.41 0 209Ac 7.7251 0.1938 −1.03 −1.11 −0.79 −1.04 0 211Ac 7.5641 0.1820 −0.67 −0.60 −0.27 −0.53 0 213Ac 7.4981 0.1637 −0.13 −0.36 −0.08 −0.34 0 215Ac 7.7461 0.1301 −0.77 −1.11 −0.96 −1.24 0 217Ac 9.8311 0.2172 −7.16 −6.81 −6.81 −7.12 0 219Ac 8.8271 0.2166 −5.03 −4.49 −4.30 −4.60 0 221Ac 7.7901 0.2087 −1.28 −1.56 −1.21 −1.51 0 223Ac 6.7831 0.1695 2.10 2.73 2.46 2.54 2 225Ac 5.9351 0.1535 5.93 6.45 6.25 6.34 2 227Ac 5.0423 0.1491 10.70 10.69 11.24 10.97 0 211Th 7.9451 0.1662 −1.32 −1.38 −1.12 −1.12 0 213Th 7.8371 0.1401 −0.84 −1.00 −0.80 −0.81 0 215Th 7.6641 0.1411 0.13 0.20 −0.25 −0.00 2 217Th 9.4351 0.1215 −3.61 −3.82 −5.49 −3.93 5 219Th 9.5031 0.1892 −5.99 −5.73 −5.69 −5.53 0 221Th 8.6251 0.1869 −2.76 −2.88 −3.38 −3.02 2 223Th 7.5661 0.1798 −0.22 0.28 −0.05 0.19 2 225Th 6.9211 0.1555 2.77 2.63 2.33 2.48 2 227Th 6.1467 0.1457 6.21 5.91 5.69 5.71 2 229Th 5.1676 0.1488 11.40 11.10 10.99 10.82 2 211Pa 8.4751 0.2424 −2.22 −2.73 −2.36 −2.62 0 213Pa 8.3851 0.1981 −2.13 −2.42 −2.13 −2.39 0 215Pa 8.2351 0.1934 −1.85 −2.01 −1.70 −1.97 0 217Pa 8.4891 0.1545 −2.42 −2.68 −2.51 −2.78 0 219Pa 10.1241 0.2367 −7.25 −6.86 −6.81 −7.10 0 221Pa 9.2431 0.2245 −5.23 −4.88 −4.68 −4.98 0 223Pa 8.3451 0.2099 −2.28 −2.50 −2.17 −2.47 0 225Pa 7.4051 0.1739 0.23 1.22 0.94 1.02 2 227Pa 6.5801 0.1561 3.43 3.73 4.20 3.91 0 229Pa 5.8351 0.1548 7.43 7.57 7.73 7.57 1 231Pa 5.1499 0.1520 12.01 11.03 11.63 11.35 0 219U 9.9501 0.1401 −4.22 −4.42 −6.04 −4.43 5 221U 9.8891 0.1800 −6.18 −5.95 −5.93 −5.73 0 223U 9.1651 0.1833 −4.19 −3.60 −4.13 −3.71 2 225U 8.0071 0.1862 −1.21 −0.40 −0.72 −0.43 2 227U 7.2351 0.1586 1.82 2.26 1.99 2.18 2 229U 6.4761 0.1485 4.24 4.63 5.11 4.90 0 231U 5.5763 0.1481 9.95 9.73 9.63 9.54 2 233U 4.9087 0.1348 12.70 13.16 13.76 13.23 0 223Np 9.6551 0.2334 −5.60 −5.23 −5.03 −5.32 0 225Np 8.8251 0.2306 −2.22 −3.18 −2.83 −3.12 0 227Np 7.8151 0.1888 −0.29 0.85 0.32 0.78 3 229Np 7.0151 0.1691 2.55 3.17 3.28 3.11 1 231Np 6.3651 0.1631 5.14 5.90 6.08 5.92 1 233Np 5.6281 0.1439 8.49 9.25 9.85 9.55 0 235Np 5.1938 0.1265 12.12 12.23 12.42 12.25 1 237Np 4.9573 0.1272 13.83 13.74 13.95 13.77 1 229Pu 7.5931 0.1707 2.26 1.73 1.51 1.74 2 231Pu 6.8391 0.1530 3.58 3.93 4.44 4.29 0 233Pu 6.4141 0.1271 6.00 6.50 6.31 6.37 2 235Pu 5.9511 0.1182 7.72 8.07 8.58 8.26 0 239Pu 5.2444 0.1161 11.88 12.03 12.60 12.13 0 241Pu 5.1401 0.1053 13.26 13.38 13.24 13.02 2 229Am 8.1351 0.2148 0.26 0.23 0.05 0.14 2 233Am 7.0651 0.1485 3.62 3.82 3.93 3.76 1 235Am 6.5751 0.1334 5.18 5.89 6.02 5.85 1 237Am 6.1951 0.1204 7.24 7.68 7.81 7.63 1 239Am 5.9225 0.1230 8.63 9.01 9.18 9.00 1 241Am 5.6378 0.1082 10.14 10.59 10.73 10.54 1 243Am 5.4391 0.1098 11.37 11.71 11.88 11.68 1 233Cm 7.4751 0.1544 2.11 2.27 2.76 2.70 0 235Cm 7.2761 0.1467 3.99 3.68 3.50 3.69 2 241Cm 6.1852 0.1074 8.45 8.75 8.30 8.58 3 243Cm 6.1688 0.0972 8.96 8.56 8.35 8.34 2 245Cm 5.6245 0.1158 11.42 11.37 11.28 11.16 2 247Cm 5.3535 0.1159 14.69 12.67 12.90 12.52 1 245Bk 6.4546 0.1228 8.55 7.52 7.40 7.45 2 247Bk 5.8901 0.1190 10.64 10.34 10.27 10.32 2 249Bk 5.5210 0.1209 12.29 12.40 12.38 12.42 2 239Cf 7.7651 0.1369 1.63 1.99 2.46 2.43 0 241Cf 7.4551 0.1128 2.97 3.17 3.60 3.53 0 243Cf 7.4151 0.1106 3.66 4.26 3.73 4.21 3 245Cf 7.2585 0.1180 3.88 3.84 4.32 4.21 0 247Cf 6.5022 0.1209 7.50 7.73 7.63 7.68 2 249Cf 6.2933 0.1102 10.04 8.45 8.63 8.44 1 251Cf 6.1771 0.1104 10.45 10.13 9.19 10.29 5 253Cf 6.0776 0.1201 8.69 9.05 9.68 9.36 0 241Es 8.2551 0.1402 0.71 0.69 1.12 0.82 0 243Es 8.0751 0.1327 1.55 1.27 1.71 1.40 0 245Es 7.8651 0.1367 2.13 1.94 2.43 2.11 0 247Es 7.4431 0.1371 3.59 3.45 4.00 3.68 0 249Es 6.9413 0.1199 6.03 6.47 6.06 6.48 3 251Es 6.5971 0.1153 7.36 7.02 7.60 7.27 0 253Es 6.7393 0.1224 6.25 6.31 6.91 6.56 0 255Es 6.4001 0.1282 7.63 7.84 8.50 8.15 0 243Fm 8.6951 0.1398 −0.60 0.05 0.06 0.24 1 245Fm 8.4351 0.1230 0.62 1.45 0.87 1.49 3 247Fm 8.2551 0.1154 1.69 2.30 1.44 2.41 4 251Fm 7.4251 0.1148 6.03 4.34 4.45 4.46 1 253Fm 7.0529 0.1219 6.33 6.92 5.98 7.23 5 257Fm 6.8631 0.1253 6.94 6.81 6.75 6.85 2 245Md 9.0151 0.1583 −0.42 −0.32 −0.57 −0.50 2 247Md 8.7651 0.1426 0.08 0.14 0.17 −0.02 1 249Md 8.4351 0.1490 1.53 1.39 1.21 1.27 2 251Md 7.9641 0.1337 3.40 2.70 2.83 2.63 1 253Md 7.5651 0.1351 5.01 4.12 4.31 4.10 1 255Md 7.9051 0.1164 4.36 3.19 2.98 3.02 2 257Md 7.5571 0.1313 5.11 4.09 4.28 4.06 1 251No 8.7551 0.1163 −0.02 0.16 0.54 0.64 0 253No 8.4151 0.1186 2.23 1.58 1.63 1.78 1 255No 8.2281 0.1081 2.84 2.50 2.24 2.55 2 257No 8.4766 0.1192 1.46 1.61 1.36 1.70 2 259No 7.8541 0.1224 3.66 3.68 3.54 3.79 2 253Lr 8.9151 0.1460 −0.15 −0.08 0.40 0.08 0 255Lr 8.5021 0.1273 1.49 1.23 1.71 1.39 0 257Lr 9.0151 0.1364 0.78 0.83 0.02 0.94 4 259Lr 8.5751 0.1360 0.90 0.90 1.40 1.07 0 255Rf 9.0551 0.1210 0.49 0.31 0.32 0.56 1 257Rf 8.9141 0.1170 0.75 1.00 0.74 1.14 2 259Rf 9.1331 0.1319 0.49 0.27 0.02 0.45 2 261Rf 8.6481 0.1252 1.06 1.05 1.54 1.62 0 257Db 9.2051 0.1455 0.39 0.12 0.22 0.03 1 259Db 9.5671 0.1599 −0.29 −0.97 −0.89 −1.08 1 263Db 8.8351 0.1390 1.89 2.28 1.29 2.83 5 261Sg 9.7141 0.1262 −0.73 −0.66 −0.96 −0.46 2 263Sg 9.4051 0.1275 0.03 −0.53 −0.09 0.09 0 265Sg 9.0451 0.1244 1.26 2.02 0.99 2.52 5 261Bh 10.5051 0.1648 −1.89 −2.16 −2.73 −2.30 3 265Hs 10.4701 0.1278 −2.71 −2.67 −2.35 −2.04 0 269Hs 9.2751 0.1264 1.18 0.85 0.98 1.24 1 Table 6. Same as Table 5 but for odd-A nuclei. The column of the l term that appears for the first time is the angular momentum carried away by an
$\alpha$ particle.For a more intuitive comparison of the results, Figs. 2−4 plot the differences between the experimental
$ \alpha $ decay half-lives and those calculated using our model, UDL, and DZR in logarithmic form. It is evident that the differences calculated by our model are more concentrated near zero, indicating that our calculation results are closer to the experimental values. Except for a few nuclei, the differences for all 559 nuclei fall between –0.5 and 0.5. For 185Pt, 268Hs, and 282Ds, it may be caused by deformation effects [82]. Meanwhile, for 209Bi, 210Po, 245Bk, 247Cm, 249Cf, 251Fm, 255Md, 257Md, and 258Md, the larger errors are likely influenced by the shell effects at N = 126 and N = 152 [83].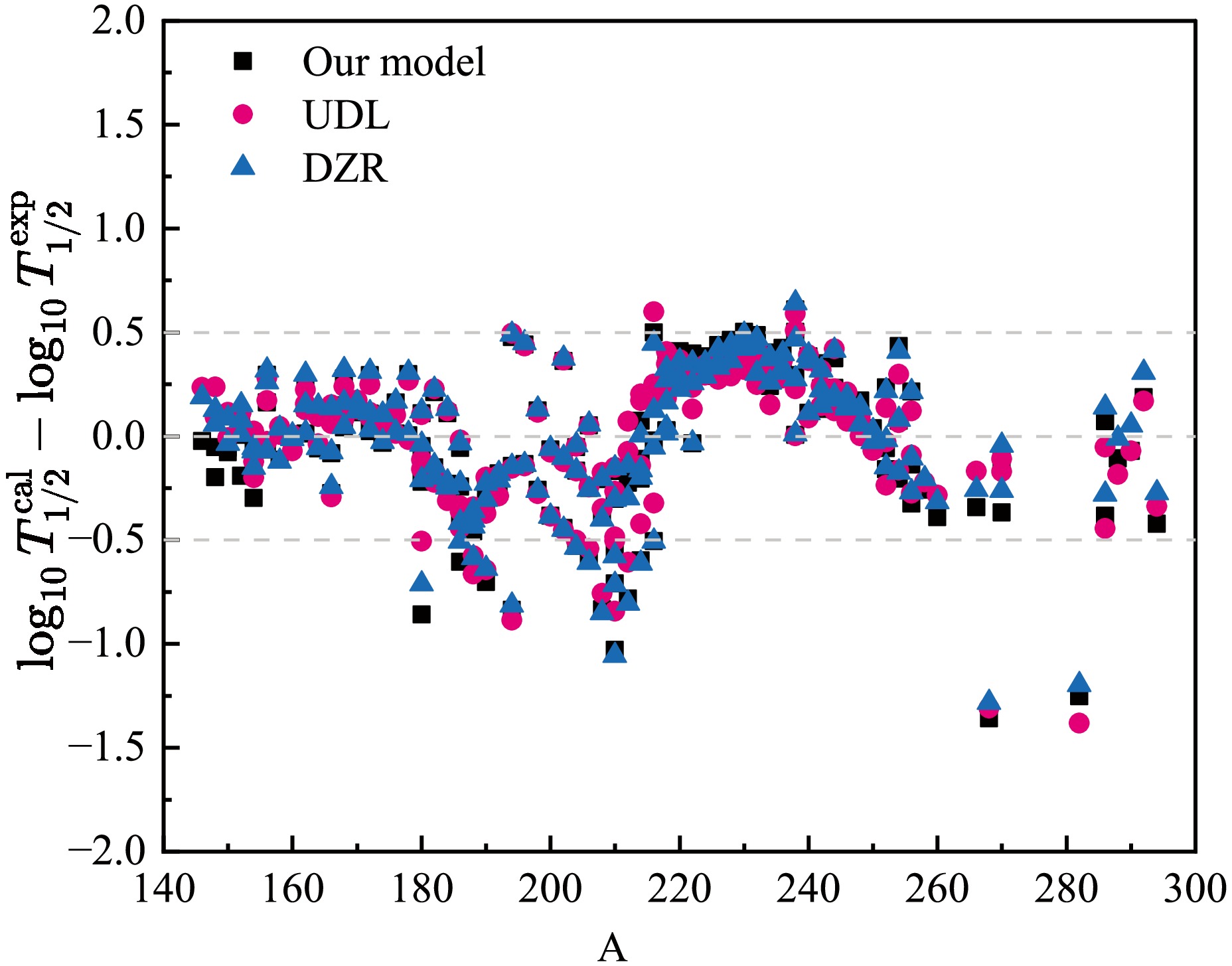
Figure 2. (color online) Deviations between the experimental
$\alpha$ decay half-lives and the calculated ones obtained using our model, UDL, and DZR in logarithmic form.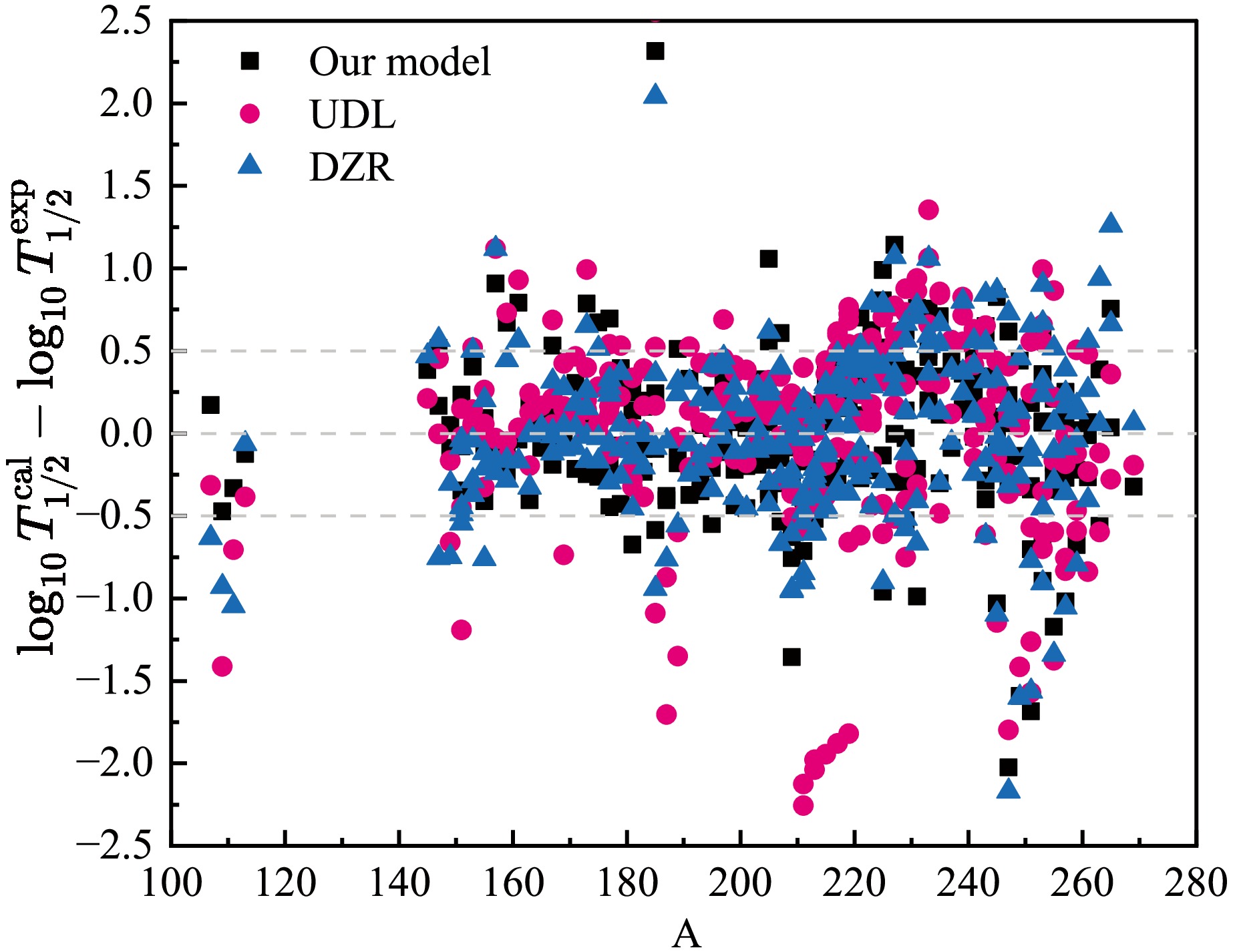
Figure 3. (color online) Same as Fig. 2 but for odd-A nuclei.
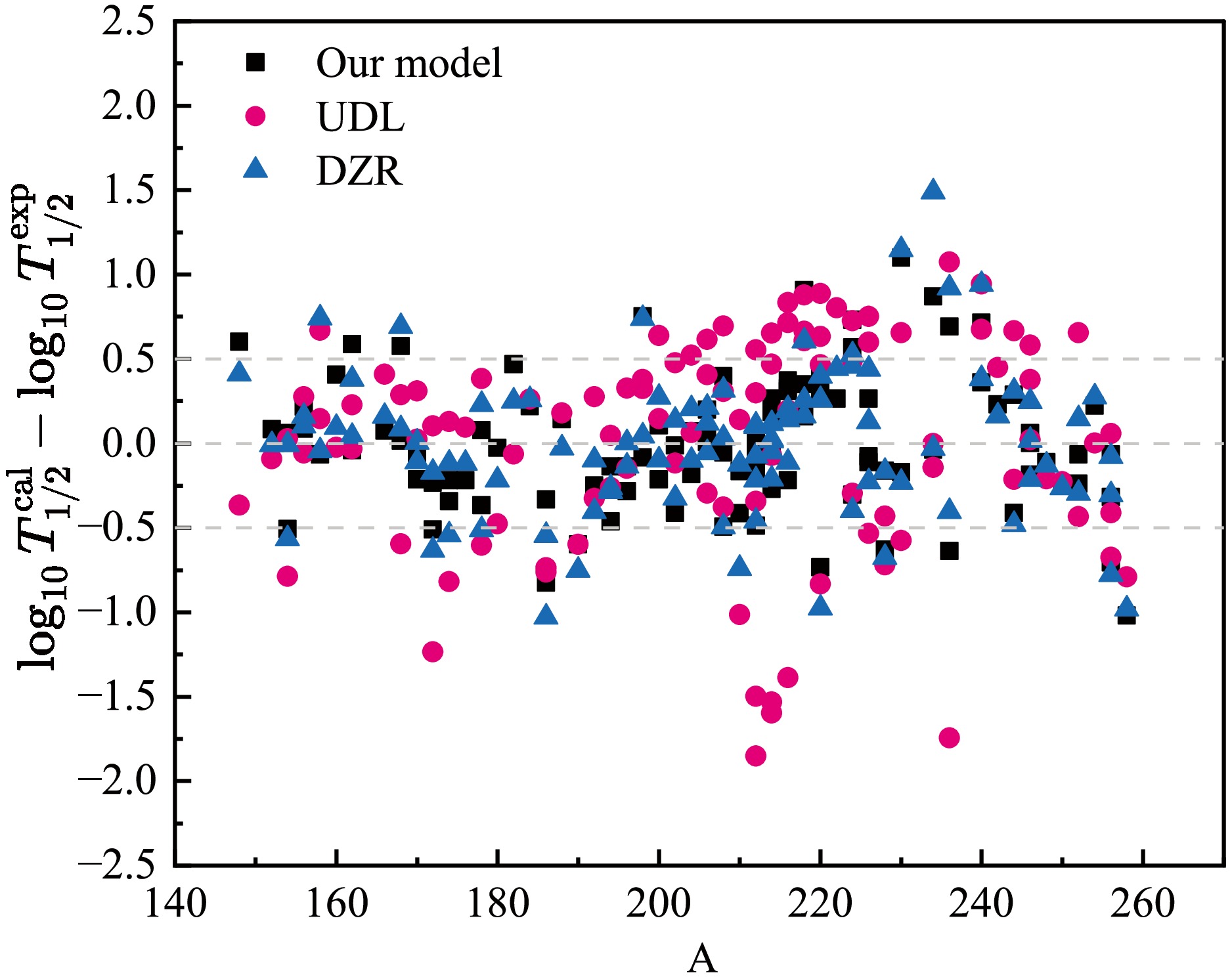
Figure 4. (color online) Same as Fig. 2 but for odd-odd nuclei.
As is known, the half-lives of
$ \alpha $ decay show a very strong sensitivity to the$ \alpha $ decay energy$ Q_\alpha $ . Therefore, selecting a precise$ Q_\alpha $ becomes one of the key problems in prediction. In 2016, Sobiczewski et al. systematically compared nine different mass models: Möller et al. (FRDM) [84], Duflo and Zuker (DZ) [85], Nayak and Satpathy (INM) [86], Wang and Liu (WS3+) [87], Wang et al. (WS4+) [88, 89], Muntian et al. (HN) [90, 91], Kuzmina et al. (TCSM) [92], Goriely et al. (HFB31) [93], and Liran et al. (SE) [94] and came to the conclusion that the WS3+ model is the most accurate in reproducing the experimental$ Q_\alpha $ of superheavy nuclei. In this work, we use our model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120. The predicted results are listed in Table 8. In this table, the first to fourth columns represent the parent nucleus,$ \alpha $ decay energy$ Q_\alpha $ calculated using WS3+, angular momentum l carried away by the$ \alpha $ particle, and$ \alpha $ preformation factors calculated by the CFM, respectively. The last three,$ \log_{10} T^{{\rm{cal}}}_{1/2} $ ,$ \log_{10} T^{{\rm{UDL}}}_{1/2} $ ,$ \log_{10} T^{{\rm{DZR}}}_{1/2} $ , represent the predicted$ \alpha $ decay half-lives in logarithmic form calculated by our model, UDL, and DZR, respectively. From this table, we can clearly see that the three predictions are quite close to each other. To visually illustrate their relationship, the logarithmic form of$ \alpha $ decay half-lives and the$ Q_\alpha $ values calculated by the WS3+ mass model with Z = 119 and 120 versus the neutron numbers of the daughter nucleus$ N_d $ , as well as the curve of the relationship between the$ \alpha $ decay preformation factors and neutron number of the parent nucleus N, are plotted in Figs. 5−7, respectively. From Fig 5, it can be seen that the trends of the$ \alpha $ decay half-lives for the isotopic chains with proton numbers Z = 119 and 120 predicted by our model, UDL, and DZR are consistent, and our predicted results are close to those of UDL. Furthermore, as shown in Fig. 5, for the isotope chains with Z = 119 and 120, when the neutron number of the daughter nucleus$ N_d $ is less than 176, the half-lives of$ \alpha $ decay exhibit a slow upward trend, followed by a gradual decrease to a minimum value at$ N_d $ = 178. From$ N_d $ = 178 to$ N_d $ = 182, it keeps a steady change. Then, it suddenly drops to the lowest point at$ N_d $ = 184, after which an upward trend appears again. A similar phenomenon can also be observed on$ Q_\alpha $ in Fig. 6. In addition, Fig. 7 clearly shows that the$ \alpha $ decay preformation factors of even-even nuclei with Z = 120, odd-A nuclei with Z = 119, and odd-odd nuclei with Z = 119 show a trend of first decreasing and then increasing near the neutron number N = 184 of the parent nuclei. However, this variation trend is not obvious in odd-A nuclei with Z = 120. When the neutron number is closer to the neutron magic number, the$ \alpha $ decay preformation factor is smaller, while it increases as the neutron number deviates further from this magic shell closure [95]. Moreover, during$ \alpha $ decay, when the neutron or proton numbers of the corresponding daughter nucleus are magic numbers, the half-life reaches its minimum value [96, 97]. When the neutron number exceeds the neutron magic number by two nucleons, the parent nucleus tends to become stable by emitting an$ \alpha $ particle. In this case, the half-life will reach its minimum value. The depth of the minimum value depends on the stability of the daughter nucleus, meaning that the more stable nucleus corresponds to a deeper minimum value. From the above content, we can conclude that N = 184 is the possible neutron magic number, while N = 178 can be considered the neutron submagic number [97].Nuclide $ Q_{\alpha} $ 

l $P_\alpha$ 

$\log_{10} T_{1/2}^{{\rm{cal}}}$ 

$\log_{10} T_{1/2}^{{\rm{UDL}}}$ 

$\log_{10} T_{1/2}^{{\rm{DZR}}}$ 

Nuclei with Z=119 284119 13.7747 4 0.2181 −5.44 −6.38 −5.41 285119 13.6461 2 0.2940 −5.93 −6.15 −5.65 286119 13.4606 2 0.1831 −5.38 −5.80 −5.72 287119 13.2830 2 0.2852 −5.31 −5.47 −4.97 288119 13.1697 2 0.1838 −4.87 −5.25 −5.18 289119 13.0764 2 0.2539 −4.91 −5.08 −4.58 290119 12.9211 2 0.1679 −4.38 −4.77 −4.71 291119 12.8677 2 0.2525 −4.54 −4.68 −4.18 292119 12.7053 2 0.1706 −3.99 −4.35 −4.29 293119 12.5103 2 0.2395 −3.85 −3.94 −3.45 294119 12.5217 2 0.1672 −3.64 −3.98 −3.93 295119 12.5701 2 0.2196 −3.96 −4.10 −3.61 296119 12.3096 2 0.1553 −3.19 −3.54 −3.50 297119 12.3025 2 0.1922 −3.39 −3.54 −3.05 298119 12.5862 2 0.1416 −3.75 −4.18 −4.14 299119 12.7275 2 0.2167 −4.33 −4.50 −4.03 300119 12.5259 2 0.1596 −3.70 −4.08 −4.05 301119 12.3748 0 0.2040 −4.31 −3.76 −3.66 302119 12.3960 0 0.1540 −4.11 −3.83 −4.17 303119 12.3691 2 0.2036 −3.64 −3.78 −3.31 304119 12.8958 1 0.1608 −4.78 −4.94 −5.16 305119 13.4495 2 0.2078 −5.73 −6.08 −5.62 306119 13.2476 0 0.1632 −5.86 −5.69 −6.04 307119 12.8167 0 0.2162 −5.30 −4.82 −4.73 308119 12.0652 0 0.1688 −3.52 −3.17 −3.53 309119 11.3386 3 0.2282 −1.24 −1.42 −0.57 310119 10.8335 3 0.1829 0.29 −0.10 0.27 311119 10.6003 0 0.1697 −0.26 0.53 0.63 312119 10.4397 2 0.1386 1.17 0.97 0.95 313119 9.4978 2 0.1562 3.61 3.87 4.36 314119 9.1165 1 0.1286 4.98 5.16 4.87 315119 9.3054 1 0.1420 3.95 4.49 4.72 316119 8.7705 2 0.1192 6.50 6.39 6.33 317119 9.2532 3 0.1826 4.55 4.64 5.49 318119 9.1841 0 0.1549 4.23 4.86 4.44 319119 8.4849 6 0.1484 8.17 7.44 10.18 Nuclei with Z=120 287120 13.9149 4 0.1680 −5.36 −6.39 −4.79 288120 13.7471 0 0.2526 −6.59 −6.87 −6.67 289120 13.6763 0 0.1661 −6.22 −5.97 −5.32 290120 13.6305 0 0.2470 −6.41 −6.69 −6.49 291120 13.4054 2 0.1639 −5.08 −5.47 −4.57 292120 13.3084 0 0.2505 −5.88 −6.09 −5.90 293120 13.2366 2 0.1701 −4.82 −5.16 −4.27 294120 13.0718 0 0.2382 −5.45 −5.65 −5.47 295120 13.0989 2 0.1648 −4.58 −4.91 −4.03 296120 13.1873 0 0.2326 −5.69 −5.92 −5.74 297120 13.0230 0 0.1621 −5.14 −4.78 −4.20 298120 12.9002 0 0.2271 −5.17 −5.37 −5.19 299120 13.1851 0 0.1633 −5.48 −5.15 −4.55 300120 13.2871 0 0.2420 −5.95 −6.19 −6.01 301120 13.0349 2 0.1736 −4.57 −4.87 −4.00 302120 12.8782 0 0.2369 −5.21 −5.39 −5.22 303120 12.7949 2 0.1737 −4.14 −4.40 −3.55 304120 12.7451 0 0.2371 −4.99 −5.14 −4.98 305120 13.2712 2 0.1827 −5.09 −5.42 −4.53 306120 13.8225 0 0.2446 −6.98 −7.31 −7.14 307120 13.5776 4 0.1861 −5.11 −6.06 −4.49 308120 13.0359 0 0.2652 −5.65 −5.81 −5.65 309120 12.1724 0 0.1994 −3.71 −3.10 −2.60 310120 11.4753 0 0.2312 −2.38 −2.34 −2.20 311120 11.1018 2 0.1802 −0.57 −0.49 0.18 312120 11.0535 0 0.2029 −1.35 −1.29 −1.17 313120 10.9229 2 0.1603 −0.10 −0.04 0.61 314120 9.9714 0 0.2273 1.47 1.73 1.83 315120 10.1487 0 0.1807 1.23 2.15 2.42 316120 9.9651 0 0.1873 1.54 1.72 1.81 317120 9.9639 3 0.1513 2.77 2.69 3.50 318120 9.9875 0 0.1785 1.47 1.62 1.71 319120 9.8887 3 0.1454 2.98 2.90 3.70 320120 9.7100 0 0.1861 2.25 2.45 2.53 Table 8. Predicted results of the
$\alpha$ decay half-lives in logarithmic form for 70 even-even, odd-even, and odd-odd nuclei with Z = 119 and 120 using our model, UDL, and DZR. The$\alpha$ decay energy and half-lives are in units of MeV and s, respectively. The mass excesses are taken from the WS3+ mass model [87]. The spin and parity values of these nuclei are taken from Ref. [98].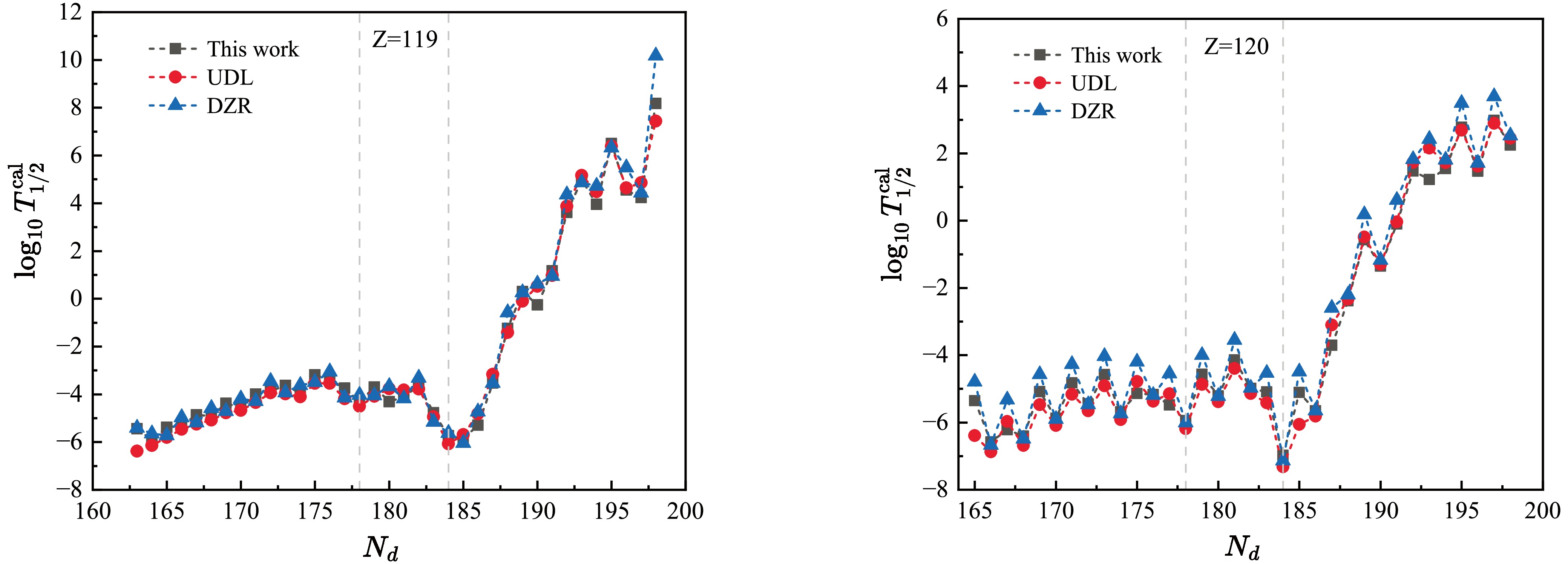
Figure 5. (color online) Predicted
$\alpha$ decay half-lives for the even-even, odd-even, and odd-odd nuclei with Z = 119 and 120 are presented in logarithmic form using our model, UDL, and DZR. -
Based on WKB theory, considering the
$ \alpha $ decay preformation factors$ P_\alpha $ , we propose a model to calculate$ \alpha $ decay half-lives of 559 nuclei from the ground state. Using the minimum standard deviation between experimental data and calculated data as the objective, function whose detailed information is provided later, we obtain the coefficients a, b, c, and d, as shown in the Table 1. To compare the calculated results under the same conditions, we refitted the experimental data and obtained the parameter results for the UDL and DZR, as shown in Tables 2−3. In this study, the standard deviation$ \sigma $ can be defined as follows:Parameters e-e e-o o-o a 21.1958 23.4998 26.7499 b −1.8435 0.7241 2.25913 c 0.5001 −2.8591 −8.4193 d 0 0.2784 0.2721 Table 1. Parameter fitting results of Eq. (13) for three different types of nuclei.
Parameters e-e e-o o-o a 0.4101 0.418 0.4062 b −0.4218 −0.4024 −0.3724 c −21.9524 −23.8632 −24.0723 Table 2. Same as Table 1 but for the UDL.
Parameters e−e e−o o−e o−o a −25.627 −28.22089 −27.1408 28.0910 b −1.1559 −1.0000 −1.1410 −1.1270 c 1.5912 1.5625 1.6251 1.6408 d 0 0.0468 0.0625 0.0625 Table 3. Same as Table 1 but for the DZR.
$ \sigma= \left[ \frac{1}{n} \sum\limits_{i=1}^n \left( \log_{10} T^{{\rm{exp}}}_{1/2} - \log_{10} T^{{\rm{cal}}}_{1/2} \right)^2 \right]^{1/2}, $
(27) where
$ \log_{10} T_{1/2}^{{\rm{exp}}} $ and$ \log_{10} T_{1/2}^{{\rm{cal}}} $ are the logarithmic forms of experimental$ \alpha $ decay half-lives and the calculated ones, respectively. n is the number of nuclei involved in different decay cases. The standard deviation$ \sigma $ of the calculated results for the three models and/or formulas is shown in Table 4. From this table, we can clearly see that the standard deviation$ \sigma $ of our model only is 0.408 for all 559 nuclei, 0.323 for 177 even-even nuclei, 0.459 for 277 odd-A nuclei, and 0.391 for 105 odd-odd nuclei. These values are smaller than those of the UDL and DZR results, which proves that our model achieves satisfactory results.Formulas Total e-e e-o o-o Our model 0.408 0.323 0.459 0.391 UDL 0.589 0.349 0.633 0.632 DZR 0.436 0.337 0.493 0.423 Table 4. Standard deviations
$\sigma$ between experimental$\alpha$ decay half-lives and those calculated using our model, the UDL and the DZR for 177 even-even nuclei, 277 odd-A nuclei, and 105 odd-odd nuclei.To show the concrete results, we use these formulas to calculate
$ \alpha $ decay half-lives of even-even, odd-A, and odd-odd nuclei. The detailed calculated results are listed in Tables 5−7. In these tables, the first three columns represent the parent nucleus, experimentally measured$ \alpha $ decay energy$ Q_\alpha $ , and$ \alpha $ decay preformation factors calculated using the CFM, respectively. The fourth to seventh columns represent the experimental half-life data for$ \alpha $ decay, as well as those calculated using our model, UDL, and DZR in logarithmic form, denoted as$ \log_{10} T^{{\rm{exp}}}_{1/2} $ ,$ \log_{10} T_{1/2}^{{\rm{cal}}} $ ,$ \log_{10} T_{1/2}^{{\rm{UDL}}} $ ,$ \log_{10} T_{1/2}^{{\rm{DZR}}} $ , respectively. For Tables 6−7, the eighth column represents the angular momentum l taken away by the$ \alpha $ particle. These three tables show that our calculated results agree closely with the experimental data for most nuclei, with some exceptions such as 185Pt, 205Ac, 209Bi, 210Po, 227Np, 230Np, 245Bk, 247Cm, 249Cf, 251Fm, 255Md, 257Md, 258Md, 268Hs, and 282Ds.Nuclide $Q_{\alpha}$ $P_\alpha$ $\log_{10} T_{1/2}^{{\rm{exp}}}$ $\log_{10} T_{1/2}^{{\rm{cal}}}$ $\log_{10} T_{1/2}^{{\rm{UDL}}}$ $\log_{10} T_{1/2}^{{\rm{DZR}}}$ 146Sm 2.5292 0.1979 15.33 15.31 15.57 15.52 148Sm 1.9870 0.1954 23.30 23.10 23.54 23.43 148Gd 3.2713 0.2017 9.35 9.30 9.44 9.41 150Gd 2.8071 0.2021 13.75 13.67 13.87 13.84 152Gd 2.2039 0.2213 21.53 21.34 21.65 21.61 150Dy 4.3511 0.2360 3.11 3.05 3.10 3.07 152Dy 3.7265 0.2403 6.93 7.01 7.04 7.08 154Dy 2.9451 0.2379 13.98 13.68 13.77 13.83 152Er 4.9341 0.2389 1.06 1.06 1.11 1.06 154Er 4.2801 0.2568 4.68 4.57 4.55 4.60 156Er 3.4811 0.2521 9.99 10.15 10.16 10.25 154Yb 5.4741 0.2349 −0.35 −0.41 −0.33 −0.41 156Yb 4.8091 0.2572 2.41 2.70 2.69 2.73 156Hf 6.0251 0.2703 −1.64 −1.70 −1.66 −1.71 158Hf 5.4051 0.2463 0.81 0.83 0.85 0.85 160Hf 4.9021 0.2546 3.28 3.24 3.21 3.26 162Hf 4.4171 0.2411 5.69 5.94 5.91 5.98 158W 6.6151 0.2408 −2.84 −2.96 −2.84 −2.97 160W 6.0651 0.2732 −0.99 −0.99 −0.98 −0.98 162W 5.6781 0.2441 0.42 0.56 0.57 0.57 164W 5.2781 0.2506 2.22 2.34 2.31 2.36 166W 4.8561 0.2309 4.74 4.46 4.44 4.49 168W 4.5001 0.2357 6.20 6.48 6.44 6.52 180W 2.5153 0.1621 25.70 24.84 25.19 24.99 162Os 6.7651 0.2373 −2.68 −2.67 −2.55 −2.66 164Os 6.4851 0.2708 −1.66 −1.72 −1.70 −1.72 166Os 6.1421 0.2472 −0.59 −0.46 −0.44 −0.46 168Os 5.8161 0.2474 0.68 0.83 0.82 0.85 170Os 5.5361 0.2373 1.89 2.04 2.02 2.05 172Os 5.2241 0.2397 3.21 3.50 3.45 3.52 174Os 4.8711 0.2259 5.25 5.33 5.29 5.36 186Os 2.8212 0.1569 22.80 22.19 22.46 22.29 166Pt 7.2951 0.2381 −3.53 −3.61 −3.47 −3.61 168Pt 6.9851 0.2725 −2.69 −2.65 −2.61 −2.65 170Pt 6.7081 0.2420 −1.86 −1.74 −1.68 −1.74 172Pt 6.4631 0.2545 −0.99 −0.89 −0.88 −0.88 174Pt 6.1833 0.2471 0.06 0.16 0.15 0.16 176Pt 5.8851 0.2605 1.20 1.36 1.30 1.37 178Pt 5.5731 0.2267 2.43 2.72 2.70 2.73 180Pt 5.2761 0.2051 4.03 4.14 4.13 4.15 182Pt 4.9511 0.1868 5.62 5.83 5.85 5.85 184Pt 4.5991 0.1858 7.77 7.88 7.89 7.90 186Pt 4.3201 0.1732 9.73 9.67 9.71 9.70 188Pt 4.0067 0.2161 12.53 11.91 11.86 11.94 190Pt 3.2686 0.2031 19.18 18.48 18.54 18.54 172Hg 7.5251 0.2767 −3.64 −3.61 −3.55 −3.60 174Hg 7.2331 0.2487 −2.70 −2.73 −2.66 −2.72 176Hg 6.8971 0.2674 −1.65 −1.64 −1.64 −1.63 178Hg 6.5773 0.2584 −0.53 −0.52 −0.54 −0.51 180Hg 6.2581 0.2651 0.73 0.68 0.62 0.69 182Hg 5.9951 0.2540 1.89 1.74 1.67 1.75 184Hg 5.6601 0.2418 3.44 3.21 3.13 3.22 186Hg 5.2041 0.2469 5.70 5.46 5.34 5.47 188Hg 4.7091 0.2387 8.72 8.26 8.15 8.29 180Pb 7.4191 0.2476 −2.39 −2.61 −2.55 −2.60 182Pb 7.0651 0.2342 −1.26 −1.47 −1.43 −1.46 184Pb 6.7741 0.2357 −0.21 −0.47 −0.46 −0.46 186Pb 6.4711 0.2301 1.07 0.65 0.63 0.66 188Pb 6.1091 0.2215 2.47 2.10 2.06 2.11 190Pb 5.6971 0.2155 4.24 3.93 3.87 3.94 192Pb 5.2211 0.2040 6.55 6.32 6.26 6.33 194Pb 4.7381 0.1946 9.94 9.11 9.06 9.13 210Pb 3.7927 0.1066 16.57 15.86 16.08 15.85 188Po 8.0831 0.2750 −3.57 −3.97 −3.91 −3.97 190Po 7.6931 0.2619 −2.61 −2.84 −2.81 −2.84 192Po 7.3201 0.2571 −1.49 −1.67 −1.68 −1.67 194Po 6.9871 0.2352 −0.41 −0.55 −0.56 −0.55 196Po 6.6581 0.2160 0.78 0.64 0.63 0.64 198Po 6.3101 0.2032 2.27 2.01 1.99 2.00 200Po 5.9811 0.1837 3.79 3.41 3.41 3.41 202Po 5.7001 0.1767 5.14 4.70 4.69 4.69 204Po 5.4851 0.1579 6.27 5.75 5.77 5.74 206Po 5.3271 0.1452 7.14 6.55 6.60 6.54 208Po 5.2157 0.1350 7.96 7.13 7.20 7.11 210Po 5.4075 0.1059 7.08 6.05 6.23 6.02 212Po 8.9542 0.2210 −6.53 −6.76 −6.46 −6.83 214Po 7.8335 0.2134 −3.79 −3.71 −3.58 −3.78 216Po 6.9063 0.2046 −0.84 −0.65 −0.63 −0.72 218Po 6.1148 0.1956 2.27 2.49 2.45 2.43 194Rn 7.8631 0.2614 −3.11 −2.63 −2.61 −2.62 196Rn 7.6161 0.2563 −2.33 −1.89 −1.89 −1.88 198Rn 7.3501 0.2390 −1.16 −1.04 −1.05 −1.03 200Rn 7.0441 0.2213 0.07 0.00 −0.01 0.01 202Rn 6.7731 0.2094 1.09 0.99 0.97 0.99 204Rn 6.5471 0.1912 2.01 1.85 1.84 1.84 206Rn 6.3841 0.1803 2.74 2.49 2.49 2.48 208Rn 6.2611 0.1626 3.37 2.98 3.02 2.97 210Rn 6.1591 0.1515 3.95 3.39 3.45 3.38 212Rn 6.3853 0.1206 3.16 2.37 2.55 2.35 214Rn 9.2082 0.2291 −6.59 −6.70 −6.42 −6.75 216Rn 8.1975 0.2368 −4.54 −4.04 −3.94 −4.09 218Rn 7.2625 0.2342 −1.47 −1.10 −1.12 −1.15 220Rn 6.4048 0.2208 1.75 2.15 2.06 2.11 222Rn 5.5904 0.2218 5.52 5.92 5.75 5.87 202Ra 7.8801 0.2477 −2.39 −2.03 −2.02 −2.01 204Ra 7.6361 0.2309 −1.22 −1.28 −1.27 −1.26 206Ra 7.4161 0.2186 −0.62 −0.57 −0.57 −0.56 208Ra 7.2731 0.1954 0.10 −0.10 −0.07 −0.10 210Ra 7.1511 0.1871 0.60 0.30 0.34 0.30 214Ra 7.2731 0.1384 0.39 −0.21 −0.36 −0.23 216Ra 9.5251 0.2390 −6.76 −6.79 −6.51 −6.82 218Ra 8.5411 0.2426 −4.59 −4.28 −4.18 −4.32 220Ra 7.5941 0.2393 −1.74 −1.42 −1.45 −1.46 222Ra 6.6777 0.1991 1.53 1.91 1.86 1.88 224Ra 5.7889 0.1840 5.50 5.88 5.79 5.85 226Ra 4.8707 0.1816 10.70 11.09 10.98 11.06 210Th 8.0691 0.2341 −1.80 −1.96 −1.95 −1.95 212Th 7.9581 0.1957 −1.50 −1.65 −1.57 −1.64 214Th 7.8271 0.1951 −1.06 −1.27 −1.20 −1.26 216Th 8.0731 0.1585 −1.58 −2.09 −1.90 −2.09 218Th 9.8491 0.2506 −6.91 −6.89 −6.62 −6.90 220Th 8.9741 0.2432 −4.99 −4.75 −4.62 −4.77 222Th 8.1321 0.2324 −2.65 −2.38 −2.35 −2.39 224Th 7.2991 0.1981 0.02 0.37 0.36 0.35 226Th 6.4531 0.1822 3.27 3.70 3.64 3.68 228Th 5.5202 0.1831 7.78 8.24 8.12 8.22 230Th 4.7700 0.1826 12.38 12.82 12.70 12.80 232Th 4.0816 0.1601 17.65 18.10 18.07 18.07 218U 8.7751 0.1880 −3.45 −3.42 −3.25 −3.41 222U 9.4781 0.2446 −5.33 −5.36 −5.20 −5.36 224U 8.6281 0.2472 −3.40 −3.11 −3.08 −3.11 226U 7.7011 0.2075 −0.57 −0.24 −0.26 −0.24 228U 6.7991 0.1905 2.75 3.12 3.04 3.11 230U 5.9921 0.1871 6.24 6.74 6.61 6.73 232U 5.4136 0.1688 9.34 9.82 9.71 9.81 234U 4.8576 0.1502 12.89 13.29 13.23 13.27 236U 4.5730 0.1532 14.87 15.29 15.23 15.27 238U 4.2698 0.1374 17.15 17.65 17.66 17.62 230Pu 7.1781 0.2015 2.02 2.45 2.36 2.46 232Pu 6.7161 0.1647 4.00 4.31 4.25 4.31 234Pu 6.3101 0.1517 5.72 6.10 6.05 6.10 236Pu 5.8672 0.1398 7.96 8.27 8.24 8.26 238Pu 5.5932 0.1450 9.44 9.73 9.67 9.72 240Pu 5.2558 0.1293 11.32 11.70 11.68 11.68 242Pu 4.9843 0.1326 13.07 13.42 13.39 13.39 244Pu 4.6656 0.1268 15.41 15.64 15.64 15.60 234Cm 7.3651 0.1943 2.28 2.53 2.43 2.54 236Cm 7.0671 0.1573 3.35 3.67 3.64 3.68 238Cm 6.6701 0.1366 5.31 5.32 5.32 5.32 240Cm 6.3978 0.1373 6.42 6.53 6.51 6.53 242Cm 6.2157 0.1222 7.15 7.38 7.39 7.37 244Cm 5.9016 0.1444 8.76 8.96 8.88 8.94 246Cm 5.4751 0.1421 11.17 11.33 11.25 11.31 248Cm 5.1618 0.1462 13.08 13.25 13.15 13.22 238Cf 8.1331 0.1854 −0.08 0.53 0.51 0.57 240Cf 7.7111 0.1496 1.61 1.98 2.00 2.00 242Cf 7.5171 0.1451 2.53 2.66 2.68 2.68 244Cf 7.3290 0.1527 3.19 3.36 3.33 3.37 246Cf 6.8616 0.1551 5.11 5.26 5.18 5.26 248Cf 6.3613 0.1382 7.46 7.52 7.46 7.52 250Cf 6.1285 0.1358 8.62 8.65 8.59 8.64 252Cf 6.2170 0.1463 7.94 8.17 8.07 8.15 254Cf 5.9261 0.1543 9.22 9.66 9.52 9.63 244Fm 8.5461 0.1656 −0.51 −0.13 −0.09 −0.09 246Fm 8.3791 0.1536 0.22 0.37 0.43 0.41 248Fm 7.9950 0.1637 1.54 1.65 1.63 1.67 250Fm 7.5569 0.1491 3.27 3.23 3.20 3.24 252Fm 7.1541 0.1539 4.96 4.80 4.72 4.81 254Fm 7.3073 0.1350 4.07 4.14 4.13 4.15 256Fm 7.0255 0.1546 5.06 5.28 5.18 5.28 252No 8.5481 0.1581 0.56 0.50 0.53 0.54 254No 8.2261 0.1404 1.75 1.55 1.59 1.58 256No 8.5811 0.1533 0.47 0.33 0.37 0.36 256Rf 8.9261 0.1557 0.33 0.00 0.05 0.06 258Rf 9.1961 0.1737 −0.59 −0.85 −0.82 −0.80 260Sg 9.9001 0.1716 −1.77 −2.16 −2.06 −2.09 266Hs 10.3461 0.1566 −2.41 −2.75 −2.58 −2.66 268Hs 9.7651 0.1711 0.15 −1.21 −1.16 −1.14 270Hs 9.0651 0.1555 0.95 0.85 0.84 0.91 270Ds 11.1151 0.1793 −3.69 −4.06 −3.86 −3.95 282Ds 9.1451 0.1958 2.40 1.15 1.02 1.21 286Cn 9.2351 0.1836 1.48 1.55 1.42 1.62 286Fl 10.3551 0.2085 −0.66 −1.04 −1.10 −0.94 288Fl 10.0751 0.1976 −0.19 −0.29 −0.37 −0.20 290Lv 10.9951 0.2069 −2.05 −2.12 −2.12 −1.99 292Lv 10.7851 0.2016 −1.80 −1.61 −1.63 −1.49 294Og 11.8353 0.2112 −3.15 −3.58 −3.49 −3.43 Table 5. Comparison of experimental
$\alpha$ decay half-lives of even-even nuclei with the calculated ones using our model, UDL, and DZR in logarithmic form. The experimental$\alpha$ decay half-lives are taken from Ref. [79]. The$\alpha$ decay energy and mass excess are taken from the latest evaluated atomic mass table AME2020 [80, 81]. The$\alpha$ decay energy and half-lives are in units of MeV and s, respectively.Nuclide $Q_{\alpha} $ /MeV$P_\alpha$ $\log_{10} T^{{\rm{exp}}}_{1/2}$ $\log_{10} T^{{\rm{cal}}}_{1/2}$ $\log_{10} T_{1/2}^{{\rm{UDL}}}$ $\log_{10} T_{1/2}^{{\rm{DZR}}}$ l 148Eu 4.5071 0.1400 14.70 15.30 14.33 15.11 0 152Ho 4.0421 0.1682 3.12 3.20 3.03 3.11 0 154Ho 5.0941 0.1714 6.56 6.05 5.77 6.00 0 154Tm 4.3461 0.1709 1.17 1.23 1.20 1.17 0 156Tm 5.5951 0.1835 5.12 5.20 5.06 5.22 0 156Lu 4.7901 0.1678 −0.31 −0.09 −0.03 −0.15 0 158Lu 6.1251 0.1842 3.07 3.76 3.73 3.81 0 158Ta 5.0071 0.1946 −1.31 −1.38 −1.17 −1.35 0 162Ta 6.6951 0.1828 3.68 4.27 3.65 4.06 2 160Re 6.2451 0.1727 −2.26 −1.85 −2.28 −2.17 2 162Re 5.0681 0.1977 −0.95 −0.99 −0.72 −0.91 0 168Re 6.7151 0.1655 4.94 5.52 4.35 5.64 4 166Ir 6.3751 0.1965 −1.95 −1.87 −1.54 −1.79 0 168Ir 5.9551 0.1781 −0.64 −0.62 −0.35 −0.55 0 170Ir 5.9851 0.1792 1.24 1.03 1.27 1.13 0 172Ir 5.6931 0.1711 2.34 1.83 1.11 1.71 3 174Ir 7.1851 0.1730 3.17 2.83 2.36 2.63 2 170Au 6.9251 0.1977 −2.58 −2.67 −2.27 −2.58 0 172Au 6.6951 0.1743 −1.55 −1.79 −1.45 −1.72 0 174Au 6.4351 0.1843 −0.81 −1.03 −0.68 −0.93 0 176Au 6.0581 0.1781 0.14 −0.08 0.24 0.02 0 178Au 5.8311 0.1875 1.32 1.40 1.71 1.56 0 180Au 5.5251 0.1625 3.13 3.11 2.66 2.92 2 182Au 5.2341 0.1464 4.06 4.53 4.00 4.31 2 184Au 4.9121 0.1327 5.19 5.41 5.45 5.45 0 186Au 7.0251 0.1316 7.89 7.56 7.16 7.35 1 178Tl 7.7571 0.1934 −0.39 −0.75 −0.99 −0.90 2 186Bi 7.2631 0.1751 −1.83 −2.66 −2.59 −2.86 1 188Bi 6.8621 0.1691 −1.22 −1.08 −1.04 −1.25 1 190Bi 6.3811 0.1620 0.91 0.31 0.31 0.16 1 192Bi 5.9181 0.1567 2.44 2.17 2.12 2.04 1 194Bi 5.2611 0.1475 4.31 4.17 4.05 4.05 1 196Bi 6.2073 0.1401 7.43 7.14 7.28 7.29 0 212Bi 5.6211 0.0786 4.00 3.98 2.51 4.11 5 214Bi 7.6961 0.0815 6.75 6.68 5.15 6.87 5 192At 7.3341 0.1895 −1.94 −2.19 −1.66 −2.04 0 194At 7.1951 0.1860 −0.54 −1.01 −0.50 −0.83 0 196At 6.8891 0.1695 −0.41 −0.55 −0.09 −0.41 0 198At 6.5961 0.1545 0.66 0.58 0.99 0.71 0 200At 6.3541 0.1447 1.92 1.70 2.06 1.82 0 202At 6.0711 0.1309 3.16 2.75 3.04 2.84 0 204At 5.8871 0.1252 4.16 3.97 4.22 4.06 0 206At 5.7511 0.1116 5.31 5.50 5.01 5.25 2 208At 5.6311 0.1022 6.02 5.53 5.65 5.53 0 210At 7.8172 0.0946 7.22 6.81 6.21 6.48 2 212At 8.9880 0.0784 −0.50 −0.99 −2.35 −0.96 5 214At 7.9500 0.1542 −6.25 −5.99 −5.60 −6.24 0 216At 6.8761 0.1501 −3.52 −3.21 −2.81 −3.33 0 218At 6.0531 0.1438 0.11 1.02 0.71 0.71 2 220At 7.8711 0.1376 3.43 3.78 4.07 3.83 0 198Fr 7.6151 0.1864 −1.82 −1.07 −1.45 −1.08 3 200Fr 7.3861 0.1729 −1.32 −1.22 −0.69 −1.05 0 202Fr 7.1701 0.1594 −0.43 −0.44 0.05 −0.29 0 204Fr 6.9231 0.1502 0.26 0.33 0.78 0.46 0 206Fr 6.7851 0.1368 1.26 1.27 1.66 1.38 0 208Fr 6.6701 0.1283 1.82 1.77 2.13 1.85 0 210Fr 6.5291 0.1152 2.43 2.26 2.57 2.30 0 212Fr 8.5891 0.1068 3.44 3.51 3.10 3.23 2 214Fr 9.1742 0.0893 −2.26 −2.53 −3.79 −2.47 5 216Fr 8.0131 0.1610 −6.15 −5.78 −5.32 −5.95 0 218Fr 6.8001 0.1661 −2.85 −2.69 −2.19 −2.69 0 220Fr 7.9531 0.1635 1.44 1.83 1.90 1.70 1 206Ac 7.7281 0.1668 −1.60 −1.56 −0.99 −1.39 0 208Ac 7.5401 0.0903 −1.01 −0.61 −0.32 −0.70 0 212Ac 7.3521 0.1334 −0.05 −0.21 0.25 −0.12 0 214Ac 9.2411 0.1212 0.94 1.13 0.87 0.90 2 216Ac 9.3831 0.1027 −3.36 −3.58 −4.74 −3.47 5 218Ac 8.3481 0.1688 −6.00 −5.65 −5.12 −5.74 0 220Ac 7.1381 0.1710 −1.58 −2.31 −2.41 −2.55 2 222Ac 6.3271 0.1667 0.70 0.97 1.50 1.15 0 224Ac 5.5061 0.1386 5.02 4.72 4.73 4.62 1 226Ac 8.4151 0.1279 9.23 9.12 8.70 9.00 2 212Pa 8.2751 0.1688 −2.24 −2.31 −1.68 −2.14 0 214Pa 8.0991 0.1404 −1.77 −1.84 −1.30 −1.75 0 216Pa 9.7031 0.1392 −0.98 −0.65 −0.78 −0.84 2 220Pa 7.6931 0.1785 −6.07 −5.78 −5.18 −5.82 0 224Pa 6.9871 0.1623 −0.07 0.49 0.42 0.38 2 226Pa 6.2651 0.1372 2.16 2.43 2.91 2.60 0 228Pa 5.4401 0.1264 6.63 6.47 5.91 6.47 3 230Pa 9.3291 0.1274 10.67 10.50 10.09 10.44 2 224Np 8.3351 0.1742 −4.32 −3.59 −3.59 −3.79 2 226Np 7.5431 0.1739 −1.46 −1.54 −0.86 −1.33 0 228Np 6.7811 0.1451 2.17 1.54 1.74 1.49 1 230Np 5.0081 0.1328 3.96 5.06 4.62 5.11 3 236Np 6.7951 0.1049 15.47 14.83 13.72 15.07 4 234Am 6.2551 0.1153 5.55 6.42 5.41 7.04 5 236Am 5.4691 0.1054 6.73 7.43 7.81 7.65 0 240Am 8.1051 0.1006 10.98 11.70 11.93 11.92 0 234Bk 8.2651 0.1480 1.40 1.36 1.40 1.37 2 240Es 8.1551 0.1308 0.93 1.29 1.61 1.32 1 242Es 7.9451 0.1057 1.49 1.72 1.94 1.66 1 244Es 7.4951 0.1022 2.84 2.43 2.63 2.36 1 246Es 7.6451 0.1068 3.66 3.66 4.24 3.90 0 246Es 7.1611 0.1068 3.66 3.47 3.68 3.44 1 248Es 6.7351 0.1087 5.76 5.65 5.55 5.63 2 252Es 8.9451 0.0958 7.72 7.48 7.28 7.42 2 244Md 8.8951 0.1347 −0.44 −0.16 0.22 −0.14 1 246Md 8.1551 0.1170 −0.04 0.03 0.34 −0.02 1 250Md 7.7451 0.1139 2.88 2.64 2.66 2.62 2 256Md 7.2709 0.0951 4.70 4.38 4.03 4.40 3 258Md 9.1651 0.1081 6.65 5.63 5.86 5.67 1 252Lr 8.8251 0.1096 −0.42 −0.49 0.23 −0.28 0 254Lr 8.8551 0.1102 1.22 1.44 1.23 1.50 3 256Lr 9.3351 0.0992 1.52 0.81 1.10 0.74 1 256Db 9.3351 0.1152 0.38 0.32 0.44 0.31 2 Table 7. Same as Table 6 but for odd-odd nuclei.
Nuclide $Q_{\alpha} $ /MeV$P_\alpha$ $\log_{10} T^{{\rm{exp}}}_{1/2}$ $\log_{10} T^{{\rm{cal}}}_{1/2}$ $\log_{10} T_{1/2}^{{\rm{UDL}}}$ $\log_{10} T_{1/2}^{{\rm{DZR}}}$ l 107Te 4.0051 0.1721 −2.34 −2.17 −2.65 −2.97 0 109I 3.9171 0.2638 −0.19 −0.66 −1.60 −1.12 2 113I 2.7061 0.2190 7.30 7.17 6.91 7.24 0 111Xe 3.7151 0.1794 0.85 0.52 0.15 −0.19 0 145Pm 2.3221 0.1659 17.30 17.68 17.51 17.77 0 147Sm 2.3114 0.1588 18.53 18.69 18.52 17.77 0 147Eu 2.9912 0.1723 10.96 11.48 11.41 11.53 0 151Eu 1.9640 0.1789 26.16 25.81 24.97 25.67 2 149Gd 3.0995 0.1581 11.27 11.18 11.10 10.52 0 151Gd 2.6522 0.1611 15.63 15.86 15.78 15.09 0 149Tb 4.0781 0.1835 4.95 5.00 4.29 4.64 2 151Tb 3.4957 0.1799 8.82 9.06 8.38 8.79 2 151Dy 4.1800 0.1796 4.28 4.26 4.24 3.83 0 153Dy 3.5591 0.1864 8.39 8.49 8.53 8.02 0 151Ho 4.6441 0.2212 2.20 2.12 2.18 2.11 0 153Ho 4.0161 0.2207 5.37 5.77 5.89 5.87 0 153Er 4.8021 0.1777 1.84 1.91 1.89 1.56 0 155Er 4.1181 0.1946 6.15 5.73 5.82 5.39 0 153Tm 5.2481 0.2314 0.21 0.19 0.27 0.17 0 155Tm 4.5721 0.2435 3.41 3.50 3.68 3.62 0 157Tm 3.8091 0.2352 7.46 8.37 8.58 8.58 0 155Yb 5.3381 0.1704 0.30 0.39 0.36 0.09 0 155Lu 5.8021 0.2359 −1.12 −1.20 −1.12 −1.24 0 157Hf 5.8751 0.1918 −0.91 −0.96 −0.95 −1.15 0 159Hf 5.2251 0.1778 1.16 1.83 1.89 1.61 0 161Hf 4.6791 0.1871 3.79 4.59 4.72 4.36 0 157Ta 6.2751 0.2821 −1.98 −2.16 −2.01 −2.14 0 159Ta 5.6601 0.2504 0.48 0.24 0.43 0.32 0 159W 6.4551 0.1658 −2.09 −2.16 −2.23 −2.37 0 161W 5.9251 0.1929 −0.25 −0.29 −0.22 −0.42 0 163W 5.5181 0.1747 1.27 1.43 1.51 1.26 0 167W 4.7511 0.1706 4.69 5.22 5.37 5.00 0 163Re 6.0121 0.2520 0.08 −0.32 −0.11 −0.25 0 165Re 5.6951 0.2537 1.03 0.94 1.20 1.07 0 169Re 5.0141 0.2280 5.18 5.12 4.45 5.09 3 163Os 6.6651 0.1625 −2.24 −2.08 −2.12 −2.24 0 165Os 6.3351 0.1892 −1.10 −1.01 −0.94 −1.10 0 167Os 5.9851 0.1750 0.21 0.33 0.42 0.22 0 169Os 5.7131 0.1778 1.40 1.43 1.56 1.33 0 171Os 5.3711 0.1731 2.66 2.97 3.13 2.84 0 173Os 5.0551 0.1765 3.73 4.51 4.72 4.38 0 167Ir 6.5051 0.2598 −1.17 −1.36 −1.14 −1.29 0 169Ir 6.1411 0.2543 −0.18 −0.02 0.24 0.09 0 171Ir 5.8651 0.2397 1.31 1.09 1.37 1.22 0 173Ir 5.5411 0.2365 2.41 2.50 2.81 2.67 0 175Ir 5.4301 0.2195 3.02 3.69 3.30 3.54 2 177Ir 5.0821 0.1885 4.69 4.80 5.06 4.92 0 167Pt 7.1651 0.1611 −3.04 −2.93 −2.99 −3.05 0 169Pt 6.8651 0.1883 −2.16 −2.07 −2.01 −2.11 0 171Pt 6.6051 0.1694 −1.28 −1.17 −1.11 −1.24 0 173Pt 6.3581 0.1808 −0.35 −0.33 −0.21 −0.37 0 177Pt 5.6431 0.1888 2.24 2.54 2.78 2.52 0 179Pt 5.4121 0.1658 3.94 4.34 3.86 3.84 2 181Pt 5.1501 0.1521 4.85 4.98 5.18 4.84 0 183Pt 4.8221 0.1405 6.61 6.80 7.00 6.60 0 185Pt 4.2801 0.1414 7.93 10.24 10.48 9.97 0 173Au 6.8361 0.2665 −1.53 −1.78 −1.52 −1.70 0 175Au 6.5851 0.2543 −0.65 −0.91 −0.64 −0.81 0 177Au 6.2971 0.2617 0.57 0.12 0.44 0.27 0 179Au 5.9811 0.2240 1.51 1.43 1.73 1.56 0 181Au 5.7511 0.1988 2.70 2.45 2.72 2.56 0 183Au 5.4661 0.1768 3.89 3.79 4.06 3.89 0 185Au 5.1800 0.1725 4.98 5.22 5.51 5.34 0 173Hg 7.3751 0.1887 −3.10 −2.95 −2.90 −2.94 0 175Hg 7.0751 0.1720 −2.00 −2.00 −1.94 −2.02 0 177Hg 6.7351 0.1878 −0.93 −0.24 −0.77 −0.61 2 179Hg 6.3511 0.1845 0.14 0.48 0.68 0.51 0 181Hg 6.2841 0.1915 1.12 1.37 0.91 1.01 2 183Hg 6.0381 0.1851 1.90 1.67 1.91 1.70 0 185Hg 5.7721 0.1792 2.91 2.81 3.07 2.82 0 177Tl 7.0671 0.2827 −1.61 −1.81 −1.50 −1.68 0 179Tl 6.7051 0.2677 −0.14 −0.57 −0.23 −0.40 0 181Tl 6.3221 0.2671 1.52 0.85 1.24 1.07 0 181Pb 7.2451 0.1716 −1.41 −1.15 −1.73 −1.51 2 183Pb 6.9281 0.1654 −0.27 −0.11 −0.66 −0.48 2 185Pb 6.6951 0.1686 1.26 0.68 0.17 0.32 2 187Pb 6.3931 0.1663 2.20 1.80 1.33 1.44 2 189Pb 5.9151 0.1622 3.97 3.78 3.37 3.41 2 187Bi 7.7791 0.2413 −1.43 −1.81 −3.14 −1.48 5 189Bi 7.2681 0.2261 −0.16 −0.24 −1.51 0.15 5 191Bi 6.4471 0.2144 1.39 1.17 1.52 1.32 0 193Bi 6.0211 0.1986 3.26 2.95 3.32 3.12 0 195Bi 5.5351 0.1858 5.78 5.23 5.64 5.44 0 209Bi 3.1373 0.0938 26.80 25.45 24.12 25.85 5 211Bi 6.7501 0.0903 2.11 1.56 −0.02 1.57 5 213Bi 5.9881 0.0924 5.12 4.60 3.14 4.73 5 189Po 7.6941 0.1906 −2.46 −1.95 −2.48 −2.22 2 191Po 7.4931 0.1849 −1.66 −2.03 −1.86 −1.90 0 193Po 7.0941 0.1840 −0.40 −0.75 −0.53 −0.61 0 195Po 6.7491 0.1699 0.69 0.48 0.72 0.59 0 197Po 6.4111 0.1577 1.80 1.79 2.05 1.87 0 199Po 6.0741 0.1498 3.64 3.20 3.48 3.25 0 201Po 5.7991 0.1368 4.92 4.46 4.74 4.46 0 203Po 5.4961 0.1329 6.29 6.62 6.24 6.19 2 205Po 5.3251 0.1198 7.19 6.85 7.13 6.76 0 207Po 5.2151 0.1111 7.99 7.46 7.71 7.32 0 209Po 4.9770 0.1037 9.59 8.84 9.08 8.65 0 211Po 7.5946 0.0884 −0.29 −0.85 −2.54 −1.19 5 213Po 8.5357 0.1804 −5.43 −5.35 −5.37 −5.33 0 215Po 7.5263 0.1775 −2.75 −2.53 −2.39 −2.45 0 217Po 6.6621 0.1726 0.20 0.42 0.69 0.53 0 219Po 5.9161 0.1673 3.34 3.51 3.88 3.60 0 191At 7.7141 0.1984 −2.68 −2.35 −2.15 −2.37 0 193At 7.3891 0.2661 −1.54 −1.49 −1.11 −1.33 0 195At 7.1021 0.2380 −0.54 −0.51 −0.14 −0.36 0 197At 7.1051 0.2142 −0.39 −0.51 −0.18 −0.41 0 199At 6.7781 0.1974 0.89 0.67 1.01 0.78 0 201At 6.4731 0.1748 2.07 1.88 2.20 1.97 0 203At 6.2101 0.1656 3.15 2.96 3.30 3.07 0 205At 6.0191 0.1456 4.20 3.83 4.14 3.90 0 207At 5.8731 0.1318 4.81 4.51 4.79 4.56 0 209At 5.7571 0.1209 5.69 5.07 5.33 5.09 0 211At 5.9825 0.0938 4.79 4.08 4.21 3.95 0 213At 9.2537 0.1871 −6.90 −6.73 −6.84 −7.16 0 215At 8.1771 0.1779 −4.43 −4.06 −3.99 −4.30 0 217At 7.2021 0.1679 −1.49 −1.08 −0.87 −1.17 0 219At 6.3421 0.1582 1.78 2.14 2.46 2.17 0 195Rn 7.6941 0.1830 −2.15 −1.93 −1.73 −1.75 0 197Rn 7.4101 0.1814 −1.27 −1.05 −0.81 −0.86 0 199Rn 7.1321 0.1706 −0.23 −0.12 0.14 0.05 0 203Rn 6.6301 0.1527 1.82 1.72 2.00 1.85 0 205Rn 6.3861 0.1407 2.84 3.39 2.99 3.08 2 207Rn 6.2511 0.1340 3.42 3.27 3.55 3.33 0 209Rn 6.1551 0.1219 4.00 3.70 3.95 3.71 0 211Rn 5.9661 0.1142 5.28 5.23 4.79 4.81 2 213Rn 8.2451 0.0978 −1.71 −2.06 −3.75 −2.32 5 215Rn 8.8386 0.1821 −5.64 −5.43 −5.44 −5.36 0 217Rn 7.8881 0.1921 −3.23 −2.92 −2.73 −2.75 0 219Rn 6.9462 0.1932 0.60 0.82 0.49 0.64 2 221Rn 6.1631 0.1851 3.84 3.95 3.71 3.75 2 197Fr 7.8841 0.2692 −2.64 −2.32 −1.95 −2.18 0 199Fr 7.8161 0.2474 −2.18 −2.11 −1.77 −2.00 0 201Fr 7.5191 0.2245 −1.20 −1.17 −0.82 −1.06 0 203Fr 7.2741 0.2080 −0.26 −0.35 0.00 −0.24 0 205Fr 7.0541 0.1858 0.60 0.44 0.78 0.53 0 207Fr 6.8891 0.1724 1.19 1.04 1.37 1.12 0 209Fr 6.7781 0.1527 1.75 1.48 1.77 1.52 0 211Fr 6.6621 0.1400 2.33 1.93 2.21 1.95 0 213Fr 6.9051 0.1096 1.54 1.07 1.21 0.94 0 215Fr 9.5403 0.2012 −7.05 −6.76 −6.82 −7.13 0 217Fr 8.4701 0.2040 −4.66 −4.21 −4.06 −4.37 0 219Fr 7.4491 0.1976 −1.65 −1.20 −0.89 −1.19 0 221Fr 6.4571 0.1823 2.46 3.16 2.90 2.99 2 223Fr 5.5614 0.1799 7.34 7.88 7.17 8.14 4 203Ra 7.7361 0.1746 −1.44 −1.39 −1.15 −1.16 0 205Ra 7.4861 0.1646 −0.66 −0.59 −0.34 −0.38 0 207Ra 7.2691 0.1574 0.21 0.81 0.40 0.61 2 209Ra 7.1431 0.1418 0.67 0.59 0.83 0.74 0 211Ra 7.0421 0.1372 1.10 0.93 1.17 1.07 0 213Ra 6.8621 0.1263 2.27 2.29 1.84 1.99 2 215Ra 8.8621 0.1092 −2.78 −3.04 −4.72 −3.22 5 217Ra 9.1611 0.1850 −5.71 −5.56 −5.54 −5.43 0 219Ra 8.1381 0.1911 −2.05 −2.24 −2.71 −2.41 2 221Ra 6.8801 0.1899 1.40 1.90 1.64 1.78 2 223Ra 5.9790 0.1608 5.99 5.77 5.55 5.55 2 205Ac 7.8061 0.0991 −1.10 −0.04 −0.99 −0.48 3 207Ac 7.8491 0.2218 −1.51 −1.53 −1.16 −1.41 0 209Ac 7.7251 0.1938 −1.03 −1.11 −0.79 −1.04 0 211Ac 7.5641 0.1820 −0.67 −0.60 −0.27 −0.53 0 213Ac 7.4981 0.1637 −0.13 −0.36 −0.08 −0.34 0 215Ac 7.7461 0.1301 −0.77 −1.11 −0.96 −1.24 0 217Ac 9.8311 0.2172 −7.16 −6.81 −6.81 −7.12 0 219Ac 8.8271 0.2166 −5.03 −4.49 −4.30 −4.60 0 221Ac 7.7901 0.2087 −1.28 −1.56 −1.21 −1.51 0 223Ac 6.7831 0.1695 2.10 2.73 2.46 2.54 2 225Ac 5.9351 0.1535 5.93 6.45 6.25 6.34 2 227Ac 5.0423 0.1491 10.70 10.69 11.24 10.97 0 211Th 7.9451 0.1662 −1.32 −1.38 −1.12 −1.12 0 213Th 7.8371 0.1401 −0.84 −1.00 −0.80 −0.81 0 215Th 7.6641 0.1411 0.13 0.20 −0.25 −0.00 2 217Th 9.4351 0.1215 −3.61 −3.82 −5.49 −3.93 5 219Th 9.5031 0.1892 −5.99 −5.73 −5.69 −5.53 0 221Th 8.6251 0.1869 −2.76 −2.88 −3.38 −3.02 2 223Th 7.5661 0.1798 −0.22 0.28 −0.05 0.19 2 225Th 6.9211 0.1555 2.77 2.63 2.33 2.48 2 227Th 6.1467 0.1457 6.21 5.91 5.69 5.71 2 229Th 5.1676 0.1488 11.40 11.10 10.99 10.82 2 211Pa 8.4751 0.2424 −2.22 −2.73 −2.36 −2.62 0 213Pa 8.3851 0.1981 −2.13 −2.42 −2.13 −2.39 0 215Pa 8.2351 0.1934 −1.85 −2.01 −1.70 −1.97 0 217Pa 8.4891 0.1545 −2.42 −2.68 −2.51 −2.78 0 219Pa 10.1241 0.2367 −7.25 −6.86 −6.81 −7.10 0 221Pa 9.2431 0.2245 −5.23 −4.88 −4.68 −4.98 0 223Pa 8.3451 0.2099 −2.28 −2.50 −2.17 −2.47 0 225Pa 7.4051 0.1739 0.23 1.22 0.94 1.02 2 227Pa 6.5801 0.1561 3.43 3.73 4.20 3.91 0 229Pa 5.8351 0.1548 7.43 7.57 7.73 7.57 1 231Pa 5.1499 0.1520 12.01 11.03 11.63 11.35 0 219U 9.9501 0.1401 −4.22 −4.42 −6.04 −4.43 5 221U 9.8891 0.1800 −6.18 −5.95 −5.93 −5.73 0 223U 9.1651 0.1833 −4.19 −3.60 −4.13 −3.71 2 225U 8.0071 0.1862 −1.21 −0.40 −0.72 −0.43 2 227U 7.2351 0.1586 1.82 2.26 1.99 2.18 2 229U 6.4761 0.1485 4.24 4.63 5.11 4.90 0 231U 5.5763 0.1481 9.95 9.73 9.63 9.54 2 233U 4.9087 0.1348 12.70 13.16 13.76 13.23 0 223Np 9.6551 0.2334 −5.60 −5.23 −5.03 −5.32 0 225Np 8.8251 0.2306 −2.22 −3.18 −2.83 −3.12 0 227Np 7.8151 0.1888 −0.29 0.85 0.32 0.78 3 229Np 7.0151 0.1691 2.55 3.17 3.28 3.11 1 231Np 6.3651 0.1631 5.14 5.90 6.08 5.92 1 233Np 5.6281 0.1439 8.49 9.25 9.85 9.55 0 235Np 5.1938 0.1265 12.12 12.23 12.42 12.25 1 237Np 4.9573 0.1272 13.83 13.74 13.95 13.77 1 229Pu 7.5931 0.1707 2.26 1.73 1.51 1.74 2 231Pu 6.8391 0.1530 3.58 3.93 4.44 4.29 0 233Pu 6.4141 0.1271 6.00 6.50 6.31 6.37 2 235Pu 5.9511 0.1182 7.72 8.07 8.58 8.26 0 239Pu 5.2444 0.1161 11.88 12.03 12.60 12.13 0 241Pu 5.1401 0.1053 13.26 13.38 13.24 13.02 2 229Am 8.1351 0.2148 0.26 0.23 0.05 0.14 2 233Am 7.0651 0.1485 3.62 3.82 3.93 3.76 1 235Am 6.5751 0.1334 5.18 5.89 6.02 5.85 1 237Am 6.1951 0.1204 7.24 7.68 7.81 7.63 1 239Am 5.9225 0.1230 8.63 9.01 9.18 9.00 1 241Am 5.6378 0.1082 10.14 10.59 10.73 10.54 1 243Am 5.4391 0.1098 11.37 11.71 11.88 11.68 1 233Cm 7.4751 0.1544 2.11 2.27 2.76 2.70 0 235Cm 7.2761 0.1467 3.99 3.68 3.50 3.69 2 241Cm 6.1852 0.1074 8.45 8.75 8.30 8.58 3 243Cm 6.1688 0.0972 8.96 8.56 8.35 8.34 2 245Cm 5.6245 0.1158 11.42 11.37 11.28 11.16 2 247Cm 5.3535 0.1159 14.69 12.67 12.90 12.52 1 245Bk 6.4546 0.1228 8.55 7.52 7.40 7.45 2 247Bk 5.8901 0.1190 10.64 10.34 10.27 10.32 2 249Bk 5.5210 0.1209 12.29 12.40 12.38 12.42 2 239Cf 7.7651 0.1369 1.63 1.99 2.46 2.43 0 241Cf 7.4551 0.1128 2.97 3.17 3.60 3.53 0 243Cf 7.4151 0.1106 3.66 4.26 3.73 4.21 3 245Cf 7.2585 0.1180 3.88 3.84 4.32 4.21 0 247Cf 6.5022 0.1209 7.50 7.73 7.63 7.68 2 249Cf 6.2933 0.1102 10.04 8.45 8.63 8.44 1 251Cf 6.1771 0.1104 10.45 10.13 9.19 10.29 5 253Cf 6.0776 0.1201 8.69 9.05 9.68 9.36 0 241Es 8.2551 0.1402 0.71 0.69 1.12 0.82 0 243Es 8.0751 0.1327 1.55 1.27 1.71 1.40 0 245Es 7.8651 0.1367 2.13 1.94 2.43 2.11 0 247Es 7.4431 0.1371 3.59 3.45 4.00 3.68 0 249Es 6.9413 0.1199 6.03 6.47 6.06 6.48 3 251Es 6.5971 0.1153 7.36 7.02 7.60 7.27 0 253Es 6.7393 0.1224 6.25 6.31 6.91 6.56 0 255Es 6.4001 0.1282 7.63 7.84 8.50 8.15 0 243Fm 8.6951 0.1398 −0.60 0.05 0.06 0.24 1 245Fm 8.4351 0.1230 0.62 1.45 0.87 1.49 3 247Fm 8.2551 0.1154 1.69 2.30 1.44 2.41 4 251Fm 7.4251 0.1148 6.03 4.34 4.45 4.46 1 253Fm 7.0529 0.1219 6.33 6.92 5.98 7.23 5 257Fm 6.8631 0.1253 6.94 6.81 6.75 6.85 2 245Md 9.0151 0.1583 −0.42 −0.32 −0.57 −0.50 2 247Md 8.7651 0.1426 0.08 0.14 0.17 −0.02 1 249Md 8.4351 0.1490 1.53 1.39 1.21 1.27 2 251Md 7.9641 0.1337 3.40 2.70 2.83 2.63 1 253Md 7.5651 0.1351 5.01 4.12 4.31 4.10 1 255Md 7.9051 0.1164 4.36 3.19 2.98 3.02 2 257Md 7.5571 0.1313 5.11 4.09 4.28 4.06 1 251No 8.7551 0.1163 −0.02 0.16 0.54 0.64 0 253No 8.4151 0.1186 2.23 1.58 1.63 1.78 1 255No 8.2281 0.1081 2.84 2.50 2.24 2.55 2 257No 8.4766 0.1192 1.46 1.61 1.36 1.70 2 259No 7.8541 0.1224 3.66 3.68 3.54 3.79 2 253Lr 8.9151 0.1460 −0.15 −0.08 0.40 0.08 0 255Lr 8.5021 0.1273 1.49 1.23 1.71 1.39 0 257Lr 9.0151 0.1364 0.78 0.83 0.02 0.94 4 259Lr 8.5751 0.1360 0.90 0.90 1.40 1.07 0 255Rf 9.0551 0.1210 0.49 0.31 0.32 0.56 1 257Rf 8.9141 0.1170 0.75 1.00 0.74 1.14 2 259Rf 9.1331 0.1319 0.49 0.27 0.02 0.45 2 261Rf 8.6481 0.1252 1.06 1.05 1.54 1.62 0 257Db 9.2051 0.1455 0.39 0.12 0.22 0.03 1 259Db 9.5671 0.1599 −0.29 −0.97 −0.89 −1.08 1 263Db 8.8351 0.1390 1.89 2.28 1.29 2.83 5 261Sg 9.7141 0.1262 −0.73 −0.66 −0.96 −0.46 2 263Sg 9.4051 0.1275 0.03 −0.53 −0.09 0.09 0 265Sg 9.0451 0.1244 1.26 2.02 0.99 2.52 5 261Bh 10.5051 0.1648 −1.89 −2.16 −2.73 −2.30 3 265Hs 10.4701 0.1278 −2.71 −2.67 −2.35 −2.04 0 269Hs 9.2751 0.1264 1.18 0.85 0.98 1.24 1 Table 6. Same as Table 5 but for odd-A nuclei. The column of the l term that appears for the first time is the angular momentum carried away by an
$\alpha$ particle.For a more intuitive comparison of the results, Figs. 2−4 plot the differences between the experimental
$ \alpha $ decay half-lives and those calculated using our model, UDL, and DZR in logarithmic form. It is evident that the differences calculated by our model are more concentrated near zero, indicating that our calculation results are closer to the experimental values. Except for a few nuclei, the differences for all 559 nuclei fall between –0.5 and 0.5. For 185Pt, 268Hs, and 282Ds, it may be caused by deformation effects [82]. Meanwhile, for 209Bi, 210Po, 245Bk, 247Cm, 249Cf, 251Fm, 255Md, 257Md, and 258Md, the larger errors are likely influenced by the shell effects at N = 126 and N = 152 [83].
Figure 2. (color online) Deviations between the experimental
$\alpha$ decay half-lives and the calculated ones obtained using our model, UDL, and DZR in logarithmic form.
Figure 3. (color online) Same as Fig. 2 but for odd-A nuclei.

Figure 4. (color online) Same as Fig. 2 but for odd-odd nuclei.
As is known, the half-lives of
$ \alpha $ decay show a very strong sensitivity to the$ \alpha $ decay energy$ Q_\alpha $ . Therefore, selecting a precise$ Q_\alpha $ becomes one of the key problems in prediction. In 2016, Sobiczewski et al. systematically compared nine different mass models: Möller et al. (FRDM) [84], Duflo and Zuker (DZ) [85], Nayak and Satpathy (INM) [86], Wang and Liu (WS3+) [87], Wang et al. (WS4+) [88, 89], Muntian et al. (HN) [90, 91], Kuzmina et al. (TCSM) [92], Goriely et al. (HFB31) [93], and Liran et al. (SE) [94] and came to the conclusion that the WS3+ model is the most accurate in reproducing the experimental$ Q_\alpha $ of superheavy nuclei. In this work, we use our model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120. The predicted results are listed in Table 8. In this table, the first to fourth columns represent the parent nucleus,$ \alpha $ decay energy$ Q_\alpha $ calculated using WS3+, angular momentum l carried away by the$ \alpha $ particle, and$ \alpha $ preformation factors calculated by the CFM, respectively. The last three,$ \log_{10} T^{{\rm{cal}}}_{1/2} $ ,$ \log_{10} T^{{\rm{UDL}}}_{1/2} $ ,$ \log_{10} T^{{\rm{DZR}}}_{1/2} $ , represent the predicted$ \alpha $ decay half-lives in logarithmic form calculated by our model, UDL, and DZR, respectively. From this table, we can clearly see that the three predictions are quite close to each other. To visually illustrate their relationship, the logarithmic form of$ \alpha $ decay half-lives and the$ Q_\alpha $ values calculated by the WS3+ mass model with Z = 119 and 120 versus the neutron numbers of the daughter nucleus$ N_d $ , as well as the curve of the relationship between the$ \alpha $ decay preformation factors and neutron number of the parent nucleus N, are plotted in Figs. 5−7, respectively. From Fig 5, it can be seen that the trends of the$ \alpha $ decay half-lives for the isotopic chains with proton numbers Z = 119 and 120 predicted by our model, UDL, and DZR are consistent, and our predicted results are close to those of UDL. Furthermore, as shown in Fig. 5, for the isotope chains with Z = 119 and 120, when the neutron number of the daughter nucleus$ N_d $ is less than 176, the half-lives of$ \alpha $ decay exhibit a slow upward trend, followed by a gradual decrease to a minimum value at$ N_d $ = 178. From$ N_d $ = 178 to$ N_d $ = 182, it keeps a steady change. Then, it suddenly drops to the lowest point at$ N_d $ = 184, after which an upward trend appears again. A similar phenomenon can also be observed on$ Q_\alpha $ in Fig. 6. In addition, Fig. 7 clearly shows that the$ \alpha $ decay preformation factors of even-even nuclei with Z = 120, odd-A nuclei with Z = 119, and odd-odd nuclei with Z = 119 show a trend of first decreasing and then increasing near the neutron number N = 184 of the parent nuclei. However, this variation trend is not obvious in odd-A nuclei with Z = 120. When the neutron number is closer to the neutron magic number, the$ \alpha $ decay preformation factor is smaller, while it increases as the neutron number deviates further from this magic shell closure [95]. Moreover, during$ \alpha $ decay, when the neutron or proton numbers of the corresponding daughter nucleus are magic numbers, the half-life reaches its minimum value [96, 97]. When the neutron number exceeds the neutron magic number by two nucleons, the parent nucleus tends to become stable by emitting an$ \alpha $ particle. In this case, the half-life will reach its minimum value. The depth of the minimum value depends on the stability of the daughter nucleus, meaning that the more stable nucleus corresponds to a deeper minimum value. From the above content, we can conclude that N = 184 is the possible neutron magic number, while N = 178 can be considered the neutron submagic number [97].Nuclide $ Q_{\alpha} $ l $P_\alpha$ $\log_{10} T_{1/2}^{{\rm{cal}}}$ $\log_{10} T_{1/2}^{{\rm{UDL}}}$ $\log_{10} T_{1/2}^{{\rm{DZR}}}$ Nuclei with Z=119 284119 13.7747 4 0.2181 −5.44 −6.38 −5.41 285119 13.6461 2 0.2940 −5.93 −6.15 −5.65 286119 13.4606 2 0.1831 −5.38 −5.80 −5.72 287119 13.2830 2 0.2852 −5.31 −5.47 −4.97 288119 13.1697 2 0.1838 −4.87 −5.25 −5.18 289119 13.0764 2 0.2539 −4.91 −5.08 −4.58 290119 12.9211 2 0.1679 −4.38 −4.77 −4.71 291119 12.8677 2 0.2525 −4.54 −4.68 −4.18 292119 12.7053 2 0.1706 −3.99 −4.35 −4.29 293119 12.5103 2 0.2395 −3.85 −3.94 −3.45 294119 12.5217 2 0.1672 −3.64 −3.98 −3.93 295119 12.5701 2 0.2196 −3.96 −4.10 −3.61 296119 12.3096 2 0.1553 −3.19 −3.54 −3.50 297119 12.3025 2 0.1922 −3.39 −3.54 −3.05 298119 12.5862 2 0.1416 −3.75 −4.18 −4.14 299119 12.7275 2 0.2167 −4.33 −4.50 −4.03 300119 12.5259 2 0.1596 −3.70 −4.08 −4.05 301119 12.3748 0 0.2040 −4.31 −3.76 −3.66 302119 12.3960 0 0.1540 −4.11 −3.83 −4.17 303119 12.3691 2 0.2036 −3.64 −3.78 −3.31 304119 12.8958 1 0.1608 −4.78 −4.94 −5.16 305119 13.4495 2 0.2078 −5.73 −6.08 −5.62 306119 13.2476 0 0.1632 −5.86 −5.69 −6.04 307119 12.8167 0 0.2162 −5.30 −4.82 −4.73 308119 12.0652 0 0.1688 −3.52 −3.17 −3.53 309119 11.3386 3 0.2282 −1.24 −1.42 −0.57 310119 10.8335 3 0.1829 0.29 −0.10 0.27 311119 10.6003 0 0.1697 −0.26 0.53 0.63 312119 10.4397 2 0.1386 1.17 0.97 0.95 313119 9.4978 2 0.1562 3.61 3.87 4.36 314119 9.1165 1 0.1286 4.98 5.16 4.87 315119 9.3054 1 0.1420 3.95 4.49 4.72 316119 8.7705 2 0.1192 6.50 6.39 6.33 317119 9.2532 3 0.1826 4.55 4.64 5.49 318119 9.1841 0 0.1549 4.23 4.86 4.44 319119 8.4849 6 0.1484 8.17 7.44 10.18 Nuclei with Z=120 287120 13.9149 4 0.1680 −5.36 −6.39 −4.79 288120 13.7471 0 0.2526 −6.59 −6.87 −6.67 289120 13.6763 0 0.1661 −6.22 −5.97 −5.32 290120 13.6305 0 0.2470 −6.41 −6.69 −6.49 291120 13.4054 2 0.1639 −5.08 −5.47 −4.57 292120 13.3084 0 0.2505 −5.88 −6.09 −5.90 293120 13.2366 2 0.1701 −4.82 −5.16 −4.27 294120 13.0718 0 0.2382 −5.45 −5.65 −5.47 295120 13.0989 2 0.1648 −4.58 −4.91 −4.03 296120 13.1873 0 0.2326 −5.69 −5.92 −5.74 297120 13.0230 0 0.1621 −5.14 −4.78 −4.20 298120 12.9002 0 0.2271 −5.17 −5.37 −5.19 299120 13.1851 0 0.1633 −5.48 −5.15 −4.55 300120 13.2871 0 0.2420 −5.95 −6.19 −6.01 301120 13.0349 2 0.1736 −4.57 −4.87 −4.00 302120 12.8782 0 0.2369 −5.21 −5.39 −5.22 303120 12.7949 2 0.1737 −4.14 −4.40 −3.55 304120 12.7451 0 0.2371 −4.99 −5.14 −4.98 305120 13.2712 2 0.1827 −5.09 −5.42 −4.53 306120 13.8225 0 0.2446 −6.98 −7.31 −7.14 307120 13.5776 4 0.1861 −5.11 −6.06 −4.49 308120 13.0359 0 0.2652 −5.65 −5.81 −5.65 309120 12.1724 0 0.1994 −3.71 −3.10 −2.60 310120 11.4753 0 0.2312 −2.38 −2.34 −2.20 311120 11.1018 2 0.1802 −0.57 −0.49 0.18 312120 11.0535 0 0.2029 −1.35 −1.29 −1.17 313120 10.9229 2 0.1603 −0.10 −0.04 0.61 314120 9.9714 0 0.2273 1.47 1.73 1.83 315120 10.1487 0 0.1807 1.23 2.15 2.42 316120 9.9651 0 0.1873 1.54 1.72 1.81 317120 9.9639 3 0.1513 2.77 2.69 3.50 318120 9.9875 0 0.1785 1.47 1.62 1.71 319120 9.8887 3 0.1454 2.98 2.90 3.70 320120 9.7100 0 0.1861 2.25 2.45 2.53 Table 8. Predicted results of the
$\alpha$ decay half-lives in logarithmic form for 70 even-even, odd-even, and odd-odd nuclei with Z = 119 and 120 using our model, UDL, and DZR. The$\alpha$ decay energy and half-lives are in units of MeV and s, respectively. The mass excesses are taken from the WS3+ mass model [87]. The spin and parity values of these nuclei are taken from Ref. [98].
Figure 5. (color online) Predicted
$\alpha$ decay half-lives for the even-even, odd-even, and odd-odd nuclei with Z = 119 and 120 are presented in logarithmic form using our model, UDL, and DZR. -
Based on WKB theory, considering the
$ \alpha $ decay preformation factors$ P_\alpha $ , we propose a model to calculate$ \alpha $ decay half-lives of 559 nuclei from the ground state. Using the minimum standard deviation between experimental data and calculated data as the objective, function whose detailed information is provided later, we obtain the coefficients a, b, c, and d, as shown in the Table 1. To compare the calculated results under the same conditions, we refitted the experimental data and obtained the parameter results for the UDL and DZR, as shown in Tables 2−3. In this study, the standard deviation$ \sigma $ can be defined as follows:Parameters e-e e-o o-o a 21.1958 23.4998 26.7499 b −1.8435 0.7241 2.25913 c 0.5001 −2.8591 −8.4193 d 0 0.2784 0.2721 Table 1. Parameter fitting results of Eq. (13) for three different types of nuclei.
Parameters e-e e-o o-o a 0.4101 0.418 0.4062 b −0.4218 −0.4024 −0.3724 c −21.9524 −23.8632 −24.0723 Table 2. Same as Table 1 but for the UDL.
Parameters e−e e−o o−e o−o a −25.627 −28.22089 −27.1408 28.0910 b −1.1559 −1.0000 −1.1410 −1.1270 c 1.5912 1.5625 1.6251 1.6408 d 0 0.0468 0.0625 0.0625 Table 3. Same as Table 1 but for the DZR.
$ \sigma= \left[ \frac{1}{n} \sum\limits_{i=1}^n \left( \log_{10} T^{{\rm{exp}}}_{1/2} - \log_{10} T^{{\rm{cal}}}_{1/2} \right)^2 \right]^{1/2}, $
(27) where
$ \log_{10} T_{1/2}^{{\rm{exp}}} $ and$ \log_{10} T_{1/2}^{{\rm{cal}}} $ are the logarithmic forms of experimental$ \alpha $ decay half-lives and the calculated ones, respectively. n is the number of nuclei involved in different decay cases. The standard deviation$ \sigma $ of the calculated results for the three models and/or formulas is shown in Table 4. From this table, we can clearly see that the standard deviation$ \sigma $ of our model only is 0.408 for all 559 nuclei, 0.323 for 177 even-even nuclei, 0.459 for 277 odd-A nuclei, and 0.391 for 105 odd-odd nuclei. These values are smaller than those of the UDL and DZR results, which proves that our model achieves satisfactory results.Formulas Total e-e e-o o-o Our model 0.408 0.323 0.459 0.391 UDL 0.589 0.349 0.633 0.632 DZR 0.436 0.337 0.493 0.423 Table 4. Standard deviations
$\sigma$ between experimental$\alpha$ decay half-lives and those calculated using our model, the UDL and the DZR for 177 even-even nuclei, 277 odd-A nuclei, and 105 odd-odd nuclei.To show the concrete results, we use these formulas to calculate
$ \alpha $ decay half-lives of even-even, odd-A, and odd-odd nuclei. The detailed calculated results are listed in Tables 5−7. In these tables, the first three columns represent the parent nucleus, experimentally measured$ \alpha $ decay energy$ Q_\alpha $ , and$ \alpha $ decay preformation factors calculated using the CFM, respectively. The fourth to seventh columns represent the experimental half-life data for$ \alpha $ decay, as well as those calculated using our model, UDL, and DZR in logarithmic form, denoted as$ \log_{10} T^{{\rm{exp}}}_{1/2} $ ,$ \log_{10} T_{1/2}^{{\rm{cal}}} $ ,$ \log_{10} T_{1/2}^{{\rm{UDL}}} $ ,$ \log_{10} T_{1/2}^{{\rm{DZR}}} $ , respectively. For Tables 6−7, the eighth column represents the angular momentum l taken away by the$ \alpha $ particle. These three tables show that our calculated results agree closely with the experimental data for most nuclei, with some exceptions such as 185Pt, 205Ac, 209Bi, 210Po, 227Np, 230Np, 245Bk, 247Cm, 249Cf, 251Fm, 255Md, 257Md, 258Md, 268Hs, and 282Ds.Nuclide $Q_{\alpha}$ $P_\alpha$ $\log_{10} T_{1/2}^{{\rm{exp}}}$ $\log_{10} T_{1/2}^{{\rm{cal}}}$ $\log_{10} T_{1/2}^{{\rm{UDL}}}$ $\log_{10} T_{1/2}^{{\rm{DZR}}}$ 146Sm 2.5292 0.1979 15.33 15.31 15.57 15.52 148Sm 1.9870 0.1954 23.30 23.10 23.54 23.43 148Gd 3.2713 0.2017 9.35 9.30 9.44 9.41 150Gd 2.8071 0.2021 13.75 13.67 13.87 13.84 152Gd 2.2039 0.2213 21.53 21.34 21.65 21.61 150Dy 4.3511 0.2360 3.11 3.05 3.10 3.07 152Dy 3.7265 0.2403 6.93 7.01 7.04 7.08 154Dy 2.9451 0.2379 13.98 13.68 13.77 13.83 152Er 4.9341 0.2389 1.06 1.06 1.11 1.06 154Er 4.2801 0.2568 4.68 4.57 4.55 4.60 156Er 3.4811 0.2521 9.99 10.15 10.16 10.25 154Yb 5.4741 0.2349 −0.35 −0.41 −0.33 −0.41 156Yb 4.8091 0.2572 2.41 2.70 2.69 2.73 156Hf 6.0251 0.2703 −1.64 −1.70 −1.66 −1.71 158Hf 5.4051 0.2463 0.81 0.83 0.85 0.85 160Hf 4.9021 0.2546 3.28 3.24 3.21 3.26 162Hf 4.4171 0.2411 5.69 5.94 5.91 5.98 158W 6.6151 0.2408 −2.84 −2.96 −2.84 −2.97 160W 6.0651 0.2732 −0.99 −0.99 −0.98 −0.98 162W 5.6781 0.2441 0.42 0.56 0.57 0.57 164W 5.2781 0.2506 2.22 2.34 2.31 2.36 166W 4.8561 0.2309 4.74 4.46 4.44 4.49 168W 4.5001 0.2357 6.20 6.48 6.44 6.52 180W 2.5153 0.1621 25.70 24.84 25.19 24.99 162Os 6.7651 0.2373 −2.68 −2.67 −2.55 −2.66 164Os 6.4851 0.2708 −1.66 −1.72 −1.70 −1.72 166Os 6.1421 0.2472 −0.59 −0.46 −0.44 −0.46 168Os 5.8161 0.2474 0.68 0.83 0.82 0.85 170Os 5.5361 0.2373 1.89 2.04 2.02 2.05 172Os 5.2241 0.2397 3.21 3.50 3.45 3.52 174Os 4.8711 0.2259 5.25 5.33 5.29 5.36 186Os 2.8212 0.1569 22.80 22.19 22.46 22.29 166Pt 7.2951 0.2381 −3.53 −3.61 −3.47 −3.61 168Pt 6.9851 0.2725 −2.69 −2.65 −2.61 −2.65 170Pt 6.7081 0.2420 −1.86 −1.74 −1.68 −1.74 172Pt 6.4631 0.2545 −0.99 −0.89 −0.88 −0.88 174Pt 6.1833 0.2471 0.06 0.16 0.15 0.16 176Pt 5.8851 0.2605 1.20 1.36 1.30 1.37 178Pt 5.5731 0.2267 2.43 2.72 2.70 2.73 180Pt 5.2761 0.2051 4.03 4.14 4.13 4.15 182Pt 4.9511 0.1868 5.62 5.83 5.85 5.85 184Pt 4.5991 0.1858 7.77 7.88 7.89 7.90 186Pt 4.3201 0.1732 9.73 9.67 9.71 9.70 188Pt 4.0067 0.2161 12.53 11.91 11.86 11.94 190Pt 3.2686 0.2031 19.18 18.48 18.54 18.54 172Hg 7.5251 0.2767 −3.64 −3.61 −3.55 −3.60 174Hg 7.2331 0.2487 −2.70 −2.73 −2.66 −2.72 176Hg 6.8971 0.2674 −1.65 −1.64 −1.64 −1.63 178Hg 6.5773 0.2584 −0.53 −0.52 −0.54 −0.51 180Hg 6.2581 0.2651 0.73 0.68 0.62 0.69 182Hg 5.9951 0.2540 1.89 1.74 1.67 1.75 184Hg 5.6601 0.2418 3.44 3.21 3.13 3.22 186Hg 5.2041 0.2469 5.70 5.46 5.34 5.47 188Hg 4.7091 0.2387 8.72 8.26 8.15 8.29 180Pb 7.4191 0.2476 −2.39 −2.61 −2.55 −2.60 182Pb 7.0651 0.2342 −1.26 −1.47 −1.43 −1.46 184Pb 6.7741 0.2357 −0.21 −0.47 −0.46 −0.46 186Pb 6.4711 0.2301 1.07 0.65 0.63 0.66 188Pb 6.1091 0.2215 2.47 2.10 2.06 2.11 190Pb 5.6971 0.2155 4.24 3.93 3.87 3.94 192Pb 5.2211 0.2040 6.55 6.32 6.26 6.33 194Pb 4.7381 0.1946 9.94 9.11 9.06 9.13 210Pb 3.7927 0.1066 16.57 15.86 16.08 15.85 188Po 8.0831 0.2750 −3.57 −3.97 −3.91 −3.97 190Po 7.6931 0.2619 −2.61 −2.84 −2.81 −2.84 192Po 7.3201 0.2571 −1.49 −1.67 −1.68 −1.67 194Po 6.9871 0.2352 −0.41 −0.55 −0.56 −0.55 196Po 6.6581 0.2160 0.78 0.64 0.63 0.64 198Po 6.3101 0.2032 2.27 2.01 1.99 2.00 200Po 5.9811 0.1837 3.79 3.41 3.41 3.41 202Po 5.7001 0.1767 5.14 4.70 4.69 4.69 204Po 5.4851 0.1579 6.27 5.75 5.77 5.74 206Po 5.3271 0.1452 7.14 6.55 6.60 6.54 208Po 5.2157 0.1350 7.96 7.13 7.20 7.11 210Po 5.4075 0.1059 7.08 6.05 6.23 6.02 212Po 8.9542 0.2210 −6.53 −6.76 −6.46 −6.83 214Po 7.8335 0.2134 −3.79 −3.71 −3.58 −3.78 216Po 6.9063 0.2046 −0.84 −0.65 −0.63 −0.72 218Po 6.1148 0.1956 2.27 2.49 2.45 2.43 194Rn 7.8631 0.2614 −3.11 −2.63 −2.61 −2.62 196Rn 7.6161 0.2563 −2.33 −1.89 −1.89 −1.88 198Rn 7.3501 0.2390 −1.16 −1.04 −1.05 −1.03 200Rn 7.0441 0.2213 0.07 0.00 −0.01 0.01 202Rn 6.7731 0.2094 1.09 0.99 0.97 0.99 204Rn 6.5471 0.1912 2.01 1.85 1.84 1.84 206Rn 6.3841 0.1803 2.74 2.49 2.49 2.48 208Rn 6.2611 0.1626 3.37 2.98 3.02 2.97 210Rn 6.1591 0.1515 3.95 3.39 3.45 3.38 212Rn 6.3853 0.1206 3.16 2.37 2.55 2.35 214Rn 9.2082 0.2291 −6.59 −6.70 −6.42 −6.75 216Rn 8.1975 0.2368 −4.54 −4.04 −3.94 −4.09 218Rn 7.2625 0.2342 −1.47 −1.10 −1.12 −1.15 220Rn 6.4048 0.2208 1.75 2.15 2.06 2.11 222Rn 5.5904 0.2218 5.52 5.92 5.75 5.87 202Ra 7.8801 0.2477 −2.39 −2.03 −2.02 −2.01 204Ra 7.6361 0.2309 −1.22 −1.28 −1.27 −1.26 206Ra 7.4161 0.2186 −0.62 −0.57 −0.57 −0.56 208Ra 7.2731 0.1954 0.10 −0.10 −0.07 −0.10 210Ra 7.1511 0.1871 0.60 0.30 0.34 0.30 214Ra 7.2731 0.1384 0.39 −0.21 −0.36 −0.23 216Ra 9.5251 0.2390 −6.76 −6.79 −6.51 −6.82 218Ra 8.5411 0.2426 −4.59 −4.28 −4.18 −4.32 220Ra 7.5941 0.2393 −1.74 −1.42 −1.45 −1.46 222Ra 6.6777 0.1991 1.53 1.91 1.86 1.88 224Ra 5.7889 0.1840 5.50 5.88 5.79 5.85 226Ra 4.8707 0.1816 10.70 11.09 10.98 11.06 210Th 8.0691 0.2341 −1.80 −1.96 −1.95 −1.95 212Th 7.9581 0.1957 −1.50 −1.65 −1.57 −1.64 214Th 7.8271 0.1951 −1.06 −1.27 −1.20 −1.26 216Th 8.0731 0.1585 −1.58 −2.09 −1.90 −2.09 218Th 9.8491 0.2506 −6.91 −6.89 −6.62 −6.90 220Th 8.9741 0.2432 −4.99 −4.75 −4.62 −4.77 222Th 8.1321 0.2324 −2.65 −2.38 −2.35 −2.39 224Th 7.2991 0.1981 0.02 0.37 0.36 0.35 226Th 6.4531 0.1822 3.27 3.70 3.64 3.68 228Th 5.5202 0.1831 7.78 8.24 8.12 8.22 230Th 4.7700 0.1826 12.38 12.82 12.70 12.80 232Th 4.0816 0.1601 17.65 18.10 18.07 18.07 218U 8.7751 0.1880 −3.45 −3.42 −3.25 −3.41 222U 9.4781 0.2446 −5.33 −5.36 −5.20 −5.36 224U 8.6281 0.2472 −3.40 −3.11 −3.08 −3.11 226U 7.7011 0.2075 −0.57 −0.24 −0.26 −0.24 228U 6.7991 0.1905 2.75 3.12 3.04 3.11 230U 5.9921 0.1871 6.24 6.74 6.61 6.73 232U 5.4136 0.1688 9.34 9.82 9.71 9.81 234U 4.8576 0.1502 12.89 13.29 13.23 13.27 236U 4.5730 0.1532 14.87 15.29 15.23 15.27 238U 4.2698 0.1374 17.15 17.65 17.66 17.62 230Pu 7.1781 0.2015 2.02 2.45 2.36 2.46 232Pu 6.7161 0.1647 4.00 4.31 4.25 4.31 234Pu 6.3101 0.1517 5.72 6.10 6.05 6.10 236Pu 5.8672 0.1398 7.96 8.27 8.24 8.26 238Pu 5.5932 0.1450 9.44 9.73 9.67 9.72 240Pu 5.2558 0.1293 11.32 11.70 11.68 11.68 242Pu 4.9843 0.1326 13.07 13.42 13.39 13.39 244Pu 4.6656 0.1268 15.41 15.64 15.64 15.60 234Cm 7.3651 0.1943 2.28 2.53 2.43 2.54 236Cm 7.0671 0.1573 3.35 3.67 3.64 3.68 238Cm 6.6701 0.1366 5.31 5.32 5.32 5.32 240Cm 6.3978 0.1373 6.42 6.53 6.51 6.53 242Cm 6.2157 0.1222 7.15 7.38 7.39 7.37 244Cm 5.9016 0.1444 8.76 8.96 8.88 8.94 246Cm 5.4751 0.1421 11.17 11.33 11.25 11.31 248Cm 5.1618 0.1462 13.08 13.25 13.15 13.22 238Cf 8.1331 0.1854 −0.08 0.53 0.51 0.57 240Cf 7.7111 0.1496 1.61 1.98 2.00 2.00 242Cf 7.5171 0.1451 2.53 2.66 2.68 2.68 244Cf 7.3290 0.1527 3.19 3.36 3.33 3.37 246Cf 6.8616 0.1551 5.11 5.26 5.18 5.26 248Cf 6.3613 0.1382 7.46 7.52 7.46 7.52 250Cf 6.1285 0.1358 8.62 8.65 8.59 8.64 252Cf 6.2170 0.1463 7.94 8.17 8.07 8.15 254Cf 5.9261 0.1543 9.22 9.66 9.52 9.63 244Fm 8.5461 0.1656 −0.51 −0.13 −0.09 −0.09 246Fm 8.3791 0.1536 0.22 0.37 0.43 0.41 248Fm 7.9950 0.1637 1.54 1.65 1.63 1.67 250Fm 7.5569 0.1491 3.27 3.23 3.20 3.24 252Fm 7.1541 0.1539 4.96 4.80 4.72 4.81 254Fm 7.3073 0.1350 4.07 4.14 4.13 4.15 256Fm 7.0255 0.1546 5.06 5.28 5.18 5.28 252No 8.5481 0.1581 0.56 0.50 0.53 0.54 254No 8.2261 0.1404 1.75 1.55 1.59 1.58 256No 8.5811 0.1533 0.47 0.33 0.37 0.36 256Rf 8.9261 0.1557 0.33 0.00 0.05 0.06 258Rf 9.1961 0.1737 −0.59 −0.85 −0.82 −0.80 260Sg 9.9001 0.1716 −1.77 −2.16 −2.06 −2.09 266Hs 10.3461 0.1566 −2.41 −2.75 −2.58 −2.66 268Hs 9.7651 0.1711 0.15 −1.21 −1.16 −1.14 270Hs 9.0651 0.1555 0.95 0.85 0.84 0.91 270Ds 11.1151 0.1793 −3.69 −4.06 −3.86 −3.95 282Ds 9.1451 0.1958 2.40 1.15 1.02 1.21 286Cn 9.2351 0.1836 1.48 1.55 1.42 1.62 286Fl 10.3551 0.2085 −0.66 −1.04 −1.10 −0.94 288Fl 10.0751 0.1976 −0.19 −0.29 −0.37 −0.20 290Lv 10.9951 0.2069 −2.05 −2.12 −2.12 −1.99 292Lv 10.7851 0.2016 −1.80 −1.61 −1.63 −1.49 294Og 11.8353 0.2112 −3.15 −3.58 −3.49 −3.43 Table 5. Comparison of experimental
$\alpha$ decay half-lives of even-even nuclei with the calculated ones using our model, UDL, and DZR in logarithmic form. The experimental$\alpha$ decay half-lives are taken from Ref. [79]. The$\alpha$ decay energy and mass excess are taken from the latest evaluated atomic mass table AME2020 [80, 81]. The$\alpha$ decay energy and half-lives are in units of MeV and s, respectively.Nuclide $Q_{\alpha} $ /MeV$P_\alpha$ $\log_{10} T^{{\rm{exp}}}_{1/2}$ $\log_{10} T^{{\rm{cal}}}_{1/2}$ $\log_{10} T_{1/2}^{{\rm{UDL}}}$ $\log_{10} T_{1/2}^{{\rm{DZR}}}$ l 148Eu 4.5071 0.1400 14.70 15.30 14.33 15.11 0 152Ho 4.0421 0.1682 3.12 3.20 3.03 3.11 0 154Ho 5.0941 0.1714 6.56 6.05 5.77 6.00 0 154Tm 4.3461 0.1709 1.17 1.23 1.20 1.17 0 156Tm 5.5951 0.1835 5.12 5.20 5.06 5.22 0 156Lu 4.7901 0.1678 −0.31 −0.09 −0.03 −0.15 0 158Lu 6.1251 0.1842 3.07 3.76 3.73 3.81 0 158Ta 5.0071 0.1946 −1.31 −1.38 −1.17 −1.35 0 162Ta 6.6951 0.1828 3.68 4.27 3.65 4.06 2 160Re 6.2451 0.1727 −2.26 −1.85 −2.28 −2.17 2 162Re 5.0681 0.1977 −0.95 −0.99 −0.72 −0.91 0 168Re 6.7151 0.1655 4.94 5.52 4.35 5.64 4 166Ir 6.3751 0.1965 −1.95 −1.87 −1.54 −1.79 0 168Ir 5.9551 0.1781 −0.64 −0.62 −0.35 −0.55 0 170Ir 5.9851 0.1792 1.24 1.03 1.27 1.13 0 172Ir 5.6931 0.1711 2.34 1.83 1.11 1.71 3 174Ir 7.1851 0.1730 3.17 2.83 2.36 2.63 2 170Au 6.9251 0.1977 −2.58 −2.67 −2.27 −2.58 0 172Au 6.6951 0.1743 −1.55 −1.79 −1.45 −1.72 0 174Au 6.4351 0.1843 −0.81 −1.03 −0.68 −0.93 0 176Au 6.0581 0.1781 0.14 −0.08 0.24 0.02 0 178Au 5.8311 0.1875 1.32 1.40 1.71 1.56 0 180Au 5.5251 0.1625 3.13 3.11 2.66 2.92 2 182Au 5.2341 0.1464 4.06 4.53 4.00 4.31 2 184Au 4.9121 0.1327 5.19 5.41 5.45 5.45 0 186Au 7.0251 0.1316 7.89 7.56 7.16 7.35 1 178Tl 7.7571 0.1934 −0.39 −0.75 −0.99 −0.90 2 186Bi 7.2631 0.1751 −1.83 −2.66 −2.59 −2.86 1 188Bi 6.8621 0.1691 −1.22 −1.08 −1.04 −1.25 1 190Bi 6.3811 0.1620 0.91 0.31 0.31 0.16 1 192Bi 5.9181 0.1567 2.44 2.17 2.12 2.04 1 194Bi 5.2611 0.1475 4.31 4.17 4.05 4.05 1 196Bi 6.2073 0.1401 7.43 7.14 7.28 7.29 0 212Bi 5.6211 0.0786 4.00 3.98 2.51 4.11 5 214Bi 7.6961 0.0815 6.75 6.68 5.15 6.87 5 192At 7.3341 0.1895 −1.94 −2.19 −1.66 −2.04 0 194At 7.1951 0.1860 −0.54 −1.01 −0.50 −0.83 0 196At 6.8891 0.1695 −0.41 −0.55 −0.09 −0.41 0 198At 6.5961 0.1545 0.66 0.58 0.99 0.71 0 200At 6.3541 0.1447 1.92 1.70 2.06 1.82 0 202At 6.0711 0.1309 3.16 2.75 3.04 2.84 0 204At 5.8871 0.1252 4.16 3.97 4.22 4.06 0 206At 5.7511 0.1116 5.31 5.50 5.01 5.25 2 208At 5.6311 0.1022 6.02 5.53 5.65 5.53 0 210At 7.8172 0.0946 7.22 6.81 6.21 6.48 2 212At 8.9880 0.0784 −0.50 −0.99 −2.35 −0.96 5 214At 7.9500 0.1542 −6.25 −5.99 −5.60 −6.24 0 216At 6.8761 0.1501 −3.52 −3.21 −2.81 −3.33 0 218At 6.0531 0.1438 0.11 1.02 0.71 0.71 2 220At 7.8711 0.1376 3.43 3.78 4.07 3.83 0 198Fr 7.6151 0.1864 −1.82 −1.07 −1.45 −1.08 3 200Fr 7.3861 0.1729 −1.32 −1.22 −0.69 −1.05 0 202Fr 7.1701 0.1594 −0.43 −0.44 0.05 −0.29 0 204Fr 6.9231 0.1502 0.26 0.33 0.78 0.46 0 206Fr 6.7851 0.1368 1.26 1.27 1.66 1.38 0 208Fr 6.6701 0.1283 1.82 1.77 2.13 1.85 0 210Fr 6.5291 0.1152 2.43 2.26 2.57 2.30 0 212Fr 8.5891 0.1068 3.44 3.51 3.10 3.23 2 214Fr 9.1742 0.0893 −2.26 −2.53 −3.79 −2.47 5 216Fr 8.0131 0.1610 −6.15 −5.78 −5.32 −5.95 0 218Fr 6.8001 0.1661 −2.85 −2.69 −2.19 −2.69 0 220Fr 7.9531 0.1635 1.44 1.83 1.90 1.70 1 206Ac 7.7281 0.1668 −1.60 −1.56 −0.99 −1.39 0 208Ac 7.5401 0.0903 −1.01 −0.61 −0.32 −0.70 0 212Ac 7.3521 0.1334 −0.05 −0.21 0.25 −0.12 0 214Ac 9.2411 0.1212 0.94 1.13 0.87 0.90 2 216Ac 9.3831 0.1027 −3.36 −3.58 −4.74 −3.47 5 218Ac 8.3481 0.1688 −6.00 −5.65 −5.12 −5.74 0 220Ac 7.1381 0.1710 −1.58 −2.31 −2.41 −2.55 2 222Ac 6.3271 0.1667 0.70 0.97 1.50 1.15 0 224Ac 5.5061 0.1386 5.02 4.72 4.73 4.62 1 226Ac 8.4151 0.1279 9.23 9.12 8.70 9.00 2 212Pa 8.2751 0.1688 −2.24 −2.31 −1.68 −2.14 0 214Pa 8.0991 0.1404 −1.77 −1.84 −1.30 −1.75 0 216Pa 9.7031 0.1392 −0.98 −0.65 −0.78 −0.84 2 220Pa 7.6931 0.1785 −6.07 −5.78 −5.18 −5.82 0 224Pa 6.9871 0.1623 −0.07 0.49 0.42 0.38 2 226Pa 6.2651 0.1372 2.16 2.43 2.91 2.60 0 228Pa 5.4401 0.1264 6.63 6.47 5.91 6.47 3 230Pa 9.3291 0.1274 10.67 10.50 10.09 10.44 2 224Np 8.3351 0.1742 −4.32 −3.59 −3.59 −3.79 2 226Np 7.5431 0.1739 −1.46 −1.54 −0.86 −1.33 0 228Np 6.7811 0.1451 2.17 1.54 1.74 1.49 1 230Np 5.0081 0.1328 3.96 5.06 4.62 5.11 3 236Np 6.7951 0.1049 15.47 14.83 13.72 15.07 4 234Am 6.2551 0.1153 5.55 6.42 5.41 7.04 5 236Am 5.4691 0.1054 6.73 7.43 7.81 7.65 0 240Am 8.1051 0.1006 10.98 11.70 11.93 11.92 0 234Bk 8.2651 0.1480 1.40 1.36 1.40 1.37 2 240Es 8.1551 0.1308 0.93 1.29 1.61 1.32 1 242Es 7.9451 0.1057 1.49 1.72 1.94 1.66 1 244Es 7.4951 0.1022 2.84 2.43 2.63 2.36 1 246Es 7.6451 0.1068 3.66 3.66 4.24 3.90 0 246Es 7.1611 0.1068 3.66 3.47 3.68 3.44 1 248Es 6.7351 0.1087 5.76 5.65 5.55 5.63 2 252Es 8.9451 0.0958 7.72 7.48 7.28 7.42 2 244Md 8.8951 0.1347 −0.44 −0.16 0.22 −0.14 1 246Md 8.1551 0.1170 −0.04 0.03 0.34 −0.02 1 250Md 7.7451 0.1139 2.88 2.64 2.66 2.62 2 256Md 7.2709 0.0951 4.70 4.38 4.03 4.40 3 258Md 9.1651 0.1081 6.65 5.63 5.86 5.67 1 252Lr 8.8251 0.1096 −0.42 −0.49 0.23 −0.28 0 254Lr 8.8551 0.1102 1.22 1.44 1.23 1.50 3 256Lr 9.3351 0.0992 1.52 0.81 1.10 0.74 1 256Db 9.3351 0.1152 0.38 0.32 0.44 0.31 2 Table 7. Same as Table 6 but for odd-odd nuclei.
Nuclide $Q_{\alpha} $ /MeV$P_\alpha$ $\log_{10} T^{{\rm{exp}}}_{1/2}$ $\log_{10} T^{{\rm{cal}}}_{1/2}$ $\log_{10} T_{1/2}^{{\rm{UDL}}}$ $\log_{10} T_{1/2}^{{\rm{DZR}}}$ l 107Te 4.0051 0.1721 −2.34 −2.17 −2.65 −2.97 0 109I 3.9171 0.2638 −0.19 −0.66 −1.60 −1.12 2 113I 2.7061 0.2190 7.30 7.17 6.91 7.24 0 111Xe 3.7151 0.1794 0.85 0.52 0.15 −0.19 0 145Pm 2.3221 0.1659 17.30 17.68 17.51 17.77 0 147Sm 2.3114 0.1588 18.53 18.69 18.52 17.77 0 147Eu 2.9912 0.1723 10.96 11.48 11.41 11.53 0 151Eu 1.9640 0.1789 26.16 25.81 24.97 25.67 2 149Gd 3.0995 0.1581 11.27 11.18 11.10 10.52 0 151Gd 2.6522 0.1611 15.63 15.86 15.78 15.09 0 149Tb 4.0781 0.1835 4.95 5.00 4.29 4.64 2 151Tb 3.4957 0.1799 8.82 9.06 8.38 8.79 2 151Dy 4.1800 0.1796 4.28 4.26 4.24 3.83 0 153Dy 3.5591 0.1864 8.39 8.49 8.53 8.02 0 151Ho 4.6441 0.2212 2.20 2.12 2.18 2.11 0 153Ho 4.0161 0.2207 5.37 5.77 5.89 5.87 0 153Er 4.8021 0.1777 1.84 1.91 1.89 1.56 0 155Er 4.1181 0.1946 6.15 5.73 5.82 5.39 0 153Tm 5.2481 0.2314 0.21 0.19 0.27 0.17 0 155Tm 4.5721 0.2435 3.41 3.50 3.68 3.62 0 157Tm 3.8091 0.2352 7.46 8.37 8.58 8.58 0 155Yb 5.3381 0.1704 0.30 0.39 0.36 0.09 0 155Lu 5.8021 0.2359 −1.12 −1.20 −1.12 −1.24 0 157Hf 5.8751 0.1918 −0.91 −0.96 −0.95 −1.15 0 159Hf 5.2251 0.1778 1.16 1.83 1.89 1.61 0 161Hf 4.6791 0.1871 3.79 4.59 4.72 4.36 0 157Ta 6.2751 0.2821 −1.98 −2.16 −2.01 −2.14 0 159Ta 5.6601 0.2504 0.48 0.24 0.43 0.32 0 159W 6.4551 0.1658 −2.09 −2.16 −2.23 −2.37 0 161W 5.9251 0.1929 −0.25 −0.29 −0.22 −0.42 0 163W 5.5181 0.1747 1.27 1.43 1.51 1.26 0 167W 4.7511 0.1706 4.69 5.22 5.37 5.00 0 163Re 6.0121 0.2520 0.08 −0.32 −0.11 −0.25 0 165Re 5.6951 0.2537 1.03 0.94 1.20 1.07 0 169Re 5.0141 0.2280 5.18 5.12 4.45 5.09 3 163Os 6.6651 0.1625 −2.24 −2.08 −2.12 −2.24 0 165Os 6.3351 0.1892 −1.10 −1.01 −0.94 −1.10 0 167Os 5.9851 0.1750 0.21 0.33 0.42 0.22 0 169Os 5.7131 0.1778 1.40 1.43 1.56 1.33 0 171Os 5.3711 0.1731 2.66 2.97 3.13 2.84 0 173Os 5.0551 0.1765 3.73 4.51 4.72 4.38 0 167Ir 6.5051 0.2598 −1.17 −1.36 −1.14 −1.29 0 169Ir 6.1411 0.2543 −0.18 −0.02 0.24 0.09 0 171Ir 5.8651 0.2397 1.31 1.09 1.37 1.22 0 173Ir 5.5411 0.2365 2.41 2.50 2.81 2.67 0 175Ir 5.4301 0.2195 3.02 3.69 3.30 3.54 2 177Ir 5.0821 0.1885 4.69 4.80 5.06 4.92 0 167Pt 7.1651 0.1611 −3.04 −2.93 −2.99 −3.05 0 169Pt 6.8651 0.1883 −2.16 −2.07 −2.01 −2.11 0 171Pt 6.6051 0.1694 −1.28 −1.17 −1.11 −1.24 0 173Pt 6.3581 0.1808 −0.35 −0.33 −0.21 −0.37 0 177Pt 5.6431 0.1888 2.24 2.54 2.78 2.52 0 179Pt 5.4121 0.1658 3.94 4.34 3.86 3.84 2 181Pt 5.1501 0.1521 4.85 4.98 5.18 4.84 0 183Pt 4.8221 0.1405 6.61 6.80 7.00 6.60 0 185Pt 4.2801 0.1414 7.93 10.24 10.48 9.97 0 173Au 6.8361 0.2665 −1.53 −1.78 −1.52 −1.70 0 175Au 6.5851 0.2543 −0.65 −0.91 −0.64 −0.81 0 177Au 6.2971 0.2617 0.57 0.12 0.44 0.27 0 179Au 5.9811 0.2240 1.51 1.43 1.73 1.56 0 181Au 5.7511 0.1988 2.70 2.45 2.72 2.56 0 183Au 5.4661 0.1768 3.89 3.79 4.06 3.89 0 185Au 5.1800 0.1725 4.98 5.22 5.51 5.34 0 173Hg 7.3751 0.1887 −3.10 −2.95 −2.90 −2.94 0 175Hg 7.0751 0.1720 −2.00 −2.00 −1.94 −2.02 0 177Hg 6.7351 0.1878 −0.93 −0.24 −0.77 −0.61 2 179Hg 6.3511 0.1845 0.14 0.48 0.68 0.51 0 181Hg 6.2841 0.1915 1.12 1.37 0.91 1.01 2 183Hg 6.0381 0.1851 1.90 1.67 1.91 1.70 0 185Hg 5.7721 0.1792 2.91 2.81 3.07 2.82 0 177Tl 7.0671 0.2827 −1.61 −1.81 −1.50 −1.68 0 179Tl 6.7051 0.2677 −0.14 −0.57 −0.23 −0.40 0 181Tl 6.3221 0.2671 1.52 0.85 1.24 1.07 0 181Pb 7.2451 0.1716 −1.41 −1.15 −1.73 −1.51 2 183Pb 6.9281 0.1654 −0.27 −0.11 −0.66 −0.48 2 185Pb 6.6951 0.1686 1.26 0.68 0.17 0.32 2 187Pb 6.3931 0.1663 2.20 1.80 1.33 1.44 2 189Pb 5.9151 0.1622 3.97 3.78 3.37 3.41 2 187Bi 7.7791 0.2413 −1.43 −1.81 −3.14 −1.48 5 189Bi 7.2681 0.2261 −0.16 −0.24 −1.51 0.15 5 191Bi 6.4471 0.2144 1.39 1.17 1.52 1.32 0 193Bi 6.0211 0.1986 3.26 2.95 3.32 3.12 0 195Bi 5.5351 0.1858 5.78 5.23 5.64 5.44 0 209Bi 3.1373 0.0938 26.80 25.45 24.12 25.85 5 211Bi 6.7501 0.0903 2.11 1.56 −0.02 1.57 5 213Bi 5.9881 0.0924 5.12 4.60 3.14 4.73 5 189Po 7.6941 0.1906 −2.46 −1.95 −2.48 −2.22 2 191Po 7.4931 0.1849 −1.66 −2.03 −1.86 −1.90 0 193Po 7.0941 0.1840 −0.40 −0.75 −0.53 −0.61 0 195Po 6.7491 0.1699 0.69 0.48 0.72 0.59 0 197Po 6.4111 0.1577 1.80 1.79 2.05 1.87 0 199Po 6.0741 0.1498 3.64 3.20 3.48 3.25 0 201Po 5.7991 0.1368 4.92 4.46 4.74 4.46 0 203Po 5.4961 0.1329 6.29 6.62 6.24 6.19 2 205Po 5.3251 0.1198 7.19 6.85 7.13 6.76 0 207Po 5.2151 0.1111 7.99 7.46 7.71 7.32 0 209Po 4.9770 0.1037 9.59 8.84 9.08 8.65 0 211Po 7.5946 0.0884 −0.29 −0.85 −2.54 −1.19 5 213Po 8.5357 0.1804 −5.43 −5.35 −5.37 −5.33 0 215Po 7.5263 0.1775 −2.75 −2.53 −2.39 −2.45 0 217Po 6.6621 0.1726 0.20 0.42 0.69 0.53 0 219Po 5.9161 0.1673 3.34 3.51 3.88 3.60 0 191At 7.7141 0.1984 −2.68 −2.35 −2.15 −2.37 0 193At 7.3891 0.2661 −1.54 −1.49 −1.11 −1.33 0 195At 7.1021 0.2380 −0.54 −0.51 −0.14 −0.36 0 197At 7.1051 0.2142 −0.39 −0.51 −0.18 −0.41 0 199At 6.7781 0.1974 0.89 0.67 1.01 0.78 0 201At 6.4731 0.1748 2.07 1.88 2.20 1.97 0 203At 6.2101 0.1656 3.15 2.96 3.30 3.07 0 205At 6.0191 0.1456 4.20 3.83 4.14 3.90 0 207At 5.8731 0.1318 4.81 4.51 4.79 4.56 0 209At 5.7571 0.1209 5.69 5.07 5.33 5.09 0 211At 5.9825 0.0938 4.79 4.08 4.21 3.95 0 213At 9.2537 0.1871 −6.90 −6.73 −6.84 −7.16 0 215At 8.1771 0.1779 −4.43 −4.06 −3.99 −4.30 0 217At 7.2021 0.1679 −1.49 −1.08 −0.87 −1.17 0 219At 6.3421 0.1582 1.78 2.14 2.46 2.17 0 195Rn 7.6941 0.1830 −2.15 −1.93 −1.73 −1.75 0 197Rn 7.4101 0.1814 −1.27 −1.05 −0.81 −0.86 0 199Rn 7.1321 0.1706 −0.23 −0.12 0.14 0.05 0 203Rn 6.6301 0.1527 1.82 1.72 2.00 1.85 0 205Rn 6.3861 0.1407 2.84 3.39 2.99 3.08 2 207Rn 6.2511 0.1340 3.42 3.27 3.55 3.33 0 209Rn 6.1551 0.1219 4.00 3.70 3.95 3.71 0 211Rn 5.9661 0.1142 5.28 5.23 4.79 4.81 2 213Rn 8.2451 0.0978 −1.71 −2.06 −3.75 −2.32 5 215Rn 8.8386 0.1821 −5.64 −5.43 −5.44 −5.36 0 217Rn 7.8881 0.1921 −3.23 −2.92 −2.73 −2.75 0 219Rn 6.9462 0.1932 0.60 0.82 0.49 0.64 2 221Rn 6.1631 0.1851 3.84 3.95 3.71 3.75 2 197Fr 7.8841 0.2692 −2.64 −2.32 −1.95 −2.18 0 199Fr 7.8161 0.2474 −2.18 −2.11 −1.77 −2.00 0 201Fr 7.5191 0.2245 −1.20 −1.17 −0.82 −1.06 0 203Fr 7.2741 0.2080 −0.26 −0.35 0.00 −0.24 0 205Fr 7.0541 0.1858 0.60 0.44 0.78 0.53 0 207Fr 6.8891 0.1724 1.19 1.04 1.37 1.12 0 209Fr 6.7781 0.1527 1.75 1.48 1.77 1.52 0 211Fr 6.6621 0.1400 2.33 1.93 2.21 1.95 0 213Fr 6.9051 0.1096 1.54 1.07 1.21 0.94 0 215Fr 9.5403 0.2012 −7.05 −6.76 −6.82 −7.13 0 217Fr 8.4701 0.2040 −4.66 −4.21 −4.06 −4.37 0 219Fr 7.4491 0.1976 −1.65 −1.20 −0.89 −1.19 0 221Fr 6.4571 0.1823 2.46 3.16 2.90 2.99 2 223Fr 5.5614 0.1799 7.34 7.88 7.17 8.14 4 203Ra 7.7361 0.1746 −1.44 −1.39 −1.15 −1.16 0 205Ra 7.4861 0.1646 −0.66 −0.59 −0.34 −0.38 0 207Ra 7.2691 0.1574 0.21 0.81 0.40 0.61 2 209Ra 7.1431 0.1418 0.67 0.59 0.83 0.74 0 211Ra 7.0421 0.1372 1.10 0.93 1.17 1.07 0 213Ra 6.8621 0.1263 2.27 2.29 1.84 1.99 2 215Ra 8.8621 0.1092 −2.78 −3.04 −4.72 −3.22 5 217Ra 9.1611 0.1850 −5.71 −5.56 −5.54 −5.43 0 219Ra 8.1381 0.1911 −2.05 −2.24 −2.71 −2.41 2 221Ra 6.8801 0.1899 1.40 1.90 1.64 1.78 2 223Ra 5.9790 0.1608 5.99 5.77 5.55 5.55 2 205Ac 7.8061 0.0991 −1.10 −0.04 −0.99 −0.48 3 207Ac 7.8491 0.2218 −1.51 −1.53 −1.16 −1.41 0 209Ac 7.7251 0.1938 −1.03 −1.11 −0.79 −1.04 0 211Ac 7.5641 0.1820 −0.67 −0.60 −0.27 −0.53 0 213Ac 7.4981 0.1637 −0.13 −0.36 −0.08 −0.34 0 215Ac 7.7461 0.1301 −0.77 −1.11 −0.96 −1.24 0 217Ac 9.8311 0.2172 −7.16 −6.81 −6.81 −7.12 0 219Ac 8.8271 0.2166 −5.03 −4.49 −4.30 −4.60 0 221Ac 7.7901 0.2087 −1.28 −1.56 −1.21 −1.51 0 223Ac 6.7831 0.1695 2.10 2.73 2.46 2.54 2 225Ac 5.9351 0.1535 5.93 6.45 6.25 6.34 2 227Ac 5.0423 0.1491 10.70 10.69 11.24 10.97 0 211Th 7.9451 0.1662 −1.32 −1.38 −1.12 −1.12 0 213Th 7.8371 0.1401 −0.84 −1.00 −0.80 −0.81 0 215Th 7.6641 0.1411 0.13 0.20 −0.25 −0.00 2 217Th 9.4351 0.1215 −3.61 −3.82 −5.49 −3.93 5 219Th 9.5031 0.1892 −5.99 −5.73 −5.69 −5.53 0 221Th 8.6251 0.1869 −2.76 −2.88 −3.38 −3.02 2 223Th 7.5661 0.1798 −0.22 0.28 −0.05 0.19 2 225Th 6.9211 0.1555 2.77 2.63 2.33 2.48 2 227Th 6.1467 0.1457 6.21 5.91 5.69 5.71 2 229Th 5.1676 0.1488 11.40 11.10 10.99 10.82 2 211Pa 8.4751 0.2424 −2.22 −2.73 −2.36 −2.62 0 213Pa 8.3851 0.1981 −2.13 −2.42 −2.13 −2.39 0 215Pa 8.2351 0.1934 −1.85 −2.01 −1.70 −1.97 0 217Pa 8.4891 0.1545 −2.42 −2.68 −2.51 −2.78 0 219Pa 10.1241 0.2367 −7.25 −6.86 −6.81 −7.10 0 221Pa 9.2431 0.2245 −5.23 −4.88 −4.68 −4.98 0 223Pa 8.3451 0.2099 −2.28 −2.50 −2.17 −2.47 0 225Pa 7.4051 0.1739 0.23 1.22 0.94 1.02 2 227Pa 6.5801 0.1561 3.43 3.73 4.20 3.91 0 229Pa 5.8351 0.1548 7.43 7.57 7.73 7.57 1 231Pa 5.1499 0.1520 12.01 11.03 11.63 11.35 0 219U 9.9501 0.1401 −4.22 −4.42 −6.04 −4.43 5 221U 9.8891 0.1800 −6.18 −5.95 −5.93 −5.73 0 223U 9.1651 0.1833 −4.19 −3.60 −4.13 −3.71 2 225U 8.0071 0.1862 −1.21 −0.40 −0.72 −0.43 2 227U 7.2351 0.1586 1.82 2.26 1.99 2.18 2 229U 6.4761 0.1485 4.24 4.63 5.11 4.90 0 231U 5.5763 0.1481 9.95 9.73 9.63 9.54 2 233U 4.9087 0.1348 12.70 13.16 13.76 13.23 0 223Np 9.6551 0.2334 −5.60 −5.23 −5.03 −5.32 0 225Np 8.8251 0.2306 −2.22 −3.18 −2.83 −3.12 0 227Np 7.8151 0.1888 −0.29 0.85 0.32 0.78 3 229Np 7.0151 0.1691 2.55 3.17 3.28 3.11 1 231Np 6.3651 0.1631 5.14 5.90 6.08 5.92 1 233Np 5.6281 0.1439 8.49 9.25 9.85 9.55 0 235Np 5.1938 0.1265 12.12 12.23 12.42 12.25 1 237Np 4.9573 0.1272 13.83 13.74 13.95 13.77 1 229Pu 7.5931 0.1707 2.26 1.73 1.51 1.74 2 231Pu 6.8391 0.1530 3.58 3.93 4.44 4.29 0 233Pu 6.4141 0.1271 6.00 6.50 6.31 6.37 2 235Pu 5.9511 0.1182 7.72 8.07 8.58 8.26 0 239Pu 5.2444 0.1161 11.88 12.03 12.60 12.13 0 241Pu 5.1401 0.1053 13.26 13.38 13.24 13.02 2 229Am 8.1351 0.2148 0.26 0.23 0.05 0.14 2 233Am 7.0651 0.1485 3.62 3.82 3.93 3.76 1 235Am 6.5751 0.1334 5.18 5.89 6.02 5.85 1 237Am 6.1951 0.1204 7.24 7.68 7.81 7.63 1 239Am 5.9225 0.1230 8.63 9.01 9.18 9.00 1 241Am 5.6378 0.1082 10.14 10.59 10.73 10.54 1 243Am 5.4391 0.1098 11.37 11.71 11.88 11.68 1 233Cm 7.4751 0.1544 2.11 2.27 2.76 2.70 0 235Cm 7.2761 0.1467 3.99 3.68 3.50 3.69 2 241Cm 6.1852 0.1074 8.45 8.75 8.30 8.58 3 243Cm 6.1688 0.0972 8.96 8.56 8.35 8.34 2 245Cm 5.6245 0.1158 11.42 11.37 11.28 11.16 2 247Cm 5.3535 0.1159 14.69 12.67 12.90 12.52 1 245Bk 6.4546 0.1228 8.55 7.52 7.40 7.45 2 247Bk 5.8901 0.1190 10.64 10.34 10.27 10.32 2 249Bk 5.5210 0.1209 12.29 12.40 12.38 12.42 2 239Cf 7.7651 0.1369 1.63 1.99 2.46 2.43 0 241Cf 7.4551 0.1128 2.97 3.17 3.60 3.53 0 243Cf 7.4151 0.1106 3.66 4.26 3.73 4.21 3 245Cf 7.2585 0.1180 3.88 3.84 4.32 4.21 0 247Cf 6.5022 0.1209 7.50 7.73 7.63 7.68 2 249Cf 6.2933 0.1102 10.04 8.45 8.63 8.44 1 251Cf 6.1771 0.1104 10.45 10.13 9.19 10.29 5 253Cf 6.0776 0.1201 8.69 9.05 9.68 9.36 0 241Es 8.2551 0.1402 0.71 0.69 1.12 0.82 0 243Es 8.0751 0.1327 1.55 1.27 1.71 1.40 0 245Es 7.8651 0.1367 2.13 1.94 2.43 2.11 0 247Es 7.4431 0.1371 3.59 3.45 4.00 3.68 0 249Es 6.9413 0.1199 6.03 6.47 6.06 6.48 3 251Es 6.5971 0.1153 7.36 7.02 7.60 7.27 0 253Es 6.7393 0.1224 6.25 6.31 6.91 6.56 0 255Es 6.4001 0.1282 7.63 7.84 8.50 8.15 0 243Fm 8.6951 0.1398 −0.60 0.05 0.06 0.24 1 245Fm 8.4351 0.1230 0.62 1.45 0.87 1.49 3 247Fm 8.2551 0.1154 1.69 2.30 1.44 2.41 4 251Fm 7.4251 0.1148 6.03 4.34 4.45 4.46 1 253Fm 7.0529 0.1219 6.33 6.92 5.98 7.23 5 257Fm 6.8631 0.1253 6.94 6.81 6.75 6.85 2 245Md 9.0151 0.1583 −0.42 −0.32 −0.57 −0.50 2 247Md 8.7651 0.1426 0.08 0.14 0.17 −0.02 1 249Md 8.4351 0.1490 1.53 1.39 1.21 1.27 2 251Md 7.9641 0.1337 3.40 2.70 2.83 2.63 1 253Md 7.5651 0.1351 5.01 4.12 4.31 4.10 1 255Md 7.9051 0.1164 4.36 3.19 2.98 3.02 2 257Md 7.5571 0.1313 5.11 4.09 4.28 4.06 1 251No 8.7551 0.1163 −0.02 0.16 0.54 0.64 0 253No 8.4151 0.1186 2.23 1.58 1.63 1.78 1 255No 8.2281 0.1081 2.84 2.50 2.24 2.55 2 257No 8.4766 0.1192 1.46 1.61 1.36 1.70 2 259No 7.8541 0.1224 3.66 3.68 3.54 3.79 2 253Lr 8.9151 0.1460 −0.15 −0.08 0.40 0.08 0 255Lr 8.5021 0.1273 1.49 1.23 1.71 1.39 0 257Lr 9.0151 0.1364 0.78 0.83 0.02 0.94 4 259Lr 8.5751 0.1360 0.90 0.90 1.40 1.07 0 255Rf 9.0551 0.1210 0.49 0.31 0.32 0.56 1 257Rf 8.9141 0.1170 0.75 1.00 0.74 1.14 2 259Rf 9.1331 0.1319 0.49 0.27 0.02 0.45 2 261Rf 8.6481 0.1252 1.06 1.05 1.54 1.62 0 257Db 9.2051 0.1455 0.39 0.12 0.22 0.03 1 259Db 9.5671 0.1599 −0.29 −0.97 −0.89 −1.08 1 263Db 8.8351 0.1390 1.89 2.28 1.29 2.83 5 261Sg 9.7141 0.1262 −0.73 −0.66 −0.96 −0.46 2 263Sg 9.4051 0.1275 0.03 −0.53 −0.09 0.09 0 265Sg 9.0451 0.1244 1.26 2.02 0.99 2.52 5 261Bh 10.5051 0.1648 −1.89 −2.16 −2.73 −2.30 3 265Hs 10.4701 0.1278 −2.71 −2.67 −2.35 −2.04 0 269Hs 9.2751 0.1264 1.18 0.85 0.98 1.24 1 Table 6. Same as Table 5 but for odd-A nuclei. The column of the l term that appears for the first time is the angular momentum carried away by an
$\alpha$ particle.For a more intuitive comparison of the results, Figs. 2−4 plot the differences between the experimental
$ \alpha $ decay half-lives and those calculated using our model, UDL, and DZR in logarithmic form. It is evident that the differences calculated by our model are more concentrated near zero, indicating that our calculation results are closer to the experimental values. Except for a few nuclei, the differences for all 559 nuclei fall between –0.5 and 0.5. For 185Pt, 268Hs, and 282Ds, it may be caused by deformation effects [82]. Meanwhile, for 209Bi, 210Po, 245Bk, 247Cm, 249Cf, 251Fm, 255Md, 257Md, and 258Md, the larger errors are likely influenced by the shell effects at N = 126 and N = 152 [83].
Figure 2. (color online) Deviations between the experimental
$\alpha$ decay half-lives and the calculated ones obtained using our model, UDL, and DZR in logarithmic form.
Figure 3. (color online) Same as Fig. 2 but for odd-A nuclei.

Figure 4. (color online) Same as Fig. 2 but for odd-odd nuclei.
As is known, the half-lives of
$ \alpha $ decay show a very strong sensitivity to the$ \alpha $ decay energy$ Q_\alpha $ . Therefore, selecting a precise$ Q_\alpha $ becomes one of the key problems in prediction. In 2016, Sobiczewski et al. systematically compared nine different mass models: Möller et al. (FRDM) [84], Duflo and Zuker (DZ) [85], Nayak and Satpathy (INM) [86], Wang and Liu (WS3+) [87], Wang et al. (WS4+) [88, 89], Muntian et al. (HN) [90, 91], Kuzmina et al. (TCSM) [92], Goriely et al. (HFB31) [93], and Liran et al. (SE) [94] and came to the conclusion that the WS3+ model is the most accurate in reproducing the experimental$ Q_\alpha $ of superheavy nuclei. In this work, we use our model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120. The predicted results are listed in Table 8. In this table, the first to fourth columns represent the parent nucleus,$ \alpha $ decay energy$ Q_\alpha $ calculated using WS3+, angular momentum l carried away by the$ \alpha $ particle, and$ \alpha $ preformation factors calculated by the CFM, respectively. The last three,$ \log_{10} T^{{\rm{cal}}}_{1/2} $ ,$ \log_{10} T^{{\rm{UDL}}}_{1/2} $ ,$ \log_{10} T^{{\rm{DZR}}}_{1/2} $ , represent the predicted$ \alpha $ decay half-lives in logarithmic form calculated by our model, UDL, and DZR, respectively. From this table, we can clearly see that the three predictions are quite close to each other. To visually illustrate their relationship, the logarithmic form of$ \alpha $ decay half-lives and the$ Q_\alpha $ values calculated by the WS3+ mass model with Z = 119 and 120 versus the neutron numbers of the daughter nucleus$ N_d $ , as well as the curve of the relationship between the$ \alpha $ decay preformation factors and neutron number of the parent nucleus N, are plotted in Figs. 5−7, respectively. From Fig 5, it can be seen that the trends of the$ \alpha $ decay half-lives for the isotopic chains with proton numbers Z = 119 and 120 predicted by our model, UDL, and DZR are consistent, and our predicted results are close to those of UDL. Furthermore, as shown in Fig. 5, for the isotope chains with Z = 119 and 120, when the neutron number of the daughter nucleus$ N_d $ is less than 176, the half-lives of$ \alpha $ decay exhibit a slow upward trend, followed by a gradual decrease to a minimum value at$ N_d $ = 178. From$ N_d $ = 178 to$ N_d $ = 182, it keeps a steady change. Then, it suddenly drops to the lowest point at$ N_d $ = 184, after which an upward trend appears again. A similar phenomenon can also be observed on$ Q_\alpha $ in Fig. 6. In addition, Fig. 7 clearly shows that the$ \alpha $ decay preformation factors of even-even nuclei with Z = 120, odd-A nuclei with Z = 119, and odd-odd nuclei with Z = 119 show a trend of first decreasing and then increasing near the neutron number N = 184 of the parent nuclei. However, this variation trend is not obvious in odd-A nuclei with Z = 120. When the neutron number is closer to the neutron magic number, the$ \alpha $ decay preformation factor is smaller, while it increases as the neutron number deviates further from this magic shell closure [95]. Moreover, during$ \alpha $ decay, when the neutron or proton numbers of the corresponding daughter nucleus are magic numbers, the half-life reaches its minimum value [96, 97]. When the neutron number exceeds the neutron magic number by two nucleons, the parent nucleus tends to become stable by emitting an$ \alpha $ particle. In this case, the half-life will reach its minimum value. The depth of the minimum value depends on the stability of the daughter nucleus, meaning that the more stable nucleus corresponds to a deeper minimum value. From the above content, we can conclude that N = 184 is the possible neutron magic number, while N = 178 can be considered the neutron submagic number [97].Nuclide $ Q_{\alpha} $ l $P_\alpha$ $\log_{10} T_{1/2}^{{\rm{cal}}}$ $\log_{10} T_{1/2}^{{\rm{UDL}}}$ $\log_{10} T_{1/2}^{{\rm{DZR}}}$ Nuclei with Z=119 284119 13.7747 4 0.2181 −5.44 −6.38 −5.41 285119 13.6461 2 0.2940 −5.93 −6.15 −5.65 286119 13.4606 2 0.1831 −5.38 −5.80 −5.72 287119 13.2830 2 0.2852 −5.31 −5.47 −4.97 288119 13.1697 2 0.1838 −4.87 −5.25 −5.18 289119 13.0764 2 0.2539 −4.91 −5.08 −4.58 290119 12.9211 2 0.1679 −4.38 −4.77 −4.71 291119 12.8677 2 0.2525 −4.54 −4.68 −4.18 292119 12.7053 2 0.1706 −3.99 −4.35 −4.29 293119 12.5103 2 0.2395 −3.85 −3.94 −3.45 294119 12.5217 2 0.1672 −3.64 −3.98 −3.93 295119 12.5701 2 0.2196 −3.96 −4.10 −3.61 296119 12.3096 2 0.1553 −3.19 −3.54 −3.50 297119 12.3025 2 0.1922 −3.39 −3.54 −3.05 298119 12.5862 2 0.1416 −3.75 −4.18 −4.14 299119 12.7275 2 0.2167 −4.33 −4.50 −4.03 300119 12.5259 2 0.1596 −3.70 −4.08 −4.05 301119 12.3748 0 0.2040 −4.31 −3.76 −3.66 302119 12.3960 0 0.1540 −4.11 −3.83 −4.17 303119 12.3691 2 0.2036 −3.64 −3.78 −3.31 304119 12.8958 1 0.1608 −4.78 −4.94 −5.16 305119 13.4495 2 0.2078 −5.73 −6.08 −5.62 306119 13.2476 0 0.1632 −5.86 −5.69 −6.04 307119 12.8167 0 0.2162 −5.30 −4.82 −4.73 308119 12.0652 0 0.1688 −3.52 −3.17 −3.53 309119 11.3386 3 0.2282 −1.24 −1.42 −0.57 310119 10.8335 3 0.1829 0.29 −0.10 0.27 311119 10.6003 0 0.1697 −0.26 0.53 0.63 312119 10.4397 2 0.1386 1.17 0.97 0.95 313119 9.4978 2 0.1562 3.61 3.87 4.36 314119 9.1165 1 0.1286 4.98 5.16 4.87 315119 9.3054 1 0.1420 3.95 4.49 4.72 316119 8.7705 2 0.1192 6.50 6.39 6.33 317119 9.2532 3 0.1826 4.55 4.64 5.49 318119 9.1841 0 0.1549 4.23 4.86 4.44 319119 8.4849 6 0.1484 8.17 7.44 10.18 Nuclei with Z=120 287120 13.9149 4 0.1680 −5.36 −6.39 −4.79 288120 13.7471 0 0.2526 −6.59 −6.87 −6.67 289120 13.6763 0 0.1661 −6.22 −5.97 −5.32 290120 13.6305 0 0.2470 −6.41 −6.69 −6.49 291120 13.4054 2 0.1639 −5.08 −5.47 −4.57 292120 13.3084 0 0.2505 −5.88 −6.09 −5.90 293120 13.2366 2 0.1701 −4.82 −5.16 −4.27 294120 13.0718 0 0.2382 −5.45 −5.65 −5.47 295120 13.0989 2 0.1648 −4.58 −4.91 −4.03 296120 13.1873 0 0.2326 −5.69 −5.92 −5.74 297120 13.0230 0 0.1621 −5.14 −4.78 −4.20 298120 12.9002 0 0.2271 −5.17 −5.37 −5.19 299120 13.1851 0 0.1633 −5.48 −5.15 −4.55 300120 13.2871 0 0.2420 −5.95 −6.19 −6.01 301120 13.0349 2 0.1736 −4.57 −4.87 −4.00 302120 12.8782 0 0.2369 −5.21 −5.39 −5.22 303120 12.7949 2 0.1737 −4.14 −4.40 −3.55 304120 12.7451 0 0.2371 −4.99 −5.14 −4.98 305120 13.2712 2 0.1827 −5.09 −5.42 −4.53 306120 13.8225 0 0.2446 −6.98 −7.31 −7.14 307120 13.5776 4 0.1861 −5.11 −6.06 −4.49 308120 13.0359 0 0.2652 −5.65 −5.81 −5.65 309120 12.1724 0 0.1994 −3.71 −3.10 −2.60 310120 11.4753 0 0.2312 −2.38 −2.34 −2.20 311120 11.1018 2 0.1802 −0.57 −0.49 0.18 312120 11.0535 0 0.2029 −1.35 −1.29 −1.17 313120 10.9229 2 0.1603 −0.10 −0.04 0.61 314120 9.9714 0 0.2273 1.47 1.73 1.83 315120 10.1487 0 0.1807 1.23 2.15 2.42 316120 9.9651 0 0.1873 1.54 1.72 1.81 317120 9.9639 3 0.1513 2.77 2.69 3.50 318120 9.9875 0 0.1785 1.47 1.62 1.71 319120 9.8887 3 0.1454 2.98 2.90 3.70 320120 9.7100 0 0.1861 2.25 2.45 2.53 Table 8. Predicted results of the
$\alpha$ decay half-lives in logarithmic form for 70 even-even, odd-even, and odd-odd nuclei with Z = 119 and 120 using our model, UDL, and DZR. The$\alpha$ decay energy and half-lives are in units of MeV and s, respectively. The mass excesses are taken from the WS3+ mass model [87]. The spin and parity values of these nuclei are taken from Ref. [98].
Figure 5. (color online) Predicted
$\alpha$ decay half-lives for the even-even, odd-even, and odd-odd nuclei with Z = 119 and 120 are presented in logarithmic form using our model, UDL, and DZR. -
In summary, based on the WKB theory, considering the
$ \alpha $ decay preformation factors$ P_\alpha $ , we systematically investigate the$ \alpha $ decay half-lives of 559 nuclei, including 177 even-even, 277 odd-A, and 105 odd-odd nuclei. The$ \alpha $ decay preformation factors$ P_\alpha $ are calculated using the CFM. The assault frequency$ \nu $ is analytically parameterized using experimental$ \alpha $ decay energies and charge radii of the parent nucleus. For all 559 nuclei taken from NUBASE2020, the standard deviation calculated by our model is 0.408. In addition, we extend this model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120 and compare the predicted results with those calculated by UDL and DZR. The results predicted by these three formulas are consistent in trend, indicating that our model has a certain reliability. The predicted$ \alpha $ decay energies and half-lives for isotopes with Z = 119 and 120 exhibit similar behavior at N = 178 and N = 184. Besides, the predicted$ \alpha $ decay preformation factors for isotopes with Z = 119 and 120 exhibit similar phenomena at N = 184. These indicate that both 178 and 184 are possible neutron magic and submagic numbers, respectively. The results of this work can provide some information for future experimental studies, such as the synthesis of elements with Z = 119 and 120 and will also prompt inquiries about the nuclear structure. -
In summary, based on the WKB theory, considering the
$ \alpha $ decay preformation factors$ P_\alpha $ , we systematically investigate the$ \alpha $ decay half-lives of 559 nuclei, including 177 even-even, 277 odd-A, and 105 odd-odd nuclei. The$ \alpha $ decay preformation factors$ P_\alpha $ are calculated using the CFM. The assault frequency$ \nu $ is analytically parameterized using experimental$ \alpha $ decay energies and charge radii of the parent nucleus. For all 559 nuclei taken from NUBASE2020, the standard deviation calculated by our model is 0.408. In addition, we extend this model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120 and compare the predicted results with those calculated by UDL and DZR. The results predicted by these three formulas are consistent in trend, indicating that our model has a certain reliability. The predicted$ \alpha $ decay energies and half-lives for isotopes with Z = 119 and 120 exhibit similar behavior at N = 178 and N = 184. Besides, the predicted$ \alpha $ decay preformation factors for isotopes with Z = 119 and 120 exhibit similar phenomena at N = 184. These indicate that both 178 and 184 are possible neutron magic and submagic numbers, respectively. The results of this work can provide some information for future experimental studies, such as the synthesis of elements with Z = 119 and 120 and will also prompt inquiries about the nuclear structure. -
In summary, based on the WKB theory, considering the
$ \alpha $ decay preformation factors$ P_\alpha $ , we systematically investigate the$ \alpha $ decay half-lives of 559 nuclei, including 177 even-even, 277 odd-A, and 105 odd-odd nuclei. The$ \alpha $ decay preformation factors$ P_\alpha $ are calculated using the CFM. The assault frequency$ \nu $ is analytically parameterized using experimental$ \alpha $ decay energies and charge radii of the parent nucleus. For all 559 nuclei taken from NUBASE2020, the standard deviation calculated by our model is 0.408. In addition, we extend this model to predict the$ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120 and compare the predicted results with those calculated by UDL and DZR. The results predicted by these three formulas are consistent in trend, indicating that our model has a certain reliability. The predicted$ \alpha $ decay energies and half-lives for isotopes with Z = 119 and 120 exhibit similar behavior at N = 178 and N = 184. Besides, the predicted$ \alpha $ decay preformation factors for isotopes with Z = 119 and 120 exhibit similar phenomena at N = 184. These indicate that both 178 and 184 are possible neutron magic and submagic numbers, respectively. The results of this work can provide some information for future experimental studies, such as the synthesis of elements with Z = 119 and 120 and will also prompt inquiries about the nuclear structure.
Systematic study of α decay half-life within cluster-formation model
- Received Date: 2025-05-11
- Available Online: 2026-01-15
Abstract: In this study, based on the Wentzel-Kramers-Brillouin (WKB) theory, by parameterizing the assault frequency $ \nu $ as a function of the $ \alpha $ decay energy and charge radius of parent nucleus, with the $ \alpha $ decay preformation factor $ P_\alpha $ being calculated through the cluster-formation model (CFM), we systematically investigate the $ \alpha $ decay half-lives of 559 nuclei from the ground state, including 177 even-even, 277 odd-A, and 105 odd-odd nuclei. The calculated results indicate that our model can effectively reproduce the experimental data, with a corresponding standard deviation of 0.408. In addition, we use this model to predict the $ \alpha $ decay half-lives of 70 even-even, odd-A, and odd-odd nuclei with Z = 119 and 120. For comparison, we also use the universal decay law (UDL) proposed by Qi et al. [Phys. Rev. Lett 103, 072501 (2009)] and the unitary Royer formula (DZR) proposed by Deng et al. [Phys. Rev. C 101, 034307 (2020)]. The calculated results are in good agreement.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
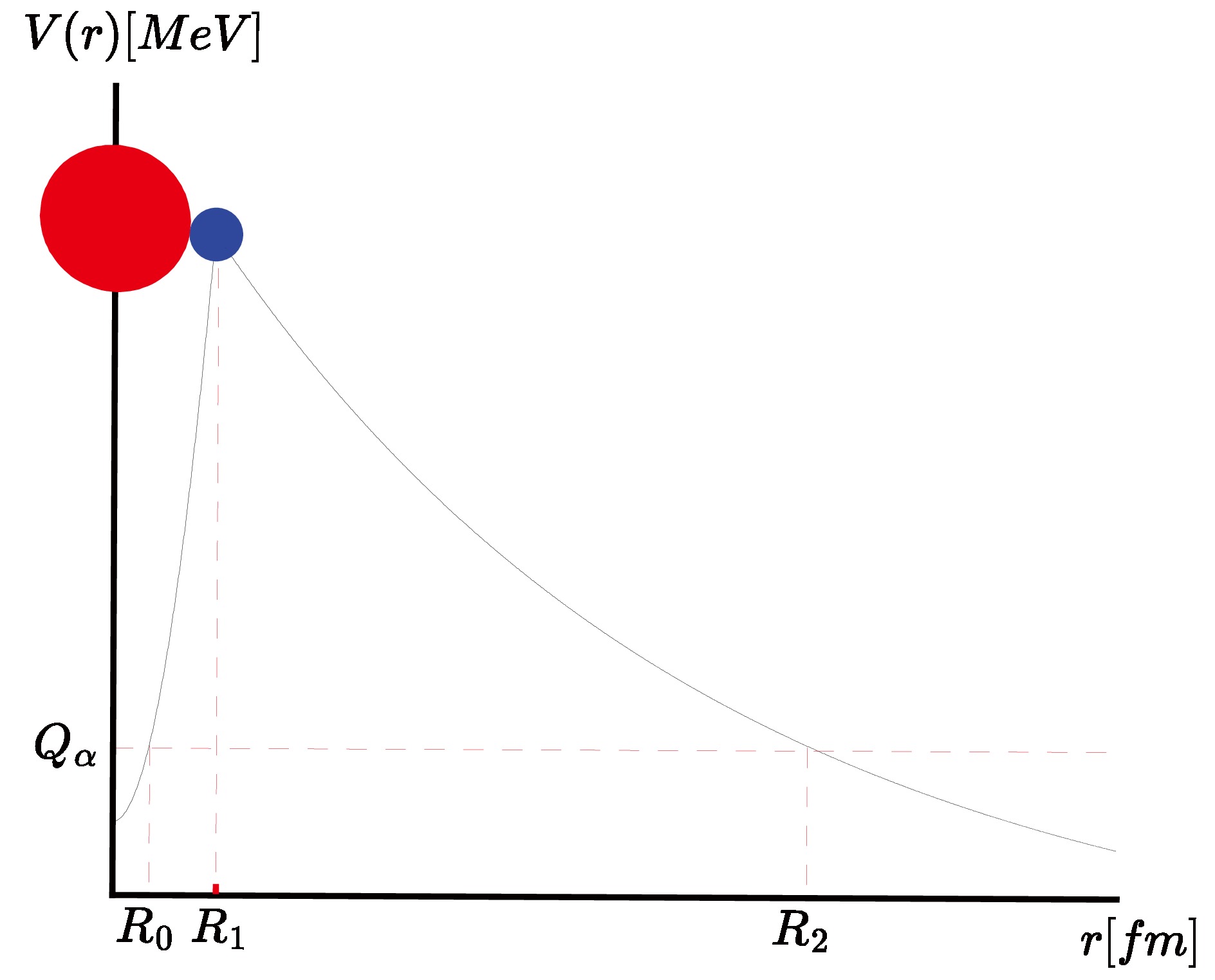










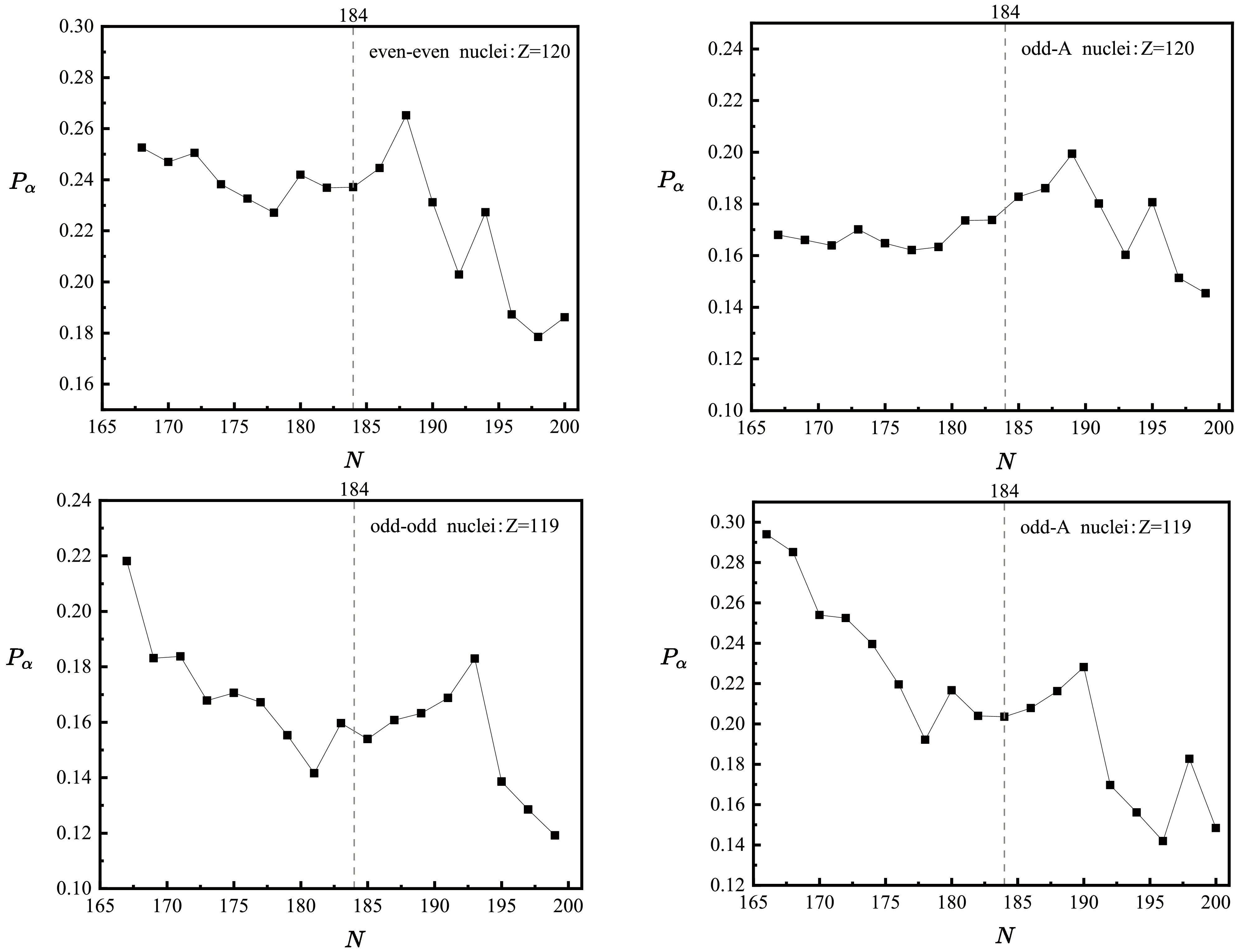
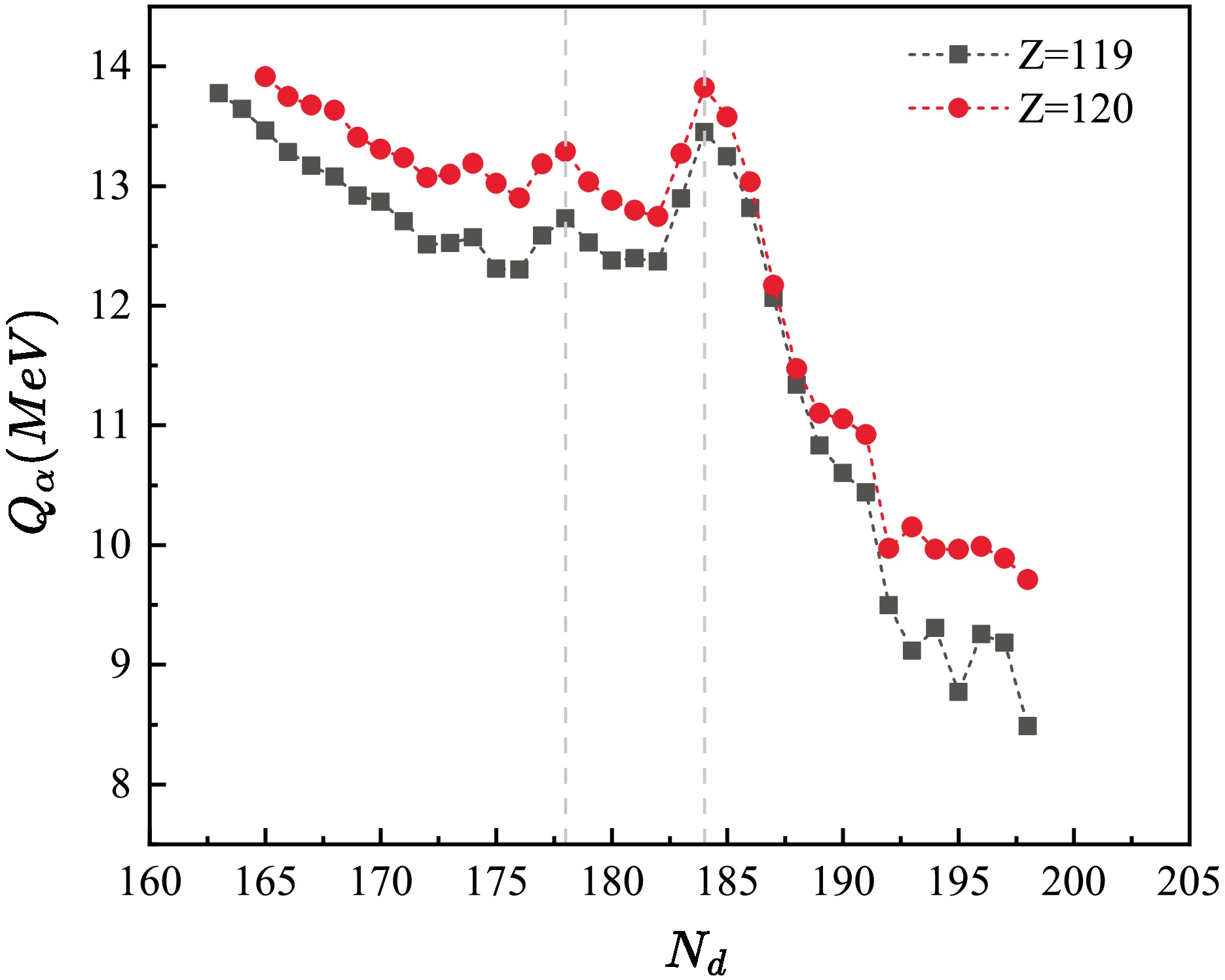



 DownLoad:
DownLoad: