Tilted-axis-cranking covariant density functional theory for the high-spin spectroscopy in ⁶⁹Ga

The spectroscopic properties of nuclei in the $ A\approx 70 $ mass region have caught much attention of experimental and theoretical studies in the past few decades. They provide an ideal laboratory for the study of the interplay between the single-nucleon and collective motions. Generally, at low spins, the properties of the $ A\approx 70 $ nuclei are governed by single-particle excitations involving low-j orbitals, such as $ 1f_{5/2} $, $ 2p_{3/2} $, and $ 2p_{1/2} $. At intermediate and high spins, the high-j deformation-driving $ 1g_{9/2} $ orbitals come into play and induce the collective behavior. The interplay between the single-nucleon and collective motions in this mass region generates many interesting phenomena, such as the superdeformed bands [1−3] and the magnetic rotations [4, 5].

Compared to the widely studied even-even nuclei [6−12], studies on the spectroscopic properties of the odd-mass nuclei with $ A\approx 70 $ are less performed. It is worthwhile to explore the spectroscopic properties of odd-mass nuclei, since the existence of the unpaired nucleon would result in additional complexity and more interesting physics. In fact, available studies of the odd-mass nuclei in the $ A\approx 70 $ mass region have already provided valuable insights in the evolution of the single-particle states around the $ Z=28 $ closed shell [13, 14] and the effects of collective motions [15, 16].

With three protons beyond the $ Z=28 $ closed shell, the odd-mass Ga isotopes present a diverse spectral structures and has caught much attention [17−20]. Many experimental efforts have been devoted to measure the spectra of ⁶⁹Ga since 1956 [21]. These investigations reported various low-lying negative-parity states generated by single-particle excitations involving $ 1f_{5/2} $, $ 2p_{3/2} $, $ 2p_{1/2} $ and $ 1f_{7/2} $ orbitals [22−26]. Very recently, through the $ ^{26}\text{Mg}(^{48}\text{Ca},p4n\gamma) $ multi-nucleon transfer reaction, the negative-parity level scheme of ⁶⁹Ga has been considerably extended. In addition, three positive-parity bands, namely bands SI, SII, and SIII, were observed[27], and better understanding for their nature necessitates the further theoretical studies.

Theoretically, the spectroscopic properties of nuclei in the $ A\approx 70 $ mass region have been investigated with many approaches, e.g., the interacting boson-fermion model [28, 29], the configuration-interaction shell model [30, 31], and the tilted-axis-cranking covariant density functional theory (TAC-CDFT) [32−34]. The TAC-CDFT [35, 36] starts from a universal density functional and, thus, could provide a microscopic understanding on the nuclear single-nucleon and collective motions without introducing adjustable parameters. Moreover, the TAC-CDFT exploits the Lorentz symmetry and, thus, nuclear currents that are important for the description of nuclear rotations [35, 37−39] can be considered self-consistently.

In this work, the TAC-CDFT is applied to investigate the three newly-observed positive-parity bands SI, SII, and SIII in ⁶⁹Ga. A microscopic interpretation for the collective structures in ⁶⁹Ga will be provided.

The detailed formalism of the CDFT and TAC-CDFT can be found in Refs. [32, 35, 36, 40]. Here, a brief introduction is presented.

The starting point of the CDFT is a universal density functional [41−44]. To realize the TAC calculations based on the CDFT, the functional is transformed into a body-fixed frame rotating with a constant angular velocity $ {\boldsymbol{\omega}} $, whose direction is determined by minimizing self-consistently the total energy in the rotating frame. The relativistic Kohn-Sham equation in the rotating body-fixed frame reads,

where $ {{{\hat{\boldsymbol{J}}}}} $ is the nuclear total angular momentum. The scalar field S and vector field $ V^{\mu} $ are connected in a self-consistent way to the nucleon densities and currents [32]. The iterative solution of Eq. (1) yields single-particle states and single-particle energies. The obtained single-particle states are then used to calculate the expectation values of three components $ \langle J_i\rangle $ of the angular momentum, total binding energies, $ B(E2) $ transition probabilities, etc. The magnitude of the angular velocity $ {\boldsymbol{\omega}} $ is connected to the total angular momentum quantum number I by the semiclassical relation $ \langle \hat{{\boldsymbol{J}}}\rangle\cdot\langle \hat{{\boldsymbol{J}}}\rangle=I(I+1) $.

In the TAC-CDFT framework, the pairing correlations are often treated by the Bogoliubov method [42, 44] and the shell-model-like approach (SLAP) [45]. In comparison, the SLAP treats the pairing correlations exactly by diagonalizing the many-body Hamiltonian in a properly truncated many-particle configuration (MPC) space and, thus, has the advantage to conserve the particle number and avoid the pairing collapse, for details, see Refs. [45−48].

Here, to investigate the collective structures in ⁶⁹Ga, the relativistic Kohn-Sham equation is solved using a three-dimensional harmonic-oscillator basis in Cartesian coordinates with ten major shells, which ensures convergence for nuclei in the $ A\approx 70 $ mass region [32]. The PC-PK1 relativistic density functional [49] is adopted. Such a functional has demonstrated high predictive power in describing nuclear masses [50, 51] and shapes [52−54], magnetic and antimagnetic rotations [32, 36, 55−57], chiral rotation [58−61], and nuclear fission [62, 63], etc.

To identify suitable configurations for the positive-parity bands SI, SII, and SIII, cranking calculations using the configuration constrained approach [35] are performed without taking into account the pairing correlations. By comparing the obtained results with the experimental data, the two most likely configurations are identified. Their energies and quadrupole deformation parameters β and γ at rotational frequency $ \hbar\omega = 0 $ MeV are listed in Table 1. The configuration $ \nu(g_{9/2})^4(pf)^6\otimes \pi(g_{9/2})^1(pf)^2 $ is assigned to band SI. The configuration $ \nu(g_{9/2})^4(pf)^6\otimes\pi(g_{9/2})^3 $ with positive and negative signatures is assigned to bands SII and SIII, respectively. Both configurations involve several valence $ g_{9/2} $ protons and neutrons that would induce nuclear collective rotations. The γ deformations for these two configurations are zero, and the corresponding β deformations are large. The particle nature of these configurations generates principal axis rotations, which are consistent with the $ \Delta I=2 $ character of the bands under consideration.

Band	E (MeV)	β	γ	Configuration
SI	−596.2	0.41	$0.0^{\circ}$	$\nu(g_{9/2})^4(pf)^6\otimes \pi(g_{9/2})^1(pf)^2$
SII, SIII	−595.6	0.57	$0.0^{\circ}$	$\nu(g_{9/2})^4(pf)^6\otimes\pi(g_{9/2})^3$

Table 1.  Calculated total energies, deformations β and γ, and assigned configurations for positive-parity bands SI-SIII in ⁶⁹Ga.

The calculated energy spectra and angular momenta for the positive-parity band SI are shown in Fig. 1, in comparison with the experimental data [27]. Without taking into account the pairing correlations, the theoretical results give a good description for the states with spin $ I> 23/2\hbar $. Nevertheless, the observed excitation energies and the total angular momenta for the states with $ I \leq 23/2\hbar $ are overestimated, which might be related to the lack of pairing correlations. To better clarify this point, calculations with pairing correlations considered by the SLAP are performed. In the calculations, the monopole pairing force is adopted. The effective neutron and proton pairing strengths are respectively 0.7 MeV and 0.75 MeV, determined by reproducing the experimental odd-even mass differences. The MPC space is truncated at an excitation energy cutoff [64] of $ E_c=10 $MeV. A larger MPC space with a renormalized pairing strength gives essentially the same results, indicating the convergence of the MPC space. It can be seen that the calculated energy spectra and angular momenta are in better agreement with the experimental data after the inclusion of the pairing correlations. It should be noted that for $ I\geq 29/2\hbar $ region, two $ g_{9/2} $ neutrons can be easily excited to the negative-parity $ 2p_{3/2} $ orbitals, which leads to an oblate configuration labeled as $ \nu (g_{9/2})^2(pf)^8\otimes \pi (g_{9/2})^1(pf)^2 $. Therefore, to maintain the same configuration as the low-spin region, configuration constrained calculations must be carried out.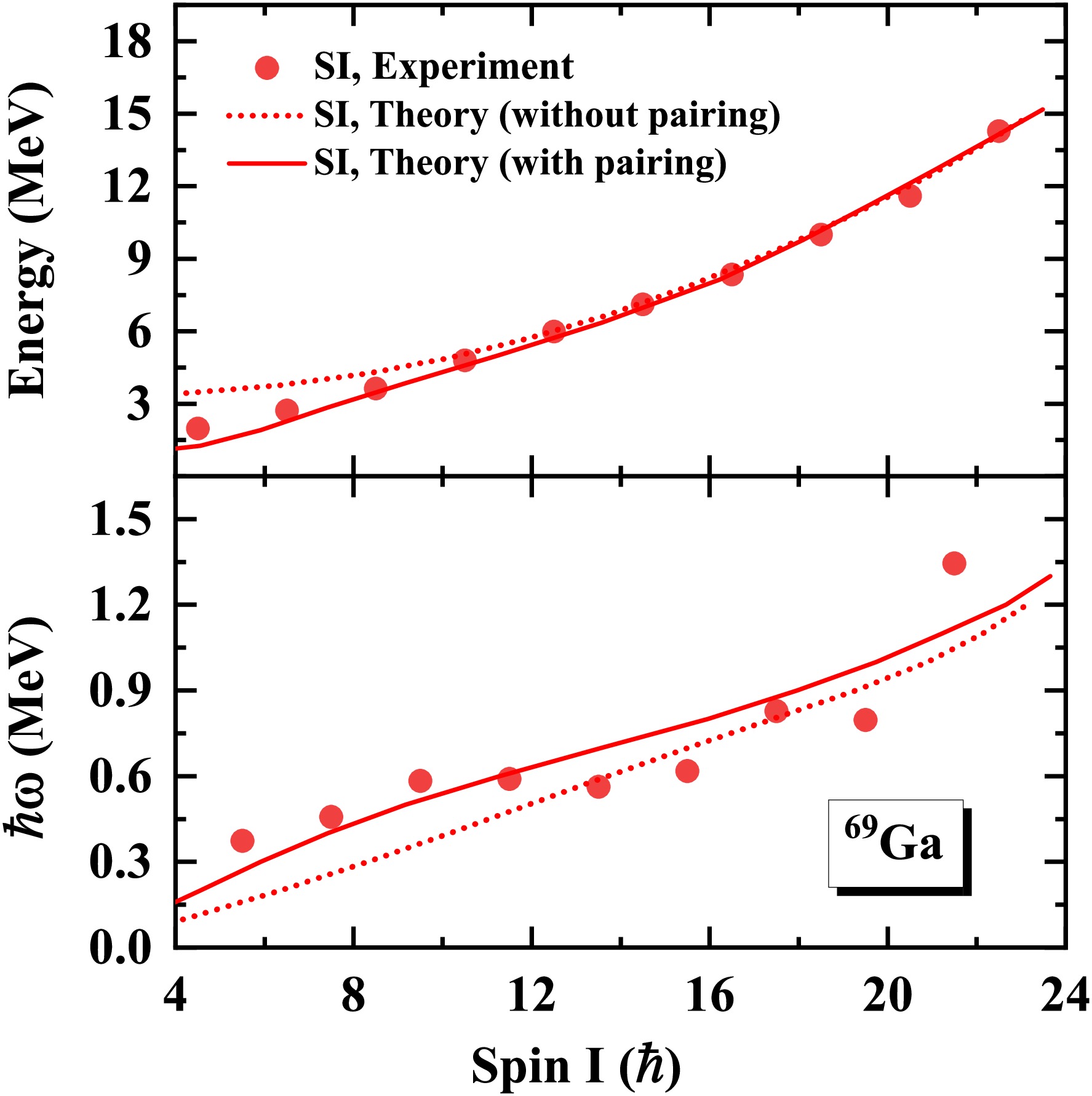

Figure 1.  (color online) Calculated excitation energies (upper panel) and rotational frequency (lower panel) as functions of the angular momenta for the positive-parity band SI in ⁶⁹Ga with and without pairing, in comparison with the data [27].

The calculated energy spectra and angular momenta for the positive-parity bands SII and SIII in ⁶⁹Ga as well as their comparison with the data [27] are shown in Fig. 2. The spins for the band heads of SII and SIII are already larger than $ 23/2\hbar $, leading to the fact that the pairing correlations are negligible for these two bands. The experimental energies and angular momenta for both SII and SIII are properly reproduced by the present calculations. Since these two bands are based on the same configuration with opposite signatures, they are suggested as signature partner bands, in which the one with negative signature is more energy favored. There is a signature inversion in bands SII and SIII at $ 35/2\hbar $, which cannot be reproduced by the present calculation, in which these two bands are calculated independently based on two different configurations. The interactions between these two configurations may be important for reproducing such a signature inversion phenomenon. Beyond-mean-field methods, such as relativistic configuration-interaction density functional theory (ReCD) [67−70], may be helpful to resolve the discrepancy between the calculated results and data.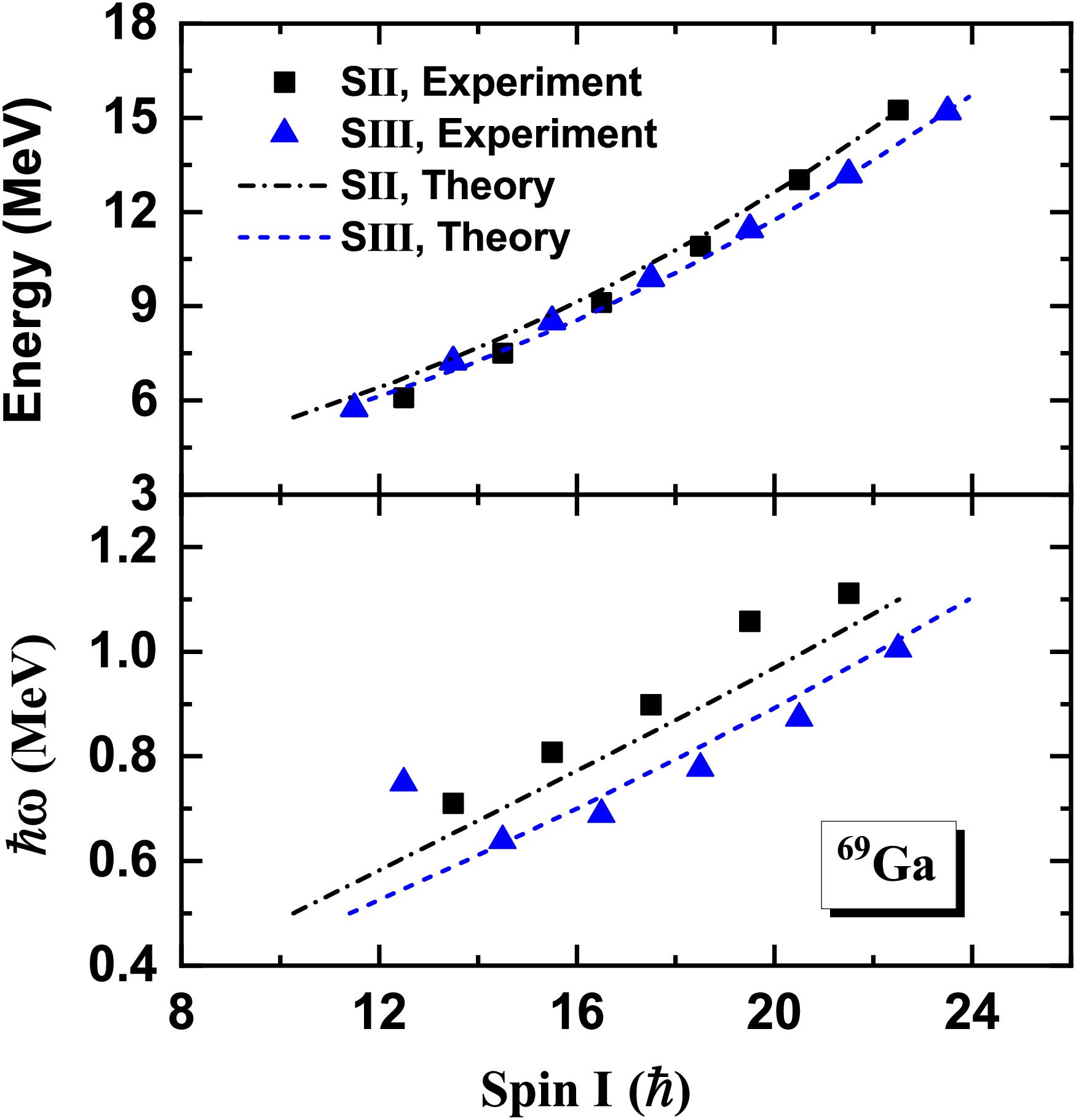

Figure 2.  (color online) Calculated excitation energies (upper panel) and rotational frequency (lower panel) as functions of the angular momenta for the positive-parity bands SII and SIII in ⁶⁹Ga, in comparison with the data.

As mentioned before, all the studied bands involves nucleons in $ g_{9/2} $ orbitals, and the reasonable description of these bands gives us confidence to give a microscopic interpretation of the role of the $ g_{9/2} $ orbitals in the collective structures in ⁶⁹Ga. In the present microscopic calculations, the nuclear total angular momenta are generated from all the individual nucleons inside of a self-consistent meanfield potential. For band SI, there are four $ g_{9/2} $ valence neutrons and one $ g_{9/2} $ valence proton. For bands SII and SIII, there are four $ g_{9/2} $ valence neutrons and three $ g_{9/2} $ valence protons. The angular momentum alignments of these $ g_{9/2} $ nucleons calculated by the TAC-CDFT without the pairing correlations are shown in Fig. 3. For band SI as shown in Fig. 3 (a), the contribution from the four neutrons in the $ g_{9/2} $ orbitals increases with the rotational frequency ω, and make a principal contribution in generating the total angular momentum. In contrast, the alignment of the unpaired $ g_{9/2} $ proton is almost constant. For band SII as shown in Fig. 3 (b), the alignments of the valence $ g_{9/2} $ neutrons and protons increase simultaneously with ω and their contributions to the total angular momentum are about the same order. The behavior of band SIII is similar with its signature partner band SII and is shown in Fig. 3 (c).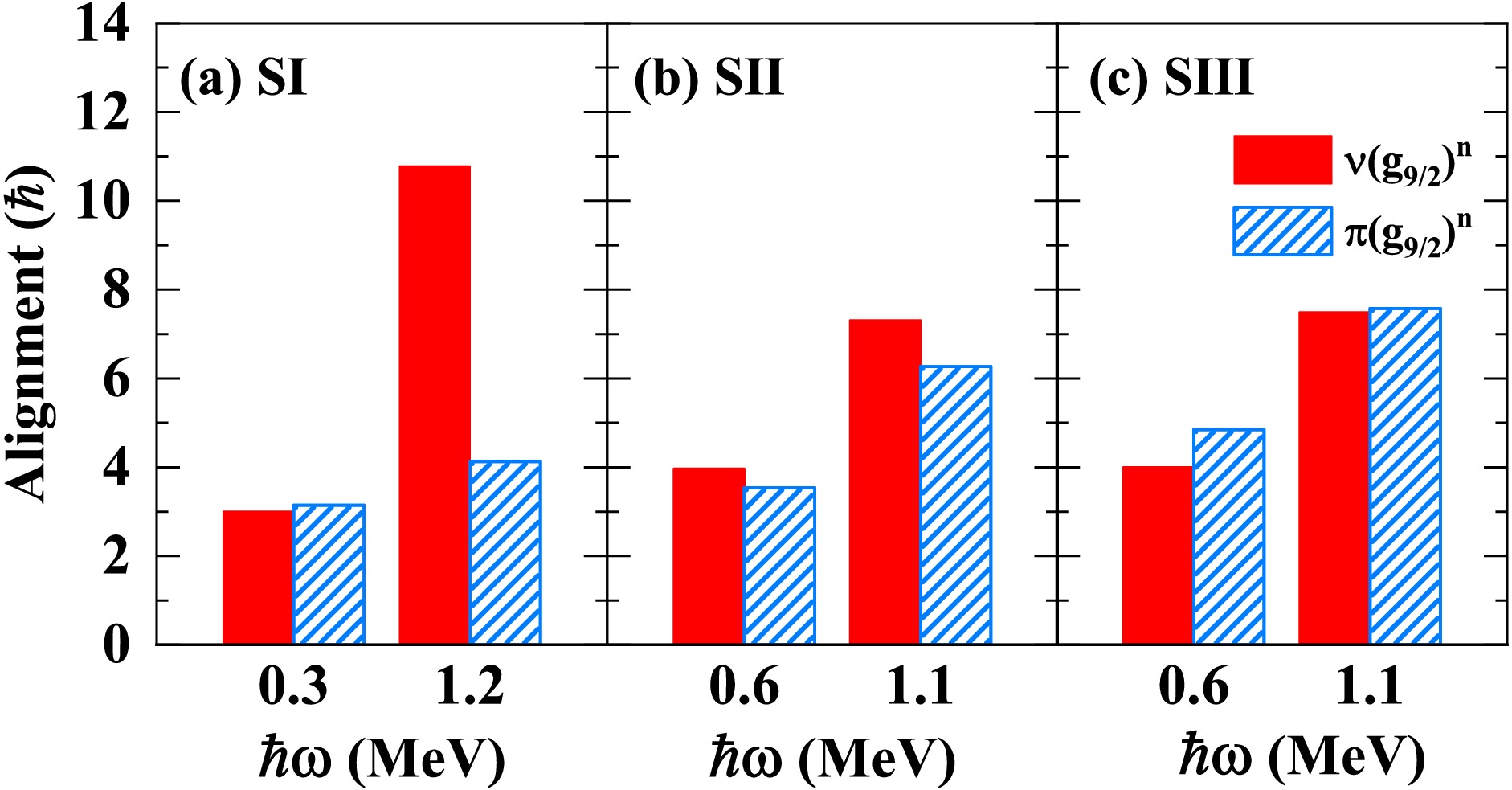

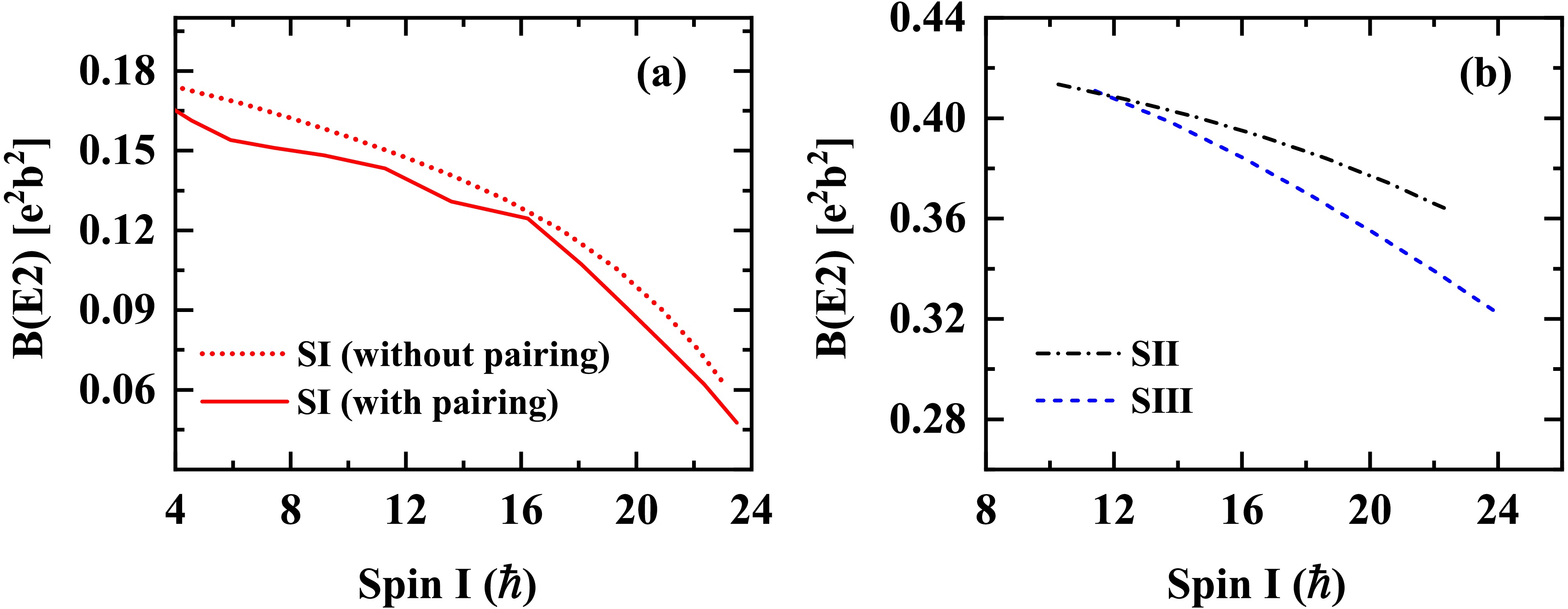
Figure 3.  (color online) Angular momentum alignments of the $ g_{9/2} $ proton and neutron particles for the bands SI (a), SII (b) and SIII (c), calculated by the TAC-CDFT without the pairing correlations.

Finally, the B(E2) values for the positive-parity bands SI, SII and SIII are predicted and are shown as functions of the angular momenta in Fig. 4. The $ B(E2) $ values exhibit a decreasing tendency for all these bands. This is caused by the fact that their deformation parameters β decrease with the total angular momenta. For band SI, when taking into account the pairing correlations, the $ B(E2) $ values are slightly reduced. For the signature partner bands SII and SIII, the calculated $ B(E2) $ values are close at spin $ I \approx 23/2\hbar $. At higher spins, however, the $ B(E2) $ values of band SII become larger than those of band SIII. Future experimental efforts including the measurement of lifetimes of these states are required to validate our predictions.

Figure 4.  (color online) Calculated $ B(E2) $ values as functions of the angular momenta for the positive-parity bands (a) SI, as well as (b) SII and SIII.

In summary, the tilted-axis-cranking covariant density functional theory is applied to investigate the three newly-observed positive-parity bands SI, SII, and SIII in ⁶⁹Ga. The energy spectra and angular momenta are calculated and compared with the experimental data. For the band SI, pairing correlations play a crucial role for the states with spin $ I\leq 23/2\hbar $. The bands SII and SIII are suggested to be signature partner bands with positive and negative signatures, respectively. By analyzing the angular momentum alignments, it is revealed that the $ g_{9/2} $ protons and neutrons play an important role in the collective structures of ⁶⁹Ga. For band SI, the two neutrons in the $ g_{9/2} $ orbitals make a principal contribution to the generation of the total angular momentum. For bands SII and SIII, the alignments of the valence $ g_{9/2} $ neutrons and protons increase simultaneously with ω and their contributions to the total angular momentum are about the same order. The transition probabilities $ B(E2) $ for these bands are predicted, and await further experimental verification.

The authors would like to express gratitude to A. D. Ayangeakaa for fruitful discussions.