Studying the proton rms radii of Li and B isotope through elastic scattering

The nuclear radii stand as a pivotal observable parameter for elucidating nuclear structure [1]. By definition, the charge distribution of a nucleus is characterized by the $ \langle r^{2}\rangle_{ch} $, whereas the neutron and proton distributions are described by the $ \langle r^{2}\rangle_{n} $ and $ \langle r^{2}\rangle_{p} $, respectively.

Experimentally, several techniques have been used to determine the rms nuclear charge radii. Three methods have proven particularly effective: electron scattering experiments, muonic spectra analyses, and measurements of optical and $ K_{\alpha} $ X-ray isotope shifts [2]. For example, electron scattering experiments with energies up to 125 and 150 MeV have been conducted [3]. These experiments measured the angular distribution of cross sections related to form factors. This measurement, in turn, enables the deduction of the nuclear charge distribution.

Muonic spectra offer an alternative approach to determine $ \langle r^{2}\rangle_{ch} $. Muons are 207 times heavier than electrons. Due to this greater mass, they have smaller orbital radii and a higher degree of overlap with the nuclear wave function. Spectra from the $ 2p\rightarrow1s $ muon de-excitation process have been used to extract $ \langle r^{2}\rangle_{ch} $ [4]. Additionally, isotope shifts cause differences in atomic spectra. When these spectral differences are combined with precise atomic structure calculations, they can also yield the rms nuclear charge radius [5].

The rms nuclear matter radii can be determined from analysis of the interaction cross sections in heavy ion collisions at high energies, classically the interaction cross section $ \sigma $ is given by the formula $ \sigma=\pi(R_{T}+R_{P})^{2} $, with $ R_{T} $ and $ R_{P} $ denoting the radii of the target and projectile nuclei, respectively [6−8], quantization analysis is accomplished through Glauber-model [9−11]. Using peripheral collisions, the rms radii of point proton distributions can be obtained from charge-changing interaction cross sections at intermediate energies, as these cross sections are related to both proton and neutron distributions [12, 13]. Moreover, the rms radii of point proton distributions can be derived from charge radii data using the relation [14]: $ \sqrt{\langle r^{2}\rangle_{p}}=\sqrt{\langle r^{2}\rangle_{ch}-0.76+0.11(N/Z)} $.

Theoretically, advanced approaches such as ab initio theory [15, 16], shell model theory [17], and mean field theory [18−20] have been extensively used to calculate the rms nuclear charge, neutron, and proton radii.

Optical Model Potentials (OMPs) play a critical role in understanding nuclear reaction mechanisms. OMPs are obtained by fitting experimental data. Systematic OMPs are derived from a broad range of target nuclei and projectile energies [21−23]. They significantly reduce uncertainties and enhance the reliability of predictions [21]. Xu et al. conducted sensitivity tests of potential parameters in 2013 [23], while Zhang et al. reported on the sensitivity of neutron density distributions for OMPs in 2014 [24]. In 2023, Yang et al. applied systematic OMPs to heavy ions [21]. These previous studies make it possible to extract the rms nuclear proton radii with the optical model analyses of elastic scattering data. Regarding the isotopes under investigations, elastic electron scattering measurements for ⁶Li and ⁷Li, ¹⁰B and ¹¹B were reported by F.A. Bumiller in 1972 [25] and T. Stovall in 1966 [26]. However, ⁸Li is unstable with a half-life of 837.7 ms [27], rendering elastic electron scattering unsuitable for measuring its charge radius. Instead, by using stable Lithium isotopes (⁶Li or ⁷Li) as references through isotope shift measurements, the charge radius of ⁸Li can be determined [28]. In 2019, Bernhard Maass achieved the first isotope shift measurements for ¹⁰B and ¹¹B, providing an improvement of the experimental precision compared to that of the elastic electron scattering [29]. As of now, only the rms radius of the point proton distribution for ¹¹B has been analyzed from charge-changing interactions, as reported by Yoshiko in 2015 [15]. This paper is structured as follows. Section II details the formalism considered in the present work, encompassing the nucleus-nucleus potential used to extract the rms nuclear proton radii. Section III presents the descriptions of the angular distributions of elastic scattering with different nucleon density distributions. Section IV presents results of the proton radii, accompanied by comparisons with other experimental and theoretical results. Finally, in Section V, a summary of this study is given.

The angular distributions of elastic scattering were analyzed within the framework of the optical model. The effective interactions are characterized by a long-range repulsive Coulomb potential $ V_{C}(R) $ and a short-range attractive nuclear potential $ U_{N}(R) $ which are combined as follows:

Here, R denotes the vector connecting the center of mass (c.m.) of the target nucleus to that of the projectile, while $ E_{\rm{lab}} $ represents the incident energy in the laboratory frame. It should be noted that $ U_{N}(R,E_{\rm{lab}}) $ is derived from the Bruyères Jeukenne-Lejeune-Mahaux (JLMB) effective interaction. Thus, it represents an optical potential rather than a bare potential. For the Coulomb component $ V_{C}(R) $, we adopted a conventional model. This model assumes a uniform charge distribution in spherical nuclei, and it is defined as follows:

In this equation, the charge radius $ R_{C} $ was assumed to be 1.3 $ \times (A_{P}^{1/3}+A_{T}^{1/3}) $ fm, with $ A_{P} $ and $ A_{T} $ signifying the mass numbers of the projectile and target nuclei, respectively. For the nuclear component, the systematic nucleus-nucleus potential proposed in Ref. [21] was employed. The real and imaginary parts of the complex $ U_{N}(R,E_{\rm{lab}}) $ potential were computed using the single-folding model. The renormalization factors $ N_{r} $ and $ N_{i} $ were determined through analysis of experimental data for stable nuclei [21]:

Here, $ U_{{\rm{sf}}} $ represents the single-folding model potential experienced by a projectile nucleus during its collision with a target nucleus at the incident energy $ E_{\rm{lab}} $. This potential requires renormalization due to the composite nature of the projectile nucleus and is expressed by the formula:

In this expression, $ {\boldsymbol{s}} = {\boldsymbol{R}}+{\boldsymbol{r}} $ is the vector from the c.m. of the target to the nucleon of the projectile. The interaction $ v(E_{\rm{lab}}/A_{P},|{\boldsymbol{s}}|) $ between a free nucleon and the target nucleus was assumed to follow the semimicroscopic Lane-consistent JLMB model potential in the present calculations. Additionally, $ \rho_{i}({\boldsymbol{r}}) $ denotes the nucleon density distribution (i = p for proton and i = n for neutron) within the projectile at position r relative to the c.m. of the projectile. In this study, the proton and neutron density distributions of both projectile and target nuclei were obtained from Hartree-Fock calculations based on the SkX parametrization [30].This parameter set is used to explain binding energy differences of mirror nuclei [31], interaction cross section [32], transfer reactions [33] and nuclear charge density distributions [34]. The calculated proton rms radii for ⁶Li, ⁷Li, ⁸Li, ¹⁰B and ¹¹B, are 2.104, 2.092, 2.090, 2.325, and 2.303 fm, respectively. In contrast, the corresponding experimental values are 2.46 ± 0.04, 2.315 ± 0.044, 2.212 ± 0.047, 2.29 ± 0.05, and 2.272 ± 0.031 fm [2]. This disparity highlights a significant discrepancy between theoretical predictions and experimental data, especially for lithium isotopes. Notably, single-folding model calculations with smaller rms proton radii yield predicted angular distributions that are shifted towards larger angles compared to those obtained using the experimental values. This observation suggests that by optimizing the fit between experimental data and theoretical cross sections through adjustments of the nucleon density distributions, it is feasible to extract the rms proton radii of nuclei with enhanced accuracy.

The elastic scattering experimental data for ^6,7,8Li and ^10,11B projectiles utilized in this study were collected from the EXFOR[35] nuclear reaction database. The data involved target nuclei with mass numbers ranging from 40 to 209 and incident energies exceeding the Coulomb barriers. With these data, the rms proton radii were extracted through optical model analysis based on an updated systematic nucleus-nucleus potential (USNP). This potential has demonstrated success in reproducing elastic scattering and total reaction cross-section data for projectiles with mass numbers up to A ~ 40, including both stable and radioactive nuclei, for incident energies from the vicinity of the Coulomb barrier to about 100 MeV/nucleon [21]. In the analysis procedure, each set of angular distribution data was individually fitted by altering the nucleon density distributions. The standard minimum $ \chi^{2} $ was employed to achieve an optimal description of the experimental data. Mathematically, the $ \chi^{2} $ is defined as:

where N represents the total number of data points in each angular distribution dataset, $ \sigma_{i}^{{\rm{th}}} $ denotes the theoretical cross section at the scattering angle $ \theta_{i} $, and $ \sigma_{i}^{{\rm{exp}}} $ and $ \Delta\sigma_{i}^{{\rm{exp}}} $ are the corresponding experimental cross section and its associated uncertainty, respectively. Notably, $ \sigma_{i}^{{\rm{th}}} $ was calculated using the USNP with various projectile density distributions. These distributions were generated by rescaling the original Hartree-Fock densities, where the rms radii of the resulting nucleon density distributions were varied by a factor $ \alpha $ in the range of 0.60 - 1.40 with a step size of 0.01. The rescaling process was accomplished by replacing the original density distribution $ \rho(r) $ with $ \rho(r/\alpha)/\alpha^{3} $. Here is a brief justification of this method. Density distribution $ \rho(r) $ has a simple conservation law:

Replace $ \rho(r) $ with $ \rho(r/\alpha) $ and add a factor $ \lambda $ to maintain conservation:

Change variables as $ t=\dfrac{r}{\alpha} $:

It's easy to get that:

The rescaled density distribution is $ \rho(r/\alpha)/\alpha^{3} $. Then we are going to reach the relationship between rms radii, by definition the rms radii is:

Rescaling the density distribution will change rms radii:

Implement $ \langle r^{2}\rangle/\langle r'^{2}\rangle $ and change variables as $ t=\dfrac{r}{\alpha} $:

After rescaling the density distribution, rms radii are represented as:

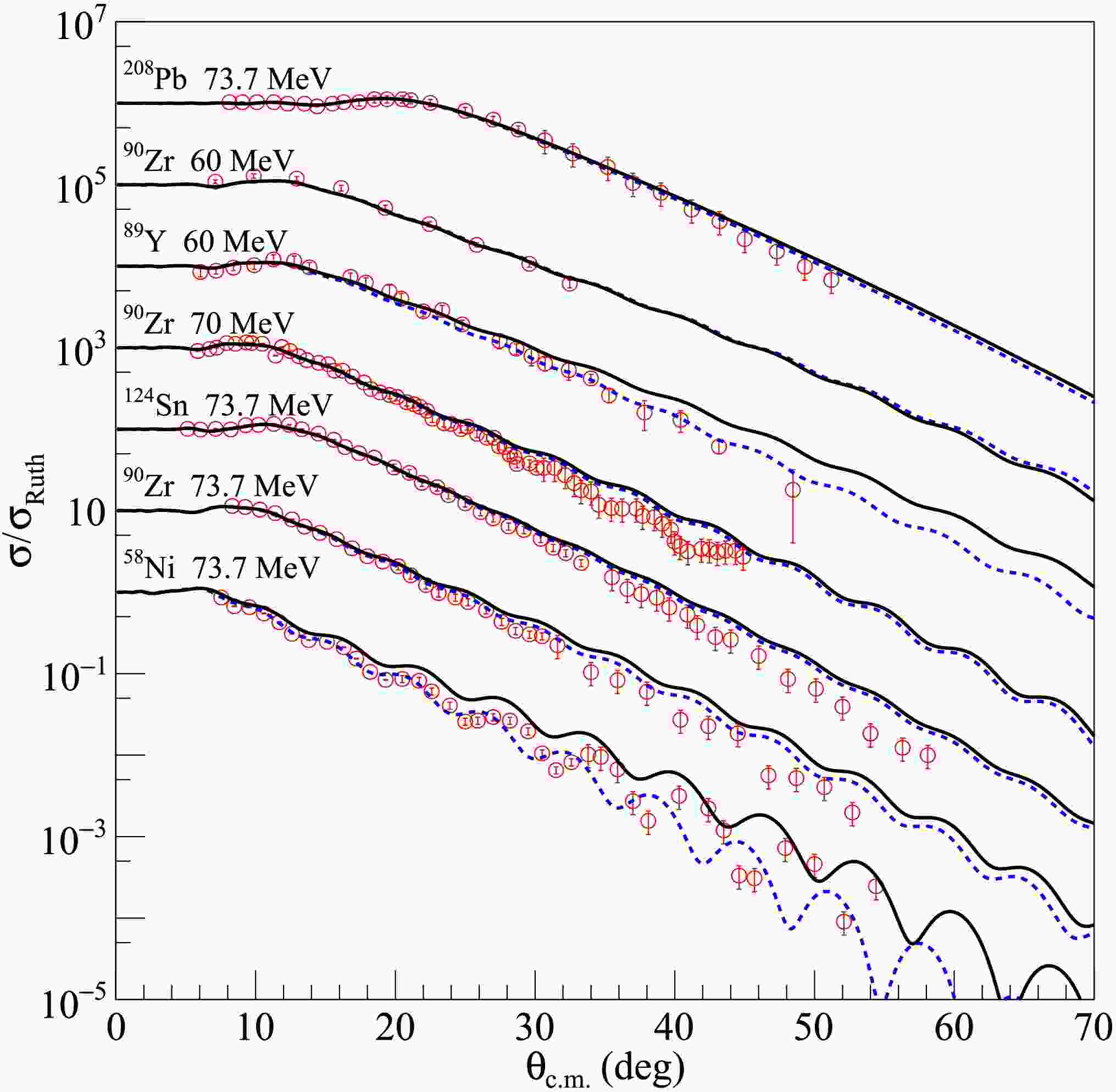
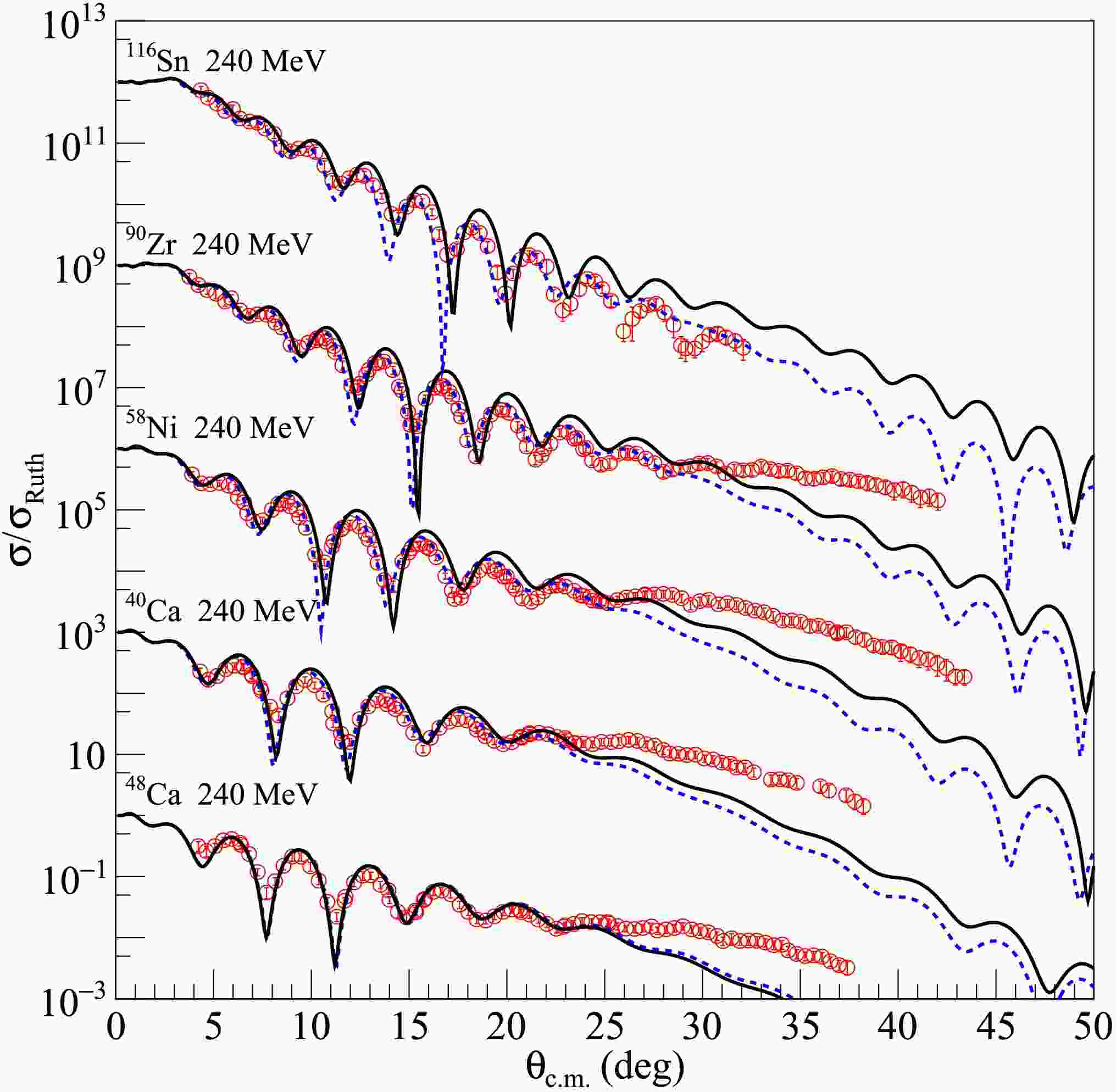
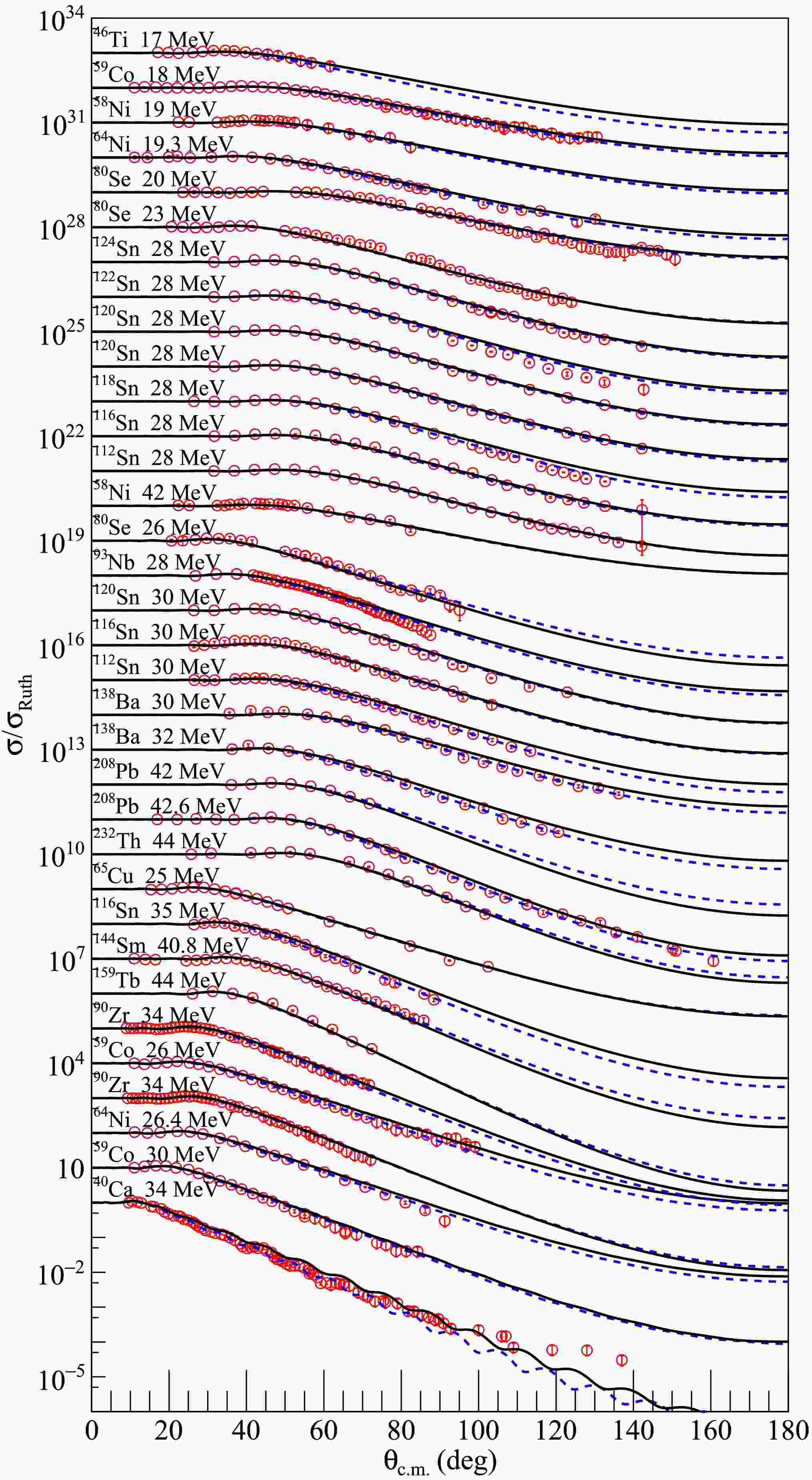
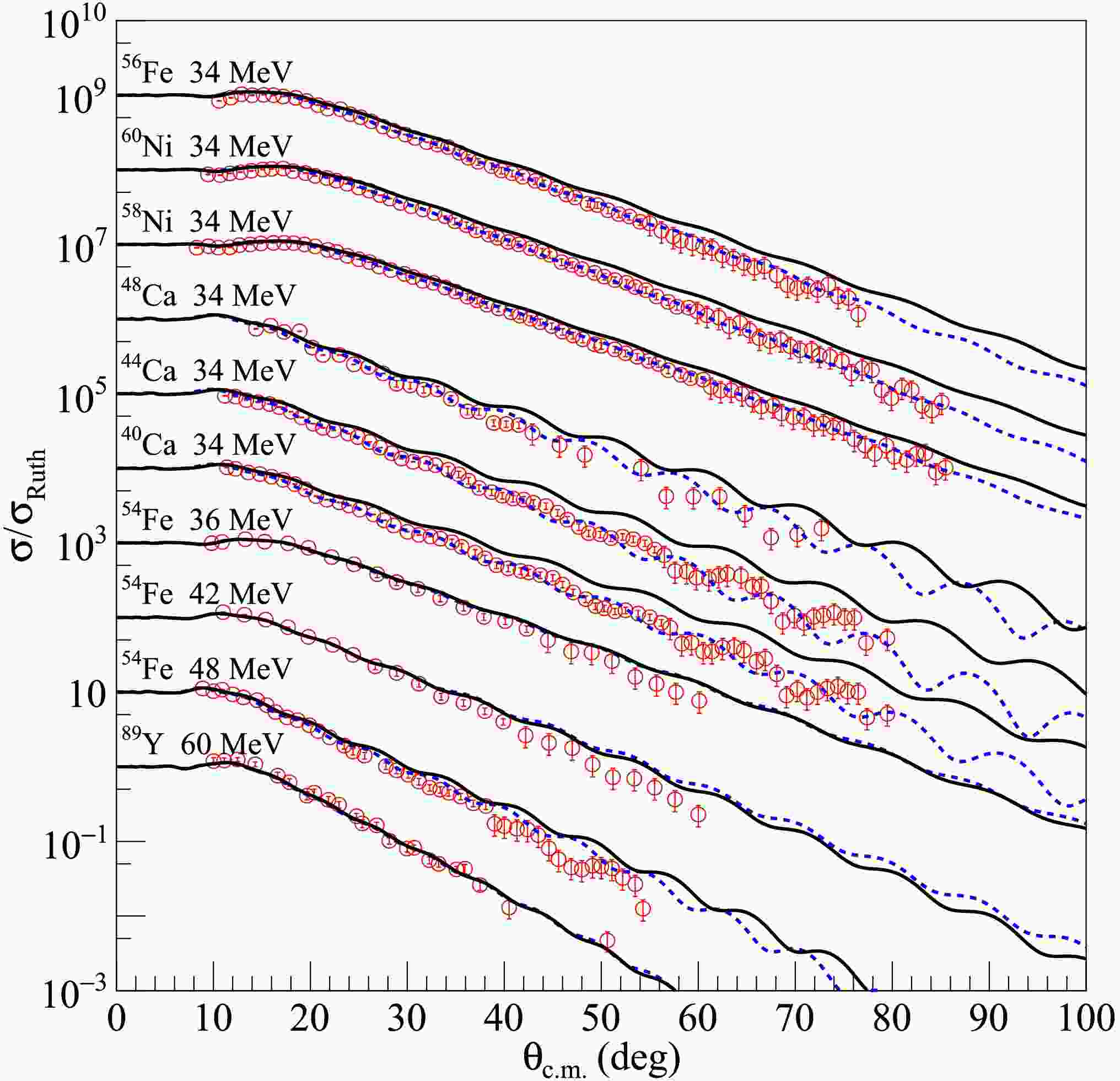
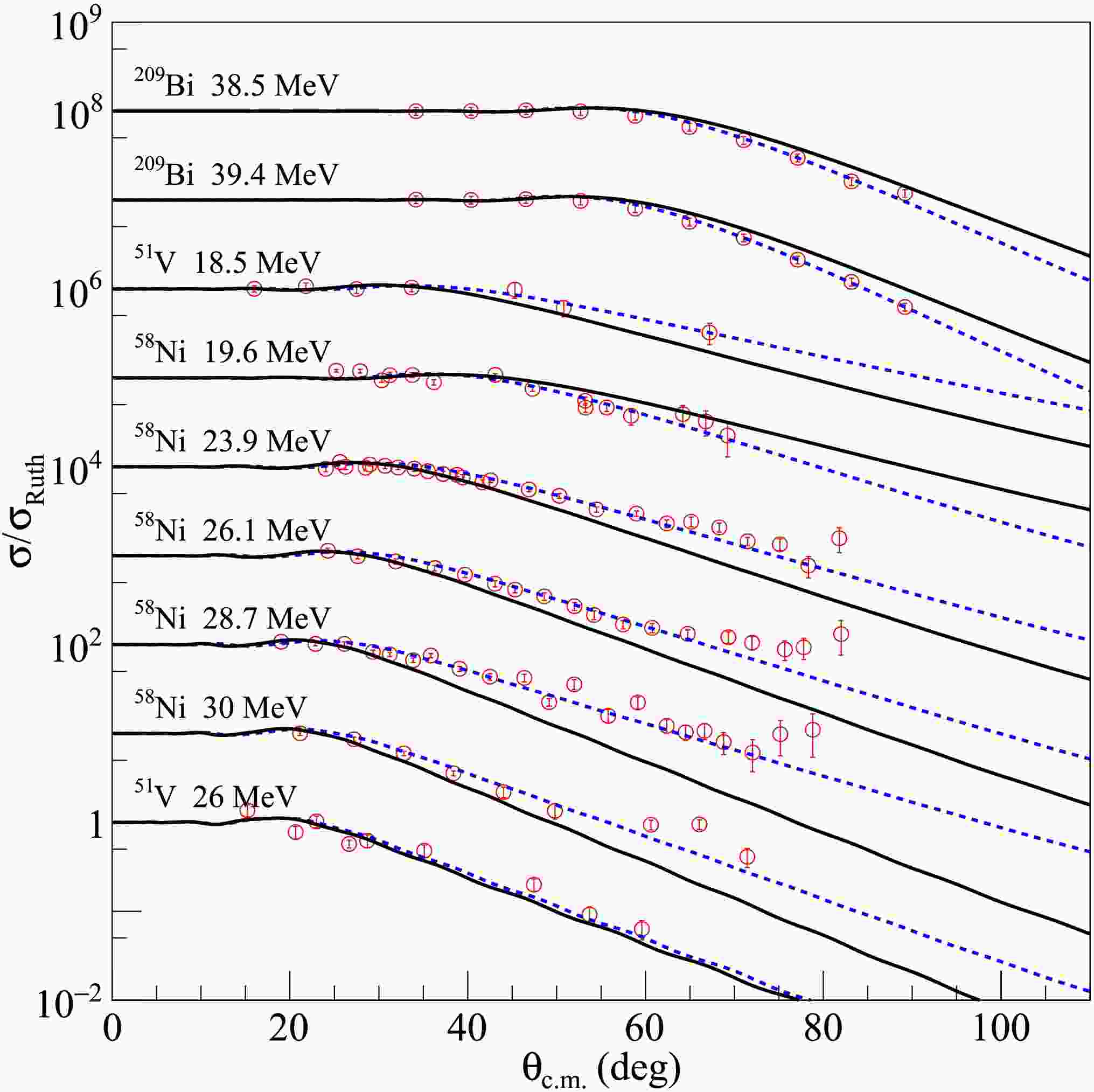
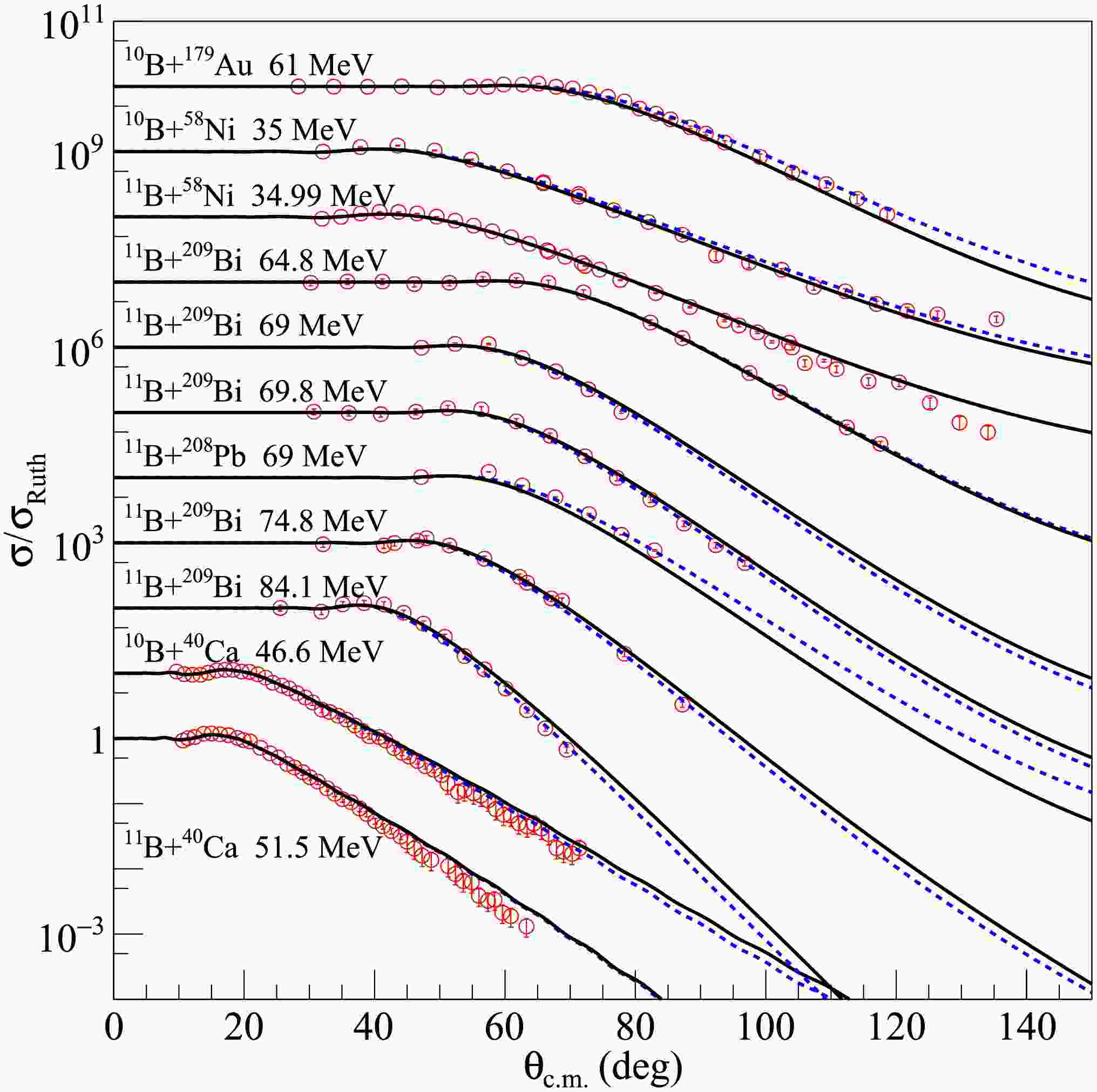
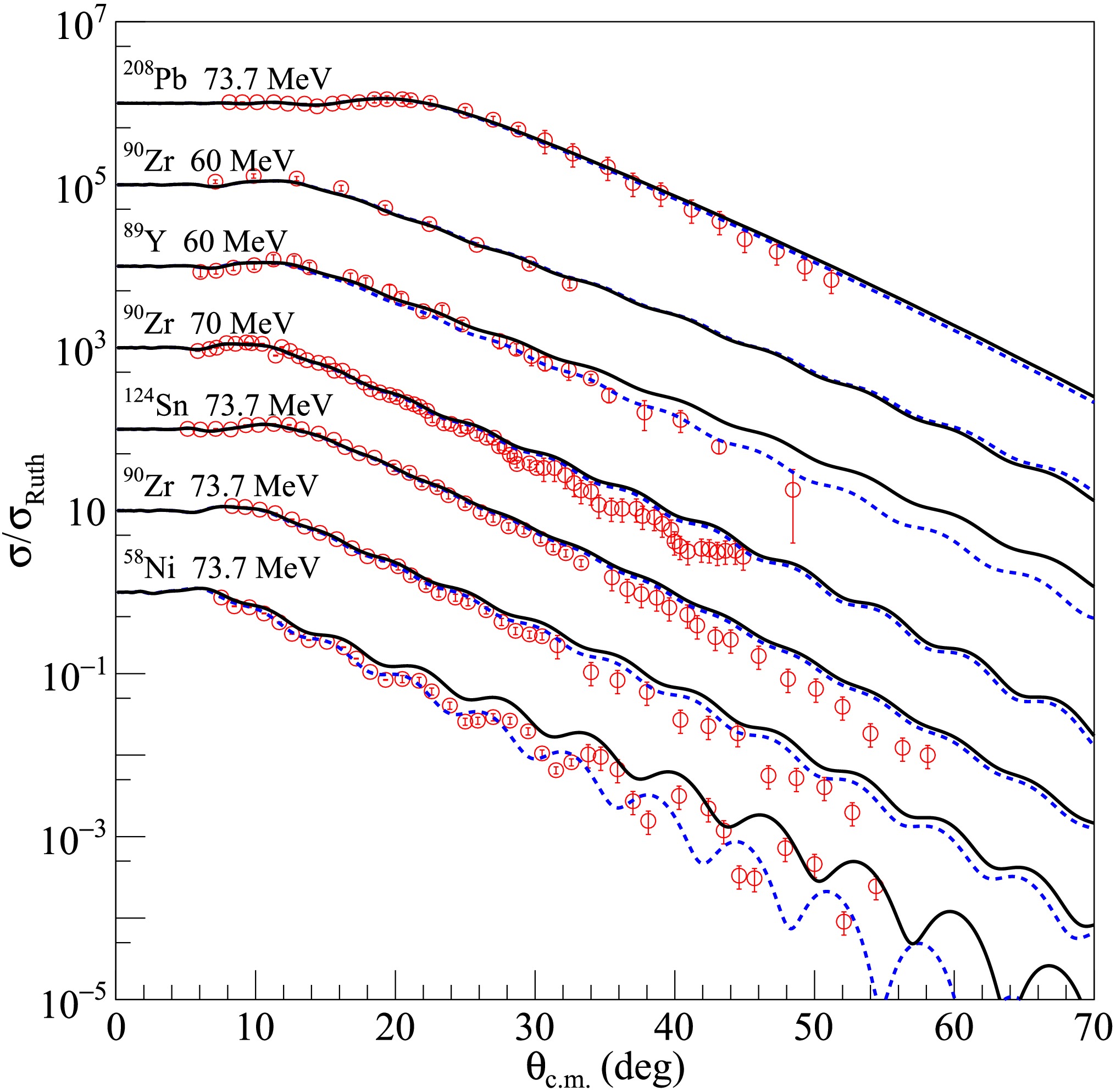
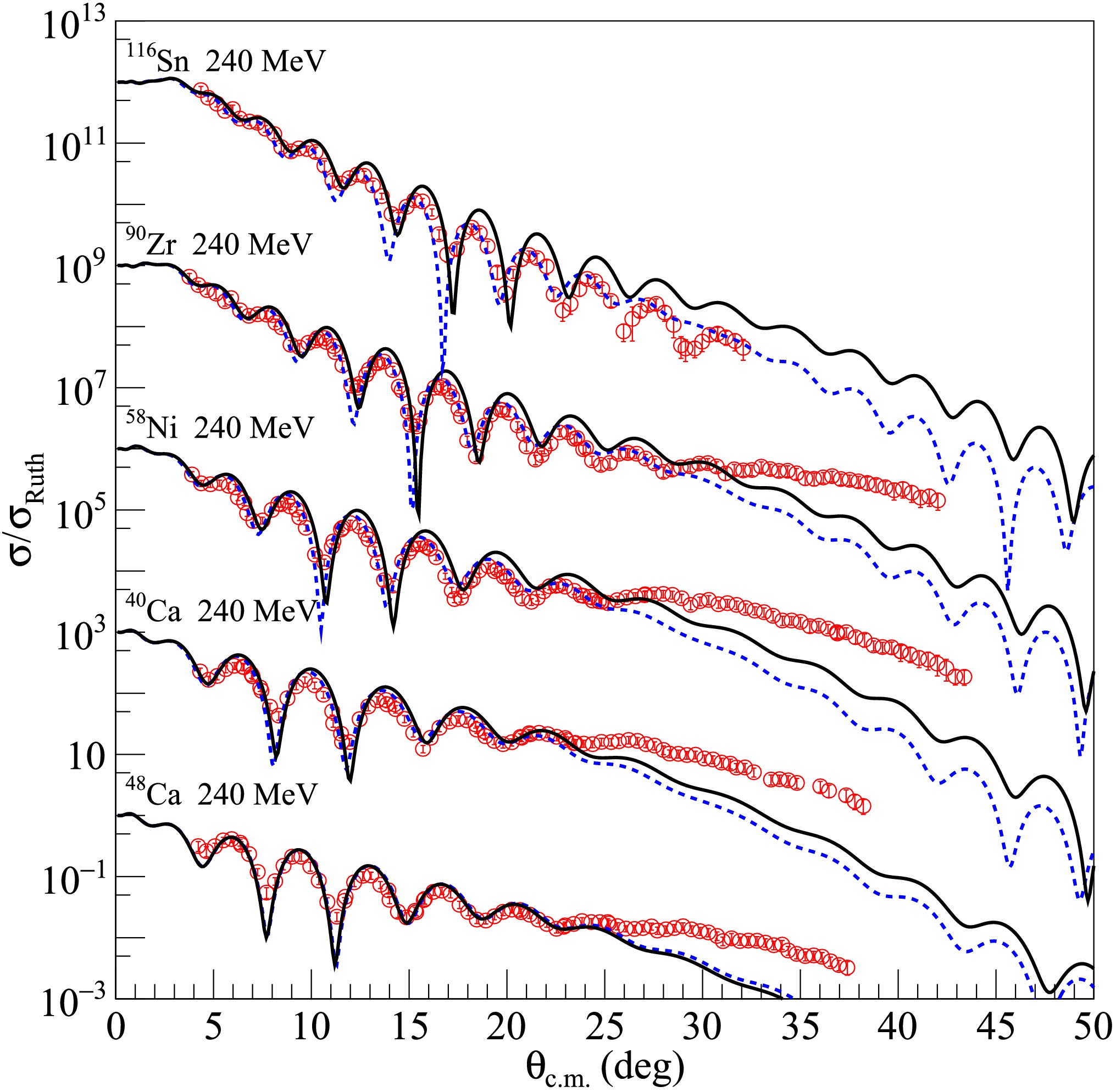
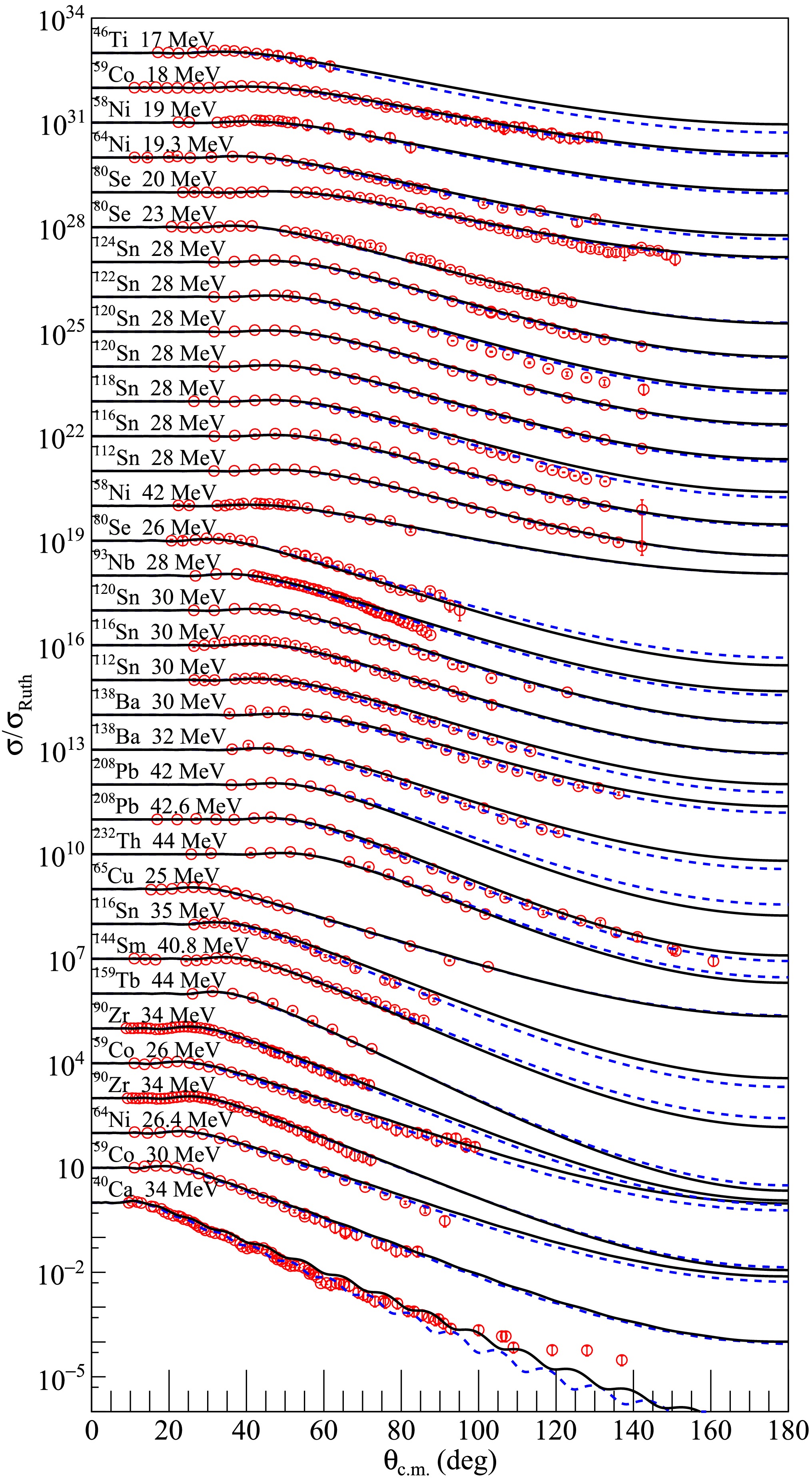
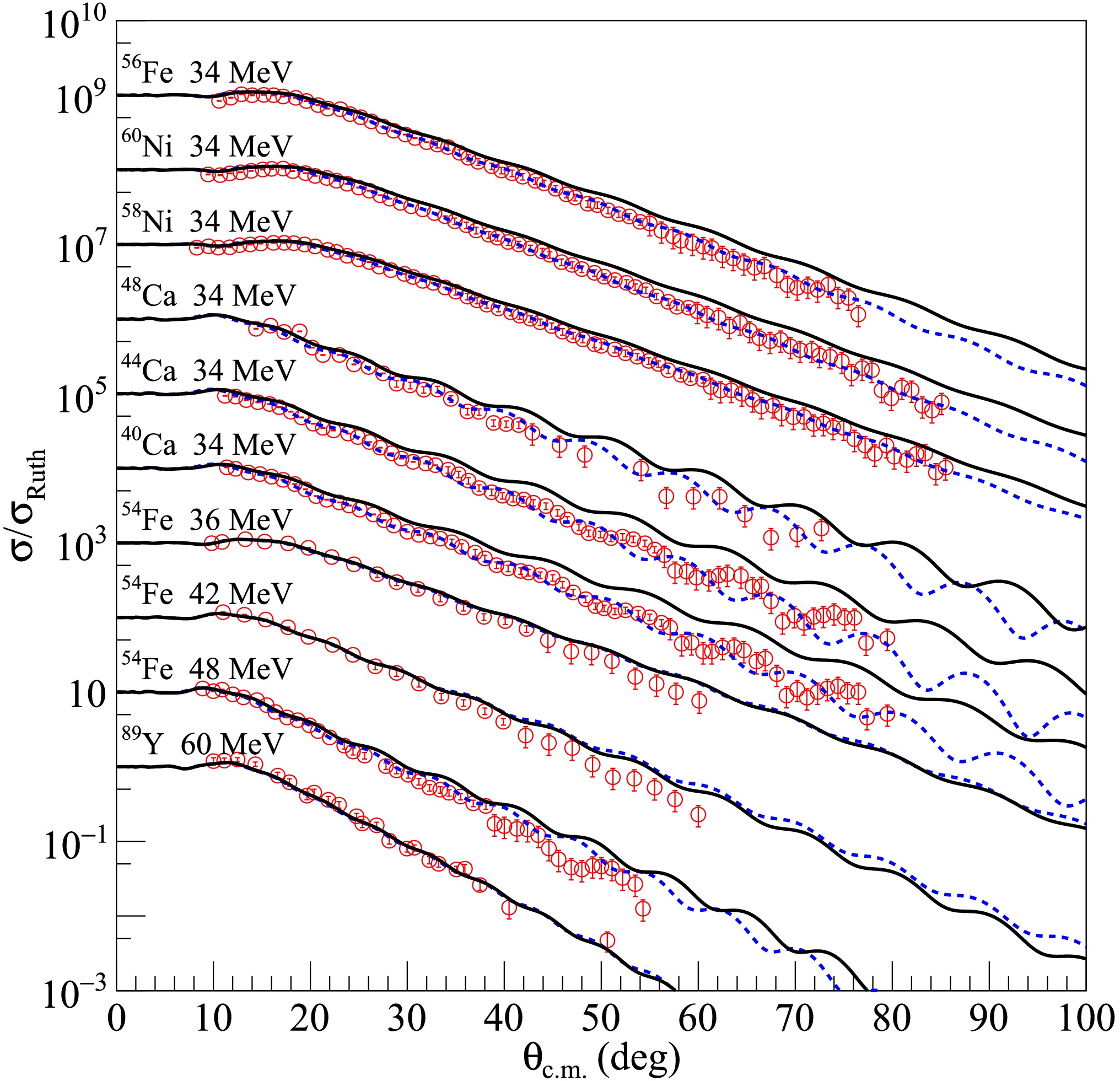
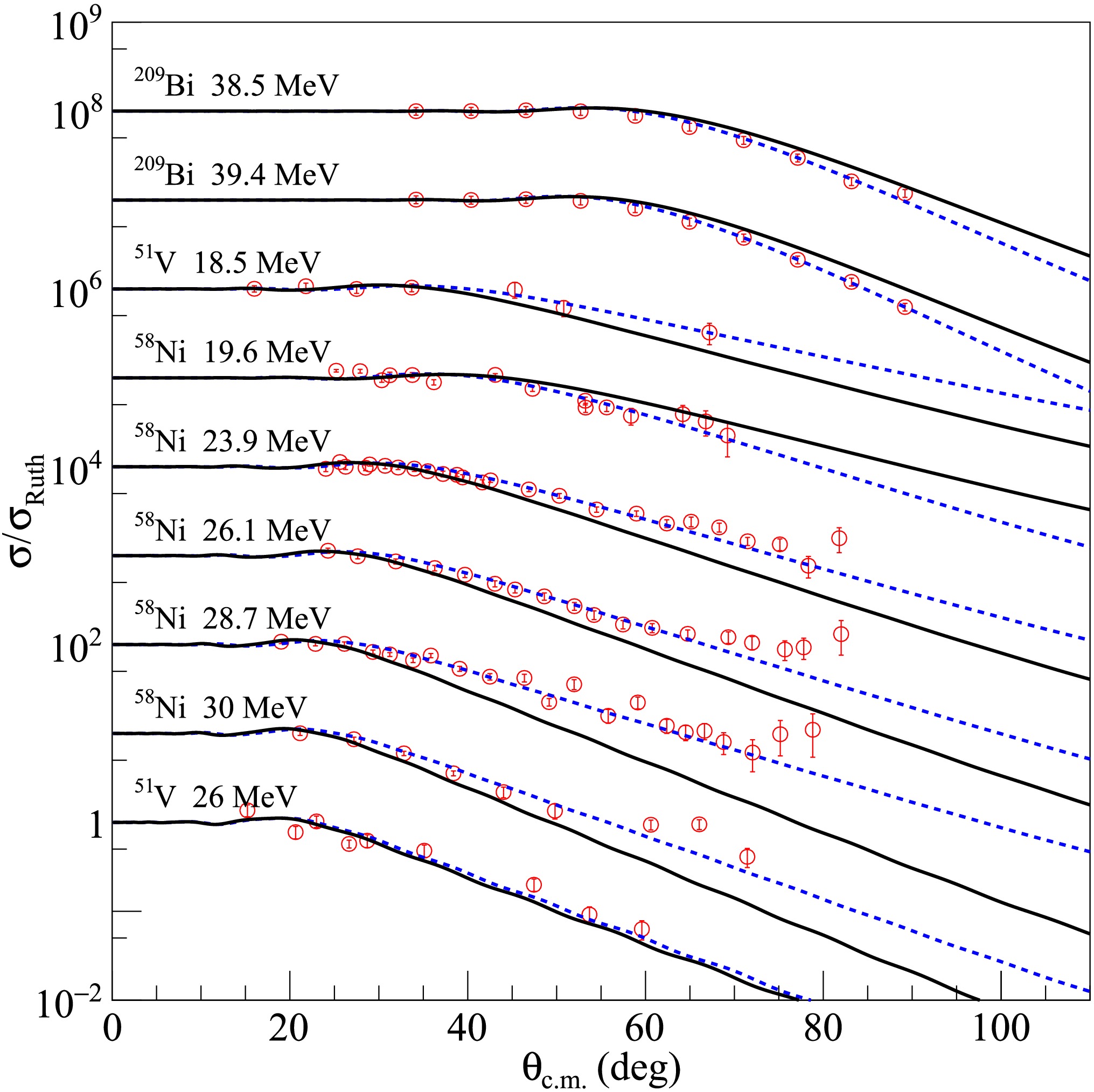
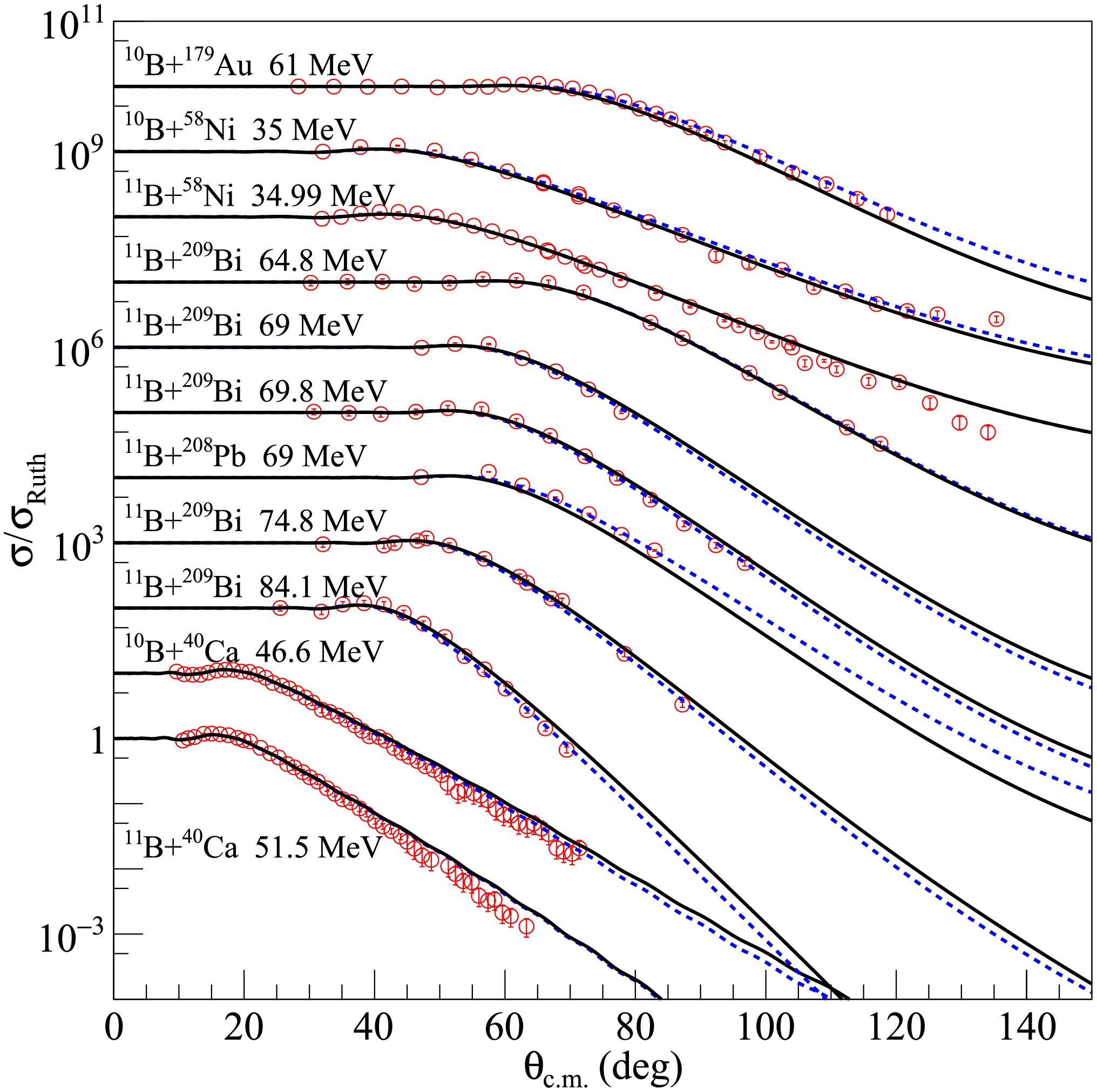
Subsequently, the newly created density distribution for each dataset was input into the SFRESCO computer code to compute the differential cross sections and determine the optimal value of the rms radii. To obtain more accurate rms proton radii for the nuclei under investigation, extensive comparisons were made between the experimental data and the results of optical model calculations with modified nucleon density distributions. The findings are presented in Figs. 1, 2, and 3 for ⁶Li elastic scattering from medium - mass and heavy targets, in Figs. 4 and 5 for ⁷Li, in Fig. 6 for ⁸Li and in Fig. 7 for ¹⁰B and ¹¹B. The blue dashed curves represent the optical model calculation results using the searched nucleon density distributions, without any adjustments to the optical model parameters of the USNP. The overall agreement between the experimental data and the fitted angular distributions is quite satisfactory, as further corroborated by the $ \chi^{2} $ values tabulated in Table 1. Compared with the calculations using the original nucleon distributions, significant improvements in describing the elastic cross sections were observed.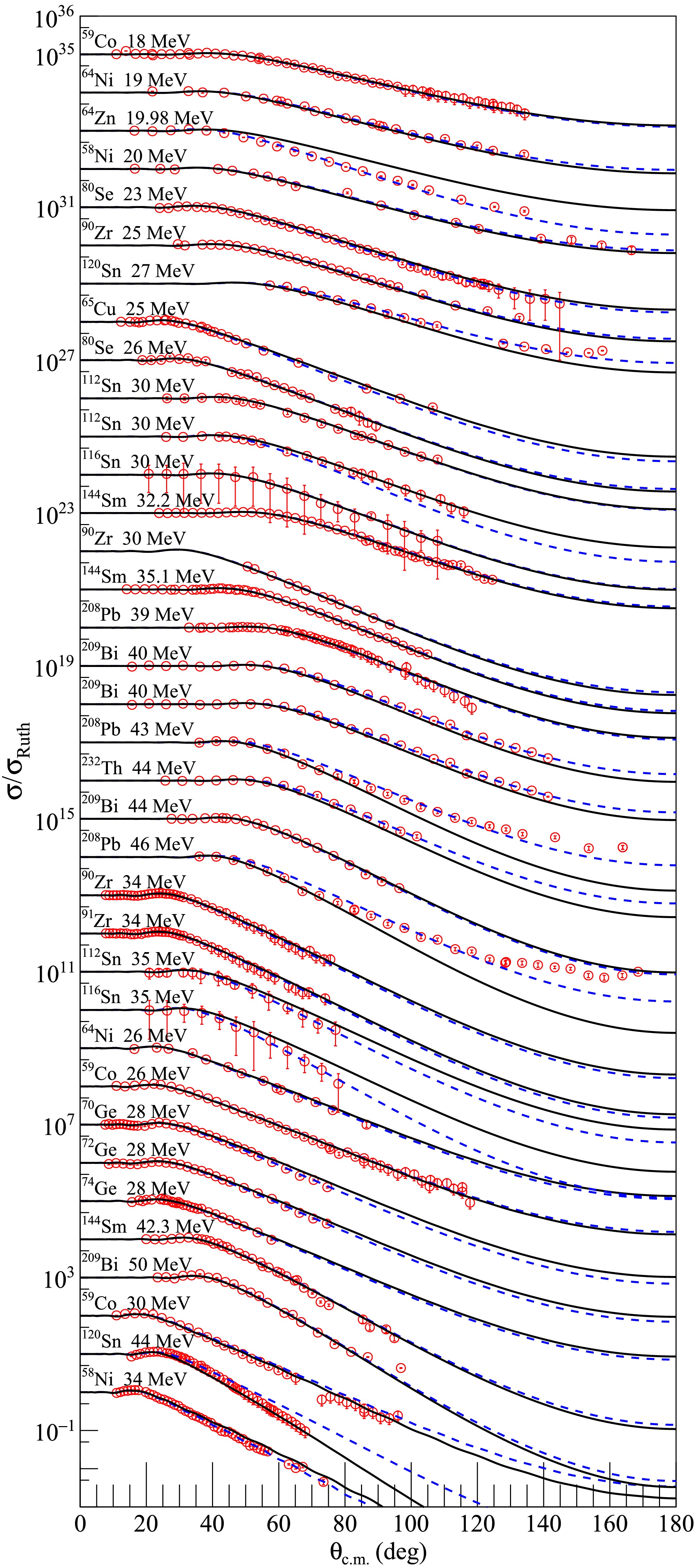

Figure 1.  (color online) Comparisons between optical model calculations and experimental data for ⁶Li elastic scattering from medium mass and heavy targets at incident energies indicated in the figure. The blue dashed and black solid curves represent results calculated with optimal and average values of rms proton radii, respectively. The data sets are offset for optimum view. The experimental data are from Refs. [36−55].

Figure 2.  (color online) Same as Fig. 1, but for ⁶Li at higher energies. The experimental data are from Refs. [56−58].

Figure 3.  (color online) Same as Fig. 1, but for ⁶Li at higher energies. The experimental data are from Refs. [59−61].

Figure 4.  (color online) Same as Fig. 1, but for ⁷Li projectile. The experimental data are from Refs. [39, 40, 45, 48, 53, 54, 62−74].

Figure 5.  (color online) Same as Fig. 1, but for ⁷Li at higher energies. The experimental data are from Refs. [58, 67].

Figure 6.  (color online) Same as Fig. 1, but for ⁸Li projectile. The experimental data are from Refs. [75−79].

Figure 7.  (color online) Same as Fig. 1, but for ¹⁰B and ¹¹B projectiles. The experimental data are from Refs. [80−85].

Projectile	Target	Energy(MeV)	Radii(fm)	$ {\chi^{2}} $	Ref.
6Li	40Ca	240	2.55	11.72	[60]
	48Ca	240	2.25	9.85	[60]
	58Ni	20	2.18	1.96	[52]
	58Ni	34	2.48	2.46	[44]
	58Ni	73.7	2.88	22.39	[56]
	58Ni	240	2.69	12.11	[61]
	59Co	18	2.4	9.86	[48]
	59Co	26	2.23	5.21	[48]
	59Co	30	2.13	12.29	[48]
	64Ni	19	2.15	3.22	[52]
	64Ni	26	2.42	0.88	[52]
	64Zn	19.98	2.88	31.66	[55]
	65Cu	25	2.44	54.75	[54]
	70Ge	28	2.46	1.03	[50]
	72Ge	28	2.44	0.98	[50]
	74Ge	28	2.42	0.74	[50]
	80Se	23	2.42	1.00	[53]
	80Se	26	2.21	1.03	[53]
	89Y	60	2.59	0.92	[58]
	90Zr	25	2.19	169.56	[49]
	90Zr	30	2.23	62.23	[49]
	90Zr	34	2.42	0.44	[45]
	90Zr	60	2.21	2.84	[58]
	90Zr	70	2.42	19.99	[57]
	90Zr	73.7	2.46	8.73	[56]
	90Zr	240	2.67	6.99	[61]
	91Zr	34	2.42	0.84	[45]
	112Sn	30	2.38	0.62	[46]
	112Sn	30	2.57	7.82	[47]
	112Sn	35	2.52	0.09	[43]
	116Sn	30	2.31	0.06	[43]
	116Sn	35	2.8	0.03	[43]
	116Sn	240	2.88	5.21	[59]
	120Sn	27	2.1	34.80	[51]
	120Sn	44	1.73	11.11	[38]
	124Sn	73.7	2.42	11.31	[56]
	144Sm	32.2	2.23	2.82	[40]
	144Sm	35.1	2.23	3.26	[40]
	144Sm	42.3	2.23	9.50	[40]
	208Pb	39	2.4	1.57	[42]
	208Pb	43	1.79	9.65	[37]
	208Pb	46	1.77	18.63	[37]
	208Pb	73.7	2.42	2.26	[56]
	209Bi	40	2.13	10.08	[36]
	209Bi	40	2.13	10.03	[41]
	209Bi	44	2.4	2.51	[36]
	209Bi	50	2.21	42.61	[36]
	232Th	44	2.08	0.48	[39]
7Li	40Ca	34	2.41	11.26	[66]
	40Ca	34	2.59	9.23	[67]
	44Ca	34	2.64	8.26	[67]
	46Ti	17	2.34	3.09	[74]
	48Ca	34	2.38	58.71	[67]
	54Fe	36	2.09	5.14	[67]
	54Fe	42	2.05	11.27	[67]
	54Fe	48	2.3	10.11	[67]
	56Fe	34	2.36	19.08	[67]
	58Ni	19	2.15	5.25	[74]
	58Ni	34	2.32	7.79	[67]
	58Ni	42	2.07	0.90	[64]
	59Co	18	2.15	2.81	[48]
	59Co	26	2.3	2.01	[48]
	59Co	30	2.2	8.01	[48]
	60Ni	34	2.41	19.32	[67]
	64Ni	19.3	2.2	0.23	[73]
	64Ni	26.4	2.26	2.05	[73]
	65Cu	25	2.09	27.99	[54]
	80Se	20	2.09	3.03	[53]
	80Se	23	2.07	2.37	[53]
	80Se	26	1.99	1.99	[53]
	89Y	60	2.09	1.50	[58]
	90Zr	34	2.09	0.96	[67]
	90Zr	34	2.24	0.47	[45]
	93Nb	28	2.18	173.53	[72]
	112Sn	28	2.07	130.56	[71]
	112Sn	30	2.28	0.21	[69]
	116Sn	28	2.09	893.60	[71]
	116Sn	30	2.09	1.17	[65]
	116Sn	35	2.3	0.94	[65]
	118Sn	28	2.22	266.41	[71]
	120Sn	28	2.09	92.42	[70]
	120Sn	28	2.11	86.61	[71]
	120Sn	30	2.09	226.13	[70]
	122Sn	28	2.13	599.16	[71]
	124Sn	28	2.09	184.44	[71]
	138Ba	30	2.24	1.20	[68]
	138Ba	32	2.28	0.89	[68]
	144Sm	40.8	2.01	1.96	[40]
	159Tb	44	2.07	9.17	[62]
	208Pb	42	1.92	19.04	[63]
	208Pb	42.6	2.2	0.92	[87]
	232Th	44	2.01	7.38	[39]
8Li	58Ni	19.6	2.59	5.68	[75]
	58Ni	23.9	1.69	2.40	[76]
	58Ni	26.1	1.65	1.80	[76]
	58Ni	27.8	1.32	2.93	[76]
	58Ni	30	1.65	4.48	[76]
	51V	18.5	1.65	0.35	[77]
	51V	26	2.03	3.21	[78]
	209Bi	38.5	2.42	0.82	[79]
	209Bi	39.4	2.45	0.34	[79]
10B	40Ca	46.6	2.42	4.39	[80]
	58Ni	35	2.26	10.14	[81]
	197Au	61	2.19	10.49	[82]
11B	40Ca	51.5	2.33	9.40	[80]
	58Ni	34.99	2.3	107.94	[85]
	208Pb	69	2.1	184.11	[83]
	209Bi	64.8	2.28	0.31	[84]
	209Bi	69	2.37	7.66	[84]
	209Bi	69.8	2.37	0.67	[84]
	209Bi	74.8	2.4	1.51	[84]
	209Bi	84.1	2.44	1.39	[84]

Table 1.  Experimental data analyzed in the present work for ^6,7,8Li, and ^10,11B from different targets, their references, and corresponding $ \chi^{2} $ values calculated with the extracted rms proton radii.

This outcome indicates that nucleon density distributions deviating from those predicted by Hartree-Fock calculations are necessary to more accurately reproduce the elastic scattering data. It is important to note that several factors, including experimental uncertainties, channel coupling effects, and the values of target nuclei radii, can influence the angular distributions of elastic scattering, thereby affecting the precision of the extracted projectile rms proton radii. Nevertheless, the systematic analysis incorporating a comprehensive set of experimental data is expected to yield relatively reliable rms proton radius values. As clearly illustrated in Figs. 1, 2, and 3, for most of the ⁶Li elastic scattering data, the angular distributions of the optimal fit exhibit a significant shift towards forward angles. This observation implies that, for ⁶Li projectiles, larger rms proton radii than those obtained from Hartree-Fock calculations should be adopted in optical model calculations. A similar trend was also evident in the ⁷Li elastic scattering results, although some angular distributions showed shifts towards larger angles, as depicted in Figs. 4 and 5. Conversely, the fitting results for most of the ⁸Li data suggest that the differential cross sections calculated using the original density distributions need to be enhanced to better match the experimental data. However, this does not necessarily imply that the rms proton radius of ⁸Li is smaller than the Hartree-Fock prediction. First, the potential parameters used in the fitting procedure were derived from the elastic scattering data analysis of the stable nucleus ⁹Be, and their applicability to ⁸Li elastic scattering data remains uncertain. Second, as discussed in Ref. [76], the ⁸Li + ⁵⁸Ni elastic scattering is strongly influenced by coupled direct reaction channels. Coupled-reaction channels calculations, which consider the coupling between elastic scattering and neutron transfer channels populating bound and unbound states of ⁵⁹Ni, have revealed that neutron stripping channels significantly impact the elastic cross sections, particularly enhancing the cross sections at large angles. Regarding the results for the stable nuclei ¹⁰B and ¹¹B shown in Fig. 7, the discrepancies between the fitted angular distributions and the calculations with unaltered density distributions were negligible, and both approaches could reasonably reproduce the experimental data. This result may suggest that the rms proton radii of these two nuclei do not require substantial modifications for use in optical model analysis of elastic scattering data. However, due to the limited availability of experimental data, additional investigations are warranted to extract more conclusive rms proton radii for ¹⁰B and ¹¹B nuclei.

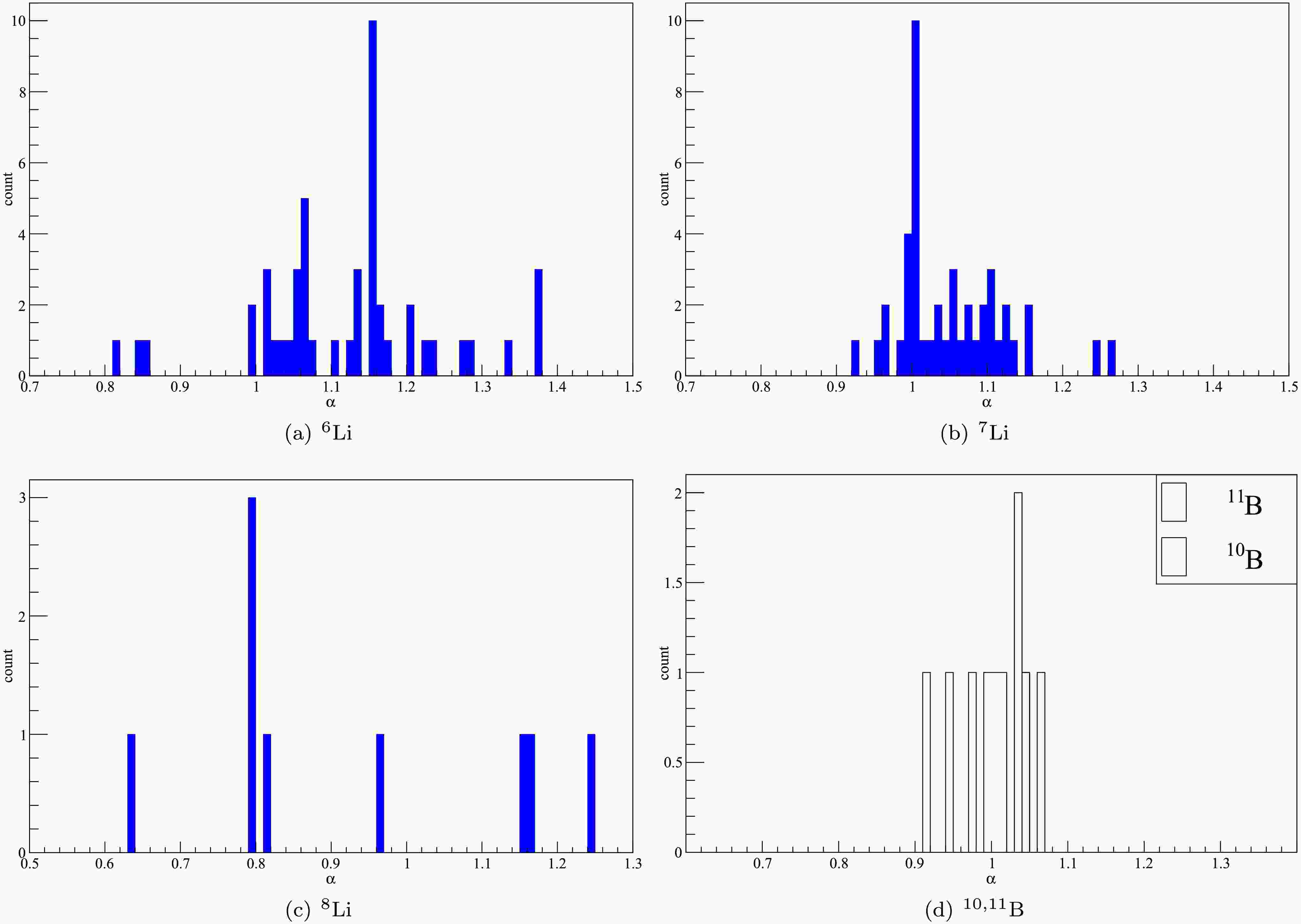
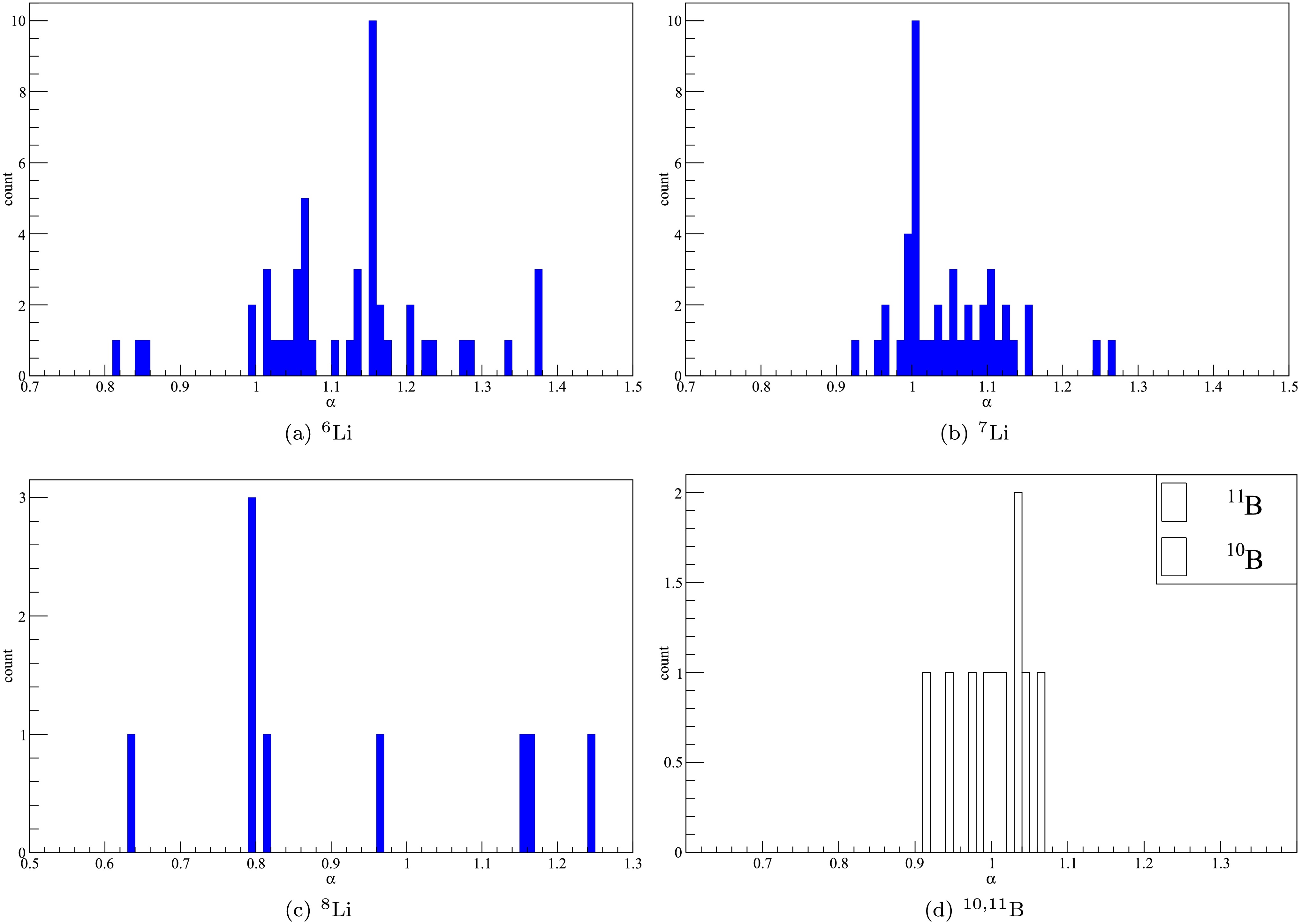
Distributions of the rms proton radii values of ^6,7,8Li and ^10,11B extracted from individual elastic scattering data fittings are presented in Fig. 9.

Figure 9.  (color online) Distributions of the rms proton radii values of ^6,7,8Li and ^10,11B.

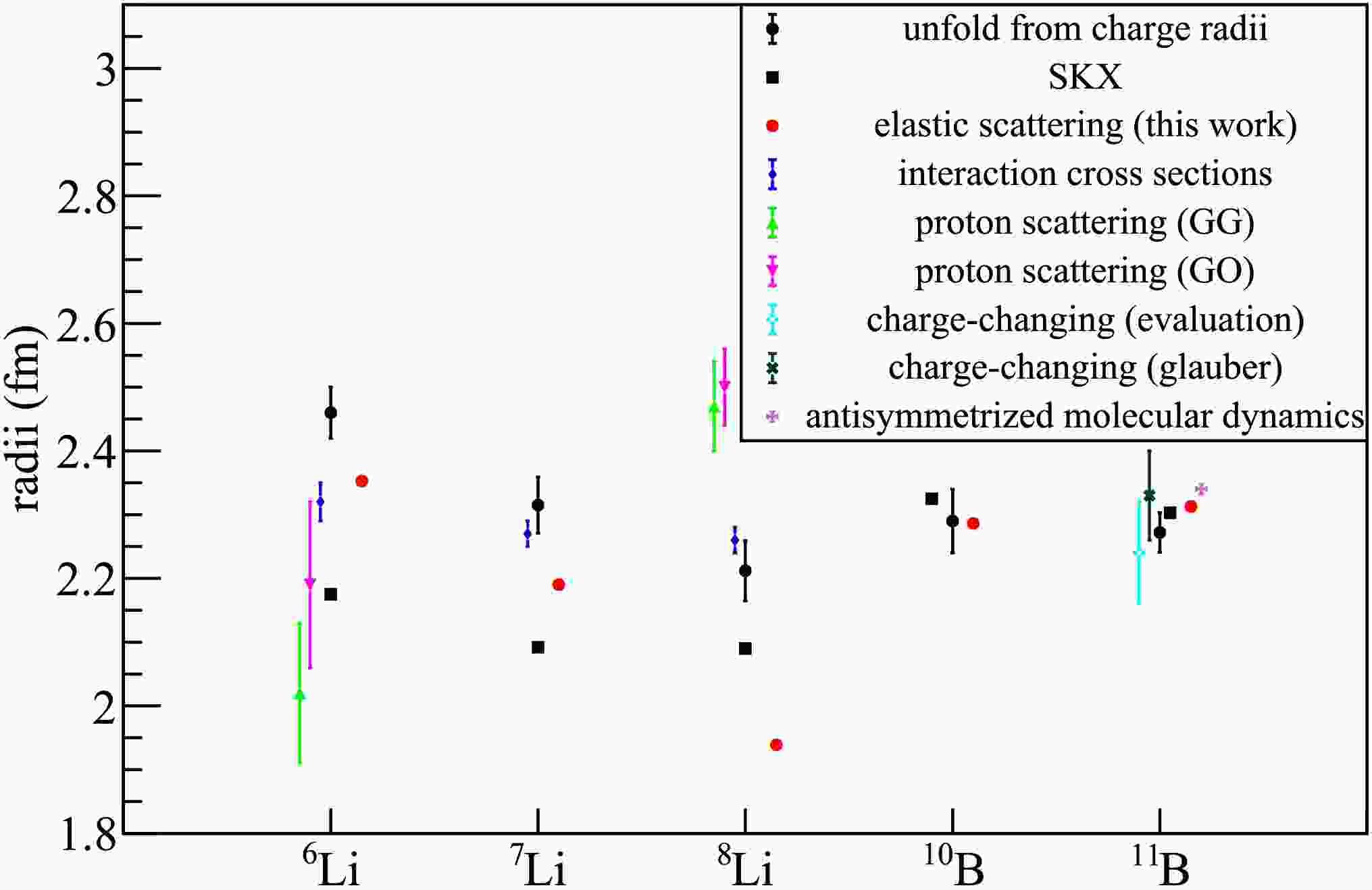
Notably, the optimal rescaling factors for ⁶Li and ⁷Li predominantly cluster in the range of $ \alpha > 1.00 $. In contrast, the rescaling factors for ⁸Li exhibit significant dispersion, and due to the limited number of data points, definitive conclusions remain a elusive challenge similarly encountered with ¹⁰B and ¹¹B. The average values of these distributions are adopted as the final rescaling factors for each projectile, demonstrating close correspondence to the central values of Gaussian functions fitted to the distributions. The final rescaling factors provide recommended rms proton radii for ⁶Li, ⁷Li, ⁸Li, ¹⁰B and ¹¹B, are 2.35, 2.19, 1.94, 2.29, and 2.31 fm.

The extracted proton rms radii from elastic scattering data analysis for ^6,7,8Li and ^10,11B are shown in Fig. 8. The average rms proton radii (red filled circles) for ⁶Li and ⁷Li exceed the Hartree-Fock predictions (black filled squares), whereas an opposite trend is observed for ⁸Li, consistent with the angular distribution results discussed earlier. Comparisons with experimental data derived from interaction cross sections [7], charge radii [2], and charge-changing cross sections [15] reveal that the extracted rms proton radii align more closely with experimental values than Hartree-Fock calculations, particularly for ¹⁰B and ¹¹B. This finding underscores the effectiveness of optical model analysis based on USNP systematics for extracting nuclear rms proton radii from elastic scattering data.

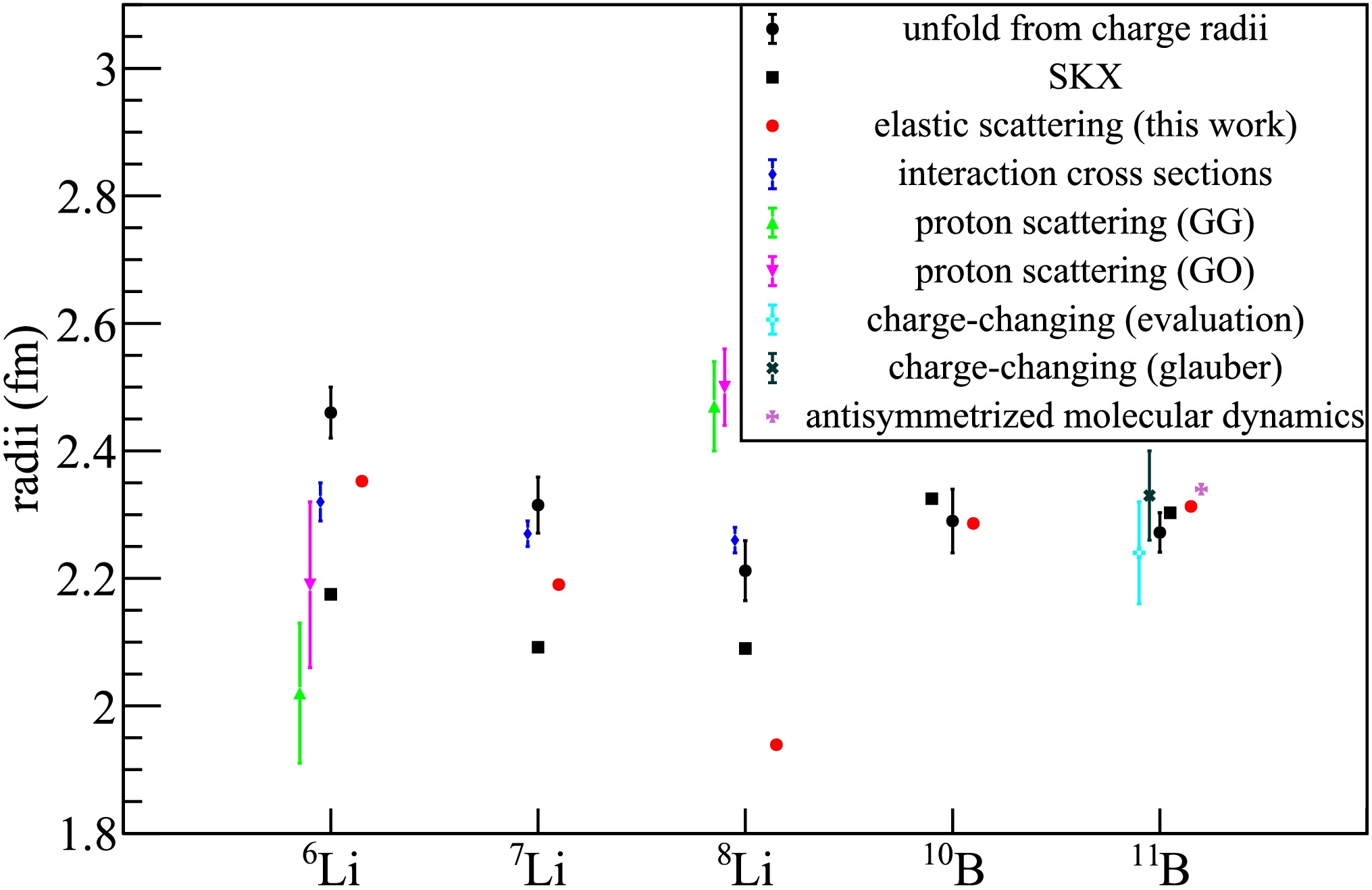
Figure 8.  (color online) Comparison of this work with other experimental and theoretical rms proton radii. References are listed as follow: unfold from charge radii[2]. interaction cross sections[7].charge-changing(Glauber)[15]. charge-changing(evaluation)[15]. anti-symmetrized molecular dynamic[15]. isotope shift[86]. proton scattering(GG)[86]. proton scattering(GO)[86]. Skyrme Hartree-Fock [20].

The optical model was employed to analyze the elastic scattering angular distributions of 112 datasets involving ^6,7,8Li and ^10,11B projectiles interacting with medium-mass and heavy targets at incident energies exceeding the Coulomb barriers. Subsequently, the root-mean-square (rms) proton radii of these projectiles were extracted. For the stable nuclei ^6,7Li and ^10,11B, the rms proton radii derived from the present analysis exhibit a more favorable agreement with experimental data than the predictions obtained from Hartree-Fock calculations. This outcome strongly suggests that systematic analysis of elastic scattering data represents an effective approach for extracting nuclear rms proton radii. In contrast, the extracted rms proton radius of ⁸Li is smaller, indicating the necessity of considering more intricate influences. These include the effects of strong couplings and the applicability of optical model parameters to weakly bound nuclei. Additionally, the current elastic scattering data for ⁸Li are limited in terms of the incident energy range and the variety of target nuclei investigated. Consequently, further experimental studies on ⁸Li are imperative to enable the extraction of rms proton radii using a systematic methodology.