-
The tensor force has been demonstrated to be crucial in accurately reproducing the properties of nuclear matter and explaining the D-wave mixing and binding energy in deuterons [1−6]. Studies have shown that the tensor force may play a significant role in the properties of neutron-rich nuclei with the new magic number, as well as in the order changes of single-particle orbits. The tensor force causes variations in single-particle energy, leading to shell evolution [3, 4]. It also contributes to the reduction of spin-orbit splitting [2, 3] and plays an attractive role in nuclear binding energy [1, 2].
The study of short-range correlations has revealed that the high-momentum component in the wave functions of nucleon momentum distribution, which is greater than the Fermi momentum, is primarily due to the tensor force inductions of proton-neutron correlated pairs [7−9]. The spins of the neutron and proton (
$ {\boldsymbol{s}}_{\boldsymbol{n}} $ ,$ {\boldsymbol{s}}_{\boldsymbol{p}} $ ) can be either parallel (I=1; l=0, 1, 2) or antiparallel (I=0; l=1), where$ {\boldsymbol{I}}={\boldsymbol{s}}_{\boldsymbol{n}}+{\boldsymbol{s}}_{\boldsymbol{p}} $ and$ {\boldsymbol{J}}={\boldsymbol{I}}+{\boldsymbol{l}} $ . There are four ways to couple$ {\boldsymbol{s}}_{\boldsymbol{n}} $ ,$ {\boldsymbol{s}}_{\boldsymbol{p}} $ , and$ {\boldsymbol{l}} $ to obtain a measured total J = 1 for the deuteron. The parity of the deuteron is linked to the orbital motion of (-1)$ ^{l} $ . The observed even parity for the deuteron eliminates the combination of spins that include l=1, leaving only l=0 and l=2 as possibilities. The wave function of the deuteron is therefore a mixture of S and D components.The spin and isospin of nucleons in a proton-neutron (
$ pn $ ) pair can be combined into different channels. The tensor force has a strong population strength for the spin and isospin in the$ J, T $ = 1, 0 channel but a weaker one for the$ J, T $ = 0, 1 channel [6]. The proton-neutron tensor monopole interaction (T = 0) is twice as strong as the T = 1 interaction [3, 4]. For the same radial condition of the wave function, larger orbital angular momenta of the proton and neutron subshell may intensively enhance the tensor monopole effect when their relative momentum becomes higher [1, 8].The interaction properties of the tensor force component are determined by the orientation direction of the spins of the proton and neutron relative to the direction of the vector connecting them [10]. The tensor force operates between two nucleons with their spins aligned, and the interaction is attractive when the spins are parallel to the line connecting the two nucleons and repulsive when the spins are perpendicular to this line [10].
The configuration of the two-body cluster in
$ ^{6} $ Li can be represented by p-shell nucleons of a$ pn $ pair (deuteron) coupled to s-shell nucleons of the α core with intrinsic spin 1 and intrinsic orbital angular momentum l = 0, as well as relative momentum L = 0, resulting in the 1$ ^{+} $ ground state and the excited triplet states 1$ ^{+} $ , 2$ ^{+} $ , 3$ ^{+} $ with isospin T = 0 of$ ^{6} $ Li from L = 2 [11]. The cluster-cluster spin-orbit force splits the L = 2 into these triplet states, where L is the orbital momentum coupling of the$ pn $ pair and α. The small magnitude, with a negative sign, for the electric quadrupole moment of$ ^{6} $ Li was proposed to be explained by the inclusion of the cluster-cluster tensor interaction, which introduces a small L = 2 component into the$ ^{6} $ Li states [11].In this letter, we present an inspired aspect of the tensor force effect enhancement derived from the isospin T = 0 state with large spin
$ J^{\pi} $ = 3$ ^{+} $ in the free$ ^{6} $ Li, while a shrinking effect is evident in the$ ^{6} $ Li cluster inside the nucleus due to the nuclear medium. In contrast, the isospin T=1 with$ J^{\pi} $ = 0$ ^{+} $ state maintains an equal excitation strength in these two different$ ^{6} $ Li formations. -
The tensor force has been demonstrated to be crucial in accurately reproducing the properties of nuclear matter and explaining the D-wave mixing and binding energy in deuterons [1−6]. Studies have shown that the tensor force may play a significant role in the properties of neutron-rich nuclei with the new magic number, as well as in the order changes of single-particle orbits. The tensor force causes variations in single-particle energy, leading to shell evolution [3, 4]. It also contributes to the reduction of spin-orbit splitting [2, 3] and plays an attractive role in nuclear binding energy [1, 2].
The study of short-range correlations has revealed that the high-momentum component in the wave functions of nucleon momentum distribution, which is greater than the Fermi momentum, is primarily due to the tensor force inductions of proton-neutron correlated pairs [7−9]. The spins of the neutron and proton (
$ {\boldsymbol{s}}_{\boldsymbol{n}} $ ,$ {\boldsymbol{s}}_{\boldsymbol{p}} $ ) can be either parallel (I=1; l=0, 1, 2) or antiparallel (I=0; l=1), where$ {\boldsymbol{I}}={\boldsymbol{s}}_{\boldsymbol{n}}+{\boldsymbol{s}}_{\boldsymbol{p}} $ and$ {\boldsymbol{J}}={\boldsymbol{I}}+{\boldsymbol{l}} $ . There are four ways to couple$ {\boldsymbol{s}}_{\boldsymbol{n}} $ ,$ {\boldsymbol{s}}_{\boldsymbol{p}} $ , and$ {\boldsymbol{l}} $ to obtain a measured total J = 1 for the deuteron. The parity of the deuteron is linked to the orbital motion of (-1)$ ^{l} $ . The observed even parity for the deuteron eliminates the combination of spins that include l=1, leaving only l=0 and l=2 as possibilities. The wave function of the deuteron is therefore a mixture of S and D components.The spin and isospin of nucleons in a proton-neutron (
$ pn $ ) pair can be combined into different channels. The tensor force has a strong population strength for the spin and isospin in the$ J, T $ = 1, 0 channel but a weaker one for the$ J, T $ = 0, 1 channel [6]. The proton-neutron tensor monopole interaction (T = 0) is twice as strong as the T = 1 interaction [3, 4]. For the same radial condition of the wave function, larger orbital angular momenta of the proton and neutron subshell may intensively enhance the tensor monopole effect when their relative momentum becomes higher [1, 8].The interaction properties of the tensor force component are determined by the orientation direction of the spins of the proton and neutron relative to the direction of the vector connecting them [10]. The tensor force operates between two nucleons with their spins aligned, and the interaction is attractive when the spins are parallel to the line connecting the two nucleons and repulsive when the spins are perpendicular to this line [10].
The configuration of the two-body cluster in
$ ^{6} $ Li can be represented by p-shell nucleons of a$ pn $ pair (deuteron) coupled to s-shell nucleons of the α core with intrinsic spin 1 and intrinsic orbital angular momentum l = 0, as well as relative momentum L = 0, resulting in the 1$ ^{+} $ ground state and the excited triplet states 1$ ^{+} $ , 2$ ^{+} $ , 3$ ^{+} $ with isospin T = 0 of$ ^{6} $ Li from L = 2 [11]. The cluster-cluster spin-orbit force splits the L = 2 into these triplet states, where L is the orbital momentum coupling of the$ pn $ pair and α. The small magnitude, with a negative sign, for the electric quadrupole moment of$ ^{6} $ Li was proposed to be explained by the inclusion of the cluster-cluster tensor interaction, which introduces a small L = 2 component into the$ ^{6} $ Li states [11].In this letter, we present an inspired aspect of the tensor force effect enhancement derived from the isospin T = 0 state with large spin
$ J^{\pi} $ = 3$ ^{+} $ in the free$ ^{6} $ Li, while a shrinking effect is evident in the$ ^{6} $ Li cluster inside the nucleus due to the nuclear medium. In contrast, the isospin T=1 with$ J^{\pi} $ = 0$ ^{+} $ state maintains an equal excitation strength in these two different$ ^{6} $ Li formations. -
The tensor force has been demonstrated to be crucial in accurately reproducing the properties of nuclear matter and explaining the D-wave mixing and binding energy in deuterons. Studies have shown that the tensor force may play a significant role in the properties of neutron-rich nuclei with the new magic number, as well as in the order changes of single-particle orbits. The tensor force causes variations in single-particle energy, leading to shell evolution [1]. It also contributes to the reduction of spin-orbit splitting [2, 3] and plays an attractive role in nuclear binding energy [4].
The study of short-range correlations has revealed that the high-momentum component in the wave functions of nucleon momentum distribution, which is greater than the Fermi momentum, is primarily due to the tensor force inductions of proton-neutron correlated pairs [5, 6]. The spins of the neutron and proton (
$ {\boldsymbol{s}}_{\boldsymbol{n}} $ ,$ {\boldsymbol{s}}_{\boldsymbol{p}} $ ) can be either parallel (I=1; l=0, 1, 2) or antiparallel (I=0; l=1), where$ {\boldsymbol{I}}={\boldsymbol{s}}_{\boldsymbol{n}}+{\boldsymbol{s}}_{\boldsymbol{p}} $ and$ {\boldsymbol{J}}={\boldsymbol{I}}+{\boldsymbol{l}} $ . There are four ways to couple$ {\boldsymbol{s}}_{\boldsymbol{n}} $ ,$ {\boldsymbol{s}}_{\boldsymbol{p}} $ , and$ {\boldsymbol{l}} $ to obtain a measured total J = 1 for the deuteron. The parity of the deuteron is linked to the orbital motion of (-1)$ ^{l} $ . The observed even parity for the deuteron eliminates the combination of spins that include l=1, leaving only l=0 and l=2 as possibilities. The wave function of the deuteron is therefore a mixture of S and D components.The spin and isospin of nucleons in a proton-neutron (
$ pn $ ) pair can be combined into different channels. The tensor force has a strong population strength for the spin and isospin in the$ J, T $ = 1, 0 channel but a weaker one for the$ J, T $ = 0, 1 channel [7]. The proton-neutron tensor monopole interaction (T = 0) is twice as strong as the T = 1 interaction [8]. For the same radial condition of the wave function, larger orbital angular momenta of the proton and neutron subshell may intensively enhance the tensor monopole effect when their relative momentum becomes higher [1, 8].The interaction properties of the tensor force component are determined by the orientation direction of the spins of the proton and neutron relative to the direction of the vector connecting them [9]. The tensor force operates between two nucleons with their spins aligned, and the interaction is attractive when the spins are parallel to the line connecting the two nucleons and repulsive when the spins are perpendicular to this line [9].
The configuration of the two-body cluster in
$ ^{6} $ Li can be represented by p-shell nucleons of a$ pn $ pair (deuteron) coupled to s-shell nucleons of the α core with intrinsic spin 1 and intrinsic orbital angular momentum l = 0, as well as relative momentum L = 0, resulting in the 1$ ^{+} $ ground state and the excited triplet states 1$ ^{+} $ , 2$ ^{+} $ , 3$ ^{+} $ with isospin T = 0 of$ ^{6} $ Li from L = 2 [10]. The cluster-cluster spin-orbit force splits the L = 2 into these triplet states, where L is the orbital momentum coupling of the$ pn $ pair and α. The small magnitude, with a negative sign, for the electric quadrupole moment of$ ^{6} $ Li was proposed to be explained by the inclusion of the cluster-cluster tensor interaction, which introduces a small L = 2 component into the$ ^{6} $ Li states [10].In this letter, we present an inspired aspect of the tensor force effect enhancement derived from the isospin T = 0 state with large spin
$ J^{\pi} $ = 3$ ^{+} $ in the free$ ^{6} $ Li, while a shrinking effect is evident in the$ ^{6} $ Li cluster inside the nucleus due to the nuclear medium. In contrast, the isospin T=1 with$ J^{\pi} $ = 0$ ^{+} $ state maintains an equal excitation strength in these two different$ ^{6} $ Li formations. -
The tensor force, a critical component of the nucleon-nucleon (NN) interaction [1, 2, 12−14], arises from the exchange of pions and other mesons. Its operator form is distinct from central and spin-orbit forces and is given by:
$ \begin{aligned} \begin{split} V_{\rm tensor}=S_{12}(\frac{3({\boldsymbol{\sigma}}_{1}\cdot{\boldsymbol{r}})({\boldsymbol{\sigma}}_{2}\cdot{\boldsymbol{r}})}{r^{2}}-{\boldsymbol{\sigma}}_{1}\cdot{\boldsymbol{\sigma}}_{2})\cdot V(r), \end{split} \end{aligned} $
(1) where
$ S_{12} $ is the tensor operator,$ \sigma_{i} $ are the Pauli spin matrices, and$ V(r) $ is the radial dependence. This force dominates in spin-triplet (S=1) channels and drives key nuclear phenomena such as the deuteron D-state admixture, shell evolution, and high-momentum nucleon pairs. Unlike central forces, the tensor interaction depends on the orientation of nucleon spins relative to their separation vector, leading to anisotropic coupling. Its isospin dependence (T=0 is stronger than T=1) is pivotal in explaining the observed asymmetry in excitation strengths between$ J^{\pi}(T)=3^{+}(0) $ and$ 0^{+}(1) $ states in$ ^{6} $ Li. -
The tensor force, a critical component of the nucleon-nucleon (NN) interaction, arises from the exchange of pions and other mesons. Its operator form is distinct from central and spin-orbit forces and is given by:
$ \begin{aligned} \begin{split} V_{tensor}=S_{12}(\frac{3({\boldsymbol{\sigma}}_{1}\cdot{\boldsymbol{r}})({\boldsymbol{\sigma}}_{2}\cdot{\boldsymbol{r}})}{r^{2}}-{\boldsymbol{\sigma}}_{1}\cdot{\boldsymbol{\sigma}}_{2})\cdot V(r), \end{split} \end{aligned} $

(1) where
$ S_{12} $ is the tensor operator,$ \sigma_{i} $ are the Pauli spin matrices, and$ V(r) $ is the radial dependence. This force dominates in spin-triplet (S=1) channels and drives key nuclear phenomena such as the deuteron D-state admixture, shell evolution, and high-momentum nucleon pairs. Unlike central forces, the tensor interaction depends on the orientation of nucleon spins relative to their separation vector, leading to anisotropic coupling. Its isospin dependence (T=0 is stronger than T=1) is pivotal in explaining the observed asymmetry in excitation strengths between$ J^{\pi}(T)=3^{+}(0) $ and$ 0^{+}(1) $ states in$ ^{6} $ Li. -
The tensor force, a critical component of the nucleon-nucleon (NN) interaction [1, 2, 12−14], arises from the exchange of pions and other mesons. Its operator form is distinct from central and spin-orbit forces and is given by:
$ \begin{aligned} \begin{split} V_{\rm tensor}=S_{12}(\frac{3({\boldsymbol{\sigma}}_{1}\cdot{\boldsymbol{r}})({\boldsymbol{\sigma}}_{2}\cdot{\boldsymbol{r}})}{r^{2}}-{\boldsymbol{\sigma}}_{1}\cdot{\boldsymbol{\sigma}}_{2})\cdot V(r), \end{split} \end{aligned} $
(1) where
$ S_{12} $ is the tensor operator,$ \sigma_{i} $ are the Pauli spin matrices, and$ V(r) $ is the radial dependence. This force dominates in spin-triplet (S=1) channels and drives key nuclear phenomena such as the deuteron D-state admixture, shell evolution, and high-momentum nucleon pairs. Unlike central forces, the tensor interaction depends on the orientation of nucleon spins relative to their separation vector, leading to anisotropic coupling. Its isospin dependence (T=0 is stronger than T=1) is pivotal in explaining the observed asymmetry in excitation strengths between$ J^{\pi}(T)=3^{+}(0) $ and$ 0^{+}(1) $ states in$ ^{6} $ Li. -
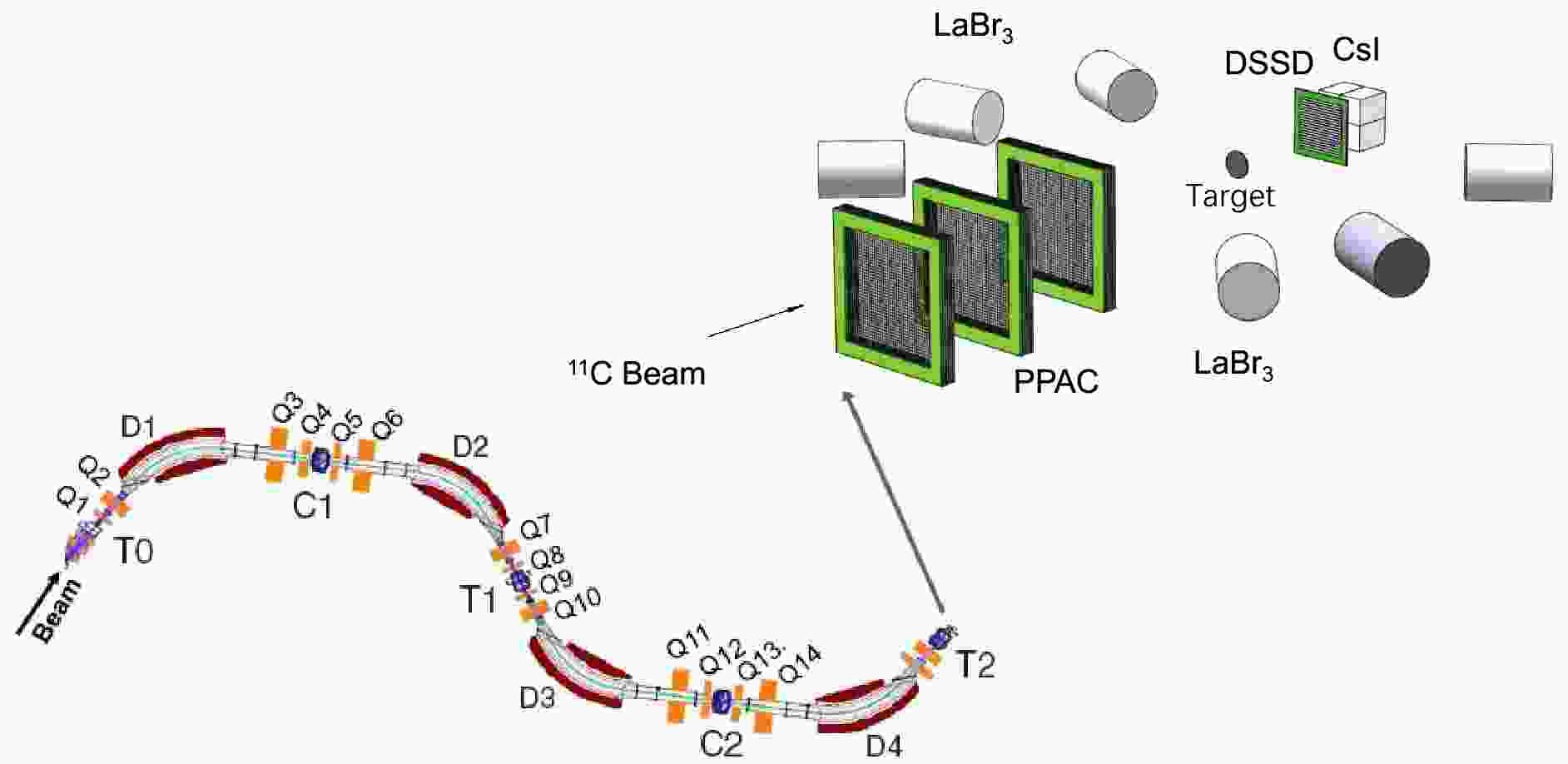
The present experimental measurement was performed at the Radioactive Ion Beam Line at the Heavy Ion Research Facility in Lanzhou (HIRFL-RIBLL) [15, 16], as shown in Fig. 1. A 60 MeV/nucleon
$ ^{12} $ C beam was transferred to bombard a 3.5 mm$ ^{9} $ Be target to produce about a 25 MeV/nucleon$ ^{11} $ C secondary beam with a purity of about 99% and an intensity of about 10$ ^{4} $ particles per second. The beam particles were identified using the$ B\rho- $ TOF$ -\Delta E $ method with the magnets and two plastic scintillator detectors in the beam line. The$ ^{11} $ C secondary beam was bombarded on a 50 mg/cm$ ^{2} $ carbon target to produce the breakup reaction.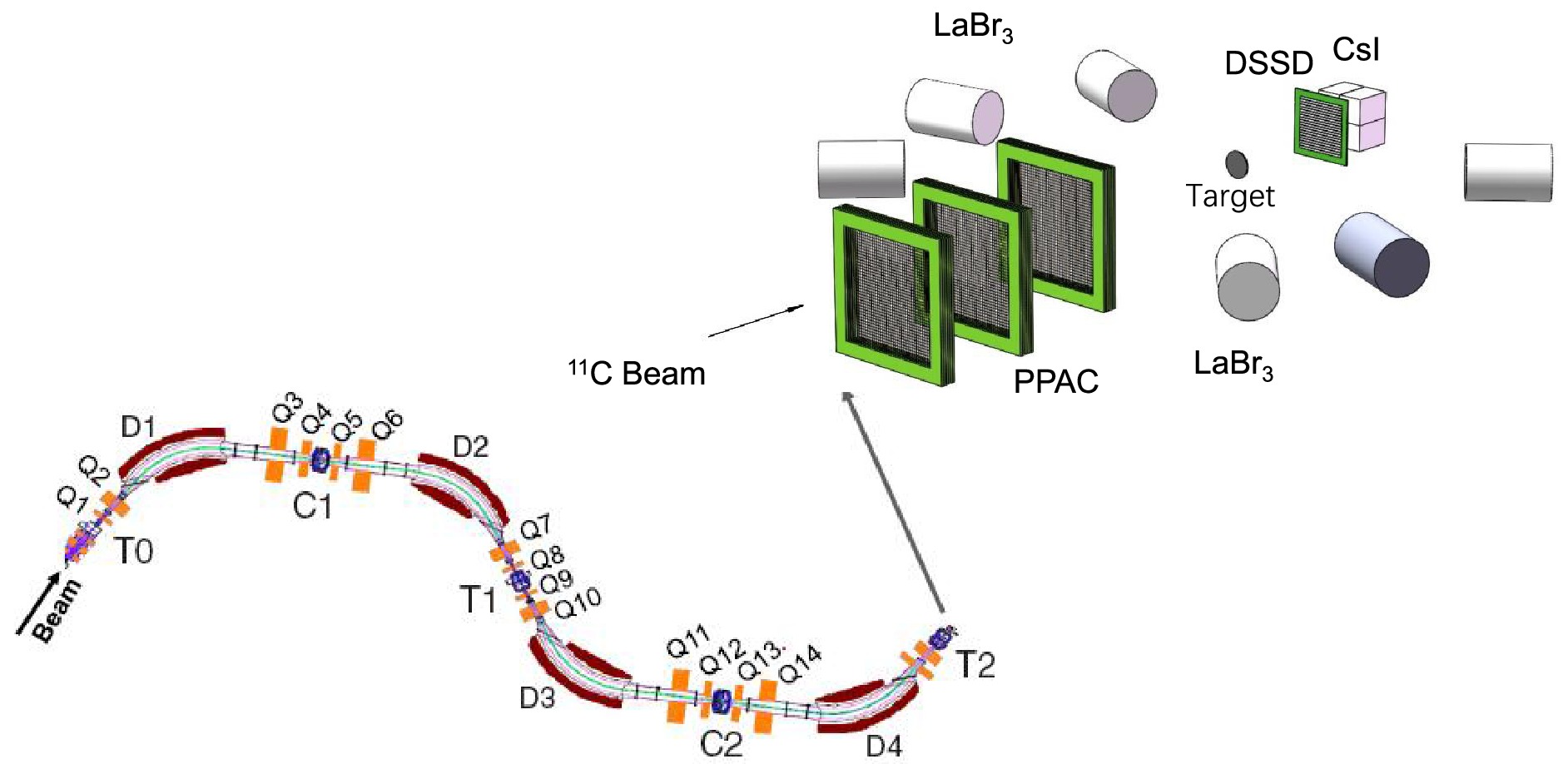
Figure 1. (color online) The experimental equipment consists of three PPACs for determining the reaction position of the beam particle on the target. The reaction products were detected by a DSSD silicon detector combined with a 2
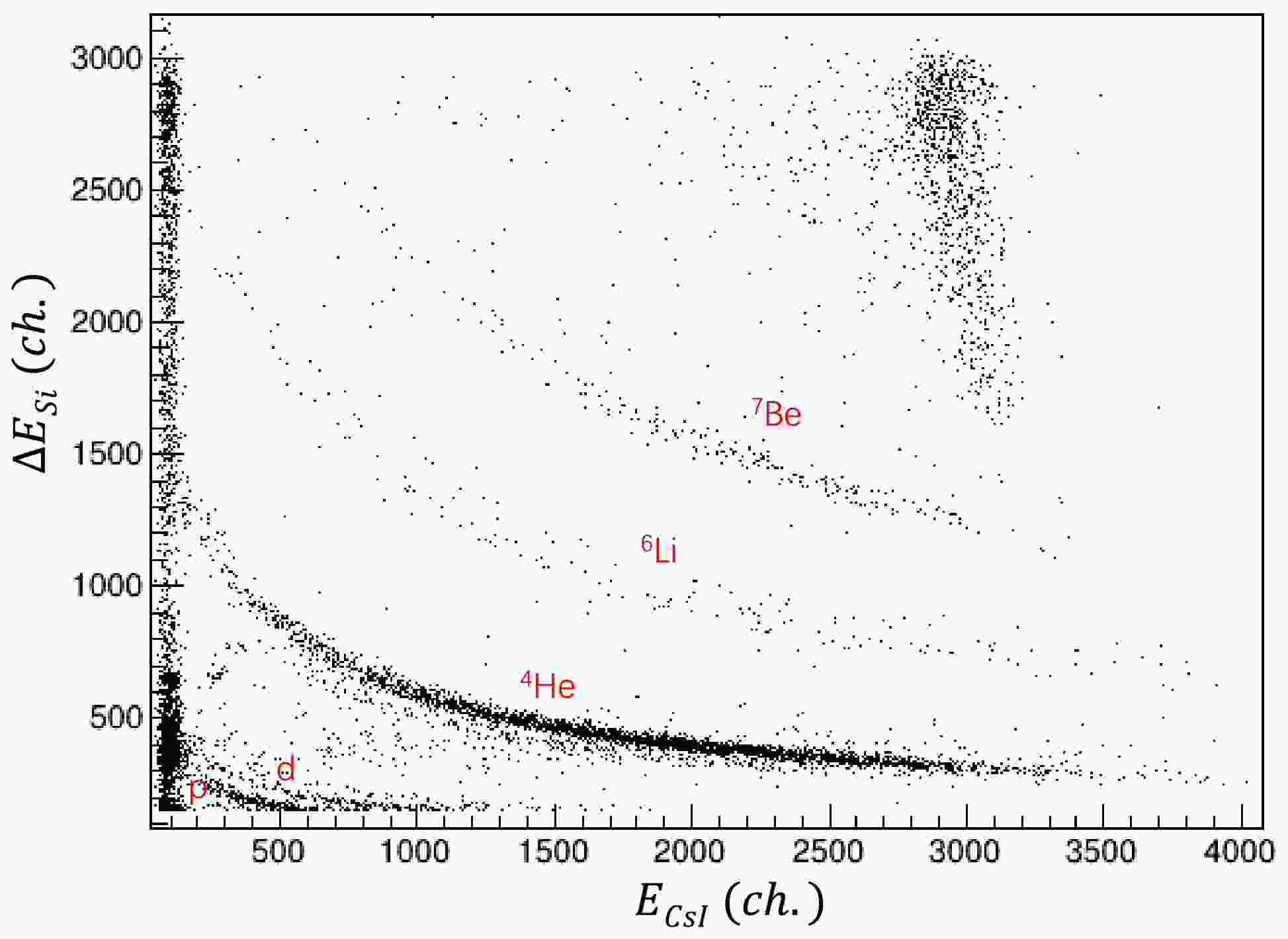
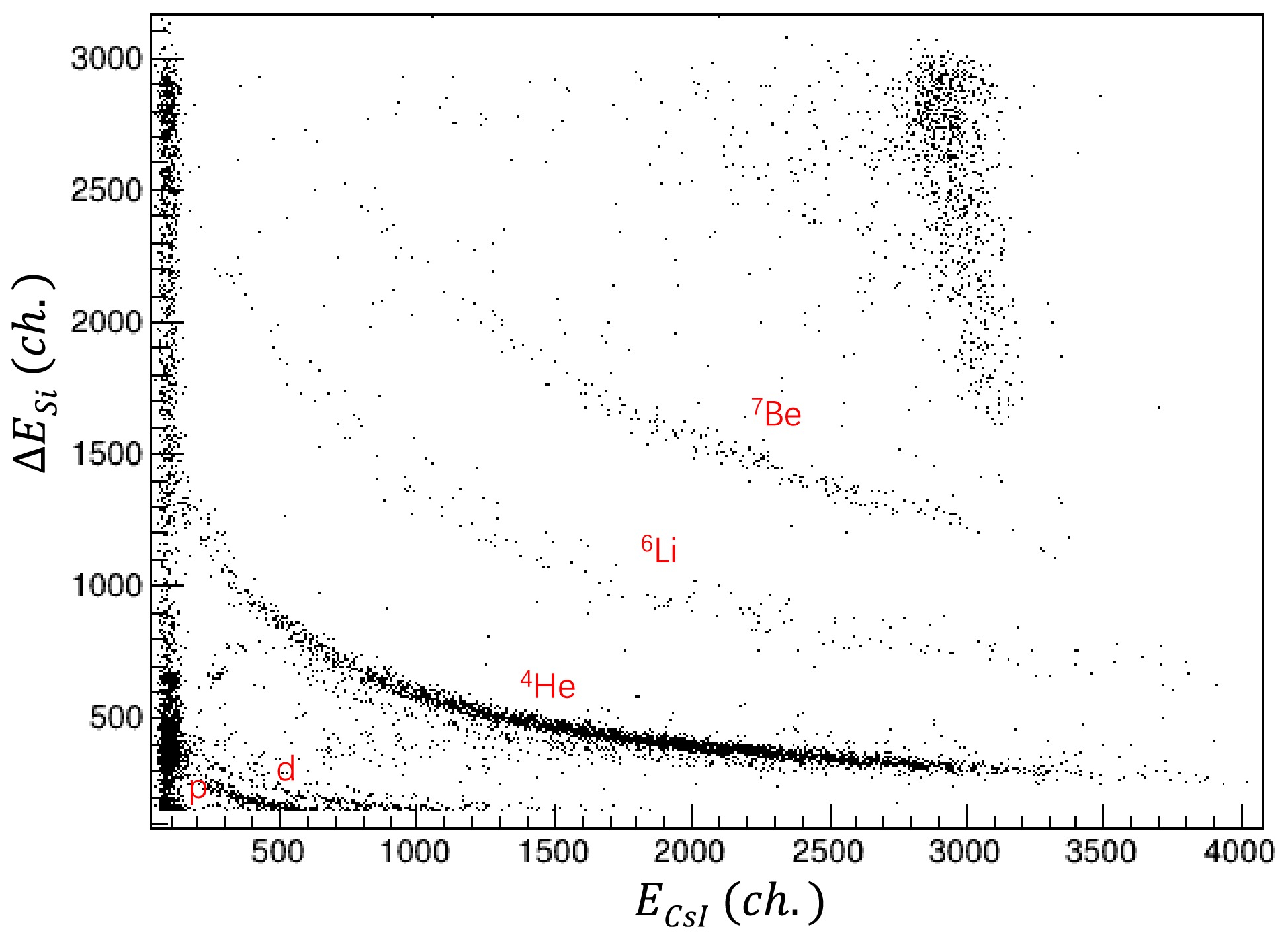
$ \times $ 2 CsI(Tl) scintillator array, and the decay γs were detected by five LaBr$ _{3} $ (Ce) and one NaI scintillator detector.Three parallel plate avalanche chambers (PPACs) with a 50×50 mm2 active area and position resolutions of about 1 mm (FWHM) in both the X and Y directions were placed in front of the target to track the incident 11C beam and subsequently determine the reaction vertex in the target. d and α particles are detected by the zero-degree telescope system, which consists of a double-sided silicon strip detector (DSSD, 148 μm in thickness and 50×50 mm2 in cross-sectional area) with 32 strips on both the front and back sides, and a 2×2 photodiode (PD) readout CsI (Tl) scintillator (25×25×30 mm3 size for each unit) array. Each CsI (Tl) scintillator is covered by two layers of high-reflection Tyvek paper and a 10 μm aluminum-coated Mylar film as a window. The PD is coupled to the CsI (Tl) scintillator with photoconductive silicone grease. The angular coverage of the zero-degree telescope is about 0−9°. Five LaBr3 (Ce) and one NaI scintillator detectors were placed around the target to measure the decayed γs from the excited fragments. The DSSD was utilized to record the ΔE energy and the position of the detecting fragments; therefore, the emission angle may be obtained by combining with the reaction vertex in the target. The CsI (Tl) detection system provides the residual E energy of the fragments. Particle identifications (PID) for α particles and d were performed using the ΔE-E contour as shown in Fig. 2. The energy resolution with sigma of this ΔE-E detection system is estimated to be ~0.8 MeV from numerical simulation.
-
The present experimental measurement was performed at the Radioactive Ion Beam Line at the Heavy Ion Research Facility in Lanzhou (HIRFL-RIBLL) [11], as shown in Fig. 1. A 60 MeV/nucleon
$ ^{12} $ C beam was transferred to bombard a 3.5 mm$ ^{9} $ Be target to produce about a 25 MeV/nucleon$ ^{11} $ C secondary beam with a purity of about 99% and an intensity of about 10$ ^{4} $ particles per second. The beam particles were identified using the$ B\rho- $ TOF$ -\Delta E $ method with the magnets and two plastic scintillator detectors in the beam line [26]. The$ ^{11} $ C secondary beam was bombarded on a 50 mg/cm$ ^{2} $ carbon target to produce the breakup reaction.
Figure 1. (color online) The experimental equipment consists of three PPACs for determining the reaction position of the beam particle on the target. The reaction products were detected by a DSSD silicon detector combined with a 2
$ \times $ 2 CsI(Tl) scintillator array, and the decay γs were detected by five LaBr$ _{3} $ (Ce) and one NaI scintillator detector.Three parallel plate avalanche chambers (PPACs) with a 50
$ \times $ 50 mm$ ^{2} $ active area and position resolutions of about 1 mm (FWHM) in both the X and Y directions were placed in front of the target to track the incident$ ^{11} $ C beam [12] and subsequently determine the reaction vertex in the target. d and α particles are detected by the zero-degree telescope system, which consists of a double-sided silicon strip detector (DSSD, 148 μm in thickness and 50$ \times $ 50 mm$ ^{2} $ in cross-sectional area) with 32 strips on both the front and back sides, and a 2$ \times $ 2 photodiode (PD) readout CsI (Tl) scintillator (25$ \times $ 25$ \times $ 30 mm$ ^{3} $ size for each unit) array. Each CsI (Tl) scintillator is covered by two layers of high-reflection Tyvek paper and a 10 μm aluminum-coated Mylar film as a window. The PD is coupled to the CsI (Tl) scintillator with photoconductive silicone grease. The angular coverage of the zero-degree telescope is about 0-9$ ^{\circ} $ . Five LaBr$ _{3} $ (Ce) and one NaI scintillator detectors were placed around the target to measure the decayed γs from the excited fragments. The DSSD was utilized to record the ΔE energy and the position of the detecting fragments; therefore, the emission angle may be obtained by combining with the reaction vertex in the target. The CsI (Tl) detection system provides the residual E energy of the fragments. Particle identifications (PID) for α particles and d were performed using the ΔE-E contour as shown in Fig. 2. The energy resolution with sigma of this ΔE-E detection system is estimated to be$ \sim $ 0.8 MeV from numerical simulation. -
The present experimental measurement was performed at the Radioactive Ion Beam Line at the Heavy Ion Research Facility in Lanzhou (HIRFL-RIBLL) [15, 16], as shown in Fig. 1. A 60 MeV/nucleon
$ ^{12} $ C beam was transferred to bombard a 3.5 mm$ ^{9} $ Be target to produce about a 25 MeV/nucleon$ ^{11} $ C secondary beam with a purity of about 99% and an intensity of about 10$ ^{4} $ particles per second. The beam particles were identified using the$ B\rho- $ TOF$ -\Delta E $ method with the magnets and two plastic scintillator detectors in the beam line. The$ ^{11} $ C secondary beam was bombarded on a 50 mg/cm$ ^{2} $ carbon target to produce the breakup reaction.
Figure 1. (color online) The experimental equipment consists of three PPACs for determining the reaction position of the beam particle on the target. The reaction products were detected by a DSSD silicon detector combined with a 2
$ \times $ 2 CsI(Tl) scintillator array, and the decay γs were detected by five LaBr$ _{3} $ (Ce) and one NaI scintillator detector.Three parallel plate avalanche chambers (PPACs) with a 50×50 mm2 active area and position resolutions of about 1 mm (FWHM) in both the X and Y directions were placed in front of the target to track the incident 11C beam and subsequently determine the reaction vertex in the target. d and α particles are detected by the zero-degree telescope system, which consists of a double-sided silicon strip detector (DSSD, 148 μm in thickness and 50×50 mm2 in cross-sectional area) with 32 strips on both the front and back sides, and a 2×2 photodiode (PD) readout CsI (Tl) scintillator (25×25×30 mm3 size for each unit) array. Each CsI (Tl) scintillator is covered by two layers of high-reflection Tyvek paper and a 10 μm aluminum-coated Mylar film as a window. The PD is coupled to the CsI (Tl) scintillator with photoconductive silicone grease. The angular coverage of the zero-degree telescope is about 0−9°. Five LaBr3 (Ce) and one NaI scintillator detectors were placed around the target to measure the decayed γs from the excited fragments. The DSSD was utilized to record the ΔE energy and the position of the detecting fragments; therefore, the emission angle may be obtained by combining with the reaction vertex in the target. The CsI (Tl) detection system provides the residual E energy of the fragments. Particle identifications (PID) for α particles and d were performed using the ΔE-E contour as shown in Fig. 2. The energy resolution with sigma of this ΔE-E detection system is estimated to be ~0.8 MeV from numerical simulation.
-
The excited state of
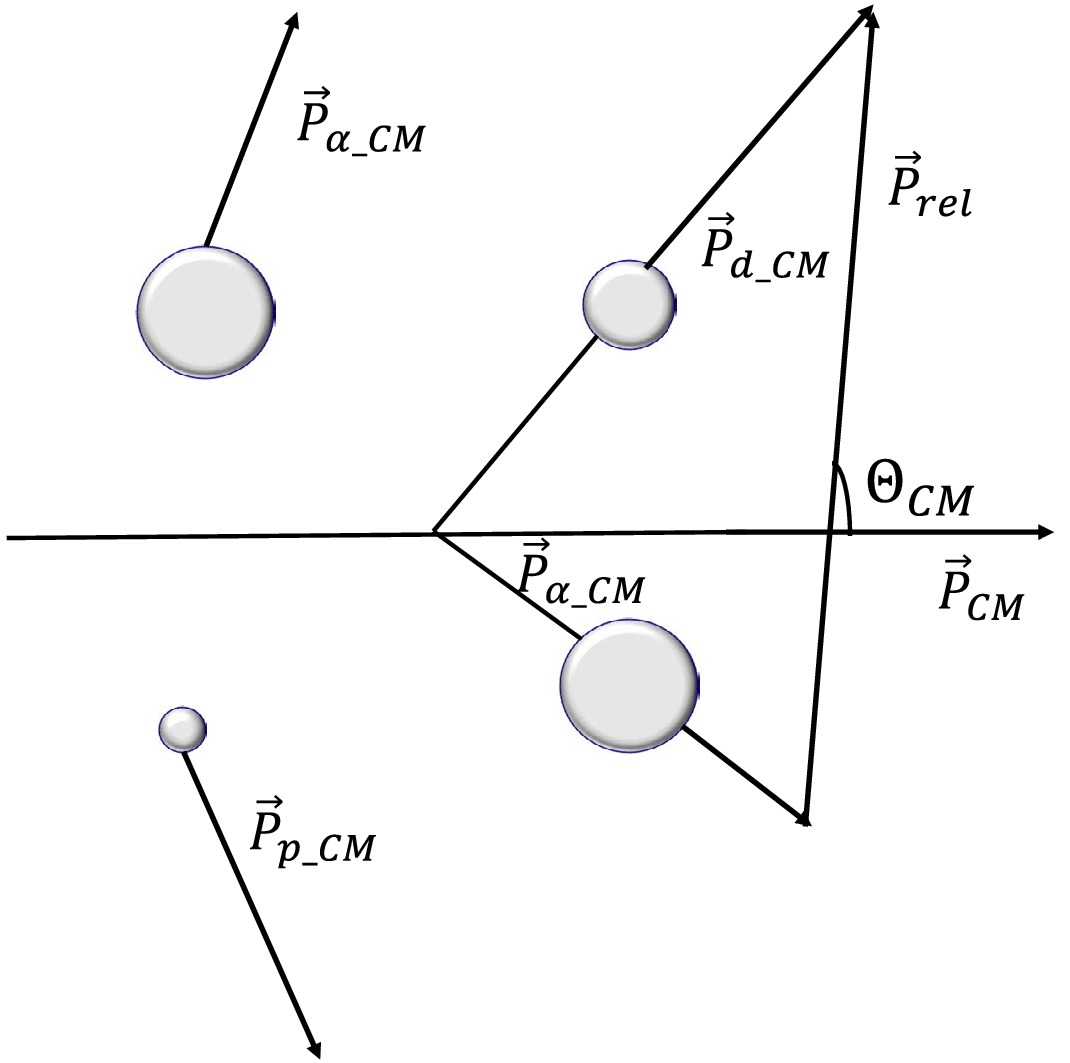
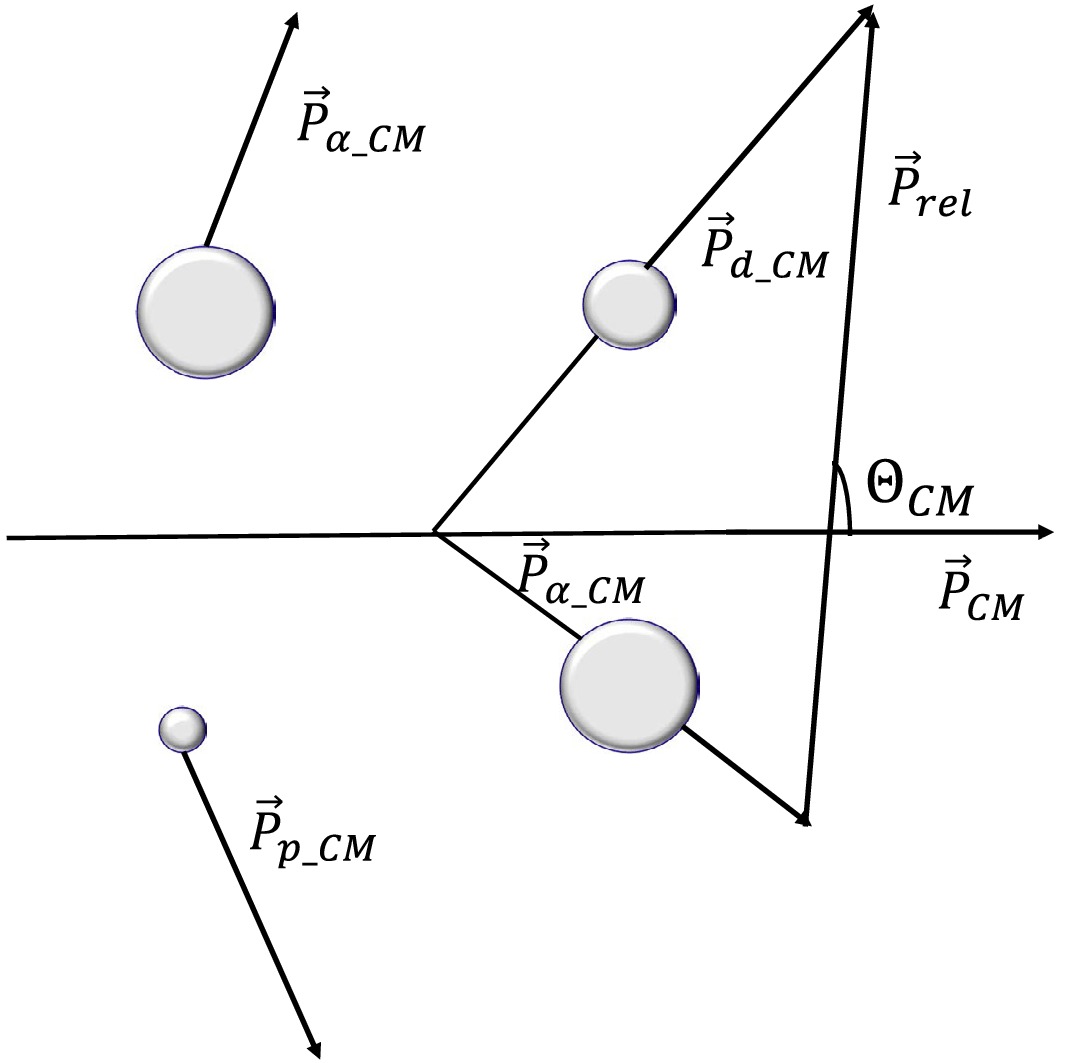
$ ^{6} $ Li$ ^* $ was reconstructed by analyzing the invariant mass of final state particles [13, 14], specifically d and α, selected from multiplicity-2 hits events recorded by the zero-degree telescope system. The excitation energy spectra of$ ^{6} $ Li$ ^* $ were investigated in two cases, as shown in Fig. 3, based on the relative emitting angle$ \Theta_{CM} $ between d and α in the center-of-mass system of the total cluster system, which is defined in Fig. 4. The first case considered$ \Theta_{CM}<120^{\circ} $ , while the second case focused on$ \Theta_{CM}>120^{\circ} $ . The angular distribution of$ \Theta_{CM} $ is displayed in Fig. 5.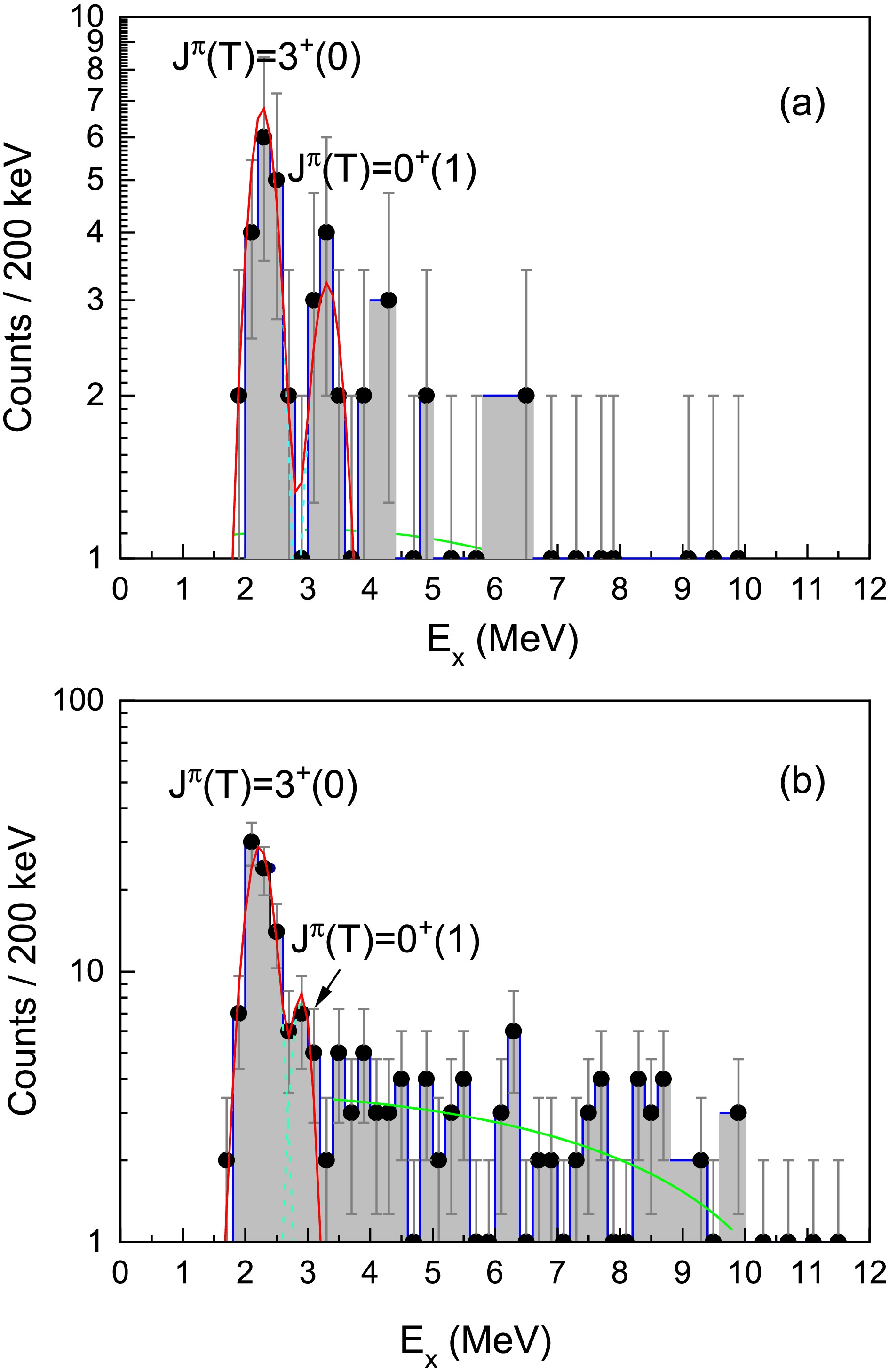
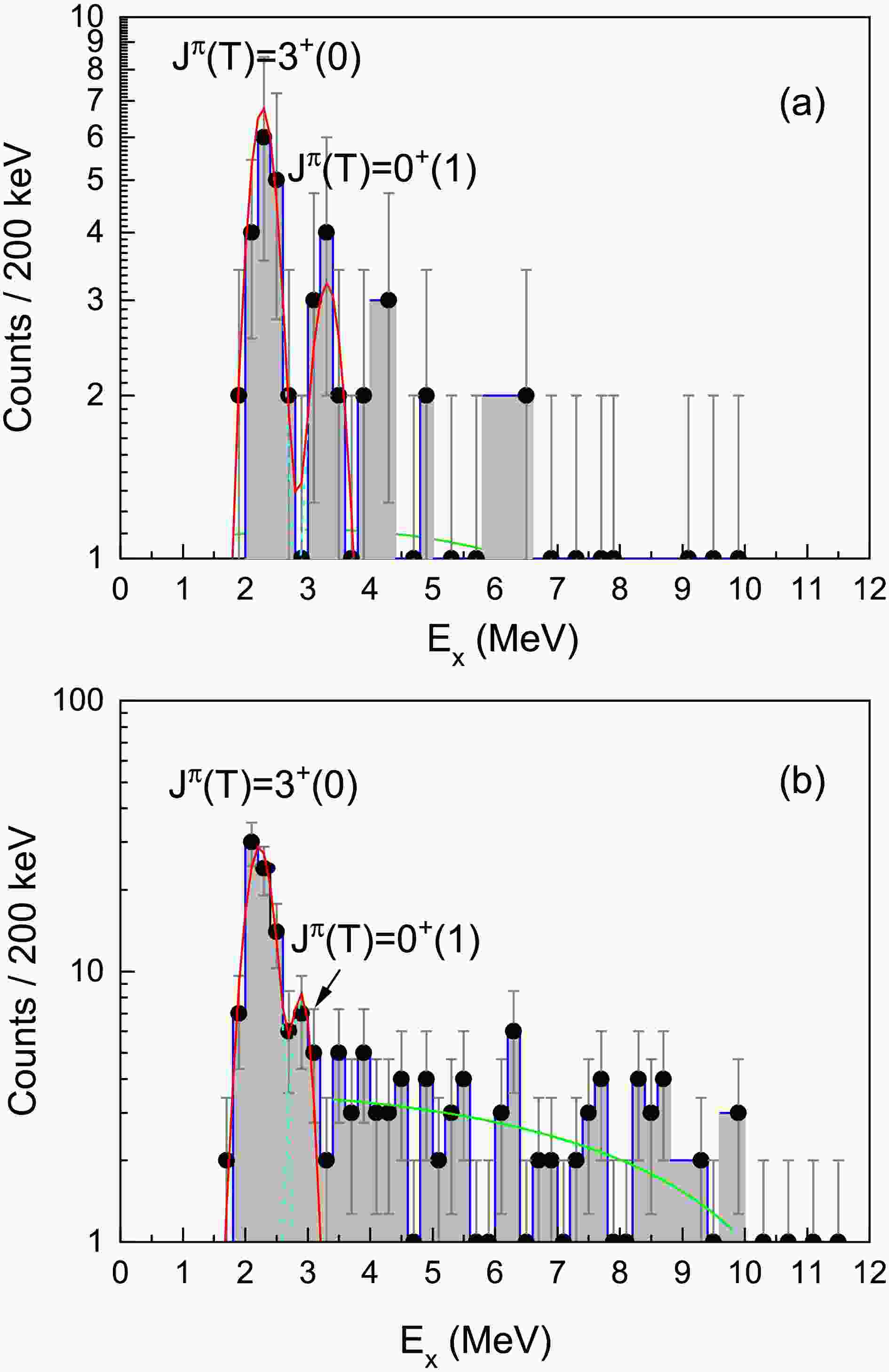
Figure 3. (color online) Excitation energy spectra of
$ ^{6} $ Li$ ^* $ : (a) Under the cut of$ \Theta_{CM}<120^{\circ} $ , where$ \Theta_{CM} $ is the relative emission angle between d and α in the center-of-mass system of all the clusters, clear excited states of$ J^{\pi}(T)=3^{+}(0) $ and$ J^{\pi}(T)=0^{+}(1) $ are observed; (b) Under the cut of$ \Theta_{CM}>120^{\circ} $ , there is an enhanced population of the$ J^{\pi}(T)=3^{+}(0) $ state, while the$ J^{\pi}(T)=0^{+}(1) $ state maintains a similar population to that in (a). The dashed lines represent the fitting for these resonances with a Breit-Wigner function, and the continuous background is depicted by the green line.
Figure 5. (color online) The relative emission angle
$ \Theta_{CM} $ between d and α is considered in the center-of-mass system of$ ^{6} $ Li. Two regions are identified, separated by$ 120^{\circ} $ . The smaller$ \Theta_{CM} $ region corresponds to d and α being emitted by the$ ^{6} $ Li cluster component initially inside$ ^{11} $ C. In contrast, the larger$ \Theta_{CM} $ reflects the back-to-back emission of d and α from$ ^{6} $ Li when it is isolated from$ ^{11} $ C.When considering the case of
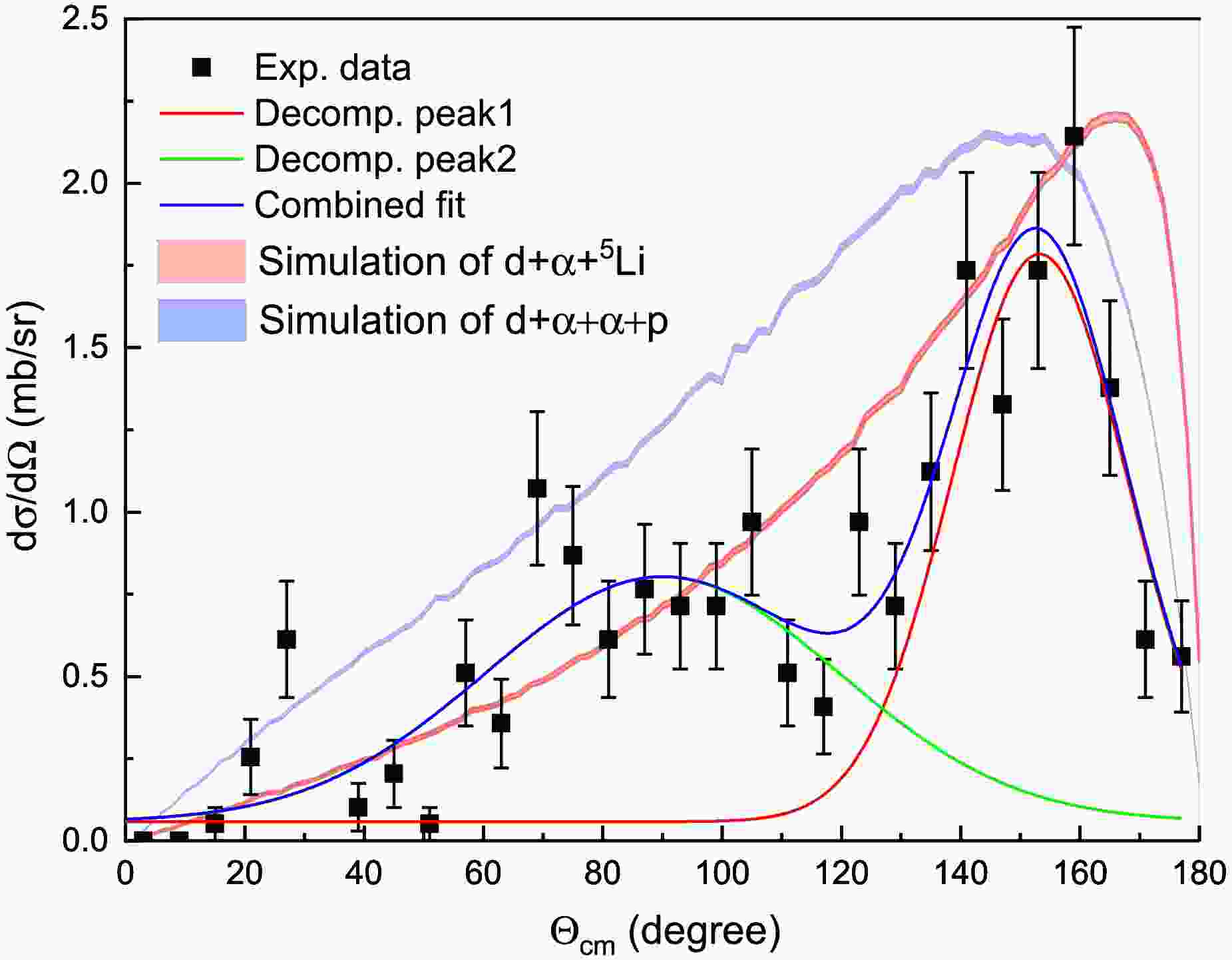
$ \Theta_{CM}<120^{\circ} $ , the resonance states of$ J^{\pi}(T)=0^{+}(1) $ and$ 3^{+}(0) $ are clearly visible, and their magnitudes are comparable, as shown in Fig. 3(a). However, in contrast, the cross-section of$ J^{\pi}(T)=3^{+}(0) $ under the case of$ \Theta_{CM}>120^{\circ} $ (Fig. 3(b)) significantly increases relative to that under the case of$ \Theta_{CM}<120^{\circ} $ (Fig. 3(a)). Despite this, the magnitudes of the cross-sections for the$ J^{\pi}(T)=0^{+}(1) $ state are similar in both cases. The small relative angle$ \Theta_{CM}<120^{\circ} $ suggests that the d and α particles arise from the direct breakup process of$ ^{11} $ C, as their momenta should be balanced by other fragments. In the case of$ \Theta_{CM}>120^{\circ} $ , the large relative emission angle suggests that the d and α particles are emitted through a back-to-back emission mode in the CM system of$ ^{6} $ Li, and are thus decay products from the sequential decay of the$ ^{6} $ Li nucleus that is isolated from$ ^{11} $ C.The cross-section ratio between the
$ J^{\pi}(T)=3^{+}(0) $ state and the$ J^{\pi}(T)=0^{+}(1) $ state varies from$ 2.7 \pm 0.3 $ at$ \Theta_{CM}<120^{\circ} $ to$ 5.5 \pm 0.6 $ at$ \Theta_{CM}>120^{\circ} $ . This indicates a remarkable property: the isospin T=0 state of$ J^{\pi}=3^{+} $ in the isolated$ ^{6} $ Li is significantly strengthened, while this state is heavily hindered in the$ ^{6} $ Li cluster component inside$ ^{11} $ C. In contrast, the isospin T=1 state of$ J^{\pi}=0^{+} $ remains relatively unchanged under these two different$ ^{6} $ Li formations.The transverse momentum
$ p_{T} $ of d or α fragments provides insight into the dynamical properties of clusters in the initial state of$ ^{6} $ Li.$ p_{T} $ is also equivalent to the transfer momentum$ \Delta p $ in the$ ^{6} $ Li breakup reaction, and, as such, it is an important parameter for understanding the reaction dynamics.$ \begin{aligned} \begin{split} {\rm sin}\Theta_{CM}=\frac{\Delta p}{p}=\frac{F\Delta t}{p}\simeq\frac{1}{p}\frac{V_{0}}{R}\frac{R}{v}=\frac{V_{0}}{pv}=\frac{V_{0}}{2E_{k}}, \end{split} \end{aligned} $
(2) where p is the momentum of the d or α fragment. F, the average force between d and α, is proportional to
$ {V_{0}}/{R} $ , where$ V_{0} $ and R are the depth and range of the potential between d and α. Assuming the velocity of the d or α cluster is v, the lifetime of the$ ^{6} $ Li excited state can be expressed as$ \tau = \Delta t = {R}/{v} $ .$ E_{k} $ is the kinetic energy of d or α. According to Eq. (1), the$ J^{\pi}(T) = 3^{+}(0) $ excited state with the opening angle of d and α,$ \Theta_{CM} < 120^{\circ} $ , corresponding to$ ^{6} $ Li inside$ ^{11} $ C, has a longer lifetime than that of$ \Theta_{CM} > 120^{\circ} $ , which corresponds to the isolated$ ^{6} $ Li. It is also reasonable to deduce that d or α exhibits slower dynamics with a smaller$ E_{k} $ in the$ ^{6} $ Li component within the nuclear medium compared to in the isolated$ ^{6} $ Li.Nucleon correlation and clustering are universal characteristics in nuclei [17−20], particularly in the presence of molecular-like states in neutron-rich light nuclei. Clusters indicate a spatially localized subsystem composed of strongly correlated nucleons, such as deuteron-like short-range correlated pairs and the compact four-nucleon correlated α cluster. The relative motion between clusters becomes a significant quantity for the fundamental motion mode of the nucleus.
The cluster model is treated based on a different degree of freedom compared to other models, typically the one-center mean field shell model. The microscopic cluster undergoes a dynamic process, constantly changing its structure due to its formation, growth, and breakup, while simultaneously complementing shell-model-like states. It is a significant fact that the description for such a transition of structure is identified in a finite quantum many-body system of the atomic nucleus. The inter-cluster relative motion and its coupling with the excitation modes of clusters correspond not only to bound states but also to highly excited states such as molecular resonances.
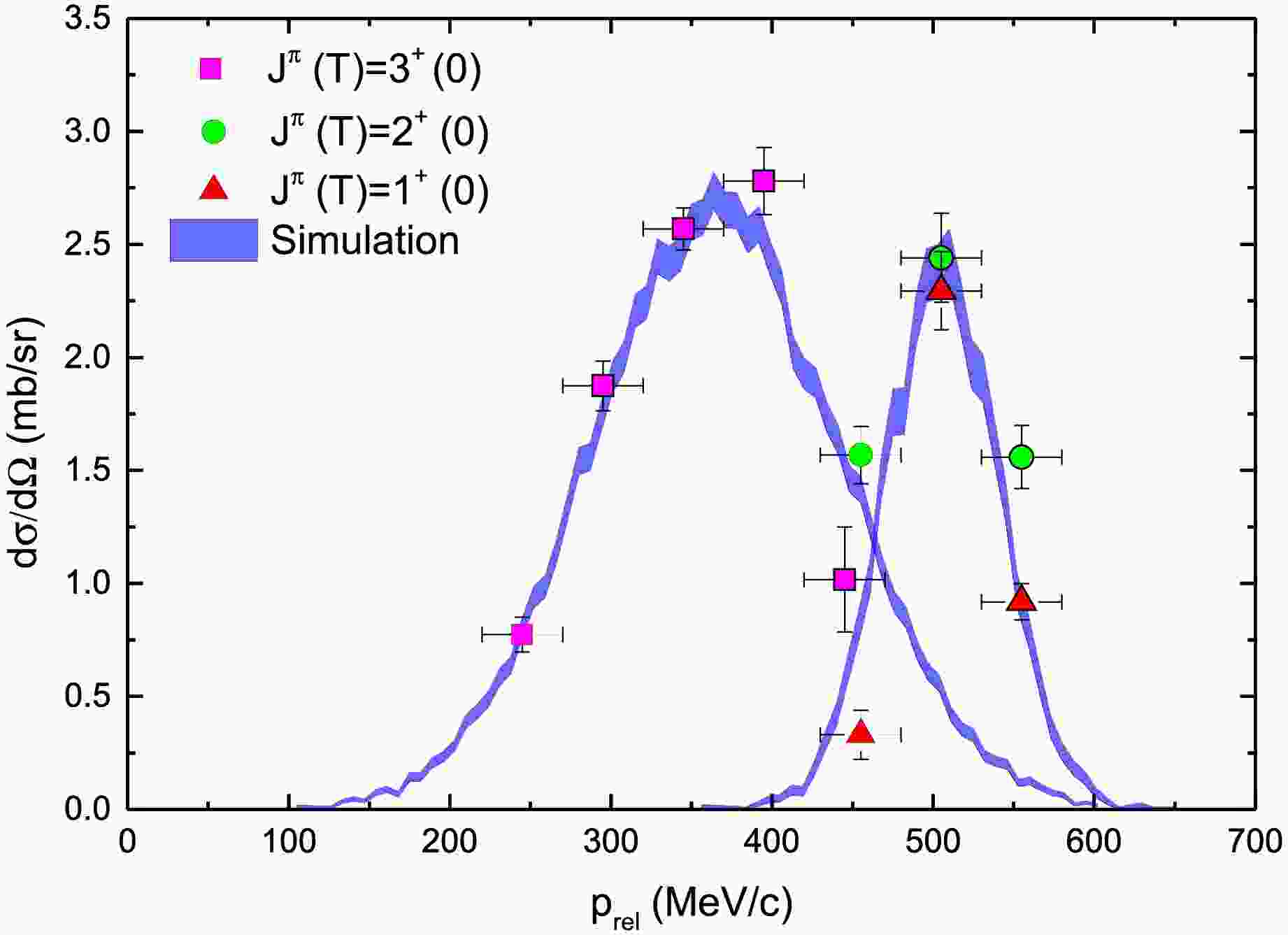
As shown in Fig. 6, the distribution of relative momentum
$ \vec{p}_{rel} = \vec{p}_{\alpha} - \vec{p}_{d} $ in the center-of-mass system of$ ^6 $ Li reveals distinct structural characteristics for different excited states. The$ 3^+(0) $ state exhibits a lower mean relative momentum ($ 361.6 \pm 12.7 $ MeV/c) but with a significantly broader distribution ($ \sigma = 77.2 \pm 5.5 $ MeV/c). According to the quantum uncertainty principle, this wide momentum distribution corresponds to a spatially compact configuration between the$ pn $ pair and α cluster. In contrast, the$ 2^+(0) $ and$ 1^+(0) $ mixing states show higher mean relative momentum ($ 517.7 \pm 9.1 $ MeV/c) with a narrower distribution ($ \sigma = 35.5 \pm 2.8 $ MeV/c), indicating a more extended spatial structure with stronger relative motion between clusters. These observations align with the expected properties: the$ 3^+(0) $ state maintains a compact structure favorable for tensor force excitation, while the$ 2^+(0) $ and$ 1^+(0) $ states represent more loosely bound molecular-like configurations.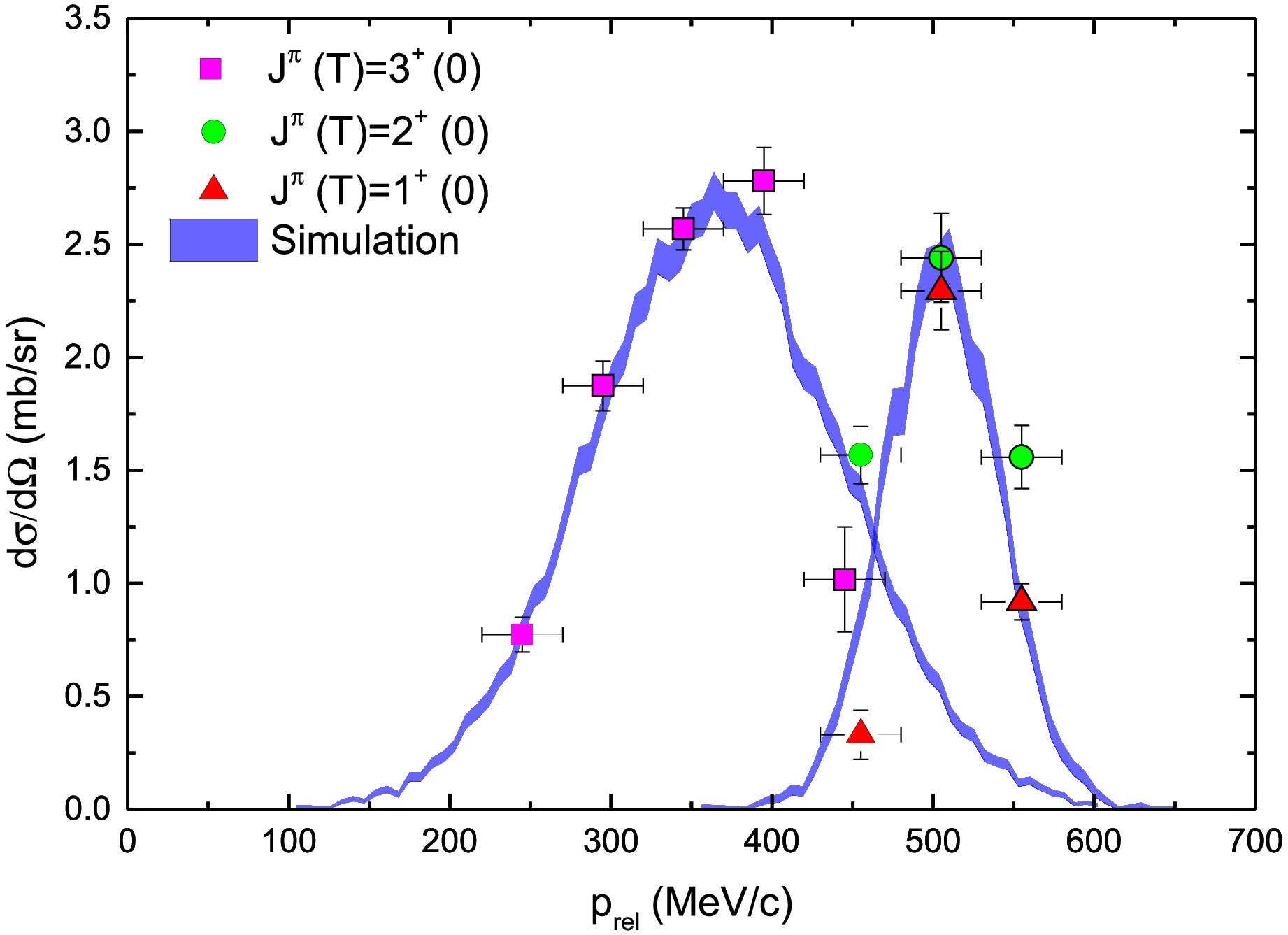
Figure 6. (color online) The relative momentum
$ p_{rel} $ between d and α depends on the spin of the triplet state with T=0. The$ J^{\pi}(T) $ =3$ ^{+}(0) $ state lies in the lower$ p_{rel} $ region with a wider width, while the$ J^{\pi}(T) $ =2$ ^{+}(0), 1^{+}(0) $ mixed states are located in the higher$ p_{rel} $ region with a narrower width. -
The excited state of
$ ^{6} $ Li$ ^* $ was reconstructed by analyzing the invariant mass of final state particles [13, 14], specifically d and α, selected from multiplicity-2 hits events recorded by the zero-degree telescope system. The excitation energy spectra of$ ^{6} $ Li$ ^* $ were investigated in two cases, as shown in Fig. 3, based on the relative emitting angle$ \Theta_{CM} $ between d and α in the center-of-mass system of the total cluster system, which is defined in Fig. 4. The first case considered$ \Theta_{CM}<120^{\circ} $ , while the second case focused on$ \Theta_{CM}>120^{\circ} $ . The angular distribution of$ \Theta_{CM} $ is displayed in Fig. 5.
Figure 3. (color online) Excitation energy spectra of
$ ^{6} $ Li$ ^* $ : (a) Under the cut of$ \Theta_{CM}<120^{\circ} $ , where$ \Theta_{CM} $ is the relative emission angle between d and α in the center-of-mass system of all the clusters, clear excited states of$ J^{\pi}(T)=3^{+}(0) $ and$ J^{\pi}(T)=0^{+}(1) $ are observed; (b) Under the cut of$ \Theta_{CM}>120^{\circ} $ , there is an enhanced population of the$ J^{\pi}(T)=3^{+}(0) $ state, while the$ J^{\pi}(T)=0^{+}(1) $ state maintains a similar population to that in (a). The dashed lines represent the fitting for these resonances with a Breit-Wigner function, and the continuous background is depicted by the green line.
Figure 5. (color online) The relative emission angle
$ \Theta_{CM} $ between d and α is considered in the center-of-mass system of$ ^{6} $ Li. Two regions are identified, separated by$ 120^{\circ} $ . The smaller$ \Theta_{CM} $ region corresponds to d and α being emitted by the$ ^{6} $ Li cluster component initially inside$ ^{11} $ C. In contrast, the larger$ \Theta_{CM} $ reflects the back-to-back emission of d and α from$ ^{6} $ Li when it is isolated from$ ^{11} $ C.When considering the case of
$ \Theta_{CM}<120^{\circ} $ , the resonance states of$ J^{\pi}(T)=0^{+}(1) $ and$ 3^{+}(0) $ are clearly visible, and their magnitudes are comparable, as shown in Fig. 3(a). However, in contrast, the cross-section of$ J^{\pi}(T)=3^{+}(0) $ under the case of$ \Theta_{CM}>120^{\circ} $ (Fig. 3(b)) significantly increases relative to that under the case of$ \Theta_{CM}<120^{\circ} $ (Fig. 3(a)). Despite this, the magnitudes of the cross-sections for the$ J^{\pi}(T)=0^{+}(1) $ state are similar in both cases. The small relative angle$ \Theta_{CM}<120^{\circ} $ suggests that the d and α particles arise from the direct breakup process of$ ^{11} $ C, as their momenta should be balanced by other fragments. In the case of$ \Theta_{CM}>120^{\circ} $ , the large relative emission angle suggests that the d and α particles are emitted through a back-to-back emission mode in the CM system of$ ^{6} $ Li, and are thus decay products from the sequential decay of the$ ^{6} $ Li nucleus that is isolated from$ ^{11} $ C.The cross-section ratio between the
$ J^{\pi}(T)=3^{+}(0) $ state and the$ J^{\pi}(T)=0^{+}(1) $ state varies from$ 2.7 \pm 0.3 $ at$ \Theta_{CM}<120^{\circ} $ to$ 5.5 \pm 0.6 $ at$ \Theta_{CM}>120^{\circ} $ . This indicates a remarkable property: the isospin T=0 state of$ J^{\pi}=3^{+} $ in the isolated$ ^{6} $ Li is significantly strengthened, while this state is heavily hindered in the$ ^{6} $ Li cluster component inside$ ^{11} $ C. In contrast, the isospin T=1 state of$ J^{\pi}=0^{+} $ remains relatively unchanged under these two different$ ^{6} $ Li formations.The transverse momentum
$ p_{T} $ of d or α fragments provides insight into the dynamical properties of clusters in the initial state of$ ^{6} $ Li.$ p_{T} $ is also equivalent to the transfer momentum$ \Delta p $ in the$ ^{6} $ Li breakup reaction, and, as such, it is an important parameter for understanding the reaction dynamics.$ \begin{aligned} \begin{split} sin\Theta_{CM}=\frac{\Delta p}{p}=\frac{F\Delta t}{p}\simeq\frac{1}{p}\frac{V_{0}}{R}\frac{R}{v}=\frac{V_{0}}{pv}=\frac{V_{0}}{2E_{k}}, \end{split} \end{aligned} $

(2) where p is the momentum of the d or α fragment. F, the average force between d and α, is proportional to
$ \frac{V_{0}}{R} $ , where$ V_{0} $ and R are the depth and range of the potential between d and α. Assuming the velocity of the d or α cluster is v, the lifetime of the$ ^{6} $ Li excited state can be expressed as$ \tau = \Delta t = \frac{R}{v} $ .$ E_{k} $ is the kinetic energy of d or α. According to Equ. (1), the$ J^{\pi}(T) = 3^{+}(0) $ excited state with the opening angle of d and α,$ \Theta_{CM} < 120^{\circ} $ , corresponding to$ ^{6} $ Li inside$ ^{11} $ C, has a longer lifetime than that of$ \Theta_{CM} > 120^{\circ} $ , which corresponds to the isolated$ ^{6} $ Li. It is also reasonable to deduce that d or α exhibits slower dynamics with a smaller$ E_{k} $ in the$ ^{6} $ Li component within the nuclear medium compared to in the isolated$ ^{6} $ Li.Nucleon correlation and clustering are universal characteristics in nuclei, particularly in the presence of molecular-like states in neutron-rich light nuclei. Clusters indicate a spatially localized subsystem composed of strongly correlated nucleons, such as deuteron-like short-range correlated pairs and the compact four-nucleon correlated α cluster. The relative motion between clusters becomes a significant quantity for the fundamental motion mode of the nucleus.
The cluster model is treated based on a different degree of freedom compared to other models, typically the one-center mean field shell model. The microscopic cluster undergoes a dynamic process, constantly changing its structure due to its formation, growth, and breakup, while simultaneously complementing shell-model-like states. It is a significant fact that the description for such a transition of structure is identified in a finite quantum many-body system of the atomic nucleus. The inter-cluster relative motion and its coupling with the excitation modes of clusters correspond not only to bound states but also to highly excited states such as molecular resonances.
As shown in Fig. 6, the distribution of relative momentum
$ \vec{p}_{rel} = \vec{p}_{\alpha} - \vec{p}_{d} $ in the center-of-mass system of$ ^6 $ Li reveals distinct structural characteristics for different excited states. The$ 3^+(0) $ state exhibits a lower mean relative momentum ($ 361.6 \pm 12.7 $ MeV/c) but with a significantly broader distribution ($ \sigma = 77.2 \pm 5.5 $ MeV/c). According to the quantum uncertainty principle, this wide momentum distribution corresponds to a spatially compact configuration between the$ pn $ pair and α cluster. In contrast, the$ 2^+(0) $ and$ 1^+(0) $ mixing states show higher mean relative momentum ($ 517.7 \pm 9.1 $ MeV/c) with a narrower distribution ($ \sigma = 35.5 \pm 2.8 $ MeV/c), indicating a more extended spatial structure with stronger relative motion between clusters. These observations align with the expected properties: the$ 3^+(0) $ state maintains a compact structure favorable for tensor force excitation, while the$ 2^+(0) $ and$ 1^+(0) $ states represent more loosely bound molecular-like configurations.
Figure 6. (color online) The relative momentum
$ p_{rel} $ between d and α depends on the spin of the triplet state with T=0. The$ J^{\pi}(T) $ =3$ ^{+}(0) $ state lies in the lower$ p_{rel} $ region with a wider width, while the$ J^{\pi}(T) $ =2$ ^{+}(0), 1^{+}(0) $ mixed states are located in the higher$ p_{rel} $ region with a narrower width. -
The excited state of
$ ^{6} $ Li$ ^* $ was reconstructed by analyzing the invariant mass of final state particles [13, 14], specifically d and α, selected from multiplicity-2 hits events recorded by the zero-degree telescope system. The excitation energy spectra of$ ^{6} $ Li$ ^* $ were investigated in two cases, as shown in Fig. 3, based on the relative emitting angle$ \Theta_{CM} $ between d and α in the center-of-mass system of the total cluster system, which is defined in Fig. 4. The first case considered$ \Theta_{CM}<120^{\circ} $ , while the second case focused on$ \Theta_{CM}>120^{\circ} $ . The angular distribution of$ \Theta_{CM} $ is displayed in Fig. 5.
Figure 3. (color online) Excitation energy spectra of
$ ^{6} $ Li$ ^* $ : (a) Under the cut of$ \Theta_{CM}<120^{\circ} $ , where$ \Theta_{CM} $ is the relative emission angle between d and α in the center-of-mass system of all the clusters, clear excited states of$ J^{\pi}(T)=3^{+}(0) $ and$ J^{\pi}(T)=0^{+}(1) $ are observed; (b) Under the cut of$ \Theta_{CM}>120^{\circ} $ , there is an enhanced population of the$ J^{\pi}(T)=3^{+}(0) $ state, while the$ J^{\pi}(T)=0^{+}(1) $ state maintains a similar population to that in (a). The dashed lines represent the fitting for these resonances with a Breit-Wigner function, and the continuous background is depicted by the green line.
Figure 5. (color online) The relative emission angle
$ \Theta_{CM} $ between d and α is considered in the center-of-mass system of$ ^{6} $ Li. Two regions are identified, separated by$ 120^{\circ} $ . The smaller$ \Theta_{CM} $ region corresponds to d and α being emitted by the$ ^{6} $ Li cluster component initially inside$ ^{11} $ C. In contrast, the larger$ \Theta_{CM} $ reflects the back-to-back emission of d and α from$ ^{6} $ Li when it is isolated from$ ^{11} $ C.When considering the case of
$ \Theta_{CM}<120^{\circ} $ , the resonance states of$ J^{\pi}(T)=0^{+}(1) $ and$ 3^{+}(0) $ are clearly visible, and their magnitudes are comparable, as shown in Fig. 3(a). However, in contrast, the cross-section of$ J^{\pi}(T)=3^{+}(0) $ under the case of$ \Theta_{CM}>120^{\circ} $ (Fig. 3(b)) significantly increases relative to that under the case of$ \Theta_{CM}<120^{\circ} $ (Fig. 3(a)). Despite this, the magnitudes of the cross-sections for the$ J^{\pi}(T)=0^{+}(1) $ state are similar in both cases. The small relative angle$ \Theta_{CM}<120^{\circ} $ suggests that the d and α particles arise from the direct breakup process of$ ^{11} $ C, as their momenta should be balanced by other fragments. In the case of$ \Theta_{CM}>120^{\circ} $ , the large relative emission angle suggests that the d and α particles are emitted through a back-to-back emission mode in the CM system of$ ^{6} $ Li, and are thus decay products from the sequential decay of the$ ^{6} $ Li nucleus that is isolated from$ ^{11} $ C.The cross-section ratio between the
$ J^{\pi}(T)=3^{+}(0) $ state and the$ J^{\pi}(T)=0^{+}(1) $ state varies from$ 2.7 \pm 0.3 $ at$ \Theta_{CM}<120^{\circ} $ to$ 5.5 \pm 0.6 $ at$ \Theta_{CM}>120^{\circ} $ . This indicates a remarkable property: the isospin T=0 state of$ J^{\pi}=3^{+} $ in the isolated$ ^{6} $ Li is significantly strengthened, while this state is heavily hindered in the$ ^{6} $ Li cluster component inside$ ^{11} $ C. In contrast, the isospin T=1 state of$ J^{\pi}=0^{+} $ remains relatively unchanged under these two different$ ^{6} $ Li formations.The transverse momentum
$ p_{T} $ of d or α fragments provides insight into the dynamical properties of clusters in the initial state of$ ^{6} $ Li.$ p_{T} $ is also equivalent to the transfer momentum$ \Delta p $ in the$ ^{6} $ Li breakup reaction, and, as such, it is an important parameter for understanding the reaction dynamics.$ \begin{aligned} \begin{split} {\rm sin}\Theta_{CM}=\frac{\Delta p}{p}=\frac{F\Delta t}{p}\simeq\frac{1}{p}\frac{V_{0}}{R}\frac{R}{v}=\frac{V_{0}}{pv}=\frac{V_{0}}{2E_{k}}, \end{split} \end{aligned} $
(2) where p is the momentum of the d or α fragment. F, the average force between d and α, is proportional to
$ {V_{0}}/{R} $ , where$ V_{0} $ and R are the depth and range of the potential between d and α. Assuming the velocity of the d or α cluster is v, the lifetime of the$ ^{6} $ Li excited state can be expressed as$ \tau = \Delta t = {R}/{v} $ .$ E_{k} $ is the kinetic energy of d or α. According to Eq. (1), the$ J^{\pi}(T) = 3^{+}(0) $ excited state with the opening angle of d and α,$ \Theta_{CM} < 120^{\circ} $ , corresponding to$ ^{6} $ Li inside$ ^{11} $ C, has a longer lifetime than that of$ \Theta_{CM} > 120^{\circ} $ , which corresponds to the isolated$ ^{6} $ Li. It is also reasonable to deduce that d or α exhibits slower dynamics with a smaller$ E_{k} $ in the$ ^{6} $ Li component within the nuclear medium compared to in the isolated$ ^{6} $ Li.Nucleon correlation and clustering are universal characteristics in nuclei [17−20], particularly in the presence of molecular-like states in neutron-rich light nuclei. Clusters indicate a spatially localized subsystem composed of strongly correlated nucleons, such as deuteron-like short-range correlated pairs and the compact four-nucleon correlated α cluster. The relative motion between clusters becomes a significant quantity for the fundamental motion mode of the nucleus.
The cluster model is treated based on a different degree of freedom compared to other models, typically the one-center mean field shell model. The microscopic cluster undergoes a dynamic process, constantly changing its structure due to its formation, growth, and breakup, while simultaneously complementing shell-model-like states. It is a significant fact that the description for such a transition of structure is identified in a finite quantum many-body system of the atomic nucleus. The inter-cluster relative motion and its coupling with the excitation modes of clusters correspond not only to bound states but also to highly excited states such as molecular resonances.
As shown in Fig. 6, the distribution of relative momentum
$ \vec{p}_{rel} = \vec{p}_{\alpha} - \vec{p}_{d} $ in the center-of-mass system of$ ^6 $ Li reveals distinct structural characteristics for different excited states. The$ 3^+(0) $ state exhibits a lower mean relative momentum ($ 361.6 \pm 12.7 $ MeV/c) but with a significantly broader distribution ($ \sigma = 77.2 \pm 5.5 $ MeV/c). According to the quantum uncertainty principle, this wide momentum distribution corresponds to a spatially compact configuration between the$ pn $ pair and α cluster. In contrast, the$ 2^+(0) $ and$ 1^+(0) $ mixing states show higher mean relative momentum ($ 517.7 \pm 9.1 $ MeV/c) with a narrower distribution ($ \sigma = 35.5 \pm 2.8 $ MeV/c), indicating a more extended spatial structure with stronger relative motion between clusters. These observations align with the expected properties: the$ 3^+(0) $ state maintains a compact structure favorable for tensor force excitation, while the$ 2^+(0) $ and$ 1^+(0) $ states represent more loosely bound molecular-like configurations.
Figure 6. (color online) The relative momentum
$ p_{rel} $ between d and α depends on the spin of the triplet state with T=0. The$ J^{\pi}(T) $ =3$ ^{+}(0) $ state lies in the lower$ p_{rel} $ region with a wider width, while the$ J^{\pi}(T) $ =2$ ^{+}(0), 1^{+}(0) $ mixed states are located in the higher$ p_{rel} $ region with a narrower width. -
The tensor force strength for the
$ J^{\pi}(T)=0^{+}(1) $ state is much smaller than that for the$ J^{\pi}(T)=3^{+}(0) $ state in the isolated$ ^{6} $ Li [11], which can be essentially explained by the tensor force properties of isospin dependence. For the$ 0^{+}(1) $ state, which has a configuration of$ (0s_{1/2})^{4}(0p_{3/2})^{2} $ , the inner$ ^{4} $ He core composed of two$ pn $ pairs with T=0 is excited from 0s to 0$ p_{1/2} $ by the tensor force via the two-particle two-hole (2p-2h) mode [12], while the outer$ pn $ pair on the 0p shell with T=1 undergoes a relatively small excitation due to the weak tensor force for the T=1 channel. For the$ 3^{+}(0) $ state, the outer$ pn $ pair in the 0p shell may undergo a tensor force excitation with a T=0 state from$ (0p_{3/2})^{2} $ to$ (0d_{3/2})^{2} $ , which satisfies the selection rule for the tensor force excitation of$ \Delta L $ =2,$ \Delta S $ =2, and$ \Delta J $ =0. From the point of view of the excitation strength of the tensor force, the coupling of the outer$ pn $ pair to the inner$ ^{4} $ He core is relatively weak for the$ 0^{+}(1) $ state, and hence the population of the$ 3^{+}(0) $ state is much higher than that of the$ 0^{+}(1) $ state in the isolated$ ^{6} $ Li nucleus, as shown in Fig. 3(b).However, when
$ ^{6} $ Li is not completely isolated but still within the domain of$ ^{11} $ C as a component, d and α in$ ^{6} $ Li are correlated two-body clusters and are essentially affected by the central interactions from the residual nucleus. Such extra interactions may reduce the strength of coupling of the$ pn $ pair with isospin T=0 to α, which leads to the shrinkage of tensor force excitation and results in comparable populations between the$ J^{\pi}(T)=0^{+}(1) $ state and the$ J^{\pi}(T)=3^{+}(0) $ state for the case of$ \Theta_{CM}<120^{\circ} $ , as shown in Fig. 3(a).Among the T=0 triplet states of
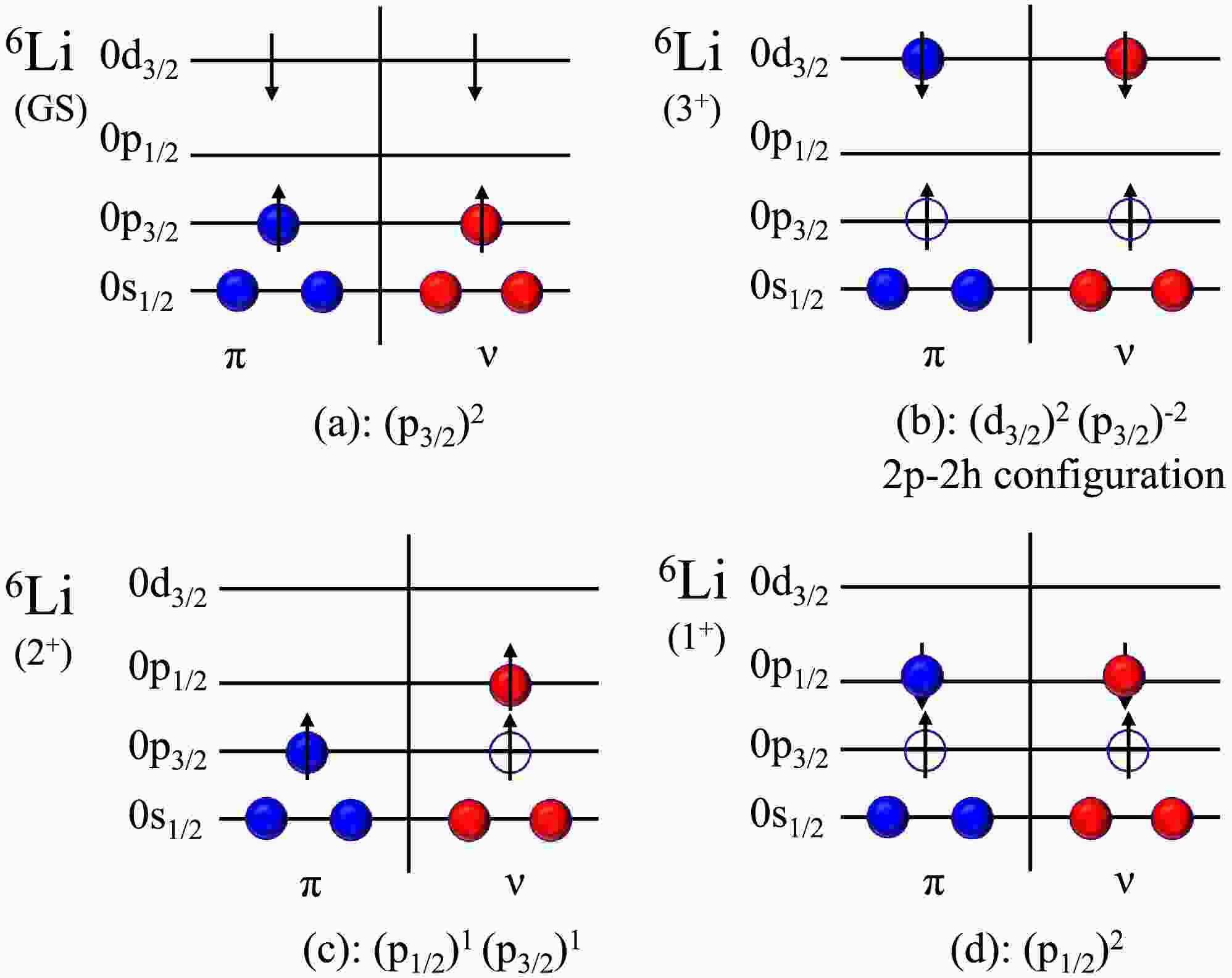
$ J^{\pi}(T)=3^{+}(0), 2^{+}(0), 1^{+}(0) $ , as shown in Fig. 7, the strong excitation of the$ 3^{+}(0) $ state with the lowest excitation energy results from the tensor force excitation from$ (0p_{3/2})^{2} $ to$ (0d_{3/2})^{2} $ with a 2p-2h excitation mode at a high spin and T=0. The highest excited energy state,$ 1^{+}(0) $ , involves the mixing configurations of$ (0s_{1/2})^{4}(0p_{3/2})^{2} $ ,$ (0s_{1/2})^{4}(0p_{1/2})^{1}(0p_{3/2})^{1} $ , and$ (0s_{1/2})^{4}(0p_{1/2})^{2} $ with a similar probability for each, and the$ 2^{+}(0) $ state only takes on a configuration of$ (0s_{1/2})^{4}(0p_{1/2})^{1}(0p_{3/2})^{1} $ with two valence nucleons of neutron and proton lying in the separated sub-shell levels, which could explain the present experimental observations of the high population of the$ 3^{+}(0) $ state and the low population of the$ 2^{+}(0) $ and$ 1^{+}(0) $ states. Additionally, this could also clarify the relatively large dynamical motion and broader density distribution of d and α, namely, a more loosely bound structure for the$ 2^{+}(0) $ and$ 1^{+}(0) $ states in$ ^{6} $ Li.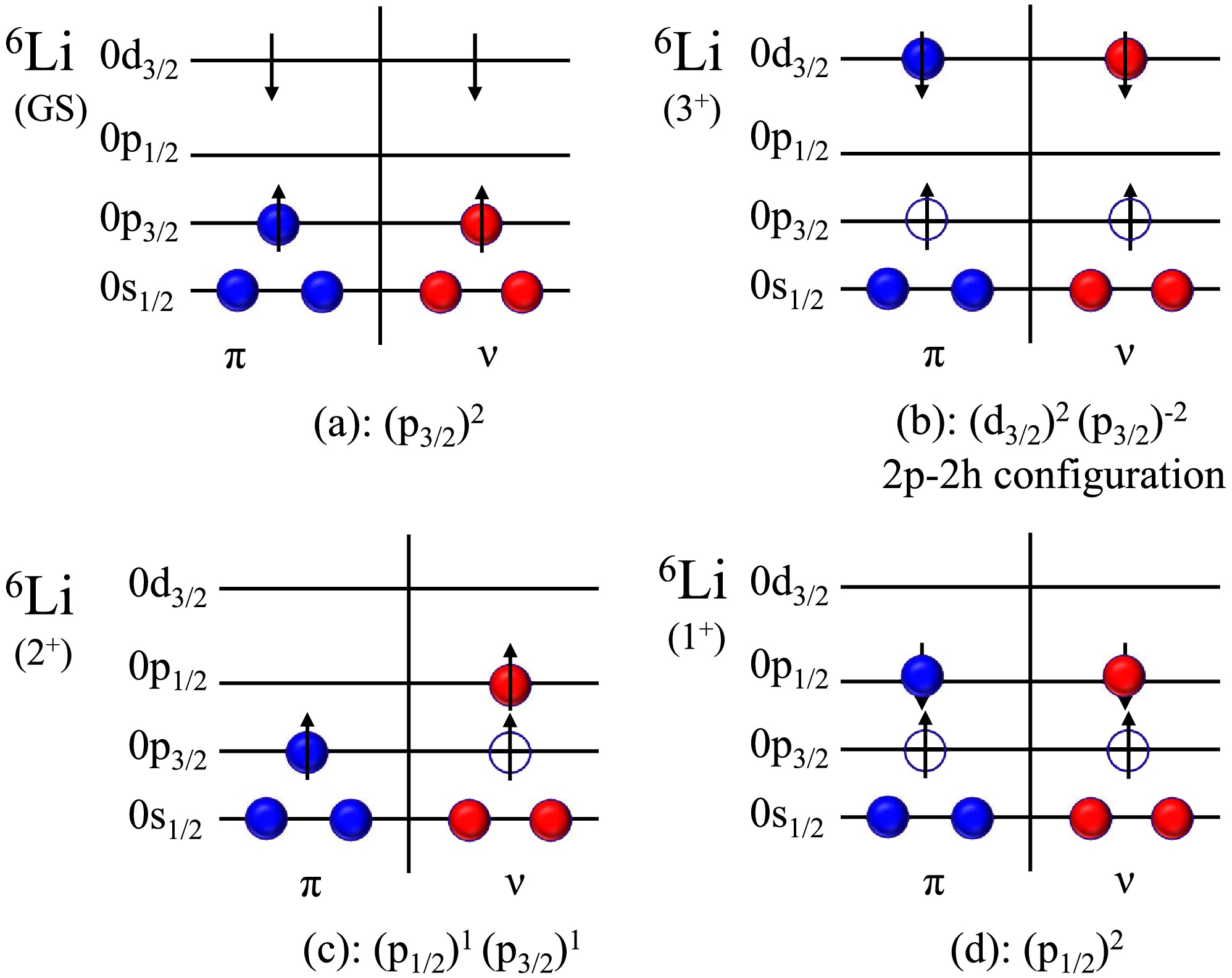
Figure 7. (color online) Configurations of
$ ^{6} $ Li for the ground state and excited states of$ J^{\pi} $ (T)=3$ ^{+} $ (0), 2$ ^{+} $ (0), and 1$ ^{+} $ (0). Notably, 3$ ^{+} $ (0) satisfies the tensor force selection rule of ΔL=2, ΔS=2, and ΔJ=0 and 2p-2h configuration.The tensor force strength [1−6], modulated by the effects of the nuclear medium, reflects the intricate interplay between the nucleons within the nucleus. As the nuclear density increases, more nucleons are packed into a given volume, leading to increased overlap and interaction between them. This enhanced interaction modifies the strength of the tensor force and its impact on the nuclear system.
$ \begin{aligned} \begin{split} \frac{f(\rho)}{f_{0}(\rho)}={\rm e}^{-(a\rho+b\rho^{2}+c\rho^{3})}. \end{split} \end{aligned} $
(3) The function
$ f(\rho)/f_{0}(\rho) $ for the nuclear medium effect on tensor force strength (NMET) in Eq. (2) captures this behavior by introducing the scaling constants a, b, and c. The positive values of these constants indicate that the tensor force strength diminishes as the nuclear density increases. This decrease is a manifestation of the saturation of the strong nuclear force at high densities, where the repulsive interactions between nucleons begin to dominate, counteracting the attractive tensor force. The density distributions of the nucleus are typically described by a Woods-Saxon type distribution as$ \begin{aligned} \begin{split} \rho_{ws}(r)=\rho_{0}\left [1+{\rm exp}\left (\frac{r-R}{a}\right )\right ]^{-1} .\end{split} \end{aligned} $
(4) With a diffuseness parameter
$ a \sim 0.53 $ fm and$ \rho_{0} \sim 0.17 $ fm$ ^{-1} $ being the density at the center of the nucleus, the radius parameter R is determined by the mass number A as$ R \sim 1.10A^{1/3} $ (fm). A charge density function was approximated as in Eq. (4), which models the shape of the nuclei as a uniform sphere with constant charge density.$ \begin{aligned} \begin{split} \rho_{ch}(r)=\frac{0.75A/\pi}{(5/3<r^{2}>)^{3/2}}. \end{split} \end{aligned} $
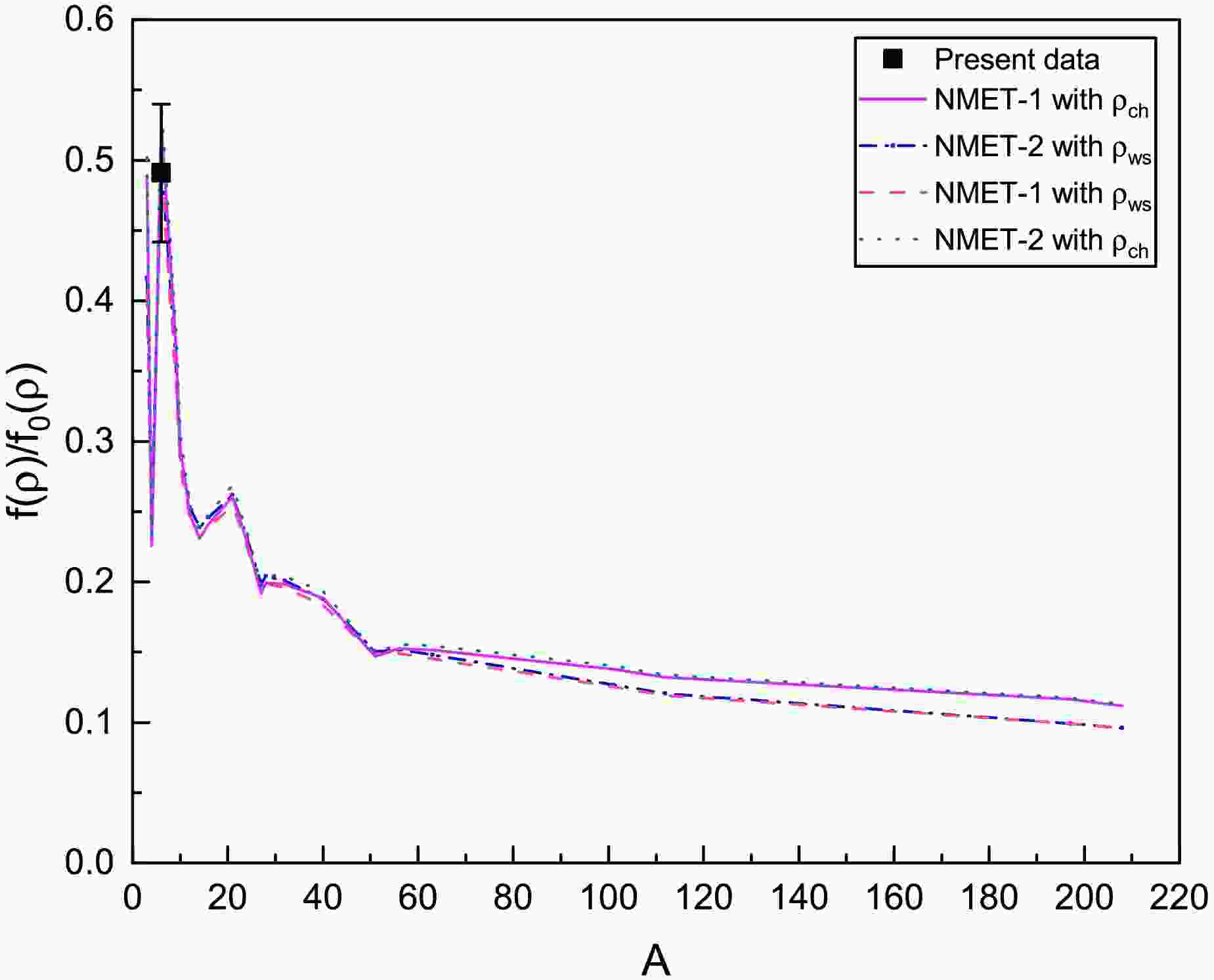
(5) The calculations with and without the b and c terms in Eq. (2), defined as the NMET-1 and NMET-2 models, have been performed using two nuclear density functions from Eq. (3) and Eq. (4), as shown in Fig. 8. The parameters were adjusted according to the scaling of the tensor force with nuclear density to be consistent with the experimental data of the 3
$ ^{+} $ (0) state of$ ^{6} $ Li. A saturation trend is achieved at high densities, reflecting the intricate behavior of the strong nuclear force within atomic nuclei.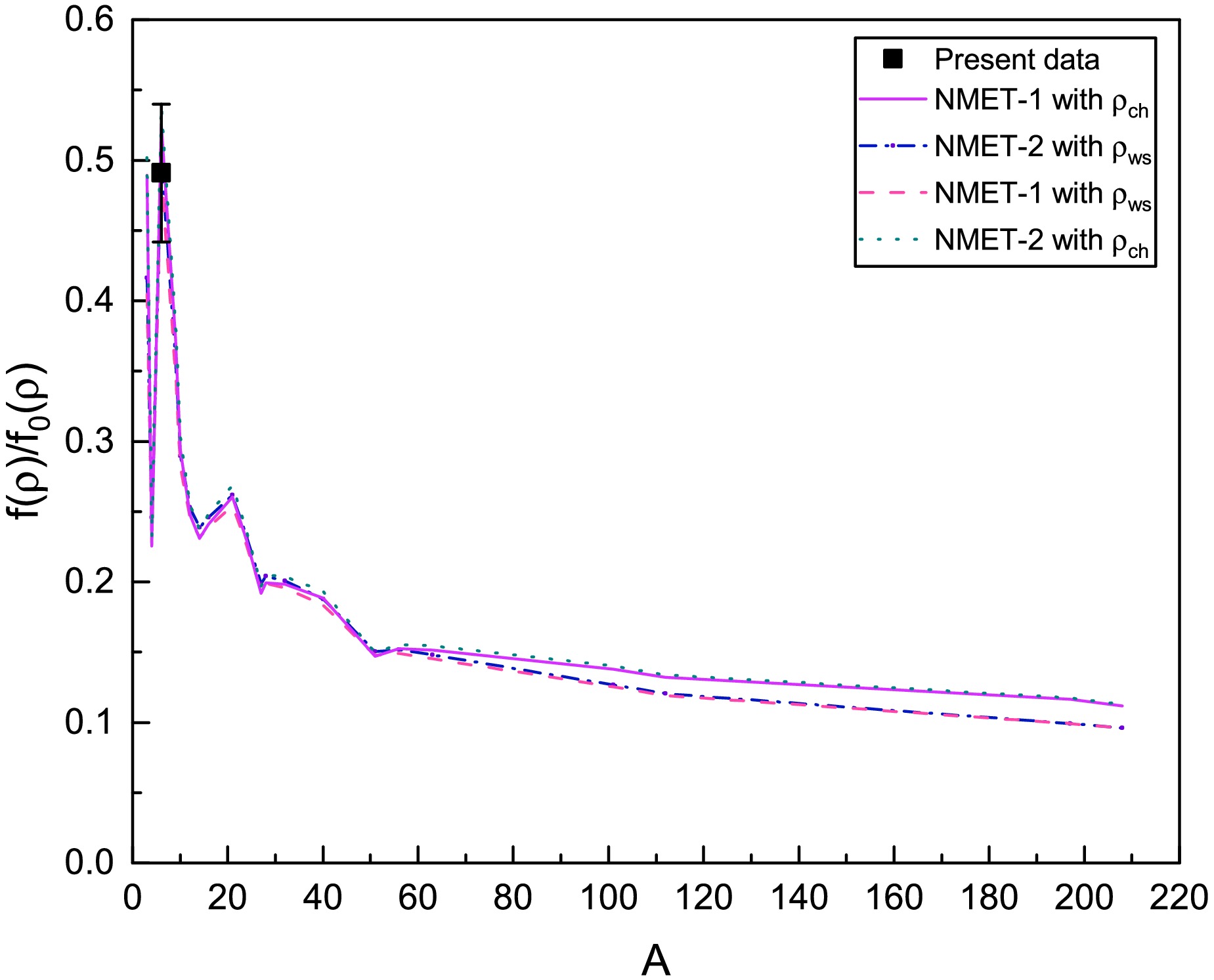
Figure 8. (color online) The tensor force strength ratio,
$ f/f_{0} $ , which compares values outside the nuclear medium to those within, is analyzed as a function of the atomic number A. NMET model calculations are conducted using two different nuclear density functions:$ \rho_{ch} $ and$ \rho_{ws} $ .The modification of tensor force strength with nuclear density becomes particularly important in extreme conditions, such as neutron stars or during heavy-ion collisions in nuclear physics experiments. In these extreme environments, the nuclear density can reach values far beyond those found in stable atomic nuclei. The modification of the tensor force strength with nuclear density influences the equation of state, nuclear structure, and transport properties of nuclear matter.
-
The tensor force strength for the
$ J^{\pi}(T)=0^{+}(1) $ state is much smaller than that for the$ J^{\pi}(T)=3^{+}(0) $ state in the isolated$ ^{6} $ Li [13], which can be essentially explained by the tensor force properties of isospin dependence [7]. For the$ 0^{+}(1) $ state, which has a configuration of$ (0s_{1/2})^{4}(0p_{3/2})^{2} $ , the inner$ ^{4} $ He core composed of two$ pn $ pairs with T=0 is excited from 0s to 0$ p_{1/2} $ by the tensor force via the two-particle two-hole (2p-2h) mode, while the outer$ pn $ pair on the 0p shell with T=1 undergoes a relatively small excitation due to the weak tensor force for the T=1 channel. For the$ 3^{+}(0) $ state, the outer$ pn $ pair in the 0p shell may undergo a tensor force excitation with a T=0 state from$ (0p_{3/2})^{2} $ to$ (0d_{3/2})^{2} $ , which satisfies the selection rule for the tensor force excitation of$ \Delta L $ =2,$ \Delta S $ =2, and$ \Delta J $ =0. From the point of view of the excitation strength of the tensor force, the coupling of the outer$ pn $ pair to the inner$ ^{4} $ He core is relatively weak for the$ 0^{+}(1) $ state, and hence the population of the$ 3^{+}(0) $ state is much higher than that of the$ 0^{+}(1) $ state in the isolated$ ^{6} $ Li nucleus, as shown in Fig. 3(b).However, when
$ ^{6} $ Li is not completely isolated but still within the domain of$ ^{11} $ C as a component, d and α in$ ^{6} $ Li are correlated two-body clusters and are essentially affected by the central interactions from the residual nucleus. Such extra interactions may reduce the strength of coupling of the$ pn $ pair with isospin T=0 to α, which leads to the shrinkage of tensor force excitation and results in comparable populations between the$ J^{\pi}(T)=0^{+}(1) $ state and the$ J^{\pi}(T)=3^{+}(0) $ state for the case of$ \Theta_{CM}<120^{\circ} $ , as shown in Fig. 3(a).Among the T=0 triplet states of
$ J^{\pi}(T)=3^{+}(0), 2^{+}(0), 1^{+}(0) $ , as shown in Fig. 7, the strong excitation of the$ 3^{+}(0) $ state with the lowest excitation energy results from the tensor force excitation from$ (0p_{3/2})^{2} $ to$ (0d_{3/2})^{2} $ with a 2p-2h excitation mode at a high spin and T=0. The highest excited energy state,$ 1^{+}(0) $ , involves the mixing configurations of$ (0s_{1/2})^{4}(0p_{3/2})^{2} $ ,$ (0s_{1/2})^{4}(0p_{1/2})^{1}(0p_{3/2})^{1} $ , and$ (0s_{1/2})^{4}(0p_{1/2})^{2} $ with a similar probability for each, and the$ 2^{+}(0) $ state only takes on a configuration of$ (0s_{1/2})^{4}(0p_{1/2})^{1}(0p_{3/2})^{1} $ with two valence nucleons of neutron and proton lying in the separated sub-shell levels [13], which could explain the present experimental observations of the high population of the$ 3^{+}(0) $ state and the low population of the$ 2^{+}(0) $ and$ 1^{+}(0) $ states. Additionally, this could also clarify the relatively large dynamical motion and broader density distribution of d and α, namely, a more loosely bound structure for the$ 2^{+}(0) $ and$ 1^{+}(0) $ states in$ ^{6} $ Li.
Figure 7. (color online) Configurations of
$ ^{6} $ Li for the ground state and excited states of$ J^{\pi} $ (T)=3$ ^{+} $ (0), 2$ ^{+} $ (0), and 1$ ^{+} $ (0). Notably, 3$ ^{+} $ (0) satisfies the tensor force selection rule of ΔL=2, ΔS=2, and ΔJ=0 and 2p-2h configuration.The tensor force strength [14, 15], modulated by the effects of the nuclear medium, reflects the intricate interplay between the nucleons within the nucleus. As the nuclear density increases, more nucleons are packed into a given volume, leading to increased overlap and interaction between them. This enhanced interaction modifies the strength of the tensor force and its impact on the nuclear system.
$ \begin{aligned} \begin{split} \frac{f(\rho)}{f_{0}(\rho)}=e^{-(a\rho+b\rho^{2}+c\rho^{3})} \end{split} \end{aligned} $

(3) The function
$ f(\rho)/f_{0}(\rho) $ for the nuclear medium effect on tensor force strength (NMET) in Equ. (2) captures this behavior by introducing the scaling constants a, b, and c. The positive values of these constants indicate that the tensor force strength diminishes as the nuclear density increases. This decrease is a manifestation of the saturation of the strong nuclear force at high densities, where the repulsive interactions between nucleons begin to dominate, counteracting the attractive tensor force. The density distributions of the nucleus are typically described by a Woods-Saxon type distribution as$ \begin{aligned} \begin{split} \rho_{ws}(r)=\rho_{0}\left [1+exp\left (\frac{r-R}{a}\right )\right ]^{-1} \end{split} \end{aligned} $

(4) With a diffuseness parameter
$ a \sim 0.53 $ fm and$ \rho_{0} \sim 0.17 $ fm$ ^{-1} $ being the density at the center of the nucleus, the radius parameter R is determined by the mass number A as$ R \sim 1.10A^{1/3} $ (fm). A charge density function was approximated as in Equation (4), which models the shape of the nuclei as a uniform sphere with constant charge density [16].$ \begin{aligned} \begin{split} \rho_{ch}(r)=\frac{0.75A/\pi}{(5/3<r^{2}>)^{3/2}} \end{split} \end{aligned} $

(5) The calculations with and without the b and c terms in Eq. (2), defined as the NMET-1 and NMET-2 models, have been performed using two nuclear density functions from Eq. (3) and Eq. (4), as shown in Fig. 8. The parameters were adjusted according to the scaling of the tensor force with nuclear density to be consistent with the experimental data of the 3
$ ^{+} $ (0) state of$ ^{6} $ Li. A saturation trend is achieved at high densities, reflecting the intricate behavior of the strong nuclear force within atomic nuclei.
Figure 8. (color online) The tensor force strength ratio,
$ f/f_{0} $ , which compares values outside the nuclear medium to those within, is analyzed as a function of the atomic number A. NMET model calculations are conducted using two different nuclear density functions:$ \rho_{ch} $ and$ \rho_{ws} $ .The modification of tensor force strength with nuclear density becomes particularly important in extreme conditions, such as neutron stars or during heavy-ion collisions in nuclear physics experiments. In these extreme environments, the nuclear density can reach values far beyond those found in stable atomic nuclei. The modification of the tensor force strength with nuclear density influences the equation of state, nuclear structure, and transport properties of nuclear matter.
-
The tensor force strength for the
$ J^{\pi}(T)=0^{+}(1) $ state is much smaller than that for the$ J^{\pi}(T)=3^{+}(0) $ state in the isolated$ ^{6} $ Li [11], which can be essentially explained by the tensor force properties of isospin dependence. For the$ 0^{+}(1) $ state, which has a configuration of$ (0s_{1/2})^{4}(0p_{3/2})^{2} $ , the inner$ ^{4} $ He core composed of two$ pn $ pairs with T=0 is excited from 0s to 0$ p_{1/2} $ by the tensor force via the two-particle two-hole (2p-2h) mode [12], while the outer$ pn $ pair on the 0p shell with T=1 undergoes a relatively small excitation due to the weak tensor force for the T=1 channel. For the$ 3^{+}(0) $ state, the outer$ pn $ pair in the 0p shell may undergo a tensor force excitation with a T=0 state from$ (0p_{3/2})^{2} $ to$ (0d_{3/2})^{2} $ , which satisfies the selection rule for the tensor force excitation of$ \Delta L $ =2,$ \Delta S $ =2, and$ \Delta J $ =0. From the point of view of the excitation strength of the tensor force, the coupling of the outer$ pn $ pair to the inner$ ^{4} $ He core is relatively weak for the$ 0^{+}(1) $ state, and hence the population of the$ 3^{+}(0) $ state is much higher than that of the$ 0^{+}(1) $ state in the isolated$ ^{6} $ Li nucleus, as shown in Fig. 3(b).However, when
$ ^{6} $ Li is not completely isolated but still within the domain of$ ^{11} $ C as a component, d and α in$ ^{6} $ Li are correlated two-body clusters and are essentially affected by the central interactions from the residual nucleus. Such extra interactions may reduce the strength of coupling of the$ pn $ pair with isospin T=0 to α, which leads to the shrinkage of tensor force excitation and results in comparable populations between the$ J^{\pi}(T)=0^{+}(1) $ state and the$ J^{\pi}(T)=3^{+}(0) $ state for the case of$ \Theta_{CM}<120^{\circ} $ , as shown in Fig. 3(a).Among the T=0 triplet states of
$ J^{\pi}(T)=3^{+}(0), 2^{+}(0), 1^{+}(0) $ , as shown in Fig. 7, the strong excitation of the$ 3^{+}(0) $ state with the lowest excitation energy results from the tensor force excitation from$ (0p_{3/2})^{2} $ to$ (0d_{3/2})^{2} $ with a 2p-2h excitation mode at a high spin and T=0. The highest excited energy state,$ 1^{+}(0) $ , involves the mixing configurations of$ (0s_{1/2})^{4}(0p_{3/2})^{2} $ ,$ (0s_{1/2})^{4}(0p_{1/2})^{1}(0p_{3/2})^{1} $ , and$ (0s_{1/2})^{4}(0p_{1/2})^{2} $ with a similar probability for each, and the$ 2^{+}(0) $ state only takes on a configuration of$ (0s_{1/2})^{4}(0p_{1/2})^{1}(0p_{3/2})^{1} $ with two valence nucleons of neutron and proton lying in the separated sub-shell levels, which could explain the present experimental observations of the high population of the$ 3^{+}(0) $ state and the low population of the$ 2^{+}(0) $ and$ 1^{+}(0) $ states. Additionally, this could also clarify the relatively large dynamical motion and broader density distribution of d and α, namely, a more loosely bound structure for the$ 2^{+}(0) $ and$ 1^{+}(0) $ states in$ ^{6} $ Li.
Figure 7. (color online) Configurations of
$ ^{6} $ Li for the ground state and excited states of$ J^{\pi} $ (T)=3$ ^{+} $ (0), 2$ ^{+} $ (0), and 1$ ^{+} $ (0). Notably, 3$ ^{+} $ (0) satisfies the tensor force selection rule of ΔL=2, ΔS=2, and ΔJ=0 and 2p-2h configuration.The tensor force strength [1−6], modulated by the effects of the nuclear medium, reflects the intricate interplay between the nucleons within the nucleus. As the nuclear density increases, more nucleons are packed into a given volume, leading to increased overlap and interaction between them. This enhanced interaction modifies the strength of the tensor force and its impact on the nuclear system.
$ \begin{aligned} \begin{split} \frac{f(\rho)}{f_{0}(\rho)}={\rm e}^{-(a\rho+b\rho^{2}+c\rho^{3})}. \end{split} \end{aligned} $
(3) The function
$ f(\rho)/f_{0}(\rho) $ for the nuclear medium effect on tensor force strength (NMET) in Eq. (2) captures this behavior by introducing the scaling constants a, b, and c. The positive values of these constants indicate that the tensor force strength diminishes as the nuclear density increases. This decrease is a manifestation of the saturation of the strong nuclear force at high densities, where the repulsive interactions between nucleons begin to dominate, counteracting the attractive tensor force. The density distributions of the nucleus are typically described by a Woods-Saxon type distribution as$ \begin{aligned} \begin{split} \rho_{ws}(r)=\rho_{0}\left [1+{\rm exp}\left (\frac{r-R}{a}\right )\right ]^{-1} .\end{split} \end{aligned} $
(4) With a diffuseness parameter
$ a \sim 0.53 $ fm and$ \rho_{0} \sim 0.17 $ fm$ ^{-1} $ being the density at the center of the nucleus, the radius parameter R is determined by the mass number A as$ R \sim 1.10A^{1/3} $ (fm). A charge density function was approximated as in Eq. (4), which models the shape of the nuclei as a uniform sphere with constant charge density.$ \begin{aligned} \begin{split} \rho_{ch}(r)=\frac{0.75A/\pi}{(5/3<r^{2}>)^{3/2}}. \end{split} \end{aligned} $
(5) The calculations with and without the b and c terms in Eq. (2), defined as the NMET-1 and NMET-2 models, have been performed using two nuclear density functions from Eq. (3) and Eq. (4), as shown in Fig. 8. The parameters were adjusted according to the scaling of the tensor force with nuclear density to be consistent with the experimental data of the 3
$ ^{+} $ (0) state of$ ^{6} $ Li. A saturation trend is achieved at high densities, reflecting the intricate behavior of the strong nuclear force within atomic nuclei.
Figure 8. (color online) The tensor force strength ratio,
$ f/f_{0} $ , which compares values outside the nuclear medium to those within, is analyzed as a function of the atomic number A. NMET model calculations are conducted using two different nuclear density functions:$ \rho_{ch} $ and$ \rho_{ws} $ .The modification of tensor force strength with nuclear density becomes particularly important in extreme conditions, such as neutron stars or during heavy-ion collisions in nuclear physics experiments. In these extreme environments, the nuclear density can reach values far beyond those found in stable atomic nuclei. The modification of the tensor force strength with nuclear density influences the equation of state, nuclear structure, and transport properties of nuclear matter.
-
In summary, a suppressed excitation for the spin
$ J^{\pi}=3^{+} $ state with isospin$ T=0 $ was observed in the$ ^{6} $ Li cluster component inside the nucleus for the first time, which differs significantly from the relatively enhanced excitation of this state in the isolated nucleus$ ^{6} $ Li. In contrast, the excitation of the reference state of$ J^{\pi}=0^{+} $ with isospin$ T=1 $ exhibits an almost equal cross section for these two$ ^{6} $ Li formations. The mechanism of this relatively weaker excitation in the$ ^{6} $ Li cluster in the$ ^{11} $ C nucleus is proposed to be due to the nuclear medium effects hindering the tensor force excitation for the isospin$ T=0 $ state, while having no impact on the$ T=1 $ state. -
In summary, a suppressed excitation for the spin
$ J^{\pi}=3^{+} $ state with isospin$ T=0 $ was observed in the$ ^{6} $ Li cluster component inside the nucleus for the first time, which differs significantly from the relatively enhanced excitation of this state in the isolated nucleus$ ^{6} $ Li. In contrast, the excitation of the reference state of$ J^{\pi}=0^{+} $ with isospin$ T=1 $ exhibits an almost equal cross section for these two$ ^{6} $ Li formations. The mechanism of this relatively weaker excitation in the$ ^{6} $ Li cluster in the$ ^{11} $ C nucleus is proposed to be due to the nuclear medium effects hindering the tensor force excitation for the isospin$ T=0 $ state, while having no impact on the$ T=1 $ state. -
In summary, a suppressed excitation for the spin
$ J^{\pi}=3^{+} $ state with isospin$ T=0 $ was observed in the$ ^{6} $ Li cluster component inside the nucleus for the first time, which differs significantly from the relatively enhanced excitation of this state in the isolated nucleus$ ^{6} $ Li. In contrast, the excitation of the reference state of$ J^{\pi}=0^{+} $ with isospin$ T=1 $ exhibits an almost equal cross section for these two$ ^{6} $ Li formations. The mechanism of this relatively weaker excitation in the$ ^{6} $ Li cluster in the$ ^{11} $ C nucleus is proposed to be due to the nuclear medium effects hindering the tensor force excitation for the isospin$ T=0 $ state, while having no impact on the$ T=1 $ state. -
We would like to acknowledge the staff of HIRFL for the operation of the cyclotron. The author T. Wang appreciates the financial support from the China Scholarship Council.
-
We would like to acknowledge the staff of HIRFL for the operation of the cyclotron. The author T. Wang appreciates the financial support from the China Scholarship Council.
-
We would like to acknowledge the staff of HIRFL for the operation of the cyclotron. The author T. Wang appreciates the financial support from the China Scholarship Council.
Nuclear medium effects for modification of tensor interaction
- Received Date: 2025-09-17
- Available Online: 2026-02-15
Abstract: The cross section for the $ J^{\pi}(T)=3^{+}(0) $ state was measured to be enhanced in an isolated $ ^{6} $Li nucleus compared to the same reduced state in a $ ^{6} $Li cluster. This difference demonstrates a nuclear medium modification of the tensor force, which is sensitively probed by the $ T=0 $ channel. In contrast, the $ J^{\pi}(T)=0^{+}(1) $ state ($ T=1 $) was found to have approximately equal excitation strength in both $ ^{6} $Li systems. We interpret this tensor force modification as a consequence of density saturation within a many-body interaction framework.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: