-
Scientists' research on the 26Al nucleus in the universe dates back to 1976. With the help of the HEAO-3 satellite, scientists were able to observe the 1809 keV characteristic
$ \gamma $ ray emitted during the$ \beta- $ decay of 26Al. Since then, scientists have continued to observe and study 26Al in the present century [1, 2]. Due to its moderate half-life ($ {\rm{T}}_{1/2} = 7 \times 10^5 $ years), the characteristic$ \gamma $ ray of 26Al has long been direct and powerful evidence of ongoing nucleosynthesis in the Milky Way, establishing its significant role in gamma-ray astronomy.However, even today, the 26Al production sites remain a subject of debate. Possible astrophysical sites include AGB stars [3], Wolf-Rayet stars [4], novae [5], and core-collapse supernovae [6]. One factor that significantly impacts the calculation of 26Al production is its isomeric state, 26mAl. Unlike the ground state 26gAl, which has a half-life of
$ 7 \times 10^5 $ years, 26mAl has a very short half-life of only 6.34 s and decays rapidly to 26Mg, subsequently becoming 27Al through the 26Mg$ (p, \gamma) $ 27Al reaction. On the other hand, the longer-lived 26gAl participates in the proton capture reaction 26Al$(p, \gamma) $ 27Si, which then decays into 27Al. Although the final products are the same, the different production sites lead to differences in the reaction rates of the two branches, which in turn affect the 26Al/27Al ratio in the universe. By studying both the reaction rate and the isotope abundance ratio, we hope to solve the mystery of the interstellar origin of 26Al. The 2017 White Paper on Nuclear Astrophysics and Low Energy Nuclear Physics [7] also pointed out that isotopic ratios are important parameters for diagnosing the multi-shell burning structure in the late stages of massive star evolution and early solar system evolution.The 26Mg
$(p, \gamma) $ 27Al reaction, as part of the Mg-Al cycle, links 26Al and 27Al through the$\beta$ -decay of 26gAl into 26Mg. The change in the reaction rate of this process will directly reflect the change in the abundance of 26Al/27Al in the interstellar medium. Based on earlier indirect measurements, the branching for the formation of 26gAl from 25Mg$(p, \gamma) $ 26Al was approximately 80% [8]. Under this assumption, the importance of 26Mg$(p, \gamma) $ 27Al reaction in the cycle was considered negligible. However, the latest direct measurement results for 25Mg$(p, \gamma) $ 26Al from LUNA [9] and JUNA [10] suggest that the branching ratio for the formation of 26gAl is only about 60%, indicating that the decay rate to 26mAl should be at least twice as high as previously believed after considering the possible measurement errors. This significantly increases the importance of the 26Mg$(p, \gamma) $ 27Al reaction branch in the cycle, and accurate measurements are needed to recalculate its impact on the 26Al / 27Al ratio.It is worth noting that globular clusters serve as ideal stellar laboratories containing a series of stars with the same initial metallicity, presenting almost every stage of stellar evolution in the same region [11]. However, the complex main-sequence stars and anomalous elemental abundances observed in globular clusters suggest that they are not simple systems [12, 13]. Currently, the Mg-Al anti-correlation phenomenon observed in massive, low-metallicity globular clusters [14] remains an unsolved mystery. The reaction rate of 26Mg
$(p, \gamma) $ 27Al in astrophysical environments has a strong direct connection with this phenomenon and may be the key to unlocking this mystery.In addition to directly measuring the
$ (p, \gamma) $ reaction, indirect measurements of single-proton transfer reactions, such as (3He, d) and (7Li, 6He), are also effective methods for studying resonance strengths and reaction rates. Based on the proton spectroscopic factor of 7Li, which has been accurately measured in previous studies [15, 16], the angular distribution can be reproduced using the Distorted Wave Born Approximation (DWBA) method to obtain the proton spectroscopic factor for 27Al, and subsequently, to investigate the information of its excited states.This work studies three excited states of 27Al near the threshold using the 26Mg (7Li, 6He) 27Al reaction, derives the corresponding proton spectroscopic factors for 27Al, and thus obtains the resonance strengths for low-energy resonances of 26Mg
$(p, \gamma) $ 27Al. The total reaction rate under astrophysical conditions is calculated, and the impact of the new resonance strengths on the total reaction rate is evaluated. -
Scientists' research on the 26Al nucleus in the universe dates back to 1976. With the help of the HEAO-3 satellite, scientists were able to observe the 1809 keV characteristic
$ \gamma $ ray emitted during the$ \beta- $ decay of 26Al. Since then, scientists have continued to observe and study 26Al in the present century [1, 2]. Due to its moderate half-life ($ {{T}}_{1/2} = 7 \times 10^5 $ years), the characteristic$ \gamma $ ray of 26Al has long been direct and powerful evidence of ongoing nucleosynthesis in the Milky Way, establishing its significant role in gamma-ray astronomy.However, even today, the 26Al production sites remain a subject of debate. Possible astrophysical sites include AGB stars [3], Wolf-Rayet stars [4], novae [5], and core-collapse supernovae [6]. One factor that significantly impacts the calculation of 26Al production is its isomeric state, 26mAl. Unlike the ground state 26gAl, which has a half-life of
$ 7 \times 10^5 $ years, 26mAl has a very short half-life of only 6.34 s and decays rapidly to 26Mg, subsequently becoming 27Al through the 26Mg$ (p, \gamma) $ 27Al reaction. On the other hand, the longer-lived 26gAl participates in the proton capture reaction 26Al$(p, \gamma) $ 27Si, which then decays into 27Al. Although the final products are the same, the different production sites lead to differences in the reaction rates of the two branches, which in turn affect the 26Al/27Al ratio in the universe. By studying both the reaction rate and the isotope abundance ratio, we hope to solve the mystery of the interstellar origin of 26Al. The 2017 White Paper on Nuclear Astrophysics and Low Energy Nuclear Physics [7] also pointed out that isotopic ratios are important parameters for diagnosing the multi-shell burning structure in the late stages of massive star evolution and early solar system evolution.The 26Mg
$(p, \gamma) $ 27Al reaction, as part of the Mg-Al cycle, links 26Al and 27Al through the$\beta$ -decay of 26gAl into 26Mg. The change in the reaction rate of this process will directly reflect the change in the abundance of 26Al/27Al in the interstellar medium. Based on earlier indirect measurements, the branching for the formation of 26gAl from 25Mg$(p, \gamma) $ 26Al was approximately 80% [8]. Under this assumption, the importance of 26Mg$(p, \gamma) $ 27Al reaction in the cycle was considered negligible. However, the latest direct measurement results for 25Mg$(p, \gamma) $ 26Al from LUNA [9] and JUNA [10] suggest that the branching ratio for the formation of 26gAl is only about 60%, indicating that the decay rate to 26mAl should be at least twice as high as previously believed after considering the possible measurement errors. This significantly increases the importance of the 26Mg$(p, \gamma) $ 27Al reaction branch in the cycle, and accurate measurements are needed to recalculate its impact on the 26Al / 27Al ratio.It is worth noting that globular clusters serve as ideal stellar laboratories containing a series of stars with the same initial metallicity, presenting almost every stage of stellar evolution in the same region [11]. However, the complex main-sequence stars and anomalous elemental abundances observed in globular clusters suggest that they are not simple systems [12, 13]. Currently, the Mg-Al anti-correlation phenomenon observed in massive, low-metallicity globular clusters [14] remains an unsolved mystery. The reaction rate of 26Mg
$(p, \gamma) $ 27Al in astrophysical environments has a strong direct connection with this phenomenon and may be the key to unlocking this mystery.In addition to directly measuring the
$ (p, \gamma) $ reaction, indirect measurements of single-proton transfer reactions, such as (3He, d) and (7Li, 6He), are also effective methods for studying resonance strengths and reaction rates. Based on the proton spectroscopic factor of 7Li, which has been accurately measured in previous studies [15, 16], the angular distribution can be reproduced using the Distorted Wave Born Approximation (DWBA) method to obtain the proton spectroscopic factor for 27Al, and subsequently, to investigate the information of its excited states.This work studies three excited states of 27Al near the threshold using the 26Mg (7Li, 6He) 27Al reaction, derives the corresponding proton spectroscopic factors for 27Al, and thus obtains the resonance strengths for low-energy resonances of 26Mg
$(p, \gamma) $ 27Al. The total reaction rate under astrophysical conditions is calculated, and the impact of the new resonance strengths on the total reaction rate is evaluated. -
Scientists' research on the 26Al nucleus in the universe dates back to 1976. With the help of the HEAO-3 satellite, scientists were able to observe the 1809 keV characteristic
$ \gamma $ ray emitted during the$ \beta- $ decay of 26Al. Since then, scientists have continued to observe and study 26Al in the present century [1, 2]. Due to its moderate half-life ($ {{T}}_{1/2} = 7 \times 10^5 $ years), the characteristic$ \gamma $ ray of 26Al has long been direct and powerful evidence of ongoing nucleosynthesis in the Milky Way, establishing its significant role in gamma-ray astronomy.However, even today, the 26Al production sites remain a subject of debate. Possible astrophysical sites include AGB stars [3], Wolf-Rayet stars [4], novae [5], and core-collapse supernovae [6]. One factor that significantly impacts the calculation of 26Al production is its isomeric state, 26mAl. Unlike the ground state 26gAl, which has a half-life of
$ 7 \times 10^5 $ years, 26mAl has a very short half-life of only 6.34 s and decays rapidly to 26Mg, subsequently becoming 27Al through the 26Mg$ (p, \gamma) $ 27Al reaction. On the other hand, the longer-lived 26gAl participates in the proton capture reaction 26Al$(p, \gamma) $ 27Si, which then decays into 27Al. Although the final products are the same, the different production sites lead to differences in the reaction rates of the two branches, which in turn affect the 26Al/27Al ratio in the universe. By studying both the reaction rate and the isotope abundance ratio, we hope to solve the mystery of the interstellar origin of 26Al. The 2017 White Paper on Nuclear Astrophysics and Low Energy Nuclear Physics [7] also pointed out that isotopic ratios are important parameters for diagnosing the multi-shell burning structure in the late stages of massive star evolution and early solar system evolution.The 26Mg
$(p, \gamma) $ 27Al reaction, as part of the Mg-Al cycle, links 26Al and 27Al through the$\beta$ -decay of 26gAl into 26Mg. The change in the reaction rate of this process will directly reflect the change in the abundance of 26Al/27Al in the interstellar medium. Based on earlier indirect measurements, the branching for the formation of 26gAl from 25Mg$(p, \gamma) $ 26Al was approximately 80% [8]. Under this assumption, the importance of 26Mg$(p, \gamma) $ 27Al reaction in the cycle was considered negligible. However, the latest direct measurement results for 25Mg$(p, \gamma) $ 26Al from LUNA [9] and JUNA [10] suggest that the branching ratio for the formation of 26gAl is only about 60%, indicating that the decay rate to 26mAl should be at least twice as high as previously believed after considering the possible measurement errors. This significantly increases the importance of the 26Mg$(p, \gamma) $ 27Al reaction branch in the cycle, and accurate measurements are needed to recalculate its impact on the 26Al / 27Al ratio.It is worth noting that globular clusters serve as ideal stellar laboratories containing a series of stars with the same initial metallicity, presenting almost every stage of stellar evolution in the same region [11]. However, the complex main-sequence stars and anomalous elemental abundances observed in globular clusters suggest that they are not simple systems [12, 13]. Currently, the Mg-Al anti-correlation phenomenon observed in massive, low-metallicity globular clusters [14] remains an unsolved mystery. The reaction rate of 26Mg
$(p, \gamma) $ 27Al in astrophysical environments has a strong direct connection with this phenomenon and may be the key to unlocking this mystery.In addition to directly measuring the
$ (p, \gamma) $ reaction, indirect measurements of single-proton transfer reactions, such as (3He, d) and (7Li, 6He), are also effective methods for studying resonance strengths and reaction rates. Based on the proton spectroscopic factor of 7Li, which has been accurately measured in previous studies [15, 16], the angular distribution can be reproduced using the Distorted Wave Born Approximation (DWBA) method to obtain the proton spectroscopic factor for 27Al, and subsequently, to investigate the information of its excited states.This work studies three excited states of 27Al near the threshold using the 26Mg (7Li, 6He) 27Al reaction, derives the corresponding proton spectroscopic factors for 27Al, and thus obtains the resonance strengths for low-energy resonances of 26Mg
$(p, \gamma) $ 27Al. The total reaction rate under astrophysical conditions is calculated, and the impact of the new resonance strengths on the total reaction rate is evaluated. -
Scientists' research on the 26Al nucleus in the universe dates back to 1976. With the help of the HEAO-3 satellite, scientists were able to observe the 1809 keV characteristic
$ \gamma $ ray emitted during the$ \beta- $ decay of 26Al. Since then, scientists have continued to observe and study 26Al in the present century [1, 2]. Due to its moderate half-life ($ {{T}}_{1/2} = 7 \times 10^5 $ years), the characteristic$ \gamma $ ray of 26Al has long been direct and powerful evidence of ongoing nucleosynthesis in the Milky Way, establishing its significant role in gamma-ray astronomy.However, even today, the 26Al production sites remain a subject of debate. Possible astrophysical sites include AGB stars [3], Wolf-Rayet stars [4], novae [5], and core-collapse supernovae [6]. One factor that significantly impacts the calculation of 26Al production is its isomeric state, 26mAl. Unlike the ground state 26gAl, which has a half-life of
$ 7 \times 10^5 $ years, 26mAl has a very short half-life of only 6.34 s and decays rapidly to 26Mg, subsequently becoming 27Al through the 26Mg$ (p, \gamma) $ 27Al reaction. On the other hand, the longer-lived 26gAl participates in the proton capture reaction 26Al$(p, \gamma) $ 27Si, which then decays into 27Al. Although the final products are the same, the different production sites lead to differences in the reaction rates of the two branches, which in turn affect the 26Al/27Al ratio in the universe. By studying both the reaction rate and the isotope abundance ratio, we hope to solve the mystery of the interstellar origin of 26Al. The 2017 White Paper on Nuclear Astrophysics and Low Energy Nuclear Physics [7] also pointed out that isotopic ratios are important parameters for diagnosing the multi-shell burning structure in the late stages of massive star evolution and early solar system evolution.The 26Mg
$(p, \gamma) $ 27Al reaction, as part of the Mg-Al cycle, links 26Al and 27Al through the$\beta$ -decay of 26gAl into 26Mg. The change in the reaction rate of this process will directly reflect the change in the abundance of 26Al/27Al in the interstellar medium. Based on earlier indirect measurements, the branching for the formation of 26gAl from 25Mg$(p, \gamma) $ 26Al was approximately 80% [8]. Under this assumption, the importance of 26Mg$(p, \gamma) $ 27Al reaction in the cycle was considered negligible. However, the latest direct measurement results for 25Mg$(p, \gamma) $ 26Al from LUNA [9] and JUNA [10] suggest that the branching ratio for the formation of 26gAl is only about 60%, indicating that the decay rate to 26mAl should be at least twice as high as previously believed after considering the possible measurement errors. This significantly increases the importance of the 26Mg$(p, \gamma) $ 27Al reaction branch in the cycle, and accurate measurements are needed to recalculate its impact on the 26Al / 27Al ratio.It is worth noting that globular clusters serve as ideal stellar laboratories containing a series of stars with the same initial metallicity, presenting almost every stage of stellar evolution in the same region [11]. However, the complex main-sequence stars and anomalous elemental abundances observed in globular clusters suggest that they are not simple systems [12, 13]. Currently, the Mg-Al anti-correlation phenomenon observed in massive, low-metallicity globular clusters [14] remains an unsolved mystery. The reaction rate of 26Mg
$(p, \gamma) $ 27Al in astrophysical environments has a strong direct connection with this phenomenon and may be the key to unlocking this mystery.In addition to directly measuring the
$ (p, \gamma) $ reaction, indirect measurements of single-proton transfer reactions, such as (3He, d) and (7Li, 6He), are also effective methods for studying resonance strengths and reaction rates. Based on the proton spectroscopic factor of 7Li, which has been accurately measured in previous studies [15, 16], the angular distribution can be reproduced using the Distorted Wave Born Approximation (DWBA) method to obtain the proton spectroscopic factor for 27Al, and subsequently, to investigate the information of its excited states.This work studies three excited states of 27Al near the threshold using the 26Mg (7Li, 6He) 27Al reaction, derives the corresponding proton spectroscopic factors for 27Al, and thus obtains the resonance strengths for low-energy resonances of 26Mg
$(p, \gamma) $ 27Al. The total reaction rate under astrophysical conditions is calculated, and the impact of the new resonance strengths on the total reaction rate is evaluated. -
The experiment was conducted at the Q3D spectrograph [17] of the HI-13 tandem accelerator in Beijing. A 100 enA, 42 MeV 7Li beam was used to bombard a 44
$ \mu {\rm{g}}/{\rm{cm}}^2 $ metal 26Mg target with an abundance of 95%, and a natural Mg target was used to analyze the influence of background. A movable Faraday cup was placed at 0° for beam normalization. A$ \Delta E-E $ counter was placed at 30° to monitor the elastic scattering events, serving as the relative normalization for the measurements of small angles. The emitted particles were momentum-analyzed by the Q3D magnetic spectrometer with a fixed solid angle of 3.26 msr and measured by the detector array on the focal plane, which included six X4 silicon detectors, each with an effective detection length of 75 mm and a minimum position resolution (FWHM) of 0.4 mm. The detectors were arranged at 55 mm intervals on a high-precision moving platform. The detector array could cover a focal plane range of 790 mm by shifting 65 mm, and two spectra measured at two positions could be combined to obtain the whole spectra. The position distortion on the edge of the detectors could be effectively eliminated by the overlaps between two adjacent detecting areas. The detector setup is shown in Fig. 1. More similar experimental setups can be found in our previous work [18−23]. In this experiment, the cross-sections of the 26Mg(7Li, 6He)27Al reaction distributed to three states near the threshold were measured in the range of$ 3^{\circ} \leqslant \theta_{\rm lab} \leqslant 15^{\circ} $ with a 1° interval, and the differential cross-section of the 26Mg(7Li, 7Li)26Mg elastic scattering was measured in the range of$ 10^{\circ} \leqslant \theta_{\rm lab} \leqslant 40^{\circ} $ with a 1° interval to obtain optical potential parameters for the entrance channel. -
The experiment was conducted at the Q3D spectrograph [17] of the HI-13 tandem accelerator in Beijing. A 100 enA, 42 MeV 7Li beam was used to bombard a 44
$ \mu {\rm{g}}/{\rm{cm}}^2 $ metal 26Mg target with an abundance of 95%, and a natural Mg target was used to analyze the influence of background. A movable Faraday cup was placed at 0° for beam normalization. A$ \Delta E-E $ counter was placed at 30° to monitor the elastic scattering events, serving as the relative normalization for the measurements of small angles. The emitted particles were momentum-analyzed by the Q3D magnetic spectrometer with a fixed solid angle of 3.26 msr and measured by the detector array on the focal plane, which included six X4 silicon detectors, each with an effective detection length of 75 mm and a minimum position resolution (FWHM) of 0.4 mm. The detectors were arranged at 55 mm intervals on a high-precision moving platform. The detector array could cover a focal plane range of 790 mm by shifting 65 mm, and two spectra measured at two positions could be combined to obtain the whole spectra. The position distortion on the edge of the detectors could be effectively eliminated by the overlaps between two adjacent detecting areas. The detector setup is shown in Fig. 1. More similar experimental setups can be found in our previous work [18−23]. In this experiment, the cross-sections of the 26Mg(7Li, 6He)27Al reaction distributed to three states near the threshold were measured in the range of$ 3^{\circ} \leqslant \theta_{\rm lab} \leqslant 15^{\circ} $ with a 1° interval, and the differential cross-section of the 26Mg(7Li, 7Li)26Mg elastic scattering was measured in the range of$ 10^{\circ} \leqslant \theta_{\rm lab} \leqslant 40^{\circ} $ with a 1° interval to obtain optical potential parameters for the entrance channel. -
The experiment was conducted at the Q3D spectrograph [17] of the HI-13 tandem accelerator in Beijing. A 100 enA, 42 MeV 7Li beam was used to bombard a 44
$ \mu {\rm{g}}/{\rm{cm}}^2 $ metal 26Mg target with an abundance of 95%, and a natural Mg target was used to analyze the influence of background. A movable Faraday cup was placed at 0° for beam normalization. A$ \Delta E-E $ counter was placed at 30° to monitor the elastic scattering events, serving as the relative normalization for the measurements of small angles. The emitted particles were momentum-analyzed by the Q3D magnetic spectrometer with a fixed solid angle of 3.26 msr and measured by the detector array on the focal plane, which included six X4 silicon detectors, each with an effective detection length of 75 mm and a minimum position resolution (FWHM) of 0.4 mm. The detectors were arranged at 55 mm intervals on a high-precision moving platform. The detector array could cover a focal plane range of 790 mm by shifting 65 mm, and two spectra measured at two positions could be combined to obtain the whole spectra. The position distortion on the edge of the detectors could be effectively eliminated by the overlaps between two adjacent detecting areas. The detector setup is shown in Fig. 1. More similar experimental setups can be found in our previous work [18−23]. In this experiment, the cross-sections of the 26Mg(7Li, 6He)27Al reaction distributed to three states near the threshold were measured in the range of$ 3^{\circ} \leqslant \theta_{\rm lab} \leqslant 15^{\circ} $ with a 1° interval, and the differential cross-section of the 26Mg(7Li, 7Li)26Mg elastic scattering was measured in the range of$ 10^{\circ} \leqslant \theta_{\rm lab} \leqslant 40^{\circ} $ with a 1° interval to obtain optical potential parameters for the entrance channel. -
The experiment was conducted at the Q3D spectrograph [17] of the HI-13 tandem accelerator in Beijing. A 100 enA, 42 MeV 7Li beam was used to bombard a 44
$ \mu {\rm{g}}/{\rm{cm}}^2 $ metal 26Mg target with an abundance of 95%, and a natural Mg target was used to analyze the influence of background. A movable Faraday cup was placed at 0° for beam normalization. A$ \Delta E-E $ counter was placed at 30° to monitor the elastic scattering events, serving as the relative normalization for the measurements of small angles. The emitted particles were momentum-analyzed by the Q3D magnetic spectrometer with a fixed solid angle of 3.26 msr and measured by the detector array on the focal plane, which included six X4 silicon detectors, each with an effective detection length of 75 mm and a minimum position resolution (FWHM) of 0.4 mm. The detectors were arranged at 55 mm intervals on a high-precision moving platform. The detector array could cover a focal plane range of 790 mm by shifting 65 mm, and two spectra measured at two positions could be combined to obtain the whole spectra. The position distortion on the edge of the detectors could be effectively eliminated by the overlaps between two adjacent detecting areas. The detector setup is shown in Fig. 1. More similar experimental setups can be found in our previous work [18−23]. In this experiment, the cross-sections of the 26Mg(7Li, 6He)27Al reaction distributed to three states near the threshold were measured in the range of$ 3^{\circ} \leqslant \theta_{lab} \leqslant 15^{\circ} $ with a 1° interval, and the differential cross-section of the 26Mg(7Li, 7Li)26Mg elastic scattering was measured in the range of$ 10^{\circ} \leqslant \theta_{lab} \leqslant 40^{\circ} $ with a 1° interval to obtain optical potential parameters for the entrance channel. -
The spectra for the 26Mg and 24Mg targets at 7° are shown in Fig. 2. The states originating from the 16O(7Li, 6He)17F and 26Mg(7Li, 6He)27Al reactions can be clearly distinguished by comparing the two spectra. To extract the entrance channel optical potential parameters, the angular distribution of 26Mg(7Li,7Li)26Mg elastic scattering was also measured and is shown in Fig. 3. Based on the position of the
$ ^{17}{\rm{F}}_0 $ and kinematic calculations, the 8.324 MeV states in 27Al, which correspond to the 52.8 keV resonance of 26Mg+p, as well as the 7.858, 8.324, 8.521, 8.597, 8.753, and 9.080 MeV states, which are located near the threshold, were accurately identified. The angular distributions of three states are shown in Fig. 4. The above excitation energies are based on literature data [24−26].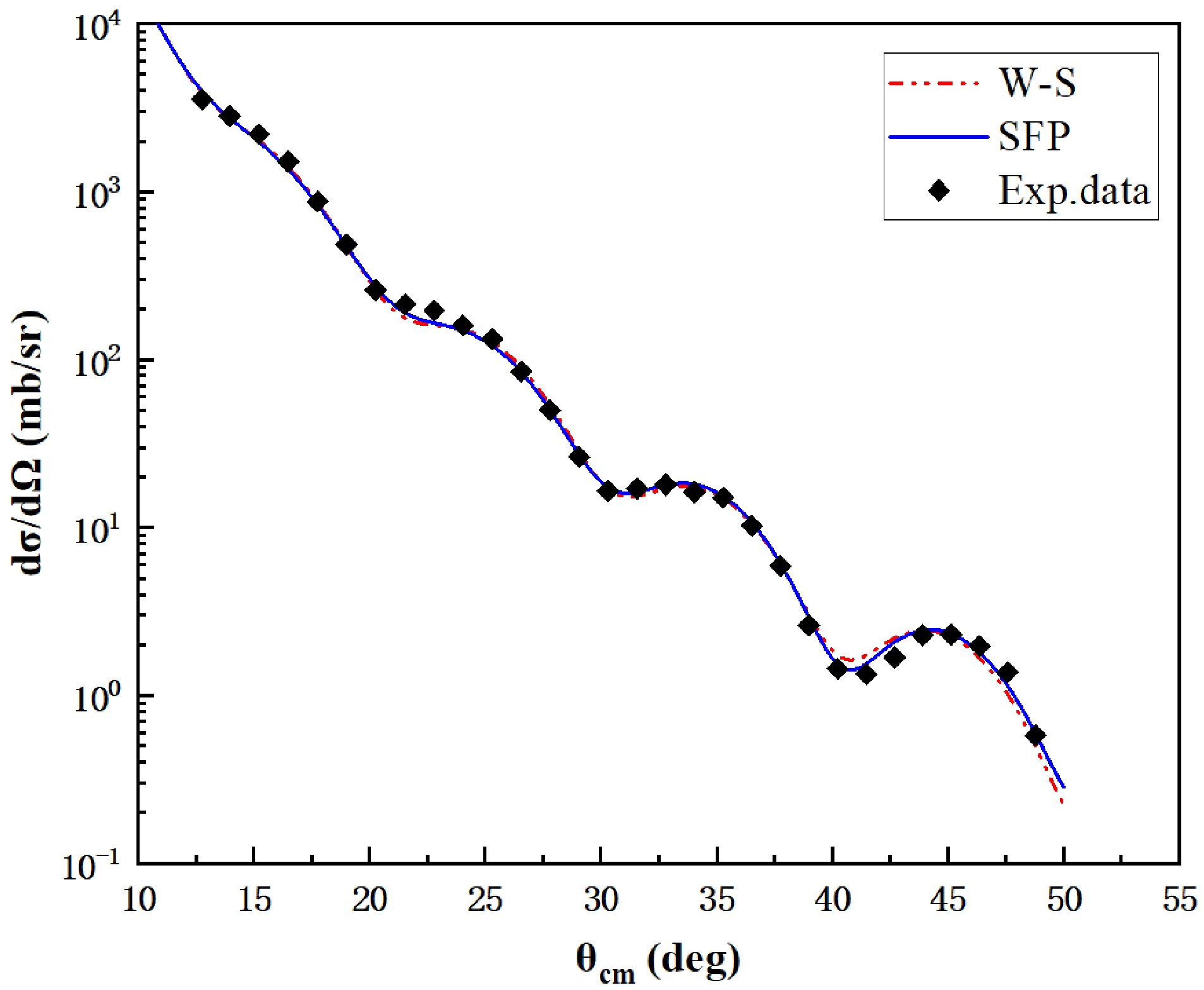
Figure 2. (color online) The total spectrum at 7°. The left figure shows the experimental spectrum measured with a 26Mg target, while the right figure shows the background spectrum obtained using a natMg target target for comparison. The six values 7.858–9.080 in the figure represent the corresponding excited states.
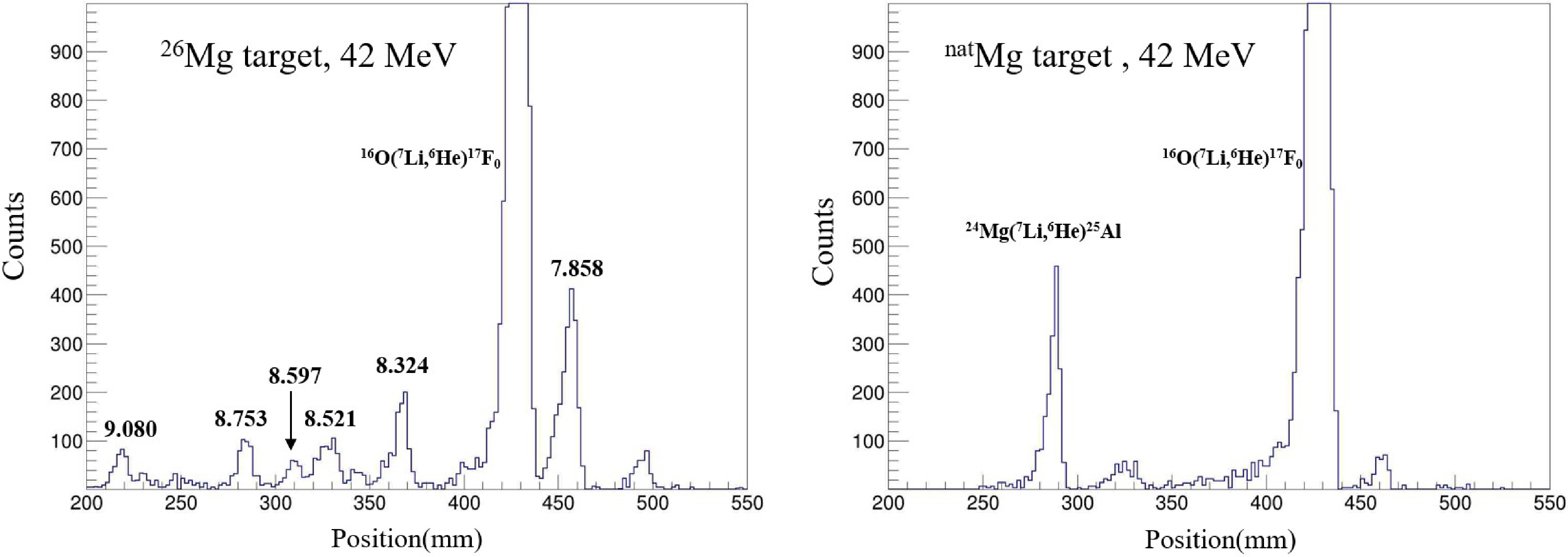
Figure 3. The fitting results of 26Mg(7Li,7Li) elastic scattering at 42 MeV. The black solid diamonds represent the experimentally measured elastic scattering angular distribution, and the blue solid line and red dashed line represent the results obtained using the SFP and the Woods-Saxon potential for fitting, respectively. The uncertainties are too minor to be discernible in the plot.
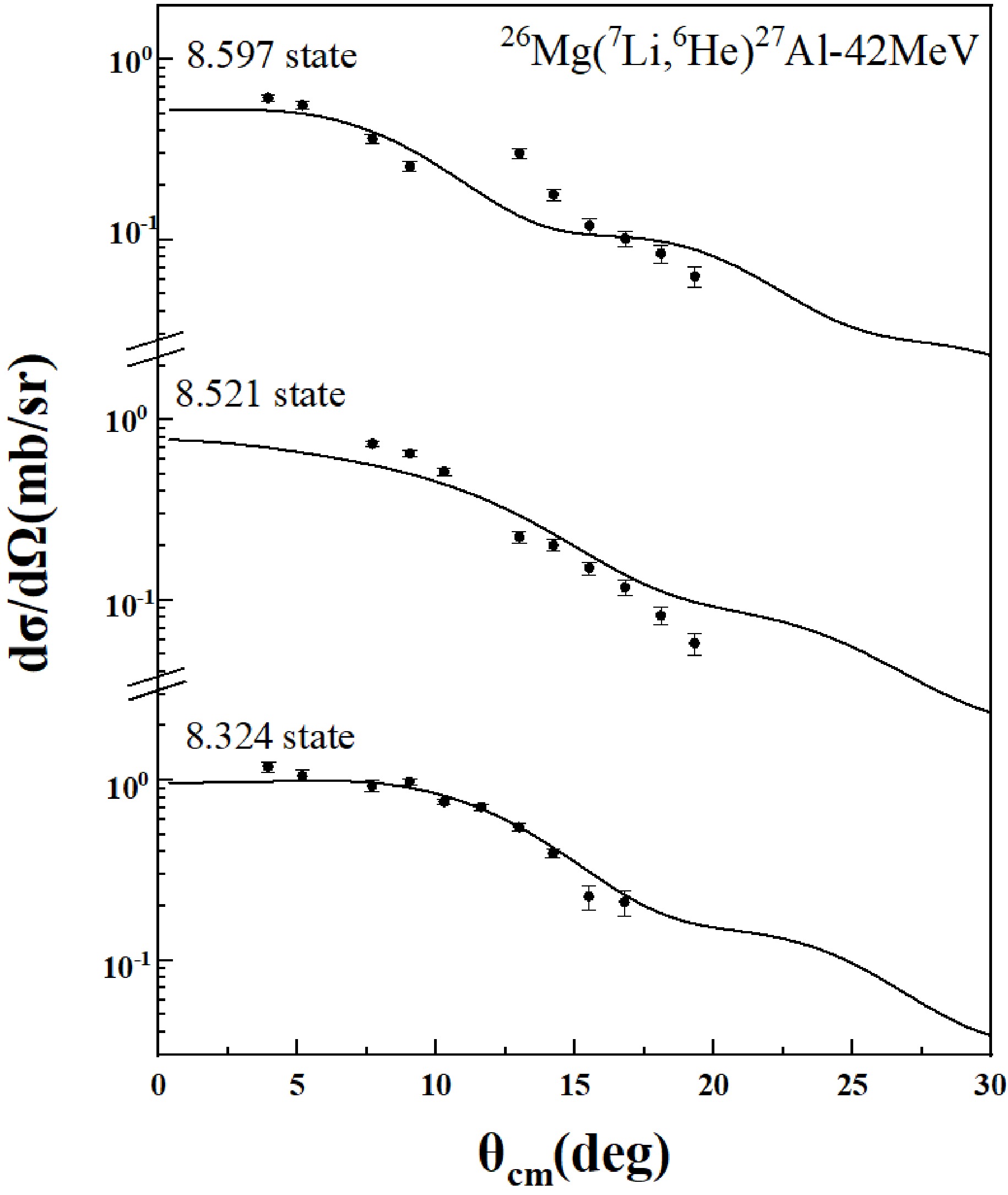
Figure 4. The angular distribution of 26Mg(7Li, 6He)27Al reaction for three different states in 27Al calculated using the DWBA program FRESCO. The selected optical potential and calculation methods are described in the article.
When determining the optical potential for the entrance, the Woods-Saxon form of the optical potential is typically used to fit the experimental angular distribution. In this work, the single-folding potential (SFP) was selected for DWBA calculation together with the Woods-Saxon form as a comparison. The SFP is obtained by folding the Lane-consistent Bruyères Jeukenne-Lejeune-Mahaux (JLMB) model nucleon-nucleus potential [27] and the nucleon density distribution of the projectile nucleus.
$ U_{\rm{sf}}(R) = \int U_{{\rm{NT}}}(| {\boldsymbol{R}} + {\boldsymbol{r}} |) \rho_{P}(r) \, {\rm d}{\boldsymbol{r}}, $
(1) where
$ {\boldsymbol{R}} $ and$ {{\boldsymbol{r}}} $ are the vectors from the center of mass (c.m.) of the target nucleus to that of the projectile, and from the constituent nucleon to the c.m. of the projectile, respectively.$ \rho_{P}(r) $ is the nucleon (proton or neutron) density distribution in the projectile at position$ {{\boldsymbol{r}}} $ from the center of mass of the projectile, and$ U_{NT}(|{\boldsymbol{R}}+{{\boldsymbol{r}}}|) $ is the JLMB model nucleon-target OMP [27, 28].$ U_{{\rm{NT}}} $ here is also a folding model potential, which is obtained by integration of an improved effective nucleon-nucleon interaction of the JLM model in nuclear matter with the nucleon density distribution of the target nucleus with a local density approximation [28]. In this work, nucleon density distributions of both the projectile and target nuclei are obtained with Hartree-Fock calculations using the Skyrme interaction SkX [29]. Although the JLMB model nucleon-nucleus potential can give good overall descriptions of nucleon scattering and reaction observables over the energy range from 1 keV to 200 MeV for spherical and near-spherical target nuclei from 40Ca to 209Bi [27], when being used in Eq. (1) for nucleus-nucleus potentials, the resulting$ U_{{\rm{sf}}} $ usually needs to be renormalized so that it can reasonably account for the elastic scattering angular distributions of the projectile-target system under study. The renormalization factors can be understood to account for the medium effects of the nucleons in the projectile [30−33] and are usually applied to both the real and imaginary parts of$ U_{{\rm{sf}}} $ with factors$ N_r $ and$ N_i $ , respectively.$ U_N(R)=N_r{\rm{Re}}[U_{{\rm{sf}}}]+N_i{\rm{Im}}[U_{{\rm{sf}}}]. $
(2) In this work,
$ N_r = 0.86 $ and$ N_i = 1.31 $ are found by fitting the angular distribution data of 6Li elastic scattering from 26Al at 42 MeV. Comparison with the experimental data and the result of the optical model calculation with these parameters is shown in Fig. 3. Also shown in this figure is the result of optical model calculations with phenomenological Woods-Saxon potentials, whose parameters are also found by fitting the experimental data.The optical potential in the Woods-Saxon form is given by:
$ U(r) = - \left[ \frac{U_V}{1 + \exp\left(\dfrac{r - R_R}{a_R}\right)} + \frac{{\rm i} W_V}{1 + \exp\left(\dfrac{r - R_I}{a_I}\right)} \right], $
(3) where
$ U_V $ and$ W_V $ represent the depths of the real and imaginary potential, respectively.$ R_{i} = r_{r} \times A^{1/3} $ , with$ A^{1/3} $ being the mass number of the target nucleus, and r and a are the radius and diffuseness parameters.For the exit channel, we used optical potentials from neighboring nuclei elastic scattering, 27Al + 6Li [34] and 28Si + 6Li [35], for the calculation. The choice is justified by the close mass and charge numbers of 6He and 6Li and by the systematic, smooth variation of OMP parameters across neighboring light-ion systems. The angular distribution of the transfer reaction was calculated using the DWBA program FRESCO [36], with standard geometric parameters
$ r=1.25 $ fm and$ a=0.65 $ fm. Table 1 shows all the parameter settings, where Set1 and Set2 correspond to two different parameter sets derived from fits to the elastic scattering data. Figure 4 presents the experimental angular distributions for all states, along with the DWBA calculation results. Since the six sets of results exhibit nearly identical profiles, only a single calculated curve is presented in the figure.Table 1. Woods-Saxon potential parameters. Set1 and Set2 represent two different sets of parameters obtained from fitting the elastic scattering angular distribution of entrance channel.
The spectroscopic factor of 27Al can be derived using the following formula:
$ \left(\frac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{exp}}}=S_{^7{\rm{Li}}}S_{^{27}{\rm{Al}}}\left(\frac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{DWBA}}}, $
(4) where
$ \left(\dfrac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{DWBA}}} $ and$ \left(\dfrac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{exp}}} $ represent the theoretical and experimental differential cross sections, respectively. The value of$ S_{^7{\rm{Li}}} $ is taken as 0.42, based on references [15, 16]. By comparing the experimental and theoretical angular distribution shapes, the spectroscopic factor$ S_{^{27}{\rm{Al}}} $ can be obtained. Figure 4 shows DWBA calculations together with all measured angular distributions. The final spectroscopic factor was obtained by averaging the outcomes of six combinations, which consisted of: two sets of Woods-Saxon potentials and a SFP in the entrance channel, and two sets of Woods-Saxon potentials in the exit channel derived from different experiments, as mentioned earlier. Table 2 presents the results for all measured excited states and their spectroscopic factors derived from the angular distribution, where l represents the transferred angular momentum.Table 2. Spin-parity values, corresponding transferred orbital angular momentum, and the final spectroscopic factor obtained by comparing the DWBA calculated angular distribution with the experimental angular distribution.
The uncertainties of spectroscopic factors for all states mainly come from the selection of optical potential parameters (10%), the error of the measurement (5%), and the error of the 7Li spectroscopic factor (10%) [15, 16].
-
The spectra for the 26Mg and 24Mg targets at 7° are shown in Fig. 2. The states originating from the 16O(7Li, 6He)17F and 26Mg(7Li, 6He)27Al reactions can be clearly distinguished by comparing the two spectra. To extract the entrance channel optical potential parameters, the angular distribution of 26Mg(7Li,7Li)26Mg elastic scattering was also measured and is shown in Fig. 3. Based on the position of the
$ ^{17}{\rm{F}}_0 $ and kinematic calculations, the 8.324 MeV states in 27Al, which correspond to the 52.8 keV resonance of 26Mg+p, as well as the 7.858, 8.324, 8.521, 8.597, 8.753, and 9.080 MeV states, which are located near the threshold, were accurately identified. The angular distributions of three states are shown in Fig. 4. The above excitation energies are based on literature data[24−26].
Figure 2. The total spectrum at 7°. The left figure shows the experimental spectrum measured with a 26Mg target, while the right figure shows the background spectrum obtained using a natMg target target for comparison. The six values 7.858 – 9.080 in the figure represent the corresponding excited states.

Figure 3. The fitting results of 26Mg(7Li,7Li) elastic scattering at 42 MeV. The black solid diamonds represent the experimentally measured elastic scattering angular distribution, and the blue solid line and red dashed line represent the results obtained using the SFP and the Woods-Saxon potential for fitting, respectively. The uncertainties are too minor to be discernible in the plot.

Figure 4. The angular distribution of 26Mg(7Li, 6He)27Al reaction for three different states in 27Al calculated using the DWBA program FRESCO. The selected optical potential and calculation methods are described in the article.
When determining the optical potential for the entrance, the Woods-Saxon form of the optical potential is typically used to fit the experimental angular distribution. In this work, the single-folding potential (SFP) was selected for DWBA calculation together with the Woods-Saxon form as a comparison. The SFP is obtained by folding the Lane-consistent Bruyères Jeukenne-Lejeune-Mahaux (JLMB) model nucleon-nucleus potential [27] and the nucleon density distribution of the projectile nucleus.
$ U_{\rm{sf}}(R) = \int U_{{\rm{NT}}}(| {\boldsymbol{R}} + {\boldsymbol{r}} |) \rho_{P}(r) \, d{\boldsymbol{r}}, $

(1) where
$ {\boldsymbol{R}} $ and$ {{\boldsymbol{r}}} $ are the vectors from the center of mass (c.m.) of the target nucleus to that of the projectile, and from the constituent nucleon to the c.m. of the projectile, respectively.$ \rho_{P}(r) $ is the nucleon (proton or neutron) density distribution in the projectile at position$ {{\boldsymbol{r}}} $ from the center of mass of the projectile, and$ U_{NT}(|{\boldsymbol{R}}+{{\boldsymbol{r}}}|) $ is the JLMB model nucleon-target OMP[27, 28].$ U_{{\rm{NT}}} $ here is also a folding model potential, which is obtained by integration of an improved effective nucleon-nucleon interaction of the JLM model in nuclear matter with the nucleon density distribution of the target nucleus with a local density approximation [28]. In this work, nucleon density distributions of both the projectile and target nuclei are obtained with Hartree-Fock calculations using the Skyrme interaction SkX [29]. Although the JLMB model nucleon-nucleus potential can give good overall descriptions of nucleon scattering and reaction observables over the energy range from 1 keV to 200 MeV for spherical and near-spherical target nuclei from 40Ca to 209Bi [27], when being used in Eq. (1) for nucleus-nucleus potentials, the resulting$ U_{{\rm{sf}}} $ usually needs to be renormalized so that it can reasonably account for the elastic scattering angular distributions of the projectile-target system under study. The renormalization factors can be understood to account for the medium effects of the nucleons in the projectile [30−33] and are usually applied to both the real and imaginary parts of$ U_{{\rm{sf}}} $ with factors$ N_r $ and$ N_i $ , respectively.$ U_N(R)=N_r{\rm{Re}}[U_{{\rm{sf}}}]+N_i{\rm{Im}}[U_{{\rm{sf}}}]. $

(2) In this work,
$ N_r = 0.86 $ and$ N_i = 1.31 $ are found by fitting the angular distribution data of 6Li elastic scattering from 26Al at 42 MeV. Comparison with the experimental data and the result of the optical model calculation with these parameters is shown in Fig. 3. Also shown in this figure is the result of optical model calculations with phenomenological Woods-Saxon potentials, whose parameters are also found by fitting the experimental data.The optical potential in the Woods-Saxon form is given by:
$ U(r) = - \left[ \frac{U_V}{1 + \exp\left(\dfrac{r - R_R}{a_R}\right)} + \frac{i W_V}{1 + \exp\left(\dfrac{r - R_I}{a_I}\right)} \right], $

(3) where
$ U_V $ and$ W_V $ represent the depths of the real and imaginary potential, respectively.$ R_{i} = r_{r} \times A^{1/3} $ , with$ A^{1/3} $ being the mass number of the target nucleus, and r and a are the radius and diffuseness parameters.For the exit channel, we used optical potentials from neighboring nuclei elastic scattering, 27Al + 6Li [34] and 28Si + 6Li [35], for the calculation. The choice is justified by the close mass and charge numbers of 6He and 6Li and by the systematic, smooth variation of OMP parameters across neighboring light-ion systems. The angular distribution of the transfer reaction was calculated using the DWBA program FRESCO [36], with standard geometric parameters
$ r=1.25 $ fm and$ a=0.65 $ fm. Table 1 shows all the parameter settings, where Set1 and Set2 correspond to two different parameter sets derived from fits to the elastic scattering data. Fig. 4 presents the experimental angular distributions for all states, along with the DWBA calculation results. Since the six sets of results exhibit nearly identical profiles, only a single calculated curve is presented in the figure.Table 1. Woods-Saxon potential parameters. Set1 and Set2 represent two different sets of parameters obtained from fitting the elastic scattering angular distribution of entrance channel.
The spectroscopic factor of 27Al can be derived using the following formula:
$ \left(\frac{d\sigma}{d\Omega}\right)_{{\rm{exp}}}=S_{^7{\rm{Li}}}S_{^{27}{\rm{Al}}}\left(\frac{d\sigma}{d\Omega}\right)_{{\rm{DWBA}}}, $

(4) where
$ \left(\dfrac{d\sigma}{d\Omega}\right)_{{\rm{DWBA}}} $ and$ \left(\dfrac{d\sigma}{d\Omega}\right)_{{\rm{exp}}} $ represent the theoretical and experimental differential cross sections, respectively. The value of$ S_{^7{\rm{Li}}} $ is taken as 0.42, based on references [15, 16]. By comparing the experimental and theoretical angular distribution shapes, the spectroscopic factor$ S_{^{27}{\rm{Al}}} $ can be obtained. Fig. 4 shows DWBA calculations together with all measured angular distributions. The final spectroscopic factor was obtained by averaging the outcomes of six combinations, which consisted of: two sets of Woods-Saxon potentials and a SFP in the entrance channel, and two sets of Woods-Saxon potentials in the exit channel derived from different experiments, as mentioned earlier. Table 2 presents the results for all measured excited states and their spectroscopic factors derived from the angular distribution, where l represents the transferred angular momentum.Table 2. Spin-parity values, corresponding transferred orbital angular momentum, and the final spectroscopic factor obtained by comparing the DWBA calculated angular distribution with the experimental angular distribution.
The uncertainties of spectroscopic factors for all states mainly come from the selection of optical potential parameters (10%), the error of the measurement (5%), and the error of the 7Li spectroscopic factor (10%) [15, 16].
-
The spectra for the 26Mg and 24Mg targets at 7° are shown in Fig. 2. The states originating from the 16O(7Li, 6He)17F and 26Mg(7Li, 6He)27Al reactions can be clearly distinguished by comparing the two spectra. To extract the entrance channel optical potential parameters, the angular distribution of 26Mg(7Li,7Li)26Mg elastic scattering was also measured and is shown in Fig. 3. Based on the position of the
$ ^{17}{\rm{F}}_0 $ and kinematic calculations, the 8.324 MeV states in 27Al, which correspond to the 52.8 keV resonance of 26Mg+p, as well as the 7.858, 8.324, 8.521, 8.597, 8.753, and 9.080 MeV states, which are located near the threshold, were accurately identified. The angular distributions of three states are shown in Fig. 4. The above excitation energies are based on literature data [24−26].
Figure 2. (color online) The total spectrum at 7°. The left figure shows the experimental spectrum measured with a 26Mg target, while the right figure shows the background spectrum obtained using a natMg target target for comparison. The six values 7.858–9.080 in the figure represent the corresponding excited states.

Figure 3. The fitting results of 26Mg(7Li,7Li) elastic scattering at 42 MeV. The black solid diamonds represent the experimentally measured elastic scattering angular distribution, and the blue solid line and red dashed line represent the results obtained using the SFP and the Woods-Saxon potential for fitting, respectively. The uncertainties are too minor to be discernible in the plot.

Figure 4. The angular distribution of 26Mg(7Li, 6He)27Al reaction for three different states in 27Al calculated using the DWBA program FRESCO. The selected optical potential and calculation methods are described in the article.
When determining the optical potential for the entrance, the Woods-Saxon form of the optical potential is typically used to fit the experimental angular distribution. In this work, the single-folding potential (SFP) was selected for DWBA calculation together with the Woods-Saxon form as a comparison. The SFP is obtained by folding the Lane-consistent Bruyères Jeukenne-Lejeune-Mahaux (JLMB) model nucleon-nucleus potential [27] and the nucleon density distribution of the projectile nucleus.
$ U_{\rm{sf}}(R) = \int U_{{\rm{NT}}}(| {\boldsymbol{R}} + {\boldsymbol{r}} |) \rho_{P}(r) \, {\rm d}{\boldsymbol{r}}, $
(1) where
$ {\boldsymbol{R}} $ and$ {{\boldsymbol{r}}} $ are the vectors from the center of mass (c.m.) of the target nucleus to that of the projectile, and from the constituent nucleon to the c.m. of the projectile, respectively.$ \rho_{P}(r) $ is the nucleon (proton or neutron) density distribution in the projectile at position$ {{\boldsymbol{r}}} $ from the center of mass of the projectile, and$ U_{NT}(|{\boldsymbol{R}}+{{\boldsymbol{r}}}|) $ is the JLMB model nucleon-target OMP [27, 28].$ U_{{\rm{NT}}} $ here is also a folding model potential, which is obtained by integration of an improved effective nucleon-nucleon interaction of the JLM model in nuclear matter with the nucleon density distribution of the target nucleus with a local density approximation [28]. In this work, nucleon density distributions of both the projectile and target nuclei are obtained with Hartree-Fock calculations using the Skyrme interaction SkX [29]. Although the JLMB model nucleon-nucleus potential can give good overall descriptions of nucleon scattering and reaction observables over the energy range from 1 keV to 200 MeV for spherical and near-spherical target nuclei from 40Ca to 209Bi [27], when being used in Eq. (1) for nucleus-nucleus potentials, the resulting$ U_{{\rm{sf}}} $ usually needs to be renormalized so that it can reasonably account for the elastic scattering angular distributions of the projectile-target system under study. The renormalization factors can be understood to account for the medium effects of the nucleons in the projectile [30−33] and are usually applied to both the real and imaginary parts of$ U_{{\rm{sf}}} $ with factors$ N_r $ and$ N_i $ , respectively.$ U_N(R)=N_r{\rm{Re}}[U_{{\rm{sf}}}]+N_i{\rm{Im}}[U_{{\rm{sf}}}]. $
(2) In this work,
$ N_r = 0.86 $ and$ N_i = 1.31 $ are found by fitting the angular distribution data of 6Li elastic scattering from 26Al at 42 MeV. Comparison with the experimental data and the result of the optical model calculation with these parameters is shown in Fig. 3. Also shown in this figure is the result of optical model calculations with phenomenological Woods-Saxon potentials, whose parameters are also found by fitting the experimental data.The optical potential in the Woods-Saxon form is given by:
$ U(r) = - \left[ \frac{U_V}{1 + \exp\left(\dfrac{r - R_R}{a_R}\right)} + \frac{{\rm i} W_V}{1 + \exp\left(\dfrac{r - R_I}{a_I}\right)} \right], $
(3) where
$ U_V $ and$ W_V $ represent the depths of the real and imaginary potential, respectively.$ R_{i} = r_{r} \times A^{1/3} $ , with$ A^{1/3} $ being the mass number of the target nucleus, and r and a are the radius and diffuseness parameters.For the exit channel, we used optical potentials from neighboring nuclei elastic scattering, 27Al + 6Li [34] and 28Si + 6Li [35], for the calculation. The choice is justified by the close mass and charge numbers of 6He and 6Li and by the systematic, smooth variation of OMP parameters across neighboring light-ion systems. The angular distribution of the transfer reaction was calculated using the DWBA program FRESCO [36], with standard geometric parameters
$ r=1.25 $ fm and$ a=0.65 $ fm. Table 1 shows all the parameter settings, where Set1 and Set2 correspond to two different parameter sets derived from fits to the elastic scattering data. Figure 4 presents the experimental angular distributions for all states, along with the DWBA calculation results. Since the six sets of results exhibit nearly identical profiles, only a single calculated curve is presented in the figure.Table 1. Woods-Saxon potential parameters. Set1 and Set2 represent two different sets of parameters obtained from fitting the elastic scattering angular distribution of entrance channel.
The spectroscopic factor of 27Al can be derived using the following formula:
$ \left(\frac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{exp}}}=S_{^7{\rm{Li}}}S_{^{27}{\rm{Al}}}\left(\frac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{DWBA}}}, $
(4) where
$ \left(\dfrac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{DWBA}}} $ and$ \left(\dfrac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{exp}}} $ represent the theoretical and experimental differential cross sections, respectively. The value of$ S_{^7{\rm{Li}}} $ is taken as 0.42, based on references [15, 16]. By comparing the experimental and theoretical angular distribution shapes, the spectroscopic factor$ S_{^{27}{\rm{Al}}} $ can be obtained. Figure 4 shows DWBA calculations together with all measured angular distributions. The final spectroscopic factor was obtained by averaging the outcomes of six combinations, which consisted of: two sets of Woods-Saxon potentials and a SFP in the entrance channel, and two sets of Woods-Saxon potentials in the exit channel derived from different experiments, as mentioned earlier. Table 2 presents the results for all measured excited states and their spectroscopic factors derived from the angular distribution, where l represents the transferred angular momentum.Table 2. Spin-parity values, corresponding transferred orbital angular momentum, and the final spectroscopic factor obtained by comparing the DWBA calculated angular distribution with the experimental angular distribution.
The uncertainties of spectroscopic factors for all states mainly come from the selection of optical potential parameters (10%), the error of the measurement (5%), and the error of the 7Li spectroscopic factor (10%) [15, 16].
-
The spectra for the 26Mg and 24Mg targets at 7° are shown in Fig. 2. The states originating from the 16O(7Li, 6He)17F and 26Mg(7Li, 6He)27Al reactions can be clearly distinguished by comparing the two spectra. To extract the entrance channel optical potential parameters, the angular distribution of 26Mg(7Li,7Li)26Mg elastic scattering was also measured and is shown in Fig. 3. Based on the position of the
$ ^{17}{\rm{F}}_0 $ and kinematic calculations, the 8.324 MeV states in 27Al, which correspond to the 52.8 keV resonance of 26Mg+p, as well as the 7.858, 8.324, 8.521, 8.597, 8.753, and 9.080 MeV states, which are located near the threshold, were accurately identified. The angular distributions of three states are shown in Fig. 4. The above excitation energies are based on literature data [24−26].
Figure 2. (color online) The total spectrum at 7°. The left figure shows the experimental spectrum measured with a 26Mg target, while the right figure shows the background spectrum obtained using a natMg target target for comparison. The six values 7.858–9.080 in the figure represent the corresponding excited states.

Figure 3. The fitting results of 26Mg(7Li,7Li) elastic scattering at 42 MeV. The black solid diamonds represent the experimentally measured elastic scattering angular distribution, and the blue solid line and red dashed line represent the results obtained using the SFP and the Woods-Saxon potential for fitting, respectively. The uncertainties are too minor to be discernible in the plot.

Figure 4. The angular distribution of 26Mg(7Li, 6He)27Al reaction for three different states in 27Al calculated using the DWBA program FRESCO. The selected optical potential and calculation methods are described in the article.
When determining the optical potential for the entrance, the Woods-Saxon form of the optical potential is typically used to fit the experimental angular distribution. In this work, the single-folding potential (SFP) was selected for DWBA calculation together with the Woods-Saxon form as a comparison. The SFP is obtained by folding the Lane-consistent Bruyères Jeukenne-Lejeune-Mahaux (JLMB) model nucleon-nucleus potential [27] and the nucleon density distribution of the projectile nucleus.
$ U_{\rm{sf}}(R) = \int U_{{\rm{NT}}}(| {\boldsymbol{R}} + {\boldsymbol{r}} |) \rho_{P}(r) \, {\rm d}{\boldsymbol{r}}, $
(1) where
$ {\boldsymbol{R}} $ and$ {{\boldsymbol{r}}} $ are the vectors from the center of mass (c.m.) of the target nucleus to that of the projectile, and from the constituent nucleon to the c.m. of the projectile, respectively.$ \rho_{P}(r) $ is the nucleon (proton or neutron) density distribution in the projectile at position$ {{\boldsymbol{r}}} $ from the center of mass of the projectile, and$ U_{NT}(|{\boldsymbol{R}}+{{\boldsymbol{r}}}|) $ is the JLMB model nucleon-target OMP [27, 28].$ U_{{\rm{NT}}} $ here is also a folding model potential, which is obtained by integration of an improved effective nucleon-nucleon interaction of the JLM model in nuclear matter with the nucleon density distribution of the target nucleus with a local density approximation [28]. In this work, nucleon density distributions of both the projectile and target nuclei are obtained with Hartree-Fock calculations using the Skyrme interaction SkX [29]. Although the JLMB model nucleon-nucleus potential can give good overall descriptions of nucleon scattering and reaction observables over the energy range from 1 keV to 200 MeV for spherical and near-spherical target nuclei from 40Ca to 209Bi [27], when being used in Eq. (1) for nucleus-nucleus potentials, the resulting$ U_{{\rm{sf}}} $ usually needs to be renormalized so that it can reasonably account for the elastic scattering angular distributions of the projectile-target system under study. The renormalization factors can be understood to account for the medium effects of the nucleons in the projectile [30−33] and are usually applied to both the real and imaginary parts of$ U_{{\rm{sf}}} $ with factors$ N_r $ and$ N_i $ , respectively.$ U_N(R)=N_r{\rm{Re}}[U_{{\rm{sf}}}]+N_i{\rm{Im}}[U_{{\rm{sf}}}]. $
(2) In this work,
$ N_r = 0.86 $ and$ N_i = 1.31 $ are found by fitting the angular distribution data of 6Li elastic scattering from 26Al at 42 MeV. Comparison with the experimental data and the result of the optical model calculation with these parameters is shown in Fig. 3. Also shown in this figure is the result of optical model calculations with phenomenological Woods-Saxon potentials, whose parameters are also found by fitting the experimental data.The optical potential in the Woods-Saxon form is given by:
$ U(r) = - \left[ \frac{U_V}{1 + \exp\left(\dfrac{r - R_R}{a_R}\right)} + \frac{{\rm i} W_V}{1 + \exp\left(\dfrac{r - R_I}{a_I}\right)} \right], $
(3) where
$ U_V $ and$ W_V $ represent the depths of the real and imaginary potential, respectively.$ R_{i} = r_{r} \times A^{1/3} $ , with$ A^{1/3} $ being the mass number of the target nucleus, and r and a are the radius and diffuseness parameters.For the exit channel, we used optical potentials from neighboring nuclei elastic scattering, 27Al + 6Li [34] and 28Si + 6Li [35], for the calculation. The choice is justified by the close mass and charge numbers of 6He and 6Li and by the systematic, smooth variation of OMP parameters across neighboring light-ion systems. The angular distribution of the transfer reaction was calculated using the DWBA program FRESCO [36], with standard geometric parameters
$ r=1.25 $ fm and$ a=0.65 $ fm. Table 1 shows all the parameter settings, where Set1 and Set2 correspond to two different parameter sets derived from fits to the elastic scattering data. Figure 4 presents the experimental angular distributions for all states, along with the DWBA calculation results. Since the six sets of results exhibit nearly identical profiles, only a single calculated curve is presented in the figure.Table 1. Woods-Saxon potential parameters. Set1 and Set2 represent two different sets of parameters obtained from fitting the elastic scattering angular distribution of entrance channel.
The spectroscopic factor of 27Al can be derived using the following formula:
$ \left(\frac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{exp}}}=S_{^7{\rm{Li}}}S_{^{27}{\rm{Al}}}\left(\frac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{DWBA}}}, $
(4) where
$ \left(\dfrac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{DWBA}}} $ and$ \left(\dfrac{{\rm d}\sigma}{{\rm d}\Omega}\right)_{{\rm{exp}}} $ represent the theoretical and experimental differential cross sections, respectively. The value of$ S_{^7{\rm{Li}}} $ is taken as 0.42, based on references [15, 16]. By comparing the experimental and theoretical angular distribution shapes, the spectroscopic factor$ S_{^{27}{\rm{Al}}} $ can be obtained. Figure 4 shows DWBA calculations together with all measured angular distributions. The final spectroscopic factor was obtained by averaging the outcomes of six combinations, which consisted of: two sets of Woods-Saxon potentials and a SFP in the entrance channel, and two sets of Woods-Saxon potentials in the exit channel derived from different experiments, as mentioned earlier. Table 2 presents the results for all measured excited states and their spectroscopic factors derived from the angular distribution, where l represents the transferred angular momentum.Table 2. Spin-parity values, corresponding transferred orbital angular momentum, and the final spectroscopic factor obtained by comparing the DWBA calculated angular distribution with the experimental angular distribution.
The uncertainties of spectroscopic factors for all states mainly come from the selection of optical potential parameters (10%), the error of the measurement (5%), and the error of the 7Li spectroscopic factor (10%) [15, 16].
-
For discrete narrow resonances, the reaction rate can be calculated using the following equation:
$ N_A\langle\sigma\upsilon\rangle=\sum\limits_{i}N_A\left(\frac{2\pi}{\mu kT}\right)^{3/2}\hbar^2{\rm e}^{-E^i_R/kT}\omega\gamma_i. $
(5) $ N_A $ is Avogadro's constant, k is Boltzmann's constant,$ \mu $ is the reduced mass, T is the stellar temperature,$ E_R $ is the resonance energy, and$ \omega\gamma $ is the resonance strength. The resonance strength for narrow resonances is calculated as follows:$ \omega\gamma_i=\frac{2J_i+1}{(2J_p+1)(2J_t+1)}\frac{\Gamma_p\Gamma_{\gamma}}{\Gamma_{{\rm{total}}}}, $
(6) where
$ J_i, J_t, J_p $ are the spins of the resonance state, target nucleus, and projectile nucleus, respectively.$ \Gamma_p, \Gamma_{\gamma}, \Gamma_{{\rm{total}}} $ represent the proton width, gamma width, and total width, respectively. When the gamma width is much larger than the proton width,$ \Gamma_{\gamma}/\Gamma_{{\rm{total}}} $ can be approximated as 1.The proton width is given by:
$ \Gamma_p = S\Gamma_{sp} = 2\frac{\hbar^2}{\mu a^2_c}SP_l\theta^2_{sp}. $
(7) In this context,
$ a_c=r\times A^{1/3} $ , S represents the proton spectroscopic factor, and$ P_l $ is the corresponding penetration coefficient for angular momentum l. The single-particle reduced width$ \theta^2 $ equals$ a_c\phi(a_c)^2/2 $ [38], where$ \phi(a_c) $ is the value of the bound-state wave function at$ a_c $ .Figure 5 shows the variations in the spectroscopic factor S,
$ \Gamma_p $ , and$ \Gamma_{sp} $ with changes in the radius parameter r. It can be seen that S and$ \Gamma_{sp} $ change significantly with radius, while$ \Gamma_p $ remains almost unchanged (fluctuations are less than 5%), indicating that the proton width for the excited states studied is nearly independent of the model.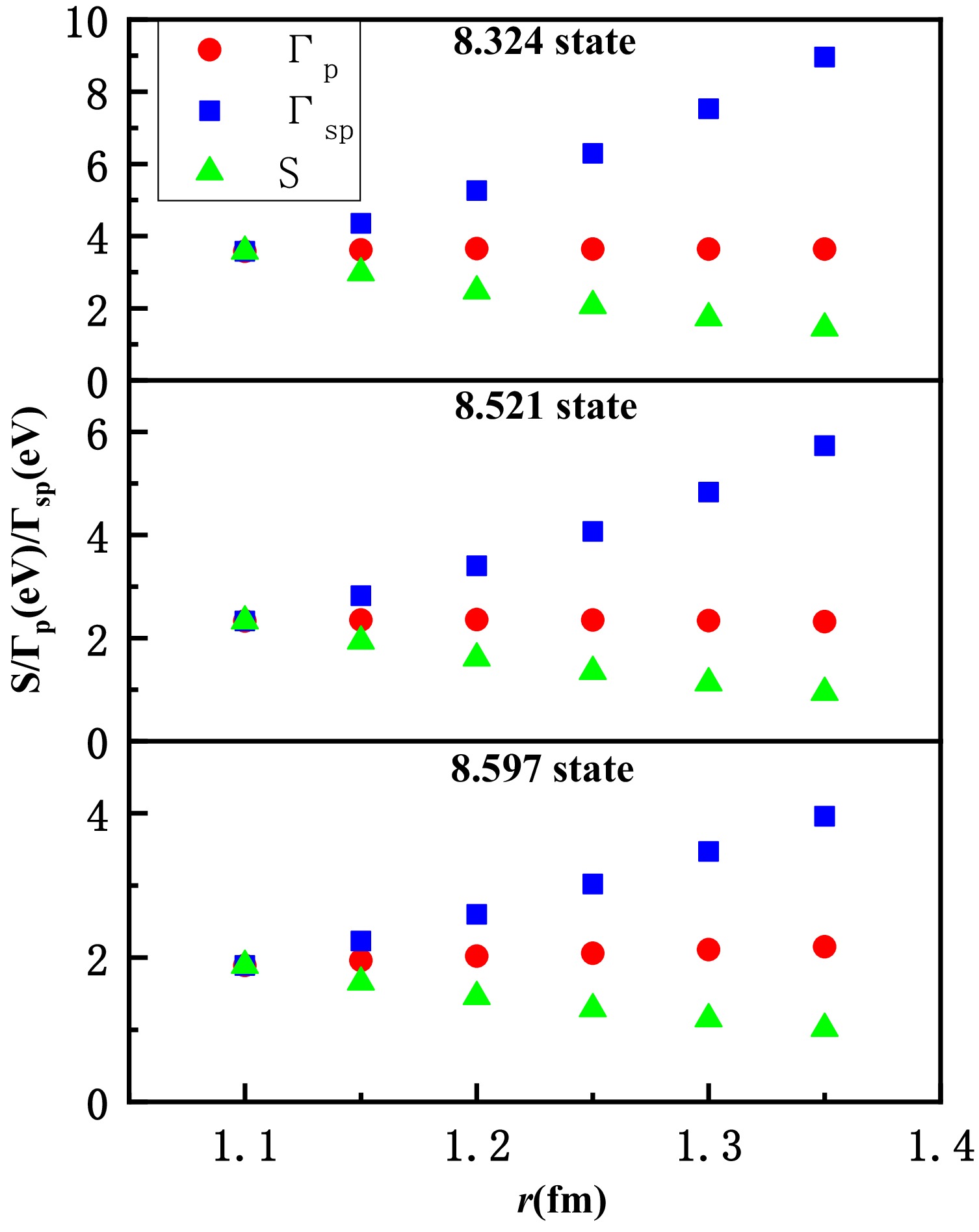
Figure 5. (color online) The variation of S,
$\Gamma_p$ , and$\Gamma_{sp}$ with the radius. At r=1.1 fm,$\Gamma_{sp}$ and S are normalized to$\Gamma_p$ . The red circles, blue squares and green triangles represent$\Gamma_p$ ,$\Gamma_{sp}$ and S, respectively.At the temperatures where the Mg-Al cycle is active (
$ T_9 \approx 0.1 $ ), the contribution from direct capture is much smaller than that from low-energy resonances. The reaction rate for direct capture is referenced from Iliadis [37]. Table 3 shows the proton width and resonance strength for the 52.8,250, and 325.8 keV resonances measured in the energy region of interest. Figure 6 shows the calculated reaction rates for 26Mg($ p, \gamma $ )27Al as a function of temperature, using the updated resonance strengths. Parameters for resonances not measured in this experiment were adopted from values in the literature [25]. The contribution of different resonances to the total reaction rate is shown in Fig. 7. Champagne et al. [24] derived the proton width and resonance strength for the 52.8 keV resonance using a scaling relation, and their results differ by a factor of 10 from those calculated using the spectroscopic factor in our work. This divergence leads to a significant increase in the total reaction rate at temperatures ($ T_9 < 0.03 $ ) where this resonance dominates. However, at$ T_9 \approx 0.1 $ , there remains considerable uncertainty in the total reaction rate due to the 90 keV and 136.7 keV resonances, especially the 90 keV resonance, which only has an upper limit. Figure 8 shows a comparison between the present reaction rates around the temperature of$ T_9=0.1 $ and the reaction rates reported by Iliadis [25] and Angulo [40]. The calculated reaction rates are listed in Table 4.$ E_x $
/keV$ E_{cm} $ [24−26]
/keV$ J^{\pi}_r $ $ \Gamma_{\gamma} $ /eV [24]$ \Gamma_p $ /eV$ \omega \gamma $ /eVliterature [24] this work literature [24, 37, 39] this work 8324(1) 52.8(10) $ \left(\dfrac{3}{2},\dfrac{5}{2}\right)^+ $ 0.1-1 $ 1.8 \times 10^{-17} $ $ 3.26(46) \times 10^{-16} $ $ 5.3 \times 10^{-17} $ $ 6.51(91) \times 10^{-16} $ 8521(2) 250(2) $ \dfrac{5}{2}^+ $ 0.1-1 $ 2.11(29) \times 10^{-4} $ $ \leqslant 1 \times 10^{-6} $ $ 6.32(85) \times 10^{-4} $ 8597.6(3) 325.8(3) $ \dfrac{3}{2}^- $ 0.56(4) 0.42(20) 0.179(28) 0.25(3) 0.049(13) Table 3. Summary of resonance parameters.
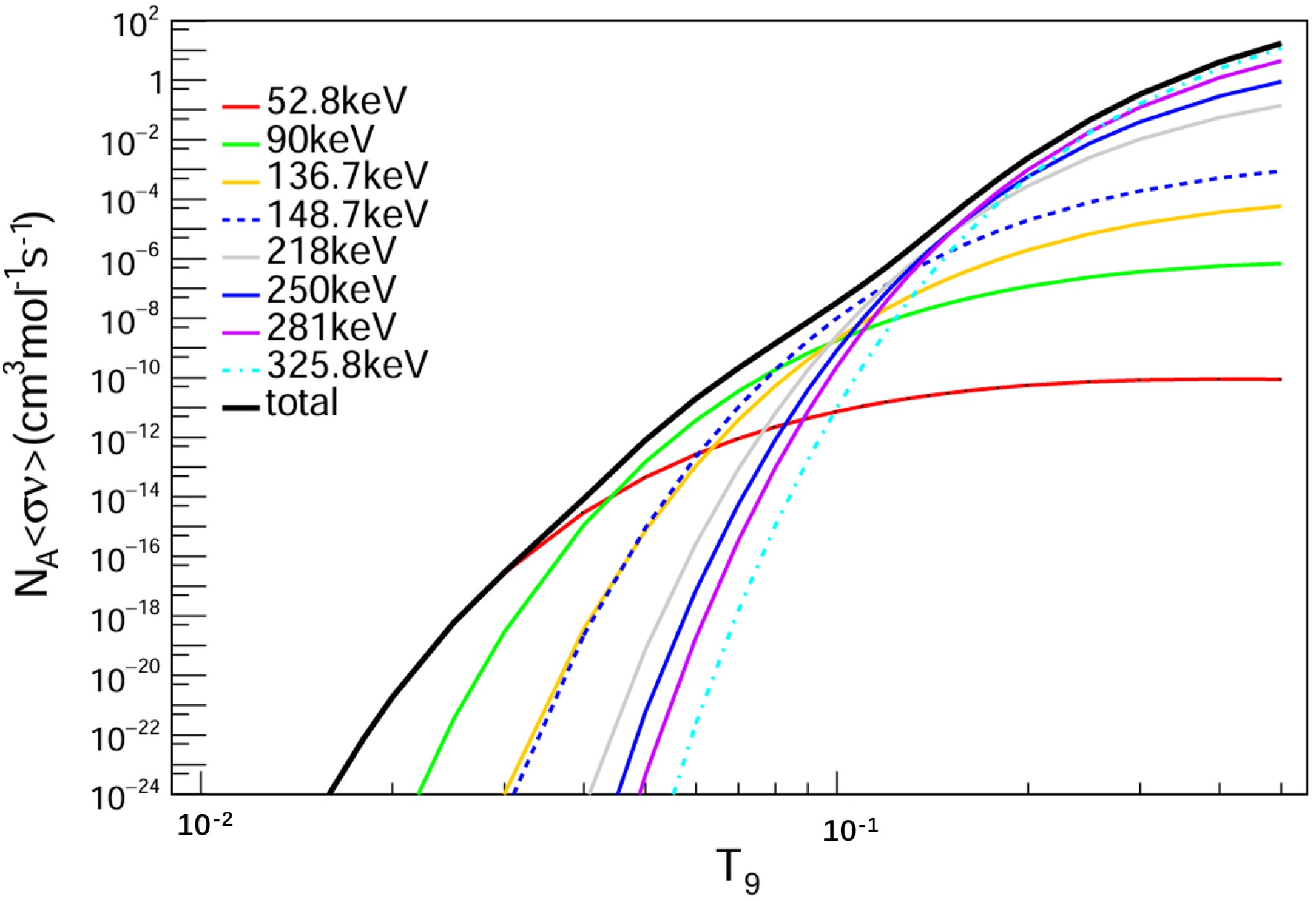
Figure 6. (color online) Present total reaction rates. For unknown resonances, the resonance strength is taken as 1/10 of the upper limit value. The solid black line represents the total reaction rate, corresponding to the "median" values in Table 4, and does not include uncertainties.
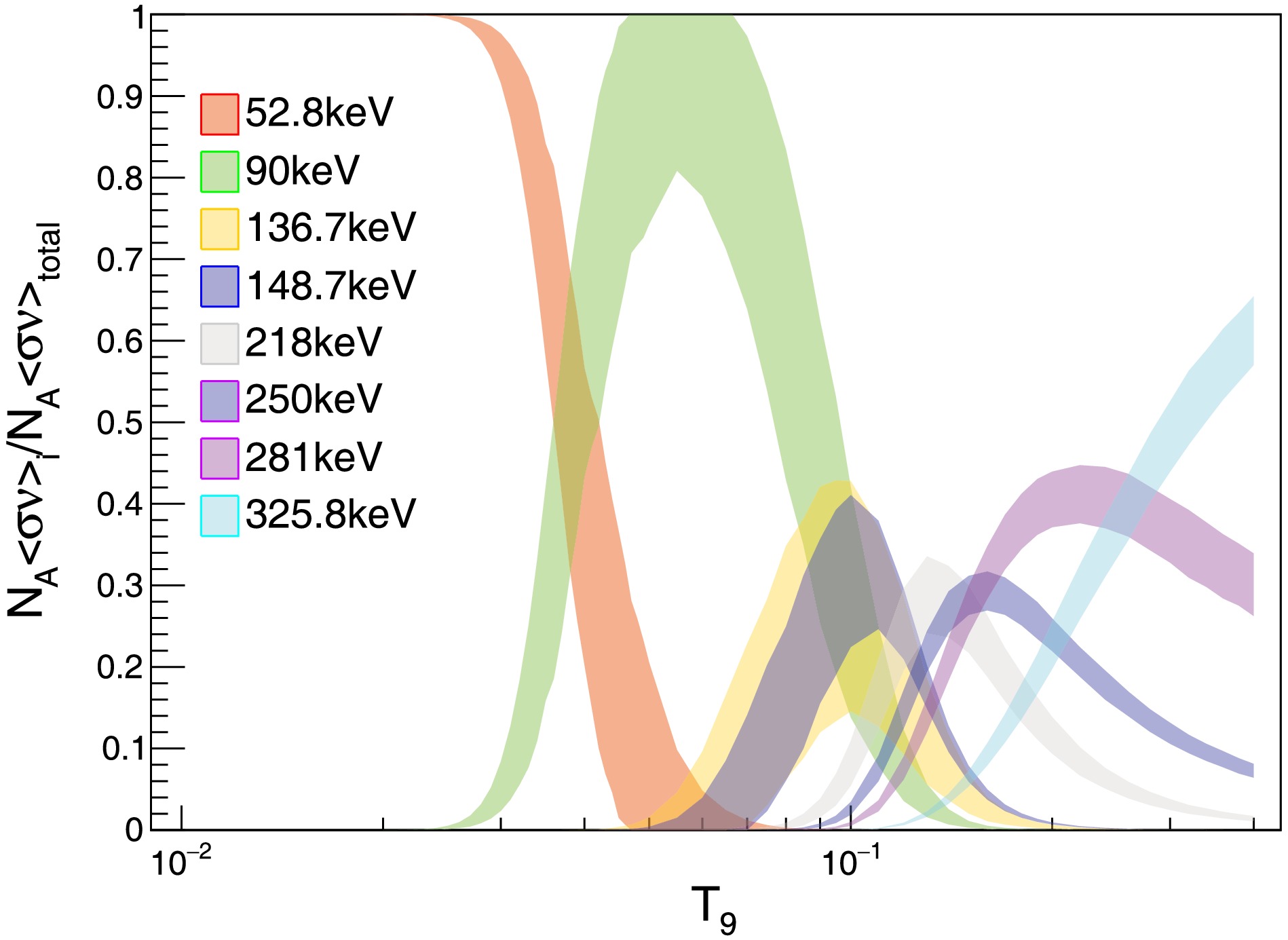
Figure 7. (color online) The contribution of the main resonances to the total reaction rate in
$\pm 1\sigma$ confidence interval.$ T_9 $ Low Median High 0.010 2.28E-34 2.65E-34 3.02E-34 0.011 5.17E-32 6.02E-32 6.85E-32 0.012 4.70E-30 5.47E-30 6.23E-30 0.013 2.12E-28 2.46E-28 2.80E-28 0.014 5.48E-27 6.37E-27 7.26E-27 0.015 9.13E-26 1.06E-25 1.21E-25 0.016 1.06E-24 1.24E-24 1.41E-24 0.018 6.27E-23 7.30E-23 8.31E-23 0.020 1.61E-21 1.87E-21 2.13E-21 0.025 5.27E-19 6.13E-19 7.02E-19 0.03 2.38E-17 2.79E-17 3.44E-17 0.04 2.56E-15 4.11E-15 1.47E-14 0.05 4.42E-14 2.02E-13 1.56E-12 0.06 5.93E-13 4.56E-12 3.88E-11 0.07 1.16E-11 5.45E-11 4.08E-10 0.08 1.67E-10 4.64E-10 2.67E-09 0.09 1.54E-09 3.14E-09 1.33E-08 0.10 1.03E-08 1.78E-08 5.58E-08 0.11 5.77E-08 9.02E-08 2.14E-07 0.12 2.89E-07 4.21E-07 7.87E-07 0.13 1.31E-06 1.80E-06 2.83E-06 0.14 5.23E-06 6.92E-06 9.68E-06 0.15 1.85E-05 2.36E-05 3.08E-05 Table 4. The present reaction rate for 26Mg(
$ p, \gamma $ )27Al(in$ {\rm{cm}}^3{\rm{mol}}^{-1}{\rm{s}}^{-1}) $ -
For discrete narrow resonances, the reaction rate can be calculated using the following equation:
$ N_A\langle\sigma\upsilon\rangle=\sum\limits_{i}N_A\left(\frac{2\pi}{\mu kT}\right)^{3/2}\hbar^2e^{-E^i_R/kT}\omega\gamma_i. $

(5) $ N_A $ is Avogadro's constant, k is Boltzmann's constant,$ \mu $ is the reduced mass, T is the stellar temperature,$ E_R $ is the resonance energy, and$ \omega\gamma $ is the resonance strength. The resonance strength for narrow resonances is calculated as follows:$ \omega\gamma_i=\frac{2J_i+1}{(2J_p+1)(2J_t+1)}\frac{\Gamma_p\Gamma_{\gamma}}{\Gamma_{{\rm{total}}}}, $

(6) where
$ J_i, J_t, J_p $ are the spins of the resonance state, target nucleus, and projectile nucleus, respectively.$ \Gamma_p, \Gamma_{\gamma}, \Gamma_{{\rm{total}}} $ represent the proton width, gamma width, and total width, respectively. When the gamma width is much larger than the proton width,$ \Gamma_{\gamma}/\Gamma_{{\rm{total}}} $ can be approximated as 1.The proton width is given by:
$ \Gamma_p = S\Gamma_{sp} = 2\frac{\hbar^2}{\mu a^2_c}SP_l\theta^2_{sp}. $

(7) In this context,
$ a_c=r\times A^{1/3} $ , S represents the proton spectroscopic factor, and$ P_l $ is the corresponding penetration coefficient for angular momentum l. The single-particle reduced width$ \theta^2 $ equals$ a_c\phi(a_c)^2/2 $ [39], where$ \phi(a_c) $ is the value of the bound-state wave function at$ a_c $ .Fig. 5 shows the variations in the spectroscopic factor S,
$ \Gamma_p $ , and$ \Gamma_{sp} $ with changes in the radius parameter r. It can be seen that S and$ \Gamma_{sp} $ change significantly with radius, while$ \Gamma_p $ remains almost unchanged (fluctuations are less than 5%), indicating that the proton width for the excited states studied is nearly independent of the model.
Figure 5. The variation of S,
$\Gamma_p$ , and$\Gamma_{sp}$ with the radius. At r=1.1 fm,$\Gamma_{sp}$ and S are normalized to$\Gamma_p$ . The red circles, blue squares and green triangles represent$\Gamma_p$ ,$\Gamma_{sp}$ and S, respectively.At the temperatures where the Mg-Al cycle is active (
$ T_9 \approx 0.1 $ ), the contribution from direct capture is much smaller than that from low-energy resonances. The reaction rate for direct capture is referenced from Iliadis [37]. Table 3 shows the proton width and resonance strength for the 52.8,250, and 325.8 keV resonances measured in the energy region of interest. Fig. 6 shows the calculated reaction rates for 26Mg($ p, \gamma $ )27Al as a function of temperature, using the updated resonance strengths. Parameters for resonances not measured in this experiment were adopted from values in the literature [25]. The contribution of different resonances to the total reaction rate is shown in Fig. 7. Champagne et al. [24] derived the proton width and resonance strength for the 52.8 keV resonance using a scaling relation, and their results differ by a factor of 10 from those calculated using the spectroscopic factor in our work. This divergence leads to a significant increase in the total reaction rate at temperatures ($ T_9 < 0.03 $ ) where this resonance dominates. However, at$ T_9 \approx 0.1 $ , there remains considerable uncertainty in the total reaction rate due to the 90 keV and 136.7 keV resonances, especially the 90 keV resonance, which only has an upper limit. Fig. 8 shows a comparison between the present reaction rates around the temperature of$ T_9=0.1 $ and the reaction rates reported by Iliadis [25] and Angulo [40]. The calculated reaction rates are listed in Table 4.$ E_x $ 

(keV)$ E_{cm} $ [24−26]

(keV)$ J^{\pi}_r $ 

$ \Gamma_{\gamma} $ (eV)[24]

$ \Gamma_p $ (eV)

$ \omega \gamma $ (eV)

literature[24] this work literature[24, 37, 38] this work 8324(1) 52.8(10) $ \left(\dfrac{3}{2},\dfrac{5}{2}\right)^+ $ 

0.1-1 $ 1.8 \times 10^{-17} $ 

$ 3.26(46) \times 10^{-16} $ 

$ 5.3 \times 10^{-17} $ 

$ 6.51(91) \times 10^{-16} $ 

8521(2) 250(2) $ \dfrac{5}{2}^+ $ 

0.1-1 $ 2.11(29) \times 10^{-4} $ 

$ \leqslant 1 \times 10^{-6} $ 

$ 6.32(85) \times 10^{-4} $ 

8597.6(3) 325.8(3) $ \dfrac{3}{2}^- $ 

0.56(4) 0.42(20) 0.179(28) 0.25(3) 0.049(13) Table 3. Summary of resonance parameters.

Figure 6. Present total reaction rates. For unknown resonances, the resonance strength is taken as 1/10 of the upper limit value. The solid black line represents the total reaction rate, corresponding to the "median" values in Table 4, and does not include uncertainties.

Figure 7. The contribution of the main resonances to the total reaction rate in
$\pm 1\sigma$ confidence interval.$ T_9 $ 

Low Median High 0.010 2.28E-34 2.65E-34 3.02E-34 0.011 5.17E-32 6.02E-32 6.85E-32 0.012 4.70E-30 5.47E-30 6.23E-30 0.013 2.12E-28 2.46E-28 2.80E-28 0.014 5.48E-27 6.37E-27 7.26E-27 0.015 9.13E-26 1.06E-25 1.21E-25 0.016 1.06E-24 1.24E-24 1.41E-24 0.018 6.27E-23 7.30E-23 8.31E-23 0.020 1.61E-21 1.87E-21 2.13E-21 0.025 5.27E-19 6.13E-19 7.02E-19 0.03 2.38E-17 2.79E-17 3.44E-17 0.04 2.56E-15 4.11E-15 1.47E-14 0.05 4.42E-14 2.02E-13 1.56E-12 0.06 5.93E-13 4.56E-12 3.88E-11 0.07 1.16E-11 5.45E-11 4.08E-10 0.08 1.67E-10 4.64E-10 2.67E-09 0.09 1.54E-09 3.14E-09 1.33E-08 0.10 1.03E-08 1.78E-08 5.58E-08 0.11 5.77E-08 9.02E-08 2.14E-07 0.12 2.89E-07 4.21E-07 7.87E-07 0.13 1.31E-06 1.80E-06 2.83E-06 0.14 5.23E-06 6.92E-06 9.68E-06 0.15 1.85E-05 2.36E-05 3.08E-05 Table 4. The present reaction rate for 26Mg(
$ p, \gamma $ )27Al(in$ {\rm{cm}}^3{\rm{mol}}^{-1}{\rm{s}}^{-1}) $ -
For discrete narrow resonances, the reaction rate can be calculated using the following equation:
$ N_A\langle\sigma\upsilon\rangle=\sum\limits_{i}N_A\left(\frac{2\pi}{\mu kT}\right)^{3/2}\hbar^2{\rm e}^{-E^i_R/kT}\omega\gamma_i. $
(5) $ N_A $ is Avogadro's constant, k is Boltzmann's constant,$ \mu $ is the reduced mass, T is the stellar temperature,$ E_R $ is the resonance energy, and$ \omega\gamma $ is the resonance strength. The resonance strength for narrow resonances is calculated as follows:$ \omega\gamma_i=\frac{2J_i+1}{(2J_p+1)(2J_t+1)}\frac{\Gamma_p\Gamma_{\gamma}}{\Gamma_{{\rm{total}}}}, $
(6) where
$ J_i, J_t, J_p $ are the spins of the resonance state, target nucleus, and projectile nucleus, respectively.$ \Gamma_p, \Gamma_{\gamma}, \Gamma_{{\rm{total}}} $ represent the proton width, gamma width, and total width, respectively. When the gamma width is much larger than the proton width,$ \Gamma_{\gamma}/\Gamma_{{\rm{total}}} $ can be approximated as 1.The proton width is given by:
$ \Gamma_p = S\Gamma_{sp} = 2\frac{\hbar^2}{\mu a^2_c}SP_l\theta^2_{sp}. $
(7) In this context,
$ a_c=r\times A^{1/3} $ , S represents the proton spectroscopic factor, and$ P_l $ is the corresponding penetration coefficient for angular momentum l. The single-particle reduced width$ \theta^2 $ equals$ a_c\phi(a_c)^2/2 $ [38], where$ \phi(a_c) $ is the value of the bound-state wave function at$ a_c $ .Figure 5 shows the variations in the spectroscopic factor S,
$ \Gamma_p $ , and$ \Gamma_{sp} $ with changes in the radius parameter r. It can be seen that S and$ \Gamma_{sp} $ change significantly with radius, while$ \Gamma_p $ remains almost unchanged (fluctuations are less than 5%), indicating that the proton width for the excited states studied is nearly independent of the model.
Figure 5. (color online) The variation of S,
$\Gamma_p$ , and$\Gamma_{sp}$ with the radius. At r=1.1 fm,$\Gamma_{sp}$ and S are normalized to$\Gamma_p$ . The red circles, blue squares and green triangles represent$\Gamma_p$ ,$\Gamma_{sp}$ and S, respectively.At the temperatures where the Mg-Al cycle is active (
$ T_9 \approx 0.1 $ ), the contribution from direct capture is much smaller than that from low-energy resonances. The reaction rate for direct capture is referenced from Iliadis [37]. Table 3 shows the proton width and resonance strength for the 52.8,250, and 325.8 keV resonances measured in the energy region of interest. Figure 6 shows the calculated reaction rates for 26Mg($ p, \gamma $ )27Al as a function of temperature, using the updated resonance strengths. Parameters for resonances not measured in this experiment were adopted from values in the literature [25]. The contribution of different resonances to the total reaction rate is shown in Fig. 7. Champagne et al. [24] derived the proton width and resonance strength for the 52.8 keV resonance using a scaling relation, and their results differ by a factor of 10 from those calculated using the spectroscopic factor in our work. This divergence leads to a significant increase in the total reaction rate at temperatures ($ T_9 \lt 0.03 $ ) where this resonance dominates. However, at$ T_9 \approx 0.1 $ , there remains considerable uncertainty in the total reaction rate due to the 90 keV and 136.7 keV resonances, especially the 90 keV resonance, which only has an upper limit. Figure 8 shows a comparison between the present reaction rates around the temperature of$ T_9=0.1 $ and the reaction rates reported by Iliadis [25] and Angulo [40]. The calculated reaction rates are listed in Table 4.$ E_x $
/keV$ E_{cm} $ [24−26]
/keV$ J^{\pi}_r $ $ \Gamma_{\gamma} $ /eV [24]$ \Gamma_p $ /eV$ \omega \gamma $ /eVliterature [24] this work literature [24, 37, 39] this work 8324(1) 52.8(10) $ \left(\dfrac{3}{2},\dfrac{5}{2}\right)^+ $ 0.1-1 $ 1.8 \times 10^{-17} $ $ 3.26(46) \times 10^{-16} $ $ 5.3 \times 10^{-17} $ $ 6.51(91) \times 10^{-16} $ 8521(2) 250(2) $ \dfrac{5}{2}^+ $ 0.1-1 $ 2.11(29) \times 10^{-4} $ $ \leqslant 1 \times 10^{-6} $ $ 6.32(85) \times 10^{-4} $ 8597.6(3) 325.8(3) $ \dfrac{3}{2}^- $ 0.56(4) 0.42(20) 0.179(28) 0.25(3) 0.049(13) Table 3. Summary of resonance parameters.

Figure 6. (color online) Present total reaction rates. For unknown resonances, the resonance strength is taken as 1/10 of the upper limit value. The solid black line represents the total reaction rate, corresponding to the "median" values in Table 4, and does not include uncertainties.

Figure 7. (color online) The contribution of the main resonances to the total reaction rate in
$\pm 1\sigma$ confidence interval.$ T_9 $ Low Median High 0.010 2.28E-34 2.65E-34 3.02E-34 0.011 5.17E-32 6.02E-32 6.85E-32 0.012 4.70E-30 5.47E-30 6.23E-30 0.013 2.12E-28 2.46E-28 2.80E-28 0.014 5.48E-27 6.37E-27 7.26E-27 0.015 9.13E-26 1.06E-25 1.21E-25 0.016 1.06E-24 1.24E-24 1.41E-24 0.018 6.27E-23 7.30E-23 8.31E-23 0.020 1.61E-21 1.87E-21 2.13E-21 0.025 5.27E-19 6.13E-19 7.02E-19 0.03 2.38E-17 2.79E-17 3.44E-17 0.04 2.56E-15 4.11E-15 1.47E-14 0.05 4.42E-14 2.02E-13 1.56E-12 0.06 5.93E-13 4.56E-12 3.88E-11 0.07 1.16E-11 5.45E-11 4.08E-10 0.08 1.67E-10 4.64E-10 2.67E-09 0.09 1.54E-09 3.14E-09 1.33E-08 0.10 1.03E-08 1.78E-08 5.58E-08 0.11 5.77E-08 9.02E-08 2.14E-07 0.12 2.89E-07 4.21E-07 7.87E-07 0.13 1.31E-06 1.80E-06 2.83E-06 0.14 5.23E-06 6.92E-06 9.68E-06 0.15 1.85E-05 2.36E-05 3.08E-05 Table 4. The present reaction rate for 26Mg(
$ p, \gamma $ )27Al(in$ {\rm{cm}}^3{\rm{mol}}^{-1}{\rm{s}}^{-1}) $ -
For discrete narrow resonances, the reaction rate can be calculated using the following equation:
$ N_A\langle\sigma\upsilon\rangle=\sum\limits_{i}N_A\left(\frac{2\pi}{\mu kT}\right)^{3/2}\hbar^2{\rm e}^{-E^i_R/kT}\omega\gamma_i. $
(5) $ N_A $ is Avogadro's constant, k is Boltzmann's constant,$ \mu $ is the reduced mass, T is the stellar temperature,$ E_R $ is the resonance energy, and$ \omega\gamma $ is the resonance strength. The resonance strength for narrow resonances is calculated as follows:$ \omega\gamma_i=\frac{2J_i+1}{(2J_p+1)(2J_t+1)}\frac{\Gamma_p\Gamma_{\gamma}}{\Gamma_{{\rm{total}}}}, $
(6) where
$ J_i, J_t, J_p $ are the spins of the resonance state, target nucleus, and projectile nucleus, respectively.$ \Gamma_p, \Gamma_{\gamma}, \Gamma_{{\rm{total}}} $ represent the proton width, gamma width, and total width, respectively. When the gamma width is much larger than the proton width,$ \Gamma_{\gamma}/\Gamma_{{\rm{total}}} $ can be approximated as 1.The proton width is given by:
$ \Gamma_p = S\Gamma_{sp} = 2\frac{\hbar^2}{\mu a^2_c}SP_l\theta^2_{sp}. $
(7) In this context,
$ a_c=r\times A^{1/3} $ , S represents the proton spectroscopic factor, and$ P_l $ is the corresponding penetration coefficient for angular momentum l. The single-particle reduced width$ \theta^2 $ equals$ a_c\phi(a_c)^2/2 $ [38], where$ \phi(a_c) $ is the value of the bound-state wave function at$ a_c $ .Figure 5 shows the variations in the spectroscopic factor S,
$ \Gamma_p $ , and$ \Gamma_{sp} $ with changes in the radius parameter r. It can be seen that S and$ \Gamma_{sp} $ change significantly with radius, while$ \Gamma_p $ remains almost unchanged (fluctuations are less than 5%), indicating that the proton width for the excited states studied is nearly independent of the model.
Figure 5. (color online) The variation of S,
$\Gamma_p$ , and$\Gamma_{sp}$ with the radius. At r=1.1 fm,$\Gamma_{sp}$ and S are normalized to$\Gamma_p$ . The red circles, blue squares and green triangles represent$\Gamma_p$ ,$\Gamma_{sp}$ and S, respectively.At the temperatures where the Mg-Al cycle is active (
$ T_9 \approx 0.1 $ ), the contribution from direct capture is much smaller than that from low-energy resonances. The reaction rate for direct capture is referenced from Iliadis [37]. Table 3 shows the proton width and resonance strength for the 52.8,250, and 325.8 keV resonances measured in the energy region of interest. Figure 6 shows the calculated reaction rates for 26Mg($ p, \gamma $ )27Al as a function of temperature, using the updated resonance strengths. Parameters for resonances not measured in this experiment were adopted from values in the literature [25]. The contribution of different resonances to the total reaction rate is shown in Fig. 7. Champagne et al. [24] derived the proton width and resonance strength for the 52.8 keV resonance using a scaling relation, and their results differ by a factor of 10 from those calculated using the spectroscopic factor in our work. This divergence leads to a significant increase in the total reaction rate at temperatures ($ T_9 < 0.03 $ ) where this resonance dominates. However, at$ T_9 \approx 0.1 $ , there remains considerable uncertainty in the total reaction rate due to the 90 keV and 136.7 keV resonances, especially the 90 keV resonance, which only has an upper limit. Figure 8 shows a comparison between the present reaction rates around the temperature of$ T_9=0.1 $ and the reaction rates reported by Iliadis [25] and Angulo [40]. The calculated reaction rates are listed in Table 4.$ E_x $
/keV$ E_{cm} $ [24−26]
/keV$ J^{\pi}_r $ $ \Gamma_{\gamma} $ /eV [24]$ \Gamma_p $ /eV$ \omega \gamma $ /eVliterature [24] this work literature [24, 37, 39] this work 8324(1) 52.8(10) $ \left(\dfrac{3}{2},\dfrac{5}{2}\right)^+ $ 0.1-1 $ 1.8 \times 10^{-17} $ $ 3.26(46) \times 10^{-16} $ $ 5.3 \times 10^{-17} $ $ 6.51(91) \times 10^{-16} $ 8521(2) 250(2) $ \dfrac{5}{2}^+ $ 0.1-1 $ 2.11(29) \times 10^{-4} $ $ \leqslant 1 \times 10^{-6} $ $ 6.32(85) \times 10^{-4} $ 8597.6(3) 325.8(3) $ \dfrac{3}{2}^- $ 0.56(4) 0.42(20) 0.179(28) 0.25(3) 0.049(13) Table 3. Summary of resonance parameters.

Figure 6. (color online) Present total reaction rates. For unknown resonances, the resonance strength is taken as 1/10 of the upper limit value. The solid black line represents the total reaction rate, corresponding to the "median" values in Table 4, and does not include uncertainties.

Figure 7. (color online) The contribution of the main resonances to the total reaction rate in
$\pm 1\sigma$ confidence interval.$ T_9 $ Low Median High 0.010 2.28E-34 2.65E-34 3.02E-34 0.011 5.17E-32 6.02E-32 6.85E-32 0.012 4.70E-30 5.47E-30 6.23E-30 0.013 2.12E-28 2.46E-28 2.80E-28 0.014 5.48E-27 6.37E-27 7.26E-27 0.015 9.13E-26 1.06E-25 1.21E-25 0.016 1.06E-24 1.24E-24 1.41E-24 0.018 6.27E-23 7.30E-23 8.31E-23 0.020 1.61E-21 1.87E-21 2.13E-21 0.025 5.27E-19 6.13E-19 7.02E-19 0.03 2.38E-17 2.79E-17 3.44E-17 0.04 2.56E-15 4.11E-15 1.47E-14 0.05 4.42E-14 2.02E-13 1.56E-12 0.06 5.93E-13 4.56E-12 3.88E-11 0.07 1.16E-11 5.45E-11 4.08E-10 0.08 1.67E-10 4.64E-10 2.67E-09 0.09 1.54E-09 3.14E-09 1.33E-08 0.10 1.03E-08 1.78E-08 5.58E-08 0.11 5.77E-08 9.02E-08 2.14E-07 0.12 2.89E-07 4.21E-07 7.87E-07 0.13 1.31E-06 1.80E-06 2.83E-06 0.14 5.23E-06 6.92E-06 9.68E-06 0.15 1.85E-05 2.36E-05 3.08E-05 Table 4. The present reaction rate for 26Mg(
$ p, \gamma $ )27Al(in$ {\rm{cm}}^3{\rm{mol}}^{-1}{\rm{s}}^{-1}) $ -
This work utilized the Q3D spectrograph to measure the angular distributions of the 26Mg(7Li, 6He)27Al proton transfer reaction with a 7Li beam at an energy of 42 MeV. The angular distributions calculated using the DWBA method provided the proton spectroscopic factors for three excited states near the threshold, from which the corresponding resonance strengths were derived. The newly obtained resonance strength at 52.8 keV is an order of magnitude higher than previous results, leading to a significant increase in the total reaction rate at
$ T_{9}< 0.03 $ . However, the total reaction rate at astrophysical temperatures for the Mg-Al cycle remains highly uncertain due to the upper limits for the 90 keV and 136.7 keV resonances. Further studies are needed to address this uncertainty. Additionally, the updated reaction rates should be further calculated and discussed to assess their impact on the Mg-Al cycle and the nuclear reaction network in globular clusters. -
This work utilized the Q3D spectrograph to measure the angular distributions of the 26Mg(7Li, 6He)27Al proton transfer reaction with a 7Li beam at an energy of 42 MeV. The angular distributions calculated using the DWBA method provided the proton spectroscopic factors for three excited states near the threshold, from which the corresponding resonance strengths were derived. The newly obtained resonance strength at 52.8 keV is an order of magnitude higher than previous results, leading to a significant increase in the total reaction rate at
$ T_{9}< 0.03 $ . However, the total reaction rate at astrophysical temperatures for the Mg-Al cycle remains highly uncertain due to the upper limits for the 90 keV and 136.7 keV resonances. Further studies are needed to address this uncertainty. Additionally, the updated reaction rates should be further calculated and discussed to assess their impact on the Mg-Al cycle and the nuclear reaction network in globular clusters. -
This work utilized the Q3D spectrograph to measure the angular distributions of the 26Mg(7Li, 6He)27Al proton transfer reaction with a 7Li beam at an energy of 42 MeV. The angular distributions calculated using the DWBA method provided the proton spectroscopic factors for three excited states near the threshold, from which the corresponding resonance strengths were derived. The newly obtained resonance strength at 52.8 keV is an order of magnitude higher than previous results, leading to a significant increase in the total reaction rate at
$ T_{9}< 0.03 $ . However, the total reaction rate at astrophysical temperatures for the Mg-Al cycle remains highly uncertain due to the upper limits for the 90 keV and 136.7 keV resonances. Further studies are needed to address this uncertainty. Additionally, the updated reaction rates should be further calculated and discussed to assess their impact on the Mg-Al cycle and the nuclear reaction network in globular clusters. -
This work utilized the Q3D spectrograph to measure the angular distributions of the 26Mg(7Li, 6He)27Al proton transfer reaction with a 7Li beam at an energy of 42 MeV. The angular distributions calculated using the DWBA method provided the proton spectroscopic factors for three excited states near the threshold, from which the corresponding resonance strengths were derived. The newly obtained resonance strength at 52.8 keV is an order of magnitude higher than previous results, leading to a significant increase in the total reaction rate at
$ T_{9}< 0.03 $ . However, the total reaction rate at astrophysical temperatures for the Mg-Al cycle remains highly uncertain due to the upper limits for the 90 keV and 136.7 keV resonances. Further studies are needed to address this uncertainty. Additionally, the updated reaction rates should be further calculated and discussed to assess their impact on the Mg-Al cycle and the nuclear reaction network in globular clusters. -
We thank the staff of the HI-13 tandem accelerator for the smooth operation of the machine.
-
We thank the staff of the HI-13 tandem accelerator for the smooth operation of the machine.
-
We thank the staff of the HI-13 tandem accelerator for the smooth operation of the machine.
-
We thank the staff of the HI-13 tandem accelerator for the smooth operation of the machine.
New determination of astrophysical 26Mg(p, γ)27Al reaction rate through the 26Mg(7Li, 6He)27Al transfer reaction
- Received Date: 2025-09-01
- Available Online: 2026-03-15
Abstract: The 26Mg$(p,\,\gamma)$27Al reaction, as part of the Mg-Al cycle, is closely related to the abundance ratio of 26Al to 27Al in stars. It also has a direct connection to the Mg-Al anti-correlation observed in globular clusters (GCs). Its reaction rate is determined by multiple known and unknown low-energy resonances. In this work, we measured the angular distributions of the proton transfer reaction 26Mg(7Li, 6He)27Al populating three levels at excitation energies from 8.324 MeV to 8.597 MeV using the HI-13 tandem accelerator and a high-precision magnetic spectrograph. Proton spectroscopic factors were extracted from the angular distributions corresponding to these three states, and the resonance strengths contributing to the reaction rate were updated. At the same time, the latest calculated reaction rate shows that the result for the 52.8 keV resonance significantly increases the total reaction rate at $T_{9}<0.03$.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
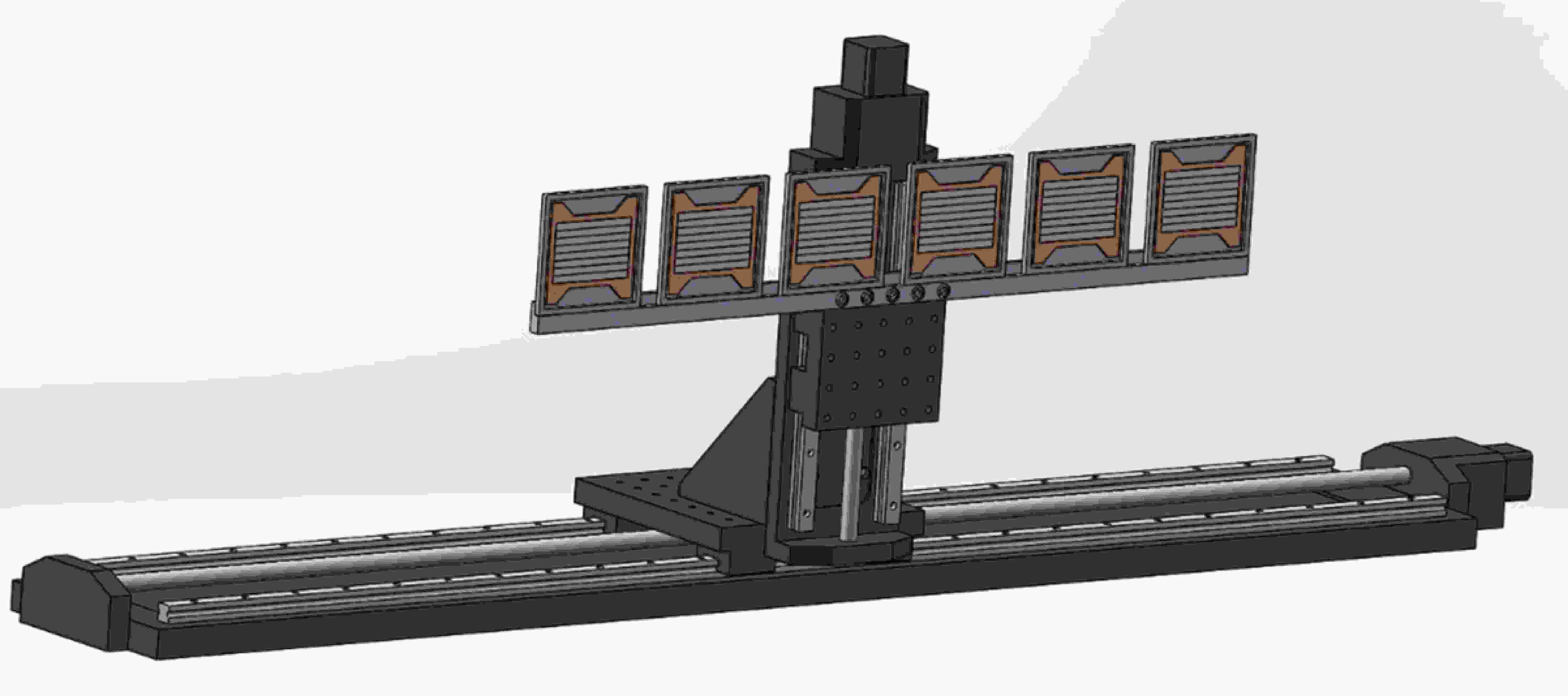










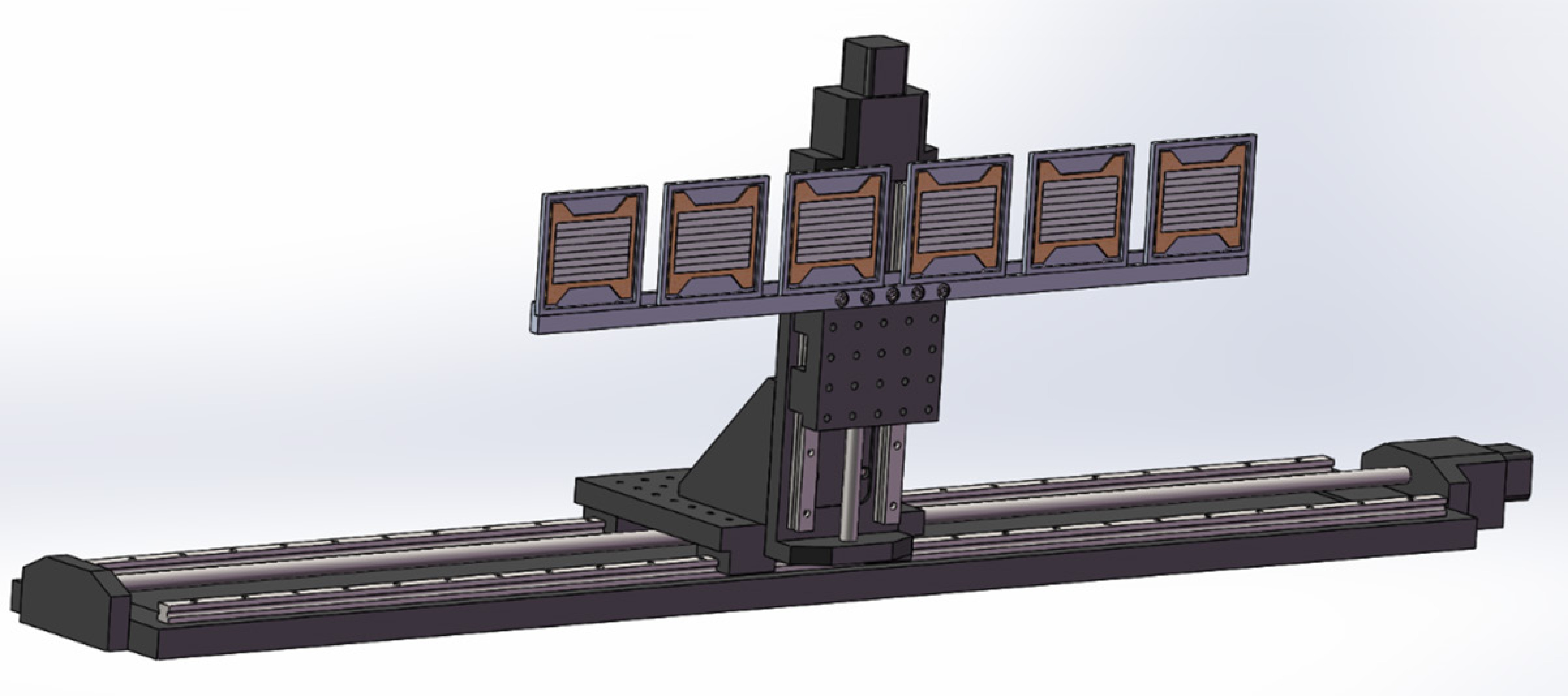
























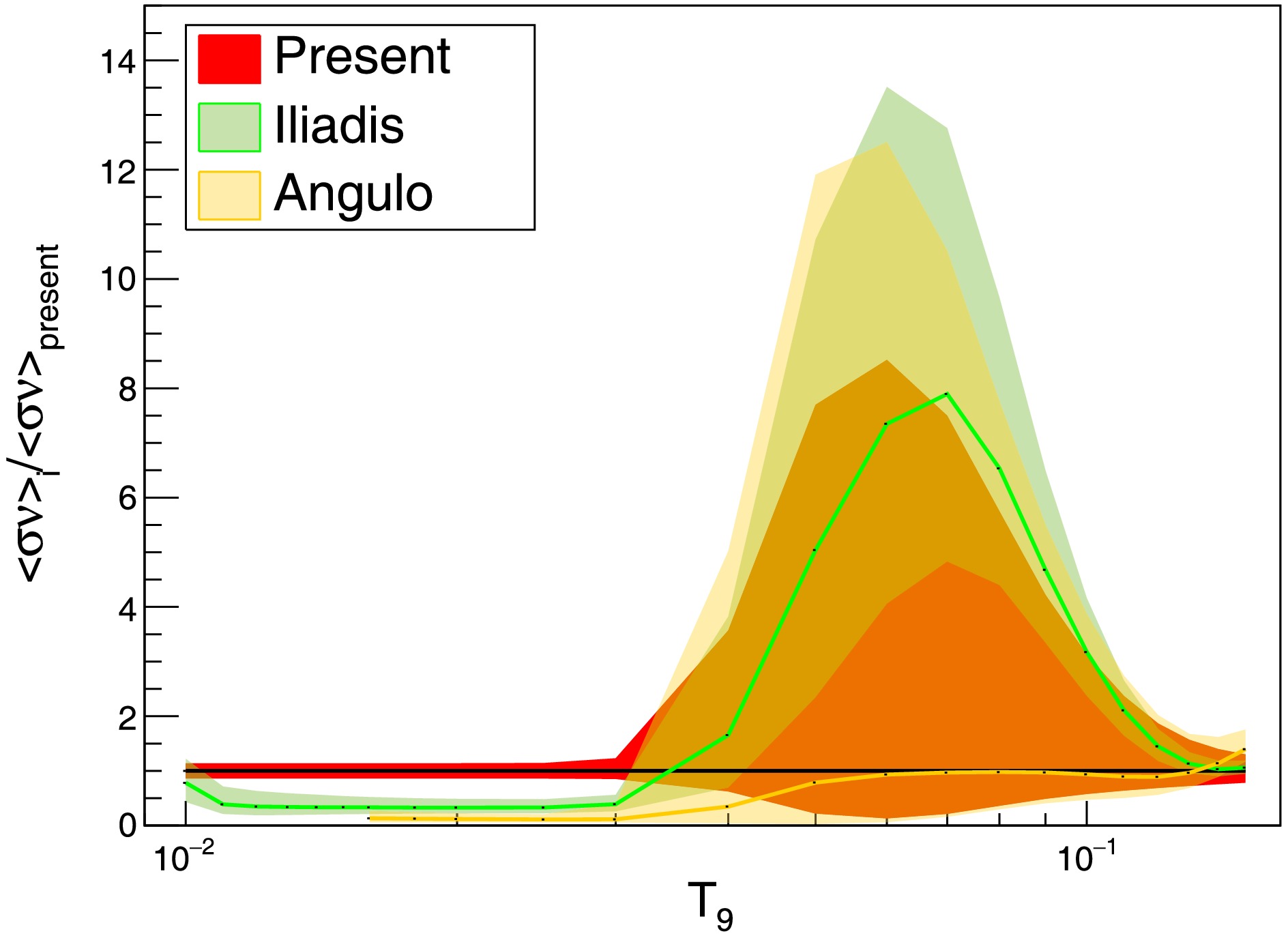



 DownLoad:
DownLoad: