-
In modern nuclear physics, exploring exotic nuclei with extreme proton-to-neutron ratios has become a crucial avenue for deepening our understanding of nuclear structure beyond the region of stability. On the proton-rich side of the nuclear chart, the proton dripline marks a fundamental boundary where nuclei cannot bind any additional protons. Nuclei near this limit often undergo proton emission as a mode of decay, naturally shedding excess protons to move toward greater stability [1, 2]. The idea of proton emission can be traced back to the early days of the nuclear theory, even before the internal structure of the atomic nucleus was fully understood. However, significant experimental interest in this phenomenon re-emerged in the 1960s. The first clear evidence originated from the observation of proton emission from a high-spin isomer in 53Co [3, 4], followed by ground-state emissions identified in 151Lu [5] and 147Tm [6]. Thus far, approximately 28 ground-state proton emitters (ranging from 105Sb to 185Bi) and around 20 isomeric emitters have been confirmed [1, 7]. Continued advances in experimental technology promise the discovery of more proton emitters, offering deeper insights into nuclear forces and the limits of nuclear existence at the proton dripline.
Driplines represent the boundaries of the nuclear chart, determined by the binding energies of nuclei. The proton dripline defines the limit beyond which nuclei are no longer bound with respect to proton emission from their ground states [1]. Beyond this boundary, the proton separation energy becomes negative, indicating that the nucleus lacks sufficient binding energy to retain its protons. Consequently, proton-rich nuclei situated past the dripline exhibit positive Q-values for proton decay, reflecting a natural tendency to emit excess protons spontaneously. These nuclei are characterized by a severe neutron deficiency. Accurately describing the properties of such unstable, proton-emitting nuclei presents a significant challenge for nuclear theory.
Proton emission decay rates are highly sensitive to the decay energy (Q value) and orbital angular momentum of the emitted proton, making proton radioactivity a powerful tool for probing nuclear properties. This includes determining nuclear masses, exploring single-particle level structures, and extracting spectroscopic information for nuclei far from stability [1]. Furthermore, proton-rich nuclei serve as useful identifiers in recoil-decay tagging experiments, providing structural insights into exotic systems.
Numerous theoretical models have been successfully employed to estimate the half-lives of proton-emitting nuclei. These include the Wentzel-Kramers-Brillouin (WKB) approximation with a Woods-Saxon–type potential combined with the Coulomb potential [8], the generalized liquid-drop model (GLDM) [9], the single-folding model (SFM) [10], the two-potential approach (TPA) [11], and models like the Coulomb and proximity potential model (CPPM) [12, 13]. Based on the WKB method for calculating barrier penetration probability, various models have been developed to estimate proton emission half-lives [8−10, 14, 15]. These include the Woods-Saxon-type potential [8, 14]; density-dependent Michigan three-range Yukawa (DDM3Y) effective interactions [10]; Jeukenne, Lejeune, and Mahaux (JLM) interactions [15]; and generalized liquid-drop model [9].
In this study, we present a microscopic investigation of proton decay half-lives for neutron-deficient nuclei using the Hartree-Fock-Bogolyubov (HFB) framework with the Gogny D1S effective interaction. The half-lives for proton emission are calculated from both ground and isomeric states using a single-folding potential based on the realistic M3Y-Paris nucleon-nucleon (NN) interaction. The deformed density distributions of the daughter nuclei are obtained microscopically through HFB calculations with the Gogny D1S force. The resulting half-lives are then compared with available experimental data and other theoretical models to assess the reliability and predictive power of this microscopic approach in modeling proton radioactivity.
The structure of the paper is organized as follows. Section II provides a detailed description of the Coulomb and nuclear potentials governing the interaction between the emitted proton and daughter nucleus. This section outlines procedures used to compute the assault frequency, penetration probability, preformation factor, and decay width. In Section III, the calculated results are analyzed and discussed. Finally, a concise summary of the study is presented in Section IV.
-
In modern nuclear physics, exploring exotic nuclei with extreme proton-to-neutron ratios has become a crucial avenue for deepening our understanding of nuclear structure beyond the region of stability. On the proton-rich side of the nuclear chart, the proton dripline marks a fundamental boundary where nuclei can no longer bind additional protons. Nuclei near this limit often undergo proton emission as a mode of decay, naturally shedding excess protons to move toward greater stability [1, 2]. The idea of proton emission dates back to the early days of nuclear theory, even before the internal structure of the atomic nucleus was fully understood. However, significant experimental interest in this phenomenon re-emerged in the 1960s. The first clear evidence came from the observation of proton emission from a high-spin isomer in 53Co [3, 4], followed by ground-state emissions identified in 151Lu [5] and 147Tm [6]. To date, approximately 28 ground-state proton emitters (ranging from 105Sb to 185Bi) and around 20 isomeric emitters have been confirmed [1, 7]. Continued advances in experimental technology promise the discovery of more proton emitters, offering deeper insights into nuclear forces and the limits of nuclear existence at the proton dripline.
Driplines represent the boundaries of the nuclear chart, determined by the binding energies of nuclei. The proton dripline defines the limit beyond which nuclei are no longer bound with respect to proton emission from their ground states [1]. Beyond this boundary, the proton separation energy becomes negative, indicating that the nucleus lacks sufficient binding energy to retain its protons. As a result, proton-rich nuclei situated past the dripline exhibit positive Q-values for proton decay, reflecting a natural tendency to emit excess protons spontaneously. These nuclei are characterized by a severe neutron deficiency. Accurately describing the properties of such unstable, proton-emitting nuclei presents a significant challenge for nuclear theory.
Proton emission decay rates are highly sensitive to the decay energy (Q value) and the orbital angular momentum of the emitted proton, making proton radioactivity a powerful tool for probing nuclear properties. This includes determining nuclear masses, exploring single-particle level structures, and extracting spectroscopic information for nuclei far from stability [1]. Furthermore, proton-rich nuclei serve as useful identifiers in recoil-decay tagging experiments, providing structural insights into exotic systems.
Numerous theoretical models have been successfully employed to estimate the half-lives of proton-emitting nuclei. These include the Wentzel-Kramers-Brillouin (WKB) approximation with a Woods-Saxon–type potential combined with the Coulomb potential [8], the generalized liquid-drop model (GLDM) [9], the single-folding model (SFM) [10], the two-potential approach (TPA) [11], and models like the Coulomb and proximity potential model (CPPM) [12, 13]. Based on the Wentzel-Kramers-Brillouin (WKB) method for calculating barrier penetration probability, various models have been developed to estimate proton emission half-lives [8−10, 14, 15]. These include the Woods-Saxon-type potential [8, 14], density-dependent M3Y (DDM3Y) effective interactions [10], Jeukenne, Lejeune, and Mahaux (JLM) interactions [15], and the generalized liquid-drop model [9].
In this study, we present a microscopic investigation of proton decay half-lives for neutron-deficient nuclei using the Hartree-Fock-Bogolyubov (HFB) framework with the Gogny D1S effective interaction. The half-lives for proton emission are calculated from both ground and isomeric states using a single-folding potential based on the realistic M3Y-Paris nucleon-nucleon interaction. The deformed density distributions of the daughter nuclei are obtained microscopically through HFB calculations with the Gogny D1S force. The resulting half-lives are then compared with available experimental data and other theoretical models to assess the reliability and predictive power of this microscopic approach in modeling proton radioactivity.
The structure of the paper is organized as follows. Section II provides a detailed description of the Coulomb and nuclear potentials governing the interaction between the emitted proton and the daughter nucleus. This section also outlines the procedures used to compute the assault frequency, penetration probability, preformation factor, and decay width. In Section III, the calculated results are analyzed and discussed. Finally, a concise summary of the study is presented in Section IV.
-
Within the density-dependent cluster model, the interaction potential between the proton particle and the daughter nucleus is a sum of the nuclear,
$ V_N $ , interaction part, the Coulomb,$ V_C $ , interaction part, and the centrifugal barrier part.$ V_T(R ,\theta)= \lambda(\theta) \, V_{N}(R ,\theta)+ V_{C}(R ,\theta) + \frac{\hbar^{2}(\ell+1 / 2)^{2}}{2 \mu R^{2}}, $

(1) where μ represents the reduced mass of the proton-daughter system. The last term of Eq. (1) is the Langer modification to the centrifugal potential which is essential for the validity of the first-order WKB integral [16, 17].
Assuming an axially symmetric deformation for the daughter nucleus and treating the emitted proton as a point particle, the nuclear potential is derived through a single-folding integral involving the daughter nucleus’s density distribution and an effective nucleon-nucleon (NN) interaction [18]:
$ V_{N}(R, \theta) = \int \mathrm{d}\vec{r}_1 \, \rho_{d}(\vec{r}_1) \, \upsilon_{NN}\left(|\vec{s} = \vec{R} - \vec{r}_1|\right), $

(2) Here, R denotes the separation between the emitted proton and the center of mass of the daughter nucleus, while θ defines the orientation angle of the proton with respect to the symmetric axis of the deformed daughter nucleus.
By utilizing the Fourier transform of the NN interaction
$ \upsilon_{NN} $ , the integral in Eq. (2) can be simplified in a momentum space method as [19, 20],$ V_{N}(R ,\theta)=\int \mathrm{d} \vec{k} \, \mathrm{e}^{\mathrm{i} \vec{k} \cdot \vec{R}} \, \tilde{\upsilon}_{NN}(k) \left[\int \mathrm{\; d} \vec{r}_{1} \mathrm{e}^{-\mathrm{i} \vec{k} \cdot \vec{r}_{1}} \rho_{d}\left(\vec{r}_{1}\right)\right] $

(3) where
$ \tilde{\upsilon}_{NN}(k)=\frac{1}{(2 \pi)^{3}} \int \mathrm{e}^{-\mathrm{i} \vec{k} \cdot \vec{r}}\upsilon_{NN}(r) \mathrm{d} \vec{r} . $

(4) The nuclear interaction potential given in Eq. (3) can be formulated using the multipole expansion of the deformed density distribution, resulting in
$ \begin{aligned}[b] V_N(R,\theta) =\;& \frac{2}{\pi} \sum\limits_{\ell} Y_{\ell 0}(\theta) \int_0^{\infty} dk\, k^2 j_{\ell}(kR)\, \tilde{\upsilon}_{NN}(k) \\& \times 2\pi\int_0^{\infty} dr_1\, r_1^2 j_{\ell}(kr_1) \int_0^{\pi} d\theta_1\, \sin\theta_1\, \rho_d(r_1,\theta_1) Y_{\ell 0}(\theta_1) \end{aligned} $

(5) The Coulomb potential is calculated using an analogous double-folding approach, as given in Eq. (5), in which the effective nucleon–nucleon interaction
$ \upsilon_{NN}(s) $ is replaced by the proton–proton Coulomb interaction$ {e^{2}}/{|\vec{s}|} $ , and the matter density of the daughter nucleus is substituted with its corresponding charge density distribution.The renormalization factor
$ \lambda(\theta) $ of the nuclear potential, Eq. (1), is not an adjustable parameter but it is determined separately for each decay by applying the Bohr–Sommerfeld quantization condition [17, 21, 22],$ \int_{R_{1}(\theta)}^{R_{2}(\theta)} \mathrm{d}r \, k(r, \theta)= (G-\ell+1) \frac{\pi}{2} $

(6) where
$ k(r, \theta)=\sqrt{2 \mu\left|V_{T}(R, \theta)-Q_{p}\right| / \hbar^{2}} $ is the wave number.$ R_{i}(\theta)(i=1,2,3) $ are the three turning points for the proton-daughter potential barrier where$ \left.V_{T}(R, \theta)\right|_{R=R_{i}}=Q_{p} $ . To reflect the primary influence of the Pauli exclusion principle, the number of nodes in the wave function—represented by the quantum number n—is determined using the Wildermuth condition [23−25]:$ G = 2n + \ell. $

(7) In this study, the value of G is chosen as either 4 or 5 based on shell model considerations as discussed in Refs. [7, 8], depending on the specific proton-emitting nucleus under investigation.
For the effective NN interaction,
$ \upsilon(s) $ , we use the popular Michigan three-range Yukawa (M3Y)-Paris-type interaction with zero-range exchange contribution [18] which has the form,$ \begin{aligned}[b] \upsilon_{NN}(s)=\;& {\left[11061.625 \frac{e^{-4 s}}{4 s}-2537.5 \frac{e^{-2.5 s}}{2.5 s}\right] } \\& -590\left[1-0.002 E/A_{p}\right] \delta(\vec{s}) \end{aligned} $

(8) where
$ E/A_{p} $ is the proton energy per mass number of proton ($ A_p=1 $ ). The last term in Eq. (8) accounts for the knock-on exchange by using zero-range pseudo-potential.The matter density distribution of the daughter nucleus is modeled using a two-parameter Fermi function:
$ \rho_{d}\left(r,\theta^{\prime}\right) = \frac{\rho_{0}}{1 + \exp\left(\dfrac{r - R(\theta^{\prime})}{a}\right)}, $

(9) where
$ \rho_{0} $ is the central density, determined by normalizing the distribution to match the mass number of the daughter nucleus$ A_d $ . The angle$ \theta^{\prime} $ denotes the orientation between the position vector$ \vec{r} $ and the symmetry axis of the deformed nucleus.The orientation-dependent half-density radius
$ R(\theta^{\prime}) $ is expressed as:$ R(\theta^{\prime}) = R_0 \left[1 + \beta_2 Y_{2,0}(\theta^{\prime}) + \beta_4 Y_{4,0}(\theta^{\prime}) + \beta_6 Y_{6,0}(\theta^{\prime}) \right], $

(10) where
$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ are the deformation parameters adopted from the evaluated values provided by WS4 [26]. The spherical equivalent of the half-density radius is given by$ R_0 = 1.07\,A_d^{1/3} \, \mathrm{fm} $ , and the surface diffuseness parameter is set to$ a = 0.54 \, \mathrm{fm} $ [27−31]. For spherical nuclei,$ R(\theta^{\prime}) $ simplifies to a constant value equal to$ R_0 $ .An alternative representation of nuclear matter and charge densities involves the microscopically calculated neutron (
$ \rho_n $ ) and proton ($ \rho_p $ ) distributions, obtained using the Hartree-Fock-Bogoliubov (HFB) mean-field approach with the BSk14 Skyrme energy-density functional (HFB-BSk14). In this work, we also incorporate the deformed density distributions predicted by the axially deformed HFB method employing the Gogny D1S effective interaction (HFB-D1S Gogny). The resulting axial densities are expanded in terms of spherical harmonics$ Y_{\lambda_m0} $ , including contributions up to$ \lambda_m=8 $ multipole components.For a given emission angle θ, the assault (knocking) frequency
$ \nu(\theta) $ and the penetration probability$ P(\theta) $ are calculated using the Wentzel–Kramers–Brillouin (WKB) approximation as follows:$ \nu(\theta) = \left[\int_{R_1(\theta)}^{R_2(\theta)} \frac{2\mu}{\hbar\, k(r,\theta)}\,dr\right]^{-1}, $

(11) $ P(\theta) = \exp\left(-2\int_{R_2(\theta)}^{R_3(\theta)} k(r,\theta)\,dr\right), $

(12) The total penetration probability, P, and total knocking frequency ν are obtained by averaging
$ P(\theta) $ and$ \nu(\theta) $ over all possible orientations of the involving deformed nuclei as follows:$ \begin{align} & P=\frac{1}{2} \int_{0}^{\pi} P(\theta) \sin \theta \mathrm{d} \theta \end{align} $

(13) $ \begin{align} & \nu=\frac{1}{2} \int_{0}^{\pi} \nu(\theta) \sin \theta \mathrm{d} \theta \end{align} $

(14) The spectroscopic factor
$ S_p $ was determined using the empirical relation expressed as [32]:$ \log_{10} S_p = \begin{cases} a \beta_2' + b & \text{for } \beta_2' > 0 \\ c \beta_2' + d & \text{for } \beta_2' < 0 \end{cases} $

(15) Here, different sets of parameters
$(a, b)$ and$(c, d)$ were applied depending on the sign of the parent deformation parameter$\beta_2'$ . Specifically, for$\beta_2' > 0$ , the coefficients are$ a = -5.819 $ and$ b = 0.421 $ , while for$\beta_2' < 0$ , the coefficients are$ c = -7.827 $ and$ d = -1.137 $ . These new values were obtained by fitting the experimental spectroscopic factor data using the least-squares method. The standard deviations for the different theoretical models—spherical, deformed, Gogny, and BSk14—are relatively small, indicating that the deformation-dependent formula reliably describes the behavior of the spectroscopic factor across the studied nuclei.The total decay width is defined as
$ \Gamma = \hbar\, \; \mathrm{S}_{\mathrm{p}} \nu\, P $ and is related to the proton decay half-life by$ T_{1 / 2}=\frac{\hbar \ln 2}{ \Gamma} $

(16) -
Within the density-dependent cluster model, the interaction potential between the proton particle and daughter nucleus is a sum of the nuclear interaction part
$ V_N $ , Coulomb interaction part$ V_C $ , and centrifugal barrier part.$ V_T(R ,\theta)= \lambda(\theta) \, V_{N}(R ,\theta)+ V_{C}(R ,\theta) + \frac{\hbar^{2}(\ell+1 / 2)^{2}}{2 \mu R^{2}}, $
(1) where μ represents the reduced mass of the proton-daughter system. The last term of Eq. (1) is the Langer modification to the centrifugal potential. This is essential for the validity of the first-order WKB integral [16, 17].
Assuming an axially symmetric deformation for the daughter nucleus and treating the emitted proton as a point particle, the nuclear potential can be derived through a single-folding integral involving the daughter nucleus’s density distribution and effective NN interaction [18].
$ V_{N}(R, \theta) = \int \mathrm{d}\boldsymbol{r}_1 \, \rho_{d}(\boldsymbol{r}_1) \, \upsilon_{NN}\left(|\boldsymbol{s} = \boldsymbol{R} - \boldsymbol{r}_1|\right), $
(2) where R denotes the separation between the emitted proton and the center of mass of the daughter nucleus, while θ defines the orientation angle of the proton with respect to the symmetric axis of the deformed daughter nucleus.
By utilizing the Fourier transform of the NN interaction
$ \upsilon_{NN} $ , the integral in Eq. (2) can be simplified in a momentum space method as [19, 20]$ V_{N}(R ,\theta)=\int \mathrm{d} \boldsymbol{k} \, \mathrm{e}^{\mathrm{i} \boldsymbol{k} \cdot \boldsymbol{R}} \, \tilde{\upsilon}_{NN}(k) \left[\int \mathrm{\; d} \boldsymbol{r}_{1} \mathrm{e}^{-\mathrm{i} \boldsymbol{k} \cdot \boldsymbol{r}_{1}} \rho_{d}\left(\boldsymbol{r}_{1}\right)\right], $
(3) where
$ \tilde{\upsilon}_{NN}(k)=\frac{1}{(2 \pi)^{3}} \int \mathrm{e}^{-\mathrm{i} \boldsymbol{k} \cdot \boldsymbol{r}}\upsilon_{NN}(r) \mathrm{d} \boldsymbol{r} . $
(4) The nuclear interaction potential given in Eq. (3) can be formulated using the multipole expansion of the deformed density distribution, which results in
$ \begin{aligned}[b]V_N(R,\theta)=\; & \frac{2}{\pi}\sum\limits_{\ell}^{ }Y_{\ell0}(\theta)\int_0^{\infty}\mathrm{d}k\, k^2j_{\ell}(kR)\, \tilde{\upsilon}_{NN}(k) \\ & \times2\pi\int_0^{\infty} \mathrm{d}r_1\, r_1^2j_{\ell}(kr_1)\int_0^{\pi}\mathrm{d}\theta_1\, \sin\theta_1\, \rho_d(r_1,\theta_1)Y_{\ell0}(\theta_1).\end{aligned} $
(5) The Coulomb potential is calculated using an analogous double-folding approach, as given in Eq. (5), wherein the effective NN interaction
$ \upsilon_{NN}(s) $ is replaced by the proton–proton Coulomb interaction$ {e^{2}}/{|\boldsymbol{s}|} $ , and the matter density of the daughter nucleus is substituted with its corresponding charge density distribution.The renormalization factor
$ \lambda(\theta) $ of the nuclear potential, Eq. (1), is not an adjustable parameter. However, it is separately determined for each decay by applying the Bohr–Sommerfeld quantization condition [17, 21, 22]$ \int_{R_{1}(\theta)}^{R_{2}(\theta)} \mathrm{d}r \, k(r, \theta)= (G-\ell+1) \frac{\pi}{2}, $
(6) where
$ k(r, \theta)=\sqrt{2 \mu\left|V_{T}(R, \theta)-Q_{p}\right| / \hbar^{2}} $ represents the wave number.$ R_{i}(\theta)(i=1,2,3) $ represents the three turning points for the proton-daughter potential barrier where$ \left.V_{T}(R, \theta)\right|_{R=R_{i}}=Q_{p} $ . To reflect the primary influence of the Pauli exclusion principle, the number of nodes in the wave function—represented by quantum number n—is determined using the Wildermuth condition [23−25]$ G = 2n + \ell. $
(7) In this study, the value of G is chosen as either 4 or 5. This choice is based on shell model considerations discussed in Refs. [7, 8] and depends on the specific proton-emitting nucleus under investigation.
For an effective NN interaction
$ \upsilon(s) $ , we use the popular Michigan three-range Yukawa (M3Y)-Paris-type interaction with zero-range exchange contribution [18], which has the form$ \begin{aligned}[b] \upsilon_{NN}(s)=\;& {\left[11061.625 \frac{{\rm e}^{-4 s}}{4 s}-2537.5 \frac{{\rm e}^{-2.5 s}}{2.5 s}\right] } \\& -590\left[1-0.002 E/A_{p}\right] \delta(\boldsymbol{s}) \end{aligned}, $
(8) where
$ E/A_{p} $ represents the proton energy per mass number of proton ($ A_p=1 $ ). The last term in Eq. (8) accounts for the knock-on exchange using the zero-range pseudo-potential.The matter density distribution of the daughter nucleus is modeled using a two-parameter Fermi function
$ \rho_{d}\left(r,\theta^{\prime}\right) = \frac{\rho_{0}}{1 + \exp\left(\dfrac{r - R(\theta^{\prime})}{a}\right)}, $
(9) where
$ \rho_{0} $ represents the central density, which is determined by normalizing the distribution to match the mass number of the daughter nucleus$ A_d $ . The angle$ \theta^{\prime} $ denotes the orientation between the position vector$ \boldsymbol{r} $ and symmetry axis of the deformed nucleus.The orientation-dependent half-density radius
$ R(\theta^{\prime}) $ is expressed as$ R(\theta^{\prime}) = R_0 \left[1 + \beta_2 Y_{2,0}(\theta^{\prime}) + \beta_4 Y_{4,0}(\theta^{\prime}) + \beta_6 Y_{6,0}(\theta^{\prime}) \right], $
(10) where
$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ represent the deformation parameters adopted from the evaluated values provided by WS4 [26]. The spherical equivalent of the half-density radius is given by$ R_0 = 1.07\,A_d^{1/3} \, \mathrm{fm} $ , and the surface diffuseness parameter is set to$ a = 0.54 \, \mathrm{fm} $ [27−31]. For spherical nuclei,$ R(\theta^{\prime}) $ simplifies to a constant value equal to$ R_0 $ .An alternative representation of nuclear matter and charge densities involves the microscopically calculated neutron (
$ \rho_n $ ) and proton ($ \rho_p $ ) distributions obtained using the HFB mean-field approach with the BSk14 Skyrme energy-density functional (HFB-BSk14). In this study, we incorporate the deformed density distributions predicted by the axially deformed HFB method by employing the Gogny D1S effective interaction (HFB-D1S Gogny). The resulting axial densities are expanded in terms of spherical harmonics$ Y_{\lambda_m0} $ , including contributions up to$ \lambda_m=8 $ multipole components.For a given emission angle θ, the assault (knocking) frequency
$ \nu(\theta) $ and penetration probability$ P(\theta) $ are calculated using the WKB approximation as$ \nu(\theta)=\left[\int_{R_1(\theta)}^{R_2(\theta)}\frac{2\mu}{\hbar\, k(r,\theta)}\, \mathrm{d}r\right]^{-1}, $
(11) $ P(\theta)=\exp\left(-2\int_{R_2(\theta)}^{R_3(\theta)}k(r,\theta)\, \mathrm{d}r\right), $
(12) The total penetration probability P and total knocking frequency ν are obtained by averaging
$ P(\theta) $ and$ \nu(\theta) $ over all possible orientations of the involving deformed nuclei as$ \begin{align} & P=\frac{1}{2} \int_{0}^{\pi} P(\theta) \sin \theta \mathrm{d} \theta ,\end{align} $
(13) $ \begin{align} & \nu=\frac{1}{2} \int_{0}^{\pi} \nu(\theta) \sin \theta \mathrm{d} \theta. \end{align} $
(14) The spectroscopic factor
$ S_p $ is determined using the empirical relationship expressed as [32]$ \log_{10} S_p = \begin{cases} a \beta_2' + b & \text{for } \beta_2' \gt 0 \\ c \beta_2' + d & \text{for } \beta_2' \lt 0 \end{cases}. $
(15) Here, the different sets of parameters
$(a, b)$ and$(c, d)$ are applied based on the sign of the parent deformation parameter$\beta_2'$ . Specifically, for$\beta_2' \gt 0$ , the coefficients are$ a = -5.819 $ and$ b = 0.421 $ , while for$\beta_2' \lt 0$ , the coefficients are$ c = -7.827 $ and$ d = -1.137 $ . These new values are obtained by fitting the experimental spectroscopic factor data using the least-squares method. The standard deviations for the different theoretical models—spherical, deformed, Gogny, and BSk14—are relatively small, indicating that the deformation-dependent formula reliably describes the behavior of the spectroscopic factor across the studied nuclei.The total decay width is defined as
$ \Gamma = \hbar\, \; \mathrm{S}_{\mathrm{p}} \nu\, P $ and is related to the proton decay half-life by$ T_{1 / 2}=\frac{\hbar \ln 2}{ \Gamma}. $
(16) -
The Hartree-Fock-Bogolyubov (HFB) approach, formulated using the Gogny D1S effective interaction, serves as a powerful and consistent framework for performing large-scale nuclear structure computations [33]. This technique has been extensively refined and employed in numerous studies, facilitating detailed investigations of nuclear characteristics such as ground-state shapes, binding energies, and potential energy surfaces (PES). The Gogny–HFB model has been extensively discussed in several previous studies (see Refs. [33−36] and the references therein). Below, we outline the key aspects of the methodology and its evolution.
The Gogny effective nucleon-nucleon interaction was originally formulated by Dechargé and Gogny in 1980 to address key features of nuclear matter, particularly saturation and pairing effects [37]. This interaction incorporates finite-range Gaussian components along with a density-dependent zero-range term, allowing for accurate modeling of a wide range of nuclei. The analytical form of the D1 Gogny interaction is expressed as [38]:
$ \begin{aligned}[b] V_{12}(\rho)=\;& \sum\limits_{j=1}^2\left(W_j+B_j P_\sigma-H_j P_\tau-M_j P_\sigma P_\tau\right) e^{-\frac{\left({\boldsymbol{r}}_1-{\boldsymbol{r}}_2\right)^2}{\mu_j^2}} \\ & +t_3\left(1+x_0 P_\sigma\right) \delta\left({\boldsymbol{r}}_1-{\boldsymbol{r}}_2\right) \rho^\alpha\left(\frac{{\boldsymbol{r}}_1+{\boldsymbol{r}}_2}{2}\right) \\& +i W_{L S} \overleftarrow{\nabla}_{12} \delta\left({\boldsymbol{r}}_1-{\boldsymbol{r}}_2\right) \wedge \vec{\nabla}_{12}\left({\boldsymbol{\sigma}}_1+{\boldsymbol{\sigma}}_2\right), \end{aligned} $

(17) where
$ P_\sigma $ and$ P_\tau $ are the spin and isospin exchange operators, respectively. The first term in Eq. (17) represents the finite-range central potential, independent of density, and allows for full spin-isospin exchange. It contributes to multiple channels:$ (S=0, T=1) $ ,$ (S=1, T=1) $ ,$ (S=0, T=0) $ , and$ (S=1, T=0) $ . The second term is the density-dependent central component, included to effectively represent N-body interactions. It involves a$ \delta(\vec{r}_1 - \vec{r}_2) $ spatial form and is the most general structure for such an exchange. When the parameter$ x_0 = 1 $ , this term acts only in the$ (S = 1, T = 0) $ channel. The third term accounts for the spin-orbit interaction and also includes a$ \delta(\vec{r}_1 - \vec{r}_2) $ dependence. This term contributes predominantly in the$ (S=1, T=1) $ channel, relevant to proton-proton and neutron-neutron interactions. The latter two terms bear resemblance to terms used in Skyrme-type interactions. -
The HFB approach, formulated using the Gogny D1S effective interaction, serves as a powerful and consistent framework to perform large-scale nuclear structure computations [33]. This technique has been extensively refined and employed in numerous studies, facilitating the detailed investigations of nuclear characteristics such as ground-state shapes, binding energies, and potential energy surfaces (PES). The Gogny–HFB model has been extensively discussed in several previous studies (see Refs. [33−36] and the references therein). Below, we outline the key aspects of the methodology and its evolution.
The Gogny effective NN interaction was originally formulated by Dechargé and Gogny in 1980 to address key features of nuclear matter, particularly saturation and pairing effects [37]. This interaction incorporates finite-range Gaussian components along with a density-dependent zero-range term, which enables the accurate modeling of a wide range of nuclei. The analytical form of the D1 Gogny interaction is expressed as [38]
$ \begin{aligned}[b]V_{12}(\rho)=\; & \sum\limits_{j=1}^2\left(W_j+B_jP_{\sigma}-H_jP_{\tau}-M_jP_{\sigma}P_{\tau}\right)\mathrm{e}^{-\frac{\left(\boldsymbol{r}_1-\boldsymbol{r}_2\right)^2}{\mu_j^2}} \\ & +t_3\left(1+x_0P_{\sigma}\right)\delta\left(\boldsymbol{r}_1-\boldsymbol{r}_2\right)\rho^{\alpha}\left(\frac{\boldsymbol{r}_1+\boldsymbol{r}_2}{2}\right) \\ & +\mathrm{i}W_{LS}\overleftarrow{\nabla}_{12}\delta\left(\boldsymbol{r}_1-\boldsymbol{r}_2\right)\wedge\boldsymbol{\nabla}_{12}\left(\boldsymbol{\sigma}_1+\boldsymbol{\sigma}_2\right),\end{aligned} $
(17) where
$ P_\sigma $ and$ P_\tau $ represent the spin and isospin exchange operators, respectively. The first term in Eq. (17) represents the finite-range central potential, independent of density, and enables a full spin-isospin exchange. This contributes to multiple channels:$ (S=0, T=1) $ ,$ (S=1, T=1) $ ,$ (S=0, T=0) $ , and$ (S=1, T=0) $ . The second term is the density-dependent central component included to effectively represent N-body interactions. It involves a$ \delta(\boldsymbol{r}_1 - \boldsymbol{r}_2) $ spatial form and is the most general structure for such an exchange. When the parameter$ x_0 = 1 $ , this term acts only in the$ (S = 1, T = 0) $ channel. The third term accounts for the spin-orbit interaction and includes a$ \delta(\boldsymbol{r}_1 - \boldsymbol{r}_2) $ dependence. This term contributes predominantly in the$ (S=1, T=1) $ channel, which is relevant to proton-proton and neutron-neutron interactions. The latter two terms bear resemblance to terms used in Skyrme-type interactions. -
This study presents a fully microscopic investigation of proton-decay half-lives in neutron-deficient nuclei using the HFB framework with the Gogny D1S effective interaction. To our knowledge, this is the first application of the Gogny-D1S HFB model to the context of proton radioactivity. The decay half-lives from both ground and isomeric states are calculated using a single-folding potential constructed from the M3Y-Paris NN interaction. The proton-daughter interaction incorporates deformed nuclear densities obtained self-consistently from the same HFB model. The predictive capability of this approach is assessed through a systematic comparison with recent experimental data and other theoretical models. This comprehensive methodology offers valuable insight into the interplay between nuclear structure and decay dynamics in proton-rich nuclei near the dripline.
Figure 1 presents the multipole components of the axially deformed neutron and proton density distributions in
$ ^{160} $ W ($ Z = 74 $ ,$ N = 86 $ ) calculated using the HFB method with the Gogny D1S effective interaction. The total intrinsic densities are expanded in terms of spherical harmonics$ Y_{\lambda_m 0} $ up to the eighth multipole, which permit the detailed examination of nuclear shape deformation. The first multipole ($ \lambda_m = 0 $ ) shown in Fig. 1(a) represents the spherical part of the density. It displays the expected saturation in the nuclear interior and gradual fall-off near the surface, with neutron density extending slightly further because of the neutron-rich nature of the nucleus. The second multipole component [Fig. 1(b)] captures the dominant deformation and reveals a clear prolate pattern in both proton and neutron densities. Although their radial shapes are similar, slight amplitude differences are noticeable at larger radii. This component is largely responsible for the global deformation of the nucleus. The fourth, sixth, and eighth multipole components [Figs. 1(c)–1(e)] exhibit increasingly oscillatory structures, reflecting finer details in the density distribution and surface geometry. The fourth multipole introduces surface modulations, whereas the sixth and eighth multipoles show more pronounced oscillations and radial sign changes, particularly in the surface region ($ r \sim 5 $ –10 fm). These higher-order multipoles, though smaller in magnitude, are essential for accurately reproducing the detailed shape and structure of the nucleus. Observed differences between the neutron and proton components at each multipole order underscore the presence of isovector deformation effects. These findings highlight the importance of including both isoscalar and isovector contributions when modeling deformed nuclei, particularly in the transitional regions of the nuclear chart such as tungsten isotopes.
Figure 1. (color online) Predictions of the deformed proton and neutron densities based on the Hartree-Fock-Bogoliubov model with the D1S Gogny interaction. The axial densities are expanded in terms of spherical harmonics
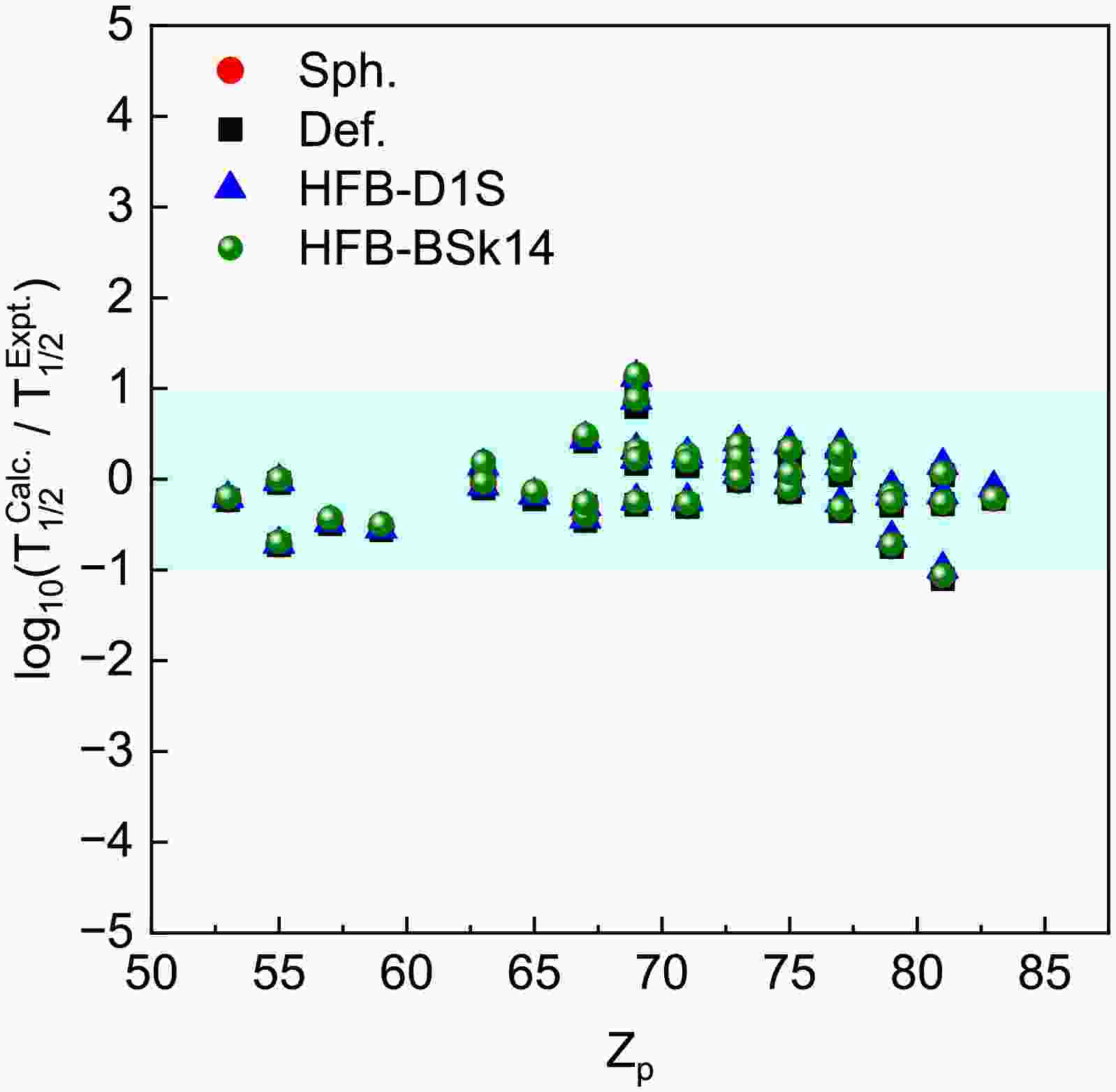
$ Y_{\lambda_m 0} $ up to$ \lambda_m = 8 $ for 160W ($ Z = 74 $ ,$ N = 86 $ ).Figure 2 presents the logarithmic deviation between the calculated and experimental proton-decay half-lives as a function of the parent nucleus atomic number
$ Z_p $ . Theoretical predictions are generated using four models: the double-folding model (DFM) with spherical (Sph.) and deformed (Def.) Fermi-type daughter density profiles, as well as the self-consistent densities from the HFB-D1S Gogny and HFB-BSk14 frameworks. The plotted variable$ \log_{10}(T_{1/2}^{\mathrm{Calc.}} / T_{1/2}^{\mathrm{Exp.}}) $ serves as a quantitative indicator of each model’s performance in reproducing the experimental half-lives. The majority of the calculated values lie within the shaded band bounded by$ \pm1 $ on the logarithmic scale, indicating agreement with experimental data within one order of magnitude. All models exhibit a good agreement with experimental data, confirming their overall reliability in describing proton radioactivity. Among them, the HFB-based approaches, particularly those employing the Gogny D1S and BSk14 interactions, exhibit a consistently good agreement with experimental observations across the full range of nuclei investigated. These microscopic models not only reproduce the global systematics of proton emission but also capture finer local variations, especially for heavier nuclei where deformation effects become significant. This similarity arises from the fact that effective interactions are carefully optimized to reproduce essential bulk nuclear properties such as binding energies, charge radii, saturation density, and pairing correlations. Although the Gogny D1S force employs a finite-range interaction while the Skyrme BSk14 force is based on a zero-range formulation, both frameworks provide a self-consistent treatment of the mean field and pairing effects, which leads to comparable nuclear density distributions and potential barriers in proton-decay calculations. Consequently, similar predictive behavior can be expected from other modern parametrizations within the Gogny and Skyrme families because they share comparable functional forms. This consistency supports the robustness of the microscopic HFB framework and confirms that the reliability of the calculated proton-decay half-lives is not limited to a specific choice of effective interaction. The accuracy of each model was quantified further by computing the standard deviation σ of the decimal logarithmic deviations using Eq. (18). We calculate the standard deviation σ given by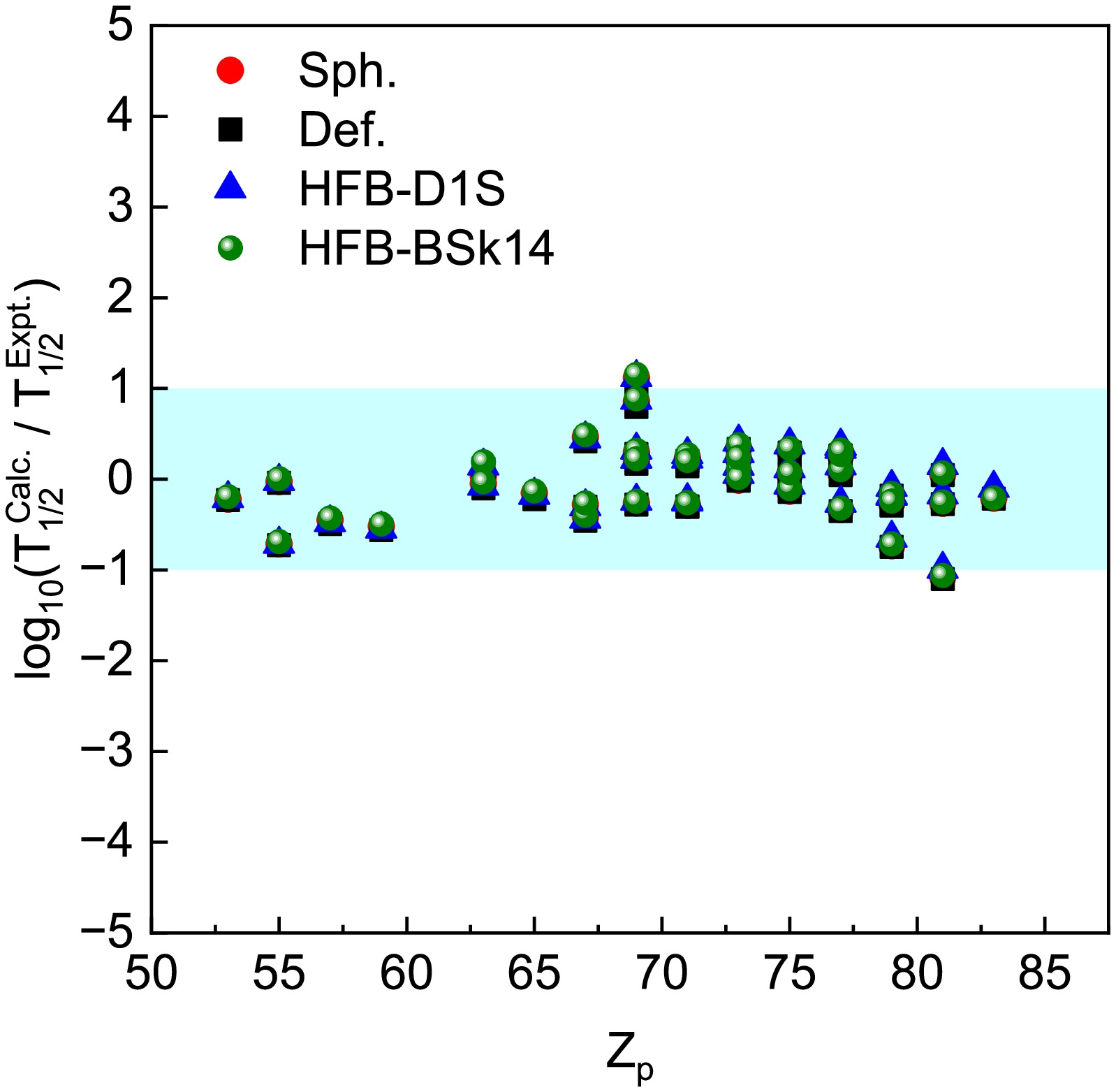
Figure 2. (color online) Deviation of the predicted proton-decay half-lives from the latest experimental values, calculated using the spherical, deformed, HFB-D1S Gogny, and HFB-BSk14 models plotted as a function of the atomic number
$ Z_p $ of parent nuclei.$ \sigma=\left[\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(\log_{10}T_{1/2}^{ \text{calc.}}-\log_{10}T_{1/2}^{ \text{expt.}}\right)^2\right]^{1/2}, $
(18) where
$ n=40 $ indicates the number of considered experimental nuclei and σ represents the root-mean-square (rms) deviation of the decimal logarithmic values. The statistical analysis shows that the HFB–D1S Gogny model provides the smallest standard deviation of$ \sigma = 0.4093 $ , which indicates the highest agreement with experimental data, closely followed by the deformed ($ \sigma = 0.4094 $ ) and spherical ($ \sigma = 0.4111 $ ) folding models. The HFB–BSk14 approach exhibits a slightly larger deviation ($ \sigma = 0.4130 $ ) but remains competitive within the same accuracy range. Overall, the results in Fig. 2 demonstrate the reliability of the HFB-based models in describing proton radioactivity. Although numerical differences among these models are small, they consistently demonstrate the reliability of the HFB-based frameworks in reproducing experimental half-lives, as shown in Fig. 2. The main advantage of the HFB–Gogny D1S model lies not in a large statistical improvement but in its microscopic and self-consistent treatment of nuclear densities, which provides a more physically grounded description of the proton emission process. The inclusion of realistic nuclear structure effects—particularly deformation—remains crucial for accurately modeling proton decay in neutron-deficient nuclei.Table 1 provides a comprehensive comparison between the experimental and theoretical proton-decay half-lives (
$\log_{10} T_{1/2}^p$ ) for a wide range of neutron-deficient nuclei. The parent nuclei are listed in the first column, with the superscript m denoting isomeric states. Subsequent columns include the experimental proton-decay energy$Q_p$ (MeV), deformation parameters of the daughter nucleus ($\beta_2$ ,$\beta_4$ , and$\beta_6$ ) adopted from the WS4 mass model [26], global quantum number G, orbital angular momentum$\ell_p$ of the emitted proton, and spectroscopic factor$S_p$ calculated using Eq. (15). The remaining columns present the theoretical half-lives obtained from various models alongside the experimental values. The spherical (Sph.) and deformed (Def.) models represent double-folding calculations employing the M3Y–Paris NN interaction with a zero-range exchange term.Parent $ Q_p $ $ \beta_2 $ $ \beta_4 $ $ \beta_6 $ G $ \ell_p $ $ S_p $ $ \log_{10}T_{1/2}^{p} $ Expt. Sph. Def. Gogny BSk14 IGM[39] RMF[40] RCHB[41] CDFT[42] $ ^{109} \text{I} $ 0.8200 0.1233 0.0161 −0.0028 4 2 0.405 −4.032 −4.252 −4.261 −4.242 −4.223 −3.558 −5.897 −4.442 − $ ^{112} \text{Cs} $ 0.8160 0.1524 0.0102 −0.0059 4 2 0.311 −3.310 −3.335 −3.349 −3.333 −3.304 −2.681 −3.555 −3.638 − $ ^{113} \text{Cs} $ 0.9728 0.1527 0.0066 −0.0053 4 2 0.306 −4.771 −5.482 −5.495 −5.485 −5.457 −4.836 −5.803 −5.759 − $ ^{117} \text{La} $ 0.8200 0.2459 0.0567 0.0044 4 2 0.089 −1.664 −2.113 −2.156 −2.141 −2.090 −1.991 −2.504 − − $ ^{121} \text{Pr} $ 0.8900 0.2521 0.0338 0.0020 4 2 0.082 −1.921 −2.438 −2.481 −2.468 −2.415 −2.456 − − − $ ^{130} \text{Eu} $ 1.5300 0.2846 0.0089 −0.0043 4 2 0.059 −3.000 −2.967 −2.884 −2.854 −2.807 −2.828 − − − $ ^{131} \text{Eu} $ 0.9470 0.2827 0.0037 −0.0035 4 2 0.060 −1.699 −1.745 −1.800 −1.774 −1.729 −1.800 −2.764 − − $ ^{135} \text{Tb} $ 1.1880 0.2769 −0.0152 −0.0035 4 3 0.067 −2.996 −3.147 −3.216 −3.171 −3.126 −3.408 − − − $ ^{140} \text{Ho} $ 1.0940 0.2278 −0.0175 −0.0019 4 3 0.127 −2.222 −1.755 −1.803 −1.775 −1.732 −1.702 −2.132 − − $ ^{141} \text{Ho} $ 1.1770 0.2148 −0.0162 −0.0015 4 3 0.150 −2.387 −2.803 −2.845 −2.827 −2.784 −2.747 −3.298 − − $ ^{141} \text{Ho}^m $ 1.2430 0.2148 −0.0162 −0.0015 4 0 0.150 −5.137 −5.415 −5.440 −5.439 −5.398 −5.115 −6.846 − − $ ^{144} \text{Tm} $ 1.7120 0.2061 −0.0291 −0.0017 5 5 0.168 −5.569 −4.449 −4.515 −4.446 −4.414 −5.263 − −5.315 − $ ^{145} \text{Tm} $ 1.7360 0.1995 −0.0318 0.0000 5 5 0.181 −5.499 −4.642 −4.703 −4.626 −4.611 −5.467 −4.698 −5.513 − $ ^{146} \text{Tm} $ 0.8960 0.1876 −0.0298 0.0002 5 0 0.214 −0.810 −0.510 −0.532 −0.487 −0.489 −0.854 1.945 −0.887 −1.003 $ ^{147} \text{Tm} $ 1.0590 −0.1596 −0.0203 0.0013 5 5 1.311 0.587 0.792 0.757 0.810 0.813 0.752 2.775 0.784 0.645 $ ^{147} \text{Tm}^m $ 1.1270 −0.1596 −0.0203 0.0013 5 2 1.311 −3.444 −3.706 −3.723 −3.684 −3.687 −3.181 −3.546 −3.203 −3.350 $ ^{150} \text{Lu} $ 1.2696 −0.1562 −0.0237 0.0016 5 5 1.162 −1.347 −1.111 −1.146 −1.074 −1.074 −1.186 0.360 −1.053 −1.169 $ ^{150} \text{Lu}^m $ 1.2718 −0.1562 −0.0237 0.0016 5 2 1.162 −4.398 −4.684 −4.702 −4.648 −4.654 −4.454 −5.038 −4.447 −4.553 $ ^{151} \text{Lu} $ 1.2410 −0.1465 −0.0184 0.0023 5 5 0.957 −0.896 −0.722 −0.752 −0.672 −0.690 −0.877 0.694 −0.754 −0.869 $ ^{151} \text{Lu}^m $ 1.3190 −0.1465 −0.0184 0.0023 5 2 0.957 −4.796 −5.081 −5.096 −5.031 −5.054 −4.561 −5.227 −4.744 −4.824 $ ^{155} \text{Ta} $ 1.4530 0.0620 0.0000 −0.0019 5 5 1.222 −2.495 −2.417 −2.423 −2.351 −2.374 −2.427 −4.238 −2.280 −2.367 $ ^{156} \text{Ta} $ 1.0200 0.0742 0.0060 −0.0018 5 2 0.931 −0.826 −0.836 −0.841 −0.773 −0.807 −0.654 −0.800 −3.470 −0.607 $ ^{156} \text{Ta}^m $ 1.1220 0.0742 0.0060 −0.0018 5 5 0.931 0.933 1.277 1.267 1.343 1.315 1.205 3.035 1.404 1.269 $ ^{157} \text{Ta} $ 0.9350 0.0874 0.0101 −0.0008 5 0 0.783 −0.527 −0.302 −0.308 −0.243 −0.284 −0.145 −0.982 0.048 −0.420 $ ^{160} \text{Re} $ 1.2670 0.0990 0.0010 −0.0014 5 2 0.744 −3.163 −3.294 −3.303 −3.225 −3.266 −3.786 −3.602 −3.041 −3.128 $ ^{161} \text{Re} $ 1.1970 0.1084 0.0005 −0.0028 5 0 0.653 −3.357 −3.304 −3.312 −3.239 −3.285 −3.223 −4.089 −3.073 −3.481 $ ^{161} \text{Re}^m $ 1.3208 0.1084 0.0005 −0.0028 5 5 0.653 −0.678 −0.363 −0.384 −0.298 −0.336 −0.712 0.710 −0.434 −0.539 $ ^{165} \text{Ir}^m $ 1.7210 0.1246 0.0036 0.0020 5 5 0.593 −3.433 −3.359 −3.387 −3.283 −3.327 −3.626 −2.914 −3.260 −3.310 $ ^{166} \text{Ir} $ 1.1520 0.1336 0.0015 0.0007 5 2 0.519 −0.824 −1.158 −1.175 −1.088 −1.141 −1.198 −1.545 −0.976 −1.102 $ ^{166} \text{Ir}^m $ 1.3240 0.1336 0.0015 0.0007 5 5 0.519 −0.076 0.221 0.188 0.291 0.246 −0.318 1.183 0.233 0.143 $ ^{167} \text{Ir} $ 1.0700 0.1390 −0.0006 −0.0001 5 0 0.485 −1.120 −0.858 −0.873 −0.788 −0.848 −0.967 −1.798 −0.919 −1.367 $ ^{167} \text{Ir}^m $ 1.2453 0.1390 −0.0006 −0.0001 5 5 0.485 0.842 1.138 1.102 1.203 1.154 0.611 2.176 1.103 1.009 $ ^{170} \text{Au} $ 1.4720 0.1168 0.0035 −0.0019 5 2 0.649 −3.487 −4.219 −4.232 −4.134 −4.199 −4.074 − −3.771 −3.842 $ ^{170} \text{Au}^m $ 1.7570 0.1168 0.0035 −0.0019 5 5 0.649 −2.971 −3.231 −3.257 −3.147 −3.203 −3.499 − −2.824 −2.842 $ ^{171} \text{Au} $ 1.4480 0.1187 −0.0012 −0.0021 5 0 0.628 −4.652 −4.823 −4.834 −4.739 −4.808 −4.669 −5.641 −4.582 −4.987 $ ^{171} \text{Au}^m $ 1.7070 0.1187 −0.0012 −0.0021 5 5 0.628 −2.587 −2.850 −2.876 −2.772 −2.827 −3.025 −2.344 −2.456 −2.472 $ ^{176} \text{Tl} $ 1.2650 −0.0866 −0.0121 0.0004 5 0 0.930 −2.208 −2.474 −2.480 −2.379 −2.458 −2.194 − −2.059 −2.509 $ ^{177} \text{Tl} $ 1.1560 −0.1166 −0.0007 −0.0006 5 0 1.018 −1.176 −1.118 −1.129 −1.023 −1.107 −0.901 −1.925 −0.787 −1.252 $ ^{177} \text{Tl}^m $ 1.9630 −0.1166 −0.0007 −0.0006 5 5 1.018 −3.346 −4.423 −4.446 −4.336 −4.405 −4.431 −4.178 −3.420 −3.304 $ ^{185} \text{Bi} $ 1.5300 −0.0580 0.0117 −0.0014 5 0 0.456 −4.191 −4.401 −4.404 −4.289 −4.397 −4.011 −6.179 −5.237 − Table 1. Comparison between experimental and theoretical proton-decay half-lives (
$\log_{10} T_{1/2}^p$ ) for a wide range of neutron-deficient nuclei. Parent nuclei (with “m” denoting isomers); proton-decay energy$Q_p$ (MeV); deformation parameters of daughter nuclei$\beta_2$ ,$\beta_4$ , and$\beta_6$ ; global quantum number G; orbital angular momentum$\ell_p$ ; and spectroscopic factor$S_p$ (calculated using Eq. (15)) are listed. Calculations are performed using the spherical and deformed folding models with the M3Y–Paris interaction, and the microscopic HFB–Gogny D1S and HFB–BSk14 frameworks. For comparison, results from the improved Gamow model (IGM) [39], relativistic mean field (RMF) model [40], relativistic continuum Hartree–Bogoliubov (RCHB) approach [41], and covariant density functional theory (CDFT) framework [42] are included alongside the experimental data.The spherical model uses a two-parameter Fermi density for the daughter nucleus, while the deformed model incorporates the deformation parameters (
$\beta_2$ ,$\beta_4$ ,$\beta_6$ ) to consider shape effects on the potential barrier. The HFB–D1S Gogny and HFB–BSk14 frameworks provide fully microscopic predictions, where nuclear densities are obtained self-consistently within the HFB method using the Gogny D1S and Skyrme BSk14 effective interactions, respectively. For comparison, additional theoretical results from the improved Gamow model (IGM) [39], relativistic mean field (RMF) model [40], relativistic continuum Hartree–Bogoliubov (RCHB) approach [41], and covariant density functional theory (CDFT) framework [42] are also included. The results show that incorporating deformation leads to noticeably improved agreement with experimental data, particularly for mid- and heavy-mass nuclei where deformation significantly affects the potential barrier and penetrability. Among microscopic approaches, the HFB–Gogny D1S and HFB–BSk14 models yield results comparable to, and in some cases slightly better than, those obtained from phenomenological folding models. Although differences in the standard deviation values among the models are relatively small, HFB-based frameworks exhibit consistent reliability and a strong physical foundation. Their primary advantage lies in the microscopic and self-consistent treatment of nuclear densities and pairing correlations rather than that in a substantial numerical reduction of the deviation. Moreover, the majority of the calculated values differ from experiment by less than one logarithmic unit, which confirms the overall accuracy and reliability of the microscopic folding potential approach. Overall, the results highlight that proton-decay half-lives are highly sensitive to the underlying nuclear density distributions, deformation parameters, and shell structure of both the parent and daughter nuclei.The concept of a universal decay curve, originally developed for α- and cluster decays, can be examined in the context of proton radioactivity. This approach involves plotting the decimal logarithm of the experimental half-life time
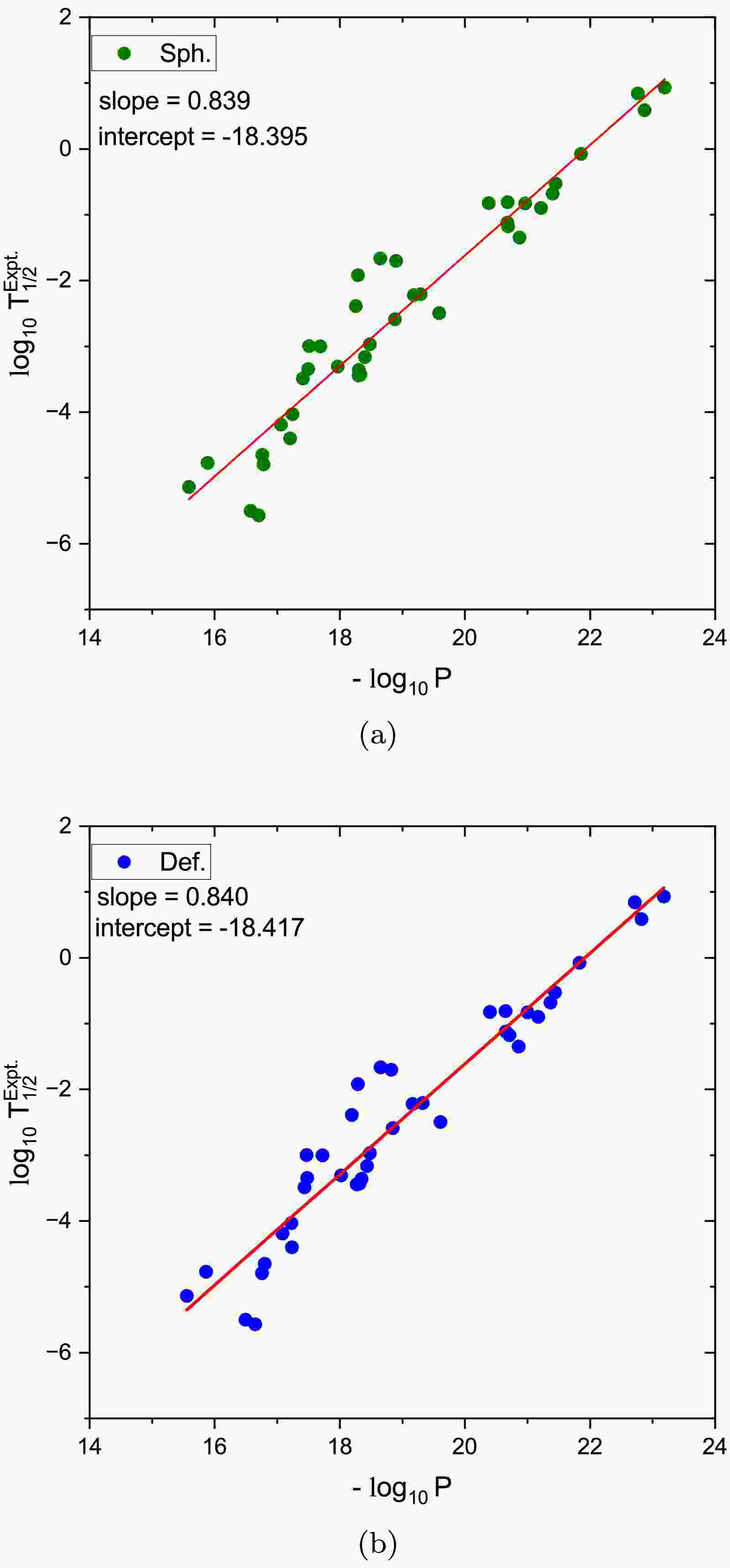
$ \log_{10} T_{1/2}^{\text{expt.}} $ against the negative decimal logarithm of the theoretical barrier penetrability$ -\log_{10} P $ . Figure 3 illustrates such correlations for proton emitters using penetrability values computed via the WKB approximation with a nuclear interaction potential derived from the M3Y-Paris NN force, including a zero-range exchange component. Figure 3(a) shows results using spherical two-parameter Fermi densities for the daughter nuclei (Sph.), while panel (b) incorporates nuclear deformation effects through deformation parameters$ (\beta_2, \beta_4, \beta_6) $ (Def.). In both cases, a clear linear trend is observed, confirming the expected exponential dependence of the half-life on penetration probability. The fitted lines yield nearly identical slopes (0.839 for Sph. and 0.840 for Def.) and similar intercepts, indicating the consistency of the model regardless of the inclusion of deformation. The tight correlation supports the validity of the WKB-based formalism in describing proton decay and confirms the reliability of the M3Y-Paris-based double-folding approach to model the nuclear interaction potential. The linear behavior of these plots provides strong evidence for the applicability of the universal decay curve concept to proton radioactivity. Moreover, the slight improvement observed with the inclusion of deformation suggests that shape effects contribute modestly to fine-tuning theoretical predictions. Overall, the results reinforce the predictive power of the current formalism and its potential usefulness in identifying new proton emitters yet to be observed experimentally.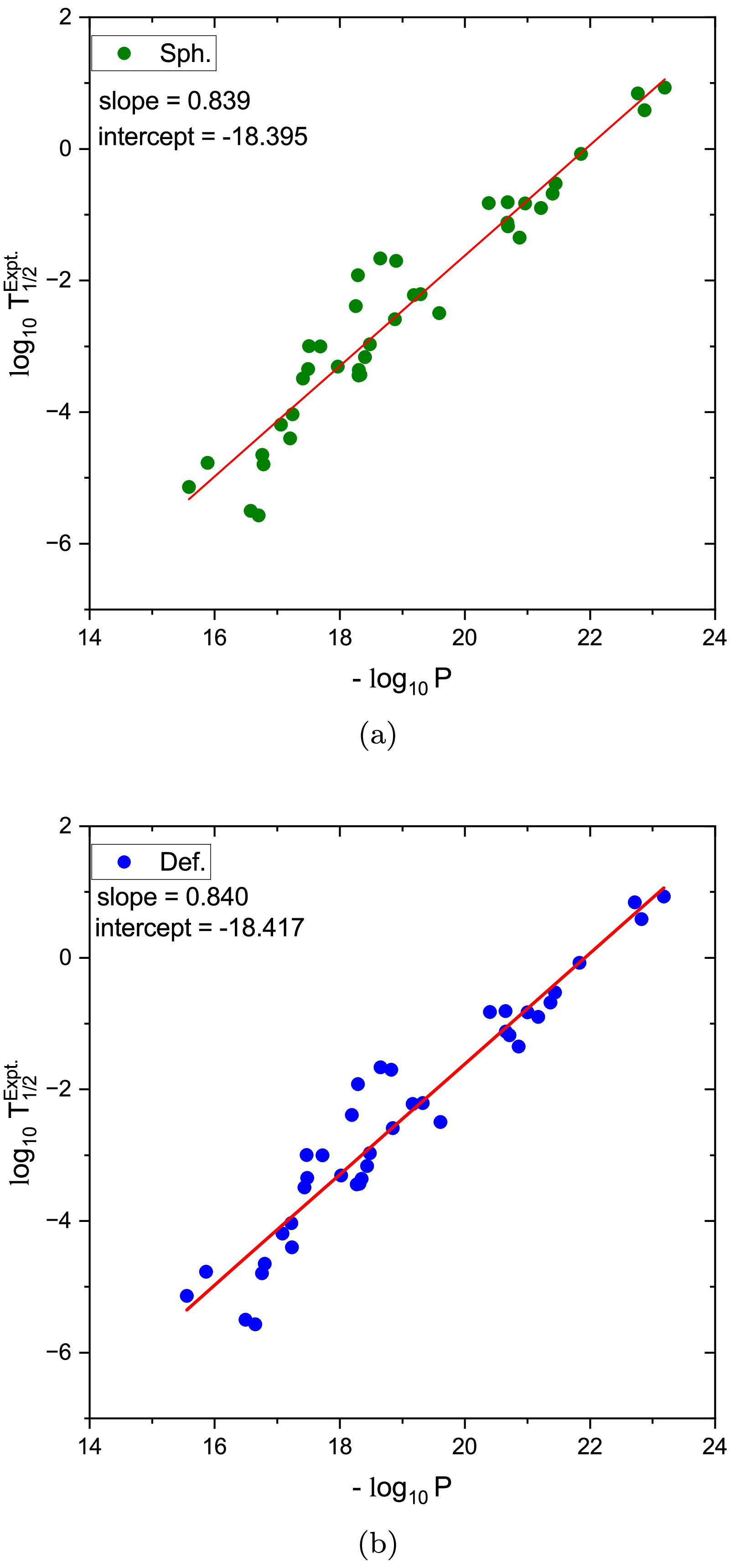
Figure 3. (color online) Universal curve based on the WKB penetration probability using the M3Y-Paris NN interaction supplemented with a zero range exchange contribution. The decimal logarithm of the experimental half-life times are plotted versus the
$ - \log_{10} P $ for proton decay listed in Table 1. (a) Spherical and (b) deformed. The slope and intercept of the fitted solid line for each case are shown in the corresponding figure.Following the establishment of a universal linear trend between decay half-lives and penetration probabilities, further efforts have been made to develop generalized formulations that can describe a broader class of radioactive decay processes. One such advancement is the universal decay law (UDL) proposed by Qi et al. [43, 44], which has proven effective in modeling the ground-state to ground-state transitions across various cluster emissions, including proton radioactivity. The UDL provides a simple yet physically meaningful linear relationship that incorporates key variables governing the decay process, including the effects of the Coulomb and centrifugal barriers. For proton radioactivity, the logarithmic half-life can be analytically expressed as
$ \log_{10} T_{1/2} = a\,\chi^{\prime} + b\,\rho^{\prime} + d\,\frac{\ell(\ell+1)}{\rho^{\prime}} + c, $
(19) where
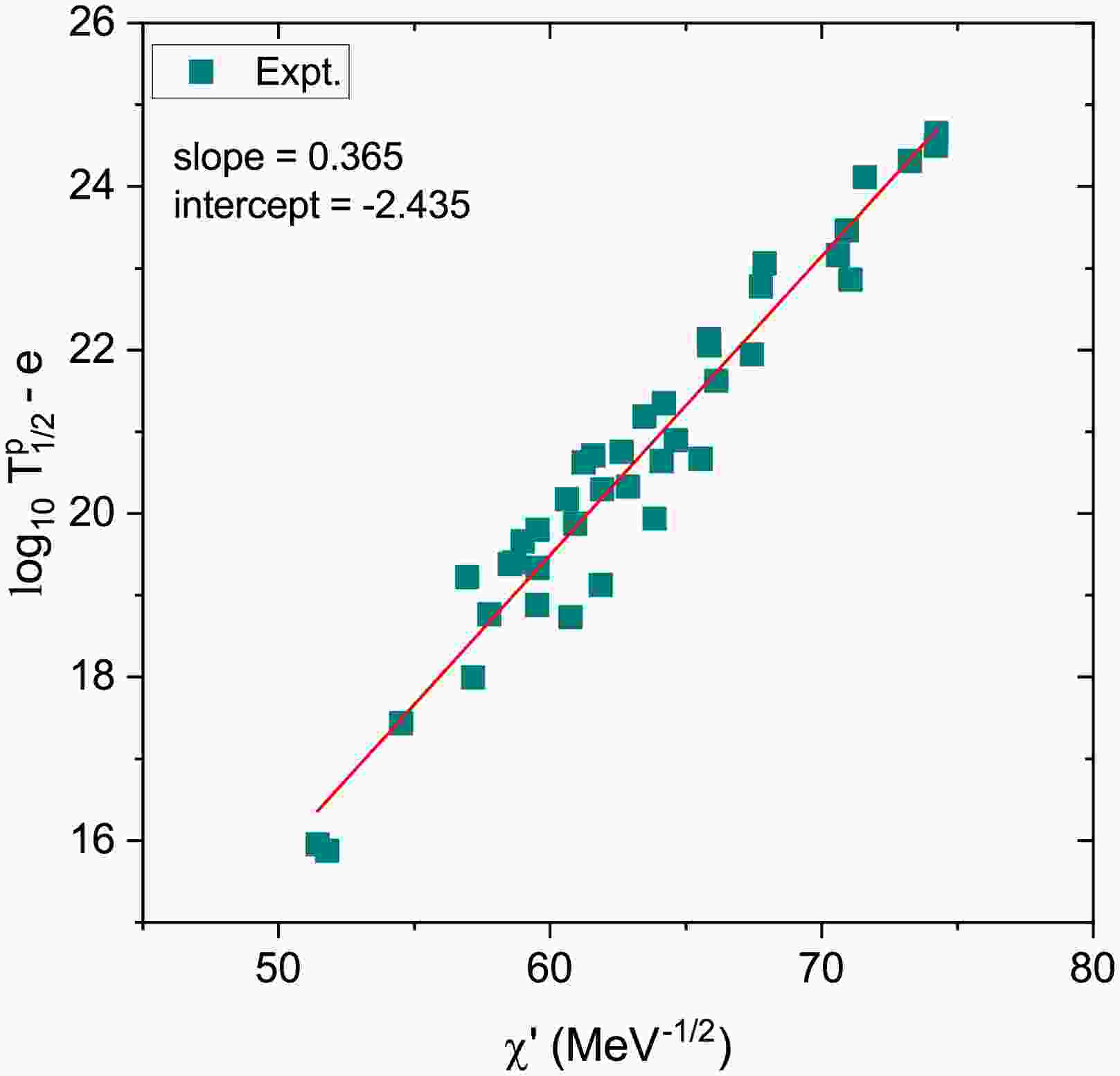
$ \chi^{\prime} = A^{1/2} Z_d Q_p^{-1/2} $ ,$ \rho^{\prime} = \sqrt{A Z_d (A_d^{1/3} + 1)} $ , and$ A = A_d / (A_d + 1) $ . The constants a, b, c, and d are determined by fitting to either experimental half-life data or calculated values from various theoretical approaches.Figure 4 presents the correlation between
$ \log_{10} T_{1/2} - e $ and$ \chi^{\prime} $ , where the term$ e = b\,\rho^{\prime} + d\,\ell(\ell+1)/\rho^{\prime} + c $ accounts for contributions beyond the leading dependence on$ \chi^{\prime} $ . A clear linear trend is observed, validating the form of Eq. (19) for proton decay. When fitting the expression to experimental data, the resulting coefficients are found to be$ a = 0.328420 $ ,$ b = -0.316392 $ ,$ c = -18.4231 $ , and$ d = $ 13.0002. These values yield the fitted line shown in the figure with a slope of 0.365 and an intercept of -2.435. The strong correlation further supports the relevance and predictive power of the UDL framework in the study of proton emission processes.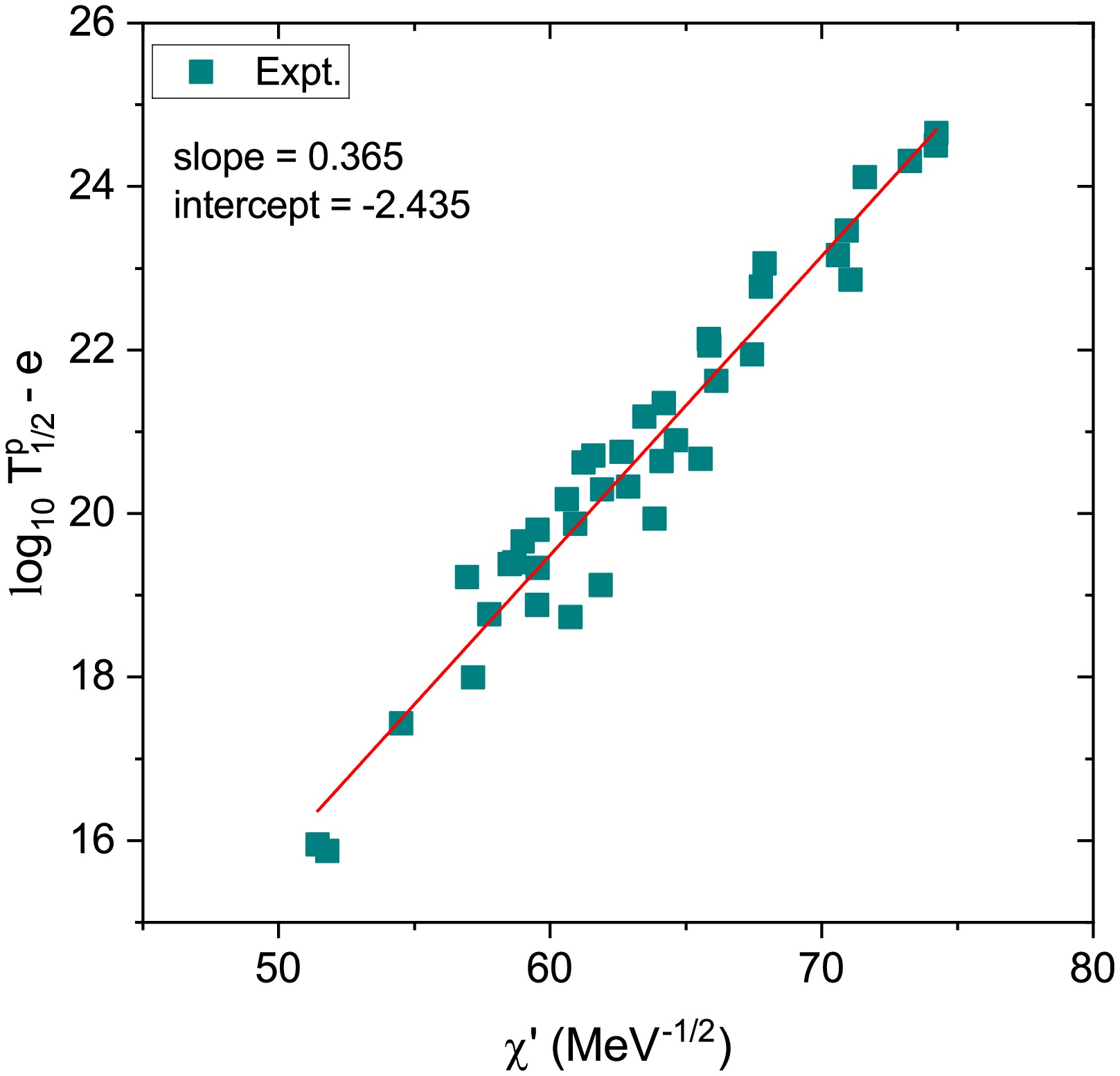
Figure 4. (color online) Universal decay law (UDL) plot for proton emission illustrating the relationship between the quantity
$ \log T_{1/2}^p - e $ and$ \chi^{\prime} $ , where$ e = b \rho^{\prime} + d \ell(\ell+1)/\rho^{\prime} + c $ . The data points represent experimentally measured half-lives.In addition to the universal curve and UDL, which successfully correlate decay half-lives with theoretical penetrability and structural parameters, further attempts have been made to refine classical empirical relations for specific decay modes. One such classical relation is the Geiger–Nuttall (GN) law, originally formulated for α-decay, which expresses a linear dependence between the logarithm of the half-life and inverse square root of the decay energy. To extend this framework to proton radioactivity, a modified version of the GN law was proposed by Chen et al. [45], incorporating angular momentum and daughter nuclear charge effects. It is expressed as
$ \log_{10}T_{1/2} = A \left(Z_d^{0.8} + \ell_p \right) Q_p^{-1/2} + B, $
(20) where
$ Z_d $ denotes the atomic number of the daughter nucleus,$ \ell_p $ represents the orbital angular momentum carried by the emitted proton, and$ Q_p $ is the proton decay energy. Constants A and B are fitted parameters.Figure 5 displays the modified GN plots for all proton emitters under consideration using four different theoretical frameworks. Each subplot corresponds to a specific model used for the single-folding potential or the daughter nuclear density: (a) Spherical folding potential using a Fermi distribution (Sph.), (b) folded potential incorporating deformation effects (Def.), (c) microscopic HFB calculation with the Gogny D1S interaction, and (d) HFB approach using the Skyrme BSk14 force. The x-axis in all panels represents
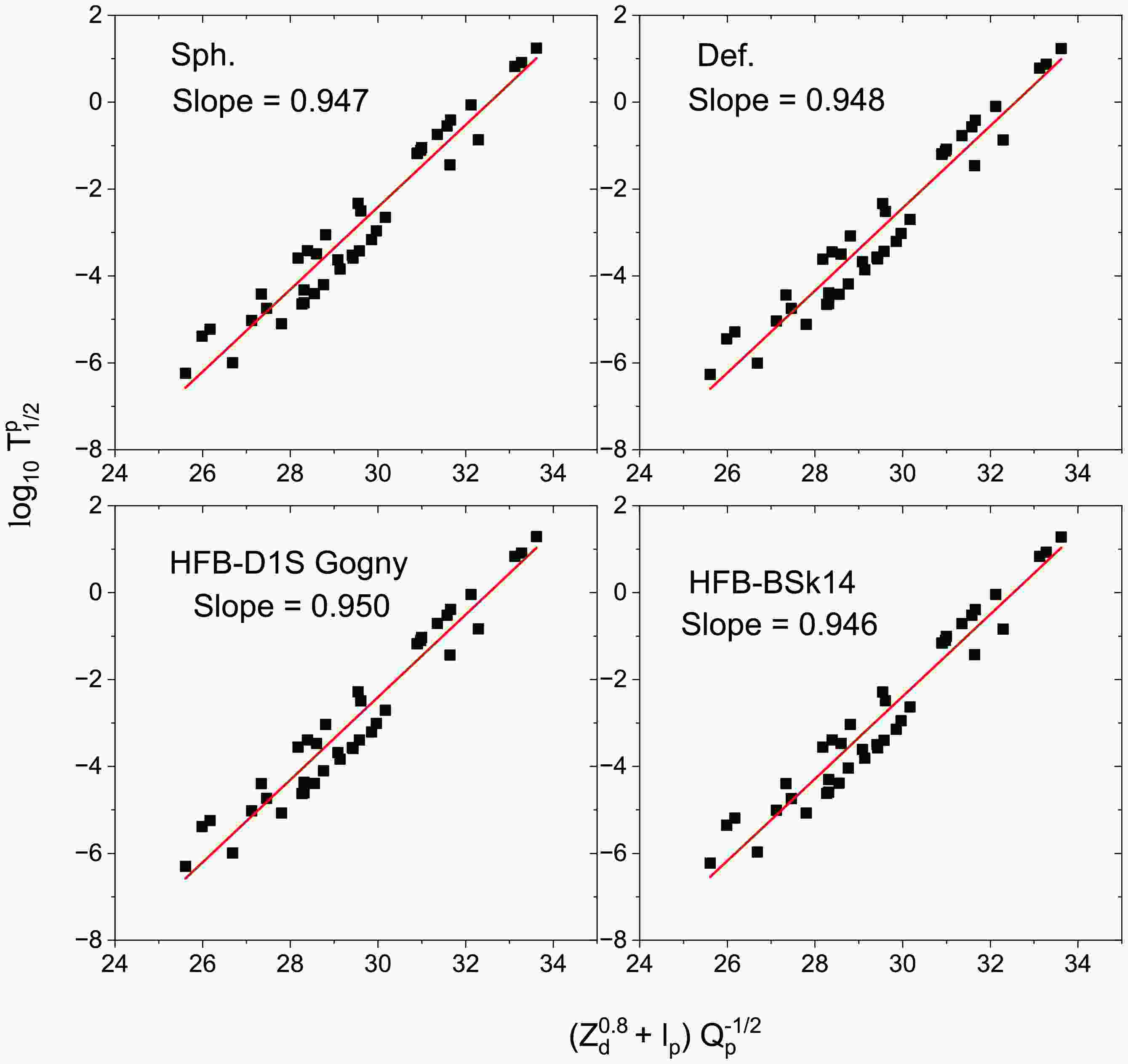
$ (Z_d^{0.8} + \ell_p) Q_p^{-1/2} $ , while the y-axis shows the decimal logarithm of the computed proton-decay half-life$ \log_{10} T_{1/2}^p $ . In all four cases, a clear linear trend is observed, confirming the validity of the GN-type correlation for proton radioactivity. The fitted straight lines are plotted in red, and the slope values are annotated in each subplot. The obtained slopes range narrowly around 0.946–0.950, indicating that the linear dependence is largely independent of the nuclear model employed. This consistent behavior reinforces the robustness of the modified GN law in describing proton radioactivity across different theoretical approaches. The linearity observed supports the predictive strength of the models and suggests that such GN-type plots can serve as a reliable diagnostic tool to assess theoretical predictions and identify new candidate proton emitters. These findings demonstrate that the essential physics of the decay process is well captured by the effective potential barrier and decay energy dependence, regardless of the microscopic origin of input density.The consistency of the modified GN correlations obtained for all models highlights the robustness and predictive capability of the present microscopic approach. Having verified that the theoretical framework accurately reproduces both global systematics and local decay properties, it is natural to extend its application to unexplored regions of the nuclear chart. The current model has been employed to predict proton-decay half-lives for nuclei that are energetically allowed but have not yet been experimentally observed. The results of these predictions are summarized in Table 2, which includes both ground and isomeric states of potential proton emitters near the proton dripline. The calculations performed using the spherical, deformed, HFB–Gogny D1S, and HFB–BSk14 models incorporate the deformation-dependent spectroscopic factor from Eq. (15) to consider nuclear structure effects. The overall consistency among four models demonstrates the reliability of the present approach and provides a theoretical basis for future experimental searches for new proton-emitting nuclei.
Parent $ Q_p $ G $ \ell_p $ $ S_p $ $ \log_{10}T_{1/2}^{p} $ Sph. Def. Gogny BSk14 $ ^{111} {\rm{Cs}}$ 1.740 4 2 0.303 −11.364 −11.377 −11.353 −11.325 $ ^{116} {\rm{La}}$ 1.591 4 2 0.102 −9.621 −9.635 −9.636 −9.591 $ ^{127} {\rm{Pm}}$ 0.792 4 2 0.060 0.043 −0.010 0.008 0.055 $ ^{159} {\rm{Re}}$ 1.606 5 0 0.828 −7.333 −7.339 −7.259 −7.301 $ ^{162} {\rm{Re}}$ 0.760 5 2 0.542 5.034 5.019 5.093 5.048 $ ^{165} {\rm{Ir}}$ 1.547 5 0 0.593 −6.208 −6.219 −6.133 −6.187 $ ^{169} {\rm{Ir}}^{m} $ 0.782 5 5 0.437 8.891 8.851 8.945 8.892 $ ^{169} {\rm{Au}}$ 1.947 5 0 0.669 −8.628 −8.637 −8.538 −8.603 $ ^{172} {\rm{Au}}$ 0.877 5 2 0.644 3.907 3.893 3.985 3.917 $ ^{184} {\rm{Bi}}$ 1.330 5 0 0.437 −2.332 −2.333 −2.221 −2.324 $ ^{185} {\rm{Bi}}$ 1.541 5 5 0.456 −0.425 −0.431 −0.333 −0.418 Table 2. Predicted proton-decay half-lives (
$\log_{10} T_{1/2}^p$ ) for possible or unobserved proton emitters near the proton dripline. The parent nuclei (''m'' denotes first isomeric state), proton-decay energy$Q_p$ (MeV) adopted from Ref. [32], global quantum number G, orbital angular momentum$\ell_p$ , and spectroscopic factor$S_p$ (from Eq. (15)) are listed. Half-lives are calculated using the spherical, deformed, HFB–Gogny D1S, and HFB–BSk14 models. -
This study presents a fully microscopic investigation of proton-decay half-lives in neutron-deficient nuclei using the Hartree-Fock-Bogoliubov (HFB) framework with the Gogny D1S effective interaction. To our knowledge, this is the first application of the Gogny-D1S HFB model to the context of proton radioactivity. The decay half-lives from both ground and isomeric states are calculated using a single-folding potential constructed from the M3Y-Paris nucleon-nucleon interaction. Importantly, the proton-daughter interaction incorporates deformed nuclear densities obtained self-consistently from the same HFB model. The predictive capability of this approach is assessed through a systematic comparison with recent experimental data and other theoretical models. This comprehensive methodology offers valuable insight into the interplay between nuclear structure and decay dynamics in proton-rich nuclei near the dripline.
Figure 1 presents the multipole components of the axially deformed neutron and proton density distributions in
$ ^{160} $ W ($ Z = 74 $ ,$ N = 86 $ ), calculated using the Hartree-Fock-Bogoliubov (HFB) method with the Gogny D1S effective interaction. The total intrinsic densities are expanded in terms of spherical harmonics$ Y_{\lambda_m 0} $ up to the eighth multipole, allowing for the detailed examination of nuclear shape deformation. The first multipole ($ \lambda_m = 0 $ ), shown in Fig. 1(a), represents the spherical part of the density. It displays the expected saturation in the nuclear interior and a gradual fall-off near the surface, with the neutron density extending slightly further due to the neutron-rich nature of the nucleus. The second multipole component (Fig. 1(b)) captures the dominant deformation and reveals a clear prolate pattern in both proton and neutron densities. While their radial shapes are similar, slight amplitude differences are noticeable at larger radii. This component is largely responsible for the global deformation of the nucleus. The fourth, sixth, and eighth multipole components [Figs. 1(c)–1(e)] exhibit increasingly oscillatory structures, reflecting finer details in the density distribution and surface geometry. The fourth multipole introduces surface modulations, whereas the sixth and eighth multipoles show more pronounced oscillations and radial sign changes, particularly in the surface region ($ r \sim 5 $ –10 fm). These higher-order multipoles, though smaller in magnitude, are essential for accurately reproducing the detailed shape and structure of the nucleus. The observed differences between the neutron and proton components at each multipole order underscore the presence of isovector deformation effects. These findings highlight the importance of including both isoscalar and isovector contributions when modeling deformed nuclei, particularly in transitional regions of the nuclear chart such as tungsten isotopes.
Figure 1. (color online) Predictions of the deformed proton and neutron densities based on the Hartree-Fock-Bogoliubov model with the D1S Gogny interaction. The axial densities are expanded in terms of spherical harmonics
$ Y_{\lambda_m 0} $ up to$ \lambda_m = 8 $ for 160W ($ Z = 74 $ ,$ N = 86 $ ).Figure 2 presents the logarithmic deviation between the calculated and experimental proton-decay half-lives as a function of the parent nucleus atomic number
$ Z_p $ . The theoretical predictions are generated using four models: the double-folding model (DFM) with spherical (Sph.) and deformed (Def.) Fermi-type daughter density profiles, as well as self-consistent densities from the HFB-D1S Gogny and HFB-BSk14 frameworks. The plotted variable,$ \log_{10}(T_{1/2}^{\mathrm{Calc.}} / T_{1/2}^{\mathrm{Exp.}}) $ , serves as a quantitative indicator of each model’s performance in reproducing the experimental half-lives. The majority of the calculated values lie within the shaded band bounded by$ \pm1 $ on the logarithmic scale, indicating agreement with experimental data within one order of magnitude. All models exhibit a good agreement with the experimental data, confirming their overall reliability in describing proton radioactivity. Among them, the HFB-based approaches—particularly those employing the Gogny D1S and BSk14 interactions exhibit a consistently good agreement with experimental observations across the full range of nuclei investigated. These microscopic models not only reproduce the global systematics of proton emission but also capture finer local variations, especially for heavier nuclei where deformation effects become significant. This similarity arises from the fact that both effective interactions are carefully optimized to reproduce essential bulk nuclear properties such as binding energies, charge radii, saturation density, and pairing correlations. Although the Gogny D1S force employs a finite-range interaction while the Skyrme BSk14 force is based on a zero-range formulation, both frameworks provide a self-consistent treatment of the mean field and pairing effects, leading to comparable nuclear density distributions and potential barriers in proton-decay calculations. Consequently, similar predictive behavior can be expected from other modern parametrizations within the Gogny and Skyrme families, as they share comparable functional forms. This consistency supports the robustness of the microscopic HFB framework and confirms that the reliability of the calculated proton-decay half-lives is not limited to a specific choice of effective interaction. To further quantify the accuracy of each model, the standard deviation σ of the decimal logarithmic deviations was computed using Eq. (18). We calculate the standard deviation σ given by:
Figure 2. (color online) Deviation of the predicted proton-decay half-lives from the latest experimental values, calculated using the Spherical, Deformed, HFB-D1S Gogny, and HFB-BSk14 models, plotted as a function of the atomic number
$ Z_p $ of the parent nuclei.$ \sigma=\left[\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(\log_{10}T_{1/2}^{ \text{calc.}}-\log_{10}T_{1/2}^{ \text{expt.}}\right)^2\right]^{1/2}, $

(18) where
$ n=40 $ is the number of considered experimental nuclei and σ represents the root-mean-square (rms) deviation of the decimal logarithmic values. The statistical analysis shows that the HFB–D1S Gogny model provides the smallest standard deviation of$ \sigma = 0.4093 $ , indicating the highest agreement with experimental data, closely followed by the Deformed ($ \sigma = 0.4094 $ ) and Spherical ($ \sigma = 0.4111 $ ) folding models. The HFB–BSk14 approach exhibits a slightly larger deviation ($ \sigma = 0.4130 $ ) but remains competitive within the same accuracy range. Overall, the results in Fig. 2 demonstrate the reliability of the HFB-based models in describing proton radioactivity. Although the numerical differences among these models are small, they consistently demonstrate the reliability of the HFB-based frameworks in reproducing experimental half-lives, as shown in Fig. 2. The main advantage of the HFB–Gogny D1S model lies not in a large statistical improvement but in its microscopic and self-consistent treatment of nuclear densities, which provides a more physically grounded description of the proton emission process. The inclusion of realistic nuclear structure effects—particularly deformation—remains crucial for accurately modeling proton decay in neutron-deficient nuclei.Table 1 provides a comprehensive comparison between the experimental and theoretical proton-decay half-lives (
$\log_{10} T_{1/2}^p$ ) for a wide range of neutron-deficient nuclei. The parent nuclei are listed in the first column, with the superscript m denoting isomeric states. The subsequent columns include the experimental proton-decay energy$Q_p$ (MeV), the deformation parameters of the daughter nucleus ($\beta_2$ ,$\beta_4$ , and$\beta_6$ ) adopted from the WS4 mass model [26], the global quantum number G, the orbital angular momentum$\ell_p$ of the emitted proton, and the spectroscopic factor$S_p$ calculated using Eq. (15). The remaining columns present the theoretical half-lives obtained from various models alongside the experimental values. The Spherical (Sph.) and Deformed (Def.) models represent double-folding calculations employing the M3Y–Paris nucleon–nucleon interaction with a zero-range exchange term.Parent $ Q_p $ 

$ \beta_2 $ 

$ \beta_4 $ 

$ \beta_6 $ 

G $ \ell_p $ 

$ S_p $ 

$ \log_{10}T_{1/2}^{p} $ 

Expt. Sph. Def. Gogny BSk14 IGM[39] RMF[40] RCHB[41] CDFT[42] $ ^{109} \text{I} $ 

0.8200 0.1233 0.0161 −0.0028 4 2 0.405 −4.032 −4.252 −4.261 −4.242 −4.223 −3.558 −5.897 −4.442 − $ ^{112} \text{Cs} $ 

0.8160 0.1524 0.0102 −0.0059 4 2 0.311 −3.310 −3.335 −3.349 −3.333 −3.304 −2.681 −3.555 −3.638 − $ ^{113} \text{Cs} $ 

0.9728 0.1527 0.0066 −0.0053 4 2 0.306 −4.771 −5.482 −5.495 −5.485 −5.457 −4.836 −5.803 −5.759 − $ ^{117} \text{La} $ 

0.8200 0.2459 0.0567 0.0044 4 2 0.089 −1.664 −2.113 −2.156 −2.141 −2.090 −1.991 −2.504 − − $ ^{121} \text{Pr} $ 

0.8900 0.2521 0.0338 0.0020 4 2 0.082 −1.921 −2.438 −2.481 −2.468 −2.415 −2.456 − − − $ ^{130} \text{Eu} $ 

1.5300 0.2846 0.0089 −0.0043 4 2 0.059 −3.000 −2.967 −2.884 −2.854 −2.807 −2.828 − − − $ ^{131} \text{Eu} $ 

0.9470 0.2827 0.0037 −0.0035 4 2 0.060 −1.699 −1.745 −1.800 −1.774 −1.729 −1.800 −2.764 − − $ ^{135} \text{Tb} $ 

1.1880 0.2769 −0.0152 −0.0035 4 3 0.067 −2.996 −3.147 −3.216 −3.171 −3.126 −3.408 − − − $ ^{140} \text{Ho} $ 

1.0940 0.2278 −0.0175 −0.0019 4 3 0.127 −2.222 −1.755 −1.803 −1.775 −1.732 −1.702 −2.132 − − $ ^{141} \text{Ho} $ 

1.1770 0.2148 −0.0162 −0.0015 4 3 0.150 −2.387 −2.803 −2.845 −2.827 −2.784 −2.747 −3.298 − − $ ^{141} \text{Ho}^m $ 

1.2430 0.2148 −0.0162 −0.0015 4 0 0.150 −5.137 −5.415 −5.440 −5.439 −5.398 −5.115 −6.846 − − $ ^{144} \text{Tm} $ 

1.7120 0.2061 −0.0291 −0.0017 5 5 0.168 −5.569 −4.449 −4.515 −4.446 −4.414 −5.263 − −5.315 − $ ^{145} \text{Tm} $ 

1.7360 0.1995 −0.0318 0.0000 5 5 0.181 −5.499 −4.642 −4.703 −4.626 −4.611 −5.467 −4.698 −5.513 − $ ^{146} \text{Tm} $ 

0.8960 0.1876 −0.0298 0.0002 5 0 0.214 −0.810 −0.510 −0.532 −0.487 −0.489 −0.854 1.945 −0.887 −1.003 $ ^{147} \text{Tm} $ 

1.0590 −0.1596 −0.0203 0.0013 5 5 1.311 0.587 0.792 0.757 0.810 0.813 0.752 2.775 0.784 0.645 $ ^{147} \text{Tm}^m $ 

1.1270 −0.1596 −0.0203 0.0013 5 2 1.311 −3.444 −3.706 −3.723 −3.684 −3.687 −3.181 −3.546 −3.203 −3.350 $ ^{150} \text{Lu} $ 

1.2696 −0.1562 −0.0237 0.0016 5 5 1.162 −1.347 −1.111 −1.146 −1.074 −1.074 −1.186 0.360 −1.053 −1.169 $ ^{150} \text{Lu}^m $ 

1.2718 −0.1562 −0.0237 0.0016 5 2 1.162 −4.398 −4.684 −4.702 −4.648 −4.654 −4.454 −5.038 −4.447 −4.553 $ ^{151} \text{Lu} $ 

1.2410 −0.1465 −0.0184 0.0023 5 5 0.957 −0.896 −0.722 −0.752 −0.672 −0.690 −0.877 0.694 −0.754 −0.869 $ ^{151} \text{Lu}^m $ 

1.3190 −0.1465 −0.0184 0.0023 5 2 0.957 −4.796 −5.081 −5.096 −5.031 −5.054 −4.561 −5.227 −4.744 −4.824 $ ^{155} \text{Ta} $ 

1.4530 0.0620 0.0000 −0.0019 5 5 1.222 −2.495 −2.417 −2.423 −2.351 −2.374 −2.427 −4.238 −2.280 −2.367 $ ^{156} \text{Ta} $ 

1.0200 0.0742 0.0060 −0.0018 5 2 0.931 −0.826 −0.836 −0.841 −0.773 −0.807 −0.654 −0.800 −3.470 −0.607 $ ^{156} \text{Ta}^m $ 

1.1220 0.0742 0.0060 −0.0018 5 5 0.931 0.933 1.277 1.267 1.343 1.315 1.205 3.035 1.404 1.269 $ ^{157} \text{Ta} $ 

0.9350 0.0874 0.0101 −0.0008 5 0 0.783 −0.527 −0.302 −0.308 −0.243 −0.284 −0.145 −0.982 0.048 −0.420 $ ^{160} \text{Re} $ 

1.2670 0.0990 0.0010 −0.0014 5 2 0.744 −3.163 −3.294 −3.303 −3.225 −3.266 −3.786 −3.602 −3.041 −3.128 $ ^{161} \text{Re} $ 

1.1970 0.1084 0.0005 −0.0028 5 0 0.653 −3.357 −3.304 −3.312 −3.239 −3.285 −3.223 −4.089 −3.073 −3.481 $ ^{161} \text{Re}^m $ 

1.3208 0.1084 0.0005 −0.0028 5 5 0.653 −0.678 −0.363 −0.384 −0.298 −0.336 −0.712 0.710 −0.434 −0.539 $ ^{165} \text{Ir}^m $ 

1.7210 0.1246 0.0036 0.0020 5 5 0.593 −3.433 −3.359 −3.387 −3.283 −3.327 −3.626 −2.914 −3.260 −3.310 $ ^{166} \text{Ir} $ 

1.1520 0.1336 0.0015 0.0007 5 2 0.519 −0.824 −1.158 −1.175 −1.088 −1.141 −1.198 −1.545 −0.976 −1.102 $ ^{166} \text{Ir}^m $ 

1.3240 0.1336 0.0015 0.0007 5 5 0.519 −0.076 0.221 0.188 0.291 0.246 −0.318 1.183 0.233 0.143 $ ^{167} \text{Ir} $ 

1.0700 0.1390 −0.0006 −0.0001 5 0 0.485 −1.120 −0.858 −0.873 −0.788 −0.848 −0.967 −1.798 −0.919 −1.367 $ ^{167} \text{Ir}^m $ 

1.2453 0.1390 −0.0006 −0.0001 5 5 0.485 0.842 1.138 1.102 1.203 1.154 0.611 2.176 1.103 1.009 $ ^{170} \text{Au} $ 

1.4720 0.1168 0.0035 −0.0019 5 2 0.649 −3.487 −4.219 −4.232 −4.134 −4.199 −4.074 − −3.771 −3.842 $ ^{170} \text{Au}^m $ 

1.7570 0.1168 0.0035 −0.0019 5 5 0.649 −2.971 −3.231 −3.257 −3.147 −3.203 −3.499 − −2.824 −2.842 $ ^{171} \text{Au} $ 

1.4480 0.1187 −0.0012 −0.0021 5 0 0.628 −4.652 −4.823 −4.834 −4.739 −4.808 −4.669 −5.641 −4.582 −4.987 $ ^{171} \text{Au}^m $ 

1.7070 0.1187 −0.0012 −0.0021 5 5 0.628 −2.587 −2.850 −2.876 −2.772 −2.827 −3.025 −2.344 −2.456 −2.472 $ ^{176} \text{Tl} $ 

1.2650 −0.0866 −0.0121 0.0004 5 0 0.930 −2.208 −2.474 −2.480 −2.379 −2.458 −2.194 − −2.059 −2.509 $ ^{177} \text{Tl} $ 

1.1560 −0.1166 −0.0007 −0.0006 5 0 1.018 −1.176 −1.118 −1.129 −1.023 −1.107 −0.901 −1.925 −0.787 −1.252 $ ^{177} \text{Tl}^m $ 

1.9630 −0.1166 −0.0007 −0.0006 5 5 1.018 −3.346 −4.423 −4.446 −4.336 −4.405 −4.431 −4.178 −3.420 −3.304 $ ^{185} \text{Bi} $ 

1.5300 −0.0580 0.0117 −0.0014 5 0 0.456 −4.191 −4.401 −4.404 −4.289 −4.397 −4.011 −6.179 −5.237 − Table 1. Comparison between experimental and theoretical proton-decay half-lives (
$\log_{10} T_{1/2}^p$ ) for a wide range of neutron-deficient nuclei. Listed are the parent nuclei (with “m” denoting isomers), proton-decay energy$Q_p$ (MeV), deformation parameters of daughter nuclei$\beta_2$ ,$\beta_4$ , and$\beta_6$ , global quantum number G, orbital angular momentum$\ell_p$ , and spectroscopic factor$S_p$ (calculated using Eq. (15)). Calculations are performed using the Spherical and Deformed folding models with the M3Y–Paris interaction, and the microscopic HFB–Gogny D1S and HFB–BSk14 frameworks. For comparison, results from the Improved Gamow Model (IGM) [39], Relativistic Mean Field (RMF) model [40], Relativistic Continuum Hartree–Bogoliubov (RCHB) approach [41], and Covariant Density Functional Theory (CDFT) framework [42] are included alongside the experimental data.The Spherical model uses a two-parameter Fermi density for the daughter nucleus, while the Deformed model incorporates the deformation parameters (
$\beta_2$ ,$\beta_4$ ,$\beta_6$ ) to account for shape effects on the potential barrier. The HFB–D1S Gogny and HFB–BSk14 frameworks provide fully microscopic predictions, where the nuclear densities are obtained self-consistently within the Hartree–Fock–Bogoliubov (HFB) method using the Gogny D1S and Skyrme BSk14 effective interactions, respectively. For comparison, additional theoretical results from the Improved Gamow Model (IGM) [39], the Relativistic Mean Field (RMF) model [40], the Relativistic Continuum Hartree–Bogoliubov (RCHB) approach [41], and the Covariant Density Functional Theory (CDFT) framework [42] are also included. The results show that incorporating deformation leads to noticeably improved agreement with experimental data, particularly for mid- and heavy-mass nuclei where deformation significantly affects the potential barrier and penetrability. Among the microscopic approaches, the HFB–Gogny D1S and HFB–BSk14 models yield results that are comparable to, and in some cases slightly better than, those obtained from the phenomenological folding models. Although the differences in the standard deviation values among the models are relatively small, the HFB-based frameworks exhibit consistent reliability and a strong physical foundation. Their primary advantage lies in the microscopic and self-consistent treatment of nuclear densities and pairing correlations rather than in a substantial numerical reduction of the deviation. Moreover, the majority of the calculated values differ from experiment by less than one logarithmic unit, confirming the overall accuracy and reliability of the microscopic folding potential approach. Overall, the results highlight that proton-decay half-lives are highly sensitive to the underlying nuclear density distributions, deformation parameters, and shell structure of both the parent and daughter nuclei.The concept of a universal decay curve, originally developed for α- and cluster decays, can also be examined in the context of proton radioactivity. This approach involves plotting the decimal logarithm of the experimental half-life time,
$ \log_{10} T_{1/2}^{\text{expt.}} $ , against the negative decimal logarithm of the theoretical barrier penetrability,$ -\log_{10} P $ . Figure 3 illustrates such correlations for proton emitters, using penetrability values computed via the WKB approximation with a nuclear interaction potential derived from the M3Y-Paris nucleon-nucleon force, including a zero-range exchange component. Figure 3(a) shows results using spherical two-parameter Fermi densities for the daughter nuclei (Sph.), while panel (b) incorporates nuclear deformation effects through deformation parameters$ (\beta_2, \beta_4, \beta_6) $ (Def.). In both cases, a clear linear trend is observed, confirming the expected exponential dependence of the half-life on the penetration probability. The fitted lines yield nearly identical slopes (0.839 for Sph. and 0.840 for Def.) and similar intercepts, indicating the consistency of the model regardless of the inclusion of deformation. The tight correlation supports the validity of the WKB-based formalism in describing proton decay and confirms the reliability of the M3Y-Paris-based double-folding approach for modeling the nuclear interaction potential. The linear behavior of these plots provides strong evidence for the applicability of the universal decay curve concept to proton radioactivity. Moreover, the slight improvement observed with the inclusion of deformation suggests that shape effects contribute modestly to fine-tuning theoretical predictions. Overall, the results reinforce the predictive power of the current formalism and its potential usefulness in identifying new proton emitters yet to be experimentally observed.
Figure 3. (color online) A universal curve based on the WKB penetration probability using the M3Y-Paris NN interaction supplemented with a zero range exchange contribution. The decimal logarithm of the experimental half-life times are plotted versus the
$ - \log_{10} P $ for proton decay listed in Table 1.(a) Spherical and (b) Deformed. The slope and intercept of the fitted solid line for each case are shown in the corresponding figure.Following the establishment of a universal linear trend between decay half-lives and penetration probabilities, further efforts have been made to develop generalized formulations that can describe a broader class of radioactive decay processes. One such advancement is the Universal Decay Law (UDL), proposed by Qi et al. [43, 44], which has proven effective in modeling ground-state to ground-state transitions across various cluster emissions, including proton radioactivity. The UDL provides a simple yet physically meaningful linear relationship that incorporates key variables governing the decay process, including the effects of the Coulomb and centrifugal barriers. For proton radioactivity, the logarithmic half-life can be expressed analytically as:
$ \log_{10} T_{1/2} = a\,\chi^{\prime} + b\,\rho^{\prime} + d\,\frac{\ell(\ell+1)}{\rho^{\prime}} + c, $

(19) where
$ \chi^{\prime} = A^{1/2} Z_d Q_p^{-1/2} $ ,$ \rho^{\prime} = \sqrt{A Z_d (A_d^{1/3} + 1)} $ , and$ A = A_d / (A_d + 1) $ . The constants a, b, c, and d are determined by fitting to either experimental half-life data or calculated values from various theoretical approaches.Figure 4 presents the correlation between
$ \log_{10} T_{1/2} - e $ and$ \chi^{\prime} $ , where the term$ e = b\,\rho^{\prime} + d\,\ell(\ell+1)/\rho^{\prime} + c $ accounts for contributions beyond the leading dependence on$ \chi^{\prime} $ . A clear linear trend is observed, validating the form of Eq. (19) for proton decay. When fitting the expression to the experimental data, the resulting coefficients are found to be$ a = 0.328420 $ ,$ b = -0.316392 $ ,$ c = -18.4231 $ , and$ d = 13.0002 $ . These values yield the fitted line shown in the figure with a slope of 0.365 and an intercept of -2.435. The strong correlation further supports the relevance and predictive power of the UDL framework in the study of proton emission processes.
Figure 4. (color online) Universal Decay Law (UDL) plot for proton emission, showing the relationship between the quantity
$ \log T_{1/2}^p - e $ and$ \chi^{\prime} $ , where$ e = b \rho^{\prime} + d \ell(\ell+1)/\rho^{\prime} + c $ . The data points represent experimentally measured half-lives.In addition to the universal curve and the Universal Decay Law (UDL), which successfully correlate decay half-lives with theoretical penetrability and structural parameters, further attempts have been made to refine classical empirical relations for specific decay modes. One such classical relation is the Geiger–Nuttall (GN) law, originally formulated for α-decay, which expresses a linear dependence between the logarithm of the half-life and the inverse square root of the decay energy. To extend this framework to proton radioactivity, a modified version of the GN law was proposed by Chen et al. [45], incorporating angular momentum and daughter nuclear charge effects, and is expressed as:
$ \log_{10}T_{1/2} = A \left(Z_d^{0.8} + \ell_p \right) Q_p^{-1/2} + B, $

(20) where
$ Z_d $ is the atomic number of the daughter nucleus,$ \ell_p $ is the orbital angular momentum carried by the emitted proton, and$ Q_p $ is the proton decay energy. The constants A and B are fitted parameters.Figure 5 displays the modified Geiger–Nuttall plots for all proton emitters under consideration, using four different theoretical frameworks. Each subplot corresponds to a specific model used for the single-folding potential or the daughter nuclear density: (a) spherical folding potential using a Fermi distribution (Sph.), (b) folded potential incorporating deformation effects (Def.), (c) microscopic HFB calculation with the Gogny D1S interaction, and (d) HFB approach using the Skyrme BSk14 force. The x-axis in all panels represents
$ (Z_d^{0.8} + \ell_p) Q_p^{-1/2} $ , while the y-axis shows the decimal logarithm of the computed proton-decay half-life,$ \log_{10} T_{1/2}^p $ . In all four cases, a clear linear trend is observed, confirming the validity of the GN-type correlation for proton radioactivity. The fitted straight lines are plotted in red, and the slope values are annotated in each subplot. The obtained slopes range narrowly around 0.946–0.950, indicating that the linear dependence is largely independent of the nuclear model employed. This consistent behavior reinforces the robustness of the modified GN law in describing proton radioactivity across different theoretical approaches. The linearity observed supports the predictive strength of the models and suggests that such Geiger–Nuttall-type plots can serve as a reliable diagnostic tool for assessing theoretical predictions and identifying new candidate proton emitters. These findings also demonstrate that the essential physics of the decay process is well captured by the effective potential barrier and the decay energy dependence, regardless of the microscopic origin of the input density.The consistency of the modified Geiger–Nuttall correlations obtained for all models highlights the robustness and predictive capability of the present microscopic approach. Having verified that the theoretical framework accurately reproduces both global systematics and local decay properties, it is natural to extend its application to unexplored regions of the nuclear chart. In this regard, the current model has been employed to predict proton-decay half-lives for nuclei that are energetically allowed but have not yet been experimentally observed. The results of these predictions are summarized in Table 2, which includes both ground and isomeric states of potential proton emitters near the proton dripline. The calculations, performed using the Spherical, Deformed, HFB–Gogny D1S, and HFB–BSk14 models, incorporate the deformation-dependent spectroscopic factor from Eq. (15) to account for nuclear structure effects. The overall consistency among the four models demonstrates the reliability of the present approach and provides a theoretical basis for future experimental searches for new proton-emitting nuclei.
Parent $ Q_p $ 

G $ \ell_p $ 

$ S_p $ 

$ \log_{10}T_{1/2}^{p} $ 

Sph. Def. Gogny BSk14 $ ^{111} {\rm{Cs}}$ 

1.740 4 2 0.303 −11.364 −11.377 −11.353 −11.325 $ ^{116} {\rm{La}}$ 

1.591 4 2 0.102 −9.621 −9.635 −9.636 −9.591 $ ^{127} {\rm{Pm}}$ 

0.792 4 2 0.060 0.043 −0.010 0.008 0.055 $ ^{159} {\rm{Re}}$ 

1.606 5 0 0.828 −7.333 −7.339 −7.259 −7.301 $ ^{162} {\rm{Re}}$ 

0.760 5 2 0.542 5.034 5.019 5.093 5.048 $ ^{165} {\rm{Ir}}$ 

1.547 5 0 0.593 −6.208 −6.219 −6.133 −6.187 $ ^{169} {\rm{Ir}}^{m} $ 

0.782 5 5 0.437 8.891 8.851 8.945 8.892 $ ^{169} {\rm{Au}}$ 

1.947 5 0 0.669 −8.628 −8.637 −8.538 −8.603 $ ^{172} {\rm{Au}}$ 

0.877 5 2 0.644 3.907 3.893 3.985 3.917 $ ^{184} {\rm{Bi}}$ 

1.330 5 0 0.437 −2.332 −2.333 −2.221 −2.324 $ ^{185} {\rm{Bi}}$ 

1.541 5 5 0.456 −0.425 −0.431 −0.333 −0.418 Table 2. Predicted proton-decay half-lives (
$\log_{10} T_{1/2}^p$ ) for possible or unobserved proton emitters near the proton dripline. Listed are the parent nuclei (“m” denotes first isomeric state), proton-decay energy$Q_p$ (MeV) adopted from Ref. [32], global quantum number G, orbital angular momentum$\ell_p$ , and spectroscopic factor$S_p$ (from Eq. (15)). Half-lives are calculated using the Spherical, Deformed, HFB–Gogny D1S, and HFB–BSk14 models. -
In this study, we presented a comprehensive microscopic study of proton radioactivity in neutron-deficient nuclei using several theoretical approaches. The proton decay half-lives were calculated by employing a single-folding potential derived from the M3Y-Paris NN interaction, both with and without nuclear deformation effects. In addition, daughter nuclear densities were obtained self-consistently using the HFB method with the Gogny D1S and Skyrme BSk14 effective interactions. Our analysis included a systematic comparison of the theoretical predictions with experimental half-lives. The results demonstrate that incorporating nuclear deformation and employing microscopic HFB densities improves the agreement with experimental data. Among the models tested, the HFB-D1S approach consistently yields more accurate half-life estimates across a wide range of proton emitters.
Further, we explored universal trends in proton radioactivity by constructing a universal decay curve and evaluating the applicability of the UDL. A clear linear correlation between the logarithmic half-lives and decay penetrability was established, supporting the robustness of the models used. Furthermore, the modified GN law was successfully applied to proton decay, reinforcing its empirical reliability when extended to charged-particle emission processes beyond α decay. The accuracy and consistency of our theoretical framework suggested that it can serve as a reliable tool for predicting proton decay half-lives in unknown or unmeasured nuclei. These predictions can be valuable in guiding future experimental investigations near the proton dripline and enhancing our understanding of nuclear structure and decay in exotic systems.
-
In this work, we have presented a comprehensive microscopic study of proton radioactivity in neutron-deficient nuclei using several theoretical approaches. The proton decay half-lives were calculated by employing a single-folding potential derived from the M3Y-Paris nucleon-nucleon interaction, both with and without nuclear deformation effects. Additionally, daughter nuclear densities were obtained self-consistently using the Hartree-Fock-Bogoliubov (HFB) method with the Gogny D1S and Skyrme BSk14 effective interactions. Our analysis included a systematic comparison of the theoretical predictions with experimental half-lives. The results demonstrate that incorporating nuclear deformation and employing microscopic HFB densities improves the agreement with experimental data. Among the models tested, the HFB-D1S approach consistently yields more accurate half-life estimates across a wide range of proton emitters.
We also explored universal trends in proton radioactivity by constructing a universal decay curve and evaluating the applicability of the Universal Decay Law (UDL). A clear linear correlation between the logarithmic half-lives and decay penetrability was established, supporting the robustness of the models used. Furthermore, the modified Geiger–Nuttall (GN) law was successfully applied to proton decay, reinforcing its empirical reliability when extended to charged-particle emission processes beyond α decay. The accuracy and consistency of our theoretical framework suggest that it can serve as a reliable tool for predicting proton decay half-lives in unknown or unmeasured nuclei. These predictions can be valuable in guiding future experimental investigations near the proton dripline and in enhancing our understanding of nuclear structure and decay in exotic systems.
Microscopic modeling of proton radioactivity through Hartree-Fock- Bogolyubov calculations with Gogny interaction
- Received Date: 2025-07-22
- Available Online: 2026-03-15
Abstract: In this study, we perform a microscopic study of proton decay half-lives in neutron-deficient nuclei using the Hartree-Fock-Bogolyubov (HFB) approach with the Gogny D1S effective interaction. Proton emission half-lives from ground and isomeric states are computed by employing a single-folding potential constructed from a realistic M3Y-Paris nucleon-nucleon interaction. Deformed density distributions of daughter nuclei are calculated self-consistently within the same HFB framework. The resulting decay half-lives are systematically compared with recent experimental measurements and other theoretical models for evaluating the accuracy and predictive capacity of this fully microscopic methodology in describing proton radioactivity near the proton dripline.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF











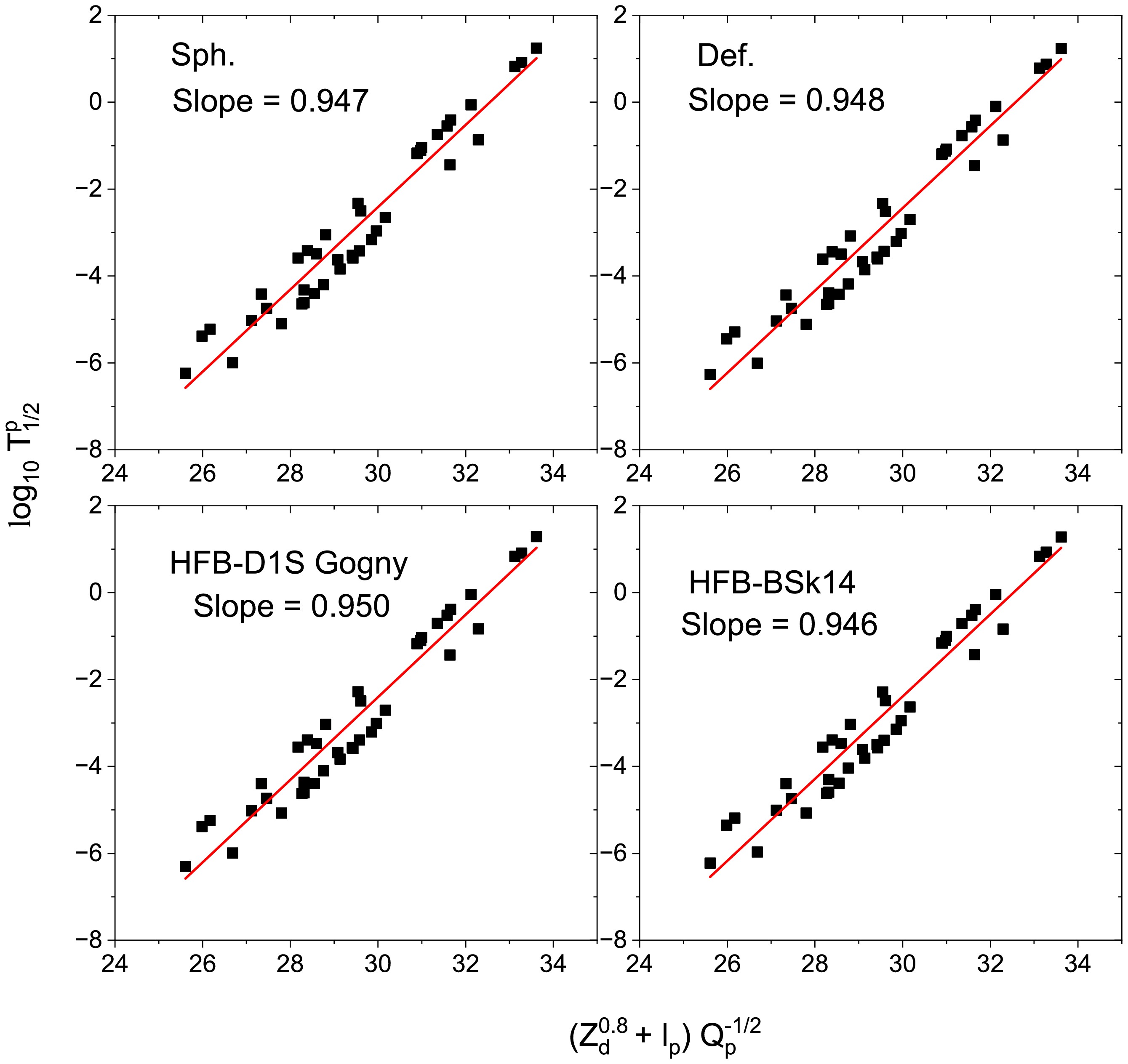



 DownLoad:
DownLoad: