Nuclear matter properties from chiral-scale effective theory including a dilatonic scalar meson

Study on nuclear matter (NM) has long been crucial for understanding both nuclear force and neutron star (NS) mass-radius (M-R) relations (see, e.g., Refs. [1−7] and references therein). The properties of NM are highly sensitive to details of nucleon interactions. A popular and widely used approach to describe these interactions is the one-boson-exchange (OBE) model and its variants, such as the Walecka-type models [8−11]. These models typically involve π, σ, ω and ρ meson exchanges, covering the effective range of nucleon forces from $0.5\ {\rm{fm}}$ to $2\ {\rm{fm}}$. Utilizing these models, NM properties can be calculated using the relativistic mean field (RMF) approach [12−15], which is the most practical and economical framework to introduce density effects.

It is recognized that Walecka-type models lack the consideration of QCD symmetry patterns, the valid region of effective operators, and theoretical errors. While Chiral effective field theory (χEFT), thanks to the pioneering works by Weinberg [16, 17], offers a powerful framework for studying nuclear forces at long ranges, anchored on QCD symmetry by treating the pion as the Nambu-Goldstone (NG) boson of spontaneous chiral symmetry breaking. Due to the derivative couplings [18, 19], operators can be organized systematically according to the chiral expansion by $q/\Lambda$, where q is the momentum scale carried by the NG bosons and $\Lambda = 4\pi f_\pi\sim 1{\rm{GeV}}$ being the scale of chiral symmetry breaking. The valid region and theoretical errors of χEFT can be determined by estimating the truncation of the chiral expansion [20−22].

To develop a realistic model of nuclear forces, it is accepted that vector mesons—ρ and ω— and isoscalar-scalar meson σ are indispensable. However, the original (χ EFT), which only contains NG modes, will encounter divergence due to the emergence of σ, ρ and ω mesons [23, 24]. To avoid this and extend the valid region of effective operators, hidden local symmetry (HLS) in χEFT [25−27] plays a crucial role to include the vector mesons. But the inclusion of the σ meson as an independent degree of freedom in χEFT is not straightforward, since the fourth scalar component of the chiral four-vector is integrated out when transitioning from the linear sigma model to the nonlinear sigma model—the leading term of χEFT. Considering that the lowest-lying scalar meson σ has a mass roughly equivalent to that of the kaon, which is a NG boson of chiral symmetry breaking in three-flavor χEFT ($\chi\rm EFT_3$), by supposing that QCD has a nonperturbative infrared fixed point, Crewther and Tunstall [28, 29] proposed that the lowest-lying scalar meson can be considered as the NG boson (dilaton) of the spontaneous breaking of scale symmetry. Consequently, χEFT is extended to include the scalar meson, resulting in the scale-chiral effective theory ($\chi \rm EFT_{\sigma}$). This approach is different from the Walecka-type models where these hadron resonances and the corresponding interactions are added by the necessity of the phenomenological analysis, without considering the symmetry argument and power counting.

Based on the terminologies of $\chi \rm EFT_{\sigma}$ and HLS, the $\chi \rm EFT$ with baryons is constructed in Refs. [30, 31] at the leading chiral order to discuss nucleon interactions. It is denoted as bsHLS, with 'b' for baryon and 's' for scale. In bsHLS, the potential from meson exchanges in OBE models can be reproduced by expanding bsHLS to the first order of linear field couplings but with additional symmetry considerations. By using the low-momentum potential $ V_{\rm{low k}} $ renormalization group approach [32, 33], taking the ''leading order scale symmetry (LOSS)” approximation where the trace anomaly effect enters only through the dilaton potential, which breaks scale symmetry explicitly and spontaneously, we found that the chiral-scale EFT with few parameters can successfully describe not only NM at the saturation density but also the compact-star matter at $ n=(5-7)n_0 $ [6]. A novel phenomena, which was not realized before, is that in nuclear matter at densities $ n=(2-4)n_0 $ the sound velocity of NM may saturate the conformal limit $ v_s^2 =1/3 $, but the trace of the energy-momentum tensor does not vanish, that is, the NM exhibits a pseudo-conformal structure [34−36]. And the corrections to LOSS in the baryonic part have been found crucial for understanding the quenched $ g_A $ value in the super-allowed Gamow-Teller transitions of heavy nuclei [37, 38].

In this work, we study NM properties using bsHLS with the RMF method. After identifying the NM properties around $n_0$, it was found that bsHLS using the RMF method can yield reasonable results. The data can be reproduced with the choice of $\beta'=\frac{\partial\beta}{\partial\alpha}\sim 1$, consistent with the results of Refs. [39, 40], where a dilaton limit fixed point is assumed in the medium. The combination of $ f_{\chi}m_{\sigma} $ is constrained to be $ \simeq 2.3 \times 10^{5} $ MeV$ ^2 $ which is consistent with what estimated before in the skyrmion crystal approach such that physically interesting results can be obtained [41, 42]. By comparing the symmetry energy $E_{\rm{sym}}$ and incompressibility coefficient $K(n)$ obtained from our bsHLS and Walecka-type models, we find that the bsHLS can make the symmetry energy stiff at subsaturation density but soft at intermediate densities to meet the constraints of GW170817 [43] and the neutron skin thickness of $ ^{208} \rm Pb $ [44] simultaneously, without introducing additional freedoms such as the δ meson in Refs. [45, 46]. In addition, we find that the incompressibility coefficient of bsHLS surges at intermediate densities, while the Walecka-type models exhibit gentler behaviors, resulting in a better description of NS M-R relation using bsHLS. The maximum mass of NS can nearly reach $3M_{\odot}$ with a pure hadron phase, meeting the constraints of GW170817 [43, 47] and PSR J0740+6620 [48, 49], whereas the Walecka-type models compared in this work, which saturates these constraints, yield maximum mass around $2.2 M_{\odot}$ [50−52]. We find that this is due to the kink behavior of σ expectations at intermediate densities, induced by the nonlinear realization of scale symmetry. Moreover, the value of $\beta'$, behavior of $\langle\chi\rangle^*$ and Brown-Rho scaling (B-R scaling) at different densities can significantly affect NS M-R relations, indicating a relationship between QCD symmetry patterns and macroscopic phenomena.

This article is organized as follows: In Sec. II, we introduce the theoretical framework of bsHLS and the equation of state (EoS) of NM under the RMF approximation. In Sec. III, we provide a phenomenological analysis by pinning the experimental data of nuclear matter and neutron star observations. A comparison with the Walecka-type models is also made. Our summary and discussion are presented in Sec. IV.

In this section, we establish the theoretical framework of bsHLS and derive the EoS for NM within the RMF approach. Focusing on NM only composed of nucleons, we restrict the bsHLS Lagrangian to the two-flavor case, involving only u and d quarks. The leading order bsHLS Lagrangian $\mathcal{L}$ can be decomposed into the baryonic part $\mathcal{L}_B$ and the mesonic part $\mathcal{L}_{M}$:

The mesonic part $\mathcal{L}_M$, consisting of σ, ρ, ω and π mesons, is constructed as follows [31],

where $ V_{\mu \nu}=\partial_\mu V_\nu-\partial_\nu V_\mu-i\left[V_\mu, V_\nu\right] $, $ V_\mu=\dfrac{1}{2}(g_\omega \omega_\mu+ g_\rho \rho_\mu^a \tau^a) $. $ m_\rho $, $ m_\omega $ and $\mathcal{M}=m_{\pi}^2 I_{2\times2}$ are the masses of ρ, ω and π mesons, respectively. The dilaton field χ is introduced as a nonlinear representation $ \chi=f_\chi\Phi= $ $ f_\chi \exp \left(\sigma / f_\chi\right) $, and $\beta'$ accounts for the anomalous dimension of gluon field operators, representing the deviation from the IR fixed point. According to Ref. [53], $ h_i $s, except $ h_5 $ and $ h_6 $, are chosen to be $ 1 $ for simplification and the anomalous dimension $\gamma_m$ is simply taken to be $ 1 $ (denoted as LOSS). $ h_5 $ and $ h_6 $ are constrained by the saddle point equations,

In Lagrangian (2), pions are introduced as a nonlinear field $ \xi=\sqrt{U}=e^{i \frac{\pi}{f_{\pi}}} $, where $ \pi=\pi^a \frac{\tau^a}{2} $ with $ a=1,2,3 $ representing the isospin indices. Its covariant derivative is defined as

The Murrer-Cartan 1-forms $ \hat{\alpha}_{\perp}^\mu $ and $ \hat{\alpha}_{\|}^\mu $ are defined as

The baryonic part Lagrangian $\mathcal{L}_B$ is written as [31]

where N is the iso-doublet of baryon field, and $ g_1 $ and $ g_2 $ are set to $ 1 $ as suggested in Ref. [53]. For convenience, we introduce the combinations of the parameters:

By regarding the NM as homogeneous matter, the RMF approximation can be applied. Using Lagrangian (1), the EOMs of ω and ρ can be obtained as

where ρ and ω fields are denoted, respectively, as ρ and ω for brevity. Similarly, the EOM of σ field is derived as

where $ \dfrac{m_N^3 \Phi^3}{\pi^2}F\left(\dfrac{k_{p(n)}}{m_N \Phi}\right) $ refers to scalar density $ \langle\bar{p} p\rangle $ or $ \langle\bar{n} n\rangle $ and $k_{p(n)}$ is the Fermi momentum of nucleons at zero temperature.

The energy density can be obtained via Lagrangian (1) with the solutions of EOMs mentioned above

where $f\left(\dfrac{k_p(n)}{m_N \Phi}\right)=\int_0^{\frac{k_p(n)}{m_N}} x^{\prime 2} \sqrt{1+x^{\prime 2}} {{\rm{d}}} x^{\prime}$. It should be noted that the nonlinear Lagrangian (1) will lead to nonzero constant vacuum energy $\mathcal{E}_0=-f_\pi^{2} m_\pi^2-h_5-h_6$, which is neglected in our EOS calculations.

The above bsHLS (1) is constructed in a matter-free space. When applying it to a medium, it's natural to expect that the parameters in the Lagrangian should be changed by medium, here density. We implement this density effect via Brown-Rho scaling (B-R scaling) [2, 54], and refer to this density effect as intrinsic density dependence (IDD). Explicitly, the parameters in Lagrangian (1) scale as

A possible choice of $\Phi^*$ is $1/(1+r \frac{\rho_n+\rho_p}{n_0})$. Pion-nuclei bound state data [55] indicates $r\approx 0.2$, but we set it as a free parameter to fit the NM properties in this work. Chiral dynamics indicates that pion mass is not changed by medium, so we set $m_{\pi}^*/m_{\pi}\approx 1$. The saddle point equation (3) leads to

After the above discussions, we finally obtain the energy density for phenomenological analysis as

In the phenomenological analysis, we choose vacuum values $f_{\pi}=92.4 {\rm{MeV}}$, $m_N=939 {\rm{MeV}}$, $m_{\pi}=140 {\rm{MeV}}$, $m_{\omega}=783 {\rm{MeV}}$ and $m_{\rho}=765 {\rm{MeV}}$ [56]. The free parameters are $M_{\sigma}=m_{\sigma}f_{\chi}$, $\beta'$, r, $g_{\omega NN}$, $g_{\rho NN}$, $g^{SSB}_{\omega NN}$ and $g^{SSB}_{\rho NN}$, which can be estimated by the properties of NM around saturation density $n_0$. The calculated results of NM properties are listed in Table 1, and the corresponding low energy constants (LECs) are given in Table 2. It can be seen that NM properties obtained from both bsHLS-L and bsHLS-H are consistent with empirical values.

	Empirical	bsHLS-L	bsHLS-H
$ n_0 $	$ 0.155\pm0.050 $ [57]	0.159	0.159
$e_0$	$ -15.0\pm1.0 $ [57]	$ -16.0 $	$ -16.0 $
$ K_0 $	$ 230\pm30 $ [58]	232	284
$ E_{{\rm{sym}}}(n_c) $	$ 22.4\pm2.3 $ [59, 60]	20.8	20.9
$ E_{{\rm{sym}}}(n_0) $	$ 30.9\pm1.9 $ [61]	30.5	29.2
$ E_{{\rm{sym}}}(2n_0) $	$ 46.9\pm10.1 $ [62]	51.5	50.2
$ L(n_c) $	$ 43.7\pm7.8 $ [63]	53.2	54.2
$ L(n_0) $	$ 52.5\pm17.5 $ [57, 61]	85.9	68.3
$ J_0 $	$ -400\pm390 $ [64]	$ -767 $	$ -599 $

Table 1.  The properties of nuclear matter: $e_0$ is the binding energy of nucleon at $n_0$, $ E_{{\rm{sym}}}(n)=\left.\frac{1}{2} \frac{\partial^2 E(n, \alpha)}{\partial \alpha^2}\right|_{\alpha=0} $ is the symmetry energy, $ \left.K_0=9 n^2 \frac{\partial^2 E(n, 0)}{\partial n^2}\right|_{n=n_0} $ is the incompressibility coefficient, $ \left.J_0=27 n^3 \frac{\partial^{3} E(n, 0)}{\partial n^3}\right|_{n=n_0} $ is the skewness coefficient and $ L(n)=3 n \frac{\partial E_{{\rm{sym}}}(n)}{\partial n} $ is the symmetry energy density slope. $n_c\approx 0.11{\rm{fm^{-3}}} $ is subsaturation cross density. Two sets of predictions are shown: bsHLS-L refers to the case, where the surge of $K(n)$ located at lower density regions, and bsHLS-H refers to the higher density case. $n_0$ is in the unit of ${\rm{fm}}^{-3}$, and the others are in the unit of ${\rm{MeV}}$.

	$M_{\sigma}(10^5{\rm{MeV}}^2)$	$\beta'$	r	$g_{\omega NN}$	$g_{\rho NN}$	$g^{SSB}_{\omega NN}$	$g^{SSB}_{\rho NN}$
bsHLS-L	1.05	0.395	0.161	11.5	3.78	16.3	9.45
bsHLS-H	2.30	1.15	0.191	11.0	4.17	8.85	4.85

Table 2.  The estimation of parameters for bsHLS-L and bsHLS-H.

To illustrate the features of bsHLS, we consider a Walecka-type model [65] for comparison

The choices of parameters from some references are listed in Table 3.

	NL3 [66]	TM1 [67]	FSU-$\delta 6.7$ [45]	BKA22 [68]	BSR12 [69]
$n_0({\rm{fm}}^{-3})$	0.148	0.145	0.148	0.147	0.147
$m_N$(MeV)	939	938	938	939	939
$m_{\sigma}$(MeV)	508	511	492	498	499
$m_{\omega}$(MeV)	783	783	783	782	783
$m_{\rho}$(MeV)	763	770	763	770	763
$m_{\delta}$(MeV)	0	0	980	0	0
$g_{\sigma}$	10.2	10.0	10.2	10.6	10.6
$g_{\omega NN}$	12.9	12.6	13.4	13.9	13.9
$g_{\rho NN}$	4.47	4.63	7.27	6.47	5.48
$g_{\delta}$	0	0	6.70	0	0
$g_2({\rm{fm}}^{-1})$	10.4	7.23	8.09	11.0	10.6
$g_3$	-28.9	0.618	5.88	11.3	10.2259
$c_3(10^{-3})$	0	2.82	5.28	5.00	5.00
$\alpha_1({\rm{fm}}^{-1}\cdot10^{-3})$	0	0	0	1.32	1.26
$\alpha_1'(10^{-3})$	0	0	0	0.124	0.00520
$\alpha_2({\rm{fm}}^{-1})$	0	0	0	0.150	0.0475
$\alpha_2'(10^{-2})$	0	0	0	0	5.10
$\alpha_3'(10^{-2})$	0	0	2.14	0	1.16
$C_{\delta\sigma}(10^{-2})$	0	0	3.85	0	0

Table 3.  The choice of parameters for Walekca-type models in Eq. (14).

The properties of NM is analyzed at first. From Table 1, one can see that, with appropriate choices of parameters in Table 2, our bsHLS can yield NM properties around (sub)saturation density, satisfying the constraints from empirical data.

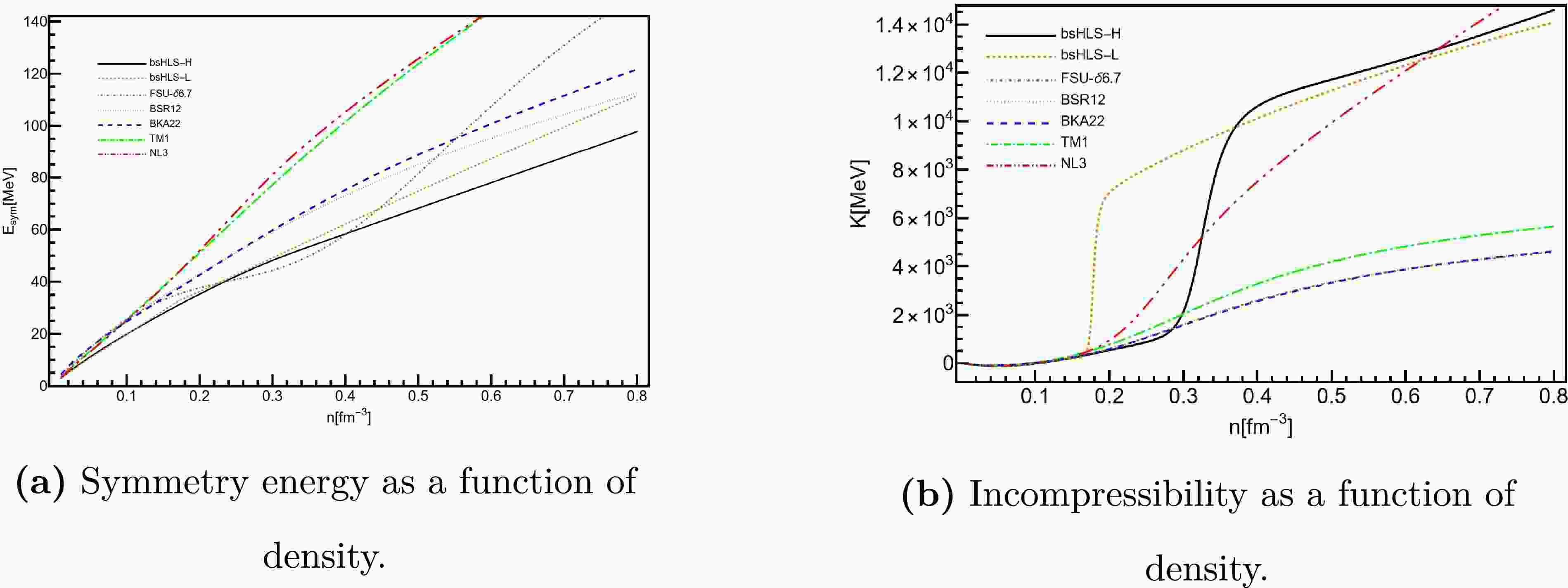
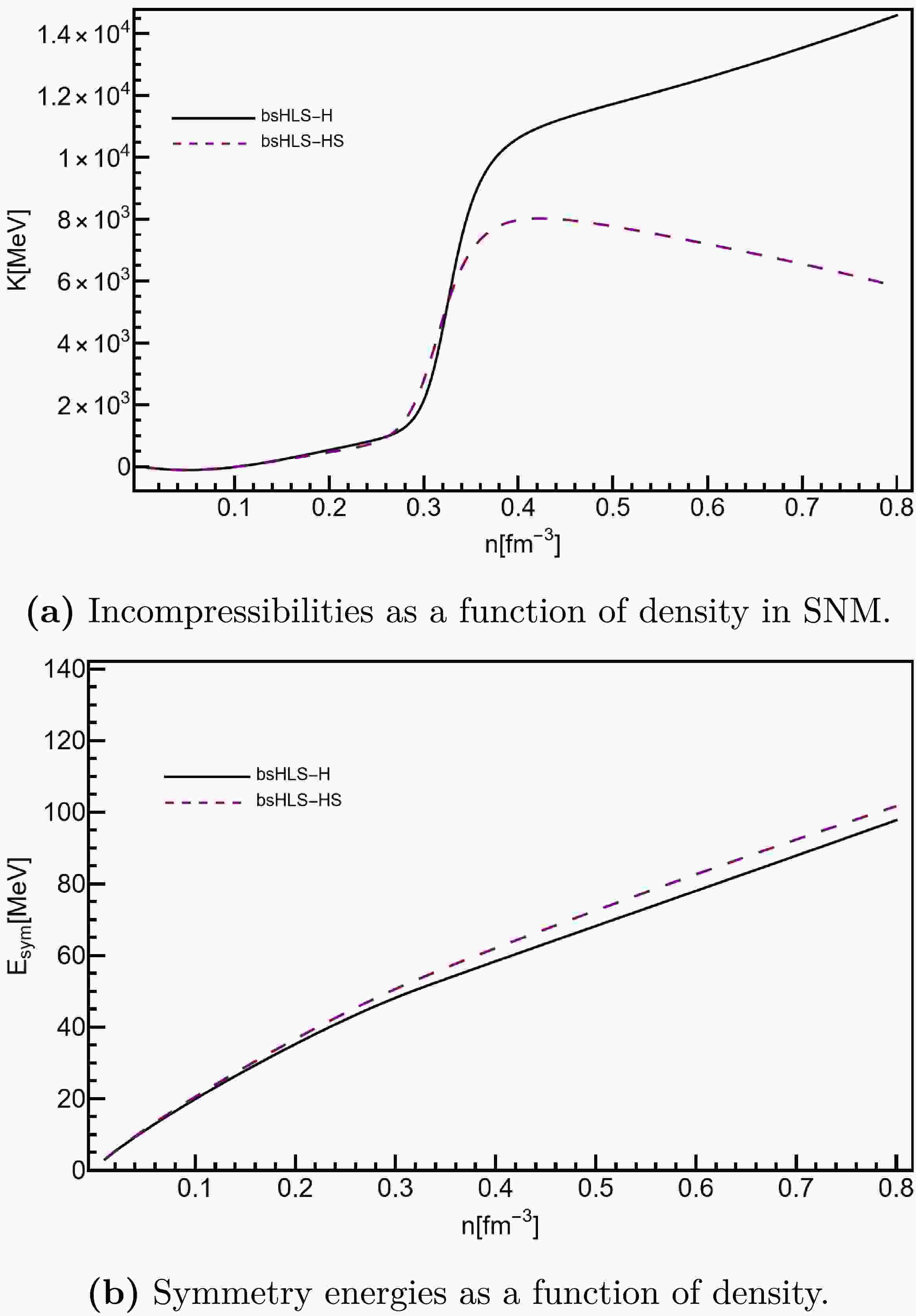
Regarding the $L(n_c)$ results listed in Table 1, both bsHLS-L and bsHLS-H exhibit the stiffness to align with the neutron skin thickness of $\rm Pb^{208}$ [44], as well as the Walecka-type models compared in this work, shown in Fig. 1. Moreover, the $E_{\rm{sym}}$ behavior of bsHLS is quite similar to that of the compared Walecka-type models at low densities $n\lesssim n_0$. However, at intermediate densities, around $2n_0$, the models can be categorized into three sets: bsHLS and FSU-$\delta6.7$ yield the most soft $E_{\rm{sym}}$, whereas NL3 and TM1 gives most stiff one, and BSR12 and BKA22 fall in between. The Walecka-type models without the δ meson are not soft enough at the intermediate densities, while bsHLS provides a more reasonable behavior without introducing δ.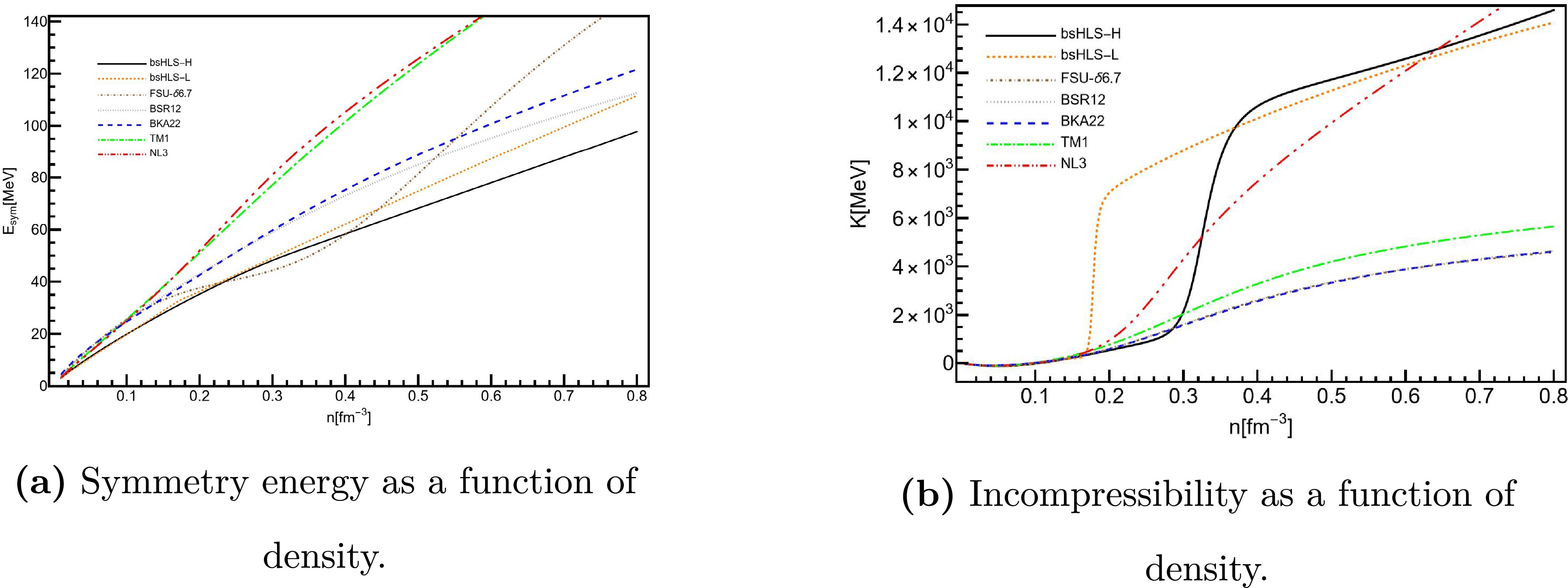

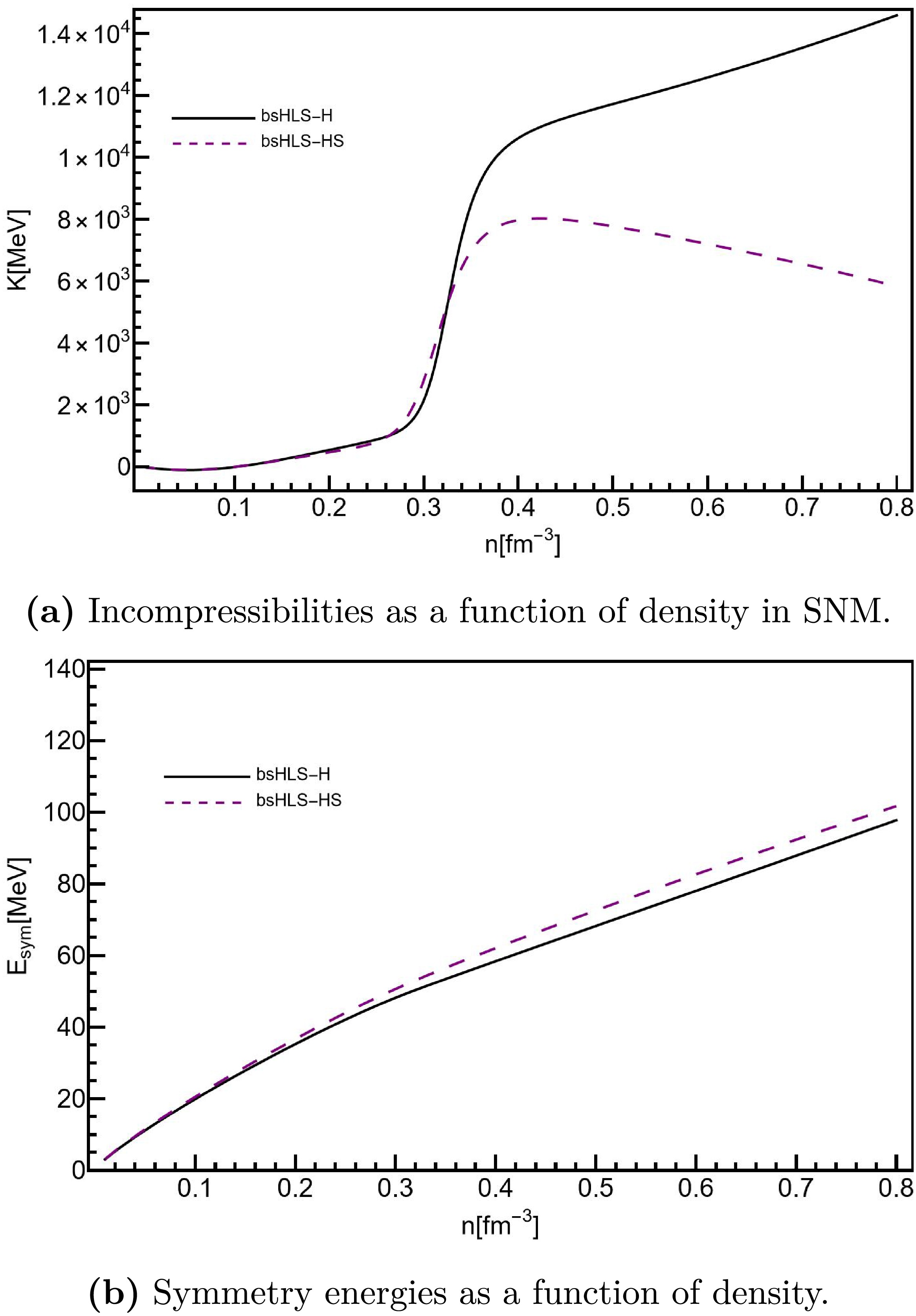
Figure 1.  (color online) Incompressibility, $ K=9\frac{{\rm{d}}P}{{\rm{d}}n} $, which is reduced to $ K_0 $ at $ n_0 $, and symmetry energy of symmetric NM from bsHLS and Walecka-type models.

It will be seen later that this difference can affect the tidal deformation of NS.

For the incompressibility, the results of bsHLS and the compared Walekca-type models show significant differences at intermediate densities: Walecka-type models exhibit a monotonic behavior with density, whereas bsHLS shows a kink behavior around $(1\sim2)n_0$. This kink behavior results in a peak structure in the sound velocity, which plays an important role in determining the M-R relation of NS, and is attributed to manifestation of scale symmetry in nuclear matter [70].

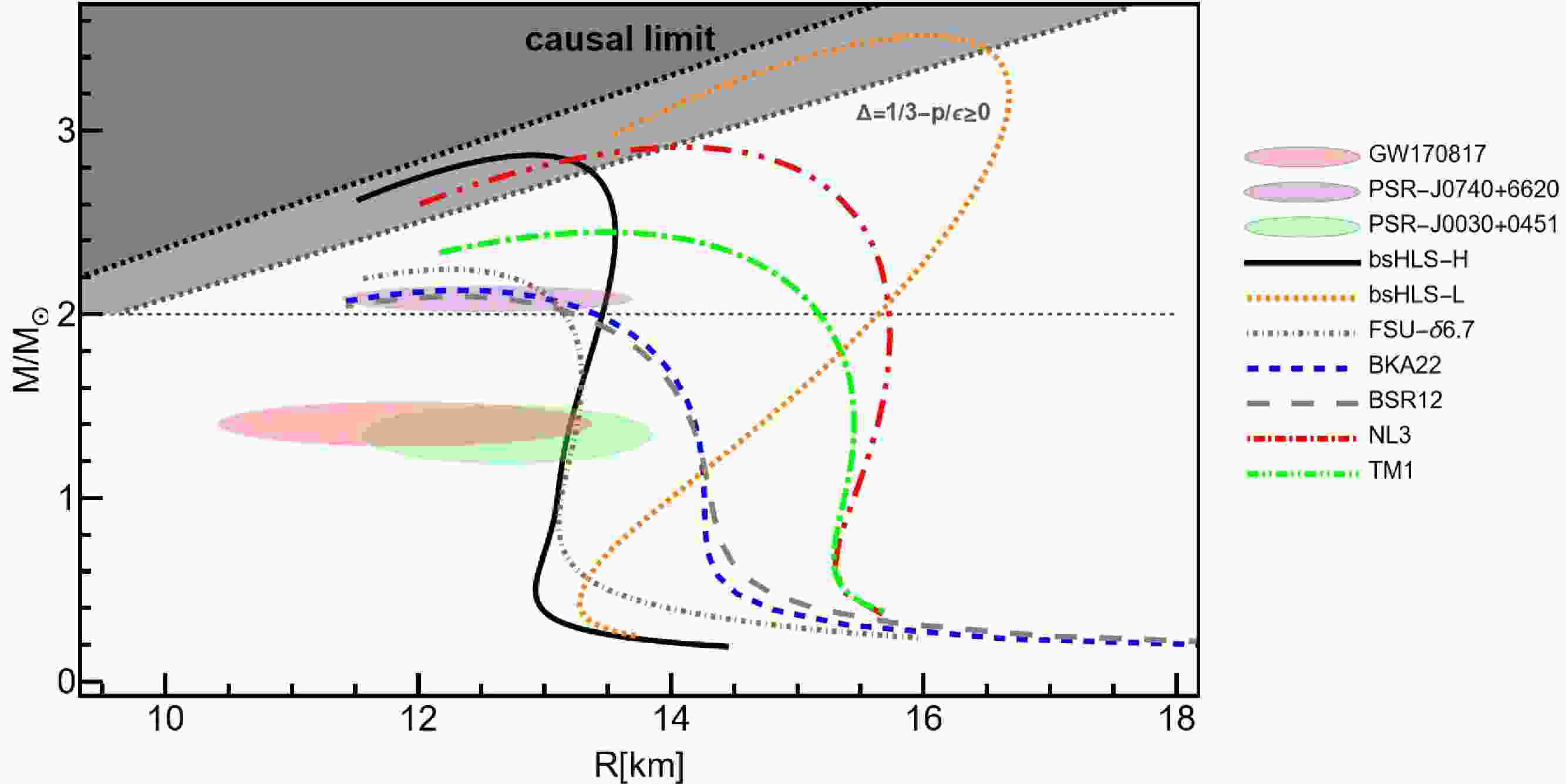
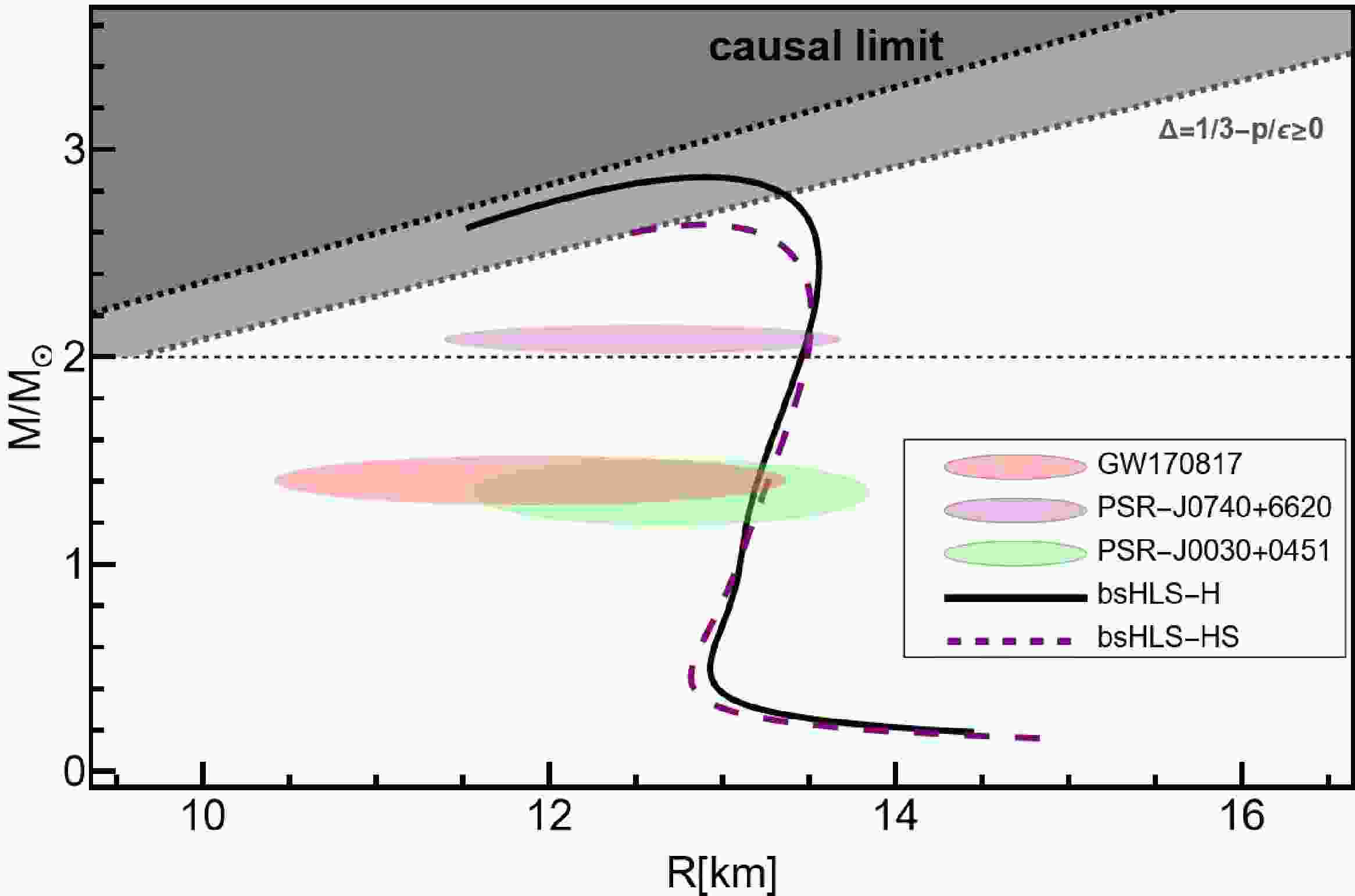
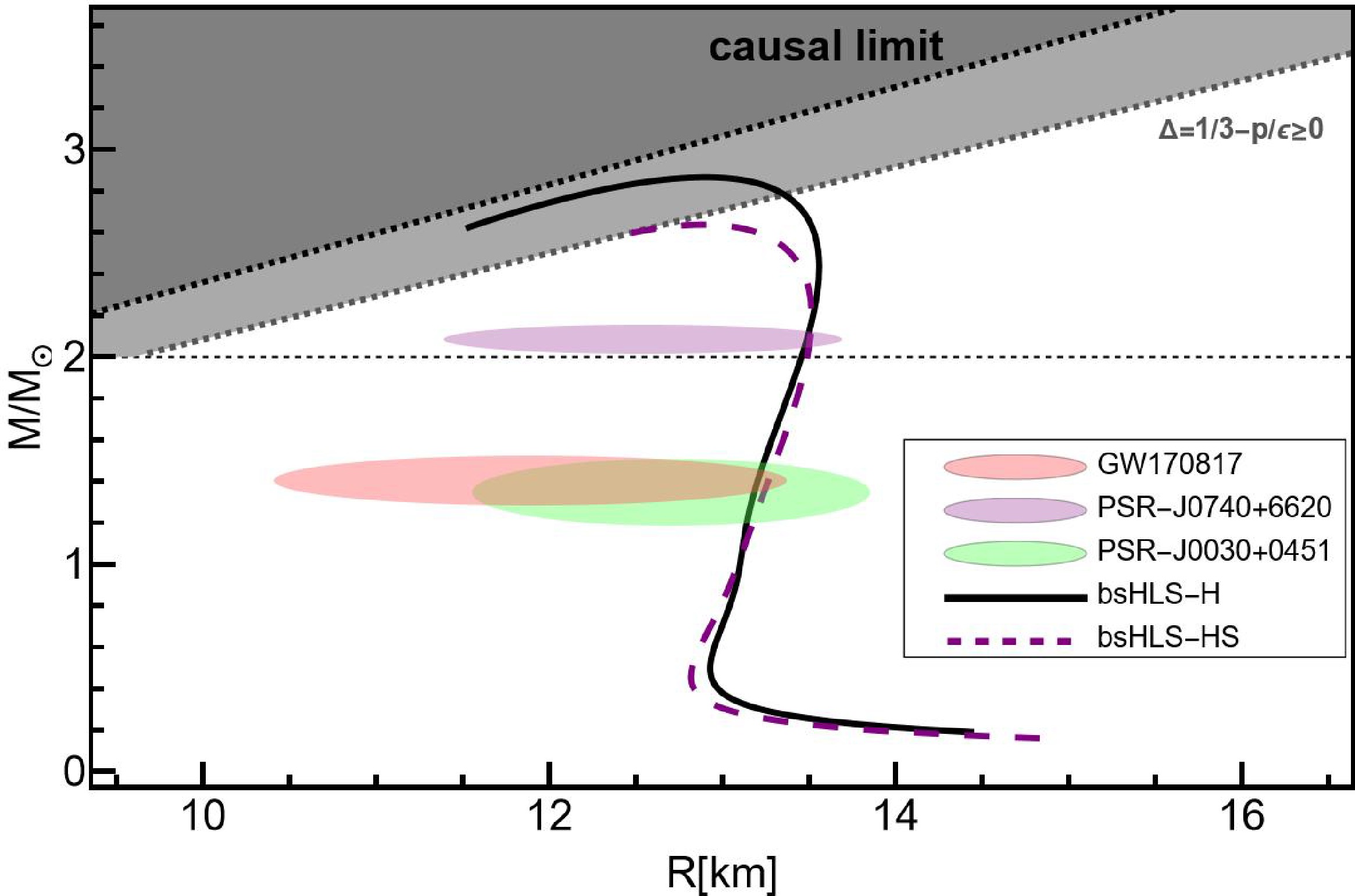
Next, the NS M-R relations are studied using the EOSs discussed above for pure neutron matter (PNM). The results of NS M-R relations are shown in Fig. 2 and Table 4

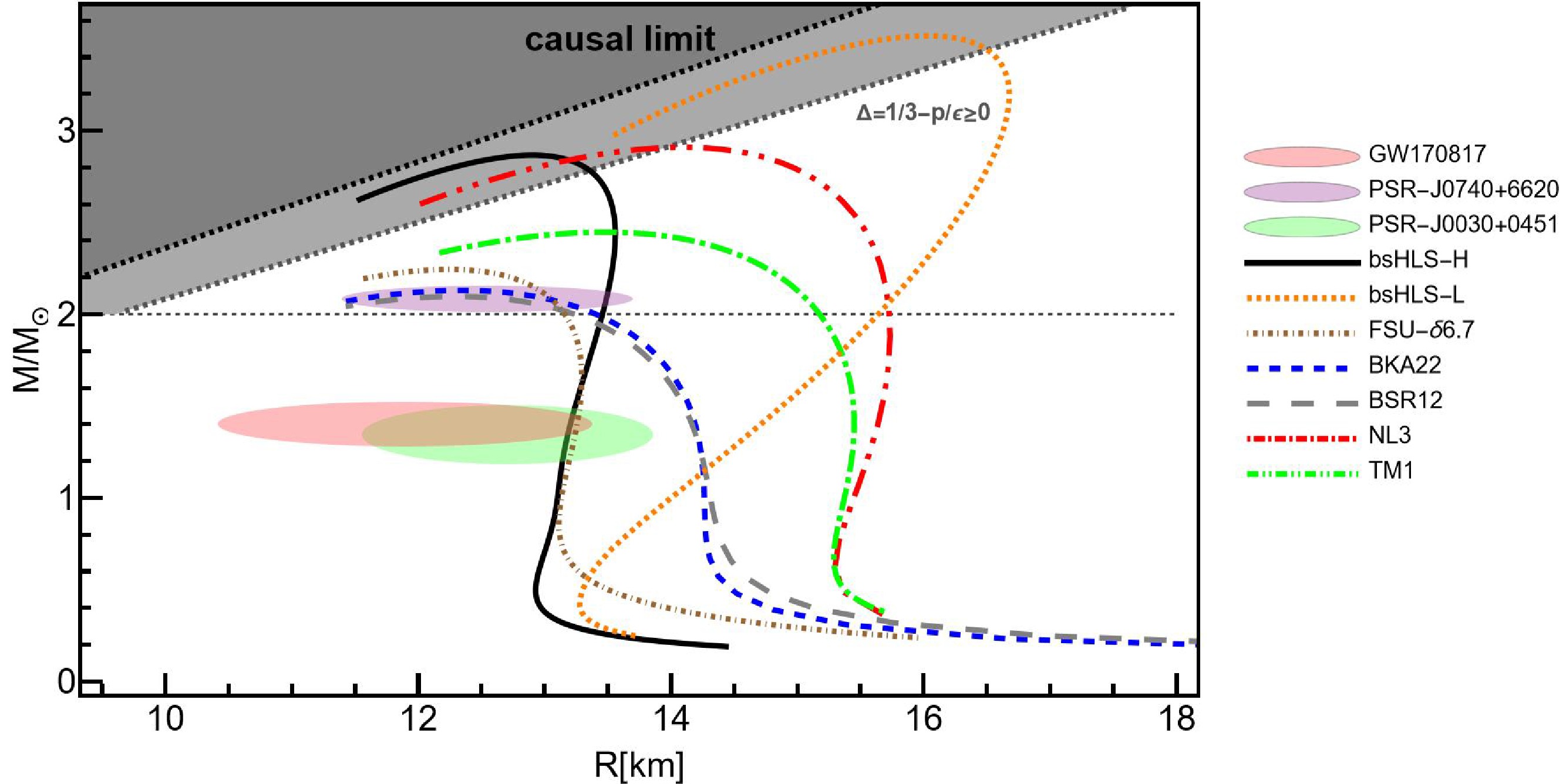
Figure 2.  (color online) The M-R relations from bsHLS and Walecka-type models. The constraints are estimated from Refs. [43, 47, 49, 71, 72]. The M-R relation is calculated by solving the Tolman-Oppenheimer-Volkoff (TOV) equation [73, 74]. All EoSs for TOV equation calculation are interpolated to a BPS EoS [75] below $0.01\ \rm fm^{-3}$ [76].

	Empirical [43]	bsHLS-L	bsHLS-H	TM1	NL3	FSU-$\delta6.7$	BKA22	BSR12
$\Lambda_{1.4}$	$190^{+390}_{-120}$	2120	910	2240	2826	878	1348	1245

Table 4.  Tidal deformations from bsHLS and Walecka-type models defined in Eq. (14) and Table III for NS with mass of $1.4\ M_{\odot}$. They are calculated from the EOSs used for the M-R relation in Fig. 2, using the formalisms in Ref. [77].

From Fig. 2, all the M-R relations satisfy the casual limits, but the parts of bsHLS and NL3 near and past the maximum mass point fall into negative trace anomaly region. However, the trace anomaly constraint is estimated from the pQCD side, whose corresponding density region is above $(20-30)n_0$ [78], which is far from the central density of a NS core. Actually, M-R relations can be improved by correcting the scale symmetry pattern to have a physically reasonable hebaviour at high density region, which will be discussed in the section. Besides, one can see that the mass-radius (M-R) relation obtained from bsHLS-L cannot satisfy the radius constraint, which will be also discussed in detail in the next section.

For bsHLS-H, it predicts a M-R relation falls within the constraints of astro-observations with an obviously larger maximum mass around $2.8 M_{\odot}$, compared to Walecka-type models: When meeting the NS constraints, the $M_{\rm{max}}$ of NSs predicted by these Walecka-type models is around or slightly above $2.2 M_{\odot}$, as discussed in Refs. [50−52, 79, 80].

Although the result from FSU-$\delta6.7$ satisfies these constraints, it requires introducing a new degree of freedom δ. The Walecka-type models without δ considered in this work cannot provide consistent results with the constraints of NSs, though they reproduce the NM properties around $n_0$ [67, 81]. This highlights the advantage of bsHLS in interpreting the structures of nuclei and NSs within a unified framework. In addition, because of the larger predicted $M_{\rm{max}}$, $\sim 2.8M_{\odot}$, which is close to the upper limit of NS of gap problem in the continuous mass distribution of supernova remnants [82, 83], by pure hadron matter with bsHLS-H, this new approach may have profound implications for understanding the gravitational wave event GW190814 [84].

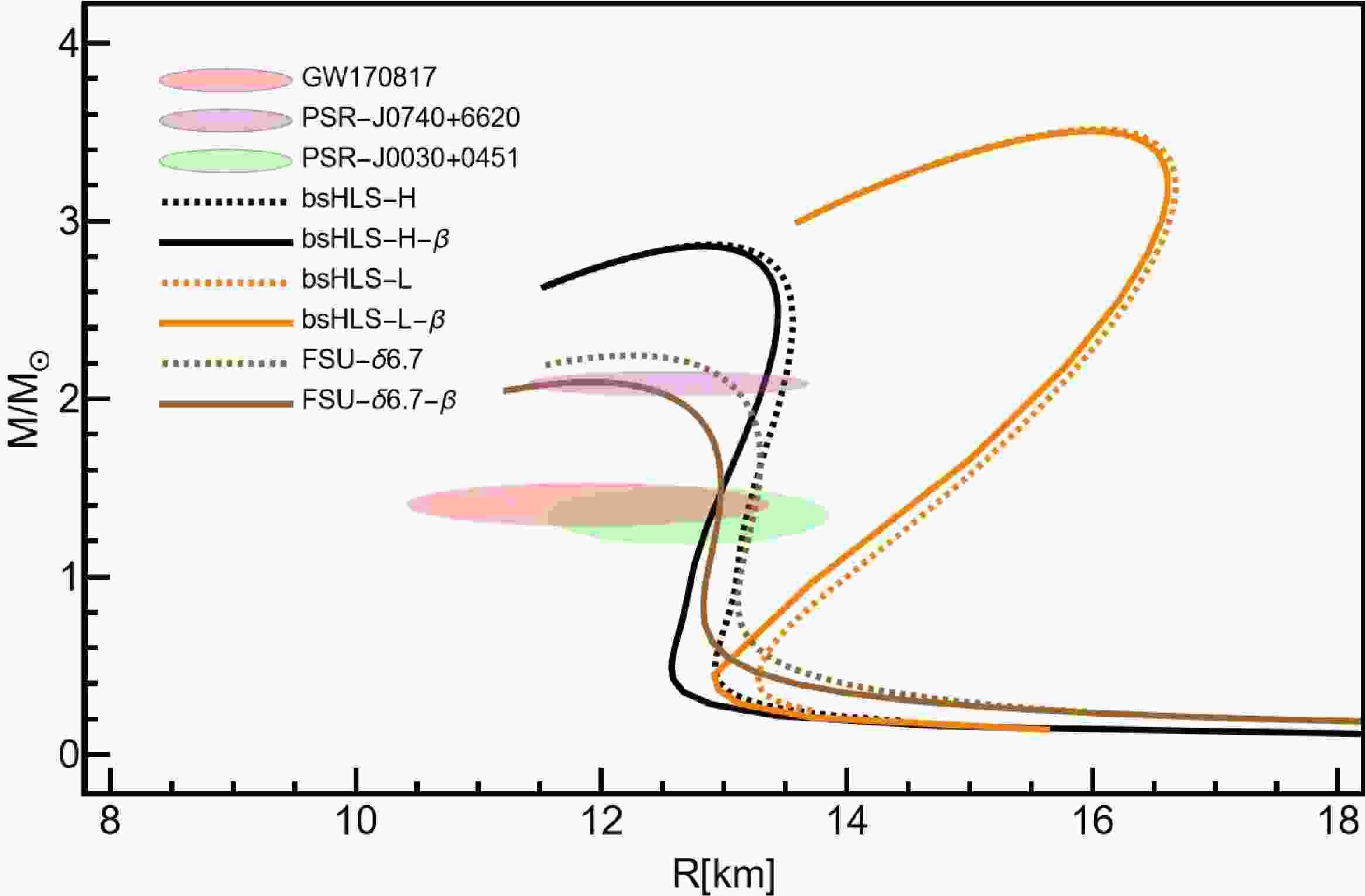
For tidal deformations from Table 4, one can conclude that only the results of bsHLS-H and FSU-$\delta6.7$ are close to the constraints of GW170817 [43]. This is due to the softness of $E_{\rm{sym}}$ from these two at intermediate densities, as shown in Fig. 1. However, the tidal deformation of bsHLS-L is very large, though the symmetry energy at intermediate densities is also soft. The reason lies in the very early surge of incompressibility, as shown in Fig. 1 leading to large maximum mass of NS, resulting a more distorted M-R relation: compact NSs for small mass ones but loose NSs to reach such a large maximum mass. The same reasoning applies to the Walecka-type models, NL3, TM1, BKA22, BSR12.

In order to show the rationality of the above discussions, we also plot the M-R relations in beta equilibrium matter—a more realistic case but beyond the present framework—in Fig. 3. One can see that the maximum mass of a NS doesn't change much, while the M-R relations all become more compact, favored by observations. So, the inclusion of beta equilibrium matter doesn't change the main conclusion drawn above.

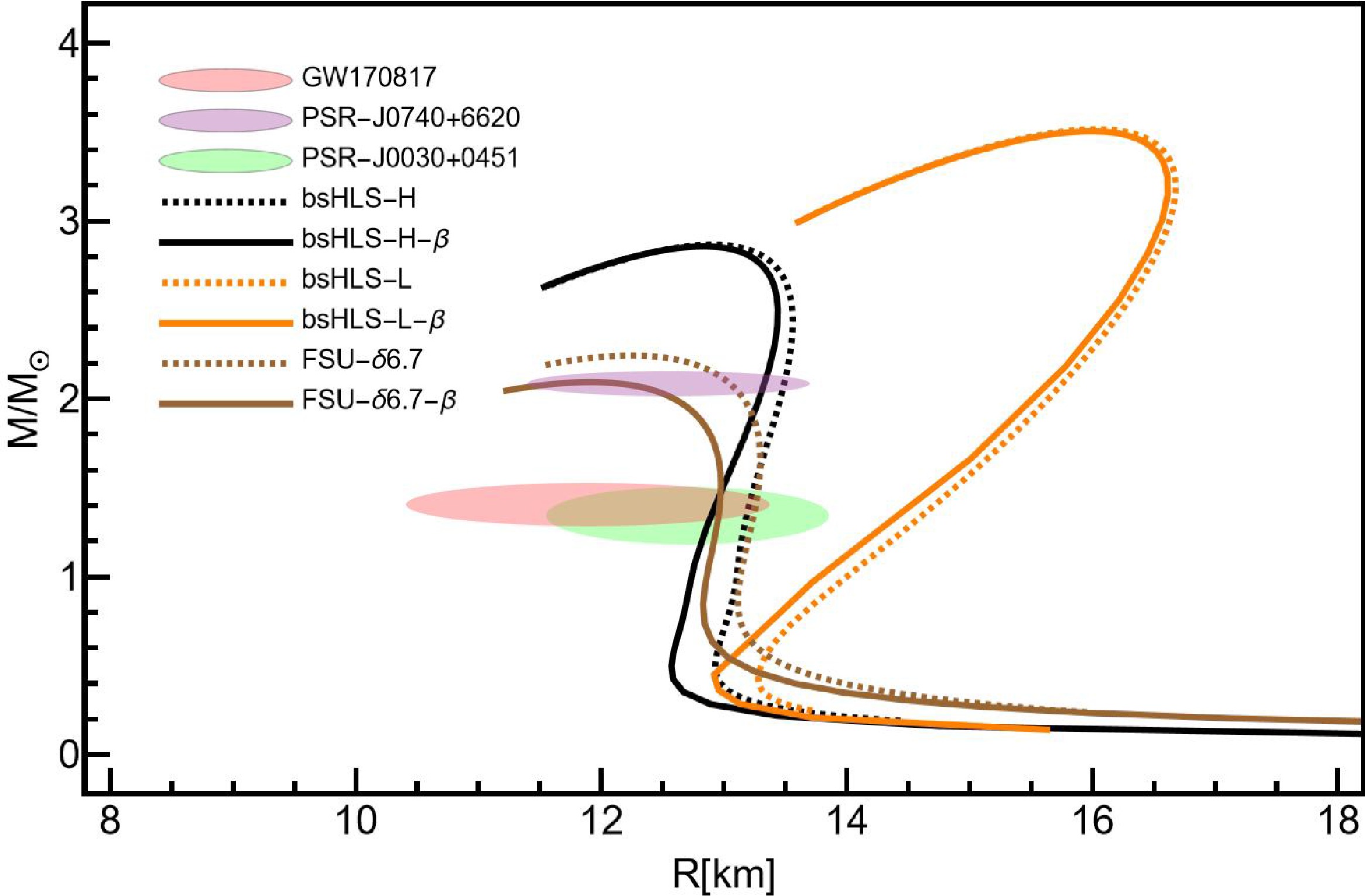
Figure 3.  (color online) The M-R relations from bsHLS and Walecka-type models based on PNM and beta equilibrium matter calculations.

In summary, the above discussion stresses that, in contrast to the Walecka-type models where the isovector scalar δ is needed, and the bsHLS anchored on the chiral and scale symmetries of QCD with self-consistent power counting can yield phenomenological results aligh with the observation data and predict the maximum mass above $2.5 M_{\odot}$. And it implies that the scaling parameter $r\approx0.19$, $\beta'\approx1.15$, $M_{\sigma}=m_{\sigma}f_{\chi}\approx 2.3\times10^{5} {\rm{MeV}}^2$, and the couplings between vector mesons and nucleons $g_{\rho NN}\approx4.17$, $g_{\omega NN}\approx 11.0$. The scaling parameter $r\approx0.19$ is consistent with pion-nuclei bound state data [55], while the $\beta'\approx1.15$ agrees with estimates from skyrmion crystal approach [39, 40]. If $f_{\chi}$ is taken to be $3f_{\pi}\approx270 {\rm{MeV}}$, $m_{\sigma}\approx 850 {\rm{MeV}}$, while the power-counting mechanism of Crewther and Tuntall remains valid [28]. The coupling constant $g_{\rho NN}\approx4.17$ aligns with the results from the OBE potential analysis of nucleon interactions [9], and $g_{\omega NN}\approx 11.0$ is in agreement with the analyses of nucleon-nucleon scatterings [85].

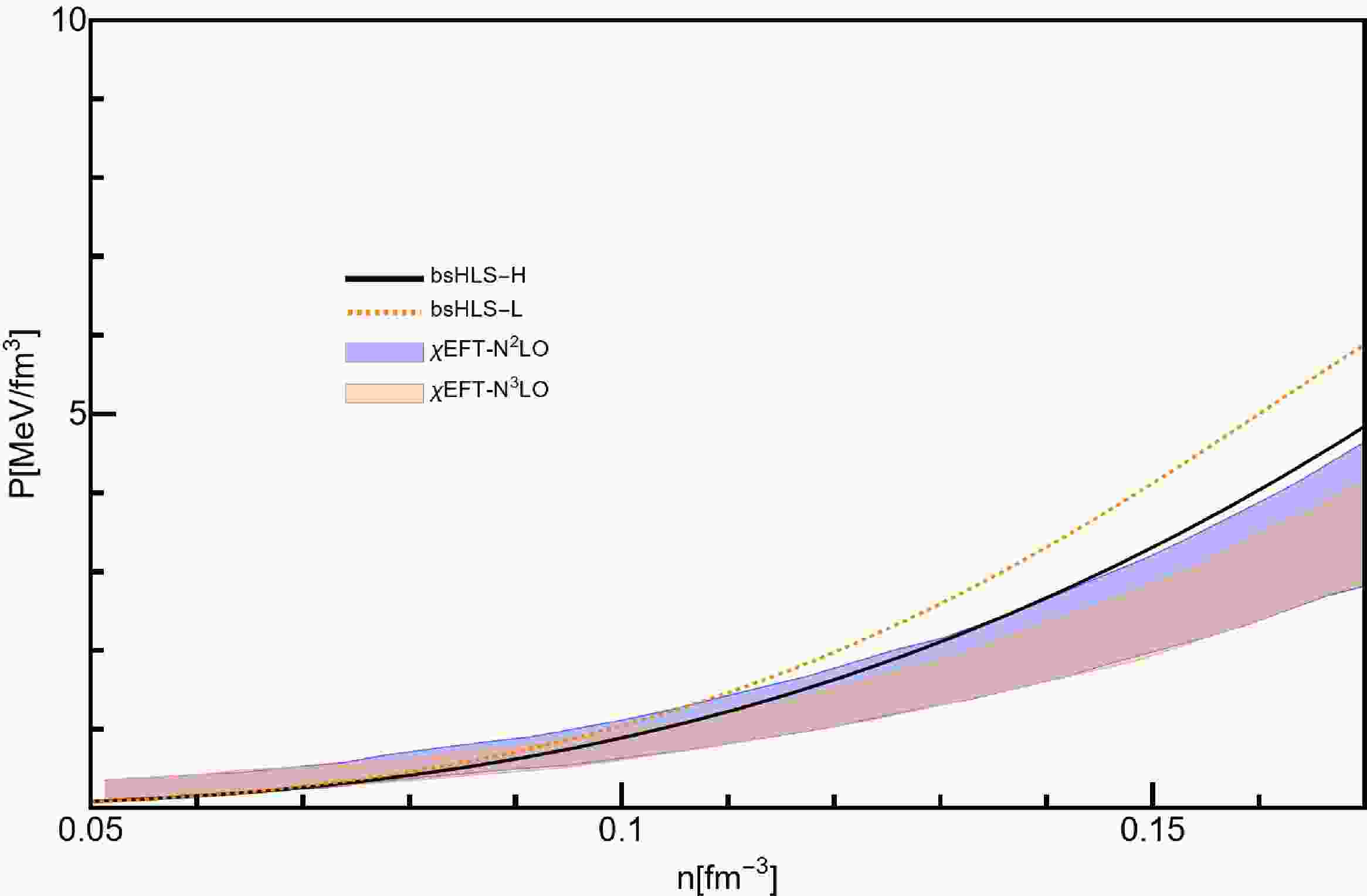
The difference between bsHLS-L and bsHLS-H becomes significant in the M-R relation, as shown in Fig. 2 and discussed in the previous section, though it is not distinguishable from the NM properties around saturation density. In order to understand these more deeply, the pressure of PNM is calculated around and below saturation density, and compared with the results of the conventional chiral nuclear force, as shown in Fig. 4. One can see that the pressure of bsHLS-H can align with the constraints up to saturation density, while bsHLS-L is a little higher around $n_0$. But at low densities, below $0.1 {\rm{fm}}^{-3}$, the chiral nuclear force and bsHLS results are consistent with each other due to the fact that the mesons can be integrated out at this region in the description of nucleon interactions, leading to the equivalence of the two approaches. It strengthens the solidness of our results.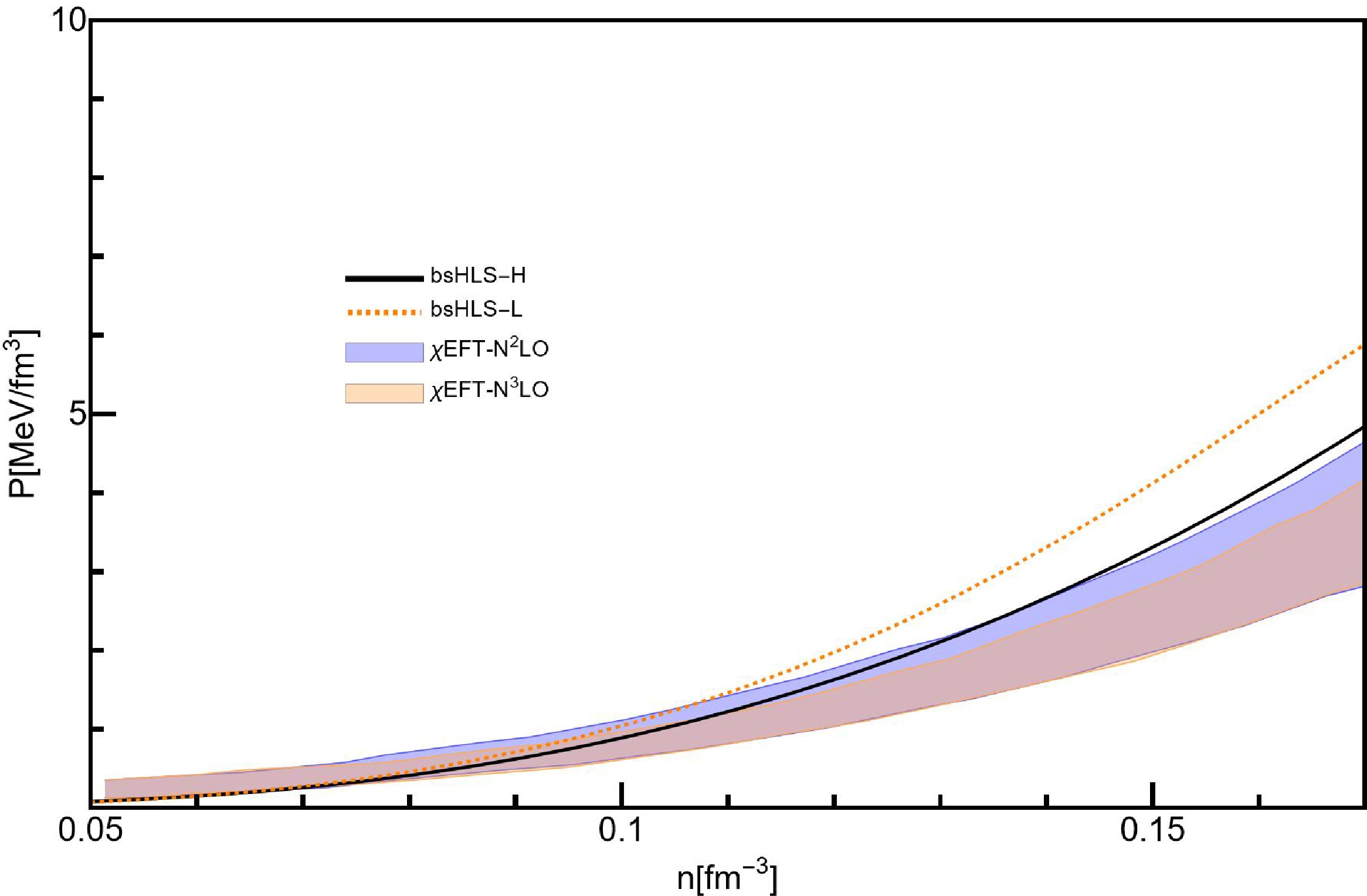

Figure 4.  (color online) Pressure as a function of density for PNM. The orange and blue shaded region comes from N²LO and N³LO of chiral nulear force results [86].

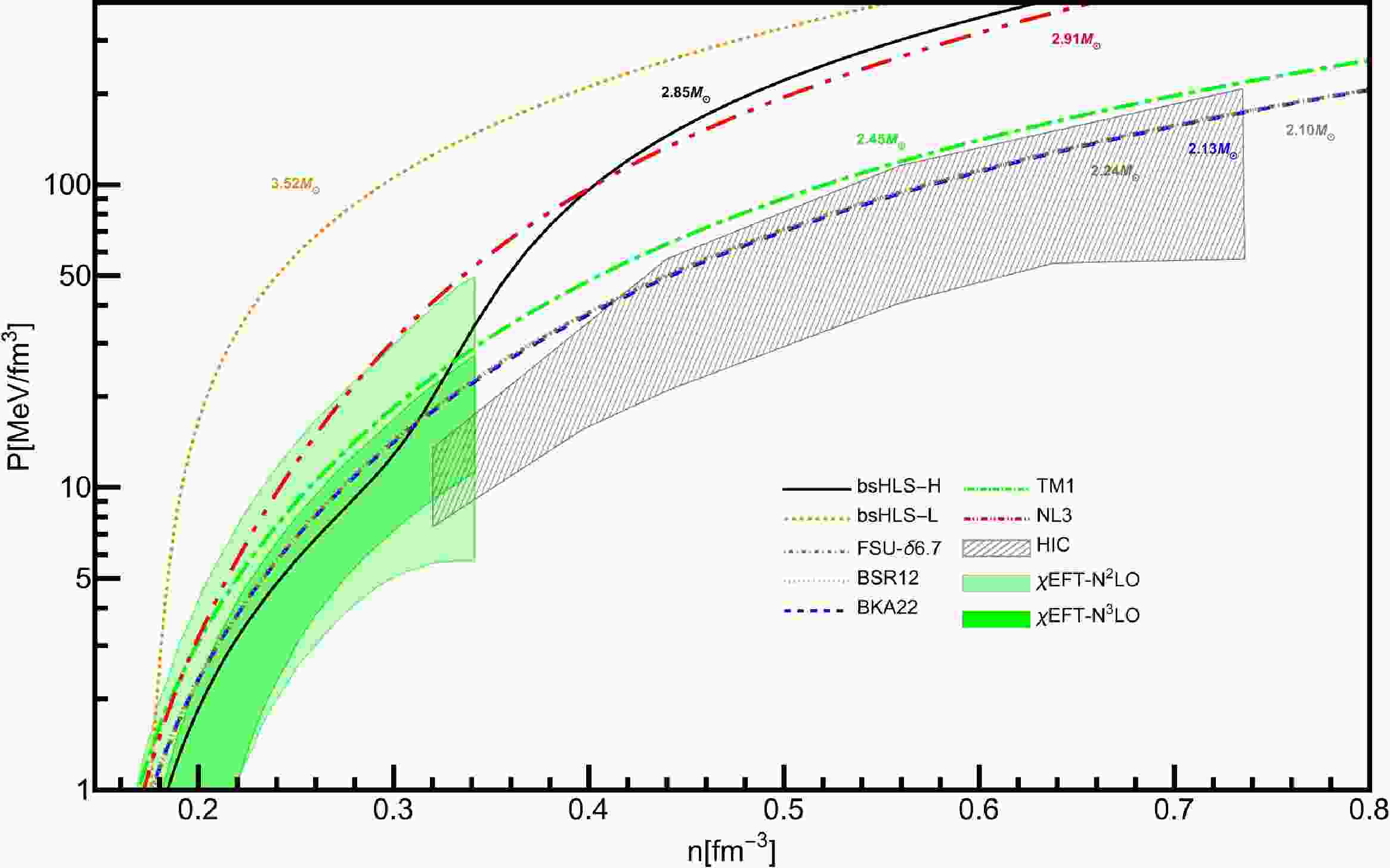
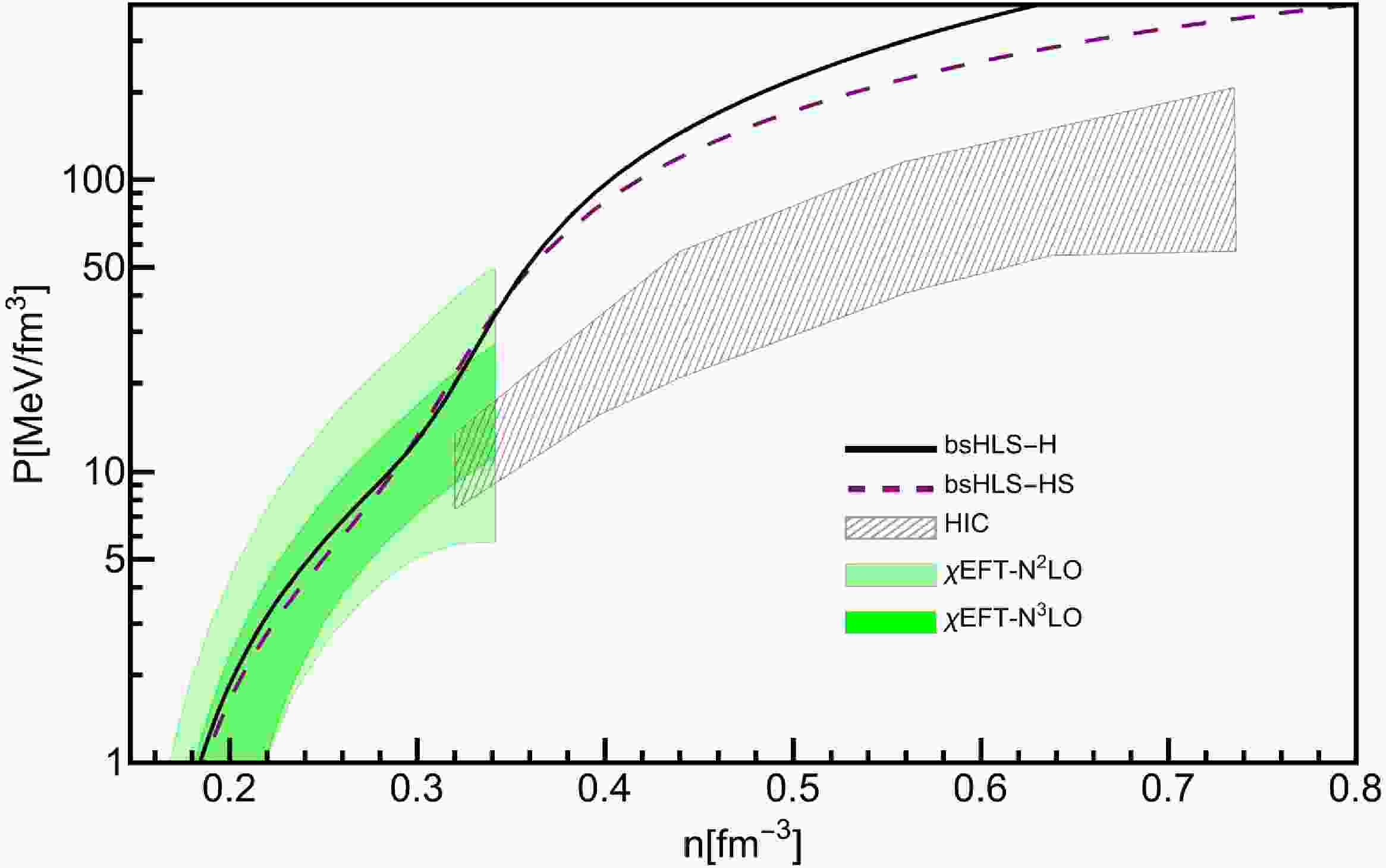
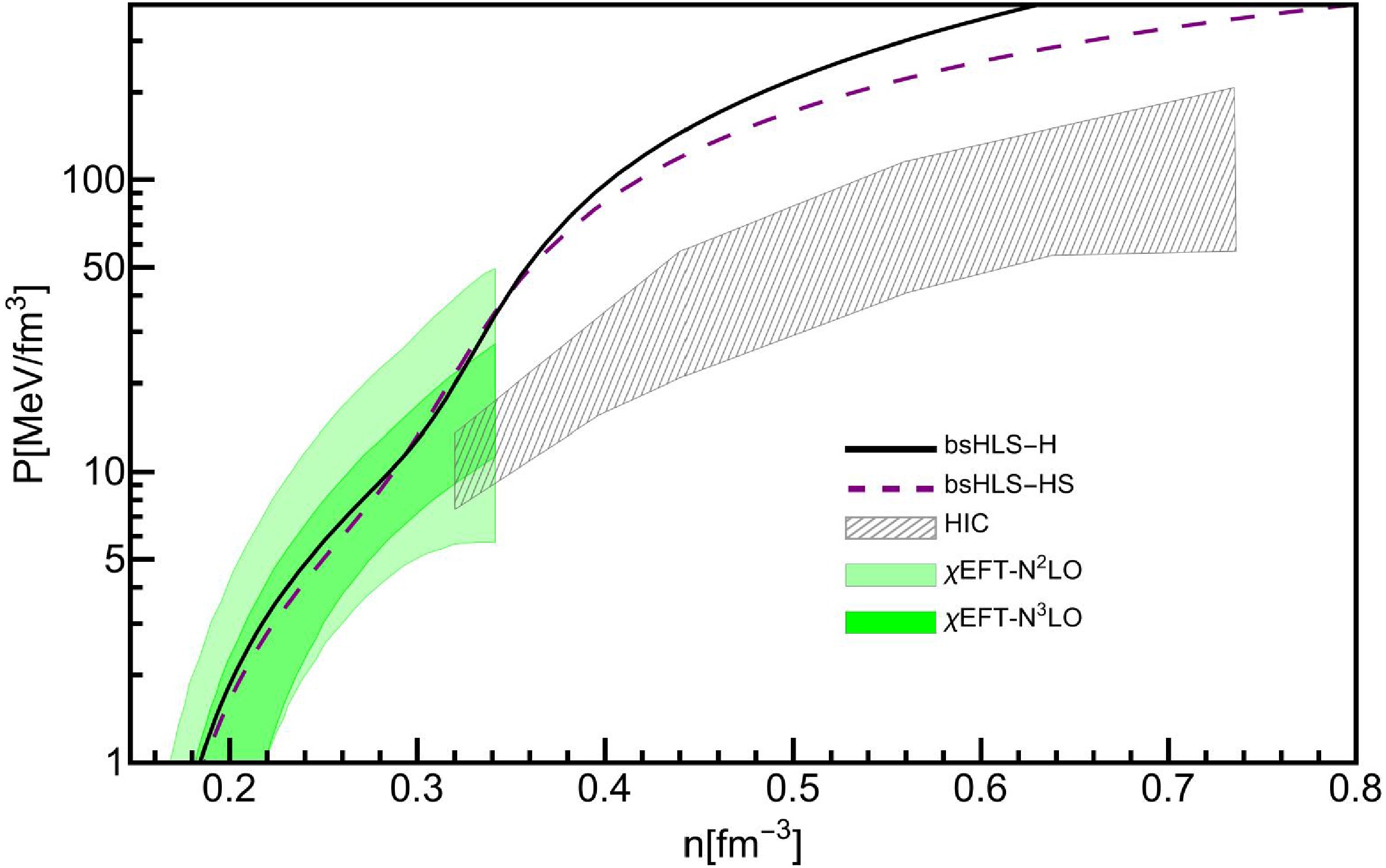
Furthermore, we plot the SNM pressure beyond the saturation density, and compare it with the heavy ion collision (HIC) analysis and chiral nuclear force results in Fig. 5. It can be seen that the results of BSR12, BKA22 and FSU-$\delta 6.7$ can fall in the region above $2.5 n_0$, which mostly influences the maximum mass of neutron star: The ones in the constraints have smaller maximum mass, and the ones above the constraints have larger maximum mass. The results of bsHLS-L and bsHLS-H are both above the constraints, and bsHLS-L is even above the chiral nuclear force results. One reason is that the HIC flow-data constraints are not included in our fitting process, and possible ways to fix the discrepancy will be discussed latter in this section.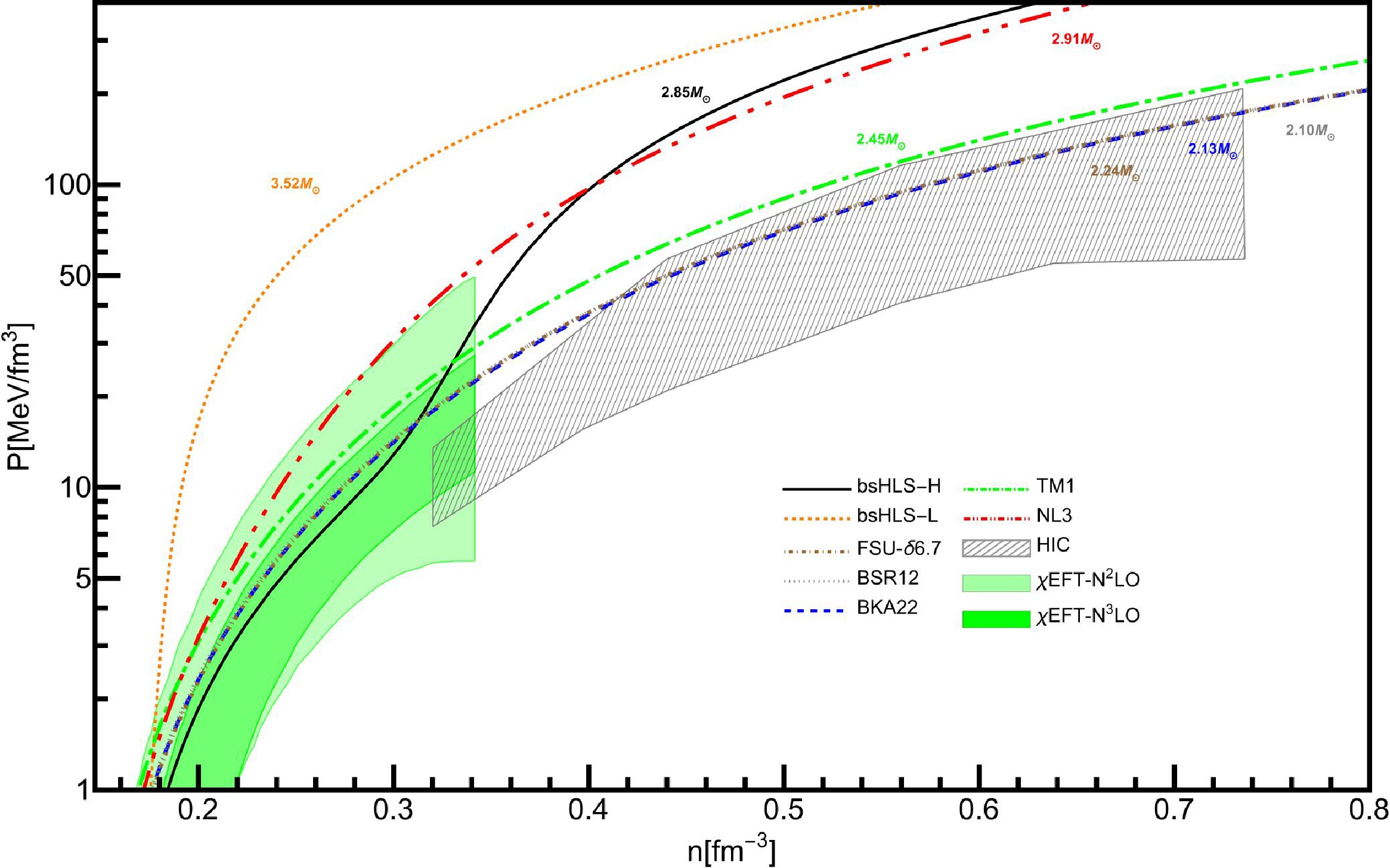

Figure 5.  (color online) Pressure as a function of density for SNM. The gray hatched area represent constraint from Au+Au flow-data analysis [87]. The green shaded region comes from chiral nuclear force results [88]. The numbers next to the curves represent the predicted maximum masses of neutron stars.

But before the kink of the incompressibility at $\sim 2 n_0$ (also the kink of pressure) in Fig. 1, the pressure of bsHLS is smaller than all the compared Walecka-type models, and such kink behavior is not excluded by the constraints, which offers the opportunity of a compact but heavy NS.

The key difference lies in $\beta'$ for bsHLS-H and bsHLS-L, which is connected to the existence of the pseudo-conformal structure at high densities [40]. The $\beta'$ of bsHLS-H aligns with the constraints of the pseudo-conformal limit, whereas the $\beta'$ of bsHLS-L does not. This highlights the impact of scale symmetry patterns on NS M-R relations.

Moreover, since σ is nonlinearly coupled with other mesons (see Eq. (8)) through a conformal compensator, its density dependence shows a kink behavior that is not observed in Walecka-type models [70]. As the result, the order parameter $ \langle\chi\rangle^* $, calculated based on bsHLS does not approach zero throughout the density regions, which is necessary for the (pseudo-)conformal limits of QCD at high densities [35, 40, 89]. Considering the derivation of bsHLS to HIC flow-data analysis, and to recover the expected behavior of $ \langle\chi\rangle^* $, a possible approach is to couple an additional factor to $ g_{\omega NN} $ to obtain the effective coupling $ \tilde{g}_{\omega NN}=g_{\omega NN}/(1+R\frac{\rho_p+\rho_n}{n_0}) $ [70, 90].

It is found that, as listed in Table 5, the NM properties can be reproduced with the parameter set bsHLS-HS: $M_{\sigma}=2.25\times10^5\ {\rm{MeV}}^2$, $\beta'=1.14$, $g_{\omega NN}=11.5$, $g_{\rho NN}=4.27$, $g^{SSB}_{\omega NN}=8.70$, $g^{SSB}_{\rho NN}=4.85$, $r=0.20 $ and $R=0.02 $. And, as shown in Fig. 6, the M-R relations for PNM are roughly consistent with observational constraints, but there is a decrease of $ M_{\rm{max}} $ compared to bsHLS-H, which makes the M-R relation fall within the positive trace anomaly region.

	$ n_0 $	$e_0$	$ K_0 $	$ E_{{\rm{sym}}}(n_c) $	$ E_{{\rm{sym}}}(n_0) $	$ E_{{\rm{sym}}}(2n_0) $	$ L(n_c) $	$ L(n_0) $	$ J_0 $
bsHLS-HS	0.159	-16.0	259	21.6	30.3	52.9	55.4	74.5	-720

Table 5.  The quantities of nuclear matter with additional suppressions of $\tilde{g}_{\omega NN}$, and the definitions and constraints are the same as Table 1.

Figure 6.  (color online) NS M-R relation results with/without $ g_{\omega NN} $ suppression.

In order to understand the discrepancies in the M-R relations, the incompressibilities and symmetry energies are also calculated for bsHLS-H and bsHLS-HS, shown in Fig. 7.

Figure 7.  (color online) NM property results with/without $ g_{\omega NN} $ suppression.

It can be seen that the symmetry energy remains almost the same in both cases. However, the incompressibility of bsHLS-HS is much softer than that of bsHLS-H at high densities, leading to a decrease in $M_{\rm{max}}$. And it gives us a hint to find a model compatible with the HIC SNM pressure constraint by introducing a suppression factor as shown in Fig. 8, which also provides the rationality from the phenomenological side to add such suppression at high densities.

Figure 8.  (color online) Pressure as a function of density for SNM with bsHLS model.

At low or intermediate densities, the incompressibilities of both cases are similar, which results in the M-R relations being comparable in the region of NS constraints.

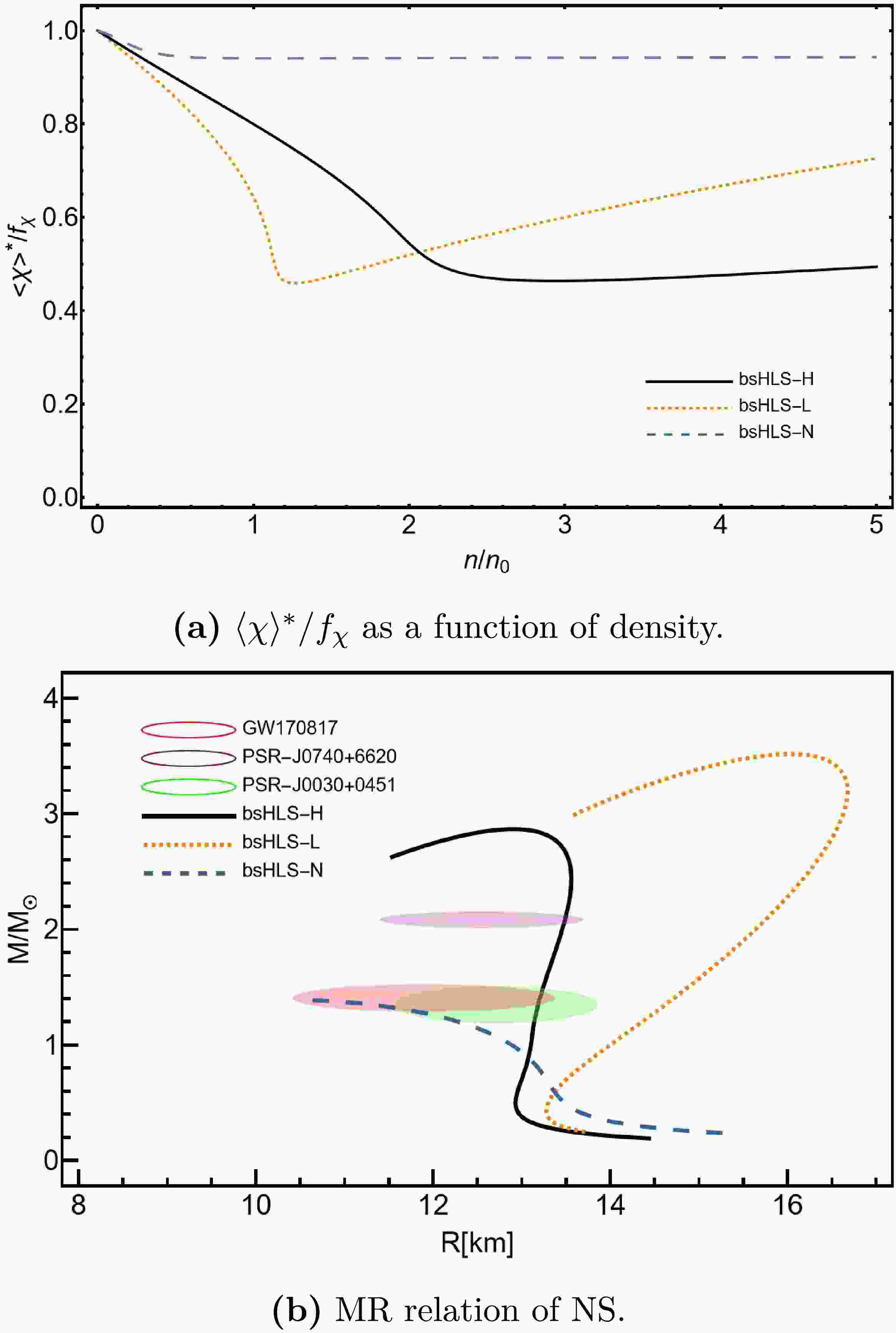
Additionally, the NM properties are investigated with B-R scaling turned off. We find that with the parameter set bsHLS-N: $M_{\sigma}=1.11\times10^5\ {\rm{MeV}}^2$, $\beta'=1.10$, $g_{\omega NN}=-11.0$, $g_{\rho NN}=4.17$, $g^{SSB}_{\omega NN}=-192$ and $g^{SSB}_{\rho NN}=4.85$, the NM properties can still be reproduced (e.g., $ n_0=0.16\ {\rm{fm}}^{-3} $, $ e_0=-16.0\ {\rm{MeV}} $, $ K_0=241\ {\rm{MeV}} $, $ E_{{\rm{sym}}}(n_0)=29.3\ {\rm{MeV}} $). However, this approach results in a much softer scale symmetry parameter $ \langle\chi\rangle^* $ flow compared to the cases with B-R scaling. As a result, the M-R relation becomes unnatural and deviates from the constraints, as shown in Fig. 9.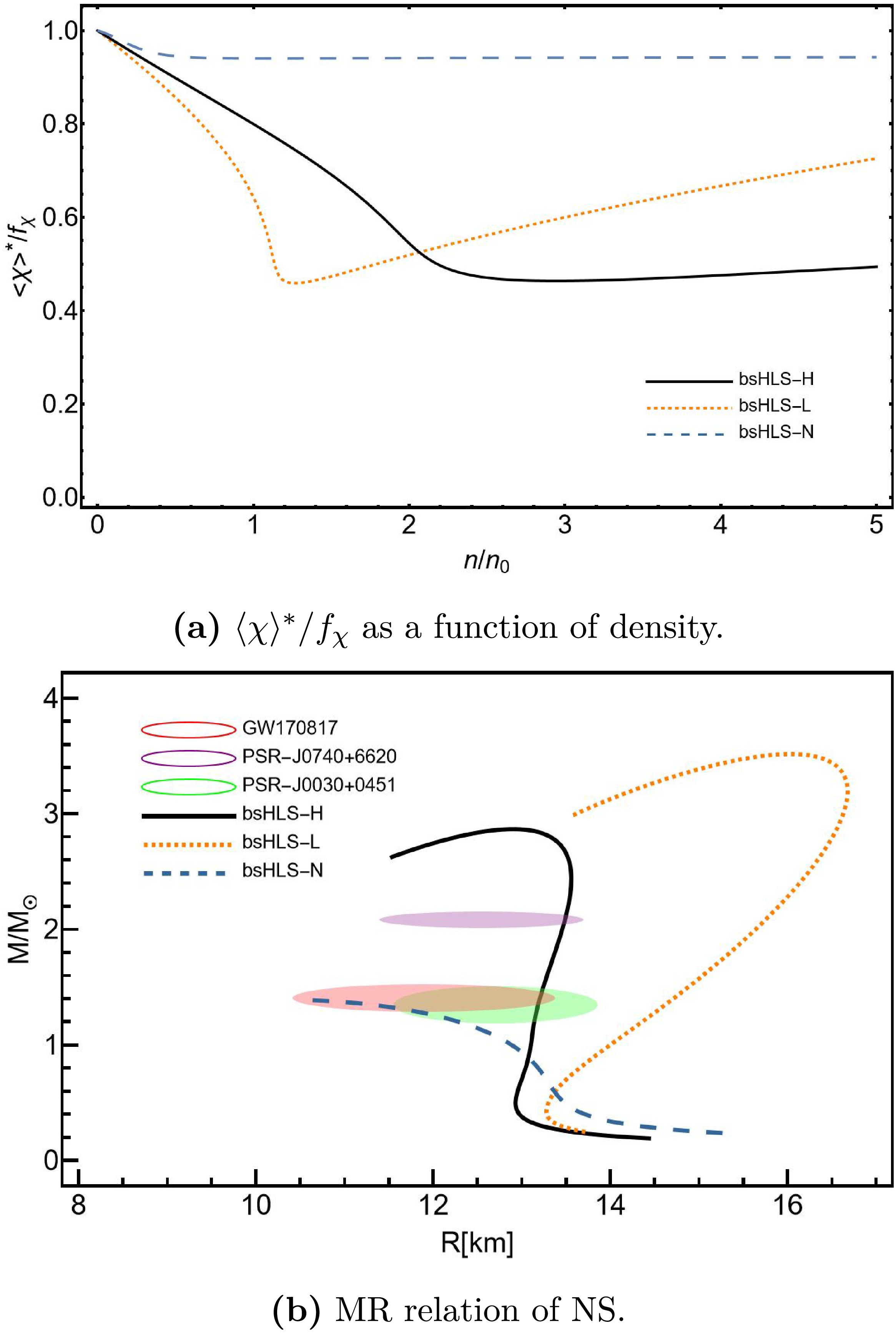

Figure 9.  (color online) The $ \langle\chi\rangle^*/f_{\chi} $ in pure neutron matter and NS M-R relation results with/without B-R scaling.

All these findings, including the necessity of introducing $ \tilde{g}_{\omega NN} $ suppression and B-R scaling, signify the importance of properly parameterizing the scale symmetry in densities. This reminds us of the past work on the quenching factors of $ g_A $ which affect the β decay of neutrons in dense environments (see Ref. [38] for details). From the comparison among the various cases discussed above, valuable lessons about NS and NM properties have been learned, providing guidance on hadron interaction parameterization to describe dense NM. Since the differences between bsHLS and Walecka-type models in our analysis are at intermediate density regions, not far from $n_0$, it is expected that examining bsHLS in dense systems will be promising in future experiments.

In this work, the bsHLS, constructed based on the philosophy of $\chi \rm EFT$ with HLS and a possible IR fixed point of QCD at low energies, is applied to dense environments using the RMF approximation, with free parameters fixed by pinning the nuclei structure data around $n_0$. The NM properties and NS M-R relations can be well reproduced, closely matching empirical values in bsHLS-H case.

Without introducing many freedoms, such as the δ meson, and with operators organized to respect chiral and scale symmetry considerations and expanded by chiral-scale orders, the bsHLS can provide a reasonable behavior of NM properties from subsaturation to intermediate densities, e.g., $K(n)$ and $E_{\rm{sym}}(n) $, compared to Walecka-type models. And the NS M-R relations are sensitive to NM properties at these density regions, making bsHLS outperform Walecka-type models in describing a wider range of densities. More specifically, the kink behavior of the σ field in bsHLS at intermediate densities allows the $M_{\rm{max}}$ to reach nearly $3\ M_{\odot}$ for PNM, while other NS observational constraints are still satisfied.

However, the above discussions are all based on the analysis where parameter sets are fitted to the nuclear matter properties around saturation density, then EOSs are extended to neutron star matter. In principle, the parameter sets may describe the neutron star matter better if they include the neutron star observations in the fitting process. The further study on this topic will be improved by a more systematic fitting procedure, as discussed in Ref. [50], which will help to refine the parameter sets and enhance the predictive power of the model.

Besides, the behaviors of symmetry patterns in dense environments are also found to be pivotal to macroscopic phenomena: If there is no restoration point of scale symmetry at certain densities, such as the $\beta'$ value of bsHLS-L, the NS M-R relations will fall outside observational constraints; The $M_{\rm{max}}$ of predicted NSs is influenced by the behavior of order parameter of scale symmetry, $\langle\chi\rangle^*$.

Furthermore, the study on the flow of $\langle\chi\rangle^*$ with densities suggests the necessity of introducing an additional suppression factor for $ \tilde{g}_{\omega NN} $ to recover the scale symmetry, and it could be an interesting problem for further investigation. As a good starting point, recovering the expected scale symmetry behavior has been shown to be a possible way to heal the discrepancy with the HIC flow-data analysis. A more systematic study on the analysis of HIC flow data with the bsHLS can be done in the future via: I. Including the potential induced by our approach, where the σ meson is introduced as a exponential field χ, in the transport model [91]; II. Including the HIC flow-data constraints in our fitting process in addition to the NM properties around saturation density; III. Introducing the additional suppression from a more fundamental consideration of QCD.

In summary, introducing bsHLS to NM studies is a promising approach due to its close relation to QCD symmetry patterns and the effective potentials organized by chiral-scale orders, which have already proven successful in describing scattering experiments at vacuum. The relationship between microscopic symmetries and macroscopic phenomena found in this work is also a valuable topic to be further studied.

We would like to thank Yi-Zhong Fan for his valuable comments.