-
Investigation into the characteristics and synthesis of superheavy nuclei (SHN) has emerged as a prominent area of research in nuclear physics over the past few decades. The exploration of these elements offers a distinctive opportunity to probe the limits of the periodic table and explore the "island of stability," which is characterized by magic numbers Z=120,126 and N=184 [1−6]. Numerous theoretical and experimental studies have offered valuable insights into the synthesis of SHN via heavy-ion-induced reactions. These studies revealed several factors that influence the dynamics of these reactions within the low-energy domain [7−15]. Firstly, the synthesis of SHN requires the interacting nuclei to overcome the repulsive Coulomb barrier in order to create a compound nucleus through the exchange of nucleons and energy. The characteristics of this Coulomb barrier, i.e. the barrier height
$ V_B $ and barrier position$ R_B $ , play a significant role, as they can hinder the formation of the new entity [16−19]. Studies examining the Coulomb barrier of such interactions suggest that numerous parameters such as mass, charge, energy, deformations, orientations, and angular momentum of the interacting nuclei can significantly influence the barrier height$ V_B $ and barrier position$ R_B $ of the Coulomb barrier [20−24]. Among these degrees of freedom, deformations of the interacting nuclei significantly influence both the barrier characteristics and the production of heavy and superheavy nuclei. Numerous investigations have been conducted to study the influence of quadrupole ($ \beta_2 $ ) deformations of interacting nuclei on the barrier characteristics and the capture cross-sections$ \sigma_{\mathrm{cap}} $ [25−29]. To expand on the promising results of these investigations, we perform an in depth study of the influence of these higher-order deformations to explore adequate assessment of the reaction dynamics.Recent studies have examined the effects of higher-order deformations on the synthesis of SHN, specifically focusing on octupole (
$ \beta_3 $ ) and hexadecapole ($ \beta_4 $ ) deformations [25, 30−38]. To date, very few studies have analyzed and discussed the influence of hexacontatetrapole ($ \beta_6 $ ) and octacontatetrapole ($ \beta_8 $ ) deformations on the dynamics of heavy-ion induced reactions. Thus, an explicit analysis and comprehension concerning the influence of$ \beta_6 $ and$ \beta_8 $ deformations is lacking in literature. Furthermore, while the experimental evidence for the presence of$ \beta_6 $ in proton and alpha scattering from 238U [39, 40] and 154Sm [41] and on fusion reaction dynamics [37, 38, 42, 43] intrigues interest in the characteristics of$ \beta_6 $ , similar insights regarding the$ \beta_8 $ deformation cannot be made due to the absence of experimental data. Therefore, investigating the influence and effect of the$ \beta_6 $ deformation on the synthesis of SHN via heavy-ion induced fusion reactions is of high interest.In view of the deformations of the interacting nuclei, the elongated and compact configurations, determined by the extremes of the interaction barrier height (
$ V_B $ ) and the barrier position ($ R_B $ ), significantly influence the reaction dynamics [17, 29, 36]. While the configuration containing the maximum$ V_B $ and minimal$ R_B $ values is termed a compact configuration, the configuration with the minimal$ V_B $ and the maximal$ R_B $ values is referred to as the elongated configuration. The influence of these configurations has been discussed and established in Refs. [17, 36, 44−47]. These configurations are significantly influenced by the incorporation of higher-order deformations. Therefore, this work analyzes the relevance of the$ \beta_6 $ deformation and associated orientations in reference to the barrier characteristics and capture cross-sections in the context of reactions leading to the synthesis of SHN.For our analysis, we have considered the P-T combinations 48Ca+248Cm, 48Ca+244Pu, 48Ca+238U, 36S+238U , and 48Ti+238U leading to the formation of SHN 296Lv, 292Fl, 286Cn, 274Hs, and 286Fl, respectively. The barrier characteristics of the modified nuclear shape due to the collective influence of the magnitude and sign (
$ \pm $ ) of the deformations (up to$ \beta_6 $ ) of the actinide target nuclei and their corresponding orientations are then used to determine the capture cross-sections ($ \sigma_{\mathrm{cap}} $ ) for the considered P-T combinations using the$ \ell $ -summed Wong formula [48, 49]. The static deformation parameters$ \beta_2,\, \beta_4,\, \beta_6 $ are referenced from the data table provided by M$ \rm\ddot{o} $ ller et al. [50]. The capture cross-sections ($ \sigma_{\mathrm{cap}} $ ) are calculated for center of mass energies ($ E_{\rm{c.m.}} $ ) that spread across the Coulomb barrier and are subsequently compared with the experimental data provided in Ref. [51]. Furthermore, we consider the P-T combination 48Ca+246Es with significant deformation magnitudes across the energy range of 180−220 MeV spanning the Coulomb barrier, to examine the effect of the magnitude and sign of the$ \beta_2^+\beta_4^\pm\beta_6^\pm $ deformation. Thus, this work provides a thorough analysis of the modified barrier characteristics and reaction dynamics with the incorporation of$ \beta_2^+ $ ,$ \beta_4^\pm $ , and$ \beta_6^\pm $ deformations. The findings advance our understanding of the dynamics associated with heavy-ion-induced reactions leading to the formation of SHN.This manuscript is structured as follows: Section II provides a theoretical framework. Section III presents and discusses the results, emphasizing the role of the magnitude and signs (
$ \pm $ ) of hexacontatetrapole deformations ($ \beta_6 $ ) on the nuclear shape of deformed nuclei, the barrier characteristics, and the fusion reaction dynamics of actinides. Finally, Section IV presents a summary of the work done. -
The investigation of the characteristics and synthesis of superheavy nuclei (SHN) has emerged as a prominent area of research in nuclear physics over the past few decades. The exploration of these elements offers a distinctive opportunity to probe the limits of the periodic table and explore the "island of stability", characterized by magic numbers Z = 120,126 and N= 184 [1−6]. Numerous theoretical and experimental studies have offered valuable insights into the synthesis of SHN via heavy-ion-induced reactions. These studies revealed several factors that influence the dynamics of these reactions within the low-energy domain [7−15]. Firstly, for the synthesis of SHN, the interacting nuclei need to overcome the repulsive Coulomb barrier to subsequently create a compound nucleus through the exchange of nucleons and energy. The characteristics of this Coulomb barrier, i.e the barrier height
$ V_B $ and barrier position$ R_B $ , play a significant role, as they can hinder the formation of the new entity [16−19]. Studies around the Coulomb barrier of such interactions suggest that numerous parameters like mass, charge, energy, deformations, orientations, and angular momentum of the interacting nuclei can significantly influence the barrier height$ V_B $ and barrier position$ R_B $ of the Coulomb barrier [20−24]. Among these degrees of freedom, deformations of the interacting nuclei have been found to play a critical role in influencing both the barrier characteristics and the production of heavy and superheavy nuclei. Numerous investigations have been conducted in the literature studying the influence of quadrupole ($ \beta_2 $ ) deformations of interacting nuclei, on the barrier characteristics and the capture cross-sections$ \sigma_{cap} $ [25−29]. The promising results of these investigations encourage us to study in depth the influence of these higher-order deformations to explore adequate assessment of the reaction dynamics.Recent studies have examined the effects of higher-order deformations on the synthesis of SHN, specifically focusing on octupole (
$ \beta_3 $ ) and hexadecapole ($ \beta_4 $ ) deformations [25, 30−38]. Till date a very few studies have analyzed and discussed the influence of hexacontatetrapole ($ \beta_6 $ ) and octacontatertrapole ($ \beta_8 $ ) deformations on the dynamics of heavy-ion induced reactions. So there remains a lack of explicit analysis and comprehension concerning the influence of$ \beta_6 $ and$ \beta_8 $ deformations. Furthermore, while the experimental evidence for the presence of$ \beta_6 $ in proton and alpha scattering from 238U [39, 40] and 154Sm [41] and on fusion reaction dynamics [37, 38, 42, 43], intrigues interest in the characteristics of$ \beta_6 $ , similar insights regarding the$ \beta_8 $ deformation cannot be made due to the absence of experimental data. In view of this, it is of interest to investigate the influence and effect of the$ \beta_6 $ deformation on the synthesis of SHN via heavy-ion induced fusion reactions.In view of the deformations of the interacting nuclei, the elongated and compact configurations, determined by the extremes of the interaction barrier height (
$ V_B $ ) and the barrier position ($ R_B $ ), play a critical role in influencing the reaction dynamics [17, 29, 36]. While the configuration with the maximum$ V_B $ and minimal$ R_B $ is termed a compact configuration, the configuration with the minimal$ V_B $ and the maximal$ R_B $ is referred to as the elongated configuration. The influence of these configurations has been discussed and established in [17, 36, 44−47]. These configurations are significantly influenced by the incorporation of higher-order deformations. Therefore, in the present work, the relevance of the$ \beta_6 $ deformation and associated orientations will be analyzed in reference to the barrier characteristics and capture cross-sections in the context of reactions leading to the synthesis of SHN.For our analysis, we have considered the P-T combinations 48Ca+248Cm, 48Ca+244Pu, 48Ca+238U, 36S+238U and 48Ti+238U leading to the formation of SHN 296Lv, 292Fl, 286Cn, 274Hs and 286Fl respectively. The barrier characteristics of the modified nuclear shape due to the collective influence of the magnitude and sign (
$ \pm $ ) of the deformations (up to$ \beta_6 $ ) of the actinide target nuclei and their corresponding orientations are then used to determine the capture cross-sections ($ \sigma_{cap} $ ) for the considered P-T combinations using the$ \ell $ -summed Wong formula [48, 49]. The static deformation parameters$ \beta_2,\beta_4,\beta_6 $ are is taken from the Data Table of M$ \ddot{o} $ ller et al. [50]. The capture cross-sections ($ \sigma_{cap} $ ) are calculated for center of mass energies ($ E_{c.m.} $ ) spread across the Coulomb barrier, and are subsequently compared with the experimental data available as referenced in [51]. Furthermore, the influence of magnitude and signs of$ \beta_2^+\beta_4^\pm\beta_6^\pm $ deformation is studied by considering the P-T combination 48Ca+246Es having significant magnitude of all deformations at energy range of$ E_{c.m.} $ = 180-220 MeV spanning the Coulomb barrier. Thus, the present work provides a thorough analysis of the modified barrier characteristics and reaction dynamics incorporating the$ \beta_2^+ $ ,$ \beta_4^\pm $ , and$ \beta_6^\pm $ deformations. These findings advance our comprehension further in the direction of understanding and unraveling the complexity of the dynamics associated with heavy-ion-induced reactions leading to the formation of SHN.This manuscript is structured as follows: Section II provides a theoretical framework. Section III presents and discusses the results, emphasizing the role of the magnitude and signs (
$ \pm $ ) of hexacontatetrapole deformations ($ \beta_6 $ ) on the nuclear shape of deformed nuclei, the barrier characteristics, and the fusion reaction dynamics of actinides. Finally, Section Ⅳ presents a summary of the work done. -
The shape of the deformed nuclei can be expressed through the radial vector
$ R_i(\alpha_i) $ equation in terms of the spherical harmonics$ Y_{\lambda i}^{(0)}(\alpha_i) $ and the magnitude of the deformation$ \beta_{\lambda i} $ [43, 50, 52, 53] as$ \begin{aligned}[b] R_i(\alpha_i)&=R_{0i}\left[1+\sum_{\lambda=2,3,4,6}\beta_{\lambda i}Y_{\lambda i}^{(0)}(\alpha_i)\right]\\&=R_{0i}\left[1+\sum_{\lambda=2,3,4,6}\beta_{\lambda i}\sqrt{\frac{2\lambda+1}{4\pi}}P_{\lambda}(\cos{\alpha_i})\right],\end{aligned} $
(1) where
$ i=1,2 $ denotes the projectile and target of the interacting systems, respectively. The term$ R_{0i} $ signifies the radius of the corresponding spherical nuclei, defined by the equation$ R_{0i} = 1.28A^{1/3}_i - 0.76 + 0.8A^{-1/3}_i $ , measured in femtometers (fm) [54]. The variable λ indicates the order of deformation present in the nuclei, with values$ \lambda=2,3,4,6 $ corresponding to quadrupole, octupole, hexadecapole, and hexacontatetrapole deformations, respectively. The static deformation parameter$ \beta_{\lambda i} $ is taken from the data table provided by M$ \ddot{o} $ ller et al. [50]. The function$ P_{\lambda}(\cos{\alpha_i}) $ represents the Legendre polynomial. -
The shape of the deformed nuclei can be expressed by the radial vector
$ R_i(\alpha_i) $ equation in terms of the spherical harmonics$ Y_{\lambda i}^{(0)}(\alpha_i) $ and the magnitude of the deformation$ \beta_{\lambda i} $ [43, 50, 52, 53], as$ \begin{aligned}[b] R_i(\alpha_i)&=R_{0i}\left[1+\sum_{\lambda=2,3,4,6}\beta_{\lambda i}Y_{\lambda i}^{(0)}(\alpha_i)\right]\\&=R_{0i}\left[1+\sum_{\lambda=2,3,4,6}\beta_{\lambda i}\sqrt{\frac{2\lambda+1}{4\pi}}P_{\lambda}(\cos{\alpha_i})\right],\end{aligned} $

(1) Here, the
$ i=1,2 $ denotes the projectile and target of the interacting systems, respectively. The term$ R_{0i} $ signifies the radius of the spherical nuclei, defined by the equation$ R_{0i} = 1.28A^{1/3}_i - 0.76 + 0.8A^{-1/3}_i $ , measured in femtometers (fm) [54]. The variable λ indicates the degree of deformation present in the nuclei, with values$ \lambda=2,3,4,6 $ corresponding to quadrupole, octupole, hexadecapole, and hexacontatetrapole deformations, respectively. The static deformation parameter$ \beta_{\lambda i} $ is taken from the Data Table of M$ \ddot{o} $ ller et al. [50]. The function$ P_{\lambda}(\cos{\alpha_i}) $ represents the Legendre polynomial. -
The colliding nuclei interact through an interaction potential (
$ V_T $ ), which comprises the sum of the attractive nuclear potential ($ V_N $ ), repulsive Coulomb potential ($ V_C $ ), and centrifugal potential ($ V_\ell $ ). The total interaction potential$ V_T $ is quantitatively expressed as follows:$ \begin{aligned}[b]V_T(R_i,A_i,\beta_{\lambda i},\theta_i)=\; & V_N(R_i,A_i,\beta_{\lambda i},\theta_i) \\ & +V_C(R_i,A_i,\beta_{\lambda i},\theta_i)+V_{\ell}(R_i,A_i,\beta_{\lambda i},\theta_i).\end{aligned} $
(2) In Eq.(2), the attractive nuclear potential is represented by
$ V_{N} $ among the two interacting nuclei and is calculated using a generalized theorem for proximity forces, given by Blocki and collaborators in 1977, called Prox77 [54]. The nuclear potential$ V_{N}(R,A_i,\beta_{\lambda i},\theta_i) $ reads as [54−58]$ V_{N}(R,A_i,\beta_{\lambda i},\theta_i)=4\pi\bar{R}\gamma b\Phi(s_0), $
(3) where 'b' is the surface diffuseness parameter and has a constant value of 0.99 fm.
The mean curvature radius (
$ \bar{R} $ ) is evaluated in terms of the radius vector of curvatures$ R_{i1} $ and$ R_{i2} $ for projectile and target nuclei, respectively, as follows:$ \frac{1}{\bar{R}^2}=\frac{1}{R_{11}R_{12}}+\frac{1}{R_{21}R_{22}}+\frac{1}{R_{11}R_{22}}+\frac{1}{R_{21}R_{12}}. $
(4) The principal radii of curvature (
$ R_{i1} $ and$ R_{i2} $ ) for deformed-deformed or spherical-deformed cases is given [56] as$ R_{i1}(\alpha_i)=\frac{\left[R_i^2(\alpha_i)+R_i^{' 2}(\alpha_i)\right]^{3/2}}{R_i^2(\alpha_i)+2R_i^{' 2}(\alpha_i)-R_i(\alpha_i)R_i^{''}(\alpha_i)}, \quad $
(5) $ R_{i2}(\alpha_i)=\frac{R_i(\alpha_i)\sin{\alpha_i}}{\cos{(\pi/2-\alpha_i-\delta_i)}} \quad (i = 1,2). $
(6) For the spherical projectiles, Eq. (5) is simplified as
$ R_{11}(\alpha_1) $ =$ R_{12}(\alpha_1)=R_1(\alpha_1) $ . In Eq. (3), the surface energy constant (γ) is expressed in terms of the asymmetry of nucleons as$ \gamma=0.9517\left[1-1.7826\left(\frac{N-Z}{A}\right)^2\right]\quad\rm{MeVfm}^{-2}. $
(7) The term 4
$ \pi\bar{R}\gamma b $ in Eq. (3) takes care of the shape and geometry of the colliding nuclei. The universal function, which depends on the shortest distance parameter ($ s_0 $ ) between the colliding nuclei along the collision axis, is given as [55, 56]$ \Phi(s_0) = \begin{cases} \begin{aligned} -\frac{1}{2}(s_0-2.54)^2-0.0852&(s_0-2.54)^3, \\&s_0\leq1.2511 \quad {\rm{fm}} \end{aligned} \\ -3.437\exp\left({-\dfrac{s_0}{0.75}}\right), s_0>1.2511 \quad {\rm{fm}}. \end{cases} $
(8) Here,
$ s_0 $ denotes the shortest distance between the two interacting nuclei [56], which is defined as$ s_0= R-X_1-X_2, $
(9) where 'R' represents the distance between the interacting nuclei and
$ X_1 $ ,$ X_2 $ are the projections of the P-T nuclei w.r.t. the colliding axis. These projections are determined as$ \begin{aligned}[b] & X_1=R_1(\alpha_1)\mathrm{cos}(\theta_1-\alpha_1); \\ & X_2=R_2(\alpha_2)\mathrm{cos}(180+\theta_2-\alpha_2).\end{aligned} $
(10) Applying the minimization conditions on
$ s_0 $ yields$ \begin{aligned}[b] \tan(\theta_1-\alpha_1)&=\tan(\delta_1)=-\frac{R_1^{'}(\alpha_1)}{R_1(\alpha_1)},\\ \tan(180+\theta_2-\alpha_2)=&\tan(\delta_2)=-\frac{R_2^{'}(\alpha_2)}{R_2(\alpha_2)}. \end{aligned}$
(11) The repulsive Coulomb potential (
$ V_C $ ) in Eq. (2) is defined for deformed-deformed colliding nuclei as follows [59, 60]:$ \begin{aligned}[b] \label{col_pot} V_{C}(R)=\;&\frac{Z_1Z_2e^2}{R}+ Z_1Z_2e^2\sum\limits_{\lambda=2,3,4,6}^{i=1,2}\left(\frac{R_i^{\lambda}(\alpha_i)}{R^{\lambda+1}}\right)\beta_{\lambda}Y_\lambda^{(0)}(\theta_i)\\& \times\left[\frac{3}{2\lambda+1}+\left(\frac{12}{7(2\lambda+1)}\right)\beta_{\lambda}Y_\lambda^{(0)}(\theta_i)\right]. \end{aligned} $
(12) The centrifugal potential in Eq. (2) is the rotational kinetic energy. This potential is dependent on the angular momentum
$ \ell $ and is expressed as follows [61, 62]:$ V_\ell(R,A_i,\beta_{\lambda i},\theta_i)=\frac{\hbar^2{\ell(\ell+1)}}{2I}; \quad I = \mu R^2. $
(13) Eqs. (2)−(13), which define the total interaction potential, provide significant insights into the characteristics of the interacting nuclei, which encompass barrier characteristics, including the barrier height
$ V_B $ , barrier position$ R_B $ , and barrier curvature$ \hbar\omega_B $ . These parameters are affected by the degrees of freedom related to deformation and orientation, as indicated in the radius vector presented in Eq. (1). As a result, these parameters play a crucial role in determining the capture cross-sections, which is calculated using the$ \ell $ -Wong formula [48, 49] for different combinations of the interacting P-T. This concept is discussed in the next section. -
The colliding nuclei interact through an interaction potential (
$ V_T $ ), which comprises the sum of the attractive nuclear potential ($ V_N $ ), repulsive Coulomb potential ($ V_C $ ), and centrifugal potential ($ V_\ell $ ). The total interaction potential$ V_T $ is quantitatively expressed as follows:$ \begin{aligned}[b]V_T(R_i,A_i,\beta_{\lambda i},\theta_i) =\;& V_N(R_i,A_i,\beta_{\lambda i},\theta_i)\\&+ V_C(R_i,A_i,\beta_{\lambda i},\theta_i) + V_{\ell}(R_i,A_i,\beta_{\lambda i},\theta_i) ,\end{aligned} $

(2) In Eq.2, the attractive nuclear potential is represented by
$ V_{N} $ , among the two interacting nuclei. It is calculated using a generalized theorem for proximity forces, given by Blocki and collaborators in 1977, called Prox77 [54]. The nuclear potential$ V_{N}(R,A_i,\beta_{\lambda i},\theta_i) $ reads as[54−58]$ V_{N}(R,A_i,\beta_{\lambda i},\theta_i)=4\pi\bar{R}\gamma b\Phi(s_0), $

(3) Here,b' is the surface diffuseness parameter and has a constant value of 0.99 fm.
The mean curvature radius (
$ \bar{R} $ ) is evaluated in terms of radius vector of curvatures$ R_{i1} $ and$ R_{i2} $ for projectile and target nuclei respectively, as follows:$ \frac{1}{\bar{R}^2}=\frac{1}{R_{11}R_{12}}+\frac{1}{R_{21}R_{22}}+\frac{1}{R_{11}R_{22}}+\frac{1}{R_{21}R_{12}}. $

(4) The principal radii of curvature (
$ R_{i1} $ and$ R_{i2} $ ) for deformed-deformed or spherical-deformed cases is given [56] as$ R_{i1}(\alpha_i)=\frac{\left[R_i^2(\alpha_i)+R_i^{' 2}(\alpha_i)\right]^{3/2}}{R_i^2(\alpha_i)+2R_i^{' 2}(\alpha_i)-R_i(\alpha_i)R_i^{''}(\alpha_i)}, \quad $

(5) $ R_{i2}(\alpha_i)=\frac{R_i(\alpha_i)\sin{\alpha_i}}{\cos{(\pi/2-\alpha_i-\delta_i)}} \quad (i = 1,2). $

(6) For the spherical projectiles, this Eq. 5 is simplified as
$ R_{11}(\alpha_1) $ =$ R_{12}(\alpha_1)=R_1(\alpha_1) $ . In Eq.(3) the surface energy constant (γ) is expressed in terms of the asymmetry of nucleons as,$ \gamma=0.9517\left[1-1.7826\left(\frac{N-Z}{A}\right)^2\right] \quad {\rm{MeVfm}}^{-2}, $

(7) The term 4
$ \pi\bar{R}\gamma b $ in Eq.(3) takes care of the shape and geometry of the colliding nuclei. While the universal function dependent on the shortest distance parameter ($ s_0 $ ) between the colliding nuclei along the collision axis is given as [55, 56],$ \Phi(s_0) = \begin{cases} \begin{aligned} -\frac{1}{2}(s_0-2.54)^2-0.0852&(s_0-2.54)^3, \\&s_0\leq1.2511 \quad {\rm{fm}} \end{aligned} \\ -3.437\exp\left({-\dfrac{s_0}{0.75}}\right), s_0>1.2511 \quad {\rm{fm}}. \end{cases} $

(8) Here, the
$ s_0 $ is the shortest distance between the two interacting nuclei [56], which is defined as$ s_0= R-X_1-X_2, $

(9) Where 'R' represents the distance between the interacting nuclei and
$ X_1 $ ,$ X_2 $ are the projections of P-T nuclei w.r.t. the colliding axis. These projections are determined as$ \begin{aligned}[b]& X_1=R_1(\alpha_1)cos(\theta_1-\alpha_1);\\& X_2=R_2(\alpha_2)cos(180+\theta_2-\alpha_2) \end{aligned} $

(10) With the minimization conditions on
$ s_0 $ we get,$ \begin{aligned}[b] \tan(\theta_1-\alpha_1)&=\tan(\delta_1)=-\frac{R_1^{'}(\alpha_1)}{R_1(\alpha_1)},\\ \tan(180+\theta_2-\alpha_2)=&\tan(\delta_2)=-\frac{R_2^{'}(\alpha_2)}{R_2(\alpha_2)}. \end{aligned}$

(11) The repulsive Coulomb potential (
$ V_C $ ) in Eq.(2) is defined for deformed-deformed colliding nuclei as follows[59, 60]:$ \begin{aligned}[b] \label{col_pot} V_{C}(R)=\;&\frac{Z_1Z_2e^2}{R}+ Z_1Z_2e^2\sum\limits_{\lambda=2,3,4,6}^{i=1,2}\left(\frac{R_i^{\lambda}(\alpha_i)}{R^{\lambda+1}}\right)\beta_{\lambda}Y_\lambda^{(0)}(\theta_i)\\& \times\left[\frac{3}{2\lambda+1}+\left(\frac{12}{7(2\lambda+1)}\right)\beta_{\lambda}Y_\lambda^{(0)}(\theta_i)\right]. \end{aligned} $

(12) The centrifugal potential (
$ V_{\ell} $ ), mentioned in Eq. 12 is the rotational kinetic energy. This potential is dependent on the angular momentum$ \ell $ and is formulated as follows [61, 62]:$ V_\ell(R,A_i,\beta_{\lambda i},\theta_i)=\frac{\hbar^2{\ell(\ell+1)}}{2I}; \quad I = \mu R^2. $

(13) The equations (2) - (13) that define the total interaction potential provide significant insights into the characteristics of the interacting nuclei. This encompasses barrier characteristics, including the barrier height
$ V_B $ , the barrier position$ R_B $ , and the barrier curvature$ \hbar\omega_B $ . These parameters are affected by the degrees of freedom related to deformation and orientation, as indicated in the radius vector presented in Eq.(1). As a result, these parameters play a crucial role in finding the capture cross-sections, which is calculated by using the$ \ell $ -Wong formula [48, 49] for different combinations of the interacting P-T, briefed in the next section. -
The capture cross-section for deformed and oriented nuclei, interacting at the center of mass energies (
$ E_{c.m.} $ ), is evaluated using the Wong formula [59, 63], which reads as$ \sigma_{cap}\ =\frac{R_B^2\hbar\omega_B}{2E_{c.m.}}\ln\left[1+\exp\left(\frac{2\pi}{\hbar\omega_B}(E_{c.m.}-V_B)\right)\right], $

(14) which further, transforms to the extended
$ \ell $ -summed Wong Model [48, 49]. This model incorporates the summation of the cross-section associated with each$ \ell $ -partial wave, which can be mathematically represented as follows:$ \sigma_{cap}(E_{c.m.},\theta_i)=\sum\limits_{\ell=0}^{\ell_{max}}\sigma_{\ell}=\frac{\pi}{k^2}\sum\limits_{\ell=0}^{\ell_{max}}(2\ell+1)P_{\ell}, $

(15) where
$ k=\sqrt{\dfrac{2\mu E_{c.m.}}{\hbar^2}} $ and μ represents the reduced mass. The sharp cut-off approximation [55, 64] is employed to determine the maximum angular momentum, denoted as$ \ell_{max} $ . Here, the barrier penetration or tunneling probability$ P_{\ell} $ for each angular momentum ($ \ell $ ) is derived using the Hill-Wheeler approximation [65].$ P^{HW}_{\ell}(E_{c.m})=\Bigg[1+\exp{\bigg(\frac{2 \pi [V_{B}^{\ell}(E_{c.m.})-E_{c.m.}]}{\hbar\omega_{B}^{\ell}(E_{c.m.})}\bigg)}\bigg]^{-1}, $

(16) In this Eq. the
$ V_{B}^{\ell}(E_{c.m.}) $ ,$ R_{B}^{\ell}(E_{c.m.}) $ and$ \hbar\omega_{B}^{\ell}(E_{c.m.}) $ are obtained from the total interaction potential between the two interacting nuclei determined in Eq. 2.In addition, the integrated or average capture cross-sections are obtained by integrating over the range of orientations
$ \theta_i $ of the deformed nuclei having$ \beta_2,\beta_4, \beta_6 $ deformations [47], which is represented as$ \sigma_{int}(E_{c.m.})=\int_{\theta_1 =0}^{\pi/2}\int_{\theta_2 =0}^{\pi/2}\sigma(E_{c.m.},\theta_i)\sin{\theta_1}\sin{\theta_2}d\theta_1d\theta_2. $

(17) -
The capture cross-section for deformed and oriented nuclei, interacting at the center of mass energies (
$ E_{\rm{c.m.}} $ ), is evaluated using the Wong formula [59, 63], which is expressed as$ \sigma_{\mathrm{cap}}\ =\frac{R_B^2\hbar\omega_B}{2E_{\rm{c.m.}}}\ln\left[1+\exp\left(\frac{2\pi}{\hbar\omega_B}(E_{\rm{c.m.}}-V_B)\right)\right], $
(14) and further transforms to the extended
$ \ell $ -summed Wong Model [48, 49]. This model incorporates the summation of the cross-section associated with each$ \ell $ -partial wave, which can be mathematically represented as follows:$ \sigma_{\mathrm{cap}}(E_{\mathrm{c.m.}},\theta_i)=\sum\limits_{\ell=0}^{\ell_{\mathrm{max}}}\sigma_{\ell}=\frac{\pi}{k^2}\sum\limits_{\ell=0}^{\ell_{\mathrm{max}}}(2\ell+1)P_{\ell}, $
(15) where
$ k=\sqrt{\dfrac{2\mu E\mathrm{_{c.m.}}}{\hbar^2}} $ and μ represents the reduced mass. The sharp cut-off approximation [55, 64] is employed to determine the maximum angular momentum, denoted as$ \ell_{\rm max} $ . Here, the barrier penetration or tunneling probability$ P_{\ell} $ for each angular momentum ($ \ell $ ) is derived using the Hill-Wheeler approximation [65]:$ P^{HW}_{\ell}(E_{\rm c.m})=\Bigg[1+\exp{\bigg(\frac{2 \pi [V_{B}^{\ell}(E_{\rm c.m.})-E_{\rm c.m.}]}{\hbar\omega_{B}^{\ell}(E_{\rm c.m.})}\bigg)}\bigg]^{-1}, $
(16) where
$ V_{B}^{\ell}(E_{\rm c.m.}) $ ,$ R_{B}^{\ell}(E_{\rm c.m.}) $ , and$ \hbar\omega_{B}^{\ell}(E_{\rm c.m.}) $ are obtained from the total interaction potential between the two interacting nuclei as determined in Eq. (2).In addition, the integrated or average capture cross-sections are obtained by integrating over the range of orientations
$ \theta_i $ of the deformed nuclei having$ \beta_2,\beta_4, \beta_6 $ deformations [47], which is represented as$ \sigma_{\rm int}(E_{\rm c.m.})=\int_{\theta_1 =0}^{\pi/2}\int_{\theta_2 =0}^{\pi/2}\sigma(E_{\rm c.m.},\theta_i)\sin{\theta_1}\sin{\theta_2}\mathrm{d}\theta_1\mathrm{d}\theta_2. $
(17) -
In the present work, we aim to explore the influence of modifications in the nuclear shape due to the incorporation of hexacontatetrapole deformation (
$ \beta_6 $ ) along with ($ \beta_2 $ ), ($ \beta_4 $ ) deformed target nuclei. This study systematically investigates the collective influence of the magnitude and sign ($ \pm $ ) of these higher-order deformations (up to$ \beta_6 $ ) on barrier characteristics of heavy-ion induced fusion reactions. Further, the elongated and compact configurations obtained from these modified barrier characteristics corresponding to$ \beta_4 $ and$ \beta_6 $ deformations are used to calculate the capture cross-sections ($ \sigma_{\mathrm{cap}} $ ). The results are compared with available experimental data for center of mass energies$ E_{\mathrm{c.m.}} $ spread across the Coulomb barrier. The analysis takes into account both spherical+ deformed and deformed+deformed P-T combinations. This comprehensive study offers new insights into the influence of higher-order deformations up to the order of hexacontatetrapole deformation ($ \beta_6 $ ) on the fusion reaction dynamics. This section presents and discusses the findings of this study. -
In the present work, we aim to explore the influence of the modified nuclear shape due to the incorporation of hexacontatetrapole deformation (
$ \beta_6 $ ) along with ($ \beta_2 $ ), ($ \beta_4 $ ) deformed target nuclei. This study systematically investigates the collective influence of magnitude and sign ($ \pm $ ) of these higher-order deformations (up to$ \beta_6 $ ) on barrier characteristics of heavy-ion induced fusion reactions. Further, the elongated and compact configurations obtained from these modified barrier characteristics corresponding to$ \beta_4 $ and$ \beta_6 $ deformations are used to calculate the capture cross-sections ($ \sigma_{cap} $ ) which are compared with available experimental data, for center of mass energies$ E_{c.m.} $ spread across the Coulomb barrier. The analysis takes into account both spherical+deformed and deformed+deformed P-T combinations. This comprehensive study offers new insights into the influence of higher-order deformations up to the order of hexacontatetrapole deformation ($ \beta_6 $ ) on the fusion reaction dynamics. The findings of this work are presented and discussed in the following sections. -
The nuclear shape usually shows deviations from perfect spherical symmetry. These deviations arise from dipole moments linked to the neutron-to-proton ratio within the nuclei, leading to a deformed nuclear shape. These nuclear deformations (
$ \beta_{\lambda} $ ) associated with the multipole order i.e.$ \lambda=2,3,4,6 $ provides quadrupole, octupole, hexadexapole and hexacontatetrapole deformed shapes of nuclei respectively. The influence of these higher-order deformations is included in the nuclear shape via the radial vector as defined in Eq. (1). To visualize the influence of$ \beta_6 $ deformation on nuclear shape, we considered 246Es nuclei having significant magnitude of$ \beta_2 $ taken from the data table of M$ \ddot{o} $ ller et al. [50], while deformations$ \beta_4 $ =$ \pm $ 0.05 and$ \beta_6 $ =$ \pm $ 0.1 are assumed to analyze the significant effect of$ \beta_6 $ , shown in Fig.(1). The figure illustrates the evolution of the nuclear shape of 246Es by incorporating different orders of deformations. One can see the evolution of prolate-deformed nuclei with the incorporation of$ \beta_4^{\pm} $ and$ \beta_6^{\pm} $ deformations associated with the nuclei. It is known that the incorporation of$ \beta_4^+ $ with$ \beta_2^+ $ leads to elongation, whereas the inclusion of$ \beta_4^- $ with$ \beta_2^+ $ leads to contraction of the prolate deformed nuclei. While Fig.1(a) illustrates the modification in nuclear shape after the inclusion of$ \beta_6^{\pm} $ in$ \beta_2^+\beta_4^+ $ deformed nuclei, figure 1(b) represents similar modifications in shape of$ \beta_2^+\beta_4^- $ deformed nuclei due to the incorporation of$ \beta_6^{\pm} $ . It can be seen from the figures that the incorporation of$ \beta_6^{\pm} $ deformation introduces complexity to both the elongated shape of$ \beta_2^+\beta_4^{+} $ deformed nuclei and the compressed shape of$ \beta_2^+\beta_4^{-} $ deformed nuclei. Specifically, the presence of$ \beta_6^+ $ in both$ \beta_4^{\pm} $ , leads to further elongation of nuclear shape along its poles, and slight compression along the belly region of the nuclei. This elongation due to$ \beta_6^+ $ is more pronounced in the$ \beta_2^+\beta_4^+ $ case than the$ \beta_2^+\beta_4^- $ deformed nuclei. On the other hand,$ \beta_6^- $ leads to compression on the poles and elongation along the belly, when incorporated in both$ \beta_4^+ $ and$ \beta_4^- $ . This flatness is more prominent at poles for$ \beta_2^+\beta_4^- $ deformed nuclei than$ \beta_2^+\beta_4^+ $ , as shown in Fig1.
Figure 1. (color online) Schematic diagram of shape evolution of the nucleus 246Es incorporating the quadrupole (
$ \beta_2 $ ), hexadecapole ($ \beta_4^\pm $ ) and hexacontatetrapole ($ \beta_6^\pm $ ); with$ \beta_2 $ =0.248, considering$ \beta_4 $ =$ \pm $ 0.05 and$ \beta_6 $ =$ \pm $ 0.1In other words, the incorporation of
$ \beta_6^{+} $ leads to elongation at the poles region and compression at the belly region, whereas$ \beta_6^{-} $ leads to the elongation at the belly region and compression at poles. In addition to the sign ($ \pm $ ) of the hexacontatertapole deformation, the extent of the elongation and compression in the deformed nuclear shape is also influenced by the magnitudes of the deformation associated with the nuclei. The above observations highlight the sensitivity of nuclear shapes to the magnitude and signs of higher-order deformations, specifically$ \beta_6 $ in conjunction with$ \beta_2 $ and$ \beta_4 $ deformations. These modifications due to the collective influence of$ \beta_2\beta_4\beta_6 $ deformations provide significant modifications on the nuclear barrier characteristics that govern the heavy-ion fusion dynamics. The upcoming section discusses the effect of these deformed nuclear shapes on the barrier characteristics relative to the angle of orientations of the deformed nuclei with respect to the collision axis. -
Typically, the nuclear shape deviates from perfect spherical symmetry. These deviations arise from dipole moments linked to the neutron-to-proton ratio within the nuclei, which leads to a deformed nuclear shape. These nuclear deformations (
$ \beta_{\lambda} $ ) associated with the multipole order i.e.,$ \lambda=2,3,4,6 $ provide quadrupole, octupole, hexadexapole and hexacontatetrapole deformed nuclei shapes, respectively. The influence of these higher-order deformations is included in the nuclear shape via the radial vector, as defined in Eq. (1). To visualize the influence of$ \beta_6 $ deformation on the nuclear shape, we considered 246Es nuclei subject to a significant magnitude of$ \beta_2 $ , which is referenced from the data table provided by M$ \rm\ddot{o} $ ller et al. [50], while deformations$ \beta_4 $ =$ \pm $ 0.05 and$ \beta_6 $ =$ \pm $ 0.1 are assumed to analyze the significant effect of$ \beta_6 $ , as shown in Fig. 1. The figure illustrates the evolution of the nuclear shape of 246Es under various orders of deformations. The figure clearly illustrates the evolution of prolate-deformed nuclei with the incorporation of$ \beta_4^{\pm} $ and$ \beta_6^{\pm} $ deformations associated with the nuclei. The incorporation of$ \beta_4^+ $ with$ \beta_2^+ $ causes elongation, whereas the inclusion of$ \beta_4^- $ with$ \beta_2^+ $ causes the contraction of the prolate deformed nuclei. While Fig. 1(a) illustrates the modification in nuclear shape after the inclusion of$ \beta_6^{\pm} $ in$ \beta_2^+\beta_4^+ $ deformed nuclei, Fig. 1(b) represents similar modifications in the shape of$ \beta_2^+\beta_4^- $ deformed nuclei due to the incorporation of$ \beta_6^{\pm} $ . The figure shows that the incorporation of$ \beta_6^{\pm} $ deformation introduces complexity to both the elongated shape of$ \beta_2^+\beta_4^{+} $ deformed nuclei and the compressed shape of$ \beta_2^+\beta_4^{-} $ deformed nuclei. Specifically, the presence of$ \beta_6^+ $ in both$ \beta_4^{\pm} $ further elongates the nuclear shape along its poles and causes slight compression along the belly region of the nuclei. This elongation due to$ \beta_6^+ $ is more pronounced in the$ \beta_2^+\beta_4^+ $ case than the$ \beta_2^+\beta_4^- $ deformed nuclei. On the other hand,$ \beta_6^- $ leads to compression on the poles and elongation along the belly, when incorporated in both$ \beta_4^+ $ and$ \beta_4^- $ . This flatness is more prominent at the poles for$ \beta_2^+\beta_4^- $ deformed nuclei than$ \beta_2^+\beta_4^+ $ , as shown in Fig. 1.
Figure 1. (color online) Schematic diagram showing the shape evolution of the nucleus 246Es incorporating the quadrupole (
$ \beta_2 $ ), hexadecapole ($ \beta_4^\pm $ ), and hexacontatetrapole ($ \beta_6^\pm $ ); with$ \beta_2 $ =0.248, considering$ \beta_4 $ =$ \pm $ 0.05 and$ \beta_6 $ =$ \pm $ 0.1.In other words, the incorporation of
$ \beta_6^{+} $ leads to elongation at the pole region and compression at the belly region, whereas$ \beta_6^{-} $ leads to the elongation at the belly region and compression at the poles. In addition to the sign ($ \pm $ ) of the hexacontatertapole deformation, the extent of the elongation and compression in the deformed nuclear shape is also influenced by the magnitudes of the deformation associated with the nuclei. These observations highlight the sensitivity of nuclear shapes to the magnitude and signs of higher-order deformations, specifically$ \beta_6 $ in conjunction with$ \beta_2 $ and$ \beta_4 $ deformations. These modifications due to the collective influence of$ \beta_2\beta_4\beta_6 $ deformations significantly modify the nuclear barrier characteristics that govern the heavy-ion fusion dynamics. The next section discusses the effect of these deformed nuclear shapes on the barrier characteristics relative to the angle of orientations of the deformed nuclei with respect to the collision axis. -
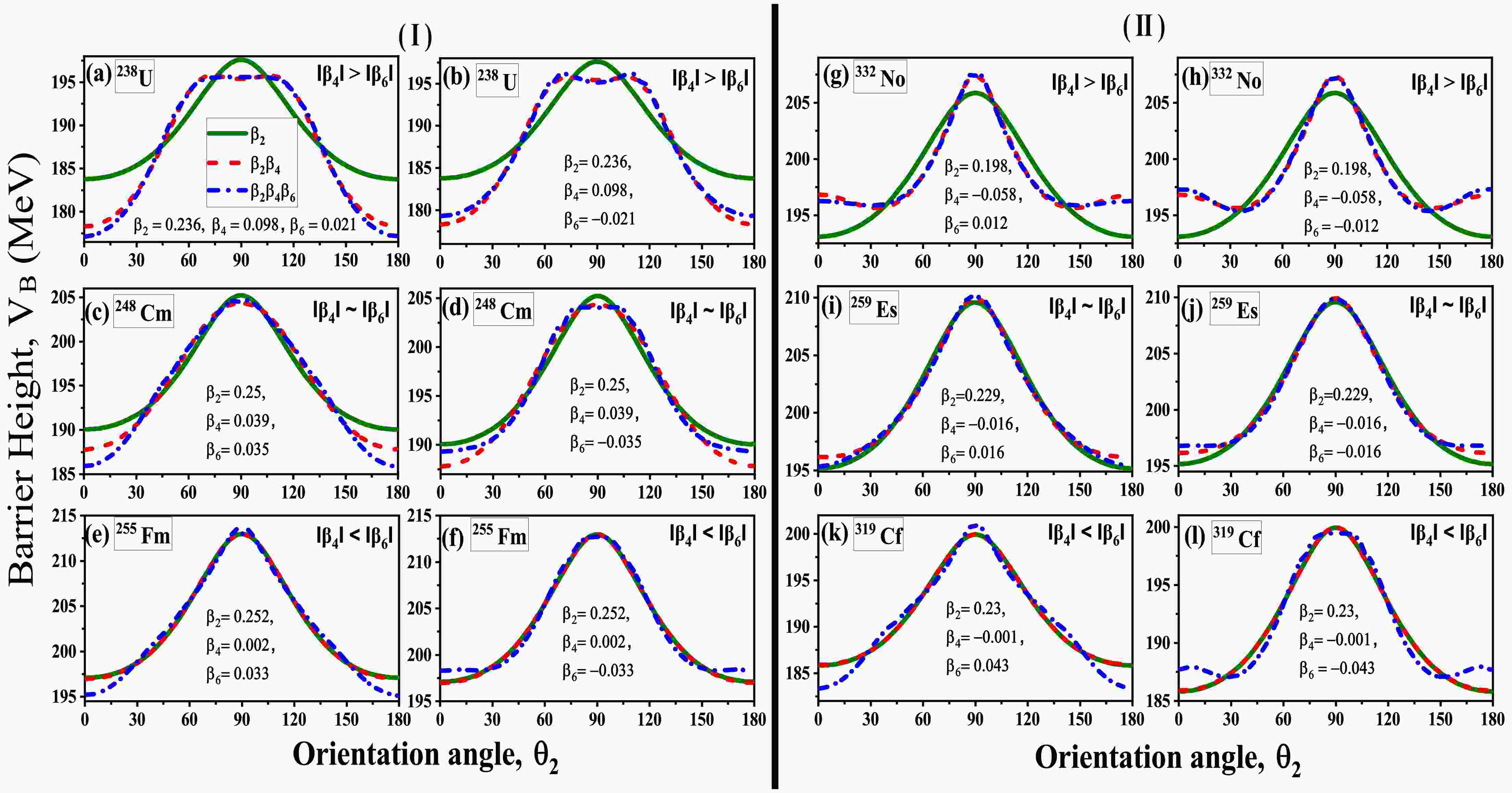
In the previous section, we discussed the influence of the magnitude and sign of the
$ \beta_6^{\pm} $ on the shape of the nuclei along with the$ \beta_2^+ $ and$ \beta_4^{\pm} $ deformations. This current section aims to broaden the analysis by investigating the comprehensive effect of the modified shape of$ \beta_4^{\pm} $ and$ \beta_6^{\pm} $ deformed nuclei on the barrier characteristics i.e. barrier height ($ V_B $ ) and barrier position($ R_B $ ) of the interacting nuclei. The objective of this analysis is to determine how the incorporation of$ \beta_4^{\pm} $ and$ \beta_6^{\pm} $ deformations modifies the barrier characteristics when compared to a prolate deformed ($ \beta_2^+ $ ) case. For this analysis, we investigated the barrier characteristics for the 48Ca-induced reactions with deformed actinide nuclei having non-zero values of$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ deformations. The variation in$ V_B $ and$ R_B $ with respect to target orientation ($ \theta_2 $ ) ranging from$ 0^\circ $ to$ 180^\circ $ for different combinations of$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ deformations are illustrated in Fig.2 and Fig.3 respectively. From these figures, one can see that here the cases are divided into two panels with panel (Ⅰ) representing the barrier characteristics of$ \beta_2^+\beta_4^{+}\beta_6^{\pm} $ deformed nuclei while panel (Ⅱ) represents the barrier characteristics of$ \beta_2^+\beta_4^{-}\beta_6^{\pm} $ deformed nuclei. Each panel of the analyzed actinide nuclei is classified into three distinct groups based on the values of$ \beta_4 $ and$ \beta_6 $ deformations. In particular, Fig.2(a, b, g and h) illustrates the scenarios where the magnitude of$ \beta_4 $ is greater than$ \beta_6 $ , while Fig.2(c, d, i and j) depicts the cases where magnitude of$ \beta_4 $ is approximately equal to magnitude of$ \beta_6 $ deformation. Additionally, Fig.2(e, f, k and l) showcases the instances where the magnitude of$ \beta_6 $ deformation exceeds the magnitude of$ \beta_4 $ deformation. To conduct a thorough analysis of both the sign and magnitude of the associated$ \beta_6 $ deformation, both positive and negative$ \beta_6 $ deformations of equal magnitude are considered.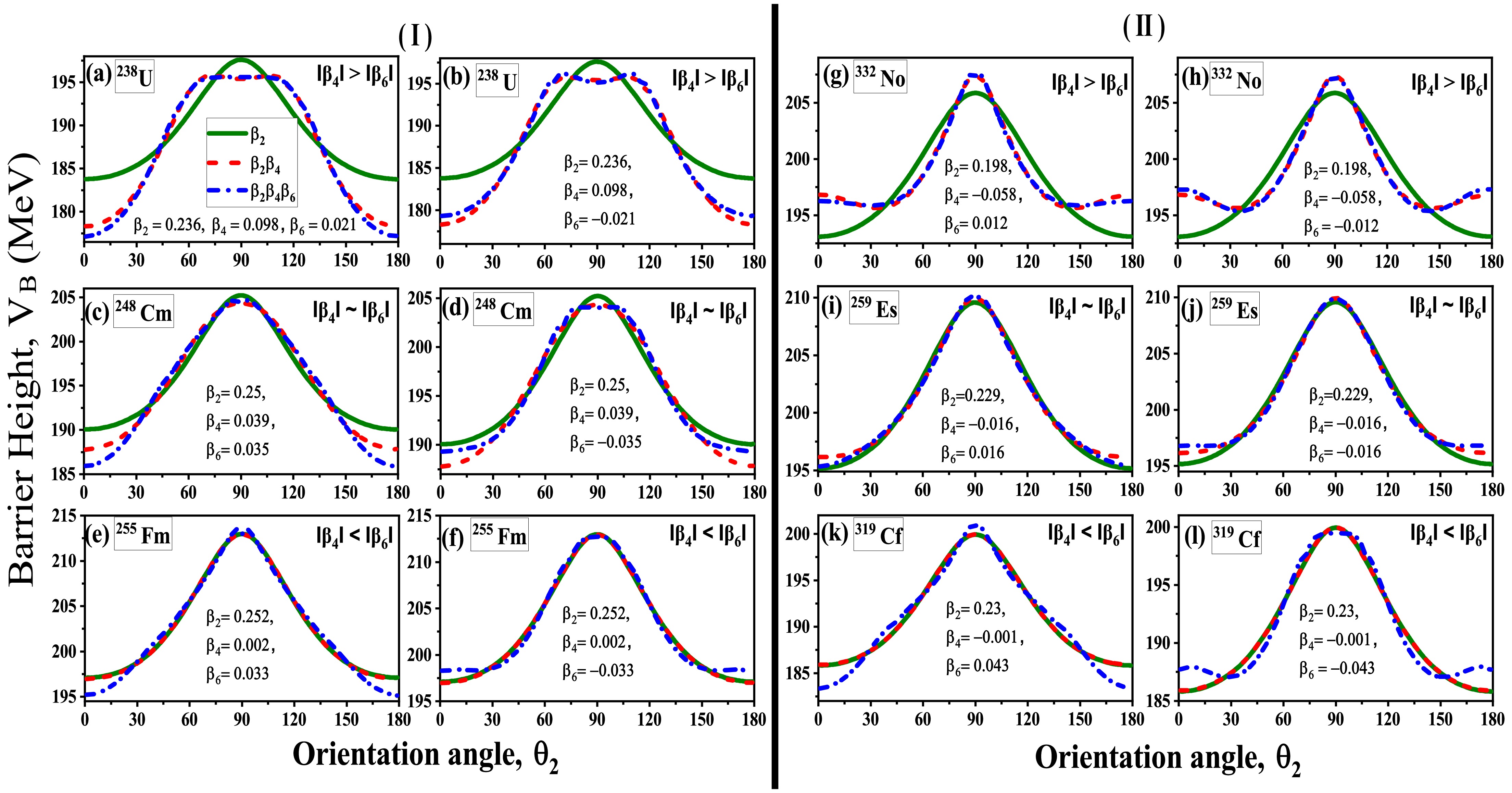
Figure 2. (color online) A schematic representation illustrating the changes in barrier height (
$ V_B $ ) in relation to the orientation angle ($ \theta_2 $ ) of deformed actinide nuclei. Panel (Ⅰ) features nuclei with configurations$ \beta_2^+\beta_4^+\beta_6^\pm $ , while Panel (Ⅱ) showcases$ \beta_2^+\beta_4^-\beta_6^\pm $ deformed nuclei.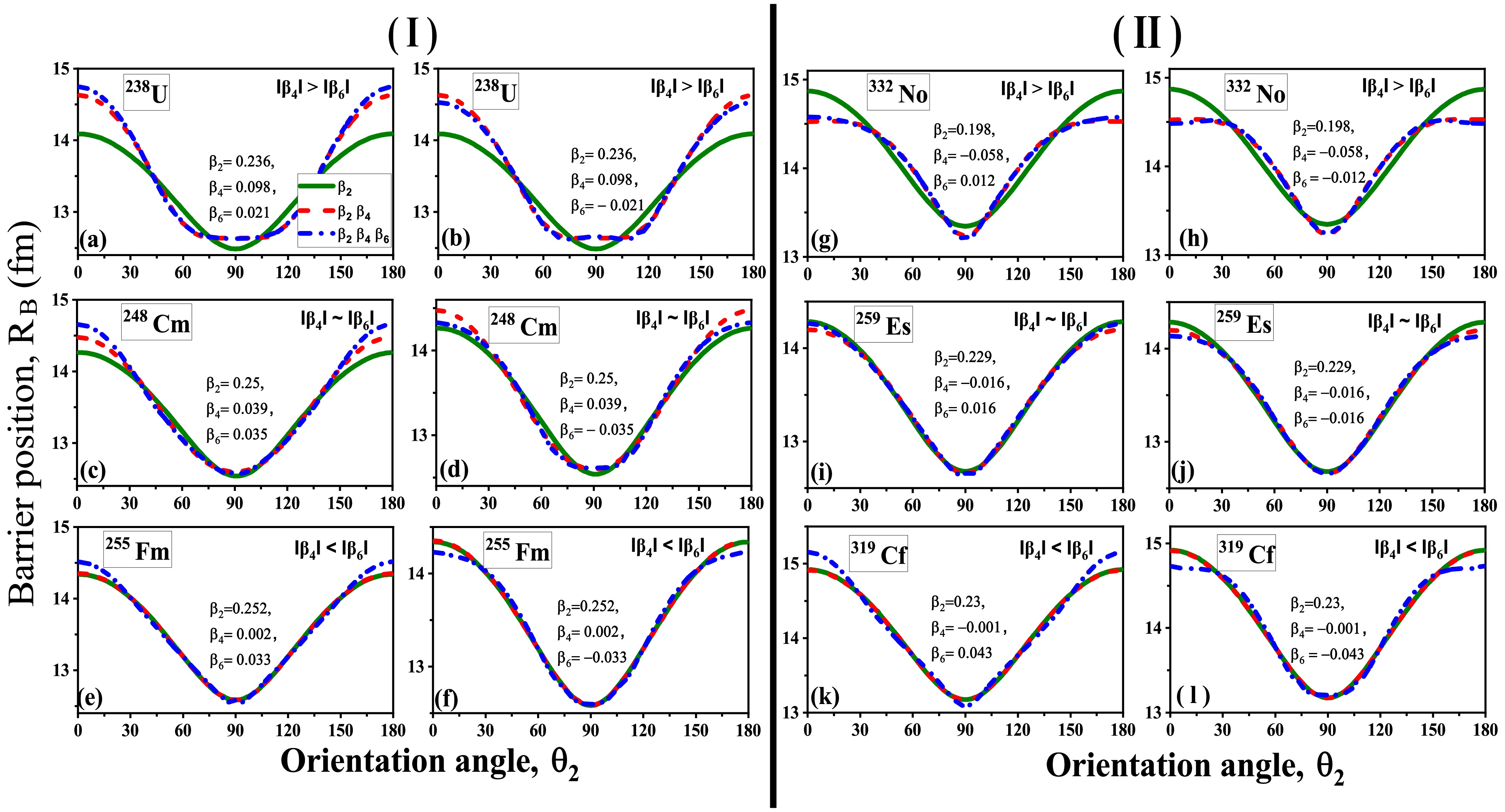
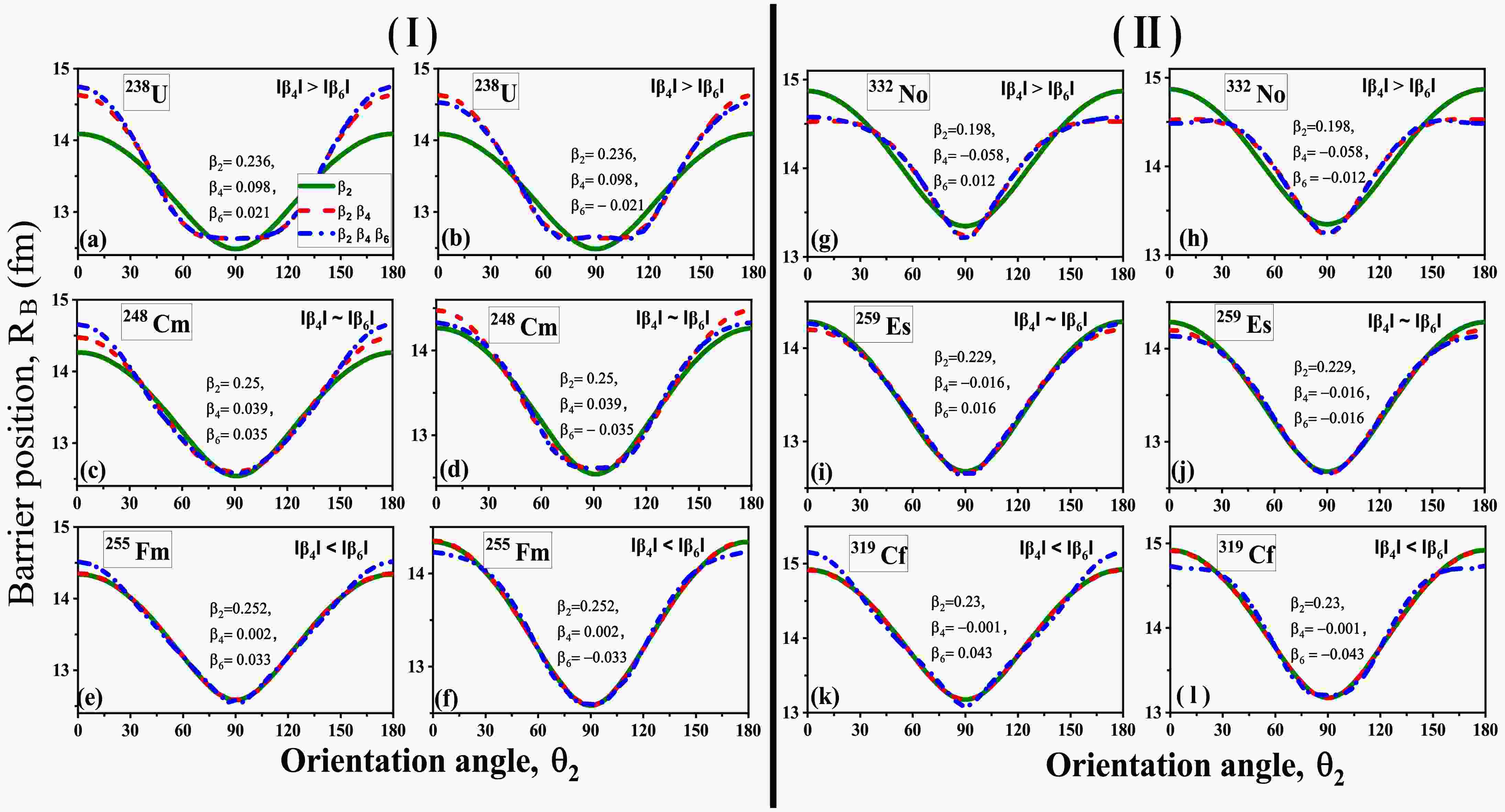
Figure 3. (color online) A schematic representation illustrating the changes in barrier position (
$ R_B $ ) in relation to the orientation angle ($ \theta_2 $ ) of deformed actinide nuclei. Panel (Ⅰ) features nuclei with configurations$ \beta_2^+\beta_4^+\beta_6^\pm $ , while Panel (Ⅱ) showcases$ \beta_2^+\beta_4^-\beta_6^\pm $ deformed nuclei.From these figures, one can observe that the introduction of
$ \beta_4^+ $ in quadrupole deformed nuclei leads to a lowering of the barrier height$ V_B $ . Conversely, the incorporation of$ \beta_4^- $ in$ \beta_2 $ deformed nuclei leads to an increase in$ V_B $ . The relative variation in the$ V_B $ is influenced by the magnitudes of the$ \beta_2 $ and$ \beta_4 $ deformation parameters. Along with the barrier characteristics, a noticeable change in the orientation angle of the compact and elongated configurations has also been observed [36]. Further, the incorporation of$ \beta_6^{\pm} $ in conjunction with$ \beta_2 $ and$ \beta_4 $ deformation modifies the shape of the nuclei at both the pole and belly positions, leading to variation in the barrier characteristics$ V_B $ and$ R_B $ . For instance, incorporation of$ \beta_6^+ $ to$ \beta_2^+\beta_4^{\pm} $ deformed nuclei lowers the barrier height$ V_B $ specifically at target orientation$ \theta_2 $ =0° or 180°. Meanwhile,$ \beta_6^- $ increases the barrier height due to compression of the shape of the nuclei around the poles at$ \theta_2 $ =0° or 180°. The impact of$ \beta_6 $ deformations is more pronounced for the orientations in the range of$ 0^\circ $ -$ 40^\circ $ for all the cases. However, as$ \theta_2 $ surpasses this range, there is a slight change in the$ V_B $ corresponding to$ \beta_2\beta_4\beta_6 $ deformed nuclei as compared to$ \beta_2\beta_4 $ deformed nuclei. Conversely, an interesting variation can be observed at target orientation$ \theta_2=90^\circ $ . At this orientation, the barrier height$ V_B $ increases for the$ \beta_6^+ $ cases while a decrease in$ V_B $ can be observed for the$ \beta_6^- $ cases relative to$ \beta_4 $ . This variation, as discussed in the previous section, is linked to compression and elongation of the nuclear shape at the belly of the nuclei due to the incorporation of$ \beta_6^+ $ and$ \beta_6^- $ deformations, respectively. It is important to note that the variation of$ V_B $ is not very significant at$ 90^\circ $ for all the cases. Additionally, in scenarios where the value of$ \beta_4 $ is greater than$ \beta_6 $ and$ \beta_4 $ is approximately equal to$ \beta_6 $ , the changes in barrier characteristics resulting from the inclusion of$ \beta_6 $ correspond to the deformation trend of$ \beta_4 $ . Conversely, in instances where$ \beta_4 $ is less than$ \beta_6 $ , as illustrated in Fig.2(e,f,k,l), the substantial impact of$ \beta_6 $ is evident due to its significantly larger magnitude relative to$ \beta_4 $ . In a similar manner, an inverse variation with respect to$ V_B $ is observed in the analysis of barrier position$ R_B $ for all the considered reactions. The variation of$ R_B $ for the considered reactions w.r.t orientation angle ($ \theta_2 $ ) are illustrated in Fig.3.Along with the variation in the barrier characteristics
$ V_B $ and$ R_B $ , a significant shift in the optimum orientation can also be observed with the incorporation of$ \beta_6 $ . These modified optimum orientations of the compact or elongated configuration of the$ \beta_6 $ deformed nuclei can impose a significant influence on the overall dynamics of the nuclear interaction. These modified compact or elongated configurations are characterized by the maximal and minimum values of barrier height ($ V_B $ ) and barrier position($ R_B $ ). While the elongated configuration corresponds to the configuration with the minimum$ V_B $ and maximum$ R_B $ , whereas the compact configuration is the configuration associated with the maximum$ V_B $ and minimum$ R_B $ . The analysis of the barrier height corresponding to$ \beta_2,\beta_4,\beta_6 $ in relation to the orientation angle ($ \theta_2 $ ) is shown in Fig.2. The figure clearly demonstrates that the variation in the barrier height$ V_B $ due to incorporation of$ \beta_6 $ deformation in comparison to the$ \beta_4 $ deformation is significantly more pronounced in the orientation range$ \theta_2 $ =$ 0^\circ $ to$ 40^\circ $ than those at$ \theta_2 $ =$ 70^\circ $ to$ 90^\circ $ . The orientation range$ \theta_2 $ =$ 0^\circ $ to$ 40^\circ $ represents the region with the minimum barrier height or the elongated configuration, while the orientation range$ \theta_2 $ =$ 70^\circ $ to$ 90^\circ $ represents the region with the maximum barrier height or the compact configuration for the$ \beta_2\beta_4\beta_6 $ deformation combinations, respectively. Based on these results, additional emphasis will be placed on evaluating the impact of$ \beta_6 $ on the barrier characteristics at orientation angles ranging from$ 0^\circ $ to$ 40^\circ $ .Till now, we have established that the incorporation of
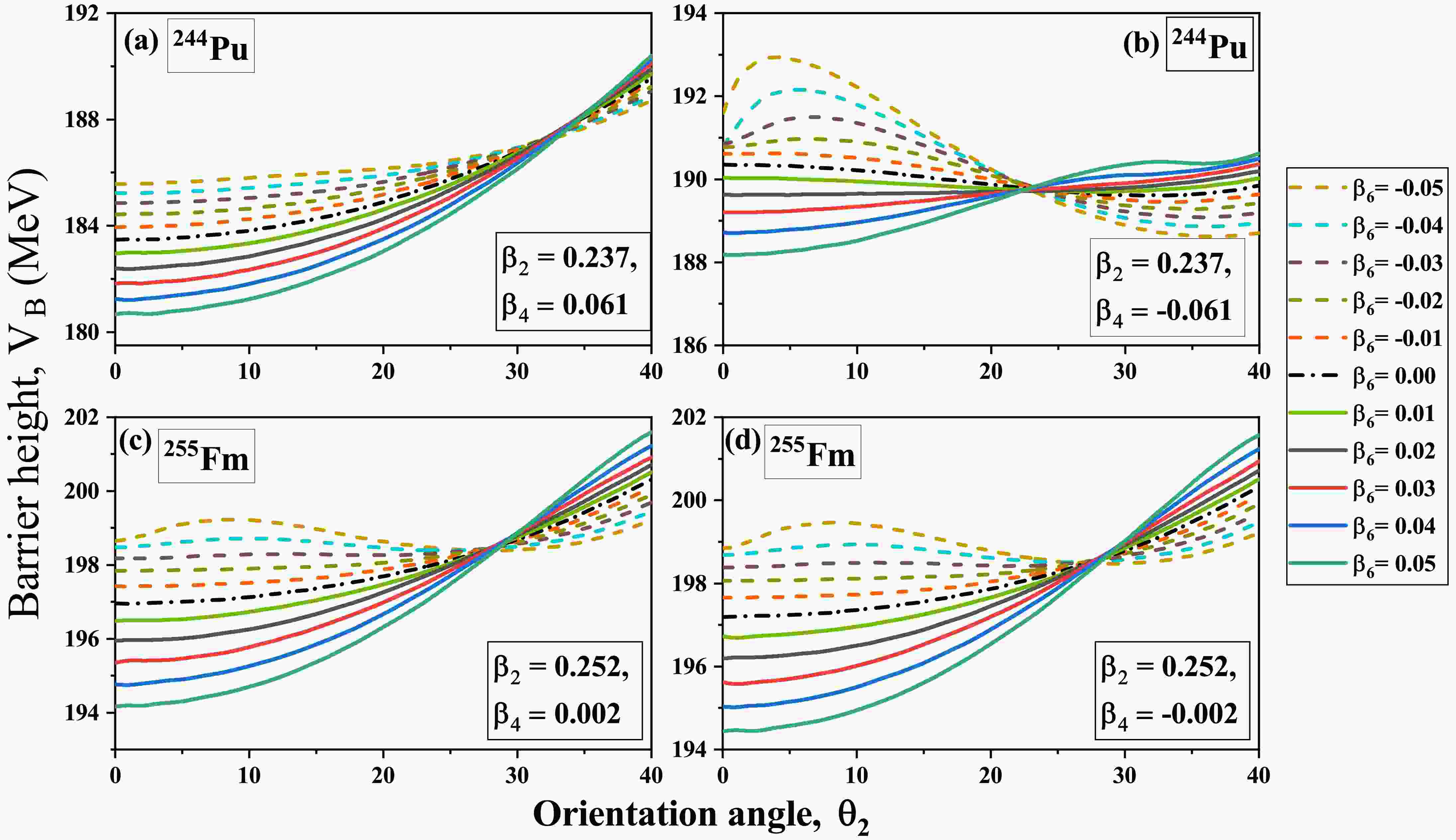
$ \beta_6 $ deformation along with$ \beta_2 $ and$ \beta_4 $ provides noticeable alterations in the barrier characteristics for orientation angles ranging from$ 0^\circ $ to$ 40^\circ $ . Further to explore the influence of the magnitude of$ \beta_6 $ we studied the variation in the$ V_B $ for the above-mentioned range of orientation angle by varying the magnitude of$ \beta_6 $ deformation from -0.05 to 0.05 as demonstrated in Fig.4. For the analysis, we consider the actinide nuclei having a significant magnitude of$ \beta_4 $ deformation as compared to the magnitude of$ \beta_6 $ (e.g. 244Pu), and the nuclei with a smaller magnitude of$ \beta_4 $ deformation as compared to the magnitude of$ \beta_6 $ (e.g. 255Fm). Note that the study assumes both positive and negative signs for the magnitude of$ \beta_4 $ of the same nuclei. From Fig.4, it can be observed that an increase in the magnitude of$ \beta_6^+ $ introduces much significant elongation to the nucleus along its poles, leading to a decrease in barrier height with respect to$ \beta_4^\pm $ at$ \theta_2 $ =$ 0^\circ $ or$ 180^\circ $ . Conversely, an increase in the magnitude of$ \beta_6^- $ induces an increase in the barrier height due to an enhanced compression effect along the poles. As we move towards the target orientation$ \theta_2 $ =$ 30^\circ $ , variations in barrier height$ V_B $ can be observed for both$ \beta_6^+ $ and$ \beta_6^- $ cases. It is observed that increasing the positive value of$ \beta_6^+ $ leads to a high$ V_B $ while increasing the negative value of$ \beta_6^- $ results in a lower$ V_B $ at$ 30^\circ $ or above, compared to$ \beta_2 $ $ \beta_4 $ deformed nuclei. These variations are due to shape modifications caused by the incorporation of$ \beta_6^{\pm} $ . In Fig.4(a), 244Pu have a significant magnitude of$ \beta_4^+ $ , the elongated shape always appears at orientation angle$ \theta_2 $ =$ 0^\circ $ , regardless of the magnitude of$ \beta_6^\pm $ . However, in Fig.4(b), a large negative$ \beta_4^- $ induces the compression in the nuclear shape, and the orientation angle for the elongated configuration shifts to around$ \theta_2=30^\circ $ . When$ \beta_6^+ $ is added, it reduces this compression and brings back elongation at the poles$ \theta_2=0^\circ $ as its values increase. On the other hand,$ \beta_6^- $ makes the compression at the poles even stronger, reinforcing the minimum barrier height around$ \theta_2=30^\circ $ .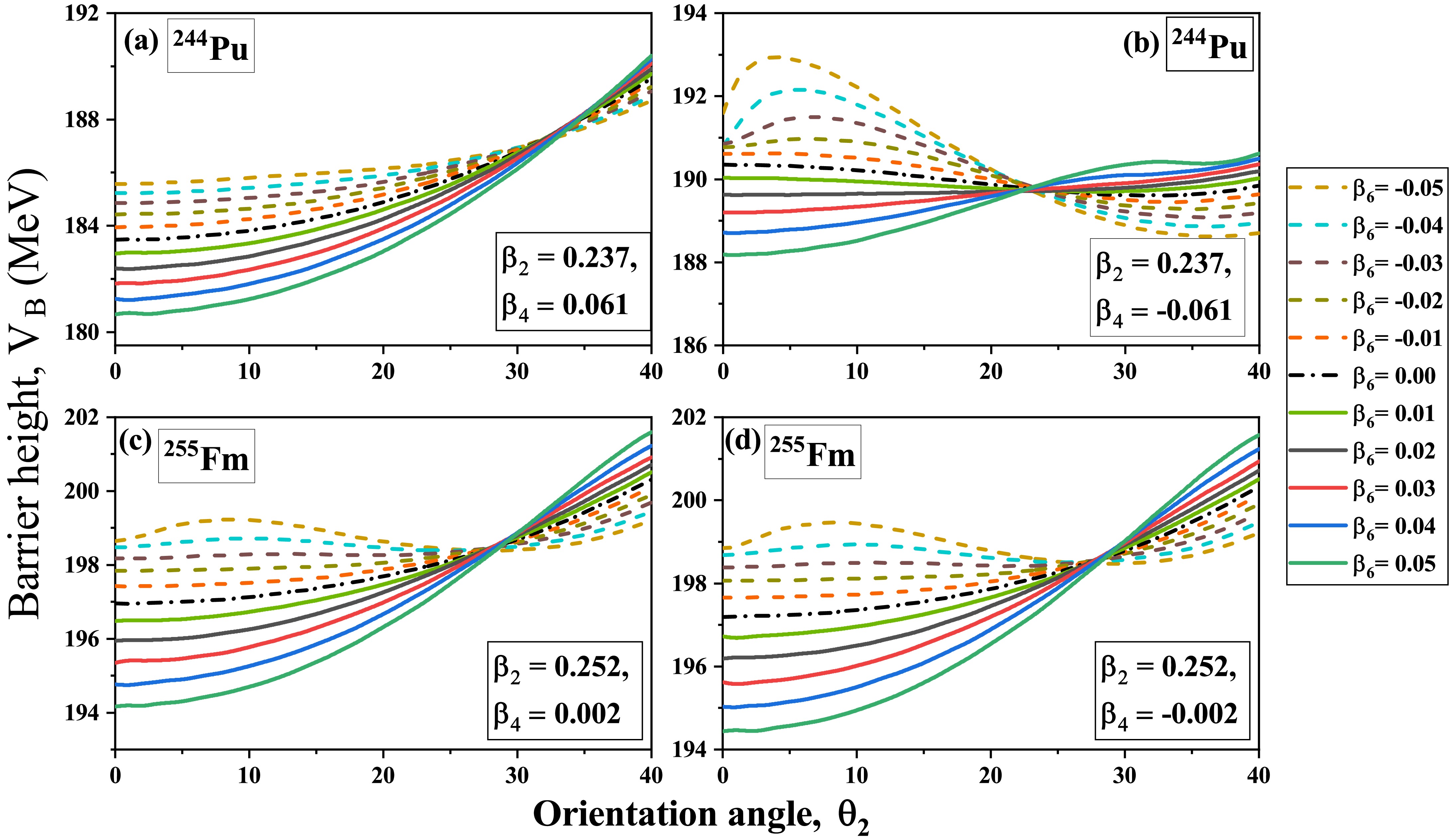
Figure 4. (color online) Schematic diagram showing the variation of barrier height with respect to the orientation angle of the target varying from 0°–40°, under different values of
$ \beta_6 $ ranging from –0.05 to +0.05 for nucleus with significant$ \beta_4^\pm $ (244Pu) and nucleus with small magnitude of$ \beta_4^\pm $ (255Fm).On the other hand, for a smaller magnitude of
$ \beta_4^\pm $ , the shape of nuclei is majorly influenced by the magnitude and sign of$ \beta_6 $ deformation. For instance, for both the cases of$ \beta_6 $ , the elongated configuration is observed at$ \theta_2 $ =$ 0^\circ $ or$ 180^\circ $ as illustrated in Fig.4(c,d). However, this orientation angle for elongation configuration gets shifted towards$ \theta_2\approx30^\circ $ for the higher magnitude of$ \beta_6^- $ . This analysis indicates that the magnitude and sign of the$ \beta_6 $ deformation have a significant influence on the barrier height$ V_B $ at the elongated configuration and also can shift the elongated configuration from$ 0^\circ $ to around$ 30^\circ $ , in conjunction with the influence of$ \beta_2^+\beta_4^{\pm} $ deformations.In order to conduct an in-depth analysis of the variation in barrier height
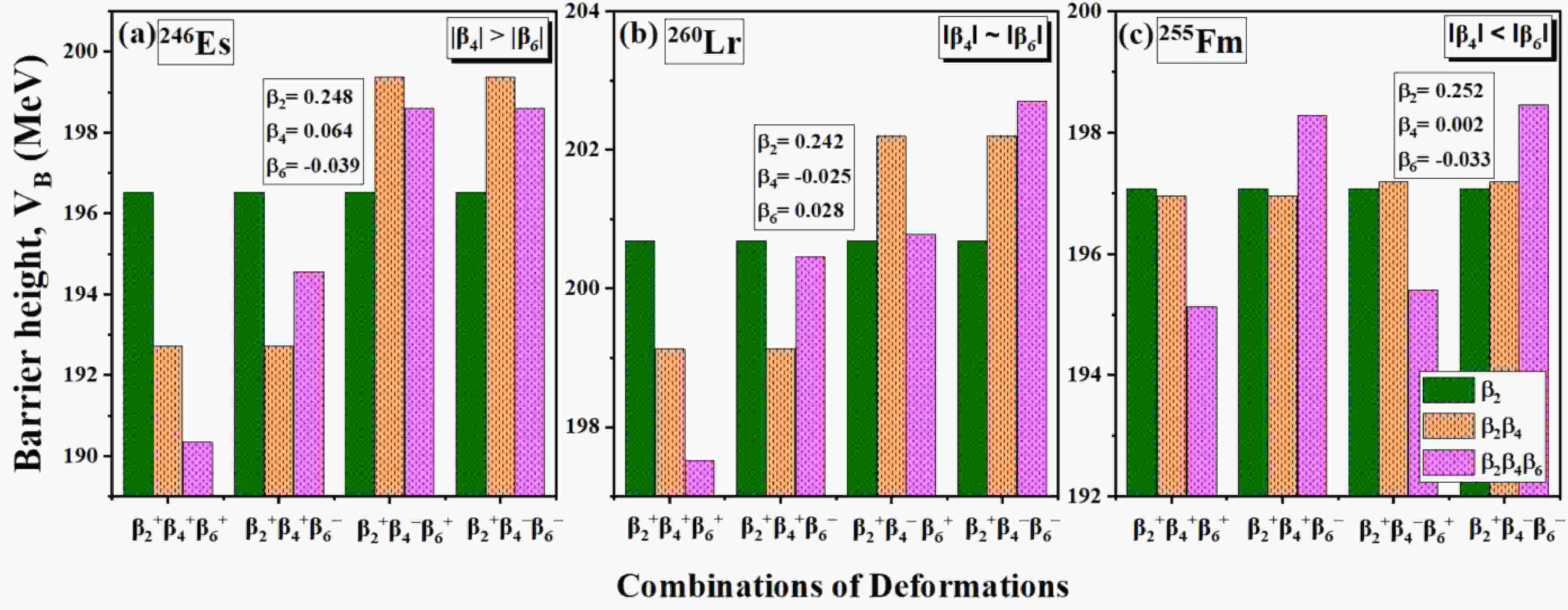
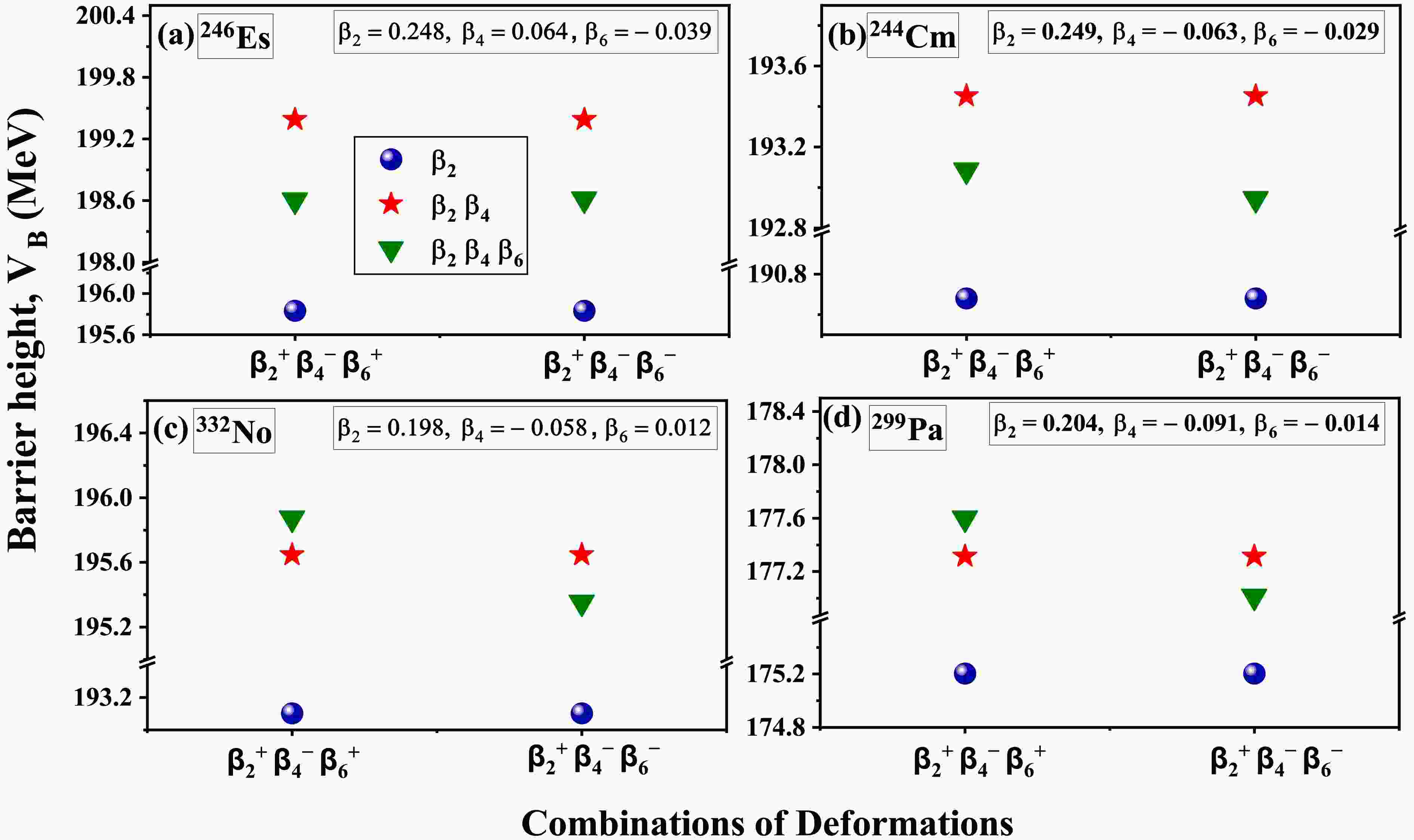
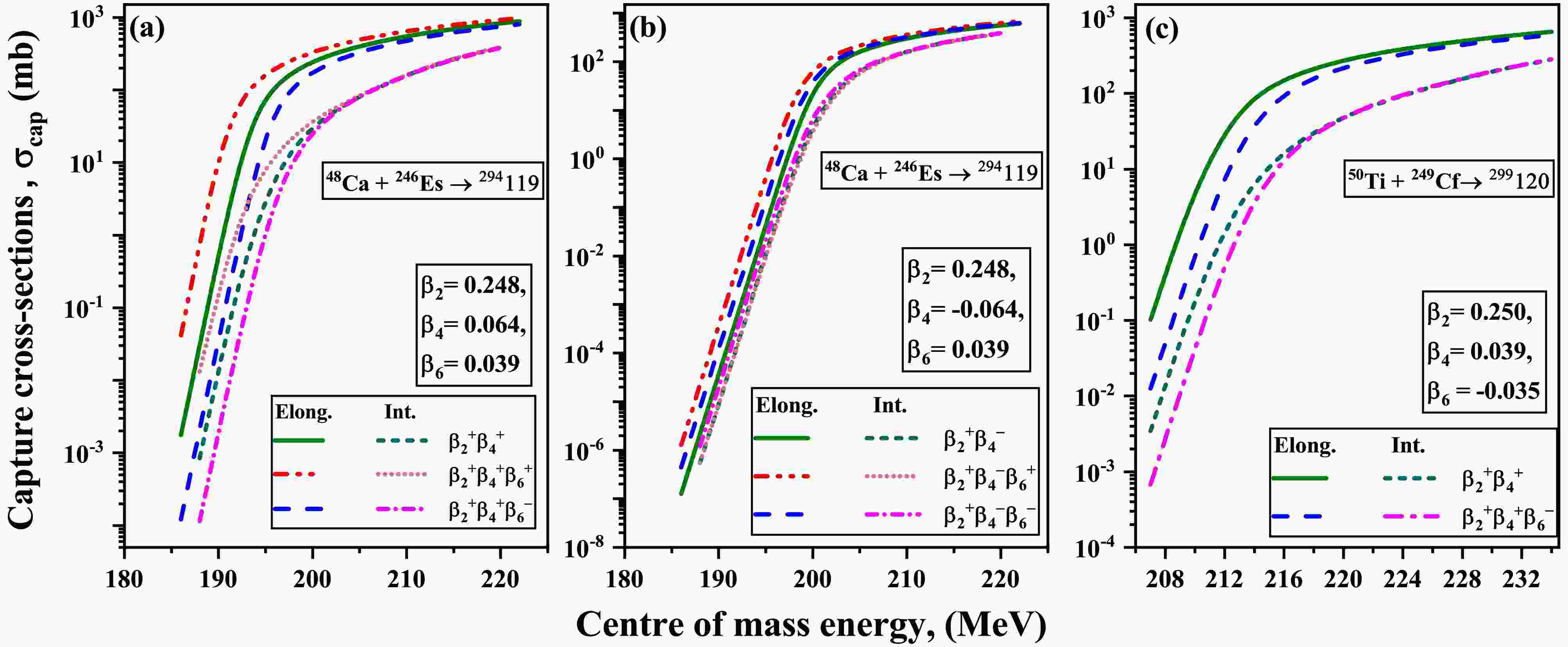
$ V_B $ at the elongated configuration, we examined different sign combinations of quadrupole ($ \beta_2 $ ), hexadecapole ($ \beta_4 $ ), and hexacontatetrapole ($ \beta_6 $ ) deformations. This investigation focuses on several actinide nuclei to provide a comprehensive analysis of magnitudes and signs of deformations. Considered nuclei are examined by comparing the magnitudes of$ \beta_4 $ and$ \beta_6 $ deformation, categorized into three sets: (a)$ \beta_4 $ >$ \beta_6 $ , (b)$ \beta_4\approx\beta_6 $ , and (c)$ \beta_4 $ <$ \beta_6 $ . These three sets are analyzed for the deformation combinations specifically$ \beta_2^+\beta_4^+\beta_6^+ $ ,$ \beta_2^+\beta_4^+\beta_6^- $ ,$ \beta_2^+\beta_4^-\beta_6^+ $ , and$ \beta_2^+\beta_4^-\beta_6^- $ , as presented in Fig.5. The deformations of the considered nuclei are taken from the data table of M$ \ddot{o} $ ller et al. [50], and the magnitudes of$ \beta_4 $ and$ \beta_6 $ are considered with both positive and negative signs for the analysis. The analysis of the figure reveals that for the combinations$ \beta_2^+\beta_4^+\beta_6^+ $ and$ \beta_2^+\beta_4^+\beta_6^- $ , the incorporation of$ \beta_6^+ $ results in a reduction of the barrier height ($ V_B $ ), whereas incorporation of$ \beta_6^- $ counteracts the influence of$ \beta_4^+ $ , thus resulting in an increase in$ V_B $ when added to the deformed nuclei of$ \beta_2^+\beta_4^+ $ . This result is consistent across all sets of magnitudes of$ \beta_4 $ and$ \beta_6 $ , as depicted in Fig.5. While the same trend of variation in barrier height is obtained for$ \beta_6^+ $ and$ \beta_6^- $ when incorporated in the$ \beta_2^+\beta_4^- $ deformed nuclei. These effects of$ \beta_6^+ $ and$ \beta_6^- $ are consistent when incorporated with$ \beta_2^+\beta_4^- $ deformation combination but specific to scenarios where$ \beta_4 \approx \beta_6 $ and$ \beta_4 < \beta_6 $ , where the magnitude of$ \beta_4 $ is not much significant, as illustrated in Fig.5(b,c). However, besides this, a minor deviation in this trend occurs when$ \beta_4 > \beta_6 $ case is considered, as shown in Fig.5(a). Contrary to expectations, the addition of$ \beta_6^+ $ and$ \beta_6^- $ does not yield the anticipated decrease and increase in$ V_B $ when combined with$ \beta_4^- $ . This seems to indicate that the predominance of$ \beta_4 $ over$ \beta_6 $ induces a structural modification. Further explicit analysis is necessary to quantify the interactions among these deformation parameters in the case of$ \beta_4 > \beta_6 $ and to assess their collective impact on the barrier characteristics, specifically at the elongation configuration.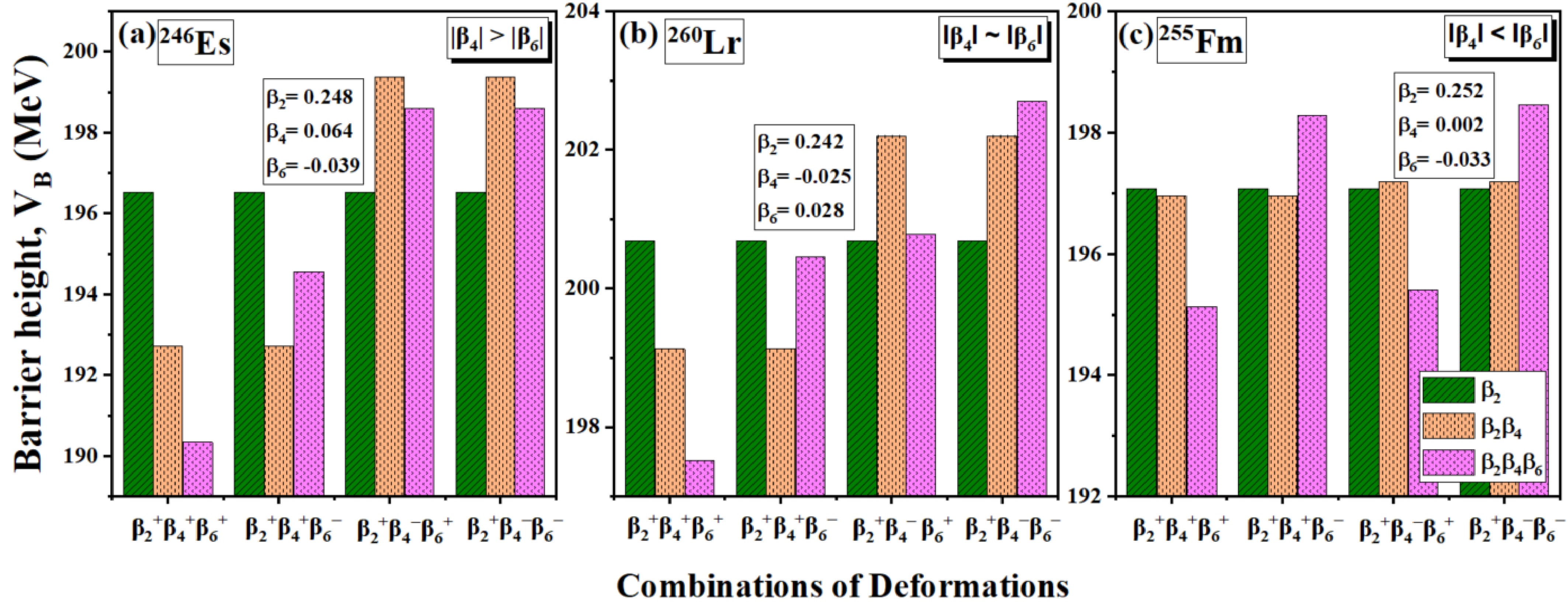
Figure 5. (color online) Schematic diagram of comparison of the barrier heights of nuclei at elongated configuration corresponding to different combinations of deformations
$ \beta_2^+\beta_4^+\beta_6^+ $ ,$ \beta_2^+\beta_4^+\beta_6^- $ ,$ \beta_2^+\beta_4^-\beta_6^+ $ , and$ \beta_2^+\beta_4^-\beta_6^- $ for the considered nuclei having variation of magnitudes such as (a)$ \beta_4 $ >$ \beta_6 $ , (b)$ \beta_4 $ $ \approx $ $ \beta_6 $ , (c)$ \beta_4 < \beta_6 $ .To further examine the influence of the
$ \beta_6^\pm $ deformation in the presence of a substantial$ \beta_4^- $ deformation, we conducted an analysis of the variations in$ V_B $ at elongated configurations for several nuclei illustrated in Fig.6. In this context, we refer to Fig.4(b), which demonstrates that the magnitude of$ \beta_4^- $ is considerable to the magnitude of the$ \beta_6^\pm $ where the presence of$ \beta_4^- $ deformation contributes to the overall shape of the nuclei. As previously mentioned, an increase in the magnitude of$ \beta_6^+ $ is associated with a decrease in$ V_B $ , leading to elongation at an angle of$ 0^\circ $ . However, for lower magnitudes of$ \beta_6^+ $ , both compression and elongation effects arise due to$ \beta_4^- $ and$ \beta_6^+ $ , respectively, creating a balance in the shape that results in a higher$ V_B $ than that produced solely by$ \beta_4^- $ . On the other hand, the$ \beta_6^- $ deformation intensifies the compression at poles but continues the elongation near$ \theta_2 $ $ \approx $ $ 30^\circ $ , resulting in a decrease in$ V_B $ as its magnitude increases. The relevant evidence for this behavior in the nuclei is depicted in Fig.6(c,d). Meanwhile, as the magnitudes of both$ \beta_6^+ $ and$ \beta_6^- $ deformations rise, the values of$ V_B $ become comparable. This behavior is illustrated in Fig.6(a,b), which shows the comparable and lower values of$ V_B $ for$ \beta_6^\pm $ in relation to$ \beta_4^- $ . Nevertheless, the relative change in$ V_B $ for$ \beta_6^\pm $ compared to$ \beta_4^- $ is not significant.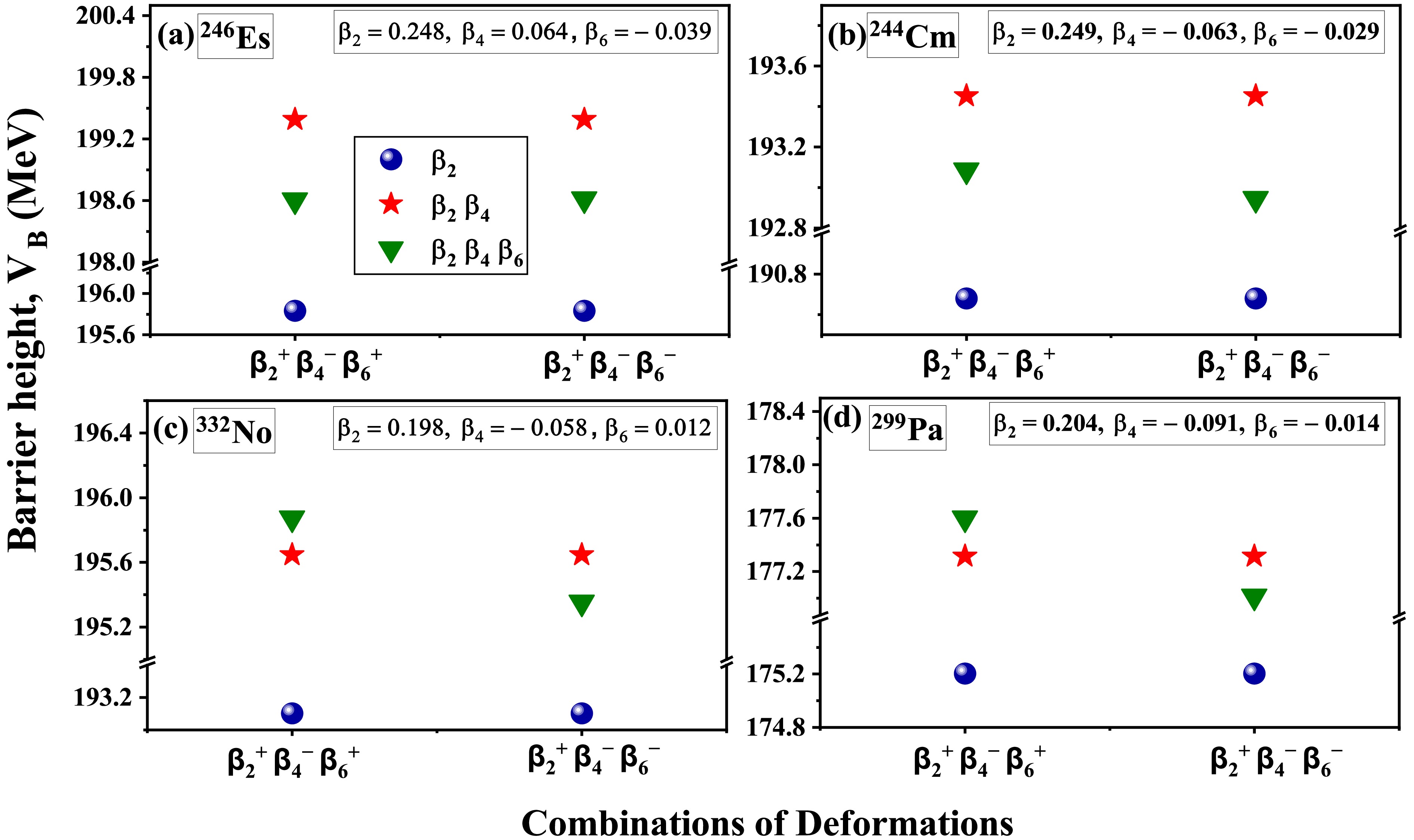
Figure 6. (color online) Schematic diagram of comparison of the barrier heights of different actinides with 48Ca projectile at the elongated configuration for the
$ \beta_2^+\beta_4^-\beta_6^+ $ , and$ \beta_2^+\beta_4^-\beta_6^- $ combination of deformations in the case of$ \beta_4 $ >$ \beta_6 $ .The above discussion explored the role of hexacontatetrapole deformations in heavy-ion induced reactions for a spherical projectile (48Ca) with
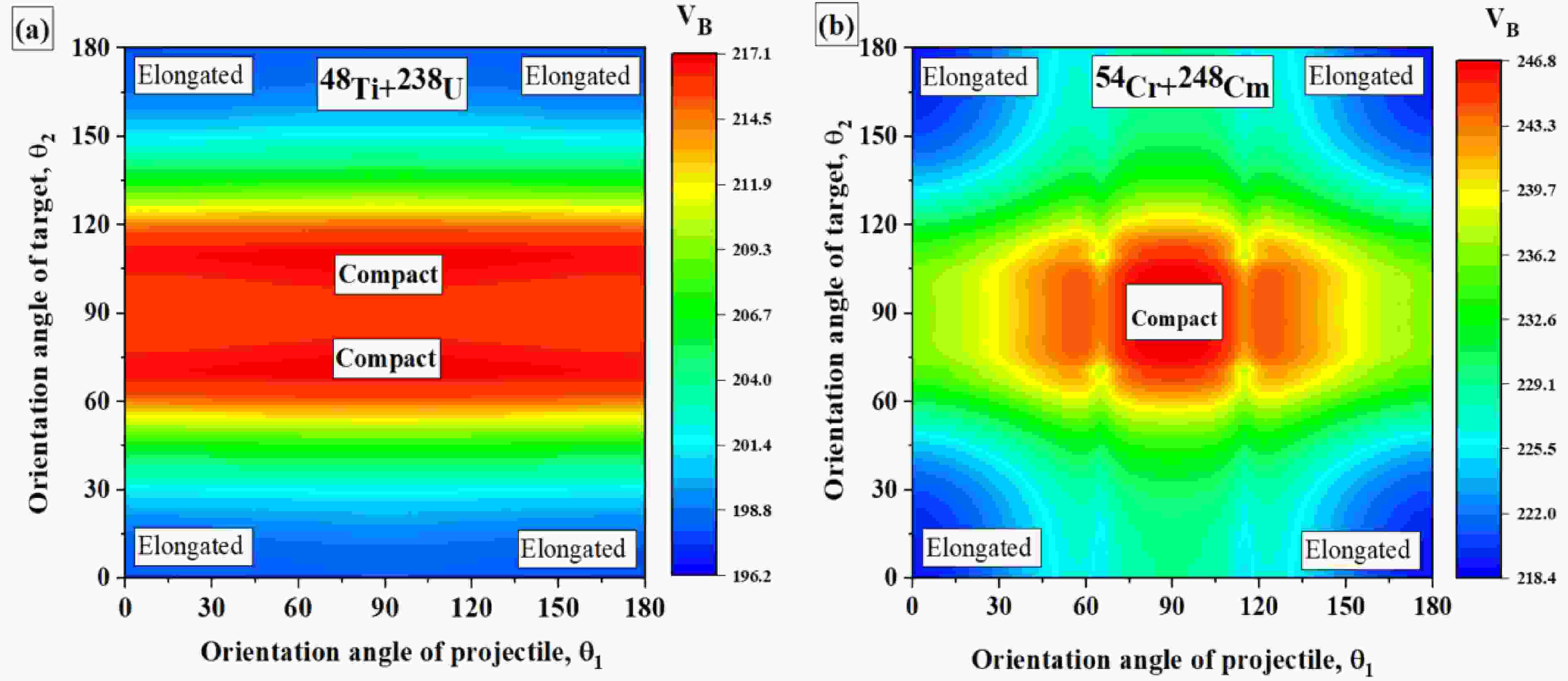
$ \beta_6 $ deformed target actinide nuclei and provided significant results. Furthermore, we intend to analyze the influence of the projectile orientation ($ \theta_1 $ ) on barrier characteristics for deformed-deformed P-T combinations. Therefore, the variation of the barrier height$ V_B $ with respect to the orientation angle of both the deformed target and projectile nuclei is systematically analyzed through the color-mapped contour plots for the reactions having minimum and significant magnitude of projectile deformation, respectively, in Fig.7. For the reaction 48Ti ($ \beta_2 $ = 0.011) +238U ($ \beta_2 $ = 0.236,$ \beta_4 $ = 0.098,$ \beta_6 $ = -0.021), as the magnitude of$ \beta_2 $ deformation of projectile is smaller, therefore the barrier height$ V_B $ is less sensitive to the projectile orientation and there is no significant change in the orientation angles for the compact and elongated configurations, as shown in Fig.7(a). While the compact configuration with the highest barrier height occurs at$ \theta_1= 97^\circ,\theta_2= 110^\circ $ , the elongated configuration with the lowest barrier is observed at$ \theta_1=1^\circ,\theta_2= 0^\circ $ . These configurations are dependent on the target orientation i.e., a change in the projectile orientation for such a P-T combination would not impose any significant change in the barrier height for both configurations. Meanwhile, for reaction 54Cr ($ \beta_2 $ = 0.161,$ \beta_4 $ = 0.048,$ \beta_6 $ = -0.024) +248Cm ($ \beta_2 $ = 0.250,$ \beta_4 $ = 0.039,$ \beta_6 $ = -0.035), where both the P-T have significant deformations, the barrier height$ V_B $ is sensitive to the orientation angle of both projectile and target nuclei, as shown in Fig.7(b). While the compact configuration with the highest$ V_B $ is observed at$ \theta_1,\theta_2 $ =$ 90^\circ, 101^\circ $ , the elongated configuration with the lowest$ V_B $ occurs at$ \theta_1,\theta_2 $ =$ 180^\circ, 0^\circ $ . For this P-T combination, a slight change in the projectile orientation$ \theta_1 $ can impose a significant change in the barrier height$ V_B $ , signifying the influence of projectile orientation$ \theta_1 $ along with the target orientation$ \theta_2 $ . These findings point out the possible influence of the projectile deformation on the barrier characteristics of deformed-deformed P-T combinations.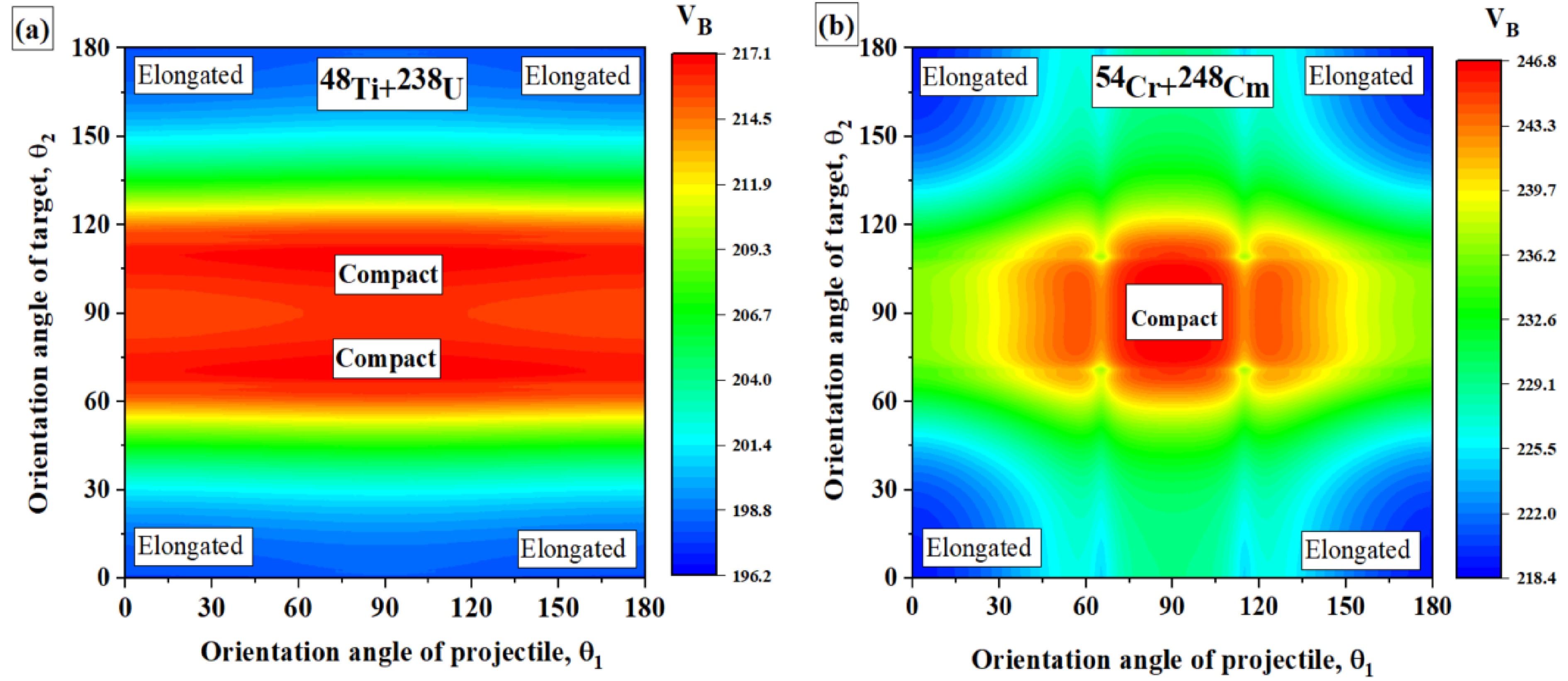
Figure 7. (color online) Schematic representation of the variation in interaction barrier height as a function of the projectile (
$ \theta_1 $ ) and target ($ \theta_2 $ ) orientation angles for deformed–deformed P-T combinations: (a) 48Ti+238U, and (b) 54Cr+248Cm.Till now, we discussed the influence of
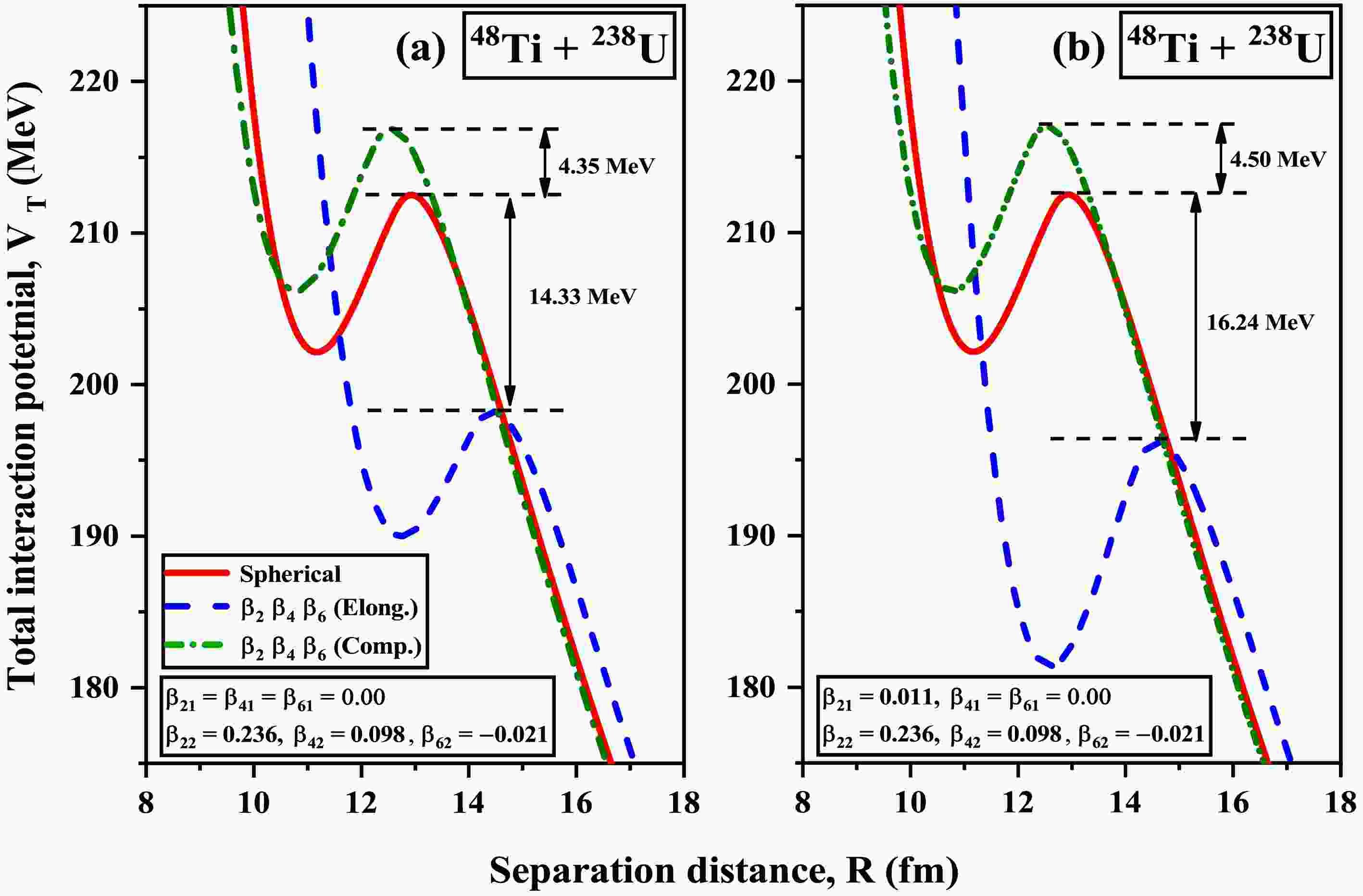
$ \beta_2\beta_4\beta_6 $ deformations on the barrier characteristics of spherical+deformed and deformed+deformed P-T nuclei, along with their modified compact and elongated configurations. To further examine the role of these configurations on the fusion dynamics of the considered P-T combinations, we study the total interaction potential$ V_T $ ($ =V_C+V_N $ ) as a function of the separation distance R for the reaction 48Ti + 238U, shown in Fig.8. The total interaction potential$ V_T $ directly reflects the effect of nuclear deformations and orientations introduced through both the Coulomb potential$ V_C $ and nuclear potential$ V_N $ . It is worth noting that both the projectile, 48Ti, and the target, 238U, are prolate deformed. The Fig.8, demonstrates the variation of the$ V_T $ for the elongated and compact configurations of the deformed projectile and target (P-T) in comparison to the spherical scenario. Fig.8(a) represents the case where the projectile nucleus is considered spherical, while Fig.8(b) includes the deformation of both projectile and target nuclei. In both cases, the elongated configuration lowers the barrier height$ V_B $ compared to the compact and spherical configurations (P-T are spherical), thereby reducing the extra push energy required for fusion. This lowering of the barrier is more pronounced when projectile deformation is taken into account, as seen in Fig.8(b). These results are due to the modification in the shape of the nuclei by the incorporation of deformations. Consequently, the inclusion of higher-order deformations for both projectile and target nuclei leads to a lowering of the fusion barrier and enhances the probability of fusion at elongated configurations.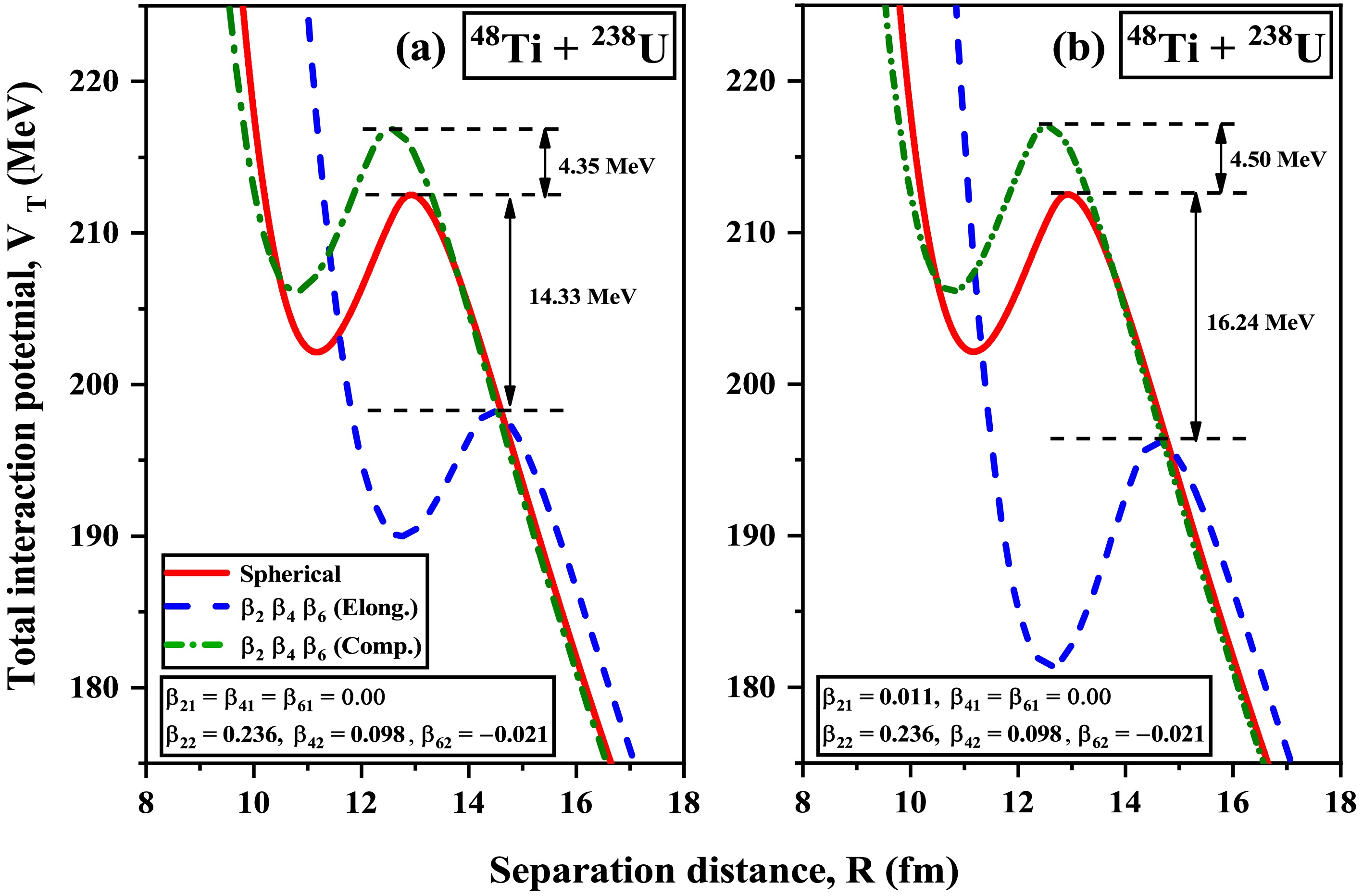
Figure 8. (color online) Total interaction potential
$ V_T $ (MeV) is represented as a function of separation distance R (fm) for the P-T combination of (a) 48Ti ($ \beta_{21}=\beta_{41}=\beta_{61}=0.00 $ ) + 238U ($ \beta_{22}= 0.236,\beta_{42}=0.098,\beta_{62}= -0.021 $ ) and (b) 48Ti ($ \beta_{21}= 0.011,\beta_{41}=\beta_{61}=0.00 $ ) + 238U ($ \beta_{22}= 0.236,\beta_{42}=0.098,\beta_{62}= -0.021 $ ). The variations of$ V_T $ and R are illustrated for both elongated and compact configurations of the deformed nuclei, along with the case where both projectile and target are considered spherical (red line).So far, the impact of both the magnitude and sign (
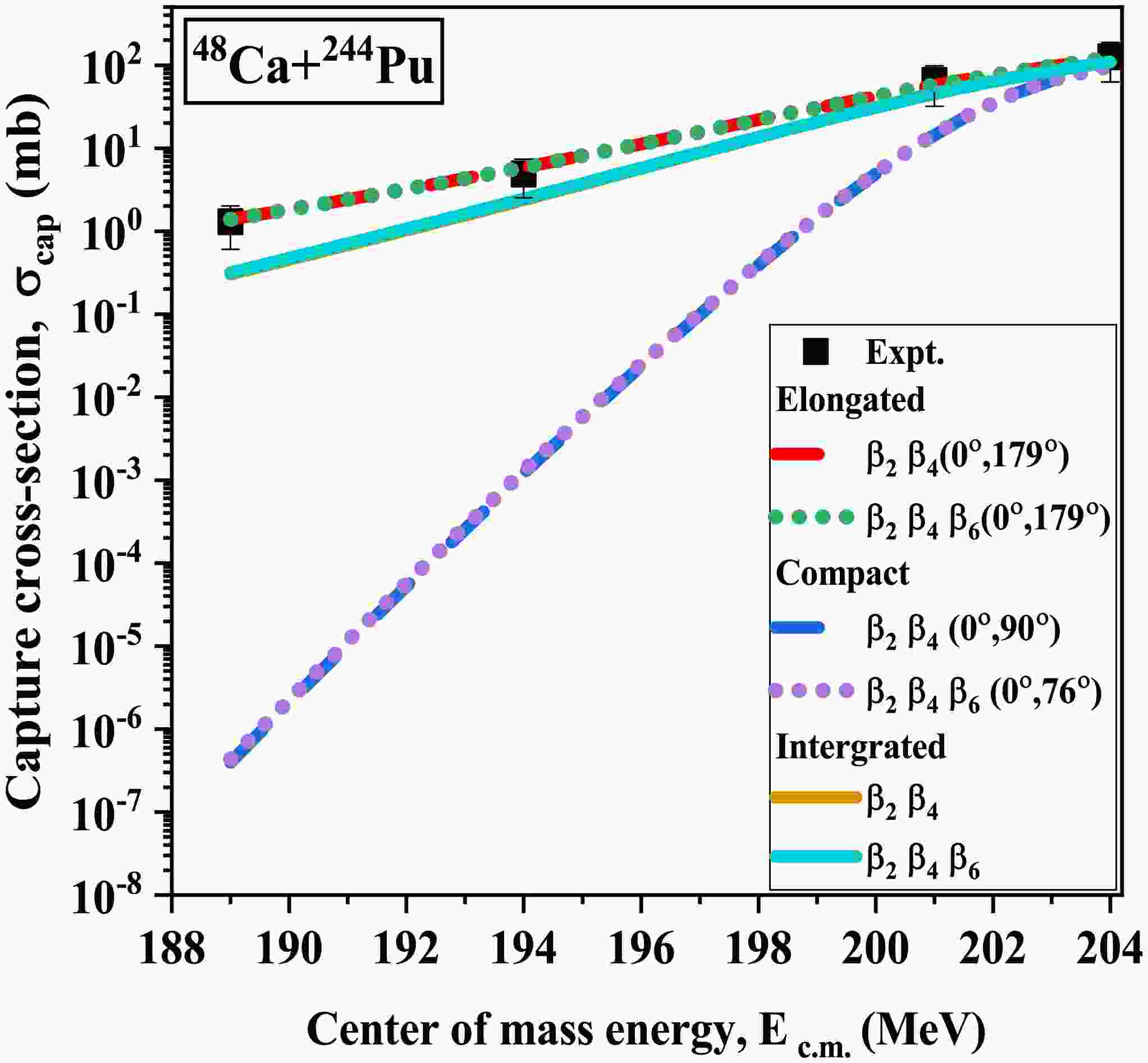
$ \pm $ ) of symmetric higher-order deformations (up to$ \beta_6 $ ) on barrier characteristics, i.e. barrier height ($ V_B $ ) and barrier position ($ R_B $ ), has been systematically analysed for both spherical+deformed and deformed+deformed P-T combinations. In further calculations, we have implemented these modified barrier characteristics and their corresponding compact and elongated configurations to determine the capture cross-sections$ \sigma_{cap} $ , which reflect the combined influence of hexacontatetrapole deformations$ \beta_6^\pm $ over a wide range of incident energies$ E_{c.m.} $ , spanning across the Coulomb barrier. -
In the previous section, we discussed the influence of the magnitude and sign of
$ \beta_6^{\pm} $ on the shape of the nuclei along with the$ \beta_2^+ $ and$ \beta_4^{\pm} $ deformations. This section aims to broaden the analysis by investigating the comprehensive effect of the modified shape of$ \beta_4^{\pm} $ and$ \beta_6^{\pm} $ deformed nuclei on the barrier characteristics, i.e., barrier height ($ V_B $ ) and barrier position ($ R_B $ ) of the interacting nuclei. The objective of this analysis is to determine how$ \beta_4^{\pm} $ and$ \beta_6^{\pm} $ deformations modify the barrier characteristics when compared to a prolate deformed ($ \beta_2^+ $ ) case. For this analysis, we investigated the barrier characteristics for the 48Ca-induced reactions with deformed actinide nuclei having non-zero values of$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ deformations. The variations in$ V_B $ and$ R_B $ with respect to target orientation ($ \theta_2 $ ) ranging from$ 0^\circ $ to$ 180^\circ $ for different combinations of$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ deformations are illustrated in Fig. 2 and Fig. 3, respectively. These figures are divided into two panels, where panel (I) represents the barrier characteristics of$ \beta_2^+\beta_4^{+}\beta_6^{\pm} $ deformed nuclei and panel (II) represents the barrier characteristics of$ \beta_2^+\beta_4^{-}\beta_6^{\pm} $ deformed nuclei. Each panel of the analyzed actinide nuclei is classified into three distinct groups based on the values of$ \beta_4 $ and$ \beta_6 $ deformations. In particular, Fig. 2(a, b, g, and h) illustrates the scenarios in which the magnitude of$ \beta_4 $ is greater than$ \beta_6 $ , while Fig. 2(c, d, i and j) depicts the cases in which the magnitude of$ \beta_4 $ is approximately equal to magnitude of$ \beta_6 $ deformation. Additionally, Fig. 2(e, f, k and l) showcases the instances in which the magnitude of$ \beta_6 $ deformation exceeds the magnitude of$ \beta_4 $ deformation. To conduct a thorough analysis of both the sign and magnitude of the associated$ \beta_6 $ deformation, both positive and negative$ \beta_6 $ deformations of equal magnitude were considered.
Figure 2. (color online) A schematic representation illustrating the changes in barrier height (
$ V_B $ ) in relation to the orientation angle ($ \theta_2 $ ) of deformed actinide nuclei. Panel (I) features nuclei with configurations$ \beta_2^+\beta_4^+\beta_6^\pm $ , while Panel (II) showcases$ \beta_2^+\beta_4^-\beta_6^\pm $ deformed nuclei.
Figure 3. (color online) A schematic representation illustrating the changes in barrier position (
$ R_B $ ) in relation to the orientation angle ($ \theta_2 $ ) of deformed actinide nuclei. Panel (I) features nuclei with configurations$ \beta_2^+\beta_4^+\beta_6^\pm $ , while Panel (II) showcases$ \beta_2^+\beta_4^-\beta_6^\pm $ deformed nuclei.These figures show that the introduction of
$ \beta_4^+ $ in quadrupole deformed nuclei lowers the barrier height$ V_B $ . Conversely, the incorporation of$ \beta_4^- $ in$ \beta_2 $ deformed nuclei increases$ V_B $ . The relative variation in$ V_B $ is influenced by the magnitudes of the$ \beta_2 $ and$ \beta_4 $ deformation parameters. A noticeable change in the orientation angle of the compact and elongated configurations has been observed alongside the barrier characteristics [36]. Further, the incorporation of$ \beta_6^{\pm} $ in conjunction with$ \beta_2 $ and$ \beta_4 $ deformation modifies the shape of the nuclei at both the pole and belly positions, which causes variation in the barrier characteristics$ V_B $ and$ R_B $ . For instance, the addition of$ \beta_6^+ $ to$ \beta_2^+\beta_4^{\pm} $ deformed nuclei lowers the barrier height$ V_B $ specifically at the target orientation$ \theta_2 $ =0° or 180°. Meanwhile,$ \beta_6^- $ increases the barrier height, as it compresses the shape of the nuclei around the poles at$ \theta_2 $ =0° or 180°. The impact of$ \beta_6 $ deformations is more pronounced for the orientations in the range of$ 0^\circ $ −$ 40^\circ $ across all cases. However, as$ \theta_2 $ surpasses this range, the value of$ V_B $ corresponding to$ \beta_2\beta_4\beta_6 $ deformed nuclei changes slightly as compared to$ \beta_2\beta_4 $ deformed nuclei. Conversely, an interesting variation can be observed at the target orientation$ \theta_2=90^\circ $ , wherein the barrier height$ V_B $ increases for the case of$ \beta_6^+ $ , while$ V_B $ decreases for the case of$ \beta_6^- $ relative to$ \beta_4 $ . This variation, as discussed in the previous section, is linked to the compression and elongation of the nuclear shape at the belly of the nuclei due to the incorporation of$ \beta_6^+ $ and$ \beta_6^- $ deformations, respectively. It is important to note that the variation in$ V_B $ is not very significant at$ 90^\circ $ for all cases. Additionally, in scenarios where the value of$ \beta_4 $ is greater than$ \beta_6 $ and$ \beta_4 $ is approximately equal to$ \beta_6 $ , the changes in barrier characteristics resulting from the inclusion of$ \beta_6 $ correspond to the deformation trend of$ \beta_4 $ . Conversely, for cases in which$ \beta_4 $ is less than$ \beta_6 $ , as illustrated in Fig. 2(e,f,k,l), the substantial impact of$ \beta_6 $ is evident because its magnitude is significantly larger than$ \beta_4 $ . In a similar manner, an inverse variation with respect to$ V_B $ is observed in the analysis of barrier position$ R_B $ for all considered reactions. The variation in$ R_B $ for the considered reactions w.r.t orientation angle ($ \theta_2 $ ) is shown in Fig. 3.The incorporation of
$ \beta_6 $ causes a significant shift in the optimum orientation in addition to variations in the barrier characteristics. These modified optimum orientations of the compact or elongated configuration of the$ \beta_6 $ deformed nuclei can significantly affect the overall dynamics of the nuclear interaction. These configurations are characterized by the maximal and minimum values of barrier height ($ V_B $ ) and barrier position ($ R_B $ ). The elongated configuration corresponds to the configuration with the minimum$ V_B $ and maximum$ R_B $ , whereas the compact configuration is associated with the configuration corresponding to the maximum$ V_B $ and minimum$ R_B $ . The analysis of the barrier height corresponding to$ \beta_2,\beta_4,\beta_6 $ in relation to the orientation angle ($ \theta_2 $ ) is shown in Fig. 2. The figure clearly demonstrates that the variation in the barrier height$ V_B $ due to the incorporation of$ \beta_6 $ deformation in comparison to the$ \beta_4 $ deformation is significantly more pronounced in the orientation range$ \theta_2 $ =$ 0^\circ $ to$ 40^\circ $ than those at$ \theta_2 $ =$ 70^\circ $ to$ 90^\circ $ . The orientation range$ \theta_2 $ =$ 0^\circ $ to$ 40^\circ $ represents the region with the minimum barrier height or the elongated configuration, while the orientation range$ \theta_2 $ =$ 70^\circ $ to$ 90^\circ $ represents the region with the maximum barrier height or the compact configuration for the$ \beta_2\beta_4\beta_6 $ deformation combinations, respectively. Based on these results, additional emphasis will be placed on evaluating the impact of$ \beta_6 $ on the barrier characteristics at orientation angles ranging from$ 0^\circ $ to$ 40^\circ $ .Thus far, we have established that the addition of
$ \beta_6 $ deformation along with$ \beta_2 $ and$ \beta_4 $ provides noticeable alterations in the barrier characteristics for orientation angles ranging from$ 0^\circ $ to$ 40^\circ $ . To further explore the influence of the magnitude of$ \beta_6 $ , we studied the variation in$ V_B $ for the previously mentioned range of orientation angle by varying the magnitude of$ \beta_6 $ deformation from -0.05 to 0.05, as demonstrated in Fig. 4. For the analysis, we consider the actinide nuclei having a significant magnitude of$ \beta_4 $ deformation as compared to the magnitude of$ \beta_6 $ (e.g. 244Pu), and the nuclei with a smaller magnitude of$ \beta_4 $ deformation as compared to the magnitude of$ \beta_6 $ (e.g. 255Fm). The study assumes both positive and negative signs for the magnitude of$ \beta_4 $ of the same nuclei. The results in Fig. 4 show that an increase in the magnitude of$ \beta_6^+ $ significantly elongates the nucleus along its poles, thereby leading to a decrease in barrier height with respect to$ \beta_4^\pm $ at$ \theta_2 $ =$ 0^\circ $ or$ 180^\circ $ . Conversely, an increase in the magnitude of$ \beta_6^- $ causes an increase in the barrier height, which is due to an enhanced compression effect along the poles. Moving towards the target orientation$ \theta_2 $ =$ 30^\circ $ , variations in barrier height$ V_B $ can be observed for both$ \beta_6^+ $ and$ \beta_6^- $ cases. Increasing the positive value of$ \beta_6^+ $ yields a high value of$ V_B $ , while increasing the negative value of$ \beta_6^- $ results in a lower value of$ V_B $ at$ 30^\circ $ or above, compared to$ \beta_2 $ $ \beta_4 $ deformed nuclei. These variations are due to shape modifications that are caused by the incorporation of$ \beta_6^{\pm} $ . In Fig. 4(a) 244Pu has a significant magnitude of$ \beta_4^+ $ , and the elongated shape always appears at the orientation angle$ \theta_2 $ =$ 0^\circ $ regardless of the magnitude of$ \beta_6^\pm $ . However, in Fig. 4(b), a large negative value of$ \beta_4^- $ causes compression in the nuclear shape, and the orientation angle for the elongated configuration shifts to approximately$ \theta_2=30^\circ $ . The addition of$ \beta_6^+ $ reduces this compression and brings back elongation at the poles$ \theta_2=0^\circ $ with increasing values. On the other hand,$ \beta_6^- $ further increases the compression at the poles, thus reinforcing the minimum barrier height at approximately$ \theta_2=30^\circ $ .
Figure 4. (color online) Schematic diagram showing the variation of barrier height with respect to the orientation angle of the target varying from 0°−40° for values of
$ \beta_6 $ ranging from –0.05 to +0.05 for nucleus with significant$ \beta_4^\pm $ (244Pu) and nucleus with a small magnitude of$ \beta_4^\pm $ (255Fm).On the other hand, for a smaller magnitude of
$ \beta_4^\pm $ , the shape of the nuclei is mainly influenced by the magnitude and sign of the$ \beta_6 $ deformation. For instance, for both cases of$ \beta_6 $ , the elongated configuration is observed at$ \theta_2 $ =$ 0^\circ $ or$ 180^\circ $ , as illustrated in Fig. 4(c, d). However, this orientation angle for the elongation configuration shift towards$ \theta_2\approx30^\circ $ for higher magnitudes of$ \beta_6^- $ . This analysis indicates that the magnitude and sign of the$ \beta_6 $ deformation have a significant influence on the barrier height$ V_B $ at the elongated configuration and also can shift the elongated configuration from$ 0^\circ $ to approximately$ 30^\circ $ , in conjunction with the influence of$ \beta_2^+\beta_4^{\pm} $ deformations.In order to conduct an in-depth analysis of the variation in barrier height
$ V_B $ at the elongated configuration, we examined different sign combinations of quadrupole ($ \beta_2 $ ), hexadecapole ($ \beta_4 $ ), and hexacontatetrapole ($ \beta_6 $ ) deformations. This investigation focuses on several actinide nuclei to provide a comprehensive analysis of magnitudes and signs of deformations. The considered nuclei are examined by comparing the magnitudes of$ \beta_4 $ and$ \beta_6 $ deformation, which are categorized into three sets: (a)$ \beta_4 $ >$ \beta_6 $ , (b)$ \beta_4\approx\beta_6 $ , and (c)$ \beta_4 $ <$ \beta_6 $ . These three sets are analyzed for the deformation combinations of$ \beta_2^+\beta_4^+\beta_6^+ $ ,$ \beta_2^+\beta_4^+\beta_6^- $ ,$ \beta_2^+\beta_4^-\beta_6^+ $ , and$ \beta_2^+\beta_4^-\beta_6^- $ , as presented in Fig. 5. The deformations of the considered nuclei are taken from the data table provided in M$ \ddot{o} $ ller et al. [50], and both positive and negative signs of$ \beta_4 $ and$ \beta_6 $ are considered. The figure reveals that for the combinations$ \beta_2^+\beta_4^+\beta_6^+ $ and$ \beta_2^+\beta_4^+\beta_6^- $ , the incorporation of$ \beta_6^+ $ results in a reduction of the barrier height ($ V_B $ ), whereas the incorporation of$ \beta_6^- $ counteracts the influence of$ \beta_4^+ $ , thus resulting in an increase in$ V_B $ when added to the deformed nuclei of$ \beta_2^+\beta_4^+ $ . This result is consistent across all sets of magnitudes of$ \beta_4 $ and$ \beta_6 $ , as depicted in Fig. 5. The same trend of variation in barrier height is obtained for$ \beta_6^+ $ and$ \beta_6^- $ when incorporated in the$ \beta_2^+\beta_4^- $ deformed nuclei. These effects of$ \beta_6^+ $ and$ \beta_6^- $ are consistent when incorporated with$ \beta_2^+\beta_4^- $ deformation combination for the cases in which$ \beta_4 \approx \beta_6 $ and$ \beta_4 \lt \beta_6 $ , where the magnitude of$ \beta_4 $ is not significant, as illustrated in Fig. 5(b, c). However, a minor deviation in this trend occurs when$ \beta_4 \gt \beta_6 $ , as shown in Fig. 5(a). Contrary to expectations, the addition of$ \beta_6^+ $ and$ \beta_6^- $ does not yield the anticipated decrease and increase in$ V_B $ when combined with$ \beta_4^- $ . This result seems to indicate that the predominance of$ \beta_4 $ over$ \beta_6 $ induces a structural modification. Further explicit analysis is necessary to quantify the interactions among these deformation parameters in the case of$ \beta_4 \gt \beta_6 $ and to assess their collective impact on the barrier characteristics, specifically at the elongation configuration.
Figure 5. (color online) Schematic diagram comparing the barrier heights of nuclei at elongated configuration corresponding to different combinations of deformations
$ \beta_2^+\beta_4^+\beta_6^+ $ ,$ \beta_2^+\beta_4^+\beta_6^- $ ,$ \beta_2^+\beta_4^-\beta_6^+ $ , and$ \beta_2^+\beta_4^-\beta_6^- $ for the considered nuclei having variation of magnitudes such as (a)$ \beta_4 $ >$ \beta_6 $ , (b)$ \beta_4 $ $ \approx $ $ \beta_6 $ , (c)$ \beta_4 \lt \beta_6 $ .To further examine the influence of the
$ \beta_6^\pm $ deformation in the presence of a substantial$ \beta_4^- $ deformation, we analyzed the variations in$ V_B $ at elongated configurations for several nuclei illustrated in Fig. 6. In this context, we refer to Fig. 4(b), which demonstrates that the magnitude of$ \beta_4^- $ is significant than the magnitude of$ \beta_6^\pm $ and the presence of$ \beta_4^- $ deformation contributes to the overall shape of the nuclei. As previously mentioned, an increase in the magnitude of$ \beta_6^+ $ is associated with a decrease in$ V_B $ and results in elongation at an angle of$ 0^\circ $ . However, for lower magnitudes of$ \beta_6^+ $ , both compression and elongation effects arise due to$ \beta_4^- $ and$ \beta_6^+ $ , respectively, creating a balance in the shape, which results in a higher$ V_B $ than that produced solely by$ \beta_4^- $ . On the other hand, the$ \beta_6^- $ deformation intensifies the compression at the poles but continues the elongation near$ \theta_2 $ $ \approx $ $ 30^\circ $ , thus resulting in a decrease in$ V_B $ as its magnitude increases. The relevant evidence for this behavior in the nuclei is depicted in Fig. 6(c,d). Meanwhile, as the magnitudes of both$ \beta_6^+ $ and$ \beta_6^- $ deformations increase, the values of$ V_B $ become comparable. This behavior is illustrated in Fig. 6(a, b), which shows the comparable and lower values of$ V_B $ for$ \beta_6^\pm $ in relation to$ \beta_4^- $ . Nevertheless, the relative change in$ V_B $ for$ \beta_6^\pm $ compared to$ \beta_4^- $ is not significant.
Figure 6. (color online) Schematic diagram comparing the barrier heights of different actinides with 48Ca projectile at the elongated configuration for the
$ \beta_2^+\beta_4^-\beta_6^+ $ , and$ \beta_2^+\beta_4^-\beta_6^- $ combination of deformations in the case of$ \beta_4 $ >$ \beta_6 $ .The previous discussion highlighted impactful results on the role of hexacontatetrapole deformations in heavy-ion induced reactions for a spherical projectile (48Ca) with
$ \beta_6 $ deformed target actinide nuclei. Next, we aim to analyze the influence of the projectile orientation ($ \theta_1 $ ) on barrier characteristics for deformed-deformed P-T combinations. To this end, the variations in the barrier height$ V_B $ with respect to the orientation angle of both the deformed target and projectile nuclei are systematically analyzed using color-mapped contour plots for cases in which the reactions having minimum and significant magnitude of projectile deformation, as shown in Fig. 7. The first case is shown in Fig. 7(a) for the reaction of 48Ti ($ \beta_2 $ = 0.011) +238U ($ \beta_2 $ = 0.236,$ \beta_4 $ = 0.098,$ \beta_6 $ = -0.021), in which the magnitude of$ \beta_2 $ deformation of the projectile is smaller and thus the barrier height$ V_B $ is less sensitive to the projectile orientation and there is no significant change in the orientation angles for the compact and elongated configurations. While the compact configuration with the highest barrier height occurs at$ \theta_1= 97^\circ,\theta_2= 110^\circ $ , the elongated configuration with the lowest barrier is observed at$ \theta_1=1^\circ,\theta_2= 0^\circ $ . These configurations are dependent on the target orientation, i.e., a change in the projectile orientation for such a P-T combination would not impose any significant change in the barrier height for both configurations. Meanwhile, for the reaction of 54Cr ($ \beta_2 $ = 0.161,$ \beta_4 $ = 0.048,$ \beta_6 $ = -0.024) +248Cm ($ \beta_2 $ = 0.250,$ \beta_4 $ = 0.039,$ \beta_6 $ = -0.035), where both P-T have significant deformations, the barrier height$ V_B $ is sensitive to the orientation angle of both projectile and target nuclei, as shown in Fig. 7(b). While the compact configuration with the highest$ V_B $ is observed at$ \theta_1,\theta_2 $ =$ 90^\circ, 101^\circ $ , the elongated configuration with the lowest$ V_B $ occurs at$ \theta_1,\theta_2 $ =$ 180^\circ, 0^\circ $ . For this P-T combination, a slight change in the projectile orientation$ \theta_1 $ can impose a significant change in the barrier height$ V_B $ , which signifies the influence of projectile orientation$ \theta_1 $ along with the target orientation$ \theta_2 $ . These findings underline the possible influence of the projectile deformation on the barrier characteristics of deformed-deformed P-T combinations.
Figure 7. (color online) Schematic representation of the variation in interaction barrier height as a function of the projectile (
$ \theta_1 $ ) and target ($ \theta_2 $ ) orientation angles for deformed–deformed P-T combinations: (a) 48Ti+238U, and (b) 54Cr+248Cm.The previous sections discussed the influence of
$ \beta_2\beta_4\beta_6 $ deformations on the barrier characteristics of spherical+deformed and deformed+deformed P-T nuclei, along with their modified compact and elongated configurations. To further examine the role of these configurations on the fusion dynamics of the considered P-T combinations, we study the total interaction potential$ V_T $ ($ =V_C+V_N $ ) as a function of the separation distance R for the reaction 48Ti + 238U, shown in Fig. 8. The total interaction potential$ V_T $ directly reflects the effect of nuclear deformations and orientations introduced through both the Coulomb potential$ V_C $ and nuclear potential$ V_N $ . It is worth noting that both the projectile, 48Ti, and the target, 238U, are prolate deformed. Fig. 8 demonstrates the variations in$ V_T $ for the elongated and compact configurations of the deformed projectile and target (P-T) in comparison to the spherical scenario. Fig. 8(a) shows the variations for a spherical projectile nucleus, while Fig. 8(b) includes the deformation of both the projectile and target nuclei. In both cases, the elongated configuration lowers the barrier height$ V_B $ compared to the compact and spherical configurations (P-T are spherical), thereby reducing the extra push energy required for fusion. This lowering of the barrier is more pronounced when projectile deformation is taken into account, as seen in Fig. 8(b). These results are attributed to the modification in the shape of the nuclei as a result of the addition of the deformations. Consequently, the inclusion of higher-order deformations for both projectile and target nuclei leads to a lowering of the fusion barrier and enhances the probability of fusion at elongated configurations.
Figure 8. (color online) Total interaction potential
$ V_T $ (MeV) as a function of separation distance R (fm) for the P-T combination of (a) 48Ti ($ \beta_{21}=\beta_{41}=\beta_{61}=0.00 $ ) + 238U ($ \beta_{22}= 0.236,\beta_{42}=0.098,\beta_{62}= -0.021 $ ) and (b) 48Ti ($ \beta_{21}= 0.011,\beta_{41}=\beta_{61}=0.00 $ ) + 238U ($ \beta_{22}= 0.236,\beta_{42}=0.098,\beta_{62}= -0.021 $ ). The variations in$ V_T $ and R are illustrated for both elongated and compact configurations of the deformed nuclei, along with the case in which both projectile and target are considered spherical (red line).So far, we have systematically analyzed the impact of both the magnitude and sign (
$ \pm $ ) of symmetric higher-order deformations (up to$ \beta_6 $ ) on barrier characteristics, i.e., barrier height ($ V_B $ ) and barrier position ($ R_B $ ), for both spherical+deformed and deformed+deformed P-T combinations. In the next section, we discuss our implementation of these modified barrier characteristics and their corresponding compact and elongated configurations to determine the capture cross-sections$ \sigma_{\mathrm{cap}} $ , which reflect the combined influence of hexacontatetrapole deformations$ \beta_6^\pm $ over a wide range of incident energies$ E\mathrm{_{c.m.}} $ spanning across the Coulomb barrier. -
In this section, the relevance of the obtained modified barrier characteristics and their corresponding compact and elongated configurations for both spherical+deformed and deformed+deformed projectile–target (P–T) combinations is exercised to calculate the capture cross-sections. The capture cross-sections (
$ \sigma_{\mathrm{cap}} $ ) are obtained using the$ \ell $ -summed Wong model for the center of mass energies$ E_{\mathrm{c.m}.} $ lying across the Coulomb barrier. Initially, the$ \sigma_{\mathrm{cap}} $ for the P-T combination 48Ca + 244Pu is calculated using$ \beta_4 $ and$ \beta_6 $ deformed nuclei at their respective elongated and compact configurations in comparison to the available experimental data [51], as shown in Fig. 9. This figure illustrates the variation in$ \sigma_{\mathrm{cap}} $ for the reaction under consideration at their optimum as well as integrated orientations across various values of$ E_{\mathrm{c.m}.} $ . The figure shows that the elongated configuration yields an enhanced value of$ \sigma_{\mathrm{cap}} $ compared to that of the compact configuration for both$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ deformations. This difference is attributed to the lower$ V_B $ for capture at the elongated configuration, which is associated with the shape modifications induced by these deformations. Additionally, the calculated integrated cross-sections reflect the average effect of the cross-sections obtained at various orientations, which lie between the compact and elongated configurations. As the elongated configuration yields better agreement with experimental data,$ \sigma_{\mathrm{cap}} $ is calculated at the elongated configuration for all considered P-T combinations involving 48Ca induced reactions with 238U and 248Cm, as well as 36S and 48Ti induced reactions with 238U. The obtained$ \sigma_{\mathrm{cap}} $ values corresponding to both the elongated and integrated configurations of$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ deformations are compared with available experimental data, as shown in Fig. 10. However, the center of mass energies of the reactions depicted in Fig. 10(a, d) lie above the barrier, beyond the$ V_B $ corresponding to the elongated configuration for both$ \beta_4 $ and$ \beta_6 $ deformations; thus, the cross-sections calculated at elongated configurations align well with the experimental cross-sections. For the reaction involving 48Ca+238U, the presence of$ \beta_6^- $ in 238U hinders$ \sigma_{\mathrm{cap}} $ for energies$ E\mathrm{_{c.m}} $ lying below and near the Coulomb barrier, which is caused by an increase in$ V_B $ in comparison to the case for$ \beta_4^+ $ , as shown in Fig. 10(b). Meanwhile, the presence of the deformed projectile 36S with$ \beta_6^+ $ deformation enhances the capture cross-sections compared to the case that only contains the$ \beta_4 $ deformation [Fig. 10(c)]. Furthermore, the integrated capture cross-sections hold significant value in light of experimental studies. However, the integrated cross-sections calculated for these considered reactions, which account for the averaged contributions from all P–T orientations, exhibit a suppression relative to those obtained for the elongated configurations, as shown in Fig. 10. To address this suppression and to determine the relevance of all orientations of$ \beta_2\beta_4\beta_6 $ through integrated cross-sections from an experimental perspective, we analyzed$ \sigma_{\mathrm{cap}} $ using the Wong Model. The obtained results are compared with experimental cross-sections as well as values of$ \sigma_{\mathrm{cap}} $ , which were calculated at the elongated configuration using the$ \ell $ -summed Wong Model for the reaction 48Ca+238U, as illustrated in Fig. 11. The analysis reveals that the integrated cross-sections derived from the Wong Model offer a decent agreement with experimental data when the deformation up to$ \beta_6 $ is incorporated, while the integrated cross-sections determined using the$ \ell $ -summed Wong Model are notably suppressed as partial waves are included up to$ \ell\mathrm{_{max}} $ only. Thus, we can conclude that the inclusion of$ \beta_6 $ alongside$ \beta_2\beta_4 $ can significantly affect$ \sigma_{\mathrm{cap}} $ at both elongated and integrated orientations.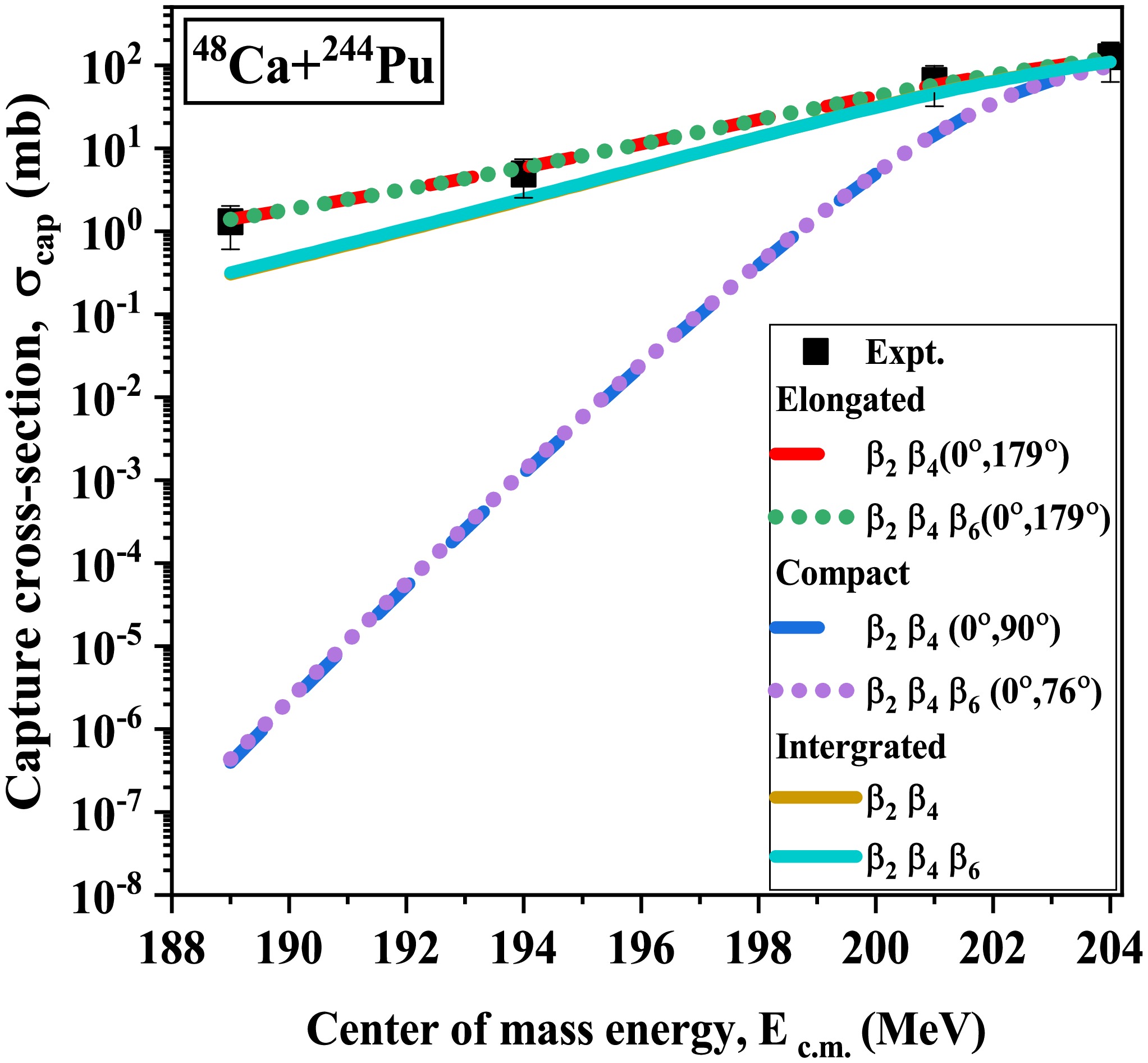
Figure 9. (color online) Schematic diagram of Capture cross-sections (
$ \sigma_{\mathrm{cap}} $ ) calculated using$ \ell $ -summed Wong model as a function of$ E\mathrm{_{c.m.}} $ at compact and elongated configurations of$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ along with the cross-sections integrated over all orientations for reaction 48Ca+244Pu.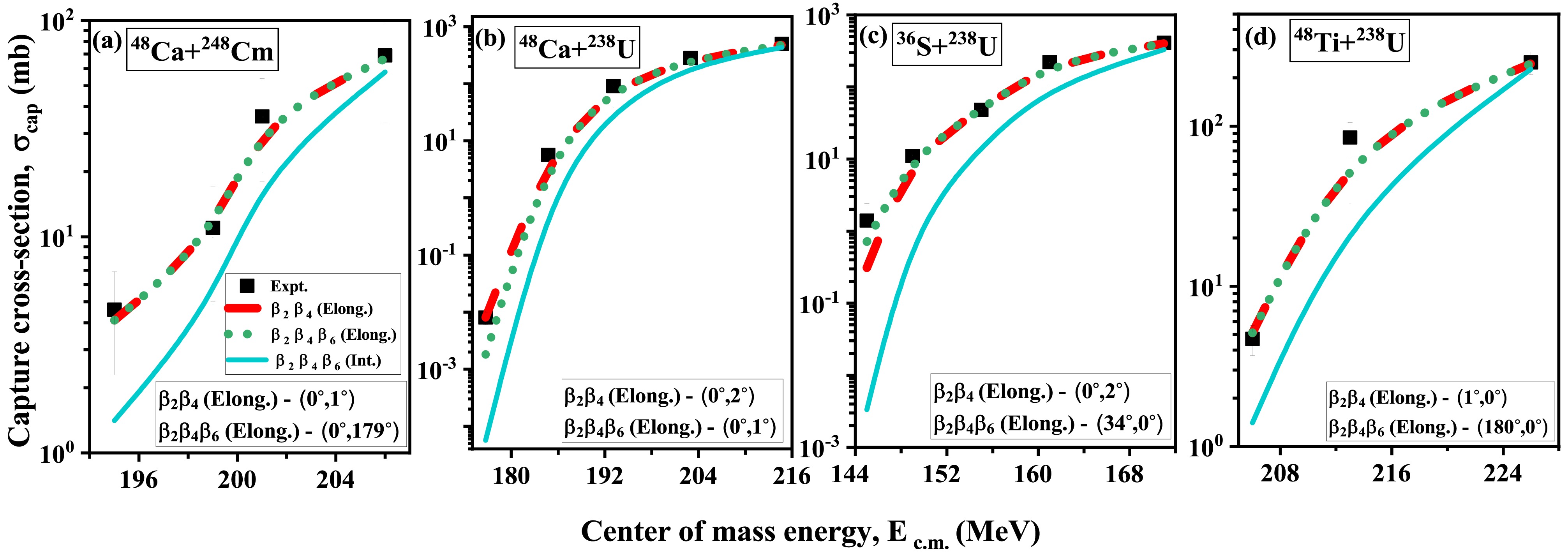
Figure 10. (color online) Schematic diagram of capture cross-sections (
$ \sigma_{\mathrm{cap}} $ ) obtained using$ \ell $ -summed Wong model as a function of$ E_{\mathrm{c.m}.} $ at elongated configurations and integrated over all orientations of$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ for considered P-T combinations and compared with available experimental data.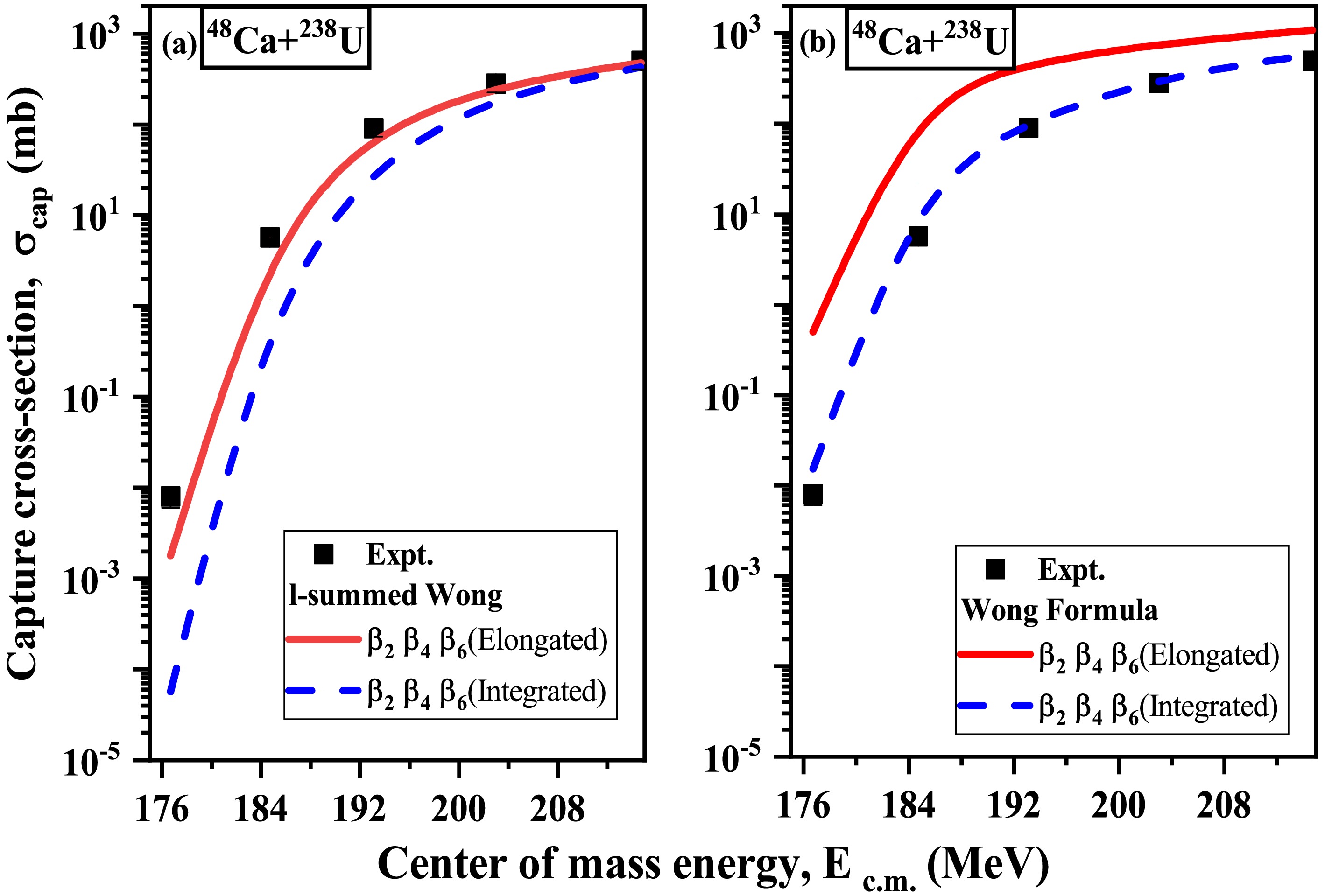
Figure 11. (color online) Schematic representation of capture cross-sections (
$ \sigma_{\mathrm{cap}} $ ) calculated using (a)$ \ell $ -summed Wong model and (b) Wong Model as a function of$ E\mathrm{_{c.m.}} $ . Results are shown for elongated configurations as well as integrated calculations for$ \beta_2\beta_4\beta_6 $ deformed case, and compared with the available experimental data for the considered P–T combination of 48Ca+238U.The considered reactions have experimental data available for energies lying above the barrier. To quantify the impact of
$ \beta_6^\pm $ relative to$ \beta_4^\pm $ , we evaluated the capture cross-sections for the reaction 48Ca+246Es forming the CN with Z=119 at centre-of-mass energies ($ E_{\mathrm{c.m.}} $ ) ranging from 180 to 220 MeV, which spans across the barrier. These capture cross-sections are calculated using the Wong formula at the elongated configurations and integrated cross-sections of all orientations of P-T of$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ with both positive and negative signs. As seen in Fig. 12(a), incorporating$ \beta_6^+ $ into$ \beta_2^+\beta_4^+ $ markedly enhances$ \sigma_{\mathrm{cap}} $ , whereas$ \beta_6^- $ introduces a noticeable suppression. Conversely, in Fig. 12(b), the value of$ \sigma_{\mathrm{cap}} $ for the$ \beta_2^+\beta_4^- $ deformation in the presence of$ \beta_6^\pm $ is enhanced owing to variations in$ V_B $ , which is caused by the shape modification in the case of$ \beta_2^+\beta_4^-\beta_6^\pm $ , as discussed in the previous section. On the other hand, the integrated cross-sections follow a similar trend to the elongated configurations upon the inclusion of$ \beta_2\beta_4^\pm\beta_6^\pm $ deformations; however, they show suppression comparatively to elongated configurations, as illustrated in Fig. 12 and discussed in the previous paragraph. Furthermore, according to the analysis presented in Refs. [11, 66], regarding the synthesis of superheavy nuclei (SHN) with Z = 120, the combination of 50Ti and 249Cf as the projectile and target is identified as the most favourable configuration for achieving SHN with Z = 120. Consequently, the estimated capture cross-sections are derived using Wong's formula, which incorporates higher-order deformations$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ at their elongated and integrated cross-sections as a function of the range of center of mass energies that lie across the Coulomb barrier, as depicted in Fig. 12 (c). The figure shows that the addition of$ \beta_6^- $ in conjunction with$ \beta_2^+ $ and$ \beta_4^+ $ results in a reduction in the cross-sections in both configurations when compared to the scenario involving$ \beta_2^+\beta_4^+ $ alone. Nevertheless, this reduction is less significant in the integrated configuration owing to the collective effects across all orientations.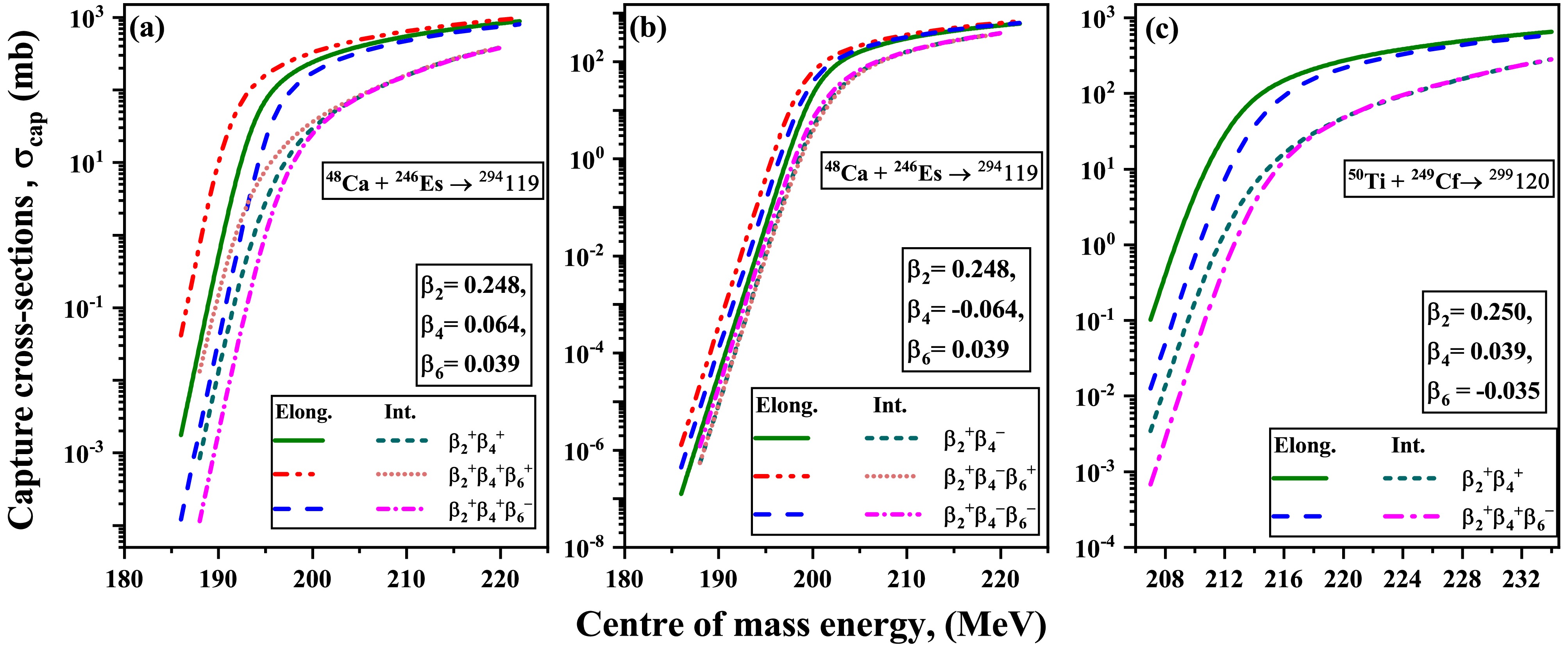
Figure 12. (color online) Schematic diagram of capture cross-sections (
$ \sigma_{\mathrm{cap}} $ ) as a function of center-of-mass energy for the reaction (a) 48Ca+246Es (Z=119) with$ \beta_2^+\beta_4^+ $ ,$ \beta_2^+\beta_4^+\beta_6^{\pm} $ combinations, (b) 48Ca+246Es (Z=119) with$ \beta_2^+\beta_4^- $ ,$ \beta_2^+\beta_4^-\beta_6^{\pm} $ combinations, (c) 50Ti+249Cf (Z=120) calculated using the Wong's formula. The results are shown for combinations of the deformations considered at their elongated configuration and integrated cross-section over all orientations.Furthermore, we comprehensively compared our calculated results with those derived from the microscopic Time-Dependent Hartree–Fock (TDHF) method. This comparison is illustrated in Fig. 13, which depicts the capture cross-sections (
$ \sigma_{\mathrm{cap}} $ ) calculated using the$ \ell $ -summed Wong model and compares them with results acquired using the Density-Constrained Frozen Hartree–Fock (DC-FHF) potential within the TDHF framework [67], alongside experimental data from [68] available for the reaction 48Ca + 238U forming the compound nucleus 286Cn. This recent TDHF-based study is particularly important, as it investigates the influence of higher-order deformations ($ \beta_2 $ ,$ \beta_4 $ ,$ \beta_6 $ ) and their orientation effects on the capture dynamics. Therefore, this work is chosen for comparison and analysis in our study. The results in Fig. 13 indicate that cross-sections obtained using the$ \ell $ -summed Wong model for the elongated configuration are in closer agreement with the experimental data compared to the integrated cross-sections$ \sigma_{\mathrm{cap}} $ , as well as the integrated and elongated cross-sections obtained from the TDHF calculations.
Figure 13. (color online) Schematic representation of the capture cross-sections (
$ \sigma_{\mathrm{cap}} $ ) obtained from the$ \ell $ -summed Wong model as a function of the center-of-mass energy ($ E\mathrm{_{c.m.}} $ ) for the reaction 48Ca+238U evaluated at elongated configurations and integrated over all orientations for deformations$ \beta_2 $ $ \beta_4 $ $ \beta_6 $ . The calculated results are compared with the corresponding experimental data and with$ \sigma_{\mathrm{cap}} $ values extracted from the DC-FHF model at both configurations.Overall, these findings underscore the crucial role of higher-order
$ \beta_6 $ deformations, alongside$ \beta_2 $ and$ \beta_4 $ , in modifying barrier characteristics and capture cross-sections in heavy-ion reactions that lead to the formation of superheavy nuclei. -
In this section, the relevance of the obtained modified barrier characteristics and their corresponding compact and elongated configurations for both spherical+deformed and deformed+deformed projectile–target (P–T) combinations is exercised to calculate the capture cross-sections. The capture cross-sections (
$ \sigma_{cap} $ ) are obtained using the$ \ell $ -summed Wong model for the center of mass energies$ E_{c.m.} $ lying across the Coulomb barrier. Initially, the$ \sigma_{cap} $ for P-T combination 48Ca + 244Pu are calculated using$ \beta_4 $ and$ \beta_6 $ deformed nuclei at their respective elongated and compact configurations in comparison to the available experimental data [51], as shown in Fig.9. This figure illustrates the variation in the$ \sigma_{cap} $ for the reaction under consideration at their optimum as well as integrated orientations across a range of$ E_{c.m.} $ . One can observe that the elongated configuration yields an enhanced$ \sigma_{cap} $ compared to that of the compact configuration for both$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ deformations. This difference is attributed to the lower$ V_B $ for capture at the elongated configuration, which is associated with the shape modifications induced by these deformations. Also, the calculated integrated cross-sections reflect the average effect of the cross-sections obtained at various orientations, which lie between the compact and elongated configurations. As the elongated configuration yields better agreement with experimental data, therefore, the$ \sigma_{cap} $ are calculated at their elongated configuration for all considered P-T combinations involving 48Ca induced reactions with 238U and 248Cm, as well as 36S and 48Ti induced reactions with 238U. The obtained$ \sigma_{cap} $ values corresponding to both configurations are compared with available experimental data, as shown in Fig.10. However, the reactions depicted in Fig.10(a,d) exhibit center of mass energies$ E_{c.m.} $ lying above the barrier, beyond the$ V_B $ corresponding to the elongated configuration for both$ \beta_4 $ and$ \beta_6 $ deformations; thus aligning well with the experimental cross-sections. For the reaction involving 48Ca+238U, the presence of$ \beta_6^- $ in 238U induces the hindrance to$ \sigma_{cap} $ for energies$ E_{c.m} $ lying below and near the Coulomb barrier, due to increased$ V_B $ in comparison to$ \beta_4^+ $ case as shown in Fig.10(b). Meanwhile, the presence of the deformed projectile 36S with$ \beta_6^+ $ deformation leads to an enhancement of the capture cross-sections compared to the case with$ \beta_4 $ deformation alone [Fig.10(c)]. Furthermore, the integrated capture cross-sections hold significant value in light of experimental studies. However, the integrated cross-sections calculated for these considered reactions, which account for the averaged contributions from all P–T orientations, exhibit a suppression relative to those obtained for the elongated configurations, as shown in Fig.10. To address this suppression and to determine the relevance of all orientations of$ \beta_2\beta_4\beta_6 $ through integrated cross-sections from an experimental perspective, we explored the$ \sigma_{cap} $ using the Wong Model. The obtained results are compared with experimental cross-sections as well as$ \sigma_{cap} $ calculated at the elongated configuration using the$ \ell $ -summed Wong Model for the reaction 48Ca+238U, as illustrated in Fig.11. The analysis reveals that the integrated cross-sections derived from the Wong Model offer a decent agreement with experimental data as we incorporate deformation up to$ \beta_6 $ , while the integrated cross-sections from the$ \ell $ -summed Wong Model are notably suppressed as partial waves are included up to$ \ell_{max} $ only. Thus, leading to the conclusion that the inclusion of$ \beta_6 $ alongside$ \beta_2\beta_4 $ can significantly affect$ \sigma_{cap} $ at elongated configuration and integrated orientations.
Figure 9. (color online) Schematic diagram of Capture cross-sections (
$ \sigma_{cap} $ ) calculated using$ \ell $ -summed Wong model as a function of$ E_{c.m.} $ at compact and elongated configurations of$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ along with the cross-sections integrated over all orientations for reaction 48Ca+244Pu.
Figure 10. (color online) Schematic diagram of Capture cross-sections (
$ \sigma_{cap} $ ) obtained using$ \ell $ -summed Wong model as a function of$ E_{c.m.} $ at elongated configurations and integrated over all orientations of$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ for considered P-T combinations, then compared with available experimental data.
Figure 11. (color online) Schematic representation of capture cross-sections (
$ \sigma_{cap} $ ) calculated using (a)$ \ell $ -summed Wong model and (b) Wong Model as a function of$ E_{c.m.} $ . Results are shown for elongated configurations as well as integrated calculations for$ \beta_2\beta_4\beta_6 $ deformed case, and compared with the available experimental data for the considered P–T combination of 48Ca+238U.The considered reactions have experimental data available for energies lying above the barrier. To quantify the impact of
$ \beta_6^\pm $ relative to$ \beta_4^\pm $ , we evaluate the capture cross-sections for the reaction 48Ca+246Es forming the CN with Z=119 at centre-of-mass energies ($ E_{c.m.} $ ) ranging from 180 to 220 MeV, spanning across the barrier. These capture cross-sections are calculated using the Wong formula at the elongated configurations and integrated cross-sections of all the orientations of P-T of$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ with both positive and negative signs. As seen in Fig.12(a), incorporating$ \beta_6^+ $ into$ \beta_2^+\beta_4^+ $ markedly enhances$ \sigma_{cap} $ , whereas$ \beta_6^- $ introduces a noticeable suppression. Conversely, in Fig.12(b), the$ \sigma_{cap} $ for the$ \beta_2^+\beta_4^- $ deformation, when$ \beta_6^\pm $ is present, is enhanced due to variation in the$ V_B $ resulting from the shape modification in$ \beta_2^+\beta_4^-\beta_6^\pm $ case as discussed in the preceding section. On the other hand, the integrated cross-sections follow a similar trend to the elongated configurations upon the inclusion of$ \beta_2\beta_4^\pm\beta_6^\pm $ deformations, though they show suppression comparatively to elongated configurations, as illustrated in Fig.12 and discussed in the previous paragraph. Furthermore, according to the analysis presented in [11, 66] regarding the synthesis of superheavy nuclei (SHN) with Z=120, the combination of 50Ti and 249Cf as projectile and target is identified as the most favourable for achieving SHN with Z=120. Consequently, the estimated capture cross-sections are derived using Wong's formula, which incorporates higher-order deformations$ \beta_2\beta_4 $ and$ \beta_2\beta_4\beta_6 $ at their elongated and integrated cross-sections, as a function of the range of center of mass energies that lie across the Coulomb barrier, as depicted in Fig.12 (c). From this figure, it is evident that the addition of$ \beta_6^- $ in conjunction with$ \beta_2^+ $ and$ \beta_4^+ $ results in a reduction of the cross-sections in both configurations when compared to the scenario involving solely$ \beta_2^+\beta_4^+ $ . Nevertheless, this reduction is less significant in the integrated configuration, due to the collective effects from all orientations.
Figure 12. (color online) Schematic diagram of Capture cross-sections (
$ \sigma_{cap} $ ) as a function of center-of-mass energy for the reaction (a) 48Ca+246Es (Z=119) with$ \beta_2^+\beta_4^+ $ ,$ \beta_2^+\beta_4^+\beta_6^{\pm} $ combinations, (b) 48Ca+246Es (Z=119) with$ \beta_2^+\beta_4^- $ ,$ \beta_2^+\beta_4^-\beta_6^{\pm} $ combinations, (c) 50Ti+249Cf (Z=120) calculated using the Wong's formula. The results are shown for combinations of the deformations considered at their elongated configuration and integrated cross-section over all orientations.Furthermore, we have incorporated a comprehensive comparison of our calculated results with those derived from the microscopic Time-Dependent Hartree–Fock (TDHF) method. This comparison is illustrated in the Fig.13. In this Figure, we depict the capture cross-sections (
$ \sigma_{cap} $ ) calculated using the$ \ell $ -summed Wong model and compare them with results from the Density-Constrained Frozen Hartree–Fock (DC-FHF) potential within the TDHF framework [67], alongside experimental data from [68] available for the reaction 48Ca + 238U forming the compound nucleus 286Cn. This recent TDHF-based study is particularly important as it investigates the influence of higher-order deformations ($ \beta_2 $ ,$ \beta_4 $ ,$ \beta_6 $ ) and their orientation effects on the capture dynamics. Therefore, this work is chosen for comparison and analysis in our study. The results of Fig.13 indicate that cross-sections obtained with the$ \ell $ -summed Wong model for the elongated configuration are in closer agreement with the experimental data compared to the integrated cross-sections$ \sigma_{cap} $ , as well as the integrated and elongated cross-sections obtained from the TDHF calculations.
Figure 13. (color online) Schematic representation of the capture cross-sections (
$ \sigma_{cap} $ ) obtained from the$ \ell $ -summed Wong model as a function of the center-of-mass energy ($ E_{c.m.} $ ) for the reaction 48Ca+238U, evaluated at elongated configurations and integrated over all orientations for deformations$ \beta_2 $ $ \beta_4 $ $ \beta_6 $ . The calculated results are compared with the corresponding experimental data and with$ \sigma_{cap} $ values extracted from the DC-FHF model at both configurations.Overall, these findings underscore the crucial role of higher-order
$ \beta_6 $ deformations, alongside$ \beta_2 $ and$ \beta_4 $ , in modifying barrier characteristics and capture cross-sections in heavy-ion reactions that lead to the formation of superheavy nuclei. -
The present work offers a deep insight into the higher-order deformations (up to hexacontatetrapole deformations
$ \beta_6 $ ) and their corresponding orientations on the synthesis of superheavy nuclei (SHN). The analysis provides an explicit role of different signs and magnitudes of$ \beta_6 $ on the heavy-ion induced reactions in conjunction with quadrupole ($ \beta_2 $ ) and hexadecapole ($ \beta_4 $ ) deformations of the target nuclei. We consider the P-T combinations 48Ca+248Cm, 48Ca+244Pu, 48Ca+238U, 36S+238U and 48Ti+238U leading to the formation of SHN 296Lv, 292Fl, 286Cn, 274Hs and 286Fl. The shape evolution of the deformed actinide target nuclei due to incorporation of these deformations alters the barrier characteristics, i.e, the barrier height$ V_B $ and barrier position$ R_B $ of the interactions influencing the formation of the SHN, with variations depending on the sign of$ \beta_6^\pm $ . For instance, incorporation of$ \beta_6^+ $ leads to simultaneous elongation along the poles and compression at the belly, whereas incorporation of$ \beta_6^- $ leads to elongation at the belly and compression along the poles in the$ \beta_2^+\beta_4^ \pm $ deformed nuclei. The influence of$ \beta_6 $ is further analyzed for three magnitude relations: (a)$ \beta_4 $ >$ \beta_6 $ , (b)$ \beta_4 \approx \beta_6 $ , and (c)$ \beta_4 < \beta_6 $ respectively. The analysis indicates notable differences in the barrier characteristics for the elongated configuration, while no such differences are observed for the compact configuration, shifting the focus towards the elongated configuration, considering various combinations of$ \beta_2, \beta_4, \beta_6 $ deformations. The findings indicate that the incorporation of$ \beta_6^+ $ deformation lowers the$ V_B $ , whereas the incorporation of$ \beta_6^- $ increases the$ V_B $ when integrated with$ \beta_2^+\beta_4^\pm $ deformation for the cases where$ \beta_4\approx\beta_6 $ and$ \beta_4<\beta_6 $ . These results are in agreement with the previously defined behaviour of$ \beta_4^\pm $ deformed nuclei. However, for the cases with$ \beta_4>\beta_6 $ , deviations from this trend are observed in$ \beta_2^+\beta_4^-\beta_6^\pm $ deformed nuclei due to the predominance of$ \beta_4 $ over$ \beta_6 $ . The possible influence of the orientation of the deformed projectile nuclei has also been discussed. These modified barrier characteristics are then utilized to calculate the capture cross-sections for the considered P-T combinations, showing better agreement with available experimental data at elongated configurations, for the synthesis of SHE. While the above-mentioned results provide significant understanding of the reaction dynamics of the nuclei involving$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ deformations having the axially symmetric shape, it will be of future interest to investigate the relevance of octupole ($ \beta_3 $ ) deformations where reflection asymmetry becomes significant. -
The present work offers a deep insight into the higher-order deformations (up to hexacontatetrapole deformations
$ \beta_6 $ ) and their corresponding orientations on the synthesis of superheavy nuclei (SHN). The analysis highlights the explicit roles of different signs and magnitudes of$ \beta_6 $ on the heavy-ion induced reactions in conjunction with quadrupole ($ \beta_2 $ ) and hexadecapole ($ \beta_4 $ ) deformations of the target nuclei. We consider the P-T combinations 48Ca+248Cm, 48Ca+244Pu, 48Ca+238U, 36S+238U , and 48Ti+ 238U leading to the formation of SHN 296Lv, 292Fl, 286Cn, 274Hs, and 286Fl. The shape evolution of the deformed actinide target nuclei due to the incorporation of these deformations alters the barrier characteristics, i.e, the barrier height$ V_B $ and barrier position$ R_B $ , of the interactions that influence the formation of the SHN, where variations depend on the sign of$ \beta_6^\pm $ . For instance, the incorporation of$ \beta_6^+ $ leads to simultaneous elongation along the poles and compression at the belly, whereas the incorporation of$ \beta_6^- $ leads to elongation at the belly and compression along the poles in the$ \beta_2^+\beta_4^ \pm $ deformed nuclei. The influence of$ \beta_6 $ is further analyzed for three magnitude relations: (a)$ \beta_4 $ >$ \beta_6 $ , (b)$ \beta_4 \approx \beta_6 $ , and (c)$ \beta_4 \lt \beta_6 $ . The analysis indicates notable differences in the barrier characteristics for the elongated configuration, while no such differences are observed for the compact configuration, which shifts the focus towards the elongated configuration considering various combinations of$ \beta_2, \beta_4, \beta_6 $ deformations. The findings indicate that the incorporation of$ \beta_6^+ $ deformation lowers$ V_B $ , whereas the incorporation of$ \beta_6^- $ increases$ V_B $ when integrated with$ \beta_2^+\beta_4^\pm $ deformation for the cases in which$ \beta_4\approx\beta_6 $ and$ \beta_4<\beta_6 $ . These results are in agreement with the previously defined behavior of$ \beta_4^\pm $ deformed nuclei. However, for the cases with$ \beta_4>\beta_6 $ , deviations from this trend are observed in$ \beta_2^+\beta_4^-\beta_6^\pm $ deformed nuclei owing to the predominance of$ \beta_4 $ over$ \beta_6 $ . The possible influence of the orientation of the deformed projectile nuclei has also been discussed. These modified barrier characteristics are utilized to calculate the capture cross-sections for the considered P-T combinations. The results show better agreement with available experimental data at elongated configurations for the synthesis of SHN. While the above-mentioned results provide significant understanding of the reaction dynamics of the nuclei involving$ \beta_2 $ ,$ \beta_4 $ , and$ \beta_6 $ deformations having an axially symmetric shape, future work will investigate the relevance of octupole ($ \beta_3 $ ) deformations where reflection asymmetry becomes significant.
Influence of hexadecapole and hexacontatetrapole deformations and associated orientations on the synthesis of superheavy nuclei
- Received Date: 2025-08-15
- Available Online: 2026-03-15
Abstract: This study examines the impact of higher-order deformations up to hexacontatetrapole ($ \beta_6 $) deformation on the synthesis of superheavy nuclei (SHN) through heavy-ion induced fusion reactions. The main objective of the study is to examine the impact of modified nuclear shapes that result from the collective influence of deformations (up to $ \beta_6 $) on the barrier characteristics $ V_B $ and $ R_B $ and overall dynamics of nuclear reactions leading to the synthesis of SHN. The analysis takes into account both spherical+deformed and deformed+deformed projectile-target (P-T) combinations that lead to the synthesis of SHN. Furthermore, the analysis examines the influence of the sign ($ \pm $) and magnitude of $ \beta_6 $ on the barrier characteristics and overall reaction dynamics. This analysis is performed by utilizing 48Ca, 36S, and 48Ti induced reactions with $ \beta_6 $-deformed actinide targets. The compact and elongated orientations, influenced by the sign and magnitude of $ \beta_2 $, $ \beta_4 $, and $ \beta_6 $ deformations, respectively, introduce further modifications in the reaction dynamics.The calculated capture cross-sections ($ \sigma_{\mathrm{cap}} $) result in better agreement with the experimental data for the case which incorporates $ \beta_6 $ along with $ \beta_2 $ and $ \beta_4 $ deformations than for the $ \beta_2\beta_4 $ deformations due to modified barrier characteristics, particularly at near-barrier energies. The findings underscore the importance and impact of incorporating deformations (up to $ \beta_6 $) and their corresponding orientations to achieve a thorough understanding of the dynamics of heavy-ion induced reactions pertaining to the superheavy mass region.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: