-
Double beta decay (
$ \beta\beta $ decay) is one of the hottest topics in nuclear and particle physics [1, 2]. There are two types of$ \beta\beta $ decay: one is two neutrino$ \beta\beta $ decay ($ 2\nu\beta\beta $ decay) and another one is zero neutrino$ \beta\beta $ decay ($ 0\nu\beta\beta $ decay). The$ 0\nu\beta\beta $ decay is predicted by the nature of Majorana neutrino hypothesis, in which the neutrino is identical to the anti-neutrino. Experimental observations of the$ 0\nu\beta\beta $ decay will justify the existence of Majorana neutrinos and provide important information on the new physics beyond standard model.The
$ 2\nu\beta\beta $ decay has been detected for decades [3], but the$ 0\nu\beta\beta $ decay has no experimental evidence so far, as the$ 0\nu\beta\beta $ decay may have an extremely long half-life, longer than the age of our universe. The precise prediction of the half-life can help to design related experiment facilities. The accurate simulation of such experiments requires the knowledge of neutrino mass term as well as the phase space parameter and nuclear matrix element (NME) of decaying nuclei. While the phase space parameter can be evaluated with high accuracy [4, 5], the NME still has a large variety depending on nuclear many-body models and also adopted effective interactions.A lot of many-body methods were adopted to calculate the
$ 0\nu\beta\beta $ NME, see for examples the recent reviews [6−8]. In these models, the so-called closure approximation is often adopted without the explicit inclusion of excited states of intermediate odd-odd nuclei. Meanwhile, the quasi-particle random phase approximation(QRPA) has been applied extensively to study the$ \beta\beta $ decay processes, without adopting the closure approximation [9−16].In the past decades, the self-consistent spherical QRPA model have been applied to study the
$ \beta\beta $ decays [17−23], with stress on the overlap factor, IS pairing interaction, the paths of calculation.$ \beta\beta $ decay is direct a decay, but QRPA calculations are done through a virtual processes, both$ (Z,N)\rightarrow(Z,N-2)\rightarrow(Z+2,N-2) $ and$ (Z,N)\rightarrow(Z+1,N-1)\rightarrow(Z+2,N-2) $ are different calculaitons paths. The axially symmetric deformations is taken into account in Refs.[24, 25]. A highly efficient finite amplitude method QRPA model including axially symmetric deformation and large model space are developed to calculate the$ 2\nu\beta\beta $ decay in Ref.[26]. However, only the central and spin-orbit components of the effective interactions are adopted in the calcualtions, and the effects of tensor force have not been studied.As an important component of nucleon-nucleon interaction, the tensor force was reported to play an important role in the evolution of nuclear shell structure [27−30], the nuclear collective excitations [31−35] such as the charge-exchange Gamow-Teller (GT) and spin-dipole (SD) transitions, and the relevant single beta decay half-lives [36, 37]. As the
$ \beta\beta $ decay is closely related to the charge-exchange excitations, it is of interest to explore the effect of tensor force on the$ \beta\beta $ decay. In this article, the$ 2\nu\beta\beta $ and$ 0\nu\beta\beta $ NMEs,$ M^{2\nu} $ and$ M^{0\nu} $ , of$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{136} {\rm{Xe}}$ and$ ^{130} {\rm{Te}}$ are studied by the HFB+QRPA model based on the Skyrme energy density function (EDF) with the tensor force.We sketch briefly the basic theoretical framework and details of calculations in Sec. II. In Sec. III, we report the effect of the tensor force on
$ M^{2\nu} $ and$ M^{0\nu} $ , and also report on the low-energy GT states. A summary is given in Sec. IV. -
The
$ \beta\beta $ decays take place between the even-even nuclei, in which the initial and final states are denoted by 0$ ^+_i $ and 0$ _f^+ $ , respectively. It is a second-order weak process from the initial to the final nuclei through virtual states of the intermediate odd-odd nucleus. Throughout we assume that the$ 0\nu\beta\beta $ decay exists, and that the light neutrino-exchange mechanism dominates. The half-life of the$ 2\nu\beta\beta $ decay and$ 0\nu\beta\beta $ decay can be separately written as [38, 39]:$ [T_{1/2}^{2\nu}(0_i^+\rightarrow 0_f^+)]^{-1} = G^{(2\nu)}(0_f^+)\left|M^{(2\nu)}_{\text{GT}}\right|^2, $

(1) $ [T_{1/2}^{0\nu}]^{-1} = G^{(0\nu)}\left|M^{(0\nu)}\right|^2{\left(\frac{\langle m_{\beta\beta} \rangle}{m_e}\right)}^2, $

(2) where
$ G^{(2\nu)}(0_f^+) $ and$ G^{(0\nu)} $ are the phase space factors denoting the contribution from the outgoing leptons,$ {\langle m_{\beta\beta}\rangle} $ is the effective neutrino mass.For
$ 2\nu\beta\beta $ decay NME, because of isospin symmetry, Fermi transition is highly suppressed so that only the NME of Gamow-Teller (GT) transition,$ M_{\text{GT}}^{2\nu} $ , is actually considered in calculations. The GT NME, in the QRPA approach is expressed as [40]:$ M_{\text{GT}}^{2\nu} = \sum\limits_{\mu\nu}\frac{\langle 0^+_{f}||O_{\text{GT}}^{(-)}||1^+_{\mu}\rangle \langle 1_{\mu}^+|1_{\nu}^+\rangle \langle 1_{\nu}^+||O_{\text{GT}}^{(-)}||0^+_{i}\rangle} {\frac{1}{2}[\omega_{\mu}+\omega_{\nu}]} , $

(3) where
$ 1^+_{\nu} $ and$ 1_{\mu}^+ $ are two sets of$ 1^+ $ intermediate states constructed on the ground states of initial and final nuclei by the QRPA method, respectively. In QRPA calculations, the HFB ground states are set as the initial ($ 0^+_i $ ) and final states ($ 0_{f}^+ $ ). Here$ \omega_{\nu} $ and$ \omega_{\mu} $ in the energy denominator are the corresponding excitation energies with respect to the ground states of initial and final nuclei [38]. In Eq. (3),$ O_{\text{GT}}^{(\pm)} = \sum\limits_{i}\sigma_i t^{(\pm)}_i , $

(4) is the Gamow-Teller transition operator. The GT transition matrix element for QRPA can be expressed as
$ \begin{array}{l} \langle 1_{\nu}^+||O_{\text{GT}}^{(-)}||0^+_{i}\rangle = -\sum\limits_{pn}\langle p||\sigma||n\rangle(X_{pn}^{i\nu}u_pv_n+Y_{pn}^{i\nu}v_pu_n), \end{array} $

(5) $ \begin{aligned}[b]\langle 0^+_{f}||O_{\text{GT}}^{(-)}||1^+_{\mu}\rangle =\;& \langle 1^+_{\mu}||O_{\text{GT}}^{(+)}||0^+_{f}\rangle\\ =\;& \sum\limits_{pn}\langle n||\sigma||p\rangle(X_{pn}^{f\mu}u_nv_p+Y_{pn}^{f\mu}v_nu_p). \end{aligned} $

(6) The overlap factor in Eq.(3) is evaluated as [40]:
$ \langle 1_{\mu}^+|1_{\nu}^+\rangle = {\cal{N}}\sum\limits_{p,n,p^\prime n^\prime}(X_{pn}^{i\nu}X_{p^\prime n^\prime}^{f\mu}-Y_{pn}^{i\nu}Y_{p^\prime n^\prime}^{f\mu}) \langle p|p^\prime\rangle\langle n|n^\prime\rangle. $

(7) In the above expressions, X and Y are the forward and backward amplitudes of the QRPA states and u and v are the unoccupation and occupation amplitudes of the HFB single-particle states in canonical basis [41]. The overlap of two single-particle states in canonical basis can be expressed as
$ \langle k|k^\prime\rangle = \delta_{l_k,l_{k^\prime}}\delta_{j_k,j_{k^\prime}}(u_ku_{k^\prime}+v_kv_{k^\prime})\int_0^\infty u_k(r)u_{k^\prime}(r)dr. $

(8) $ {\cal{N}} $ is the overlap factor between the initial and final ground state calculated in canonical basis by the approach introduced in Ref.[40].The
$ 0\nu\beta\beta $ NME,$ M^{0\nu} $ , is usually presented as a sum of three parts of two-body currents: Gamow-Teller(GT), Fermi(FM), and Tensor(T) NMEs, function into separable form:$ M^{0\nu} = M_{\text{GT}}^{0\nu}-(\frac{g_V}{g_A})^2M_{\text{F}}^{0\nu}+M_{\text{T}}^{0\nu}, $

(9) where
$ g_V $ is the vector constant, and$ g_{A} $ is taken to be$ g_A^{\rm eff} = 1.0 $ consistent to the one used in$ 2\nu\beta\beta $ NME. Since the tensor term$ M_{\text{T}}^{0\nu} $ is negligibly small [39], we just calculate the GT and Fermi ones.$ \begin{aligned}[b]& M_{\text{F}}^{0\nu} = \sum\limits_k \langle 0_f^+\mid\mid h_{\text{F}} (r_{12},E_k) t_{1}^- t_{2}^-\mid\mid 0_i^+\rangle,\\& M_{\text{GT}}^{0\nu} = \sum\limits_k \langle 0_f^+\mid\mid h_{\text{GT}} (r_{12},E_k)(\sigma_{1} \cdot \sigma_{2})t_{1}^- t_{2}^-\mid\mid 0_i^+\rangle, \end{aligned} $

(10) where
$ r_{12} = |{{\boldsymbol{r}}_{\bf{1}}}-{{\boldsymbol{r}}_{\bf{2}}}| $ is the relative coordinates of the two nucleons. The neutrino potential reads$ h_{\text{K}}(r_{12},E_k) = \frac{2R}{\pi}\int dq\frac{qh_{\text{K}}(q^2)}{q+E_k-(M_i+M_f)/2} j_0(qr_{12}), $

(11) where K denotes Fermi or GT, and R is the radius of the initial nuclei.
In QRPA method, the spherical Bessel function
$ j_0(qr_{12}) $ is expanded by the formula,$ \begin{equation} j_0(qr_{12}) = 4\pi\sum\limits_{lm}j_l(qr_1)j_l(qr_2)Y_{lm}^*(\Omega_1)Y_{lm}(\Omega_2), \end{equation} $

(12) and the NME can be written as:
$ \begin{aligned}[b] M_{\text{GT}}^{0\nu} =\;& 8R\int dqqh_{\text{GT}}(q^2)\sum\limits_{k_1k_2}\sum\limits_{lJ}\frac{1}{2J+1}\\&\times \frac{1}{q+(E_{k_1}+E_{k_2})/2-(M_i+M_f)/2}\\&\times [\langle J_{k_1}\mid\mid j_l(qr_1)(Y_l\otimes\sigma_1)^{(J)}t_{1}^+\mid\mid0_f^+\rangle\langle J_{k_1}\mid J_{k_2}\rangle \\ & \langle J_{k_2}\mid\mid j_l(qr_{2})(Y_l\otimes\sigma_{2})^{(J)}t_{2}^-\mid\mid0_i^+\rangle], \end{aligned}$

$ \begin{aligned}[b] M_{\text{F}}^{0\nu} =\;& 8R\int dqqh_{\text{F}}(q^2)\sum\limits_{k_1k_2}\sum\limits_{lJ}\frac{1}{2J+1}\\ & \times \frac{1}{q+(E_{k_1}+E_{k_2})/2-(M_i+M_f)/2}\\& \times [\langle J_{k_1}\mid\mid j_l(qr_1)Y_lt_{1}^+\mid\mid0_f^+\rangle\langle J_{k_1}\mid J_{k_2}\rangle \\& \langle J_{k_2}\mid\mid j_l(qr_{2})Y_lt_{2}^-\mid\mid0_i^+\rangle], \end{aligned}$

(13) where
$ J_{k_1} $ and$ J_{k_2} $ are the QRPA excited states with total angular momentum J, calculated from the ground states of the final and initial nuclei, respectively. Details expressions of$ h_{\text{GT}}(q^2) $ and$ h_{\text{F}}(q^2) $ are found in Ref.[39].For the details of QRPA solutions and the Skyrme HFB, one could refer to [42, 43]. In this work, we adopt the volume pairing interaction, which can be divided into the IV and IS components:
$ V^{IV}_q = V_0^q\frac{1-P_\sigma}{2}\delta({{\boldsymbol{r}}}), $

(14) $ V^{IS} = fV_0\frac{1+P_\sigma}{2}\delta({{\boldsymbol{r}}}), $

(15) where
$ {{\boldsymbol{r}}} = {{\boldsymbol{r}}}_{{1}}-{{\boldsymbol{r}}}_{{2}} $ is the distance between the two nucleons,$ P_\sigma $ is the spin exchange operator. The IV pairing is included in both HFB and QRPA calculations, and the strength$ V_0^q (q = n,p) $ is fixed in HFB calculation by empirical pairing gaps of neutron and proton, respectively. The IS pairing interaction is included only in the$ pp $ chanel of QRPA equation, and the strength is decided by two factors,$ V_0 $ is the mean value of$ V_0^n $ and$ V_0^p $ , and f is a free parameter.The Skyrme-type tensor interaction is adopted on top of the central part of EDF in our calculations,
$ \begin{aligned}[b] V^{\text{T}} =\;& \frac{\text{T}}{2}\{[({\sigma _{{\bf{1}}}\cdot {{\bf{k}}}^{\prime })(\sigma _{{\bf{2}}}\cdot {{\bf{k}}}^{\prime })-\frac{{\bf{1}}}{{\bf{3}}}\left( \sigma _{{\bf{1}}}\cdot \sigma _{{\bf{2}}}\right) {{\bf{k}}}^{\prime {\bf{2}}}]\delta({\bf{r}}) }\\ &+ \delta ({\bf{r}})[ ({\sigma _{{\bf{1}}}\cdot {{{\bf{k}}}})(\sigma _{{\bf{2}}}\cdot {{{\bf{k}}}})-\frac{{\bf{1}}}{{\bf{3}}}\left( \sigma _{{\bf{1}}}\cdot \sigma _{{\bf{2}}}\right) {{{\bf{k}}}}^{{\bf{2}}}}] \}\\& + \frac{\text{U}}{2}\{\left( \sigma _{1}\cdot {\bf{k}}^{\prime }\right) \delta ({\bf{r}}) (\sigma _{{\bf{2}}}\cdot {\bf{k}}) +\left( \sigma _{{\bf{2}}}\cdot {\bf{k}}^{\prime }\right) \delta ({\bf{r}})(\sigma _{{\bf{1}}}\cdot {{\bf{k}}})\\ & - \frac{{{2}}}{{{3}}}\left[ ({\sigma }_{{\bf{1}}}\cdot {\sigma }_{{\bf{2}}}) {\bf{k}}^{\prime }\cdot \delta ({\bf{r}}){\bf{k}} \right] \} , \end{aligned} $

(16) where the operator
$ {\bf{k}} = \left( \nabla_{\bf{1}}- \nabla_{\bf{2}}\right)/2i $ acts on the right and$ {\bf{k}}^\prime = -\left( \nabla_{\bf{1}}^{\prime}-\bf \nabla_{\bf{2}}^{\prime}\right)/2i $ acts on the left. The parameters T and U denote the strengths of triplet-even (TE) and triplet-odd (TO) tensor force, respectively. This type of tensor interactions was firstly presented by T. H. R. Skyrme in 1950s [44, 45]. -
In
$ \beta\beta $ decay experiments,$ ^{76} {\rm{Ge}}$ has been used in LEGEND[46] and CDEX[47],$ ^{82} {\rm{Se}}$ will be used in NvDEx[48],$ ^{136} {\rm{Xe}}$ has been used in KamLAND-Zen collaboration[49], PandaX[50], EXO-200[51] and NEXT[52], and$ ^{130} {\rm{Te}}$ has been used in CUORE[53]. We perform the self-consistent HFB+QRPA for the$ 2\nu $ and$ 0\nu\beta\beta $ decays in$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ , and the calculated results converge when the cutoff energy of the intermediate state is taken to be 60 MeV. In the calculations, the Skyrme interaction SGII is adopted [54], which gives a reasonable Landau-migdal parameter for the spin-isospin channel,$ g^\prime_0 = 0.498 $ , having the effective mass$ m^*/m $ = 0.786. The tensor interaction is added with (T,U) = (500,-350) MeV$ \cdot {\rm{fm}}^5 $ . This tensor parameter is named ”Te1”. This strength is optimized by the study of the centroid energies of GT and charge-exchange spin-dipole (SD) giant resonances [55−58], which have reasonable descriptions of the low-lying 0+, 2+, and 3− states, and giant Gamow-Teller transition in subtracted second random phase approximation (SSRPA) calcualtion [59, 60]. -
The dependence of
$ \beta\beta $ decay NME on IV and IS pairings has been well studied in QRPA [15, 24, 61]. These studies suggest that$ M_{\text{GT}}^{2\nu} $ is affected by the IS pairing but not sensitive to IV pairing [15, 61]. As the tensor force has strong effect on the low-lying GT transitions[31], it is valuable to study the effect of the tensor force on the$ M_{\text{GT}}^{2\nu} $ .Before proceeding to discuss the NME, we show first the overlap factors
$ {\cal{N}} $ calculated with and without tensor force in Table 1. The average value of these overlap factors for open shell nuclei is around 0.8 and agrees with that obtained by deformed calculations [14, 16, 40]. The presence of tensor force does not largely affect this factor. For$ ^{136} {\rm{Xe}}$ , a strong suppression for the overlap factor is observed due to the neutron magicity$ N = 82 $ of this nucleus. For this nucleus, we find that the tensor force changes this factor by more than 5%. This implies that for magic nuclei, the tensor force may affect the structure of ground state. On the other hand, it was suggested in Ref.[62] that such suppression for magic nuclei may be overestimated due to the particle number non-conservation nature of HFB theory, and a larger overlap factor is expected when the number projection is applied to the calculation. To confirm this point, the number projected HFB is needed for further investigation.Nuclei w/o w/i $ ^{76} {\rm{Ge}}$ 

0.789 0.784 $ ^{82} {\rm{Se}}$ 

0.780 0.773 $ ^{130} {\rm{Te}}$ 

0.808 0.814 $ ^{136} {\rm{Xe}}$ 

0.447 0.473 Table 1. The overlap factor
$ {\cal{N}} $ between the initial and final ground states obtained by HFB calculations employing SGII+Te1 interaction with (w/i) and without (w/o) tensor force.We present the dependence of
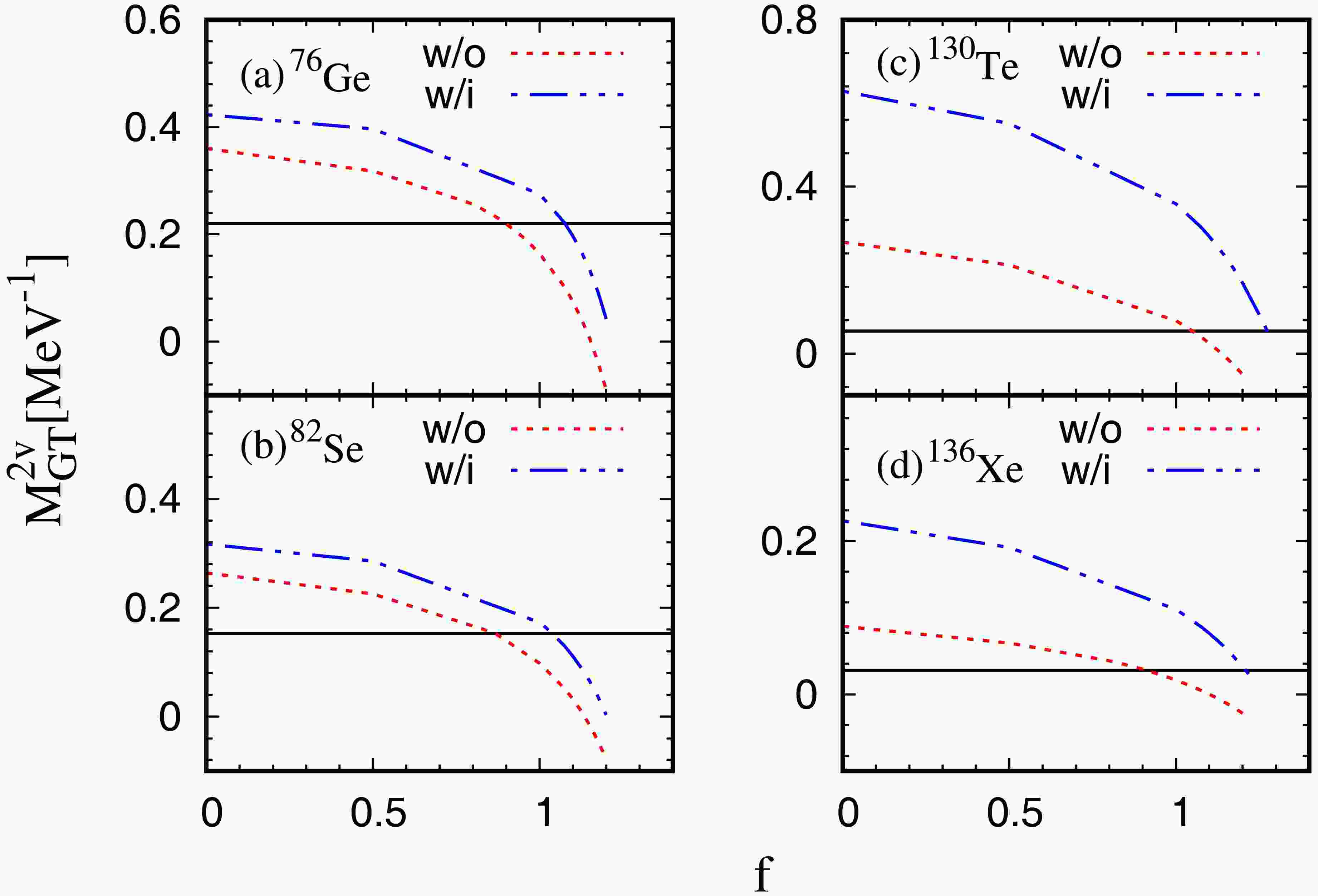
$ M^{2\nu}_{\text{GT}} $ on the IS pairing strength and the tensor force for$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ in Fig. 1. The two different curves are obtained with and without the tensor interaction in the HFB+QRPA calculations, labeled by ”w/i” or ”w/o” respectively. For the IS pairing strength dependence, we obtain similar results to other QRPA calculations [40, 64, 65]. The NME changes smoothly when the IS pairing strength is small and then at a certain value of f close to the critical point, the NME starts to change drastically untill the collapse of QRPA solutions. This general trend is not affected by the inclusion of tensor force.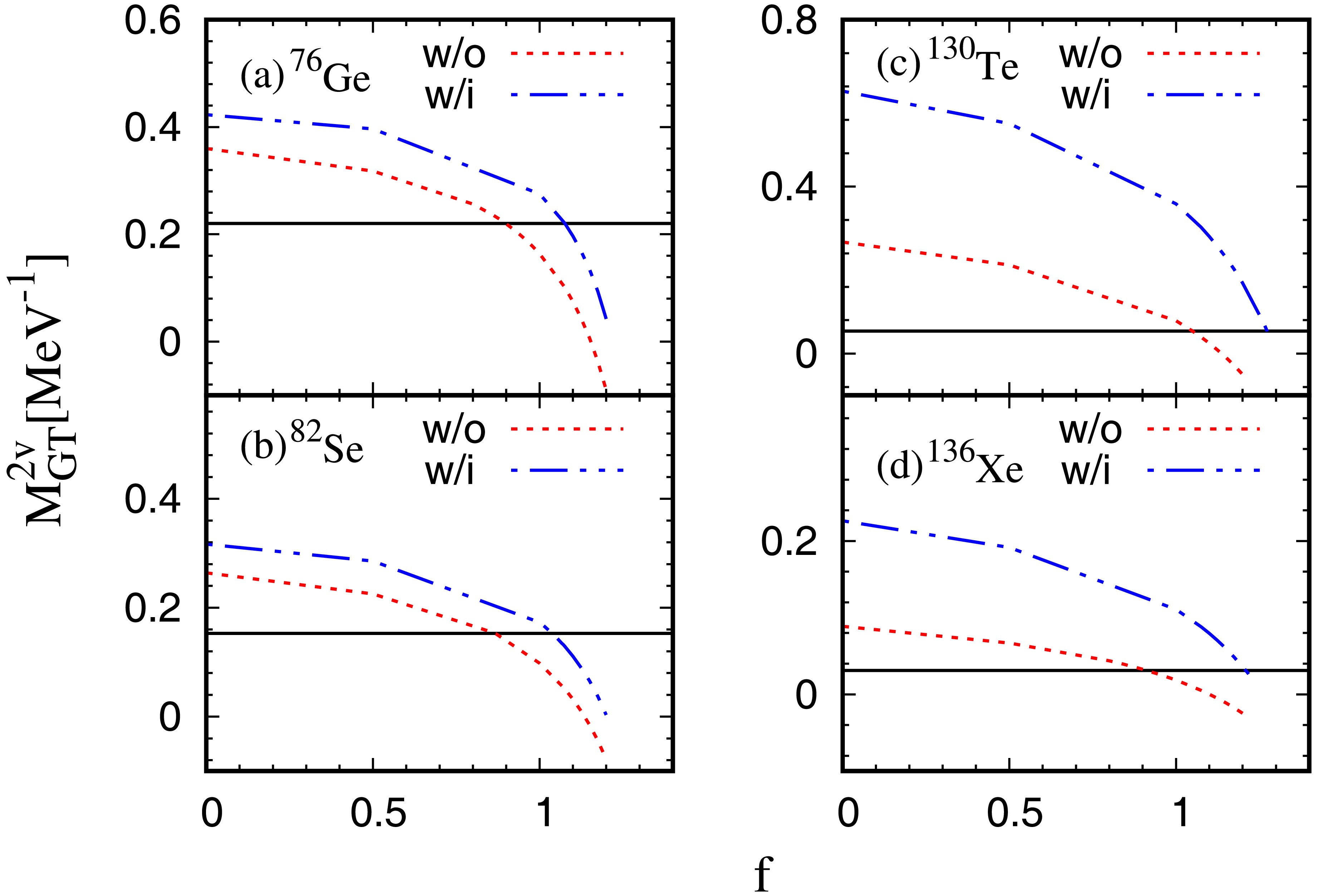
Figure 1. (color online) The
$ M^{2\nu}_{\text{GT}} $ values of$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ obtained by the HFB+QRPA calculation for different strengths of the IS pairing interaction. The results obtained by the calculations with (blue dash-dot-dot line) or without (red dotted line) tensor interaction are labeled by ”w/i” or ”w/o”, respectively. The experimental result is given by a black horizontal line [63].For the NMEs of
$ ^{76} {\rm{Ge}}$ and$ ^{82} {\rm{Se}}$ , as shown in Fig. 1(a) and (b), the results show that the tensor force enhances the NMEs notably. In$ ^{76} {\rm{Ge}}$ and$ ^{82} {\rm{Se}}$ , the tensor force enhances about 20% the NMEs when the IS pairing is absent. For$ ^{76} {\rm{Ge}}$ , when we increase the strength of IS pairing up to$ f = $ 1.0, the NME is enhanced by constant amount about 0.1 by the tensor force. Near the critical value$ f = $ 1.1, the NMEs both without and with the tensor force drop rapidly and become 0.075 and 0.197 without and with the tensor force at$ f = $ 1.1, respectively. For$ ^{82} {\rm{Se}}$ , the effect of tensor force is similar to the case of$ ^{76} {\rm{Ge}}$ ; it increases the NME always by 0.05$ \sim $ 0.07. When the value f is approaching to 1.1, the NME is enhanced even more by the tensor force, i.e., the NME becomes 0.032 and 0.111 without and with the tensor force at$ f = $ 1.1, respectively. For$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ , as shown Fig. 1(c) and (d), We can see much larger enhancement of NME by the tensor force compared to those of$ ^{76} {\rm{Ge}}$ and$ ^{82} {\rm{Se}}$ . For no IS pairing, NMEs are enhanced by more than a factor 2. This enhancement continues even with a large IS pairing with$ f = $ 1.0. When the IS pairing is approaching$ f = $ 1.1, the NMEs of both$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ are changed from negative to positive values by the tensor force.The f values, which reproduce the experimental NMEs are tabulated in Table 2. As was noticed already, these results show that the tensor force enhances the NME and therefore a larger f value is needed to reproduce the measured NME.
Nuclei $ M^{2\nu}_{\text{exp}} $ 

Tensor $ f_1 $ or

$ f_2 $ 

$ M^{2\nu}_{\text{GT}} $ 

$ ^{76} {\rm{Ge}}$ 

0.220 w/o $ f_1= $ 0.900

0.219 w/i $ f_2= $ 1.075

0.221 $ ^{82} {\rm{Se}}$ 

0.153 w/o $ f_1= $ 0.866

0.153 w/i $ f_2= $ 1.038

0.153 $ ^{130} {\rm{Te}}$ 

0.054 w/o $ f_1= $ 1.050

0.054 w/i $ f_2= $ 1.274

0.053 $ ^{136} {\rm{Xe}}$ 

0.031 w/o $ f_1= $ 0.920

0.030 w/i $ f_2= $ 1.211

0.030 Table 2. The values of IS pairing strength f to reproduce the experimental NMEs and the corresponding
$ M_{\text{GT}}^{2\nu} $ .$ f_1 $ and$ f_2 $ are the optimized values without (w/o) and with (w/i) the tensor force, respectively.The GT− strength distributions in
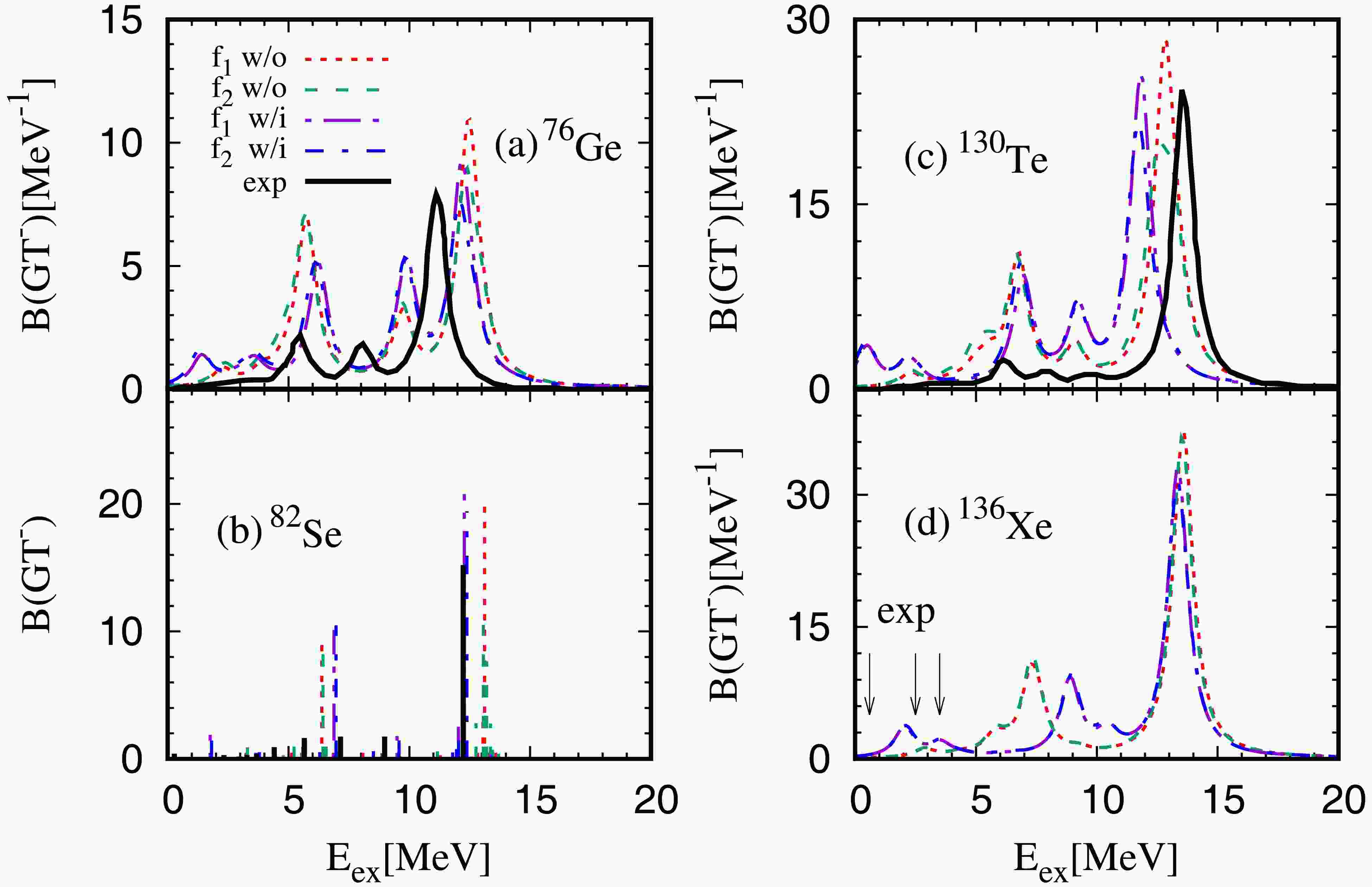
$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ calculated by using the IS pairing strengths listed in Table 2, in cases with or without including tensor force are shown in Fig. 2. For$ ^{76} {\rm{Ge}}$ as shown in the Fig. 2(a), the QRPA calculations give the three-peak structure observed also in the experimental data. The inclusion of the tensor force shifts the main peak energy downwords by about 0.5 MeV and obtains an excitation energy about 1 MeV higher than that of experiment. Basically, the change of IS pairing from${\rm{f}} _1 $ to${\rm{f}} _2 $ reduces the strengths in the giant GT resonances, which is the reason why the increasing of IS pairing rapidly reduces the$ 2\nu\beta\beta $ NME. On the other hand, the inclusion of tensor force changes the excitation energies in both low and high energy region. For$ ^{82} {\rm{Se}}$ as shown in panel (b), the main peak energy is about 1 MeV higher than the experimental data when the tensor force is absent, while the inclusion of the tensor force shifts down the peak by 1 MeV gives a good agreement with the experimental data. For$ ^{130} {\rm{Te}}$ , the main peak energy obtained with tensor force is about 1.8 MeV lower than the experimental one, which is partly due to the strong IS pairing required to reproduce the NME. For$ ^{136} {\rm{Xe}}$ , the calculation with tensor force produces the low excitation energy distribution at about 2 MeV, which is consistent with the experimental observation. The calculated main peak energies of three nuclei$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ and$ ^{130} {\rm{Te}}$ obtained with the inclusion of the tensor force are within 2 MeV difference to the experimental data. This is reasonable since the strength of the tensor force was optimized to reproduce the main GT peak energies of doubly-closed shell nuclei within 2.5 MeV differences in Ref.[55]. For all four nuclei in Fig. 2, the inclusion of the tensor force shifts main peak energies and bring the low-energy states downwards. In addition, it increases the strength in the low-energy states, this might be the reason that the tensor force enhance the NME.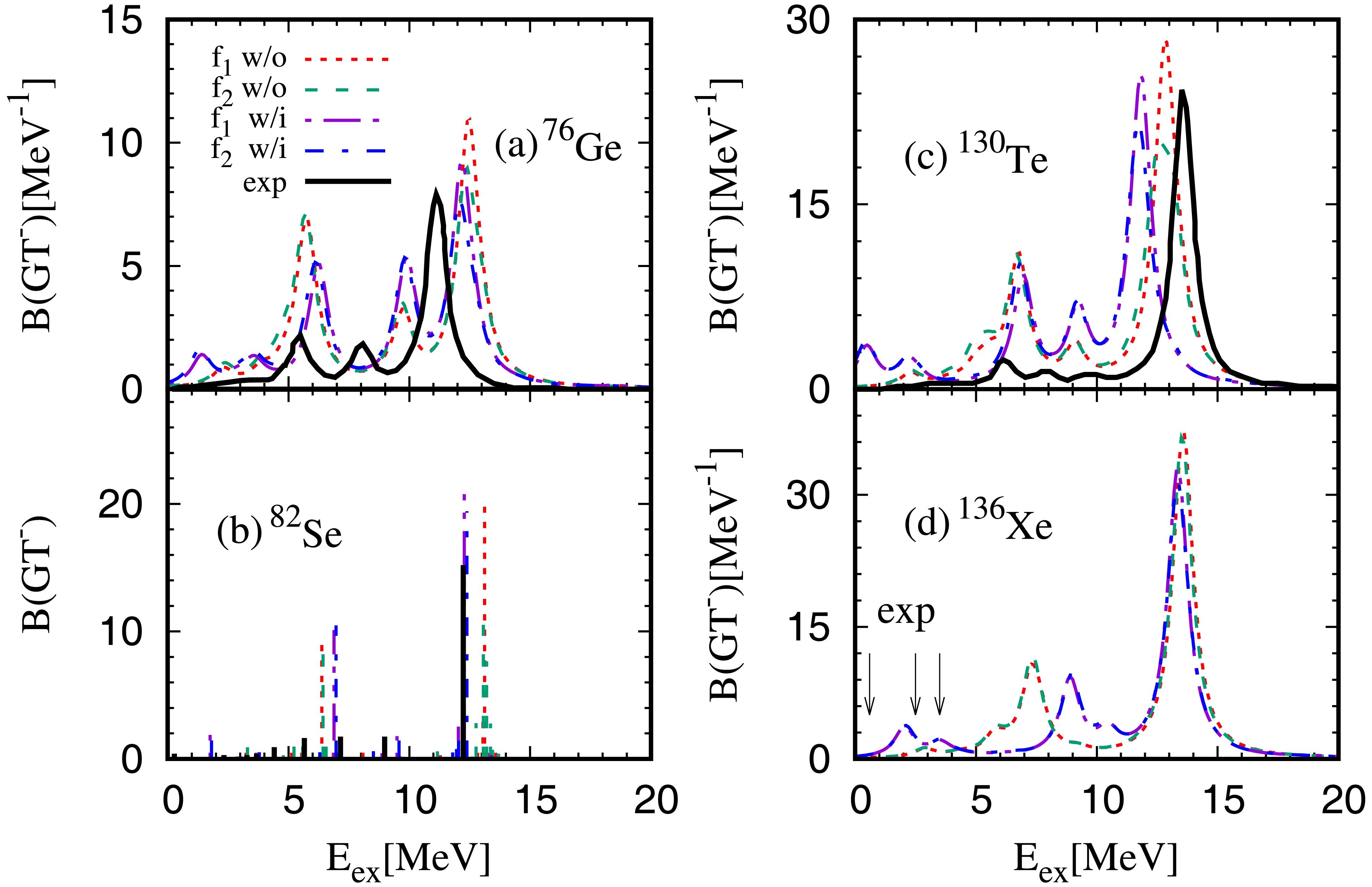
Figure 2. (color online) The
$ \text{GT}^- $ transition strength function for$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ .$ E_{ex} $ is the excitation energy of the final nuclei. The results obtained by the calculations with ($ f_1 $ -purple dash-dot-dot line,$ f_2 $ -blue dash-dot line) or without ($ f_1 $ -red dotted line,$ f_2 $ -green dashed line) tensor interaction are labeled by ”w/i” or ”w/o”, respectively, and$ f_1 $ and$ f_2 $ are the IS pairing strengths. Experimental data are shown by black lines for$ ^{76} {\rm{Ge}}$ , and$ ^{130} {\rm{Te}}$ , while the data are given by black horizontal lines for$ ^{82} {\rm{Se}}$ [69, 70].For more comprehensive understanding the effect of tensor force on the M
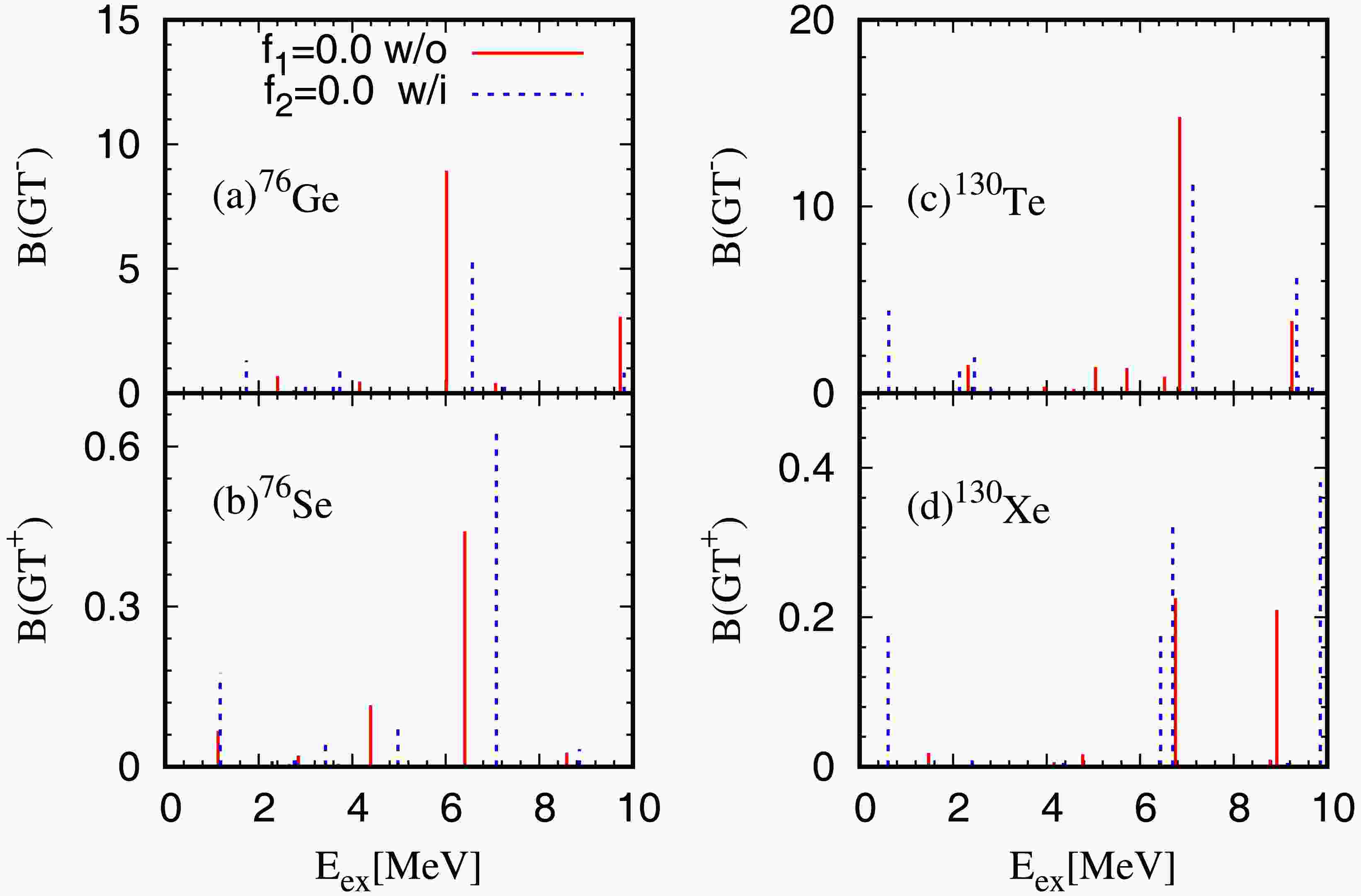
$ _{GT}^{2\nu} $ , we show in Fig. 3 the$ \text{GT}^\pm $ strength distributions for the initial and final nuclei$ ^{76} {\rm{Ge}}$ and$ ^{76} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{130} {\rm{Xe}}$ obtained with and without tensor force without the pn pairing. Since the cases of$ ^{76} {\rm{Ge}}$ and$ ^{130} {\rm{Te}}$ are similar to$ ^{82} {\rm{Se}}$ and$ ^{136} {\rm{Xe}}$ respectively,$ ^{76} {\rm{Ge}}$ and$ ^{130} {\rm{Te}}$ are chosen as representatives to examine effects of tensor force on the NMEs. For$ ^{76} {\rm{Ge}}$ with the inclusion of tensor force as shown in panel (a), the lowest GT state is shifted downwards by about 0.8 MeV. For$ ^{76} {\rm{Se}}$ as shown in panel (b), the excitation energy of the lowest GT+ state is kept unchanged. The strengths in the lowest states are enhance by about a factor 2 by the inclusion of tensor force. These two effects of tensor force are the main reason that the tensor force obviously enhances the M$ _{GT}^{2\nu} $ of$ ^{76} {\rm{Ge}}$ . On the other hand, for$ ^{130} {\rm{Te}}$ and$ ^{130} {\rm{Xe}}$ as shown in panels (c) and (d), the lowest GT− and GT+ states are shifted downwards by about 2.0 and 0.8 MeV by the inclusion of tensor force. In addition, the GT strengths in the lowest states are dramatically increased, particularly the GT+ strength which is increased by about one order of magnitude. As a result, a much stronger effect of tensor force on the NME of$ ^{130} {\rm{Te}}$ is observed in Fig. 1.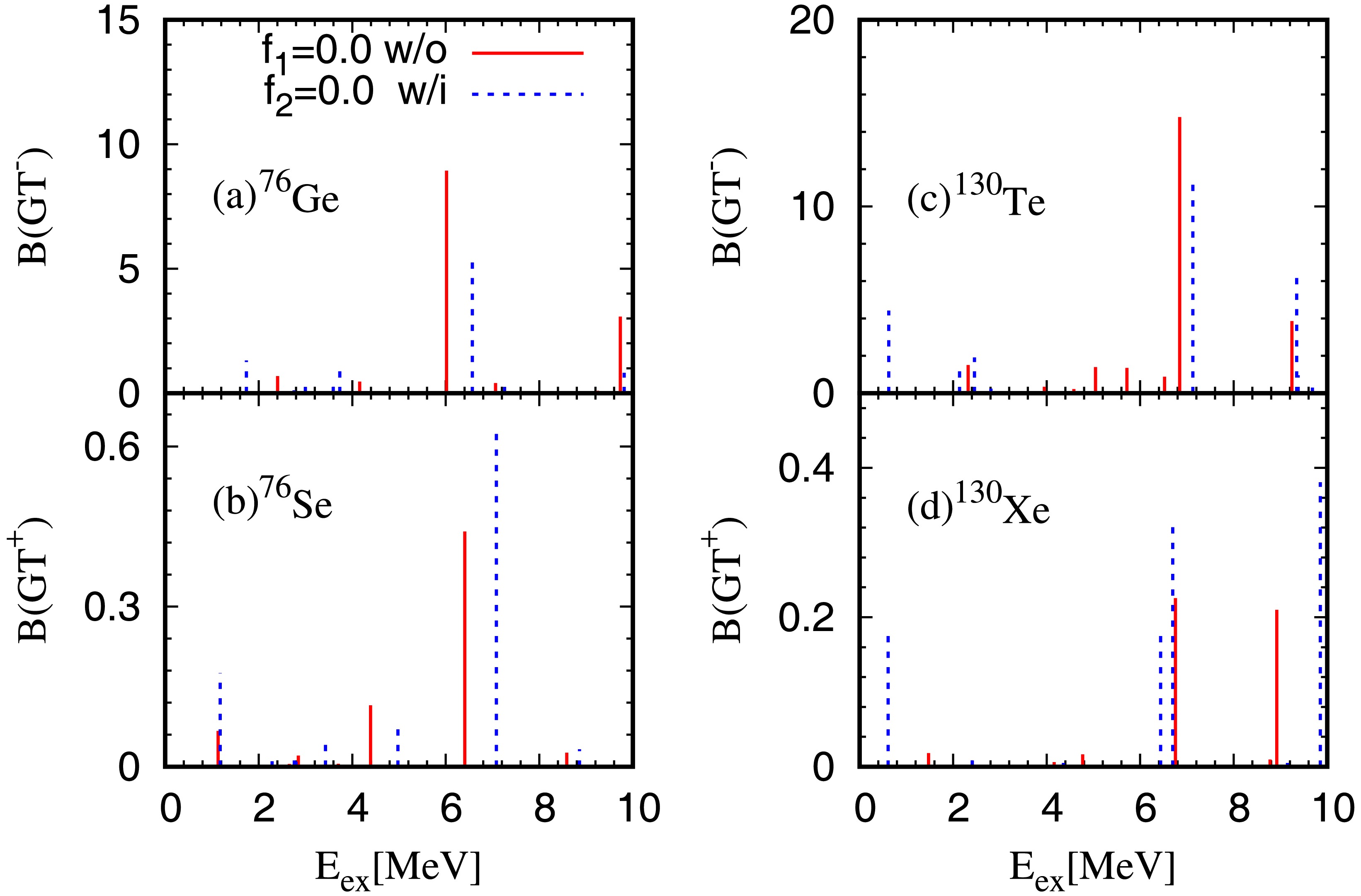
Figure 3. (color online) The
$ \text{GT}^\pm $ strength distributions for the initial and final nuclei$ ^{76} {\rm{Ge}}$ and$ ^{76} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{130} {\rm{Xe}}$ obtained with pn pairing strength f = 0 in cased with (blue dotted lines) and without (red solid lines) including tensor force.For further clarification of the effect of tensor force on the GT states, the important configurations of
$ ^{76} {\rm{Ge}}$ ,$ ^{76} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ ,$ ^{130} {\rm{Xe}}$ are listed in Table 3. For$ ^{76} {\rm{Ge}}$ ,$ ^{76} {\rm{Se}}$ , the most important configuration is$ (\pi2p_{3/2},\nu2p_{1/2}) $ , while it is$ (\pi2d_{5/2},\nu2d_{3/2}) $ for$ ^{130} {\rm{Te}}$ and$ ^{130} {\rm{Xe}}$ . As reported in Ref.[27], the tensor force produces an attractive effect between proton and neutron in j$ {_\gtrless} $ and j$ _{\lessgtr} $ orbits, and a repulsive effect between protons and neutrons in j$ {_\gtrless} $ and j$ _{\gtrless} $ orbits. As a result, the tensor force shifts the lowest GT states downwards. We should point out some difference among the nuclei listed in the table. For$ ^{76} {\rm{Ge}}$ ,$ ^{76} {\rm{Se}}$ , there are appreciable contributions from$ (\pi2p_{1/2},\nu2p_{1/2}) $ configuration after the tensor force is included, which cancels slightly the attractive effect. However, for$ ^{130} {\rm{Te}}$ and$ ^{130} {\rm{Xe}}$ all the important configurations receive the attractive effect of the tensor force. This is the reason that the effects of the tensor force are stronger in$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ .Nuclei Tensor $ E_{ex} $ 

B(GT $ \pm $ )

configuration $ X^2-Y^2 $ 

$ ^{76} {\rm{Ge}}$ 

w/o 2.40 0.69 $ (\pi2p_{3/2},\nu2p_{1/2}) $ 

0.948 $ (\pi2p_{1/2},\nu2p_{3/2}) $ 

0.016 $ (\pi2p_{3/2},\nu2p_{3/2}) $ 

0.022 w/i 1.73 1.31 $ (\pi2p_{1/2},\nu2p_{1/2}) $ 

0.045 $ (\pi2p_{3/2},\nu2p_{1/2}) $ 

0.895 $ (\pi2p_{3/2},\nu1f_{5/2}) $ 

0.052 $ ^{76} {\rm{Se}}$ 

w/o 1.13 0.07 $ (\pi2p_{3/2},\nu2p_{1/2}) $ 

0.964 $ (\pi2p_{1/2},\nu2p_{3/2}) $ 

0.015 $ (\pi2p_{3/2},\nu2p_{3/2}) $ 

0.011 w/i 1.17 0.18 $ (\pi2p_{1/2},\nu2p_{1/2}) $ 

0.089 $ (\pi2p_{3/2},\nu2p_{1/2}) $ 

0.887 $ (\pi2p_{3/2},\nu1f_{5/2}) $ 

0.016 $ ^{130} {\rm{Te}}$ 

w/o 2.32 1.50 $ (\pi3s_{1/2},\nu3s_{1/2}) $ 

0.010 $ (\pi2d_{3/2},\nu2d_{3/2}) $ 

0.006 $ (\pi2d_{5/2},\nu2d_{3/2}) $ 

0.925 $ (\pi2d_{5/2},\nu2d_{5/2}) $ 

0.022 w/i 0.62 4.42 $ (\pi3s_{1/2},\nu2d_{3/2}) $ 

0.046 $ (\pi2d_{5/2},\nu2d_{3/2}) $ 

0.883 $ (\pi2d_{5/2},\nu1g_{7/2}) $ 

0.046 $ ^{130} {\rm{Xe}}$ 

w/o 1.47 0.02 $ (\pi3s_{1/2},\nu3s_{1/2}) $ 

0.011 $ (\pi2d_{3/2},\nu2d_{3/2}) $ 

0.006 $ (\pi2d_{5/2},\nu2d_{3/2}) $ 

0.932 $ (\pi2d_{5/2},\nu2d_{5/2}) $ 

0.020 w/i 0.61 0.19 $ (\pi3s_{1/2},\nu2d_{3/2}) $ 

0.049 $ (\pi2d_{5/2},\nu2d_{3/2}) $ 

0.894 $ (\pi2d_{5/2},\nu1g_{7/2}) $ 

0.035 Table 3. The important configurations in the lowest GT states of initial and final nuclei obtained with f = 0.0, in cases with and without tensor force.
Recent
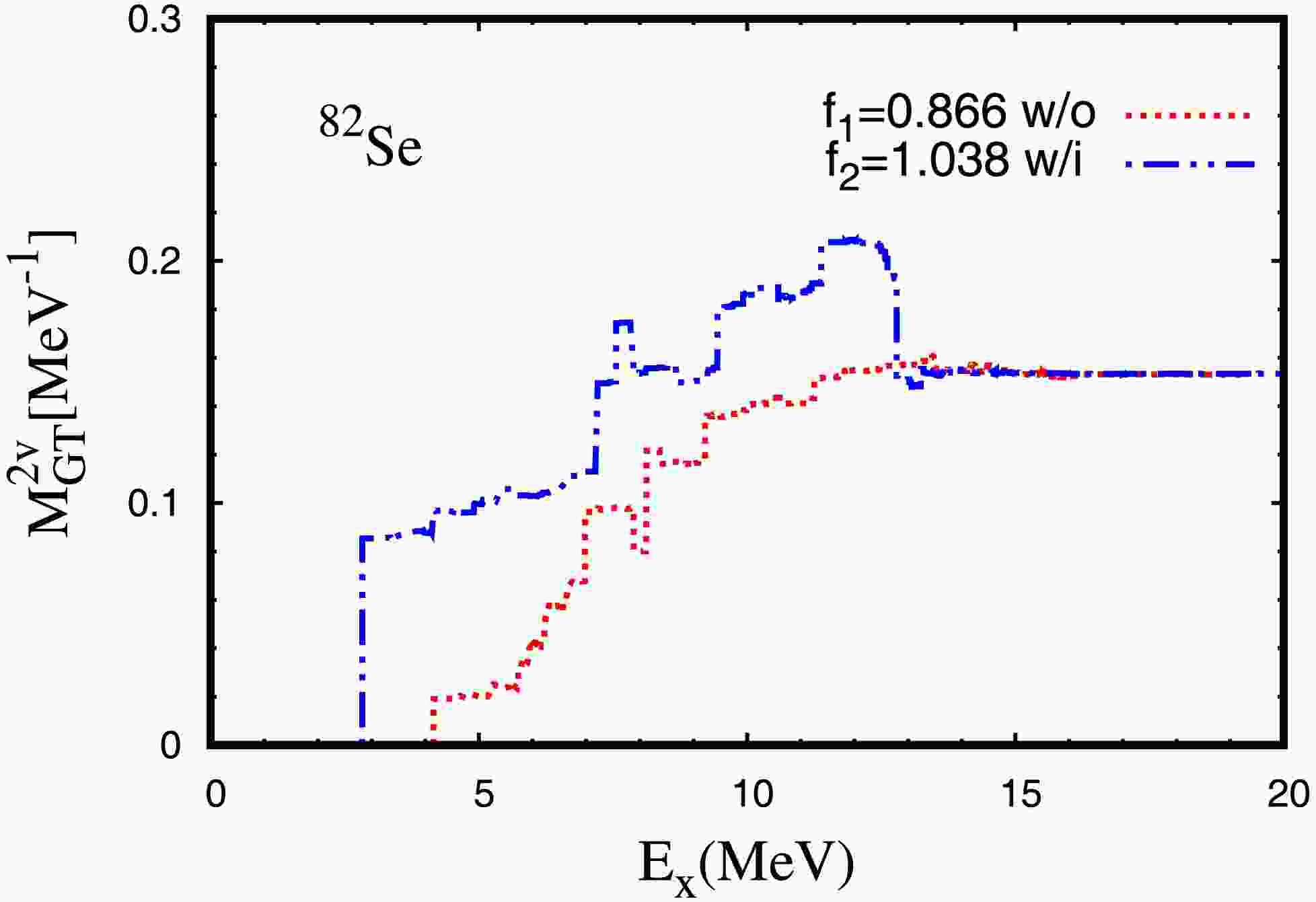
$ 2\nu\beta\beta $ decay experiments offer rich information of the electron spectra which provide precious information about the contributions from states with different excitation energies and could be used to further constrain the nuclear structure calculations other than the NME [66]. The running sums of NMEs in$ ^{82} {\rm{Se}}$ and$ ^{136} {\rm{Xe}}$ are measured [67, 68]. However, the results in$ ^{136} {\rm{Xe}}$ are still with a large uncertainty which could not uniquely determine the running sum yet [66]. For$ ^{82} {\rm{Se}}$ , a strong preference to the single-state dominance (SSD) feature for the running sum is observed, i.e. contribution from the lowest$ 1^+ $ state exhausts almost all the total$ M_{\text{GT}}^{2\nu} $ . The running sums of$ M^{2\nu}_{\text{GT}} $ for$ ^{82} {\rm{Se}}$ are shown in Fig. 4. Without the tensor force, the running sum starts at about 0.02 and increases steadily up to the final value about 0.15, most of the contribution comes from high-lying states. When the tensor force is included, the running sum starts at about 0.08, which contributes more than 50% to the total$ M_{\text{GT}}^{2\nu} $ . This could be an implication of necessity to include the tensor force in the NME calculations.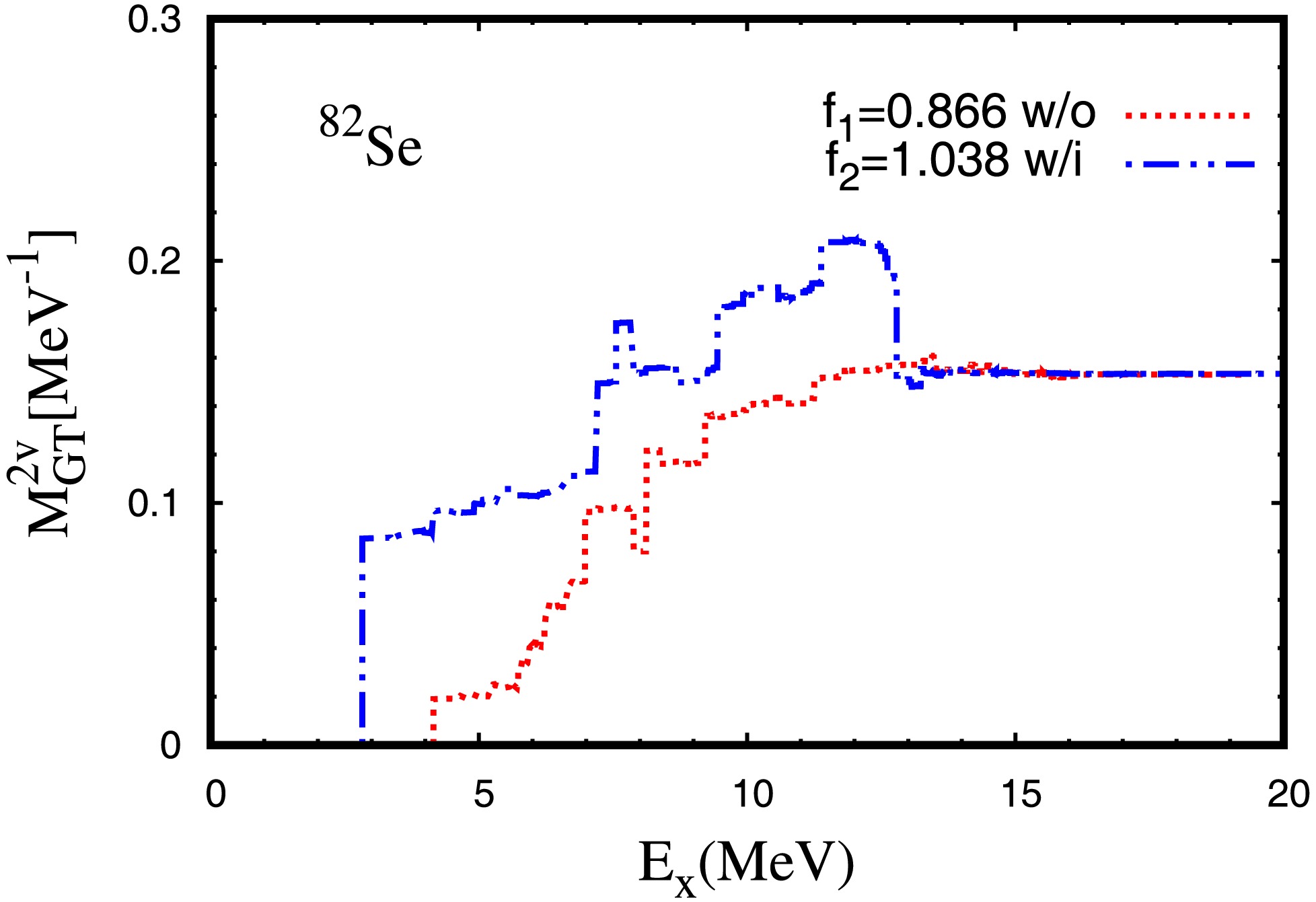
Figure 4. (color online) The running sum of the NME
$ M^{2\nu}_{\text{GT}} $ in$ ^{82} {\rm{Se}}$ as a function of the excitation energy$ E_x $ with the optimized IS pairing strength$ f_1 $ or$ f_2 $ .$ E_x $ = ($ \omega_{\mu}+\omega_{\nu} $ )/2 is the averaged excitation energy given in Eq. (3). The results with (blue dash-dot-dot line) or without (red dotted line) tensor interaction are labeled by ”w/i” or ”w/o”, respectively. -
After the strength parameter f of IS pairing interaction is fixed by the
$ 2\nu\beta\beta $ NME, we performed the calcualtion on the NMEs of$ 0\nu\beta\beta $ for$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ . In the calcualations, the intermediate states from${\rm{J}} ^{\pi} $ = 0± to 10± are taken into account.The
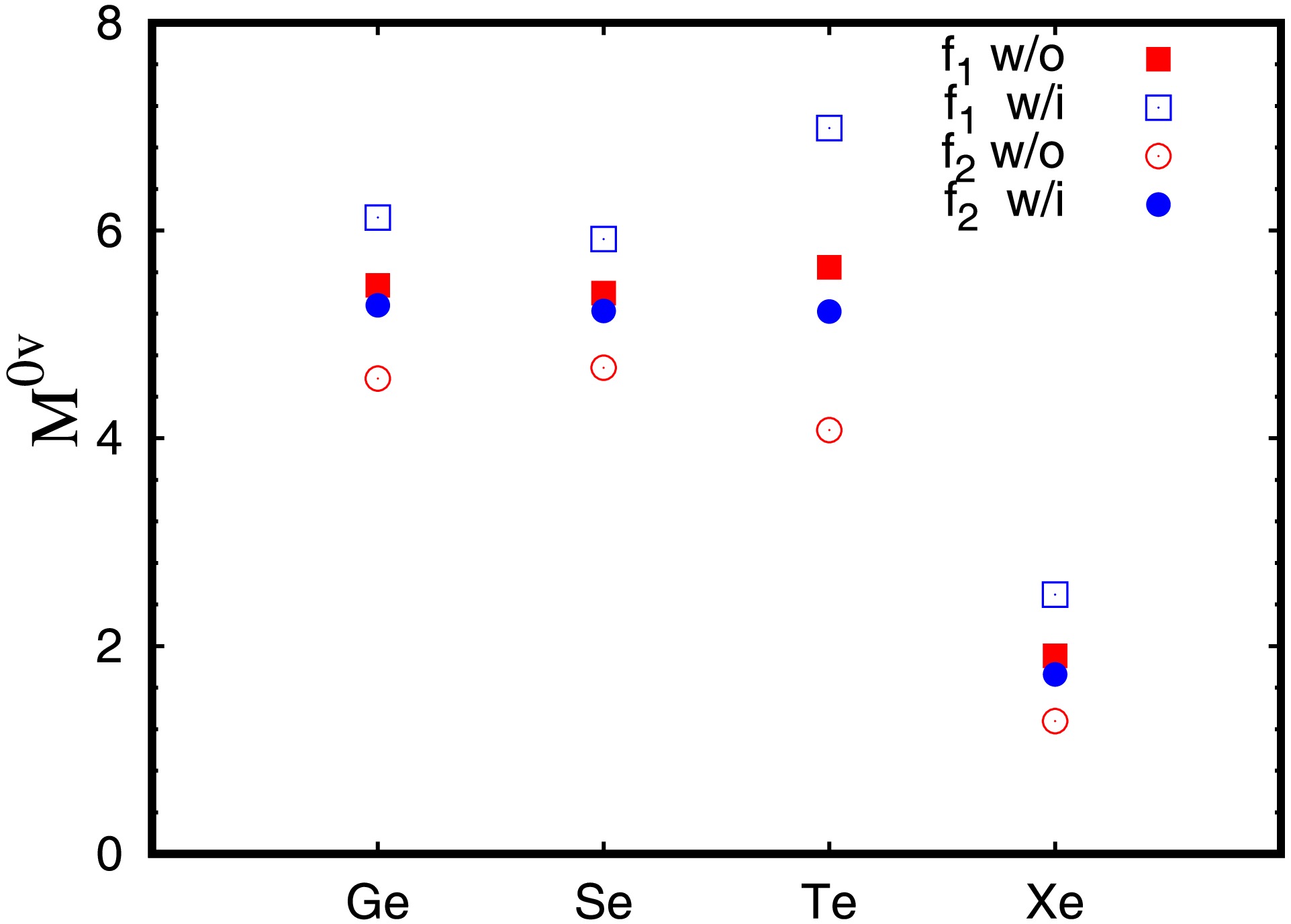
$ M^{0\nu} $ values for$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ calculated with different IS pairing strength factor f, including tensor force or not are shown in Fig. 5. As shown in Fig. 1, reproducing$ M_{\text{GT}}^{2\nu} $ in the calculations with or without tensor force need different IS pairing strengths. In Fig. 5 the IS pairing strength factor fixed by the$ M_{\text{GT}}^{2\nu} $ in the calculations without and with tensor force are labeled by$ f_1 $ and$ f_2 $ , respectively. One can see from the figure when$ M_{\text{GT}}^{2\nu} $ are reproduced, i.e. the filled symbols, including tensor force make small changes on the$ M^{0\nu} $ , which is consistent to Ref.[23]. While in the calculations using the same factor f but including tensor force or not, i.e. the results shown in the same symbol but with filled or empty styles, the including of tensor force lead to obvious difference of$ M^{0\nu} $ values.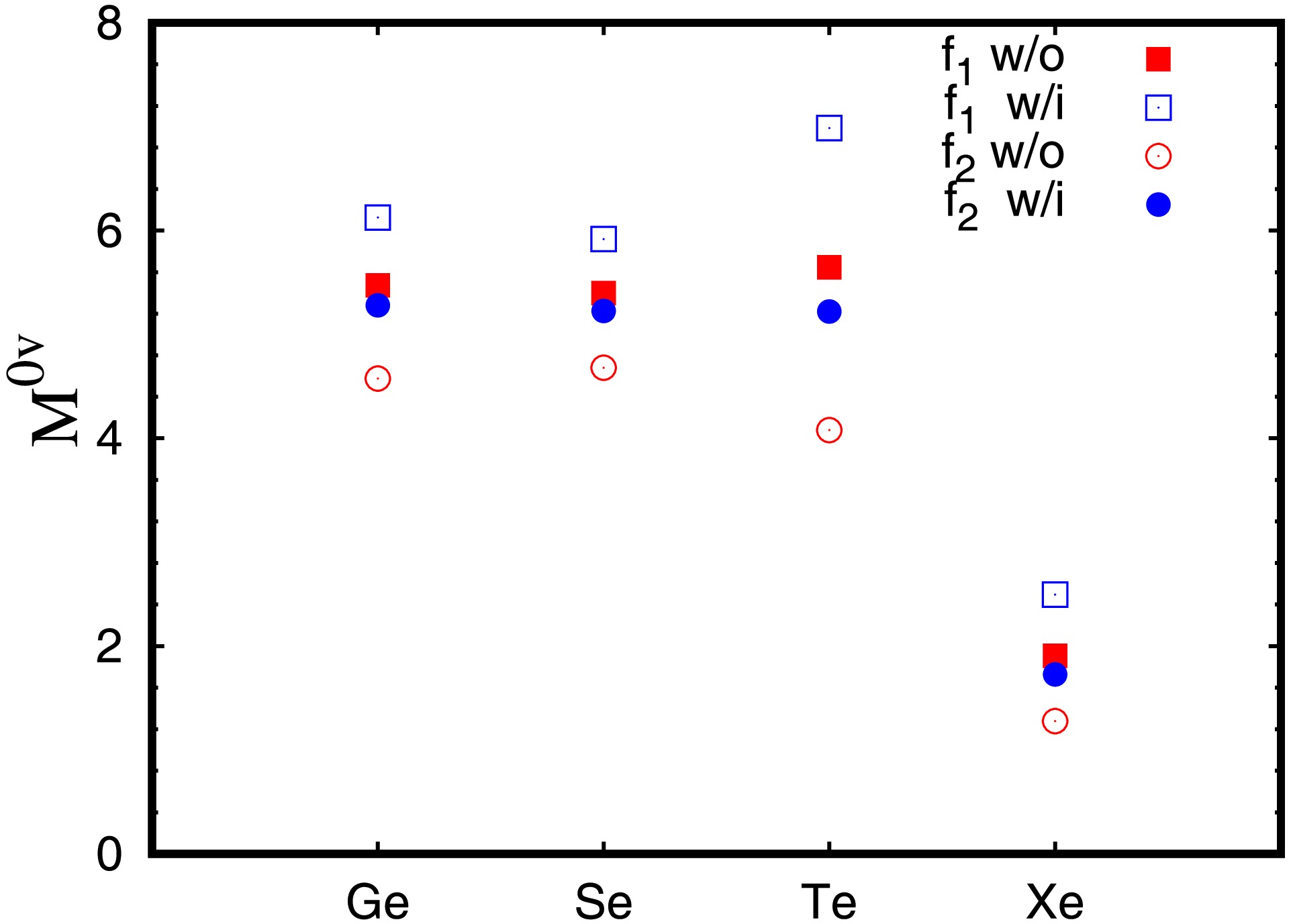
Figure 5. (color online) The
$ M^{0\nu} $ values for$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ . The results obtained by the calculations with (blue) or without (red) tensor interaction are labeled by ”w/i” or ”w/o”, respectively.The relative change of
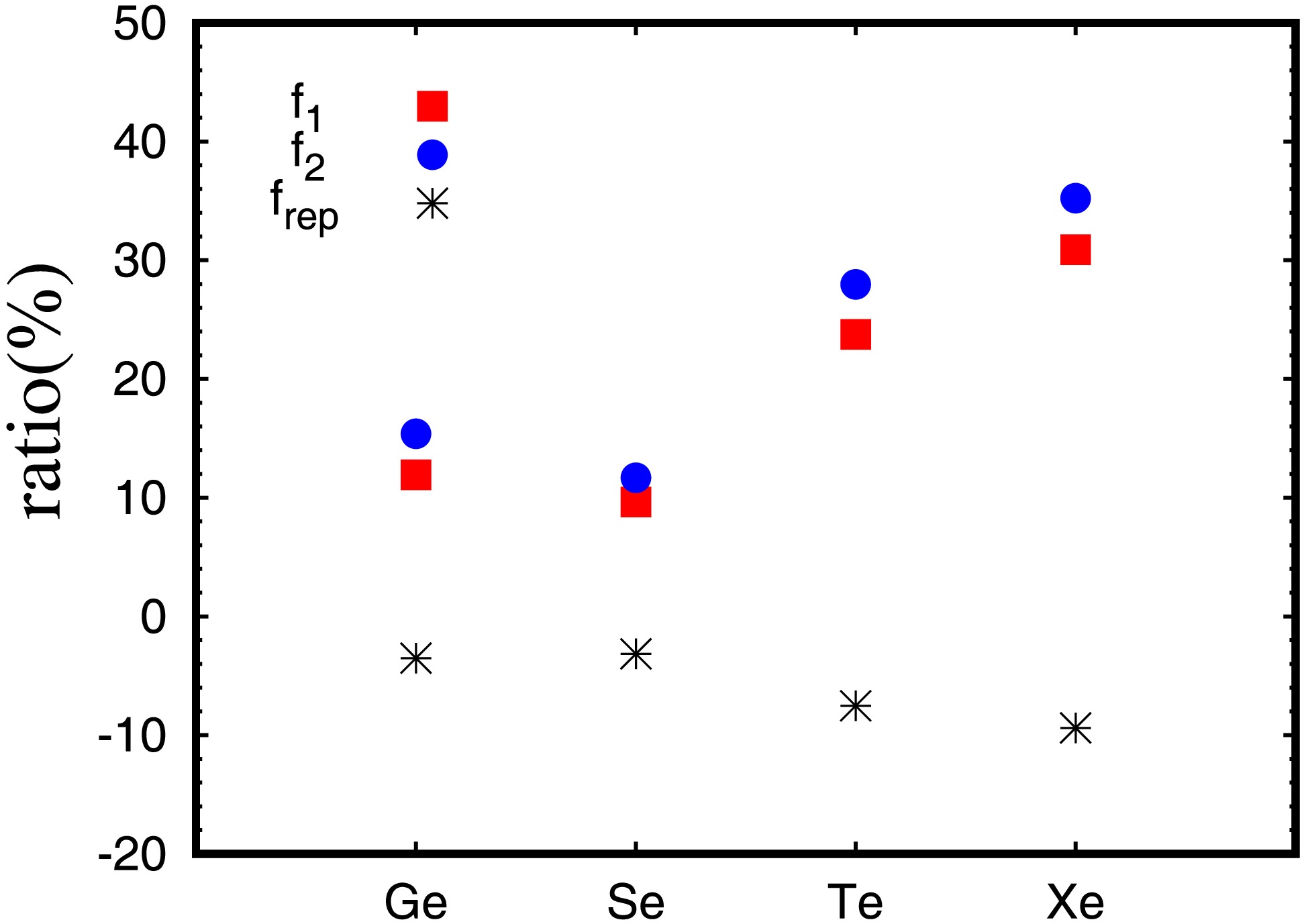
$ M^{0\nu} $ caused by the inclusion of tensor force are depicted in Fig. 6 as the ratio$ (M_{w/i}^{0\nu}(f)-M_{w/o}^{0\nu}(f))/M_{w/o}^{0\nu}(f) $ . For the fixed IS pairing strength$ f_1 $ or$ f_2 $ , the tensor force increases the ratio about 13% for$ ^{76} {\rm{Ge}}$ and$ ^{82} {\rm{Se}}$ , and about 30% for$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ . However, the ratio$ (M_{w/i}^{0\nu}(f_2)-M_{w/o}^{0\nu}(f_1))/M_{w/o}^{0\nu}(f_1) $ varies only slightly with the change of f factor from$ f_1 $ w/o tensor to$ f_2 $ with tensor; if the pairing strengths are optimized by the experimental$ M_{\text{GT}}^{2\nu} $ with or without tensor force, the net results of IS paring and tensor coupling for$ M_{0\nu} $ cause only small changes, i.e., about -3% for$ ^{76} {\rm{Ge}}$ and$ ^{82} {\rm{Se}}$ , -8.0% and -9.0% for$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ , respectively, compared with those with the optimized value$ f_1 $ for no tensor interaction. As noticed before, this is due to the fact that the inclusion of tensor force requires stronger IS pairing strength so as to reproduce the$ M_{\text{GT}}^{2\nu} $ , but the stronger IS pairing will cancel the effect of tensor force.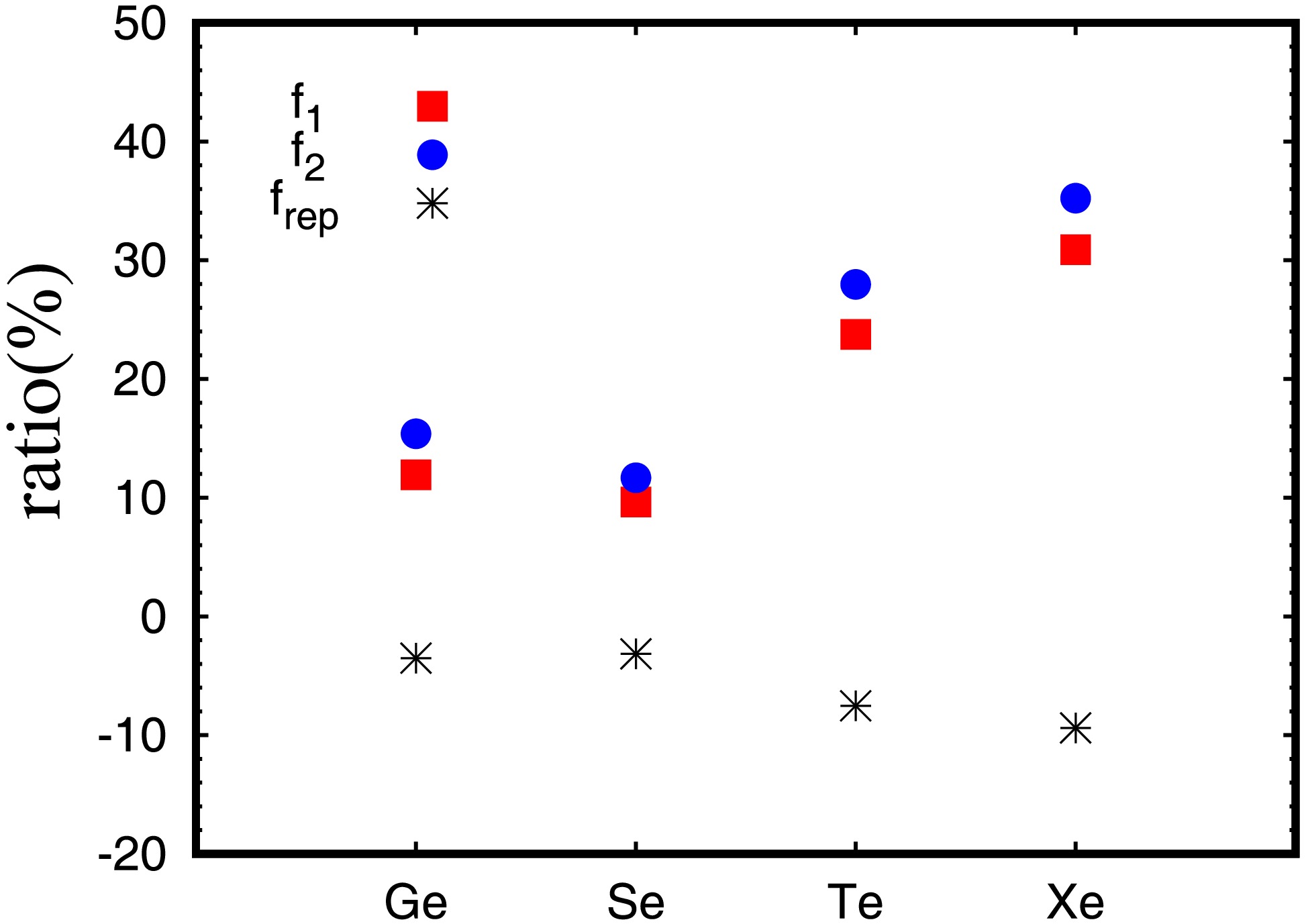
Figure 6. (color online) Relative change of
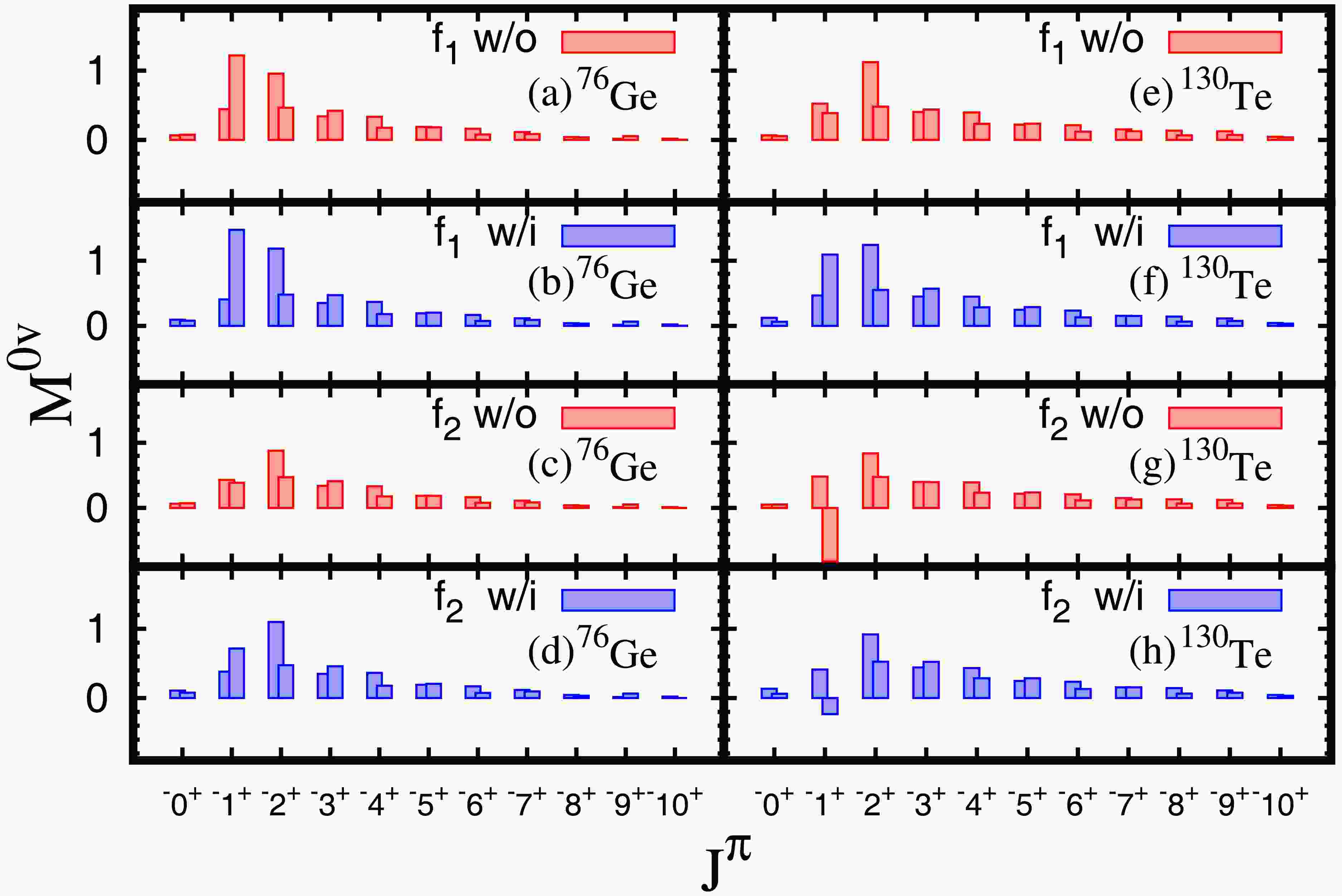
$ M^{0\nu} $ caused by the inclusion of tensor force, the ratio is defined by$ \frac{M_{w/i}^{0\nu}(f)-M_{w/o}^{0\nu}(f)}{M_{w/o}^{0\nu}(f)} $ , for$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ . The results are labeled by the IS strength$ f_1 $ or$ f_2 $ , while$ f_{rep} $ represents the ratio$ \frac{M_{w/i}^{0\nu}(f_2)-M_{w/o}^{0\nu}(f_1)}{M_{w/o}^{0\nu}(f_1)} $ .For more details, the contributions of all the intermediate states to
$ M^{0\nu} $ calculated with different f values$ f_1 $ and$ f_2 $ are displayed in Fig. 7. For each f value, we examine the effect of tensor interaction without introducing the closure approximation. Since the cases of$ ^{76} {\rm{Ge}}$ and$ ^{130} {\rm{Te}}$ are similar to$ ^{82} {\rm{Se}}$ and$ ^{136} {\rm{Xe}}$ respectively,$ ^{76} {\rm{Ge}}$ and$ ^{130} {\rm{Te}}$ are chosen as representatives to examine the interplay between IS pairing and tensor interactions. Basically, the tensor force and IS pairing interaction make small contribution to the NME through the state with$ J>2 $ , this is due to the exchange momentum q in the neutrino potential in Eq. (11); for larger J, larger q is needed to contribute to the matrix element of$ j_l(qr) $ . For$ ^{76} {\rm{Ge}}$ , as shown in panels (a) and (b), or (c) and (d), when calculated with the fixed IS pairing strength factor$ f_1 $ or$ f_2 $ , the tensor force obviously increases NMEs through 1+ and 2− intermediate states. As a result, including tensor force enhances the NME as can be seen in comparisons between panels (a) and (b) or between (c) and (d). While comparing panels (a) and (d), in which experimental$ M^{2\nu}_{\text{GT}} $ are reproduced by optimized IS pairing strengths, the larger IS pairing$ f_2 $ reduces the NME largely through 1+ states, while the tensor interaction increases the contribution of 2− states. Therefore, the effects of tensor force and IS pairing on the NME are largely canceled by each other in the panels (a) and (d).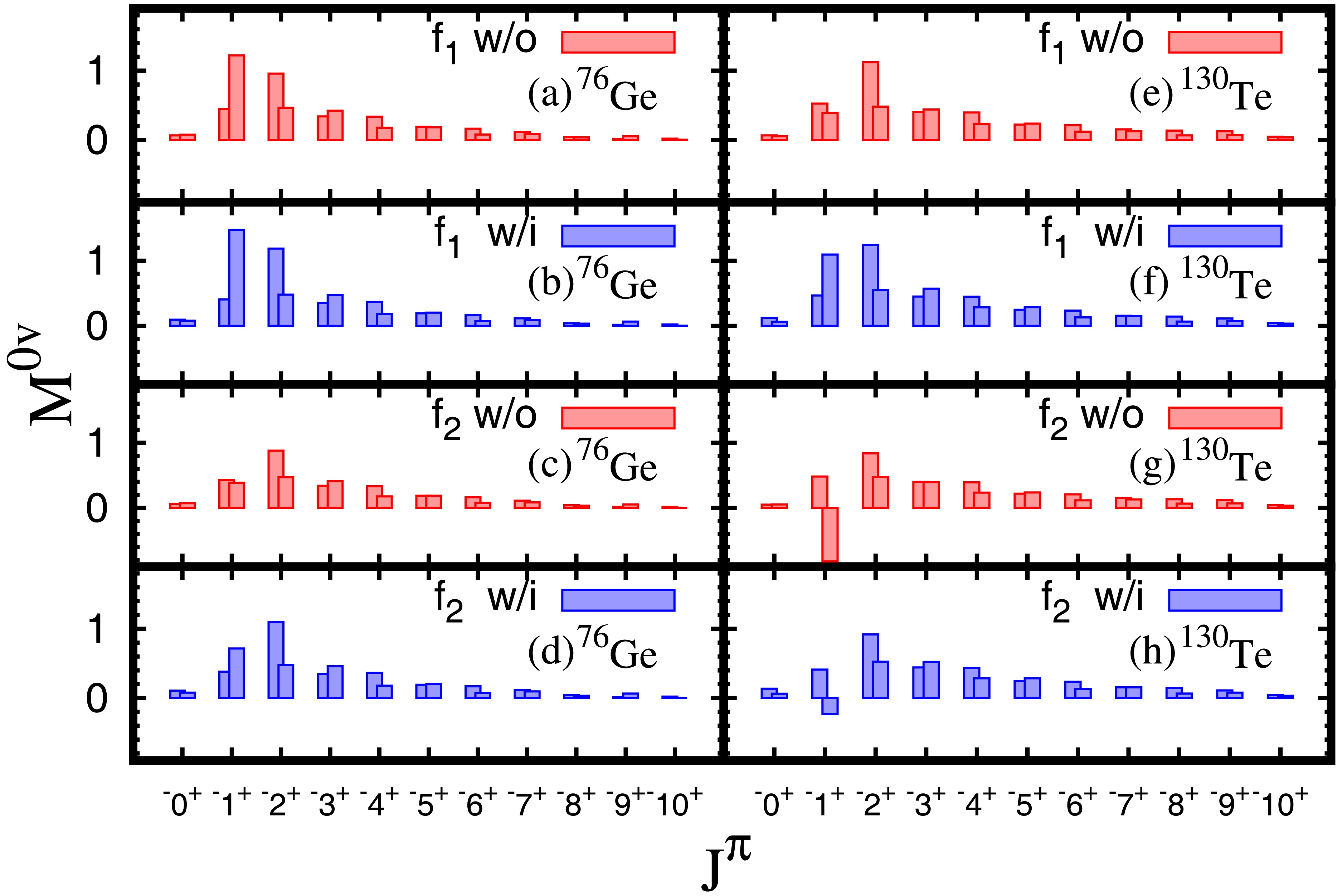
Figure 7. (color online) The
$ M^{0\nu} $ value of each$ J^{\pi} $ for$ ^{76} {\rm{Ge}}$ and$ ^{130} {\rm{Te}}$ in different f with or without the tensor force is shown above,$ f_1 $ is determined by the experimental value of w/o (red rectangle), and$ f_2 $ is determined by the experimental value of w/i (blue rectangle).In the case of
$ ^{130} {\rm{Te}}$ , we can see clearly in comparisons between panels (e) and (f) or (g) and (h) of Fig. 7 that the inclusion of the tensor force increases substantially the NME through 1+ and 2− intermediate states even more than the case of$ ^{76} {\rm{Ge}}$ . For 2− states, in calculations with both${\rm{f}} _1 $ and${\rm{f}} _2 $ cases, the tensor force slightly enhances the NME. While for 1+ states, with the increasing of IS pairing strength from${\rm{f}} _1 $ to${\rm{f}} _2 $ , the contribution is reduced rapidly from the magnitude similar to 2− state with${\rm{f}} _1 $ to very small with${\rm{f}} _2 $ , even negative in some cases. As a net effect, we can see that the inclusion of the tensor interaction enhances the contribution, but cancels largely the effect of IS pairing. On the other hand, the larger IS pairing$ f_2 $ reduces the NME, especially through 1+ states, in comparison with the weaker IS pairing$ f_1 $ as seen between (e) and (g) or (f) and (h).The present results are different from what reported by Ref.[10] in which the 1− states also makes important contribution. The difference might be due to the differences in the single-particle states and residual interaction in the calculations. Moreover in our calculations, the 1− states are located at higher energies which reduce the contribution to the NME.
In this work, the
$ \beta\beta $ NMEs are studied in the spherical approximation, but the initial and final nuclei of the present four double β decay candidates might be deformed. It was reported that the NMEs are reduced when there are very different deformations between the initial and final nuclei[71], as the overlap factor of two nuclei is reduced by this difference. It was also reported empirically that similar deformations of the initial and final nuclei for$ ^{82} {\rm{Se}}$ and$ ^{136} {\rm{Xe}}$ , but obvious different values for$ ^{76} {\rm{Ge}}$ and$ ^{130} {\rm{Te}}$ . The$ 0\nu\beta\beta $ NMEs are studied by using Skyrme interaction with axial deformation in Ref.[24]. It was found that the M$ ^{0\nu} $ value of$ ^{76} {\rm{Ge}}$ is very close to our results without including tensor force since similar deformations of the initial and final nuclei are obtained, but M$ ^{0\nu} $ values in$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ are much suppressed due to the obvious different deformations in terms of absolute values or signs. Since the quadrupole deformation factor$ \beta_2 $ is not well reproduced in the HFB calculation even qualitatively, it is valuable to check the$ \beta\beta $ NMEs with realistic deformations in qualitatively and quantitatively in our forthcoming work. -
HFB+QRPA calculations employing Skyrme interaction SGII have been performed to study the
$ 2\nu\beta\beta $ and$ 0\nu\beta\beta $ decay NMEs in$ ^{76} {\rm{Ge}}$ ,$ ^{82} {\rm{Se}}$ ,$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ taking into account the tensor interaction. Together with the tensor interaction, the IV pairing interaction was adopted in the HFB and QRPA calculations, while the IS pairing interaction was included only in the QRPA calculations. The$ 2\nu\beta\beta $ decay is dominated by the intermediate 1+ states, and the inclusion of the tensor force enhances$ M^{2\nu}_{\text{GT}} $ largely because the tensor force shifts low energy GT states downwards, which makes the$ M^{2\nu}_{\text{GT}} $ larger. Thus, a stronger IS pairing is required to reproduce the experimental$ 2\nu\beta\beta $ NMEs,$ M^{2\nu}_{\text{GT}} $ , with the tensor interaction compared with the case without the tensor interaction. That is, the optimized IS strength$ f_1 $ is around 0.9 to 1.0 when the tensor force is absent, but the value$ f_2 $ becomes around 15% larger to be about 1.0 for$ ^{76} {\rm{Ge}}$ and$ ^{82} {\rm{Se}}$ , and 1.2 for$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ with the inclusion of the tensor force. The experimental$ 2\nu\beta\beta $ electron spectra of$ ^{82} {\rm{Se}}$ for the running sum is dominated by the lowest 1+ state, and the calculated results are largely improved by the tensor interaction showing a substantially large contribution from the lowest 1+ state.The
$ 0\nu\beta\beta $ NMEs,$ M^{0\nu} $ , was calculated including the full spectra of intermediate states with$ J^{\pi} = 0^{\pm}\sim 10^{\pm} $ up to the energy cutoff E = 60 MeV, which is enough to attain the converge to calculate NME without introducing the closure approximation. In calculations with the fixed IS pairing strength, the inclusion of tensor interaction enhances the NME by about 13% for$ ^{76} {\rm{Ge}}$ and$ ^{82} {\rm{Se}}$ , and by about 30% for$ ^{130} {\rm{Te}}$ and$ ^{136} {\rm{Xe}}$ . However, if we adopt the optimized IS pairing strengths fixed by the experimental$ 2\nu\beta\beta $ NME, i.e.,$ f_1 $ or$ f_2 $ ($ f_1<f_2 $ ) without or with tensor force, the tensor effect cancels the larger IS pairing effect, and the net effect of the tensor and IS pairing interactions becomes smaller, at most 10% effect. We found that the 2− state makes the important contribution to$ 0\nu\beta\beta $ NME, which is slightly affected by the IS and tensor force. But one should pay much attention to the 1+ state since its contribution to the NME may be affected largely by the IS pairing and tensor interaction, i.e. the inclusion of tensor force enhances largely its contribution to the NME, but its contribution is reduced significantly by the IS pairing: the increase of IS pairing strength from${\rm{f}} _1 $ to${\rm{f}} _2 $ changes the contribution of 1+ states from the similar magnitude to that of 2− state to very small, even to be negative contribution. In other words, the inclusion of tensor force enhances the contributions of 1+ and 2− intermediate states to the$ M^{0\nu} $ , but the larger IS pairing interaction in the case with the tensor interaction reduces largely the contribution from these low spin states.
Effect of tensor force on the 2νββ and 0νββ decays in 76Ge,82Se, 130Te and 136Xe
- Received Date: 2025-01-27
- Available Online: 2025-09-01
Abstract: The effects of the tensor force on the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: