-
The study of protons and neutrons is the primary focus of atomic physics, which studies nucleons and their constituent parts. Nuclear deformation is one of the most thoroughly researched topics; in it, the non-spherical shape of a nucleus is described by quadrupole and octupole moments. Nuclear dynamics and organization are known to be significantly impacted by such deformation. The study of quadrupole [1] and octupole [2−4] deformations in nuclei has advanced recently, particularly in cases when these two anharmonic forms interact. Nonuniform spatial charge distributions are the driving force underlying this interaction, and deformations affect nuclear characteristics including energy levels and electromagnetic moments. Several models have been presented to investigate the collective dynamics of nuclei [5−8] (such as those with Davidson potentials and the analytical quadrupole-octupole axially symmetric model enclosed in an infinite well potential). Alternative possibilities are still being investigated, although these models have limitation and do not always perform better than others.
Quadrupole deformations have long been linked to nuclear rotational spectra, and octupole deformations, or pear-shaped nuclei, are known to occur in some places, most notably among light actinides. A negative-parity band with levels
$L^\pi = 1^-, 3^-, 5^-, \cdots$ , etc., that are near in energy to the ground-state band and form a single band with$L^\pi = 0^+, 1^-, 2^+, 3^-, 4^+, \cdots$ , etc., is one of the characteristics of octupole deformation [1]. Octupole vibrations are indicated by a negative-parity band that is higher than the ground-state band. Numerous authors have examined the shift from octupole vibrations to octupole deformation [9−11]. Although it has movable parameters, the spdf-interacting boson model (IBM) [12, 13] is a comprehensive algebraic classification of states in the presence of both quadrupole and octupole degrees of freedom.According to a recent review [14] and its references, machine learning (ML) has been combined with statistical techniques over the past ten years to address nuclear physics problems ranging from fundamental particles to the behavior of dense celestial bodies. A few of the applications focus on teaching ML models to predict nuclear observables directly, including fission yields [15], nuclear masses [16−20], charge radii [21−23], and beta-decay half-lives [24, 25]. Other applications of ML seek to enhance nuclear many-body simulations by using ML models to replace computationally intensive procedures. For example, collective Hamiltonians for low-lying nuclear states have been refined using deep neural networks [26], and density profiles for nuclear radii and binding energies calculations using density functional theory have been determined using back-propagation neural networks [27] and kernel Ridge regression [28].
One of the most well-known potentials in nuclear physics is the Woods-Saxon potential [29]. This potential has deep roots in nuclear physics studies. However, it presents a significant challenge: the lack of an appropriate analytical solution. In other words, no exact analytical solution exists for such a potential for general angular momentum. One way to address this problem is to use the Pekeris approximation, but this approach leads to solutions involving Jacobi polynomials. Owing to the limitations on the arguments of Jacobi polynomials, these solutions cannot be used for our purposes and multiple bands [30]. However, the aforementioned problem can be resolved using a different method, which we will discuss in detail later in the paper.
Our objective in this paper is to use the Woods-Saxon potential to investigate excited states resulting from quadrupole and octupole deformations. We aim to investigate the nuclei
$ ^{226} $ Ra and$ ^{226} $ Th by considering the Woods-Saxon potential in a Hamiltonian that includes quadrupole and octupole deformations. Additionally, the optimization process required to reproduce experimental data relies on optimization algorithms, for which we will employ ML techniques. Furthermore, the steps for obtaining eigenvalues and eigenvectors will be implemented using a numerical approach. Therefore, we have organized the paper as follows: Sec. II presents the theoretical foundations necessary for investigating such states. To reproduce the experimental data, which is the subject of Sec. III, we first examine the foundations of numerical calculations based on ML algorithms and then reproduce experimental data, including the excitation spectrum and multipole transitions. -
Two basic assumptions underlie the analytic quadrupole-octupole axially symmetric model [5, 6]. First, the axes of the quadrupole and octupole deformations are expected to align. In other words, the γ degree of freedom is ignored, but axial symmetry is assumed. Moreover, because they occur at extremely high energy levels, levels with none zero K (where K represents the projection of angular momentum along the body-fixed z-axis) are excluded [31]. In contrast, this simplification makes the system easier to analyze. Thus, the form of the corresponding Hamiltonian is [31, 32]
$ \begin{align} H = - \sum_{\lambda = 2,3} \frac{\hbar^2}{2 B_\lambda} \frac{1}{\beta_\lambda ^3} \frac{\partial}{\partial \beta_\lambda} \beta_\lambda ^3 \frac{\partial}{\partial \beta_\lambda} + \frac{\hbar^2 \hat{L}^2}{6(B_2 \beta_2 ^2 + 2 B_3 \beta_3 ^2)} + V(\beta_2, \beta_3), \end{align} $

(1) where the quadrupole and octupole deformations are denoted by
$ \beta_2 $ and$ \beta_3 $ , respectively. The related masses that are connected to these distortions are$ B_2 $ and$ B_3 $ . In the intrinsic reference frame,$ \hat{L} $ is the angular momentum operator.The following consideration can be used to determine the answers to the Schrödinger equation [32]:
$ \begin{align} \Phi_L ^{\pm} (\beta_2, \beta_3, \theta) = (\beta_2 \beta_3)^{-3/2} \Psi_L ^{\pm} (\beta_2, \beta_3) | {L M 0 , \pm} \rangle, \end{align} $

(2) where the set of Euler angles, θ, is necessary to understand and illustrate the orientation of the body-fixed coordinate system, defined by the axes
$ x', y' $ , and$ z' $ , with respect to the fixed laboratory coordinate system, defined by the axes$ x, y $ , and z. This model uses the mathematical expression$ | {L M 0, \pm} \rangle $ to illustrate the rotation associated with an axially symmetric nucleus, focusing on the angular momentum projection M along the laboratory-fixed z axis and maintaining a projection K equal to$ 0 $ along the body-fixed$ z' $ axis [1]. The explicit form of the functions$ | {L M 0, +} \rangle $ and$ | {L M 0, -} \rangle $ are provided in [1, 5]. These functions transform in accordance with the irreducible representations (irreps) A and$ B_1 $ of the group$ D_2 $ , respectively [31, 32].$ \begin{align} | {L M 0, \pm} \rangle = \sqrt{\frac{2L+1}{32\pi^2}} (1 \pm (-1)^L) {\cal{D}}_{0,M} ^L (\theta) \end{align} $

(3) where Wigner functions of Euler angles are represented by
$ {\cal{D}}(\theta) $ . The$ + $ label indicates positive parity states with$L = 0,2,4,\cdots$ , whereas the$ - $ label denotes those with$L = 1,3,5,\cdots$ .We can simplify the Schrödinger equation by considering new deformation variables.
$ \begin{align} \tilde{\beta}_2 = \beta_2 \sqrt{\frac{B_2}{B}}, \qquad \tilde{\beta}_3 = \beta_3 \sqrt{\frac{B_3}{B}}, \qquad B = \frac{B_2 + B_3}{2}, \end{align} $

(4) the polar coordinates in the range of
$ 0 \le \tilde{\beta} < \infty $ and$ -\pi/2 \le \phi \le \pi/2 $ with the goal of the new deformation variables$ \begin{align} \tilde{\beta}_2 = \tilde{\beta} \cos \phi, \qquad \tilde{\beta}_3 = \tilde{\beta} \sin \phi, \qquad \tilde{\beta} = \sqrt{\tilde{\beta}_2 ^2 + \tilde{\beta}_3 ^2}, \end{align} $

(5) with the reduced energy
$ \epsilon = (2B/\hbar^2)E $ , and the reduced potential$ u=(2B/\hbar^2)V $ . Thus, we have$ \begin{aligned}[b]& \Bigg[ - \frac{\partial^2}{\partial \tilde{\beta}^2} - \frac{1}{\tilde{\beta}} \frac{\partial}{\partial \tilde{\beta}} + \frac{L(L+1)}{3\tilde{\beta}^2 (1+\sin^2 \phi)} - \frac{1}{\tilde{\beta}^2} \frac{\partial^2}{\partial \phi^2}\\&\quad +u(\tilde{\beta},\phi) + \frac{3}{\tilde{\beta}^2 \sin^2 2\phi} - \epsilon_L \Bigg] \Psi_L ^{\pm} (\tilde{\beta}, \phi) = 0. \end{aligned} $

(6) As a simplification, let us assume that the potential energy
$ u(\tilde{\beta},\phi) $ can be separated into the form$ u(\tilde{\beta},\phi) = u(\tilde{\beta}) + u(\phi)/ \tilde{\beta}^2 $ : a function of only$ u(\tilde{\beta}) $ and a function of$ {\phi} $ . Such a hypothesis permits us to separate Eq. (6) into two independent equations. We further assume that$ u({\phi}) $ is a very steep, double-well potential centered around$ \pm \phi_0 $ . Thus, we have$ \begin{align} \tilde{\beta}^2\left[ - \frac{ \text{d}^2}{ \text{d} \tilde{\beta}^2} - \frac{1}{\tilde{\beta}} \frac{ \text{d}}{ \text{d} \tilde{\beta}} + u(\tilde{\beta}) - \epsilon_{\tilde{\beta}}(L) \right] \psi_L ^\pm (\tilde{\beta}) = -\varrho^2 \psi_L ^\pm (\tilde{\beta}), \end{align} $

(7) and
$ \begin{align} &\left[ \frac{ \text{d}^2}{ \text{d} \phi^2} - u(\phi) - u_L (\phi) \right] \chi ^\pm (\phi) = -\varrho^2 \chi ^\pm (\phi), \end{align} $

(8) $ \begin{align} & u_L(\phi) = \frac{L(L+1)}{3 (1+\sin^2 \phi)} + \frac{3}{\sin^2 2\phi}, \end{align} $

(9) where the total wave function has been assumed as
$ \Psi_L ^\pm (\tilde{\beta}, \phi) = \psi_L (\tilde{\beta}) \chi_L ^\pm (\phi) $ , the separation constant$ \varrho^2 $ . Hereafter, for the sack of simplicity,$ \pm $ will be omitted. An important exciting a periodic term,$ u_L (\phi) $ , exists. It will impact the later calculation of the electromagnetic transitions.Equation (8) contains the function
$ u_L(\phi) $ in this separation process. Having a term such as that in the equation makes it much more difficult to solve and analyze. Becauseit is a well-defined, smooth, and differentiable function, this problem can be solved by applying the Taylor expansion of this function around its minimum value, as described in [33]. Consequently, we have$ \begin{align} u_L (\phi) \approx u_L (\phi_L) + \frac{u''(\phi_L)}{2}(\phi - \phi_L)^2, \end{align} $

(10) where, for a given L,
$ \phi_L $ is the minimum of$ u_L(\phi) $ . Note that because$ u_L(\phi) $ attains its minimum value at$ \phi_L $ , the first derivative of$ u_L(\phi) $ at$ \phi_L $ will be zero. Consequently, the first derivative does not appear in the Taylor expansion. To transform the differential equation into the familiar form of the harmonic oscillator differential equation, we must not only substitute the Taylor expansion into the differential Eq. (8), but also, as outlined in [33], neglect the potential$ u(\phi) $ . Thus, we have$ \begin{align} - \frac{ \text{d}^2 \chi}{ \text{d} \zeta^2} + \zeta^2 \chi = \varepsilon_L \chi, \end{align} $

(11) which introduces the following new parameters:
$ \begin{align} \zeta^2 _L (\phi) = \sqrt{\frac{u_L ''(\phi_L)}{2}} (\phi - \phi_L)^2, \quad \varepsilon_L = \frac{\varrho^2 - u_L(\phi_L)}{\sqrt{\frac{u_L ''(\phi_L)}{2}}}. \end{align} $

(12) This differential equation has eigenvalues given by
$ \varepsilon_L = 2 n + 1 $ , where n is the oscillation quantum number. Therefore, we may have$ \begin{align} \varrho ^2 = \varrho_L ^2 = \sqrt{\frac{u_L''(\phi_L)}{2}} (2n+1) + u_L(\phi_L). \end{align} $

(13) Additionally, henceforth, we will restrict our analysis to the case
$ n = 0 $ . We emphasize here that the parameter$\varrho $ is dependent on the angular momentum,$\varrho_L$ . This dependence is evident in our calculations of electromagnetic transitions. This is because this parameter appears in the eigen function of the ϕ part:$ \begin{align} \chi_{n_{\phi}, L} (\phi) = N_{n_{\phi}, L} \exp\left(-\frac{\zeta_L ^2 (\phi)}{2} \right) H_{n_{\phi}} \left(\zeta_L ^2 (\phi) \right), \end{align} $

(14) where
$ N_{n_{\phi}, L} $ is the normalization constant, and Hermit polynomials are represented by$ H_{n_{\phi}} $ . If the arguments of the Hermite and polynomial functions were independent of angular momentum, the normalization constant would be simplified to a function of$ n_{\phi} $ . However, this is not true in our case. The angular momentum dependence adds difficulties that prevent us from obtaining an analytical solution for the normalizing constant. However, a numerical calculation can be easily used to calculate its value:$ \begin{align} N_{n_{\phi}, L} = \left[ \int_{-\pi/2}^{\pi/2} \left|\chi_{n_{\phi}, L} (\phi)\right|^2 \text{d} \phi \right]^{-1/2}. \end{align} $

(15) Now that the separation parameter has been determined based on the problem's known information, we can analyze the beta part of the differential equation.
We can now present the potential that we are interested in: the Woods-Saxon potential [1, 29, 30].
$ \begin{align} u(\tilde{\beta}) = \frac{-U_0}{1+ {\rm e}^{a(\tilde{\beta} - \tilde{\beta}_0)}}, \end{align} $

(16) where the non-negative parameters
$ U_0 $ , a, and$ \tilde{\beta}_0 $ are present. This potential lacks a hard core, and its shape simplifies to a square well potential in the limit of$ a \to \infty $ . The Schrödinger equation including such potential cannot be solved correctly and analytically, although it satisfies physical predictions well. This is another significant mathematical point regarding this potential [30]. Naturally, approximations such as the Pekeris approximation have been used to present analytical solutions for this purpose. However, the final answer contains Jacobi polynomials, which impose restrictions on their parameters. Upon numerical evaluation of the physical constants, we find that these restrictions are not satisfied, and practically, we are unable to extract appropriate experimental data from those analytical solutions. Stated differently, we can only address a limited amount of the experimental data using these answers. This is because the system in question cannot be sufficiently described by such mathematical approximations.We employ an alternative approach to obtain the solution of the differential Eq. (7) in the presence of the Woods-Saxon potential (16). This method has been applied to several problems. The problem of single-particle levels in deformed nuclei is among the most significant of them [34−36]. In essence, we want to use this method to estimate the solution to a specific degree of precision. Hence, we begin by assuming appropriate basic functions. We indicate whole sets of functions that enable us to fully expand a function by using the proper base functions. We may save only a few selected terms of this infinite expansion, as the name approximation implies. This is achieved when the results no longer differ significantly for a certain number of terms considered in the expansion. Therefore, we must begin by adopting suitable basic functions. A strong basis is one that can accurately characterize the system states across the same domain. The harmonic oscillator the basis provided by is among the most often used bases.
$ \begin{align} g_{\nu,n_\phi,L}(\tilde{\beta}) &= \sqrt{\frac{2 \nu!}{\Gamma(\nu + \varrho + 1)}} \tilde{\beta}^{\varrho} {\rm e}^{-\tilde{\beta}^2/2} \mathscr{L}_\nu ^{\varrho} (\tilde{\beta}^2), \end{align} $

(17) where v indicates the number of nodes in the
$ \tilde{\beta} $ direction, Γ represents the gamma function, a known special function, and$ \mathscr{L} $ is the corresponding laguerre polynomials. By solving Eq. (7) for a system with the potential$ u(\tilde{\beta}) = \tilde{\beta}^2 $ , we can directly obtain this particular basis set.We can obtain the answer as follows by applying this principle [37]:
$ \begin{align} \psi_{n,L} (\tilde{\beta}) = \sum_{\nu} C_{\nu,L} ^{a,\tilde{\beta}_0, U_0} g_{\nu, L} (\tilde{\beta}), \qquad \sum_\nu \left(C_{\nu,L} ^{a,\tilde{\beta}_0, U_0}\right) ^2 = 1, \end{align} $

(18) The numerical values of the free parameters in the differential Eq. (7) have a significant impact on the coefficients
$ C_{\nu,L} ^{a,\tilde{\beta}_0,U_0} $ . Essentially, for any distinct state of Eq. (7), we will have an appropriate linear combination of the harmonic oscillator basis functions. The matrix eigenvalue problem is solved to obtain the coefficients of this expansion, and the elements are computed as follows:$ \begin{align} \left\langle\nu^{\prime}\right| \hat{H}_{\tilde{\beta}}|\nu\rangle &\equiv \int_{0}^{\infty} \tilde{\beta} \text{d} \tilde{\beta} \; g_{\nu' L} (\tilde{\beta}) \hat{H}_{\tilde{\beta}} g_{\nu L} (\tilde{\beta}), \end{align} $

(19) $ \begin{align} \hat{H}_{\tilde{\beta}} &= - \frac{ \text{d}^2 }{ \text{d} \tilde{\beta}^2} - \frac{1}{\tilde{\beta}} \frac{ \text{d} }{ \text{d} \tilde{\beta}} + \frac{\varrho_L ^2 }{\tilde{\beta}^2} - \frac{U_0}{1+ {\rm e}^{a(\tilde{\beta} - \tilde{\beta}_0)}} \end{align} $

(20) as we know,
$ \begin{align} \hat{H}_{\tilde{\beta}} | {n,L;\phi_L; a, \tilde{\beta}_0, U_0} \rangle = \epsilon_{\tilde{\beta}} | {n,L;\phi_L; a, \tilde{\beta}_0, U_0} \rangle. \end{align} $

(21) The following is a description of the methods used to address this problem: The matrix elements, as expressed in Eq. (19), must be calculated for each quantized angular momentum inside each nucleus. Subsequently, by solving the eigenvalue problem, we may obtain the relevant eigenvalues and eigenvectors, which can be used to determine the energy levels of states with different numbers of nodes according to the given angular momentum. The manner in which the solution's numerical precision is considered is another important aspect of this. The number of terms considered in the expansion (18) has a direct correlation with accuracy. We easily observe that the results converge to a certain value when more terms are added to this expansion. The degree of precision required to solve the problem determines the degree of convergence. Consequently, we estimate 10 terms in this expansion based on the facts considered in this study. This number of terms renders a level of precision to our answer that is sufficient. In contrast, the ideal values for the free parameters must be determined for this process. Although the factors involved in this methodology will be explained in the next part, the observations of this segment are summarized in the appendix, the specifics of which are discussed in the section on numerical calculations.
The experimental results can now be reproduced using numerical computations in the following section.
-
In this section, we aim to reproduce the experimental data of some nuclei using the information gathered in the previous section. As mentioned in the introduction, ML techniques form the basis of the computational investigations in this work. Specifically, our objective is to use a ML optimization technique to determine the optimal values for the problem-relevant free parameters to reproduce the experimental results. Gradient descent [38], an algorithm for determining a function's minimum value that is frequently used to lower errors in prediction models, is one of the most significant optimization strategies in ML. Gradient descent reduces the difference between the model's predictions and the real empirical data (i.e., the loss function or the deviation function) by progressively changing the parameters during the model's training phase.
Gradient descent systematically refines the model parameters from an initial approximation by moving toward error minimization. According to [38], if we gather all of the parameters that affect the deviation function or the loss function in a vector notation
${\boldsymbol{\vartheta}} = (\vartheta_1,\vartheta_2, \cdots)$ , they are revised after each iteration:$ \begin{align} {\boldsymbol{\vartheta}} \to {\boldsymbol{\vartheta}} - \eta \cdot {\boldsymbol{\nabla}} \sigma, \end{align} $

(22) where σ is the deviation function defined according to our objective, and η is the learning rate.
$ \begin{align} \sigma = \sqrt{ \frac{1}{N} \left( \frac{E_{\text{exp}} (L_i ^\pi)}{E_{\text{exp}} (2^+)} - \frac{E_{\text{theo}} (L_i ^\pi) - E_{\text{theo}} (0^+) }{E_{\text{theo}} (2^+) - E_{\text{theo}} (0 ^+) } \right)^2 }, \qquad \pi = \pm , \end{align} $

(23) where N is the number of data used for each isotope, and
$ E_{\text{exp}} $ (from Ref. [39]) and$ E_{\text{theo}} $ represent the experimental and theoretical energies, respectively. By determining how steeply the loss function changes in relation to each parameter, we can obtain the slope or rate of adjustment. The method basically "descends" towards a minimum error threshold by traveling in the opposite direction of the gradient to arrive at an optimal or nearly optimal solution [38]. Unlike instructional resources such as [38], textbook optimization tasks often employ a simple mathematical function. However, the function we are attempting to improve is not mathematical and does not have a continuous domain. This is because, to retrieve the energies, we must first determine the matrix of each angular momentum in (19) and then calculate the pertinent energies using diagonalization. Consequently, the optimization technique must incorporate district theoretical data. -
After describing the fundamental computations in the previous section, we now present the findings. Only the isotopes of
$ ^{226} $ Ra and$ ^{226} $ Th are examined in this article. Table 1 shows the values that were acquired during the optimization procedure for every isotope. Each row in the table corresponds to a distinct isotope because the isotopes are identified in the table. The number of digits in free parameters to the right of the decimal point is a highly special feature of the ML approach. In other words, using more basic approaches, such as search algorithms, obtaining free parameters with such accuracy would require time that cannot be quantified in normal units of time to accomplish the level of accuracy offered in the preceding equations. The last column also shows the σ parameter for each isotope.Isotope a $\tilde{\beta}_0$ 

$U_0$ 

$\sigma_{\text{Ours}}$ 

σRef. [33] $^{226}\text{Ra}$ 

5.558247546040683 5.836410397132373 10.03477806863556 0.949 1.163 $^{226}\text{Th}$ 

19.654234566878788 6.574464293524817 12.356356546357798 0.942 1.093 Table 1. Values of free parameters for each isotope.
The appendix to this paper provides a summary of the outcomes obtained using these values. The tables in the appendix give the state's angular momentum value in the first column, the experimental normalized energy value in the second, the theoretical normalized energy in the third, and the coefficients in the wave function expansion in the remaining columns. These tables are organized according to the isotopes discussed in this work, and locating the information required for each isotope and angular momenta value in each of them is reasonably simple. Note that only the level of
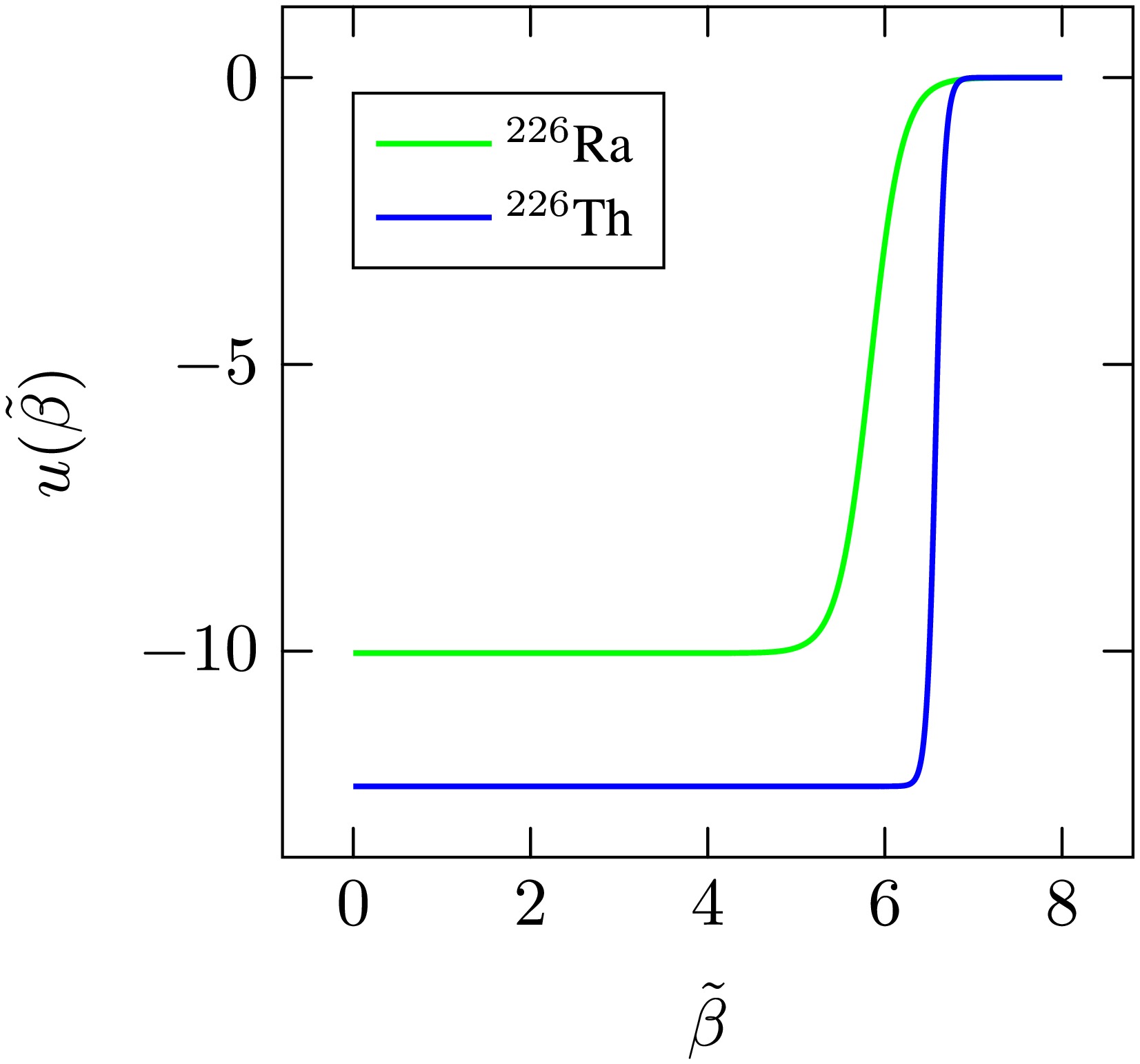
$ n_{\tilde{\beta}} = 0 $ , and hence$ n_{\phi} = 0 $ , has been included in the energy level computations. Therefore, in the subsequent discussions, these will not be included when using the aforementioned numbers as indices.The first step in analyzing the study's findings is plotting the potential that produced the best fit for each isotope. Figure 1 is plotted using the information in Table 1 and Eq. (16). Each isotope's potential is shown in a different color in this picture. An interesting pattern is observed: the potential shape shifts from the well-known Woods-Saxon form to a finite well as the mass number increases. The reason for this behavior is in increase in the parameter a as the optimization process progresses.
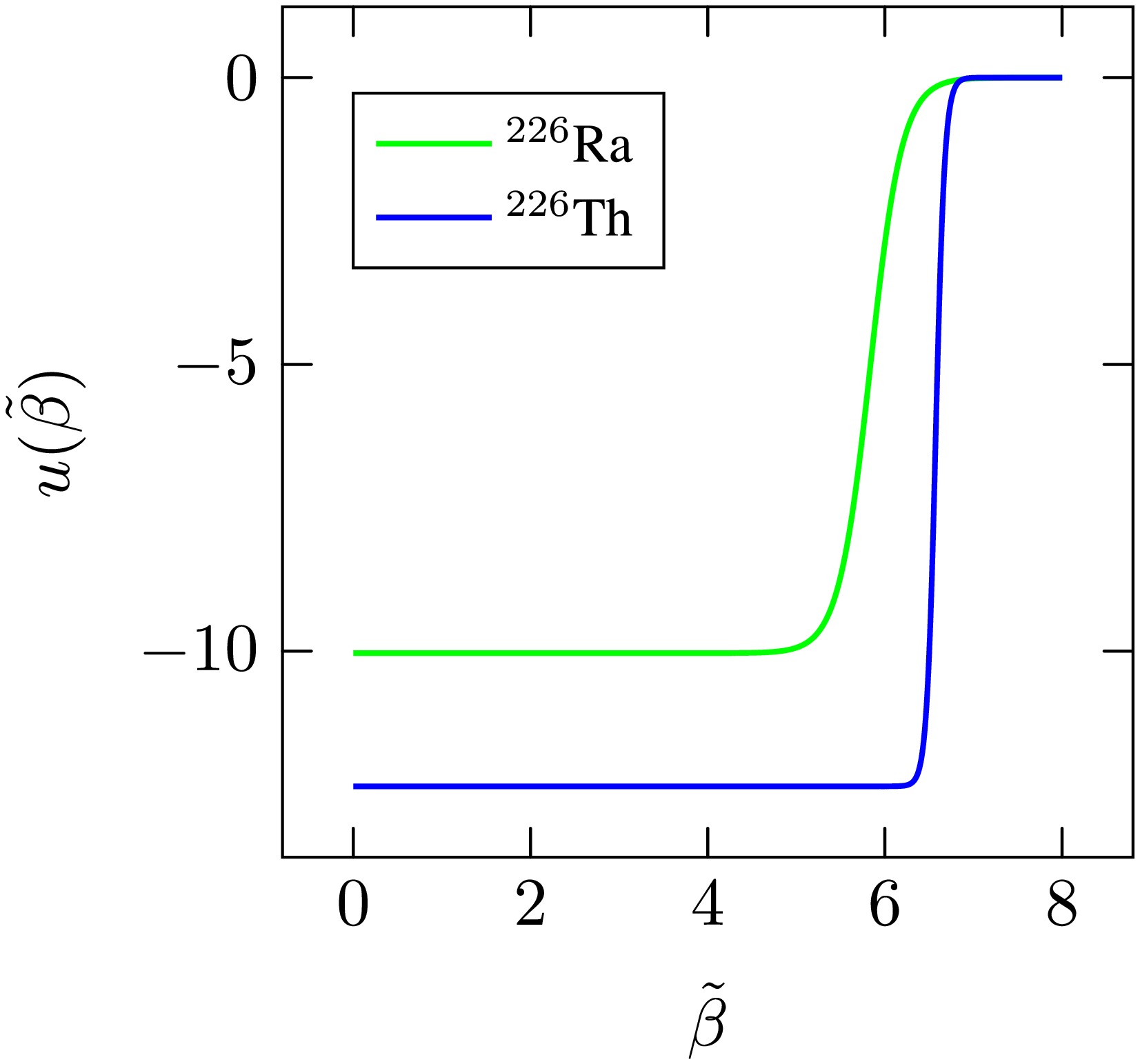
Figure 1. (color online) Visualization of the potential energy shape for each isotope after optimizing the parameters.
The following step shows the experimental and expected spectra for the nuclei under consideration in Fig. 2. The precision of the theoretical predictions in comparison to the experimental data is better shown in this image. The graphical representations display the theoretical predictions in red and the experimental data in black. Additionally, to better compare excitation states with different parities, we plot them separately. For better comparison and understanding of the discrepancy between the theoretical prediction and experimental data, these levels are connected by dotted lines. Naturally, the steeper the slope of these dotted lines, the greater the difference between them. Furthermore, we have shown the predictions from Ref. [33] (indicates as PFM) in green in this figure for a visual comparison between our calculations and the reference.

Figure 2. (color online) Comparison of predicted and experiments spectra of the considered nuclei and predictions of the parameter-free model [33] (PFM).
A noteworthy finding from this figure is that, in every instance, the trend of the experimental values in the positive parity band is correctly predicted. However, in the negative parity band, this tendency is slightly different. The theoretical predicted values are typically marginally lower than the experimental results for the lowest few levels of the negative parity band. This is because, as other investigations have shown, these levels require slightly more energy to reproduce, which is not achievable with this Hamiltonian structure and potential [30].
Before we calculate electromagnetic transitions, we must examine the wave functions that have been computed for these isotopes. The wave functions of the
$ {\phi} $ part are Hermite polynomial expressions, whereas those of the$ \tilde{\beta} $ section are obtained using linear combinations of the basis functions given in Eq. (17). The corresponding expansion coefficients for$^{224}$ Ra and$^{226}$ Th are given in full detail in Table 2 and Table 3, respectively, in the appendix. To illustrate their differences, we have included both the basis and wave functions for$ ^{224} $ Ra in Fig. 3. This figure consists of four panels. The upper panels show positive parity, whereas the lower panels show negative parity. The left panels display the wave functions as a function of$ \tilde{\beta} $ , and the right panels display the basis functions. The difference between the basis and wave functions is evident. For instance, they have different values at different places. To understand this, consider the size of the vertical axis.L Exp. [38] Theo. $\nu=0$ 

$\nu=1$ 

$\nu=2$ 

$\nu=3$ 

$\nu=4$ 

$\nu=5$ 

$\nu=6$ 

$\nu=7$ 

$\nu=8$ 

$\nu=9$ 

0 0.000 0.000 −0.3356183853 0.4601163135 −0.4897062874 0.4505819956 −0.3670331573 0.2617959960 −0.1562957389 0.0698176536 −0.0158171870 −0.0036560333 1 3.747 0.337 −0.3320798429 0.4588960446 −0.4906960185 0.4524808776 −0.3685330316 0.2621360470 −0.1554623931 0.0684309260 −0.0146942714 −0.0040865223 2 1.000 1.000 −0.3258283252 0.4567842794 −0.4925691799 0.4559291880 −0.3711134798 0.2624601534 −0.1535905963 0.0656267032 −0.0125342736 −0.0048592957 3 4.749 1.966 −0.3181701537 0.4543356854 −0.4951707502 0.4603620583 −0.3740962562 0.2622124328 −0.1503969407 0.0614196291 −0.0095288033 −0.0058106949 4 3.127 3.196 −0.3104089198 0.4521519106 −0.4983574091 0.4651875797 −0.3767783229 0.2608595358 −0.1456856596 0.0559497979 −0.0059731975 −0.0067370896 5 6.603 4.647 −0.3034832001 0.4507078368 −0.5020251254 0.4699358412 −0.3786183631 0.2580482922 −0.1394337654 0.0494828575 −0.0022099817 −0.0074480610 6 6.155 6.279 −0.2978828667 0.4502802754 −0.5061049946 0.4743048841 −0.3792904112 0.2536284057 −0.1317636229 0.0423417616 0.0014445236 −0.0078060662 7 9.264 8.063 −0.2937684445 0.4509789661 −0.5105450086 0.4781224346 −0.3786343987 0.2475922793 −0.1228755534 0.0348448023 0.0047389883 −0.0077356502 8 9.891 9.980 −0.2911225829 0.4528090055 −0.5152941648 0.4812886357 −0.3765869515 0.2400118015 −0.1130003916 0.0272794881 0.0074909379 −0.0072145040 9 12.677 12.017 −0.2898522236 0.4557199787 −0.5202944199 0.4837358483 −0.3731341605 0.2310003354 −0.1023777809 0.0198980530 0.0095777500 −0.0062611990 10 14.185 14.165 −0.2898416927 0.4596353243 −0.5254787416 0.4854080602 −0.3682873158 0.2206944582 −0.0912475785 0.0129188438 0.0109273192 −0.0049249123 11 16.743 16.418 −0.2909767098 0.4644682759 −0.5307723062 0.4862524582 −0.3620721758 0.2092454854 −0.0798454475 0.0065273832 0.0115110616 −0.0032772609 12 18.931 18.774 −0.2931540960 0.4701303256 −0.5360948090 0.4862169665 −0.3545246386 0.1968148841 −0.0683991739 0.0008762172 0.0113385347 −0.0014053723 13 21.388 21.227 −0.2962849584 0.4765356481 −0.5413627981 0.4852502783 −0.3456890948 0.1835710565 −0.0571249543 −0.0039158050 0.0104526333 0.0005943711 14 24.061 23.776 −0.3002949086 0.4836031641 −0.5464915222 0.4833027678 −0.3356178941 0.1696867046 −0.0462238274 −0.0077640914 0.0089247470 0.0026221047 15 26.536 26.419 −0.3051229136 0.4912571029 −0.5513961416 0.4803276121 −0.3243713360 0.1553366406 −0.0358785697 −0.0106182512 0.0068496610 0.0045797499 16 29.523 29.155 −0.3107194183 0.4994264887 −0.5559923535 0.4762820060 −0.3120180934 0.1406960933 −0.0262512452 −0.0124612649 0.0043402161 0.0063756938 17 32.126 31.982 −0.3170441321 0.5080439460 −0.5601966237 0.4711284630 −0.2986359878 0.1259394558 −0.0174814083 −0.0133078987 0.0015218372 0.0079288019 18 35.300 34.900 0.3240636677 −0.5170441108 0.5639262645 −0.4648363124 0.2843130580 −0.1112393430 0.0096848575 0.0132024602 0.0014729501 −0.0091717132 19 38.099 37.908 0.3317492415 −0.5263619768 0.5670995962 −0.4573833940 0.2691487135 −0.0967656947 0.0029527646 0.0122159930 0.0045099233 −0.0100533940 20 41.375 41.004 0.3400745900 −0.5359314254 0.5696363501 −0.4487579085 0.2532547646 −0.0826847141 −0.0026489130 0.0104429634 0.0074583951 −0.0105409236 21 44.412 44.189 0.3490142425 −0.5456841613 0.5714584266 −0.4389602818 0.2367560076 −0.0691573910 −0.0070798083 0.0079974640 0.0101961966 −0.0106204913 22 47.750 47.461 0.3585422406 −0.5555491722 0.5724909946 −0.4280048536 0.2197901432 −0.0563375345 −0.0103252426 0.0050089378 0.0126142910 −0.0102975738 23 51.032 50.820 0.3686313576 −0.5654527299 0.5726638342 −0.4159212049 0.2025068956 −0.0443693649 −0.0123959303 0.0016174647 0.0146208643 −0.0095962763 24 54.440 54.264 0.3792527612 −0.5753188862 0.5719128145 −0.4027549597 0.1850662718 −0.0333847854 −0.0133271586 −0.0020313086 0.0161447311 −0.0085578541 25 57.931 57.793 −0.3903760680 0.5850703179 −0.5701813272 0.3885679874 −0.1676360901 0.0235006007 0.0131773165 0.0057914419 −0.0171378832 0.0072384763 26 61.421 61.405 0.4019696321 −0.5946293545 0.5674215611 −0.3734380233 0.1503889877 −0.0148159501 −0.0120257155 −0.0095219709 0.0175770381 −0.0057063461 27 65.080 65.099 −0.4140009176 0.6039189998 −0.5635955390 0.3574578295 −0.1334991990 0.0074102215 0.0099696929 0.0130919993 −0.0174642277 0.0040383838 28 68.696 68.875 −0.4264368134 0.6128638365 −0.5586759102 0.3407340429 −0.1171393576 0.0013416049 0.0071211407 0.0163852607 −0.0168261299 0.0023165600 Table 2. Normalized energies and wave function coefficients expansion of 224Ra.
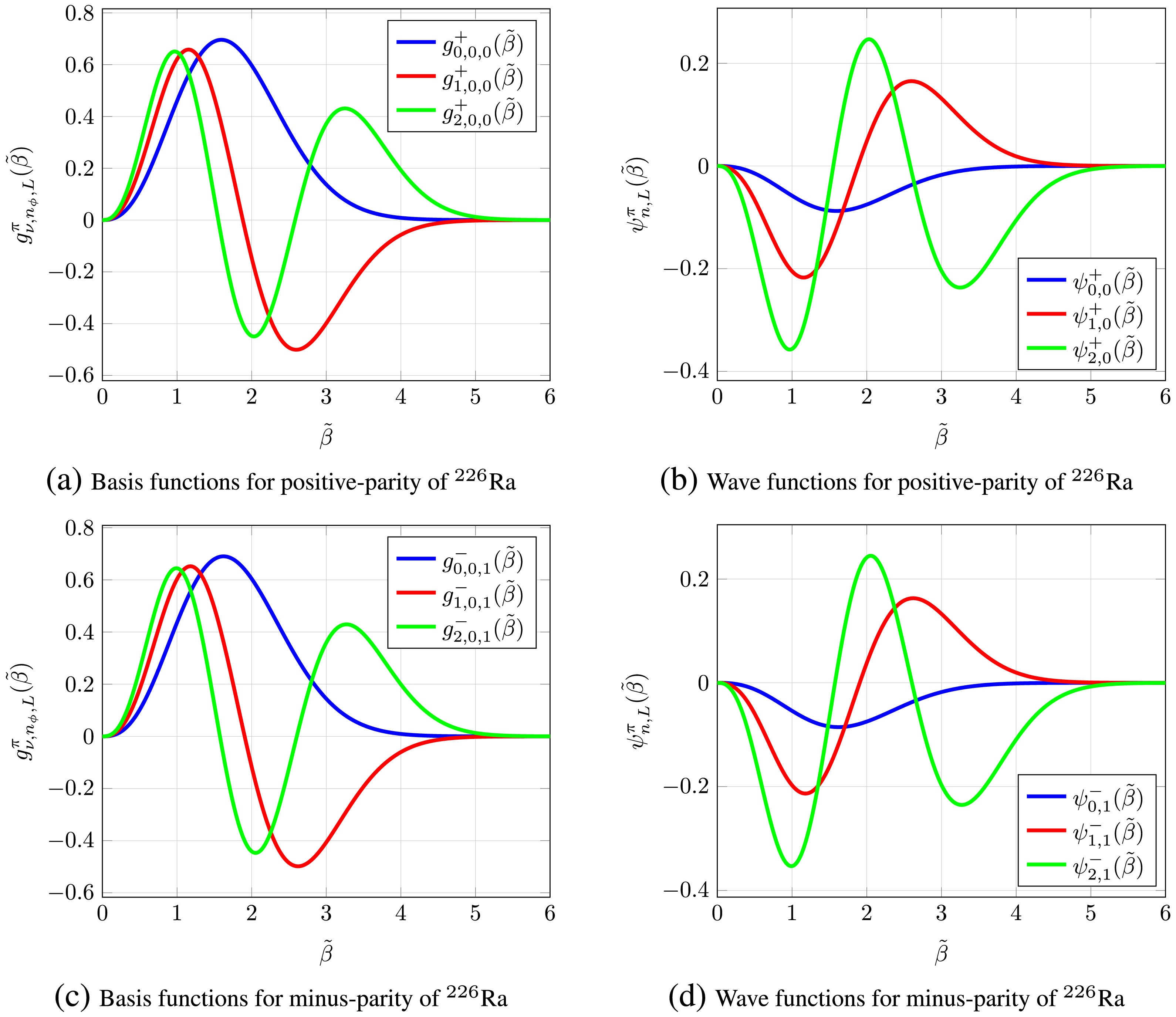
Figure 3. (color online) Graphical comparison between the bases and actual wave functions obtained as linear combinations of basis functions.
L Exp. [38] Theo. $\nu=0$ 

$\nu=1$ 

$\nu=2$ 

$\nu=3$ 

$\nu=4$ 

$\nu=5$ 

$\nu=6$ 

$\nu=7$ 

$\nu=8$ 

$\nu=9$ 

0 0 0 −0.2395120670 0.3559161264 −0.4168675898 0.4317728657 −0.4102009018 0.3615599332 −0.2946027497 0.2173350179 −0.1373294897 0.0622594713 1 3.191 0.337 −0.2347460754 0.3522489586 −0.4153924990 0.4323338587 −0.4121163322 0.3640157644 −0.2968752351 0.2189234152 −0.1380506017 0.0623199329 2 1 1 −0.2262173660 0.3455604256 −0.4126413509 0.4333082761 −0.4155812866 0.3684534943 −0.3009236226 0.2216482034 −0.1391441107 0.0622489320 3 4.259 1.967 −0.2155319442 0.3369686717 −0.4090277811 0.4345232447 −0.4200301774 0.3740978412 −0.3059144655 0.2247430537 −0.1400209454 0.0617285121 4 3.136 3.201 −0.2043223174 0.3277437296 −0.4051266748 0.4359075183 −0.4249209185 0.3801316652 −0.3109355854 0.2273599579 −0.1400380959 0.0604270161 5 6.24 4.663 −0.1937919498 0.3189566985 −0.4015237592 0.4375202995 −0.4298874664 0.3859160824 −0.3152376323 0.2287971408 −0.1386811965 0.0581045254 6 6.195 6.317 −0.1845829070 0.3112901985 −0.3986687729 0.4394873418 −0.4347571971 0.3910674987 −0.3183429784 0.2286099732 −0.1356527178 0.0546590166 7 9.112 8.136 −0.1769067195 0.3050641250 −0.3968269787 0.4419252052 −0.4394787392 0.3954027341 −0.3200098183 0.2265909499 −0.1308592842 0.0501156184 8 9.999 10.103 −0.1707306153 0.3003508937 −0.3961030571 0.4448988204 −0.4440445545 0.3988517281 −0.3201520984 0.2227043921 −0.1243628049 0.0445961692 9 12.785 12.206 −0.1659084369 0.2970776374 −0.3964835370 0.4484109497 −0.4484466992 0.4013989594 −0.3187790354 0.2170306955 −0.1163343955 0.0382888834 10 14.409 14.434 −0.1622588851 0.2951031893 −0.3978844733 0.4524149482 −0.4526603437 0.4030472496 −0.3159499487 0.2097209402 −0.1070134992 0.0314200313 11 17.152 16.779 0.1596031067 −0.2942633184 0.4001866849 −0.4568327131 0.4566442716 −0.4038039311 0.3117505220 −0.2009659091 0.0966751091 −0.0242295329 12 19.324 19.234 0.1577818511 −0.2943974213 0.4032614432 −0.4615724989 0.4603479756 −0.4036770906 0.3062768270 −0.1909714022 0.0856021786 −0.0169506972 13 22.105 21.793 −0.1566645815 0.2953670348 −0.4069911061 0.4665445850 −0.4637176702 0.4026697861 −0.2996210697 0.1799378660 −0.0740641712 0.0097957416 14 24.675 24.451 −0.1561518008 0.2970646830 −0.4112806056 0.4716703963 −0.4666993692 0.4007768897 −0.2918624359 0.1680473271 −0.0623040648 0.0029480798 15 27.554 27.205 −0.1561709405 0.2994124000 −0.4160587331 0.4768853849 −0.4692422894 0.3979857329 −0.2830633124 0.1554575712 −0.0505333259 −0.0034395301 16 30.413 30.053 −0.1566752713 0.3023631518 −0.4212804209 0.4821393766 −0.4712952542 0.3942708562 −0.2732659605 0.1423010674 −0.0389330870 −0.0092424746 17 33.418 32.994 −0.1576387716 0.3058952543 −0.4269217619 0.4873926502 −0.4728044852 0.3895947381 −0.2624953576 0.1286899267 −0.0276600065 −0.0143595883 18 36.497 36.029 −0.1590503593 0.3100049881 −0.4329730238 0.4926112280 −0.4737128258 0.3839092797 −0.2507642554 0.1147235416 −0.0168538790 −0.0187082043 19 39.627 39.16 −0.1609106851 0.3147020939 −0.4394332374 0.4977612698 −0.4739559244 0.3771580279 −0.2380805277 0.1004980382 −0.0066453337 −0.0222202960 20 42.896 42.387 −0.1632277474 0.3200033587 −0.4463035656 0.5028044624 −0.4734615174 0.3692805926 −0.2244557872 0.0861154723 0.0028383058 −0.0248406398 Table 3. Same as Table 2, but for 226Th.
-
The electric dipole, quadrupole, and octupole operators in the presence of axial symmetry are [31]
$ \begin{align} T^{(E1)} _\mu &= t_1 \beta_2 \beta_3 {\cal{D}}_{\mu,0} ^{(1)} (\theta) = t_1 \frac{B}{\sqrt{B_2 B_3}} \tilde{\beta}^2 \frac{\sin 2 \phi}{2} {\cal{D}}_{0,\mu} ^{(1)} (\theta), \end{align} $

(24a) $ T^{(E2)} _\mu = t_2 \beta_2 {\cal{D}}_{\mu,0} ^{(2)} (\theta), = t_2 \sqrt{\frac{B}{B_2}} \tilde{\beta} \cos \phi {\cal{D}}_{0,\mu} ^{(2)} (\theta), $

(24b) $ \begin{align} T^{(E3)} _\mu &= t_3 \beta_3 {\cal{D}}_{\mu,0} ^{(3)} (\theta) = t_3 \sqrt{\frac{B}{B_3}} \tilde{\beta} \sin \phi {\cal{D}}_{0,\mu} ^{(3)} (\theta), \end{align} $

(24c) where
$ t_1 $ is a constant, and$ \begin{align} t_2 = \frac{3 Ze}{4 \pi} R^2, \quad t_3 = \frac{3 Ze}{4 \pi} R^3, \quad R = (1.2) A^{1/3}. \end{align} $

(25) Combining Eq. (3) and
$ \Psi_L ^{\pm} (\tilde{\beta}, \phi) $ results in the final wave function. To obtain the transition rate B(EL) for this wave function, we use the following formula:$ \begin{align} B(\text{E}L; L_i a_i \to L_f a_f) = \frac{\left|\left(L_f a_f\left\|T^{(\text{E} L)}\right\| L_i a_i\right)\right|^2}{2L_i +1} \end{align} $

(26) in which the Wigner-Eckart theorem [40] is applied to calculate the reduced matrix element.
$ \begin{align} \left\langle L f \mu_f a_f\right| T^{(\text{E} L)}\left|L_i \mu_i a_i\right\rangle = \frac{(L_i L L_f|\mu_i \mu \mu_f)}{\sqrt{2L_f+1}} \left(L_f a_f\left\|T^{\text{E} L}\right\| L_i a_i\right) \end{align} $

(27) where
$ (L_i L L_f|\mu_i \mu \mu_f) $ represents the Clebsch-Gordan coefficient.In Eq. (26), the integration over angles θ uses a typical integral over three Wigner functions [40], yielding
$ (L_i L L_f|000) $ . The remaining integrations are performed across$ \iint \beta_2^3 \text{d} \beta_2 \; \beta_3 ^3 \text{d} \beta_3 $ , where the$ \beta_2^3 $ and$ \beta_3^3 $ factors are obtained from the volume element. The integration is over$ \int \tilde{\beta} \text{d} \tilde{\beta} \text{d} \phi $ , up to constant factors, according to Eqs. (4) and (5) and the relevant Jacobian.By examining the formulas in (24), we observe that the calculation of the electromagnetic transition can be decomposed into four factors. The first factor is a purely constant parameter that depends only on the fundamental properties of the isotope in question. However, the other three factors depend entirely on the initial and final state information and the transition order. Thus, the formula for calculating the electromagnetic transition can be expressed as follows [6]:
$ \begin{align} B(\text{E}\lambda; L_i \to L_f) = C \left( I_{\tilde{\beta}} ^{(\text{E}\lambda)} \right) ^2 \left( I_{\phi} ^{(\text{E}\lambda)} \right)^2 (L_i L L_f|000)^2, \end{align} $

(28) where C is a constant, and
$ \begin{align} I_{\tilde{\beta}} ^{(\text{E}2)} = I_{\tilde{\beta}} ^{(\text{E}3)} &= \int \tilde{\beta}^2 \psi_{n_i,L_i} \psi_{n_f,L_f} \text{d} \tilde{\beta}, \end{align} $

(29) $ \begin{align} I_{\tilde{\beta}} ^{(\text{E}1)} &= \int \tilde{\beta}^3 \psi_{n_i,L_i} \psi_{n_f,L_f} \text{d} \tilde{\beta}, \end{align} $

(30) $ \begin{align} I_{\phi} ^{(\text{E}1)} &= \int_{- \frac{\pi}{2}}^{\frac{\pi}{2}} \sin 2 \phi \chi_{{n_{\phi}}_i, L_i} \chi_{{n_{\phi}}_f, L_f} \; \text{d} \phi, \end{align} $

(31) $ \begin{align} I_{\phi} ^{(\text{E}2)} &= \int_{- \frac{\pi}{2}}^{\frac{\pi}{2}} \cos \phi \chi_{{n_{\phi}}_i, L_i} \chi_{{n_{\phi}}_f, L_f} \; \text{d} \phi, \end{align} $

(32) $ \begin{align} I_{\phi} ^{(\text{E}3)} &= \int_{- \frac{\pi}{2}}^{\frac{\pi}{2}} \sin \phi \chi_{{n_{\phi}}_i, L_i} \chi_{{n_{\phi}}_f, L_f} \; \text{d} \phi, \end{align} $

(33) and we suggest readers to see Ref. [6] for more valuable information on the integrals and equations.
Unfortunately, we could not find sufficient experimental data for electromagnetic transitions of the considered nuclei in Ref. [38]. However, a comparison of the trends obtained in this study would still be interesting and informative. If readers refer to the section on solving differential equations in this article, they will observe that, unlike the case of approximate separation, electromagnetic transitions are influenced by both parts of the solution, namely
$ \tilde{\beta} $ and ϕ. For approximate separation, because the ϕ part is merely a constant factor, it is automatically eliminated by calculating the ratio of electromagnetic transitions. However, this is no longer applicable here. Although we have limited ourselves to$ n_{\phi} = 0 $ and we have$ H_0 = 1 $ in the Hermite functions, the normalization constant will be a function of the angular momentum value because the argument of the exponential function$ \zeta^2 $ contains$ \phi_L $ , which takes a specific value for each value of angular momentum. This is what causes the difference in the trend of theoretical predictions in the calculation of electromagnetic transitions in the present model.To illustrate the trend of theoretical predictions of our model, we have plotted the calculated electromagnetic transitions in Figs. 4, 5, and 6. In Fig. 4, we have calculated the electromagnetic transitions
$ B(\text{E}1, L \to L-1) $ for the model [33] and our results, and we finally normalize them to the value of$ B(\text{E}1, 1^- \to 0^+) $ . We believe that the authors of [33] used the same approximate separation [5] formulae of$ B(\text{E}L) $ transitions because the values of their electromagnetic transitions were obtained similarly. In this case, the theoretical prediction predicts an upward trend with increasing L, but this is not the case for the predictions made by the results of this article. If we examine this trend more closely, the theoretical predictions for the$ B(\text{E}1) $ transition suggest an oscillatory trend, but overall, this trend is upward. The change in this oscillatory trend is more significant and severe in$ ^{226} $ Th than in$ ^{226} $ Ra, whereas for the parameter-free model, the theoretical prediction trend for the$ B(\text{E}1) $ transition is strictly upward.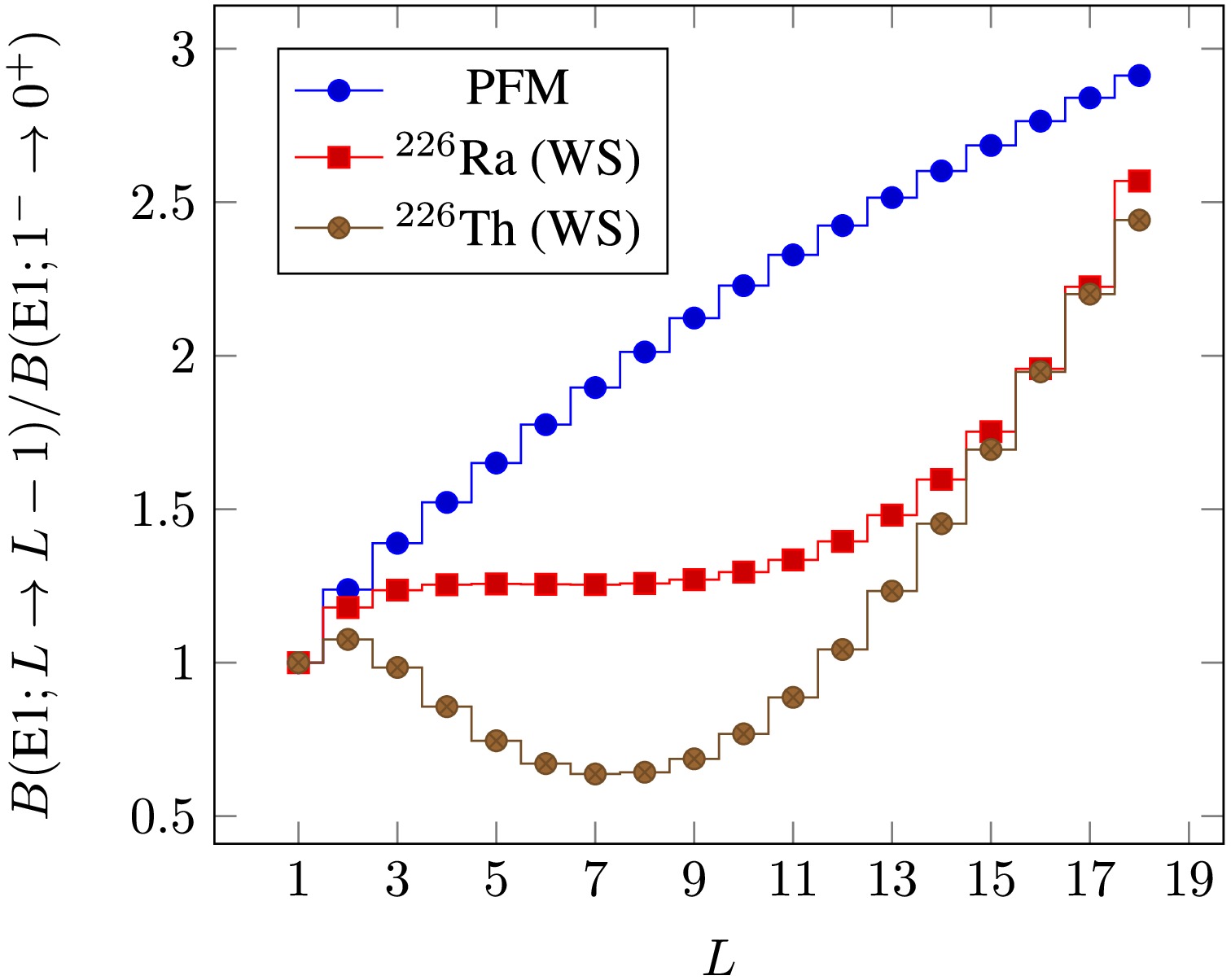
Figure 4. (color online) Comparison of theoretical calculations of
$ B(\text{E}1) $ electromagnetic transitions in parameter-free and WS models.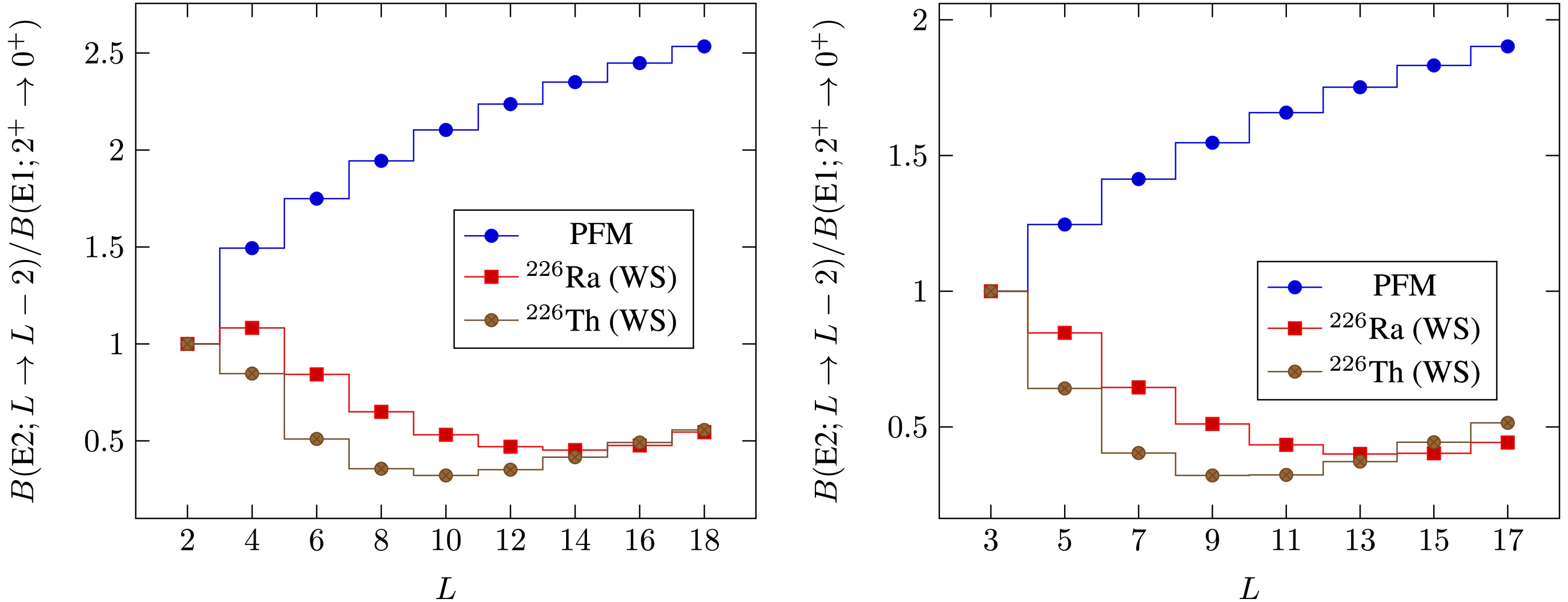
Figure 5. (color online) Same as Fig. 4, but for
$ B(\text{E}2) $ electromagnetic transitions. The left panel belongs to the positive-parity sates, whereas the right panel is for the minus-parity states.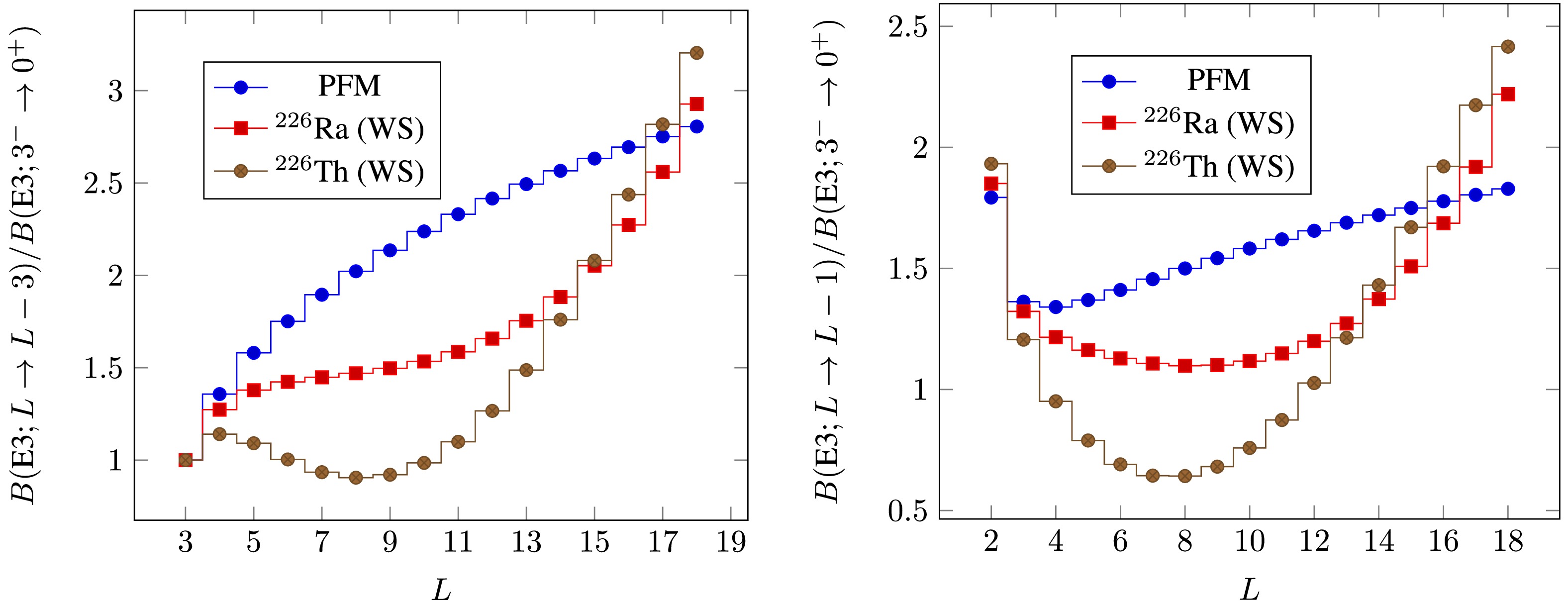
Figure 6. (color online) Same as Fig. 4, but for
$ B(\text{E}3) $ electromagnetic transitions. The left panel shows transitions with a$ \Delta L $ of three units between initial and final states, whereas the right panel shows transitions with a$ \Delta L $ of one unit.For the
$ B(\text{E}2) $ electromagnetic transition, a behavior different from the parameter-free model is predicted. In this case, for transitions involving positive parity states, an initial increase in the transition value is predicted, followed by a decrease. In contrast, for$ B(\text{E}2) $ electromagnetic transitions involving negative parity states, an initial decrease followed by a relative growth is predicted. In contrast, the parameter-free model does not predict any decrease in$ B(\text{E}2) $ transition values with increasing angular momentum. This is clearly shown in Fig. 5. The transition values in this figure are normalized$ B(\text{E}2, 2^+ \to 0^+) $ . The left panel of this figure shows electromagnetic transitions involving states with positive parity, whereas the right panel corresponds to states with negative parity.However, the predicted trends for
$ B(\text{E}3) $ electromagnetic transitions in the parameter-free model and the model discussed in this paper are somewhat similar. We have examined these transitions in two different categories. All values considered in this figure are normalized to the$ B(\text{E3}; 3^- \to 0^+) $ transition. This category includes transitions in which the difference in angular momentum between the starting and ending states is three units. In the left panel of Fig. 6, we observe the predicted behavior for these transitions. The figure shows that the model predicts an increasing trend for these transitions, and the slope becomes gentler as the angular momentum value increases. However, in our calculations, although the overall behavior is upward, the rate of change is significantly different. For$ ^{226} $ Ra, for angular momenta less than 15, the slope of this change is gentle, but for angular momenta greater than 15, the slope of this trend becomes steeply upward. In contrast, for$ ^{226} $ Th, in the angular momentum range of$ 4 \le L_i \le 9 $ , this trend experiences a relative decline, then either a steep upward slope.The second category of
$ B(\text{E}3) $ electromagnetic transitions is those with a one-unit difference between the initial and final states. The result of this investigation is shown in the right panel of Fig. 6. The overall trend for all three cases is similar but not identical. In all three cases, the values of these transitions initially experience a decrease, and then an increase. This trend for the parameter-free model has a nearly uniform rate, whereas for our model, both the decreasing trend is more pronounced and the slope of the increasing values is steeper. -
In this study, we investigate the application of the Woods-Saxon potential to describe excited states arising from quadrupole and octupole deformations. Hence, we employ a numerical method to compute the eigenfunctions and eigenvalues of the Hamiltonian. This process is coupled with a machine learning optimization algorithm to evaluate the optimal solutions. Subsequently, we analyze the results. Energy levels with different parities for
$ ^{226} $ Ra and$ ^{226} $ Th are examined using both this model and the parameter-free model. Thereafter, we calculate electromagnetic transitions and discuss the effect of the exact separation of variables in the model presented in this paper on the calculation of electromagnetic transition values. Electric dipole, quadrupole, and octupole transitions are extensively analyzed and visualized. We observe that the trend predicted by our model differs significantly from that predicted by the parameter-free model. The reason for this difference is investigated, we find that the angular part of the Hamiltonian becomes a function of angular momentum in the exact separation. This manifests itself in the overlap of wave functions during the calculation of electromagnetic transitions. -
The authors are grateful to the referee for helpful comments and suggestions on this work.
-
The appendix contains a detailed list of each isotope's normalized energies and wave function expansions. For more information on how to understand this data, refer to the main text of the article.
Application of the Woods-Saxon potential in studying quadrupole and octupole excited states using machine learning
- Received Date: 2024-12-01
- Available Online: 2025-04-15
Abstract: In this study, the energy bands of quadrupole and octupole excited states are investigated. This is achieved by employing the Bohr Hamiltonian, incorporating quadrupole and octupole deformations whose variables are accurately separated. Subsequently, the Woods-Saxon potential is added to the problem. Because this problem cannot yield suitable solutions using conventional approximations, we solve it numerically using machine learning. A detailed description is given of how wave functions and their associated energies are obtained. Throughout this procedure, we demonstrate how machine learning aids us in easily accomplishing our objective. We examine and analyze the energy spectrum and possible multipole transitions for candidate isotopes





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: