On the structure in the ΛN cross section at the ΣN threshold

There has been a revival of interest in threshold phenomena over the last two decades triggered not least by the discovery of the so-called XYZ states [1, 2]. Many of the new states seen in the charm or bottom sectors, which do not fit into the standard quark-antiquark or three-quark classification, have been observed close to thresholds. The perhaps most famous one is the $\chi_{c1} (3872)$, formerly known as $X(3872)$, whose mass coincides with the $D \bar D^*$/$D^* \bar D$ threshold within the experimental uncertainty [3]. Threshold anomalies are standard textbook knowledge for a long time, see e.g. Ref. [4], but have been revisited in various works since they are considered as possible explanation for the nature and structure of some XYZ and other exotic states, see, e.g. [5, 6] and the reviews [7, 8] for very recent examples.

In the light of this development and also because of its intrinsic interest we re-examine one of the longest known threshold effects, namely the structure observed in the ${\Lambda} p$ cross section (invariant mass spectrum) at the threshold of the ${\Sigma} N$ channel. First evidence of it was already reported as early as 1961 [9], but the first convincing signal and still one of the most prominent examples is from the measurement of the reaction $K^- d \to \pi^- {\Lambda} p$ by Tan in 1969 [10]. A review of other early observations can be found in Ref. [11] and an overview of later measurements is provided by Machner et al. [12]. More recent examples for the presence of a ${\Sigma} N$ threshold effect, in the reaction $pp \to K^+ {\Lambda} p$, can be found in Refs. [13-16]. Very recently evidence of the threshold structure has been also observed in measurements of the ${\Lambda} p$ correlation function in $pp$ collisions at $T = 13$ GeV by the ALICE Collaboration [17]. Let us mention that there are also data for the ${\Lambda} p$ elastic cross section itself in the ${\Sigma} N$ threshold region [18, 19]. However, in that case the energy resolution is rather poor so that no conclusion on a possible structure could be drawn [12].

In the present work we discuss the predictions for ${\Lambda} N$ observables around the ${\Sigma} N$ threshold, utilizing hyperon-nucleon ($YN$) interactions that yield the presently best description of low-energy ${\Lambda} p$ [20, 21], ${\Sigma}^- p$ [22-25] and ${\Sigma}^+ p$ [23] scattering data. This condition is met by the $YN$ potentials derived within chiral effective field theory (EFT) up to next-to-leading order (NLO) by the Jülich-Bonn-Munich group [26, 27] and by the Nijmegen NSC97 meson-exchange potentials [28]. In all those cases the achieved $\chi^2$ value is in the order of $16$ for the $36$ (or $35$) “best” $YN$ data taken into account. The coupling of the ${\Sigma} N$ channel to ${\Lambda} N$ dominates the dynamics around the ${\Sigma} N$ threshold, where the angular-momentum coupled partial waves $^3S_1$ and $^3D_1$ play an important role. A further facet is added by the mass splitting between the $\Sigma$ baryons which implies that there are actually two physical ${\Sigma} N$ thresholds so that, in principle, one faces a six-channel problem. Thus, the ${\Lambda} N$-${\Sigma} N$ system is an excellent textbook example to illustrate issues and complications of coupled-channel dynamics that might be also instructive for interpreting threshold structures seen in the charm and/or bottom sector.

We also re-address the question regarding a strangeness $S = -1$, isospin-$1/2$, spin-$1$ dibaryon [29-31], building on those aforementioned $YN$ interactions. Indeed, the dispute about whether there is a dibaryon - in form of a deuteron-like ${\Sigma} N$ bound state - or not has a varied history. In the past, studies where the possibility of such a dibaryon was discussed focused primarily on the reaction $K^- d \to \pi^- {\Lambda} p$ [11, 32-38]. While initial investigations were more or less inconclusive, in the latest works [35, 37, 38] the unanimous conclusion has been drawn that a ${\Sigma} N$ bound state does not exist near the ${\Sigma} N$ threshold. However, one must keep in mind that in those studies simplified models of the $YN$ interaction were employed. Specifically, with regard to the $^3S_1$-$^3D_1$ partial wave where that dibaryon should occur, the tensor coupling mediated by the long-ranged one-pion exchange was ignored and usually only the S-wave component was taken into account. Realistic $YN$ potentials suggest that the ${\Lambda} N \to {\Sigma} N$ transition occurs predominantly from the ${\Lambda} N$ $^3D_1$ state [26-28, 39-44]. Furthermore, often no constraints from SU(3) flavor symmetry were implemented. Though SU(3) symmetry is certainly broken, may be on the level of 20% - 30% [45], one should not abandon it altogether.

The paper is structured in the following way: In Sect. II we provide the main results of our study. We start with a brief description of the employed $YN$ potentials and summarize the achieved $\chi^2$. Then we examine in detail the ${\Lambda} p$ cross section near the ${\Sigma} N$ threshold based on three selected $YN$ interactions, the chiral EFT potentials NLO13 (600) [26] and NLO19 (600) [27], and the Nijmegen NSC97f potential [28], in order to expose subtle differences in the dynamics. Subsequently, we determine the pole positions in the complex plane near the ${\Sigma} N$ thresholds for the $^3S_1$-$^3D_1$ partial wave, and we discuss possible evidence for a dibaryon. Finally, we compare the structures in the ${\Lambda} p$ and ${\Lambda} n$ cross sections around the ${\Sigma} N$ threshold. In Sect. III predictions for the level shifts and widths of ${\Sigma}^-p$ atomic states are given. The paper ends with a brief summary.

Let us start by noting that $YN$ potentials which include the ${\Lambda} N$-${\Sigma} N$ coupling [26-28, 39-44] are established by considering data from channels with different charge Q, namely those for $Q = 0$ (${\Sigma}^-p$), $Q = 1$ (${\Lambda} p$), and $Q = 2$ (${\Sigma}^+p$). Thus, the predictions of the potentials for ${\Lambda} p$ near the ${\Sigma} N$ threshold, and specifically of the threshold structure, are actually predominantly determined by the available cross sections for the ${\Sigma}^-p$ elastic [23] and charge exchange (${\Sigma}^-p\to {\Sigma}^0 n$) [22] channels, and the one of the transition ${\Sigma}^-p\to {\Lambda} n$ [22]. In addition there is the capture ratio at rest [24, 25]. The latter is defined by [46]

where $\sigma_s$ ($\sigma_t$) is the total reaction cross section in the singlet $^1S_0$ (triplet $^3S_1$-$^3D_1$) partial wave. The cross sections are the ones at zero momentum, but in calculations it is common practice [28] to evaluate the cross sections at a small non-zero momentum, namely $p_{\rm{lab}} = 10$ MeV/c. As mentioned already, available ${\Lambda} p$ cross sections in the ${\Sigma} N$ threshold region [18, 19] are afflicted by a poor momentum resolution and usually not taken into account in the fitting procedure.

For a detailed description of the utilized $YN$ interactions (NLO13, NLO19, NSC97f) we refer the reader to the original publications [26-28]. Here we focus only on the essential features and differences. For all potentials SU(3) flavor symmetry is used as an essential guideline in the derivation. However, in the actual calculations it is broken in various ways, notably by the mass differences of the pseudoscalar mesons $\pi$, $\eta$ and K. In the NSC97 potentials there is also an explicit SU(3) breaking in the baryon-baryon-meson coupling constants. In the $YN$ potentials from chiral EFT there is no additional breaking of SU(3) symmetry. In particular, the short-distance dynamics, represented in that approach by contact terms, fulfills strict SU(3) symmetry in the original potential (NLO13) [26] and also in the version from 2019 (NLO19) [27]. However, in both cases there is an explicit SU(3) symmetry breaking with respect to the $NN$ interaction. Specifically, while in case of NLO13 all S-wave contact terms where determined by a fit to ${\Lambda} N$ and ${\Sigma} N$ data, without any recourse to the $NN$ system, the NLO19 interaction was guided by the objective to reduce the number of free parameters and some of the contact terms were inferred from the $NN$ sector by exploiting the underlying (broken) SU(3) symmetry [27].

In the EFT interactions the empirical binding energy of the hypertriton $^3_ {\Lambda} {\rm{H}}$ is used as a further constraint. It is utilized to fix the relative strength of the spin-singlet and spin-triplet S-wave contributions to the $\Lambda p$ interaction. Because of that, all NLO interactions yield practically identical values for the $^1S_0$ and $^3S_1$ scattering length, respectively. In the NSC97 potentials there is no such constraint and, consequently, there is a fairly large variation in the $\Lambda p$ scattering lengths for the versions a-f presented in Ref. [28], correlated with the magnitude of explicit SU(3) symmetry breaking. Anyway, as we will see below, this aspect has very little influence on the $\Lambda p$ results near the ${\Sigma} N$ threshold. Finally, we want to mention that isospin symmetry is fulfilled by the EFT potentials [26, 27]. In case of the NSC97 interactions there is an isospin breaking in the ${\Lambda} N$ sector via ${\Sigma}^0$-${\Lambda}$ mixing [47] which allows for contributions from the exchange of isovector mesons ($\pi$, $\rho$,...) to the ${\Lambda} N \to {\Lambda} N$ potential. Also this is relevant only for the ${\Lambda} N$ results at low energies but not at the ${\Sigma} N$ threshold.

Note that a regularization is required when solving the scattering equation for interactions derived from chiral EFT [48] which is usually done by introducing an exponential regulator function involving a cutoff. In case of the EFT potentials employed in the present study cutoff values of $500 - 650$ MeV have been used [26, 27] and we present here results for that range. As we will see, there is a small but noticeable cutoff dependence.

Because of the important role played by the ${\Sigma} N$ data we summarize the relevant $\chi^2$ values for the potentials considered in the present work in Table 1. The best results achieved correspond to $\chi^2 \approx 12-13$ for the $24$ ${\Sigma} N$ data points included. The NLO19 interactions with cutoffs of $500$ and $550$ MeV deviate already noticeably from the best values, which has consequences as we will see later. In case of the Jülich '04 interaction, considered here for illustration, the $\chi^2$ is very large, though mostly due to the fact that the capture ratio $r_R$, which has been determined to very high precision [24, 25], was not included in the fitting procedure. The Nijmegen potentials NSC97a-e yield a $\chi^2$ very close to that of NSC97f [28].

reaction	NLO13					NLO19				Jülich '04	NSC97f
	500	550	600	650		500	550	600	650
$\Sigma^- p \to \Lambda n$ [22]	3.7	3.9	4.1	4.4		4.7	4.7	4.0	4.4	8.3	3.9
$\Sigma^- p \to \Sigma^0 n$ [22]	6.0	5.8	5.8	5.7		5.5	5.5	6.0	5.7	6.4	6.0
$\Sigma^- p \to \Sigma^- p$ [23]	2.0	1.8	1.9	1.9		3.0	2.9	2.2	1.9	1.6	2.3
$\Sigma^+ p \to \Sigma^+ p$ [23]	0.3	0.4	0.5	0.3		0.3	0.4	0.4	0.3	0.1	0.2
$r_R$ [24, 25]	0.1	0.2	0.1	0.2		1.1	0.7	0.1	0.5	53.6	0.0
total $\chi^2$	12.2	12.0	12.3	12.5		14.6	14.2	12.7	12.8	70(16.4)	12.4

Table 1.  Obtained $\chi^2$ for the NLO13 [26] and NLO19 [27] interactions (for cutoffs $500$-$650$ MeV) and the Jülich '04 [44] and Nijmegen NSC97f [28] $YN$ potentials. The set includes 24 $\Sigma N$ data points. For Jülich '04, the result without $r_R$ is given in brackets.

It is instructive to first look at the ${\Lambda} p$ cross section in the ${\Sigma} N$ threshold region. Corresponding predictions are presented in Fig. 1 for the NLO13 (600), the NLO19 (600), and the NSC97f potentials. The dash-double-dotted lines representing the full results make clear that the cross sections are remarkably similar, especially close to the threshold of the lower channel (${\Sigma}^+ n$). Furthermore, for all three potentials the $^3S_1$-$^3D_1$ partial wave (cf. the solid lines) is responsible for about 90% of the cross section. Differences in the dynamics are reflected primarily in the individual components of this angular-momentum coupled partial wave, i.e. the $^3S_1$ (dotted), the $^3D_1$ (dashed) and the S-D (dash-dotted) transition amplitude. Obviously, the NSC97f result is by far dominated by the $^3D_1$ amplitude while for the EFT interactions the largest contribution comes from the S-D transition amplitude. Moreover, there are differences in the very details. In case of NLO13 all three contributions exhibit a cusp-like structure at the ${\Sigma}^+ n$ threshold. On the other hand, for NLO19 and NSC97f a rounded step appears in the $^3S_1$ amplitude, which is clearly visible for the EFT interaction but difficult to see for NSC97f because for the latter the contribution of the $^3S_1$ is fairly small.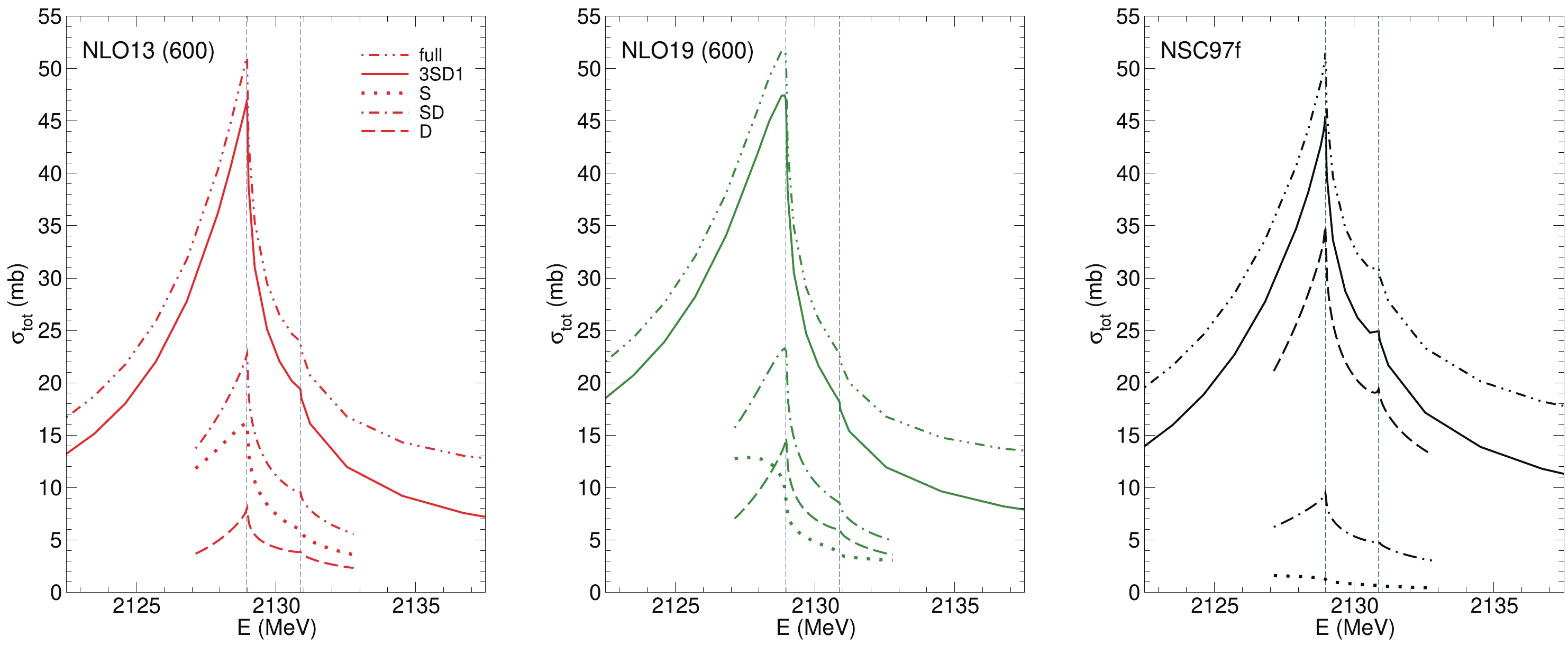

Figure 1.  (color online) Partial-wave contributions to the ${\Lambda} p$ cross section for NLO13 (600) (left), NLO19 (600) (middle), and Nijmegen NSC97f (right) around the ${\Sigma} N$ threshold. The dash-double-dotted line represents the full result, while the solid line is that of the $^3S_1$-$^3D_1$ partial wave alone. The dotted, dash-dotted, and dashed lines represent the individual contributions from $^3S_1$, the $S-D$ transition, and $^3D_1$ amplitudes, respectively. The vertical lines indicate the ${\Sigma}^+ n$ and ${\Sigma}^0 p$ thresholds, respectively.

Evidently, with a measurement of the ${\Lambda} p$ cross section across the ${\Sigma} N$ threshold region, even with an excellent energy resolution, it will be difficult to resolve the dynamical differences represented by these scenarios. The only promising tool for a discrimination are measurements of differential observables. This is exemplified in Fig. 2 with predictions at $p_{\rm lab} = 633$ MeV/c, i.e. at the ${\Sigma}^+ n$ threshold. Of course, the observables are also influenced by the P waves (and higher partial waves) which have uncertainties, too [26, 39]. However, as one can see, there is definitely a qualitative difference in case where the $^3D_1$ contribution is dominant. Note that the NLO13 and NLO19 potentials differ only in the $^1S_0$ and $^3S_1$-$^3D_1$ partial waves [27]. The interactions in the higher partial waves are identical. With regard to the Jülich '04 potential it should be said that its ${\Lambda} p$ cross section in the ${\Sigma} N$ threshold region differs drastically from those shown in Fig. 1 [44]. Let us mention that measurements of differential observables for ${\Lambda} p$ are planned at J-PARC [49, 50], also for energies in the ${\Sigma} N$ threshold region.

Figure 2.  (color online) Differential cross sections, polarization, and depolarization $D_{NN}$ for ${\Lambda} p$ scattering at $633$ MeV/c (i.e., at the ${\Sigma}^+ n$ threshold). Predictions for NLO13 (600) (solid line), NLO19 (600) (dash-dotted), Jülich '04 (dashed), and Nijmegen NSC97f (dotted) are presented.

In this context we want to emphasize that the subtle differences discussed above will have an impact on the outcome for reactions like $K^-d \to \pi^- {\Lambda} p$ and/or $pp \to$$K^+ {\Lambda} p$, too. Depending on the (principally unknown) reaction mechanism the relative weight of the S and D waves will differ in those processes as compared to ${\Lambda} p$ elastic scattering. Accordingly, the structure or line shape in elastic scattering and in the ${\Lambda} p$ invariant mass spectrum can certainly be different. Most of the past studies of $K^-d \to \pi^- {\Lambda} p$ relied on ${\Lambda} p$ interactions that include only the $^3S_1$ partial wave [31-35] and, thus, the above aspect is not accounted for.

Let us now come to the pole positions for the ${\Lambda} N$-${\Sigma} N$ system in the $^3S_1$-$^3D_1$ partial wave. We determine those based on the multichannel effective range expansion, discussed, e.g., in Refs. [46, 51, 52] and also in the textbook by Newton [4], performed at the ${\Sigma} N$ threshold. Such methods are also used in lattice QCD to determine resonance parameters, see e.g. [53]. In the single-channel case the effective range expansion (ERE) of the scattering amplitude $f(q) = (S-1) / 2 i q$ is introduced via $f(q) = 1/$$(q\cot\delta - {\rm i}q)$, where $q\cot\delta = -1/a + r\,q^2 / 2 + \cdots$. Here, S is the S-matrix, q is the on-shell momentum, $\delta$ is the phase shift and a and r are the scattering length and the effective range, respectively. In the multichannel case the S-matrix is connected with the scattering matrix F via $S_{ij} = \delta_{ij} + 2i \sqrt{q_iq_j} F_{ij}$, where the indices i and j denote the channels and coupled partial waves. The scattering amplitude F can be written in matrix form as

with symmetric and real valued matrices A, R and P. A and R correspond to the usual scattering length and effective range. We included also the next term in the expansion, P, for testing purposes. Switching it on and off allowed us to check that the pole positions from the expansion have been extracted reliably. The quantity q in Eq. (2) is a diagonal matrix with the on-shell momenta of the individual channels. $q_0$ is the momentum relative to the threshold at which the expansion is performed. Note that the ERE of M in Eq. (2) can be also written in symmetric (matrix) form [52] utilizing diagonal momentum matrices of the form $(q^2 - q^2_{(th)})^{1/2}$, etc.. Here $q_{(th)}$ are the momenta $q_i$ for each channel that correspond to the energy of the threshold at which the effective range expansion is performed [46]. The two ways of writing the expansion are equivalent [52].

Because of the tensor coupling of the $^3S_1$ and $^3D_1$ state, F and accordingly M are $6\times 6$ matrices (or $4\times 4$ when isospin is conserved and the isospin $I = 1/2$ system is considered). Near the ${\Sigma} N$ threshold the $^3D_1$ components of the two ${\Sigma} N$ channels are very small and can be safely neglected. However, this is not the case for the $^3D_1$ ${\Lambda} N$ partial waves which yields an essential contribution at energies around the ${\Sigma} N$ threshold. Thus, our multichannel ERE involves $4\times 4$ matrices ($3\times 3$ in the isospin symmetric case).

An extensive discussion of the ${\Lambda} N$-${\Sigma} N$ coupled channels in terms of the effective range approximation, within different scenarios, can be found in [52]. The expansion facilitates a reliable determination of the pole positions when they are within the analyticity circle bounded by the nearest dynamical singularity which for ${\Sigma} N$ is due to the left-hand cut caused by one-pion exchange. That cut starts at $E = -m^2_{\pi}/8 \mu_{ {\Sigma} N} \approx -5.1$ MeV below the ${\Sigma} N$ threshold [52], so that $|q_0| \lesssim 70$ MeV/c. In our study the expansion is performed at the higher of the two ${\Sigma} N$ thresholds, i.e. at the one of the ${\Sigma}^0 p$ channel for $Q = 1$ and of the ${\Sigma}^- p$ channel in case of $Q = 0$.

Our results are summarized in Fig. 3 where we show the ${\Sigma} N$ poles in the complex $q_{ {\Sigma} N}$ plane for calculations with isospin-averaged masses (left), for $Q = 1$ (middle) and for $Q = 0$ (right). In the presentation and discussion of the pole positions we adopt the definitions and conventions of Badalyan et al. [52]. Specifically, we use the following classification of sheets in the complex q plane,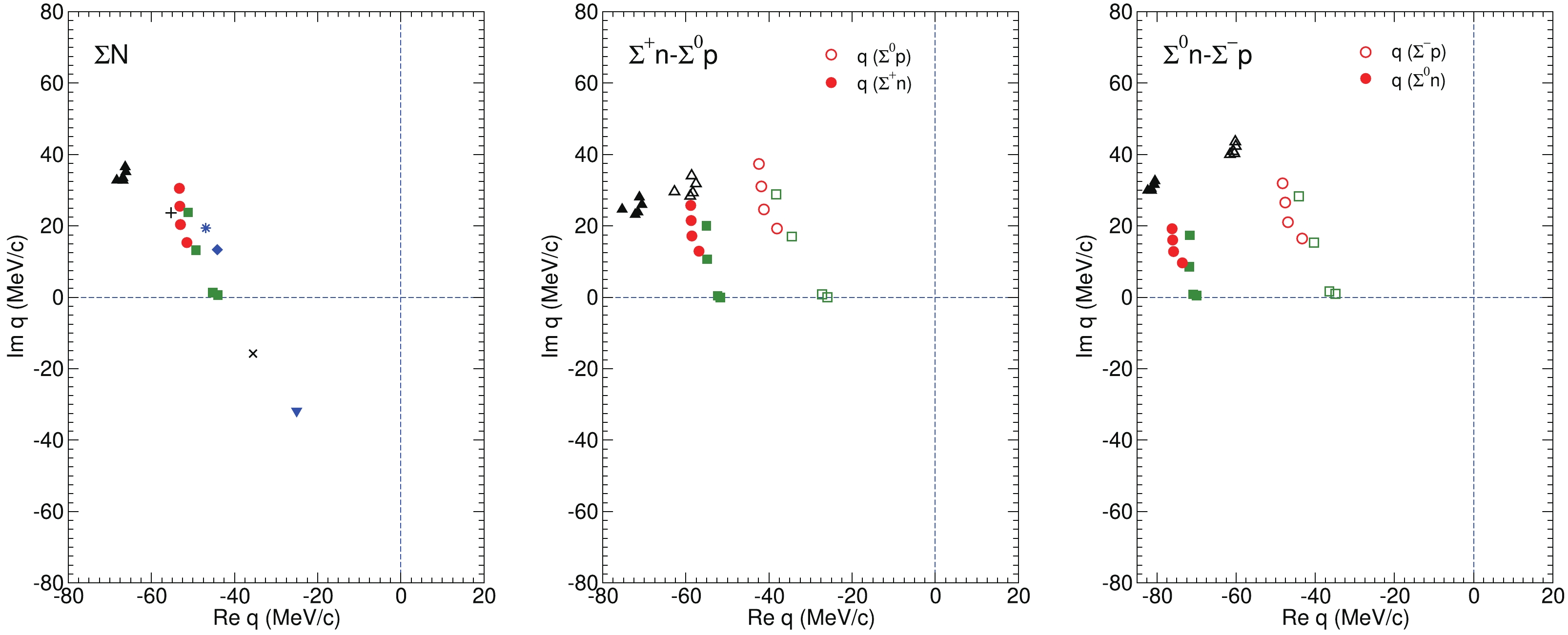

Figure 3.  (color online) ${\Sigma} N$ poles for isospin averaged masses (left), for $Q = 1$ (${\Sigma}^+ n$, ${\Sigma}^0 p$) (middle) and $Q = 0$ (${\Sigma}^0 n$, ${\Sigma}^- p$) (right). Results are presented for NLO19 (green squares), NLO13 (red circles), and Nijmegen NSC97b-f (black triangles) potentials. The filled (open) symbols are for the ${\Sigma} N$ channel with the lower (higher) threshold. In the case of isospin averaged masses, results for the Jülich meson-exchange potentials '04 [44] (blue inverted triangle), $\tilde A$ [43] (blue diamond), A [42] (blue star), and the Nijmegen potentials ND [40] (cross) and NF [41] (plus) are included.

appropriate for two channels. We focus here on the poles for the ${\Sigma} N$ channels. For all considered $YN$ interactions the poles are located either on sheet II or IV, that correspond to the sheets [bt] and [tb] in another popular labeling scheme [54]. Specifically, they lie in the second or third quadrant in the complex $q_{ {\Sigma} N}$ plane. Thus, in practice, they classify as unstable bound states (UBS) or inelastic virtual states (IVS) in the terminology of Ref. [52]. In principle, they correspond to what is termed coupled-channel (CC) poles in that work because their position is significantly influenced by the strong channel coupling between ${\Lambda} N$ and ${\Sigma} N$ and there are no poles near the ${\Sigma} N$ thresholds for the $YN$ interactions discussed here when the coupling is switched off. Accordingly, the essential question is whether the poles appear and remain on sheet IV in the full coupled-channel calculation or whether the ${\Sigma} N$ interaction together with the ${\Lambda} N$-${\Sigma} N$ coupling is strong enough so that the poles are on sheet II.

Note that eight sheets appear in the three-channel case [52] and the notation has to be generalized accordingly. However, since in our study the poles for ${\Sigma}^+ n$ and ${\Sigma}^0 p$ (${\Sigma}^0 n$ and ${\Sigma}^- p$) turn out to be always on the same respective sheets we refrain from introducing a more complicated notation and we show the poles in the same panel in Fig. 3.

Miyagawa and Yamamura have determined the poles for some of the Nijmegen potentials directly by solving the scattering equation, analytically continued into the complex plane [55]. Specifically, results for the NSC97f potential are provided. Our value of $q_{ {\Sigma} N} = (-68.3,\,32.8)$ MeV/c for NSC97f compares rather well with $q_{ {\Sigma} N} =$$(-69,\,30)$ MeV/c quoted in Table 1 of [55], which gives us confidence that the ERE is quite reliable for establishing the position of the near-threshold poles. The agreement is particularly remarkable in view of the fact that the pole lies already close to the formal boundary where the ERE is expected to work reliably, see above.

We start with the poles found for isospin-averaged masses, summarized in the left panel of Fig. 3. In this case isospin symmetry is fulfilled and the poles reflect directly the strength of the coupled-channel ${\Lambda} N$-${\Sigma} N$ interaction with $I = 1/2$. Evidently for all the NLO EFT interactions and also for the NSC97 potentials the poles lie on sheet II, i.e. all of them predict a UBS [52]. It is certainly remarkable that the poles lie all in a narrow region. Thus, despite the large experimental uncertainties for some of the $YN$ cross sections, the ${\Sigma}^- p$ data as a whole seem to impose rather strong restrictions. Indeed the potentials with the lowest $\chi^2$ (cf. Table 1) yield also similar pole positions. Two of the NLO19 potentials, the ones with cutoff $500$ and $550$ MeV, stick out because they yield poles where Im $q_{ {\Sigma} N}$ is very close to zero, i.e. the poles are close to sheet IV where the IVS are located. But in these two cases the achieved $\chi^2$ is already noticeable larger as seen in Table 1. For illustration we include here the pole positions for other $YN$ interactions like the Jülich '04 [44], $\tilde A$ [43], and A [42] potentials. In addition, results for the Nijmegen potentials ND [40] and NF [41] (taken from Ref. [55]), are included. Among those only ND and Jülich '04 predict an IVS. But in the former case the $\chi^2$ is noticeable larger [40] than the best values in Table 1 because the ${\Sigma}^- p$ cross section is somewhat low and the latter yields a too low ${\Sigma}^- p\to {\Lambda} n$ transition cross section [26] and a too large capture ratio.

When we use physical masses and consider the $Q = 0$ and $Q = 1$ systems the overall picture does not change qualitatively. This is not too surprising because the ${\Sigma} N$ interaction in the $^3S_1$-$^3D_1$ partial wave is dominated by the $I = 1/2$ component. The $I = 3/2$ contribution is small [28] and, in case of the EFT potentials, the corresponding interaction is even weakly repulsive [26, 27]. With the mass splitting taken into account, there are poles for ${\Sigma}^+ n$ and ${\Sigma}^0 p$, and for ${\Sigma}^0 n$ and ${\Sigma}^- p$, respectively, but they all lie in the same quadrant as before, i.e. correspond again to a UBS. The poles for the ${\Sigma}^0 n$ and ${\Sigma}^- p$ channels, displayed in the right-hand panel of Fig. 3, are somewhat closer together than those for ${\Sigma}^+ n$ and ${\Sigma}^0 p$. It is a consequence of the fact that the ${\Sigma} N$ interaction is primarily determined by the scattering data in the ${\Sigma}^- p$ channel. The results for Nijmegen NSC97 potentials are particularly close together. Presumably, due to the absence of constraints on the relative strength of the singlet- and triplet ${\Lambda} N$ interactions, an optimal description of the ${\Sigma} N$ data could be achieved for all versions a-f. Overall, the largest variations occur for NLO19, where, however, as said, here is also a larger difference in the achieved $\chi^2$, cf. Table 1,

As manifested by Fig. 3, for the EFT interactions and the NSC97 potentials all poles lie in the lower half of the second quadrant of the complex $q_{ {\Sigma} N}$ plane, so that Im $q_{ {\Sigma} N}$ $<$ -Re $q_{ {\Sigma} N}$. This means that the real part of the corresponding energy, $E = \sqrt{M^2_N+ q^2_{ {\Sigma} N}} + \sqrt{M^2_{ {\Sigma}}+ q^2_{ {\Sigma} N}}$, is larger than $M_N+M_{ {\Sigma}}$, i.e. the “bound” states lie actually above the ${\Sigma} N$ threshold. We summarize the pole positions in the energy plane in Table 2 for the calculation with physical masses. As expected in all cases (except for the Jülich '04 potential) the poles are indeed located above the ${\Sigma} N$ thresholds.

In any case, we interpret our results as strong evidence for the existence of a dibaryon, in form of a (unstable) ${\Sigma} N$ bound state in the vicinity of the ${\Sigma} N$ threshold. It is supported by all $YN$ interactions that provide the best possible reproduction of the near-threshold ${\Sigma} N$ data. In this context we note that the important role of the ${\Sigma} N$ data for the appearance of a ${\Lambda} p$ resonance was already pointed out long time ago [56]. Admittedly, what we obtain here is not the kind of dibaryon one ideally wants to have. The position of the pole in the energy plane is above the ${\Sigma} N$ threshold. There is no Breit-Wigner type peak that is well separated from and well below the ${\Sigma} N$ thresholds. Furthermore, there is no “pre-existing” ${\Sigma} N$ bound state, i.e. there is no bound state when the ${\Lambda} N$-${\Sigma} N$ coupling is switched off. Nonetheless the position of the poles is in all cases in the second quadrant of the complex $q_{ {\Sigma} N}$ plane, i.e. where unstable bound states are to be found [52].

In this context let us mention that the existence of near-threshold resonances or bound states has been also suggested for the analogon in the charm sector, i.e. for the $\Lambda_c N$-$\Sigma_c N$ system [57, 58]. However, so far neither lattice QCD calculations (for unphysical quark masses corresponding to $m_\pi \geqslant 410$ MeV) [59] nor extrapolations of those lattice results to the physical point [60, 61] produced any evidence for such states in the $\Sigma_c N$ channel.

Detailed discussions of the shape of the ${\Lambda} N$ cross section depending on the position of the poles can be found in Refs. [54, 55, 62]. Here we focus on the shape of the ${\Lambda} p$ and ${\Lambda} n$ cross sections for the $YN$ potentials NLO19 and NSC97f, see Fig. 4. Indeed, the results for NLO13 are well within the variations found for NLO19. Furthermore, the differences between the NSC97a-f predictions are rather small, so that concentrating on results for NSC97f is sufficient. Generally speaking, a pole on sheet IV (third quadrant of $q_{ {\Sigma} N}$) leads to a cusp at the ${\Lambda} N$ threshold while a pole on sheet II (second quadrant of $q_{ {\Sigma} N}$) produces a rounded (Breit-Wigner type) peak. In practice, this happens only for ideal cases where the pole is sufficiently close to the ${\Sigma} N$ threshold and specifically close to the negative or positive Im $q_{ {\Sigma} N}$ axis. As one can see in Fig. 3 the second condition is not fulfilled by any of the $YN$ potentials considered here. Thus, we are far from the mentioned ideal cases and that means, citing Pearce and Gibson [54], in “a gray area where it is not obvious whether the effect will be cusp or peak”.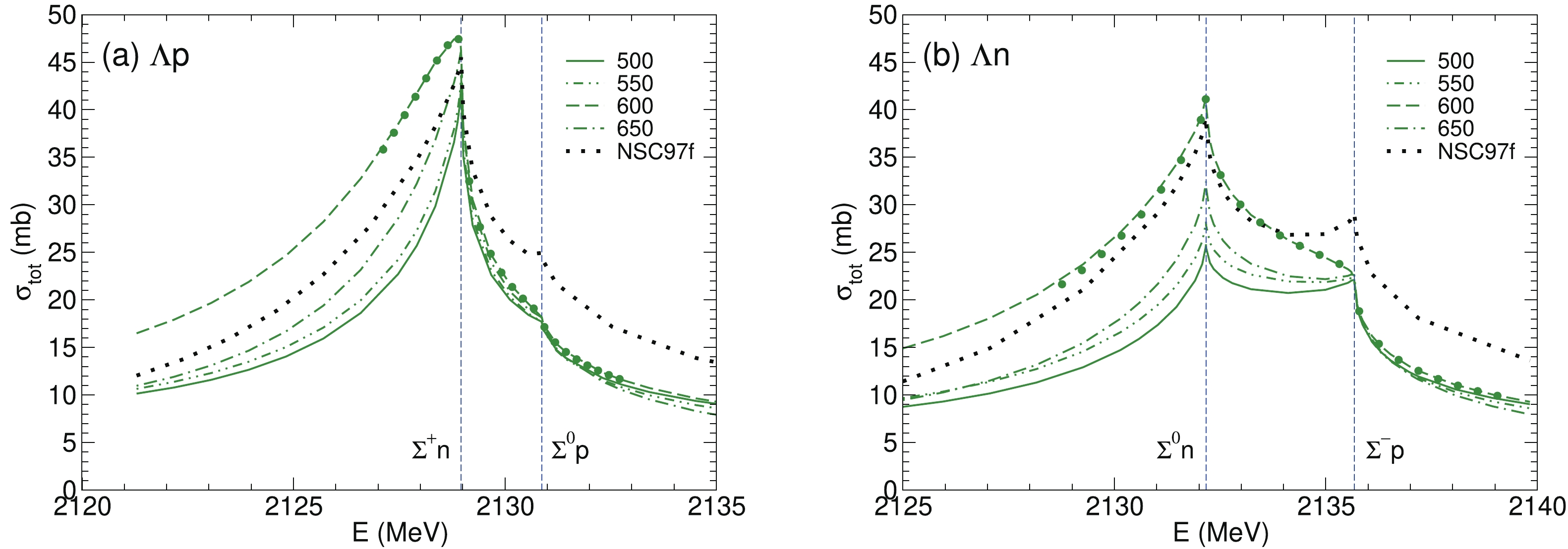

Figure 4.  (color online) Results for ${\Lambda} p$ (a) and ${\Lambda} n$ (b) cross sections for the NLO19 interaction with cutoffs $500$-$650$ MeV and for the NSC97f potential. Circles indicate the results for NLO19 (600) based on the effective range expansion (2). The vertical lines indicate the ${\Sigma} N$ thresholds.

Starting with the ${\Lambda} n$ cross section at the ${\Sigma}^0 n$ threshold (Fig. 4(b)) one can see that a cusp is produced by all potentials, despite the fact that the poles for NSC97f and for the NLO19 potentials lie on sheet II. In case of NLO19 (550) and NLO19 (500) the poles are very close to the Re $q_{ {\Sigma} N}$ axis which separates sheet II and IV, so that a cusp is may be not too surprising. At the ${\Sigma}^- p$ threshold some potentials produce a cusp while others lead to a rounded step. The latter is the expected behavior based on the pole position. In any case, the presence of a lower near-by threshold distorts the signal strongly so that no rounded peak appears.

In case of the ${\Lambda} p$ cross section (Fig. 4(a)) most of the potentials produce again a cusp at the lower ${\Sigma} N$ threshold, despite of having the poles on sheet II. The only exception is NLO19 (600) where a rounded peak is visible, at least on the scale chosen for the figure. Note that the peak is barely $100$ keV below the threshold and certainly is not of Breit-Wigner type. A similar shape was reported in Ref. [55] for the NSC97f potential in a calculation using isospin-averaged masses. At the ${\Sigma}^0 p$ threshold cusps as well as rounded steps occur. However, the actual signals are obscured by the large effect at the ${\Sigma}^+ n$ threshold and the subsequent steep fall-off of the ${\Lambda} p$ cross section.

Since for ${\Lambda} n$ the separation of the ${\Sigma} N$ thresholds is significantly larger than for the $Q = 1$ channels, the details of both threshold structures appear more prominently. Moreover, the interaction in the ${\Sigma}^- p$ channel is stronger than that for ${\Sigma}^0 n$ because the crucial $I = 1/2$ contribution enters with a weight $2/3$ in the former and with $1/3$ in the latter [42]. For $Q = 0$ the contribution to the lower channel, ${\Sigma}^+ n$, is weighted by $2/3$. Both aspects make the ${\Lambda} n$ channel to be a good testing ground for details of the $YN$ interaction. Unfortunately, there is little hope to perform pertinent experiments. In any case, we want to emphasize that in the ${\Sigma}^- p$ channel the real situation will be more complicated, because the presence of the attractive Coulomb interaction leads to an accumulation of Coulomb bound states at the threshold. In this case there is a discontinuity of the cross sections at the ${\Sigma}^- p$ threshold and, as a consequence, no cusp (or rounded step) is expected but a jump in the cross sections of the open channels. For a detailed discussion see Ref. [4]. We do not consider this complication here.

Finally, in order to demonstrate the quality of the ERE, we indicate in the figure corresponding results for NLO19 (600) (circles). As one can see, the representation of the amplitudes in terms of such an expansion works remarkably well, down to and even below the lower ${\Sigma} N$ threshold.

Measurements of ${\Sigma}^- p$ scattering with reduced uncertainty would be rather useful for corroborating the existence of a $S = -1$ dibaryon suggested by the present study. An alternative source of information is offered by measurements of level shifts and widths of ${\Sigma}^- p$ atoms. In Table 3 we present predictions for those quantities, for the $YN$ potentials considered in the present work. In the calculation the Trueman formula [63] was applied (with the second-order term taken into account) which relates these quantities to the ${\Sigma}^- p$ scattering lengths:

$\Lambda$/MeV	NLO13					NLO19				Jülich '04	NSC97f
	500	550	600	650		500	550	600	650
$E_{^1S_0}$	−248	−231	−146	−106		−249	−234	−146	−107	−130	−498
$\Gamma_{^1S_0}$	1401	1391	1357	1317		1471	1455	1381	1309	1788	1809
$E_{^3S_1}$	−1286	−1256	−1211	−1159		−944	−942	−1210	−1141	884	−825
$\Gamma_{^3S_1}$	2338	2514	2657	2865		3506	3406	2620	2975	4782	2605
$E_{1S}$	−1026	−1000	−945	−896		−770	−765	−944	−882	630	−743
$\Gamma_{1S}$	2104	2233	2332	2478		2997	2918	2310	2558	4034	2406

Table 3.  Hadronic shifts and broadenings of S-wave states of $\Sigma ^-$p atoms (in eV). Results for the $^1S_0$ and $^3S_1$ partial waves, and for the spin average, are presented.

Here ${a^{sc}}$ is the Coulomb-modified ${\Sigma}^- p$ ($^1S_0$ and/or $^3S_1$) scattering length, $\mu_{ {\Sigma}^- p}$ is the reduced mass, and $r_{\rm B}$ is the Bohr radius which amounts to $51.4$ fm for ${\Sigma}^- p$. The quantity $\beta$ is given by $\beta = 2(1-\Psi(1)) \approx 3.1544$ for S waves, where $\Psi$ is the digamma function. According to a detailed study of antiprotonic atoms [64] the above formula yields rather reliable results once the Coulomb interaction is explicitly taken into account in the calculation of the hadronic reaction amplitude and/or scattering length.

It is interesting to compare our results with those for similar atomic systems where measurements have been already performed. This is possible for antiprotonic hydrogen and deuterium [65] as well for kaonic hydrogen [66]. It reveals that the predicted widths for ${\Sigma}^- p$, being of the order of ($2100$-$3000$) eV, are noticeable larger than those for antiprotonic atoms ($\Gamma_{\bar pp} \approx 1000$ eV) [65] and $K^-$ atoms ($\Gamma_{K^- p} \approx 500$ eV) [66]. Most likely this is due to the fact that the threshold of the neutral “partner” channel (${\Sigma}^0 n$) is slightly below the one of ${\Sigma}^- p$ whereas in the other two systems the corresponding channels ($\bar nn$ and $\bar K^0 n$) are slightly above. In any case a large width as predicted here certainly reduces the prospects for an experimental determination of the level shifts and widths of ${\Sigma}^- p$ atoms. So far such measurements have been only performed for carbon and heavier nuclei [67, 68].

In the present work we studied the threshold structure seen in the ${\Lambda} p$ cross section (invariant mass spectrum) around the ${\Sigma} N$ threshold. For that purpose we utilized $YN$ interactions that yield the presently best description of low-energy ${\Lambda} p$, ${\Sigma}^- p$ and ${\Sigma}^+ p$ scattering data.

The $YN$ potentials in question are interactions established within chiral effective field theory up to next-to-leading order by the Jülich-Bonn-Munich group in 2013 and 2019 [26, 27] and the Nijmegen NSC97 meson-exchange potentials [28] from 1999. In all those cases the achieved $\chi^2$ value is in the order of $16$ for the $36$ (or $35$) “best” $YN$ data taken into account.

Our work revealed that (i) if one takes into account the full complexity of the $YN$ interaction (tensor forces, ${\Lambda} N$-${\Sigma} N$ coupling) as well as constraints from (broken) SU(3) flavor symmetry [26-28] and (ii) one takes the presently available low-energy ${\Sigma} N$ data serious and aims at their best possible reproduction, then the appearance of a dibaryon in form of a (unstable) ${\Sigma} N$ bound state close to the ${\Sigma} N$ threshold seems to be practically unavoidable.

Unfortunately, our study also indicates that it might be wishful thinking to expect a truly convincing evidence for a strangeness $S = -1$ dibaryon, i.e. a peak that is well separated from the (and well below the) ${\Sigma} N$ threshold. Nonetheless, to confirm our result and to reliably establish that there is a pole in the second quadrant of the complex ${\Sigma} N$ momentum plane which signals a ${\Sigma} N$ bound state, additional and more accurate near-threshold ${\Sigma}^- p$ data would be rather useful.

It would be also interesting to get experimental data or at least tighter constraints on the charge $Q = 1$ ${\Sigma} N$ channels. Pertinent information has been already acquired at the COSY accelerator in Jülich, from the reactions $pp \to K^+ {\Sigma}^0 p$ [69, 70] and $pp \to K^+ {\Sigma}^+ n$ [71-73], and also by the ALICE Collaboration where the ${\Sigma}^0 p$ momentum correlation function was determined in $pp$ collisions at $13$ TeV [74]. But the present quality of the data together with uncertainties in the tools for analyzing final-state interactions [75, 76] prevent more quantitative conclusions. Most promising are certainly planned scattering experiments at J-PARC, where among other things the reactions ${\Lambda} p \to {\Sigma}^0 p, {\Sigma}^+ n$ could be measured [50]. Such cross sections would provide independent information on the ${\Lambda} N\leftrightarrow {\Sigma} N$ transition, complementing available data for ${\Sigma}^- p \to {\Lambda} n$, and, thus, could allow one to pin down the actual strength of the ${\Lambda} N$-${\Sigma} N$ coupling more accurately.

We would like to thank Michael Döring for the code for searching for zeros in the complex plane.