-
The study on the formation of superheavy elements via heavy ion fusion reactions is an interesting topic in nuclear physics. Heavy ion fusion reactions can be adopted to study the different properties of the compound nucleus [1-5]. Using projectile and target nuclei, the compound nucleus can be formed. To obtain a heavy nucleus, a heavy projectile is required to be fused with a heavy target. There are two experimental methods for synthesizing superheavy elements. The cold fusion method is used to synthesize superheavy elements with Z = 107-112 [6, 7]. Another method is the hot fusion reaction method, which is used to produce elements with Z = 113-118 [8-12]. It should be noted that an element with Z = 113 was also produced via the cold fusion reaction [13, 14].
For the synthesis of a superheavy element with Z = 119, Zagrebaev and Greiner experimentally reported the upper cross sectional 50 fb in the reaction 50Ti+249Bk, and no indication for the discovery of an element with Z = 119 was observed. Recently, Khuyagbaatar et al. [15] investigated the production of superheavy elements with Z = 119 and 120 in the reactions 50Ti+249Bk and 50Ti+249Cf. They discussed the nonobservation of the elements (with Z = 119 and 120) using the concept of fusion evaporation reactions, addressing different theoretical calculations on the fission barrier heights of superheavy elements. Different theoretical works exist with different models such as the multidimensional stochastic [16, 17], dinuclear system [18, 19], and fusion-by-diffusion models [20, 21]. In Ref. [22], within the dinuclear system model, the production of hassium isotopes is studied in the reactions 22Ne + 249Cf, 25,26Mg + 24824Cm, 30Si + 244Pu, 34,36S + 238U, 40Ar+232Th, and 48Ca+226Ra.
It is clear that synthesizing superheavy nuclei is very difficult experimentally because the evaporation residue cross section of these reactions is negligible. Consequently, the study on the effective parameters of evaporation residue cross section is crucial. These parameters are different, and they include incident energy, combination of the projectile and target, deformation of the colliding nuclei, etc. Recently, we calculated the evaporation residue cross section for superheavy elements with Z = 120, considering the projectile and target deformations [23].
In heavy ions collision, the quasifission processes occur on short time scales at approximately 10−20 s [24-26], while fusion-fission usually occurs on longer time scales, from approximately 10−20 to 10−16 s. There is a close relationship between the production of superheavy elements and entrance channels. In other words, the effects of entrance channel and the competition between the quasifission processes and complete fusion can facilitate the elucidation of heavy ion collisions. This subject has been studied in several publications [27-30]. In addition, several studies exist on the influence of the neutron numbers of projectile and target on the evaporation residue cross sections in hot fusion reactions [31-34].
In this study, using the Coulomb and proximity potential, we investigated the role of the entrance channel of colliding nuclei on the evaporation residue cross section of a superheavy element 296119 formed in heavy ion fusion reactions. We also investigated the relationship between the mean fission parameter, quasi-fission, and evaporation residue cross section. This paper is organized as follows. In Sec. II, the theoretical method is provided. Then, the obtained results are presented in Sec. III. Finally, the summary and conclusion of our results are provided in Sec. IV.
-
The potential between the target and the projectile can be calculated based on the Coulomb and proximity potential model as [35]
$ V(r) = V_c+V_P+\frac{\hbar^2l(l+1)}{2\mu r^2}, $

(1) where, l is the angular momentum, r represents the distance between the centers of the projectile and target, and μ is the reduced mass. The Coulomb potential is given as
$ V_c = \frac{Z_PZ_Te^2}{r}, $

(2) where,
$ Z_P $ and$ Z_T $ are the atomic numbers of the projectile and target, respectively.$ V_P $ is the proximity potential given by [36]$ V_P = 4 \pi \gamma b \left(\frac{C_1 C_2}{C_1+C_2}\right) \Phi (z/b), $

(3) where z is the short separation distance and the nuclear surface thickness is given as
$ b\approx1\;{\rm fm} $ . In addition, the surface energy constant is expressed as$ \gamma = 0.9517\left[1-1.7826\left(\frac{N-Z}{A}\right)^2\right]{\rm MeV fm}^{-2}, $

(4) where, N, Z, and A represent the neutron, proton, and atomic numbers of the parent nucleus, respectively.
$ C_i $ can be calculated as$ C_i = R_i-\frac{b^2}{R_i^2}, $

(5) with
$ R_i = 1.24A_i^{1/3}-0.76+0.8A_i^{-1/3}. $

(6) The universal function
$ \Phi(z/b) $ can be calculated as [36]$ \Phi(z/b) = \left\{ \begin{array}{*{20}l} -1.7817+0.9270z+0.0143z^2 -0.09z^3 &z\leqslant 0,\\ -1.7817+0.9270z+0.01696z^2 -0.05148z^3& 0<z<1.9475, \\ -4.41{\rm exp}(-z/0.7176)& z\geqslant 1.9475. \end{array} \right. $ 
(7) -
By multiplying three quantities, the capture cross section, fusion probability, and survival probability, we can calculate the evaporation cross section for a superheavy element as [37]
$ \sigma_{\rm ER}^{xn}(E_{\rm cm}) = \sigma_{cap}(E_{\rm cm})P_{\rm CN}(E_{\rm cm})W_{\rm sur}^{xn}(E^*,l). $

(8) This is an estimation because the total process of the compound nucleus formation and decay is separated here into three single reaction stages even if they are related to each other; in addition, they are treated and evaluated separately. In the fusion of heavy nuclei, it is the fission channels that considerably determine the dynamics of the total process; the fusion probability value can be significantly smaller than unity, whereas its exact calculation is difficult. Furthermore, currently, there is no agreement for the mechanism of the compound nucleus formation itself, and relatively different, occasionally opposite in their physics sense, models are used for the description.
In contrast to the excessively available data in the study on the initial stage of the heavy ion fusion reactions and the processes of statistical decay of weakly excited compound nuclei, an accurate description of these reaction stages in the synthesis of superheavy elements is also difficult, which introduces an additional uncertainty in the cross section calculations of the evaporation residue formation. Here, the uncertainty is related with the convolution of the mechanisms of the first and last reaction stages, as well as with the fact that a number of quantities and nuclear specifications are not properly determined in this region.
The capture cross section can be evaluated using the sum of the cross section for each partial wave l as
$ \sigma_{\rm cap} = \frac{\pi}{k^2}\Sigma_{l = 0}^\infty (2l+1)T(E,l), $

(9) where,
$ k = \sqrt{\dfrac{2\mu E}{\hbar^2}} $ and μ denote the reduced mass of the target and projectile systems. In addition,$ T(E,l) $ is the penetration probability of the lth partial wave, which can be calculated using the Hill-Wheeler formula [38]$ T(E,l) = \Big\{1+{\rm exp}[2\pi(E_l-E)/\hbar\omega_l]\Big\}^{-1}. $

(10) Substituting the penetration probability in Eq. (9) by an integral, Wong obtained the following relationship for the capture cross section [39]
$ \sigma_{\rm cap} = \frac{R_0^2 \hbar\omega_0}{2E}{\rm ln}\Big\{1+{\rm exp}[2\pi(E-E_0)/\hbar\omega_0]\Big\}, $

(11) here
$ E_0 $ is the barrier height.$ R_0 $ is the barrier radius and can be calculated as$ \left(\frac{{\rm d}V(r)}{{\rm d}r}\right)_{r = R_0} = 0. $

(12) The curvature of the potential can be calculated as
$ \hbar\omega_0 = \hbar\sqrt{\frac{1}{\mu}\left(\frac{{\rm d}^2V(r)}{ {\rm d}r^2}\right)_{r = R_0}}. $

(13) Based on Ref. [40], we evaluated the fusion probability by the following relationship:
$ P_{\rm CN} = \frac{{\rm exp}(-c(x_{\rm e}-x_{\rm thr}))}{1+{\rm exp}\left[\dfrac{E^*_{\rm B}-E^*}{\Delta}\right]}, $

(14) where ∆ is an adjustable parameter.
$ E^*_{\rm B} $ is the excitation energy of the compound nucleus when the center of mass beam energy is equal to the Coulomb and proximity energy.$ x_{\rm e} $ can be evaluated as$ x_{\rm e} = \left[\frac{(Z^2/A)}{(Z^2/A)_{\rm crit}}\right]\big[1-\alpha+\alpha f(K)\big], $

(15) here
$ \alpha = 1/3 $ and$ (Z^2/A)_{\rm crit} $ is given by$ (Z^2/A)_{\rm crit} = 50.883\left[1-1.7826\left(\frac{N-Z}{A}\right)^2\right], $

(16) $ f(K) = \frac{4}{K^2+K+\dfrac{1}{K^2}+\dfrac{1}{K}}, $

(17) $ K = (A_P/A_T)^{1/3}. $

(18) Equation (14) was proposed by Zagrebaev to investigate the cold fusion reactions; however, this equation has also been adopted in various studies for the hot fusion reactions. For the best fit to the cold fusion reaction, it is inferred that the values of c and
$ x_{\rm e} $ are 136.5 and 0.79, respectively. For the hot fusion reaction, the best fit for$ x_{\rm e}\leqslant 0.8 $ is$ c = 104 $ and$ x_{\rm thr} = 0.69 $ ; while for$ x_{\rm e}>0.8 $ , the values are$ c = 82 $ and$ x_{\rm thr} = 0.69 $ [41].We calculated the value of the survival probability under the evaporation of the x neutron as [42]
$ W_{\rm sur} = P_{xn}(E_{\rm CN}^*)\prod\limits_{i = 0}^{i_{\rm max} = x}\left(\frac{\Gamma_n}{\Gamma_n+\Gamma_f}\right)_{i,E^*}, $

(19) where the index i is the number of emitted neutron, and
$ \Gamma_n $ and$ \Gamma_f $ present the decay widths of the neutron evaporation and fission, respectively. Vandenbosch and Huizenga suggested that$ {\Gamma_n}/{\Gamma_f} $ can be calculated as [42]$ \begin{aligned}[b]\frac{\Gamma_n}{\Gamma_f} =& \frac{4A^{2/3}a_f(E^*-B_n)}{K_0a_n[2a_n^{1/2}(E^*-B_f)^{1/2}-1]} \\& \times {\rm exp}[2a_n^{1/2}(E^*-B_n)^{1/2}\\&-2a_f^{1/2}(E^*-B_f)^{1/2}], \end{aligned}$

(20) here
$ k = 9.8 $ MeV, and$ a_n = A/10 $ represents the level density parameter for the neutron evaporation channel. The level density parameter for fission is$ a_f = 1.1a_n $ . In addition,$ B_n $ and$ B_f $ represent the neutron separation energy and fission barrier, respectively.$ B_f $ is evaluated using the shell correction as$ B_f(E^*) = B_f^{\rm LD}+S {\rm exp}(-E^*/E_D), $

(21) where
$ B_f^{\rm LD} $ is the liquid drop fission barrier that is equal to zero for heavy elements with$ Z>109 $ , and the shell correction, S, is obtained from Ref. [43]. In addition, the shell damping energy,$ E_D $ , is evaluated as$ E_D = 5.48 A^{1/3}/(1+1.3A^{-1/3}). $

(22) In Eq. (19),
$ P_{xn}(E_{\rm CN}^*) $ is calculated based on the method presented in Refs. [42, 44, 45] as$ P_{xn}(E_{\rm CN}^*) = P[x]-P[x+1], $

(23) where
$ P(x) $ is the probability that at least x neutrons are evaporated at a given$ E^{\star} $ and can be calculated by the following relationship$ P[x] = 1-{\rm exp}(-\Delta_x/T)\left[1+\Sigma_{i = 1}^{2x-3}\frac{(\Delta_x/T)^i}{i!}\right], $

(24) with
$ \Delta_x = E^{\star}_{\rm CN}-\sum\limits_{k = 1}^x B_k, $

(25) here
$ B_k $ is the evaporation neutron separation energy and$ T = \sqrt{\dfrac{E^{\star}_{\rm CN}}{(2a_n)}} $ . -
We theoretically investigated the formation of the superheavy element 296119 using the Coulomb and proximity potential models. We selected 29 reactions with different targets and projectiles, including convenient half lives. The evaporation residue cross section of the 3n and 4n channels is calculated. The entrance channel influences the production of the superheavy element via the Q value and entrance asymmetry. The mass and neutron asymmetries are defined as
$ \alpha_A = (A_T-A_P)/A $ and$ \alpha_N = (N_T-N_P)/N $ , respectively. The effect of the entrance channel is studied in comparison with the evaporation residue cross sections for the reactions triggering the formation of the same compound nucleus. The calculated results are presented in Figs. 1 to 12 and Table 1.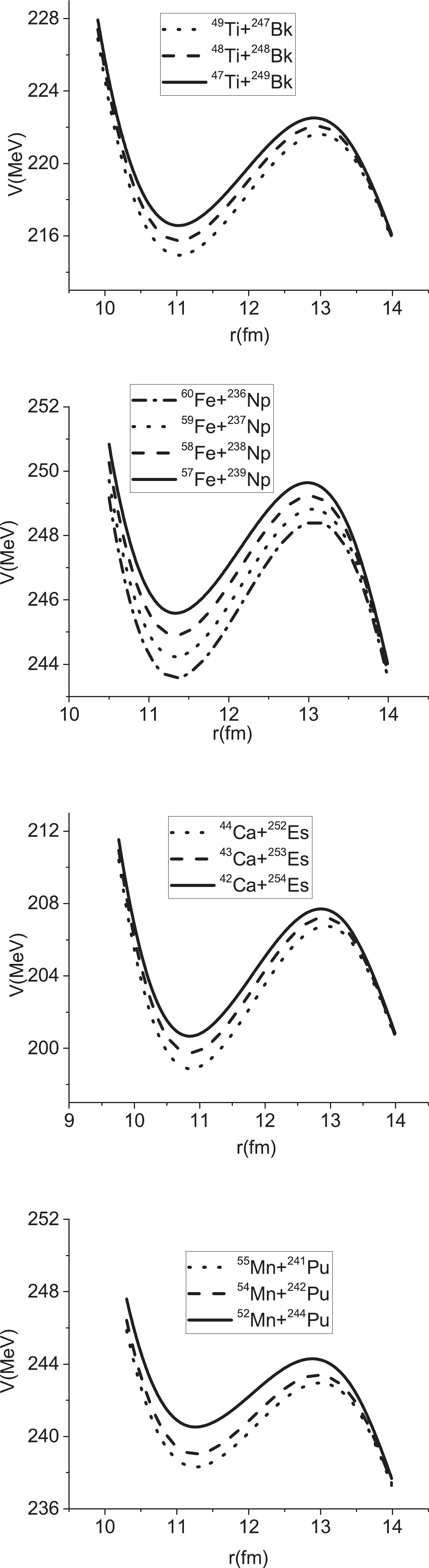
Figure 1. Calculated dependence of the potential energy on the distance between the projectile and target.
Reaction $\mid Q\mid/{\rm{MeV} }$ 

$\alpha_A = (A_T-A_P)/A$ 

$\alpha_N = (N_T-N_P)/N$ 

$\chi_m$ 

${{E}}^*_{3n}/{\rm {MeV}}$ 

$\sigma_{3n}^{\rm max}/{\rm {fb}}$ 

${{E}}^*_{4n}/{\rm {MeV}}$ 

$\sigma_{4n}^{\rm max}/{\rm {fb}}$ 

$^{38}_{18}{\rm{Ar}}+^{258}_{101}{\rm{Md}} \rightarrow ^{296}119$ 

147.576 0.7432 0.7740 0.8049 45.26 54.26 46.17 125.84 $^{36}_{18}{\rm{Ar}}+^{260}_{101}{\rm{Md}} \rightarrow ^{296}119$ 

138.229 0.7567 0.7966 0.8160 55.92 0.03 58.13 0.27 $^{39}_{19}{\rm{K}} + ^{257}_{100}{\rm{Fm}} \rightarrow ^{296}119$ 

149.766 0.7364 0.7740 0.8243 52.02 0.07 55.32 0.54 $^{44}_{20}{\rm{Ca}}+^{252}_{99}{\rm{Es}} \rightarrow ^{296}119$ 

168.723 0.7027 0.7288 0.8230 39.36 169.97 41.82 42.15 $^{43}_{20}{\rm{Ca}}+^{253}_{99}{\rm{Es}} \rightarrow ^{296}119$ 

163.944 0.7094 0.7401 0.8277 44.63 2.92 45.59 5.77 $^{42}_{20}{\rm{Ca}}+^{254}_{99}{\rm{Es}} \rightarrow ^{296}119$ 

161.105 0.7162 0.7514 0.8326 48.01 0.24 48.57 0.93 $^{46}_{21}{\rm{Sc}}+^{250}_{98}{\rm{Cf}} \rightarrow ^{296}119$ 

175.138 0.6891 0.7175 0.8369 40.71 25.64 42.61 4.74 $^{45}_{21}{\rm{Sc}}+^{251}_{98}{\rm{Cf}} \rightarrow ^{296}119$ 

171.484 0.6959 0.7288 0.8414 44.86 2.5 45.78 1.44 $^{49}_{22}{\rm{Ti}}+^{247}_{97}{\rm{Bk}} \rightarrow ^{296}119$ 

187.62 0.6689 0.6949 0.8445 35.59 106.3 40.17 4.7 $^{48}_{22}{\rm{Ti}}+^{248}_{97}{\rm{Bk}} \rightarrow ^{296}119$ 

184.96 0.6756 0.7062 0.7953 38.49 10.5 41.35 2.2 $^{47}_{22}{\rm{Ti}}+^{249}_{97}{\rm{Bk}} \rightarrow ^{296}119$ 

179.635 0.6824 0.7175 0.8012 44.25 0.12 45.27 0.22 $^{51}_{23}{\rm{V}}+^{245}_{96}{\rm{Cm}} \rightarrow ^{296}119$ 

194.295 0.6554 0.6838 0.8566 34.82 27.64 39.93 0.53 $^{50}_{23}{\rm{V}}+^{246}_{96}{\rm{Cm}} \rightarrow ^{296}119$ 

193.332 0.6621 0.6949 0.8607 39.61 10.62 41.93 0.4 $^{54}_{24}{\rm{Cr}}+^{242}_{95}{\rm{Am}} \rightarrow ^{296}119$ 

206.014 0.6351 0.6610 0.8642 32.63 70.34 39.06 0.21 $^{53}_{24}{\rm{Cr}}+^{243}_{95}{\rm{Am}} \rightarrow ^{296}119$ 

202.659 0.6418 0.6723 0.8701 35.08 12.02 40.13 0.13 $^{55}_{25}{\rm{Mn}}+^{241}_{94}{\rm{Pu}} \rightarrow ^{296}119$ 

209.304 0.6283 0.6610 0.8791 35.31 0.98 40.09 0.04 $^{54}_{25}{\rm{Mn}}+^{242}_{94}{\rm{Pu}} \rightarrow ^{296}119$ 

205.388 0.6351 0.6723 0.8830 39.41 0.04 41.82 0.013 $^{52}_{25}{\rm{Mn}}+^{244}_{94}{\rm{Pu}} \rightarrow ^{296}119$ 

195.450 0.6486 0.6949 0.8912 50.37 1.02 $\times 10^{-5}$ 

50.91 6 $\times 10^{-5}$ 

$^{60}_{26}{\rm{Fe}}+^{236}_{93}{\rm{Np}} \rightarrow ^{296}119$ 

222.583 0.5945 0.6185 0.8789 30.55 11.0 38.00 0.03 $^{59}_{26}{\rm{Fe}}+^{237}_{93}{\rm{Np}} \rightarrow ^{296}119$ 

220.340 0.6013 0.6271 0.8823 31.46 3.4 38.9 0.02 $^{58}_{26}{\rm{Fe}}+^{238}_{93}{\rm{Np}} \rightarrow ^{296}119$ 

219.248 0.6081 0.6384 0.8859 32.55 1.8 39.2 0.015 $^{57}_{26}{\rm{Fe}}+^{239}_{93}{\rm{Np}} \rightarrow ^{296}119$ 

215.418 0.6148 0.6497 0.8896 34.95 0.28 40.3 0.007 $^{60}_{27}{\rm{Co}}+^{235}_{92}{\rm{U}} \rightarrow ^{296}119$ 

223.753 0.5912 0.6214 0.8975 33.91 0.27 39.61 0.0016 $^{59}_{27}{\rm{Co}}+^{237}_{92}{\rm{U}} \rightarrow ^{296}119$ 

221.387 0.6013 0.6384 0.8996 36.3 0.05 40.41 0.001 $^{64}_{28}{\rm{Ni}}+^{232}_{91}{\rm{Pa}} \rightarrow ^{296}119$ 

235.700 0.5675 0.5932 0.8991 30.83 0.49 38.93 7.3 $\times 10^{-4}$ 

$^{63}_{28}{\rm{Ni}}+^{233}_{91}{\rm{Pa}} \rightarrow ^{296}119$ 

232.572 0.5743 0.6045 0.9023 31.98 0.02 38.31 5.3 $\times 10^{-4}$ 

$^{65}_{29}{\rm{Cu}}+^{231}_{90}{\rm{Th}} \rightarrow ^{296}119$ 

237.995 0.5608 0.5932 0.9116 32.42 0.04 39.1 1.2 $\times 10^{-4}$ 

$^{70}_{30}{\rm{Zn}}+^{226}_{89}{\rm{Ac}} \rightarrow ^{296}119$ 

249.804 0.5270 0.5480 0.9114 30.19 0.50 37.68 5.7 $\times 10^{-5}$ 

$^{71}_{31}{\rm{Ga}}+^{225}_{88}{\rm{Ra}} \rightarrow ^{296}119$ 

252.695 0.5202 0.5480 0.9229 30.90 0.007 8.33 2 $\times 10^{-5}$ 

Table 1. Obtained results for 3n, 4n channels evaporation. Columns two, three, four, and five are
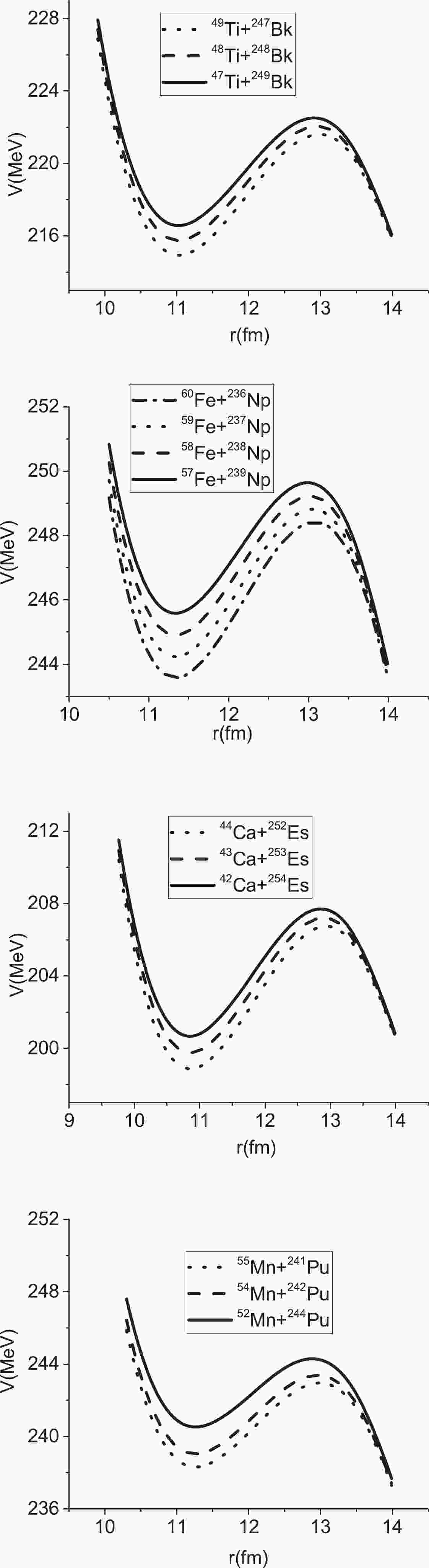
$ \mid Q\mid = \mid(M_P+M_T-M_{\rm CN})c^2\mid $ [43], the mass asymmetry, neutron asymmetry, and mean fissility, respectively. The position of the maximum value of the 3n channel ($ E^*_{3n} $ ) and the maximum value of the evaporation residue of the 3n channel ($ \sigma_{3n}^{\rm max} $ ) are presented in the sixth and seventh columns. In addition, the results for the 4n channel ($ E^*_{4n} $ and$ \sigma_{4n}^{\rm max} $ ) are presented in columns eight and nine.In Fig. 1, we display the variation of the potential energy with the distance between the projectile and the target for the reactions
$ ^{49-47} {\rm{Ti}} + ^{247-249} {\rm{Bk}}$ ,$ ^{60-57} {\rm{Fe}}+ $ $ ^{236-239} {\rm{Np}}$ ,$ ^{44-42} {\rm{Ca}}+ ^{252-254} {\rm{Es}}$ , and$ ^{55,54,52} {\rm{Mn}}+ ^{241,242,244} {\rm{Pu}}$ . In these reactions, with an increase in the entrance channel (mass or neutron) asymmetry, the fusion barrier height increases; however, the barrier radius decreases. The capture cross section as a function of energy is plotted in Fig. 2 for these reactions. The maximum capture cross section is related to the reaction 49Ti+247Bk. The vertical arrows demonstrate the excitation energies of$ E^{*} = E_0+Q $ for different reactions. The neutron asymmetry parameters for the reactions, 49Ti+247Bk, 48Ti+248Bk, and 47Ti+249Bk, are 0.668, 0.675, and 0.682, respectively. Because the reaction 49Ti+247Bk has the highest Q value at energies below the Coulomb barrier, the capture cross section is larger. In addition, the neutron asymmetry via the barrier hight, barrier radius, and curvature of the potential influence the capture cross section. In other words, owing to the effects of the Q value and Coulomb barriers, the capture cross sections are different. By increasing the energy, the capture cross section increases at low energies and then reaches the maximum value at higher energies. The same results can be concluded for other reactions.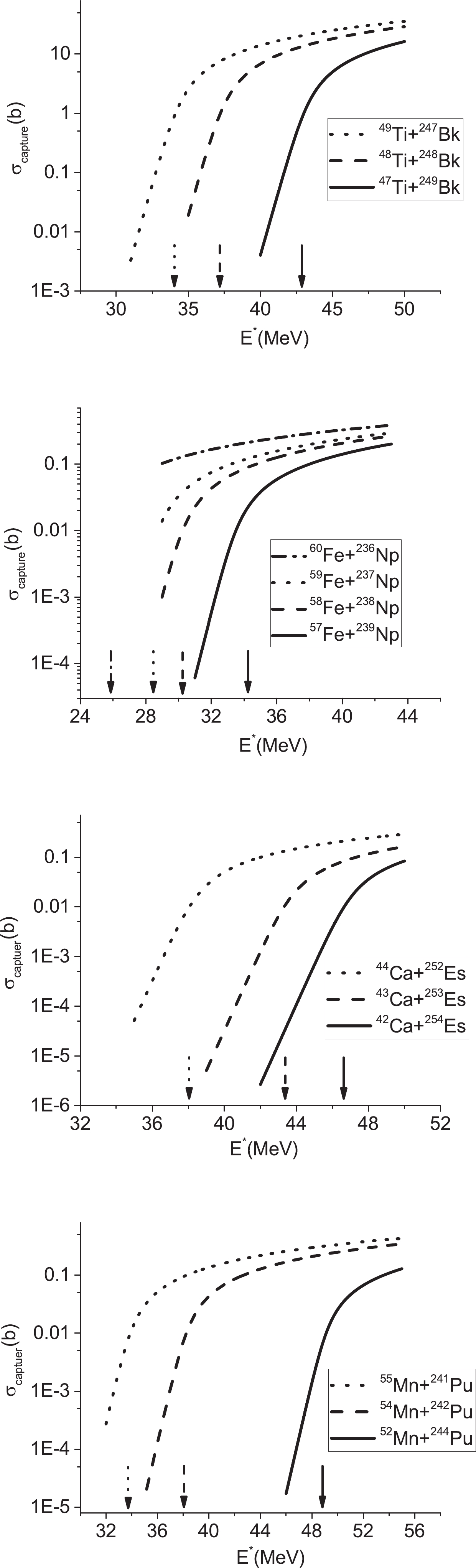
Figure 2. Calculated dependence of the capture cross section on the energy. The arrows denote the positions of the corresponding Coulomb barriers.
The probability of the compound nucleus formation with the excitation energy is calculated in Fig. 3. At lower energies, with the increase in the Q value, the probability of the compound nucleus formation increases. At higher energies, the obtained results for the formation probability are approximately close together. It should be noted that in Fig. 3, the reaction 44Ca+252Es exhibits the highest fusion probability.
In Fig. 4, we have demonstrated the 3n evaporation residue cross sections as a function of energy for the reactions
$ ^{49-47} {\rm{Ti}}+ ^{247-249} {\rm{Bk}}$ ,$ ^{60-57} {\rm{Fe}}+ ^{236-239} {\rm{Np}}$ ,$ ^{44-42} {\rm{Ca}}+ ^{252-254} {\rm{Es}}$ , and$ ^{55,54,52} {\rm{Mn}}+ ^{241,242,244} {\rm{Pu}}$ . For each of these reactions, the maximum value of the evaporation residue occurs for the case where the Q value is the highest. In addition, owing to the increase in the asymmetry parameter, the maximum cross section of the 3n evaporation residue is created at larger energies. We can observe that the evaporation residue cross sections reach the maximum value at the energy of approximately$ E^{*} = E_0+Q $ . The obtained results for the 4n evaporation residue are presented in Fig. 5. The same results can be inferred from Fig. 5, in comparison with Fig. 4.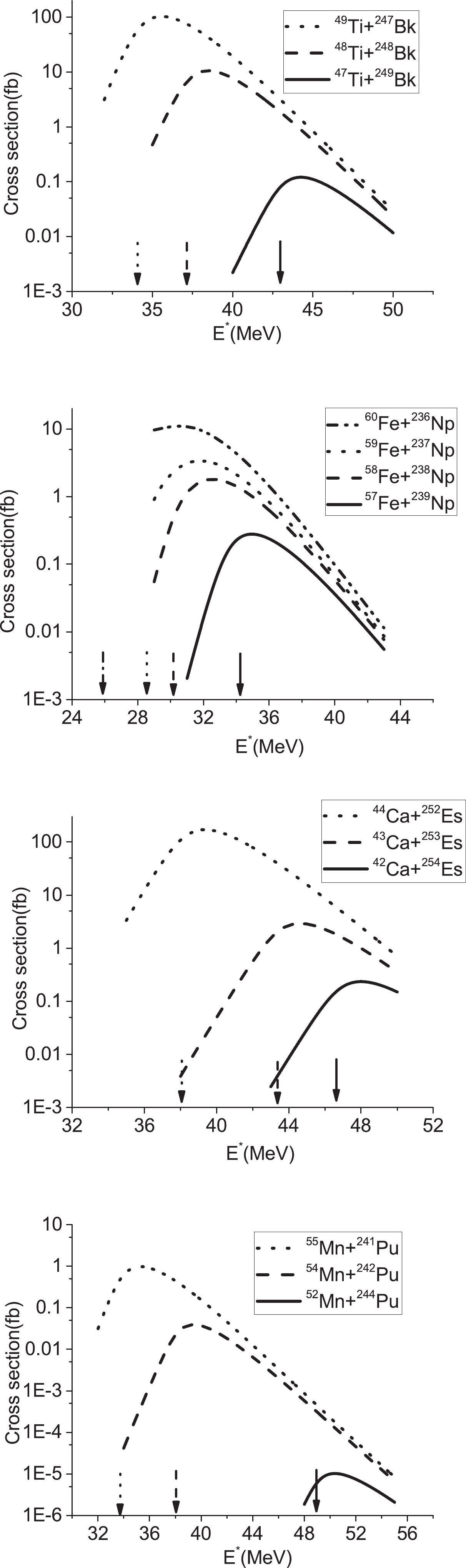
Figure 4. Plot of the 3n evaporation residue cross sections as a function of energy. The arrows indicate the positions of the corresponding Coulomb barriers.
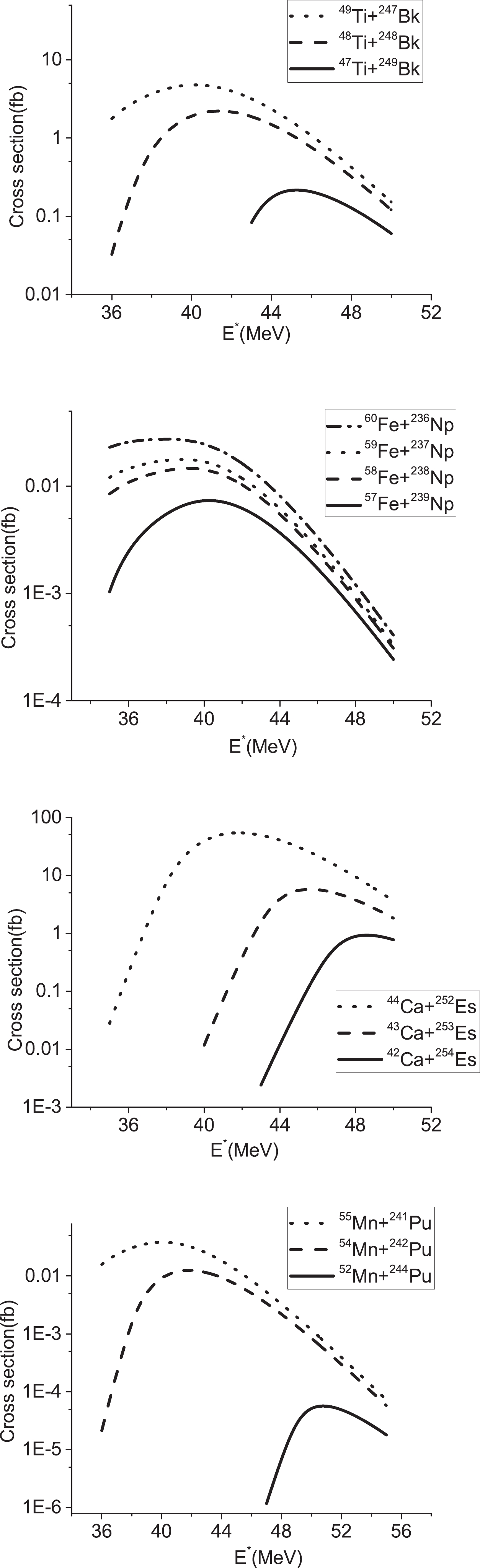
Figure 5. Same as Fig. 3 but for the 4n channel.
In the aforementioned reactions, the difference between the mass asymmetry parameters is low. Consequently, to investigate the role of mass asymmetry, we compared the obtained results for the reactions 44Ca+252Es and 60Fe+236Np. The mass asymmetry parameters for these reactions are 0.702 and 0.594, respectively. The calculated results are presented in Fig. 6. For the reaction 44Ca+252Es, the fusion probability is higher than that for the reaction 60Fe+236Np. In other words, for the reaction with larger asymmetry parameters, the fusion probability is higher than that for the reaction with lower asymmetry parameters. The capture cross section for the reaction 44Ca+252Es is lower than that for the reaction 60Fe+236Np. The barrier height and Q value for the reaction 44Ca+252Es are 206.747 and 168.723 MeV, respectively; however, for the reaction 60Fe+236Np, the barrier height and Q value are 248.424 and 222.583 MeV, respectively. Consequently, at energies below the Coulomb barrier, the capture cross section for the reaction 60Fe+236Np is larger than that for the reaction 44Ca+252Es. The maximum
$ \sigma_{3n} $ values for the reactions 44Ca+252Es and 60Fe+236Np are 169.97 and 11.0 MeV, respectively, whereas for the maximum$ \sigma_{4n} $ values, we have 42.15 and 0.03 fb, respectively. It can be inferred that for the combinations with the large discrepancy of mass asymmetry, the effect of the mass asymmetry on the evaporation residue cross section is elucidated.In Fig. 7, for clarity, we demonstrated the results for the reaction 44Ca+248Cm. Here, we presented the fusion probability, capture cross section, and survival probability. In addition, the 3n and 4n evaporation residue cross sections as a function of excitation energy are calculated. At energies lower than
$ E_0+Q $ , the evaporation residue cross section decreases because the capture cross section and fusion probability are small. At energies higher than$ E_0+Q $ , the evaporation residue cross section decreases because the survival probability decreases.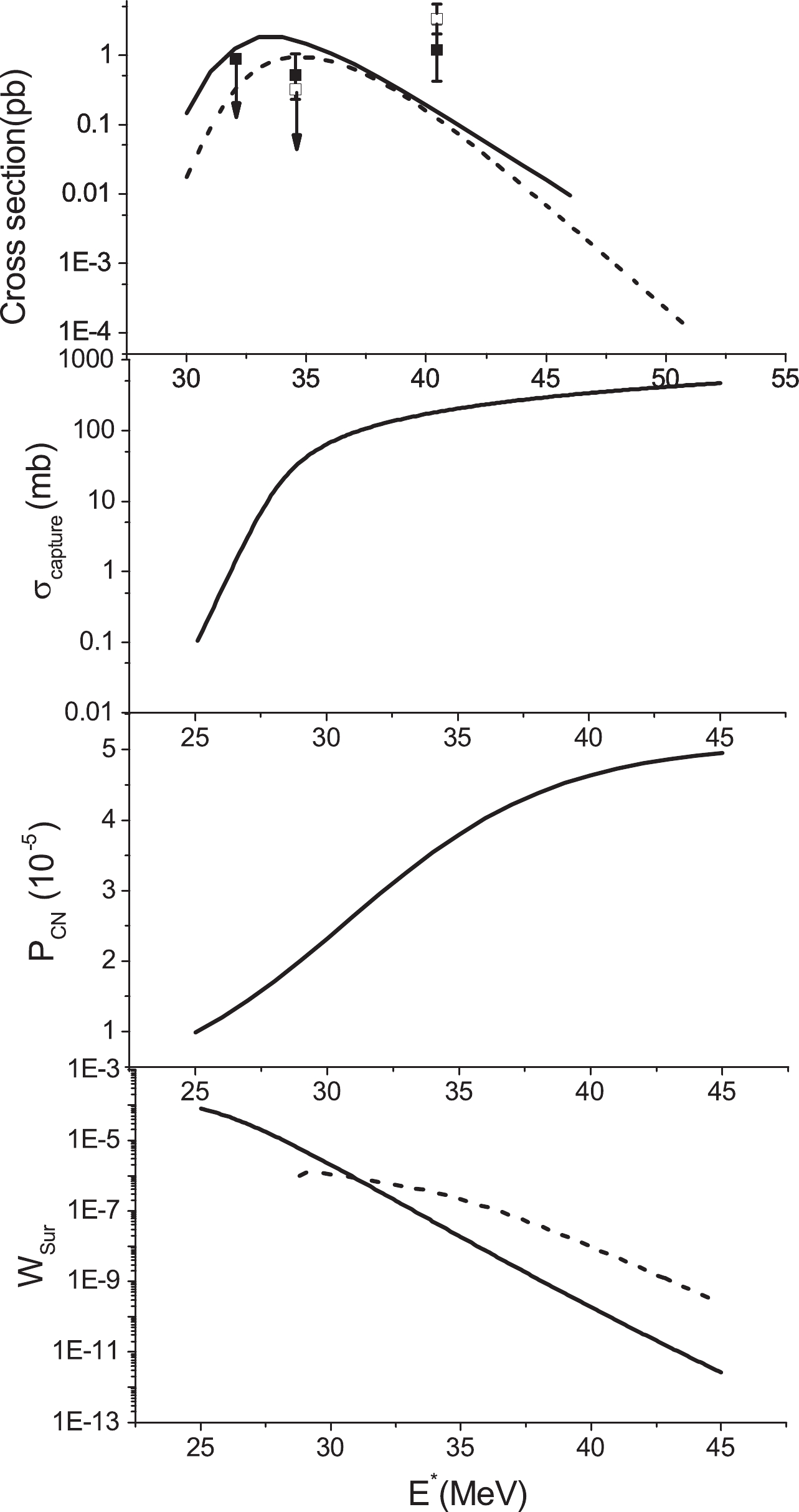
Figure 7. Plot of the survival probability, fusion probability, capture cross section, and the 3n and 4n evaporation residue cross section as a function of energy for the reaction 48Ca+248Cm. Solid and dashed curves are results for the 3n and 4n channels, respectively. Experimental data are obtained from Ref. [56].
To better investigate the influence of the Q value, we demonstrated the variations in the maximum value of the evaporation residue cross section with the
$ |Q| $ in Fig. 8. As observed from Fig. 8, with an increase in$ |Q| $ , the maximum value of the evaporation residue cross section for the 3n and 4n channels increases. In this study, the Q values are obtained from Ref. [43]. To study the role of mass table on the evaporation residue cross section, we used the mass based on Ref. [46] for the reaction 49Ti+247Bk. The obtained results are presented in Fig. 9. The$ |Q| $ values based on Refs. [43] and [46] are 187.62 and 182.19 MeV, respectively. It is clear that the Q value has an important effect on the evaporation residue cross section. The evaporation residue cross section based on the Q value of Ref. [43] is higher than that based on Ref. [46].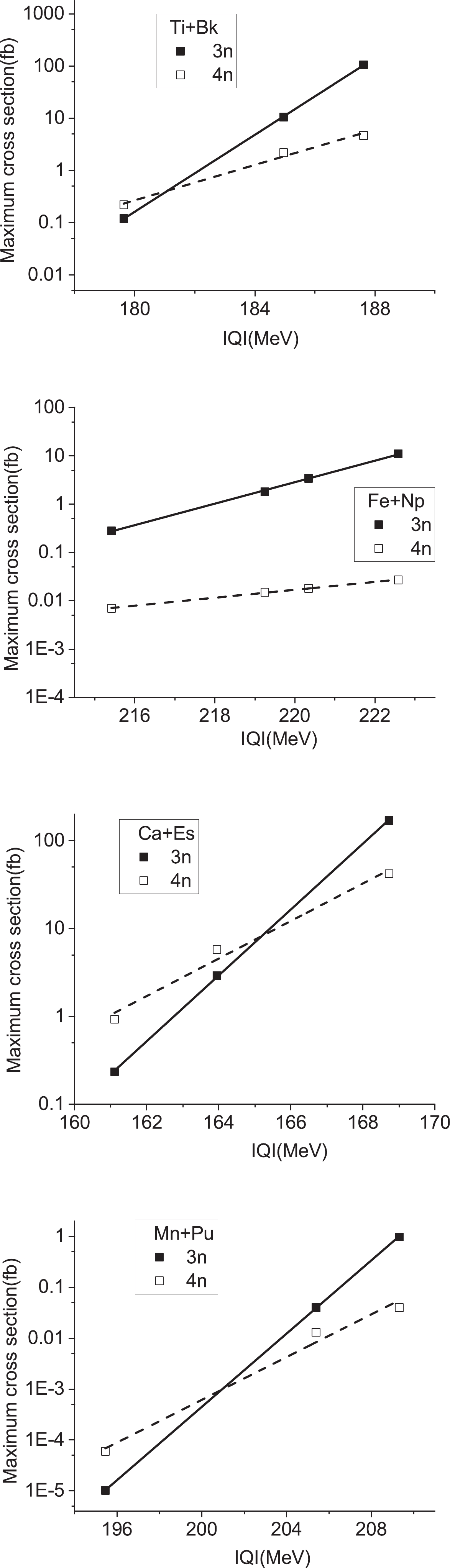
Figure 8. Plot of the maximum evaporation residue cross section versus Q-value of the reaction. Solid and open squares are results for the 3n and 4n channels, respectively. In addition, the solid and dashed lines represent liner fits on the theoretical results of 3n and 4n channels, respectively.
The obtained results for all reactions are presented in Table 1. Among all reactions, the 44Ca+252Es combination has the maximum value (169.97 fb) for the evaporation residue for the 3n channel. The asymmetry parameter and
$ |Q| $ for this reaction are 0.662 and 192.012 MeV, respectively.There are different processes in the heavy ion reactions that hinder the fusion process, such as deep inelastic, quasifission, and fast fission processes. Quasifission occurs when the dinuclear system starts to break down into two fragments without attaining the compound nucleus formation. In other words, the quasifission competes with the compound nucleus formation. The effective entrance channel fissility is defined as
$ \chi_{\rm eff} = \frac{\dfrac{4Z_PZ_T}{(A_P^{1/3}+A_T^{1/3})\times(A_PA_T)^{1/3}}}{50.883\left[1-1.7826\left(\dfrac{A-2Z}{A}\right)^2\right]}. $

(26) The mean fissility that indicates the appearance of the quasifission can be calculated as [47, 48]
$ \chi_{m} = 0.25\chi_{\rm CN}+0.75\chi_{\rm eff}, $

(27) where
$ \chi_{\rm CN} $ is the compound nucleus fissility that indicates the stability of the compound nuclei against the fission as$ \chi_{\rm CN} = \frac{Z^2/A}{50.883\left[1-1.7826\left(\dfrac{A-2Z}{A}\right)^2\right]}. $

(28) The reactions studied in this research have
$ \chi_{\rm CN} = 1.009 $ . Consequently, the mean fissility depends solely on the effective entrance channel fissility. It is clear that the possibility of the quasifission depends on the asymmetry of the entrance channel. The critical asymmetry parameter is defined as$\alpha _{\rm as}^{\rm CR} = \left\{ {\begin{array}{*{20}{l}} 0&{{\chi _{\rm CN}} < 0.396,}\\ {1.12\sqrt {\dfrac{{{\chi _{\rm CN}} - 0.396}}{{{\chi _{\rm CN}} - 0.156}}} }&{{\chi _{\rm CN}} > 0.396.} \end{array}} \right. $

(29) If we have
$ \alpha< \alpha_{\rm as}^{\rm CR} $ , the quasifission process can occur. Here, we have$ \alpha_{\rm as}^{\rm CR} = 0.949 $ . Because$ \alpha_{\rm as}^{\rm CR} $ is the same for the suggested reactions, we use another parameter ($ \chi_{m} $ ) to investigate the quasifission process. As mentioned in Ref. [48], the quasifission becomes primary for$ \chi_{m}>0.765 $ . We present the mean fissility for all reactions in Table 1. The lowest and highest values of$ \chi_{m} $ are 0.7953 and 0.9229, related to the reactions$ ^{48}_{22} {\rm{Ti}}+ ^{248}_{97} {\rm{Bk}}$ and$ ^{71}_{31} {\rm{Ga}}+ ^{225}_{88} {\rm{Ra}}$ , respectively.Figure 10 presents the maximum values of the 3n and 4n evaporation residue cross sections as a function of mean fissility. It is important to note here that as mean fissility increases, the maximum value of evaporation residue cross section decreases. It can be inferred that with an increase in the mean fissility, the quasifission becomes dominant. We obtained the following relationships for evaporation residue cross sections versus the mean fissility as
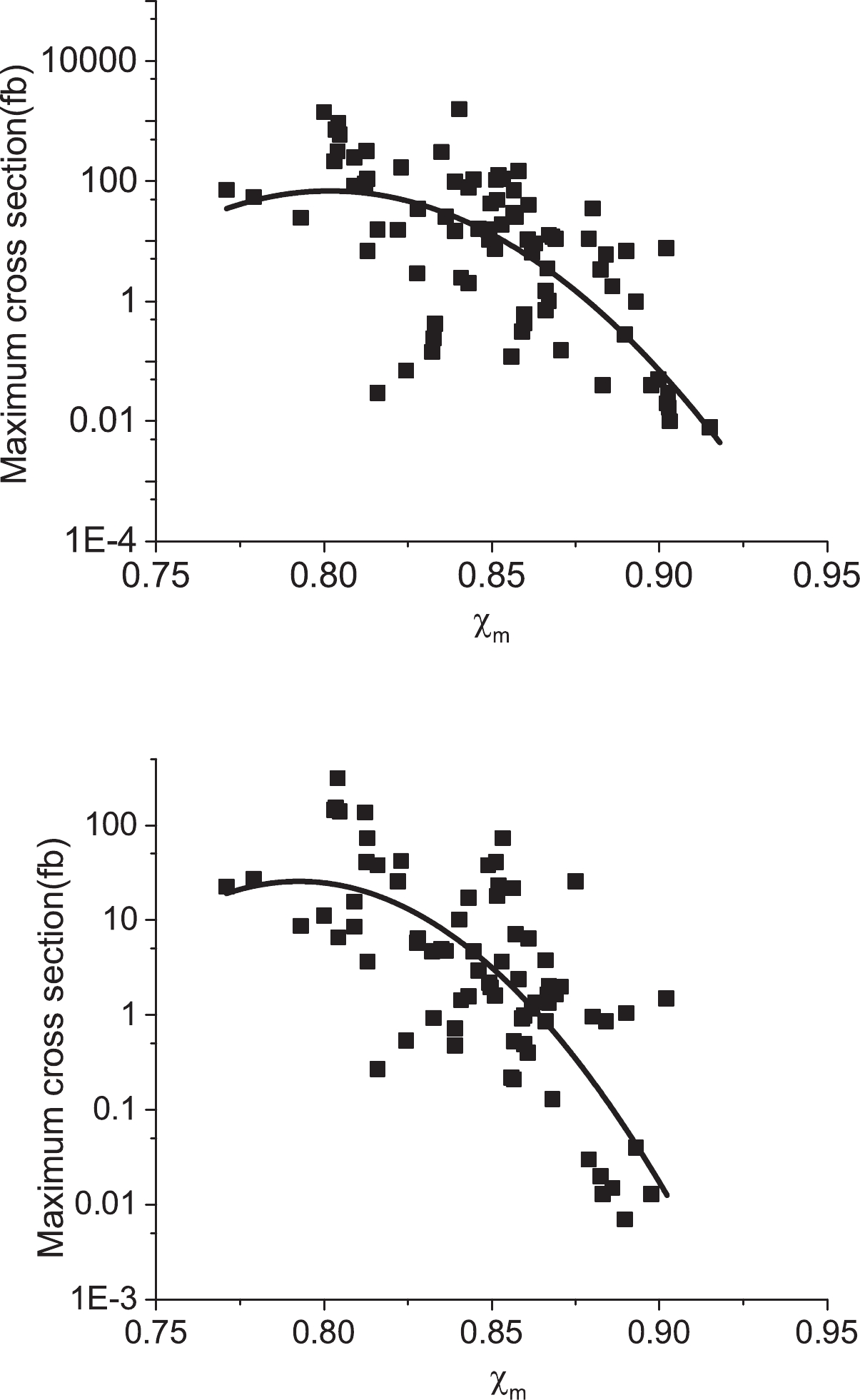
Figure 10. Variations of the maximum evaporation residue cross section versus the mean fissility. Solid curves represent the second order fit for the theoretical results.
$ \sigma_{3n}^{\rm max} = 10^{-310.23\chi_m^2+497.467\chi_m-197.58}, $

(30) and
$ \sigma_{4n}^{\rm max} = 10^{-274.834\chi_m^2+435.622\chi_m-171.211}. $

(31) We checked Eqs. (30) and (31) for the reactions 50Ti+249Bk, 48Ca+252Es, 48Ca+254Es, 47Ti+249Cf, and 50Ti+249Cf. The obtained results for 3n channel are 25.92, 70.20, 70.07, 13.36, and 24.77 fb, while the results for the 4n channel are 6.46, 23.68, 23.47, 3.16, and 6.14 fb. Eqs. (30) and (31) are important because they determine the relationship between the maximum evaporation cross section and the quasifission process (via mean fissility).
It should be noted that the synthesis of superheavy elements is influenced by dynamical effects such as friction, inertia mass, and the dissipation of the kinetic energy. These effects have been investigated in several studies [49-52]. The formation of a superheavy nucleus can be dynamically evaluated using multidimensional Langevin equations. Nuclear dissipation delays fission, which enhances prescission particle multiplicities and evaporation residue cross sections relative to the standard statistical model predictions. In Ref. [52], it is inferred that the evaporation residue cross section is a very sensitive probe for nuclear friction. The decay of superheavy elements can be evaluated using statistical models, where the Kramers factor plays a decisive role [30, 53]. The Kramers factor depends on the nuclear friction coefficient, and it is inferred as a constraint in the phase space around the saddle point owing to friction.
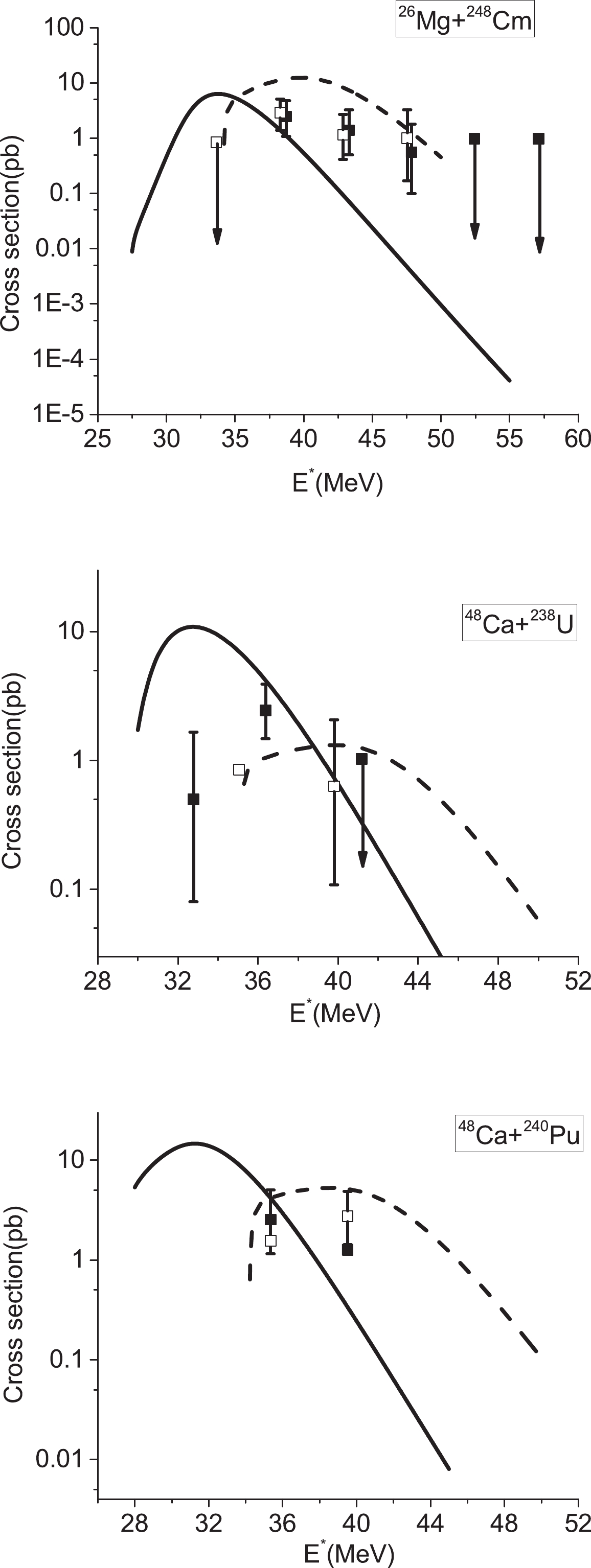
We checked the reliability of the model by comparing the evaporation residue cross section and the experimental data for the reactions 26Mg+248Cm, 48Ca+238U, 48Ca+240Pu, 48Ca+237Np, 48Ca+
$ ^{242,244} {\rm{Pu}}$ , and 48Ca+249Bk. The results of the 3n and 4n channels are presented in Figs. 11 and 12. The solid and open squares represent the experimental data for the 3n and 4n channels, respectively. The agreement between theoretical results and experimental data is satisfactory. -
We theoretically studied the effect of entrance channel on the production of supherheavy
$ ^{296}119 $ via the calculation of the evaporation residue cross sections for the 3n and 4n channels. The synthesis of superheavy elements significantly depends on the entrance channel effects. The asymmetry parameter and the Q value play important roles in the formation of superheavy elements. With an increase in the asymmetry parameter, the evaporation residue cross section of the 3n and 4n channels decreases. In addition, with an increase in$ |Q| $ , the evaporation residue cross section increases. There are linear relationships between$ \log_{10}\sigma_{3n}^{\rm max} $ and$ \log_{10}\sigma_{4n}^{\rm max} $ with the$ |Q| $ value, for the reactions$ ^{49-47} {\rm{Ti}}+ ^{247-249} {\rm{Bk}}$ ,$ ^{60-57} {\rm{Fe}}+ $ $ ^{236-239} {\rm{Np}}$ ,$ ^{44-42} {\rm{Ca}}+ ^{252-254} {\rm{Es}}$ , and$ ^{55,54,52} {\rm{Mn}}+ $ $ ^{241,242,244} {\rm{Pu}}$ . The major distinction is owing to the different capture and fusion probabilities.The sensitivity of the evaporation residue cross section to the mass models was investigated. It was observed that a change in the Q value can trigger significant changes in the evaporation residue cross section. Hence, such changes must be considered while calculating the evaporation residue cross section.
We investigated the role of mass asymmetry using the comparison of results for the reactions 44Ca+252Es and 60Fe+236Np. It was inferred that the reactions with larger mass asymmetries are more desirable for fusion than those with smaller mass asymmetries.
It should be noted that in heavy ion reactions, the role of quasifission is important and should be considered. This inference is expressed by the mean fissility parameter. By increasing the mean fissility parameter, the fusion probability decreases. In other words, for the reactions with larger values of the mean fissility parameter, the probability of the quasifission process increases. The quasifission probability is significant as it facilitates the probability analysis of the compound nucleus formation in the synthesis of superheavy nuclei. In general, to study the formation of superheavy elements, it is crucial to consider the three quantities as the asymmetry parameters, Q value and mean fissility.
The entrance channel effect on the synthesis of a superheavy element 296119
- Received Date: 2021-03-06
- Available Online: 2021-09-15
Abstract: In this study, we investigated the entrance channel effect on the evaporation residue cross section of a superheavy element 296119. Using 29 projectile-target combinations, we investigated the role of the entrance channel on the 3n and 4n evaporation channels in hot combinations. This effect can be evaluated based on the entrance channel asymmetry and Q value of complete fusion. We calculated the variation of the maximum evaporation residue cross sections (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
























 DownLoad:
DownLoad: