-
The OZI suppressed light hadron pair decays of vector charmonia occur via annihilation of three gluons, whereas the dilepton decays occur via a virtual photon. An estimation based on perturbative QCD yields
$ R={\mathcal{B}(\psi^\prime\to h)\over \mathcal{B}(J/\psi\to h)} =\frac{\mathcal{B}(\psi^\prime\to \ell^+ \ell^-)}{ \mathcal{B}(J/\psi\to \ell^+ \ell^-)} \sim 12{\text%}, $

(1) which is referred to as the "
$ 12 $ % rule". Severe violation of the "$ 12 $ % rule" was first observed in the$ \rho \pi $ channel, which was measured to be$ (0.19 \pm 0.08) $ % by Mark II Collaboration in 1983 [1]; subsequently, it was observed in more channels. This anomalous phenomenon is named "$ \rho-\pi $ puzzle." In Table 1, we list the measured branching fractions of$ J/\psi \to VP $ and$ \psi^\prime \to VP $ along with their ratios.Channel Branch ratio Channel Branch ratio Ratio $ J/\psi \to \rho \pi $ 

$ (1.69\pm0.15)\times10^{-2} $ 

$ \psi^\prime \to \rho \pi $ 

$ (3.2\pm1.2)\times10^{-5} $ 

$(0.19\pm0.08)$ %

$ J/\psi \to \rho^0 \pi^0 $ 

$ (5.6\pm0.7)\times10^{-3} $ 

$ \psi^\prime \to \rho^0 \pi^0 $ 

$ J/\psi \to K^{*+}\bar{K}^- +c.c. $ 

$ (6.0^{+0.8}_{-1.0})\times10^{-3} $ 

$ \psi^\prime \to K^{*+}\bar{K}^- +c.c. $ 

$ (2.9\pm0.4)\times10^{-5} $ 

$ (0.48\pm0.10) $ %

$ J/\psi \to K^{*0}\bar{K}^0 +c.c. $ 

$ (4.2\pm0.4)\times10^{-3} $ 

$ \psi^\prime \to K^{*0}\bar{K}^0 +c.c. $ 

$ (1.09\pm0.20)\times10^{-4} $ 

$ (2.60\pm0.54) $ %

$ J/\psi \to \omega \eta $ 

$ (1.74\pm0.20)\times10^{-3} $ 

$ \psi^\prime \to \omega \eta $ 

$<1.1\times10^{-5} $ 

$< (0.63\pm0.07)$ %

$ J/\psi \to \phi \eta $ 

$ (7.4\pm0.8)\times10^{-4} $ 

$ \psi^\prime \to \phi \eta $ 

$ (3.10\pm0.31)\times10^{-5} $ 

$(4.19\pm0.62)$ %

$ J/\psi \to \phi \eta' $ 

$ (4.6\pm0.5)\times10^{-4} $ 

$ \psi^\prime \to \phi \eta' $ 

$ (1.54\pm0.20)\times10^{-5} $ 

$ (3.35\pm0.57) $ %

$ J/\psi \to \omega \pi $ 

$ (4.5\pm0.5)\times10^{-4} $ 

$ \psi^\prime \to \omega \pi^0 $ 

$ (2.1\pm0.6)\times10^{-5} $ 

$ (4.67\pm1.43) $ %

$ J/\psi \to \rho \eta $ 

$ (1.93\pm0.23)\times10^{-4} $ 

$ \psi^\prime \to \rho \eta $ 

$ (2.2\pm0.6)\times10^{-5} $ 

$(11.40\pm3.40)$ %

$ J/\psi \to \phi \pi $ 

$ 3\times10^{-6} $ 

$ \psi^\prime \to \phi \pi^0 $ 

$<4\times10^{-7} $ 

$<13.33 $ %

$ J/\psi \to \omega \eta' $ 

$ (1.89\pm0.18)\times10^{-4} $ 

$ \psi^\prime \to \omega \eta' $ 

$ 3.2^{+2.5}_{-2.1}\times10^{-5} $ 

$ (16.93\pm13.33) $ %

$ J/\psi \to \rho \eta' $ 

$ (8.1\pm0.8)\times10^{-5} $ 

$ \psi^\prime \to \rho \eta' $ 

$ 1.9^{+1.7}_{-1.2}\times10^{-5} $ 

$ (23.46\pm21.12) $ %

Table 1. Measured branching fractions of
$ J/\psi\to PV $ and$ \psi^\prime\to PV $ , where P and V refer to pseudoscalar and vector light mesons, respectively [26].To solve the "
$ \rho-\pi $ puzzle", various schemes have been proposed. In essence, there are two different major methods to address the discrepancy between experimental measurements and the "$ 12 $ % rule" expectation: introducing some additional mechanisms in the decays of either$ \psi^\prime $ or$ J/\psi $ . For example, in Ref. [2], the author suggested that$ \psi^\prime $ is a$ 2S-1D $ mixing state rather than a pure 2S state. The destructive interference greatly suppresses the branching fractions of$ \psi^\prime\to \rho\pi $ . This type of suppression could also result from the possible final state interaction [3−14]. The estimations in previous studies suggested that the branching fractions of light hadron decays of$ J/\psi $ are enhanced by some mechanisms. For example, Freund and Nambu [15] considered that$ J/\psi $ might mix with a$ 1^{--} $ glueball with a mass of$ 1.4\sim 1.8 $ GeV that could also transit into$ \rho \pi $ . Thus, the rate of$ J/\psi\to \rho\pi $ could be enhanced by constructive interference [16−24].As an important light hadron production platform, the
$ J/\psi $ decays exhibit anomalous phenomena besides the "$ \rho-\pi $ puzzle". For example, the branching ratio of$ J/\psi\to f_0(1710)\phi\to K\bar K\phi $ was measured to be$(3.6\pm 0.6)\times 10^{-4}$ [25], which is higher than that of$J/\psi\to f_0(980)\phi$ , which is$ (3.2\pm0.9)\times10^{-4} $ [26]. Similarly, the branching ratio for$ J/\psi\to f_0(1710)\omega\to K\bar K\omega $ is also greater than that of$ J/\psi\to f_0(980)\omega $ , which are$(4.8\pm 1.1)\times10^{-4}$ [25] and$ (1.4\pm0.5)\times10^{-4} $ [27], respectively. Generally, the branching ratios for processes involving higher excited states are smaller than those only involving ground states in the$ J/\psi $ decays owing to the effect of nodes and a smaller phase space for the former processes. Thus, larger$ f_0(1710) \omega $ and$ f_0 (1710) \phi $ branching ratios indicate anomalous strong coupling between$ J/\psi $ and$ f_0(1710) \omega/ f_0(1710) \phi $ . Additionally, the thresholds of$ f_0(1710) \omega $ and$ f_0 (1710) \phi $ are 2487 MeV and 2723 MeV, respectively. In the vicinity of the$ f_0(1710) \omega $ threshold, a resonance$ X(2440) $ with$ M=2440\pm10 $ MeV and$ \Gamma=310\pm20 $ MeV [28] was reported. Recently, a resonance state around$ 2.4 $ GeV was observed in$ \pi^+\pi^-\phi $ and$ f_0(980)\phi $ invariant mass spectra with quantum number$1^{--}$ [29−34]. We hypothesize that this state may be$ X(2440) $ observed decades ago and consider it a molecular state in this study. In the vicinity of the$ f_0(1710) \phi $ threshold, a resonance$ X(2680) $ with$ M=2676\pm27 $ MeV,$ \Gamma=150 $ MeV [35] was reported. Therefore, these two states could be molecular candidates of$ f_0(1710) \omega $ and$ f_0 (1710) \phi $ , respectively.Additionally, Table 1 shows that the branching ratios of
$ \psi(2S) $ to various$ PV $ final states are in the ranges of$ (1.5\sim5.5)\times10^{-5} $ (expect$ \psi(2S) \to \phi\pi $ ). The branching ratios of$ J/\psi $ to various$ PV $ final states vary from$ 5.6\times10^{-3} $ to$ 8.1\times10^{-5} $ (expect$ J/\psi\to \phi\pi $ ). Recently,$\mathcal{B}(\psi(3686)\to \phi K^0_SK^0_S)/\mathcal{B}(J/\psi\to \phi K^0_SK^0_S)=6.0\pm1.6 $ % was experimentally measured [36]. This ratio was also suppressed in relation to the$ 12\ $ % rule. There may be some type of mechanistic effect in the decays of$ J/\psi $ to$ PV $ . Thus, we suppose that the experimentally observed state$ J/\psi $ may contain extremely small molecular state components, which only affect some hadronic decay channels of$ J/\psi $ and not others such as leptonic decays. In this scenario, we expect that a mixing scheme for$ J/\psi $ could elucidate the long standing "$ \rho-\pi $ puzzle".In this paper, we propose that the experimentally observed
$ J/\psi $ is a mixture of$ c\bar c $ and hadronic molecules$ X_{f_0(1710)\omega} $ and$ X_{f_0(1710)\phi} $ (hereinafter denoted as$ X_{f_0\omega} $ and$ X_{f_0\phi} $ , respectively). In the$ J/\psi $ light hadron decays, the molecular components break down into on-shell$ f_0(1710) $ and$ \phi(\omega) $ , which then transition into light hadron pairs by exchanging an appropriate light hadron. It is important to note that the exchanged light hadron is also on-shell, potentially increasing the rescattering contributions. Consequently, although the proportion of hadronic molecules$ X_{f_0\phi} $ and$ X_{f_0\omega} $ in$ J/\psi $ state may be small, they still have a significant impact on the light hadron decays.The rest of this paper is organized as follows. After the introduction, we analyze the mixing between
$ c\bar c $ and hadronic molecules in Sec. II. Then, we estimate the fractions of$ X_{f_0\phi} $ and$ X_{f_0\omega} $ components in$ J/\psi $ in Sec. III. In Sec. IV, we calculate branching fractions of$ J/\psi\to VP $ considering the components$ X_{f_0\phi} $ and$ X_{f_0\omega} $ . The last section presents a short summary. -
Based on the ansatz that the physical states
$ X(2440) $ ,$ X(2680) $ , and$ J/\psi $ are the mixtures of the molecular states$ X_{f_0\omega} $ ,$ X_{f_0\phi} $ and the charmonium$ c\bar c(1S) $ through a unitary matrix U transformation, we have the following relation:$ \begin{array}{*{20}{l}} \left( \begin{array}{ccc} |X(2440)\rangle \\ |X(2680)\rangle \\ |J/\psi\rangle \\ \end{array} \right) = U \left( \begin{array}{ccc} |X_{f_0\omega }\rangle \\ |X_{f_0\phi }\rangle \\ |c\bar c(1S)\rangle \\ \end{array} \right) \end{array} $

(2) where U is a unitary matrix with compact form as
$ \begin{array}{*{20}{l}} U=\left( \begin{array}{ccc} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33}\\ \end{array} \right). \end{array} $

(3) Thus, we have
$ \begin{array}{*{20}{l}} |J/\psi\rangle= c_{31} | X_{f_0 \omega}\rangle + c_{32} | X_{f_0 \phi}\rangle + c_{33} | c\bar{c}(1S)\rangle. \end{array} $

(4) The mass of
$ \psi^\prime $ notably differs from that of the molecular states$ X_{f_0 \omega} $ and$ X_{f_0 \phi} $ . Thus, the mixing between$ c\bar{c} (2S) $ and the molecular states should be dismissible. One can suppose that the magnitudes of$ c\bar{c}(1S) \to PV $ and$ c\bar{c}(2S) \to PV $ satisfy the "$ 12 $ % rule", while the violations at least partly result from the mixing of the charmonium and light meson-meson molecular states. To estimate the mixing between the charmonium and the molecular states, we first investigated the spectra of charmonium and molecular states individually. -
According to Ref. [37], the mass spectra of charmonia can be obtained by solving Schrödinger equation with one-gluon-exchange plus a linear confinement potential which manifests the non-perturbative QCD effects. The Hamiltonian for
$1^{--}$ states is$ \begin{array}{*{20}{l}} H=H_0 +H' \end{array} $

(5) with
$ \begin{array}{*{20}{l}} H_0=\sum\limits^2_{i=1} \left(m_i+\dfrac{p^2}{2m_i}\right)+\dfrac{-4}{3}\dfrac{\alpha_s (r)}{r} +\kappa r + c \end{array} $

(6) and
$ \begin{array}{*{20}{l}} H'=\dfrac{1}{4}\dfrac{32\pi}{9m_1 m_2}\alpha_s(r)\left(\dfrac{\sigma}{\sqrt\pi}\right)^3 {\rm e}^{-\sigma^2 r^2}, \end{array} $

(7) where
$ \kappa=0.18 $ GeV$ ^2 $ ,$ \sigma=3.0996 $ GeV, and$ m_c=1.628 $ GeV [37]. The constant c denotes zero-point energy set by fitting experimental data. From the aforementioned Hamiltonian, the mass of the$ 1S $ and$ 2S $ states can be obtained, while their mass difference is independent of the constant c. By setting$ \psi(2S) $ to be a pure$ c \bar{c}(2S) $ state, i.e.,$ m_{c \bar{c}(2S)}=(m_{\psi(2S)})_{\mathrm{exp}} $ , one has$ c=(448.93 \pm 0.06) $ MeV. For this value of c,$ m_{c\bar c(1S)}=(3088.19 \pm 0.06) $ MeV, which is approximately 10 MeV below the PDG average [26]. Additionally, the masses of the ground and first excited states of$ c\bar c(0^-) $ are$ m_{\eta_c}=3022.02 $ MeV and$m_{\eta_c(2S)}= 3641.90$ MeV, respectively. -
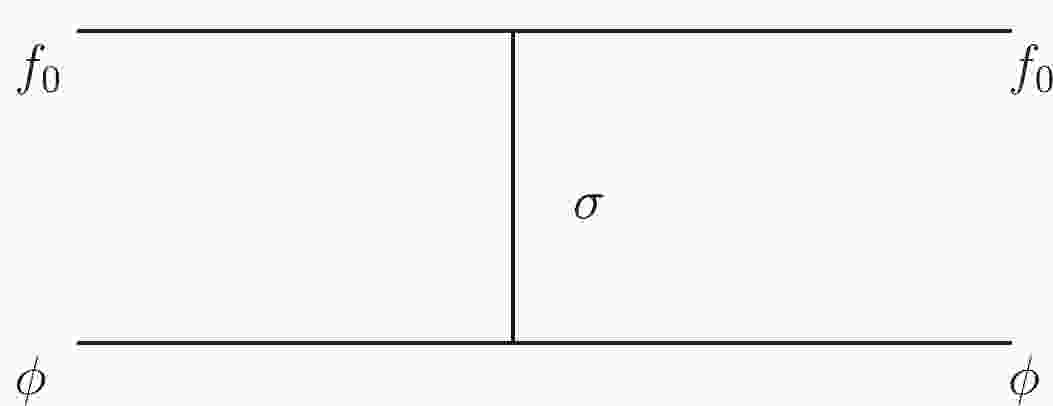
The mass spectra of the light meson-meson bound states can also be estimated by solving the non-relativistic Schrödinger equation, where the potentials between the meson components could be induced by one-boson exchange, as shown in Fig. 1 [38, 39]. In Refs. [40, 41], the authors considered σ and
$ f_0(980) $ as mixture of$ (u\bar u+d\bar d)/ \sqrt2 $ and$ s\bar s $ . Thus, we consider that σ can couple with$ f_0(1710) $ and ϕ. Taking the$ f_0(1710) \phi $ system as an example, one can transform the scattering amplitude of the elastic scattering process in the momentum space into a non-relativistic effective potential in the coordinate space. To obtain the amplitude corresponding to the diagram in Fig. 1, the following effective Lagrangians are employed:$ \begin{array}{*{20}{l}} &\mathcal{L}_{f_0 f_0 \sigma}= g_\sigma m_{f_0} \langle f_0 f_0 \sigma \rangle ,\end{array} $

(8) $ \begin{array}{*{20}{l}} &\mathcal{L}_{\phi \phi \sigma}= g_\sigma m_{\phi} \langle \phi \phi \sigma \rangle. \end{array} $

(9) Unlike hadronic scattering, where incoming and outgoing mesons are on their mass shells, the ingredient mesons in the bound state are off-shell; thus, a form factor which partly compensates the off-shell effect is introduced as follows:
$ \mathcal{F} (q^2, m^2_\sigma)=\frac{\Lambda^2-m^2_\sigma}{\Lambda^2-q^2}, $

(10) where
$ m_\sigma $ and q are the mass and four momenta of the exchanged σ meson, respectively. The resultant effective potential reads as [38]$ \begin{array}{*{20}{l}} V(\Lambda, m_\sigma, r) =-g^2_\sigma \left[\dfrac{1}{4\pi r}\left({\rm e}^{-m_\sigma r} -{\rm e}^{-\Lambda r}\right) - \dfrac{\Lambda^2 -m_\sigma^2}{8\pi \Lambda} {\rm e}^{-\Lambda r} \right]. \end{array} $

(11) According to Ref. [38], the relations
$ g_\sigma=2/3 g_{\sigma NN} $ and$ g_{\sigma NN}^2/4\pi=5.69 $ are assumed. However, note that in Ref. [38] the mesons in the corresponding effective Lagrangians are all ground states, namely$ f_0(980) $ . However,$ f_0(1710) $ is a higher excited state in the$ f_0 $ family. For σ exchanging, the interaction between heavy and light quarks is ignored, in general; in other words, only the contributions of light quarks are considered [42]. Thus, for meson scattering, the effective coupling constant is$ 2/3 $ times smaller than that from baryons. This is suitable for$ f_0(1710) $ as well. Moreover, according to Refs. [43, 44], we have$ g^2/4\pi=3.20 $ ,$ 4.45 $ , and$ 0.085 $ for three$ N^*(1440)N\sigma $ ,$ N^*(1680)N\sigma $ , and$ N^*(1710)N\sigma $ vertices, respectively. Thus, to obtain an estimate, we adopt$g_\sigma(f_0(1710))\sim g_\sigma(f_0(980))$ here. According to Ref. [39], we set$ \Lambda=1.5\sim2.0 $ GeV.After setting
$ m_{f_0(1710)}=1704 $ MeV and$ m_\phi=1019 $ MeV, we obtain$ m_{X_{f_0\phi}}=2647\sim 2701 $ MeV. Adopting a similar method, we obtain$ m_{X_{f_0\omega}}=2440\sim2477 $ MeV. -
In the present estimation, we impose the following conditions for the unitray matrix as mandatory conditions: the determinant of the matrix must be unity, and all the matrix elements must be real. According to Eq. (2), the unitary matrix U transforms the unphysical states
$|X_{f_0\omega}\rangle,\; |X_{f_0\phi}\rangle$ and$ |c\bar c(1S)\rangle $ into the physical eigenstates$|X(2440)\rangle,\; |X(2680)\rangle$ and$ |J/\psi\rangle $ and simultaneously diagonalizes the mass matrix$ \tilde M_q $ as$ \begin{array}{*{20}{l}} M_{\mathrm{mass}}=U \tilde M_q U^\dagger \end{array} $

(12) with
$ \begin{array}{*{20}{l}} M_{\rm mass}= \left( \begin{array}{ccc} m_{X(2440)} & 0 & 0 \\ 0 & m_{X(2680)} & 0 \\ 0 & 0 & m_{J/\psi} \\ \end{array} \right), \end{array} $

(13) and
$ \begin{array}{*{20}{l}} \tilde M_q= \left( \begin{array}{ccc} m_{X_{f_0\omega}} & \lambda_1 & \lambda_2 \\ \lambda_1 & m_{X_{f_0\phi}} & \lambda_3 \\ \lambda_2 & \lambda_3 & m_{c\bar c(1S)} \\ \end{array} \right). \end{array} $

(14) Namely,
$ m_{X(2440)},\: m_{X(2680)} $ , and$ m_{J/\psi} $ are the three roots of equation,$ \begin{split} \\[-8pt] &m^3 - m^2\left(m_{c\bar c(1S)}+m_{X_{f_0\phi}}+m_{X_{f_0\omega}}\right) +m\left(m_{c\bar c(1S)} m_{X_{f_0\omega}}+ m_{c\bar c(1S)} m_{X_{f_0\phi}}+ m_{X_{f_0\omega}} m_{X_{f_0\phi}} -\lambda_1^2- \lambda_2^2- \lambda_3^2\right)\\ & +\left(\lambda_1^2 m_{c\bar c(1S)}+ \lambda_2^2 m_{X_{f_0\phi}}+ \lambda_3^2 m_{X_{f_0\omega}}- 2\lambda_1\lambda_2\lambda_3- m_{X_{f_0\omega}} m_{X_{f_0\phi}} m_{c\bar c(1S)}\right) =0. \\ \end{split}$ 
(15) Generally, we have three unknown variables in the Hermitian matrix
$ \tilde M_q $ , namely$ \lambda_1,\; \lambda_2 $ , and$ \lambda_3 $ . While there are three independent equations by which we set these three unknown variables. In principle, we could simultaneously set the values of three non-diagonal matrix elements by setting the physical masses of$ m_{X(2440)},\: m_{X(2680)} $ , and$ m_{J/\psi} $ as the eigen-values of the mass matrix. However, note that the secular equation cannot be solved in a normal manner. Thus, we adopt an alternative method to obtain the ranges of three non-diagonal matrix elements. We pre-determine the ranges of the elements of the unitary transformation matrix U that diagonalizes the mass matrix$ \tilde M_q $ and then substitute them into the secular equation to check whether the equation can be satisfied, that is, whether all the requirements (unitarity, etc.) are fulfilled. Then, we can obtain the unitary transformation matrix U and mass matrix$ \tilde M_q $ as$ \begin{array}{*{20}{l}}\\ U=\left( \begin{array}{ccc} -0.990\sim-0.985 & -0.147\sim-0.049 & -0.099\sim0.141 \\ 0.056\sim0.159 & -0.976\sim-0.997 & 0.050\sim0.150 \\ 0.061\sim0.133 & 0.057\sim0.161 & 0.985\sim0.990 \\ \end{array} \right) \end{array} $ 
(16) and
$ \begin{array}{*{20}{l}} M_q=\left( \begin{array}{ccc} 2438\sim2463 & -33\sim-7 & 45\sim86 \\ -33\sim-7 & 2645\sim2708 & 24\sim74 \\ 45\sim86 & 24\sim51 & 3079\sim3087 \\ \end{array} \right) \; \mathrm{MeV}. \end{array} $

(17) From these two matrices, the pre-determined ranges of the mass of
$ X_{f_0\omega} $ and$ X_{f_0\phi} $ are$ (2438\sim 2463) $ MeV and$ (2645 \sim 2708) $ MeV. respectively, which are very close to those obtained by potential model estimations. Moreover, the value of$ m_{c\bar{c}(1S)} $ is fitted to be$ (3079\sim3087)\; \mathrm{MeV} $ , which is also very close to the one obtained from the quark model, which is$ (3088.19 \pm 0.06) $ MeV. -
Besides the contributions from
$ c\bar{c} $ annihilation, the molecular components in$ J/\psi $ should also have an important effect on the decay$ J/\psi \to PV $ . For the molecular state, its components transit into light pseoduscalar and vector mesons exchanging a proper light meson. This meson loop connects the molecular and final states. Taking$ |f_0 \phi\rangle $ as an example, the Feynman diagrams contributing to the decays$ X_{f_0 \phi} \to PV $ are presented in Fig. 2. In the present study, these diagram were estimated at the hadron level, and the relevant vertices read [38]$\begin{split} \langle X_{f_0 V} | f_0 V\rangle &= g_X \;\Lambda_0\; X_{f_0 V} V f_0 ,\\ \langle f_0 | PP\rangle &= g_{f_0} m_P\; \mathrm{Tr}[ PP] f_0,\\ \langle f_0 | VV\rangle &= g_{f_0} m_V\; \mathrm{Tr}[ VV] f_0,\\ \langle\phi | PV\rangle &= \frac{G}{\sqrt2}\;\varepsilon^{\lambda\nu\alpha\beta} \mathrm{Tr}[ \partial_\lambda V_\nu \partial_\alpha V_\beta P ], \end{split} $

(18) $ \Lambda_0=1 $ GeV is a dimensional parameter to ensure that the effective coupling constant$ g_X $ is dimensionless;$ m_V $ and$ m_P $ denote the masses of vector and pseudoscalar mesons, respectively. The matrix form of the psedoscalar and vector mesons are$ \begin{array}{*{20}{l}} &P = \left( \begin{array}{ccc} \dfrac{\pi^0}{\sqrt2}+ \dfrac{\eta_8}{\sqrt6}+ \dfrac{\eta_1}{\sqrt3} & \pi^+ & K^+ \\ \pi^- & -\dfrac{\pi^0}{\sqrt2}+ \dfrac{\eta_8}{\sqrt6}+ \dfrac{\eta_1}{\sqrt3} & K^0 \\ K^- & \bar K^0 & -\dfrac{2\eta_8}{\sqrt6}+ \dfrac{\eta_1}{\sqrt3} \\ \end{array} \right) \\ \\ &V = \left( \begin{array}{ccc} \dfrac{\rho^0}{\sqrt2}+ \dfrac{\omega_8}{\sqrt6}+ \dfrac{\omega_1}{\sqrt3} & \rho^+ & K^{*+} \\ \rho^- & -\dfrac{\rho^0}{\sqrt2}+ \dfrac{\omega_8}{\sqrt6}+ \dfrac{\omega_1}{\sqrt3} & K^{*0} \\ K^{*-} & \bar K^{*0} & -\dfrac{2\omega_8}{\sqrt6}+ \dfrac{\omega_1}{\sqrt3} \\ \end{array} \right) . \label{} \end{array} $ 
with mixing parameters
$\begin{split} \eta_8&= \eta\cos\theta+ \eta'\sin\theta,\quad \eta_1= -\eta\sin\theta+ \eta'\cos\theta,\\ \omega_8&= \omega\cos\varphi+ \phi\sin\varphi,\quad \omega_1=-\omega\sin\varphi+ \phi\cos\varphi, \end{split} $

(19) and mixing angles θ and φ fulfilling
$ \sin\theta=-0.31\pm0.11 $ [26] and$ \sin\varphi=-0.76 $ [45].According to the above vertices, we can obtain the amplitudes corresponding to diagrams (a) and (b) in Fig. 2,
$ \begin{split} \mathcal{M}_a =& \int\frac{{\rm d}^4k}{(2\pi)^4} \frac{g_{f_0} m_P}{(p_1+k)^2- m^2_{f_0} } \frac{g_X g^{\mu\nu} \varepsilon_X^\mu }{(p_2-k)^2- m^2_\phi } \\ &\times \dfrac{g_{\phi PV} \varepsilon^{\lambda\nu\alpha\beta} (p_2-k)^\lambda p_2^\alpha \varepsilon^{*^\beta}_V }{k^2-m_P^2}\\ \mathcal{M}_b =& \int\frac{{\rm d}^4k}{(2\pi)^4} \dfrac{g_{\phi PV} \varepsilon^{\lambda\nu\alpha\sigma} (p_1-k)^\lambda k^\alpha }{(p_1-k)^2- m^2_\phi } \dfrac{g_X g^{\mu\nu} \varepsilon_X^\mu }{(p_2+k)^2- m^2_{f_0} }\\ &\times \dfrac{g_{f_0} m_V g^{\sigma\beta} \varepsilon^{*^\beta}_V }{k^2-m_V^2}, \end{split}$

(20) respectively.
-
Considering the
$S U(3)$ symmetry, the coupling constants in the hadron vertex in Eq. (18) satisfy$ G=(3g^2)/ (4\pi^2 f_\pi) $ ,$ f_\pi=93 $ MeV, and$ g=(12)/(2\sqrt2) $ [38]. In the mixing scenario,$ X(2240) $ and$ X(2680) $ are molecular states with a very small$ c\bar{c}(1S) $ component, and the decays of$ c\bar{c} $ components into light$ PV $ are further suppressed by the OZI suppression rule. Thus, we estimate$ X(2240)/X(2680) \to PV $ ; the$ c\bar{c}(1S) $ components can be ignored and$ X(2240)/ X(2680) $ can be considered as a pure$ f_0(1710) \omega/f_0(1710) \phi $ molecular state. In the molecular scenario, the coupling constant of the molecular state and its components can be estimated as follows [46, 47]:$ \begin{array}{*{20}{l}} g_{X}^2 = \dfrac{16\pi(m_{f_0(1710)}+ m_V)^2}{\mu}\sqrt{2\mu E_B} \dfrac{1}{ \Lambda_0^2}. \end{array} $

(21) where
$ \mu=(m_{f_0(1710)} m_V)/(m_{f_0(1710)}+ m_V) $ and$ E_B=m_{f_0(1710)}+ m_V-m_{X} $ . Setting$ m_{f_0(1710)}=1704 $ MeV,$ m_\omega=783 $ MeV,$ m_\phi=1019 $ MeV,$ m_{X_{f_0\omega}}=(2440\sim 2477) $ MeV and$m_{X_{f_0\phi}}= (2647 \sim 2701)$ MeV, we obtain$ g_{X_{f_0\omega}}=9.6\pm1.8 $ and$ g_{X_{f_0\phi}}= 11.7\pm1.8 $ .Concerning the value of the coupling constant
$ g_{f_0} $ , reproducing the experimental data$ \Gamma(f_0(1710))=123 $ MeV [26] and$ \mathcal{B}(f_0(1710) \to KK) = 0.38\pm0.19 $ [48],$ \mathcal{B}(f_0(1710) \to \eta\eta)= 0.22\pm0.12 $ [49] and$ \mathcal{B}(f_0(1710) \to \pi\pi)= 0.039\pm 0.024 $ [48], we have$ g_{f_0}=2.24\pm 0.56 $ ,$ g_{f_0}=3.17\pm 0.86 $ , and$ g_{f_0}= 4.68\pm 1.44 $ , respectively. As a matter of fact [50], the three experimental values were not reliably measured, and the values of$ g_{f_0} $ obtained from different experimental data are not consistent with each other. Thus, in our calculations, we considered$ g_{f_0} $ as a free parameter for the first step.It should be noted that some channels in Table 1 are isospin violated. Thus, in the present study, some isospin violated vertices were also considered. From the branching fraction
$ \mathcal{B}(\phi \to \omega\pi)_{\rm exp}= (4.7\pm0.5)\times10^{-5} $ , we obtain$ g_{\phi\omega\pi}=0.04 $ . Concerning the other involved isospin violation vertices, for example$ g_{\phi\rho\eta} $ ,$ g_{\phi\rho\eta'} $ ,$ g_{\omega\rho\eta} $ ,$ g_{\omega\rho\eta'} $ and$ g_{\omega\omega\pi} $ , given the lack of corresponding experimental data, we consider that they are of the same order as$ g_{\phi\omega\pi} $ and set$ g_{\phi\rho\eta}=g_{\phi\rho\eta'}=g_{\omega\rho\eta}=g_{\omega\rho\eta'}=g_{\omega\omega\pi}=0.04 $ in the present calculations. -
As we discussed in the previous subsection, the coupling constant
$ g_{f_0} $ is considered as a free parameter for the first step. The partial width of$ X(2440) \to VP $ satisfies$\begin{split} \Gamma(X(2440) \to VP)_{\mathrm{Theory} } =& \frac{1}{2\;m_{X(2440)} } \int {\rm d}\Pi_2 \\& |c_{11} \; \mathcal{M}(X_{f_0\omega} \to VP) \end{split} $

$\begin{split} & + c_{12}\; \mathcal{M}(X_{f_0\phi} \to VP)\\ & + c_{13}\; \mathcal{M}(c\bar c(1S) \to VP)|^2, \end{split} $

(22) with the amplitude for
$ c \bar c(1S)\to PV $ being$ \begin{array}{*{20}{l}} \mathcal{M}(c\bar c(1S) \to VP)=g_{c\bar c PV} \varepsilon^{\lambda\nu\alpha\beta} p_\psi^\lambda \varepsilon^\nu_\psi p_V^\alpha \varepsilon^{*^\beta}_V . \end{array} $

(23) The constants
$ g_{c\bar c PV} $ are obtained by fitting$ \mathcal{B}(c\bar c(1S)\to PV)_{\mathrm{Exp}} $ data with the relation$ \begin{array}{*{20}{l}} \mathcal{B}(c\bar c(1S)\to PV)_{\mathrm{Exp}}= {\mathcal{B}(\psi^\prime\to PV)_{\mathrm{Exp}}}/{(13.3\%\times c_{33}^2)}, \end{array} $

(24) where
$ 13.3\ $ % comes from$ \mathcal{B}(\psi'\to l^+l^-)_{\mathrm{ Exp}}/\mathcal{B}(J/\psi\to l^+l^-)_{\mathrm{ Exp}} $ with$ l=e,\;\mu $ . Table 2 lists the corresponding data and values. The partial width of$ X(2680) \to VP $ is similar, and we omit it for simplification.Decay channel Branch ratio Decay channel Branch ratio Ratio $J/\psi \to e^+e^-$ 

$ (5.971\pm0.032)\times10^{-2}$ 

$\psi' \to e^+e^-$ 

$(7.93\pm0.17)\times10^{-3}$ 

$(13.28\pm0.29)$ %

$J/\psi \to \mu^+\mu^-$ 

$(5.961\pm0.033)\times10^{-2}$ 

$\psi' \to \mu^+\mu^-$ 

$(8.0\pm0.6)\times10^{-3}$ 

$(13.42\pm1.01)$ %

Table 2. Experimental data of
$ J/\psi $ and$ \psi' $ to lepton pair [26].Setting
$ \Gamma_{X(2440)}=310 $ MeV and$ \Gamma_{X(2680)}=150 $ MeV [26], one can obtain the branching fractions of$ X(2240)/ X(2680) \to PV $ . Next, we briefly discuss the effective coupling constant$ g_{f_0} $ . Although its value is not well measured, its approximate range is$ 2\sim4 $ . Here, we set$ g_{f_0}=2 $ and$ 3 $ as examples and list the estimated results in Table 3.Channel $\mathcal{B}(X(2440)\to PV)_{\rm theory}$ 

$\mathcal{B}(X(2680)\to PV)_{\rm theory}$ 

$g_{f_0}=2$ 

$g_{f_0}=3$ 

$g_{f_0}=2$ 

$g_{f_0}=3$ 

$\rho^0 \pi^0$ 

$(7.97\pm0.14)\times10^{-3}$ 

$(1.78\pm0.03)\times10^{-2}$ 

$(1.45\pm0.73)\times10^{-3}$ 

$(3.21\pm1.59)\times10^{-3}$ 

$K^{*+}\bar{K}^-$ 

$(1.05\pm0.18)\times10^{-3}$ 

$(2.31\pm0.40)\times10^{-3}$ 

$(1.29\pm0.09)\times10^{-2}$ 

$(2.88\pm0.19)\times10^{-2}$ 

$K^{*0}\bar{K}^0$ 

$(1.13\pm0.20)\times10^{-3}$ 

$(2.42\pm0.43)\times10^{-3}$ 

$(1.31\pm0.10)\times10^{-2}$ 

$(2.92\pm0.21)\times10^{-2}$ 

$\omega \eta$ 

$(2.89\pm0.13)\times10^{-4}$ 

$(6.22\pm0.25)\times10^{-4}$ 

$(1.35\pm0.51)\times10^{-4}$ 

$(2.85\pm1.04)\times10^{-4}$ 

$\phi \eta $ 

$(4.85\pm1.38)\times10^{-5}$ 

$(9.07\pm2.52)\times10^{-5}$ 

$(9.16\pm0.87)\times10^{-5}$ 

$(1.98\pm0.16)\times10^{-3}$ 

$\phi \eta'$ 

$(2.15\pm0.83)\times10^{-6}$ 

$(2.39\pm0.96)\times10^{-6}$ 

$(1.19\pm0.40)\times10^{-5}$ 

$(2.08\pm0.55)\times10^{-5}$ 

$\omega \pi$ 

$(3.19\pm0.97)\times10^{-6}$ 

$(3.68\pm1.07)\times10^{-6}$ 

$(3.75\pm2.42)\times10^{-6}$ 

$(4.85\pm2.87)\times10^{-6}$ 

$\rho \eta$ 

$(2.62\pm0.87)\times10^{-6}$ 

$(2.71\pm0.89)\times10^{-6}$ 

$(2.48\pm1.87)\times10^{-6}$ 

$(2.69\pm1.98)\times10^{-6}$ 

$\omega \eta'$ 

$(1.41\pm0.26)\times10^{-5}$ 

$(2.21\pm0.34)\times10^{-5}$ 

$(1.13\pm0.74)\times10^{-5}$ 

$(1.74\pm1.07)\times10^{-5}$ 

$\rho \eta'$ 

$(2.16\pm0.73)\times10^{-6}$ 

$(2.19\pm0.74)\times10^{-6}$ 

$(1.95\pm1.52)\times10^{-6}$ 

$(2.04\pm1.56)\times10^{-6}$ 

$\omega K\bar K$ 

$(9.92\pm0.04)\times10^{-2}$ 

$(2.23\pm0.01)\times10^{-1}$ 

$\phi K\bar K$ 

$(2.02\pm0.01)\times10^{-1}$ 

$(4.55\pm0.02)\times10^{-1}$ 

Table 3. Branching fractions of
$ X(2440) $ and$ X(2680) $ decaying into a light pseudoscalar and vector meson, where we set$ g_{f_0}=2 $ and$ 3 $ as examples. The branching fractions of the decay channels$ X(2440)\to \omega K\bar K $ and$ X(2680)\to \phi K\bar K $ are also listed. The uncertainties of the present estimations result from$ c_{ij} $ .For
$ X(2440) $ , our estimations indicate that the branching ratio of$ X(2440)\to \rho \pi^0 $ is up to the order of$ 10^{-2} $ , and the one for$ X(2440)\to K^{\ast0} \bar{K}^0 $ is approximately one order of magnitude smaller than that of$ X(2440)\to \rho \pi^0 $ . The branching fractions of the other seven$ PV $ channel are even smaller. Regarding$ X(2680) $ , the branching fractions of$ K^\ast \bar{K}^0 $ channel are of the order of$ 10^{-2} $ , which is approximately one order of magnitude larger than that of$ X(2680)\to \rho \pi^0 $ .Besides the two body
$ PV $ decay process, the branching ratios of the three body decay processes, that is,$ X(2440)\to \omega K\bar{K} $ and$ X(2680)\to \phi K\bar{K} $ , are also estimated, where$ K\bar{K} $ are the daughter particles of$ f_0(1710) $ . Our estimations indicate that the branching fractions of these three body decay processes are of the order of$ 10^{-1} $ . To date, the decay properties of$ X(2440) $ and$ X(2680) $ have been poorly measured; we hope our results shown in Table 3 can be confirmed by future measurements from BESIII, BELLE, LHCb, and probably the future charm-tau factory (FCTF). -
In the mixing scheme, the physical
$ J/\psi $ state is the mixture of$ |c\bar{c}(1S)\rangle $ ,$ |X_{f_0 \omega}\rangle $ and$ |X_{f_0 \phi}\rangle $ molecular states, as shown in Eq. (4). Considering the fact that the molecular state$ X_{f_0 \omega}/X_{f_0 \phi} $ can decay into a light pseudoscalar and a light vector meson, as shown in the previous subsection, it can be concluded that the$ X_{f_0 \omega}/X_{f_0 \phi} $ molecular components in the$ J/\psi $ state should also contribute to the processes$ J/\psi \to PV $ , and the partial widths of$ J/\psi \to VP $ satisfy$\begin{split} \Gamma(J/\psi \to VP)_{\mathrm{Theory} } =& \frac{1}{2\;m_{J/\psi}} \int {\rm d}\Pi_2 \\ & \times |c_{31} \; \mathcal{M}(X_{f_0\omega} \to VP)\\ & + c_{32}\; \mathcal{M}(X_{f_0\phi} \to VP)\\ & + c_{33}\; \mathcal{M}(c\bar c(1S) \to VP)|^2 . \end{split} $

(25) Given that the mass of
$ \psi^\prime $ is notably larger than those of the$ X_{f_0 \omega} $ and$ X_{f_0 \phi} $ molecular states,$ \psi^\prime $ could be considered as a pure$ c\bar{c} (2S) $ charmonium state. Then, the partial width of$ \psi^\prime \to PV $ should be dominated by$ c\bar{c} $ annihilation. In the present calculations, we estimate$ \Gamma(c \bar c(1S) \to VP) $ using$ \Gamma(\psi^\prime \to VP) $ and the "$ 12 $ % rule". The terms of$ \Gamma(X_{f_0 \omega}\to VP) $ and$ \Gamma(X_{f_0 \phi}\to VP) $ are estimated in the same manner as the molecular decay. However, in the physical$ J/\psi $ state,$ X_{f_0 \omega} $ and$ X_{f_0 \phi} $ are off-shell. Thus, the coupling constants$ g_X $ estimated in Eq. (21) are not valid, and we set$ g_X $ as an undetermined parameter. Regarding the factors$ c_{31} $ ,$ c_{32} $ , and$ c_{33} $ , they are determined by the unitary transformation matrix U in Eq. (16) as follows:$ \begin{array}{*{20}{l}} \begin{aligned} c_{31}^2&=0.0107\pm0.0070,\\ c_{32}^2&=0.0146\pm0.0114,\\ c_{33}^2&=0.9747\pm0.0050.\\ \end{aligned} \end{array} $

For better understanding of the contributions of the different terms in Eq. (25), we have the following relations and definitions:
$\begin{split} \mathcal{B}(c\bar c(1S)\to PV)_{\mathrm{Theory}}&= {\mathcal{B}(\psi^\prime\to PV)_{\mathrm{Exp}}}/{(13.3\%} \times c_{33}^2), \\ \mathcal{B}(J/\psi\to PV)_{\mathrm{Theory}}&= \mathcal{B}(c\bar c(1S)\to PV)_{\mathrm{Theory}} + \mathcal{B}(X\to PV)_{\mathrm{Theory}} +\mathcal{B}(INT\to PV)_{\mathrm{Theory}}, \end{split}$ 
(26) where
$ INT $ denotes the interference terms that form molecular states with$ c\bar c(1S) $ . The estimated branching fractions defined above are listed in Table 4. In this table, the branching fraction of the process$ \psi^\prime \to \rho^0 \pi^0 $ is estimated by$ \mathcal{B}(\psi^\prime\to \rho^0\pi^0)=\mathcal{B}(\psi^\prime \to \rho\pi)/3 $ . The decay processes$ \psi^\prime \to \phi \pi $ and$ J/\psi \to \phi \pi $ are not included because the branching fractions of these two channels are extremely small. Concerning the decay channels$ J/\psi(\psi^\prime)\to \rho\eta $ ,$ J/\psi(\psi^\prime)\to \omega\eta^\prime $ , and$ \psi^\prime \to \rho \eta^\prime $ , according to Table 1, they satisfy the$ 12\ $ % rule within the experimental error range. Thus, we estimate that the components of the$ X\to \rho\eta $ ,$ X\to \omega\eta' $ , and$ X\to \rho\eta' $ contributions in$ J/\psi $ are not larger than$ 10^{-5} $ . Therefore, our estimations in Table 4 are consistent with the expectations.Channel $\mathcal{B}(\psi'\to PV)_{\mathrm{Exp}}$ 

$\mathcal{B}(J/\psi\to PV)_{\mathrm{Exp}}$ 

$\mathcal{B}(c\bar c(1S)\to PV)_{\mathrm{Theory}}$ 

$\mathcal{B}(X\to PV)_{\mathrm{Theory}}/(g_{f_0}g_X)^2$ 

$\mathcal{B}(INT\to PV)_{\mathrm{Theory}}/(g_{f_0}g_X)$ 

$\rho^0 \pi^0$ 

$(1.1\pm0.4)\times10^{-5}$ 

$(5.6\pm0.7)\times10^{-3}$ 

$(7.82\pm2.93)\times10^{-5}$ 

$(3.03\pm2.02)\times10^{-3}$ 

$(9.89\pm3.76)\times10^{-4}$ 

$K^{*+}\bar{K}^-$ 

$(1.5\pm0.2)\times10^{-5}$ 

$(3.0\pm0.5)\times10^{-3}$ 

$(1.06\pm0.15)\times10^{-4}$ 

$(3.29\pm2.42)\times10^{-3}$ 

$(1.21\pm0.53)\times10^{-3}$ 

$K^{*0}\bar{K}^0$ 

$(5.5\pm1.0)\times10^{-5}$ 

$(2.1\pm0.2)\times10^{-3}$ 

$(3.99\pm0.73)\times10^{-4}$ 

$(3.29\pm2.42)\times10^{-3}$ 

$(2.34\pm1.02)\times10^{-3}$ 

$\omega\eta$ 

$ <1.1\times10^{-5}$ 

$(1.74\pm0.20)\times10^{-3}$ 

$ <8.06\times10^{-5}$ 

$(1.96\pm1.33)\times10^{-4}$ 

$(2.52\pm0.98)\times10^{-4}$ 

$\phi\eta $ 

$(3.10\pm0.31)\times10^{-5}$ 

$(7.4\pm0.8)\times10^{-4}$ 

$(2.27\pm0.23)\times10^{-4}$ 

$(2.10\pm1.57)\times10^{-4}$ 

$(4.40\pm1.98)\times10^{-4}$ 

$\phi\eta'$ 

$(1.54\pm0.20)\times10^{-5}$ 

$(4.6\pm0.5)\times10^{-4}$ 

$(1.13\pm0.15)\times10^{-4}$ 

$(2.26\pm1.74)\times10^{-6}$ 

$(3.29\pm1.55)\times10^{-5}$ 

$\omega\pi$ 

$(2.1\pm0.6)\times10^{-5}$ 

$(4.5\pm0.5)\times10^{-4}$ 

$(1.54\pm0.44)\times10^{-4}$ 

$(8.18\pm5.88)\times10^{-8}$ 

$(7.30\pm3.12)\times10^{-6}$ 

$\rho\eta$ 

$(2.2\pm0.6)\times10^{-5}$ 

$(1.93\pm0.23)\times10^{-4}$ 

$(1.61\pm0.44)\times10^{-4}$ 

$(6.54\pm4.71)\times10^{-9}$ 

$(2.00\pm0.85)\times10^{-6}$ 

$\omega\eta'$ 

$(3.1\pm2.5)\times10^{-5}$ 

$(1.89\pm0.18)\times10^{-4}$ 

$(2.35\pm1.83)\times10^{-4}$ 

$(9.39\pm6.41)\times10^{-6}$ 

$(9.60\pm3.13)\times10^{-5}$ 

$\rho\eta'$ 

$(1.9\pm1.7)\times10^{-5}$ 

$(8.1\pm0.8)\times10^{-5}$ 

$(1.39\pm1.25)\times10^{-4}$ 

$(2.41\pm1.72)\times10^{-9}$ 

$(1.16\pm0.49)\times10^{-6}$ 

Table 4. Experimental values of the branching ratios of
$ J/\psi\to PV $ and$ X\to PV $ , where X stands for both$ X_{f_0\omega} $ and$ X_{f_0\phi} $ . The uncertainties of$ \mathcal{B}(X\to PV)_{\mathrm{Theory}} $ and$ \mathcal{B}(INT\to PV)_{\mathrm{Theory}} $ result from$ c_{ij} $ . The uncertainties of$ \mathcal{B}(c\bar c(1S)\to PV)_{\mathrm{Theory}} $ result from experimental data through the "$12$ % rule".To better understand the contributions of molecular states to
$ J/\psi $ hadronic decays, we define the ratio$ \mathcal{R} $ as$ \begin{array}{*{20}{l}} \mathcal{R}&=&\dfrac{\mathcal{B}(J/\psi\to PV)_{\mathrm{Theory}} }{\mathcal{B}(J/\psi\to PV)_{\mathrm{Exp}} } . \end{array} $

(27) Next, we briefly discuss the effective coupling constant
$ g_X $ and$ g_{f_0} $ , which are different from those of the decay processes$ X(2680) \to PV $ and$ X(2440) \to PV $ in which the effective coupling constant$ g_X $ is evaluated through the wave function of the physical state. In the$ J/\psi \to PV $ process, we set$ g_X $ as a free undetermined coupling constants for the off-shell effect. From the effective Lagrangian in Eq. (18), one has$ \mathcal{B}(J/\psi\to f_0(1710)\phi)_{\mathrm{theory} }= g_X^2\;(6.92\pm 5.40)\times 10^{-1} $ and$ \mathcal{B}(J/\psi\to f_0(1710)\omega)_{\mathrm{theory} }= g_X^2\;(10.38 \pm6.79)\times 10^{-1} $ , respectively, with the uncertainties resulting from$ c_{ij} $ . In other words, the upper limit of$ g_X^2 $ is of the order of$ 10^{-1} $ ; thus, one has$ g_X^2 g^2_{f_0}\sim 1 $ .The ratios
$ \mathcal{R} $ defined above are listed in Table 5, where$ g_X g_{f_0} $ varies in the range of$ 0.5\sim1.5 $ . According to Table 5, the estimated branching fractions of$ J/\psi\to \rho^0 \pi^0 $ ,$ J/\psi\to K^*\bar{K} $ ,$ J/\psi\to\phi\eta $ ,$ J/\psi\to \rho\eta $ ,$ J/\psi\to \omega\eta' $ and$ J/\psi\to \rho\eta' $ are consistent with the experimental expectations. The channels$ J/\psi\to\omega\eta $ can only meet experimental expectations within$ 3\sigma $ error ranges. Regarding$ J/\psi\to\phi\eta' $ and$ J/\psi\to\omega\pi $ , the theoretical values are several times smaller than the corresponding experimental expectations.Channel $g_X g_{f_0}= 0.5$ 

$g_X g_{f_0}= 1.0$ 

$g_X g_{f_0}= 1.5$ 

$\rho^0 \pi^0$ 

$0.24\pm0.13$ 

$0.73\pm0.44$ 

$1.50\pm0.94$ 

$K^{*+}\bar{K}^-$ 

$0.52\pm0.31$ 

$1.55\pm1.03$ 

$3.11\pm2.15$ 

$K^{*0}\bar{K}^0$ 

$1.14\pm0.58$ 

$2.89\pm1.71$ 

$5.39\pm3.40$ 

$\omega\eta$ 

$0.15\pm0.05$ 

$0.30\pm0.14$ 

$0.52\pm0.26$ 

$\phi\eta $ 

$0.68\pm0.23$ 

$1.19\pm0.53$ 

$1.84\pm0.93$ 

$\phi\eta'$ 

$0.28\pm0.06$ 

$0.32\pm0.08$ 

$0.36\pm0.10$ 

$\omega\pi$ 

$0.35\pm0.11$ 

$0.36\pm0.11$ 

$0.37\pm0.12$ 

$\rho\eta$ 

$0.84\pm0.25$ 

$0.85\pm0.25$ 

$0.85\pm0.26$ 

$\omega\eta'$ 

$1.51\pm1.09$ 

$1.80\pm1.21$ 

$2.11\pm1.31$ 

$\rho\eta'$ 

$1.73\pm1.55$ 

$1.73\pm1.55$ 

$1.74\pm1.56$ 

Table 5. Values of
$ \mathcal{R} $ with$ g_X g_{f_0} $ set to$ 0.5 $ ,$ 1.0 $ , and$ 1.5 $ as examples.Note that the experimental data for
$J/\psi\to f_0 (1710)\phi\to \phi K\bar K$ and$ J/\psi\to f_0(1710)\omega\to \omega K\bar K $ may have a confinement to$ c_{ij}g_X g_{f_0} $ through the$ f_0(1710)\to K\bar K $ process. The corresponding coupling constants can be fitted through the following relations and equations derived from Eq. (18):$ \begin{split} \mathcal{M}(J/\psi\to f_0(1710)\phi\to \phi K\bar K)=2g_{f_0} m_K\dfrac{1}{q^2-m_{f_0}^2}\epsilon^{*\mu}_\phi g_{\mu\nu}\epsilon^\nu_X g_X \Lambda_0 \sqrt3 \cos\varphi, \end{split} $ 
(28) $ \begin{split} \Gamma(J/\psi\to f_0(1710)\phi\to \phi K\bar K)=\frac{1}{2\;m_{J/\psi}}\int {\rm d}\Pi_3 |c_{32}\mathcal{M}(J/\psi\to f_0(1710)\phi\to \phi K\bar K)|^2. \end{split} $

(29) By fitting
$\mathcal{B}(J/\psi\to f_0(1710)\phi\to \phi K\bar K)_{\rm Exp}=(3.6\pm0.6)\times 10^{-4}$ [25] , we obtain$ g_X g_{f_0}=0.09\pm0.02 $ . Likewise, by fitting$\mathcal{B}(J/\psi\to f_0(1710)\omega\to \omega K\bar K)_{\rm Exp}=(4.8\pm1.1)\times10^{-4}$ [25] we have$ g_X g_{f_0}=0.08\pm0.02 $ . When taking the two values into the relation$ \mathcal{B}(J/\psi\to PV)_{\mathrm{Theory}} $ , we obtain numerical results which are independent of$ c_{ij} $ , given that$ c_{ij} $ and$ g_X g_{f_0} $ exist in both Eqs. (25) and (29).Finally, note that the values of
$ g_X g_{f_0} $ fitted from the experiments are much smaller. Although$ g_X g_{f_0} $ was fitted using experimental data of the final state of three$ J/\psi $ hadrons ,$ g_X $ and$ g_{f_0} $ are off shell values, and the running of those effective coupling constants is difficult to handle. It may affect the numerical values. This point have also been mentioned above, especially for$ g_X $ . Regarding the value of$ g_{f_0} $ , there are no experimental data, and more data about$ f_0(1710)\to PP(VV) $ and$ f_0(1710) $ hadronic decays are needed. Moreover, we expect that many more$ J/\psi $ hadronic and radiative decays containing the$ f_0(1710) $ resonance peak will be experimentally observed and measured to fit the effective coupling constants. Finally, for the$ \omega-\phi $ mixing, we assume$ \sin\varphi=-0.76 $ , although its value is not well studied. -
Motivated by recent observations of a series of light exotic candidates and the anomalous large branching fraction of
$ J/\psi\to f_0(1710)\phi/f_0(1710)\omega $ , we suppose that the experimentally observed resonances$ X(2440) $ and$ X(2680) $ are of the$ 1^{--} $ state and mainly composed of$ X_{f_0\omega} $ and$ X_{f_0\phi} $ molecular states, respectively. Meanwhile, the two molecular states$ X_{f_0\omega} $ and$ X_{f_0\phi} $ can mix with$ c\bar c(1S) $ to form experimentally observed states$ X(2440) $ ,$ X(2680) $ , and$ J/\psi $ . In the present study, we first evaluated the mass spectra of$ c\bar c $ bound states with the Godfrey-Isgur model [37]. Then, the masses of two molecular states$ X_{f_0\omega} $ and$ X_{f_0\phi} $ were also evaluated within the framework of the OBE model [38, 39]. Finally, we investigated the mixing of the$ c\bar c(1S) $ bound state with the molecular states$ X_{f_0\omega} $ and$ X_{f_0\phi} $ and obtained the mixing parameters by reproducing experimental data.Moreover, we estimated the branching fraction of
$ X(2680)/X(2440)\to PV $ and the three body final states$ K\bar K\phi(\omega) $ . Our estimations indicate that the results strongly depend on the effective coupling constants$ g_{f_0} $ and$ g_X $ as well as on the$ \omega-\phi $ mixing angle$ {\rm sin}\varphi $ . With a certain parameter range, the rate of some$ J/\psi\to PV $ channels can be naturally understood with the present ansatz.The experimental data for
$\mathcal{B}(J/\psi \to f_0(1710)\phi \to \phi K\bar K)$ [25] and$ \mathcal{B}(J/\psi\to f_0(1710)\omega\to \omega K\bar K) $ [25] were observed in the invariant mass spectra of$ J/\psi\to \phi K\bar K $ and$ J/\psi\to \omega K\bar K $ . Therefore, we expect that the$ f_0(1710) $ resonance will be observed in other three body hadronic decays of$ J/\psi $ , such as$ \mathcal{B}(/\psi\to \phi(\omega)\pi\pi) $ ,$ \mathcal{B}(J/\psi\to \phi(\omega)\eta\eta) $ ,$\mathcal{B}(J/\psi\to \phi(\omega)\rho\rho)$ , and$ \mathcal{B}(J/\psi\to \phi(\omega)\omega\omega) $ .Unfortunately, the measurement of the hadronic decays of the resonances still presents large uncertainties, which hinder setting definite values of the coupling constants. Therefore, it is still too early for drawing conclusions about the present ansatz. More precise measurements on those hadronic decays in future will provide crucial information to test the present ansatz.
-
X. D. Guo is very grateful to K. Chen for helpful discussions.
Molecular components in J/ψ and ρ-π puzzle
- Received Date: 2023-12-19
- Available Online: 2024-05-15
Abstract: Motivated by the large branching fractions of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


























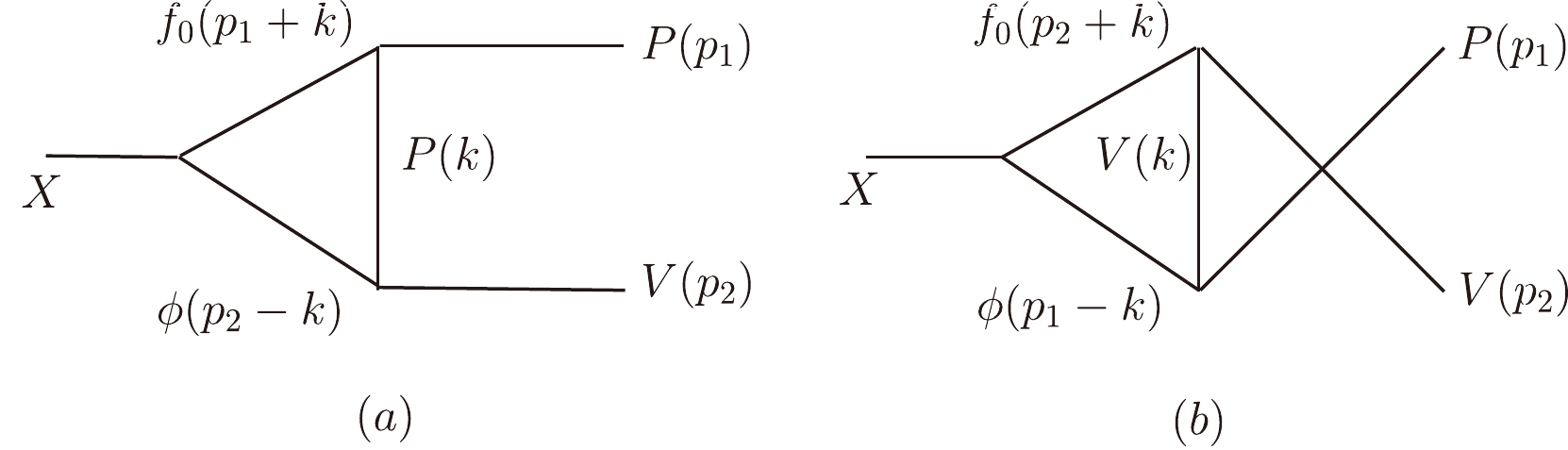



 DownLoad:
DownLoad: