Analytic continuation in the coupling constant for resonances in ${{}^{{\boldsymbol{9}}}_{{\boldsymbol{\Lambda}}}}$Be

In nuclear physics, investigations related to resonance are among the most important topics. Among the approaches that can address resonant states, a traditional estimation theory corresponds to the analytic continuation in the coupling constant (ACCC) method [1, 2]. This method is based on the property of the analytic continuation: the S-matrix [3] pole of a resonant state is defined as the analytic continuation of a bound-state pole in the coupling constant of the attractive part of the Hamiltonian.

The microscopic cluster model is a popular model in nuclear physics that considers the microscopic structure of clusters and Pauli principle between nucleons. In addressing the problems about resonant state, the traditional ACCC method has also been applied within the cluster model. For example, the ACCC method can be implemented by incorporating an additional pseudo potential [4, 5] or by modifying the effective nucleon-nucleon interaction adopted in the microscopic cluster model [6, 7]. With respect to the latter, the exchange parameters in conventional Volkov interaction [8] and Minnesota interaction [9] are adjusted to implement the ACCC method. The potentials used in the microscopic cluster model generally contain the exchange operator, and therefore, we refer to such variant of ACCC method as the exchange parameter dependent-ACCC (EPD-ACCC) method.

The complex scaling method (CSM) [10, 11] is another powerful theoretical approach, in which the resonant states of quantum systems are transformed into bound states via complex scaling transformations, without changing their complex eigenenergies. This method has also been extensively developed and applied in the study of bound states, resonant states, and scattering states in nuclear physics [12−23]. In this study, with EPD-ACCC method and CSM, we consider the hypernucleus $ {}^9_{\Lambda} $Be with $ \alpha+\alpha+{\Lambda} $ three cluster model as a proof-of-concept example.

Hypernuclear system is an important research subject in nuclear physics, and significant studies have been conducted on the production, decay, and structure of hypernuclei [24, 25]. Various theoretical studies, including the generator coordinate method (GCM) [26, 27], the orthogonality condition model [28−30], the Tohsaki-Horiuchi-Schuck-Röpke (THSR) wave function [31−33], antisymmetrized molecular dynamics [34, 35], the variational Monte Carlo (VMC) method [36], the Gaussian expansion method [37−44], the cluster orbit shell model [45], the particle rotor model [46], and mean-field approaches [47−56], have been proposed to investigate different aspects of the nature of hypernuclei. Additionally, the harmonic trap method [57] has also been successfully applied to the study of nuclear resonances and scattering [58−71], and it demonstrates potential for making valuable contributions to future research on hypernuclei. In hypernuclear physics, one of the main aspects involves studying the new dynamical and structural properties by an addition of a hyperon (or more than one hyperon). The systematic study of binding energy of light Λ-hypernuclei has traditionally been a key topic in hypernuclear physics. In addition to investigations on the bound states and the structural properties, the resonant states have also been studied with theoretical approaches.

In this study, through the EPD-ACCC method, we calculate the resonant states within the $ \alpha+\alpha+{\Lambda} $ three cluster model for $ {}^9_{\Lambda} $Be. Here, the investigations about decay indicates the particle emission of light hypernuclei. The weak decay lifetime of a free Λ hyperon is approximately 260 $ {\rm ps} $, and the lifetime of a hyperon in hypernuclei is also on this order. Such a lifetime is much longer than the time for particle decay and does not affect the discussion in this study. To verify that the EPD-ACCC method can provide a good estimation, we select some resonant states of $ {}^9_{\Lambda} $Be as examples. Additionally, the CSM is applied as a benchmark to extract the resonant state.

The rest of the paper is organized as follows. In Sec. II, the microscopic cluster model for the $ \alpha+\alpha+\Lambda $ three cluster system is briefly introduced. Furthermore, we illustrate the framework of EPD-ACCC, along with the CSM, which is applied as a benchmark. In Sec. III, the numerical results are presented and discussed. Sec. IV summarizes the article. The overlap and Hamiltonian kernels evaluated in the framework of the generator coordinate method (GCM) are provided in the Appendix.

$ {}^9_{\Lambda} $Be within the $ \alpha+\alpha+\Lambda $ three cluster system is described by the GCM, and the configurations of $ {}^5_{\Lambda} $He and $ {}^9_{\Lambda} $Be are shown in Fig. 1. The Pauli principle between two α clusters is considered with the GCM, whereas antisymmetrization between Λ hyperon and other nucleons is not required. Therefore, the wave functions of $ {}^5_{\Lambda} $He and $ {}^9_{\Lambda} $Be can be expressed as

Figure 1.  (color online) Coordinate systems and angular momentum labels for (a) $ {}^5_{\Lambda}\mathrm{He} $ and (b) $ {}^9_{\Lambda}\mathrm{Be} $

where $ \phi_{\alpha} $ and $ \Phi_{l,\alpha\alpha} $ denote the wave functions of α particle and $ {}^8_{} $Be with total angular momentum l, respectively. Some details of the calculation for the $ \alpha + \alpha $ part can be found in the Appendix or in [17, 72, 73].

The size parameters b appropriate for the coordinates in Fig. 1 are chosen such that combinations with the corresponding reduced massed lead to an identical value of $ \hbar/\omega $:

The total Hamiltonian of $ {}^9_{\Lambda} $Be can be divided as

with

where T denotes the total kinetic energy of 8 nucleons in $ {}^8 $Be, and $ T_G $ denotes the center-of-mass kinetic energy of $ {}^8 $Be. Furthermore, $ T_R $denotes the kinetic energy associated with the coordinate R. $ V_N $ is the effective two-body nuclear interaction energy and $ V_C $ is the Coulomb interaction energy. $ V_{\Lambda N}^i $ denotes the $ \Lambda N $ interaction between the hyperon Λ and i-th nucleon.

Practically, we adopt Volkov (or Minnesota) interaction as the effective two-body nuclear potential, which has the general form

where parameters of Volkov and Minnesota interactions are all as listed in Table 1. In our calculations, Volkov No.1 is utilized as $ NN $ interaction.

Interaction	k	$ V^0_{k} $	$ a_k $	$ W_k $	$ M_k $	$ B_k $	$ H_k $
Volkov No.1	1	−83.34	1.60	1-M	M	0	0
	2	144.86	0.82	1-M	M	0	0
Volkov No.2	1	−60.65	1.80	1-M	M	0	0
	2	61.14	1.01	1-M	M	0	0
Minnesota	1	200	1/ $ \sqrt{1.487} $	u/2	1-u/2	0	0
	2	−178	1/ $ \sqrt{0.639} $	u/4	1/2-u/4	u/4	1/2-u/4
	3	−91.85	1/ $ \sqrt{0.465} $	u/4	1/2-u/4	-u/4	u/4-1/2

Table 1.  Amplitudes $ V^0_{k} $ (in MeV) and ranges $ a_k $(in fm) of Volkov No.1, Volkov No.2, and Minnesota interactions. The standard values are $ M=0.6 $ and $ u=1 $. However, these parameters can be modified to reproduce some important properties of the system.

The Coulomb interaction can be expressed as

where the isospin z-component equals $ t_z=+{1}/{2} $ for proton and $ t_z=-{1}/{2} $ for the neutron.

The two-body $ \Lambda N $ interaction is selected as YNG interaction, which can be provided by

where $ P_r $ denotes the space exchange parameter and

The parameters of the YNG model used in this study are taken from [24] and listed in Table 2. With the parameters adopted in the $ \Lambda N $ potential, the binding energy of $ {}^{5}_{\Lambda} $He can be reproduced as 3.10 MeV, which is in good agreement with the experimental value 3.12$ \pm $0.02 MeV [74].

$ \beta_i $	$ V^0(E) $	$ V^0(O) $	$ V^0_D $	$V^0_{\rm EX}$
1.5	−9.93	−7.66	−8.795	−1.135
0.9	−227.73	−82.55	−155.140	−72.590
0.5	1021.17	717.40	869.285	151.885

Table 2.  $ \Lambda N $interaction depth of the YNG model. The Fermi momentum $ k_F $ is 0.9 fm⁻¹.

The following restrictions on the channels and generator coordinates are adopted in the calculation of $ {}^{5}_{\Lambda} $He:

In this study, the Λ particle is treated as spinless because$ \Lambda N $spin-spin interaction does not contribute to the coupling potential between the Λ particle and spin-saturated α cluster. Additionally, the Λ one-body spin-orbit potential was found to be very weak in the experiment.

In the GCM framework, complex scaling can be introduced by letting the generator coordinate be a complex scaled one. This type of transformation has been used in [17] for the two cluster system $ \alpha+\alpha $. Here, for the three cluster system, the transformation is extended to $d_{\theta}={\rm e}^{{\rm i}\theta}d$ and $D_{\theta}={\rm e}^{{\rm i}\theta}D$. Additionally, owing to the non-hermitian property due to the CSM, we need to use the c-product (bi-orthogonal product) [75] as opposed to the normal inner product to calculate the matrix elements. More detailed information regarding the implementation of the CSM in the framework of the GCM can be found in [18].

There are many practical methods to select the resonance states among positive energy eigenstates. One of them is the analytic continuation in the coupling constant (ACCC) method, which is based on the analytic continuation from a bound-state pole to an S-matrix pole of a resonant state. As a variant of ACCC, inverse ACCC (IACCC) [76, 77] can also complete the task of analytic continuation.

Explicitly speaking, this can be realized by adding an artificial attractive pseudo potential V to the original Hamiltonian H:

where δ denotes a coupling constant to vary the strength of the pseudo potential, or from another point of view, the original Hamiltonian can be written as

where $V_{\rm att}$ denotes an attractive potential and $ \lambda=1 $ denotes the physical value. Then, we have $ \delta=\lambda-1 $ and $V=V_{\rm att}$. When there is a bound state with a value of λ, the binding energy will decrease with the shrinking of λ, and this bound state will reach the threshold at$ \lambda = \lambda_0 $, where $ E(\lambda = \lambda_0)=0 $. Beyond this critical point, the bound state will become a resonant or a virtual state.

For a two-body system $ (n=2) $, it can be shown that the square root of the binding energy, $ k_l=\sqrt{-E} $, behaves near the threshold$ \lambda = \lambda_0 $as

Therefore, one can consider $ k_l $ as a function of complex variable x:

and $ k_l $ analytically continues from the $ \lambda>\lambda_0 $ region to the $ \lambda<\lambda_0 $ region.

In practice, we generally use the Padé approximant to formulate $ k_l $:

In general, for systems with $ n>2 $, $ k_l $ denotes the relative momenta to the nearest desintegration threshold $ k_l=\sqrt{-(E_n-E_{\rm{thr}})} $. In the calculations, we consider the threshold energy as the sum of the intrinsic energies of two free α particles, namely $E_{\rm thr}=2E_{\alpha}$. Contrary to the $ n=2 $ case, for $ n>2 $ systems, l can no longer determine if a bound state turns into a resonant state or a virtual one when $ \lambda<\lambda_0 $.

In this study, the EPD-ACCC method applied is based on the effective N-N interaction adopted in microscopic cluster model:

where $ F(r) $ is typically in the form of a Gaussian function.

In the EPD-ACCC method, M(or u) becomes the new coupling constant. In the conventional ACCC method, as the coupling constant δ (or λ) increases, the attraction effect of the potential must be stronger, and thereby, the binding energy of the bound state increases gradually. This is also true if parameter u in Minnesota interaction is adopted as the coupling constant. However, conversely, for Volkov interaction, we can observe that the binding energy of the bound state will decrease as the coupling constant M increases. As M decreases from its physical value (0.573 in our calculations), the system becomes increasingly bound, and the resonant energy approaches the threshold. A further decrease in M causes the system to cross the threshold and become bound, allowing us to obtain a series of bound states and their corresponding M parameters. The complex variable that we should utilize is$ \sqrt{M-M_0} $, where $ E(M_0)-E_{\rm thr}=0 $ and $ M<M_0 $ for bound state.

Compared to introducing an auxiliary attractive potential, using parameters from the original interaction as the coupling constant has the advantage that the results do not depend on the choice of the attractive potential. Additionally, for a single α cluster, the nuclear potential energy is only dependent on $ M+W $, and $ M+W $ is generally restricted as a constant. Therefore, the internal energy of a single free α particle is independent of the choice of M and u in Volkov and Minnesota interactions, respectively. This is very convenient when we use the ACCC method to estimate resonant states in the $ \alpha+\alpha+\Lambda $ system.

To test the reliability of EPD-ACCC method, we choose the $ 4_1^{+} $ state of $ {}^9_{\Lambda} $Be as a proof-of-concept example. The single and coupled channel cases are both considered. For the single channel case, namely $(l,L)= (4,0)$, the generator coordinates are considered as $d=1,\;2,\;3,\cdots,\;25\ \rm{fm}$ and $D=1,\;2,\;3,\cdots,\;20\ \rm{fm}$. In the coupled channel calculations, the following restrictions on the channels and generator coordinates are adopted:

We solve the coupled channel Hill–Wheeler equations and reproduce the so called $ {}^8 $Be analog states, where the configurations are $ {}^8 $Be($ 0^+ $) + Λ, $ {}^8 $Be($ 2^+ $) + Λ, and $ {}^8 $Be($ 4^+ $) + Λ for the $ 0_1^{+} $, $ 2_1^{+} $, and $ 4_1^{+} $ states of $ {}^9_{\Lambda} $Be, respectively. The results are listed in Table 3. It is noticeable that the binding energy of the Λ particle is defined as $ B_{\Lambda} $= $E(^9_\Lambda {\rm Be})-E(^8 {\rm Be}(0^+_1))$. We can determine that the Λ particle occupies the $ 0s $ orbit coupling to the $ {}^8 $Be core with a high probability, which can be observed from the large s-wave components $ 0.9735 $, $ 0.9680 $, and $ 0.9274 $for the $ 0_1^{+} $, $ 2_1^{+} $, and $ 4_1^{+} $ states, respectively. Additionally, we can find that $ 0_1^{+} $ and $ 2_1^{+} $ are bound states among $ {}^8 $Be analog states. However, the $ 4_1^{+} $state, calculated by the bound state approximation, has a positive binding energy of the Λ particle, which indicates that this state might be a resonance. More specifically, to clarify the nature of the excited states, we should compare their energies with the lowest $ {}^{5}_{\Lambda} $He + α threshold. Furthermore, $ B_{\Lambda} $ values alone are insufficient to determine whether the excited states are bound or unbound. Additionally, $ 0^+_{1} $ and $ 2^+_{1} $ states are below the lowest $ {}^{5}_{\Lambda} $He + α threshold, indicating that they are bound states. No excited states are found between $ {}^{5}_{\Lambda} $He + α and α + α + Λ thresholds, which suggests that potential $ ^{5}_\Lambda $He + α resonance states are not within the scope of this study. Additionally, we refer to the resonance states found above the α + α + Λ threshold as "α + α + Λ resonances."

$ J^{\pi} $	Energy/MeV	$ B_{\Lambda} $/MeV	momenta			$ w_{l,L}^2 $
$ 0_1^{+} $	−61.13(−60.45)	−7.056	$ (l,L) $	(0,0)0.9735		(2,2)0.02596		(4,4)5$ \times10^{-4} $
$ 2_1^{+} $	−58.18(−57.5)	−4.106	$ (l,L) $	(2,0)0.9680	(0,2)0.01248	(2,2)0.01149	(2,4)3$ \times10^{-4} $	(4,2)0.007596	(4,4)2$ \times10^{-4} $
$ 4_1^{+} $	−50.62(−50.02)	3.454	$ (l,L) $	(4,0)0.9274	(0,4)7$ \times10^{-4} $	(2,2)0.06105	(2,4)6$ \times10^{-4} $	(4,2)0.009859	(4,4)3$ \times10^{-4} $

Table 3.  Weight $ w_{l,L}^2 $ of a channel specified by the angular momenta of α-α part $ (l) $ and Λ-$ { }^8 $Be part $ (L) $, defined by Eq. (1). The total binding energy E and Λ binding energy $ B_{\Lambda} $ are also listed. It should be noted that $ B_{\Lambda} $is defined as the binding energy measured from the calculated $ { }^8 \mathrm{Be}(0^+) $ energy $ -54.074 \;\mathrm{MeV} $. Energies in parentheses are the results of the single channel calculation of $ (l,L)=(J, 0) $.$ \Lambda N $ interaction of the YNG form is used.

Therefore, we utilize the EPD-ACCC method and CSM to obtain the complex energy of the $ 4_1^{+} $ state. Initially, we use the EPD-ACCC method to estimate the resonance of the $ 4_1^{+} $ state with single channel calculations; the order of the Padé approximant is denoted by $ [N_1,N_2] $.

Choosing $ N_1+N_2 $ bound state energies of $ {}^9_{\Lambda} $Be close to the $ \alpha+\alpha $ threshold, the coefficients in the Padé rational function can be determined. The trajectories of resonance with a coupling constant λ (here, λ denotes Majorana parameter M) with several Padé orders $ [N_1,N_2] $ are plotted in Fig. 2(a), where the values of the coupling constant M corresponding to the points on the trajectories are taken as 0.515, 0.520, 0.525, 0.530, 0.535, 0.540, 0.545, 0.550, 0.555, 0.560, 0.565, 0.570, and 0.573 from left to right. The rightmost point of the trajectory represents a real physical situation, namely the resonance we desire. Figure 2(b) is similar to Fig. 2(a) but for coupled channel case. The resonant energies and decay widths obtained by the CSM are also marked in the figures with red stars, which shows good agreement between our two theoretical methods.

Figure 2.  (color online) Positions of the resonance poles with the $ 4_1^{+} $ state for different orders of the Padé approximant $ [N_1,N_2] $ (the approximant order is indicated in square brackets): (a) single channel case ($ (l,L)=(4,0) $); (b) coupled channel case. The values of the coupling constant M corresponding to points on the trajectories are taken as 0.515, 0.520, 0.525, 0.530, 0.535, 0.540, 0.545, 0.550, 0.555, 0.560, 0.565, 0.570, and 0.573, from left to right. The rightmost point of the trajectory represents a real physical situation. The positions of the resonance poles obtained by the CSM are also marked in the figures with red stars.

To further corroborate the validity of this technique, we can artificially manipulate M to a higher value (namely broader resonance). Subsequently, employing the same Padé approximant, we can estimate the resonant state corresponding to the new parameter M. Furthermore, the CSM is applied as a benchmark during this process. For instance, we can set the value of M to be larger and use the original bound states obtained in the coupled channel case; the complex energies of resonant states are listed in Table 5. Based on the aforementioned calculations, we can observe that this method can also extrapolate reliable values for resonance states with broad decay widths.

M	$ E_{r} $/MeV	Γ /MeV	$ E^{\rm CSM}_{r} $/MeV	$ \Gamma^{\rm CSM} $/MeV
0.575	3.8592	0.4969	3.9311	0.5205
0.585	4.5075	0.7287	4.5345	0.7822
0.595	5.1320	1.0004	5.0928	1.0822
0.605	5.7350	1.3091	5.6057	1.4107
0.615	6.3182	1.6523	6.0734	1.7549
0.625	6.8831	2.0276	6.4966	2.0981

Table 5.  Resonant energies and decay widths for the $ 4_1^{+} $ state of $ {}^9_{\Lambda} $Be with coupled channel calculations. Several different values of M are considered to test the stabilization and reliability of the EPD-ACCC method. The results obtained by the EPD-ACCC method are listed in the second and third columns. Here, the order of the Padé approximant is taken as $ [N_1,N_2] $=[3,3]. In the fourth and fifth columns, we display the results extracted by the CSM.

Complex scaling is introduced using the complex scaled generator coordinates $d_{\theta}={\rm e}^{{\rm i}\theta}d$ and $D_{\theta}={\rm e}^{{\rm i}\theta}D$ in the three cluster system. We calculate the single and coupled channel cases for the $ 4_1^{+} $ state of $ {}^9_{\Lambda} $Be with the CSM and extract the resonances from the complex energy spectra with respect to angle θ.

First, we show the results in the single channel case, which dominates the $ 4_{1}^{+} $ state observed in Table 3. In Fig. 3(a), we display a complex energy spectrum, where the scaling angles are taken to be $ {12}^{\circ} $, $ {14}^{\circ} $, and $ {16}^{\circ} $. We can observe that the α + α + Λ resonance appears above the $ {}^8 $Be$ (0^+)+\Lambda $threshold. Using the conventional stability condition, the accurate value is extracted from the θ trajectory in Fig. 3(b); the optimal scaling angle is also marked. With this optimal angle, the location of the resonance is determined as $E-{\rm i}\Gamma/2=4.0766-0.05096{\rm i}$ MeV (energy of two free α particles already subtracted), which is a considerably narrow resonance. By comparing the real part of this complex energy $ -50.06 $ MeV with the positive energy $ -50.02 $ MeV obtained by bound approximation in Table 3, the good reliability of the bound state approximation for narrow resonance is confirmed.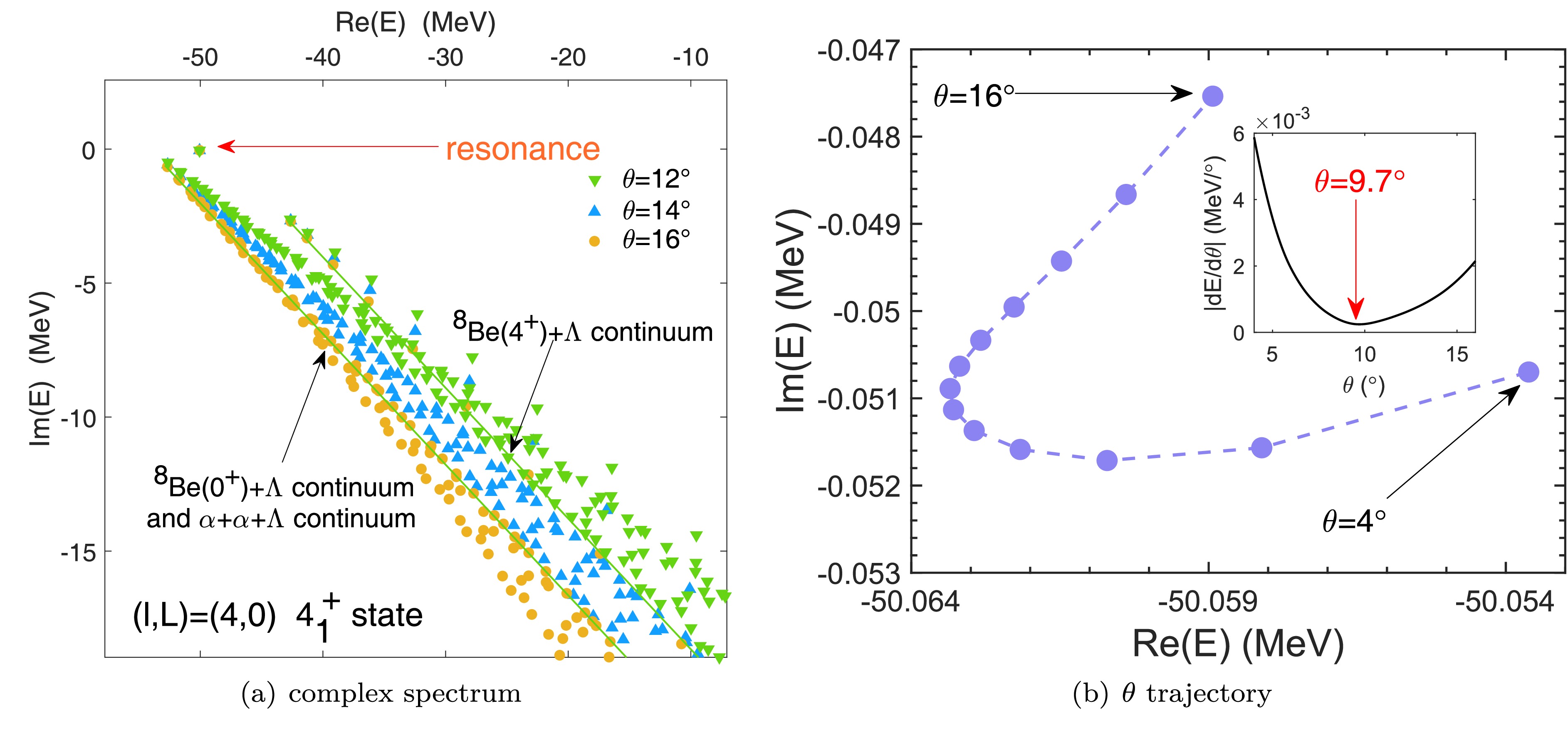

Figure 3.  (color online) Complex energy spectrum for the $ 4_1^+ $ state with GCM wave functions in a single channel case. The blue square, red circle, and orange triangle correspond to $ \theta=12^{\circ},14^{\circ},16^{\circ} $, respectively. Due to the small resonance energy of $ {}^8 $Be($ 0^+ $) above the $ \alpha+\alpha $ threshold, the $ {}^8 $Be($ 0^+ $)$ +\Lambda $ continuum and $ \alpha+\alpha+\Lambda $ continuum are indistinguishable, which can be observed from Fig. 3(a). The $ {}^8 $Be($ 4^+ $)$ +\Lambda $ continuum is also marked in Fig. 3(a). In Fig. 3(b), we plot the θ trajectory of the complex resonant energy. Angle θ is taken from 4$ {}^{\circ} $ to 16$ {}^{\circ} $with steps of 1$ {}^{\circ} $. It can be observed that the optimal energy of the resonant state is approximately $ \theta={9.7}^{\circ} $.

Similarly, in Fig. 4(a), (b), we show the complex energy spectra of the $ 4_1^{+} $ state calculated with the coupled channel and θ trajectory, respectively. The resonance marked by the red circle is located at $E-{\rm i}\Gamma/2= 3.8050-0.2368{\rm i}$ MeV with the θ stabilization condition. This broader resonance indicates that there is a stronger repulsive effect caused by the coupled channel, or more explicitly, due to higher D wave Λ particle coupling to $ {}^8 $Be$ (2^+) $.

Figure 4.  (color online) Complex energy spectrum for the $ 4_1^+ $ state with GCM wave functions in the coupled channel case. The blue square, red circle, and orange triangle correspond to $ \theta=20^{\circ},23^{\circ},26^{\circ} $, respectively. The angle θ is taken from 12.5$ {}^{\circ} $ to 15$ {}^{\circ} $with steps of 0.25$ {}^{\circ} $. It can be observed from Fig. 4(b) that the optimal energy of the resonant state is approximately at $ \theta={13.6}^{\circ} $.

The results of two theoretical methods, EPD-ACCC and CSM, for $ 4_1^{+} $ resonance are listed in Table 4. We can observe that the resonances obtained by these two methods are highly consistent with each other. Additionally, through the investigation of $ 4_1^+ $ resonance in the range of $ M>0.573 $, as observed in Table 5, the good stabilization of the EPD-ACCC method is confirmed by the good consistency between two theoretical methods.

$ J^{\pi}=4_1^{+} $	CSM			EPD-ACCC
	$ E_r $/MeV	Γ/MeV		$ E_r $/MeV	Γ/MeV
single channel	4.0766	0.1020		4.2847	0.1068
coupled channel	3.8050	0.4736		3.7265	0.4556

Table 4.  Resonant energies and decay widths for the $ 4_1^{+} $ state of $ {}^9_{\Lambda} $Be. The theoretical values are provided by CSM and EPD-ACCC, respectively.

Finally, we present the energy levels of $ {}^8 $Be and $ {}^9_{\Lambda} $Be in Fig. 5, including both experimental data and theoretical results. The first column shows the experimental data for $ {}^8 $Be. The shaded areas represent the decay widths, whose values are also indicated in parentheses. The second column contains our numerical results obtained using the microscopic R-matrix method, which are in good agreement with the experimental values. The third to seventh columns display the energy spectra for $ {}^9_{\Lambda} $Be. The third column shows the energies of the bound states $ 0_1^{+} $ and $ 2_1^{+} $, along with the resonance state $ 4_1^{+} $ obtained using the EPD-ACCC method and CSM. The fourth column contains the $ {}^8 $Be analog states from [43]. The fifth and sixth columns present the experimental data corresponding to Exp.(1) and Exp.(2) taken from [79−81] and [82, 83], respectively. The final column shows the recalibrated experimental data Exp.(2)* [74] from Exp.(2). It is important to note that the resonant energies of $ {}^8 $Be displayed in Fig. 5 differ from those in [17, 19]; this is because, in [17, 19], we did not use $ b=1.36 $ fm for the free α particle. Instead, we used $ b^{*}=1.3748 $ fm for free α particle to maximize its binding energy, which results in a difference of approximately 0.0316 MeV in the resonant energies.

Figure 5.  (color online) Low lying energy levels of $ {}^8 $Be and $ {}^9_{\Lambda} $Be. Here, we take the $ \alpha+\alpha+\Lambda $ threshold as the zero point of energy. The black solid lines represent the binding energies of bound states and resonant energies of resonances, and the shaded areas indicate the corresponding decay widths. The first column corresponds to experimental data of $ {}^8 $Be [78]; the second column presents the energy levels of $ 0^{+} $, $ 2^{+} $, and $ 4^{+} $ states calculated based on the microscopic R-matrix method; the third column represents $ 0_1^{+} $, $ 2_1^{+} $, and $ 4_1^{+} $ states of $ {}^9_{\Lambda} $Be obtained via EPD-ACCC calculations; and the fourth column displays the theoretical results taken from [43]. The observed energies of $ {}^9_{\Lambda} $Be in column Exp.(1) are taken from [79−81], and the observed energies in column Exp.(2) are taken from [82, 83]. Additionally, in column Exp.(2)*, we present the recalibration of the observed values in column Exp.(2) according to [74].

Our results for $ 0_1^{+} $ and $ 2_1^{+} $ bound states show consistency with those obtained using the orthogonality condition model and Gaussian expansion method in [43]; they also align well with the experimental data. Additionally, our results for the $ 4_1^{+} $ resonant state are also in good agreement with those from [43]. The consistent resonances obtained from the EPD-ACCC method and CSM validate the good reliability of the EPD-ACCC method.

In this study, we use the EPD-ACCC method to evaluate the resonances of light hypernuclei within the microscopic cluster model and generator coordinate method. We consider the resonant state $ 4_1^{+} $ of $ {}^9_{\Lambda} $Be as an example to investigate the validity and reliability of the EPD-ACCC method. For both narrow and broad decay widths, the resonant energies and decay widths obtained from the EPD-ACCC method are in good agreement with those calculated by the three cluster complex scaling method, which encourages us to extract the resonant energies and decay widths in multi-cluster systems with the EPD-ACCC method. This study provides a reliable approach based on the ACCC method to investigate the resonances of light hypernuclei in the microscopic cluster model, and our EPD-ACCC method can be extended to examine resonant states in more complex multi-cluster systems.

The matrix elements required are listed as follows:

The $ {}^5_{\Lambda} $He case

Matrix elements of overlap:

Matrix elements of kinetic:

Matrix elements of $ \Lambda N $ potential:

The notations used above are defined by

with

The wave functions of two α clusters are constructed by the Brink wave functions. The matrix elements involving two α clusters can be expressed as follows:

Kernels of $\alpha+\alpha$ Norm kernel:

Kinetic kenrel:

where A denotes the nucleon number of $ {}^8 $Be.

$ NN $ interaction kernel:

with

The $ NN $ interaction used here is of the form

The $ {}^9_{\Lambda} $Be case

Matrix elements of overlap:

Matrix elements of kinetic $ T_R $:

Matrix elements of $ \Lambda N $ potential:

where

and

with $ (ab|c)=(a0b0|c0) $ and $ \hat{d}=2d+1 $.

The notations used above are defined by