-
The study of black holes has advanced significantly in recent decades, primarily due to breakthroughs in observational astronomy and numerical simulations. The detection of gravitational waves from black hole mergers by LIGO/Virgo [1], along with the direct imaging of event horizons by the Event Horizon Telescope (EHT), has provided compelling evidence for the existence of black holes and their strong-field relativistic effects [2].
Astrophysical black holes are typically surrounded by accretion disks, which serve as the primary sources of electromagnetic radiation. The structure and dynamics of these disks have been extensively studied through numerical simulations, particularly in the context of magnetized accretion flows [3]. Moreover, high-resolution observations of M87* have revealed a bright, ring-like structure associated with the accretion flow and jet base, reinforcing the theoretical connection between jet dynamics and accretion disk physics [4].
In 1963, Maarten Schmidt observed the spectrum of 3C-273 using the Palomar Telescope and discovered that its Balmer line redshift reached
$ z = 0.158 $ . This finding overturned the "nearby star" hypothesis and confirmed that quasars are extremely high-energy celestial objects on cosmological scales. With luminosities far exceeding those of normal galaxies, quasars prompted scholars to propose the supermassive black hole (SMBH) accretion hypothesis [5]. Subsequently, Donald Lynden-Bell pioneered the concept of accretion disks, demonstrating how black holes release gravitational energy by accreting matter [6]. While Lynden-Bells ideas established the foundation, the standard Shakura-Sunyaev Disk (SSD) model was mathematically formalized in 1973 by Shakura and Sunyaev [7]. In the same year, Novikov and Thorne enriched the SSD framework by incorporating general relativity, most critically through the concept of the innermost stable circular orbit (ISCO). This refinement clarified the dynamical boundaries and energy extraction mechanisms of accretion disks [8]. Soon after, Thorne and Page systematically introduced general relativity into accretion disk theory for the first time, creating the basis of modern black hole accretion disk models. They re-derived the thin-disk structure within the relativistic framework and established rigorous mathematical formulations for mass, angular momentum transport, and radiative efficiency, paving the way for the practical application of the standard accretion disk model (SSD) [9]. Then, Shapiro proposed the two-temperature accretion disk model, resolving the high-energy spectrum puzzle of black hole X-ray binaries; by abandoning the standard thin-disk thermal equilibrium assumption, they addressed the low-luminosity black hole spectra unexplained by standard thin disks and successfully predicted the origin of hard X-ray radiation and radio jets [10].The Blandford-Znajek (BZ) mechanism, proposed in 1977, became the cornerstone of relativistic jet physics by leveraging black hole spin-energy extraction via magnetic fields [11]. In the next year, Abramowicz pioneered the mathematical model of thick accretion disks, revealing novel accretion regimes under extreme conditions through rigorous hydrodynamic analysis. His proposed toroidal structures and sub-Keplerian rotation concepts remain foundational tools in high-energy astrophysics, providing irreplaceable theoretical value for understanding super-Eddington accretion, thermal accretion flows, and multi-wavelength radiation mechanisms [12]. Blandford and Konigl then expanded this paradigm by constructing a relativistic jet analytical model. Assuming a power-law electron energy distribution (
$ N(\gamma) \propto \gamma^{-p} $ ), they derived the relationship between radio spectral indices and the electron index p, laying the groundwork for unified jet radiation theory [13]. Later, in 1982, Blandford and Payne introduced the Blandford-Payne (BP) mechanism, explaining centrifugal launching of jets from accretion disks. This complemented the BZ mechanism by addressing jets in non- or weakly spinning black hole systems [14].In 1985, Uchida and Shibata were the first to use numerical simulations to demonstrate how magnetohydrodynamic (MHD) processes generate collimated jets from accretion disks. This work provided the first numerical verification of the magnetic field-driven jet hypothesis and has inspired decades of subsequent research on jet dynamics [15]. Stone and Norman then developed the ZEUS-2D numerical code, followed later by the implementation of ZEUS-3D. Utilizing this 3D MHD framework, Stone and Hardee simulated magnetized astrophysical jets and discovered that their propagation is significantly disrupted by kink-mode instabilities, leading to lateral distortion and fragmentation. These simulations predicted the formation of knot-like structures closely resembling the observed quasi-periodic shock features and bright knots in radio galaxies such as M87 [16]. By 1994, Rees fireball model tied jet dynamics to ultrarelativistic expansion, explaining gamma-ray burst (GRB) prompt emission and later evolving into baryonic jet models to account for heavy particle-dominated outflows [17]. At the same time, Narayan and Yi systematically developed the first self-similar analytical model for advection-dominated accretion flows (ADAF), revolutionizing the theoretical framework for low-accretion-rate systems. They unified viscous heating, electron-ion energy exchange, and radial energy advection under a two-temperature framework for the first time, extending the Shakura-Sunyaev α-viscosity hypothesis to ADAF [18].
In 1999, Koide pioneered the implementation of general relativistic magnetohydrodynamics (GRMHD) in numerical simulations of black hole jets. Building upon this foundation, Gammie et al. introduced the High-Accuracy Relativistic Magnetohydrodynamics (HARM) code in 2003 - the first fully general relativistic MHD framework capable of self-consistently modeling black hole accretion flows and their coupled jets within curved spacetime, thereby validating the governing equations of relativistic plasma dynamics in strong gravitational fields [19]. Not long after, Komissarov proposed an analytical solution model for magnetized tori around black holes, revealing the profound impact of magnetic fields on accretion disk morphology and stability [20]. Subsequently, Tchekhovskoy, Narayan, and McKinney leveraged HARM to systematically simulate black holes across a range of spin parameters. Their computations revealed a striking dependence of normalized jet efficiency on spin: for extreme spins (
$ a = 0.99 $ ), the BZ mechanism dominates, surpassing the canonical 10% accretion energy limit; conversely, for non-spinning holes ($ a = 0 $ ), jet power originates solely from disk magnetic dissipation. These results align with statistical trends in radio-loud quasars, where high-spin systems exhibit significantly higher jet power at fixed accretion rates [21]. In 2012, McKinney's HARM simulations uncovered that under magnetically arrested disk (MAD) conditions, accumulated magnetic flux near the horizon saturates into flux-tube structures. The large-scale field anchored to these tubes continuously extracts rotational energy via the BZ process, explaining why rapidly spinning black holes launch ultra-relativistic, tightly collimated jets [3]. In the same year, Tejeda developed an innovative analytical framework to construct a concise relativistic accretion model for Kerr black holes, bridging the gap between complex numerical simulations and classical theories [22].Thereafter, Compere proposed a self-similar theory for steady-state thin accretion disks around near-extremal Kerr black holes. By combining the symmetries of extremal black hole spacetimes with accretion flow dynamics, he revealed the unique properties of accretion structures in such strong gravitational environments [23]. Addressing computational limitations, Porth developed the BHAC code, incorporating adaptive mesh refinement (AMR) and multi-physics coupling. This advancement enabled high-fidelity studies of blazar jet morphology and black hole merger magnetospheric interactions [24]. The 2019 EHT imaging of M87*s shadow, combined with polarized emission maps, resolved a toroidal magnetic field morphology at the jet base, providing direct observational evidence corroborating BZ mechanism predictions [2]. In a seminal follow-up investigation, Mitra pioneered a breakthrough exploration of black hole accretion flows using GRMHD simulations, employing high-fidelity numerical algorithms to unravel the nonlinear coupling between large-scale magnetic fields, extreme gravitational fields, and turbulent accretion plasmas [25]. A groundbreaking study recently presents an intriguing analytical formulation for steady-state axisymmetric magnetized accretion disk configurations surrounding Kerr black holes, transcending previous methodologies exclusively reliant on numerical simulations or weakly magnetized approximations [26].
Several mechanisms have been proposed to explain jet formation and energy extraction. The BZ mechanism [11] describes how rotating black holes power jets via magnetic fields, whereas the BP mechanism [14] suggests that jets can originate from the accretion disk itself. Recent studies [27] have indicated that jet formation is strongly coupled to accretion flow properties, suggesting a non-negligible contribution of jet luminosity to the observed emission. However, most existing accretion disk models, including the classical Novikov-Thorne model [8–9], neglect the impact of jet radiation.
To bridge this gap, we propose a "jet-modified Novikov-Thorne disk model," which explicitly incorporates jet luminosity into the accretion disk radiation framework. By integrating synchrotron emission from relativistic electrons in the jet [28], we derive a modified luminosity function and analyze its impact on the observed flux. Our work aims to provide a more complete description of accretion disk radiation, which is crucial for accurately interpreting black hole observations.
-
In this section, we investigate a static spherically symmetric black hole metric described by the equation
$ {\rm d}s^{2}=-f(r){\rm d}t^{2}+f(r)^{-1}{\rm d}r^{2}+r^{2}({\rm d}\theta^{2}+\sin^{2}\theta {\rm d}\phi^{2}). $

(1) Here,
$ f(r) $ represents the black hole metric potential, which can be expressed as$ f(r) = 1 - \frac{2M}{r}, $

(2) where M represents the mass of the black hole. Assuming a geometrically thin and optically thick accretion disk surrounding the black hole, we calculate the electromagnetic radiation flux (
$ \rm ergs^{-1}cm^{-2}str^{-1}Hz^{-1} $ ) emitted from a specific radial position r on the disk using the following equation [29]:$ F = - \frac{\dot{M}}{4\pi \sqrt{\rm -I}} \frac{\Omega_{,\rm r}}{(E-\Omega L)^{2}} \int_{r_{\rm in}}^{r} (E- \Omega L)L_{,\rm r} {\rm d} r, $

(3) where
$ \dot{M} $ represents the mass accretion rate, I is the determinant of the induced metric in the equatorial plane, and$ r_{\rm in} $ denotes the inner edge of the accretion disk. The parameters E, Ω, and L represent the angular velocity, energy, and angular momentum of the particles in a circular orbit, respectively [30]:$ \begin{eqnarray} &&E= - \frac{g_{\rm tt} + g_{\rm t \phi} \Omega}{\sqrt{-g_{\rm tt} + 2g_{\rm t \phi}\Omega - g_{\rm \phi \phi}\Omega^{2}}}, \end{eqnarray} $

(4) $ \begin{eqnarray} &&L= \frac{g_{\rm t \phi} + g_{\rm \phi \phi} \Omega}{\sqrt{-g_{\rm tt} + 2g_{\rm t \phi}\Omega - g_{\rm \phi \phi}\Omega^{2}}}, \end{eqnarray} $

(5) $ \begin{eqnarray} &&\Omega=\frac{{\rm d}\phi}{{\rm d}t}=\frac{-g'_{\rm t \phi} + \sqrt{(g'_{\rm t \phi})^{2} - g'_{\rm tt}g'_{\rm \phi \phi}}}{g'_{\rm \phi \phi}}. \end{eqnarray} $

(6) According to Eqs. (2)−(6), the radiation flux over the disk for a Schwarzschild black hole is [9]
$ F_{\rm disk}(r) = - \frac{3 \dot{M} \sqrt{{M}/{r^{3}}}}{\pi r(24M - 8r)} \int_{r_{\rm in}}^{r} \frac{(6M-r)\sqrt{{M}/{r^{3}}}r}{6M-2r} \mathrm{d}r. $

(7) Meanwhile, the luminosity of a black hole jet is produced by high-energy particles that emit synchrotron radiation in a magnetic field. The resulting radiation spectrum depends on factors such as the magnetic field strength, energy distribution of electrons, and angle between the electron velocity and magnetic field. The total luminosity of the jet is obtained by integrating the synchrotron radiation from all electrons in the jet. By combining the accretion disk and jet luminosity models, we investigate how the jet affects the optical appearance of the accretion disk. To construct our jet model, we assume that the relativistic electrons in the jet follow a power-law energy distribution [13]:
$ N(\gamma) = N_0 \gamma^{-p}, $

(8) where γ is the Lorentz factor, p is the spectral index, and
$ N_0 $ is the normalization factor. The synchrotron radiation power emitted per unit frequency is given by [31]$ P_{\nu} = \frac{\sqrt{3} q_e^3 B \sin{\theta}}{m_e c^2} \int\limits_{\gamma_{\min}}^{\gamma_{\max}} N(\gamma) F\left( \frac{\nu}{\nu_c(\gamma)} \right) \mathrm{d}\gamma, $

(9) where B is the magnetic field strength, θ is the pitch angle, and
$ \nu_c $ is the critical frequency [31].$ \nu_c(\gamma) = \frac{3 q_e B}{4 \pi m_e c} \gamma^2. $

(10) Full derivations are provided in Appendix A. We incorporate this emission mechanism into the Novikov-Thorne model to account for the additional contribution of the jet to the total flux. Furthermore, the interaction between the jet and accretion disk introduces an additional radiative component due to Compton upscattering of disk photons by relativistic electrons in the jet. This process enhances the observed flux and modifies the spectral energy distribution (SED) of the accretion disk emission. The observed flux incorporating jet contributions is given by
$ F_{\rm total} = F_{\rm disk} + F_{\rm jet}, $

(11) where
$ F_{\rm jet} $ includes both synchrotron and inverse Compton contributions.To visualize the effects of jet contributions, we compare the standard Novikov-Thorne model with our modified model in Fig. 1. It is evident that jet radiation significantly enhances the observed luminosity, particularly at higher frequencies.
-
To obtain the observable radiant flux for a distant observer, the correction for gravitational redshift must be considered. The redshift factor, denoted by
$ d = 1 + z $ , is the ratio of emitted photon energy$ E_{\rm em} $ to observed photon energy$ E_{\rm obs} $ and accounts for the gravitational potential difference between the source and observer. In general relativity, the projection of photon four-momentum$ k_{\mu} $ onto the four-velocities of the source$ p_{\rm source}^{\mu} $ and observer$ p_{\rm obs}^{\mu} $ must be taken into account to calculate$ E_{\rm obs} $ . The redshift factor can be calculated as follows [32]:$ d = 1 + z = \frac{E_{\rm em}}{E_{\rm obs}}. $

(12) The emitted energy
$ E_{\rm em} $ is given by$ E_{\rm em} = p_{\rm t} u^{\rm t} + p_{\rm \phi} u^{\rm \phi} = p_{\rm t} u^{\rm t} \Bigg(1 + \Omega \frac{p_{\rm \phi}}{p_{\rm t}}\Bigg), $

(13) where
$ p_{\rm t} $ and$ p_{\rm \phi} $ represent the photon four-momentum. For observers at a large distance, the ratio$ p_{\rm t}/p_{\rm \phi} $ represents the impact parameter of the photons relative to the z-axis. The redshift factor d can be rewritten as$ d = 1 + z = \frac{E_{\rm em}}{E_{\rm obs}} = \frac{1 + b \Omega \cos \theta_{0}}{\sqrt{-g_{\rm tt} - 2 g_{\rm t \phi} g^{\rm t \phi} - g_{\rm \phi\phi}}}, $

(14) where b represents the impact parameter, derived from the determination of the photon orbit around the black hole.
$ \theta_{0} $ is the observing inclination angle.From the above discussion, the observed flux of the accretion disk can be expressed in terms of the redshift factor as follows [33]:
$ F_{\rm obs} = \frac{F_{\rm total}}{(1 + z)^{4}}. $

(15) Our model accounts for the contribution of the jet to the accretion disk luminosity, resulting in a brighter accretion disk image for a distant observer compared to the standard Novikov-Thorne model, which considers only accretion material. We present the impact of the jet flow on the observed brightness of the accretion disk in Fig. 2. Our findings demonstrate noticeable differences in brightness at various observation angles (
$ \theta_{0} $ ). Specifically, we show that the jet flow contributes approximately 25.3% of the total luminosity, resulting in a 33.8% increase in the brightness of the accretion disk compared to the standard Novikov-Thorne model.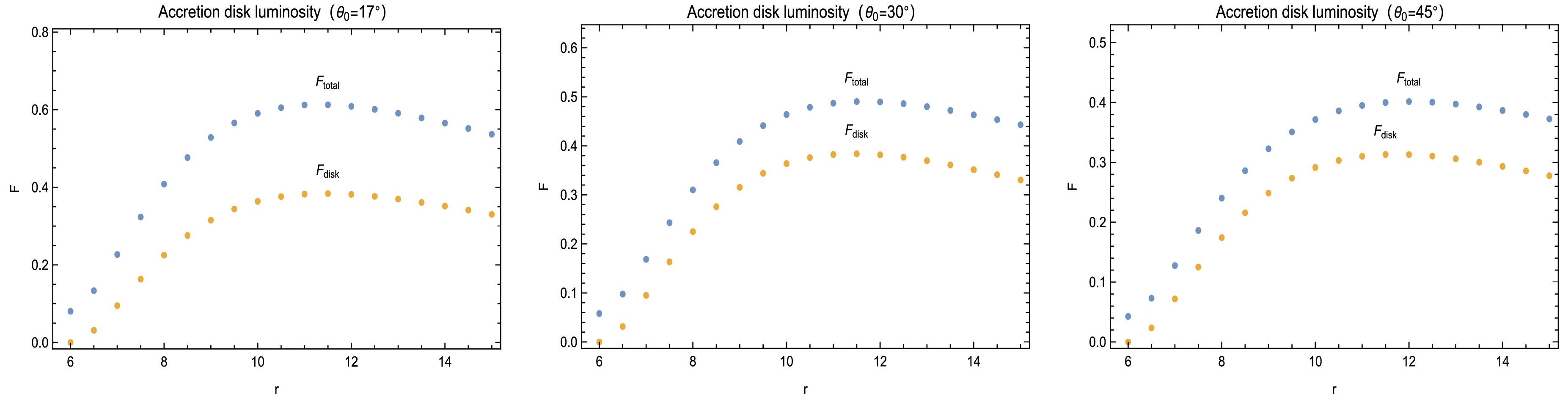
Figure 2. (color online) Observable luminosity of the Novikov-Thorne model and jet model of Novikov-Thorne disk.
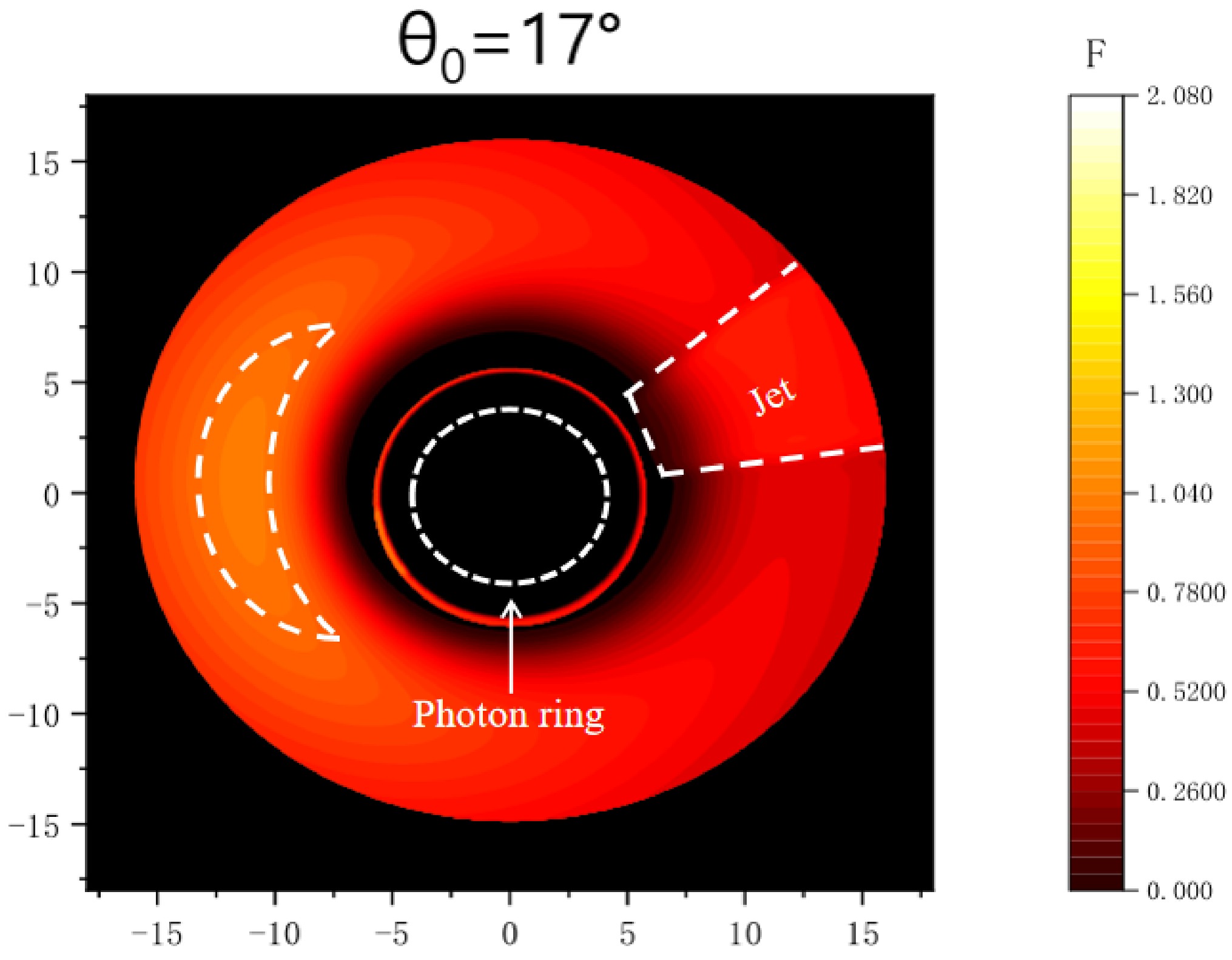
We employed an optical tracking code to generate visual representations of a Novikov-Thorne disk model that includes jet contributions. Our results, as depicted in Fig. 3, demonstrate a distinct concentration of brightness on the left side of the accretion disk, a consequence of the complex geometric interplay between the movement of matter and propagation of light within the disk. Notably, there is also a pronounced accumulation of brightness in the northeast region of the image, which we attribute to the jet. To further investigate this phenomenon, we captured images from different observation angles and found that the additional luminosity persists regardless of the observation angle, confirming its dependence on the physical properties of the source itself. Furthermore, our analysis revealed a significant increase in brightness due to the jet flow in the southwest region of the secondary image shown in Fig. 4.
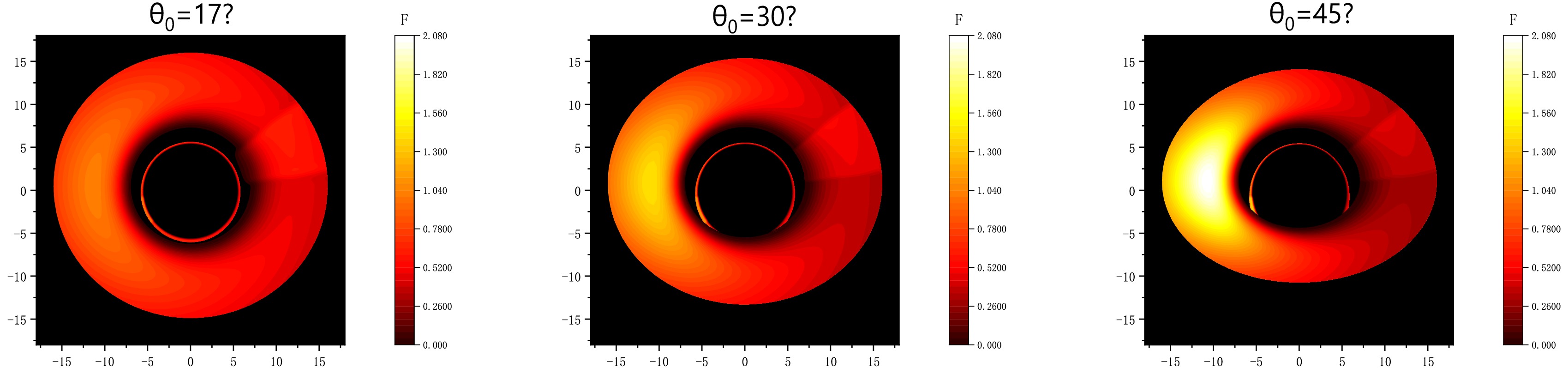
Figure 4. (color online) Images of an accretion disk with different observation angles. The position of the secondary image corresponds to the inner edge of the disk at
$ r_{\rm in} = 6M $ , and the outer edge of the disk is at$ r_{\rm out} = 15M $ .We applied a Gaussian blur to the jet model of the Novikov-Thorne disk and obtained the image shown in Fig. 5. This image clearly shows the black hole shadow as a dark region surrounding the black hole. The halo surrounding the shadow is also significant and results from the gravitational lensing effect. Moreover, our analysis identified two bright regions in the western and northeastern directions of the direct image, which can be attributed to the accretion and jet flow of matter around the black hole. This result also revealed that the observed images of the accretion disk are closely related to the observing inclination angle.
-
In this letter, we introduce a novel jet model of the Novikov-Thorne disk and derive a general formula for the accretion disk luminosity that includes the jet contribution. Our findings demonstrate that black hole jets have a significant impact on the observable characteristics of black holes. While the motion of material in the accretion disk of a black hole is influenced by its gravitational and magnetic fields, resulting in the emission of radiation such as X-rays and ultraviolet light, the contribution of black hole jet luminosity to this radiation has not been taken into account in the conventional Novikov-Thorne model. Consequently, the observable flux function can be written as
$ F_{\rm total} = F_{\rm disk} + F_{\rm jet}. $

(16) Our analysis demonstrates that after incorporating the black hole jet luminosity, the luminosity of black hole radiation can increase by approximately 33.8%. This result suggests that accurately estimating the luminosity of black hole jets can provide a means of determining the observable radiant flux. The contribution of the jet persists at different observed inclinations, as shown by our comparison of the Novikov-Thorne model with our jet model. By extending the Novikov-Thorne model, our approach provides a more precise representation of observational data. Our work underscores the importance of considering black hole jet luminosity when estimating the observable radiant flux, which could advance our understanding of black hole behavior.
Our findings indicate that the inclusion of jet luminosity leads to a substantial increase in the observed brightness of the accretion disk. This is consistent with recent EHT observations of M87*, which revealed that jet-disk interactions significantly enhance millimeter-wavelength emissions [27].
Compared to previous models [3, 34], our approach explicitly accounts for the angle-dependent jet contribution to the observed flux. However, our model does not yet incorporate the time-dependent evolution of the jet, which can be explored in future work using full GRMHD simulations. Additionally, investigating the impact of jet precession and variability could further refine our understanding of jet-disk interactions.
-
Here, we present the detailed derivation of Eqs. (9) and (10). For a single relativistic electron, the spectral power peaks near the critical frequency
$ \nu_c $ , governed by the function$ P_{\nu}(\gamma)\propto\gamma^2B^2F \Big(\frac{\nu}{\nu_c(\gamma)}\Big). $

(A1) Maximizing
$ F(x) $ at$ x = 1 $ (i.e.,$ \nu = \nu_c $ ) gives$ \frac{\mathrm{d}F(x)}{\mathrm{d}x}\Big|_{x=1}=0, $

(A2) to
$ \nu=\nu_c(\gamma). $

(A3) Nonrelativistic gyrofrequency is as follows:
$ \nu_g=\frac{q_eB}{2\pi m_ec}. $

(A4) Time dilation increases the observed orbital period by γ:
$ \Delta t_{\rm obs}=\gamma\Delta t_{\rm rest}. $

(A5) Lorentz contraction shortens radiation pulse duration by γ:
$ \Delta t\sim\frac{1}{\gamma^2\nu_g}. $

(A6) Combined, the observed critical frequency scales as follows:
$ \nu_c(\gamma)\propto\gamma^2\nu_g=\gamma^2\frac{q_eB}{2\pi m_ec}. $

(A7) By rigorously computing the Fourier transform of the radiation field, the peak corresponds to the integral of the Bessel function
$ K_{5/3}(x) $ :$ F \left(\frac{\nu}{\nu_c}\right)\propto\int_{0}^{\infty}K_\frac{5}{3}(x)\mathrm{d}x, $

(A8) which introduces the factor
$ {3}/{4\pi} $ . Substituting back gives$ \nu_c(\gamma) = \frac{3 q_e B}{4 \pi m_e c} \gamma^2. $

(A9)
A novel jet model for the Novikov-Thorne disk and its observable impact
- Received Date: 2024-11-27
- Available Online: 2025-08-15
Abstract: Recent high-resolution observations have established a strong link between black hole jets and accretion disk structures, particularly in the 3.5 mm wavelength band [Nature. 616,686 (2023)]. In this work, we propose a "jet-modified Novikov-Thorne disk model" that explicitly incorporates jet luminosity into the accretion disk radiation framework. By integrating synchrotron radiation from relativistic electrons in the jet, we derive a modified luminosity function that accounts for both the accretion disk and jet contributions. Our analysis demonstrates that the inclusion of jet luminosity enhances the total accretion disk luminosity by approximately 33.5%, as derived from the integration of radiative flux. Furthermore, we compare our modified model with the standard Novikov-Thorne model and find that the jet contribution remains significant across different observational inclinations. These results highlight the necessity of incorporating jet effects when estimating the observable flux of black hole accretion systems, which has direct implications for future astronomical observations.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: