-
The possibility of additional Higgs states beyond the Standard Model (SM) is an open question. The emergence of experimental anomalies hinting at a scalar resonance around 95.4 GeV has generated significant interest within the high-energy physics community. Hints of a light scalar near 95.4 GeV first appeared in searches at the Large Electron–Positron (LEP) collider, where a 2.3σ excess in the
$ e^+ e^-\to Z\phi $ process with$ \phi\to b\bar{b} $ was reported [1]. Recently, the CMS collaboration has observed a local significance of 2.9σ in the diphoton invariant mass spectrum around 95.4 GeV using a full Run 2 data set of the Large Hardon Collider (LHC) [2]. The ATLAS experiment has also observed an excess in the diphoton channel, albeit with a lower significance [3]. Neglecting possible correlations, the combined signal strength of ATLAS and CMS has a$ 3.1\sigma $ local excess in the diphoton channel around 95.4 GeV [4]. There are numerous explanations of the excesses in the new physics models [4−62].In contrast, current observations from several pulsar timing array (PTA) collaborations have yielded strong statistical evidence for a stochastic gravitational wave background (SGWB) in the nano-Hertz regime, including NANOGrav [63, 64], the European Pulsar Timing Array (EPTA) [65, 66], the Parkes Pulsar Timing Array (PPTA) [67], and the Chinese Pulsar Timing Array (CPTA) [68]. In addition to the supermassive black hole binaries interpretation [69], there are various cosmological sources of the gravitational waves (GWs), such as cosmic strings [70−80], domain walls [81−93], primordial first-order phase transitions [94−115], and inflation [116−127].
This study explores the possibility of simultaneously explaining the observed excess of 95.4 GeV Higgs boson and the nano-Hertz SGWB within the framework of the two-Higgs-doublet model extended by a real singlet scalar, known as the next-to-two-Higgs-doublet model (N2HDM) [6−8, 128−130]. In this model, the 95.4 GeV Higgs boson arises from the mixing among three CP-even scalar fields, including the singlet field. In addition, the N2HDM respects a discrete
$ Z_2 $ symmetry, which is spontaneously broken by the non-zero vacuum expectation value (VEV) of the singlet scalar. The spontaneous breaking of this discrete$ Z_2 $ symmetry in the early Universe leads to the formation of domain walls that separate regions of distinct vacua. Sassi and Moortgat-Pick [131] studied the possibility of restoring the electroweak symmetry in the N2HDM via the domain walls. To ensure that the domain walls are unstable and eventually annihilate, the discrete symmetry is explicitly broken by introducing a very small bias term. The peak frequency of GWs produced by the domain walls is set by the time of annihilation, while the amplitude depends on the energy density of domain wall. This model has the potential to generate domain walls whose dynamics may produce GWs in the nano-Hertz frequency band, offering a possible explanation for the NANOGrav data.The remainder of this paper is organized as follows. Section II presents the key features of the N2HDM. Sections III and IV examine the relevant theoretical and experimental constraints and discuss the explanation of the diphoton and
$ b\bar{b} $ excesses at 95.4 GeV. Section V explores the domain walls and the associated GW spectra. Finally, Section VI summarizes the conclusions. -
The possibility of additional Higgs states beyond the Standard Model (SM) is an open question. The emergence of experimental anomalies hinting at a scalar resonance around 95.4 GeV has generated significant interest within the high-energy physics community. Hints of a light scalar near 95.4 GeV first appeared in searches at the Large Electron–Positron (LEP) collider, where a 2.3σ excess in the
$ e^+ e^-\to Z\phi $ process with$ \phi\to b\bar{b} $ was reported [1]. Recently, the CMS collaboration has observed a local significance of 2.9σ in the diphoton invariant mass spectrum around 95.4 GeV using a full Run 2 data set of the Large Hardon Collider (LHC) [2]. The ATLAS experiment has also observed an excess in the diphoton channel, albeit with a lower significance [3]. Neglecting possible correlations, the combined signal strength of ATLAS and CMS has a$ 3.1\sigma $ local excess in the diphoton channel around 95.4 GeV [4]. There are numerous explanations of the excesses in the new physics models [4−62].In contrast, current observations from several pulsar timing array (PTA) collaborations have yielded strong statistical evidence for a stochastic gravitational wave background (SGWB) in the nano-Hertz regime, including NANOGrav [63, 64], the European Pulsar Timing Array (EPTA) [65, 66], the Parkes Pulsar Timing Array (PPTA) [67], and the Chinese Pulsar Timing Array (CPTA) [68]. In addition to the supermassive black hole binaries interpretation [69], there are various cosmological sources of the gravitational waves (GWs), such as cosmic strings [70−80], domain walls [81−93], primordial first-order phase transitions [94−115], and inflation [116−127].
This study explores the possibility of simultaneously explaining the observed excess of 95.4 GeV Higgs boson and the nano-Hertz SGWB within the framework of the two-Higgs-doublet model extended by a real singlet scalar, known as the next-to-two-Higgs-doublet model (N2HDM) [6−8, 128−130]. In this model, the 95.4 GeV Higgs boson arises from the mixing among three CP-even scalar fields, including the singlet field. In addition, the N2HDM respects a discrete
$ Z_2 $ symmetry, which is spontaneously broken by the non-zero vacuum expectation value (VEV) of the singlet scalar. The spontaneous breaking of this discrete$ Z_2 $ symmetry in the early Universe leads to the formation of domain walls that separate regions of distinct vacua. Sassi and Moortgat-Pick [131] studied the possibility of restoring the electroweak symmetry in the N2HDM via the domain walls. To ensure that the domain walls are unstable and eventually annihilate, the discrete symmetry is explicitly broken by introducing a very small bias term. The peak frequency of GWs produced by the domain walls is set by the time of annihilation, while the amplitude depends on the energy density of domain wall. This model has the potential to generate domain walls whose dynamics may produce GWs in the nano-Hertz frequency band, offering a possible explanation for the NANOGrav data.The remainder of this paper is organized as follows. Section II presents the key features of the N2HDM. Sections III and IV examine the relevant theoretical and experimental constraints and discuss the explanation of the diphoton and
$ b\bar{b} $ excesses at 95.4 GeV. Section V explores the domain walls and the associated GW spectra. Finally, Section VI summarizes the conclusions. -
The possibility of additional Higgs states beyond the Standard Model (SM) is an open question. The emergence of experimental anomalies hinting at a scalar resonance around 95.4 GeV has generated significant interest within the high-energy physics community. Hints of a light scalar near 95.4 GeV first appeared in searches at LEP collider, where a 2.3σ excess in the
$ e^+ e^-\to Z\phi $ process with$ \phi\to b\bar{b} $ was reported [1]. Recently, the CMS collaboration has observed a local significance of 2.9σ in the diphoton invariant mass spectrum around 95.4 GeV using full Run 2 data set of LHC [2]. The ATLAS experiment has also observed an excess in the diphoton channel, albeit with a lower significance [3]. Neglecting possible correlations, the combined signal strength of ATLAS and CMS has a$ 3.1\sigma $ local excess in the diphoton channel around 95.4 GeV [4]. There are numerous explanations on the excesses in the new physics models, for example Refs. [4−62].On the other hand, current observations from several pulsar timing array (PTA) collaborations have yielded strong statistical evidence for a stochastic gravitational wave background (SGWB) in the nano-Hertz regime, including NANOGrav [63,64], the European Pulsar Timing Array (EPTA) [65,66], the Parkes Pulsar Timing Array (PPTA) [67], and the Chinese Pulsar Timing Array (CPTA) [68]. In addition to the supermassive black hole binaries interpretation [69], there are various cosmological sources of the gravitational waves (GWs), such as cosmic strings [70−80], domain walls [81−93], primordial first-order phase transitions [94−115], and inflation [116−127].
In this paper, we explore the possibility of simultaneously explaining the observed excess of 95.4 GeV Higgs boson and the nano-Hertz SGWB within the framework of the two-Higgs-doublet model extended by a real singlet scalar, commonly referred to as the N2HDM [6−8,128−130]. In this model, the 95.4 GeV Higgs boson arises from the mixing among three CP-even scalar fields, including the singlet field. In addition, the N2HDM respects a discrete
$ Z_2 $ symmetry, which is spontaneously broken by the non-zero vacuum expectation value (VEV) of the singlet scalar. The spontaneous breaking of this discrete$ Z_2 $ symmetry in the early Universe leads to the formation of domain walls that separate regions of distinct vacua. The authors of [131] studied the possibility of restoring the electroweak symmetry in the N2HDM via the domain walls. To ensure that the domain walls are unstable and eventually annihilate, the discrete symmetry is explicitly broken by introducing a very small bias term. The peak frequency of GWs produced by the domain walls is set by the time of annihilation, while the amplitude depends on the energy density of domain wall. This model has the potential to generate domain walls whose dynamics may produce GWs in the nano-Hertz frequency band, offering a possible explanation for the NANOGrav data.The remainder of this paper is organized as follows. In Section II we present the key features of the N2HDM. In Sections III and IV, we examine the relevant theoretical and experimental constraints, and discuss the explanation of the diphoton and
$ b\bar{b} $ excesses at 95.4 GeV. In Section V we explore the domain walls and the associated GW spectra. Finally, we summarize our conclusions in Section VI. -
The possibility of additional Higgs states beyond the Standard Model (SM) is an open question. The emergence of experimental anomalies hinting at a scalar resonance around 95.4 GeV has generated significant interest within the high-energy physics community. Hints of a light scalar near 95.4 GeV first appeared in searches at the Large Electron–Positron (LEP) collider, where a 2.3σ excess in the
$ e^+ e^-\to Z\phi $ process with$ \phi\to b\bar{b} $ was reported [1]. Recently, the CMS collaboration has observed a local significance of 2.9σ in the diphoton invariant mass spectrum around 95.4 GeV using a full Run 2 data set of the Large Hardon Collider (LHC) [2]. The ATLAS experiment has also observed an excess in the diphoton channel, albeit with a lower significance [3]. Neglecting possible correlations, the combined signal strength of ATLAS and CMS has a$ 3.1\sigma $ local excess in the diphoton channel around 95.4 GeV [4]. There are numerous explanations of the excesses in the new physics models [4−62].In contrast, current observations from several pulsar timing array (PTA) collaborations have yielded strong statistical evidence for a stochastic gravitational wave background (SGWB) in the nano-Hertz regime, including NANOGrav [63, 64], the European Pulsar Timing Array (EPTA) [65, 66], the Parkes Pulsar Timing Array (PPTA) [67], and the Chinese Pulsar Timing Array (CPTA) [68]. In addition to the supermassive black hole binaries interpretation [69], there are various cosmological sources of the gravitational waves (GWs), such as cosmic strings [70−80], domain walls [81−93], primordial first-order phase transitions [94−115], and inflation [116−127].
This study explores the possibility of simultaneously explaining the observed excess of 95.4 GeV Higgs boson and the nano-Hertz SGWB within the framework of the two-Higgs-doublet model extended by a real singlet scalar, known as the next-to-two-Higgs-doublet model (N2HDM) [6−8, 128−130]. In this model, the 95.4 GeV Higgs boson arises from the mixing among three CP-even scalar fields, including the singlet field. In addition, the N2HDM respects a discrete
$ Z_2 $ symmetry, which is spontaneously broken by the non-zero vacuum expectation value (VEV) of the singlet scalar. The spontaneous breaking of this discrete$ Z_2 $ symmetry in the early Universe leads to the formation of domain walls that separate regions of distinct vacua. Sassi and Moortgat-Pick [131] studied the possibility of restoring the electroweak symmetry in the N2HDM via the domain walls. To ensure that the domain walls are unstable and eventually annihilate, the discrete symmetry is explicitly broken by introducing a very small bias term. The peak frequency of GWs produced by the domain walls is set by the time of annihilation, while the amplitude depends on the energy density of domain wall. This model has the potential to generate domain walls whose dynamics may produce GWs in the nano-Hertz frequency band, offering a possible explanation for the NANOGrav data.The remainder of this paper is organized as follows. Section II presents the key features of the N2HDM. Sections III and IV examine the relevant theoretical and experimental constraints and discuss the explanation of the diphoton and
$ b\bar{b} $ excesses at 95.4 GeV. Section V explores the domain walls and the associated GW spectra. Finally, Section VI summarizes the conclusions. -
The two-Higgs-doublet model is extented by introducing a real singlet scalar,
$ \begin{aligned}[b] &\Phi_1=\left(\begin{array}{c} \phi_1^+ \\ \dfrac{(v_1+\rho_1+i\eta_1)}{\sqrt{2}}\, \end{array}\right)\,, \Phi_2=\left(\begin{array}{c} \phi_2^+ \\ \dfrac{(v_2+\rho_2+i\eta_2)}{\sqrt{2}}\, \end{array}\right),\\& \Phi_S=\rho_s+v_s, \end{aligned} $

(1) After spontaneous symmetry breaking, the fields
$ \Phi_1, \Phi_2 $ and$ \Phi_S $ acquire their VEVs$ v_1 $ ,$ v_2 $ , and$ v_s $ , with$ v\equiv \sqrt{v_1^2+v_2^2}=246 $ GeV. The ratio of the two-Higgs-doublet VEVs is defined as$ \tan\beta \equiv v_2 /v_1 $ .The Higgs potential is written as
$ \begin{aligned}[b] V =\;& m_{11}^2 |\Phi_1|^2 + m_{22}^2 |\Phi_2|^2 - m_{12}^2 (\Phi_1^\dagger \Phi_2 + \text{h.c.})\\& + \frac{\lambda_1}{2} (\Phi_1^\dagger \Phi_1)^2 + \frac{\lambda_2}{2} (\Phi_2^\dagger \Phi_2)^2 \\ & + \lambda_3 (\Phi_1^\dagger \Phi_1) (\Phi_2^\dagger \Phi_2) + \lambda_4 (\Phi_1^\dagger \Phi_2) (\Phi_2^\dagger \Phi_1) \\&+ \frac{\lambda_5}{2} [(\Phi_1^\dagger \Phi_2)^2 + \text{h.c.}] + \frac{m_S^2}{2} \Phi_S^2 + \frac{\lambda_6}{8} \Phi_S^4\\ & + \frac{\lambda_7}{2} (\Phi_1^\dagger \Phi_1) \Phi_S^2 + \frac{\lambda_8}{2} (\Phi_2^\dagger \Phi_2) \Phi_S^2. \end{aligned} $

(2) We assume that the model conserves CP-symmetry, meaning all coupling constants and mass parameters to be real. The Higgs potential in Eq. (2) respects a discrete
$ Z_2 $ symmetry,$ \begin{array}{*{20}{l}} \Phi_1\to\Phi_1\,,\ \Phi_2\to\Phi_2\,,\ \Phi_S\to -\Phi_S\,, \end{array} $

(3) which is spontaneously broken by the VEV of
$ \Phi_S $ , giving rise to domain walls in the early Universe. The conditions for minimizing the scalar potential lead to$ v_2 m_{12}^2 - v_1 m_{11}^2 = \frac{1}{2} (v_1^3 \lambda_1 + v_2^2 v_1 \lambda_{345} + v_s^2 v_1 \lambda_7)\,, $

(4) $ v_1 m_{12}^2 - v_2 m_{22}^2 = \frac{1}{2} (v_1^2 v_2 \lambda_{345} + v_2^3 \lambda_2 + v_s^2 v_2 \lambda_8)\,, $

(5) $ - v_s m_S^2 = \frac{1}{2} v_s (v_1^2 \lambda_7 + v_2^2 \lambda_8 + v_s^2 \lambda_6)\,, $

(6) where
$ \lambda_{345} \equiv \lambda_3 + \lambda_4 + \lambda_5 $ .It is necessary to introduce an energy bias in the potential, which lifts the degenerate minima connected by the discrete
$ Z_2 $ symmetry. This bias destabilizes the domain walls, thereby evading the associated cosmological constraints [132−134]. Here we introduce the$ Z_2 $ symmetry-breaking potential term by hand,$ V_{\not{Z}_2}=-a_1 v_s^2 \Phi_S + \frac{a_1}{3} \Phi_S^3 \,. $

(7) The total potential still has minima at
$ (v_1,v_2,\pm v_s) $ , but there is an energy difference between them$ V_{\rm bias}=V(v_1,v_2,-v_s)-V(v_1,v_2,v_s)=\frac{4}{3}a_1 v_s^3 \,. $

(8) In fact, since the required values of
$ a_1 $ is extremely small, we only consider it in the discussions of domain walls, and neglect it in other calculations.Once spontaneous symmetry breaking occurs, the mass eigenstates are derived from the original fields through the application of rotation matrices
$ \begin{array}{*{20}{l}} \left(\begin{array}{c}h_1,h_2,h_3 \end{array}\right) = \left(\begin{array}{c} \rho_1, \rho_2, \rho_s\end{array} \right) R^T, \end{array} $

(9) $ \begin{array}{*{20}{l}} \left(\begin{array}{c}G^0 \\ A \end{array}\right) = \left(\begin{array}{cc}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{array}\right) \left(\begin{array}{c} \eta_1 \\ \eta_2 \end{array}\right) , \end{array} $

(10) $ \begin{array}{*{20}{l}} \left(\begin{array}{c}G^{\pm} \\ H^{\pm} \end{array}\right) = \left(\begin{array}{cc}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{array}\right) \left(\begin{array}{c} \phi^{\pm}_1 \\ \phi^{\pm}_2 \end{array}\right), \end{array} $

(11) with
$ \begin{array}{*{20}{l}} R= \left( \begin{array}{*{20}{c}} c_{1} c_{2} & s_{1} c_{2} & s_{2}\\ - s_{1} c_{3}-c_{1} s_{2} s_{3} & c_{1} c_{3}-s_{1} s_{2} s_{3} & c_{2} s_{3} \\ s_{ 1} s_{3}-c_{1} s_{2} c_{3} &- s_{1} s_{2}c_{3} -c_{1} s_{3} & c_{2} c_{3} \end{array} \right). \end{array} $

(12) The shorthand notations are
$ s_{1,2,3}\equiv\sin\alpha_{1,2,3} $ and$ c_{1,2,3}\equiv\cos\alpha_{1,2,3} $ . The$ G^0 $ and$ G^\pm $ correspond to the Goldstone bosons, which are absorbed by the Z and$ W^\pm $ . The remaining physical states consist of three CP-even scalars$ h_{1,2,3} $ , one pseudoscalars A, and a pair of charged scalar$ H^{\pm} $ .The coupling constants in the Higgs potential can be expressed in terms of the scalar masses and mixing angles as
$ \begin{aligned}[b] &\lambda_1 = \frac{ m_{h_1}^2 R_{11}^2+m_{h_2}^2 R_{21}^2 +m_{h_3}^2 R_{31}^2 - m_{12}^2 t_\beta}{v^2 c_\beta^2}, \\ & \lambda_2 = \frac{ m_{h_1}^2 R_{12}^2 +m_{h_2}^2 R_{22}^2+m_{h_3}^2 R_{32}^2- m_{12}^2 t_\beta^{-1}}{v^2 s_\beta^2}, \\ &\lambda_3 = \frac{m_{h_1}^2 R_{11}R_{12}+m_{h_2}^2 R_{21}R_{22}+m_{h_3}^2 R_{31}R_{32}+ 2 m_{H^{\pm}}^2 s_\beta c_\beta - m_{12}^2}{v^2 s_\beta c_\beta }, \\ &\lambda_4 = \frac{(m_A^2-2m_{H^{\pm}}^2 ) s_\beta c_\beta + m_{12}^2}{v^2 s_\beta c_\beta }, \\ &\lambda_5= \frac{ - m_A^2 s_\beta c_\beta + m_{12}^2}{ v^2 s_\beta c_\beta }, \\ &\lambda_6= \frac{m_{h_1}^2 R_{13}^2+m_{h_2}^2 R_{23}^2+m_{h_3}^2 R_{33}^2-2 a_1 v_s}{v_s^2} , \\ &\lambda_7= \frac{m_{h_1}^2 R_{11} R_{13}+m_{h_2}^2 R_{21} R_{23}+m_{h_3}^2 R_{31} R_{33}}{v v_s c_\beta}, \\ &\lambda_8=\frac{m_{h_1}^2 R_{12} R_{13}+m_{h_2}^2 R_{22} R_{23}+m_{h_3}^2 R_{32} R_{33}}{v v_s s_\beta}, \\ \end{aligned} $

(13) with shorthand notation
$ t_{\beta}\equiv\tan\beta $ .In order to avoid the flavor changing neutral current at the tree-level, one imposes a
$ \mathbb{Z'}_2 $ symmetry (see, e.g., the recent review [135]),$ \begin{array}{*{20}{l}} u_R\to -u_R\,,\ d_R\to-d_R\,,\ e_R\to -e_R\,, \Phi_2\to -\Phi_2, \end{array} $

(14) while the other fields remain unchanged. This results in the well-known type-I Yukawa interactions,
$ \begin{array}{*{20}{l}} - {\cal L} &=&Y_{u2}\,\overline{Q}_L \, \tilde{{ \Phi}}_2 \,u_R +\,Y_{d2}\, \overline{Q}_L\,{\Phi}_2 \, d_R\, + \, Y_{\ell 2}\,\overline{L}_L \, {\Phi}_2\,e_R+\, \rm{h.c.}\,. \end{array} $

(15) Where
$ Q_L^T=(u_L\,,d_L) $ ,$ L_L^T=(\nu_L\,,l_L) $ ,$ \widetilde\Phi_{2}=i\tau_2 \Phi_{2}^* $ , and$ Y_{u2} $ ,$ Y_{d2} $ and$ Y_{\ell 2} $ are$ 3 \times 3 $ matrices in family space. However, the$ \mathbb{Z'}_2 $ symmetry is explicitly broken in the scalar potential of Eq. (2).The neutral Higgs boson couplings, normalized to the SM values, are given by
$ \begin{aligned}[b] & y^{h_1}_V=c_2 c_{\beta 1},\; y_{f}^{h_1}=c_2 \left(c_{\beta 1}- s_{\beta 1}\kappa_f\right), \\ &y^{h_2}_V = c_3 s_{\beta 1} - s_2 s_3 c_{\beta 1},\\& y^{h_2}_f =c_3 \left(s_{\beta 1}+c_{\beta 1}\kappa_f\right)- s_2 s_3\left(c_{\beta 1} - s_{\beta 1}\kappa_f\right), \\ &y^{h_3}_V = -s_3 s_{\beta 1} - s_2 c_3 c_{\beta 1},\\& y^{h_3}_f = -s_3 \left(s_{\beta 1}+ c_{\beta 1}\kappa_f\right)-s_2 c_3\left(c_{\beta 1} - s_{\beta 1}\kappa_f\right), \\ &y^{A}_V=0,\; y^{A}_{f}=-i\kappa_f\; {\rm (for}\; u),\; y_{f}^{A}=i \kappa_f\; {\rm (for}\; d,\; \ell). \end{aligned} $

(16) Here
$ \kappa_f=1/\tan\beta $ and V stands for Z or W. The shorthand notations are defined as$ c_{\beta 1}\equiv\cos(\beta-\alpha_1) $ and$ s_{\beta 1}\equiv\sin(\beta-\alpha_1) $ .The charged Higgs Yukawa couplings are given by
$ \begin{aligned}[b] \mathcal{L}_Y =\;& - \frac{\sqrt{2}}{v}\, H^+\, \Big\{\bar{u}_i \Big[\kappa_f\,(V_{CKM})_{ij}\; m_{dj} P_R \\&- \kappa_f\,m_{ui}\; (V_{CKM})_{ij} \; P_L\Big] d_j + \kappa_f\,\bar{\nu} m_\ell P_R \ell \Big\}+h.c., \end{aligned} $

(17) where
$ i,j=1,2,3 $ are the index of generation. -
The two-Higgs-doublet model is extented by introducing a real singlet scalar,
$ \begin{aligned}[b] &\Phi_1=\left(\begin{array}{c} \phi_1^+ \\ \dfrac{(v_1+\rho_1+ {\rm i} \eta_1)}{\sqrt{2}}\, \end{array}\right)\,, \Phi_2=\left(\begin{array}{c} \phi_2^+ \\ \dfrac{(v_2+\rho_2+ {\rm i} \eta_2)}{\sqrt{2}}\, \end{array}\right),\\& \Phi_S=\rho_s+v_s. \end{aligned} $
(1) After spontaneous symmetry breaking, the fields
$ \Phi_1, \Phi_2 $ and$ \Phi_S $ acquire their respective VEVs$ v_1 $ ,$ v_2 $ , and$ v_s $ , with$ v\equiv \sqrt{v_1^2+v_2^2}= 246 $ GeV. The ratio of the two-Higgs-doublet VEVs is defined as$ \tan\beta \equiv v_2 /v_1 $ .The Higgs potential is written as
$ \begin{aligned}[b] V =\;& m_{11}^2 |\Phi_1|^2 + m_{22}^2 |\Phi_2|^2 - m_{12}^2 (\Phi_1^\dagger \Phi_2 + \text{h.c.})\\& + \frac{\lambda_1}{2} (\Phi_1^\dagger \Phi_1)^2 + \frac{\lambda_2}{2} (\Phi_2^\dagger \Phi_2)^2 \\ & + \lambda_3 (\Phi_1^\dagger \Phi_1) (\Phi_2^\dagger \Phi_2) + \lambda_4 (\Phi_1^\dagger \Phi_2) (\Phi_2^\dagger \Phi_1) \\&+ \frac{\lambda_5}{2} [(\Phi_1^\dagger \Phi_2)^2 + \text{h.c.}] + \frac{m_S^2}{2} \Phi_S^2 + \frac{\lambda_6}{8} \Phi_S^4\\ & + \frac{\lambda_7}{2} (\Phi_1^\dagger \Phi_1) \Phi_S^2 + \frac{\lambda_8}{2} (\Phi_2^\dagger \Phi_2) \Phi_S^2. \end{aligned} $
(2) It is assumed that the model conserves CP-symmetry, meaning all coupling constants and mass parameters to be real. The Higgs potential in Eq. (2) respects a discrete
$ Z_2 $ symmetry,$ \begin{array}{*{20}{l}} \Phi_1\to\Phi_1\,,\ \Phi_2\to\Phi_2\,,\ \Phi_S\to -\Phi_S\,, \end{array} $
(3) which is spontaneously broken by the VEV of
$ \Phi_S $ , giving rise to domain walls in the early Universe. The conditions for minimizing the scalar potential lead to$ v_2 m_{12}^2 - v_1 m_{11}^2 = \frac{1}{2} (v_1^3 \lambda_1 + v_2^2 v_1 \lambda_{345} + v_s^2 v_1 \lambda_7)\,, $
(4) $ v_1 m_{12}^2 - v_2 m_{22}^2 = \frac{1}{2} (v_1^2 v_2 \lambda_{345} + v_2^3 \lambda_2 + v_s^2 v_2 \lambda_8)\,, $
(5) $ - v_s m_S^2 = \frac{1}{2} v_s (v_1^2 \lambda_7 + v_2^2 \lambda_8 + v_s^2 \lambda_6)\,, $
(6) where
$ \lambda_{345} \equiv \lambda_3 + \lambda_4 + \lambda_5 $ .It is necessary to introduce an energy bias in the potential, which lifts the degenerate minima connected by the discrete
$ Z_2 $ symmetry. This bias destabilizes the domain walls, thereby evading the associated cosmological constraints [132−134]. Here, the$ Z_2 $ symmetry-breaking potential term is introduced by hand,$ V_{\not{Z}_2}=-a_1 v_s^2 \Phi_S + \frac{a_1}{3} \Phi_S^3 \,. $
(7) The total potential still has minima at
$ (v_1,v_2,\pm v_s) $ , but there is an energy difference between them$ V_{\rm bias}=V(v_1,v_2,-v_s)-V(v_1,v_2,v_s)=\frac{4}{3}a_1 v_s^3 \,. $
(8) As the required values of
$ a_1 $ are extremely small, it is only considered in the discussions of domain walls, and neglected in other calculations.Once spontaneous symmetry breaking occurs, the mass eigenstates are derived from the original fields through the application of rotation matrices
$ \begin{array}{*{20}{l}} \left(\begin{array}{c}h_1,h_2,h_3 \end{array}\right) = \left(\begin{array}{c} \rho_1, \rho_2, \rho_s\end{array} \right) R^T, \end{array} $
(9) $ \begin{array}{*{20}{l}} \left(\begin{array}{c}G^0 \\ A \end{array}\right) = \left(\begin{array}{cc}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{array}\right) \left(\begin{array}{c} \eta_1 \\ \eta_2 \end{array}\right) , \end{array} $
(10) $ \begin{array}{*{20}{l}} \left(\begin{array}{c}G^{\pm} \\ H^{\pm} \end{array}\right) = \left(\begin{array}{cc}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{array}\right) \left(\begin{array}{c} \phi^{\pm}_1 \\ \phi^{\pm}_2 \end{array}\right), \end{array} $
(11) with
$ \begin{array}{*{20}{l}} R= \left( \begin{array}{*{20}{c}} c_{1} c_{2} & s_{1} c_{2} & s_{2}\\ - s_{1} c_{3}-c_{1} s_{2} s_{3} & c_{1} c_{3}-s_{1} s_{2} s_{3} & c_{2} s_{3} \\ s_{ 1} s_{3}-c_{1} s_{2} c_{3} &- s_{1} s_{2}c_{3} -c_{1} s_{3} & c_{2} c_{3} \end{array} \right). \end{array} $
(12) The shorthand notations are
$ s_{1,2,3}\equiv\sin\alpha_{1,2,3} $ and$ c_{1,2,3}\equiv \cos\alpha_{1,2,3} $ . The$ G^0 $ and$ G^\pm $ correspond to the Goldstone bosons, which are absorbed by the Z and$ W^\pm $ . The remaining physical states consist of three CP-even scalars$ h_{1,2,3} $ , one pseudoscalars A, and a pair of charged scalar$ H^{\pm} $ .The coupling constants in the Higgs potential can be expressed in terms of the scalar masses and mixing angles as
$ \begin{aligned}[b] &\lambda_1 = \frac{ m_{h_1}^2 R_{11}^2+m_{h_2}^2 R_{21}^2 +m_{h_3}^2 R_{31}^2 - m_{12}^2 t_\beta}{v^2 c_\beta^2}, \\ & \lambda_2 = \frac{ m_{h_1}^2 R_{12}^2 +m_{h_2}^2 R_{22}^2+m_{h_3}^2 R_{32}^2- m_{12}^2 t_\beta^{-1}}{v^2 s_\beta^2}, \\ &\lambda_3 = \frac{m_{h_1}^2 R_{11}R_{12}+m_{h_2}^2 R_{21}R_{22}+m_{h_3}^2 R_{31}R_{32}+ 2 m_{H^{\pm}}^2 s_\beta c_\beta - m_{12}^2}{v^2 s_\beta c_\beta }, \\ &\lambda_4 = \frac{(m_A^2-2m_{H^{\pm}}^2 ) s_\beta c_\beta + m_{12}^2}{v^2 s_\beta c_\beta }, \\ &\lambda_5= \frac{ - m_A^2 s_\beta c_\beta + m_{12}^2}{ v^2 s_\beta c_\beta }, \\ &\lambda_6= \frac{m_{h_1}^2 R_{13}^2+m_{h_2}^2 R_{23}^2+m_{h_3}^2 R_{33}^2-2 a_1 v_s}{v_s^2} , \\ &\lambda_7= \frac{m_{h_1}^2 R_{11} R_{13}+m_{h_2}^2 R_{21} R_{23}+m_{h_3}^2 R_{31} R_{33}}{v v_s c_\beta}, \\ &\lambda_8=\frac{m_{h_1}^2 R_{12} R_{13}+m_{h_2}^2 R_{22} R_{23}+m_{h_3}^2 R_{32} R_{33}}{v v_s s_\beta}, \\ \end{aligned} $
(13) with shorthand notation
$ t_{\beta}\equiv\tan\beta $ .To avoid the flavor changing neutral current at the tree-level, a
$ \mathbb{Z'}_2 $ symmetry is imposed [135],$ \begin{array}{*{20}{l}} u_R\to -u_R\,,\ d_R\to-d_R\,,\ e_R\to -e_R\,, \Phi_2\to -\Phi_2, \end{array} $
(14) while the other fields remain unchanged. This results in the well-known type-I Yukawa interactions,
$ - {\cal L} = Y_{u2}\,\overline{Q}_L \, \tilde{{ \Phi}}_2 \,u_R +\,Y_{d2}\, \overline{Q}_L\,{\Phi}_2 \, d_R\, + \, Y_{\ell 2}\,\overline{L}_L \, {\Phi}_2\,e_R+\, \rm{h.c.}\,. $
(15) where
$ Q_L^T=(u_L\,,d_L) $ ,$ L_L^T=(\nu_L\,,l_L) $ ,$ \widetilde\Phi_{2}={\rm i}\tau_2 \Phi_{2}^* $ , and$ Y_{u2} $ ,$ Y_{d2} $ and$ Y_{\ell 2} $ are$ 3 \times 3 $ matrices in family space. However, the$ \mathbb{Z'}_2 $ symmetry is explicitly broken in the scalar potential of Eq. (2).The neutral Higgs boson couplings, normalized to the SM values, are given by
$ \begin{aligned}[b] & y^{h_1}_V=c_2 c_{\beta 1},\; y_{f}^{h_1}=c_2 \left(c_{\beta 1}- s_{\beta 1}\kappa_f\right), \\ &y^{h_2}_V = c_3 s_{\beta 1} - s_2 s_3 c_{\beta 1},\\& y^{h_2}_f =c_3 \left(s_{\beta 1}+c_{\beta 1}\kappa_f\right)- s_2 s_3\left(c_{\beta 1} - s_{\beta 1}\kappa_f\right), \\ &y^{h_3}_V = -s_3 s_{\beta 1} - s_2 c_3 c_{\beta 1},\\& y^{h_3}_f = -s_3 \left(s_{\beta 1}+ c_{\beta 1}\kappa_f\right)-s_2 c_3\left(c_{\beta 1} - s_{\beta 1}\kappa_f\right), \\ &y^{A}_V=0,\; y^{A}_{f}=-i\kappa_f\; {\rm (for}\; u),\; y_{f}^{A}=i \kappa_f\; {\rm (for}\; d,\; \ell). \end{aligned} $
(16) $ \kappa_f=1/\tan\beta $ and V represents Z or W. The shorthand notations are defined as$ c_{\beta 1}\equiv\cos(\beta-\alpha_1) $ and$ s_{\beta 1}\equiv \sin(\beta-\alpha_1) $ .The charged Higgs Yukawa couplings are given by
$ \begin{aligned}[b] \mathcal{L}_Y =\;& - \frac{\sqrt{2}}{v}\, H^+\, \Big\{\bar{u}_i \Big[\kappa_f\,(V_{\rm CKM})_{ij}\; m_{dj} P_R \\&- \kappa_f\,m_{ui}\; (V_{\rm CKM})_{ij} \; P_L\Big] d_j + \kappa_f\,\bar{\nu} m_\ell P_R \ell \Big\}+ {\rm h.c.}, \end{aligned} $
(17) where
$ i,j=1,2,3 $ are the index of generation. -
The two-Higgs-doublet model is extented by introducing a real singlet scalar,
$ \begin{aligned}[b] &\Phi_1=\left(\begin{array}{c} \phi_1^+ \\ \dfrac{(v_1+\rho_1+ {\rm i} \eta_1)}{\sqrt{2}}\, \end{array}\right)\,, \Phi_2=\left(\begin{array}{c} \phi_2^+ \\ \dfrac{(v_2+\rho_2+ {\rm i} \eta_2)}{\sqrt{2}}\, \end{array}\right),\\& \Phi_S=\rho_s+v_s. \end{aligned} $
(1) After spontaneous symmetry breaking, the fields
$ \Phi_1, \Phi_2 $ and$ \Phi_S $ acquire their respective VEVs$ v_1 $ ,$ v_2 $ , and$ v_s $ , with$ v\equiv \sqrt{v_1^2+v_2^2}= 246 $ GeV. The ratio of the two-Higgs-doublet VEVs is defined as$ \tan\beta \equiv v_2 /v_1 $ .The Higgs potential is written as
$ \begin{aligned}[b] V =\;& m_{11}^2 |\Phi_1|^2 + m_{22}^2 |\Phi_2|^2 - m_{12}^2 (\Phi_1^\dagger \Phi_2 + \text{h.c.})\\& + \frac{\lambda_1}{2} (\Phi_1^\dagger \Phi_1)^2 + \frac{\lambda_2}{2} (\Phi_2^\dagger \Phi_2)^2 \\ & + \lambda_3 (\Phi_1^\dagger \Phi_1) (\Phi_2^\dagger \Phi_2) + \lambda_4 (\Phi_1^\dagger \Phi_2) (\Phi_2^\dagger \Phi_1) \\&+ \frac{\lambda_5}{2} [(\Phi_1^\dagger \Phi_2)^2 + \text{h.c.}] + \frac{m_S^2}{2} \Phi_S^2 + \frac{\lambda_6}{8} \Phi_S^4\\ & + \frac{\lambda_7}{2} (\Phi_1^\dagger \Phi_1) \Phi_S^2 + \frac{\lambda_8}{2} (\Phi_2^\dagger \Phi_2) \Phi_S^2. \end{aligned} $
(2) It is assumed that the model conserves CP-symmetry, meaning all coupling constants and mass parameters to be real. The Higgs potential in Eq. (2) respects a discrete
$ Z_2 $ symmetry,$ \begin{array}{*{20}{l}} \Phi_1\to\Phi_1\,,\ \Phi_2\to\Phi_2\,,\ \Phi_S\to -\Phi_S\,, \end{array} $
(3) which is spontaneously broken by the VEV of
$ \Phi_S $ , giving rise to domain walls in the early Universe. The conditions for minimizing the scalar potential lead to$ v_2 m_{12}^2 - v_1 m_{11}^2 = \frac{1}{2} (v_1^3 \lambda_1 + v_2^2 v_1 \lambda_{345} + v_s^2 v_1 \lambda_7)\,, $
(4) $ v_1 m_{12}^2 - v_2 m_{22}^2 = \frac{1}{2} (v_1^2 v_2 \lambda_{345} + v_2^3 \lambda_2 + v_s^2 v_2 \lambda_8)\,, $
(5) $ - v_s m_S^2 = \frac{1}{2} v_s (v_1^2 \lambda_7 + v_2^2 \lambda_8 + v_s^2 \lambda_6)\,, $
(6) where
$ \lambda_{345} \equiv \lambda_3 + \lambda_4 + \lambda_5 $ .It is necessary to introduce an energy bias in the potential, which lifts the degenerate minima connected by the discrete
$ Z_2 $ symmetry. This bias destabilizes the domain walls, thereby evading the associated cosmological constraints [132−134]. Here, the$ Z_2 $ symmetry-breaking potential term is introduced by hand,$ V_{\not{Z}_2}=-a_1 v_s^2 \Phi_S + \frac{a_1}{3} \Phi_S^3 \,. $
(7) The total potential still has minima at
$ (v_1,v_2,\pm v_s) $ , but there is an energy difference between them$ V_{\rm bias}=V(v_1,v_2,-v_s)-V(v_1,v_2,v_s)=\frac{4}{3}a_1 v_s^3 \,. $
(8) As the required values of
$ a_1 $ are extremely small, it is only considered in the discussions of domain walls, and neglected in other calculations.Once spontaneous symmetry breaking occurs, the mass eigenstates are derived from the original fields through the application of rotation matrices
$ \begin{array}{*{20}{l}} \left(\begin{array}{c}h_1,h_2,h_3 \end{array}\right) = \left(\begin{array}{c} \rho_1, \rho_2, \rho_s\end{array} \right) R^T, \end{array} $
(9) $ \begin{array}{*{20}{l}} \left(\begin{array}{c}G^0 \\ A \end{array}\right) = \left(\begin{array}{cc}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{array}\right) \left(\begin{array}{c} \eta_1 \\ \eta_2 \end{array}\right) , \end{array} $
(10) $ \begin{array}{*{20}{l}} \left(\begin{array}{c}G^{\pm} \\ H^{\pm} \end{array}\right) = \left(\begin{array}{cc}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{array}\right) \left(\begin{array}{c} \phi^{\pm}_1 \\ \phi^{\pm}_2 \end{array}\right), \end{array} $
(11) with
$ \begin{array}{*{20}{l}} R= \left( \begin{array}{*{20}{c}} c_{1} c_{2} & s_{1} c_{2} & s_{2}\\ - s_{1} c_{3}-c_{1} s_{2} s_{3} & c_{1} c_{3}-s_{1} s_{2} s_{3} & c_{2} s_{3} \\ s_{ 1} s_{3}-c_{1} s_{2} c_{3} &- s_{1} s_{2}c_{3} -c_{1} s_{3} & c_{2} c_{3} \end{array} \right). \end{array} $
(12) The shorthand notations are
$ s_{1,2,3}\equiv\sin\alpha_{1,2,3} $ and$ c_{1,2,3}\equiv \cos\alpha_{1,2,3} $ . The$ G^0 $ and$ G^\pm $ correspond to the Goldstone bosons, which are absorbed by the Z and$ W^\pm $ . The remaining physical states consist of three CP-even scalars$ h_{1,2,3} $ , one pseudoscalars A, and a pair of charged scalar$ H^{\pm} $ .The coupling constants in the Higgs potential can be expressed in terms of the scalar masses and mixing angles as
$ \begin{aligned}[b] &\lambda_1 = \frac{ m_{h_1}^2 R_{11}^2+m_{h_2}^2 R_{21}^2 +m_{h_3}^2 R_{31}^2 - m_{12}^2 t_\beta}{v^2 c_\beta^2}, \\ & \lambda_2 = \frac{ m_{h_1}^2 R_{12}^2 +m_{h_2}^2 R_{22}^2+m_{h_3}^2 R_{32}^2- m_{12}^2 t_\beta^{-1}}{v^2 s_\beta^2}, \\ &\lambda_3 = \frac{m_{h_1}^2 R_{11}R_{12}+m_{h_2}^2 R_{21}R_{22}+m_{h_3}^2 R_{31}R_{32}+ 2 m_{H^{\pm}}^2 s_\beta c_\beta - m_{12}^2}{v^2 s_\beta c_\beta }, \\ &\lambda_4 = \frac{(m_A^2-2m_{H^{\pm}}^2 ) s_\beta c_\beta + m_{12}^2}{v^2 s_\beta c_\beta }, \\ &\lambda_5= \frac{ - m_A^2 s_\beta c_\beta + m_{12}^2}{ v^2 s_\beta c_\beta }, \\ &\lambda_6= \frac{m_{h_1}^2 R_{13}^2+m_{h_2}^2 R_{23}^2+m_{h_3}^2 R_{33}^2-2 a_1 v_s}{v_s^2} , \\ &\lambda_7= \frac{m_{h_1}^2 R_{11} R_{13}+m_{h_2}^2 R_{21} R_{23}+m_{h_3}^2 R_{31} R_{33}}{v v_s c_\beta}, \\ &\lambda_8=\frac{m_{h_1}^2 R_{12} R_{13}+m_{h_2}^2 R_{22} R_{23}+m_{h_3}^2 R_{32} R_{33}}{v v_s s_\beta}, \\ \end{aligned} $
(13) with shorthand notation
$ t_{\beta}\equiv\tan\beta $ .To avoid the flavor changing neutral current at the tree-level, a
$ \mathbb{Z'}_2 $ symmetry is imposed [135],$ \begin{array}{*{20}{l}} u_R\to -u_R\,,\ d_R\to-d_R\,,\ e_R\to -e_R\,, \Phi_2\to -\Phi_2, \end{array} $
(14) while the other fields remain unchanged. This results in the well-known type-I Yukawa interactions,
$ - {\cal L} = Y_{u2}\,\overline{Q}_L \, \tilde{{ \Phi}}_2 \,u_R +\,Y_{d2}\, \overline{Q}_L\,{\Phi}_2 \, d_R\, + \, Y_{\ell 2}\,\overline{L}_L \, {\Phi}_2\,e_R+\, \rm{h.c.}\,. $
(15) where
$ Q_L^T=(u_L\,,d_L) $ ,$ L_L^T=(\nu_L\,,l_L) $ ,$ \widetilde\Phi_{2}={\rm i}\tau_2 \Phi_{2}^* $ , and$ Y_{u2} $ ,$ Y_{d2} $ and$ Y_{\ell 2} $ are$ 3 \times 3 $ matrices in family space. However, the$ \mathbb{Z'}_2 $ symmetry is explicitly broken in the scalar potential of Eq. (2).The neutral Higgs boson couplings, normalized to the SM values, are given by
$ \begin{aligned}[b] & y^{h_1}_V=c_2 c_{\beta 1},\; y_{f}^{h_1}=c_2 \left(c_{\beta 1}- s_{\beta 1}\kappa_f\right), \\ &y^{h_2}_V = c_3 s_{\beta 1} - s_2 s_3 c_{\beta 1},\\& y^{h_2}_f =c_3 \left(s_{\beta 1}+c_{\beta 1}\kappa_f\right)- s_2 s_3\left(c_{\beta 1} - s_{\beta 1}\kappa_f\right), \\ &y^{h_3}_V = -s_3 s_{\beta 1} - s_2 c_3 c_{\beta 1},\\& y^{h_3}_f = -s_3 \left(s_{\beta 1}+ c_{\beta 1}\kappa_f\right)-s_2 c_3\left(c_{\beta 1} - s_{\beta 1}\kappa_f\right), \\ &y^{A}_V=0,\; y^{A}_{f}=-i\kappa_f\; {\rm (for}\; u),\; y_{f}^{A}=i \kappa_f\; {\rm (for}\; d,\; \ell). \end{aligned} $
(16) $ \kappa_f=1/\tan\beta $ and V represents Z or W. The shorthand notations are defined as$ c_{\beta 1}\equiv\cos(\beta-\alpha_1) $ and$ s_{\beta 1}\equiv \sin(\beta-\alpha_1) $ .The charged Higgs Yukawa couplings are given by
$ \begin{aligned}[b] \mathcal{L}_Y =\;& - \frac{\sqrt{2}}{v}\, H^+\, \Big\{\bar{u}_i \Big[\kappa_f\,(V_{\rm CKM})_{ij}\; m_{dj} P_R \\&- \kappa_f\,m_{ui}\; (V_{\rm CKM})_{ij} \; P_L\Big] d_j + \kappa_f\,\bar{\nu} m_\ell P_R \ell \Big\}+ {\rm h.c.}, \end{aligned} $
(17) where
$ i,j=1,2,3 $ are the index of generation. -
The two-Higgs-doublet model is extented by introducing a real singlet scalar,
$ \begin{aligned}[b] &\Phi_1=\left(\begin{array}{c} \phi_1^+ \\ \dfrac{(v_1+\rho_1+ {\rm i} \eta_1)}{\sqrt{2}}\, \end{array}\right)\,, \Phi_2=\left(\begin{array}{c} \phi_2^+ \\ \dfrac{(v_2+\rho_2+ {\rm i} \eta_2)}{\sqrt{2}}\, \end{array}\right),\\& \Phi_S=\rho_s+v_s. \end{aligned} $
(1) After spontaneous symmetry breaking, the fields
$ \Phi_1, \Phi_2 $ and$ \Phi_S $ acquire their respective VEVs$ v_1 $ ,$ v_2 $ , and$ v_s $ , with$ v\equiv \sqrt{v_1^2+v_2^2}= 246 $ GeV. The ratio of the two-Higgs-doublet VEVs is defined as$ \tan\beta \equiv v_2 /v_1 $ .The Higgs potential is written as
$ \begin{aligned}[b] V =\;& m_{11}^2 |\Phi_1|^2 + m_{22}^2 |\Phi_2|^2 - m_{12}^2 (\Phi_1^\dagger \Phi_2 + \text{h.c.})\\& + \frac{\lambda_1}{2} (\Phi_1^\dagger \Phi_1)^2 + \frac{\lambda_2}{2} (\Phi_2^\dagger \Phi_2)^2 \\ & + \lambda_3 (\Phi_1^\dagger \Phi_1) (\Phi_2^\dagger \Phi_2) + \lambda_4 (\Phi_1^\dagger \Phi_2) (\Phi_2^\dagger \Phi_1) \\&+ \frac{\lambda_5}{2} [(\Phi_1^\dagger \Phi_2)^2 + \text{h.c.}] + \frac{m_S^2}{2} \Phi_S^2 + \frac{\lambda_6}{8} \Phi_S^4\\ & + \frac{\lambda_7}{2} (\Phi_1^\dagger \Phi_1) \Phi_S^2 + \frac{\lambda_8}{2} (\Phi_2^\dagger \Phi_2) \Phi_S^2. \end{aligned} $
(2) It is assumed that the model conserves CP-symmetry, meaning all coupling constants and mass parameters to be real. The Higgs potential in Eq. (2) respects a discrete
$ Z_2 $ symmetry,$ \begin{array}{*{20}{l}} \Phi_1\to\Phi_1\,,\ \Phi_2\to\Phi_2\,,\ \Phi_S\to -\Phi_S\,, \end{array} $
(3) which is spontaneously broken by the VEV of
$ \Phi_S $ , giving rise to domain walls in the early Universe. The conditions for minimizing the scalar potential lead to$ v_2 m_{12}^2 - v_1 m_{11}^2 = \frac{1}{2} (v_1^3 \lambda_1 + v_2^2 v_1 \lambda_{345} + v_s^2 v_1 \lambda_7)\,, $
(4) $ v_1 m_{12}^2 - v_2 m_{22}^2 = \frac{1}{2} (v_1^2 v_2 \lambda_{345} + v_2^3 \lambda_2 + v_s^2 v_2 \lambda_8)\,, $
(5) $ - v_s m_S^2 = \frac{1}{2} v_s (v_1^2 \lambda_7 + v_2^2 \lambda_8 + v_s^2 \lambda_6)\,, $
(6) where
$ \lambda_{345} \equiv \lambda_3 + \lambda_4 + \lambda_5 $ .It is necessary to introduce an energy bias in the potential, which lifts the degenerate minima connected by the discrete
$ Z_2 $ symmetry. This bias destabilizes the domain walls, thereby evading the associated cosmological constraints [132−134]. Here, the$ Z_2 $ symmetry-breaking potential term is introduced by hand,$ V_{\not{Z}_2}=-a_1 v_s^2 \Phi_S + \frac{a_1}{3} \Phi_S^3 \,. $
(7) The total potential still has minima at
$ (v_1,v_2,\pm v_s) $ , but there is an energy difference between them$ V_{\rm bias}=V(v_1,v_2,-v_s)-V(v_1,v_2,v_s)=\frac{4}{3}a_1 v_s^3 \,. $
(8) As the required values of
$ a_1 $ are extremely small, it is only considered in the discussions of domain walls, and neglected in other calculations.Once spontaneous symmetry breaking occurs, the mass eigenstates are derived from the original fields through the application of rotation matrices
$ \begin{array}{*{20}{l}} \left(\begin{array}{c}h_1,h_2,h_3 \end{array}\right) = \left(\begin{array}{c} \rho_1, \rho_2, \rho_s\end{array} \right) R^T, \end{array} $
(9) $ \begin{array}{*{20}{l}} \left(\begin{array}{c}G^0 \\ A \end{array}\right) = \left(\begin{array}{cc}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{array}\right) \left(\begin{array}{c} \eta_1 \\ \eta_2 \end{array}\right) , \end{array} $
(10) $ \begin{array}{*{20}{l}} \left(\begin{array}{c}G^{\pm} \\ H^{\pm} \end{array}\right) = \left(\begin{array}{cc}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{array}\right) \left(\begin{array}{c} \phi^{\pm}_1 \\ \phi^{\pm}_2 \end{array}\right), \end{array} $
(11) with
$ \begin{array}{*{20}{l}} R= \left( \begin{array}{*{20}{c}} c_{1} c_{2} & s_{1} c_{2} & s_{2}\\ - s_{1} c_{3}-c_{1} s_{2} s_{3} & c_{1} c_{3}-s_{1} s_{2} s_{3} & c_{2} s_{3} \\ s_{ 1} s_{3}-c_{1} s_{2} c_{3} &- s_{1} s_{2}c_{3} -c_{1} s_{3} & c_{2} c_{3} \end{array} \right). \end{array} $
(12) The shorthand notations are
$ s_{1,2,3}\equiv\sin\alpha_{1,2,3} $ and$ c_{1,2,3}\equiv \cos\alpha_{1,2,3} $ . The$ G^0 $ and$ G^\pm $ correspond to the Goldstone bosons, which are absorbed by the Z and$ W^\pm $ . The remaining physical states consist of three CP-even scalars$ h_{1,2,3} $ , one pseudoscalars A, and a pair of charged scalar$ H^{\pm} $ .The coupling constants in the Higgs potential can be expressed in terms of the scalar masses and mixing angles as
$ \begin{aligned}[b] &\lambda_1 = \frac{ m_{h_1}^2 R_{11}^2+m_{h_2}^2 R_{21}^2 +m_{h_3}^2 R_{31}^2 - m_{12}^2 t_\beta}{v^2 c_\beta^2}, \\ & \lambda_2 = \frac{ m_{h_1}^2 R_{12}^2 +m_{h_2}^2 R_{22}^2+m_{h_3}^2 R_{32}^2- m_{12}^2 t_\beta^{-1}}{v^2 s_\beta^2}, \\ &\lambda_3 = \frac{m_{h_1}^2 R_{11}R_{12}+m_{h_2}^2 R_{21}R_{22}+m_{h_3}^2 R_{31}R_{32}+ 2 m_{H^{\pm}}^2 s_\beta c_\beta - m_{12}^2}{v^2 s_\beta c_\beta }, \\ &\lambda_4 = \frac{(m_A^2-2m_{H^{\pm}}^2 ) s_\beta c_\beta + m_{12}^2}{v^2 s_\beta c_\beta }, \\ &\lambda_5= \frac{ - m_A^2 s_\beta c_\beta + m_{12}^2}{ v^2 s_\beta c_\beta }, \\ &\lambda_6= \frac{m_{h_1}^2 R_{13}^2+m_{h_2}^2 R_{23}^2+m_{h_3}^2 R_{33}^2-2 a_1 v_s}{v_s^2} , \\ &\lambda_7= \frac{m_{h_1}^2 R_{11} R_{13}+m_{h_2}^2 R_{21} R_{23}+m_{h_3}^2 R_{31} R_{33}}{v v_s c_\beta}, \\ &\lambda_8=\frac{m_{h_1}^2 R_{12} R_{13}+m_{h_2}^2 R_{22} R_{23}+m_{h_3}^2 R_{32} R_{33}}{v v_s s_\beta}, \\ \end{aligned} $
(13) with shorthand notation
$ t_{\beta}\equiv\tan\beta $ .To avoid the flavor changing neutral current at the tree-level, a
$ \mathbb{Z'}_2 $ symmetry is imposed [135],$ \begin{array}{*{20}{l}} u_R\to -u_R\,,\ d_R\to-d_R\,,\ e_R\to -e_R\,, \Phi_2\to -\Phi_2, \end{array} $
(14) while the other fields remain unchanged. This results in the well-known type-I Yukawa interactions,
$ - {\cal L} = Y_{u2}\,\overline{Q}_L \, \tilde{{ \Phi}}_2 \,u_R +\,Y_{d2}\, \overline{Q}_L\,{\Phi}_2 \, d_R\, + \, Y_{\ell 2}\,\overline{L}_L \, {\Phi}_2\,e_R+\, \rm{h.c.}\,. $
(15) where
$ Q_L^T=(u_L\,,d_L) $ ,$ L_L^T=(\nu_L\,,l_L) $ ,$ \widetilde\Phi_{2}={\rm i}\tau_2 \Phi_{2}^* $ , and$ Y_{u2} $ ,$ Y_{d2} $ and$ Y_{\ell 2} $ are$ 3 \times 3 $ matrices in family space. However, the$ \mathbb{Z'}_2 $ symmetry is explicitly broken in the scalar potential of Eq. (2).The neutral Higgs boson couplings, normalized to the SM values, are given by
$ \begin{aligned}[b] & y^{h_1}_V=c_2 c_{\beta 1},\; y_{f}^{h_1}=c_2 \left(c_{\beta 1}- s_{\beta 1}\kappa_f\right), \\ &y^{h_2}_V = c_3 s_{\beta 1} - s_2 s_3 c_{\beta 1},\\& y^{h_2}_f =c_3 \left(s_{\beta 1}+c_{\beta 1}\kappa_f\right)- s_2 s_3\left(c_{\beta 1} - s_{\beta 1}\kappa_f\right), \\ &y^{h_3}_V = -s_3 s_{\beta 1} - s_2 c_3 c_{\beta 1},\\& y^{h_3}_f = -s_3 \left(s_{\beta 1}+ c_{\beta 1}\kappa_f\right)-s_2 c_3\left(c_{\beta 1} - s_{\beta 1}\kappa_f\right), \\ &y^{A}_V=0,\; y^{A}_{f}=-i\kappa_f\; {\rm (for}\; u),\; y_{f}^{A}=i \kappa_f\; {\rm (for}\; d,\; \ell). \end{aligned} $
(16) $ \kappa_f=1/\tan\beta $ and V represents Z or W. The shorthand notations are defined as$ c_{\beta 1}\equiv\cos(\beta-\alpha_1) $ and$ s_{\beta 1}\equiv \sin(\beta-\alpha_1) $ .The charged Higgs Yukawa couplings are given by
$ \begin{aligned}[b] \mathcal{L}_Y =\;& - \frac{\sqrt{2}}{v}\, H^+\, \Big\{\bar{u}_i \Big[\kappa_f\,(V_{\rm CKM})_{ij}\; m_{dj} P_R \\&- \kappa_f\,m_{ui}\; (V_{\rm CKM})_{ij} \; P_L\Big] d_j + \kappa_f\,\bar{\nu} m_\ell P_R \ell \Big\}+ {\rm h.c.}, \end{aligned} $
(17) where
$ i,j=1,2,3 $ are the index of generation. -
The following discussions account for the following theoretical and experimental constraints:
(1) Vacuum stability. The following conditions are required by the vacuum stability [129],
$ \begin{array}{*{20}{l}} \Omega_1 \; \; {\rm or}\; \; \Omega_2 \end{array} $
(18) with
$ \begin{aligned}[b] \Omega_1 =\;& \Bigg\{ \lambda_1, \lambda_2, \lambda_6 > 0; \sqrt{\lambda_1 \lambda_6} + \lambda_7 > 0; \sqrt{\lambda_2 \lambda_6} + \lambda_8 > 0; \\ & \sqrt{\lambda_1 \lambda_2} + \lambda_3 + D > 0; \lambda_7 + \sqrt{\frac{\lambda_1}{\lambda_2}} \lambda_8 \ge 0 \Bigg\}, \\ \Omega_2 =\;& \Bigg\{ \lambda_1, \lambda_2, \lambda_6 > 0; \sqrt{\lambda_2 \lambda_6} \ge \lambda_8 > -\sqrt{\lambda_2 \lambda_6}; \\& \sqrt{\lambda_1 \lambda_6} >- \lambda_7 \ge \sqrt{\frac{\lambda_1}{\lambda_2}} \lambda_8; \\ & \sqrt{(\lambda_7^2 - \lambda_1 \lambda_6)(\lambda_8^2 -\lambda_2 \lambda_6)} > \lambda_7 \lambda_8 - (D+\lambda_3) \lambda_6 \Bigg\} \;. \end{aligned} $
(19) where
$ D = \text{min}(\lambda_4-|\lambda_5|\,,\;0) $ .(2) Tree-level perturbative unitarity. The eigenvalues of the
$ 2\to 2 $ scalar-scalar scattering matrix are below$ 8\pi $ , which are [129]$ \begin{aligned}[b] |\lambda_3 - \lambda_4| &< 8 \pi \\ |\lambda_3 + 2 \lambda_4 \pm 3 \lambda_5| &< 8 \pi \\ \left| \frac{1}{2} \left( \lambda_1 + \lambda_2 + \sqrt{(\lambda_1 - \lambda_2)^2 + 4 \lambda_4^2}\right) \right| &< 8\pi \\ \left| \frac{1}{2} \left( \lambda_1 + \lambda_2 + \sqrt{(\lambda_1 - \lambda_2)^2 + 4 \lambda_5^2}\right) \right| &< 8\pi \\ |\lambda_7|\,,\;|\lambda_8|&<8\pi, \\ \frac{1}{2}|a_{1,2,3}| &< 8\pi \;, \end{aligned} $
(20) where
$ a_{1,2,3} $ are the real roots of the cubic equation,$ \begin{aligned}[b] 0=\;&4\Big(-27 \lambda_1 \lambda_2 \lambda_6 + 12 \lambda_3^2 \lambda_6 + 12 \lambda_3 \lambda_4 \lambda_6 + 3 \lambda_4^2 \lambda_6 \\&+ 6 \lambda_2 \lambda_7^2 - 8 \lambda_3 \lambda_7 \lambda_8 - 4 \lambda_4 \lambda_7 \lambda_8 + 6 \lambda_1 \lambda_8^2 \Big) \\ &+ x (36 \lambda_1 \lambda_2 - 16\lambda_3^2 - 16\lambda_3 \lambda_4 - 4 \lambda_4^2 + 18 \lambda_1 \lambda_6 \\&+ 18 \lambda_2 \lambda_6 - 4\lambda_7^2 - 4\lambda_8^2) \\ & +x^2 \left(-6 (\lambda_1 + \lambda_2) -3 \lambda_6\right) + x^3 \;. \end{aligned} $
(21) (3) 125 GeV Higgs signal data.
$ h_2 $ is identifed as the observed 125 GeV Higgs boson and$ \textsf{HiggsTools} $ [136] is used to compute the total$ \chi^2_{125} $ based on the latest LHC measurements of signal strength of the 125 GeV Higgs boson.$ \textsf{HiggsTools} $ integrates both$ \textsf{HiggsSignals} $ [136, 137] and$ \textsf{HiggsBounds} $ [138, 139]. In particular, the calculation focuses on the parameter points that satisfy$ \chi^2_{125}-\chi^2_{\rm SM}< $ 6.18, where$ \chi^2_{\rm SM} $ represents the SM prediction value. These points are preferred over the SM at the$ 2\sigma $ confidence level, assuming a two-parameter fit.(4) Searches for additional Higgs boson at the collider and flavor observables.
$ \textsf{Higgstools} $ is used to retain only those parameter points that are consistent with the 95% confidence level exclusion limits from collider searches for additional Higgs bosons.$ \textsf{SuperIso-v4.1} $ [140] is employed to assess the bound of$ B\to X_s\gamma $ decay.(5) Oblique parameters. The oblique parameters provide important constraints on the Higgs mass spectrum within the model. To ensure consistency with experimental data, parameter points are required to lie within the
$ 2\sigma $ confidence region for both the S and T parameters. This corresponds to$ \chi^2<6.18 $ for two degrees of freedom. The corresponding fit results can be found in [141],$ \begin{array}{*{20}{l}} S=0.00\pm 0.07,\; \; T=0.05\pm 0.06, \end{array} $
(22) with a correlation coefficient
$ \rho_{ST} $ = 0.92.In the model, the approximate calculations of the S and T parameters are [142, 143]
$ \begin{aligned}[b] S=\;&\frac{1}{\pi m_Z^2}\Bigg[\sum\limits_{i=1,2,3}\left( F_S(m_Z^2,m_{h_i}^2,m_A^2) (-s_{\beta} R_{i1} + c_{\beta} R_{i2})^2 \right. \\ & +F_S(m_Z^2,m_Z^2,m_{h_i}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 \\&-m_Z^2 F_{S0}(m_Z^2,m_Z^2,m_{h_i}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 ) \\ & - F_S(m_{Z}^2,m_{H^{\pm}}^2,m_{H^{\pm}}^2) -F_S(m_Z^2,m_Z^2,m_{ref}^2) \\&+ m_Z^2 F_{S0}(m_Z^2,m_Z^2,m_{ref}^2)\Bigg], \\ T=\;&\frac{1}{16\pi m_W^2 s_W^2} \Bigg[\sum\limits_{i=1,2,3}( -F_T(m_{h_i}^2,m_{A}^2) (-s_{\beta} R_{i1} + c_{\beta} R_{i2})^2 \\ & + F_T(m_{H^{\pm}}^2,m_{h_{i}}^2) (c_\beta R_{i2} -s_\beta R_{i1})^2 \\ &+ 3 F_T(m_{Z}^2,m_{h_{i}}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 \\&-3 F_T(m_{W}^2,m_{h_{i}}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2) \\ & + F_T(m_{H^{\pm}}^2,m_A^2) -3 F_T(m_{Z}^2,m_{ref}^2) + 3F_T(m_{W}^2,m_{ref}^2)\Bigg], \end{aligned} $
(23) with
$ \begin{aligned}[b] F_T(a,b)=\;&\frac{1}{2}(a+b)-\frac{ab}{a-b}\log(\frac{a}{b}),\\ F_S(a,b,c)=\;&B_{22}(a,b,c)-B_{22}(0,b,c),\\ F_{S0}(a,b,c)=\;&B_{0}(a,b,c)-B_{0}(0,b,c), \end{aligned} $
(24) where
$ \begin{aligned}[b] &B_{22}(a,b,c)=\frac{1}{4}\left[b+c-\frac{1}{3}a\right] - \frac{1}{2}\int^1_0 {\rm d}x\; X\log(X-{\rm i}\epsilon),\\ &B_{0}(a,b,c) = -\int^1_0 {\rm d}x \; \log{(X- {\rm i} \epsilon)}\, ,\\ & X=bx+c(1-x)-ax(1-x). \end{aligned} $
(25) -
The following discussions account for the following theoretical and experimental constraints:
(1) Vacuum stability. The following conditions are required by the vacuum stability [129],
$ \begin{array}{*{20}{l}} \Omega_1 \; \; {\rm or}\; \; \Omega_2 \end{array} $
(18) with
$ \begin{aligned}[b] \Omega_1 =\;& \Bigg\{ \lambda_1, \lambda_2, \lambda_6 > 0; \sqrt{\lambda_1 \lambda_6} + \lambda_7 > 0; \sqrt{\lambda_2 \lambda_6} + \lambda_8 > 0; \\ & \sqrt{\lambda_1 \lambda_2} + \lambda_3 + D > 0; \lambda_7 + \sqrt{\frac{\lambda_1}{\lambda_2}} \lambda_8 \ge 0 \Bigg\}, \\ \Omega_2 =\;& \Bigg\{ \lambda_1, \lambda_2, \lambda_6 > 0; \sqrt{\lambda_2 \lambda_6} \ge \lambda_8 > -\sqrt{\lambda_2 \lambda_6}; \\& \sqrt{\lambda_1 \lambda_6} >- \lambda_7 \ge \sqrt{\frac{\lambda_1}{\lambda_2}} \lambda_8; \\ & \sqrt{(\lambda_7^2 - \lambda_1 \lambda_6)(\lambda_8^2 -\lambda_2 \lambda_6)} > \lambda_7 \lambda_8 - (D+\lambda_3) \lambda_6 \Bigg\} \;. \end{aligned} $
(19) where
$ D = \text{min}(\lambda_4-|\lambda_5|\,,\;0) $ .(2) Tree-level perturbative unitarity. The eigenvalues of the
$ 2\to 2 $ scalar-scalar scattering matrix are below$ 8\pi $ , which are [129]$ \begin{aligned}[b] |\lambda_3 - \lambda_4| &< 8 \pi \\ |\lambda_3 + 2 \lambda_4 \pm 3 \lambda_5| &< 8 \pi \\ \left| \frac{1}{2} \left( \lambda_1 + \lambda_2 + \sqrt{(\lambda_1 - \lambda_2)^2 + 4 \lambda_4^2}\right) \right| &< 8\pi \\ \left| \frac{1}{2} \left( \lambda_1 + \lambda_2 + \sqrt{(\lambda_1 - \lambda_2)^2 + 4 \lambda_5^2}\right) \right| &< 8\pi \\ |\lambda_7|\,,\;|\lambda_8|&<8\pi, \\ \frac{1}{2}|a_{1,2,3}| &< 8\pi \;, \end{aligned} $
(20) where
$ a_{1,2,3} $ are the real roots of the cubic equation,$ \begin{aligned}[b] 0=\;&4\Big(-27 \lambda_1 \lambda_2 \lambda_6 + 12 \lambda_3^2 \lambda_6 + 12 \lambda_3 \lambda_4 \lambda_6 + 3 \lambda_4^2 \lambda_6 \\&+ 6 \lambda_2 \lambda_7^2 - 8 \lambda_3 \lambda_7 \lambda_8 - 4 \lambda_4 \lambda_7 \lambda_8 + 6 \lambda_1 \lambda_8^2 \Big) \\ &+ x (36 \lambda_1 \lambda_2 - 16\lambda_3^2 - 16\lambda_3 \lambda_4 - 4 \lambda_4^2 + 18 \lambda_1 \lambda_6 \\&+ 18 \lambda_2 \lambda_6 - 4\lambda_7^2 - 4\lambda_8^2) \\ & +x^2 \left(-6 (\lambda_1 + \lambda_2) -3 \lambda_6\right) + x^3 \;. \end{aligned} $
(21) (3) 125 GeV Higgs signal data.
$ h_2 $ is identifed as the observed 125 GeV Higgs boson and$ \textsf{HiggsTools} $ [136] is used to compute the total$ \chi^2_{125} $ based on the latest LHC measurements of signal strength of the 125 GeV Higgs boson.$ \textsf{HiggsTools} $ integrates both$ \textsf{HiggsSignals} $ [136, 137] and$ \textsf{HiggsBounds} $ [138, 139]. In particular, the calculation focuses on the parameter points that satisfy$ \chi^2_{125}-\chi^2_{\rm SM}< $ 6.18, where$ \chi^2_{\rm SM} $ represents the SM prediction value. These points are preferred over the SM at the$ 2\sigma $ confidence level, assuming a two-parameter fit.(4) Searches for additional Higgs boson at the collider and flavor observables.
$ \textsf{Higgstools} $ is used to retain only those parameter points that are consistent with the 95% confidence level exclusion limits from collider searches for additional Higgs bosons.$ \textsf{SuperIso-v4.1} $ [140] is employed to assess the bound of$ B\to X_s\gamma $ decay.(5) Oblique parameters. The oblique parameters provide important constraints on the Higgs mass spectrum within the model. To ensure consistency with experimental data, parameter points are required to lie within the
$ 2\sigma $ confidence region for both the S and T parameters. This corresponds to$ \chi^2<6.18 $ for two degrees of freedom. The corresponding fit results can be found in [141],$ \begin{array}{*{20}{l}} S=0.00\pm 0.07,\; \; T=0.05\pm 0.06, \end{array} $
(22) with a correlation coefficient
$ \rho_{ST} $ = 0.92.In the model, the approximate calculations of the S and T parameters are [142, 143]
$ \begin{aligned}[b] S=\;&\frac{1}{\pi m_Z^2}\Bigg[\sum\limits_{i=1,2,3}\left( F_S(m_Z^2,m_{h_i}^2,m_A^2) (-s_{\beta} R_{i1} + c_{\beta} R_{i2})^2 \right. \\ & +F_S(m_Z^2,m_Z^2,m_{h_i}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 \\&-m_Z^2 F_{S0}(m_Z^2,m_Z^2,m_{h_i}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 ) \\ & - F_S(m_{Z}^2,m_{H^{\pm}}^2,m_{H^{\pm}}^2) -F_S(m_Z^2,m_Z^2,m_{ref}^2) \\&+ m_Z^2 F_{S0}(m_Z^2,m_Z^2,m_{ref}^2)\Bigg], \\ T=\;&\frac{1}{16\pi m_W^2 s_W^2} \Bigg[\sum\limits_{i=1,2,3}( -F_T(m_{h_i}^2,m_{A}^2) (-s_{\beta} R_{i1} + c_{\beta} R_{i2})^2 \\ & + F_T(m_{H^{\pm}}^2,m_{h_{i}}^2) (c_\beta R_{i2} -s_\beta R_{i1})^2 \\ &+ 3 F_T(m_{Z}^2,m_{h_{i}}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 \\&-3 F_T(m_{W}^2,m_{h_{i}}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2) \\ & + F_T(m_{H^{\pm}}^2,m_A^2) -3 F_T(m_{Z}^2,m_{ref}^2) + 3F_T(m_{W}^2,m_{ref}^2)\Bigg], \end{aligned} $
(23) with
$ \begin{aligned}[b] F_T(a,b)=\;&\frac{1}{2}(a+b)-\frac{ab}{a-b}\log(\frac{a}{b}),\\ F_S(a,b,c)=\;&B_{22}(a,b,c)-B_{22}(0,b,c),\\ F_{S0}(a,b,c)=\;&B_{0}(a,b,c)-B_{0}(0,b,c), \end{aligned} $
(24) where
$ \begin{aligned}[b] &B_{22}(a,b,c)=\frac{1}{4}\left[b+c-\frac{1}{3}a\right] - \frac{1}{2}\int^1_0 {\rm d}x\; X\log(X-{\rm i}\epsilon),\\ &B_{0}(a,b,c) = -\int^1_0 {\rm d}x \; \log{(X- {\rm i} \epsilon)}\, ,\\ & X=bx+c(1-x)-ax(1-x). \end{aligned} $
(25) -
The following discussions account for the following theoretical and experimental constraints:
(1) Vacuum stability. The following conditions are required by the vacuum stability [129],
$ \begin{array}{*{20}{l}} \Omega_1 \; \; {\rm or}\; \; \Omega_2 \end{array} $
(18) with
$ \begin{aligned}[b] \Omega_1 =\;& \Bigg\{ \lambda_1, \lambda_2, \lambda_6 > 0; \sqrt{\lambda_1 \lambda_6} + \lambda_7 > 0; \sqrt{\lambda_2 \lambda_6} + \lambda_8 > 0; \\ & \sqrt{\lambda_1 \lambda_2} + \lambda_3 + D > 0; \lambda_7 + \sqrt{\frac{\lambda_1}{\lambda_2}} \lambda_8 \ge 0 \Bigg\}, \\ \Omega_2 =\;& \Bigg\{ \lambda_1, \lambda_2, \lambda_6 > 0; \sqrt{\lambda_2 \lambda_6} \ge \lambda_8 > -\sqrt{\lambda_2 \lambda_6}; \\& \sqrt{\lambda_1 \lambda_6} >- \lambda_7 \ge \sqrt{\frac{\lambda_1}{\lambda_2}} \lambda_8; \\ & \sqrt{(\lambda_7^2 - \lambda_1 \lambda_6)(\lambda_8^2 -\lambda_2 \lambda_6)} > \lambda_7 \lambda_8 - (D+\lambda_3) \lambda_6 \Bigg\} \;. \end{aligned} $
(19) where
$ D = \text{min}(\lambda_4-|\lambda_5|\,,\;0) $ .(2) Tree-level perturbative unitarity. The eigenvalues of the
$ 2\to 2 $ scalar-scalar scattering matrix are below$ 8\pi $ , which are [129]$ \begin{aligned}[b] |\lambda_3 - \lambda_4| &< 8 \pi \\ |\lambda_3 + 2 \lambda_4 \pm 3 \lambda_5| &< 8 \pi \\ \left| \frac{1}{2} \left( \lambda_1 + \lambda_2 + \sqrt{(\lambda_1 - \lambda_2)^2 + 4 \lambda_4^2}\right) \right| &< 8\pi \\ \left| \frac{1}{2} \left( \lambda_1 + \lambda_2 + \sqrt{(\lambda_1 - \lambda_2)^2 + 4 \lambda_5^2}\right) \right| &< 8\pi \\ |\lambda_7|\,,\;|\lambda_8|&<8\pi, \\ \frac{1}{2}|a_{1,2,3}| &< 8\pi \;, \end{aligned} $
(20) where
$ a_{1,2,3} $ are the real roots of the cubic equation,$ \begin{aligned}[b] 0=\;&4\Big(-27 \lambda_1 \lambda_2 \lambda_6 + 12 \lambda_3^2 \lambda_6 + 12 \lambda_3 \lambda_4 \lambda_6 + 3 \lambda_4^2 \lambda_6 \\&+ 6 \lambda_2 \lambda_7^2 - 8 \lambda_3 \lambda_7 \lambda_8 - 4 \lambda_4 \lambda_7 \lambda_8 + 6 \lambda_1 \lambda_8^2 \Big) \\ &+ x (36 \lambda_1 \lambda_2 - 16\lambda_3^2 - 16\lambda_3 \lambda_4 - 4 \lambda_4^2 + 18 \lambda_1 \lambda_6 \\&+ 18 \lambda_2 \lambda_6 - 4\lambda_7^2 - 4\lambda_8^2) \\ & +x^2 \left(-6 (\lambda_1 + \lambda_2) -3 \lambda_6\right) + x^3 \;. \end{aligned} $
(21) (3) 125 GeV Higgs signal data.
$ h_2 $ is identifed as the observed 125 GeV Higgs boson and$ \textsf{HiggsTools} $ [136] is used to compute the total$ \chi^2_{125} $ based on the latest LHC measurements of signal strength of the 125 GeV Higgs boson.$ \textsf{HiggsTools} $ integrates both$ \textsf{HiggsSignals} $ [136, 137] and$ \textsf{HiggsBounds} $ [138, 139]. In particular, the calculation focuses on the parameter points that satisfy$ \chi^2_{125}-\chi^2_{\rm SM}< $ 6.18, where$ \chi^2_{\rm SM} $ represents the SM prediction value. These points are preferred over the SM at the$ 2\sigma $ confidence level, assuming a two-parameter fit.(4) Searches for additional Higgs boson at the collider and flavor observables.
$ \textsf{Higgstools} $ is used to retain only those parameter points that are consistent with the 95% confidence level exclusion limits from collider searches for additional Higgs bosons.$ \textsf{SuperIso-v4.1} $ [140] is employed to assess the bound of$ B\to X_s\gamma $ decay.(5) Oblique parameters. The oblique parameters provide important constraints on the Higgs mass spectrum within the model. To ensure consistency with experimental data, parameter points are required to lie within the
$ 2\sigma $ confidence region for both the S and T parameters. This corresponds to$ \chi^2<6.18 $ for two degrees of freedom. The corresponding fit results can be found in [141],$ \begin{array}{*{20}{l}} S=0.00\pm 0.07,\; \; T=0.05\pm 0.06, \end{array} $
(22) with a correlation coefficient
$ \rho_{ST} $ = 0.92.In the model, the approximate calculations of the S and T parameters are [142, 143]
$ \begin{aligned}[b] S=\;&\frac{1}{\pi m_Z^2}\Bigg[\sum\limits_{i=1,2,3}\left( F_S(m_Z^2,m_{h_i}^2,m_A^2) (-s_{\beta} R_{i1} + c_{\beta} R_{i2})^2 \right. \\ & +F_S(m_Z^2,m_Z^2,m_{h_i}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 \\&-m_Z^2 F_{S0}(m_Z^2,m_Z^2,m_{h_i}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 ) \\ & - F_S(m_{Z}^2,m_{H^{\pm}}^2,m_{H^{\pm}}^2) -F_S(m_Z^2,m_Z^2,m_{ref}^2) \\&+ m_Z^2 F_{S0}(m_Z^2,m_Z^2,m_{ref}^2)\Bigg], \\ T=\;&\frac{1}{16\pi m_W^2 s_W^2} \Bigg[\sum\limits_{i=1,2,3}( -F_T(m_{h_i}^2,m_{A}^2) (-s_{\beta} R_{i1} + c_{\beta} R_{i2})^2 \\ & + F_T(m_{H^{\pm}}^2,m_{h_{i}}^2) (c_\beta R_{i2} -s_\beta R_{i1})^2 \\ &+ 3 F_T(m_{Z}^2,m_{h_{i}}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 \\&-3 F_T(m_{W}^2,m_{h_{i}}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2) \\ & + F_T(m_{H^{\pm}}^2,m_A^2) -3 F_T(m_{Z}^2,m_{ref}^2) + 3F_T(m_{W}^2,m_{ref}^2)\Bigg], \end{aligned} $
(23) with
$ \begin{aligned}[b] F_T(a,b)=\;&\frac{1}{2}(a+b)-\frac{ab}{a-b}\log(\frac{a}{b}),\\ F_S(a,b,c)=\;&B_{22}(a,b,c)-B_{22}(0,b,c),\\ F_{S0}(a,b,c)=\;&B_{0}(a,b,c)-B_{0}(0,b,c), \end{aligned} $
(24) where
$ \begin{aligned}[b] &B_{22}(a,b,c)=\frac{1}{4}\left[b+c-\frac{1}{3}a\right] - \frac{1}{2}\int^1_0 {\rm d}x\; X\log(X-{\rm i}\epsilon),\\ &B_{0}(a,b,c) = -\int^1_0 {\rm d}x \; \log{(X- {\rm i} \epsilon)}\, ,\\ & X=bx+c(1-x)-ax(1-x). \end{aligned} $
(25) -
In our discussions, we take into account the following theoretical and experimental constraints:
(1) Vacuum stability. The following conditions are required by the vacuum stability [129],
$ \begin{array}{*{20}{l}} \Omega_1 \; \; {\rm or}\; \; \Omega_2 \end{array} $

(18) with
$ \begin{aligned}[b] \Omega_1 =\;& \Bigg\{ \lambda_1, \lambda_2, \lambda_6 > 0; \sqrt{\lambda_1 \lambda_6} + \lambda_7 > 0; \sqrt{\lambda_2 \lambda_6} + \lambda_8 > 0; \\ & \sqrt{\lambda_1 \lambda_2} + \lambda_3 + D > 0; \lambda_7 + \sqrt{\frac{\lambda_1}{\lambda_2}} \lambda_8 \ge 0 \Bigg\}, \\ \Omega_2 =\;& \Bigg\{ \lambda_1, \lambda_2, \lambda_6 > 0; \sqrt{\lambda_2 \lambda_6} \ge \lambda_8 > -\sqrt{\lambda_2 \lambda_6}; \sqrt{\lambda_1 \lambda_6} > \\&- \lambda_7 \ge \sqrt{\frac{\lambda_1}{\lambda_2}} \lambda_8; \\ & \sqrt{(\lambda_7^2 - \lambda_1 \lambda_6)(\lambda_8^2 -\lambda_2 \lambda_6)} > \lambda_7 \lambda_8 - (D+\lambda_3) \lambda_6 \Bigg\} \;. \end{aligned} $

(19) Here
$ D = \text{min}(\lambda_4-|\lambda_5|\,,\;0) $ .(2) Tree-level perturbative unitarity. The eigenvalues of the
$ 2\to 2 $ scalar-scalar scattering matrix are below$ 8\pi $ , which are [129]$ \begin{aligned}[b] |\lambda_3 - \lambda_4| &< 8 \pi \\ |\lambda_3 + 2 \lambda_4 \pm 3 \lambda_5| &< 8 \pi \\ \left| \frac{1}{2} \left( \lambda_1 + \lambda_2 + \sqrt{(\lambda_1 - \lambda_2)^2 + 4 \lambda_4^2}\right) \right| &< 8\pi \\ \left| \frac{1}{2} \left( \lambda_1 + \lambda_2 + \sqrt{(\lambda_1 - \lambda_2)^2 + 4 \lambda_5^2}\right) \right| &< 8\pi \\ |\lambda_7|\,,\;|\lambda_8|&<8\pi, \\ \frac{1}{2}|a_{1,2,3}| &< 8\pi \;, \end{aligned} $

(20) where
$ a_{1,2,3} $ are the real roots of the cubic equation,$ \begin{aligned}[b] 0=\;&4\Big(-27 \lambda_1 \lambda_2 \lambda_6 + 12 \lambda_3^2 \lambda_6 + 12 \lambda_3 \lambda_4 \lambda_6 + 3 \lambda_4^2 \lambda_6 \\&+ 6 \lambda_2 \lambda_7^2 - 8 \lambda_3 \lambda_7 \lambda_8 - 4 \lambda_4 \lambda_7 \lambda_8 + 6 \lambda_1 \lambda_8^2 \Big) \\ &+ x (36 \lambda_1 \lambda_2 - 16\lambda_3^2 - 16\lambda_3 \lambda_4 - 4 \lambda_4^2 + 18 \lambda_1 \lambda_6 \\&+ 18 \lambda_2 \lambda_6 - 4\lambda_7^2 - 4\lambda_8^2) \\ & +x^2 \left(-6 (\lambda_1 + \lambda_2) -3 \lambda_6\right) + x^3 \;. \end{aligned} $

(21) (3) The 125 GeV Higgs signal data. We identify
$ h_2 $ as the observed 125 GeV Higgs boson and use$ \textsf{HiggsTools} $ [136] to compute the total$ \chi^2_{125} $ based on the latest LHC measurements of signal strength of the 125 GeV Higgs boson.$ \textsf{HiggsTools} $ integrates both$ \textsf{HiggsSignals} $ [136,137] and$ \textsf{HiggsBounds} $ [138,139]. In particular, we focus on the parameter points that satisfy$ \chi^2_{125}-\chi^2_{SM}< $ 6.18, where$ \chi^2_{SM} $ stands for the SM prediction value. These points are preferred over the SM at the$ 2\sigma $ confidence level, assuming a two-parameter fit.(4) Searches for additional Higgs boson at the collider and flavor observables. We utilize
$ \textsf{Higgstools} $ to retain only those parameter points that are consistent with the 95% confidence level exclusion limits from collider searches for additional Higgs bosons. We employ$ \textsf{SuperIso-v4.1} $ [140] to assess the bound of$ B\to X_s\gamma $ decay.(5) The oblique parameters. The oblique parameters provide important constraints on the Higgs mass spectrum within the model. To ensure consistency with experimental data, parameter points are required to lie within the
$ 2\sigma $ confidence region for both the S and T parameters. This corresponds to$ \chi^2<6.18 $ for two degrees of freedom. The corresponding fit results can be found in Ref. [141],$ \begin{array}{*{20}{l}} S=0.00\pm 0.07,\; \; T=0.05\pm 0.06, \end{array} $

(22) with a correlation coefficient
$ \rho_{ST} $ = 0.92.In the model, the approximate calculations of the S and T parameters are [142,143]
$ \begin{aligned}[b] S=\;&\frac{1}{\pi m_Z^2}\Bigg[\sum\limits_{i=1,2,3}\left( F_S(m_Z^2,m_{h_i}^2,m_A^2) (-s_{\beta} R_{i1} + c_{\beta} R_{i2})^2 \right. \\ & +F_S(m_Z^2,m_Z^2,m_{h_i}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 \\&-m_Z^2 F_{S0}(m_Z^2,m_Z^2,m_{h_i}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 ) \\ & - F_S(m_{Z}^2,m_{H^{\pm}}^2,m_{H^{\pm}}^2) -F_S(m_Z^2,m_Z^2,m_{ref}^2) \\&+ m_Z^2 F_{S0}(m_Z^2,m_Z^2,m_{ref}^2)\Bigg], \\ T=\;&\frac{1}{16\pi m_W^2 s_W^2} \Bigg[\sum\limits_{i=1,2,3}( -F_T(m_{h_i}^2,m_{A}^2) (-s_{\beta} R_{i1} + c_{\beta} R_{i2})^2 \\ & + F_T(m_{H^{\pm}}^2,m_{h_{i}}^2) (c_\beta R_{i2} -s_\beta R_{i1})^2 \\ &+ 3 F_T(m_{Z}^2,m_{h_{i}}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2 \\&-3 F_T(m_{W}^2,m_{h_{i}}^2) (c_\beta R_{i1} +s_\beta R_{i2})^2) \\ & + F_T(m_{H^{\pm}}^2,m_A^2) -3 F_T(m_{Z}^2,m_{ref}^2) + 3F_T(m_{W}^2,m_{ref}^2)\Bigg], \end{aligned} $

(23) with
$ \begin{aligned}[b] F_T(a,b)=\;&\frac{1}{2}(a+b)-\frac{ab}{a-b}\log(\frac{a}{b}),\\ F_S(a,b,c)=\;&B_{22}(a,b,c)-B_{22}(0,b,c),\\ F_{S0}(a,b,c)=\;&B_{0}(a,b,c)-B_{0}(0,b,c) \end{aligned} $

(24) where
$ \begin{aligned}[b] &B_{22}(a,b,c)=\frac{1}{4}\left[b+c-\frac{1}{3}a\right] - \frac{1}{2}\int^1_0 dx\; X\log(X-i\epsilon),\\ &B_{0}(a,b,c) = -\int^1_0 dx \; \log{(X-i\epsilon)}\, ,\\ & X=bx+c(1-x)-ax(1-x). \end{aligned} $

(25) -
The combined analysis of ATLAS and CMS diphoton data at 95.4 GeV reveals a
$ 3.1\sigma $ local excess [4].$ \begin{array}{*{20}{l}} \mu_{\gamma\gamma}^{\rm exp}=\mu_{\gamma\gamma}^{\rm ATLAS+CMS}=0.24^{+0.09}_{-0.08}. \end{array} $
(26) Intriguingly, a persistent local excess with a significance of
$ 2.3\sigma $ was also observed in the$ e^+ e^- \to Z(\phi \to b\bar{b}) $ channel at the LEP in the same mass region [1],$ \begin{array}{*{20}{l}} \mu_{b\bar{b}}^{\rm exp}=0.117\pm 0.057. \end{array} $
(27) The observed excesses in the diphoton and
$ b\bar{b} $ channels at 95.4 GeV are attributed to resonant production of the lightest CP-even Higgs boson,$ h_1 $ . Under the narrow width approximation, the corresponding signal strengths can be formulated as follows:$ \begin{aligned}[b] \mu_{b\bar{b}}=\;&\frac{\sigma_\text{N2HDM}(e^+ e^-\rightarrow Z h_1)}{\sigma_\text{SM}(e^+ e^-\rightarrow Z h_{95.4}^\text{SM})}\times\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow b\bar{b})}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow b\bar{b})}\\=\;&|y^{h_1}_V|^2\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow b\bar{b})}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow b\bar{b})}, \end{aligned} $
(28) $ \begin{aligned}[b] \mu_{\gamma\gamma}=\;&\frac{\sigma_\text{N2HDM}(g g\rightarrow h_1)}{\sigma_\text{SM}(g g\rightarrow h_{95.4}^\text{SM})}\times \frac{\text{BR}_\text{N2HDM}(h_1\rightarrow \gamma\gamma)}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow \gamma\gamma)}\\\simeq\;& |y^{h_1}_f|^2\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow \gamma\gamma)}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow \gamma\gamma)}. \end{aligned} $
(29) To assess the capability to simultaneously account for the observed excesses in the
$ \gamma\gamma $ and$ b\bar{b} $ channels, a$ \chi^2_{95} $ analysis is conducted,$ \chi^2_{95}=\frac{(\mu_{\gamma\gamma}-0.24)^2}{0.085^2}+\frac{(\mu_{b\bar{b}}-0.117)^2}{0.057^2}, $
(30) and the diphoton and
$ b\bar{b} $ excesses within the$ 2\sigma $ ranges, namely$ \chi^2_{95}< 6.18 $ , are explainedIn the model, the decay
$ h_1 \to \gamma\gamma $ is induced at the one-loop level, whose width is calculated as$ \begin{aligned}[b] \Gamma(h_1 \to \gamma\gamma) =\; & \frac{\alpha^2 m_{h_1}^3}{256 \pi^3 v^2} \Big| y_V^{h_1} F_1(\tau_{W^\pm}) + y_{H^\pm} F_0(\tau_{H^\pm})\\& +\sum\limits_f y_f^{h_1} N_{cf} Q_f^2 F_{1/2}(\tau_f) \Big|^2, \end{aligned} $
(31) where
$ \tau_i=\dfrac{4m^2_{i}}{m^2_{h_1}} $ , and$ N_{cf} $ and$ Q_f $ are electric charge and the number of color degrees of freedom of the fermion in the loop. The factor$ y_{H^\pm} $ is$ y_{H^\pm}=\frac{v}{2m_{h^\pm}^2}g_{h_1H^+H^-} $
(32) with
$ \begin{aligned}[b] g_{h_1H^+H^-}=\;&\frac{1}{v} \Bigg( - \frac{m_{12}^2}{s_\beta c_\beta} \left[ \frac{R_{11}}{c_\beta} + \frac{R_{12}}{s_\beta} \right] + m_{h_1}^2 \left[ \frac{R_{11} s_\beta^2}{c_\beta} + \frac{R_{12} c_\beta^2}{s_\beta} \right]\\& + 2m_{H^\pm}^2 [R_{11} c_\beta + R_{12} s_\beta] \Bigg). \end{aligned} $
(33) The functions
$ F_{1,0,1/2} $ are defined as [144]$ \begin{aligned}[b]& F_1(\tau) = 2 + 3 \tau + 3\tau (2-\tau) f(\tau),\\& F_{1/2}(\tau) = -2\tau [1 + (1-\tau)f(\tau)],\\& F_0(\tau) = \tau [1 - \tau f(\tau)], \end{aligned} $
(34) with
$ \begin{array}{*{20}{l}} f(\tau) = \left\{ \begin{array}{lr} [\sin^{-1}(1/\sqrt{\tau})]^2, & \tau \geq 1 \\ -\dfrac{1}{4} [\ln(\eta_+/\eta_-) - i \pi]^2, & \, \tau < 1 \end{array} \right. \end{array} $
(35) where
$ \eta_{\pm}=1\pm\sqrt{1-\tau} $ .In the calculations, two different scenarios are considered:
Scenario A: By choosing a small value of
$ c_2 $ , the 95.4 GeV Higgs boson ($ h_1 $ ) is predominantly singlet-like, originating mainly from the singlet field$ \Phi_S $ . Under the approximation of$ s_2\simeq sgn(s_2)(1-\dfrac{c_2^2}{2}) $ , the couplings$ h_2 $ and$ h_3 $ normalized to the SM are given by$ \begin{aligned}[b] y^{h_2}_V \simeq\;& |s_2| s_{\beta 13}+\frac{c_2^2}{2}c_3 s_{\beta 1},\; y^{h_2}_f \simeq |s_2| \left(s_{\beta 13}+c_{\beta 13}\kappa_f\right)\\& +\frac{c_2^2}{2}c_3\left(s_{\beta 1} + c_{\beta 1}\kappa_f\right), \\ y^{h_3}_V \simeq\;& |s_2| c_{\beta 13}-\frac{c_2^2}{2}c_3 s_{\beta 1},\; y^{h_3}_f \simeq |s_2| \left(c_{\beta 13}-s_{\beta 13}\kappa_f\right)\\& -\frac{c_2^2}{2}c_3\left(s_{\beta 1} + c_{\beta 1}\kappa_f\right), \end{aligned} $
(36) where
$ c_{\beta 13}\equiv\cos(\beta-\alpha_1-sgn(s_2)\alpha_3) $ and$ s_{\beta 13}\equiv\sin(\beta-\alpha_1- sgn(s_2)\alpha_3) $ . The mixing parameters are chosen as follows:$ \begin{array}{*{20}{l}} 0 \leq c_2 \leq 0.4,\; \; s_{\beta 13} = 1.0,\; \; 0 \leq c_{\beta 1} \leq 1.0,\; \; 1 \leq \tan\beta \leq 15. \end{array} $
(37) When
$ s_{\beta 13} = 1.0 $ and$ c_2 $ approaches zero, the couplings of$ h_2 $ to the SM particles converge to those of the SM Higgs boson, which is favored by the observed signal data for the 125 GeV Higgs.Scenario B: The mixing parameters are scanned over the following ranges:
$ \begin{array}{*{20}{l}} 0 \leq c_{\beta 1} \leq 0.4,\; \; -0.4 \leq s_{3} \leq 0.4,\; \; 0 \leq c_2 \leq 1,\; \; 1 \leq \tan\beta \leq 15. \end{array} $
(38) In the limits of
$ c_{\beta 1} \to 0 $ and$ |s_3| \to 0 $ , the couplings of$ h_2 $ to the SM particles approach those of the SM, which is favored by the signal measurements of the 125 GeV Higgs. In addition, when$ c_2 \to 1 $ , the 95.4 GeV Higgs boson ($ h_1 $ ) predominantly originates from the mixing of the two CP-even components of the Higgs doublets.After imposing the relevant theoretical constraints, the oblique parameters, the Higgs signal data at 125 GeV, searches for additional Higgs bosons at the collider, and flavor observables, the parameter space in scenario A that accounts for the observed excesses in the
$ b\bar{b} $ and diphoton channels at 95.4 GeV in Fig. 1 is identified. As indicated by Eq. (36), within the selected parameter space of scenario A, the coupling of$ h_2 $ to vector bosons,$ y_V^{h_2} $ , tends to be smaller than its coupling to fermions,$ y_f^{h_2} $ , as shown in the left panel of Fig. 1. The Higgs signal data at 125 GeV impose a lower bound on$ y_V^{h_2} $ , requiring$ y_V^{h_2} > 0.93 $ . In the parameter space consistent with the 125 GeV Higgs measurements, collider limits on additional Higgs bosons, and constraints from flavor physics, the coupling$ y_V^{h_1} $ is restricted to values below 0.38. Furthermore, the condition$ \chi^2_{95} < 6.18 $ is satisfied in the region of$ 0.2 \le y_V^{h_1} \le 0.38 $ , with$ y_f^{h_1} $ bounded from below. In addition, the Higgs signal data at 125 GeV exclude a small corner of the parameter space characterized by$ c_{\beta 1}\to 1 $ and$ c_2\to 0.4 $ . In such a region, both$ y_V^{h_2} $ and$ y_f^{h_2} $ can exhibit significant deviations from unity.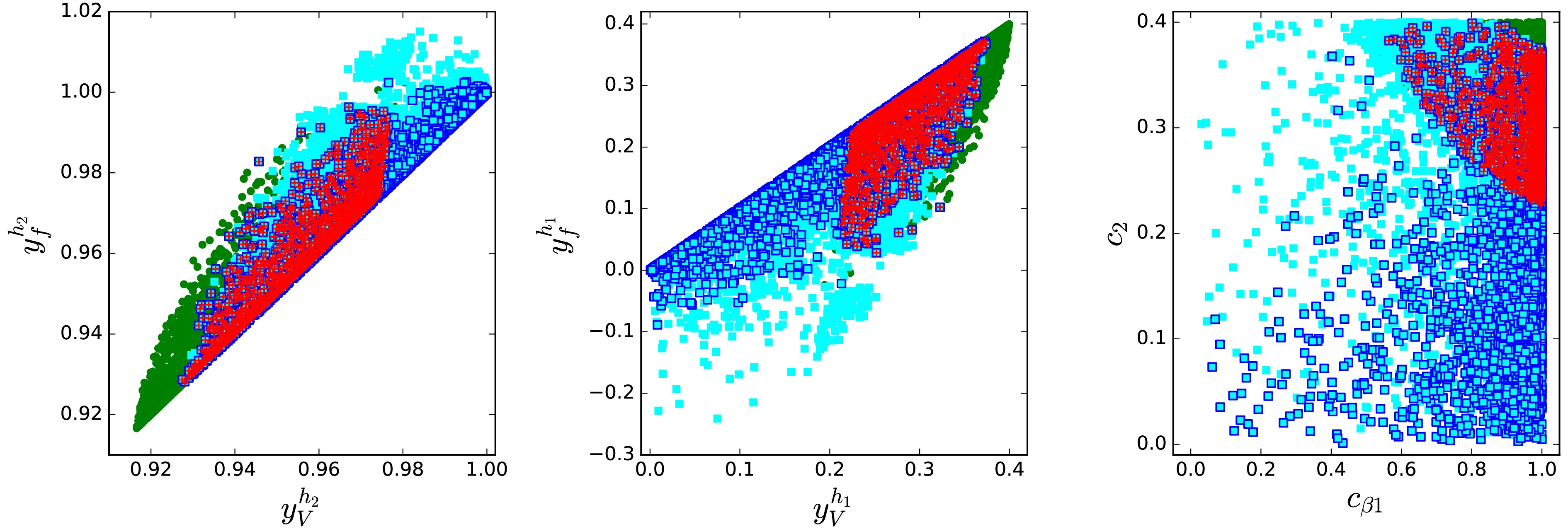
Figure 1. (color online) In scenario A, the parameter space is progressively constrained by sequentially imposing the following: theoretical requirements and the oblique parameters; the signal data of the 125 GeV Higgs boson; searches for additional Higgs bosons at the collider and flavor observables; and finally the condition
$ \chi_{95}^2<6.18 $ . The surviving parameter points at each stage are represented by green bullets, cyan squares, blue-edged squares, and red pluses, respectively.As shown in the left panel of Fig. 2, the value of
$ \chi_{95}^2 $ is sensitive to$ y^{h_1}_V $ and$ y^{h_1}_f $ , and decreases as they increase. The condition$ \chi_{95}^2<2.3 $ is satisfied in partial region of parameter space, with the minimum value attaining 1.2, which indicates that the model can explain the diphoton and$ b\bar{b} $ excesses within the$ 1\sigma $ ranges. The signal strength$ \mu_{b\bar{b}} $ is proportional to$ |y^{h_1}_V|^2 $ . Meanwhile, the W-loop can play an important contribution to the width of$ h_1\to \gamma\gamma $ , and therefore the signal strength$ \mu_{\gamma\gamma} $ is also affected by$ y^{h_1}_V $ . The interpretation of the$ b\bar{b} $ excess imposes a lower bound on$ |y_f^{h_1}| $ . Owing to$ y_V^{h_1}=c_2c_{\beta 1} $ , the value of$ \chi_{95}^2 $ tends to decrease as$ c_2 $ and$ c_{\beta 1} $ increase, as shown in the middle panel of Fig. 2. When$ c_{\beta 1} $ or$ \tan\beta $ is large, the$ y^{h_1}_f $ has a mild dependence on$ \tan\beta $ (See Eq. (16)). From the right panel of Fig. 2, it is observed that the value of$ \chi_{95}^2 $ shows limited sensitivity to$ \tan\beta $ .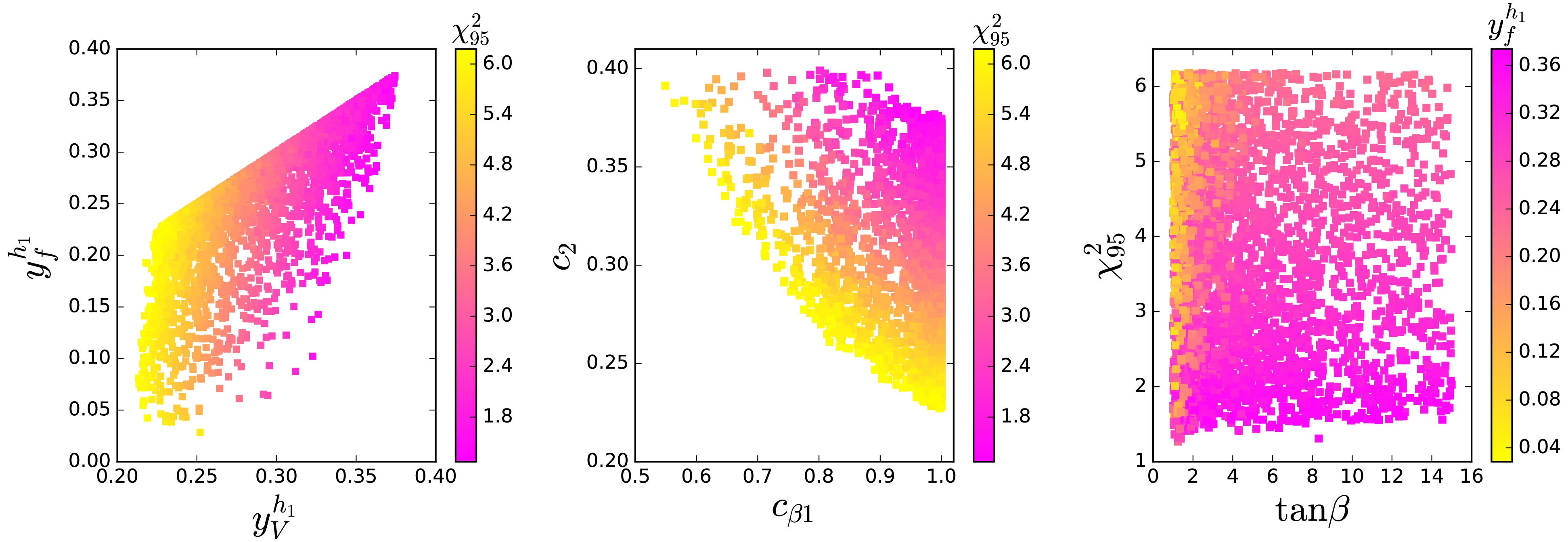
Figure 2. (color online) In scenario A, the surviving parameter points satisfy
$ \chi_{95}^2<6.18 $ and simultaneously meet the theoretical constraints, the oblique parameters, the Higgs signal data at 125 GeV, searches for additional Higgs bosons at the collider, and flavor observables.Similar to Fig. 1, the parameter points for scenario B that account for the observed excesses in the
$ b\bar{b} $ and diphoton channels at 95.4 GeV are shown in Fig. 3. Unlike scenario A, the allowed region in scenario B includes not only the positive$ y_f^{h_1} $ region but also a narrow band where$ y_f^{h_1} $ takes negative values. The signal data of the 125 GeV Higgs boson require a small$ c_{\beta 1} $ , allowing for a negative$ y_f^{h_1} $ , see Eq. (16). The condition$ \chi_{95}^2 < 6.18 $ is satisfied in the region of$ 0.18<c_{\beta 1}< 0.35 $ and$ 0.88<c_2<1 $ . For such large$ c_2 $ , the 95.4 GeV Higgs boson mainly originates from the mixing of the two CP-even components of the Higgs doublets.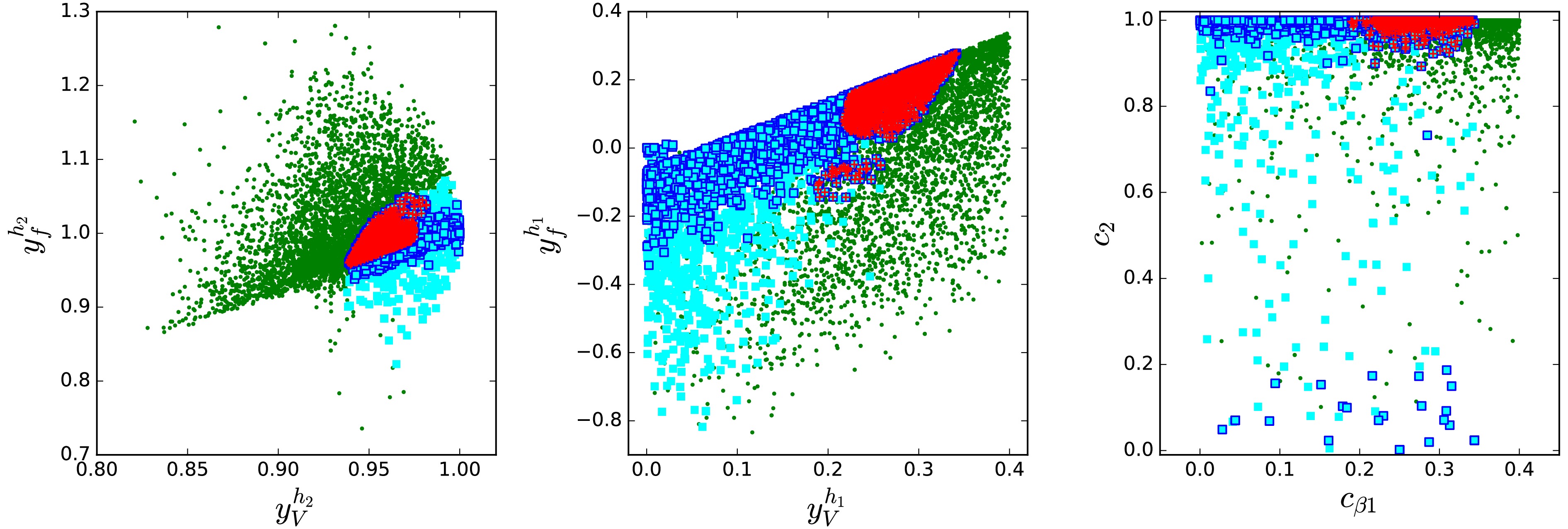
Figure 3. (color online) As Fig. 1, but for scenario B.
As in scenario A, the value of
$ \chi_{95}^2 $ in scenario B decreases as$ y^{h_1}_V $ and$ \mid y^{h_1}_f\mid $ ($ c_2 $ and$ c_{\beta 1} $ ) increase, as illustrated in the upper-left panel and upper-right panel of Fig. 4. However, different from scenario A, the minimal value of$ \chi_{95}^2 $ in scenario B only reaches 2, suggesting that the model can only marginally explain the diphoton and$ b\bar{b} $ excesses at the$ 1\sigma $ level. Furthermore, the condition$ \chi_{95}^2 < 6.18 $ disfavors a narrow region around$ \tan\beta\sim 4 $ , where the value of$ \mid y_f^{h_1}\mid $ is significantly suppressed. The parameter$ s_3 $ is favored to vary from -0.3 to 0.25, and is not sensitive to$ c_2 $ . Its absolute value decreases with increasing$ c_{\beta 1} $ to maintain a sufficiently large$ y_V^{h_2} $ to accommodate the signal data of the 125 GeV Higgs boson.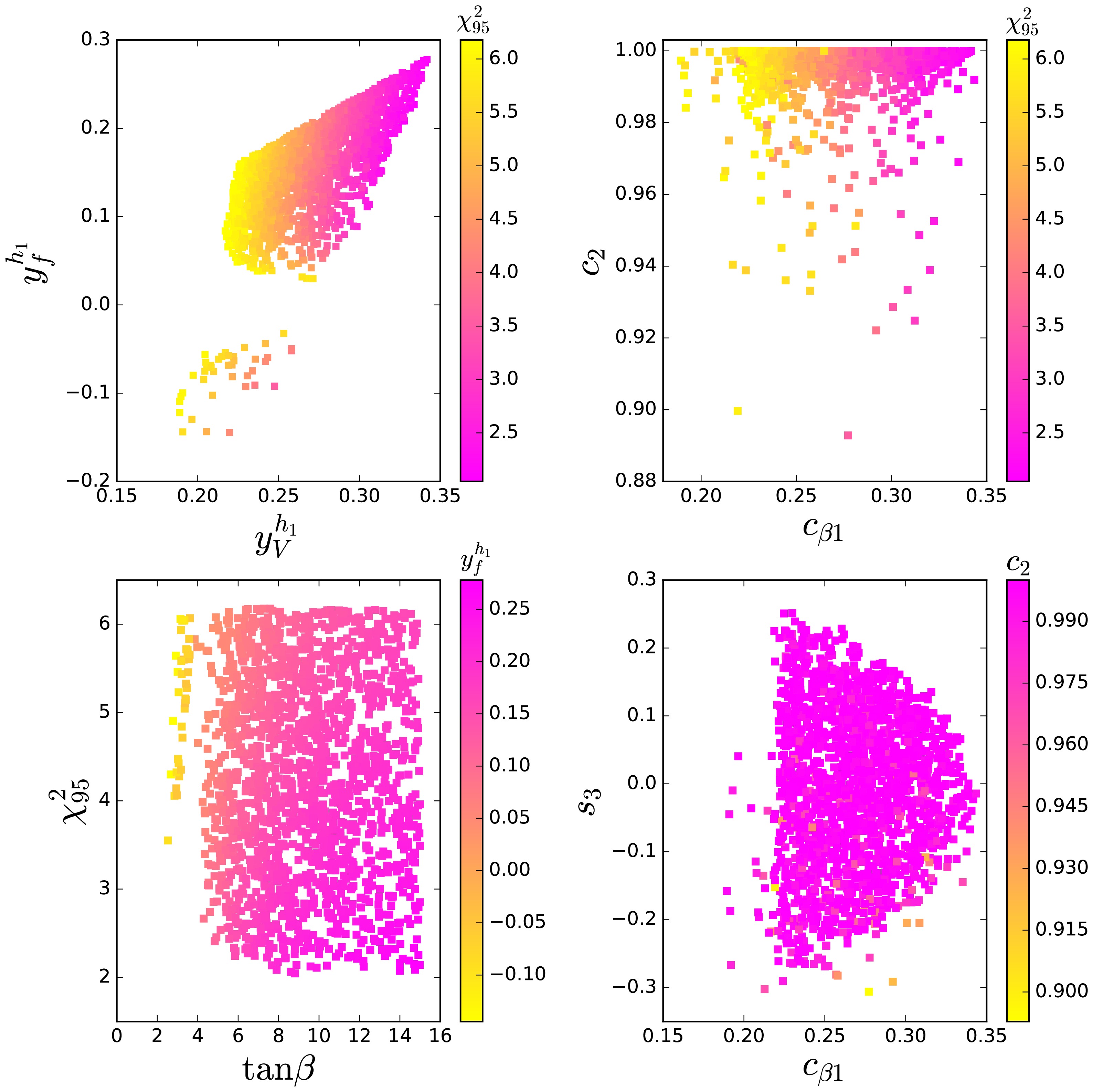
Figure 4. (color online) As Fig. 2, but for scenario B.
-
The combined analysis of ATLAS and CMS diphoton data at 95.4 GeV reveals a
$ 3.1\sigma $ local excess [4].$ \begin{array}{*{20}{l}} \mu_{\gamma\gamma}^{\rm exp}=\mu_{\gamma\gamma}^{\rm ATLAS+CMS}=0.24^{+0.09}_{-0.08}. \end{array} $
(26) Intriguingly, a persistent local excess with a significance of
$ 2.3\sigma $ was also observed in the$ e^+ e^- \to Z(\phi \to b\bar{b}) $ channel at the LEP in the same mass region [1],$ \begin{array}{*{20}{l}} \mu_{b\bar{b}}^{\rm exp}=0.117\pm 0.057. \end{array} $
(27) The observed excesses in the diphoton and
$ b\bar{b} $ channels at 95.4 GeV are attributed to resonant production of the lightest CP-even Higgs boson,$ h_1 $ . Under the narrow width approximation, the corresponding signal strengths can be formulated as follows:$ \begin{aligned}[b] \mu_{b\bar{b}}=\;&\frac{\sigma_\text{N2HDM}(e^+ e^-\rightarrow Z h_1)}{\sigma_\text{SM}(e^+ e^-\rightarrow Z h_{95.4}^\text{SM})}\times\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow b\bar{b})}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow b\bar{b})}\\=\;&|y^{h_1}_V|^2\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow b\bar{b})}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow b\bar{b})}, \end{aligned} $
(28) $ \begin{aligned}[b] \mu_{\gamma\gamma}=\;&\frac{\sigma_\text{N2HDM}(g g\rightarrow h_1)}{\sigma_\text{SM}(g g\rightarrow h_{95.4}^\text{SM})}\times \frac{\text{BR}_\text{N2HDM}(h_1\rightarrow \gamma\gamma)}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow \gamma\gamma)}\\\simeq\;& |y^{h_1}_f|^2\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow \gamma\gamma)}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow \gamma\gamma)}. \end{aligned} $
(29) To assess the capability to simultaneously account for the observed excesses in the
$ \gamma\gamma $ and$ b\bar{b} $ channels, a$ \chi^2_{95} $ analysis is conducted,$ \chi^2_{95}=\frac{(\mu_{\gamma\gamma}-0.24)^2}{0.085^2}+\frac{(\mu_{b\bar{b}}-0.117)^2}{0.057^2}, $
(30) and the diphoton and
$ b\bar{b} $ excesses within the$ 2\sigma $ ranges, namely$ \chi^2_{95}< 6.18 $ , are explainedIn the model, the decay
$ h_1 \to \gamma\gamma $ is induced at the one-loop level, whose width is calculated as$ \begin{aligned}[b] \Gamma(h_1 \to \gamma\gamma) =\; & \frac{\alpha^2 m_{h_1}^3}{256 \pi^3 v^2} \Big| y_V^{h_1} F_1(\tau_{W^\pm}) + y_{H^\pm} F_0(\tau_{H^\pm})\\& +\sum\limits_f y_f^{h_1} N_{cf} Q_f^2 F_{1/2}(\tau_f) \Big|^2, \end{aligned} $
(31) where
$ \tau_i=\dfrac{4m^2_{i}}{m^2_{h_1}} $ , and$ N_{cf} $ and$ Q_f $ are electric charge and the number of color degrees of freedom of the fermion in the loop. The factor$ y_{H^\pm} $ is$ y_{H^\pm}=\frac{v}{2m_{h^\pm}^2}g_{h_1H^+H^-} $
(32) with
$ \begin{aligned}[b] g_{h_1H^+H^-}=\;&\frac{1}{v} \Bigg( - \frac{m_{12}^2}{s_\beta c_\beta} \left[ \frac{R_{11}}{c_\beta} + \frac{R_{12}}{s_\beta} \right] + m_{h_1}^2 \left[ \frac{R_{11} s_\beta^2}{c_\beta} + \frac{R_{12} c_\beta^2}{s_\beta} \right]\\& + 2m_{H^\pm}^2 [R_{11} c_\beta + R_{12} s_\beta] \Bigg). \end{aligned} $
(33) The functions
$ F_{1,0,1/2} $ are defined as [144]$ \begin{aligned}[b]& F_1(\tau) = 2 + 3 \tau + 3\tau (2-\tau) f(\tau),\\& F_{1/2}(\tau) = -2\tau [1 + (1-\tau)f(\tau)],\\& F_0(\tau) = \tau [1 - \tau f(\tau)], \end{aligned} $
(34) with
$ \begin{array}{*{20}{l}} f(\tau) = \left\{ \begin{array}{lr} [\sin^{-1}(1/\sqrt{\tau})]^2, & \tau \geq 1 \\ -\dfrac{1}{4} [\ln(\eta_+/\eta_-) - i \pi]^2, & \, \tau < 1 \end{array} \right. \end{array} $
(35) where
$ \eta_{\pm}=1\pm\sqrt{1-\tau} $ .In the calculations, two different scenarios are considered:
Scenario A: By choosing a small value of
$ c_2 $ , the 95.4 GeV Higgs boson ($ h_1 $ ) is predominantly singlet-like, originating mainly from the singlet field$ \Phi_S $ . Under the approximation of$ s_2\simeq sgn(s_2)(1-\dfrac{c_2^2}{2}) $ , the couplings$ h_2 $ and$ h_3 $ normalized to the SM are given by$ \begin{aligned}[b] y^{h_2}_V \simeq\;& |s_2| s_{\beta 13}+\frac{c_2^2}{2}c_3 s_{\beta 1},\; y^{h_2}_f \simeq |s_2| \left(s_{\beta 13}+c_{\beta 13}\kappa_f\right)\\& +\frac{c_2^2}{2}c_3\left(s_{\beta 1} + c_{\beta 1}\kappa_f\right), \\ y^{h_3}_V \simeq\;& |s_2| c_{\beta 13}-\frac{c_2^2}{2}c_3 s_{\beta 1},\; y^{h_3}_f \simeq |s_2| \left(c_{\beta 13}-s_{\beta 13}\kappa_f\right)\\& -\frac{c_2^2}{2}c_3\left(s_{\beta 1} + c_{\beta 1}\kappa_f\right), \end{aligned} $
(36) where
$ c_{\beta 13}\equiv\cos(\beta-\alpha_1-sgn(s_2)\alpha_3) $ and$ s_{\beta 13}\equiv\sin(\beta-\alpha_1- sgn(s_2)\alpha_3) $ . The mixing parameters are chosen as follows:$ \begin{array}{*{20}{l}} 0 \leq c_2 \leq 0.4,\; \; s_{\beta 13} = 1.0,\; \; 0 \leq c_{\beta 1} \leq 1.0,\; \; 1 \leq \tan\beta \leq 15. \end{array} $
(37) When
$ s_{\beta 13} = 1.0 $ and$ c_2 $ approaches zero, the couplings of$ h_2 $ to the SM particles converge to those of the SM Higgs boson, which is favored by the observed signal data for the 125 GeV Higgs.Scenario B: The mixing parameters are scanned over the following ranges:
$ \begin{array}{*{20}{l}} 0 \leq c_{\beta 1} \leq 0.4,\; \; -0.4 \leq s_{3} \leq 0.4,\; \; 0 \leq c_2 \leq 1,\; \; 1 \leq \tan\beta \leq 15. \end{array} $
(38) In the limits of
$ c_{\beta 1} \to 0 $ and$ |s_3| \to 0 $ , the couplings of$ h_2 $ to the SM particles approach those of the SM, which is favored by the signal measurements of the 125 GeV Higgs. In addition, when$ c_2 \to 1 $ , the 95.4 GeV Higgs boson ($ h_1 $ ) predominantly originates from the mixing of the two CP-even components of the Higgs doublets.After imposing the relevant theoretical constraints, the oblique parameters, the Higgs signal data at 125 GeV, searches for additional Higgs bosons at the collider, and flavor observables, the parameter space in scenario A that accounts for the observed excesses in the
$ b\bar{b} $ and diphoton channels at 95.4 GeV in Fig. 1 is identified. As indicated by Eq. (36), within the selected parameter space of scenario A, the coupling of$ h_2 $ to vector bosons,$ y_V^{h_2} $ , tends to be smaller than its coupling to fermions,$ y_f^{h_2} $ , as shown in the left panel of Fig. 1. The Higgs signal data at 125 GeV impose a lower bound on$ y_V^{h_2} $ , requiring$ y_V^{h_2} > 0.93 $ . In the parameter space consistent with the 125 GeV Higgs measurements, collider limits on additional Higgs bosons, and constraints from flavor physics, the coupling$ y_V^{h_1} $ is restricted to values below 0.38. Furthermore, the condition$ \chi^2_{95} < 6.18 $ is satisfied in the region of$ 0.2 \le y_V^{h_1} \le 0.38 $ , with$ y_f^{h_1} $ bounded from below. In addition, the Higgs signal data at 125 GeV exclude a small corner of the parameter space characterized by$ c_{\beta 1}\to 1 $ and$ c_2\to 0.4 $ . In such a region, both$ y_V^{h_2} $ and$ y_f^{h_2} $ can exhibit significant deviations from unity.
Figure 1. (color online) In scenario A, the parameter space is progressively constrained by sequentially imposing the following: theoretical requirements and the oblique parameters; the signal data of the 125 GeV Higgs boson; searches for additional Higgs bosons at the collider and flavor observables; and finally the condition
$ \chi_{95}^2<6.18 $ . The surviving parameter points at each stage are represented by green bullets, cyan squares, blue-edged squares, and red pluses, respectively.As shown in the left panel of Fig. 2, the value of
$ \chi_{95}^2 $ is sensitive to$ y^{h_1}_V $ and$ y^{h_1}_f $ , and decreases as they increase. The condition$ \chi_{95}^2<2.3 $ is satisfied in partial region of parameter space, with the minimum value attaining 1.2, which indicates that the model can explain the diphoton and$ b\bar{b} $ excesses within the$ 1\sigma $ ranges. The signal strength$ \mu_{b\bar{b}} $ is proportional to$ |y^{h_1}_V|^2 $ . Meanwhile, the W-loop can play an important contribution to the width of$ h_1\to \gamma\gamma $ , and therefore the signal strength$ \mu_{\gamma\gamma} $ is also affected by$ y^{h_1}_V $ . The interpretation of the$ b\bar{b} $ excess imposes a lower bound on$ |y_f^{h_1}| $ . Owing to$ y_V^{h_1}=c_2c_{\beta 1} $ , the value of$ \chi_{95}^2 $ tends to decrease as$ c_2 $ and$ c_{\beta 1} $ increase, as shown in the middle panel of Fig. 2. When$ c_{\beta 1} $ or$ \tan\beta $ is large, the$ y^{h_1}_f $ has a mild dependence on$ \tan\beta $ (See Eq. (16)). From the right panel of Fig. 2, it is observed that the value of$ \chi_{95}^2 $ shows limited sensitivity to$ \tan\beta $ .
Figure 2. (color online) In scenario A, the surviving parameter points satisfy
$ \chi_{95}^2<6.18 $ and simultaneously meet the theoretical constraints, the oblique parameters, the Higgs signal data at 125 GeV, searches for additional Higgs bosons at the collider, and flavor observables.Similar to Fig. 1, the parameter points for scenario B that account for the observed excesses in the
$ b\bar{b} $ and diphoton channels at 95.4 GeV are shown in Fig. 3. Unlike scenario A, the allowed region in scenario B includes not only the positive$ y_f^{h_1} $ region but also a narrow band where$ y_f^{h_1} $ takes negative values. The signal data of the 125 GeV Higgs boson require a small$ c_{\beta 1} $ , allowing for a negative$ y_f^{h_1} $ , see Eq. (16). The condition$ \chi_{95}^2 < 6.18 $ is satisfied in the region of$ 0.18<c_{\beta 1}< 0.35 $ and$ 0.88<c_2<1 $ . For such large$ c_2 $ , the 95.4 GeV Higgs boson mainly originates from the mixing of the two CP-even components of the Higgs doublets.
Figure 3. (color online) As Fig. 1, but for scenario B.
As in scenario A, the value of
$ \chi_{95}^2 $ in scenario B decreases as$ y^{h_1}_V $ and$ \mid y^{h_1}_f\mid $ ($ c_2 $ and$ c_{\beta 1} $ ) increase, as illustrated in the upper-left panel and upper-right panel of Fig. 4. However, different from scenario A, the minimal value of$ \chi_{95}^2 $ in scenario B only reaches 2, suggesting that the model can only marginally explain the diphoton and$ b\bar{b} $ excesses at the$ 1\sigma $ level. Furthermore, the condition$ \chi_{95}^2 < 6.18 $ disfavors a narrow region around$ \tan\beta\sim 4 $ , where the value of$ \mid y_f^{h_1}\mid $ is significantly suppressed. The parameter$ s_3 $ is favored to vary from -0.3 to 0.25, and is not sensitive to$ c_2 $ . Its absolute value decreases with increasing$ c_{\beta 1} $ to maintain a sufficiently large$ y_V^{h_2} $ to accommodate the signal data of the 125 GeV Higgs boson.
Figure 4. (color online) As Fig. 2, but for scenario B.
-
The combined analysis of ATLAS and CMS diphoton data at 95.4 GeV reveals a
$ 3.1\sigma $ local excess [4].$ \begin{array}{*{20}{l}} \mu_{\gamma\gamma}^{\rm exp}=\mu_{\gamma\gamma}^{\rm ATLAS+CMS}=0.24^{+0.09}_{-0.08}. \end{array} $
(26) Intriguingly, a persistent local excess with a significance of
$ 2.3\sigma $ was also observed in the$ e^+ e^- \to Z(\phi \to b\bar{b}) $ channel at the LEP in the same mass region [1],$ \begin{array}{*{20}{l}} \mu_{b\bar{b}}^{\rm exp}=0.117\pm 0.057. \end{array} $
(27) The observed excesses in the diphoton and
$ b\bar{b} $ channels at 95.4 GeV are attributed to resonant production of the lightest CP-even Higgs boson,$ h_1 $ . Under the narrow width approximation, the corresponding signal strengths can be formulated as follows:$ \begin{aligned}[b] \mu_{b\bar{b}}=\;&\frac{\sigma_\text{N2HDM}(e^+ e^-\rightarrow Z h_1)}{\sigma_\text{SM}(e^+ e^-\rightarrow Z h_{95.4}^\text{SM})}\times\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow b\bar{b})}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow b\bar{b})}\\=\;&|y^{h_1}_V|^2\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow b\bar{b})}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow b\bar{b})}, \end{aligned} $
(28) $ \begin{aligned}[b] \mu_{\gamma\gamma}=\;&\frac{\sigma_\text{N2HDM}(g g\rightarrow h_1)}{\sigma_\text{SM}(g g\rightarrow h_{95.4}^\text{SM})}\times \frac{\text{BR}_\text{N2HDM}(h_1\rightarrow \gamma\gamma)}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow \gamma\gamma)}\\\simeq\;& |y^{h_1}_f|^2\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow \gamma\gamma)}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow \gamma\gamma)}. \end{aligned} $
(29) To assess the capability to simultaneously account for the observed excesses in the
$ \gamma\gamma $ and$ b\bar{b} $ channels, a$ \chi^2_{95} $ analysis is conducted,$ \chi^2_{95}=\frac{(\mu_{\gamma\gamma}-0.24)^2}{0.085^2}+\frac{(\mu_{b\bar{b}}-0.117)^2}{0.057^2}, $
(30) and the diphoton and
$ b\bar{b} $ excesses within the$ 2\sigma $ ranges, namely$ \chi^2_{95}< 6.18 $ , are explainedIn the model, the decay
$ h_1 \to \gamma\gamma $ is induced at the one-loop level, whose width is calculated as$ \begin{aligned}[b] \Gamma(h_1 \to \gamma\gamma) =\; & \frac{\alpha^2 m_{h_1}^3}{256 \pi^3 v^2} \Big| y_V^{h_1} F_1(\tau_{W^\pm}) + y_{H^\pm} F_0(\tau_{H^\pm})\\& +\sum\limits_f y_f^{h_1} N_{cf} Q_f^2 F_{1/2}(\tau_f) \Big|^2, \end{aligned} $
(31) where
$ \tau_i=\dfrac{4m^2_{i}}{m^2_{h_1}} $ , and$ N_{cf} $ and$ Q_f $ are electric charge and the number of color degrees of freedom of the fermion in the loop. The factor$ y_{H^\pm} $ is$ y_{H^\pm}=\frac{v}{2m_{h^\pm}^2}g_{h_1H^+H^-} $
(32) with
$ \begin{aligned}[b] g_{h_1H^+H^-}=\;&\frac{1}{v} \Bigg( - \frac{m_{12}^2}{s_\beta c_\beta} \left[ \frac{R_{11}}{c_\beta} + \frac{R_{12}}{s_\beta} \right] + m_{h_1}^2 \left[ \frac{R_{11} s_\beta^2}{c_\beta} + \frac{R_{12} c_\beta^2}{s_\beta} \right]\\& + 2m_{H^\pm}^2 [R_{11} c_\beta + R_{12} s_\beta] \Bigg). \end{aligned} $
(33) The functions
$ F_{1,0,1/2} $ are defined as [144]$ \begin{aligned}[b]& F_1(\tau) = 2 + 3 \tau + 3\tau (2-\tau) f(\tau),\\& F_{1/2}(\tau) = -2\tau [1 + (1-\tau)f(\tau)],\\& F_0(\tau) = \tau [1 - \tau f(\tau)], \end{aligned} $
(34) with
$ \begin{array}{*{20}{l}} f(\tau) = \left\{ \begin{array}{lr} [\sin^{-1}(1/\sqrt{\tau})]^2, & \tau \geq 1 \\ -\dfrac{1}{4} [\ln(\eta_+/\eta_-) - i \pi]^2, & \, \tau < 1 \end{array} \right. \end{array} $
(35) where
$ \eta_{\pm}=1\pm\sqrt{1-\tau} $ .In the calculations, two different scenarios are considered:
Scenario A: By choosing a small value of
$ c_2 $ , the 95.4 GeV Higgs boson ($ h_1 $ ) is predominantly singlet-like, originating mainly from the singlet field$ \Phi_S $ . Under the approximation of$ s_2\simeq sgn(s_2)(1-\dfrac{c_2^2}{2}) $ , the couplings$ h_2 $ and$ h_3 $ normalized to the SM are given by$ \begin{aligned}[b] y^{h_2}_V \simeq\;& |s_2| s_{\beta 13}+\frac{c_2^2}{2}c_3 s_{\beta 1},\; y^{h_2}_f \simeq |s_2| \left(s_{\beta 13}+c_{\beta 13}\kappa_f\right)\\& +\frac{c_2^2}{2}c_3\left(s_{\beta 1} + c_{\beta 1}\kappa_f\right), \\ y^{h_3}_V \simeq\;& |s_2| c_{\beta 13}-\frac{c_2^2}{2}c_3 s_{\beta 1},\; y^{h_3}_f \simeq |s_2| \left(c_{\beta 13}-s_{\beta 13}\kappa_f\right)\\& -\frac{c_2^2}{2}c_3\left(s_{\beta 1} + c_{\beta 1}\kappa_f\right), \end{aligned} $
(36) where
$ c_{\beta 13}\equiv\cos(\beta-\alpha_1-sgn(s_2)\alpha_3) $ and$ s_{\beta 13}\equiv\sin(\beta-\alpha_1- sgn(s_2)\alpha_3) $ . The mixing parameters are chosen as follows:$ \begin{array}{*{20}{l}} 0 \leq c_2 \leq 0.4,\; \; s_{\beta 13} = 1.0,\; \; 0 \leq c_{\beta 1} \leq 1.0,\; \; 1 \leq \tan\beta \leq 15. \end{array} $
(37) When
$ s_{\beta 13} = 1.0 $ and$ c_2 $ approaches zero, the couplings of$ h_2 $ to the SM particles converge to those of the SM Higgs boson, which is favored by the observed signal data for the 125 GeV Higgs.Scenario B: The mixing parameters are scanned over the following ranges:
$ \begin{array}{*{20}{l}} 0 \leq c_{\beta 1} \leq 0.4,\; \; -0.4 \leq s_{3} \leq 0.4,\; \; 0 \leq c_2 \leq 1,\; \; 1 \leq \tan\beta \leq 15. \end{array} $
(38) In the limits of
$ c_{\beta 1} \to 0 $ and$ |s_3| \to 0 $ , the couplings of$ h_2 $ to the SM particles approach those of the SM, which is favored by the signal measurements of the 125 GeV Higgs. In addition, when$ c_2 \to 1 $ , the 95.4 GeV Higgs boson ($ h_1 $ ) predominantly originates from the mixing of the two CP-even components of the Higgs doublets.After imposing the relevant theoretical constraints, the oblique parameters, the Higgs signal data at 125 GeV, searches for additional Higgs bosons at the collider, and flavor observables, the parameter space in scenario A that accounts for the observed excesses in the
$ b\bar{b} $ and diphoton channels at 95.4 GeV in Fig. 1 is identified. As indicated by Eq. (36), within the selected parameter space of scenario A, the coupling of$ h_2 $ to vector bosons,$ y_V^{h_2} $ , tends to be smaller than its coupling to fermions,$ y_f^{h_2} $ , as shown in the left panel of Fig. 1. The Higgs signal data at 125 GeV impose a lower bound on$ y_V^{h_2} $ , requiring$ y_V^{h_2} > 0.93 $ . In the parameter space consistent with the 125 GeV Higgs measurements, collider limits on additional Higgs bosons, and constraints from flavor physics, the coupling$ y_V^{h_1} $ is restricted to values below 0.38. Furthermore, the condition$ \chi^2_{95} < 6.18 $ is satisfied in the region of$ 0.2 \le y_V^{h_1} \le 0.38 $ , with$ y_f^{h_1} $ bounded from below. In addition, the Higgs signal data at 125 GeV exclude a small corner of the parameter space characterized by$ c_{\beta 1}\to 1 $ and$ c_2\to 0.4 $ . In such a region, both$ y_V^{h_2} $ and$ y_f^{h_2} $ can exhibit significant deviations from unity.
Figure 1. (color online) In scenario A, the parameter space is progressively constrained by sequentially imposing the following: theoretical requirements and the oblique parameters; the signal data of the 125 GeV Higgs boson; searches for additional Higgs bosons at the collider and flavor observables; and finally the condition
$ \chi_{95}^2<6.18 $ . The surviving parameter points at each stage are represented by green bullets, cyan squares, blue-edged squares, and red pluses, respectively.As shown in the left panel of Fig. 2, the value of
$ \chi_{95}^2 $ is sensitive to$ y^{h_1}_V $ and$ y^{h_1}_f $ , and decreases as they increase. The condition$ \chi_{95}^2<2.3 $ is satisfied in partial region of parameter space, with the minimum value attaining 1.2, which indicates that the model can explain the diphoton and$ b\bar{b} $ excesses within the$ 1\sigma $ ranges. The signal strength$ \mu_{b\bar{b}} $ is proportional to$ |y^{h_1}_V|^2 $ . Meanwhile, the W-loop can play an important contribution to the width of$ h_1\to \gamma\gamma $ , and therefore the signal strength$ \mu_{\gamma\gamma} $ is also affected by$ y^{h_1}_V $ . The interpretation of the$ b\bar{b} $ excess imposes a lower bound on$ |y_f^{h_1}| $ . Owing to$ y_V^{h_1}=c_2c_{\beta 1} $ , the value of$ \chi_{95}^2 $ tends to decrease as$ c_2 $ and$ c_{\beta 1} $ increase, as shown in the middle panel of Fig. 2. When$ c_{\beta 1} $ or$ \tan\beta $ is large, the$ y^{h_1}_f $ has a mild dependence on$ \tan\beta $ (See Eq. (16)). From the right panel of Fig. 2, it is observed that the value of$ \chi_{95}^2 $ shows limited sensitivity to$ \tan\beta $ .
Figure 2. (color online) In scenario A, the surviving parameter points satisfy
$ \chi_{95}^2<6.18 $ and simultaneously meet the theoretical constraints, the oblique parameters, the Higgs signal data at 125 GeV, searches for additional Higgs bosons at the collider, and flavor observables.Similar to Fig. 1, the parameter points for scenario B that account for the observed excesses in the
$ b\bar{b} $ and diphoton channels at 95.4 GeV are shown in Fig. 3. Unlike scenario A, the allowed region in scenario B includes not only the positive$ y_f^{h_1} $ region but also a narrow band where$ y_f^{h_1} $ takes negative values. The signal data of the 125 GeV Higgs boson require a small$ c_{\beta 1} $ , allowing for a negative$ y_f^{h_1} $ , see Eq. (16). The condition$ \chi_{95}^2 < 6.18 $ is satisfied in the region of$ 0.18<c_{\beta 1}< 0.35 $ and$ 0.88<c_2<1 $ . For such large$ c_2 $ , the 95.4 GeV Higgs boson mainly originates from the mixing of the two CP-even components of the Higgs doublets.
Figure 3. (color online) As Fig. 1, but for scenario B.
As in scenario A, the value of
$ \chi_{95}^2 $ in scenario B decreases as$ y^{h_1}_V $ and$ \mid y^{h_1}_f\mid $ ($ c_2 $ and$ c_{\beta 1} $ ) increase, as illustrated in the upper-left panel and upper-right panel of Fig. 4. However, different from scenario A, the minimal value of$ \chi_{95}^2 $ in scenario B only reaches 2, suggesting that the model can only marginally explain the diphoton and$ b\bar{b} $ excesses at the$ 1\sigma $ level. Furthermore, the condition$ \chi_{95}^2 < 6.18 $ disfavors a narrow region around$ \tan\beta\sim 4 $ , where the value of$ \mid y_f^{h_1}\mid $ is significantly suppressed. The parameter$ s_3 $ is favored to vary from -0.3 to 0.25, and is not sensitive to$ c_2 $ . Its absolute value decreases with increasing$ c_{\beta 1} $ to maintain a sufficiently large$ y_V^{h_2} $ to accommodate the signal data of the 125 GeV Higgs boson.
Figure 4. (color online) As Fig. 2, but for scenario B.
-
The combined analysis of ATLAS and CMS diphoton data at 95.4 GeV reveals a
$ 3.1\sigma $ local excess [4].$ \begin{array}{*{20}{l}} \mu_{\gamma\gamma}^{exp}=\mu_{\gamma\gamma}^{ATLAS+CMS}=0.24^{+0.09}_{-0.08}. \end{array} $

(26) Intriguingly, a persistent local excess with a significance of
$ 2.3\sigma $ was also observed in the$ e^+ e^- \to Z(\phi \to b\bar{b}) $ channel at LEP in the same mass region [1],$ \begin{array}{*{20}{l}} \mu_{b\bar{b}}^{exp}=0.117\pm 0.057. \end{array} $

(27) The observed excesses in the diphoton and
$ b\bar{b} $ channels at 95.4 GeV are attributed to resonant production of the lightest CP-even Higgs boson,$ h_1 $ . Under the narrow width approximation, the corresponding signal strengths can be formulated as follows:$ \begin{aligned}[b] \mu_{b\bar{b}}=\;&\frac{\sigma_\text{N2HDM}(e^+ e^-\rightarrow Z h_1)}{\sigma_\text{SM}(e^+ e^-\rightarrow Z h_{95.4}^\text{SM})}\times\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow b\bar{b})}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow b\bar{b})}\\=\;&|y^{h_1}_V|^2\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow b\bar{b})}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow b\bar{b})}, \end{aligned} $

(28) $ \begin{aligned}[b] \mu_{\gamma\gamma}=\;&\frac{\sigma_\text{N2HDM}(g g\rightarrow h_1)}{\sigma_\text{SM}(g g\rightarrow h_{95.4}^\text{SM})}\times \frac{\text{BR}_\text{N2HDM}(h_1\rightarrow \gamma\gamma)}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow \gamma\gamma)}\\\simeq\;& |y^{h_1}_f|^2\frac{\text{BR}_\text{N2HDM}(h_1\rightarrow \gamma\gamma)}{\text{BR}_\text{SM}(h_{95.4}^\text{SM}\rightarrow \gamma\gamma)}. \end{aligned} $

(29) To assess the capability to simultaneously account for the observed excesses in the
$ \gamma\gamma $ and$ b\bar{b} $ channels, we conduct a$ \chi^2_{95} $ analysis,$ \chi^2_{95}=\frac{(\mu_{\gamma\gamma}-0.24)^2}{0.085^2}+\frac{(\mu_{b\bar{b}}-0.117)^2}{0.057^2}, $

(30) and explain the diphoton and
$ b\bar{b} $ excesses within the$ 2\sigma $ ranges, namely$ \chi^2_{95}< 6.18 $ .In the model, the decay
$ h_1 \to \gamma\gamma $ is induced at the one-loop level, whose width is calculated as$ \begin{aligned}[b] \Gamma(h_1 \to \gamma\gamma) =\; & \frac{\alpha^2 m_{h_1}^3}{256 \pi^3 v^2} \Big| y_V^{h_1} F_1(\tau_{W^\pm}) + y_{H^\pm} F_0(\tau_{H^\pm})\\& +\sum\limits_f y_f^{h_1} N_{cf} Q_f^2 F_{1/2}(\tau_f) \Big|^2, \end{aligned} $

(31) where
$ \tau_i=\dfrac{4m^2_{i}}{m^2_{h_1}} $ , and$ N_{cf} $ and$ Q_f $ are electric charge and the number of color degrees of freedom of the fermion in the loop. The factor$ y_{H^\pm} $ is$ y_{H^\pm}=\frac{v}{2m_{h^\pm}^2}g_{h_1H^+H^-} $

(32) with
$ \begin{aligned}[b] g_{h_1H^+H^-}=\;&\frac{1}{v} \Bigg( - \frac{m_{12}^2}{s_\beta c_\beta} \left[ \frac{R_{11}}{c_\beta} + \frac{R_{12}}{s_\beta} \right] + m_{h_1}^2 \left[ \frac{R_{11} s_\beta^2}{c_\beta} + \frac{R_{12} c_\beta^2}{s_\beta} \right]\\& + 2m_{H^\pm}^2 [R_{11} c_\beta + R_{12} s_\beta] \Bigg) \end{aligned} $

(33) The functions
$ F_{1,0,1/2} $ are defined as [144]$ \begin{aligned}[b]& F_1(\tau) = 2 + 3 \tau + 3\tau (2-\tau) f(\tau),\\& F_{1/2}(\tau) = -2\tau [1 + (1-\tau)f(\tau)],\\& F_0(\tau) = \tau [1 - \tau f(\tau)], \end{aligned} $

(34) with
$ \begin{array}{*{20}{l}} f(\tau) = \left\{ \begin{array}{lr} [\sin^{-1}(1/\sqrt{\tau})]^2, & \tau \geq 1 \\ -\dfrac{1}{4} [\ln(\eta_+/\eta_-) - i \pi]^2, & \, \tau < 1 \end{array} \right. \end{array} $

(35) where
$ \eta_{\pm}=1\pm\sqrt{1-\tau} $ .In our calculations, we take two different scenarios:
Scenario A: By choosing a small value of
$ c_2 $ , the 95.4 GeV Higgs boson ($ h_1 $ ) is predominantly singlet-like, originating mainly from the singlet field$ \Phi_S $ . Under the approximation of$ s_2\simeq sgn(s_2)(1-\frac{c_2^2}{2}) $ , the couplings$ h_2 $ and$ h_3 $ normalized to the SM are given by$ \begin{aligned}[b] y^{h_2}_V \simeq\;& |s_2| s_{\beta 13}+\frac{c_2^2}{2}c_3 s_{\beta 1},\; y^{h_2}_f \simeq |s_2| \left(s_{\beta 13}+c_{\beta 13}\kappa_f\right)\\& +\frac{c_2^2}{2}c_3\left(s_{\beta 1} + c_{\beta 1}\kappa_f\right), \\ y^{h_3}_V \simeq\;& |s_2| c_{\beta 13}-\frac{c_2^2}{2}c_3 s_{\beta 1},\; y^{h_3}_f \simeq |s_2| \left(c_{\beta 13}-s_{\beta 13}\kappa_f\right)\\& -\frac{c_2^2}{2}c_3\left(s_{\beta 1} + c_{\beta 1}\kappa_f\right), \end{aligned} $

(36) where
$ c_{\beta 13}\equiv\cos(\beta-\alpha_1-sgn(s_2)\alpha_3) $ and$ s_{\beta 13}\equiv\sin(\beta-\alpha_1- sgn(s_2)\alpha_3) $ . The mixing parameters are chosen as follows:$ \begin{array}{*{20}{l}} 0 \leq c_2 \leq 0.4,\; \; s_{\beta 13} = 1.0,\; \; 0 \leq c_{\beta 1} \leq 1.0,\; \; 1 \leq \tan\beta \leq 15. \end{array} $

(37) When
$ s_{\beta 13} = 1.0 $ and$ c_2 $ approaches zero, the couplings of$ h_2 $ to the SM particles converge to those of the SM Higgs boson, which is favored by the observed signal data for the 125 GeV Higgs.Scenario B: The mixing parameters are scanned over the following ranges:
$ \begin{array}{*{20}{l}} 0 \leq c_{\beta 1} \leq 0.4,\; \; -0.4 \leq s_{3} \leq 0.4,\; \; 0 \leq c_2 \leq 1,\; \; 1 \leq \tan\beta \leq 15. \end{array} $

(38) In the limits of
$ c_{\beta 1} \to 0 $ and$ |s_3| \to 0 $ , the couplings of$ h_2 $ to the SM particles approach those of the SM, which is favored by the signal measurements of the 125 GeV Higgs. In addition, when$ c_2 \to 1 $ , the 95.4 GeV Higgs boson ($ h_1 $ ) predominantly originates from the mixing of the two CP-even components of the Higgs doublets.After imposing the relevant theoretical constraints, the oblique parameters, the Higgs signal data at 125 GeV, searches for additional Higgs bosons at the collider, and flavor observables, we identify the parameter space in scenario A that accounts for the observed excesses in the
$ b\bar{b} $ and diphoton channels at 95.4 GeV in Fig. 1. As indicated by Eq. (36), within the selected parameter space of scenario A, the coupling of$ h_2 $ to vector bosons,$ y_V^{h_2} $ , tends to be smaller than its coupling to fermions,$ y_f^{h_2} $ , as illustrated in the left panel. The Higgs signal data at 125 GeV impose a lower bound on$ y_V^{h_2} $ , requiring$ y_V^{h_2} > 0.93 $ . In the parameter space consistent with the 125 GeV Higgs measurements, collider limits on additional Higgs bosons, and constraints from flavor physics, the coupling$ y_V^{h_1} $ is restricted to values below 0.38. Furthermore, the condition$ \chi^2_{95} < 6.18 $ is satisfied in the region of$ 0.2 \le y_V^{h_1} \le 0.38 $ , with$ y_f^{h_1} $ bounded from below. In addition, the Higgs signal data at 125 GeV exclude a small corner of the parameter space characterized by$ c_{\beta 1}\to 1 $ and$ c_2\to 0.4 $ . In such region both$ y_V^{h_2} $ and$ y_f^{h_2} $ can exhibit significant deviations from unity.
Figure 1. (color online) In scenario A, the parameter space is progressively constrained by sequentially imposing the following: theoretical requirements and the oblique parameters; the signal data of the 125 GeV Higgs boson; searches for additional Higgs bosons at the collider and flavor observables; and finally the condition
$ \chi_{95}^2<6.18 $ . The surviving parameter points at each stage are represented by green bullets, cyan squares, blue-edged squares, and red pluses, respectively.As shown in the left panel of Fig. 2, the value of
$ \chi_{95}^2 $ is sensitive to$ y^{h_1}_V $ and$ y^{h_1}_f $ , and decreases as they increase. The condition$ \chi_{95}^2<2.3 $ is satisfied in partial region of parameter space, with the minimum value attaining 1.2, which indicates that the model can explain the diphoton and$ b\bar{b} $ excesses within the$ 1\sigma $ ranges. The signal strength$ \mu_{b\bar{b}} $ is proportional to$ |y^{h_1}_V|^2 $ . Meanwhile, the W-loop can play an important contribution to the width of$ h_1\to \gamma\gamma $ , and therefore the signal strength$ \mu_{\gamma\gamma} $ is also affected by$ y^{h_1}_V $ . The interpretation of the$ b\bar{b} $ excess imposes a lower bound on$ |y_f^{h_1}| $ . Because of$ y_V^{h_1}=c_2c_{\beta 1} $ , the value of$ \chi_{95}^2 $ tends to decrease as$ c_2 $ and$ c_{\beta 1} $ increase, as shown in the middle panel of Fig. 2. When$ c_{\beta 1} $ or$ \tan\beta $ is large, the$ y^{h_1}_f $ will has a mild dependence on$ \tan\beta $ (See Eq. (16)). From the right panel of Fig. 2, it is observed that the value of$ \chi_{95}^2 $ shows limited sensitivity to$ \tan\beta $ .
Figure 2. (color online) In scenario A, the surviving parameter points satisfy
$ \chi_{95}^2<6.18 $ and simultaneously meet the theoretical constraints, the oblique parameters, the Higgs signal data at 125 GeV, searches for additional Higgs bosons at the collider, and flavor observables.Similar to Fig. 1, we display the parameter points for scenario B that accounts for the observed excesses in the
$ b\bar{b} $ and diphoton channels at 95.4 GeV in Fig. 3. Unlike scenario A, the allowed region in scenario B includes not only the positive$ y_f^{h_1} $ region but also a narrow band where$ y_f^{h_1} $ takes negative values. The signal data of the 125 GeV Higgs boson requires a small$ c_{\beta 1} $ , allowing for a negative$ y_f^{h_1} $ , see Eq. (16). The condition$ \chi_{95}^2 < 6.18 $ is satisfied in the region of$ 0.18<c_{\beta 1}< 0.35 $ and$ 0.88<c_2<1 $ . For such large$ c_2 $ , the 95.4 GeV Higgs boson mainly originates from the mixing of the two CP-even components of the Higgs doublets.
Figure 3. (color online) Same as the Fig. 1, but for scenario B.
As in scenario A, the value of
$ \chi_{95}^2 $ in scenario B decreases as$ y^{h_1}_V $ and$ \mid y^{h_1}_f\mid $ ($ c_2 $ and$ c_{\beta 1} $ ) increase, as illustrated in the upper-left panel and upper-right panel of Fig. 4. However, different from scenario A, the minimal value of$ \chi_{95}^2 $ in scenario B only reaches to 2, suggesting that the model can only marginally explain the diphoton and$ b\bar{b} $ excesses at the$ 1\sigma $ level. Furthermore, the condition$ \chi_{95}^2 < 6.18 $ disfavors a narrow region around$ \tan\beta\sim 4 $ , where the value of$ \mid y_f^{h_1}\mid $ is significantly suppressed. The parameter$ s_3 $ is favored to vary from -0.3 to 0.25, and is not sensitive to$ c_2 $ . Its absolute value decreases with increasing$ c_{\beta 1} $ in order to maintain a sufficiently large$ y_V^{h_2} $ to accommodate the signal data of the 125 GeV Higgs boson.
Figure 4. (color online) Same as the Fig. 2, but for scenario B.
-
The classical scalar fields are parameterized as
$ \begin{array}{*{20}{l}} \Phi_1=\left(\begin{array}{c} 0 \\ \dfrac{\phi_1(z)}{\sqrt{2}}\, \end{array}\right)\,,\; \Phi_2=\left(\begin{array}{c} 0 \\ \dfrac{\phi_2(z)}{\sqrt{2}}\, \end{array}\right), \;\Phi_S=\phi_s(z), \end{array} $
(39) where z is a coordinate perpendicular to domain walls [145]. The expression for the energy density of the domain walls is given by
$ \begin{aligned}[b] \varepsilon_{\rm wall}=\;&\frac{1}{2}(\partial_z\phi_1)^2 + \frac{1}{2}(\partial_z\phi_2)^2 + \frac{1}{2}(\partial_z\phi_S)^2\\& + V(\phi_1,\phi_2,\phi_S) -V(v_1,v_2,v_s), \end{aligned} $
(40) with the scalar potential
$ \begin{aligned}[b] V(\phi_1,\phi_2,\phi_S)=\;&\frac{m_{11}^2}{2} \phi_1^2 +\frac{\lambda_1}{8} \phi_1^4+ \frac{m_{22}^2}{2} \phi_2^2\\&+\frac{\lambda_2}{8} \phi_2^4-m_{12}^2 \phi_1 \phi_2+\frac{\lambda_{345}}{4} \phi_1^2 \phi_2^2 \\ &+\frac{m_S^2}{2} \phi_S^2 +\frac{\lambda_6}{8} \phi_S^4+ \frac{\lambda_7}{4} \phi_1^2\phi_S^2 \\&+\frac{\lambda_8}{4} \phi_2^2 \phi_S^2-a_1 v_s^2 \phi_S+\frac{a_1}{3} \phi_S^3. \end{aligned} $
(41) The equations of motion for domain walls are
$ \frac{ \mathrm{d}^2 \phi_i }{ \mathrm{d} z^2 } = \frac{ \partial V(\phi_1,\phi_2,\phi_S) }{ \partial \phi_i }, \quad ( \phi_i=\phi_1,\phi_2,\phi_S), $
(42) with the boundary conditions
$ \begin{array}{*{20}{l}} \lim_{z\to\pm\infty}\phi_1(z)=v_1,\; \lim_{z\to\pm\infty}\phi_2(z)=v_2, \; \lim_{z\to\pm\infty}\phi_S(z)=\pm v_s. \end{array} $
(43) $ \textsf{CosmoTransitions} $ [146] is modified to approximately solve Eqs. (42) and (43), and relevant computational details are provided in [146, 147]. The domain wall tension$ \sigma_{\rm wall} $ is computed through an integration of the energy density$ \varepsilon_{\rm wall} $ over the z axis,$ \sigma_{\rm wall}=\int {\rm d}z \; \varepsilon_{\rm wall}. $
(44) Domain walls must collapse before they can overclose the Universe. The volume pressure induced by energy bias (
$ V_{\rm bias} $ ) exerts a force on the domain walls, and drives the contraction of regions occupied by the false vacuum. The collapse of domain wall occurs when the volume pressure force becomes comparable to the tension force. The characteristic temperature at which the domain walls annihilate can be estimated by [148, 149]$ T_{\rm ann} =3.41\times 10^{-2}\,{\rm GeV}\, C_{\rm ann}^{-1/2} A^{-1/2} \Big( \frac{ g_{*} (T_{\rm ann}) }{10} \Big)^{-1/4} \hat \sigma_{\rm wall}^{-1/2} \hat V_{\rm bias}^{1/2} \,, $
(45) with
$ \hat \sigma_{\rm wall} \equiv \frac{\sigma_{\rm wall}}{\rm TeV^3},\quad \hat V_{\rm bias} \equiv \frac{V_{\rm bias}}{\rm MeV^4}. $
(46) In this analysis, a constant
$ C_{\rm ann}=5 $ [149] is adopted and the area parameter$ A\simeq 0.8 $ is set for the$ Z_2 $ symmetric model [148]. The energetic particles released from the collapse of domain walls have the potential to disrupt the synthesis of light nuclei formed during Big Bang Nucleosynthesis (BBN) [150]. To preserve the successful predictions of BBN, it is therefore imperative that the domain walls annihilate before the BBN epoch,$ T_{\rm ann} > T_{\rm BBN} = 8.6 \times 10^{-3} $ GeV. In addition, to ensure that domain walls annihilate before their energy density dominates the Universe, a lower bound must be imposed on$ V_{\rm bias} $ [149]$ \begin{array}{*{20}{l}} V_{\rm{bias}}^{1/4}>2.18\times 10^{-5} ~~ C_{\rm{ann}}^{\frac{1}{4}} ~ A^{\frac{1}{2}} \hat \sigma_{\rm wall}^{\frac{1}{2}}\; . \end{array} $
(47) Following the annihilation of domain walls, a SGWB is produced, and the peak frequency is given by [148]
$ \begin{aligned}[b] f_{\rm peak} \simeq & 1.1\times 10^{-7}\,{\rm Hz}\, \Big( \frac{ g_*( T_{\rm ann} ) }{10} \Big)^{1/2} \Big( \frac{ g_{*s}( T_{\rm ann} ) }{10} \Big)^{-1/3} \Big( \frac{ T_{\rm ann} }{1\,\rm GeV } \Big)\\ \simeq & 3.75\times 10^{-9}\,{\rm Hz}\, \Big( \frac{ g_*( T_{\rm ann} ) }{10} \Big)^{1/4} \Big( \frac{ g_{*s}( T_{\rm ann} ) }{10} \Big)^{-1/3} \\&\times C_{\rm ann}^{-1/2} A^{-1/2} \hat\sigma^{-1/2}_{\rm wall} \hat V_{\rm bias}^{1/2} \,. \end{aligned} $
(48) where
$ g_*(T_{\rm ann}) $ and$ g_{*s}(T_{\rm ann}) $ count the relativistic degrees of freedom contributing to the energy and entropy densities, respectively. Within the temperature range$ 1\,\rm MeV\lesssim T_{\rm ann} \lesssim 100\,\rm MeV $ , both quantities take the value 10.75 [151].The peak amplitude of the GW spectrum at the present time is [148, 149]
$ \begin{aligned}[b] \Omega_{\rm GW}^{\rm peak} h^2 =\;& 5.3\times 10^{-20}\, \tilde \epsilon_{\rm GW} A^4 C_{\rm ann}^2 \Big( \frac{ g_{*s}(T_{\rm ann}) }{10} \Big)^{-4/3} \\&\times\Big( \frac{ g_{*} (T_{\rm ann}) }{10} \Big) \hat \sigma^4_{\rm wall} \hat V^{-2}_{\rm bias} \,. \end{aligned} $
(49) with
$ \tilde \epsilon_{\rm GW}\simeq 0.7\pm 0.4 $ [148]. Given an arbitrary frequency f, the following is used [148, 152]$ \Omega_{\text{GW}}h^2(f<f_{\text{peak}}) = \Omega_{\rm GW}^{\rm peak} h^2 \left(\frac{f}{f_{\text{peak}}}\right)^3, $
(50) $ \Omega_{\text{GW}}h^2(f>f_{\text{peak}}) = \Omega_{\rm GW}^{\rm peak} h^2 \left(\frac{f_{\text{peak}}}{f}\right). $
(51) In the discussions,
$ 10^{-9} $ Hz$ \leq f_{\rm peak}\leq $ $ 10^{-7} $ Hz are taken, and$ T_{\rm ann} $ is obtained from the first line of Eq. (48).$ \hat V_{\rm bias} $ is obtained from the second line of Eq. (48) with$ f_{\rm peak} $ and$ \hat \sigma_{\rm wall} $ calculated in the parameter points accommodating the diphoton and$ b\bar{b} $ excesses at 95.4 GeV. Fig. 5 and Fig. 6 show the parameter points that satisfy$ \chi_{95}^2 < 6.18 $ and$ \Omega_{\rm GW}^{\rm peak} h^2>10^{-15} $ for$ f_{\rm peak}=10^{-9} $ Hz while remaining consistent with relevant theoretical and experimental constraints mentioned above, for scenario A and scenario B, respectively.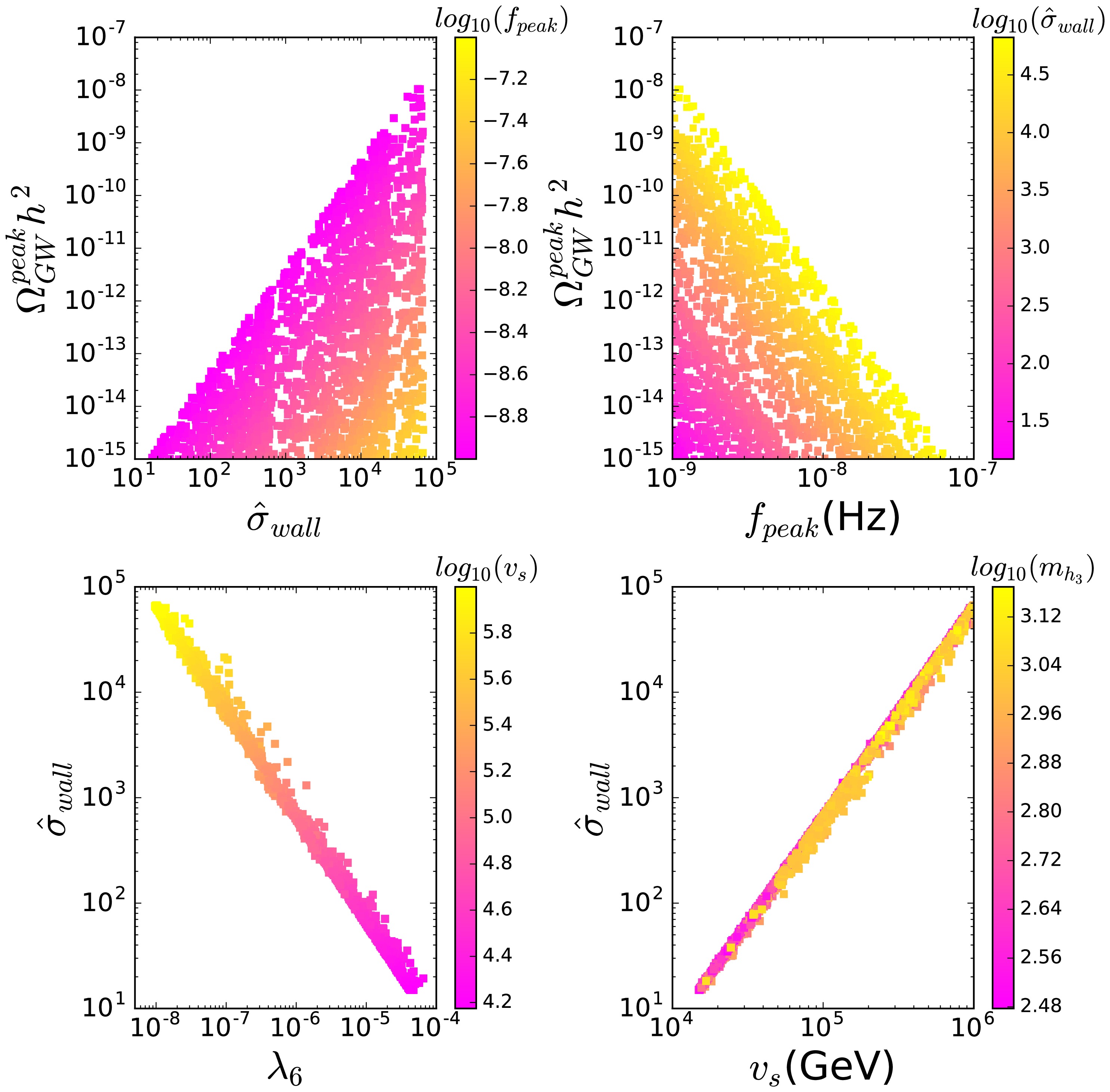
Figure 5. (color online) In scenario A, the parameter points satisfy
$ \Omega_{\rm GW}^{\rm peak} h^2>10^{-15} $ and$ \chi_{95}^2<6.18 $ , while also complying with the theoretical and experimental constraints discussed above.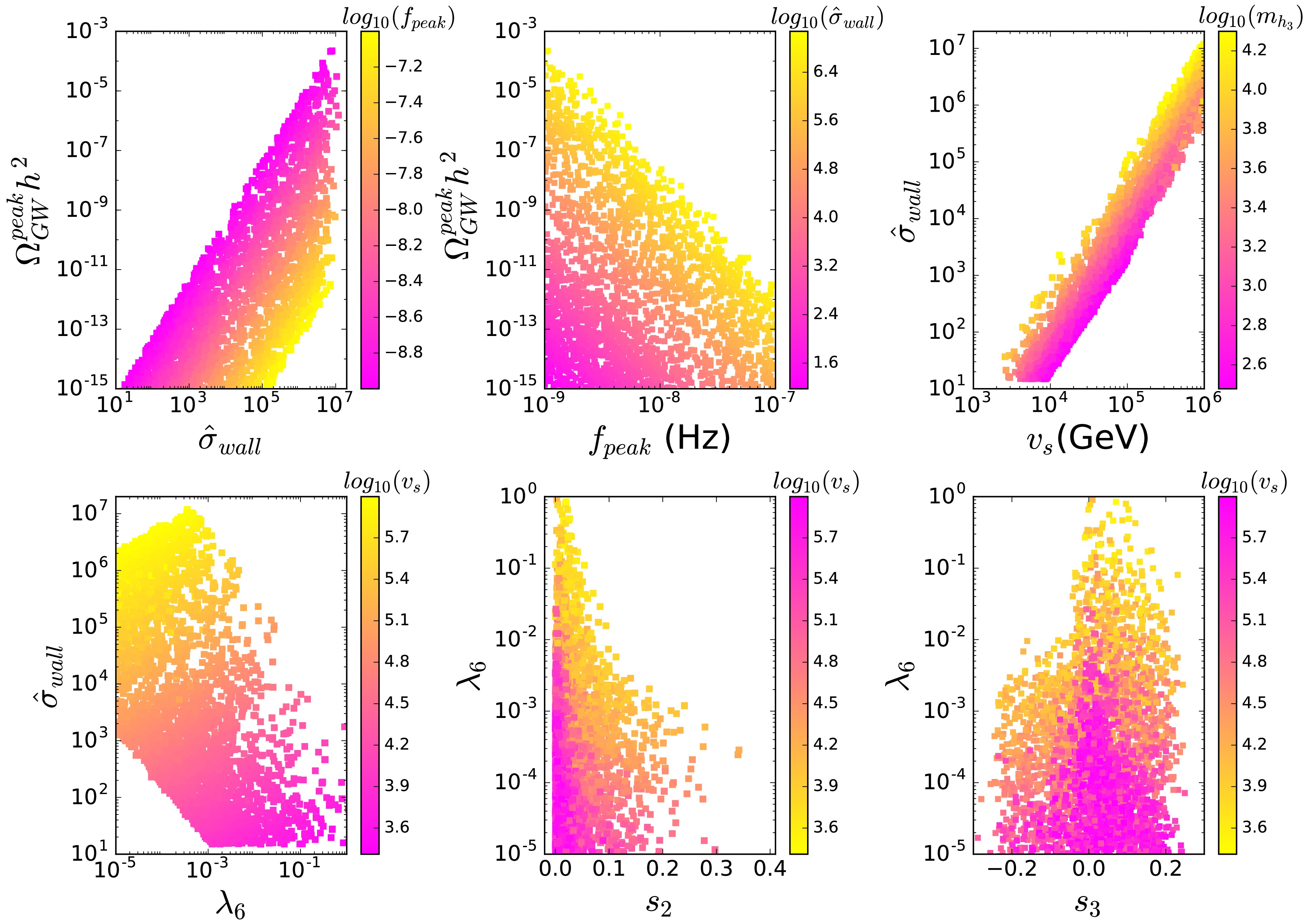
Figure 6. (color online) As Fig. 5, but for scenario B.
The peak amplitude
$ \Omega_{\rm GW}^{\rm peak} $ increases with decreasing$ f_{\rm peak} $ and increasing$ \hat\sigma_{\rm wall} $ , as indicated by the second line of Eqs. (48) and (49), and as illustrated in the upper-left and upper-right panels of Fig. 5. In scenario A, although the 95.4 GeV Higgs boson ($ h_1 $ ) predominantly originates from the real singlet field, it must include non-negligible components of the Higgs doublets to acquire the necessary couplings to gauge bosons and fermions, thereby accounting for the observed diphoton and and$ b\bar{b} $ excesses at 95.4 GeV. Thus, both$ R_{31} $ and$ R_{32} $ can not approach to zero, theoretical constraints on$ \lambda_{1,2,3} $ will impose a lower bound on$ m_{h_3} $ ,$ m_{h_3}<1.5 $ TeV (see the first three lines of Eq. (13)). As a result, according to the sixth line of Eq. (13),$ \lambda_6 $ decreases with increasing$ v_s $ , yielding a range of$ 10^{-8}<\lambda_6<10^{-4} $ for$ 14\; {\rm TeV}\; <v_s<1000 $ TeV. Although$ \lambda_6 $ decreases as$ v_s $ increases, the domain wall tension$ \hat\sigma_{\rm wall} $ still grows rapidly.In scenario B, the 95.4 GeV Higgs boson predominantly originates from the CP-even components of the Higgs doublets. Even though the mixing between the singlet and doublet components vanishes (i.e.,
$ R_{31}\to 0 $ and$ R_{32}\to 0 $ ), the 95.4 GeV Higgs boson still can interact with gauge bosons and fermions to explain the diphoton and$ b\bar{b} $ excesses at 95.4 GeV. Therefore, theoretical constraints on$ \lambda_{1,2,3} $ allow$ m_{h_3} $ to have a large value, reaching up to 20 TeV for sufficiently small$ s_2 $ and$ s_3 $ . Consequently,$ \lambda_6 $ is sensitive to$ s_2 $ ,$ s_3 $ , and$ v_s $ , and can attain larger value as$ s_2 $ ,$ s_3 $ , and$ v_s $ decrease, as illustrated in the lower-middle and lower-right panels of Fig. 6. Asthe domain wall tension$ \hat\sigma_{\rm wall} $ mainly depends on$ v_s $ and$ \lambda_6 $ , as shown in the lower-left panel of Fig. 6, the value of$ \hat\sigma_{\rm wall} $ in scenario B can be much larger than that in scenario A, thereby significantly enhancing$ \Omega_{\rm GW}^{\rm peak} $ .Four benchmark points are identified: BPA1 and BPA2 for scenario A, and BPB1 and BPB2 for scenario B, and the key input parameters and results are listed in Table 1. BPA2 is taken as an example to show the domain wall profiles of
$ \phi_1 $ ,$ \phi_2 $ , and$ \phi_s $ for the BPA2 in Fig. 7. From Fig. 7, one can deduce that the domain wall tension$ \sigma_{\rm wall} $ is predominantly determined by the singlet field$ \phi_s(z) $ when$ v_s $ is very large.$m_{h_3}$ /GeV$m_{A}$ /GeV$m_{H^\pm}$ /GeV$m_{12}^2\;/{\rm{GeV}}^2$ $\tan\beta$ $s_{1}$ $s_{2}$ $s_{3}$ $v_s$ /GeV$\lambda_6$ $\hat \sigma_{\rm wall}$ $ f_{\rm peak} $ $\Omega^{\rm peak}_{\rm GW}h^2$ $\chi^2_{95}$ BPA1 912.25 887.14 912.25 208668.96 3.51 0.9569 0.9362 −0.9998 999021 $1.01\times 10^{-8}$ $6.69\times 10^{4} $ $7.0\times 10^{-9}$ $2.00\times 10^{-8}$ 1.89 BPA2 312.53 465.11 465.11 15778.26 5.13 0.8331 0.9580 −0.9235 101267 $1.05\times 10^{-6}$ $7.10\times 10^{2} $ $1.5\times 10^{-9}$ $2.26\times 10^{-12}$ 4.61 BPB1 18418.07 414.86 414.86 553.96 12.53 0.1575 0.0046 0.0350 982846 $3.51\times 10^{-4}$ $1.19\times 10^{7} $ $1.1\times 10^{-8}$ $7.22\times 10^{-8}$ 5.77 BPB2 13474.82 476.88 476.88 1161.65 5.30 0.1081 0.0047 0.0313 728781 $3.42\times 10^{-4}$ $4.78\times 10^{6}$ $1.4\times 10^{-8}$ $1.03\times 10^{-8}$ 3.01 Table 1. Input parameters and results for the BPA1, BPA2, BPB1 and BPB2. Here
$ m_{h_1}=95.4 $ GeV and$ m_{h_2}=125.5 $ GeV are fixed.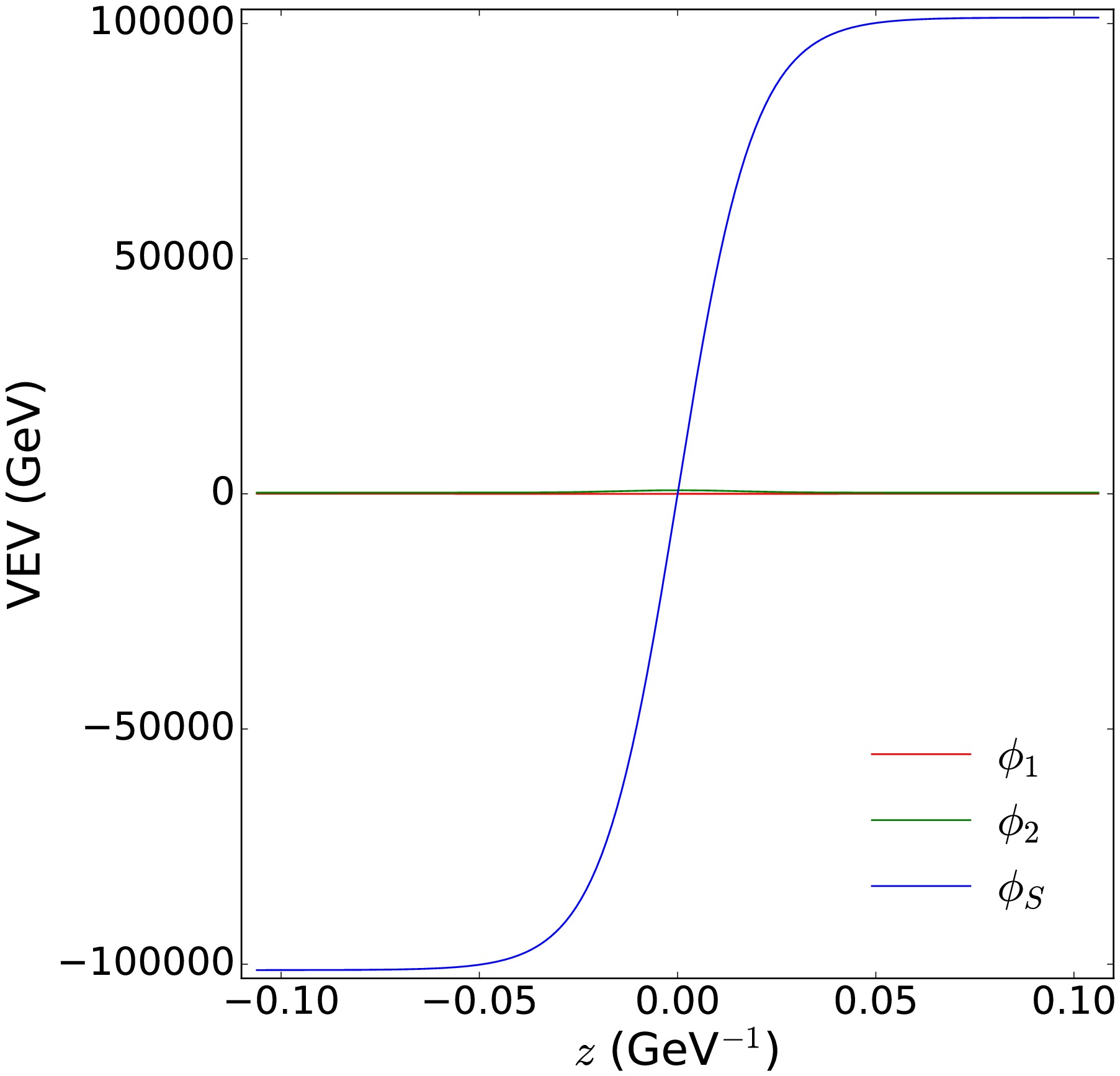
Figure 7. (color online) The domain wall profiles of
$ \phi_1 $ ,$ \phi_2 $ , and$ \phi_S $ for the BPA2.The GW spectra for the four benchmark points are examined, which are shown along with the result of the NANOGrav dataset and the sensitivity curve of SKA in Fig. 8. For the BPB1 with
$ v_s\approx $ 980 TeV, the predicted GW spectrum can account for the entire frequency range of the NANOGrav data, from low to high frequencies. For the BPB2 with$ v_s= $ 730 TeV, the predicted GW spectrum explains the NANOGrav data in the low frequency region ($ f<4\times 10^{-8} $ Hz) but fails to extend into the higher frequency range. From the parameter points shown in Fig. 5, the one with the largest domain wall tension is selected as BPA1. However, the peak amplitude of its GW spectrum only fits the edges of several low-frequency regions of the NANOGrav data. As illustrated in Fig. 8, the GW spectra corresponding to BPA1 and BPA2 exceed the SKA sensitivity curve in several low frequency regions.A Bayesian analysis of the model is performed using
$\textsf{PTArcade}$ [154] and the NANOGrav 15 year data. The$\textsf{Ceffyl}$ mode [155] is employed to derive the posterior distributions of the model parameters. The$\textsf{Enterprise}$ mode [156] is used to evaluate the Bayes factor of our model relative to the supermassive black hole binaries (SMBHB). The GW background signal from SMBHB is modeled as a power law of the form,$ \Omega_{\rm GW}(f) h^2 = \frac{ 2\pi^2 A^2_{\rm BHB}}{3H_0} \Big( \frac{ f}{f_{yr}} \Big)^{5-\gamma_{\rm BHB}} f_{yr}^2, $
(52) where
$ f_{yr}=year^{-1}=3.17\times 10^{-8} $ Hz and$ H_0 $ is the present-day value of the Hubble rate. A two-dimensional Gaussian prior is adopted for$ \gamma_{\rm BHB} $ and$ A_{\rm BHB} $ , derived from a power-law fit to the simulated SMBHB populations [69], as implemented in$\textsf{PTArcade}$ .Table 2 lists the priors for the parameters of scenario B in the model and the Bayes factor. For very large
$ v_s $ in the range of 500–1000 TeV, the domain wall tension$ \sigma_{\rm wall} $ is almost entirely determined by$ \lambda_6 $ , while being insensitive to other parameters. Consequently, all parameters except$ v_s $ and$ \lambda_6 $ are fixed for simplicity. It is assumed that the singlet scalar field exhibits mild mixings with the two Higgs doublets, leading to non-zero values of$ s_2 $ and$ s_3 $ . As a result, the couplings of the 125 GeV Higgs boson deviate slightly from the SM predictions, which may be tested in the future using the Circular Electron Positron Collider (CEPC). A detailed study of this aspect will be performed in future work. For the chosen values of$ s_2 $ and$ s_3 $ , as well as$ v_s\sim 1000 $ TeV, theoretical constraints require$ \lambda_6 < 0.0004 $ . Simultaneously, the diphoton and$ b\bar{b} $ excesses at 95.4 GeV are accommodated within the$ 2\sigma $ ranges. The Bayes factor is estimated to be approximately 22. The posterior distributions of parameters are shown in Fig. 9. The maximum posterior value of$ f_{\rm peak} $ is$ 1.2\times 10^{-8} $ Hz, while$ \lambda_{6} < 2.4\times 10^{-4} $ and$ v_s< 870 $ TeV respectively lie outside the 68% credible interval. For scenario A, even within the optimistic prior ranges, the Bayes factor is found to be nearly zero, consistent with the results shown in Fig. 8.$m_{h_1}$ /GeV$m_{h_2}$ /GeV$m_{A}=m_{H^\pm}$ /GeV$m_{12}^2\;/{\rm{GeV}}^2$ $\tan\beta$ $s_{1}$ $s_{2}$ $s_{3}$ $v_s$ (100 TeV)$\lambda_6$ ${\rm log10}(f_{\rm peak})$ ${\rm BF}_{\rm Y,X}$ scenario B 95.4 125.5 410 550 12 0.16 0.004 0.035 Uniform
[5, 10]Uniform
[0.0001,0.0004]Uniform
[-9, -7]$22.41\pm 6.75$ Table 2. Summary of model parameters and prior ranges. Bayesian factors, BF
$ _{\rm Y,X} $ , with Y representing scenario B and X denoting SMBHB. -
The classical scalar fields are parameterized as
$ \begin{array}{*{20}{l}} \Phi_1=\left(\begin{array}{c} 0 \\ \dfrac{\phi_1(z)}{\sqrt{2}}\, \end{array}\right)\,,\; \Phi_2=\left(\begin{array}{c} 0 \\ \dfrac{\phi_2(z)}{\sqrt{2}}\, \end{array}\right), \;\Phi_S=\phi_s(z), \end{array} $

(39) where z is a coordinate perpendicular to domain walls [145]. The expression for the energy density of the domain walls is given by
$ \begin{aligned}[b] \varepsilon_{\rm wall}=\;&\frac{1}{2}(\partial_z\phi_1)^2 + \frac{1}{2}(\partial_z\phi_2)^2 + \frac{1}{2}(\partial_z\phi_S)^2\\& + V(\phi_1,\phi_2,\phi_S) -V(v_1,v_2,v_s), \end{aligned} $

(40) with the scalar potential
$ \begin{aligned}[b] V(\phi_1,\phi_2,\phi_S)=\;&\frac{m_{11}^2}{2} \phi_1^2 +\frac{\lambda_1}{8} \phi_1^4+ \frac{m_{22}^2}{2} \phi_2^2\\&+\frac{\lambda_2}{8} \phi_2^4-m_{12}^2 \phi_1 \phi_2+\frac{\lambda_{345}}{4} \phi_1^2 \phi_2^2 \\ &+\frac{m_S^2}{2} \phi_S^2 +\frac{\lambda_6}{8} \phi_S^4+ \frac{\lambda_7}{4} \phi_1^2\phi_S^2 \\&+\frac{\lambda_8}{4} \phi_2^2 \phi_S^2-a_1 v_s^2 \phi_S+\frac{a_1}{3} \phi_S^3. \end{aligned} $

(41) The equations of motion for domain walls are
$ \frac{ \mathrm{d}^2 \phi_i }{ \mathrm{d} z^2 } = \frac{ \partial V(\phi_1,\phi_2,\phi_S) }{ \partial \phi_i }, \quad ( \phi_i=\phi_1,\phi_2,\phi_S), $

(42) with the boundary conditions
$ \begin{array}{*{20}{l}} \lim_{z\to\pm\infty}\phi_1(z)=v_1,\; \lim_{z\to\pm\infty}\phi_2(z)=v_2, \; \lim_{z\to\pm\infty}\phi_S(z)=\pm v_s. \end{array} $

(43) We modify
$ \textsf{CosmoTransitions} $ [146] to approximately solve Eqs. (42) and (43), and relevant computational details are provided in [146,147]. The domain wall tension$ \sigma_{\rm wall} $ is computed through an integration of the energy density$ \varepsilon_{\rm wall} $ over the z axis,$ \begin{array}{*{20}{l}} \sigma_{\rm wall}=\int dz \; \varepsilon_{\rm wall}. \end{array} $

(44) Domain walls must collapse before they can overclose the Universe. The volume pressure induced by energy bias (
$ V_{\rm bias} $ ) exerts a force on the domain walls, and drives the contraction of regions occupied by the false vacuum. The collapse of domain wall occurs when the volume pressure force becomes comparable to the tension force. The characteristic temperature at which the domain walls annihilate can be estimated by [148,149]$ T_{\rm ann} =3.41\times 10^{-2}\,{\rm GeV}\, C_{\rm ann}^{-1/2} A^{-1/2} \Big( \frac{ g_{*} (T_{\rm ann}) }{10} \Big)^{-1/4} \hat \sigma_{\rm wall}^{-1/2} \hat V_{\rm bias}^{1/2} \,, $

(45) with
$ \hat \sigma_{\rm wall} \equiv \frac{\sigma_{\rm wall}}{\rm TeV^3},\; \; \hat V_{\rm bias} \equiv \frac{V_{\rm bias}}{\rm MeV^4}. $

(46) In this analysis, we adopt a constant
$ C_{ann}=5 $ [149] and set the area parameter$ A\simeq 0.8 $ for the$ Z_2 $ symmetric model [148]. The energetic particles released from the collapse of domain walls have the potential to disrupt the synthesis of light nuclei formed during Big Bang Nucleosynthesis (BBN) [150]. To preserve the successful predictions of BBN, it is therefore imperative that the domain walls annihilate before the BBN epoch,$ T_{\rm ann} > T_{\rm BBN} = 8.6 \times 10^{-3} $ GeV. In addition, in order to ensure that domain walls annihilate before their energy density dominates the Universe, a lower bound must be imposed on$ V_{\rm bias} $ [149]$ \begin{array}{*{20}{l}} V_{\rm{bias}}^{1/4}>2.18\times 10^{-5} \quad C_{\rm{ann}}^{\frac{1}{4}} \quad A^{\frac{1}{2}} \hat \sigma_{\rm wall}^{\frac{1}{2}}\,\,. \end{array} $

(47) Following the annihilation of domain walls, a SGWB is produced, and the peak frequency is given by [148]
$ \begin{aligned}[b] f_{\rm peak} \simeq & 1.1\times 10^{-7}\,{\rm Hz}\, \Big( \frac{ g_*( T_{\rm ann} ) }{10} \Big)^{1/2} \Big( \frac{ g_{*s}( T_{\rm ann} ) }{10} \Big)^{-1/3} \Big( \frac{ T_{\rm ann} }{1\,\rm GeV } \Big)\\ \simeq & 3.75\times 10^{-9}\,{\rm Hz}\, \Big( \frac{ g_*( T_{\rm ann} ) }{10} \Big)^{1/4} \Big( \frac{ g_{*s}( T_{\rm ann} ) }{10} \Big)^{-1/3} \\&\times C_{\rm ann}^{-1/2} A^{-1/2} \hat\sigma^{-1/2}_{\rm wall} \hat V_{\rm bias}^{1/2} \,. \end{aligned} $

(48) Here,
$ g_*(T_{\rm ann}) $ and$ g_{*s}(T_{\rm ann}) $ count the relativistic degrees of freedom contributing to the energy density and the entropy density. Within the temperature range$ 1\,\rm MeV\lesssim T_{\rm ann} \lesssim 100\,\rm MeV $ , both quantities take the value 10.75 [151].The peak amplitude of the GW spectrum at the present time is [148,149]
$ \begin{aligned}[b] \Omega_{\rm GW}^{\rm peak} h^2 =\;& 5.3\times 10^{-20}\, \tilde \epsilon_{\rm GW} A^4 C_{\rm ann}^2 \Big( \frac{ g_{*s}(T_{\rm ann}) }{10} \Big)^{-4/3} \\&\times\Big( \frac{ g_{*} (T_{\rm ann}) }{10} \Big) \hat \sigma^4_{\rm wall} \hat V^{-2}_{\rm bias} \,. \end{aligned} $

(49) with
$ \tilde \epsilon_{\rm GW}\simeq 0.7\pm 0.4 $ [148]. Given an arbitrary frequency f, we use [148,152]$ \Omega_{\text{GW}}h^2(f<f_{\text{peak}}) = \Omega_{\rm GW}^{\rm peak} h^2 \left(\frac{f}{f_{\text{peak}}}\right)^3, $

(50) $ \Omega_{\text{GW}}h^2(f>f_{\text{peak}}) = \Omega_{\rm GW}^{\rm peak} h^2 \left(\frac{f_{\text{peak}}}{f}\right). $

(51) In our discussions, we take
$ 10^{-9} $ Hz$ \leq f_{\rm peak}\leq $ $ 10^{-7} $ Hz, and get$ T_{\rm ann} $ from the first line of Eq. (48).$ \hat V_{\rm bias} $ is obtained from the second line of Eq. (48) with$ f_{\rm peak} $ and$ \hat \sigma_{\rm wall} $ calculated in the parameter points accommodating the diphoton and$ b\bar{b} $ excesses at 95.4 GeV. In Fig. 5 and Fig. 6, we display the parameter points that satisfy$ \chi_{95}^2 < 6.18 $ and$ \Omega_{\rm GW}^{\rm peak} h^2>10^{-15} $ for$ f_{peak}=10^{-9} $ Hz while remaining consistent with relevant theoretical and experimental constraints mentioned above, for scenario A and scenario B, respectively.
Figure 5. (color online) In scenario A, the parameter points satisfy
$ \Omega_{\rm GW}^{\rm peak} h^2>10^{-15} $ and$ \chi_{95}^2<6.18 $ , while also complying with the theoretical and experimental constraints discussed above.
Figure 6. (color online) Same as the Fig. 5, but for scenario B.
The peak amplitude
$ \Omega_{\rm GW}^{\rm peak} $ increases with decreasing$ f_{peak} $ and increasing$ \hat\sigma_{\rm wall} $ , as indicated by the second line of Eq. (48) and Eq. (49), and as illustrated in the upper-left and upper-right panels of Fig. 5. In scenario A, although the 95.4 GeV Higgs boson ($ h_1 $ ) predominantly originates from the real singlet field, it must include non-negligible components of the Higgs doublets to acquire the necessary couplings to gauge bosons and fermions, thereby accounting for the observed diphoton and and$ b\bar{b} $ excesses at 95.4 GeV. Thus, both$ R_{31} $ and$ R_{32} $ can not approach to zero, theoretical constraints on$ \lambda_{1,2,3} $ will impose a lower bound on$ m_{h_3} $ ,$ m_{h_3}<1.5 $ TeV (see the first three lines of Eq. (13)). As a result, according to the sixth line of Eq. (13),$ \lambda_6 $ decreases with increasing$ v_s $ , yielding a range of$ 10^{-8}<\lambda_6<10^{-4} $ for$ 14\; {\rm TeV}\; <v_s<1000 $ TeV. Although$ \lambda_6 $ decreases as$ v_s $ increases, the domain wall tension$ \hat\sigma_{\rm wall} $ still grows rapidly.In scenario B, the 95.4 GeV Higgs boson predominantly originates from the CP-even components of the Higgs doublets. Even though the mixing between the singlet and doublet components vanishes (i.e.,
$ R_{31}\to 0 $ and$ R_{32}\to 0 $ ), the 95.4 GeV Higgs boson still can interact with gauge bosons and fermions to explain the diphoton and$ b\bar{b} $ excesses at 95.4 GeV. Therefore, theoretical constraints on$ \lambda_{1,2,3} $ allow$ m_{h_3} $ to have a large value, reaching up to 20 TeV for sufficiently small$ s_2 $ and$ s_3 $ . Consequently,$ \lambda_6 $ is sensitive to$ s_2 $ ,$ s_3 $ , and$ v_s $ , and can attain larger value as$ s_2 $ ,$ s_3 $ , and$ v_s $ decrease, as illustrated in the lower-middle and lower-right panels of Fig. 6. Since the domain wall tension$ \hat\sigma_{\rm wall} $ mainly depends on$ v_s $ and$ \lambda_6 $ , as shown in the lower-left panel of Fig. 6, the value of$ \hat\sigma_{\rm wall} $ in scenario B can be much larger than that in scenarioA, thereby significantly enhancing$ \Omega_{\rm GW}^{\rm peak} $ .We pick out four benchmark points: BPA1 and BPA2 for scenario A, and BPB1 and BPB2 for scenario B, and display the key input parameters and results in Table 1. We take BPA2 as an example, and show the domain wall profiles of
$ \phi_1 $ ,$ \phi_2 $ , and$ \phi_s $ for the BPA2 in Fig. 7. From Fig. 7, one can deduce that the domain wall tension$ \sigma_{\rm wall} $ is predominantly determined by the singlet field$ \phi_s(z) $ when$ v_s $ is very large.$m_{h_3}$ (GeV)

$m_{A}$ (GeV)

$m_{H^\pm}$ (GeV)

$m_{12}^2\;{\rm{(GeV)}}^2$ 

$\tan\beta$ 

$s_{1}$ 

$s_{2}$ 

$s_{3}$ 

$v_s$ (GeV)

$\lambda_6$ 

$\hat \sigma_{wall}$ 

$ f_{peak} $ 

$\Omega^{peak}_{GW}h^2$ 

$\chi^2_{95}$ 

BPA1 912.25 887.14 912.25 208668.96 3.51 0.9569 0.9362 −0.9998 999021 $1.01\times 10^{-8}$ 

$6.69\times 10^{4} $ 

$7.0\times 10^{-9}$ 

$2.00\times 10^{-8}$ 

1.89 BPA2 312.53 465.11 465.11 15778.26 5.13 0.8331 0.9580 −0.9235 101267 $1.05\times 10^{-6}$ 

$7.10\times 10^{2} $ 

$1.5\times 10^{-9}$ 

$2.26\times 10^{-12}$ 

4.61 BPB1 18418.07 414.86 414.86 553.96 12.53 0.1575 0.0046 0.0350 982846 $3.51\times 10^{-4}$ 

$1.19\times 10^{7} $ 

$1.1\times 10^{-8}$ 

$7.22\times 10^{-8}$ 

5.77 BPB2 13474.82 476.88 476.88 1161.65 5.30 0.1081 0.0047 0.0313 728781 $3.42\times 10^{-4}$ 

$4.78\times 10^{6}$ 

$1.4\times 10^{-8}$ 

$1.03\times 10^{-8}$ 

3.01 Table 1. Input parameters and results for the BPA1, BPA2, BPB1 and BPB2. Here
$ m_{h_1}=95.4 $ GeV and$ m_{h_2}=125.5 $ GeV are fixed.
Figure 7. (color online) The domain wall profiles of
$ \phi_1 $ ,$ \phi_2 $ , and$ \phi_S $ for the BPA2.We examine the GW spectra for the four benchmark points, which are shown along with the result of the NANOGrav dataset and the sensitivity curve of SKA in Fig. 8. For the BPB1 with
$ v_s\approx $ 980 TeV, the predicted GW spectrum can account for the entire frequency range of the NANOGrav data, from low to high frequencies. For the BPB2 with$ v_s= $ 730 TeV, the predicted GW spectrum explains the NANOGrav data in the low frequency region ($ f<4\times 10^{-8} $ Hz) but fails to extend into the higher frequency range. From the parameter points shown in Fig. 5, we select the one with the largest domain wall tension as BPA1. However, the peak amplitude of its GW spectrum only fits the edges of several low-frequency regions of the NANOGrav data. As illustrated in Fig. 8, the GW spectra corresponding to BPA1 and BPA2 exceed the SKA sensitivity curve in several low frequency regions.We perform a Bayesian analysis of our model using
$\textsf{PTArcade}$ [154] and the NANOGrav 15 year data. We employ the$\textsf{Ceffyl}$ mode [155] to derive the posterior distributions of the model parameters. The$\textsf{Enterprise}$ mode [156] is used to evaluate the Bayes factor of our model relative to the supermassive black hole binaries (SMBHB). The GW background signal from SMBHB is modeled as a power law of the form,$ \Omega_{\rm GW}(f) h^2 = \frac{ 2\pi^2 A^2_{BHB}}{3H_0} \Big( \frac{ f}{f_{yr}} \Big)^{5-\gamma_{BHB}} f_{yr}^2, $

(52) wheres
$ f_{yr}=year^{-1}=3.17\times 10^{-8} $ Hz and$ H_0 $ is the present-day value of the Hubble rate. We adopt a two-dimensional Gaussian prior for$ \gamma_{BHB} $ and$ A_{BHB} $ , derived from a power-law fit to the simulated SMBHB populations [69], as implemented in$\textsf{PTArcade}$ .In Table 2, we provide the priors for parameters of scenario B in our model and the Bayes factor. For very large
$ v_s $ in the range of 500 TeV and 1000 TeV, the domain wall tension$ \sigma_{\rm wall} $ is almost entirely determined by$ \lambda_6 $ , while being insensitive to other parameters. Consequently, we fix all parameters except$ v_s $ and$ \lambda_6 $ for simplicity. We assume that the singlet scalar field exhibits mild mixings with the two Higgs doublets, leading to non-zero values of$ s_2 $ and$ s_3 $ . As a result, the couplings of the 125 GeV Higgs boson deviate slightly from the SM predictions, which might be tested at the future CEPC. A detailed study of this aspect will be performed in future work. For the chosen values of$ s_2 $ and$ s_3 $ , as well as$ v_s\sim 1000 $ TeV, theoretical constraints require$ \lambda_6 < 0.0004 $ . Simultaneously, we impose that the diphoton and$ b\bar{b} $ excesses at 95.4 GeV are accommodated within the$ 2\sigma $ ranges. The Bayes factor is estimated to be approximately 22. The posterior distributions of parameters are shown in Fig. 9. The maximum posterior value of$ f_{\rm peak} $ is$ 1.2\times 10^{-8} $ Hz, while$ \lambda_{6} < 2.4\times 10^{-4} $ and$ v_s< 870 $ TeV respectively lie outside the 68% credible interval. For scenario A, even within the optimistic prior ranges, the Bayes factor is found to be nearly zero, consistent with the results shown in Fig. 8.$m_{h_1}$ (GeV)

$m_{h_2}$ (GeV)

$m_{A}=m_{H^\pm}$ (GeV)

$m_{12}^2\;{\rm{(GeV)}}^2$ 

$\tan\beta$ 

$s_{1}$ 

$s_{2}$ 

$s_{3}$ 

$v_s$ (100 TeV)

$\lambda_6$ 

${\rm log10}(f_{peak})$ 

${\rm BF}_{Y,X}$ 

scenario B 95.4 125.5 410 550 12 0.16 0.004 0.035 Uniform
[5, 10]Uniform
[0.0001,0.0004]Uniform
[−9, −7]$22.41\pm 6.75$ 

Table 2. Summary of model parameters and prior ranges. Bayesian factors, BF
$ _{Y,X} $ , with Y representing scenario B and X denoting SMBHB. -
The classical scalar fields are parameterized as
$ \begin{array}{*{20}{l}} \Phi_1=\left(\begin{array}{c} 0 \\ \dfrac{\phi_1(z)}{\sqrt{2}}\, \end{array}\right)\,,\; \Phi_2=\left(\begin{array}{c} 0 \\ \dfrac{\phi_2(z)}{\sqrt{2}}\, \end{array}\right), \;\Phi_S=\phi_s(z), \end{array} $
(39) where z is a coordinate perpendicular to domain walls [145]. The expression for the energy density of the domain walls is given by
$ \begin{aligned}[b] \varepsilon_{\rm wall}=\;&\frac{1}{2}(\partial_z\phi_1)^2 + \frac{1}{2}(\partial_z\phi_2)^2 + \frac{1}{2}(\partial_z\phi_S)^2\\& + V(\phi_1,\phi_2,\phi_S) -V(v_1,v_2,v_s), \end{aligned} $
(40) with the scalar potential
$ \begin{aligned}[b] V(\phi_1,\phi_2,\phi_S)=\;&\frac{m_{11}^2}{2} \phi_1^2 +\frac{\lambda_1}{8} \phi_1^4+ \frac{m_{22}^2}{2} \phi_2^2\\&+\frac{\lambda_2}{8} \phi_2^4-m_{12}^2 \phi_1 \phi_2+\frac{\lambda_{345}}{4} \phi_1^2 \phi_2^2 \\ &+\frac{m_S^2}{2} \phi_S^2 +\frac{\lambda_6}{8} \phi_S^4+ \frac{\lambda_7}{4} \phi_1^2\phi_S^2 \\&+\frac{\lambda_8}{4} \phi_2^2 \phi_S^2-a_1 v_s^2 \phi_S+\frac{a_1}{3} \phi_S^3. \end{aligned} $
(41) The equations of motion for domain walls are
$ \frac{ \mathrm{d}^2 \phi_i }{ \mathrm{d} z^2 } = \frac{ \partial V(\phi_1,\phi_2,\phi_S) }{ \partial \phi_i }, \quad ( \phi_i=\phi_1,\phi_2,\phi_S), $
(42) with the boundary conditions
$ \begin{array}{*{20}{l}} \lim_{z\to\pm\infty}\phi_1(z)=v_1,\; \lim_{z\to\pm\infty}\phi_2(z)=v_2, \; \lim_{z\to\pm\infty}\phi_S(z)=\pm v_s. \end{array} $
(43) $ \textsf{CosmoTransitions} $ [146] is modified to approximately solve Eqs. (42) and (43), and relevant computational details are provided in [146, 147]. The domain wall tension$ \sigma_{\rm wall} $ is computed through an integration of the energy density$ \varepsilon_{\rm wall} $ over the z axis,$ \sigma_{\rm wall}=\int {\rm d}z \; \varepsilon_{\rm wall}. $
(44) Domain walls must collapse before they can overclose the Universe. The volume pressure induced by energy bias (
$ V_{\rm bias} $ ) exerts a force on the domain walls, and drives the contraction of regions occupied by the false vacuum. The collapse of domain wall occurs when the volume pressure force becomes comparable to the tension force. The characteristic temperature at which the domain walls annihilate can be estimated by [148, 149]$ T_{\rm ann} =3.41\times 10^{-2}\,{\rm GeV}\, C_{\rm ann}^{-1/2} A^{-1/2} \Big( \frac{ g_{*} (T_{\rm ann}) }{10} \Big)^{-1/4} \hat \sigma_{\rm wall}^{-1/2} \hat V_{\rm bias}^{1/2} \,, $
(45) with
$ \hat \sigma_{\rm wall} \equiv \frac{\sigma_{\rm wall}}{\rm TeV^3},\quad \hat V_{\rm bias} \equiv \frac{V_{\rm bias}}{\rm MeV^4}. $
(46) In this analysis, a constant
$ C_{\rm ann}=5 $ [149] is adopted and the area parameter$ A\simeq 0.8 $ is set for the$ Z_2 $ symmetric model [148]. The energetic particles released from the collapse of domain walls have the potential to disrupt the synthesis of light nuclei formed during Big Bang Nucleosynthesis (BBN) [150]. To preserve the successful predictions of BBN, it is therefore imperative that the domain walls annihilate before the BBN epoch,$ T_{\rm ann} > T_{\rm BBN} = 8.6 \times 10^{-3} $ GeV. In addition, to ensure that domain walls annihilate before their energy density dominates the Universe, a lower bound must be imposed on$ V_{\rm bias} $ [149]$ \begin{array}{*{20}{l}} V_{\rm{bias}}^{1/4}>2.18\times 10^{-5} ~~ C_{\rm{ann}}^{\frac{1}{4}} ~ A^{\frac{1}{2}} \hat \sigma_{\rm wall}^{\frac{1}{2}}\; . \end{array} $
(47) Following the annihilation of domain walls, a SGWB is produced, and the peak frequency is given by [148]
$ \begin{aligned}[b] f_{\rm peak} \simeq & 1.1\times 10^{-7}\,{\rm Hz}\, \Big( \frac{ g_*( T_{\rm ann} ) }{10} \Big)^{1/2} \Big( \frac{ g_{*s}( T_{\rm ann} ) }{10} \Big)^{-1/3} \Big( \frac{ T_{\rm ann} }{1\,\rm GeV } \Big)\\ \simeq & 3.75\times 10^{-9}\,{\rm Hz}\, \Big( \frac{ g_*( T_{\rm ann} ) }{10} \Big)^{1/4} \Big( \frac{ g_{*s}( T_{\rm ann} ) }{10} \Big)^{-1/3} \\&\times C_{\rm ann}^{-1/2} A^{-1/2} \hat\sigma^{-1/2}_{\rm wall} \hat V_{\rm bias}^{1/2} \,. \end{aligned} $
(48) where
$ g_*(T_{\rm ann}) $ and$ g_{*s}(T_{\rm ann}) $ count the relativistic degrees of freedom contributing to the energy and entropy densities, respectively. Within the temperature range$ 1\,\rm MeV\lesssim T_{\rm ann} \lesssim 100\,\rm MeV $ , both quantities take the value 10.75 [151].The peak amplitude of the GW spectrum at the present time is [148, 149]
$ \begin{aligned}[b] \Omega_{\rm GW}^{\rm peak} h^2 =\;& 5.3\times 10^{-20}\, \tilde \epsilon_{\rm GW} A^4 C_{\rm ann}^2 \Big( \frac{ g_{*s}(T_{\rm ann}) }{10} \Big)^{-4/3} \\&\times\Big( \frac{ g_{*} (T_{\rm ann}) }{10} \Big) \hat \sigma^4_{\rm wall} \hat V^{-2}_{\rm bias} \,. \end{aligned} $
(49) with
$ \tilde \epsilon_{\rm GW}\simeq 0.7\pm 0.4 $ [148]. Given an arbitrary frequency f, the following is used [148, 152]$ \Omega_{\text{GW}}h^2(f<f_{\text{peak}}) = \Omega_{\rm GW}^{\rm peak} h^2 \left(\frac{f}{f_{\text{peak}}}\right)^3, $
(50) $ \Omega_{\text{GW}}h^2(f>f_{\text{peak}}) = \Omega_{\rm GW}^{\rm peak} h^2 \left(\frac{f_{\text{peak}}}{f}\right). $
(51) In the discussions,
$ 10^{-9} $ Hz$ \leq f_{\rm peak}\leq $ $ 10^{-7} $ Hz are taken, and$ T_{\rm ann} $ is obtained from the first line of Eq. (48).$ \hat V_{\rm bias} $ is obtained from the second line of Eq. (48) with$ f_{\rm peak} $ and$ \hat \sigma_{\rm wall} $ calculated in the parameter points accommodating the diphoton and$ b\bar{b} $ excesses at 95.4 GeV. Fig. 5 and Fig. 6 show the parameter points that satisfy$ \chi_{95}^2 < 6.18 $ and$ \Omega_{\rm GW}^{\rm peak} h^2>10^{-15} $ for$ f_{\rm peak}=10^{-9} $ Hz while remaining consistent with relevant theoretical and experimental constraints mentioned above, for scenario A and scenario B, respectively.
Figure 5. (color online) In scenario A, the parameter points satisfy
$ \Omega_{\rm GW}^{\rm peak} h^2>10^{-15} $ and$ \chi_{95}^2<6.18 $ , while also complying with the theoretical and experimental constraints discussed above.
Figure 6. (color online) As Fig. 5, but for scenario B.
The peak amplitude
$ \Omega_{\rm GW}^{\rm peak} $ increases with decreasing$ f_{\rm peak} $ and increasing$ \hat\sigma_{\rm wall} $ , as indicated by the second line of Eqs. (48) and (49), and as illustrated in the upper-left and upper-right panels of Fig. 5. In scenario A, although the 95.4 GeV Higgs boson ($ h_1 $ ) predominantly originates from the real singlet field, it must include non-negligible components of the Higgs doublets to acquire the necessary couplings to gauge bosons and fermions, thereby accounting for the observed diphoton and and$ b\bar{b} $ excesses at 95.4 GeV. Thus, both$ R_{31} $ and$ R_{32} $ can not approach to zero, theoretical constraints on$ \lambda_{1,2,3} $ will impose a lower bound on$ m_{h_3} $ ,$ m_{h_3}<1.5 $ TeV (see the first three lines of Eq. (13)). As a result, according to the sixth line of Eq. (13),$ \lambda_6 $ decreases with increasing$ v_s $ , yielding a range of$ 10^{-8}<\lambda_6<10^{-4} $ for$ 14\; {\rm TeV}\; <v_s<1000 $ TeV. Although$ \lambda_6 $ decreases as$ v_s $ increases, the domain wall tension$ \hat\sigma_{\rm wall} $ still grows rapidly.In scenario B, the 95.4 GeV Higgs boson predominantly originates from the CP-even components of the Higgs doublets. Even though the mixing between the singlet and doublet components vanishes (i.e.,
$ R_{31}\to 0 $ and$ R_{32}\to 0 $ ), the 95.4 GeV Higgs boson still can interact with gauge bosons and fermions to explain the diphoton and$ b\bar{b} $ excesses at 95.4 GeV. Therefore, theoretical constraints on$ \lambda_{1,2,3} $ allow$ m_{h_3} $ to have a large value, reaching up to 20 TeV for sufficiently small$ s_2 $ and$ s_3 $ . Consequently,$ \lambda_6 $ is sensitive to$ s_2 $ ,$ s_3 $ , and$ v_s $ , and can attain larger value as$ s_2 $ ,$ s_3 $ , and$ v_s $ decrease, as illustrated in the lower-middle and lower-right panels of Fig. 6. Asthe domain wall tension$ \hat\sigma_{\rm wall} $ mainly depends on$ v_s $ and$ \lambda_6 $ , as shown in the lower-left panel of Fig. 6, the value of$ \hat\sigma_{\rm wall} $ in scenario B can be much larger than that in scenario A, thereby significantly enhancing$ \Omega_{\rm GW}^{\rm peak} $ .Four benchmark points are identified: BPA1 and BPA2 for scenario A, and BPB1 and BPB2 for scenario B, and the key input parameters and results are listed in Table 1. BPA2 is taken as an example to show the domain wall profiles of
$ \phi_1 $ ,$ \phi_2 $ , and$ \phi_s $ for the BPA2 in Fig. 7. From Fig. 7, one can deduce that the domain wall tension$ \sigma_{\rm wall} $ is predominantly determined by the singlet field$ \phi_s(z) $ when$ v_s $ is very large.$m_{h_3}$ /GeV$m_{A}$ /GeV$m_{H^\pm}$ /GeV$m_{12}^2\;/{\rm{GeV}}^2$ $\tan\beta$ $s_{1}$ $s_{2}$ $s_{3}$ $v_s$ /GeV$\lambda_6$ $\hat \sigma_{\rm wall}$ $ f_{\rm peak} $ $\Omega^{\rm peak}_{\rm GW}h^2$ $\chi^2_{95}$ BPA1 912.25 887.14 912.25 208668.96 3.51 0.9569 0.9362 −0.9998 999021 $1.01\times 10^{-8}$ $6.69\times 10^{4} $ $7.0\times 10^{-9}$ $2.00\times 10^{-8}$ 1.89 BPA2 312.53 465.11 465.11 15778.26 5.13 0.8331 0.9580 −0.9235 101267 $1.05\times 10^{-6}$ $7.10\times 10^{2} $ $1.5\times 10^{-9}$ $2.26\times 10^{-12}$ 4.61 BPB1 18418.07 414.86 414.86 553.96 12.53 0.1575 0.0046 0.0350 982846 $3.51\times 10^{-4}$ $1.19\times 10^{7} $ $1.1\times 10^{-8}$ $7.22\times 10^{-8}$ 5.77 BPB2 13474.82 476.88 476.88 1161.65 5.30 0.1081 0.0047 0.0313 728781 $3.42\times 10^{-4}$ $4.78\times 10^{6}$ $1.4\times 10^{-8}$ $1.03\times 10^{-8}$ 3.01 Table 1. Input parameters and results for the BPA1, BPA2, BPB1 and BPB2. Here
$ m_{h_1}=95.4 $ GeV and$ m_{h_2}=125.5 $ GeV are fixed.
Figure 7. (color online) The domain wall profiles of
$ \phi_1 $ ,$ \phi_2 $ , and$ \phi_S $ for the BPA2.The GW spectra for the four benchmark points are examined, which are shown along with the result of the NANOGrav dataset and the sensitivity curve of SKA in Fig. 8. For the BPB1 with
$ v_s\approx $ 980 TeV, the predicted GW spectrum can account for the entire frequency range of the NANOGrav data, from low to high frequencies. For the BPB2 with$ v_s= $ 730 TeV, the predicted GW spectrum explains the NANOGrav data in the low frequency region ($ f<4\times 10^{-8} $ Hz) but fails to extend into the higher frequency range. From the parameter points shown in Fig. 5, the one with the largest domain wall tension is selected as BPA1. However, the peak amplitude of its GW spectrum only fits the edges of several low-frequency regions of the NANOGrav data. As illustrated in Fig. 8, the GW spectra corresponding to BPA1 and BPA2 exceed the SKA sensitivity curve in several low frequency regions.A Bayesian analysis of the model is performed using
$\textsf{PTArcade}$ [154] and the NANOGrav 15 year data. The$\textsf{Ceffyl}$ mode [155] is employed to derive the posterior distributions of the model parameters. The$\textsf{Enterprise}$ mode [156] is used to evaluate the Bayes factor of our model relative to the supermassive black hole binaries (SMBHB). The GW background signal from SMBHB is modeled as a power law of the form,$ \Omega_{\rm GW}(f) h^2 = \frac{ 2\pi^2 A^2_{\rm BHB}}{3H_0} \Big( \frac{ f}{f_{yr}} \Big)^{5-\gamma_{\rm BHB}} f_{yr}^2, $
(52) where
$ f_{yr}=year^{-1}=3.17\times 10^{-8} $ Hz and$ H_0 $ is the present-day value of the Hubble rate. A two-dimensional Gaussian prior is adopted for$ \gamma_{\rm BHB} $ and$ A_{\rm BHB} $ , derived from a power-law fit to the simulated SMBHB populations [69], as implemented in$\textsf{PTArcade}$ .Table 2 lists the priors for the parameters of scenario B in the model and the Bayes factor. For very large
$ v_s $ in the range of 500–1000 TeV, the domain wall tension$ \sigma_{\rm wall} $ is almost entirely determined by$ \lambda_6 $ , while being insensitive to other parameters. Consequently, all parameters except$ v_s $ and$ \lambda_6 $ are fixed for simplicity. It is assumed that the singlet scalar field exhibits mild mixings with the two Higgs doublets, leading to non-zero values of$ s_2 $ and$ s_3 $ . As a result, the couplings of the 125 GeV Higgs boson deviate slightly from the SM predictions, which may be tested in the future using the Circular Electron Positron Collider (CEPC). A detailed study of this aspect will be performed in future work. For the chosen values of$ s_2 $ and$ s_3 $ , as well as$ v_s\sim 1000 $ TeV, theoretical constraints require$ \lambda_6 < 0.0004 $ . Simultaneously, the diphoton and$ b\bar{b} $ excesses at 95.4 GeV are accommodated within the$ 2\sigma $ ranges. The Bayes factor is estimated to be approximately 22. The posterior distributions of parameters are shown in Fig. 9. The maximum posterior value of$ f_{\rm peak} $ is$ 1.2\times 10^{-8} $ Hz, while$ \lambda_{6} < 2.4\times 10^{-4} $ and$ v_s< 870 $ TeV respectively lie outside the 68% credible interval. For scenario A, even within the optimistic prior ranges, the Bayes factor is found to be nearly zero, consistent with the results shown in Fig. 8.$m_{h_1}$ /GeV$m_{h_2}$ /GeV$m_{A}=m_{H^\pm}$ /GeV$m_{12}^2\;/{\rm{GeV}}^2$ $\tan\beta$ $s_{1}$ $s_{2}$ $s_{3}$ $v_s$ (100 TeV)$\lambda_6$ ${\rm log10}(f_{\rm peak})$ ${\rm BF}_{\rm Y,X}$ scenario B 95.4 125.5 410 550 12 0.16 0.004 0.035 Uniform
[5, 10]Uniform
[0.0001,0.0004]Uniform
[-9, -7]$22.41\pm 6.75$ Table 2. Summary of model parameters and prior ranges. Bayesian factors, BF
$ _{\rm Y,X} $ , with Y representing scenario B and X denoting SMBHB. -
The classical scalar fields are parameterized as
$ \begin{array}{*{20}{l}} \Phi_1=\left(\begin{array}{c} 0 \\ \dfrac{\phi_1(z)}{\sqrt{2}}\, \end{array}\right)\,,\; \Phi_2=\left(\begin{array}{c} 0 \\ \dfrac{\phi_2(z)}{\sqrt{2}}\, \end{array}\right), \;\Phi_S=\phi_s(z), \end{array} $
(39) where z is a coordinate perpendicular to domain walls [145]. The expression for the energy density of the domain walls is given by
$ \begin{aligned}[b] \varepsilon_{\rm wall}=\;&\frac{1}{2}(\partial_z\phi_1)^2 + \frac{1}{2}(\partial_z\phi_2)^2 + \frac{1}{2}(\partial_z\phi_S)^2\\& + V(\phi_1,\phi_2,\phi_S) -V(v_1,v_2,v_s), \end{aligned} $
(40) with the scalar potential
$ \begin{aligned}[b] V(\phi_1,\phi_2,\phi_S)=\;&\frac{m_{11}^2}{2} \phi_1^2 +\frac{\lambda_1}{8} \phi_1^4+ \frac{m_{22}^2}{2} \phi_2^2\\&+\frac{\lambda_2}{8} \phi_2^4-m_{12}^2 \phi_1 \phi_2+\frac{\lambda_{345}}{4} \phi_1^2 \phi_2^2 \\ &+\frac{m_S^2}{2} \phi_S^2 +\frac{\lambda_6}{8} \phi_S^4+ \frac{\lambda_7}{4} \phi_1^2\phi_S^2 \\&+\frac{\lambda_8}{4} \phi_2^2 \phi_S^2-a_1 v_s^2 \phi_S+\frac{a_1}{3} \phi_S^3. \end{aligned} $
(41) The equations of motion for domain walls are
$ \frac{ \mathrm{d}^2 \phi_i }{ \mathrm{d} z^2 } = \frac{ \partial V(\phi_1,\phi_2,\phi_S) }{ \partial \phi_i }, \quad ( \phi_i=\phi_1,\phi_2,\phi_S), $
(42) with the boundary conditions
$ \begin{array}{*{20}{l}} \lim_{z\to\pm\infty}\phi_1(z)=v_1,\; \lim_{z\to\pm\infty}\phi_2(z)=v_2, \; \lim_{z\to\pm\infty}\phi_S(z)=\pm v_s. \end{array} $
(43) $ \textsf{CosmoTransitions} $ [146] is modified to approximately solve Eqs. (42) and (43), and relevant computational details are provided in [146, 147]. The domain wall tension$ \sigma_{\rm wall} $ is computed through an integration of the energy density$ \varepsilon_{\rm wall} $ over the z axis,$ \sigma_{\rm wall}=\int {\rm d}z \; \varepsilon_{\rm wall}. $
(44) Domain walls must collapse before they can overclose the Universe. The volume pressure induced by energy bias (
$ V_{\rm bias} $ ) exerts a force on the domain walls, and drives the contraction of regions occupied by the false vacuum. The collapse of domain wall occurs when the volume pressure force becomes comparable to the tension force. The characteristic temperature at which the domain walls annihilate can be estimated by [148, 149]$ T_{\rm ann} =3.41\times 10^{-2}\,{\rm GeV}\, C_{\rm ann}^{-1/2} A^{-1/2} \Big( \frac{ g_{*} (T_{\rm ann}) }{10} \Big)^{-1/4} \hat \sigma_{\rm wall}^{-1/2} \hat V_{\rm bias}^{1/2} \,, $
(45) with
$ \hat \sigma_{\rm wall} \equiv \frac{\sigma_{\rm wall}}{\rm TeV^3},\quad \hat V_{\rm bias} \equiv \frac{V_{\rm bias}}{\rm MeV^4}. $
(46) In this analysis, a constant
$ C_{\rm ann}=5 $ [149] is adopted and the area parameter$ A\simeq 0.8 $ is set for the$ Z_2 $ symmetric model [148]. The energetic particles released from the collapse of domain walls have the potential to disrupt the synthesis of light nuclei formed during Big Bang Nucleosynthesis (BBN) [150]. To preserve the successful predictions of BBN, it is therefore imperative that the domain walls annihilate before the BBN epoch,$ T_{\rm ann} > T_{\rm BBN} = 8.6 \times 10^{-3} $ GeV. In addition, to ensure that domain walls annihilate before their energy density dominates the Universe, a lower bound must be imposed on$ V_{\rm bias} $ [149]$ \begin{array}{*{20}{l}} V_{\rm{bias}}^{1/4}>2.18\times 10^{-5} ~~ C_{\rm{ann}}^{\frac{1}{4}} ~ A^{\frac{1}{2}} \hat \sigma_{\rm wall}^{\frac{1}{2}}\; . \end{array} $
(47) Following the annihilation of domain walls, a SGWB is produced, and the peak frequency is given by [148]
$ \begin{aligned}[b] f_{\rm peak} \simeq & 1.1\times 10^{-7}\,{\rm Hz}\, \Big( \frac{ g_*( T_{\rm ann} ) }{10} \Big)^{1/2} \Big( \frac{ g_{*s}( T_{\rm ann} ) }{10} \Big)^{-1/3} \Big( \frac{ T_{\rm ann} }{1\,\rm GeV } \Big)\\ \simeq & 3.75\times 10^{-9}\,{\rm Hz}\, \Big( \frac{ g_*( T_{\rm ann} ) }{10} \Big)^{1/4} \Big( \frac{ g_{*s}( T_{\rm ann} ) }{10} \Big)^{-1/3} \\&\times C_{\rm ann}^{-1/2} A^{-1/2} \hat\sigma^{-1/2}_{\rm wall} \hat V_{\rm bias}^{1/2} \,. \end{aligned} $
(48) where
$ g_*(T_{\rm ann}) $ and$ g_{*s}(T_{\rm ann}) $ count the relativistic degrees of freedom contributing to the energy and entropy densities, respectively. Within the temperature range$ 1\,\rm MeV\lesssim T_{\rm ann} \lesssim 100\,\rm MeV $ , both quantities take the value 10.75 [151].The peak amplitude of the GW spectrum at the present time is [148, 149]
$ \begin{aligned}[b] \Omega_{\rm GW}^{\rm peak} h^2 =\;& 5.3\times 10^{-20}\, \tilde \epsilon_{\rm GW} A^4 C_{\rm ann}^2 \Big( \frac{ g_{*s}(T_{\rm ann}) }{10} \Big)^{-4/3} \\&\times\Big( \frac{ g_{*} (T_{\rm ann}) }{10} \Big) \hat \sigma^4_{\rm wall} \hat V^{-2}_{\rm bias} \,. \end{aligned} $
(49) with
$ \tilde \epsilon_{\rm GW}\simeq 0.7\pm 0.4 $ [148]. Given an arbitrary frequency f, the following is used [148, 152]$ \Omega_{\text{GW}}h^2(f<f_{\text{peak}}) = \Omega_{\rm GW}^{\rm peak} h^2 \left(\frac{f}{f_{\text{peak}}}\right)^3, $
(50) $ \Omega_{\text{GW}}h^2(f>f_{\text{peak}}) = \Omega_{\rm GW}^{\rm peak} h^2 \left(\frac{f_{\text{peak}}}{f}\right). $
(51) In the discussions,
$ 10^{-9} $ Hz$ \leq f_{\rm peak}\leq $ $ 10^{-7} $ Hz are taken, and$ T_{\rm ann} $ is obtained from the first line of Eq. (48).$ \hat V_{\rm bias} $ is obtained from the second line of Eq. (48) with$ f_{\rm peak} $ and$ \hat \sigma_{\rm wall} $ calculated in the parameter points accommodating the diphoton and$ b\bar{b} $ excesses at 95.4 GeV. Fig. 5 and Fig. 6 show the parameter points that satisfy$ \chi_{95}^2 < 6.18 $ and$ \Omega_{\rm GW}^{\rm peak} h^2>10^{-15} $ for$ f_{\rm peak}=10^{-9} $ Hz while remaining consistent with relevant theoretical and experimental constraints mentioned above, for scenario A and scenario B, respectively.
Figure 5. (color online) In scenario A, the parameter points satisfy
$ \Omega_{\rm GW}^{\rm peak} h^2>10^{-15} $ and$ \chi_{95}^2<6.18 $ , while also complying with the theoretical and experimental constraints discussed above.
Figure 6. (color online) As Fig. 5, but for scenario B.
The peak amplitude
$ \Omega_{\rm GW}^{\rm peak} $ increases with decreasing$ f_{\rm peak} $ and increasing$ \hat\sigma_{\rm wall} $ , as indicated by the second line of Eqs. (48) and (49), and as illustrated in the upper-left and upper-right panels of Fig. 5. In scenario A, although the 95.4 GeV Higgs boson ($ h_1 $ ) predominantly originates from the real singlet field, it must include non-negligible components of the Higgs doublets to acquire the necessary couplings to gauge bosons and fermions, thereby accounting for the observed diphoton and and$ b\bar{b} $ excesses at 95.4 GeV. Thus, both$ R_{31} $ and$ R_{32} $ can not approach to zero, theoretical constraints on$ \lambda_{1,2,3} $ will impose a lower bound on$ m_{h_3} $ ,$ m_{h_3}<1.5 $ TeV (see the first three lines of Eq. (13)). As a result, according to the sixth line of Eq. (13),$ \lambda_6 $ decreases with increasing$ v_s $ , yielding a range of$ 10^{-8}<\lambda_6<10^{-4} $ for$ 14\; {\rm TeV}\; <v_s<1000 $ TeV. Although$ \lambda_6 $ decreases as$ v_s $ increases, the domain wall tension$ \hat\sigma_{\rm wall} $ still grows rapidly.In scenario B, the 95.4 GeV Higgs boson predominantly originates from the CP-even components of the Higgs doublets. Even though the mixing between the singlet and doublet components vanishes (i.e.,
$ R_{31}\to 0 $ and$ R_{32}\to 0 $ ), the 95.4 GeV Higgs boson still can interact with gauge bosons and fermions to explain the diphoton and$ b\bar{b} $ excesses at 95.4 GeV. Therefore, theoretical constraints on$ \lambda_{1,2,3} $ allow$ m_{h_3} $ to have a large value, reaching up to 20 TeV for sufficiently small$ s_2 $ and$ s_3 $ . Consequently,$ \lambda_6 $ is sensitive to$ s_2 $ ,$ s_3 $ , and$ v_s $ , and can attain larger value as$ s_2 $ ,$ s_3 $ , and$ v_s $ decrease, as illustrated in the lower-middle and lower-right panels of Fig. 6. Asthe domain wall tension$ \hat\sigma_{\rm wall} $ mainly depends on$ v_s $ and$ \lambda_6 $ , as shown in the lower-left panel of Fig. 6, the value of$ \hat\sigma_{\rm wall} $ in scenario B can be much larger than that in scenario A, thereby significantly enhancing$ \Omega_{\rm GW}^{\rm peak} $ .Four benchmark points are identified: BPA1 and BPA2 for scenario A, and BPB1 and BPB2 for scenario B, and the key input parameters and results are listed in Table 1. BPA2 is taken as an example to show the domain wall profiles of
$ \phi_1 $ ,$ \phi_2 $ , and$ \phi_s $ for the BPA2 in Fig. 7. From Fig. 7, one can deduce that the domain wall tension$ \sigma_{\rm wall} $ is predominantly determined by the singlet field$ \phi_s(z) $ when$ v_s $ is very large.$m_{h_3}$ /GeV$m_{A}$ /GeV$m_{H^\pm}$ /GeV$m_{12}^2\;/{\rm{GeV}}^2$ $\tan\beta$ $s_{1}$ $s_{2}$ $s_{3}$ $v_s$ /GeV$\lambda_6$ $\hat \sigma_{\rm wall}$ $ f_{\rm peak} $ $\Omega^{\rm peak}_{\rm GW}h^2$ $\chi^2_{95}$ BPA1 912.25 887.14 912.25 208668.96 3.51 0.9569 0.9362 −0.9998 999021 $1.01\times 10^{-8}$ $6.69\times 10^{4} $ $7.0\times 10^{-9}$ $2.00\times 10^{-8}$ 1.89 BPA2 312.53 465.11 465.11 15778.26 5.13 0.8331 0.9580 −0.9235 101267 $1.05\times 10^{-6}$ $7.10\times 10^{2} $ $1.5\times 10^{-9}$ $2.26\times 10^{-12}$ 4.61 BPB1 18418.07 414.86 414.86 553.96 12.53 0.1575 0.0046 0.0350 982846 $3.51\times 10^{-4}$ $1.19\times 10^{7} $ $1.1\times 10^{-8}$ $7.22\times 10^{-8}$ 5.77 BPB2 13474.82 476.88 476.88 1161.65 5.30 0.1081 0.0047 0.0313 728781 $3.42\times 10^{-4}$ $4.78\times 10^{6}$ $1.4\times 10^{-8}$ $1.03\times 10^{-8}$ 3.01 Table 1. Input parameters and results for the BPA1, BPA2, BPB1 and BPB2. Here
$ m_{h_1}=95.4 $ GeV and$ m_{h_2}=125.5 $ GeV are fixed.
Figure 7. (color online) The domain wall profiles of
$ \phi_1 $ ,$ \phi_2 $ , and$ \phi_S $ for the BPA2.The GW spectra for the four benchmark points are examined, which are shown along with the result of the NANOGrav dataset and the sensitivity curve of SKA in Fig. 8. For the BPB1 with
$ v_s\approx $ 980 TeV, the predicted GW spectrum can account for the entire frequency range of the NANOGrav data, from low to high frequencies. For the BPB2 with$ v_s= $ 730 TeV, the predicted GW spectrum explains the NANOGrav data in the low frequency region ($ f<4\times 10^{-8} $ Hz) but fails to extend into the higher frequency range. From the parameter points shown in Fig. 5, the one with the largest domain wall tension is selected as BPA1. However, the peak amplitude of its GW spectrum only fits the edges of several low-frequency regions of the NANOGrav data. As illustrated in Fig. 8, the GW spectra corresponding to BPA1 and BPA2 exceed the SKA sensitivity curve in several low frequency regions.A Bayesian analysis of the model is performed using
$\textsf{PTArcade}$ [154] and the NANOGrav 15 year data. The$\textsf{Ceffyl}$ mode [155] is employed to derive the posterior distributions of the model parameters. The$\textsf{Enterprise}$ mode [156] is used to evaluate the Bayes factor of our model relative to the supermassive black hole binaries (SMBHB). The GW background signal from SMBHB is modeled as a power law of the form,$ \Omega_{\rm GW}(f) h^2 = \frac{ 2\pi^2 A^2_{\rm BHB}}{3H_0} \Big( \frac{ f}{f_{yr}} \Big)^{5-\gamma_{\rm BHB}} f_{yr}^2, $
(52) where
$ f_{yr}=year^{-1}=3.17\times 10^{-8} $ Hz and$ H_0 $ is the present-day value of the Hubble rate. A two-dimensional Gaussian prior is adopted for$ \gamma_{\rm BHB} $ and$ A_{\rm BHB} $ , derived from a power-law fit to the simulated SMBHB populations [69], as implemented in$\textsf{PTArcade}$ .Table 2 lists the priors for the parameters of scenario B in the model and the Bayes factor. For very large
$ v_s $ in the range of 500–1000 TeV, the domain wall tension$ \sigma_{\rm wall} $ is almost entirely determined by$ \lambda_6 $ , while being insensitive to other parameters. Consequently, all parameters except$ v_s $ and$ \lambda_6 $ are fixed for simplicity. It is assumed that the singlet scalar field exhibits mild mixings with the two Higgs doublets, leading to non-zero values of$ s_2 $ and$ s_3 $ . As a result, the couplings of the 125 GeV Higgs boson deviate slightly from the SM predictions, which may be tested in the future using the Circular Electron Positron Collider (CEPC). A detailed study of this aspect will be performed in future work. For the chosen values of$ s_2 $ and$ s_3 $ , as well as$ v_s\sim 1000 $ TeV, theoretical constraints require$ \lambda_6 < 0.0004 $ . Simultaneously, the diphoton and$ b\bar{b} $ excesses at 95.4 GeV are accommodated within the$ 2\sigma $ ranges. The Bayes factor is estimated to be approximately 22. The posterior distributions of parameters are shown in Fig. 9. The maximum posterior value of$ f_{\rm peak} $ is$ 1.2\times 10^{-8} $ Hz, while$ \lambda_{6} < 2.4\times 10^{-4} $ and$ v_s< 870 $ TeV respectively lie outside the 68% credible interval. For scenario A, even within the optimistic prior ranges, the Bayes factor is found to be nearly zero, consistent with the results shown in Fig. 8.$m_{h_1}$ /GeV$m_{h_2}$ /GeV$m_{A}=m_{H^\pm}$ /GeV$m_{12}^2\;/{\rm{GeV}}^2$ $\tan\beta$ $s_{1}$ $s_{2}$ $s_{3}$ $v_s$ (100 TeV)$\lambda_6$ ${\rm log10}(f_{\rm peak})$ ${\rm BF}_{\rm Y,X}$ scenario B 95.4 125.5 410 550 12 0.16 0.004 0.035 Uniform
[5, 10]Uniform
[0.0001,0.0004]Uniform
[-9, -7]$22.41\pm 6.75$ Table 2. Summary of model parameters and prior ranges. Bayesian factors, BF
$ _{\rm Y,X} $ , with Y representing scenario B and X denoting SMBHB. -
After imposing relevant theoretical and experimental constraints, we studied the diphoton and
$ b\bar{b} $ excesses at 95.4 GeV, along with the nano-Hertz GW signatures originating from domain walls, within the framework of the N2HDM. We consider two scenarios: in scenario A, the 95.4 GeV Higgs boson is primarily singlet-like, whereas in scenario B, it mainly originates from the CP-even components of the Higgs doublets. We find that scenario A is able to fully reproduce both the diphoton and$ b\bar{b} $ excesses at 95.4 GeV within the$ 1\sigma $ range. However, in the parameter space that accommodates both excesses, scenario A does not offer a valid explanation for the NANOGrav data up to$ v_s = 1000 $ TeV, and the resulting GW spectrum can surpass the SKA sensitivity curve at low frequencies. Scenario B provides a marginal explanation of the diphoton and$ b\bar{b} $ excesses at 95.4 GeV at the$ 1\sigma $ level, but it can simultaneously offer a good explanation for the NANOGrav data.Our work highlights the complementary roles of collider signals and GW observables in probing the nature of the extended Higgs sector. Although the 95.4 GeV excess reported by CMS, ATLAS, and LEP has not yet reached the discovery level of statistical significance, its consistent appearance across multiple experiments has inspired extensive theoretical interest, making it a well-motivated phenomenon to investigate. To our knowledge, our work is the first to simultaneously explain both the NANOGrav data and the 95.4 GeV Higgs boson excess, realized here within a coherent N2HDM framework. We explicitly identify specific scenario within the N2HDM in which this dual explanation can be realized. Our work extends previous studies of the N2HDM by connecting collider and cosmological phenomena.
-
After imposing relevant theoretical and experimental constraints, the diphoton and
$ b\bar{b} $ excesses at 95.4 GeV, along with the nano-Hertz GW signatures originating from domain walls, were studied within the framework of the N2HDM. Two scenarios were considered: in scenario A, the 95.4 GeV Higgs boson is primarily singlet-like, whereas in scenario B, it mainly originates from the CP-even components of the Higgs doublets. Scenario A was able to fully reproduce both the diphoton and$ b\bar{b} $ excesses at 95.4 GeV within the$ 1\sigma $ range. However, in the parameter space that accommodates both excesses, scenario A did not offer a valid explanation for the NANOGrav data up to$ v_s = 1000 $ TeV, and the resulting GW spectrum can surpass the Square Kilometre Array (SKA) sensitivity curve at low frequencies. Scenario B provided a marginal explanation of the diphoton and$ b\bar{b} $ excesses at 95.4 GeV at the$ 1\sigma $ level, but it can simultaneously offer a good explanation for the NANOGrav data.This study highlights the complementary roles of collider signals and GW observables in probing the nature of the extended Higgs sector. Although the 95.4 GeV excess reported by CMS, ATLAS, and LEP has not yet reached the discovery level of statistical significance, its consistent appearance across multiple experiments has inspired extensive theoretical interest, making it a well-motivated phenomenon to investigate. To the best of the authors' knowledge, this study is the first to simultaneously explain both the NANOGrav data and the 95.4 GeV Higgs boson excess, realized here within a coherent N2HDM framework. Specific scenarios within the N2HDM in which this dual explanation can be realized were explicitly identified. This study extends previous studies of the N2HDM by connecting collider and cosmological phenomena.
-
After imposing relevant theoretical and experimental constraints, the diphoton and
$ b\bar{b} $ excesses at 95.4 GeV, along with the nano-Hertz GW signatures originating from domain walls, were studied within the framework of the N2HDM. Two scenarios were considered: in scenario A, the 95.4 GeV Higgs boson is primarily singlet-like, whereas in scenario B, it mainly originates from the CP-even components of the Higgs doublets. Scenario A was able to fully reproduce both the diphoton and$ b\bar{b} $ excesses at 95.4 GeV within the$ 1\sigma $ range. However, in the parameter space that accommodates both excesses, scenario A did not offer a valid explanation for the NANOGrav data up to$ v_s = 1000 $ TeV, and the resulting GW spectrum can surpass the Square Kilometre Array (SKA) sensitivity curve at low frequencies. Scenario B provided a marginal explanation of the diphoton and$ b\bar{b} $ excesses at 95.4 GeV at the$ 1\sigma $ level, but it can simultaneously offer a good explanation for the NANOGrav data.This study highlights the complementary roles of collider signals and GW observables in probing the nature of the extended Higgs sector. Although the 95.4 GeV excess reported by CMS, ATLAS, and LEP has not yet reached the discovery level of statistical significance, its consistent appearance across multiple experiments has inspired extensive theoretical interest, making it a well-motivated phenomenon to investigate. To the best of the authors' knowledge, this study is the first to simultaneously explain both the NANOGrav data and the 95.4 GeV Higgs boson excess, realized here within a coherent N2HDM framework. Specific scenarios within the N2HDM in which this dual explanation can be realized were explicitly identified. This study extends previous studies of the N2HDM by connecting collider and cosmological phenomena.
-
After imposing relevant theoretical and experimental constraints, the diphoton and
$ b\bar{b} $ excesses at 95.4 GeV, along with the nano-Hertz GW signatures originating from domain walls, were studied within the framework of the N2HDM. Two scenarios were considered: in scenario A, the 95.4 GeV Higgs boson is primarily singlet-like, whereas in scenario B, it mainly originates from the CP-even components of the Higgs doublets. Scenario A was able to fully reproduce both the diphoton and$ b\bar{b} $ excesses at 95.4 GeV within the$ 1\sigma $ range. However, in the parameter space that accommodates both excesses, scenario A did not offer a valid explanation for the NANOGrav data up to$ v_s = 1000 $ TeV, and the resulting GW spectrum can surpass the Square Kilometre Array (SKA) sensitivity curve at low frequencies. Scenario B provided a marginal explanation of the diphoton and$ b\bar{b} $ excesses at 95.4 GeV at the$ 1\sigma $ level, but it can simultaneously offer a good explanation for the NANOGrav data.This study highlights the complementary roles of collider signals and GW observables in probing the nature of the extended Higgs sector. Although the 95.4 GeV excess reported by CMS, ATLAS, and LEP has not yet reached the discovery level of statistical significance, its consistent appearance across multiple experiments has inspired extensive theoretical interest, making it a well-motivated phenomenon to investigate. To the best of the authors' knowledge, this study is the first to simultaneously explain both the NANOGrav data and the 95.4 GeV Higgs boson excess, realized here within a coherent N2HDM framework. Specific scenarios within the N2HDM in which this dual explanation can be realized were explicitly identified. This study extends previous studies of the N2HDM by connecting collider and cosmological phenomena.
-
The authors thank Junjie Cao, Zhaohuan Yu, Yang Zhang, and Yeling Zhou for helpful discussions, and Bo-Qiang Lu for his support in using PTArcade.
-
The authors thank Junjie Cao, Zhaohuan Yu, Yang Zhang, and Yeling Zhou for helpful discussions, and Bo-Qiang Lu for his support in using PTArcade.
-
The authors thank Junjie Cao, Zhaohuan Yu, Yang Zhang, and Yeling Zhou for helpful discussions, and Bo-Qiang Lu for his support in using PTArcade.
-
We thank Junjie Cao, Zhaohuan Yu, Yang Zhang, and Yeling Zhou for helpful discussions, and Bo-Qiang Lu for his support in using PTArcade.
95 GeV Higgs boson and nano-Hertz gravitational waves from domain walls in the next-to-two-Higgs-doublet model
- Received Date: 2025-10-10
- Available Online: 2026-01-15
Abstract: This study explores the diphoton and $b\bar{b}$ excesses at 95.4 GeV, as well as nano-Hertz gravitational waves originating from domain walls, within the framework of the next-to-two-Higgs-doublet model (N2HDM), which extends the two-Higgs-doublet model by introducing a real singlet scalar subject to a discrete $Z_2$ symmetry. The $Z_2$ symmetry is spontaneously broken by the non-zero vacuum expectation value of the singlet scalar, $v_s$, which leads to the formation of domain walls. Two different scenarios are discussed: in scenario A, the 95.4 GeV Higgs boson predominantly originates from the singlet field, while in scenario B, it arises mainly from the CP-even components of the Higgs doublets. Accounting for relevant theoretical and experimental constraints, scenario A can fully account for both the diphoton and $b\bar{b}$ excesses at 95.4 GeV within the $1\sigma$ range. In the parameter space accommodating both excesses, scenario A fails to provide a valid explanation for the NANOGrav data up to $v_s=$ 1000 TeV, and the predicted gravitational wave spectrum can exceed the SKA sensitivity curve in the low frequency region. Scenario B only marginally accounts for the diphoton and $b\bar{b}$ excesses at the $1\sigma$ level, but can simultaneously explain the NANOGrav data well.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

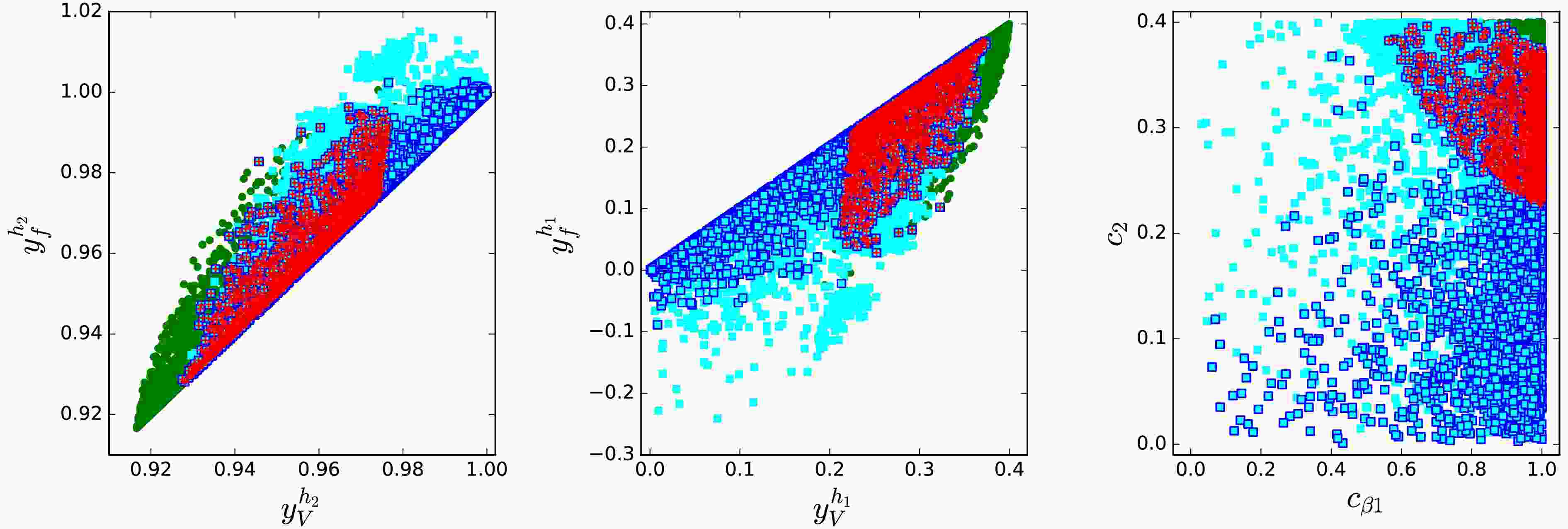










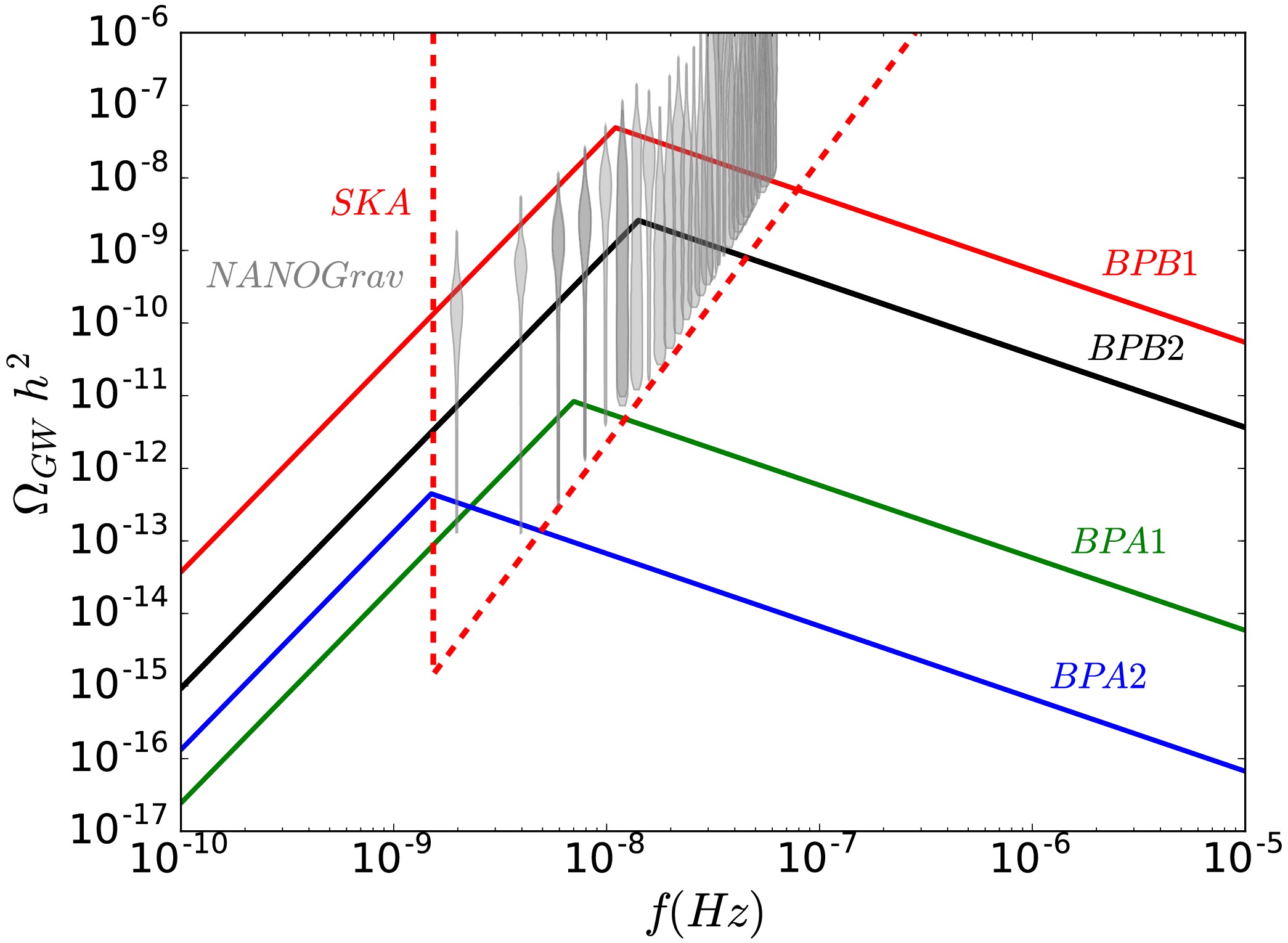
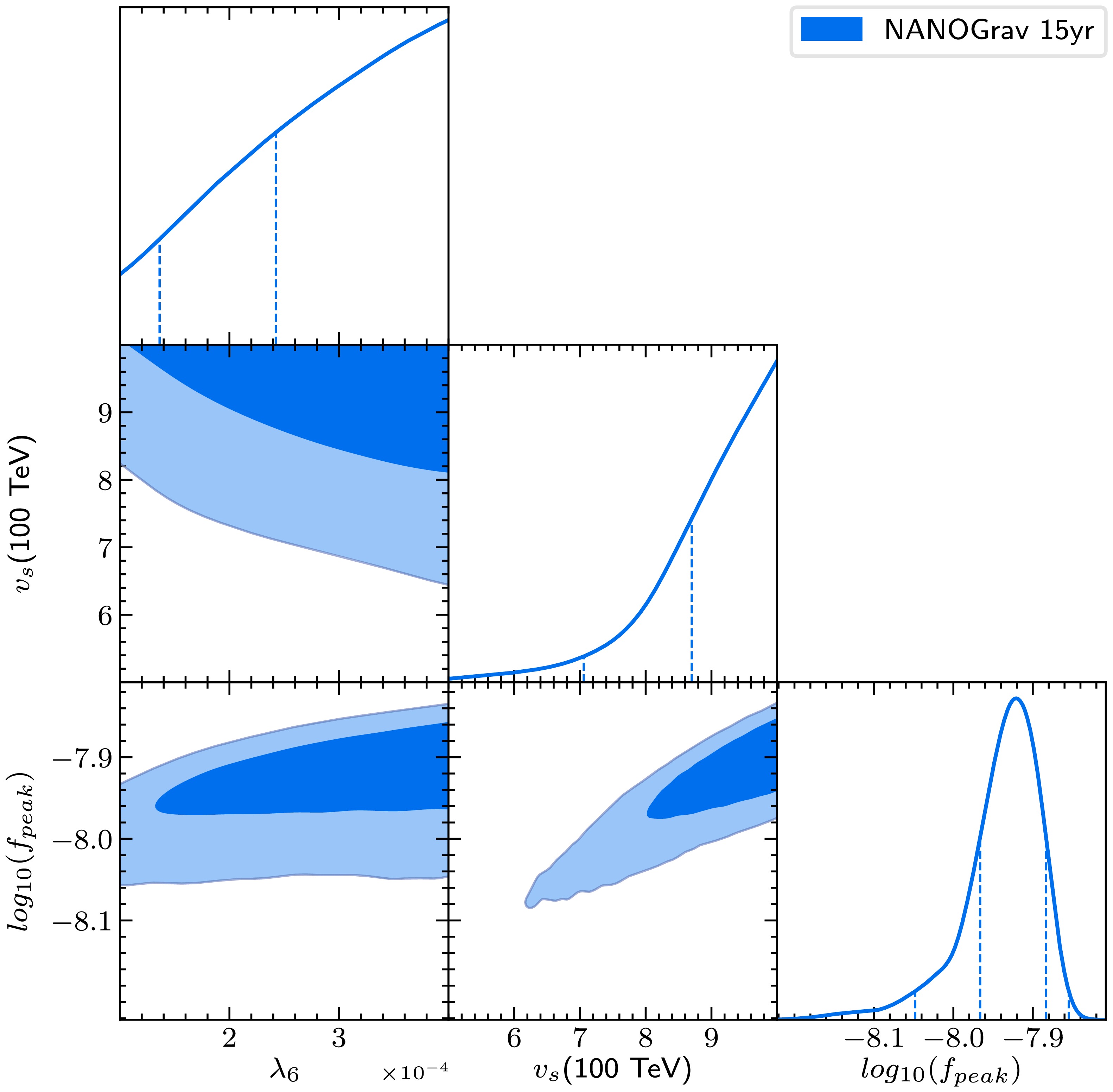



 DownLoad:
DownLoad: